Fundamental Properties of Nonlinear Stochastic Differential Equations

Abstract

The existence of solutions is used the premise of discussing other properties of dynamic systems. The goal of this paper is to investigate the fundamental properties of nonlinear stochastic differential equations via the Khasminskii test, including the local existence and global existence of the solutions. Firstly, a fundamental result is given as a lemma to verify the local existence of solutions to the considered equation. Then, the equivalent proposition for the global existence and the fundamental principle for the Khasminskii test are formally established. Moreover, the classical Khasminskii test is generalized to the cases with high-order estimates and heavy nonlinearity for the stochastic derivatives of the Lyapunov functions. The role of the noise in this aspect is especially investigated, some concrete criteria are obtained, and an application for the role of the noise in the persistence of financial systems is accordingly provided. As another application of the fundamental principle, a new version of the Khasminskii test is established for the delayed stochastic systems. Finally the conclusions obtained in the paper are verified by simulation. The results show that, under weaker conditions, the global existence of better solutions to stochastic systems to those in the existing literature can be obtained.

1. Introduction

Stochastic differential equations are widely investigated in the fields of applied mathematics and control theory, c.f. [1,2,3,4,5,6,7] etc. Differential equations can solve many practical problems in reality. The literature [8] has proposed a stochastic differential equation model of the COVID-19 epidemic for a population with five compartments. The work of [9] generalizes other authors’s stochastic model of population and renewable resources by substituting a distributed delay for the time delay. Ref. [10] discusses a kind of second-order iterative differential equation and seeks the uniqueness and existence of the solution using Banach fixed point theorem. For the real problems in engineering, fundamental theories on the uniqueness and existence of solutions is very important, and cannot be ignored. Many results have been obtained in the literature regarding this; see [11,12,13,14,15,16,17]. Ref. [11] presents some new results regarding the existence and uniqueness of mild solutions to neutral stochastic differential equations under some reasonable conditions. Literature [12] discusses the existence and uniqueness of one-dimensional, mixed stochastic delay differential equations by using a contraction principle and some priori estimations. Ref. [13] investigates the unique existence and spatial analyticity of a global mild solution to the stochastic Navier–Stokes–Coriolis equation.

The classical result says that if the linear growth condition and global Lipschitz condition are satisfied by the drift and diffusive coefficients of the systems, then the global existence of these solutions can be guaranteed. These conditions are too harsh for the practical engineering models and the real nonlinear systems were theoretically excluded. Then, an improved result was obtained in [1], which says that the local Lipschitz condition, which admits real nonlinearity, can ensure the local existence of solutions. Under this assumption, the global existence of the solutions could be guaranteed by other approaches. Fortunately, the mathematician R.Z.Khasminskii proposed such a technique, c.f. [18], called the Khasminskii test or Khasminskii-type theorem, which provides a means of ensuring the global existence of solutions to underlying equations by suppressing the explosion of the solution at a finite time based on calculations and properties of martingales. To adapt to more complex models and make the result more general, this technique was further investigated and applied in a series of the literature; see, for example, refs. [19,20,21,22,23,24,25,26,27,28] etc. In these literature, the obtained Khasminskii tests are represented as a kind of “comparison equations method” via the global existence of solutions to the deterministic comparison equations dominating the underlying systems. To date, the combination of local Lipschitz conditions to guarantee the local existence of the solutions and the Khasminskii test has provided the standard technique to guarantee the global existence of solutions to stochastic differential equations. Of course, we observe from the literature that the idea of the Khasminskii test has not been completely theorized to date, while the premise for this theorization is to investigate the substance of Khasminskii test. The comparison equations actually only provide a means of finding the suppression functions, not the suppression functions themselves.

Motivated by the above discussions, in the the present paper, authors try to focus on the idea of the Khasminskii test and establish a fundamental theoretical framework for this technique, including the equivalent proposition for the global existence and a fundamental principle, by comparing the unknown solutions and certain known functions, namely the essential suppression condition. Based on these preliminaries, the classical Khasminskii test is then generalized to the cases with high-order estimates and heavy nonlinearity for the stochastic derivatives of Lyapunov functions. The active role of noise in the persistence of the solutions is especially investigated and some concrete criteria related to this topic are obtained. An application for the role of noise in the persistence of financial systems is accordingly given. Additionally, a new version of the Khasminskii test for the delayed stochastic systems is established, which will provide the authors with some excitement. Next, we conclude with the innovations of this paper as follows.

• The stochastic differential equations admit time variance in the time variable and nonlinearity in spacial variable.
• The paper formally provides a kind of fundamental principle and some reference versions for the Khasminskii tests for the global existence of solutions for stochastic differential equations as well as from simple generalizations, which can be directly applied in future works by investigators in the areas of control theory and applied mathematics, etc.
• Two similar concepts are applied, namely, the local existence of the solutions vs. the local solutions (or the global existence of the solutions vs. the global solutions).
• The results shows that noise nearly always leads to systems persisting under the usual assumptions. The application for the role of the noise in the persistence of financial systems is innovative and interesting.

The arrangement is as follows. We will introduce notations, the system model and the assumptions in Section 2. Section 3 investigates the local existence of solutions using the truncation technique. The existence of global solutions via the Khasminskii test is investigated in Section 4. A numerical example is illustrated to verify the obtained results in Section 5. A conclusion is given in Section 6.

2. Preliminaries: Notations, Model and Assumptions

2.1. Basic Notations

In the paper, $(\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge t_0},\mathbb{P})$ is a complete probability space with a filtration ${\left\{{\mathcal{F}}_t\right\}}_{t\ge t_0}$ satisfying the usual conditions; namely, it is continuous and ${\mathcal{F}}_{t_0}$ contains all $\mathbb{P}$-null sets, c.f. [1] etc. $B(t)={[B_1(t),W_2(t),\cdots ,B_r(t)]}^{\mathrm{T}}$ is an $r-$dimensional standard Brown motion defined on $(\Omega ,\mathcal{F},{\left\{{\mathcal{F}}_t\right\}}_{t\ge t_0},\mathbb{P})$. $|·|$ stands for the Euclid norm for vectors; for the matrices, it stands for the 2-norm, spectral norm, Frobenius norm or the trace norm. As usual, $\mathcal{K}$ represents a family of the $\mathcal{K}$ class functions. ${\mathbb{R}}^{+}=[0,+\infty )$, the instant $T>0$. $\mathbb{E}$ stands for the mathematical expectation. $a\vee b$ represents the maximum of a and b. $a\wedge b$ represents the minimum of a and b. $C([-\tau ,0],{\mathbb{R}}^d)$ denotes the family of the continuous function $\varphi (\theta )$ from $[-\tau ,0]$ into ${\mathbb{R}}^d$ with norm $\parallel \varphi \parallel ={sup}_{\theta \in [-\tau ,0]}|\varphi (\theta )|$ for $\tau >0$. Some notations, including $p,q,\alpha ,\beta ,a(t),M(t),H(t)$ etc., will be used several times; there should not be any confusion with or by them.

2.2. General System Model, Basic Assumption and the It ô Formula

Consider the Itô stochastic differential equation

$$\begin{array}{c}\hfill \mathrm{d}x(t)=f(t,x(t))\mathrm{d}t+g(t,x(t))\mathrm{d}B(t),t\in {\mathbb{R}}^{+},\end{array}$$

(1)

where $x\in {\mathbb{R}}^d$, $f:{\mathbb{R}}^{+}\times {\mathbb{R}}^d\to {\mathbb{R}}^d,g:{\mathbb{R}}^{+}\times {\mathbb{R}}^d\to {\mathbb{R}}^{d\times r}$ are Borel measurable functions.

We will call $f(t,x)$ intrinsic system dynamics in the following text.

Assumption 1.

The local Lipschitz condition. There is a continuous function $L_n(t)$ depending on n with each positive integer $n>0$, such that

$$|f(t,x)-f(t,y)|\vee |g(t,x)-g(t,y)|\le L_n(t)|x-y|,$$

for $t\in {\mathbb{R}}^{+},x,y\in {\mathbb{R}}^d$ with $|x|\vee |y|\le n$.

Let $V(t,x)$ be a Lyapunov function, define the operators as follows,

$$\begin{array}{ccc}\hfill \mathcal{L}V(t,x)& =& V_t(t,x)+V_x(t,x)f(t,x)+\frac{1}{2}\mathrm{Tr}(g^{\mathrm{T}}(t,x)V_{xx}(t,x)g(t,x)),\hfill \\ \hfill \mathcal{H}V(t,x)& =& V_x(t,x)g(t,x),t\in {\mathbb{R}}^{+},x\in {\mathbb{R}}^d,\hfill \end{array}$$

then $\mathrm{d}V(t,x(t))=\mathcal{L}V(t,x(t))\mathrm{d}t+\mathcal{H}V(t,x(t))\mathrm{d}B(t)$.

2.3. General Delayed System Model, Basic Assumption and the It ô Formula

Consider the Itô stochastic functional differential equation

$$\begin{array}{c}\hfill \mathrm{d}x(t)=f(t,x_t)\mathrm{d}t+g(t,x_t)\mathrm{d}B(t),t\in {\mathbb{R}}^{+},\end{array}$$

(2)

where $x\in {\mathbb{R}}^d$, $f:{\mathbb{R}}^{+}\times C([-\tau ,0],{\mathbb{R}}^d)\to {\mathbb{R}}^d,g:{\mathbb{R}}^{+}\times C([-\tau ,0],{\mathbb{R}}^d)\to {\mathbb{R}}^{d\times r}$ are Borel measurable functionals.

Assumption 2.

The local Lipschitz condition. There is a continuous function $L_n(t)$ depending on n with each positive integer $n>0$, such that

$$|f(t,{\varphi }_2)-f(t,{\varphi }_1)|\vee |g(t,{\varphi }_2)-g(t,{\varphi }_1)|\le L_n(t)\parallel {\varphi }_2-{\varphi }_1\parallel ,$$

for $t\in {\mathbb{R}}^{+},{\varphi }_1,{\varphi }_2\in C([-\tau ,0],{\mathbb{R}}^d)$ with $\parallel {\varphi }_1\parallel \vee \parallel {\varphi }_2\parallel \le n$.

Let $V(t,x)$ be a Lyapunov function; accordingly,

$$\begin{array}{ccc}\hfill \mathcal{L}V(t,\varphi )& =& V_t(t,\varphi (0))+V_x(t,\varphi (0))f(t,\varphi )+\frac{1}{2}\mathrm{Tr}(g^{\mathrm{T}}(t,\varphi )V_{xx}(t,\varphi (0))g(t,\varphi )),\hfill \\ \hfill \mathcal{H}V(t,\varphi )& =& V_x(t,\varphi (0))g(t,\varphi ),t\in {\mathbb{R}}^{+},\varphi \in C([-\tau ,0],{\mathbb{R}}^d),\hfill \end{array}$$

then, we similarly have $\mathrm{d}V(t,x(t))=\mathcal{L}V(t,x_t)\mathrm{d}t+\mathcal{H}V(t,x_t)\mathrm{d}B(t)$.

3. Local Existence of Solutions via the Truncation Technique

We first state a fundamental result as a lemma for the local existence of solutions to stochastic differential equations.

Lemma 1.

Local existence. Assume $f(t,x)$ and $g(t,x)$ satisfy Assumption 1; then, for arbitrary given initial data $\xi \in {\mathbb{R}}^d$, there is an initial interval $[t_0,{\tau }_{\infty })$ a.s., such that there exists a local continuous maximal solution $x(t)=x(t,\xi )$ to Equation (1) on $[t_0,{\tau }_{\infty })$.

Proof. 

Firstly, define truncation function $f_n(t,x)$ as follows,

$$\begin{array}{c}\hfill f_n(t,x)=\left\{\begin{array}{cc}f(t,x),\hfill & \hfill \mathrm{if}|x|\le n,\\ f(t,nx/|x|),\hfill & \hfill \mathrm{if}|x|\ge n,\end{array}\right.\end{array}$$

where n is an arbitrarily given positive integer, and the definition of $g_n(t,x)$ is similar to $f_n(t,x)$. We can verify, for $t\in {\mathbb{R}}^{+},x,y\in {\mathbb{R}}^d$, new coefficients $f_n(t,x)$, $g_n(t,x)$ satisfy the global Lipschitz condition

$$\begin{array}{c}\hfill |f_n(t,x)-f_n(t,y)|\le 2L_{n,f}(t)|x-y|,|g_n(t,x)-g_n(t,y)|\le 2L_{n,g}(t)|x-y|.\end{array}$$

With this, we can verify that, for $t\in {\mathbb{R}}^{+},x\in {\mathbb{R}}^d$, the linear growth condition is satisfied for $f_n(t,x)$ and $g_n(t,x)$, namely,

$$\begin{array}{c}\hfill |f_n(t,x)|\le max\{|f(t,t_0)|,2L_{n,f}(t)\}|x|,|g_n(t,x)|\le max\{|g(t,t_0)|,2L_{n,g}(t)\}|x|.\end{array}$$

For an arbitrary instant $T>0$, then for $t\in [t_0,T]$, $L_{n,f}(t)$, $L_{n,g}(t)$ are bounded. If $L_{n,f}(t)\vee L_{n,g}(t)\le L_n^T,t\in [t_0,T]$ holds, by Theorem 3.1 in Chapter of [1] we get, for arbitrarily given initial data $\xi \in {\mathbb{R}}^d$, a unique continuous solution process $x_n(t)=x_n(t;t_0,\xi )$ exists to the integral equation

$$\begin{array}{c}\hfill x_n(t)=\xi +{\int }_{t_0}^t{f}_n(s,x_n(s))\mathrm{d}s+{\int }_{t_0}^t{g}_n(s,x_n(s))\mathrm{d}B(s),\end{array}$$

on $[t_0,T]$ with $\mathbb{E}\left\{{sup}_{t\in [t_0,T]}{|x_n(t)|}^2\right\}<+\infty$. Owing to the arbitrariness of $T>0$, we immediately know that the continuous solution $x_n(t)$ exists on $[t_0,+\infty )$ with $\mathbb{E}|x_n{(t)|}^2<+\infty$ for each $t\ge t_0$.

Give the definition stopping time ${\tau }_n=inf\{t\in [t_0,+\infty )||x_n(t)|\ge n\}$, thus one obtains $x_n(t)=x_{n+1}(t)$ for $t\in [t_0,{\tau }_n]$, which means $\left\{{\tau }_n\right\}$ is increasing. Define ${\tau }_{\infty }={lim}_{n\to \infty }{\tau }_n$, and $x(t)=x_n(t)$ on $[{\tau }_{n-1},{\tau }_n)$ for each $n\ge 1$, where ${\tau }_0=t_0$. Naturally, $x(t)$ is a continuous process. With this definition, we can obtain, for $t\in [t_0,{\tau }_n)$,

$$\begin{array}{ccc}\hfill x(t)& =& \xi +{\int }_{t_0}^t{f}_n(s,x(s))\mathrm{d}s+{\int }_{t_0}^t{g}_n(s,x(s))\mathrm{d}B(s)\hfill \\ & =& \xi +{\int }_{t_0}^{t}f(s,x(s))\mathrm{d}s+{\int }_{t_0}^{t}g(s,x(s))\mathrm{d}B(s),\mathrm{a}.\mathrm{s}.\hfill \end{array}$$

namely, $[t_0,{\tau }_n)$ is an existing interval of solution $x(t)$ to (1) for each n; this implies that $[t_0,{\tau }_{\infty })$ is an existing interval for the solution. If ${\tau }_{\infty }=+\infty$, then we obtain a global solution; if ${\tau }_{\infty }<+\infty$, then we obtain a local maximal solution (in time). The proof is then complete. □

Remark 1.

Under Assumption $1^{*}$, we reach the same conclusion for (2), c.f. Theorem 2.8 in Chapter 5 of [1].

4. Existence of Global Solutions via the Khasminskii Test

4.1. General Principle: Comparison by Functions

Assumption 3.

There is a $\mathcal{K}$ class function $u(·)$ and a positive number $p>0$ such that $V(t,x)\ge u(|x{|}^p)$.

Remark 2.

For each $L>0$, this condition can be replaced by ${inf}_{t\ge 0,|x|\ge L}V(t,x)>0$.

We will prove the global existence result by the contradiction under Assumption 2. To this end, we similarly define the stopping time ${\tau }_k=inf\{t\in [0,{\tau }_{\infty })||x(t)|\ge k\}$, and ${\tau }_{\infty }$ is the exploding time. If the set $\{t\in [0,{\tau }_{\infty })||x(t)|\ge k\}$ is empty, we set ${\tau }_k=\infty$. In this case, we actually obtain ${\tau }_{\infty }=+\infty$.

Lemma 2.

The equivalent proposition. A continuous solution $x(t)$ to (1) or (2) globally exists if it does not explode in a finite time under the assumption of the local existence of the solutions.

Proof. 

The necessity is obvious. We now show the sufficiency using the familiar continuation principle. We repeatedly apply the continuation technique. If the solution is extended to ∞ in a step with this technique, then we arrive at the conclusion of the lemma. Thus, we assume in the following text that we can only extend the solution to a limited interval by each step.

The assumption for the non-explosivity means that, for any increasing sequence $\left\{t_k\right\}$ in the existing interval of the solution $x(t)$, we have ${lim\; sup}_{k\to \infty }|x(t_k)|<+\infty$.

Given the initial data $\xi \in {\mathbb{R}}^d$ for (1) or $\xi \in C_{{\mathcal{F}}_{t_0}}^b([-\tau ,0];{\mathbb{R}}^d)$ for (2). Assuming local existence, there is an instant $t_1=t_1(t_0)>t_0$, such that there is a maximal solution $x(t)=x(t;t_0,\xi )$ to Equation (1) on $[t_0,t_1^{*})$ with $x(t_0)=\xi$. Denote $t_1=(t_0+t_1^{*})/2$. Similarly, one can reach that point in an instant $t_2^{*}=t_2^{*}(t_1)>t_1$, such that there is a maximal solution $x(t)=x(t;t_1,x(t_1))$ to Equation (1) on $[t_1,t_2^{*})$. Denote $t_2=(t_1+t_2^{*})/2$. Repeating this procedure, we can obtain an increasing sequence ${\left\{t_i\right\}}_{1\le i\le k-1}(k\ge 3)$, such that there is a maximal solution $x(t)=x(t;t_{k-1},x(t_{k-1}))$ to Equation (1) on $[t_{k-1},t_k^{*})$. Denote $t_k=(t_{k-1}+t_k^{*})/2$. Using this procedure, we actually reach a local solution $x(t)=x(t;t_0,\xi )$ (in time) to the system (1) on $[t_0,t_k^{*})\supset [t_0,t_k]$. If ${lim}_{k\to \infty }{t}_k=+\infty$, then we actually arrive at the conclusion of the lemma. Now, we exclude the possibility for ${lim}_{k\to \infty }{t}_k\triangleq t_{\infty }<+\infty$. ${lim}_{k\to \infty }{t}_k\triangleq t_{\infty }<+\infty$ means that we can not extend the solution to exceed $t_{\infty }$. Then, we reach a limit ${lim}_{t\to t_{\infty }}x(t)\triangleq x_{\infty }$ due the continuity and boundedness of the solution guaranteed by ${lim\; sup}_{k\to \infty }|x(t_k)|<+\infty$ using the basic principle in mathematical analysis, or by the direct assumption of this part. We can define $x(t_{\infty })=x_{\infty }$ in this case and then continue the continuation procedure to obtain a new, existing interval $[t_0,t_{\infty }^{*})\supset [t_0,t_{\infty })$, which contradicts the assumption for $t_{\infty }$. Thus, we must obtain ${lim}_{k\to \infty }{t}_k=+\infty$. The proof is complete. □

The non-explosivity of $|x(t)|$ is equivalent to arbitrary order moment ${|x(t)|}^p$, where $p>0$. We will check this via ${\mathbb{E}|x(t)|}^p$ in the following.

Lemma 3.

Comparison principle. Under Assumption 2, if, for the above stopping time ${\tau }_k$, we have an estimate $\mathbb{E}V(t\wedge {\tau }_k,x(t\wedge {\tau }_k))\le \mathbb{E}H(t\wedge {\tau }_k)$, where $H(t)$ is a stochastic process with $\mathbb{E}H(t)$ being bounded on any bounded interval, then the solution $x(t)$ for (1) or (2) exists globally.

Proof. 

Assume that our assertion was false. Then, the solution explodes in a finite time. The stopping time ${\tau }_k=inf\{t\in [0,{\tau }_{\infty }]||x(t)|\ge k\}<+\infty$ is well defined.

Consider the probability $\mathbb{P}\{{\tau }_k\le t\}$ for the index $k\ge 1$ and the time $t\ge 0$.

We can easily verify that $\mathbb{P}\{{\tau }_k\le t\}$ is non-increasing in k and non-decreasing in t. With $0\le \mathbb{P}\{{\tau }_k\le t\}\le 1$, we know that ${lim}_{k\to \infty }\mathbb{P}\{{\tau }_k\le t\}\triangleq \beta (t)$ exists and $\beta (t)$ is also non-decreasing in t with $\mathbb{P}\{{\tau }_k\le t\}\ge \beta (t)$. With $\mathbb{P}\{{\tau }_k\le t\}=\mathbb{E}\left\{I_{{\tau }_k\le t}\right\}$ and the dominated convergence theorem, one can show that $\beta (t)={lim}_{k\to \infty }\mathbb{P}\{{\tau }_k\le t\}={lim}_{k\to \infty }\mathbb{E}\left\{I_{{\tau }_k\le t}\right\}=\mathbb{E}\left\{{lim}_{k\to \infty }{I}_{{\tau }_k\le t}\right\}=\mathbb{E}\left\{I_{{\tau }_{\infty }\le t}\right\}=\mathbb{P}\{{\tau }_{\infty }\le t\}$. Similarly, based on this, we can further reach ${lim}_{t\to \infty }\beta (t)=\mathbb{P}\{{\tau }_{\infty }<\infty \}=1>p^{*}>0$ for each given constant $0<p^{*}<1$. Thus, there must be an instant $T=T(p^{*})>0$, for $t\ge T$, such that $\beta (t)\ge p^{*}$. This leads to $\mathbb{P}\{{\tau }_k\le t\}\ge \beta (t)\ge p^{*}$, including the case $\mathbb{P}\{{\tau }_k\le T\}\ge p^{*}$. We have $\mathbb{E}V(t\wedge {\tau }_k,x(t\wedge {\tau }_k))\le {\overline{H}}_T$ using this assumption, where ${\overline{H}}_T={max}_{0\le s\le T}\mathbb{E}H(s)$. From $\mathbb{E}V(T\wedge {\tau }_k,x(T\wedge {\tau }_k))\ge \mathbb{E}\left\{I_{{\tau }_k\le T}V(T\wedge {\tau }_k,x(T\wedge {\tau }_k))\right\}=\mathbb{E}\left\{I_{{\tau }_k\le T}V({\tau }_k,x({\tau }_k))\right\}\ge \mathbb{E}\{I_{{\tau }_k\le T}u(|x({\tau }_k){|}^p)\}=u^p(k)\mathbb{E}\left\{I_{{\tau }_k\le T}\right\}=u^p(k)\mathbb{P}\{{\tau }_k\le T\}\ge u^p(k)p^{*}$. Namely, $u^p(k)\le {\overline{H}}_T/p^{*}$, this contradicts $u^p(k)\to \infty$ as $k\to \infty$. Thus, our assertion is true. □

Corollary 1.

Under Assumption 2, if one presents $V(t,x(t))\le H(t)$ in the existing interval of $x(t)$, where $H(t)$ is a stochastic process with $\mathbb{E}H(t)$ being being bounded on any bounded interval, then the solution for Equations (1) or (2) exists globally.

Proof. 

From the given condition, we have $V(t\wedge {\tau }_k,x(t\wedge {\tau }_k))\le H(t\wedge {\tau }_k)$; then, we can obtain $\mathbb{E}V(t\wedge {\tau }_k,x(t\wedge {\tau }_k))\le \mathbb{E}H(t\wedge {\tau }_k)$, where the stopping time ${\tau }_k<+\infty$ guarantees the existence of the mathematical expectations involved (which simultaneously guarantees the usability of the Dynkin formula, as applied in the next text). Using Lemma 3, we obtain the desired results. □

Remark 3.

The principle established in this subsection or the Khasminskii test, including the classical ones and those generalized below, can be applied on any finite interval. If we obtain a global existence on each finite interval, then we actually have the global existence in the usual meaning.

4.2. Generalized Khasminskii Test

The Khasminskii test is often applied to determine the global existence of solutions to the stochastic systems. Here, we first discuss the test for the SDE (1). The classical version proposed by R.Z.Khasminskii is based on the estimate $\mathcal{L}V(t,x)\le C(1+V(t,x))$, where C = const. $\ge 0$. Some of the literature generalizes this to the case where $\mathcal{L}V(t,x)\le m(t,V(t,x))$, where $m(t,·)$ is assumed to be concave, and some additional assumptions are needed. However, additional assumptions are unnecessary and the conclusion can be represented more clearly. We actually have $m(t,V(t,x))\le a(t)+b(t)V(t,x)$ using the Jensen’s inequality under the convexity for $m(t,·)$, where $a(t),b(t)\ge 0$. One may provide a simple condition to guarantee $max\{a(t),b(t)\}\le C$ = const. on any bounded interval. Thus, it is suggested that the concave functions are directly replaced by linear ones using the bound technique in future works related to the global existence of the solutions. Now, we consider a more general case

$$\begin{array}{c}\hfill \mathcal{L}V(t,x)\le -{\mu }^{-}(t,|x|)+{\mu }^{+}(t,|x|),t\in {\mathbb{R}}^{+},x\in {\mathbb{R}}^d,\end{array}$$

(3)

where ${\mu }^{+}(t,|x|)\ge 0$ and ${\mu }^{-}(t,|x|)\ge 0$ are semi-positive definite functions in x, $C_L(t)={max}_{|x|\le L}{\mu }^{+}(t,|x|)$ is integrable for each $L>0$. For the global existence problem, it is unnecessary for us to transfer the $|x|$ in the right-hand side into $V(t,x)$. These kinds of estimates usually come from the robust stability analysis for the control system design problems, while in the stability analysis, we usually have ${\mu }^{+}(t,|x|)=a(t)+{b(t)|x|}^q+\Phi (t,|x|),{\mu }^{-}(t,|x|)={c(t)|x|}^p,p,q>0$, where the functions and parameters involved vary for different models and problems.

If the order of the state in ${\mu }^{+}(t,|x|)$ is higher than that in ${\mu }^{-}(t,|x|)$, namely, the disturbance ${\mu }^{+}(t,|x|)$ dominates, then we will encounter great difficulties when dealing with the nonlinear factor. Can we overcome these?

If ${\mu }^{+}(t,|x|)=0$, then $\mathcal{L}V(t,x)\le -{\mu }^{-}(t,|x|)\le 0$, if ${\mu }^{-}(t,|x|)=0,{\mu }^{+}(|x|)$$\le C(t)(1+V(t,x))$, where $C(t)\ge 0$ is bounded on any bounded interval, then the classical Khasminskii test, c.f., can be used [2]. We now enter the general case. We consider two cases in which ${\mu }^{-}(t,|x|)$ and ${\mu }^{+}(t,|x|)$ suppress each other: ${lim}_{|x|\to +\infty }{inf}_{t\ge 0}{\mu }^{-}(t,|x|)/{\mu }^{+}(t,|x|)=+\infty$ and ${lim}_{|x|\to +\infty }{inf}_{t\ge 0}{\mu }^{+}(t,|x|)/{\mu }^{-}(t,|x|)=+\infty$. The local existence of the solutions is first assumed to serve as a base, which is not further mentioned. We formulate these conditions as assumptions before the corresponding theorem.

Assumption 4.

${lim}_{s\to +\infty }{inf}_{t\ge 0}{\mu }^{-}(t,s)/{\mu }^{+}(t,s)=+\infty$.

Theorem 1.

Under Assumptions 1, 2 and 3, there is a global solution to the system (1) for the initial data $\xi \in {\mathbb{R}}^d$.

Proof. 

Assume that $x\ne 0$. We rewrite and estimate $-{\mu }^{-}(t,|x|)+{\mu }^{+}(t,|x|)$ as

$$\begin{array}{ccc}\hfill -{\mu }^{-}(t,|x|)+{\mu }^{+}(t,|x|)& =& -{\mu }^{-}(t,|x|)[1-{\mu }^{+}(t,|x|)/{\mu }^{-}(t,|x|)]\hfill \\ & \le & -{\mu }^{-}(t,|x|)[1-\underset{t\ge 0}{sup}{\mu }^{+}(t,|x|)/{\mu }^{-}(t,|x|)].\hfill \end{array}$$

Under Assumption 3, we have ${lim}_{|x|\to +\infty }{sup}_{t\ge 0}{\mu }^{+}(t,|x|)/{\mu }^{-}(t,|x|)=0<1$; thus, there is a positive number L, independent of time t, such that

$$\begin{array}{c}\hfill -{\mu }^{-}(t,|x|)+{\mu }^{+}(t,|x|)\le -{\mu }^{-}(t,|x|)[1-\underset{t\ge 0}{sup}{\mu }^{+}(t,|x|)/{\mu }^{-}(t,|x|)]\le 0,\end{array}$$

for $|x|\ge L$. For the case $|x|\le L$, we have $-{\mu }^{-}(t,|x|)+{\mu }^{+}(t,|x|)\le {\mu }^{+}(t,|x|)\le C_L(t)$. Finally, $\mathcal{L}V(t,x)\le C_L(t)$, $t\in {\mathbb{R}}^{+}$ and $x\in {\mathbb{R}}^d$. Using the Itô and Dynkin’s formulas, we can directly obtain

$$\begin{array}{c}\hfill \mathbb{E}V(t\wedge {\tau }_k,x(t\wedge {\tau }_k))\le H(t)=\mathbb{E}V(t_0,\xi )+{\int }_{t_0}^t{C}_L(s)\mathrm{d}s,\end{array}$$

for $t\ge t_0$. Using Lemma 3, we obtain the desired results.

Assumption 3 means that the positive term in the stochastic derivative dominates at infinity, which goes against the global existence of the solutions. Therefore, can we obtain any global existence result based on this kind of estimate? If the underlying system is a deterministic one (ODE), one can determine global existence in a local domain (namely, we can obtain the so-called local solutions). However, if the underlying system is a stochastic one (SDE), the problem will become much more difficult due to the randomness. How can the effect of the high-order positive terms be eliminated with the mathematical expectations? We have not found work with this kind of feature in the literature on the Khasminskii test. Here, we want to have a try. Of course, a result without any condition is inconceivable; thus, we have to impose some further assumptions on the estimate, as follows. □

Assumption 5.

${\mu }^{+}(t,s)=a(t)w_{*}(s^q),{\mu }^{-}(t,s)=a(t)\tilde{w}(s^p)$, where $q\ge p>0,a(t)\ge 0$, and $w_{*}(s^q)=\tilde{w}(s^p)w_{**}(s^m)$ for $s\ge 0$, and ${lim}_{s\to 0^{+}}{w}_{**}(s^m)<k$ where the order $m\in [0,p]$, and k is a constant with $0\le k<1$, $w_{**}(·)$ is concave. In addition, there are $\mathcal{K}$ functions $u(·)$ and $v(·)$, such that ${u(|x|}^p{)\le V(t,x)\le v(|x|}^p)$, where $u(·)$ is convex.

Theorem 2.

Under Assumptions 1, 2 and 4 and the estimate (3), there is a deterministic positive number $\delta >0$, such that there is a global solution $x(t)$ to (1) for each piece of initial data $\xi \in {\mathbb{R}}^d$ with $|\xi |\le \delta$.

Proof. 

Denote ${\sigma }_1=\frac{1}{2}(1+k),{\sigma }_2=\frac{1}{2}(1-k)$, then we have ${\sigma }_1\in [\frac{1}{2},1),{\sigma }_2\in (0,\frac{1}{2}],{\sigma }_1>k$ and ${\sigma }_1+{\sigma }_2=1$. Define $\overline{w}(|x|)={\sigma }_1\tilde{w}{(|x|}^p)-w_{*}{(|x|}^q)$, then we actually have $\overline{w}(|x|)=\tilde{w}{(|x|}^p)({\sigma }_1-w_{**}{(|x|}^m))$. With these notations, one can obtain $\mathcal{L}V(t,x)\le -{\sigma }_{2}a(t)\tilde{w}{(|x|}^p)-a(t)\overline{w}(|x|)$. We hope that $\overline{w}(|x|)\ge 0$ in the local domain. Take initial value $\xi$, which is first assumed to be a deterministic one, such that

$$\begin{array}{c}\hfill 0<|\xi |<\delta \triangleq (v^{-1}(u(w_{**}^{-1}({\sigma }_1){)}^{\frac{p}{m}}){)}^{\frac{1}{p}},\end{array}$$

(4)

namely, $0<w_{**}((u^{-1}{(v(|\xi |}^p)){)}^{\frac{m}{p}})<{\sigma }_1$. If we define $\sigma ={\sigma }_1-w_{**}((u^{-1}{(v(|\xi |}^p)){)}^{\frac{m}{p}})$, then $\sigma >0$. With this choice of initial value, we know that there is an instant $t_1=t_1(\omega )>t_0$, such that $|x(t)|>0,w_{**}{(|x(t)|}^m)<{\sigma }_1$ for $t\in [t_0,t_1)$. We now assert that, for all times, $t\ge t_0$, $|x(t)|>0,w_{**}{(|x(t)|}^m)<{\sigma }_1$ a.s.

Using the non-zero property of solutions to stochastic differential equations, c.f. [1], one can obtain $|x(t)|>0$ a.s.; therefore, we only need to show the latter assertion.

Assuming the assertion is false, there must be two instants $t^{*}=t^{*}(\omega )>t_1,$ $t^{**}=t^{**}(\omega )>t^{*}$ such that $w_{**}(|x(t^{*}){|}^m)={\sigma }_1$ and $w_{**}{(|x(t)|}^m)>{\sigma }_1$ for $t\in (t^{*},t^{**})$. Actually, $t^{*}$ can be chosen as the stopping time $t^{*}=inf\{t|w_{**}{(|x(t)|}^m)>{\sigma }_1\}$; $t^{**}$ is determined by $t^{*}$. From this we have

$$|x(t^{*}){|}^p=(w_{**}^{-1}({\sigma }_1){)}^{\frac{p}{m}},\mathbb{E}\tilde{w}(|x(t^{*}){|}^p)=\tilde{w}((w_{**}^{-1}({\sigma }_1){)}^{\frac{p}{m}})\triangleq \eta >0.$$

From the continuity of the solution in the existing interval, we can find another stopping time $t_{\Delta }=t_{\Delta }(\omega )\in (t^{*},t^{**})$ such that for $t\in (t^{*},t_{\Delta })$, $w_{**}{(|x(t)|}^m)>{\sigma }_1$, $\tilde{w}(|x(t)|)\triangleq -\frac{1}{2}{\sigma }_2\tilde{w}{(|x(t)|}^p)-\overline{w}(|x(t)|)<0$ owing to $\tilde{w}(|x(t^{*})|)=-\frac{1}{2}{\sigma }_2\tilde{w}(|x(t^{*}){|}^p)-\overline{w}(|x(t^{*})|)=-\frac{1}{2}{\sigma }_2\tilde{w}(|x(t^{*}){|}^p)<0$, in which the non-zero property is applied. We can choose $t_{\Delta }$ such that we can simultaneously have

$$\begin{array}{c}\hfill (\tilde{w}(|x(t^{*}){|}^p)-\tilde{w}(|x(t_{\Delta }){|}^p))(w_{**}(|x(t^{*}){|}^m)-w_{**}(|x(t_{\Delta }){|}^m))<\frac{1}{2}\eta \sigma .\end{array}$$

From $\tilde{w}(|x(t)|)<0$, one gets

$$\begin{array}{c}\hfill \mathcal{L}V(t,x)\le -{\sigma }_{2}a(t)\tilde{w}{(|x(t)|}^p)-a(t)\overline{w}(|x|)\le -\frac{1}{2}{\sigma }_{2}a(t)\tilde{w}{(|x(t)|}^p),t\in (t^{*},t_{\Delta }).\end{array}$$

Combined with the above estimate

$$\begin{array}{c}\hfill \mathcal{L}V(t,x)\le -{\sigma }_{2}a(t)\tilde{w}{(|x(t)|}^p)-a(t)\overline{w}(|x|)\le -\frac{1}{2}{\sigma }_{2}a(t)\tilde{w}{(|x(t)|}^p),\end{array}$$

on the interval $[t_0,t^{*}]$, we obtain a whole estimate

$$\begin{array}{c}\hfill \mathcal{L}V(t,x(t))\le -\frac{1}{2}{\sigma }_{2}a(t)\tilde{w}{(|x(t)|}^p)\le 0,t\in (t_0,t_{\Delta }).\end{array}$$

(5)

Define $\mathcal{U}(t)=V(t\wedge t_{\Delta },x(t\wedge t_{\Delta })),t\ge t_0$; then, we have

$$\begin{array}{c}\hfill \mathcal{U}(t)=V(t_0,x_0)+{\int }_{t_0}^{t\wedge t_{\Delta }}\mathcal{L}V(s,x(s))\mathrm{d}s+M(t),\end{array}$$

(6)

where $M(t)={\int }_{t_0}^{t\wedge t_{\Delta }}\mathcal{H}V(s,x(s))\mathrm{d}W(s)$. $t\wedge t_{\Delta }$ is also a stopping time with $t\wedge t_{\Delta }\le t$; thus, $\mathbb{E}[t\wedge t_{\Delta }]<+\infty$. Using the Dynkin formula, we have $\mathbb{E}M(t)=0$. Based on this, (6) combined with (5) then leads to ${[\mathbb{E}\mathcal{U}(t)]}^{\prime }=\mathbb{E}{\int }_{t_0}^{t\wedge t_{\Delta }}\mathcal{L}V(s,x(s))\mathrm{d}s\le 0,$ which means that $\mathbb{E}\mathcal{U}(t)\le \mathbb{E}\mathcal{U}(t_0)=\mathbb{E}V(t_0,\xi )\le {v(|\xi |}^p)$ by $V(t,x)\le v(|x{|}^p)$. Letting $t\to +\infty$, and using $u(|x{|}^p)\le V(t,x)$, we then obtain $u(\mathbb{E}|x(t_{\Delta }){|}^p)\le \mathbb{E}\mathcal{U}(t_{\Delta })\le {v(|\xi |}^p)$, and then

$$\begin{array}{ccc}\hfill \mathbb{E}|x(t_{\Delta }){|}^m& \le & (\mathbb{E}|x(t_{\Delta }){|}^p{)}^{\frac{m}{p}}\le (u^{-1}{(v(|\xi |}^p)){)}^{\frac{m}{p}},\hfill \\ \hfill \mathbb{E}{w}_{**}(|x(t_{\Delta }){|}^m)& \le & w_{**}(\mathbb{E}|x(t_{\Delta }){|}^m)\le w_{**}((u^{-1}{(v(|\xi |}^p)){)}^{\frac{m}{p}}),\hfill \\ \hfill {\sigma }_1-\mathbb{E}{w}_{**}(|x(t_{\Delta }){|}^m)& \ge & {\sigma }_1-w_{**}((u^{-1}{(v(|\xi |}^p)){)}^{\frac{m}{p}})=\sigma .\hfill \end{array}$$

Based on this, and using the Markov property to provide solutions to the stochastic differential equations, c.f. [1], with the fact ${\sigma }_1=w_{**}(|x(t^{*}){|}^m)$, one can obtain

$$\begin{array}{ccc}\hfill \mathbb{E}\overline{w}(|x(t_{\Delta })|)& =& \mathbb{E}\tilde{w}(|x(t_{\Delta }){|}^p)(w_{**}(|x(t^{*}){|}^m)-w_{**}(|x(t_{\Delta }){|}^m)\hfill \\ & =& \mathbb{E}\tilde{w}(|x(t^{*}){|}^p)(w_{**}(|x(t^{*}){|}^m)-w_{**}(|x(t_{\Delta }){|}^m)\hfill \\ & & -\mathbb{E}(\tilde{w}(|x(t^{*}){|}^p)-\tilde{w}(|x(t_{\Delta }){|}^p))(w_{**}(|x(t^{*}){|}^m)-w_{**}(|x(t_{\Delta }){|}^m)\hfill \\ & =& \mathbb{E}\tilde{w}(|x(t^{*}){|}^p)\mathbb{E}(w_{**}(|x(t^{*}){|}^m)-w_{**}(|x(t_{\Delta }){|}^m)\hfill \\ & & -\mathbb{E}(\tilde{w}(|x(t^{*}){|}^p)-\tilde{w}(|x(t_{\Delta }){|}^p))(w_{**}(|x(t^{*}){|}^m)-w_{**}(|x(t_{\Delta }){|}^m)\hfill \\ & \ge & \mathbb{E}\tilde{w}(|x(t^{*}){|}^p)({\sigma }_1-\mathbb{E}\{w_{**}(|x(t_{\Delta }){|}^m))-\frac{1}{2}\eta \sigma \hfill \\ & =& \eta ({\sigma }_1-\mathbb{E}\{w_{**}(|x(t_{\Delta }){|}^m))-\frac{1}{2}\eta \sigma \hfill \\ & \ge & \eta \sigma -\frac{1}{2}\eta \sigma =\frac{1}{2}\eta \sigma >0.\hfill \end{array}$$

However, at the same time, $w_{**}{(|x(t)|}^m)>{\sigma }_1$ for $t\in (t^{*},t^{**})\supseteq (t^{*},t_{\Delta })$, then $\mathbb{E}\overline{w}(|x(t_{\Delta })|)=\mathbb{E}\tilde{w}(|x(t_{\Delta }){|}^p)({\sigma }_1-w_{**}(|x(t_{\Delta }){|}^m))\le 0$, which contradicts the above estimate $\mathbb{E}\overline{w}(|x(t_{\Delta })|)>0$. Thus, our assertion is true. With this assertion, we finally obtain $\mathcal{L}V(t,x)\le -{\sigma }_{2}a(t)\tilde{w}$$(|x{|}^p)\le 0$ a.s. From Lemma 3, we obtain the desired results. Assertion $w_{**}{(|x(t)|}^m)<{\sigma }_1$, as shown above, also provides the conclusion of Lemma 3 for the case $m>0$.

If the initial data $\xi$ are a stochastic variable, then we can similarly complete the proof of the theorem by virtue of the conditional expectation w.r.t the initial data $\xi$. The proof is complete. □

4.3. Noise Leads to Persistence

Assume that $R(V):{\mathbb{R}}^{+}\to \mathbb{R}$ is an increasing and differentiable function with $R(V)\to \infty$ as $V\to \infty$; then, $R(V)$ is a generalized Lyapunov function and $R(V(t,x(t)))$ is a composite random process for the solution process $x(t)$ of (1). Therefore,

$$\begin{array}{ccc}\hfill \mathrm{d}R(t,x)& =& \mathcal{L}R(t,x)\mathrm{d}t+\mathcal{H}R(t,x)\mathrm{d}B(t),\mathrm{where}\hfill \\ \hfill \mathcal{L}R(t,x)& =& R^{\prime }(V(t,x))\mathcal{L}V(t,x)+\frac{1}{2}{R}^{″}(V(t,x))\mathrm{Tr}\left({(\mathcal{H}V(t,x))}^{\mathrm{T}}\mathcal{H}V(t,x)\right),\hfill \\ \hfill \mathcal{H}R(t,x)& =& R^{\prime }(V(t,x))\mathcal{H}V(t,x).\hfill \end{array}$$

Noticing the term $R^{″}(V(t,x))$ and the relation $\mathcal{H}V(t,x)=V_x(t,x)g(t,x)$, we can observe that, if $R^{″}(V)<0$ for $V>0$, then we may reach the negativeness of $\mathcal{L}R(t,x)$ due to the contribution of the noise, while the negativeness of $\mathcal{L}R(t,x)$ directly guarantees the global existence of the solution $x(t)$ (we also call this the persistence of the system) if the boundedness of $R(t,x)=R(V(t,x))$ via $V(t,x)$ implies the boundedness of x. Of course, appropriate conditions for $R^{\prime }(V(t,x))\mathcal{L}V(t,x)$ are needed. A typical choice for $R(V)$ is $R(V)=V^{\frac{p}{2}}$, where $p>0$. In this case,

$$\begin{array}{c}\hfill R^{\prime }(V(t,x))=\frac{p}{2}{V}^{\frac{p}{2}-1}(t,x),R^{″}(V(t,x))=\frac{p}{2}(\frac{p}{2}-1)V^{\frac{p}{2}-2}(t,x),\end{array}$$

and then we get

$$\begin{array}{c}\hfill \mathcal{L}R(t,x)=\frac{p}{2}{V}^{\frac{p}{2}-1}(t,x)\mathcal{L}V(t,x)+\frac{p}{4}(\frac{p}{2}-1)V^{\frac{p}{2}-2}(t,x)\mathrm{Tr}\left({(\mathcal{H}V(t,x))}^{\mathrm{T}}\mathcal{H}V(t,x)\right).\end{array}$$

To make good use of this formula, we consider $0<p<2$. Then, we have $\frac{p}{4}(\frac{p}{2}-1)<0$. If appropriate conditions are imposed on coefficients $f(t,x)$ and $g(t,x)$, we may reach the negativeness of $\mathcal{L}R(t,x)$, which will be illustrated below. We assume that $f(t,x)$ and $g(t,x)$ satisfy the local Lipschitz conditions, which ensures the local existence of solutions to the system.

This analysis shows that noise may lead to the persistence of the systems and one may investigate the global existence of solutions using as low an order moment as possible, which is beneficial when carrying out the intrinsic existence criterion.

Based on the above derivations, by applying the classical Khasminskii test, we can obtain:

Corollary 2.

If $\mathcal{L}R(t,x)\le C(t)(1+R(t,x))$ holds, then, for each initial piece of data $\xi \in {\mathbb{R}}^d$, there exists a global solution $x(t)$ to Equation (1).

From Theorem 1, we have:

Corollary 3.

If there are orders $p>q\ge 0$, functions $a(t)\ge 0,c(t)$ and coefficients $b>0$ such that $\mathcal{L}R(t,x)\le a(t)(|x{|}^q-b|x{|}^p)+c(t)$, then, for each initial piece of data $\xi \in {\mathbb{R}}^d$, there is a global solution $x(t)$ to Equation (1).

Case $p=q$ can be seen as a special case if $b>1$. Similarly, from Theorem 2, we have:

Corollary 4.

If there are orders $q>p>0$ with $p<q<p+1$, functions $a(t)\ge 0,c(t)$ and coefficients $b>0$, such that $\mathcal{L}R(t,x)\le a(t)(|x{|}^q-b|x{|}^p)+c(t)$; then, for each initial piece of data $\xi \in {\mathbb{R}}^d$ with $|\xi |\le \delta$, there is a deterministic positive number $\delta >0$, such that there is a global and local solution $x(t)$ to Equation (1).

We then concretely investigate the role of the noise by assuming:

Assumption 6.

$0<p<2,$$V^{\frac{p}{2}-2}(t,x)\mathrm{Tr}\left({(\mathcal{H}V(t,x))}^{\mathrm{T}}\mathcal{H}V(t,x)\right)\ge \beta {|x|}^q,\beta >0$.

If, in addition, we have $V^{\frac{p}{2}-1}(t,x)\mathcal{L}V(t,x)\le \alpha {|x|}^p$, then we have

$$\begin{array}{c}\hfill \mathcal{L}R(t,x)\le \frac{1}{2}{\alpha p|x|}^p-\frac{1}{8}(2-p)p\beta {|x|}^q.\end{array}$$

From Corollaries 3, 4 and Lemma 3 we have:

Corollary 5.

Under Assumption 5, for each of the following cases, the global existence conclusion can be described vt Corollaries 3 and 4:

(i) $q>p$ with $\beta >0$;

(ii) $q=p$ with $(2-p)\beta >2\alpha$;

(iii) $q<p$ with $q<p\le 2q$ and $\beta >0$.

The following analysis will enhance this conclusion.

We now consider a related topic: how to achieve the persistence of the system by introducing a suitable noise. To this end, we first assume:

Assumption 7.

$|f(t,x)|\le {K|x|}^{\mu }$, where $\mu \ge 1,K$ = const.

Design the noise ${\rho |x|}^{q}x\mathrm{d}B(t)$, $\beta \ne 0,B(t)$ as a scalar Browian motion. Let $V(t,x)={|x|}^2$; therefore, one can estimate

$$\begin{array}{ccc}& & V^{\frac{p}{2}-2}(t,x)\mathrm{Tr}\left({(\mathcal{H}V(t,x))}^{\mathrm{T}}\mathcal{H}V(t,x)\right)\ge {\rho }^2{|x|}^{p+2q},\hfill \\ & & V^{\frac{p}{2}-1}(t,x)\mathcal{L}V(t,x)\le {2|x|}^{p+\mu -1}+{\rho }^2{|x|}^{p+2q},\hfill \end{array}$$

and then

$$\begin{array}{ccc}\hfill \mathcal{L}R(t,x)& \le & {p|x|}^{p+\mu -1}+{\rho }^2{p|x|}^{p+2q}/2-p(2-p){\rho }^2{|x|}^{p+2q}/2\hfill \\ & =& {p|x|}^{p+\mu -1}-{\rho }^{2}p(1-p)/2{|x|}^{p+2q}.\hfill \end{array}$$

Define $\Gamma (\mu ,q)=p+\mu -1-(p+2q)=\mu -1-2q$. Then, if $q=(\mu -1)/2$, we have $\Gamma (\mu ,q)=0$. If ${\rho }^2>2$, there is a $p>0$ such that $p(1-{\rho }^2(1-p)/2)<0$, and then $\mathcal{L}R(t,x)\le p(1-{\rho }^2(1-p)/2){|x|}^{p+\mu -1}\le 0$; this leads to the global existence. If $q>(\mu -1)/2$, we have $\Gamma (\mu ,q)<0$. In this case, from Corollary 3, we have:

Corollary 6.

Under the Assumption 6, if the the noise $g(t,x)\mathrm{d}B(t)$ in (1) can be designed as ${\rho |x|}^{q}x\mathrm{d}B(t)$, where $\rho >0,q>(\mu -1)/2$; then, for each initial piece of data $\xi \in {\mathbb{R}}^d$, there is a global solution to Equation (1).

For the case $\mu =1$, the bound for q is $q>0$, namely, ${\rho |x|}^{q}x\mathrm{d}B(t)$ was intended to be multiplicative noise. In this case, Corollary 6 can be read as:

Corollary 7.

Under $|f(t,x)|\le K|x|$, namely, the linear growth condition, any multiplicative noise ${\rho |x|}^{q}x\mathrm{d}B(t)$ (with $q>0$) will lead to the persistence of the system; namely, there exists a global solution to $\mathrm{d}x=f(t,x)\mathrm{d}t+{\rho |x|}^{q}x\mathrm{d}B(t)$ for each initial piece of data $\xi \in {\mathbb{R}}^d$.

If we use a more general estimate $|f(t,x)|\le {K|x|}^{\mu }+\nu (|x|)$ for the intrinsic dynamics of the system, where $\mu >1$ and $\nu (|x|)$ is a lower-order term than ${|x|}^{\mu }$; then, we can design the same noise to realize the persistence of the system.

Interestingly, for the pure noise case, namely $f(t,x)=0$, we easily obtain a global solution. If we define $V={|x|}^2$, then we have

$$\begin{array}{c}\hfill \mathcal{L}R(t,x)=\frac{p}{2}{|x|}^{p-2}{|g(t,x)|}^2+p(\frac{p}{2}-{1)|x|}^{p-4}{|x^{\mathrm{T}}g(t,x)|}^2.\end{array}$$

With this, we see that the boundedness of $\mathcal{L}R(t,x)$ and the global existence of the solution are easily guaranteed. For example, if we use the nonlinear diffusive coefficient $g(t,x)={k|x|}^{\varrho }x$, where $\varrho \ge 0$, then $\mathcal{L}R(t,x)=-\frac{1}{2}{k}^2(1-p)p{|x|}^{p+2\varrho }$. This implies that, for each positive number $p\in (0,1)$, we have $\mathcal{L}R(t,x)\le 0$, and then we can determine the global existence of the solution. One can further show p-th moment asymptotic stability for the system. A more general case is $g(t,x)=G(t,x)x$, where $G(t,x)$ is a scalar function. By tausingking an arbitrary order $p\in (0,1)$, we can similarly obtain the global existence conclusion.

4.4. An Application to Financial Systems

The Black–Scholes model is a formula for pricing European options, proposed by two economists, Black and Scholes, in 1973. This lays a foundation for the reasonable pricing of derivative financial instruments. The Black–Scholes model is represented by the following stochastic differential equation,

$$\mathrm{d}{S}_t=\mu S_t\mathrm{d}t+\sigma S_t\mathrm{d}B(t),$$

where $B(t)$ is a Brownian motion, $\mu$ is the drift rate, and $\sigma$ is the volatility. The solution of this kind of differential equation modeling is a geometric Brownian motion. It is realistic to model the stock price change using the above stochastic differential equation. The reasons for this are as follows. Under the assumption of continuous compound interest, the stock return conforms to the normal distribution, which is consistent with the property of Brownian motion $B(t)$. In addition, the Brownian motion is mathematically non-differentiable in time and its quadratic variation is not zero, which shows that the stock yield image owns the characteristics of turning points in time.

Corollary 7 implies that this financial system must persist globally. Corollary 7 also implies that, if the noise is replaced by an arbitrary multiplicative noise $\sigma |S_t{|}^q\mathrm{d}B(t)$, where q is only desired to be a positive number, then the noised financial system $\mathrm{d}{S}_t=\mu S_t\mathrm{d}t+\sigma S_t^q\mathrm{d}B(t)$ must also persist globally.

For $q=1$, the model is only the Black–Scholes model. For the case $q=\frac{1}{2}$, we obtain a Heston model (the terminology “root process" is usually applied to the solution process $x(t)$ of this model), c.f. [29,30]. Here, we can determine the global existence of this, in which the linear growth condition is not satisfied.

4.5. Illustrating Example

Here, we illustrate the feasibility of the conditions and conclusions of the obtained criteria using a simple example, and some simulations follow this example at the end of the paper.

Example 1.

Let $f(t,x)={a|x|}^{\alpha }x,g(t,x)=\sigma {|x|}^{\beta }x$, where $a,{\sigma }^2>0,\alpha \ge 0$. $\beta >0$ is to be chosen.

Firstly, we chose $\beta >0$ such that $2\beta >\alpha$, namely, $\gamma \triangleq 2\beta -\alpha >0$.

Let $0<p<1$. Define $V(t,x)={|x|}^2$; then, $R(t,x)={|x|}^p$. We can easily show that

$$\begin{array}{c}\hfill \mathcal{L}R(t,x)=\frac{1}{2}{p[2a|x|}^{p+\alpha }-(1-p){\sigma }^2{|x|}^{p+2\beta }]=\frac{1}{2}{p|x|}^{p+\alpha }[2a-(1-p){\sigma }^2{|x|}^{\gamma }],\end{array}$$

(7)

using Corollary 2, we can determine that, for the initial data $\xi \in {\mathbb{R}}^d$, there is a global solution to Equation (1).

For $\alpha =1$, namely, $f(t,x)=a|x|x$, the condition $\gamma =2\beta -\alpha >0$ becomes $\beta >\frac{1}{2}$; for the case $\alpha =0$, namely, $f(t,x)=ax$, this condition becomes $\beta >0$.

For the case $\gamma =0$, the stability condition $a-\frac{1}{2}{\sigma }^2<0$ also provides the global existence conclusion for the reason that there is a positive number $0<p<1$, such that $2a-(1-p){\sigma }^2<0$ in this case.

For the case $\gamma =2\beta -\alpha <0$, namely, $2\beta <\alpha$ (here, $\beta =0$ is allowed), we may obtain the global existence result using Theorem 2, based on the estimate (7). That is, if $0<\alpha -2\beta <1$, or, say, $\alpha -1<2\beta <\alpha$, then, for each initial piece of data $\xi \in {\mathbb{R}}^d$ with $|\xi |\le \delta$, there is a deterministic positive number $\delta >0$, such that there is a global and local solution to Equation (1).

4.6. Khasminskii Test for Delayed Stochastic Systems

Now, we apply the fundamental principle established above to derive the corresponding Khasminskii test for the delayed stochastic systems. For the representativeness and comprehensiveness, the considered model is

$$\begin{array}{c}\hfill \mathrm{d}x(t)=f(t,x(t),x(t-\tau ),x_t)\mathrm{d}t+g(t,x(t),x(t-\tau ),x_t)\mathrm{d}B(t),t\in {\mathbb{R}}^{+},\end{array}$$

(8)

where $x\in {\mathbb{R}}^d$, $f:{\mathbb{R}}^{+}\times {\mathbb{R}}^d\times {\mathbb{R}}^d\times C([-\tau ,0],{\mathbb{R}}^d)\to {\mathbb{R}}^d,g:{\mathbb{R}}^{+}\times {\mathbb{R}}^d\times {\mathbb{R}}^d\times C([-\tau ,0],{\mathbb{R}}^d)$$\to {\mathbb{R}}^{d\times r}$ are Borel measurable functionals. The time delay $\tau >0$.

We intend to derive a typical Khasminskii test for the general delayed stochastic systems, with some individualities orientated to the delayed systems involved in related criteria, e.g., the structure and condition in the criteria, are expected in addition to the representativeness and comprehensiveness.

Assumption 8.

The partial local Lipschitz condition. For each positive integer $n>0$ and the state $y\in {\mathbb{R}}^d$, there is a continuous function $L_n(t,y)$ depending on n and y, such that

$$\begin{array}{cc}& |f(t,x_2,y,{\varphi }_2)-f(t,x_1,y,{\varphi }_1)|\\ & \vee |g(t,x_2,y,{\varphi }_2)-g(t,x_1,y,{\varphi }_1)|\le L_n(t,y)(|x_2-x_1|+\parallel {\varphi }_2-{\varphi }_1\parallel ),\end{array}$$

for $t\in {\mathbb{R}}^{+},x_1,x_2\in {\mathbb{R}}^d,{\varphi }_1,{\varphi }_2\in C([-\tau ,0],{\mathbb{R}}^d)$ with $|x_1|\vee |x_2|\vee \parallel {\varphi }_1\parallel \vee \parallel {\varphi }_2\parallel \le n$.

$V(t,x)\in C^{1\times 2}({\mathbb{R}}^{+}\times {\mathbb{R}}^d,{\mathbb{R}}^{+})$ is a Lyapunov function. As usual, we assume that there are $\mathcal{K}$ functions $u(·)$ and $v(·)$, such that ${u(|x|}^p{)\le V(t,x)\le v(|x|}^p)$, where $u(·)$ is convex. Define the differential operators

$$\begin{array}{ccc}\hfill \mathcal{L}V(t,x,y,\varphi )& =& V_t(t,x)+V_x(t,x)f(t,x,y,\varphi )+\frac{1}{2}\mathrm{Tr}(g^{\mathrm{T}}(t,x,y,\varphi )V_{xx}(t,x)g(t,x,y,\varphi )),\hfill \\ \hfill \mathcal{H}V(t,x,y,\varphi )& =& V_x(t,x)g(t,x,y,\varphi ),t\in {\mathbb{R}}^{+},x,y\in {\mathbb{R}}^d,\varphi \in C([-\tau ,0],{\mathbb{R}}^d),\hfill \end{array}$$

then, for the process $V(t,x(t))$, we have the Itô formula

$$\begin{array}{c}\hfill \mathrm{d}V(t,x(t))=\mathcal{L}V(t,x(t),x(t-\tau ),x_t)\mathrm{d}t+\mathcal{H}V(t,x(t),x(t-\tau ),x_t)\mathrm{d}B(t).\end{array}$$

Actually, $V(t,x)$ is allowed to be a Lyapunov functional.

Remark 1 tells us that, for each initial piece of data, $\xi \in C_{{\mathcal{F}}_{t_0}}^b([-\tau ,0];{\mathbb{R}}^d)$ there is a solution $x(t)=x(t;t_0,\xi )$ to (8) under Assumption 6. Based on this, we further consider the global existence.

Generally, we obtain the following estimate for $\mathcal{L}V(t,x,y,\varphi )$:

$$\begin{array}{c}\hfill \mathcal{L}V(t,x,y,\varphi )\le -{\mu }^{-}(t,|x|,y)+{\mu }^{+}(t,|x|,y,\varphi )+R(t,y),\end{array}$$

(9)

for $t\in {\mathbb{R}}^{+},x,y\in {\mathbb{R}}^d,\varphi \in C([-\tau ,0],{\mathbb{R}}^d)$, where ${\mu }^{+}(t,|x|,y,\varphi )\ge 0$ and ${\mu }^{-}(t,|x|,y)\ge 0$ are semi-positive definite functions in x; these can be estimated further. Here, we consider a typical special case, which is formulated in the following assumption.

Assumption 9.

$\mathcal{L}V(t,\varphi (0),y,\varphi )\le C(t)(1+{sup}_{\theta \in [-\tau ,0]}V(t+\theta ,\varphi (\theta )))+R(t,y)$, where $C(t)\ge 0$ is bounded on any bounded interval $[t_1,t_2]$, $R(t,y)\ge 0$ satisfies $R(t,y)\le \tilde{R}{(t,|y|}^m),m\ge 0$, and $\tilde{R}(t,s)$ is concave in s.

Remark 4.

The condition for $R(t,y)$ is not harsh due to the arbitrariness of m. If we choose m as the highest order of y in the estimate for $R(t,y)$, the condition is naturally satisfied.

Corollary 8.

Under Assumptions 7 and 8, for each piece of initial data, $\xi \in C_{{\mathcal{F}}_{t_0}}^b([-\tau ,0];{\mathbb{R}}^d)$, there exists global a solution $x(t)=x(t;t_0,\xi )$ to (8).

Proof. 

We prove the conclusion using the piecewise technique based on Lemma 3.

Consider the first interval $[t_0,t_0+\tau ]$, on which $x(t-\tau )=\xi (t-\tau )$. Using Assumption 5, we have

$$\begin{array}{c}\hfill \mathcal{L}V(t,x(t),x(t-\tau ),x_t)\le C(t)(1+\underset{\theta \in [-\tau ,0]}{sup}V(t+\theta ,x(t+\theta )))+R(t,x(t-\tau )).\end{array}$$

Define $U(t)={sup}_{\theta \in [-\tau ,0]}V(t+\theta ,x(t+\theta ))$; then, we can obtain

$$\begin{array}{ccc}\hfill V(t,x(t))& =& V(t_0,\xi )+{\int }_{t_0}^t\mathcal{L}V(s,x(s),x(s-\tau ),x_s)\mathrm{d}s+M(t)\hfill \\ & \le & V(t_0,\xi )+{\int }_{t_0}^t[C(s)(1+U(s)))+\tilde{R}(s,|x(s-\tau ){|}^m)]\mathrm{d}s+M(t)\hfill \\ \hfill & \le & \zeta +c{\int }_{t_0}^{t}U(s)\mathrm{d}s+M(t),t\in [t_0,t_0+\tau ],\hfill \end{array}$$

(10)

where $M(t)={\int }_{t_0}^t\mathcal{H}V(s,x(s),x(s-\tau ),x_s)\mathrm{d}B(s)$, which can be verified as a martingale, and

$$\begin{array}{ccc}\hfill \zeta & =& V(t_0,\xi )+\tau (c+\rho ),c=\underset{s\in [t_0,t_0+\tau ]}{sup}C(s),\hfill \\ \hfill \rho & =& \underset{s\in [t_0,t_0+\tau ]}{sup}\tilde{R}(s,\underset{\theta \in [-\tau ,0]}{sup}{|\xi (\theta )|}^m),\mathrm{with}\hfill \\ \hfill \mathbb{E}\rho & \le & \underset{s\in [t_0,t_0+\tau ]}{sup}\tilde{R}(s,\mathbb{E}\underset{\theta \in [-\tau ,0]}{sup}{|\xi (\theta )|}^m)<+\infty ,\hfill \end{array}$$

this, combined with the assumption for $V(t,x)$, guarantees $\mathbb{E}\zeta <+\infty$.

Based on (10), one can verify that, regardless of whether $t+\theta >t_0$ for $\theta \in [-\tau ,0]$, one can obtain

$$\begin{array}{c}\hfill V(t+\theta ,x(t+\theta ))\le \zeta +c{\int }_{t_0}^{t}U(s)\mathrm{d}s+\underset{\theta \in [-\tau ,0]}{sup}M(t+\theta ),t\in [t_0,t_0+\tau ];\end{array}$$

thus,

$$\begin{array}{c}\hfill U(t)\le \zeta +c{\int }_{t_0}^{t}U(s)\mathrm{d}s+\underset{s\in [t_0-\tau ,t_0+\tau ]}{sup}M(s),t\in [t_0,t_0+\tau ].\end{array}$$

(11)

By applying the stopping time ${\tau }_k$ defined above, we can obtain

$$\begin{array}{c}\hfill U(t\wedge {\tau }_k)\le \zeta +c{\int }_{t_0}^{t\wedge {\tau }_k}U(s)\mathrm{d}s+\underset{s\in [t_0-\tau ,t_0+\tau ]}{sup}M(s),t\in [t_0,t_0+\tau ].\end{array}$$

(12)

In addition, with $U(·)\ge 0$, we can verify either $t\ge {\tau }_k$ or $t<{\tau }_k$. We always have

$$\begin{array}{c}\hfill {\int }_{t_0}^{t\wedge {\tau }_k}U(s)\mathrm{d}s\le {\int }_{t_0}^{t}U(s\wedge {\tau }_k)\mathrm{d}s.\end{array}$$

Thus, (12) becomes

$$\begin{array}{c}\hfill U(t\wedge {\tau }_k)\le \zeta +c{\int }_{t_0}^{t}U(s\wedge {\tau }_k)\mathrm{d}s+\underset{s\in [t_0-\tau ,t_0+\tau ]}{sup}M(s),t\in [t_0,t_0+\tau ].\end{array}$$

(13)

In addition, given the time $t\ge t_0$ and an increment $h\ge 0$, we can obtain

$$\begin{array}{c}\hfill {\mathbb{E}|M(t+h)-M(t)|}^2=\mathbb{E}|{\int }_t^{t+h}\mathcal{H}V(s,x(s),x(s-\tau ),x_s)\mathrm{d}B(s){|}^2.\end{array}$$

Under the assumptions for both $g(t,x,y,\varphi )$ and $V(t,x)$, we can verify that $\mathbb{E}|\mathcal{H}V(t,x(t),$ $x(t-\tau ),x_t){|}^2$ is bounded on any bounded interval $[t_1,t_2]\supset [t,t+h]$ and $\mathcal{H}V(t,x(t),x(t-\tau ),x_t)$ is ${\mathcal{M}}^2$-integrable over $[t,t+h]$. This shows that, simultaneously, $M(t)$ is a martingale. Using these, with the Itô’s isometry, we can obtain

$$\begin{array}{c}\hfill {\mathbb{E}|M(t+h)-M(t)|}^2={\int }_t^{t+h}\mathbb{E}|\mathcal{H}V(s,x(s),x(s-\tau ),x_s){|}^2\mathrm{d}s,\end{array}$$

which then means that $M(t)$ is mean square continuous and is also continuous. Using this, we know that there is almost cartainly an ${\theta }^{*}\in [t_0-\tau ,t_0+\tau ]$ such that ${sup}_{s\in [t_0-\tau ,t_0+\tau ]}$$M(s)=M({\theta }^{*})$, which means that $\mathbb{E}{sup}_{s\in [t_0-\tau ,t_0+\tau ]}M(s)=\mathbb{E}M({\theta }^{*})=0$. With this fact, it follows from (13)

$$\begin{array}{c}\hfill \mathbb{E}U(t\wedge {\tau }_k)\le \mathbb{E}\zeta +c{\int }_{t_0}^t\mathbb{E}U(s\wedge {\tau }_k)\mathrm{d}s,t\in [t_0,t_0+\tau ].\end{array}$$

(14)

Making use of Gronwall’s inequality one obtains $\mathbb{E}U(t\wedge {\tau }_k)\le H(t)=\mathbb{E}\zeta e^{c(t-t_0)}$ and then $\mathbb{E}V(t\wedge {\tau }_k,x(t\wedge {\tau }_k))\le H(t)$ for $t\in [t_0,t_0+\tau ]$. From Lemma 3, we know that $x(t)$ exists over the whole interval $[t_0,t_0+\tau ]$. Repeating this procedure, we can obtain the desired results.

As a special case, using Corollary 7 and $V(x)={|x|}^2$ one can easily show that, if Assumption 4 is replaced by a global partial Lipschitz condition, then the underlying system (8) always admits a global solution in time for each given piece of initial data. These systems include

$$\begin{array}{c}\hfill \mathrm{d}x(t)=[f(t,x(t),x_t)+\tilde{f}(t,x(t-\tau ))]\mathrm{d}t+[g(t,x(t),x_t)+\tilde{g}(t,x(t-\tau ))]\mathrm{d}B(t),t\in {\mathbb{R}}^{+},\end{array}$$

where $f:{\mathbb{R}}^{+}\times {\mathbb{R}}^d\times C([-\tau ,0],{\mathbb{R}}^d)\to {\mathbb{R}}^d,g:{\mathbb{R}}^{+}\times {\mathbb{R}}^d\times C([-\tau ,0],{\mathbb{R}}^d)\to {\mathbb{R}}^{d\times r}$ are Borel measurable functionals, which satisfy the (time-varying) global Lipschitz condition. The time delay is $\tau >0$.

Corollary 8 tells us that, no matter how large the terms $\tilde{f}(t,x(t-\tau ))$ and $\tilde{g}(t,x(t-\tau ))$ are, the global existence of the solutions can always be guaranteed. Of course, this conclusion remains valid for the extremely special case $f(t,x,\varphi )=0\in {\mathbb{R}}^d,g(t,x,\varphi )=0\in {\mathbb{R}}^{d\times r}$, namely, the completely retarded systems. □

Remark 5.

In principle, Corollary 8 shows that the delayed term $R(t,y)$ in the estimate of $\mathcal{L}V(t,x,y,\varphi )$ does not affect the global existence of the solutions.

Remark 6.

$\mathcal{L}V(t,\varphi (0),y,\varphi )\le C(t)(1+V(t,\varphi (0))+R(t,y)$ is a special case of Assumption 5, so we have the global existence conclusion in this case.

5. Numerical Simulations

We continue from Example 1. All the simulations will be illustrated in finite time. We rewrite the system here for clarity

$$\begin{array}{c}\hfill \mathrm{d}x(t)={a|x|}^{\alpha }x\mathrm{d}t+\sigma {|x|}^{\beta }x\mathrm{d}B(t),t\in {\mathbb{R}}^{+},\end{array}$$

(15)

where $x\in \mathbb{R}$ and $B(t)$ is a scalar Brown motion.

Firstly, let us consider the case $2\beta >\alpha$. We simulate this for $\alpha =\beta =1,a=\sigma =1$ for $\xi =3$ in Figure 1, which shows the global existence of the solution.

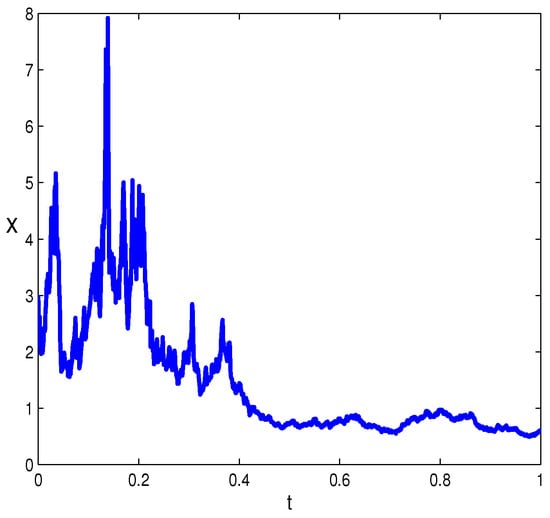
Figure 1. Dynamic responses for the first case.

Secondly, we consider the case $2\beta =\alpha$. We simulate it for $\alpha =2,\beta =1,a=1,\sigma =2$ with $a-\frac{1}{2}{\sigma }^2<0$ for $\xi =3$ in Figure 2, which also shows the global existence of the solution.

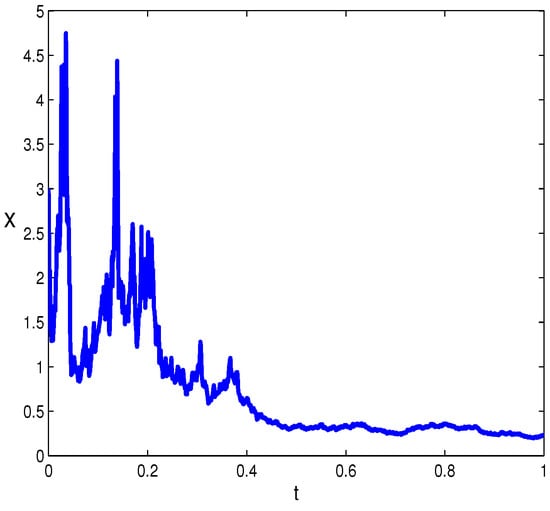
Figure 2. Dynamic responses for the second case.

Thirdly, we consider the case $2\beta <\alpha$. We simulate it for $\alpha =2,\beta =0.75,a=1,\sigma =2$ with $\alpha -1<2\beta <\alpha$ for $\xi =3$ in Figure 3, which shows the global existence of the solution.

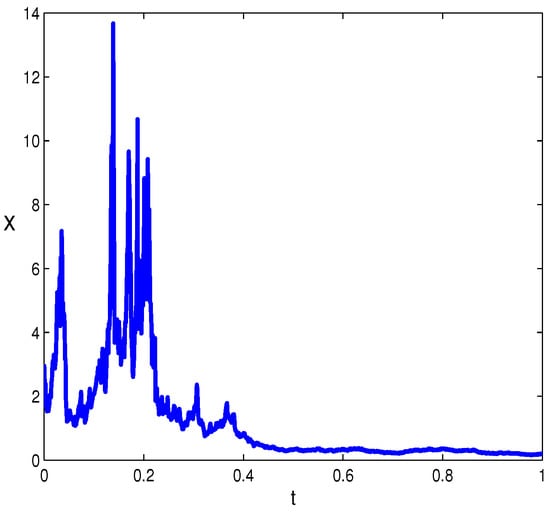
Figure 3. Dynamic responses for the third case.

Finally we consider the case $2\beta <\alpha$. We simulate it for $\alpha =2,\beta =0,a=1,\sigma =2$ with $2\beta <\alpha -1$ for $\xi =3$ in Figure 4, which shows the explosion in finite time for the solution.

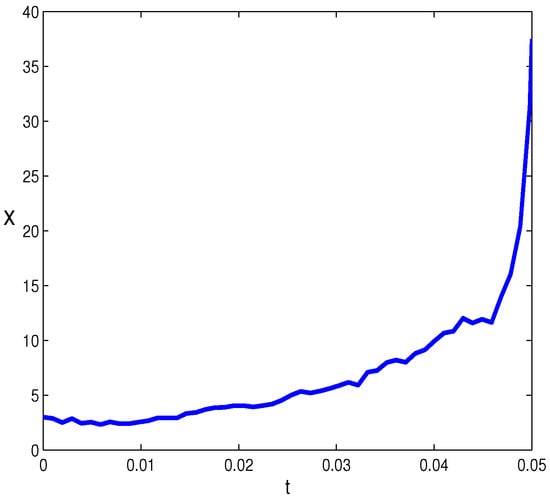
Figure 4. Dynamic responses for the explosive case.

The simulations verify the results obtained in the paper.

6. Conclusions

It is known that the existence of the solutions is fundamental to investigations on stability theory and the control of stochastic differential equations. In this paper, the global existence of solutions to stochastic differential equations via the Khasminskii tests is further theorized. As we see, the equivalent proposition for the global existence and the fundamental principle for the Khasminskii test are formally established; then, the classical Khasminskii test is generalized to the cases with high-order estimates for stochastic derivatives of Lyapunov functions. Our work, using a series of arguments to deal with the nonlinear factor for the case in which the positive term in the stochastic derivative dominates at infinity, appears to be novel. To discuss the feature of stochastic differential equations, the active role of the noise in the global existence is specifically investigated in the paper and some concrete criteria related to this topic are obtained. The analysis based on Assumption 4 shows that noise nearly always leads to system persistence under the usual assumption. The application for the role of noise in the persistence of financial systems given in the paper is obviously novel and interesting. A new version of the Khasminskii test for the delayed stochastic systems is established, in which we show a mechanism: that is, the delayed terms in the estimates for the stochastic derivatives do not affect the global existence of solutions. Finally, the conclusions obtained in this paper are verified by simulations (in finite time). In further investigations, one could consider more complicated models, e.g., neutral models. In addition, one could study some new problems regarding stronger system properties, such as the stability, dissipativity and synchronization of the underlying systems under nonlinear conditions.