Upper and Lower Bounds for the Spectral Radius of Generalized Reciprocal Distance Matrix of a Graph

Abstract

For a connected graph G on n vertices, recall that the reciprocal distance signless Laplacian matrix of G is defined to be $RQ\left(G\right)=RT\left(G\right)+RD\left(G\right)$, where $RD\left(G\right)$ is the reciprocal distance matrix, $RT\left(G\right)=diag(R{T}_1,R{T}_2,\cdots ,R{T}_n)$ and $R{T}_i$ is the reciprocal distance degree of vertex $v_i$. In 2022, generalized reciprocal distance matrix, which is defined by $R{D}_{\alpha }\left(G\right)=\alpha RT\left(G\right)+(1-\alpha )RD\left(G\right),\alpha \in [0,1]$, was introduced. In this paper, we give some bounds on the spectral radius of $R{D}_{\alpha }\left(G\right)$ and characterize its extremal graph. In addition, we also give the generalized reciprocal distance spectral radius of line graph $L\left(G\right)$.

1. Introduction

In this paper, all graphs considered are finite, simple, and connected. Let G be such a graph with vertex set $V\left(G\right)=\{v_1,v_2,\cdots ,v_n\}$ and edge set $E\left(G\right)$, where $\left|V\right(G\left)\right|=n$ and $\left|E\right(G\left)\right|=m$. Let $d_{v_i}$ denote the degree of vertex $v_i$, which is simply written as $d_i$. $N\left(v_i\right)$ denote the neighbor set of $v_i$. The distance between vertices $v_i$ and $v_j$ in G is the length of the shortest path connecting $v_i$ to $v_j$, which is denoted as $d(v_i,v_j)$. We use the notation $d_{ij}$ instead of $d(v_i,v_j)$. The diameter of G, denoted by $diam\left(G\right)$, is the maximum distance between any pair of vertices of G. The Harary matrix of G, which is also called the reciprocal distance matrix, is an $n\times n$ matrix defined as [1]

$$R{D}_{i,j}=\left\{\begin{array}{cc}\frac{1}{d(v_i,v_j)},\hfill & \mathrm{if}i\ne j,\hfill \\ 0,\hfill & \mathrm{if}i=j.\hfill \end{array}\right.$$

Henceforth, we consider $i\ne j$ for $d(v_i,v_j)$.

The transmission of vertex $v_i$, denoted by $T{r}_G\left(v_i\right)$ or $T{r}_i$, is defined to be the sum of the distances from $v_i$ to all vertices in G, that is, $T{r}_G\left(v_i\right)=T{r}_i={\displaystyle \sum _{u\in V\left(G\right)}}d(u,v_i)$. A graph G is said to be k-transmission regular graph if $T{r}_G\left(v\right)=k$ for each $v\in V\left(G\right)$. Transmission of a vertex v is also called the distance degree or the first distance degree of v.

Definition 1.

Let G be a graph with $V\left(G\right)=\{v_1,v_2,\cdots ,v_n\}$. The reciprocal distance degree of a vertex v, denoted by $RT{r}_G\left(v\right)$, is given by

$$RT{r}_G\left(v\right)=\sum _{u\in V\left(G\right),u\ne v}\frac{1}{d(u,v)}.$$

Let $RT\left(G\right)$ be the $n\times n$ diagonal matrix defined by $R{T}_{i,i}=RT{r}_G\left(v_i\right)$.

Sometimes we use the notation $R{T}_i$ instead of $RT{r}_G\left(v_i\right)$ for $i=1,\cdots ,n$.

Definition 2.

A graph G is called a k-reciprocal distance degree regular graph if $R{T}_i=k$ for all $i\in \{1,2,\cdots ,n\}.$

The Harary index of a graph G, denoted by $H\left(G\right)$, is defined in [1] as

$$H\left(G\right)=\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^{n}R{D}_{i,j}=\frac{1}{2}\sum _{u,v\in V\left(G\right),u\ne v}\frac{1}{d(u,v)}.$$

Clearly,

$$H\left(G\right)=\frac{1}{2}\sum _{i=1}^{n}R{T}_i.$$

In [2], Bapat and Panda defined the reciprocal distance Laplacian matrix as $RL\left(G\right)=RT\left(G\right)-RD\left(G\right)$. It was proved that, given a connected graph G of order n, the spectral radius of its reciprocal distance Laplacian matrix $\rho \left(RL\right(G\left)\right)\le n$ if and only if its complement graph, denoted by $\overline{G}$, is disconnected. In [3], Alhevaz et al. defined the reciprocal distance signless Laplacian matrix as $RQ\left(G\right)=RT\left(G\right)+RD\left(G\right).$ Recently, the lower and upper bounds of the spectral radius of the reciprocal distance matrices and reciprocal distance signless Laplacian matrices of graphs were given in [3,4,5,6], respectively.

In [7], the author, using the convex linear combinations of the matrices $RT\left(G\right)$ and $RD\left(G\right)$, introduces a new matrix, that is generalized reciprocal distance matrix, denoted by $R{D}_{\alpha }\left(G\right)$, which is defined by

$$R{D}_{\alpha }\left(G\right)=\alpha RT\left(G\right)+(1-\alpha )RD\left(G\right),0\le \alpha \le 1.$$

Since $R{D}_0\left(G\right)=RD\left(G\right)$, $R{D}_{\frac{1}{2}}\left(G\right)=\frac{1}{2}RQ\left(G\right)$ and $R{D}_1\left(G\right)=RT\left(G\right)$, then $R{D}_{\frac{1}{2}}\left(G\right)$ and $RQ\left(G\right)$ have the same spectral properties. To this extent these matrices $RD\left(G\right)$, $RT\left(G\right)$, and $RQ\left(G\right)$ may be understood from a completely new perspective, and some interesting topics arise. For the these matrices $RD\left(G\right)$, $RT\left(G\right)$, and $RQ\left(G\right)$, some spectral extremal graphs with fixed structure parameters have been characterized in [8,9]. It is natural to ask whether these results can be generalized to $R{D}_{\alpha }\left(G\right)$.

Since $R{D}_{\alpha }\left(G\right)$ is real symmetric matrics, we can denoted ${\lambda }_1\left(R{D}_{\alpha }\left(G\right)\right)\ge {\lambda }_2\left(R{D}_{\alpha }\left(G\right)\right)$$\ge \cdots \ge {\lambda }_n\left(R{D}_{\alpha }\left(G\right)\right)$ to the eigenvalues of $R{D}_{\alpha }\left(G\right).$ The maximum eigenvalue ${\lambda }_1\left(R{D}_{\alpha }\left(G\right)\right)$ is called the spectral radius of the matrix $R{D}_{\alpha }\left(G\right)$, denoted by $\rho \left(R{D}_{\alpha }\left(G\right)\right)$.

This paper is organized as follows. In Section 2, we give some definitions, notations, and lemmas of generalized reciprocal distance matrix. In Section 3, we give the upper and lower bounds of the spectral radius of the generalized reciprocal distance matrix $R{D}_{\alpha }\left(G\right)$ by using the reciprocal distance degree and the second reciprocal distance degree. In Section 4, we give the bounds of the spectral radius of the generalized reciprocal distance matrix of $L\left(G\right)$, where $L\left(G\right)$ is the line graph of graph G.

2. Lemmas

In this section, we give some definitions, notations, and lemmas to prepare for subsequent proofs.

Definition 3.

Let G be a graph with $V\left(G\right)=\{v_1,v_2,\cdots ,v_n\}$, the reciprocal distance matrix $RD\left(G\right)$ and the reciprocal distance degree sequence $\{R{T}_1,R{T}_2,\cdots ,R{T}_n\}.$ Then the second reciprocal distance degree of a vertex $v_i$, denoted by $T_i$, is given by

$$T_i=\sum _{j=1,j\ne i}^n\frac{1}{d_{i,j}}R{T}_j.$$

Definition 4.

A graph G is called a pseudo k-reciprocal distance degree regular graph if $\frac{T_i}{R{T}_i}=k$ for all $i\in \{1,2,\cdots ,n\}.$

Definition 5.

The Frobenius norm of an $n\times n$ matrix $M=\left(m_{i,j}\right)$ is

$${\parallel M\parallel }_F=\sqrt{\sum _{i=1}^n\sum _{j=1}^n{\left|m_{i,j}\right|}^2}.$$

We recall that, if M is a normal matrix then ${\parallel M\parallel }_F^2={\displaystyle \sum _{i=1}^n}{\left|{\lambda }_i\left(M\right)\right|}^2$ where ${\lambda }_1\left(M\right),\cdots ,{\lambda }_n\left(M\right)$ are the eigenvalues of M. In particular, $\parallel R{D}_{\alpha }{\left(G\right)\parallel }_F^2={\displaystyle \sum _{i=1}^n}\mid {\lambda }_i\left(R{D}_{\alpha }\left(G\right)\right){\mid }^2.$

Lemma 1

([6]). Let G be a graph of order n with reciprocal distance degree sequence $\{R{T}_1,R{T}_2,\cdots ,R{T}_n\}$ and second reciprocal distance degree sequence $\{T_1,T_2,\cdots ,T_n\}$. Then

$$T_1+T_2+\cdots +T_n=R{T}_1^2+R{T}_2^2+\cdots +R{T}_n^2.$$

Lemma 2

(Perron–Frobenius theorem [10]). If A is a non-negative matrix of order n, then its spectral radius $\rho \left(A\right)$ is an eigenvalue of A and it has an associated non-negative eigenvector. Furthermore, if A is irreducible, then $\rho \left(G\right)$ is a simple eigenvalue of A with an associated positive eigenvector.

Lemma 3

([7]). Let G be a graph with $n\ge 2$ vertices and Harary index $H\left(G\right)$. Then

$$\rho \left(R{D}_{\alpha }\left(G\right)\right)\ge \frac{2H\left(G\right)}{n}.$$

The equality holds if and only if G is a reciprocal distance degree regular graph.

Lemma 4

([11]). Let $A=\left(a_{i,j}\right)$ be an $n\times n$ nonnegative matrix with spectral radius $\rho \left(A\right)$ and row sums $S_1\left(A\right),S_2\left(A\right),\cdots ,S_n\left(A\right).$ Then,

$$\underset{1\le i\le n}{min}{S}_i\left(A\right)\le \rho \left(A\right)\le \underset{1\le i\le n}{max}{S}_i\left(A\right).$$

Moreover, if A is an irreducible matrix, then equality holds on either side (and hence both sides) of the equality if and only if all row sums of A are all equal.

Lemma 5

([6]). Let G be a graph on n vertices. Let $R{T}_{max}$ and $R{T}_{min}$ be the maximum and the minimum reciprocal distance degree of G, respectively. Then, for any $v_i\in V\left(G\right)$,

$$2H\left(G\right)+(R{T}_{max}-1)R{T}_i-(n-1)R{T}_{max}\le T_i\le 2H\left(G\right)+(R{T}_{min}-1)R{T}_i-(n-1)R{T}_{min}.$$

Lemma 6

(Cauchy alternating theorem [12]). Let A be a real symmetric matrix of order n and B be a principal submatrix of order m of A. Suppose A has eigenvalues ${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_n$, and B has eigenvalues ${\beta }_1\ge {\beta }_2\ge \cdots \ge {\beta }_m$. Then, for all $k=1,2,\cdots ,m$, ${\lambda }_{n-m+k}\le {\beta }_k\le {\lambda }_k$.

Lemma 7.

Let G be a graph on $n\ge 2$ vertices with $0\le \alpha <1$. The G has exactly two distinct generalized reciprocal distance eigenvalues if and only if G is a complete graph. In particular, $\rho \left(R{D}_{\alpha }\left(K_n\right)\right)=n-1$ and ${\lambda }_i\left(R{D}_{\alpha }\left(K_n\right)\right)=\alpha n-1$ for $i=2,3,\cdots ,n$.

Proof. 

Let $n\ge 2$. Clearly, the spectrum of the generalized reciprocal distance matrix of the complete graph $K_n$ is $\{n-1,{(\alpha n-1)}^{[n-1]}\}$.

Let G be a graph with generalized reciprocal distance matrix $R{D}_{\alpha }\left(G\right)$. If G has exactly two distinct $R{D}_{\alpha }$-eigenvalues, then ${\lambda }_1\left(R{D}_{\alpha }\left(G\right)\right)>{\lambda }_2\left(R{D}_{\alpha }\left(G\right)\right)$. Since G is a connected graph and $R{D}_{\alpha }\left(G\right)$ is an irreducible matrix. Then, from Lemma 2, ${\lambda }_1\left(R{D}_{\alpha }\left(G\right)\right)=\rho \left(R{D}_{\alpha }\left(G\right)\right)$ is the greatest and simple eigenvalue of $R{D}_{\alpha }\left(G\right)$. Thus, the algebraic multiplicity of ${\lambda }_2\left(R{D}_{\alpha }\left(G\right)\right)$ is $n-1$, i.e.,

$${\lambda }_2\left(R{D}_{\alpha }\left(G\right)\right)={\lambda }_3\left(R{D}_{\alpha }\left(G\right)\right)=\cdots ={\lambda }_n\left(R{D}_{\alpha }\left(G\right)\right).$$

(1)

Now, to prove that $G=K_n$, we show that the diameter of G is 1. That is, we prove that G does not contain an shortest path $P_k$, for $k\ge 3$.

We suppose that G contains an induced shortest path $P_k$, $k\ge 3$. Let B be the principal submatrix of $R{D}_{\alpha }\left(G\right)$ indexed by the vertices in $P_k$. Then by Lemma 6, we have

$${\lambda }_i\left(R{D}_{\alpha }\left(G\right)\right)\ge {\lambda }_i\left(B\right)\ge {\lambda }_{i+n-k}\left(R{D}_{\alpha }\left(G\right)\right),i=1,2,\cdots ,k.$$

Using the equalities given in (1), we obtain ${\lambda }_2\left(R{D}_{\alpha }\left(G\right)\right)\ge {\lambda }_2\left(B\right)\ge {\lambda }_3\left(B\right)\ge \cdots \ge {\lambda }_k\left(B\right)\ge {\lambda }_p\left(R{D}_{\alpha }\left(G\right)\right)={\lambda }_2\left(R{D}_{\alpha }\left(G\right)\right).$ Thus, for $k\ge 3$, the matrix $B=\left(R{D}_{\alpha }\left(P_k\right)\right)$ has at most two different eigenvalues. By definition, we can get the generalized reciprocal distance matrix of $P_3$, that is

$$R{D}_{\alpha }\left(P_3\right)=\left[\begin{array}{ccc}\frac{3}{2}\alpha & 1-\alpha & \frac{1}{2}(1-\alpha )\\ 1-\alpha & 2(1-\alpha )& 1-\alpha \\ \frac{1}{2}(1-\alpha )& 1-\alpha & \frac{3}{2}\alpha \end{array}\right].$$

Using the software Maple 18, it is easy to calculate that the generalized reciprocal distance spectrum of the path of order 3 is $\{\frac{3}{2}\alpha +\frac{1}{4}+\frac{1}{4}\sqrt{36{\alpha }^2-68\alpha +33},\frac{3}{2}\alpha +\frac{1}{4}-\frac{1}{4}\sqrt{36{\alpha }^2-68\alpha +33},2\alpha -\frac{1}{2}\}$, this is false.

Therefore, G does not have two vertices at distance two or more. Then, $G=K_n$. □

Lemma 8

([13]). If $x_1\ge x_2\ge \cdots \ge x_m$ are real numbers such that ${\displaystyle \sum _{i=1}^m}{x}_i=0$, then

$$x_1\le \sqrt{\frac{m-1}{m}\sum _{i=1}^m{x}_i^2}.$$

The equality holds if and only if $x_2=x_3=\cdots =x_m=-\frac{x_1}{m-1}$.

Lemma 9

(Rayleigh quotient theorem [14]). let M be a real symmetric matrix of order n whose eigenvalues are ${\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_n$. Then, for any n-dimensional nonzero column vector x,

$${\lambda }_1\ge \frac{x^{T}Mx}{x^{T}x}\ge {\lambda }_n.$$

Lemma 10

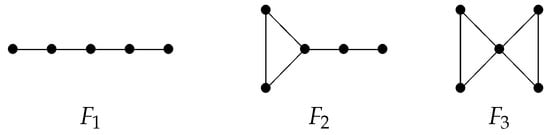
([15]). If $diam\left(G\right)\le 2$ and if none of the three graphs $F_1$, $F_2$, and $F_3$ depicted in Figure 1 are induced subgraphs of G, then $diam\left(L\right(G\left)\right)\le 2$.

Figure 1. Graphs $F_1$, $F_2$, $T_3$ in Lemma 10.

3. Bounds of $\mathit{\rho }\left({\mathit{RD}}_{\mathit{\alpha }}\left(\mathit{G}\right)\right)$ of Graphs

In this section, we find bounds of the spectral radius of generalizes reciprocal distance matrix in terms of parameters associated with the structure of the graph.

Let $\mathbf{e}$ be the n-dimensional vector of ones.

Theorem 1.

Let G be a graph with reciprocal distance degree sequence $\{R{T}_1,R{T}_2,\cdots ,R{T}_n\}$. Then

$$\rho \left(R{D}_{\alpha }\left(G\right)\right)\ge \sqrt{\frac{R{T}_1^2+R{T}_2^2+\cdots +R{T}_n^2}{n}}.$$

The equality holds if and only if G is a reciprocal distance degree regular graph.

Proof. 

Let $\mathbf{x}={[x_1,x_2,\cdots ,x_n]}^T$ be the unit positive Perron eigenvector of $R{D}_{\alpha }\left(G\right)$ corresponding to $\rho \left(R{D}_{\alpha }\left(G\right)\right)$. We take the unit vector $\mathbf{y}=\frac{1}{\sqrt{n}}\mathbf{e}$. Then, we have

$$\begin{array}{cc}\hfill \rho \left(R{D}_{\alpha }\left(G\right)\right)& =\sqrt{{\rho }^2\left(R{D}_{\alpha }\left(G\right)\right)}=\sqrt{{\mathbf{x}}^T{\left(R{D}_{\alpha }\left(G\right)\right)}^2\mathbf{x}}\ge \sqrt{{\mathbf{y}}^T{\left(R{D}_{\alpha }\left(G\right)\right)}^2\mathbf{y}}.\hfill \end{array}$$

(2)

Since $\left(R{D}_{\alpha }\left(G\right)\right)\mathbf{y}=\frac{1}{\sqrt{n}}{[R{T}_1,R{T}_2,\cdots ,R{T}_n]}^T$, we obtain

$${\mathbf{y}}^T{\left(R{D}_{\alpha }\left(G\right)\right)}^2\mathbf{y}=\frac{R{T}_1^2+R{T}_2^2+\cdots +R{T}_n^2}{n}.$$

Therefore,

$$\rho \left(R{D}_{\alpha }\left(G\right)\right)\ge \sqrt{\frac{R{T}_1^2+R{T}_2^2+\cdots +R{T}_n^2}{n}}.$$

Now, assume that the equality holds. By Equation (2), we have that $\mathbf{y}$ is the positive eigenvector corresponding to $\rho \left(R{D}_{\alpha }\left(G\right)\right)$. From $R{D}_{\alpha }\left(G\right)\mathbf{y}=\rho \left(R{D}_{\alpha }\left(G\right)\right)\mathbf{y}$, we obtain that $R{T}_i=\rho \left(R{D}_{\alpha }\left(G\right)\right)$, for $i=1,2,\cdots ,n$. Therefore, graph G is a reciprocal distance degree regular graph.

Conversely, if G is a reciprocal distance degree regular graph, then $R{T}_1=R{T}_2=\cdots =R{T}_n=k$. From Lemma 2, $k=\rho \left(R{D}_{\alpha }\left(G\right)\right)$. So

$$\rho \left(R{D}_{\alpha }\left(G\right)\right)=k=\sqrt{\frac{n{k}^2}{n}}=\sqrt{\frac{R{T}_1^2+R{T}_2^2+\cdots +R{T}_n^2}{n}}.$$

The equality holds. □

Theorem 2.

Let G be a graph with reciprocal distance degree sequence $\{R{T}_1,R{T}_2,\cdots ,R{T}_n\}$ and second reciprocal distance degree sequence $\{T_1,T_2,\cdots ,T_n\}$. Then

$$\rho \left(R{D}_{\alpha }\left(G\right)\right)\ge \sqrt{\frac{{(\alpha R{T}_1^2+(1-\alpha )T_1)}^2+{(\alpha R{T}_2^2+(1-\alpha )T_2)}^2+\cdots +{(\alpha R{T}_n^2+(1-\alpha )T_n)}^2}{{\displaystyle \sum _{i=1}^n}R{T}_i^2}}.$$

The equality holds if and only if G is a pseudo reciprocal distance degree regular graph.

Proof. 

Using $\mathbf{y}=\frac{1}{\sqrt{{\displaystyle \sum _{i=1}^n}R{T}_i^2}}{[R{T}_1,R{T}_2,\cdots ,R{T}_n]}^T$, the proof is similar to Theorem 1. □

Remark 1.

The lower bound given in Theorem 2 improves the bound given in Theorem 1, and the bound given in Theorem 1 improves the bound given in Lemma 3.

In fact, from Lemma 1, we have ${\displaystyle \sum _{i=1}^n}{T}_i={\displaystyle \sum _{i=1}^n}R{T}_i^2.$ By Cauchy–Schwarz inequality

$$\begin{array}{cc}\hfill n\sum _{i=1}^n{(\alpha R{T}_i^2+(1-\alpha )T_i)}^2& \ge {\left(\sum _{i=1}^n(\alpha R{T}_i^2+(1-\alpha )T_i)\right)}^2\hfill \\ & ={(\alpha \sum _{i=1}^{n}R{T}_i^2+(1-\alpha )\sum _{i=1}^n{T}_i)}^2\hfill \\ & ={(\alpha \sum _{i=1}^{n}R{T}_i^2+(1-\alpha )\sum _{i=1}^{n}R{T}_i^2)}^2\hfill \\ & ={\left(\sum _{i=1}^{n}R{T}_i^2\right)}^2.\hfill \end{array}$$

Moreover, we recall that, $n{\displaystyle \sum _{i=1}^n}R{T}_i^2\ge {\left({\displaystyle \sum _{i=1}^n}R{T}_i\right)}^2$. Thus

$$\sqrt{\frac{{\displaystyle \sum _{i=1}^n}{(\alpha R{T}_i^2+(1-\alpha )T_i)}^2}{{\displaystyle \sum _{i=1}^n}R{T}_i^2}}\ge \sqrt{\frac{{\left({\displaystyle \sum _{i=1}^n}R{T}_i^2\right)}^2}{n{\displaystyle \sum _{i=1}^n}R{T}_i^2}}=\sqrt{\frac{{\displaystyle \sum _{i=1}^n}R{T}_i^2}{n}}$$

and

$$\sqrt{\frac{{\displaystyle \sum _{i=1}^n}R{T}_i^2}{n}}\ge \sqrt{\frac{{\left({\displaystyle \sum _{i=1}^n}R{T}_i\right)}^2}{n^2}}=\frac{2H\left(G\right)}{n}.$$

Theorem 3.

Let G be a graph with reciprocal distance degree sequence $\{R{T}_1,R{T}_2,\cdots ,R{T}_n\}$ and second reciprocal distance degree sequence $\{T_1,T_2,\cdots ,T_n\}$. Then

$$\underset{1\le i\le n}{min}\left\{\sqrt{(1-\alpha )T_i+\alpha {\left(R{T}_i\right)}^2}\right\}\le \rho \left(R{D}_{\alpha }\left(G\right)\right)\le \underset{1\le i\le n}{max}\left\{\sqrt{(1-\alpha )T_i+\alpha {\left(R{T}_i\right)}^2}\right\}.$$

Proof. 

Let $R{D}_{\alpha }\left(G\right)=\left(b_{i,j}\right)$. Then ${\left(R{D}_{\alpha }\left(G\right)\right)}_{i,j}^2={\displaystyle \sum _{k=1}^n}{b}_{i,k}{b}_{k,j}$, and the row sum of ${\left(R{D}_{\alpha }\left(G\right)\right)}^2$ should be

$$S_i\left({\left(R{D}_{\alpha }\left(G\right)\right)}^2\right)=\sum _{j=1}^n\sum _{k=1}^n{b}_{i,k}{b}_{k,j}=\sum _{k=1}^n\left(b_{i,k}\sum _{j=1}^n{b}_{k,j}\right)=\sum _{k=1}^n\left(b_{i,k}R{T}_k\right).$$

Hence, $S_i\left({\left(R{D}_{\alpha }\left(G\right)\right)}^2\right)=(1-\alpha )T_i+\alpha R{T}_i^2.$

Now, let $\mathbf{x}$ be the unit Perron vector corresponding to $\rho \left(R{D}_{\alpha }\left(G\right)\right)$. Clearly, $R{D}_{\alpha }\left(G\right)\mathbf{x}=\rho \left(R{D}_{\alpha }\left(G\right)\right)\mathbf{x}$ and ${\left(R{D}_{\alpha }\left(G\right)\right)}^2\mathbf{x}={\left(\rho \left(R{D}_{\alpha }\left(G\right)\right)\right)}^2\mathbf{x}$. By Lemma 4, we have

$$\underset{1\le i\le n}{min}\left\{(1-\alpha )T_i+\alpha {\left(R{T}_i\right)}^2\right\}\le {\left(\rho \left(R{D}_{\alpha }\left(G\right)\right)\right)}^2\le \underset{1\le i\le n}{max}\left\{(1-\alpha )T_i+\alpha {\left(R{T}_i\right)}^2\right\}.$$

Thus

$$\underset{1\le i\le n}{min}\left\{\sqrt{(1-\alpha )T_i+\alpha {\left(R{T}_i\right)}^2}\right\}\le \rho \left(R{D}_{\alpha }\left(G\right)\right)\le \underset{1\le i\le n}{max}\left\{\sqrt{(1-\alpha )T_i+\alpha {\left(R{T}_i\right)}^2}\right\}.$$

□

Theorem 4.

Let G be a graph with n vertices, $R{T}_{max}$ and $T_{max}$ be the maximum reciprocal distance degree and the maximum second reciprocal distance degree of G, respectively. Then

$$\rho \left(R{D}_{\alpha }\left(G\right)\right)\le \frac{\alpha R{T}_{max}+\sqrt{{\left(\alpha R{T}_{max}\right)}^2+4(1-\alpha )T_{max}}}{2}.$$

The equality holds if and only if G is a reciprocal distance degree regular graph.

Proof. 

Since $R{D}_{\alpha }\left(G\right)=\alpha RT\left(G\right)+(1-\alpha )RD\left(G\right),0\le \alpha \le 1$, it can be obtained by simple calculation

$$S_i\left(R{D}_{\alpha }\left(G\right)\right)=R{T}_i,$$

$$S_i\left({\left(RT\left(G\right)\right)}^2\right)=S_i\left(RT\left(G\right)RD\left(G\right)\right)=R{T}_i^2,$$

$$S_i\left({\left(RD\left(G\right)\right)}^2\right)=S_i\left(RD\left(G\right)RT\left(G\right)\right)=T_i.$$

Then

$$\begin{array}{cc}\hfill S_i\left({\left(R{D}_{\alpha }\left(G\right)\right)}^2\right)=& S_i({\alpha }^2{\left(RT\left(G\right)\right)}^2+\alpha (1-\alpha )RT\left(G\right)RD\left(G\right)\hfill \\ & +\alpha (1-\alpha )RD\left(G\right)RT\left(G\right)+{(1-\alpha )}^{2}RD{\left(G\right)}^2)\hfill \\ \hfill =& S_i\left(\alpha RT\left(G\right)(\alpha RT\left(G\right)+(1-\alpha )RD\left(G\right))\right)\hfill \\ & +\alpha (1-\alpha )S_i\left(RD\left(G\right)RT\left(G\right)\right)+{(1-\alpha )}^2{S}_i\left(RD{\left(G\right)}^2\right)\hfill \\ \hfill =& \alpha R{T}_i{S}_i\left(R{D}_{\alpha }\left(G\right)\right)+(1-\alpha )T_i\hfill \\ \hfill \le & \alpha R{T}_{max}{S}_i\left(R{D}_{\alpha }\left(G\right)\right)+(1-\alpha )T_{max},\hfill \end{array}$$

that is,

$$S_i({\left(R{D}_{\alpha }\left(G\right)\right)}^2-\alpha R{T}_{max}R{D}_{\alpha }\left(G\right))\le (1-\alpha )T_{max}.$$

By Lemma 4,

$${\rho }^2\left(R{D}_{\alpha }\left(G\right)\right)-\alpha R{T}_{max}\rho \left(R{D}_{\alpha }\left(G\right)\right)-(1-\alpha )T_{max}\le 0.$$

For any vertex $v_i$, when the inequality is equal, $R{T}_i=R{T}_{max}$, $T_i=T_{max}$. That is, G is a reciprocal distance degree regular graph.

On the contrary, when G is a reciprocal distance degree regular graph, the inequality is equal. □

Theorem 5.

Let G be a graph with n vertices, $R{T}_{min}$ and $T_{min}$ be the minimum reciprocal distance degree and the minmum second reciprocal distance degree of G, respectively. Then

$$\rho \left(R{D}_{\alpha }\left(G\right)\right)\ge \frac{\alpha R{T}_{min}+\sqrt{{\left(\alpha R{T}_{min}\right)}^2+4(1-\alpha )T_{min}}}{2}.$$

The equality holds if and only if G is a reciprocal distance degree regular graph.

Proof. 

The method is the same as Theorem 4. □

Theorem 6.

Let G be a graph with reciprocal distance degree sequence $\{R{T}_1,R{T}_2,\cdots ,R{T}_n\}$ and second reciprocal distance degree sequence $\{T_1,T_2,\cdots ,T_n\}$. Then

$$\begin{array}{cc}\hfill & \rho \left(R{D}_{\alpha }\left(G\right)\right)\le \underset{1\le i,j\le n}{max}\left\{\frac{\alpha (R{T}_i+R{T}_j)+\sqrt{{\alpha }^2{(R{T}_i-R{T}_j)}^2+4{(1-\alpha )}^2\frac{T_i{T}_j}{R{T}_{i}R{T}_j}}}{2}\right\}.\hfill \end{array}$$

(3)

The equality holds if and only if G is a reciprocal distance degree regular graph.

Proof. 

Let $\mathbf{x}=(x_1,x_2,\cdots ,x_n)$ be the eigenvector corresponding to the eigenvalue $\rho \left(G\right)$ of the matrix $RT{\left(G\right)}^{-1}R{D}_{\alpha }\left(G\right)RT\left(G\right)$, $x_s=max\left\{x_i\right|i=1,2,\cdots ,n\}$, $x_t=max\left\{x_i\right|x_i\ne x_s,i=1,2,\cdots ,n\}$.

Through simple calculation, the value of the $(i,j)$-th element of $RT{\left(G\right)}^{-1}R{D}_{\alpha }\left(G\right)RT\left(G\right)$ is

$$\left\{\begin{array}{cc}\alpha R{T}_i,\hfill & \mathrm{if}i=j,\hfill \\ (1-\alpha )\frac{R{T}_j}{R{T}_i}\frac{1}{d_{ij}},\hfill & \mathrm{if}i\ne j.\hfill \end{array}\right.$$

Because

$$RT{\left(G\right)}^{-1}R{D}_{\alpha }\left(G\right)RT\left(G\right)\mathbf{x}=\rho \left(R{D}_{\alpha }\left(G\right)\right)\mathbf{x},$$

(4)

row s and t in Equation (4) are

$$\rho \left(R{D}_{\alpha }\left(G\right)\right)x_s=\alpha R{T}_s{x}_s+(1-\alpha )\sum _{i=1}^n\frac{R{T}_i}{R{T}_s}\frac{x_i}{d_{si}},$$

(5)

$$\rho \left(R{D}_{\alpha }\left(G\right)\right)x_t=\alpha R{T}_t{x}_t+(1-\alpha )\sum _{i=1}^n\frac{R{T}_i}{R{T}_t}\frac{x_i}{d_{ti}}.$$

(6)

After shifting the item of Equations (5) and (6), we can get

$$\begin{array}{cc}\hfill \left(\rho (R{D}_{\alpha }\left(G\right)-\alpha R{T}_s)\right)x_s& =(1-\alpha )\sum _{i=1}^n\frac{R{T}_i}{R{T}_s}\frac{x_i}{d_{si}}\hfill \\ \hfill & \le (1-\alpha )\frac{x_t}{R{T}_s}\sum _{i=1}^{n}R{T}_i\frac{1}{d_{si}}\hfill \\ \hfill & =(1-\alpha )\frac{T_s}{R{T}_s}{x}_t,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \left(\rho (R{D}_{\alpha }\left(G\right)-\alpha R{T}_t)\right)x_t& =(1-\alpha )\sum _{i=1}^n\frac{R{T}_i}{R{T}_t}\frac{x_i}{d_{ti}}\hfill \\ \hfill & \le (1-\alpha )\frac{x_s}{R{T}_t}\sum _{i=1}^{n}R{T}_i\frac{1}{d_{ti}}\hfill \\ \hfill & =(1-\alpha )\frac{T_t}{R{T}_t}{x}_s.\hfill \end{array}$$

(8)

Multiply Equation (7) and (8) to simplify $(\rho (R{D}_{\alpha }\left(G\right)-\alpha R{T}_s)(\rho (R{D}_{\alpha }\left(G\right)-\alpha R{T}_t)x_s{x}_t\le {(1-\alpha )}^2\frac{T_s{T}_t}{R{T}_{s}R{T}_t}{x}_t{x}_s$. Then

$$(\rho {\left(R{D}_{\alpha }\left(G\right)\right)}^2-\alpha (R{T}_s+R{T}_t)\rho \left(R{D}_{\alpha }\left(G\right)\right)+{\alpha }^{2}R{T}_{s}R{T}_t-{(1-\alpha )}^2\frac{T_s{T}_t}{R{T}_{s}R{T}_t}\le 0.$$

$$\rho \left(R{D}_{\alpha }\left(G\right)\right)\le \frac{\alpha (R{T}_s+R{T}_t)+\sqrt{{\alpha }^2{(R{T}_s-R{T}_t)}^2+4{(1-\alpha )}^2\frac{T_s{T}_t}{R{T}_{s}R{T}_t}}}{2}.$$

Hence

$$\rho \left(R{D}_{\alpha }\left(G\right)\right)\le \underset{1\le i,j\le n}{max}\left\{\frac{\alpha (R{T}_i+R{T}_j)+\sqrt{{\alpha }^2{(R{T}_i-R{T}_j)}^2+4{(1-\alpha )}^2\frac{T_i{T}_j}{R{T}_{i}R{T}_j}}}{2}\right\}.$$

Suppose G is a k-reciprocal distance regular graph, $R{T}_i=k,T_i=k^2,i=1,2,\cdots ,n$. According to Lemma 2, $\rho \left(R{D}_{\alpha }\left(G\right)\right)=k$, so Equation (3) holds. On the contrary, if inequality (3) is equal, $x_1=x_2=\cdots =x_n$ can be obtained from (7) and (8), that is, $\rho \left(R{D}_{\alpha }\left(G\right)\right)=\alpha R{T}_1+(1-\alpha )\frac{T_1}{R{T}_1}=\alpha R{T}_2+(1-\alpha )\frac{T_2}{R{T}_2}=\cdots =\alpha R{T}_n+(1-\alpha )\frac{T_n}{R{T}_n}$, which means that G is a reciprocal distance degree regular graph. □

Theorem 7.

Let G be a graph with reciprocal distance degree sequence $\{R{T}_1,R{T}_2,\cdots ,R{T}_n\}$ and second reciprocal distance degree sequence $\{T_1,T_2,\cdots ,T_n\}$. Then

$$\rho \left(R{D}_{\alpha }\left(G\right)\right)\ge \underset{1\le i,j\le n}{min}\left\{\frac{\alpha (R{T}_i+R{T}_j)+\sqrt{{\alpha }^2{(R{T}_i-R{T}_j)}^2+4{(1-\alpha )}^2\frac{T_i{T}_j}{R{T}_{i}R{T}_j}}}{2}\right\}.$$

The equality holds if and only if G is a reciprocal distance degree regular graph.

Proof. 

The method is the same as Theorem 6. □

Theorem 8.

Let G be a graph of order n and $0\le \alpha <1$, then

$$\rho \left(R{D}_{\alpha }\left(G\right)\right)\le \frac{2\alpha H\left(G\right)}{n}+\sqrt{\frac{n-1}{n}(\parallel R{D}_{\alpha }\left(G\right){\parallel }_F^2-\frac{{\left(2\alpha H\left(G\right)\right)}^2}{n})}.$$

The equality holds if and only if $G=K_n$.

Proof. 

We recall that ${\displaystyle \sum _{i=1}^n}{\lambda }_i\left(R{D}_{\alpha }\left(G\right)\right)=\alpha {\displaystyle \sum _{i=1}^n}R{T}_i=2\alpha H\left(G\right)$, and ${\displaystyle \sum _{i=1}^n}{\lambda }_i{\left(R{D}_{\alpha }\left(G\right)\right)}^2={\parallel R{D}_{\alpha }\left(G\right)\parallel }_F^2$. Clearly,

$${\displaystyle \sum _{i=1}^n}({\lambda }_i\left(R{D}_{\alpha }\left(G\right)\right)-\frac{2\alpha H\left(G\right)}{n})=0.$$

By Lemma 8,

$$\rho \left(R{D}_{\alpha }\left(G\right)\right)-\frac{2\alpha H\left(G\right)}{n}\le \sqrt{\frac{n-1}{n}{\displaystyle \sum _{i=1}^n}{({\lambda }_i\left(R{D}_{\alpha }\left(G\right)\right)-\frac{2\alpha H\left(G\right)}{n})}^2},$$

(9)

with equality holds if and only if

$$\begin{array}{cc}\hfill {\lambda }_2\left(R{D}_{\alpha }\left(G\right)\right)-\frac{2\alpha H\left(G\right)}{n}& =\cdots ={\lambda }_n\left(R{D}_{\alpha }\left(G\right)\right)-\frac{2\alpha H\left(G\right)}{n}=-\frac{\rho \left(R{D}_{\alpha }\left(G\right)\right)-\frac{2\alpha H\left(G\right)}{n}}{n-1}.\hfill \end{array}$$

(10)

Since

$$\begin{array}{cc}\hfill \sum _{i=1}^n{({\lambda }_i\left(R{D}_{\alpha }\left(G\right)\right)-\frac{2\alpha H\left(G\right)}{n})}^2& =\sum _{i=1}^n{\left({\lambda }_i\left(R{D}_{\alpha }\left(G\right)\right)\right)}^2-\frac{4\alpha H\left(G\right)}{n}\sum _{i=1}^n{\lambda }_i\left(R{D}_{\alpha }\left(G\right)\right)+n{(\frac{2\alpha H\left(G\right)}{n})}^2\hfill \\ & =\parallel R{D}_{\alpha }{\left(G\right)\parallel }_F^2-2\frac{{\left(2\alpha H\left(G\right)\right)}^2}{n}+\frac{{\left(2\alpha H\left(G\right)\right)}^2}{n}\hfill \\ & =\parallel R{D}_{\alpha }{\left(G\right)\parallel }_F^2-\frac{{\left(2\alpha H\left(G\right)\right)}^2}{n}.\hfill \end{array}$$

The upper bound (9) is equivalent to

$$\rho \left(R{D}_{\alpha }\left(G\right)\right)\le \frac{2\alpha H\left(G\right)}{n}+\sqrt{\frac{n-1}{n}(\parallel R{D}_{\alpha }\left(G\right){\parallel }_F^2-\frac{{\left(2\alpha H\left(G\right)\right)}^2}{n})}$$

(11)

with the necessary and sufficient condition for the equality given in (10).

Now, suppose that the equality holds. Therefore, the equality condition for (11) can be given in (10), and we obtain that G has only two distinct generalized reciprocal distance eigenvalues. Hence, from Lemma 7, $G=K_n$.

Conversely, from Lemma 7 the generalized reciprocal distance eigenvalues of $K_n$ are $\rho (R{D}_{\alpha }\left(K_n\right)=n-1$ and ${\lambda }_i\left(R{D}_{\alpha }\left(G\right)\right)=\alpha n-1$, for $i=2,3,\cdots ,n$. Then, the equality holds. □

4. Bounds of $\mathit{\rho }\left({\mathit{RD}}_{\mathit{\alpha }}\left(\mathit{G}\right)\right)$ of Line Graph $\mathit{L}\left(\mathit{G}\right)$

The line graph $L\left(G\right)$ of G is the graph whose vertices correspond to the edges of G, and two vertices of $L\left(G\right)$ are adjacent if and only if the corresponding edges of G are adjacent. In this section, we give the bounds of the spectral radius of the generalized reciprocal distance matrix of $L\left(G\right)$.

Theorem 9.

Let graph G have n vertices and m edges, and the degree of vertex $v_i$ be recorded as $d_i$. If $diam\left(G\right)\le 2$ and graphs $F_i$, $i=1,2,3$ in Lemma 10 are not induced subgraphs of G, then

$$\rho \left(R{D}_{\alpha }\left(L\left(G\right)\right)\right)\ge \frac{\frac{1}{2}(m^2-3m+{\displaystyle \sum _{i=1}^n}{d}_i^2)}{m}.$$

Proof. 

If $diam\left(G\right)\le 2$, the i-th row element of $R{D}_{\alpha }\left(G\right)$ is composed of $\{\frac{1}{2}\alpha (n+d_i-1),{(1-\alpha )}^{d_i},\frac{1}{2}{(1-\alpha )}^{[n-d_i-1]}\}$, which can be obtained from Lemma 9

$$\rho \left(R{D}_{\alpha }\left(L\left(G\right)\right)\right)\ge \frac{{\mathbf{e}}^{T}R{D}_{\alpha }\left(G\right)\mathbf{e}}{{\mathbf{e}}^T\mathbf{e}}=\frac{{\displaystyle \sum _{i=1}^n}(\frac{1}{2}n+d_i-1)}{n}=\frac{\frac{1}{2}(n^2+2m-n)}{n}.$$

Hence, line graph $L\left(G\right)$ has $n_1=m$ vertices and $m_1=\frac{1}{2}{\displaystyle \sum _{i=1}^n}{d}_i^2-m$ edges. Because graphs $F_i$, $i=1,2,3$ are not induced subgraphs of G, from Lemma 10, $diam\left(L\right(G\left)\right)\le 2$, then

$$\begin{array}{cc}\hfill \rho \left(R{D}_{\alpha }\left(L\left(G\right)\right)\right)& \ge \frac{\frac{1}{2}(n_1^2+2m_1-n_1)}{n_1}\hfill \\ & =\frac{\frac{1}{2}[m^2+2(\frac{1}{2}{\displaystyle \sum _{i=1}^n}{d}_i^2-m)-m]}{m}\hfill \\ & =\frac{\frac{1}{2}(m^2-3m+{\displaystyle \sum _{i=1}^n}{d}_i^2)}{m}.\hfill \end{array}$$

□

Theorem 10.

Let graph G be r-regular graph with n vertices, and graphs $F_i$, $i=1,2,3$ be not-induced subgraphs of G. Then

$$\rho \left(R{D}_{\alpha }\left(L\left(G\right)\right)\right)\ge \frac{nr}{4}+r-3.$$

Proof. 

Let graph G be r-regular graph with n vertices, the number of edges in graph G is $m=\frac{nr}{2}$, $d_i=deg\left(v_i\right)=r$. It is proved by Theorem 9. □

Theorem 11.

Let the vertices set and edges set of G be $V\left(G\right)=\{v_1,v_2,\cdots ,v_n\}$ and $E\left(G\right)=\{e_1,e_2,\cdots ,e_m\}$, $deg\left(e_i\right)$ represent the number of edges adjacent to edge $e_i$. Then,

$$\rho (R{D}_{\alpha }(L\left(G\right))\le \underset{1\le i\le m}{max}\left\{\frac{1}{2}(m-deg\left(e_i\right)-1)\right\}.$$

Proof. 

Let $e=uv$ be an edge of G. Then, the degree of vertex $e\in V\left(L\right(G\left)\right)$ is $de{g}_{L\left(G\right)}\left(e\right)=de{g}_G\left(u\right)+de{g}_G\left(v\right)-2.$

In graph G, if edge $e=uv$ is adjacent to $deg\left(u\right)+deg\left(v\right)-2=deg(e$), then denoted $|E_e|=m-1-deg\left(e\right)$ as the number of edges which are not adjacent to edge e. Therefore, in the graph $L\left(G\right)$, there are $|E_e|$ vertices, and their distance from vertex e is greater than 1. Thus, the maximum element of generalized reciprocal distances matrix of the corresponding vertices should be $\frac{1}{2}(1-\alpha )$. We can get

$$\begin{array}{cc}\hfill S_i\left(R{D}_{\alpha }\left(L\left(G\right)\right)\right)& \le \frac{1}{2}(1-\alpha )(m-1-deg\left(e_i\right))\hfill \\ & +(1-\alpha )deg\left(e_i\right)+\alpha (\frac{1}{2}m-\frac{1}{2}+\frac{1}{2}deg\left(e_i\right))\hfill \\ & =\frac{1}{2}(m-deg\left(e_i\right)-1).\hfill \end{array}$$

By Lemma 4, $\rho \left(R{D}_{\alpha }\left(L\left(G\right)\right)\right)\le \underset{1\le i\le m}{max}\left\{\frac{1}{2}(m-deg\left(e_i\right)-1)\right\}.$ □

5. Conclusions

In this paper, we find some bounds for the spectral radius of the generalized reciprocal distance matrix of a simple undirected connected graph G, and we also give the generalized reciprocal distance spectral radius of line graph L(G). The graphs for which those bounds are attained are characterized.