Abstract
Safety assessment of modern critical instrumentation and control systems is a complicated process considerably dependent on expert techniques, single/multiple faults consideration scope, other assumptions, invoked limitations, and support tools used during the assessment process. Ignoring these assumptions, as well as the significance of expert and tool influence, could lead to such effects as functional safety underestimation or overestimation in such a manner that functional safety assessment correctness and accuracy are affected. This paper introduces XMECA (x modes, effects, and criticality analysis, where x could be from different known techniques and domains—failures in functional safety, vulnerabilities and intrusions regarding cybersecurity, etc.) as a key technique of safety assessment. To verify the results obtained as XMECA deliverables, expert and uncertainty modes, effects, and criticality analysis (EUMECA) is performed, in particular focusing on decisions and judgments made by experts. Scenarios for processing verbal and quantitative information of XMECA tables from experts are offered. A case study of a possible functional safety assessment approach that considers the above-mentioned techniques and a supporting tool is provided. To assess the trustworthiness of safety analysis and estimation using XMECA, a set of the metrics is suggested. Features of adapting the suggested method for security assessment considering intrusions, vulnerabilities, and effects analysis (IMECA technique) are discussed.
MSC:
00A06
1. Introduction
1.1. Motivation
Safety assessment was not a trivial task in the past, but, nowadays, safety assessment challenges are significantly increased. These challenges, among other factors, result from the complexity of modern electronic systems comprising thousands of components, as well as the control platforms on which they are built [1].
Such systems and platforms comprise hundreds of documents (standards, specifications, project, verification, and validation documents and artifacts, etc.) to be analyzed by experts during safety assessment [2], giving rise to dependence on expert judgments.
The range of possible failure causes is extended due to the extensive utilization of complex electronic components, such as microprocessors and FPGA: such components are subject to hardware and software failures that should be considered during the assessment process [3]. Besides, an additional challenge is caused by the vulnerability of software and hardware components and threats of intrusions and cyber-attacks, which can be reasons for failures and blocking of performance as well [4].
As a response to the above-mentioned challenges, regulatory bodies and auditing authorities are constantly making safety requirements more exacting, in such a manner turning the assessment process into a more time- and resource-consuming activity.
Another challenge is related to the existence of a variety of safety assessment approaches and their modifications (including techniques for safety constituents, such as functional safety, cybersecurity, etc.). There are many assessment techniques (FMECA—failure modes, effects, and criticality analysis, FTA—fault tree analysis, HAZOP—hazard and operability study, HAZID—hazard identification study [5,6,7]) that can be applied separately and jointly to guarantee the trustworthiness of results. Besides, there is a problem of incompatibility and inconsistency of their outputs in the general case [8], etc.
Traditional approaches cannot be directly implied as they were not designed for complex systems incorporating a huge variety of new failure types, and, hence, they are becoming too time- and resource-consuming or even absolutely unsuitable for performing trustworthy assessment. Therefore, modifications aiming to support the safety assessment process are essential. However, simple modifications allow for solving only some tasks; for strategic ones, a new assessment platform is needed.
It is noteworthy that FMECA, among other techniques, has gained widespread attention due to its visibility and simplicity, and, to this point, it is being extensively used in various industries [9]. Therefore, regarding this method and its modifications precisely, it would be beneficial to choose it as a basis for a safety assessment orchestration platform.
In this paper, XMECA is presented as an attempt to provide such a platform that allows using different assessment techniques and has possibilities to process and evaluate expert judgments to ensure trustworthy safety assessment.
1.2. State of the Art
Failure modes, effects, and criticality analysis (FMECA) is one of the techniques for quantitative analysis of the risks recommended by the IEC/ISO 31010:2019 guidelines [10]. FMECA is a method of determining the failure types and high-level assessment of their impact on performance and the level of effects criticality. A feature of the method is the systematic and semi-formal approach, while practicality is in determining the impact of failures on the product (software, hardware, subsystem, system) or process. Some FMECA standards define not only FMECA implementation procedures but also the way they fit into overall safety assessment processes [11].
Applications of the FMECA technique nowadays are really wide and impressive: it is being used in radiotherapy [12], there are successful cases of application to cyber–physical systems [13], power electronic-based power systems [14], heating, ventilation, and air conditioning (HVAC) systems in railways [15]. FMECA could also be usefully performed on a mass vaccination process to help identify potential failures [16], as well as be used as a simple, powerful, and useful tool for quick identification of criticality in a clinical laboratory process [17].
In addition to ‘pure’ FMECA usage, it is being increasingly used in combination with other techniques. In Ref. [18], the system functional modeling, the failure propagation analysis, FMECA, and FTA are combined for ship complex systems assessment. The authors of Ref. [19] combine FMECA with the entropy and best worst method (BWM), EDAS, and system dynamics. An example of effective usage of FMECA, used along with safety block diagrams, preliminary hazard analysis, is shown in Ref. [20].
A combination of FMECA and FTA methods was successfully employed to assess the safety and reliability in the maritime sector [21]. Integrating systems theoretic process analysis with FMECA is suitable for hazard analysis and risk assessment and generation of safety requirements of modern software-intensive, complex safety-critical systems for road vehicles [22]. Research [23] highlights that condensation of several risk factors into one variable, the RPN (risk priority number), used in traditional FMECA, neglects a great deal of information; therefore, the PRISM method and some of its possible aggregation functions are presented to be more suitable for risk evaluation and prioritization in different cases.
Another modification of the FMECA model for risk analysis is proposed in Ref. [9] by using an integrated approach, which introduces Z-number, rough number, the decision-making trial, and evaluation laboratory method. Moreover, an interval-based extension of the elimination and choice translating reality (ELECTRE) TRI method is proposed in Ref. [24] for the classification of failure modes into risk categories to consider the vagueness and uncertainty of the FMECA evaluation process. In Ref. [25], it is stated that assessing the likelihood of failure, severity level, and detection rate provides a more reliable perspective for prioritizing failure modes as an adjunct to the “classic” addressing the severity of failure modes approach. The methodology proposed in Ref. [26] simplifies FMECA by automatic analysis of the effects of different faults and identifying the critical faults at the system level.
One of the modifications of FMECA is IMECA, which follows a similar procedure but aims to assess information security or cybersecurity. IMECA is based on chains “threat—vulnerability—attack/intrusion, effects, assessment of criticality in terms of violation of the cybersecurity properties (confidentiality, integrity, accessibility), and, under certain conditions, functional security as well [27,28,29]. A unified approach combining FMECA, IMECA, and other assessment methods was referred to in our previous publications as XMECA [30,31].
Even though FMECA has been used for more than half of the century, the analysis performed shows that the challenge in defining and classifying FMECA outputs applied to modern complex products and systems still takes place. The absence of any interrelation between the ranking of failures and a procedure for selection of the most critical maintenance and/or improvement tasks limits the potential of FMECA for implementation in real environments [32]. Drawbacks of the conventional FMECA method are also addressed in Ref. [33] by examples in the oil refinery field, providing a new fuzzy risk quantification approach method, “four fuzzy logic system”, that includes pre-assessment by sets of fuzzy logic systems.
According to Ref. [34], FMECA and its modification play an essential role in increasing reliability and safety, but they still undoubtedly have drawbacks regarding risk evaluation and uncertainties. A multicriteria decision-making risk evaluation model, as well as a prioritization of risks, may be used to simplify decision-makers’ judgments and to handle uncertainty caused by these judgments [35]. Using security analysis results as a factor in increasing or decreasing the risk level could affect the introduced uncertainty of probabilistic model parameters [36].
According to other authors [37,38], it is natural that different experts during the implementation of FMECA procedures provide assessments that differ in metrics of completeness (or incompleteness), accuracy (or inaccuracy), and their own definition of criticality (critical or non-critical). Another conclusion is that there are various shortcomings of FMECA, but the authors [39,40,41] do not analyze the impact of expert errors on evaluation results.
Besides, the important fact is that a specific part of FMECA operations is usually performed without the use of automatic or semi-automatic tools by experts, or using such tools without additional verification, as well as checking for updates to databases that work with these tools [42,43,44]. It can also be a source of certain errors. To address this issue in the oil and gas sector, the analytic hierarchy process is used to evaluate the ability of experts to improve the objectivity of expert judgment [45]. In Ref. [46], an attempt was made to provide an improved approach to FMECA using a method called multi-criteria decision-making (MCDM). A feature of MCDM is the ability to tolerate the hesitation of experts during the assessment by using the mathematical apparatus of an indefinite fuzzy set.
There is a method that modifies the known RPN model [47] by determining the degree of uncertainty of some expert conclusions when performing FMECA as the relative importance of each expert who assesses safety using FMECA. As tool support, different questionnaires for estimating uncertainties are provided [48].
Errors of experts and inaccuracy of assessment caused by uncertainties of the values of input parameters, influence of faults, and so on have been analyzed in Refs. [49,50,51]. This problem can be addressed by using FMECA (XMECA) and other techniques, such as FTA, fault injection testing (FIT), reliability block diagrams (RBD), and so on. Table 1 illustrates the expert impact on application of safety assessment techniques.

Table 1.
Analysis of expert impact on application of safety assessment techniques.
After performing a literature review, it is possible to recognize that:
- Although FMECA is a well-known technique that has been used in different domains for quite a long time, it is still quite complicated to use due to task dimension, not having a formalized procedure, a huge amount of modifications, etc. Therefore, recent research still provides additional clarifications to FMECA utilization, its peculiarities, etc.
- FMECA is a methodological technique, but its key drawback is semi-formalism and the need for expert support, which is not studied in detail in well-known works;
- To increase the trustworthiness of assessments, experts are needed, but procedures and tools are needed that either improve trustworthiness due to the correct combination of assessments and/or reduce the influence of individual experts by reducing non-formalized operations (tool support). Such an integrated approach requires additional formalization and development.
1.3. Objective and Research Questions
The objective of this paper is to increase the trustworthiness of XMECA-based safety assessment by minimizing risks of inaccuracy caused by assumptions that are usually used in the different modifications of traditional techniques, and potential errors of experts caused by the uncertainty of input data and their errors.
The following research questions have been formed to address this objective:
- What approach could be utilized to minimize safety assessment inaccuracy? With what limitations?
- In what way could the generic XMECA technique be applied for safety and security assessment?
- How could the criticality of assumptions usually used to implement FMECA be analyzed?
- What are the impacts of expert approaches and tool support?
- In which manner could FMECA modification (IMECA) be utilized for cybersecurity assessment within XMECA?
1.4. Paper Structure
The paper is structured as follows. Section 2 provides a description of the materials and methods. Section 3 provides the results, namely XMECA and its usage, the analysis of expert uncertainties of XMECA, a case study, XMECA application for cybersecurity assessment, and an example of a tool used to support the XMECA process. In Section 4, the discussion is provided. Finally, in Section 5, we make conclusions and outline future directions.
2. Materials and Methods
The presented approach is based on the combination of the following main principles:
- a formal description of the shortcomings and the consequences of these shortcomings for the FMECA methodology, which is combined in the form of the XMECA conception, which allows minimizing the risks of erroneous decisions and narrows the area of uncertainty. To accomplish this, we use the EUMECA analysis of XMECA (E—error; U—uncertainty). To evaluate the consequences of possible errors, we use an expert procedure for determining the importance of error and uncertainty factors;
- scenario-oriented integration of expert assessments when using XMECA, considering the complexity of such integration when using verbal, fuzzy, and quantitative assessments. This principle allows various scenarios to achieve the best result when combining expert estimates to maximize the accuracy of estimation. Moreover, the number of operations performed by an expert is being reduced;
- reducing the influence of individual experts and uncertainty factors during the assessment process by minimizing non-automated (manual) operations using improved tools. This principle is a natural addition and support for the first two.
The interrelationship of these principles is shown in Figure 1. As an input, we have assessment results with some degrees of errors and uncertainties (sets E0 and U0). After the application of EUMECA, new sets E1 and U1 can be obtained. These sets are the subsets of E0 and U0, correspondently.
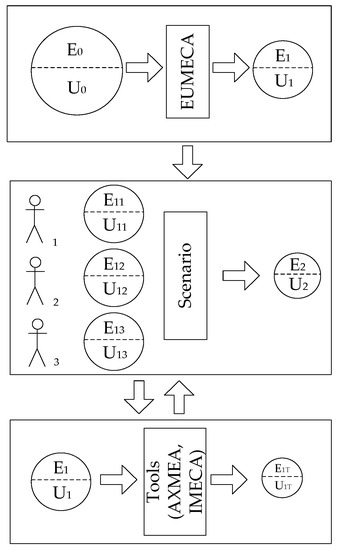
Figure 1.
Overall relation between principles and E/U sets.
This decrease can be estimated by metrics, which are determined by the ratio of the powers of the corresponding sets |E|, |U|:
hE10 = |E1|/|E0|, hU10 = |U1|/|U0|, hEU10 = (|E1| + |U1|)/(|E0| + |U0|)
During the next step, scenario-oriented approach is applied to the outputs of the previous step (sets E11 and U11 for the first expert, sets E12 and U12 for the second expert, sets E13 and U13 for the third expert, and so on). The effectiveness of this procedure is assessed by similar metrics
hE21 = |E2|/|E1|, hU21 = |U2|/|U1|, hEU21 = (|E2| + |U2|)/(|E1| + |U1|)
Alternative to this step is the usage of tools to decrease the influence of individual experts and uncertainty factors, allowing to obtain sets E1T and U1T correspondently and calculate metrics.
hET1 = |E1T|/|E1|, hUT1 = |U1T|/|U1|, hEUT1 = (|E1T| + |U1T|)/(|E1| + |U1|)
This principle could be used as an alternative to the previous one, or as an additional operation. Examples of tools that can be applied to support assessment procedures are described in Refs. [50,52] and discussed in Section 3.7.
In general, maximal decreasing for the expert and uncertainty influence on the trustworthiness of assessment due to the application of described procedures can be calculated as a multiplying of metrics
hEU = hEU10 × hEUT1 × hEU21
It should be noted that EUMECA analysis considers results of preliminary expert assessment and research of trustworthiness sensitivity for different expert and uncertainty factors. These three stages of assessment methodology are described in Section 3.4, Section 3.5, Section 3.6.
3. Results
3.1. XMECA Model
The XMECA model in this section is presented by the example of FMECA. For other techniques (for instance, IMECA), the approach would be similar, but intrusions would be used instead of failures.
An example is the FMECA table, which could be reported in terms of list FT list involving a set of T tuples:
where
fi implies failure cause (failed element);
ei is herein taken to mean a set of failure consequences (effects);
pi denotes failure probability, which can be preassigned qualitatively with the fuzzy scale (as an example, «low»–«medium»–«high») or quantitatively as a value in range 0–1;
si identifies failure severity, which can also be defined using a fuzzy scale or quantitatively;
ci stands for a failure criticality determined as a function of fuzzy variables φ, ci = φ (pi,si);
mi signifies a set of possible failure modes;
ki is the number of considered failure modes of element i; the total number of failure modes is calculated by the following expression:
k = k1 + k2 + … + kF
Figure 2 depicts the interrelation between previously mentioned fi, mi, and ei, and the relation between si, pi, and ci is shown in Figure 3.

Figure 2.
Relation between failure cause, modes, and effects.
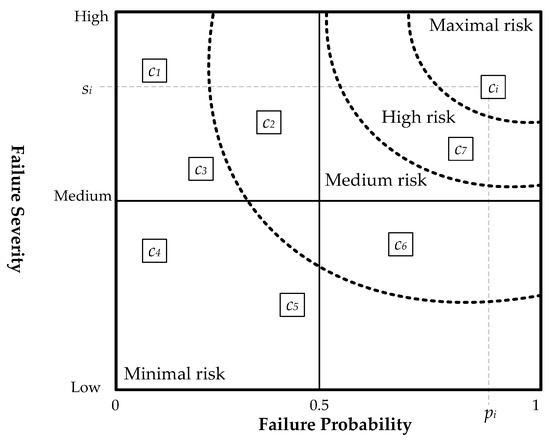
Figure 3.
Relation between failure severity and probability.
FMECA table is characterized by number of rows F* = F, if k1 = k2 = … = kF = 1; in a general way, F* = K.
In the process of FMECA execution, the following items are sequentially defined by an expert with possible tool support:
- elements fi (for instance, module components, program operators, process operations, etc.), failures of which are to be considered, that is fi ϵ ΔF, ΔF ϲ MF, where ΔF is a subset of components investigated; MF is a set of components;
- failure modes mij of element fi, which are to be considered, i.e.,
mij ϵ ΔMi, ΔMi ϲ MMi
- effects eij of failure mode mij of element fi, which are to be considered, i.e.,
eij ϵ ΔEi, ΔEi ϲ MEi
- probability pij and severity sij of failure mode mij of element fi; probability pij and severity sij are being adopted according to defined scale on the sets of values MP = {p’h} and MS = {s’g} accordingly; criticality cij of failure mode mij of element fi, which could be either explicitly evaluated by an expert using given function φ or assigned by an expert manually on the set of values MC = {c’g}.
3.2. Stages of XMECA Application
XMECA could be applied in the following stages (Figure 4): specifying system requirements, defining system structure, selection of elements, and implementation.
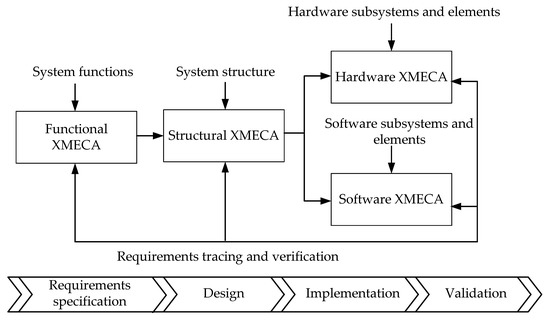
Figure 4.
XMECA application stages.
In the first stage, functional requirements are analyzed. In this case, rows in the XMECA table are represented by system functions and possible events, leading to full or partial system failure. Outcomes, received during functional XMECA, are used for requirements tracing and verification of designing results.
The second stage represents the usage of XMECA applied to sub-systems and elements, with a focus on software and hardware.
3.3. XMECA and Other Assessment Techniques
Typical assessment techniques and their modifications could be presented as the transformation of input data set I into output data set O according to requirements R with parallel or serial possible usage (Figure 5).
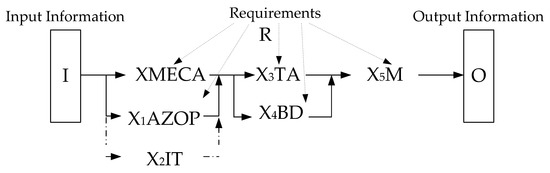
Figure 5.
XMECA and other assessment techniques.
XMECA is a set of techniques based on FMECA and its modifications (IMECA, FMEDA, etc.).
X = {F, I, …}
X1HAZOP is a set of techniques based on HAZOP and its modifications (software HAZOP, control HAZOP, etc.).
X1 = {S, C, …}
X2IT is a set of techniques intended for fault/intrusion insertion to verify XMECA or X2HAZOP assumptions and statements (fault, vulnerability, software fault, etc.).
X2 = {F, V, SF, …}
X4TA is a set of techniques based on FTA and its modifications (FTA, ETA, etc.):
X3 = {F, E, …}
X4BD is a set of techniques based on RBD and its modifications (safety, security, availability, etc.):
X4 = {R, Saf, Sec, Avail, …}
The final stage is the construction of Markov models and their modifications to obtain quantitative assessment results:
X5 = {M, SemiM, …}
Technique choice and acceptance of its particular modification (Xi) depends on the input information completeness, requirements to output information, etc.
Xi = f (I, O.R, …)
3.4. EUMECA Analysis of XMECA
3.4.1. Uncertainty Evaluation Questionnaire
The questionnaire presented in Table 2 was prepared to be distributed among experts. Each expert is expected to specify the probability and severity of the assumptions using a 1–3 scale.

Table 2.
Questionnaire for assumptions effects, probability, and severity.
3.4.2. Evaluation in Case of Equal Qualification (Self-Assessment) of Experts
Scenario-Based approach
Assuming XMECA assessment is being performed by a group of Q experts that have an identical qualification, or, in the case when expert qualification may be disregarded entirely, assessment of different experts’ opinions requires the following steps:
- analysis of divergence types associated with different constituents of the model (1);
- generation of the final version for each divergence;
- preparation of integrated version of XMECA;
- accomplishing analysis of it and provision of eventual safety assessment.
For XMECA assessment being performed by a group of Q experts, possible divergences are summarized in Table 3.

Table 3.
Divergences for a group of experts.
By this means, the following crucial assumptions are considered: firstly, all varieties of possible expert opinions are entirely covered by sets MΔF, MΔMi, and MΔEi, and, secondly, failure probabilities, severities, and criticality assessment scales (values) MP, MS, and MC are common and cannot be changed during the assessment process.
Hence, three assessment scenarios based on expert opinions are available: conservative (ScC), when the generated list of failure modes is the most comprehensive and the pessimistic way is chosen for consequences and risks assessment; optimistic (ScO), when the list of failure modes is minimal because of generation based on the intersection of sets of failure modes, and choice of best values during consequences and risks assessment; and, lastly, weighted (ScW), when a generation of the common subset of failures is performed, and, then, with complementation by modes, discovery and selection by two or more experts is conducted; consequences and risks assessment is based on averaging of obtained values.
Scenario ScC
Here, the following assessment steps are performed:
- generation of a set of elements to be included in FMECA table according to (1):
MΔF(ScC) = UΔF(q), q = 1, …, Q
- generation of sets of failure modes to be considered for all elements fi ϵ MΔF(ScC):
MΔMi(ScC) = UΔMi(q), q = 1, …, Q
- generation of sets of failure effects eij of mode mij of element fi to be considered:
MΔEi(ScC) = UΔEi(q), q = 1, …, Q
- evaluation of failure probabilities of mode mij of element fi by equation:
pij (ScC) = max {ΔPij(q)}, q = 1, …, Q
- evaluation of failure severities of mode mij of element fi by equation:
sij (ScC) = max {ΔSij(q)}, q = 1, …, Q
- evaluation of failure criticalities of mode mij of element fi by equation:
cij (ScC) = max {ΔCij(q)}, q = 1, …, Q
Scenario ScO
For this scenario, the following assessment steps are performed:
- generation of a set of elements to be included in FMECA table according to (1) using the equation:
MΔF(ScO) = ∩ ΔF(q), q = 1, …, Q
- generation of sets of failure modes for all elements fi ϵ MΔF(ScC) to be considered:
MΔMi(ScO) = ∩ ΔMi(q), q = 1, …, Q
- generation of sets of failure consequences eij of mode mij of element fi to be considered:
MΔEi(ScO) = ∩ ΔEi(q), q = 1, …, Q
- evaluation of probabilities of failure modes mij of element fi using equation:
pij (ScO) = min {ΔPij(q)}, q = 1, …, Q
- evaluation of severities of failure modes mij of element fi by equation:
sij (ScO) = min {ΔSij(q)}, q = 1, …, Q
- evaluation of failure criticalities of mode mij of element fi by equation:
cij (ScO) = min {ΔCij(q)}, q = 1, …, Q
Scenario ScW
This scenario incorporates the following steps:
- generation of set of elements, of which failures are to be included in FMECA table according to (1):
MΔF(ScW) = ∩ ΔF(q) UΔF(q) *, q = 1, …, Q
- generation of sets of failure modes for all elements fi ϵ MΔF(ScC), which have to be considered:
MΔMi(ScW) = ∩ ΔMi(q) UΔMi(q) *, q = 1, …, Q
- generation of sets of failure consequences eij of mode mij of element fi, which have to be considered:
MΔEi(ScW) = ∩ ΔEi(q) UΔEi(q) *, q = 1, …, Q
- evaluation of probabilities of failure modes mij of element fi by application of ceiling function to the average:
pij (ScW) = avermax {ΔPij(q)}, q = 1, …, Q
- evaluation of severities of failure modes mij of element fi by equation:
sij (ScW) = avermax {ΔSij(q)}, q = 1, …, Q
- evaluation of failure criticalities of mode mij of element fi by equation:
cij (ScW) = avermax {ΔCij(q)}, q = 1, …, Q
3.4.3. Evaluation in Case of Different Qualification (Self-Assessment) of Experts
Assuming that FMECA is being performed by a group of Q experts, with differences, the assessment of opinions of different experts requires the addition of MScD sets to the ScC, ScO, ScW scenarios presented above. Therefore, the following groups of scenarios could be considered, ScDT and ScDW.
Group of Scenarios ScDT
Scenarios from this group are based on ignoring of assessments provided by experts that have a qualification that is below the minimum specified level, and, further, going to execution of one of the presented above scenarios ScC, ScO, ScW, with the further transformation of them into scenarios ScTC, ScTO, ScTW, where qualification of experts is not considered anymore.
Group of Scenarios ScDW
This group of scenarios is based on the ScC scenario in the generation of MΔF (ScC), MΔMi (ScC), and MΔEi (ScC) sets and subsequently weighted failure probability, severity, and criticality assessments with ceiling function used for rounding.
3.5. Case Study. Expert-Based FMECA Assessment of Hardware/Software Module Safety
3.5.1. Results of EUMECA
Table 4 provides averaged results obtained from ten experts who have more than ten years of experience in the area of development, verification, and certification of safety-critical systems (instrumentation and control systems for NPPs). Risk is evaluated as a product of probability and severity.

Table 4.
EUMECA results.
Table 4 allows making the following considerations:
- in considered cases, higher probability and severity are assigned to hardware-related assumptions;
- by experts’ opinions, the higher risk caused by uncertain assessment of probability in respect to safety overestimation is due to failure mistakenly treated as detected, while, in respect to safety underestimation, it is due to several components used for safety assessment being given too high or excess system levels being considered;
- by experts’ opinions, the higher risk caused by uncertain assessment of severity in respect to safety overestimation is due to not all software faults being considered and hardware and software faults are not considered in respect to possible attacks, while, in respect to safety underestimation, it is due to fact that more than required software faults are considered and more than required hardware faults (physical and project) are considered;
By experts’ opinions, higher integral risk concerning safety overestimation is when the failure is mistakenly treated as detected, and, while concerning safety underestimation, when the failure modes are not considered.
3.5.2. Assumption Modes and Effects Evaluation Example
Assessment performed by several experts implies consideration of the following particular cases and appropriate responses:
- different sets of elements: sets of elements provided by different experts can be merged;
- different sets of failure modes: two scenarios of merging are possible: optimistic (intersection of sets) and conservative (union of sets);
- different sets of failure effects: to choose more critical effects, preference relation could be utilized.
Table 5 provides an example of assumption modes and effect analysis.

Table 5.
Assumption modes and effect example.
For an illustration of the scenarios described above, three examples of FMECA prepared by three different experts are provided in Table 6, Table 7 and Table 8, respectively. These tables are used further to show the application of different scenarios.

Table 6.
FMECA example prepared by expert 1.

Table 7.
FMECA example prepared by expert 2.

Table 8.
FMECA example prepared by expert 3.
Applying the conservative scenario described above to the FMECA tables in Table 6, Table 7 and Table 8, we obtain the results provided in Table 9.

Table 9.
FMECA table after ScC application.
After applying the optimistic scenario described above to the FMECA tables in Table 6, Table 7 and Table 8, we obtain the results provided in Table 10.

Table 10.
FMECA table after ScO application.
With the application of the above-mentioned weighted scenario ScW to the FMECA tables presented in Table 6, Table 7 and Table 8, we obtain the results summarized in Table 11.

Table 11.
FMECA table after ScW application.
Considering this case, we can conclude that complete automation of multi-expert assessment of safety using FMECA is impossible. To provide complete automation, a more detailed description of the procedure of hardware/software analysis and support by a database of specific parameters would be necessary.
3.6. Application of XMECA for Cybersecurity Assessment
IMECA analysis (intrusion modes, effects, and criticality analysis) is a technique within XMECA intended for cybersecurity assessment considering refinements in the system and can be applied to analyze the intrusions in the assessed object [53].
IMECA focuses on vulnerabilities that can be utilized by intrusions. In gap analysis, the detection of nonconformities and discrepancies (and related vulnerabilities in the case of cybersecurity assessment) can be implemented by separately identifying/analyzing problems caused by human factors, techniques, and tools, considering the impact of the development environment. Then, after identifying all the vulnerabilities as a priority, it is possible to ensure the cybersecurity of critical instrumentation and control systems by implementing appropriate countermeasures.
Depending on the critical instrumentation and control system considered, each space should be presented in the form of a formal description that identifies any discrepancies (between “ideal”, i.e., described in the requirements, and real). Such a formal description should be made for the set of inconsistencies identified by a gap.
The concept of a gap is one of the main concepts underlying the idea of the approach. The analyzed product development features are process, product, and cybersecurity threats. Processes are implemented through the development stages of critical instrumentation and control system lifecycle to produce products. Processes can be vulnerable due to incorrect execution. Products, in turn, can be subject (i.e., vulnerable) to intrusions of various types that can affect them as well. The results of process execution could have negative effects on possible consequential changes in the mentioned processes. Each process includes some activities and, in the case of “non-ideal” implementation of such activities, some of them can contain discrepancies. Therefore, a gap could be defined as a part of such discrepancies (related to the use of an inappropriate tool or introduced by humans, or due to shortcoming of development technique). In other words, a gap is a set of inconsistencies (discrepancies) of any single process within the critical instrumentation and control system life cycle [29] that may introduce some anomalies (e.g., vulnerabilities) to its product and/or cannot detect (and eliminate) existing anomalies in the product.
Each detected gap must be represented by the IMECA table, and each discrepancy within the gap can be represented by a row in this table, considering the characteristics of the product and/or process feature. A separate table is created for each gap that contains the vulnerabilities identified during the gap analysis. All individual tables are combined into a common IMECA table.
The overall sequence of IMECA application is depicted in Figure 6 [53]. The ideal system is represented by a requirements profile (SRS, security requirements specification), containing all the elements of the processing system at different levels of detail. Requirements can be hierarchically decomposed into different levels. After determining the number of hierarchical levels of requirements, experts compile a list of requirements for each level. The requirement levels are filled evenly from top to bottom. When completing one level, for each requirement of that level, lower-level requirements that expand, refine, or detail are created. As a result, a requirement at the level in question may correspond to one or more of the requirements of the level below (see Step 1 and Step 2).
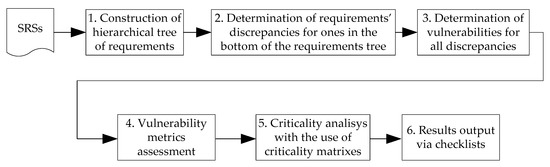
Figure 6.
Overall sequence of IMECA application.
After every requirement is entered, their analysis at the lowest level should be conducted. It is assumed that the requirement can potentially be violated, thus introducing the gap artificially with further detailing. During the requirements analysis, the specific violations that may occur are clarified. It depends on the nature of the requirement itself. In such a way, each gap is represented in a form of the set of violations that could take place in the critical instrumentation and control system of a particular requirement. After that, IMECA tables are filled in for every discrepancy (see Step 3, Step 4). More options could also be defined. They can be additionally determined by expert assessment or supporting analysis. Among the required parameters are the probability and impact on the system. Some additional parameters could also be defined via expert assessment or using the additional analysis methods as well. Above the assessed parameter, the probability and critical impact on the system are placed. Quantitative parameters can be further determined through the use of expert methods or other additional tools. A separate table is created for each gap, containing all the vulnerabilities that were identified during the analysis of this gap. Every vulnerability is supported by a criticality matrix. With the help of the criticality matrix based on vulnerability parameters, the metric should be calculated, and the resulting conclusion for vulnerability shall be made. For the criticality matrix, the set of valid parameters is defined. The analysis of vulnerabilities can be based, using open databases, on results of cybersecurity research for different applications, embedded systems, IoT, and so on [54].
If any of the vulnerability parameters are not included in the agreed range, a decision that the vulnerability is presented in the system and requires further attention should be made (see Step 5). After the discrepancy is determined based on the criticality matrix, the checklist of those requirements is formed and a conclusion about their implementation should be made (see Step 6).
3.7. The Tool for XMECA Assessment of Safety and Security
3.7.1. AXMEA Tool
AXMEA is a tool that automates XMECA techniques, providing users the possibility to utilize different failure and vulnerability sources, specify their priorities, assign failure rates for electronic components, and obtain required reliability and safety metrics [50]. The tool is intended to simplify the analysis of critical instrumentation and control systems and minimize the influence of expert judgments. AXMEA supports the usage of templates for input information (such as bills of materials with pre-defined structure, export information from electronic design software, etc.) and output information (projects, reports with configurable structure, etc.).
Figure 7 shows the AXMEA tool that has specified failure rates automatically based on component information. Information that was filled in by the expert manually in Table 6 of Section 3.5.2 is being populated by the tool automatically.
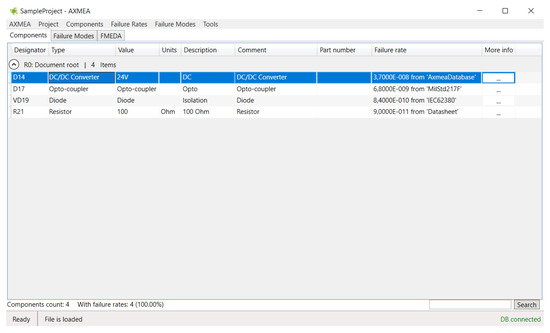
Figure 7.
AXMEA tool: automatic failure rate assignment.
All known components are assigned failure rates by AXMEA automatically from different configured failure rate sources. The database of failure rates could be updated cumulatively by users from project to project, but the basic database already contains failure rates of components appropriate to the following international normative documents supplied as AXMEA modules:
- MIL-HDBK-217F “Military Handbook Reliability Prediction of Electronic Equipment” [55];
- IEC 62380 “Reliability data handbook—Universal model for reliability prediction of electronics components, PCBs and equipment” [56].
AXMEA accounts that each component may have one or more failure modes. Each type of failure must be classified according to IEC 61508 [57] as safe detected, safe undetected, dangerous detected, and dangerous undetected (Figure 8). Default classification of failures into dangerous undetected (or any other type specified by the user) is supported.
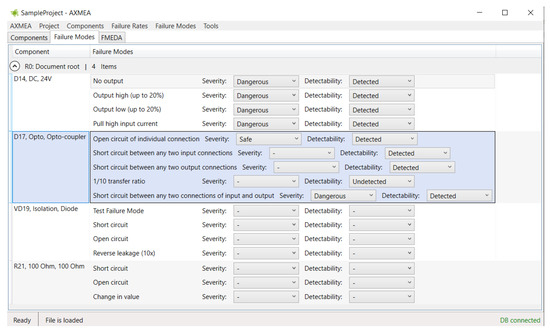
Figure 8.
AXMEA tool: specification of severity and detectability.
Basic safety and reliability metrics provided by AXMEA include failure rates classified according to IEC 61508 [57] requirements, safe failure fraction, diagnostic coverage, and safety integrity level (Figure 9).
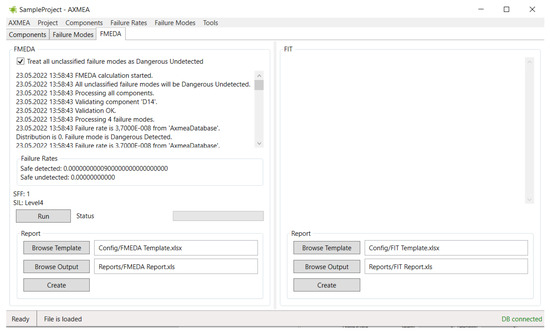
Figure 9.
AXMEA tool: safety metrics calculation.
AXMEA provides the possibility to generate reports on the work performed according to configurable templates that could be used as relevant project reliability and safety documentation. The reports include all the obtained metrics, used failure source database, and assessment process steps.
3.7.2. Assessment of Increasing Trustworthiness
AXMEA tool allows to lower expert uncertainty by providing automation support of modes presented in Table 2. For example, the following modes could be supported by AXMEA in such a manner that allows eliminating dependence on expert decisions:
- not all components are defined for safety assessment;
- number of components used for safety assessment is given too high;
- not all failure modes are considered;
- excess failure modes are considered;
- failure multiplicity is underestimated;
- failure multiplicity is overestimated;
- multiple faults of different components at one level are not considered;
- multiple faults of different components at different levels are not considered;
- multiple faults of different versions are not considered.
Using a straightforward approach based on expressions (1)–(3), we can conclude that it is possible to increase trustworthiness for nine out of the twenty-two modes presented in Table 2, or 40.9%.
Besides, the efficiency of the AXMEA tool application can be assessed by the expert involvement indicator presented in Refs. [49,50]:
EID (expert involvement degree) is evaluated as the number of operations that are performed by expert(s) divided by the total number of operations:
EID = NOE/TNO
EUD (expert uncertainty degree) is evaluated as number of operations with uncertainty that are performed by expert(s) divided by number of operations that are performed by expert(s):
EUD = NUE/NOE
ETD (expert trustworthiness (certainty) degree) is evaluated using following expression:
ETD = 1 − EID ∗ EUD
Due to the application of the AXMEA metric, ETD, in comparison with existing tools, has been increased by 16.3% (from 0.619 to 0.720).
4. Discussion
In our previous works, we presented different modifications of FMECA that could be applied to different domains. In particular, IMECA is intended for security assessment by analyzing intrusions and their effects [27,28,29].
XMECA is an extension of FMECA that can be applied to analyze other aspects related to safety and security analysis, except failures only. Among them could be, e.g., intrusions (i.e., intrusion modes, effects, and criticality analysis, IMECA), etc. [30].
The proposed methodology does not exclude the use of experts at all but aims to, on the one hand, reduce their impact in a negative sense, and, on the other hand, provide for their use when they can reduce the risk of errors or inaccuracies.
The effectiveness of the proposed method is assessed by qualitative and quantitative metrics. These metrics estimate methodological, human, and technological benefits, which improve the trustworthiness and productivity of assessment processes and results by:
- specifying and excluding traditional assumptions for FMECA and IMECA techniques (first of all, types of faults);
- minimizing errors caused by objective uncertainty of input data, the complexity of systems, and decisions of experts;
- improving part of activities based on automatically executed operations.
Besides, the cumulative effect of the method application is that it provides decreasing risks of inaccurate safety and security assessment.
5. Conclusions
A framework for safety assessment that uses XMECA as a key methodology and handles expert and tool outputs was proposed in this paper.
Based on XMECA, various functional safety and cybersecurity assessment chains can be built for embedded systems based on FPGA or CPU. To obtain a high level of trustworthiness in safety assessment, it is important to reduce the level of expert influence not only in terms of their possible mistakes but also considering situations when certain decisions are made by experts in conditions of uncertainty.
It is proposed to measure trustworthiness using several fairly simple metrics. For the examples presented in this paper, the implementation of the proposed approaches allowed to increase trustworthiness by decreasing expert influence and the degree of non-automated operations. The first group of metrics (1)–(3) outlines drawbacks in assumptions and expert errors, while the second one (14)–(16) deals with automation degree.
In terms of the use of XMECA (IMECA) to assess cybersecurity, the approach becomes more complicated as the appropriate vulnerability attacks possibility factor is being considered as the implementation of certain threats. The main stages of cybersecurity assessment are provided using a special software tool for conducting sequential application of gap analysis and IMECA.
The probability of successful attacks on the system may vary over the time period depending on the development of the attack and methods of defense, increasing knowledge about the measures of control and system protection, as well as other reasons. A common limitation of the consecutive application of analysis of gaps and further application of IMECA is the limitation in analysis of only individual causes of the particular effect. This is the reason why some multistage attacks can pass over. Thus, cybersecurity controls have a much shorter lifespan than safety measures, and they require updates more frequently.
The combined application of EUMECA and supporting tools AXMEA and IMECA (with the implementation of supporting countermeasures) will increase the functional safety and cybersecurity of the systems in time.
Therefore, the raised research questions could be answered positively. The innovativeness of the proposed method is based on the well-known statement that investing in safety is always an innovation because it reduces the risk of losses, which can significantly exceed the cost of overcoming the consequences of dangerous failures and accidents, especially when it comes to critical systems, and reduce reputational risks of companies that design safety-critical systems. The results of this research have theoretical and technological components. The innovative theoretical component, namely the development of an assessment methodology that minimizes the risks of untrue/non-trustworthy safety assessment due to (1) use of well-known and established assumptions in the assessment, (2) uncertainties in the input data, and (3) potential inaccuracies or even the mistakes of experts, is determined by the fact that some complications of the assessment process and additional costs of resources to compensate for it are addressed by reducing the probability of functional safety overestimation of unspent funds (and, hence, the actual income) to overcome the consequences of accidents.
This effect is enhanced by the use of the proposed technological tools that not only support the methodological component but also provide the opportunity to involve a limited group of professional experts to form important conclusions for safety assessment, which are related to the processing of verbal, fuzzy, and quantitative information. Therefore, the proposed theoretical and technological solutions are not limited to the XMECA methodology and define broader aspects of use for safety analysis and accident risk reduction.
Possible future work could be focused on the following directions:
- development of software platform for safety and security assessment based on the complexation of different analysis techniques with the possibility to choose their combinations, data transfer between techniques, and metrics calculation [31,58];
- provision of integration into this platform subsystem for expert assessment and tools developed earlier (IMECA, AXMEA);
- development of automatic vulnerability monitor based on vulnerability data processing from different databases of programs and programmable components;
- improving trustworthiness accuracy assessment by application of considered and new metrics and their calculation considering weights of operations, assumption severity, and so on.
Author Contributions
Conceptualization, V.K.; methodology, V.K., I.B. and O.I.; software, V.K., I.B. and O.I.; investigation and case study, K.L.; writing—original draft preparation, V.K., I.B., O.I. and K.L.; writing—review and editing, V.K., I.B. and O.I.; supervision, V.K.; project administration, V.K.; funding acquisition, O.I. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the ECHO project, which has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 830943.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Acknowledgments
The authors appreciate the scientific society of the consortium and, in particular, the staff of the Department of Computer Systems, Networks and Cybersecurity of the National Aerospace University “KhAI” for invaluable inspiration, hard work, and creative analysis during the preparation of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jiang, Z.; Zhao, T.; Wang, S.; Ren, F. A Novel Risk Assessment and Analysis Method for Correlation in a Complex System Based on Multi-Dimensional Theory. Appl. Sci. 2020, 10, 3007. [Google Scholar] [CrossRef]
- Sklyar, V. Safety-Critical Certification of FPGA-based Platform against Requirements of U.S. Nuclear Regulatory Commission (NRC): Industrial Case Study. ICTERI. 2016. Available online: http://ceur-ws.org/Vol-1614/paper_32.pdf (accessed on 28 April 2022).
- Kharchenko, V.; Illiashenko, O.; Sklyar, V. Invariant-Based Safety Assessment of FPGA Projects: Conception and Technique. Computers 2021, 10, 125. [Google Scholar] [CrossRef]
- Hajda, J.; Jakuszewski, R.; Ogonowski, S. Security Challenges in Industry 4.0 PLC Systems. Appl. Sci. 2021, 11, 9785. [Google Scholar] [CrossRef]
- Takahashi, M.; Anang, Y.; Watanabe, Y. A Safety Analysis Method for Control Software in Coordination with FMEA and FTA. Information 2021, 12, 79. [Google Scholar] [CrossRef]
- Peeters, J.; Basten, R.; Tinga, T. Improving failure analysis efficiency by combining FTA and FMEA in a recursive manner. Reliab. Eng. Syst. Saf. 2018, 172, 36–44. [Google Scholar] [CrossRef]
- Trivyza, N.L.; Cheliotis, M.; Boulougouris, E.; Theotokatos, G. Safety and Reliability Analysis of an Ammonia-Powered Fuel-Cell System. Safety 2021, 7, 80. [Google Scholar] [CrossRef]
- Ehrlich, M.; Bröring, A.; Harder, D.; Auhagen-Meyer, T.; Kleen, P.; Wisniewski, L.; Trsek, H.; Jasperneite, J. Alignment of safety and security risk assessments for modular production systems. Elektrotech. Inftech. 2021, 138, 454–461. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, R.; Deng, W.; Zhao, Y. An Integrated Approach-Based FMECA for Risk Assessment: Application to Offshore Wind Turbine Pitch System. Energies 2022, 15, 1858. [Google Scholar] [CrossRef]
- IEC/ISO 31010:2019; Risk Management—Risk Assessment Techniques. European Ed. 2.0. International Electrotechnical Commission: Geneva, Switzerland, 2019.
- Babeshko, I.; Leontiiev, K.; Kharchenko, V.; Kovalenko, A.; Brezhniev, E. Application of Assumption Modes and Effects Analysis to XMECA. In Theory and Engineering of Dependable Computer Systems and Networks; DepCoS-RELCOMEX 2021. Advances in Intelligent Systems and Computing; Zamojski, W., Mazurkiewicz, J., Sugier, J., Walkowiak, T., Kacprzyk, J., Eds.; Springer: Cham, Switzerland, 2021; Volume 1389. [Google Scholar] [CrossRef]
- Giardina, M.; Tomarchio, E.; Buffa, P.; Palagonia, M.; Veronese, I.; Cantone, M.C. FMECA Application in Tomotherapy: Comparison between Classic and Fuzzy Methodologies. Environments 2022, 9, 50. [Google Scholar] [CrossRef]
- Oliveira, J.; Carvalho, G.; Cabral, B.; Bernardino, J. Failure Mode and Effect Analysis for Cyber-Physical Systems. Future Internet 2020, 12, 205. [Google Scholar] [CrossRef]
- Peyghami, S.; Davari, P.; Firuzabad, M.; Blaabjerg, F. Failure Mode, Effects and Criticality Analysis (FMECA) in Power Electronic based Power Systems. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. 1–9. [Google Scholar] [CrossRef]
- Catelani, M.; Ciani, L.; Galar, D.; Guidi, G.; Matucci, S.; Patrizi, G. FMECA Assessment for Railway Safety-Critical Systems Investigating a New Risk Threshold Method. IEEE Access 2021, 9, 86243–86253. [Google Scholar] [CrossRef]
- Buja, A.; Manfredi, M.; De Luca, G.; Zampieri, C.; Zanovello, S.; Perkovic, D.; Scotton, F.; Minnicelli, A.; De Polo, A.; Cristofori, V.; et al. Using Failure Mode, Effect and Criticality Analysis to Improve Safety in the COVID Mass Vaccination Campaign. Vaccines 2021, 9, 866. [Google Scholar] [CrossRef] [PubMed]
- Serafini, A.; Troiano, G.; Franceschini, E.; Calzoni, P.; Nante, N.; Scapellato, C. Use of a systematic risk analysis method (FMECA) to improve quality in a clinical laboratory procedure. Ann. Ig 2016, 28, 288–295. [Google Scholar] [CrossRef] [PubMed]
- Milioulis, K.; Bolbot, V.; Theotokatos, G. Model-Based Safety Analysis and Design Enhancement of a Marine LNG Fuel Feeding System. J. Mar. Sci. Eng. 2021, 9, 69. [Google Scholar] [CrossRef]
- Di Nardo, M.; Murino, T.; Osteria, G.; Santillo, L.C. A New Hybrid Dynamic FMECA with Decision-Making Methodology: A Case Study in An Agri-Food Company. Appl. Syst. Innov. 2022, 5, 45. [Google Scholar] [CrossRef]
- Di Bona, G.; Forcina, A.; Falcone, D.; Silvestri, L. Critical Risks Method (CRM): A New Safety Allocation Approach for a Critical Infrastructure. Sustainability 2020, 12, 4949. [Google Scholar] [CrossRef]
- Shafiee, M.; Enjema, E.; Kolios, A. An Integrated FTA-FMEA Model for Risk Analysis of Engineering Systems: A Case Study of Subsea Blowout Preventers. Appl. Sci. 2019, 9, 1192. [Google Scholar] [CrossRef]
- Chen, L.; Jiao, J.; Zhao, T. A Novel Hazard Analysis and Risk Assessment Approach for Road Vehicle Functional Safety through Integrating STPA with FMEA. Appl. Sci. 2020, 10, 7400. [Google Scholar] [CrossRef]
- Bognár, F.; Hegedűs, C. Analysis and Consequences on Some Aggregation Functions of PRISM (Partial Risk Map) Risk Assessment Method. Mathematics 2022, 10, 676. [Google Scholar] [CrossRef]
- La Fata, C.M.; Giallanza, A.; Micale, R.; La Scalia, G. Improved FMECA for effective risk management decision making by failure modes classification under uncertainty. Eng. Fail. Anal. 2022, 135, 106163. [Google Scholar] [CrossRef]
- Lee, G.-H.; Akpudo, U.E.; Hur, J.-W. FMECA and MFCC-Based Early Wear Detection in Gear Pumps in Cost-Aware Monitoring Systems. Electronics 2021, 10, 2939. [Google Scholar] [CrossRef]
- Piumatti, D.; Sini, J.; Borlo, S.; Sonza Reorda, M.; Bojoi, R.; Violante, M. Multilevel Simulation Methodology for FMECA Study Applied to a Complex Cyber-Physical System. Electronics 2020, 9, 1736. [Google Scholar] [CrossRef]
- Babeshko, E.; Kharchenko, V.; Gorbenko, A. Applying F(I)MEA-technique for SCADA-Based Industrial Control Systems Dependability Assessment and Ensuring. In Proceedings of the 2008 Third International Conference on Dependability of Computer Systems DepCoS-RELCOMEX, Szklarska Poreba, Poland, 26–28 June 2008; pp. 309–315. [Google Scholar] [CrossRef]
- Androulidakis, I.; Kharchenko, V.; Kovalenko, A. IMECA-Based Technique for Security Assessment of Private Communications: Technology and Training. Inf. Secur. Int. J. 2016, 35, 99–120. [Google Scholar] [CrossRef][Green Version]
- Kharchenko, V. Gap-and-IMECA-Based Assessment of I&C Systems Cyber Security. In Complex Systems and Dependability. Advances in Intelligent and Soft Computing, 170; Kharchenko, V., Andrashov, A., Sklyar, V., Siora, A., Kovalenko, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; 334p. [Google Scholar] [CrossRef]
- Illiashenko, O.; Kharchenko, V.; Chuikov, Y. Safety analysis of FPGA-based systems using XMECA for V-model of life cycle. Radioelectron. Comput. Syst. 2016, 80, 141–147. [Google Scholar]
- Babeshko, E.; Kharchenko, V.; Leontiiev, K.; Odarushchenko, O.; Strjuk, O. NPP I&C safety assessment by aggregation of formal techniques. In Proceedings of the 2018 26th International Conference on Nuclear Engineering, London, UK, 22–26 July 2018; pp. 21–26. [Google Scholar]
- Lolli, F.; Gamberini, R.; Balugani, E.; Rimini, B.; Mai, F. FMECA-based optimization approaches under an evidential reasoning framework. DEStech Trans. Eng. Technol. Res. 2017, 1, 738–743. [Google Scholar] [CrossRef][Green Version]
- Ivančan, J.; Lisjak, D. New FMEA Risks Ranking Approach Utilizing Four Fuzzy Logic Systems. Machines 2021, 9, 292. [Google Scholar] [CrossRef]
- Fabis-Domagala, J.; Domagala, M.; Momeni, H. A Concept of Risk Prioritization in FMEA Analysis for Fluid Power Systems. Energies 2021, 14, 6482. [Google Scholar] [CrossRef]
- Pikner, H.; Sell, R.; Majak, J.; Karjust, K. Safety System Assessment Case Study of Automated Vehicle Shuttle. Electronics 2022, 11, 1162. [Google Scholar] [CrossRef]
- Piesik, E.; Sliwinski, M.; Barnert, T. Determining and verifying the safety integrity level of the safety instrumented systems with the uncertainty and security aspects. Reliab. Eng. Syst. Saf. 2016, 152, 259–272. [Google Scholar] [CrossRef]
- Chin, K.-S.; Wang, Y.-M.; Ka Kwai Poon, G.; Yang, J.-B. Failure mode and effects analysis using a group-based evidential reasoning approach. Comput. Oper. Res. 2009, 36, 1768–1779. [Google Scholar] [CrossRef]
- Liu, H.-C. FMEA Using Uncertainty Theories and MCDM Methods; Springer Science: Singapore, 2016; p. 219. [Google Scholar]
- Liu, H.-C.; Chen, X.-Q.; Duan, C.-Y.; Wang, Y.-M. Failure mode and effect analysis using multi-criteria decision making methods: A systematic literature review. Comput. Ind. Eng. 2019, 135, 881–897. [Google Scholar] [CrossRef]
- Liu, H.-C.; Liu, L.; Liu, N. Risk evaluation approaches in failure mode and effects analysis: A literature review. Expert Syst. Appl. 2013, 40, 828–838. [Google Scholar] [CrossRef]
- Dai, W.; Maropoulos, P.; Cheung, W.; Tang, X. Decision-making in product quality based on failure knowledge. Int. J. Prod. Lifecycle Manag. 2011, 5, 143–163. [Google Scholar] [CrossRef]
- Lee, Y.-S.; Kim, H.-C.; Cha, J.-M.; Kim, J.-O. A new method for FMECA using expert system and fuzzy theory. In Proceedings of the 2010 9th International Conference on Environment and Electrical Engineering, Prague, Czech Republic, 16–19 May 2010. [Google Scholar]
- Liu, H.-C.; Chen, X.-Q.; You, J.-X.; Li, Z. A New Integrated Approach for Risk Evaluation and Classification With Dynamic Expert Weights. IEEE Trans. Reliab. 2020, 70, 163–174. [Google Scholar] [CrossRef]
- Colli, M.; Sala, R.; Pirola, F.; Pinto, R.; Cavalieri, S.; Wæhrens, B.V. Implementing a Dynamic FMECA in the Digital Transformation Era; IFAC-PapersOnLine: Berlin, Germany, 2019. [Google Scholar]
- Zhang, P.; Qin, G.; Wang, Y. Risk Assessment System for Oil and Gas Pipelines Laid in One Ditch Based on Quantitative Risk Analysis. Energies 2019, 12, 981. [Google Scholar] [CrossRef]
- Heidary Dahooie, J.; Vanaki, A.S.; Firoozfar, H.R.; Zavadskas, E.K.; Čereška, A. An Extension of the Failure Mode and Effect Analysis with Hesitant Fuzzy Sets to Assess the Occupational Hazards in the Construction Industry. Int. J. Environ. Res. Public Health 2020, 17, 1442. [Google Scholar] [CrossRef]
- Zhou, X.; Tang, Y. Modeling and Fusing the Uncertainty of FMEA Experts Using an Entropy-Like Measure with an Application in Fault Evaluation of Aircraft Turbine Rotor Blades. Entropy 2018, 20, 864. [Google Scholar] [CrossRef]
- Idmessaoud, Y.; Guiochet, J.; Dubois, D. Questionnaire for Estimating Uncertainties in Assurance Cases. 2022. Available online: https://hal.laas.fr/hal-03649068/document (accessed on 28 April 2022).
- Yasko, A.; Babeshko, E.; Kharchenko, V. FMEDA-Based NPP I&C Systems Safety Assessment: Toward to Minimization of Experts’ Decisions Uncertainty. In Proceedings of the 24th International Conference on Nuclear Engineering, Charlotte, NC, USA, 26–30 June 2016. [Google Scholar]
- Yasko, A.; Babeshko, E.; Kharchenko, V. FMEDA and FIT-based safety assessment of NPP I&C systems considering expert uncertainty. In Proceedings of the 2018 26th International Conference on Nuclear Engineering, London, UK, 22–26 July 2018; pp. 231–238. [Google Scholar]
- Leontiiev, K.; Babeshko, I.; Kharchenko, V. Assumption Modes and Effect Analysis of XMECA: Expert based safety assessment. In Proceedings of the 2020 IEEE 11th International Conference on Dependable Systems, Services and Technologies (DESSERT), Kyiv, Ukraine, 14–18 May 2020; pp. 90–94. [Google Scholar]
- Illiashenko, O.; Babeshko, E. Choosing FMECA-Based Techniques and Tools for Safety Analysis of Critical Systems. Inf. Secur. Int. J. 2012, 28, 275–285. Available online: http://procon.bg/system/files/28.22_Illiashenko_Babeshko.pdf (accessed on 28 April 2022). [CrossRef]
- Kharchenko, V.; Illiashenko, O.; Kovalenko, A.; Sklyar, V.; Boyarchuk, A. Security Informed Safety Assessment of NPP I&C Systems: GAP-IMECA Technique. In Proceedings of the 2014 22nd International Conference on Nuclear Engineering, Prague, Czech Republic, 7–11 July 2014; Volume 3. [Google Scholar] [CrossRef]
- Kolisnyk, M. Vulnerability analysis and method of selection of communication protocols for information transfer in Internet of Things systems. Radioelectron. Comput. Syst. 2021, 1, 133–149. [Google Scholar] [CrossRef]
- Reliability Prediction of Electric Equipment. Department of Defense, Washington DC, USA, Tech. Rep. MIL-HDBK-217F, December 1991. Available online: https://s3vi.ndc.nasa.gov/ssri-kb/static/resources/MIL-HDBK-217F-Notice2.pdf (accessed on 28 April 2022).
- International Electro Technical Commission (Ed.) IEC TR 62380; Reliability Data Handbook—Universal Model for Reliability Prediction of Electronics Components, PCBs and Equipment; IEC: Geneva, Switzerland, 2005. [Google Scholar]
- International Electro Technical Commission (Ed.) IEC 61508; Functional Safety of Electrical/Electronic/Programmable Electronic Safety-Related Systems—Part 1–7; IEC: Geneva, Switzerland, 2010. [Google Scholar]
- Babeshko, E.; Kharchenko, V.; Leoniev, K.; Ruchkov, E. Practical aspects of operating and analytical reliability assessment of FPGA-based I&C systems. Radioelectron. Comput. Syst. 2020, 3, 75–83. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).