Uncertain Population Model with Jumps

Abstract

The uncertain population model (UPM), which has been proposed and studied, is a kind of population model driven by a Liu process that can only deal with continuous uncertain population systems. In reality, however, species systems may be suddenly shaken by earthquakes, tsunamis, epidemics, etc. The drastic changes lead to jumps in the population and make the sample path no longer continuous. In order to model the dramatic drifts embedded in an uncertain dynamic population system, this paper proposes a novel uncertain population model with jumps (UPMJ), which is described by a kind of uncertain differential equation with jumps (UDEJ). Then, the distribution function and the stability of solution for UPMJ are discussed based on uncertainty theory. Finally, a numerical example related to the transmission of Ebola virus is given to illustrate the characteristics of the distribution function and the stability of solution for UPMJ.

1. Introduction

The Malthus population model was proposed in 1798 [1], which describes how a population tends to grow at an exponential rate. The Malthus population model can only describe the population size over a short period of time because the constant growth rate cannot describe the population growth over a long period of time. For example, if the population growth rate is greater than zero, the population will always survive without extinction, which is unrealistic.

In 1923, Wiener [2] defined the Wiener process, which is a kind of random process with stationary and independent normal increments. Ito presented the Ito stochastic differential equation, which is a kind of differential equation driven by the Wiener process [3]. The stochastic population model characterized by Ito stochastic differential equation is path continuous.

In real life, the changes of many stochastic phenomena are discontinuous. The Poisson process is used to describe the stochastic discontinuous dynamic process, as shown in reference [3]. Lévy defined a class of random processes with stationary independent increments and right continuity based on probability measures, which is known as the Lévy process. Both the Wiener process and Poisson process are Lévy processes. Applications of the Lévy process can be found in reference [4].

Although the stochastic population model has been widely used in practice, stochastic population models are applied on the premise that the probability distribution function should be sufficiently close to the actual frequency of events. This requires a lot of sample data. Due to economic and technical reasons, it is sometimes impossible to obtain sample data in practice, so we can only rely on domain experts to estimate the possibilities of events’ occurrence and give their reliabilities. Because people generally overestimate the probability of unlikely events, sometimes if we use probability theory, we might make the wrong decision.

To address this issue, Liu [5] proposed uncertainty theory in 2007, which is a mathematical branch and simulates human uncertainty. In 2008, the uncertain process was introduced to describe the evolution of uncertain quantities. The uncertain differential equation is a kind of differential equation containing uncertain processes. The Liu process is a stable independent incremental process, and plays an essential role in uncertain analysis. There is also a kind of uncertain process with discontinuous path called uncertain renewal process (URP), which is used to characterize the evolution of discontinuous phenomena in an uncertain environment.

Recently, uncertain differential equations have become a main tool to handle uncertain dynamic systems. Lu et al. [6] studied a new stock model under uncertain conditions for the stock market. Shi and Sheng [7] discussed some concepts of stability of backward UDEs. Gu and Zhu [8] proposed a new Adams prediction correction method to solve UDE. Wang and Zhu [9] studied fractional delay differential equations with linear uncertainty. Yao and Liu [10] proposed the moment estimation method for parameter estimation of UDEs. Sheng et al. [11] discussed the principle of minimum noise by using the least square estimation method and obtained the parametric estimation of some special kinds of UDEs. Yao [12] presented a kind of UDE called UDEJ for dealing with discontinuous phenomena. A great number of research achievements have been obtained for UDE, see [13,14,15,16,17,18,19]. Uncertainty theory has been widely used in finance, engineering technology, physics medicine, and other fields.

In recent years, uncertainty theory has also been applied to the study of biological population models. In 2021, Jia and Liu [20] designed an optimal harvesting strategy of an uncertain logistic population model. Deng et al. [21] proved the inverse distribution theorem for the solution of an uncertain age-structured population equation. In 2017, Sheng et al. [22] proposed an UPM with age-structure. In 2020, Zhang and Yang [23] added an uncertain perturbation to the growth rate and obtained an uncertain Malthus population model. However, the above population model only applies to continuous dynamic uncertain systems because it is a kind of UDE driven by a Liu process. In practice, population systems are sometimes subjected to sudden shocks, such as droughts, floods, earthquakes, tsunamis, epidemics, etc. These phenomena can lead to jumps in the population. An UPM driven by a Liu process is no longer suitable for describing such phenomena. Based on this, this paper proposes a novel UPMJ, which is a kind of UDE driven by both a Liu process and an URP. The UPMJ can describe the dramatic drifts embedded in an uncertain population dynamic system.

The rest of this paper is arranged as follows. In Section 2, the UPMJ is developed. In Section 3, the solution of UPMJ is given, and the distribution function of solution is also discussed. In Section 4, we prove that stability of the solution in measure can be derived from stability in p-th moment for UPMJ when t is a finite number. A numerical example related to the transmission of Ebola virus is given to explain the distribution function and the stability of solution for UPMJ in Section 5. Finally, a brief summary is given in Section 6.

2. Uncertain Population Model with Jumps (UPMJ)

Suppose the number of species population at time t is P_t. The Malthus population model is

$$\frac{d{P}_t}{dt}=b{P}_t-d{P}_t,$$

(1)

where b and d are the birth and death rates, respectively, and they are constants. If we write r = b − d, then Equation (1) simplifies to

$$\frac{d{P}_t}{dt}=r{P}_t,$$

(2)

where r is called the population growth rate. For the given initial value P₀, Equation (2) has a solution

$$P_t=P_0\exp (rt).$$

Considering the various uncertainties of reality, Zhang and Yang [23] added an uncertain noise to the growth rate as follows

$$r\to r+\sigma \cdot \mathrm{noise},$$

where $\sigma$ is the intensity of the noise. The uncertain Malthus population model they presented is as follows

$$d{P}_t=r{P}_{t}dt+\sigma P_{t}d{C}_t$$

(3)

where $C_t$ is a continuous uncertain process called the Liu process, and the noise $\frac{d{C}_t}{dt}$ is an uncertain normal variable with expectation 0 and variance 1. Equation (3) has a solution

$$P_t=P_0\exp \left(rt+\sigma C_t\right).$$

In real-world situations, the species system may be subjected to sudden shocks, such as earthquakes, tsunamis, epidemics, etc. The drastic changes lead to jumps in the population, and the sample path becomes no longer continuous. An UDE driven by a Liu process is not appropriate for describing the dynamic process with jumps, while an UDEJ is available to portray such drastic drifts. Based on this, we add two different noises to the birth rate and death rate terms as follows

$$b\to b+{\sigma }_1“\mathrm{noise}1”,-d\to -d+{\sigma }_2“\mathrm{noise}2”,$$

where ${\sigma }_1$ and ${\sigma }_2$ are the intensity of noise 1 and noise 2, respectively.

Case I. Suppose the drastic drifts embedded in the death rate, then noise 2 is characterized by $\frac{d{N}_t}{dt}$, and noise 1 is characterized by $\frac{d{C}_t}{dt}$ as follows

$$b\to b+{\sigma }_1\frac{d{C}_t}{dt},-d\to -d+{\sigma }_2\frac{d{N}_t}{dt},$$

where $C_t$ is a continuous uncertain process called Liu process, and $N_t$ is a discontinuous uncertain process called URP. Thus, we propose the UPMJ as shown below

$$d{P}_t=\left(b{P}_{t}dt+{\sigma }_1{P}_{t}d{C}_t\right)+\left(-d{P}_{t}dt+{\sigma }_2{P}_{t}d{N}_t\right).$$

(4)

For simplicity,

$$d{P}_t=r{P}_{t}dt+{\sigma }_1{P}_{t}d{C}_t+{\sigma }_2{P}_{t}d{N}_t.$$

(5)

Case II. Suppose the dramatic drifts embedded in the birth rate, then noise 1 is characterized by $\frac{d{N}_t}{dt}$, and noise 2 is characterized by $\frac{d{C}_t}{dt}$ as follows

$$b\to b+{\sigma }_1\frac{d{N}_t}{dt},-d\to -d+{\sigma }_2\frac{d{C}_t}{dt}.$$

In this case, the same model as Equation (5) is obtained. Therefore, in the uncertain environment, UPMJ can be obtained whether the sharp drifts are embedded in the birth rate or the death rate. It is a proper model to deal with the uncertain discontinuous dynamic population system.

3. Solution of UPMJ

In this section, we will further discuss the solution of UPMJ and the distribution function of the solution.

Theorem 1.

Let$N_t$be an URP with iid uncertain interarrival times  ${\eta }_1,{\eta }_2,\cdots$, and  $C_t$ be a Liu process. Define $T_0=0$ and $T_n={\eta }_1+{\eta }_2+\cdots +{\eta }_n$ for  $n\ge 1.$ Suppose $r,$ ${\sigma }_1$ and ${\sigma }_2$ are three given real numbers. If the initial population size $P_0$ is given, then UPMJ

$$d{P}_t=r{P}_{t}dt+{\sigma }_1{P}_{t}d{C}_t+{\sigma }_2{P}_{t}d{N}_t,$$

has a solution

$$P_t=P_0\exp \left(rt+{\sigma }_1{C}_t\right)\cdot {(1+{\sigma }_2)}^{N_t}.$$

(6)

Proof. 

Note that $C_t(\gamma )$ is path continuous, we discuss differential equation

$$d{P}_t(\gamma )=r{P}_t(\gamma )dt+{\sigma }_1{P}_t(\gamma )d{C}_t(\gamma )+{\sigma }_2{P}_t(\gamma )d{N}_t(\gamma ),P_0(\gamma )=P_0.$$

(7)

For any given time $v$, we prove that UDE (7) has a unique solution on the interval $[0,v].$ Suppose $N_v(\gamma )=n,$ i.e., $T_n(\gamma )\le v<T_{n+1}(\gamma )$. For any $t\in \left[0,T_1(\gamma )\right)$, we have $d{N}_t(\gamma )=0$. Then, UDE (7) degenerates to

$$d{P}_t(\gamma )=r{P}_t(\gamma )dt+{\sigma }_1{P}_t(\gamma )d{C}_t(\gamma ),P_0(\gamma )=P_0.$$

(8)

UDE (8) has a solution. $P_t(\gamma )=P_0\exp \left(rt+{\sigma }_1{C}_t(\gamma )\right)$ in $\left[0,T_1(\gamma ).\right)$

At the time $T_1(\gamma )$, a jump occurs. So

$$\begin{array}{l}{P}_{T_1}(\gamma )=\underset{t\to {(T_1(\gamma ))}^{-}}{\lim }{P}_t(\gamma )+{\sigma }_2\cdot \underset{t\to {(T_1(\gamma ))}^{-}}{\lim }{P}_t(\gamma )\\ =P_0\exp \left({\displaystyle {\int }_0^{T_1(\gamma )}rds}+{\displaystyle {\int }_0^{T_1(\gamma )}{\sigma }_{1}d{C}_s(\gamma )}\right)\left(1+{\sigma }_2\right)\\ =P_0\exp \left(r{T}_1(\gamma )+{\sigma }_1{C}_{T_1}(\gamma )\right)\left(1+{\sigma }_2\right).\end{array}$$

On the interval $\left[T_1(\gamma ),T_2(\gamma )\right)$, $d{N}_t(\gamma )=0$, and UDE (7) degenerates to

$$d{P}_t(\gamma )=r{P}_t(\gamma )dt+{\sigma }_1{P}_t(\gamma )d{C}_t(\gamma ),P_0(\gamma )=P_{T_1}(\gamma ).$$

(9)

In $\left[T_1(\gamma ),T_2(\gamma )\right)$ UDE (9) has a solution

$$\begin{array}{l}{P}_t(\gamma )=P_{T_1}(\gamma )\exp \left({\displaystyle {\int }_{T_1(\gamma )}^{t}rds}+{\displaystyle {\int }_{T_1(\gamma )}^t{\sigma }_{1}d{C}_s(\gamma )}\right)\\ =P_0\exp \left({\displaystyle {\int }_0^{t}rds}+{\displaystyle {\int }_0^t{\sigma }_{1}d{C}_s(\gamma )}\right)\left(1+{\sigma }_2\right)\\ =P_0\exp \left(rt+{\sigma }_{1}d{C}_t(\gamma )\right)\left(1+{\sigma }_2\right).\end{array}$$

At the time $T_2(\gamma )$, a jump occurs. So

$$\begin{array}{l}{P}_{T_2}(\gamma )=\underset{t\to {\left(T_2(\gamma )\right)}^{-}}{\lim }{P}_t(\gamma )+{\sigma }_2\cdot \underset{t\to {\left(T_2(\gamma )\right)}^{-}}{\lim }{P}_t(\gamma )\\ =P_0\exp \left({\displaystyle {\int }_0^{T_2(\gamma )}rds}+{\displaystyle {\int }_0^{T_2(\gamma )}{\sigma }_{1}d{C}_s(\gamma )}\right){\left(1+{\sigma }_2\right)}^2\\ =P_0\exp \left(r{T}_2(\gamma )+{\sigma }_1{C}_{T_2}(\gamma )\right){\left(1+{\sigma }_2\right)}^2.\end{array}$$

Repeating the process,

$$\begin{array}{l}{P}_{T_n}(\gamma )=P_0\exp \left({\displaystyle {\int }_0^{T_n(\gamma )}rds}+{\displaystyle {\int }_0^{T_n(\gamma )}{\sigma }_{1}d{C}_s(\gamma )}\right){\displaystyle \prod _{i=1}^n\left(1+{\sigma }_2\right)}\\ =P_0\exp \left(r{T}_n(\gamma )+{\sigma }_1{C}_{T_n}(\gamma )\right){\displaystyle \prod _{i=1}^n\left(1+{\sigma }_2\right)}.\end{array}$$

On $[T_n(\gamma ),v)$, we obtain $d{N}_t(\gamma )=0$, and UDE (7) degenerates to

$$d{P}_t(\gamma )=r{P}_t(\gamma )dt+{\sigma }_1{P}_t(\gamma )d{C}_t(\gamma ),P_0(\gamma )=P_{T_n}(\gamma ).$$

(10)

In $[T_n(\gamma ),v)$, UDE (10) has a solution

$$\begin{array}{c}{P}_v(\gamma )=P_{T_n}(\gamma )\exp \left({\displaystyle {\int }_{T_n(\gamma )}^{v}rds}+{\displaystyle {\int }_{T_n(\gamma )}^v{\sigma }_{1}d{C}_s(\gamma )}\right)\\ =P_0\exp \left({\displaystyle {\int }_0^{v}rds}+{\displaystyle {\int }_0^v{\sigma }_{1}d{C}_s(\gamma )}\right){\displaystyle \prod _{i=1}^n\left(1+{\sigma }_2\right)}\\ =P_0\exp \left(rv+{\sigma }_{1}d{C}_v(\gamma )\right){\displaystyle \prod _{i=1}^{N_v(\gamma )}\left(1+{\sigma }_2\right)}.\end{array}$$

Then, UDE (7) has a unique solution on the interval $[0,v].$ Thus, UPMJ has a solution

$$P_t=P_0\exp \left(rt+{\sigma }_1{C}_t\right)\cdot {(1+{\sigma }_2)}^{N_t}.$$

The theorem is proven. □

Lemma 1

(Liu [24]). Let $N_t$ be an uncertain renewal process with iid positive uncertain interarrival times ${\eta }_1,{\eta }_2,\cdots$. If $\varphi (x)$ is the common regular uncertainty distribution of those interarrival times, then $N_t$ has an uncertainty distribution

$${\mathsf{\Upsilon }}_t(z)=1-\varphi \left(\frac{t}{\left[z\right]+1}\right),\forall z\ge 0,$$

(11)

where $\left[z\right]$ represents the maximal integer less than or equal to$z.$

Theorem 2.

Let  $N_t$ be an URP, and  $C_t$ be a Liuprocess.  $C_t$ has an uncertain distribution  ${\Phi }_t(y)$, and  $N_t$ has an uncertain distribution  ${\mathsf{\Upsilon }}_t(z)$, where $z\ge 0$. Suppose $N_t$ and $C_t$ are mutually independent uncertain variables. If  $P_t=P_0\exp \left(rt+{\sigma }_1{C}_t\right){\left(1+{\sigma }_2\right)}^{N_t}$ , where  ${\sigma }_1>0,{\sigma }_2>0,$ then the uncertain variable  $P_t$ has an uncertain distribution

$$\mathsf{\Psi }(x)=\underset{f(y,z)=x}{\sup }{\mathsf{\Phi }}_t(y)\wedge {\mathsf{\Upsilon }}_t(z),$$

(12)

where $f(y,z)=P_0\exp \left(rt+{\sigma }_{1}y\right){\left(1+{\sigma }_2\right)}^z.$

Proof. 

Because ${\sigma }_1>0,{\sigma }_2>0$ and $f(C_t,N_t)=P_0\exp \left(rt+{\sigma }_1{C}_t\right){\left(1+{\sigma }_2\right)}^{N_t}$, $f(C_t,N_t)$ increases strictly with respect to $C_t$ and $N_t$. We have

$$\left\{P_t\le x\right\}=\left\{f(C_t,N_t)\le x\right\}=\underset{f(y,z)=x}{\cup }(C_t\le y)\cap (N_t\le z).$$

(13)

Then

$$\mathsf{\Psi }(x)=M\left\{f(C_t,N_t)\le x\right\}=M\left\{\underset{f(y,z)=x}{\cup }(C_t\le y)\cap (N_t\le z)\right\}.$$

(14)

For any given number $x$, the event

$$\underset{f(y,z)=x}{\cup }(C_t\le y)\cap (N_t\le z),$$

is a polyrectangle. From the polyrectangular theorem [5], we get

$$\begin{gathered} \begin{array}{l}\mathsf{\Psi }(x)=\underset{f(y,z)=x}{\sup }M\left\{(C_t\le y)\cap (N_t\le z)\right\}\\ =\underset{f(y,z)=x}{\sup }M\left\{C_t\le y\right\}\wedge M\left\{N_t\le z\right\}\end{array} \\ =\underset{f(y,z)=x}{\sup }{\Phi }_t(y)\wedge {\Upsilon }_t(z). \end{gathered}$$

The theorem is proven. □

4. Stability Analysis

The stability of solution for UPMJ is of great significance in practice, which implies insensitivity of the uncertain dynamic population system when a small perturbation is added to the initial state. Many concepts of stability for UDEJ have been studied. Up to now, there are mainly six kinds of stability for UDEJ. The stability in measure for UDEJ was first presented by Yao [12]. Subsequently, Ji and Ke [25] investigated almost sure stability for UDEJ. Ma et al. [26] focused on the stability in p-th moment for UDEJ. Liu [27] gave exponential stability for UDEJ. Gao [28] researched the stability in mean for UDEJ. Liu et al. [29] studied a new p-th moment exponential stability for UDEJ.

When $t\ge 0$, the stability in p-th moment for UDEJ has been studied in reference [26]. By the definition, it can be proven that UPMJ is unstable in the p-th moment. However, in practice, the model is usually applied when t is a finite number. Extending the previous work on the stability of UDEJ, this paper will develop new concepts of stability in the p-th moment and stability in measure for UDEJ when t is a finite number, and the relationship between them is also discussed.

Definition 1.

Suppose$T$is a finite positive number, and$t\in \left[0,T\right]$. Let$X_t$and$Y_t$be solutions of UDEJ

$$d{P}_t=f(t,P_t)dt+g(t,P_t)d{C}_t+h(t,P_t)d{N}_t,$$

with initial values$X_0$and$Y_0$, respectively. Then we say that UDEJ is stable in p-th moment if

$$\underset{\left|X_0-Y_0\right|\to 0}{\lim }E\left\{\underset{0\le t\le T}{\sup }{\left|X_t-Y_t\right|}^p\right\}=0,p>0.$$

(15)

Definition 2.

Suppose$T$is a finite positive number, and$t\in \left[0,T\right]$. Let$X_t$and$Y_t$be solutions of UDEJ

$$d{P}_t=f(t,P_t)dt+g(t,P_t)d{C}_t+h(t,P_t)d{N}_t,$$

with initial values$X_0$and$Y_0$, respectively. Then we say that UDEJ is stable in measure if for each given number$\epsilon >0$,

$$\underset{\left|X_0-Y_0\right|\to 0}{\lim }M\left\{\underset{0\le t\le T}{\sup }\left|X_t-Y_t\right|\le \epsilon \right\}=1.$$

(16)

Theorem 3.

Suppose $T$is a finite positive number, and$t\in \left[0,T\right]$. Let$X_t$and$Y_t$be solutions of UPMJ

$$d{P}_t=r{P}_{t}dt+{\sigma }_1{P}_{t}d{C}_t+{\sigma }_2{P}_{t}d{N}_t,$$

with initial values$X_0$and$Y_0$, respectively. Then UPMJ is stable in p-th moment.

Proof. 

The solutions with initial values $X_0$ and $Y_0$ are

$$X_t=X_0\exp \left(rt+{\sigma }_1{C}_t\right){\left(1+{\sigma }_2\right)}^{N_t},$$

(17)

and

$$Y_t=Y_0\exp \left(rt+{\sigma }_1{C}_t\right){\left(1+{\sigma }_2\right)}^{N_t},$$

(18)

respectively. Since

$$\left|X_t-Y_t\right|=\left|X_0-Y_0\right|\exp \left(rt+{\sigma }_1{C}_t\right){\left(1+{\sigma }_2\right)}^{N_t}\to 0$$

(19)

when $\left|X_0-Y_0\right|\to 0$ and $0\le t\le T$, we can get

$$\underset{\left|X_0-Y_0\right|\to 0}{\lim }E\left\{\underset{0\le t\le T}{\sup }{\left|X_t-Y_t\right|}^p\right\}=0,p>0.$$

According to Definition 1, UPMJ is stable in p-th moment. □

Theorem 4.

Suppose$T$is a finite positive number, and$t\in \left[0,T\right]$. Let$X_t$and$Y_t$be solutions of UPMJ

$$d{P}_t=r{P}_{t}dt+{\sigma }_1{P}_{t}d{C}_t+{\sigma }_2{P}_{t}d{N}_t,$$

with initial values$X_0$and$Y_0$, respectively. Then UPMJ is stable in measure.

Proof. 

The solutions with initial values $X_0$ and $Y_0$ are

$$X_t=X_0\exp \left(rt+{\sigma }_1{C}_t\right){\left(1+{\sigma }_2\right)}^{N_t},$$

and

$$Y_t=Y_0\exp \left(rt+{\sigma }_1{C}_t\right){\left(1+{\sigma }_2\right)}^{N_t},$$

respectively. Since

$$\left|X_t-Y_t\right|=\left|X_0-Y_0\right|\exp \left(rt+{\sigma }_1{C}_t\right){\left(1+{\sigma }_2\right)}^{N_t}\to 0,$$

(20)

when $\left|X_0-Y_0\right|\to 0$ and $0\le t\le T$, we can get

$$\underset{\left|X_0-Y_0\right|\to 0}{\lim }M\left\{\underset{0\le t\le T}{\sup }\left|X_t-Y_t\right|\le \epsilon \right\}=1.$$

According to Definition 2, UPMJ is stable in measure. □

Next, we prove the stability in measure can be derived from the stability in p-th moment for UPMJ when t is a finite number.

Theorem 5.

Suppose$T$is a finite positive number, and$t\in \left[0,T\right]$. If UPMJ

$$d{P}_t=r{P}_{t}dt+{\sigma }_1{P}_{t}d{C}_t+{\sigma }_2{P}_{t}d{N}_t,$$

is stable in$p$-th moment, then it is stable in measure.

Proof. 

By Definition 1, for solutions $X_t$ and $Y_t$ with initial values $X_0$ and $Y_0$, respectively, we have

$$\underset{\left|X_0-Y_0\right|\to 0}{\lim }E\left\{\underset{0\le t\le T}{\sup }{\left|X_t-Y_t\right|}^p\right\}=0,p>0.$$

According to Markov inequality, for each given real number $\epsilon >0$, we have

$$\underset{\left|X_0-Y_0\right|\to 0}{\lim }M\left\{\underset{0\le t\le T}{\sup }\left|X_t-Y_t\right|\ge \epsilon \right\}\le \frac{1}{{\epsilon }^p}\underset{\left|X_0-Y_0\right|\to 0}{\lim }E\left[\underset{0\le t\le T}{\sup }{\left|X_t-Y_t\right|}^p\right]=0.$$

(21)

Thus, we can get

$$\underset{\left|X_0-Y_0\right|\to 0}{\lim }M\left\{\underset{0\le t\le T}{\sup }\left|X_t-Y_t\right|\le \epsilon \right\}=1,$$

for each given real number $\epsilon >0$. The theorem is proven. □

5. A Numerical Example

In this section, a numerical example related to the transmission of Ebola virus is given to explain the distribution function and the stability of solution for UPMJ. Ebola virus is a kind of virulent infectious disease that can cause blood fever in humans and animals and has an unusually high mortality rate. For example, a small city has seen a large number of deaths due to the spread of Ebola virus, and this leads to jumps in the population. The UPMJ proposed in this paper is suitable for dealing with such uncertain dynamic population systems with sharp drift. In Section 5.1 and Section 5.2, we discuss the disturbances on the birth and death rates resulting from the spread of the Ebola virus.

5.1. The Disturbance on Birth Rate

Due to the spread of Ebola virus, the birth rate b is disturbed as follows

$$b\to b+{\sigma }_1\frac{d{C}_t}{dt},$$

where $C_t$ is a Liu process and ${\sigma }_1$ is the intensity of disturbance. Liu process $C_t$ has an uncertain distribution

$${\mathsf{\Phi }}_t(y)={\left(1+\exp \left(1-\frac{\pi y}{\sqrt{3}t}\right)\right)}^{-1}.$$

(22)

Set $t=10$ and $t=30$. When y falls between $-150$ and $150$, we get two uncertain distributions of Liu process $C_t$, as shown in Figure 1. It can be observed in Figure 1 that ${\mathsf{\Phi }}_t(y)$ is a continuous and monotone increasing function. This indicates that the spread of Ebola virus has caused a continuous perturbation on the birth rate.

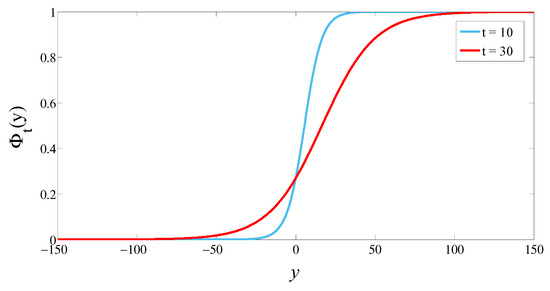
Figure 1. Uncertain distribution ${\mathsf{\Phi }}_t(y)$ of Liu process $C_t$.

5.2. The Disturbance on Death Rate

Due to the spread of Ebola virus, the death rate $d$ is disturbed as follows

$$-d\to -d+{\sigma }_2\frac{d{N}_t}{dt},$$

where $N_t$ is an URP, and ${\sigma }_2$ is the intensity of disturbance. In the following, the distribution function of URP $N_t$ is discussed.

Assume those interarrival times ${\eta }_1,{\eta }_2,\cdots$ in Lemma 1 are linear uncertain variables, and they have a same linear uncertainty distribution as follows

$$\varphi (x)=\left\{\begin{array}{cc}0,& ifx\le a;\\ (x-a)/(c-a),& ifa\le x\le c;\\ 1,& ifx\ge c.\end{array}\right.$$

(23)

Suppose $a=1$, $c=10$, $t=15$, and $z$ changes gradually from $0$ to $15$, we get the uncertain distribution ${\mathsf{\Upsilon }}_t(z)=1-\varphi \left(\frac{t}{\left[z\right]+1}\right)$ shown in Figure 2. It can be observed in Figure 2, ${\mathsf{\Upsilon }}_t(z)$ is not continuous, but is a right continuous and increasing step function. Furthermore, we can see that ${\mathsf{\Upsilon }}_t(z)$ does not jump at time $0$ and it has at most one renewal at a time. This indicates that there are dramatic shifts embedded in the death rate due to the spread of Ebola virus, and these sudden environmental disturbances are discontinuous, causing the distribution function ${\mathsf{\Upsilon }}_t(z)$ to jump intermittently again and again.

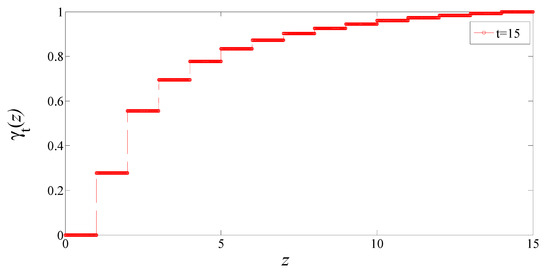
Figure 2. Uncertain distribution ${\mathsf{\Upsilon }}_t(z)$ of URP $N_t$.

Remark 1.

According to the elementary renewal theorem [24], the average renewal number

$$\frac{N_t}{t}\to \frac{1}{{\eta }_1},$$

(24)

in the sense of convergence in distribution as$t\to \infty$.

Remark 2.

According to the elementary renewal theorem [24], if$E\left[\frac{1}{{\eta }_1}\right]$exists, then

$$\underset{t\to \infty }{\lim }\frac{E\left[N_t\right]}{t}=E\left[\frac{1}{{\eta }_1}\right].$$

(25)

5.3. Uncertain Distribution $\Psi (x)$ of Solution $P_t$

Suppose the people of the small city at time $t$ is $P_t$, and the initial population size $P_0$ is 50,000. The UPMJ related to the transmission of Ebola virus is as follows

$$d{P}_t=\left(b{P}_{t}dt+{\sigma }_1{P}_{t}d{C}_t\right)+\left(-d{P}_{t}dt+{\sigma }_2{P}_{t}d{N}_t\right).$$

Since

$$r=b-d,$$

for simplicity,

$$d{P}_t=r{P}_{t}dt+{\sigma }_1{P}_{t}d{C}_t+{\sigma }_2{P}_{t}d{N}_t.$$

According to Theorem 1, the UPMJ related to the transmission of Ebola virus has a solution

$$P_t=P_0\exp \left(rt+{\sigma }_1{C}_t\right){\left(1+{\sigma }_2\right)}^{N_t},$$

where $C_t$ and $N_t$ are independent uncertain variables. In this section, the distribution function of solution $P_t$ is studied. Parameters concerning UPMJ related to the transmission of Ebola virus including $P_0$, $r$, ${\sigma }_1$, ${\sigma }_2$, $a$, $c$, $y$, and $z$ are summarized in Table 1.

Table 1. Model parameter values.

Parameters	Values	Unit	Sources
$P_0$	50,000	Person	Assumption
$t$	15	Month	Assumption
$r$	0.02	Non-dimensional	Assumption
${\sigma }_1$	0.01	Non-dimensional	Assumption
${\sigma }_2$	0.01	Non-dimensional	Assumption
$a$	1	Non-dimensional	Assumption
$c$	10	Non-dimensional	Assumption
$y$	[–150, 150]	Non-dimensional	Assumption
$z$	[0, 15]	Non-dimensional	Assumption

By Theorem 2, the solution $P_t$ has an uncertain distribution

$$\mathsf{\Psi }(x)=\underset{f(y,z)=x}{\sup }{\mathsf{\Phi }}_t(y)\wedge {\mathsf{\Upsilon }}_t(z).$$

where $f(y,z)=P_0\exp \left(rt+{\sigma }_{1}y\right){\left(1+{\sigma }_2\right)}^z$. When $x$ changes gradually from 0 to 120,000, we get the uncertain distribution $\mathsf{\Psi }(x)$ of solution $P_t$, as shown in Figure 3. It can be observed that $\mathsf{\Psi }(x)$ is a continuous and increasing function. Furthermore, Figure 3 indicates that the spread of Ebola virus has caused intermittent pauses in the population.

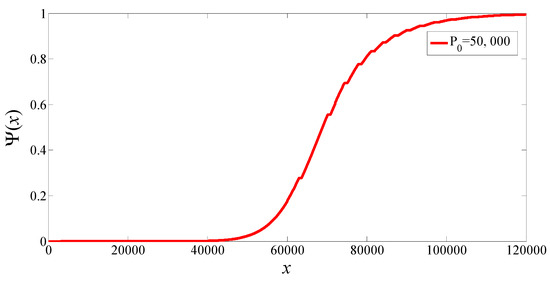
Figure 3. Uncertain distribution $\mathsf{\Psi }(x)$ of solution $P_t$.

5.4. Stability Analysis of UPMJ

The stability for UPMJ related to the transmission of Ebola virus is of great significance in practice. The UPMJ is stable, meaning that any small changes in the initial value will not result in a substantial effect on the uncertain dynamic population system. Parameters including $t$, $r$, ${\sigma }_1$, ${\sigma }_2$, $a$, $c$, $y$, and $z$ are also shown in Table 1. Let P₀ = 50,000 and P₀ = 50,500, when $x$ ranges gradually from 0 to 120,000, the uncertain distributions $\mathsf{\Psi }(x)$ of solution $P_t$ are shown in Figure 4. It can be seen that when the initial value $P_0$ increases from 50,000 to 50,500, the uncertain distribution $\mathsf{\Psi }(x)$ is not sensitive, indicating that the UPMJ under the background of Ebola virus spread is stable. Figure 4 is in line with our expectation, which can provide certain theoretical basis for decision-makers to make decisions.

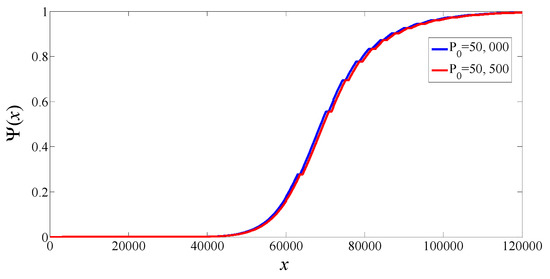
Figure 4. Stability of UPMJ related to the transmission of Ebola virus.

6. Conclusions

In this paper, an UPMJ is established to simulate dramatic drifts embedded in an uncertain population dynamic system. In addition, the characteristics of the distribution function and the stability of solution for the UPMJ are illustrated via a numerical example related to the transmission of Ebola virus.

It is obvious that our work is just the first step to study uncertain population systems subjected to sudden shocks. Recently, using mathematical models to solve practical problems has attracted the attentions of more and more scholars. This paper only discusses an UPMJ in an uncertain environment from the theoretical aspect. For future work, applications of the UPMJ could be studied.

In practice, without any historical data, Liu [24] proposed a questionnaire survey method to obtain expert experience data. Then, he proposed the linear interpolation method and Delphi method to obtain the empirical uncertainty distribution according to the obtained expert experience data. The unknown parameters in the empirical uncertainty distribution are estimated by the least square multiplication and moment method.

Of course, the researchers can further study with only a small amount of historical data. Lio and Liu [30] proposed the uncertain maximum likelihood function estimation method to estimate the unknown parameters in the model. The uncertain likelihood function was defined as

$$L(\theta \left|x_1\right.,x_2,\dots ,x_n)=\underset{i=1}{\overset{n}{\wedge }}{F}^{\prime }(x_i\left|\theta \right.),$$

(26)

where $\theta$ is a vector of unknown parameters, $x_1,x_2,\dots ,x_n$ are the observed values of the sample, and $F^{\prime }$ is the derivative of the uncertainty distribution function of the sample. According to the theory of uncertain maximum likelihood estimation, the estimation of unknown parameters is given by

$${\theta }^{\ast }=\underset{\theta }{\arg \max }L(\theta \left|x_1\right.,x_2,\dots ,x_n).$$

(27)

Our future work will apply the ideas and methods proposed by Liu [24] and Lio and Liu [30] to study the applications of the UPMJ.