Abstract
We present a DPLL SAT solver, which we call TrueSAT, developed in the verification-enabled programming language Dafny. We have fully verified the functional correctness of our solver by constructing machine-checked proofs of its soundness, completeness, and termination. We present a benchmark of the execution time of TrueSAT and we show that it is competitive against an equivalent DPLL solver implemented in C++, although it is still slower than state-of-the-art CDCL solvers. Our solver serves as a significant case study of a machine-verified software system. The benchmark also shows that auto-active verification is a promising approach to increasing trust in SAT solvers, because it combines execution speed with a high degree of trustworthiness.
MSC:
68T15; 03B35
1. Introduction
Modern high-performance SAT solvers can efficiently handle large satisfiability instances that occur in practice and they have many practical applications ranging from software and hardware verification to combinatorial optimization.
For maximal performance, state-of-the-art high-performance SAT solvers implement advanced algorithms and data structures with an inherent degree of conceptual complexity. Due to the subtleties involved in the implementation and the many possible corner cases, SAT solvers might contain bugs, which invalidate the trust in their result. Furthermore, such errors might not be found in the usual process of testing the solver, as shown by Brummayer and others [1], who have used fuzzing to find serious soundness bugs in state-of-the-art SAT solvers.
To mitigate this issue for satisfiable instances, SAT solvers can easily output a satisfying truth assignment, which serves as a witness that can be independently checked by another computer program. This increases the degree of confidence in the result of the solver.
For unsatisfiable instances, the situation is somewhat less nice. Since 2016, the annual Satisfiability Competition requires SAT solvers competing in the main track to also output UNSAT certificates [2]. These serve as witnesses for the unsatisfiability of the instance and they can also be checked independently by another computer program; however, unlike satisfiability witnesses, certificates for unsatisfiability could be exponentially large, the SAT solver might not even be able to output them due to various resource constraints, and checking the certificate could also be computationally intensive.
Additionally, checking SAT and UNSAT certificates generated by SAT solvers is not the ideal way to increase the trust in their output, because such a check must be performed for every run of the solver.
We propose a fully verified SAT solver, which is more trustworthy. We have implemented our solver, TrueSAT (for trusted and efficient SAT solver), in the Dafny system [3]. Dafny is a high-level imperative programming language with some object oriented features. Its main characteristic is that all methods in the project can be formally specified by using preconditions, postconditions, and invariants. The specifications are checked at compilation time by using the satisfiability modulo theories (SMT) solver Z3 [4]. If a postcondition cannot be established (either due to a timeout or due to the fact that it does not hold), compilation fails; therefore, we can place a high degree of trust in a program verified using the Dafny system. For readers unfamiliar with the Dafny system, we feature a brief overview in Section 3.
Typical modern high-performance SAT solvers implement a backtracking-based algorithm that searches for a truth assignment satisfying the input formula. As the search space is exponentially large, several algorithmic improvements to the search are necessary in order for the solvers to be fast:
- A
- Unit Propagation. Also called boolean constraint propagation, this is a core optimization in high-performance SAT solvers [5]. It refers to the idea of speeding up the search process by using unit clauses, which are clauses whose literals are all currently false, except for one, whose value is not yet set. For every unit clause, the value of the unset literal must be true in any satisfying assignment. Forcing these literals to be true in the current assignment is called unit propagation.
- B
- Fast Data Structures. In order to perform unit propagation as efficiently as possible, the solver must be able to quickly identify unit clauses. To this end, the solver either maintains for each clause counters with the number of literals currently known to be true (resp. false) [5], or uses lazy data structures [6,7].
- C
- Variable Ordering Heuristics. The search space might be very different depending on the order in which the propositional variables are assigned. Variable ordering heuristics use information such as the number of occurrences of a variable in the formula to guide the algorithm [8] by choosing variables in a order that typically reduces the search space.
- D
- Backjumping. In typical backtracking search algorithms, if the current truth assignment does not satisfy the formula, we go one level up in the search tree and reset the value of the last assigned variable. Backjumping [9] takes this idea a step further: if the reason that the current assignment does not satisfy the formula is a variable that has been set earlier, we may go up several levels, thereby improving speed.
- E
- Conflict Analysis. This improvement is intimately tied to backjumping. The idea is to analyze the conflict clause, a clause that is not satisfied by the current assignment, in order to identify a level to which to backjump that is as early as possible [10] in the search tree.
- F
- Clause Learning and Forgetting. Introduced in the GRASP solver [10], clause learning means that, each time a conflict is found in the search, a clause that explains the conflict is added to the initial formula. The idea is that the learned clause is logically entailed by the initial formula and therefore does not change its satisfiability status. The learned clause however prevents the same conflict from manifesting in the future, thereby reducing the search space. Because not all learned clauses are useful, a strategy to delete (forget) such clauses is also typically used.
- G
- Restart Strategy. In addition to using variable ordering heuristics, SAT solvers sometimes choose the next variable to assign in a random manner. This makes the search nondeterministic and the running times follow a heavily tailed distribution [11]. To improve on this distribution, SAT solvers regularly drop the current assignment [12] and start the search process over, a process known as restarts.
In addition to the ideas above, all of which are algorithmic in nature, careful engineering choices in the implementation are also necessary for maximum efficiency.
The algorithm consisting of items A, B, and C is usually referred to as the Davis–Putnam–Logemann–Loveland (DPLL) algorithm [13,14]. SAT solvers extending DPLL with the ideas D, E, F, and G are called conflict-driven clause learning (CDCL) solvers [10,15] and they are the most efficient solvers known.
We have implemented, specified, and fully verified in the Dafny system items A, B, and C, which make up the DPLL algorithm. We leave the further items (D–G) for future work. For variable ordering, we have chosen to base our solver on the maximum occurrence in clauses of minimum size (MOMS) heuristic [8]. Our Danny solver has machine-checked proofs of soundness, completeness, and termination. It takes as input a formula that is in conjunctive normal form (CNF); it does not perform the CNF conversion, although the CNF conversion has been verified [16] independently of this work. The parser, which reads the input formula from a file in the DIMACS format, has also been written in Dafny. The parser is therefore also verified not to contain, for example, bugs such as out-of-bounds errors; however, we do not provide a full functional specification for the parser. Specifying the parser as a function from strings to CNF formulae and proving its correctness is an orthogonal concern. Parsing is therefore the only part of our solver that must be trusted without a computer-checked proof.
Our work is part of a larger research context where artefacts such as mathematical statements [17] or computer software ranging from compilers [18] to system software [19,20,21,22] are computer-verified for correctness.
The main difference between our solver, TrueSAT, and previous work on verified or certified SAT solvers is that we have directly verified an imperative implementation of the DPLL algorithm using deductive verification. Other approaches might verify, for example, functional code, and rely on a mechanism to refine the functional code or to extract it into imperative code, but this could make the resulting solver less efficient. We have benchmarked our verified implementation and it is roughly as efficient as a C++ implementation of the same algorithm. Because it does not implement CDCL (only DPLL), it is still one order of magnitude slower than that of a state-of-the-art verified solver and two orders of magnitude slower than a state-of-the-art unverified solver. Despite currently being less efficient than the best verified solver, our solver has the potential to meet the efficiency of unverified solvers once it is extended to implement the full CDCL algorithm.
Structure. In Section 2, we recall the DPLL algorithm. In Section 3, we feature a brief overview of the Dafny system and of auto-active (assertional) proofs, the verification style used in Dafny. In Section 4, we present TrueSAT, our verified DPLL implementation in Dafny. We first present its most important data structures, together with their invariants (Section 4.1). In Section 4.2, we then go over the main operations that our data structures support. We present the core of our DPLL implementation, its specification, and discuss the guarantees that it provides in Section 4.3. In Section 5, we benchmark the performance of our solver. In Section 6, we discuss related work. We conclude in Section 7. We also discuss here the main challenges faced in the verification process, together with a set of verification patterns that we have identified and used in order to make the entire process feasible.
Contributions. We present the first (to our knowledge) assertional proof of the DPLL algorithm. The implementation is competitive in running time with an equivalent C++ solver. Our solver also has value as a significant case study for the Dafny system.
Comparison with the workshop version. This paper is a revised and extended version of our previous work [23] published in the Third Working Formal Methods Symposium, in 2019. We feature an improved presentation, additional explanations, and a benchmark of the performance of our solver. In addition, the solver has been significantly improved over the workshop version:
- The new implementation features machine integers, which improve performance approximately 10 times in our tests. Going to machine integers from unbounded integers requires proving upper bounds on indices throughout the code.
- The new implementation features mutable data structures for identifying unit clauses. Our previous approach used Dafny sequences (seq), which are immutable and cause a performance drawback because they are updated frequently. The new mutable data structures make the solver significantly faster, but they are more difficult to reason about and verify.
- We have implemented and verified a variable ordering heuristic.
- We have also improved the methodology of our verification approach. In particular we have significantly reduced verification time. By carefully specifying invariants and separating concerns in the implementation, the verification time is now approximately 5 min for the entire project.In contrast, in our previous implementation, one method (setLiteral) took approximately 10 min to verify on its own (the entire project used to take about 2 h to verify in its entirety).
2. The DPLL Algorithm
DPLL can be seen as an optimized version of searching for a truth assignment that satisfies the input formula. If such an assignment is found, then the formula is satisfiable. If no such assignment is found, the formula is unsatisfiable.
The search tree is pruned whenever the current assignment makes the formula false. The main improvement in DPLL is to use a form of deduction called unit propagation to speed up the search.
A clause is called unit if it has the following property: all of its literals are false in the current truth assignment, except for one literal, which has not yet been assigned a value. If we were to set this unknown literal to false, the assignment would make the unit clause false and then the entire formula would also be false; therefore, in a satisfying assignment extending the current one, the unknown literal in any unit clause must be true. Identifying all unit clauses and setting their single unknown literal to true is called unit propagation (or sometimes boolean constraint propagation).
Example 1.
We consider a formula with three propositional variables, , , and , which has four clauses:
The formula is satisfiable, because, for example, the truth assignment (true, false, true) makes it true.
We present the procedure [23] that we have implemented and verified in Algorithm 1; it is based on the well known DPLL algorithm [24]. We have chosen a recursive formulation of the procedure for its simplicity. In Section 7, we discuss how it can be changed into an iterative formulation, in preparation for implementing further optimizations.
| Algorithm 1: The DPLL procedure [23] that we have implemented and verified. |
 |
We describe how DPLL works in Example 1, with the search tree summarized in Figure 1. We start with the empty truth assignment (where all variables are unknown).
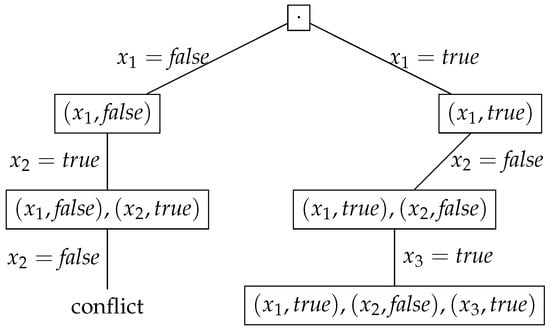
Figure 1.
The search space of the DPLL algorithm on the formula in Example 1. Each node contains the current truth assignment and the edges represent assignments made by the algorithm. Vertical edges represent unit propagations, whereas the oblique edges represent decisions.
There are no unit clauses at this point, and therefore our algorithm must choose a so-called decision variable (or branching variable) and set its value. We first set the value of the variable to false, and then, if no satisfying assignment is found, to true.
The heuristic that we have implemented based on MOMS chooses the variable (it is the most frequent to occur in the clauses that have the least number of literals) and first assigns it the value false. The first two clauses, and , become a unit. The literals and must be set to true by unit propagation, generating a conflict.
At this point, the algorithm backtracks the assignment made to the last decision variable () and changes its value from false to true. The first two clauses are satisfied and no clause becomes unit; therefore, a second decision variable is selected, , and it is set to false. The third clause, , becomes unit and the literal is set to true by unit propagation. At this point, all clauses are satisfied by the current truth assignment and therefore the DPLL algorithm returns true—the formula is satisfiable.
At any given point in the search space, any propositional variable whose value is set is either a decision variable or its value was set by unit propagation. The variables are grouped by decision levels into layers: the decision variable and the subsequent variables assigned by unit propagation belong to the same layer. The DPLL algorithm keeps track of a trace of the current assignments; each assignment is in some layer, with one layer for each decision level.
The assignments trace corresponding to the last search state in Example 1 is shown in Figure 2.

Figure 2.
The assignments trace corresponding to the last search state in Figure 1. The first layer consists only of the decision variable . The second layer consists of the decision variable and the propagated variable . Literals colored in blue are true. As each clause has at least one true literal, the formula is satisfied by the current assignment.
When a conflict is reached, the algorithm must undo all assignments in the last layer. This process of undoing all assignments is required by the data structures that we use (counters of literals that are true and false, respectively, in each clause) for identifying unit and conflict clauses. In future work, when we implement the two watched literal data structure, reverting should consist of simply decreasing the current decision level, without affecting the post-conditions significantly.
3. Brief Overview of Auto-Active Proofs in Dafny
Dafny is an imperative programming language with object-oriented features. It is special because it allows us to write code with a high degree of confidence in its correctness. This is achieved by proving that the code satisfies a specification, and the proof is machine-checked by the Dafny system.
Both the specification and the proof are given as annotations in the code. Each method in Dafny is annotated with its specification: the preconditions are given after the requires keyword, and the postconditions are given after the ensures keyword. The proof is given as a set of annotations consisting of invariants, variants, helper lemmas, and others.
Below is a typical example of Dafny code implementing the binary search algorithm, which searches for the key k in the sorted array T.
method binarySearch(T: array<int>, k : int) returns (r : int)
requires ∀ i, j • 0 ≤ i < j < T.Length ==> T[i] ≤ T[j];
ensures r ≥ 0 ==> 0 ≤ r < T.Length T[r] = k;
ensures r < 0 ==> k ∉ T[..]
{
var start : int := 0;
var end : int := T.Length - 1;
while (start ≤ end)
invariant 0 ≤ start ≤ T.Length;
invariant −1 ≤ end < T.Length;
invariant k ∉ T[..start];
invariant k ∉ T[end + 1..];
decreases end - start;
{
var mid : int := (start + end) / 2;
if (k < T[mid]) {
end := mid - 1;
} else if (k > T[mid]) {
start := mid + 1;
} else {
return mid;
}
}
return -1;
}
The precondition to the binarySearch function states that the array argument should be sorted in increasing order of values, while the two postconditions state that the result should be either an index where the key k appears in the array, or a negative number indicating that the key k is not in the array T.
At verification time (usually during compilation), Dafny establishes with mathematical certainty that whenever the method is called with arguments satisfying the preconditions, it terminates and its result satisfies the postconditions.
It achieves this by relying on Hoare logic and translating the annotations into first-order logic formulae called verification conditions or proof obligations. These formulae are sent to the Z3 SMT solver, which tries to prove their logical validity. If for whatever reason the SMT solver cannot prove a verification condition, compilation of the entire Dafny development fails.
The verification problem is undecidable: the SMT solver is in general not capable of proving the post-conditions directly from the pre-conditions. This is why helper annotations given by the programmer, such as invariants, are required. Invariants help simplify the proof obligations given to the SMT solver. Instead of a single but intractable proof obligation stating that precondition entails postcondition, Dafny generates several proof obligations that are simpler to prove. In particular, for loop invariants, Dafny generates three obligations: (1) the invariant is preserved by the loop body, (2) the invariant holds at the start of the loop, and (3) the invariant implies the postcondition after the end of the loop.
As the verification process is a mix of automatic verification (SMT solver) and interactive verification (adding annotations), the Dafny system is called an auto-active prover. Auto-active proofs are sometimes also referred to as assertional proofs.
One of the main difficulties in auto-active verification is that, when verification fails, there could be many reasons why:
- The code might not satisfy the specification, either due to
- (a)
- an error in the code or
- (b)
- an error in the specification;
- There might be missing helper annotations that are needed for Dafny to be able to perform the proof;
- The underlying SMT solver might simply not have enough computational resources to finish the proof.
Developing a sense for which of the four cases we are in is very important when developing Dafny code.
Here is an example of the same binarySearch method as above, which now fails to verify. The only difference is that the precondition stating that the array is sorted, marked by (*), is specified in a syntactically different manner:
method binarySearch(T: array<int>, k : int) returns (r : int)
requires ∀ j • 0 ≤ j < T.Length − 1 ==> T[j] ≤ T[j + 1]; // (*)
ensures r ≥ 0 ==> 0 ≤ r < T.Length Λ T[r] = k;
ensures r < 0 ==> k ∉ T[..]
{
// [...] the same code as above; the method now fails to verify
}
The precondition now states that any two elements on consecutive positions are in increasing order of values. Verification now fails, because Dafny requires help in generalizing this fact to elements which are not necessarily on consecutive positions. To establish this fact, we require a helper lemma:
lemma plusOne(T : array<int>)
requires ∀ j • 0 ≤ j < T.Length − 1 ==> T[j] ≤ T[j + 1];
ensures ∀ j, k • 0 ≤ j < k < T.Length ==> T[j] ≤ T[k];
{
∀ j | 0 ≤ j < T.Length
ensures ∀ k • j < k < T.Length ==> T[j] ≤ T[k];
{
var kp := j + 1;
while (kp < T.Length)
invariant j < kp ≤ T.Length;
invariant ∀ kpp • j < kpp < kp ==> T[j] ≤ T[kpp];
{
assert T[j] ≤ T[kp - 1]; // (**)
kp := kp + 1;
}
}
}
In Dafny, lemmas are similar to methods, but their code is erased before execution; it is only used for the verification of proofs. The lemma above helps the system understand that the initial formulation of the precondition is entailed by the later one. The implementation of the lemma acts as a proof. It starts with a construct called a forall statement, which basically implements the well-known natural deduction rule ∀-introduction. This is useful when proving universal statements, such as the one in the postcondition of the lemma. The while loop essentially works as a proof by induction, with the invariant serving as the induction hypothesis. In order to help the system prove the invariant, the helper assertion in the line marked (**) is required. This assertion is an immediate logical consequence of the invariant, obtained by instantiating the ∀ quantifier; however, it is impossible for Dafny to make all such instantiations by itself, because in general there are an infinite number of possible instantiations. This is one case where Dafny requires help on the part of the developer. With the lemma verified, it remains to call it in the binarySearch method that uses the alternative formulation of the precondition:
method binarySearch(T: array<int>, k : int) returns (r : int)
requires ∀ j • 0 ≤ j < T.Length − 1 ==> T[j] ≤ T[j + 1]; // (*)
ensures r ≥ 0 ==> 0 ≤ r < T.Length T[r] = k;
ensures r < 0 ==> k ∉ T[..]
{
plusOne(T); // helper annotation: “call” the lemma
// [...] the same code as above; the method now verifies successfully
}
The method now verifies successfully, but it required significant help on the part of the developer in the form of annotations.
Large Dafny Projects. In the example above, some important features of Dafny that make the verification of large projects feasible are not displayed. Among these, we mention reads clauses and modifies clauses, which restrict the use of the heap and are important in developments using data structures such as arrays.
A particular difficulty in verifying large projects is that, even on a very fast computer, the number of proof obligations and the intrinsic complexity of each proof obligation makes for a large verification time. This can lengthen the development loop (code, specify, verify) significantly. To achieve a reasonable verification time on a large project, several strategies need to be employed. These strategies range from technical (only verify the method being worked on) to fundamental.
A fundamental method of keeping the verification time reasonable is to structure the data structures, the code, the specification, and the helper annotations in such a way that the SMT solver can quickly discharge the verification conditions. This structuring gives rise to verification patterns, somewhat similar to design pattern in object-oriented code. We discuss a number of patterns that we have identified while developing TrueSAT in Section 7.
4. A Verified Implementation of the DPLL Algorithm
In this section, we describe our verified SAT solver. The full source code to the solver, together with instructions on how to compile and run it and how to reproduce the benchmark described in Section 5 is available at: https://github.com/andricicezar/truesat (accessed on 1 June 2022).
4.1. Data Structures
We first describe the data structures that we use to represent the formula and the current search state (decision level, truth assignment by layers). We also explain how we quickly identify unit clauses using counters.
4.1.1. Representing the CNF Formula
We represent propositional variables and literals by bounded integers, represented by values of the type Int32.t, which we define in the file int32.dfy:
module Int32 {
newtype {:nativeType "int"} t = x | -2000000 ≤ x < 2000001
const max : t := 2000000;
const min : t := -2000000;
}
The type Int32.t represents bounded integers. This type requires to prove that all computations involving values of type Int32.t remain within the bounds. The bounds themselves can be set to any larger constants without affecting the proofs. The advantage is that values of type Int32.t are represented by machine integers and hence these computations are very fast.
The mathematical integers (unbounded), represented in Dafny by the type int, have the disadvantage that they should be compiled to big integers, which have a significant performance overhead; therefore, by representing variables and literals as values of type Int32.t instead of int, we gain efficiency.
We store the CNF formula, together with the solver state, in the trait DataStructures (a trait is similar to an abstract class in other object-oriented languages), presented in Figure 3.

Figure 3.
The fields (file solver/data_structures.dfy) we use for storing the formula and the solver state. The fields are presented in a slightly different order to improve presentation.
The field variablesCount stores the number of propositional variables in the formula. The field clauses stores the formula itself, as a sequence of clauses (each clause being a sequence of literals). Sequences (seq) are immutable in Dafny, but storing clauses as sequences has no significant performance impact, because the clauses are set once at the beginning and never changed. The number of clauses is stored in clausesCount. The array clauseLength stores the number of literals in each clause.
We represent propositional variables as bounded integers with values between 0 and , positive literals by bounded integers between 1 and variablesCount, and negative literals by bounded integers between and −variablesCount.
The trait DataStructures has a number of predicates for checking the syntactical validity of propositional variables, literals, clauses, and others. Here is an example predicate that checks whether an integer represents a literal:
predicate validLiteral(literal : Int32.t)
requires validVariablesCount();
reads ‘variablesCount;
{
if literal = 0 then false
else if -variablesCount ≤ literal Λ literal ≤ variablesCount then true
else false
}
4.1.2. Representing the Current Assignment
The field decisionLevel stores the current decision level, which starts at and is incremented with each decision variable. The current assignment has three different representations, each of which has its own use:
- The field truthAssignment is an array storing for each propositional variable its current value: unknown is encoded by , false by 0 and true by 1. This field is useful for quickly (in time ) retrieving the value of a given propositional variable. At the beginning of the search, it is initialized by in all positions (no variable is set).
- The fields traceVariable and traceValue are arrays having the same size that store the current trace. The variable traceVariable[i] is the th variable to be set and it has a value of traceValue[i]. As explained in the previous section, the trace is split into layers. We store each layer j as two indices, traceDLStart[j] and traceDLEnd[j], into the trace. The layer j consists of the variables traceVariable[traceDLStart[j]] (inclusive) up to traceVariable[traceDLEnd[j]] (exclusive). This representation of the truth assignment, as a trace split into layers, is useful for backtracking. As all of these fields are arrays, lookups and updates into them are very efficient.
- The field assignmentsTrace stores the entire trace of assignments. As it is marked ghost, this field is not used at runtime, but only at verification time, in order to enable the specification and verification of certain properties; therefore, it entails no runtime overhead.
A trait-level computer-checked invariant ensures that the three different representations of the current assignment all agree with each other:
// [...] some parts elided for~brevity
truthAssignment.Length = variablesCount Λ
(∀ i • 0 ≤ i < variablesCount ==> −1 ≤ truthAssignment[i] ≤ 1) Λ
(∀ i • 0 ≤ i < variablesCount ΛtruthAssignment[i] ≠ −1 ==>
(i, convertIntToBool(truthAssignment[i])) in assignmentsTrace) Λ
(∀ i • 0 ≤ i < variablesCount ΛtruthAssignment[i] = −1 ==> (i, false) ∉ assignmentsTrace Λ (i, true) ∉ assignmentsTrace)
4.1.3. Quickly Identifying Unit Clauses
The fields trueLiteralsCount and falseLiteralsCount are arrays indexed from to that store, for each clause, the number of literals in the clause that are currently true and false, respectively. An invariant stating that the two arrays truly contain the required number is computer-checked:
|trueLiteralsCount| = |clauses| Λ ∀ i • 0 ≤ i < |clauses| ==> 0 ≤ trueLiteralsCount[i] = countTrueLiterals(truthAssignment, clauses[i])
(a similar invariant is used for falseLiteralsCount). The function countTrueLiterals serves as a mathematical specification of the number of literals currently true in a given clause, which works by actually counting one by one the literals that are true in the given clause.
We can use these arrays to efficiently check whether:
- the clause is true in the current assignment:trueLiteralsCount[i] > 0;
- the clause is false in the current assignment:falseLiteralsCount[i] == clauseLength[i];
- the clause is unit in the current assignment:trueLiteralsCount[i] == 0 ∧ clauseLength[i] - falseLiteralsCount[i] == 1.
It would be marginally more efficient to store these counters as part of the arrays representing the clauses (for example, on positions 0 and 1, with the literals starting on position 2); however, we prefer to leave out such lower-level optimizations, as they would impede readability of the code and of the specifications for a marginal gain in performance.
The final two fields of the trait DataStructures, the arrays positiveLiteralsToClauses and negativeLiteralsToClauses are used for updating as efficiently as possible the counters in trueLiteralsCount and falseLiteralsCount after a variable has been set (either due to a new decision, or due to unit propagation). These two arrays are indexed from 0 to variablesCount - 1. The sequence positiveLiteralsToClauses[i] contains the indices of the clauses in which the variable i occurs as a literal. The sequence negativeLiteralsToClauses[i] contains the indices of the clauses in which the negation of the variable i occurs as a literal.
Therefore, when a variable i is set (or unset), it is sufficient to update the counters of the clauses in positiveLiteralsToClauses[i] and negativeLiteralsToClauses[i], instead of updating all counters. The two arrays satisfy the following computer-checked invariant:
|positiveLiteralsToClauses| = variablesCount Λ (
∀ variable • 0 ≤ variable < |positiveLiteralsToClauses| ==>
ghost var s := positiveLiteralsToClauses[variable];
...
(∀ clauseIndex • clauseIndex in s ==> variable+1 in clauses[clauseIndex]) Λ
(∀ clauseIndex • 0 ≤ clauseIndex < |clauses| Λ clauseIndex ∉ s ==>
variable+1 ∉ clauses[clauseIndex]))
(a similar invariant holds for ).Class/trait invariants are represented in Dafny by using a predicate, typically called valid, which is added as a precondition and postcondition to all methods of the class/trait. In our case, the trait DataStructures has a predicate valid that consists of the conjunction of the snippets of code shown above, and some more lower-level conditions that we omit for brevity.
4.2. Verified Operations over the Data Structures
In our Dafny development, the class Formula extends the trait DataStructures by a constructor that sets up the data structures used to represent the formula and the current search state and also by a set of methods that implement several actions that can be taken by the DPLL algorithm:
- Creating a new layer (by increasing the current decision level);
- Setting the value of a propositional variable (either because it is a decision variable, or because of unit propagation);
- Build the current layer by setting a decision variable and performing all unit propagations necessary;
- Undo the assignments performed in the last layer.
Each of the four operations above is implemented as a method in the Formula class (file solver/formula.dfy). As part of the implementation of each method, we show that it preserves the data structure invariants described earlier.
4.2.1. The Method increaseDecisionLevel
This method creates a new layer in the assignments trace. It ensures that the new search state is valid, with the truth assignment remaining the same. It is used to set up the assignments trace for a new decision variable and subsequent unit propagations.
We present its signature and specification:
method increaseDecisionLevel()
requires validVariablesCount();
requires validAssignmentTrace();
requires decisionLevel < variablesCount - 1;
requires decisionLevel ≥ 0 ==>
traceDLStart[decisionLevel] < traceDLEnd[decisionLevel];
modifies ‘decisionLevel, traceDLStart, traceDLEnd;
ensures decisionLevel = old(decisionLevel) + 1;
ensures validAssignmentTrace();
ensures traceDLStart[decisionLevel] = traceDLEnd[decisionLevel];
ensures getDecisionLevel(decisionLevel) = {};
ensures ∀ i • 0 ≤ i < decisionLevel ==>
old(getDecisionLevel(i)) = getDecisionLevel(i);
The function getDecisionLevel returns all assignments performed at a given decision level:
function getDecisionLevel(dL : Int32.t) : set<(Int32.t, bool)>
reads ‘variablesCount, ‘decisionLevel, ‘traceDLStart,
‘traceDLEnd, ‘traceVariable, ‘traceValue,
traceDLStart, traceDLEnd, traceVariable,
traceValue, ‘assignmentsTrace;
requires validVariablesCount();
requires validAssignmentTrace()
requires −1 ≤ dL ≤ decisionLevel;
requires traceVariable.Length = variablesCount as int;
ensures getDecisionLevel(dL) ≤ assignmentsTrace;
{
if dL = −1 then {}
else (set j | j in assignmentsTrace Λ j.0 in
traceVariable[traceDLStart[dL]..traceDLEnd[dL]])
}
Therefore, the last postcondition of increaseDecisionLevel ensures that the current assignment remains unchanged.
4.2.2. The Method setVariable
This method changes the current truth assignment by setting the value of a variable that is currently unknown. We present its signature and its specification:
method setVariable(variable : Int32.t, value : bool)
requires valid();
requires validVariable(variable);
requires truthAssignment[variable] = -1;
requires 0 ≤ decisionLevel; // not empty
modifies truthAssignment, traceVariable, traceValue,
traceDLEnd, ‘assignmentsTrace, trueLiteralsCount,
falseLiteralsCount;
ensures valid();
ensures value = false ==> old(truthAssignment[..])[variable as int := 0]
= truthAssignment[..];
ensures value = true ==> old(truthAssignment[..])[variable as int := 1]
= truthAssignment[..];
ensures traceDLStart[decisionLevel] < traceDLEnd[decisionLevel];
ensures traceVariable[traceDLEnd[decisionLevel]-1] = variable;
ensures traceValue[traceDLEnd[decisionLevel]-1] = value;
ensures ∀ i • 0 ≤ i < variablesCount Λ i ≠ decisionLevel ==>
traceDLEnd[i] = old(traceDLEnd[i]);
ensures ∀ i • 0 ≤ i < variablesCount Λ i ≠ old(traceDLEnd[decisionLevel]) ==>
traceVariable[i] = old(traceVariable[i]) Λ traceValue[i] = old(traceValue[i]);
ensures ∀ x • 0 ≤ x < old(traceDLEnd[decisionLevel]) ==>
traceVariable[x] = old(traceVariable[x]);
ensures ∀ i • 0 ≤ i < decisionLevel ==>
old(getDecisionLevel(i)) = getDecisionLevel(i);
ensures assignmentsTrace = old(assignmentsTrace) + {(variable, value)};
ensures countUnsetVariables(truthAssignment[..]) + 1 =
old(countUnsetVariables(truthAssignment[..]));
In addition to updating the three representations of the current truth assignment in a consistent manner, the main difficulty in the method setVariable is to efficiently update the counters in the arrays trueLiteralsCount and falseLiteralsCount in a provably correct manner. To this end, the method steps over all affected clauses (stored in negativeLiteralsToClauses[variable] and in positiveLiteralsToClauses[variable]) and updates the counters only for these clauses. The technical difficulty in the proof is to reason about the clauses that are not affected and show that their counters do not need to change.
4.2.3. The Method setLiteral
This method uses setVariable to set the value of the variable correspondingly, and then performs unit propagation repeatedly, until no more unit clauses are found. We show its signature and its specification:
method setLiteral(literal : Int32.t, value : bool) requires valid(); requires validLiteral(literal); requires getLiteralValue(truthAssignment[..], literal) = -1; requires 0 ≤ decisionLevel;
modifies truthAssignment, trueLiteralsCount,
falseLiteralsCount, traceDLEnd, traceValue,
traceVariable, ‘assignmentsTrace;
ensures valid();
ensures traceDLStart[decisionLevel] < traceDLEnd[decisionLevel];
ensures ∀ x • 0 ≤ x < old(traceDLEnd[decisionLevel]) ==>
traceVariable[x] = old(traceVariable[x]);
ensures assignmentsTrace = old(assignmentsTrace) +
getDecisionLevel(decisionLevel);
ensures ∀ i • 0 ≤ i < decisionLevel ==>
old(getDecisionLevel(i)) = getDecisionLevel(i);
ensures countUnsetVariables(truthAssignment[..]) <
old(countUnsetVariables(truthAssignment[..]));
ensures (
ghost var (variable, val) := convertLVtoVI(literal, value);
isSatisfiableExtend(old(truthAssignment[..])[variable as int := val]) ⇔
isSatisfiableExtend(truthAssignment[..])
);
decreases countUnsetVariables(truthAssignment[..]), 0;
Unlike in setVariable, where a single variable is affected, several variables might be set in setLiteral as a result of unit propagation; therefore, the current truth assignment might change in several positions, hence the more complicated postconditions.
The last postcondition is the most important one, because it is directly used to prove the functional correctness of the DPLL algorithm: it states that all variables set during unit propagation are logical consequences of the assignment at the entry into setLiteral, updated with the value of the decision variable.
The method setLiteral is part of a chain of mutually recursive functions shown in Figure 4.
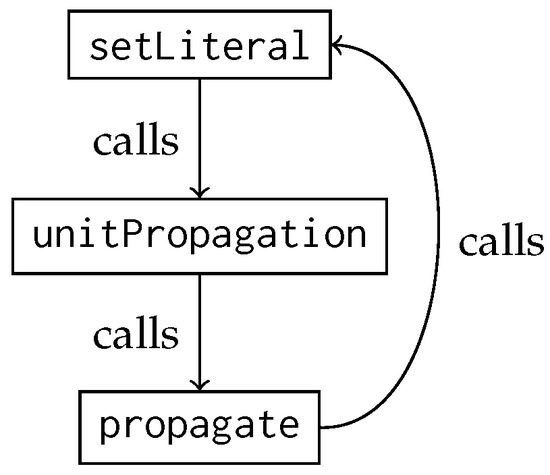
Figure 4.
Flowchart of the method setLiteral.
The method unitPropagation takes a variable and the value that is has just been assigned:
method unitPropagation(variable : Int32.t, value : bool)and checks all clauses that might have become unit after this assignment. It uses the arrays negativeLiteralsToClauses[variable] and positiveLiteralsToClauses[variable] to only inspect the relevant clauses, which ensures that, in general, just a small fraction of the clauses are accessed at this step. When it identifies a unit clause, it calls propagate:
method propagate(clauseIndex : Int32.t)which takes as input the index of a unit clause and it uses setLiteral recursively to make the unknown literal in the unit clause true. We only show the signature of the methods unitPropagation and propagate, because the specification is similar to the one for setLiteral.
We show termination of this chain of recursive functions by using a variant that is defined in the decreases annotation in the specification of the method setLiteral shown above. The variant counts the number of variables that have not yet been set, and it is guaranteed to decrease strictly at every recursion step, without ever becoming negative, thereby ensuring a machine-checked proof of termination.
4.2.4. The Method revertLastDecisionLevel
This method is used when a conflict is found and therefore we need to backtrack. It undoes all of the assignments in the last decision layer, one by one, by setting the value of the respective propositional variables to in the current truth assignment. As it needs to update the counters for the affected clauses, it makes use again of the two arrays positiveLiteralsToClauses and negativeLiteralsToClauses. Its signature and specification are:
method revertLastDecisionLevel() requires valid(); requires 0 ≤ decisionLevel;
modifies ‘assignmentsTrace, ‘decisionLevel, truthAssignment, trueLiteralsCount,
falseLiteralsCount, traceDLEnd;
ensures decisionLevel = old(decisionLevel) - 1;
ensures assignmentsTrace = old(assignmentsTrace) -
old(getDecisionLevel(decisionLevel));
ensures valid();
ensures ∀ i • 0 ≤ i ≤ decisionLevel ==>
old(getDecisionLevel(i)) = getDecisionLevel(i);
ensures decisionLevel > −1 ==>
traceDLStart[decisionLevel] < traceDLEnd[decisionLevel];
As part of the postcondition, the method is guaranteed to preserve the values of all variables on the previous decision levels.
4.3. Proof of the Main Algorithm
The entry point into our verified DPLL procedure is the solve method in the file solver/solver.dfy, which is specified as follows:
method solve() returns (result : SATUNSAT)
requires formula.valid();
requires formula.decisionLevel > −1 ==>
formula.traceDLStart[formula.decisionLevel] <
formula.traceDLEnd[formula.decisionLevel];
modifies formula.truthAssignment, formula.traceVariable, formula.traceValue,
formula.traceDLStart, formula.traceDLEnd, formula‘decisionLevel,
formula‘assignmentsTrace, formula.trueLiteralsCount,
formula.falseLiteralsCount;
ensures formula.valid();
ensures old(formula.decisionLevel) = formula.decisionLevel;
ensures old(formula.assignmentsTrace) = formula.assignmentsTrace;
ensures ∀ i • 0 ≤ i ≤ formula.decisionLevel ==>
old(formula.getDecisionLevel(i)) = formula.getDecisionLevel(i);
ensures formula.decisionLevel > −1 ==>
formula.traceDLStart[formula.decisionLevel] <
formula.traceDLEnd[formula.decisionLevel];
ensures result.SAT? ==> formula.validValuesTruthAssignment(result.tau);
ensures formula.countUnsetVariables(formula.truthAssignment[..]) =
formula.countUnsetVariables(old(formula.truthAssignment[..]));
ensures result.SAT? ==>
formula.isSatisfiableExtend(formula.truthAssignment[..]);
ensures result.UNSAT? ==>
¬formula.isSatisfiableExtend(formula.truthAssignment[..]);
decreases formula.countUnsetVariables(formula.truthAssignment[..]), 1;
This method implements the DPLL procedure as a chain of mutually recursive functions consisting of two methods, called solve and step. The implementation of the method solve closely follows Algorithm 1:
method solve() returns (result : SATUNSAT)
// [...] specification elided
{
var hasEmptyClause : bool := formula.getHasEmptyClause();
if (hasEmptyClause) {
return UNSAT;
}
var isEmpty : bool := formula.getIsEmpty();
if (isEmpty) {
result := SAT(formula.truthAssignment[..]);
return result;
}
var literal := formula.chooseLiteral();
result := step(literal, true);
if (result.SAT?) {
return result;
}
result := step(literal, false);
return result;
}
(some helper assertions are elided for brevity).One difference between our implementation and the pseudo-code in Algorithm 1 is that the data structures are stored as part of the class instead of being passed around as arguments, which helps keep the code efficient. A more important difference is that the first step in Algorithm 1, unit propagation, is delegated to the step method, for efficiency reasons: only the clauses that have a chance of becoming unit after setting the value of the chosen literal are inspected. An initial unit propagation that takes into account all clauses is also performed just before the method solve is called.
The role of the step method is to set the value of the literal, perform unit propagation, and then call the method solve recursively. The reason that we need a separate method, called step, is to have a uniform specification for both the case where the literal is set to true and the case where it is set to false. The implementation of the step method can be seen in Section 5.
A graphical depiction of the control flow of the methods solve and step is shown in Figure 5.
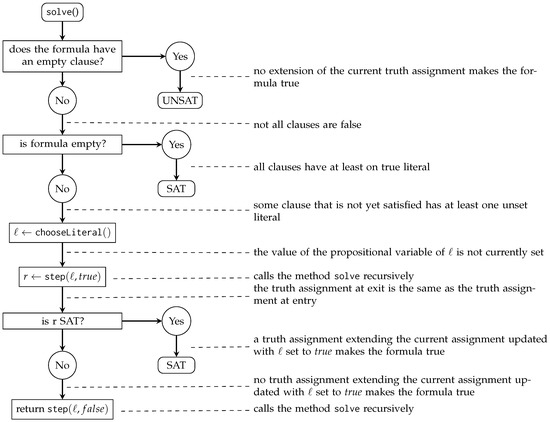
Figure 5.
Flowchart of method solve. A level-0 propagation of unit clauses is performed just before the call to the solve method and is not shown in the figure.
The method solve first checks whether the current truth assignment trivially makes the formula true or false and it simply returns SAT or UNSAT in these cases.
If the formula is not trivially true or false, a decision variable is selected by calling the chooseLiteral method. This method implements the variable ordering heuristic that we have discussed earlier. It chooses the literal that occurs most frequently in the clauses of the formula with the fewest unset literals among the clauses that are not yet satisfied. It returns the negation of this literal. The idea behind this heuristic is to speed up the algorithm by making clauses unit as quickly as possible.
Once a literal is chosen, the solve method starts the search process by first setting the literal to true and then, if needed, to false. It achieves this in a modular fashion by calling the method step, which sets the literal to the given boolean value and performs unit propagation using the previously described method setLiteral. The method step calls the method solve recursively. At the end, it reverts the assignments. The specification of the step methods closely follows the specification of the solve method:
method step(literal : Int32.t, value : bool) returns (result : SATUNSAT)
requires formula.valid();
requires formula.decisionLevel < formula.variablesCount - 1;
requires formula.decisionLevel > −1 ==>
formula.traceDLStart[formula.decisionLevel] <
formula.traceDLEnd[formula.decisionLevel];
requires ¬formula.hasEmptyClause();
requires ¬formula.isEmpty();
requires formula.validLiteral(literal);
requires formula.getLiteralValue(formula.truthAssignment[..], literal) = -1;
modifies formula.truthAssignment, formula.traceVariable, formula.traceValue,
formula.traceDLStart, formula.traceDLEnd, formula‘decisionLevel,
formula‘assignmentsTrace, formula.trueLiteralsCount,
formula.falseLiteralsCount;
ensures formula.valid();
ensures old(formula.decisionLevel) = formula.decisionLevel;
ensures old(formula.assignmentsTrace) = formula.assignmentsTrace;
ensures ∀ i • 0 ≤ i ≤ formula.decisionLevel ==>
old(formula.getDecisionLevel(i)) = formula.getDecisionLevel(i);
ensures formula.decisionLevel > −1 ==>
formula.traceDLStart[formula.decisionLevel] <
formula.traceDLEnd[formula.decisionLevel];
ensures result.SAT? ==> formula.validValuesTruthAssignment(result.tau);
ensures result.SAT? ==> (
var (variable, val) := formula.convertLVtoVI(literal, value);
formula.isSatisfiableExtend(formula.truthAssignment[..][variable := val]));
ensures result.UNSAT? ==> (
var (variable, val) := formula.convertLVtoVI(literal, value);
¬formula.isSatisfiableExtend(formula.truthAssignment[..][variable := val]));
ensures formula.countUnsetVariables(formula.truthAssignment[..]) =
formula.countUnsetVariables(old(formula.truthAssignment[..]));
decreases formula.countUnsetVariables(formula.truthAssignment[..]), 0;
The most important part of the specification of the method solve are the postconditions encoding the functional correctness of the algorithm:
- If the solve method returns SAT, then the current assignment can be extended to a satisfying assignment;
- If the solve method returns UNSAT, then no assignment extending the current assignment satisfies the formula.
We also show as a postcondition that the solve method ends with the same truth assignment as the one it starts with. This means that it reverts the changes to the truth assignment, even if it finds a satisfying assignment. Otherwise, the preconditions and postconditions for the method solve would become more verbose and less elegant. This undo process does not affect our ability to implement the two watched literals data structure in the future, because we only check that the truth assignment remains the same, not the helper data structures that help quickly identify unit clauses.
5. Benchmarks
In this section, we present the results of benchmarking our solver, in order to understand its performance. The Dafny system can either directly execute (interpret) the Dafny code, or transpile it to C# code, to obtain better performance. Figure 6 shows an example of how translation from Dafny to C# is performed.

Figure 6.
Example of how Dafny compiles the code to C#. Aside from the minor and mostly cosmetic changes, note that proofs are not copied over. We add the spacing ourselves to improve readability.
We have benchmarked the C# code generated automatically by Dafny from our solver. We call this solver TrueSAT.
5.1. Benchmarking Methodology
5.1.1. Machine
We have run all experiments on a machine with an i5-8400 CPU (2.80GHz) running Ubuntu Linux (version 22.04) with the 5.15.0-33-generic kernel. The machine features 8GiB of DDR4 RAM (2400 MHz), an L1 cache of 384KiB, an L2 cache of 1536KiB, an L3 cache of 9MiB, and a 256GB solid state drive.
5.1.2. Software
We have executed the benchmark using the BenchExec framework [25], which helps ensure reproducibility, accurate measurement of performance, and limits resource usage of the benchmarked tool. For all solvers, we have used BenchExec (https://github.com/sosy-lab/benchexec, accessed on 1 June 2022) to limit resource usage by using the following settings for each run: time limit set to 120 s, memory limit set to 1024 MB, CPU core limit set to 1.
5.1.3. Tasks
We have benchmarked the solvers using tests in SATLIB - Benchmark Problems (https://www.cs.ubc.ca/~hoos/SATLIB/benchm.html, accessed on 1 June 2022). We have chosen the sets of instances having 100, 150, 175, and 200 variables. These SAT problems are all in 3-CNF. The number of clauses in each set is chosen such that all instances sit at the satisfiability threshold [5]. There are 2000 tasks with 100 variables, 200 tasks with 150 variables, 200 tasks with 175 variables, and 199 tasks with 200 variables. The tasks are distributed evenly between satisfiable and unsatisfiable instances across the four classes (for the tasks with 200 variables, there are 100 satisfiable instances and 99 unsatisfiable instances). We have chosen these SAT instances because they are small enough for DPLL to solve in reasonable time, but big enough so that the search dominates the execution time (and not, e.g., reading the input). We have made sure that our solver parses these inputs correctly, even if they are not strictly valid DIMACS files (they end with two lines containing % and 0, respectively, which could be mistaken for the empty clause by a naive parser). All code necessary to reproduce the benchmark can be found at https://github.com/andricicezar/truesat (accessed on 1 June 2022).
5.2. Machine Integers
We have first tested what is the performance gain we obtain in TrueSAT by using machine integers for representing variables and literals instead of mathematical integers. To understand this, we have created a modified version of TrueSAT where the type representing variables and literals is changed back to Dafny type int, which represents mathematical integers. We denote this version by TrueSAT (BigInteger) in the graphs, because mathematical integers are compiled into instances of the class BigInteger (which represents integers as arrays of digits).
Figure 7 shows that there is roughly a 10× performance improvement between TrueSAT (BigInteger) and TrueSAT. We conclude that this improvement of using machine integers is therefore highly relevant for performance and the proof effort is worth it.
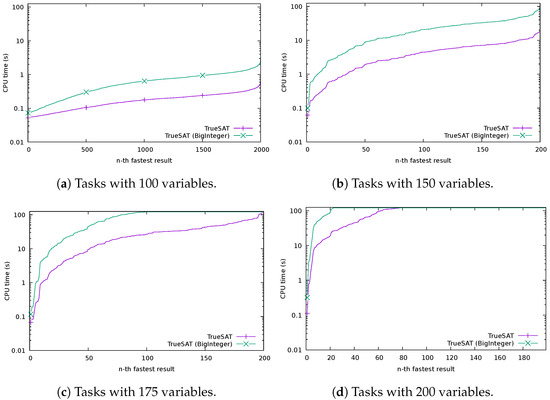
Figure 7.
Comparison of TrueSAT and a version of TrueSAT using mathematical integers instead of machine integers. There are 2000 tasks with 100 variables, 200 tasks with 150 and 175 variables each, and 199 tasks with 200 variables. We plot the running time taken by the n-th fastest result for each solver. The y axis uses a logarithmic scale.
5.3. DPLL Solvers
In this subsection, we present the results of benchmarking TrueSAT against other solvers implementing the DPLL algorithm. The TrueSAT solver has been compiled using version 3.6.0.40511 of the Dafny system and version 6.12.0.179 of the Mono just-in-time compiler. The source code can be found in the truesat_src folder of our repository.
We have first checked whether TrueSAT has any added overhead compared to a implementation written directly in C#. For this purpose, we have written by hand in C# a solver implementing the same algorithm and data structures as our Dafny solver. We denote this solver by C# solver in the graphs. The source code can be found in the cs_solver folder of our repository.
As typical high-performance SAT solvers are written in C++, not C#, we have also implemented the same DPLL algorithm directly in C++. This solver is denoted by C++ solver in the graphs. The source code can be found in the cpp_solver folder of our repository.
In this comparison, we have included the verified solver of Berger et al. [26], which is written in Minlog and compiled to Haskell. This solver also implements the DPLL algorithm. We denote it by Minlog solver; in order to run it on our benchmark we have extended it slightly by adding an unverified parser for DIMACS files.
We summarize the results of running the four solvers above in Figure 8.
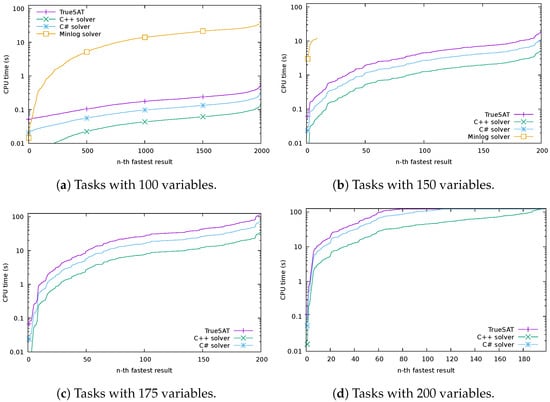
Figure 8.
Comparison of the four DPLL solvers in our benchmark (lower is better). There are 2000 tasks with 100 variables, 200 tasks with 150 and 175 variables each, and 199 tasks with 200 variables. We plot the running time taken by the n-th fastest result for each solver. The y axis uses a logarithmic scale. The Minlog solver and TrueSAT are verified, while the C++ and the C# solvers are not. The running time of any solver on any given task is capped at 120s. The Minlog solver hits the memory limit on most tasks starting with 150 variables, and is therefore not shown in tasks with 175 and 200 variables.
Comparing TrueSAT to the C# solver, we have found that there is a small overhead coming from the method we use to read files in Dafny, and not from the extraction process itself. In our results, the reading and parsing of the input file in Dafny takes at least twice as long as in C#. The overhead diminishes as longer SAT instances are used: on small inputs, the C# solver outperforms TrueSAT; on larger inputs, the performance is roughly the same.
Our results show that the (unverified) C++ solver is approximately twice as fast on large tests as our verified Dafny solver. This means that our verified solver is competitive against a handwritten C++ solver. The small performance gap between TrueSAT and the C++ solver is likely due to TrueSAT relying on the C# backend of Dafny (a 2× performance gain is typical when going from C# to C++). Our verified Dafny solver is competitive with an equivalent implementation in C++ (it is only two times slower), but the correctness guarantee offered by our verified solver makes it significantly more trustworthy. Dafny also features an extraction mechanism to C++, but this backend is unfortunately not completely implemented at the moment. Once the C++ extraction mechanism in Dafny is finished, it might improve the performance of TrueSAT to levels similar to the C++ solver.
The Minlog solver, which also implements the DPLL algorithm and is verified in the Minlog proof assistant, is slower than the three solvers above. This is expected, since emphasis is not placed on speed in its implementation: the solver is implemented as a set of recursive Haskell functions, with immutable data structures.
5.4. CDCL Solvers
To place the performance of our verified Dafny solver into context, we have also benchmarked against three CDCL solvers: the unverified solver MiniSAT (http://minisat.se/, accessed on 1 June 2022) (with the default settings), the partially verified solver versat, and the verified solver IsaSAT. As these solvers implement the full CDCL algorithm, which can be exponentially faster than DPLL, they are expected to outperform our solver. Figure 9 summarizes the performance of these four solvers.
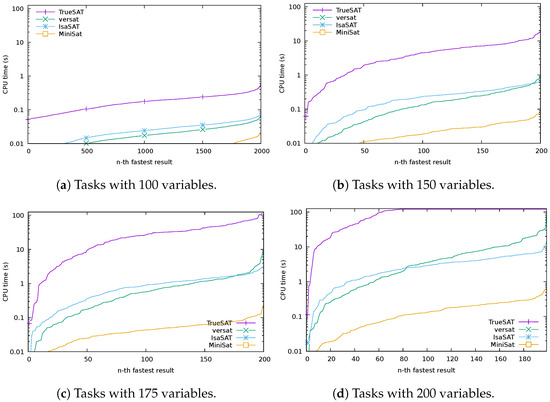
Figure 9.
Comparison of CDCL solvers against our verified DPLL solver (lower is better). There are 2000 tasks with 100 variables, 200 tasks with 150 and 175 variables each, and 199 tasks with 200 variables. We plot the running time taken by the n-th fastest result for each solver. The running time of any solver on any given task is capped at 120 s. The y axis uses a logarithmic scale. The IsaSAT solver and TrueSAT are verified, while MiniSAT is not.
We have chosen MiniSAT as the canonical unverified implementation of the CDCL algorithm in C++, including clause learning, the two watched literals data structures, variable heuristics, restarts, and so on. It is very efficient, and modern SAT solvers typically have the same structure, but differ in parameter choices or engineering improvements. Achieving performance similar to MiniSAT would be the ultimate goal of a verified solver. We have compiled MiniSAT at -O2 level using g++ version 11.2.0. We have run MiniSAT using its default options.
The solver versat is one of the earliest to be verified. It is written in the Guru dependently typed language and its code is extracted to C. It is verified formally only for soundness (not completeness, nor termination) and some checks are deferred to runtime. We have compiled the extracted C code obtained from the homepage of the author (https://homepage.divms.uiowa.edu/~astump/software.html, accessed on 1 June 2022) using the gcc compiler version 11.2.0 at -O2 optimization level. We have altered the solver slightly to read its input from a file instead of the standard input in order to be compatible with the BenchExec framework.
IsaSAT is the most compelling verified solver to date. It is part of the Isabelle Formalisation of Logic (IsaFOL) project. It is written in Isabelle/HOL (the Isabelle proof assistant, instantiated with the theory of higher-order logic) and it is verified using the Isabelle refinement framework. At the top there is the CDCL calculus, which is refined down to an executable version. We have used the IsaSAT code extracted to the programming language ML in the corresponding folder (Weidenbach_Book/IsaSAT/code/ML) of the //bitbucket.org/isafol/isafol.git repository (accessed 27 May 2022). We have compiled it using a recent version of the mlton compiler (20210117-1.amd64-linux-glibc2.31), which is known to be the ML compiler that produces the fastest executables.
The IsaSAT and versat solvers are an order of magnitude slower than MiniSAT, and the TrueSAT solver is an order of magnitude slower than IsaSAT and versat. The solver versat outperforms IsaSAT on the smaller inputs, but it seems to lose this advantage as the input becomes larger. The verified solvers are therefore still quite far of the performance of MiniSAT. The potential advantage of TrueSAT is that it is roughly as fast as a native (C++) implementation of the same algorithm, as we have discussed earlier. While not as high performance as a CDCL solver, extending it to CDCL offer a path towards a verified solver roughly as efficient as a native CDCL solver such as MiniSAT.
6. Related Work
One of the earliest verified SAT solvers is versat [27]. It has been implemented in the Guru language, which uses dependent types for verification. The solver is extracted to efficient C code, where the imperative data structures rely on reference counting and on a statically enforced read/write discipline. The solver is only verified to be sound (not verified to be complete, nor terminating). Some checks are delayed until runtime; these checks (if they fail) could be a source of incompleteness. It implements several optimizations, such as conflict analysis and clause learning, which enable it to be quite efficient. The soundness criterion in versat is slightly different from the one in TrueSAT: versat is verified to output UNSAT if the input formula allows for a resolution proof of the empty clause, while TrueSAT is verified to output UNSAT if the input formula is semantically unsatisfiable. Of course, the two criteria (existence of a resolution proof of the empty clause and the formula being semantically unsatisfiable) are equivalent in propositional logic, but functional correctness proofs that are based on one or another can be very different.
Another series of SAT solvers has been verified in Isabelle/HOL by Marić [28]. The Hoare triples associated to the solver pseudo-code are shown to be valid in the Isabelle/HOL proof assistant. In subsequent work [29], Marić and Janičić have proven in Isabelle the functional correctness of a SAT solver that is represented as an abstract transition system and also of a shallow embedding of CDCL as a set of recursive functions [30].
Berger et al. have verified a DPLL SAT solver [26] using the Minlog system. The solver is extracted to Haskell code. Berger et al. benchmark the solver against versat and they show it is roughly as efficient on small instances, but on industrial problems it can be slower, because versat implements additional optimizations, such as clause learning.
The state-of-the-art verified SAT solver today is IsaSAT [31]. IsaSAT is verified in the Isabelle/HOL proof assistant and it is part of the Isabelle Formalization of Logic project. The solver is verified using a refinement technique. At the top of the refinement chain there are logical calculi, such as CDCL, which are verified formally to be sound, complete, and terminating. These calculi are shown to be refined by lower level programs. At the bottom of the refinement chain there is an implementation in Standard ML. The framework also contains meta-theoretical results. Fleury [32] benchmarks the solver as still being two orders of magnitude slower than a state-of-the-art C solver and proposes additional optimizations. In our own solver, we do not prove any meta-theoretical properties of DPLL/CDCL; we concentrate on obtaining a verified imperative SAT solver in an auto-active manner. A key challenge is that the verification of Dafny code may take a lot of time in certain cases and we have to optimize our code for verification time as well.
Table 1 summarizes the algorithms, efficiency, and levels of trust of the certified approaches above. The unique selling point of TrueSAT is that it is written and proved directly in imperative style because it only implements DPLL, not the full CDCL, and is not currently as efficient as possible; however, it offers a path forward (namely, extending it with clause learning and the two watched literals data structure) to obtaining a verified solver that is about as efficient as state-of-the-art unverified solvers. The other approaches, even if they implement the full CDCL-based algorithm, are orders of magnitude slower than unverified solvers due to the fact they are written in essentially a functional style.

Table 1.
Summary of existing verified SAT solvers.
In other related work, Lescuyer [33] has also verified a satisfiability solver in the Coq system, extended with linear arithmetic, and exposed as a reflexive tactic. Shankar and Vaucher [34] have verified in the PVS system, a decision procedure based on DPLL using sub-typing and dependent types. Efficiency seem to be secondary concern in these last two approaches.
An alternative method to increase the trust in the output of SAT solvers is to verify the certificate checker. For this purpose, Lammich [35] proposes an efficient certificate checker for well-known DRAT format [36] that is formally verified and is also faster than unverified checkers.
7. Discussion
We have presented TrueSAT, a machine-checked implementation of the DPLL algorithm verified using the Dafny system. It is roughly as efficient as an equivalent DPLL solver written in C++, but it is still less efficient than state-of-the-art solvers, because it only implements DPLL, not the full CDCL algorithm; however, it has the advantage that it is very trustworthy, because it is fully verified: soundness, completeness, and termination are all machine-checked using the Dafny system. Our implementation shows that it is possible to build a SAT solver fully verified in assertional style that is still competitive in terms of efficiency with an equivalent solver written in a traditional imperative language such as C++ or C#. This offers a path forward to obtaining a verified solver that is about as efficient as state-of-the-art unverified solvers, by extending our solver to a CDCL solver.
The solver TrueSAT has approximately 3.9K lines of Dafny code, including the parser. Most of the code has been written by the first author in approximately one year and a half of part time work. The author also learned Dafny during that time. Table 2 contains a summary of our verified solver in numbers.

Table 2.
Various statistics for our verified DPLL solver.
The number of lines containing executable code in the entire Dafny development is 657. We obtain this number by concatenating all source files and removing by hand all annotations: invariants, variants, modifies and reads annotations, conditions, post-conditions, lemmas, functions, predicates, helper assertions, ghost variables. We keep function methods and predicate methods, which serve as both executable code and as specification. The proportion of lines containing executable code in the entire development is approximately 1 to 5 (657 to 3303). For every line of executable code we have about 4 lines of logic (proofs, specifications).
The main challenge in verifying the solver is designing the right invariants and helper assertions. This is made more difficult by some verification conditions that take a large amount of time to discharge. Furthermore, the verification time is sometimes difficult to predict. In order to minimize verification time and make it more predictable, we have developed and used a set of verification patterns:
- Patterns that improve the modularity of the code.
- Avoid nested loops, because they typically require sharing some invariants between the inner and the outer loop. This increases duplication of code, decreases elegance, and increases verification time.We have made use of this pattern in the revertLastDecisionLevel method (in the file solver/formula.dfy), whose purpose is to revert the assignments made in the last decision level. The code of the method is very simple: it calls the removeLastVariable method repeatedly in a loop, and the removeLastVariable method also has a simple loop to update the counters.It would be simple to inline it and obtain two nested loops, but this would lead to a significant increase in verification time for the revertLastDecisionLevel method.
- Use methods with few lines of code. We have found that it is better to extract basic blocks as a separate method, even if they consist of only a few lines of code. This forces to programmer to better understand the role of such basic blocks and improves modularity.In a typical imperative programming language, the programmer would simply inline these basic blocks. In our Dafny development, it is not unusual to have methods with few lines of code that have a larger specification, which might require a significant number of helper assertions to prove.
- Patterns that improve the modularity of specifications.
- Avoid nested quantifiers. We use this pattern when a formula such as occurs in the specification. For such cases, we define a new predicate, , that is equivalent to the subformula . We then use instead of .This helps improve the development in two distinct ways: firstly, it forces the developer to give a proper name, , to the subformula, thereby clarifying their intention, and (2) it helps the underlying Z3 prover, which uses pattern-based quantifier instantiation, to perform better [37].
- Use as fewmodifiesandreadsclauses as necessary. This is known to improve the verification time, sometimes significantly, because the prover knows that any object not under a modifies clause of a method remains the same after the method call. In particular, we have made extensive use of the less well-known backtick operator in modifies clauses, which allows to specify that a method is allowed to modify a particular field of an object, instead of the entire object.
It is not feasible to develop a SAT solver by running the Dafny verifier on the entire project with every change in the code or in the specification, because it can take several minutes to finish the verification of the entire project. Because of this issue, we have adopted a development methodology where we used Dafny to verify only the lemma/method being worked on, by using the /proc command line switch. Once the current lemma or method is verified, Dafny is run again on the entire project to check for other issues. We have also discovered that the Z3 axiom profiler [38], which allows to understand what verification conditions take a long time and why, does not scale well to projects the size of our solver.
Our experience in implementing and verifying TrueSAT in auto-active style is that it requires a significant amount of effort and expertise, and that it pushes the Dafny system to its limit. Based on our Dafny development, we identify three research directions for the further improvement to Dafny and other similar systems:
- Shorten the verification time for individual methods and lemmas and make verification time more predictable,
- Improve error messages for verification conditions that fail to verify, and
- Construct a method better than using helper assertions for manually guiding the verifier.
As future work, we would like to upgrade our Dafny development to the full CDCL algorithm. This is a promising way of building a verified solver that is roughly as efficient as current state-of-the-art SAT solvers. In order to upgrade our solver to CDCL, there are basically three algorithmic improvements that are necessary: (1) implement backjumping and a clause learning/forgetting strategy, (2) implement the two watched literals data structure, and (3) implement a restart strategy. Additionally, as a prerequisite for backjumping, the DPLL procedure should be implemented iteratively instead of recursively. In the iterative version, the call stack will be represented explicitly. Most of the call stack is already represented explicitly in the trace of assignments anyway. From the point of view of the implementation, we would only need to add one bit for each variable assignment, describing whether the other truth value of the propositional variable has already been checked or not. The recursive procedure will then become a loop. From the point of view of the specification, the postconditions of the recursive calls should become part of the loop invariant. A termination proof for the loop will also be necessary, and it could be based on the number of assignments that have been discarded as not satisfying the formula. The two watched literals data structure is particularly important for performance as the number of clauses increases due to the learnt clauses. Additionally, the two watched literals data structure makes reverting the assignments leading to a conflict very efficient, as it is no longer necessary to process each individual variable assigned to update counters. The structure of our solver enables the implementation of each of the three improvements in an orthogonal manner, although each of them requires significant verification effort. In addition to the algorithmic improvements above, better heuristics and engineering choices will be required to match the efficiency of state-of-the-art unverified solvers.
Author Contributions
Conceptualization, Ș.C.; methodology, C.-C.A. and Ș.C.; software, C.-C.A.; validation, C.-C.A. and Ș.C.; investigation, C.-C.A. and Ș.C.; data curation, C.-C.A.; writing—original draft preparation, C.-C.A. and Ș.C.; writing—review and editing, C.-C.A. and Ș.C.; visualization, C.-C.A.; supervision, Ș.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a grant of the Alexandru Ioan Cuza University of Iași, within the Research Grants program UAIC Grant, code GI-UAIC-2018-07.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The source code of TrueSAT is available at https://github.com/andricicezar/truesat (accessed on 1 June 2022). The SAT problems used as benchmarks and the SAT solvers against which we benchmark are available at the URL indicated in the main text.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brummayer, R.; Lonsing, F.; Biere, A. Automated Testing and Debugging of SAT and QBF Solvers. In Proceedings of the 13th International Conference on Theory and Applications of Satisfiability Testing, SAT 2010, Edinburgh, UK, 11–14 July 2010; pp. 44–57. [Google Scholar] [CrossRef]
- Balyo, T.; Heule, M.J.H.; Järvisalo, M. SAT Competition 2016: Recent Developments. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 5061–5063. [Google Scholar]
- Leino, K.R.M. Developing verified programs with Dafny. In Proceedings of the 35th International Conference on Software Engineering, ICSE ’13, San Francisco, CA, USA, 18–26 May 2013; pp. 1488–1490. [Google Scholar] [CrossRef]
- De Moura, L.M.; Bjørner, N. Z3: An Efficient SMT Solver. In Proceedings of the 14th International Conference on Tools and Algorithms for the Construction and Analysis of Systems, TACAS 2008, Budapest, Hungary, 29 March–6 April 2008; Volume 4963, pp. 337–340. [Google Scholar] [CrossRef]
- Crawford, J.M.; Auton, L.D. Experimental Results on the Crossover Point in Random 3-SAT. Artif. Intell. 1996, 81, 31–57. [Google Scholar] [CrossRef]
- Zhang, H.; Stickel, M.E. Implementing the Davis-Putnam Method. J. Autom. Reason. 2000, 24, 277–296. [Google Scholar] [CrossRef]
- Moskewicz, M.W.; Madigan, C.F.; Zhao, Y.; Zhang, L.; Malik, S. Chaff: Engineering an Efficient SAT Solver. In Proceedings of the 38th Design Automation Conference, DAC 2001, Las Vegas, NV, USA, 18–22 June 2001; pp. 530–535. [Google Scholar] [CrossRef]
- Hooker, J.N.; Vinay, V. Branching Rules for Satisfiability. J. Autom. Reason. 1995, 15, 359–383. [Google Scholar] [CrossRef]
- Prosser, P. Hybrid Algorithms for the Constraint Satisfaction Problem. Comput. Intell. 1993, 9, 268–299. [Google Scholar] [CrossRef]
- Marques Silva, J.P.; Sakallah, K.A. GRASP: A Search Algorithm for Propositional Satisfiability. IEEE Trans. Comput. 1999, 48, 506–521. [Google Scholar] [CrossRef]
- Gomes, C.P.; Selman, B.; Crato, N.; Kautz, H.A. Heavy-Tailed Phenomena in Satisfiability and Constraint Satisfaction Problems. J. Autom. Reason. 2000, 24, 67–100. [Google Scholar] [CrossRef]
- Biere, A.; Fröhlich, A. Evaluating CDCL Restart Schemes. In Proceedings of Pragmatics of SAT 2015 and 2018; Berre, D.L., Järvisalo, M., Eds.; EPiC Series in Computing; EasyChair: Austin, TX, USA, 2018; Volume 59, pp. 1–17. [Google Scholar] [CrossRef]
- Davis, M.; Putnam, H. A Computing Procedure for Quantification Theory. J. ACM 1960, 7, 201–215. [Google Scholar] [CrossRef]
- Davis, M.; Logemann, G.; Loveland, D.W. A machine program for theorem-proving. Commun. ACM 1962, 5, 394–397. [Google Scholar] [CrossRef]
- Bayardo, R.J., Jr.; Schrag, R. Using CSP Look-Back Techniques to Solve Real-World SAT Instances. In Proceedings of the Fourteenth National Conference on Artificial Intelligence and Ninth Innovative Applications of Artificial Intelligence Conference, AAAI 97, IAAI 97, Providence, RI, USA, 27–31 July 1997; pp. 203–208. [Google Scholar]
- Iordache, V.; Ciobâcă, Ş. Verifying the Conversion into CNF in Dafny. In Proceedings of the 27th International Workshop on Logic, Language, Information, and Computation, WoLLIC 2021, Virtual Event, 5–8 October 2021; Volume 13038, pp. 150–166. [Google Scholar] [CrossRef]
- Schlichtkrull, A. Formalization of Logic in the Isabelle Proof Assistant. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2018. [Google Scholar]
- Leroy, X. A Formally Verified Compiler Back-end. J. Autom. Reason. 2009, 43, 363–446. [Google Scholar] [CrossRef]
- Hawblitzel, C.; Petrank, E. Automated Verification of Practical Garbage Collectors. Log. Methods Comput. Sci. 2010, 6, 1–41. [Google Scholar] [CrossRef]
- Hawblitzel, C.; Howell, J.; Lorch, J.R.; Narayan, A.; Parno, B.; Zhang, D.; Zill, B. Ironclad Apps: End-to-End Security via Automated Full-System Verification. In Proceedings of the 11th USENIX Symposium on Operating Systems Design and Implementation, OSDI ’14, Broomfield, CO, USA, 6–8 October 2014; pp. 165–181. [Google Scholar]
- Bhargavan, K.; Fournet, C.; Kohlweiss, M. miTLS: Verifying Protocol Implementations against Real-World Attacks. IEEE Secur. Priv. 2016, 14, 18–25. [Google Scholar] [CrossRef]
- Zinzindohoué, J.K.; Bhargavan, K.; Protzenko, J.; Beurdouche, B. HACL*: A Verified Modern Cryptographic Library. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, CCS 2017, Dallas, TX, USA, 30 October–3 November 2017; pp. 1789–1806. [Google Scholar] [CrossRef]
- Andrici, C.C.; Ciobâcă, Ş. Verifying the DPLL Algorithm in Dafny. In Proceedings of the Third Symposium on Working Formal Methods, Timişoara, Romania, 3–5 September 2019; Volume 303, pp. 3–15. [Google Scholar] [CrossRef]
- Gomes, C.P.; Kautz, H.A.; Sabharwal, A.; Selman, B. Satisfiability Solvers. In Handbook of Knowledge Representation; van Harmelen, F., Lifschitz, V., Porter, B.W., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; pp. 89–134. [Google Scholar] [CrossRef]
- Beyer, D.; Löwe, S.; Wendler, P. Reliable benchmarking: Requirements and solutions. Int. J. Softw. Tools Technol. Transf. 2019, 21, 1–29. [Google Scholar] [CrossRef]
- Berger, U.; Lawrence, A.; Forsberg, F.N.; Seisenberger, M. Extracting verified decision procedures: DPLL and Resolution. Log. Methods Comput. Sci. 2015, 11, 1–18. [Google Scholar] [CrossRef]
- Oe, D.; Stump, A.; Oliver, C.; Clancy, K. versat: A Verified Modern SAT Solver. In Proceedings of the 13th International Conference on Verification, Model Checking, and Abstract Interpretation, VMCAI 2012, Philadelphia, PA, USA, 22–24 January 2012; pp. 363–378. [Google Scholar] [CrossRef]
- Marić, F. Formalization and Implementation of Modern SAT Solvers. J. Autom. Reason. 2009, 43, 81–119. [Google Scholar] [CrossRef]
- Marić, F.; Janičić, P. Formalization of Abstract State Transition Systems for SAT. Log. Methods Comput. Sci. 2011, 7, 1–37. [Google Scholar] [CrossRef]
- Marić, F. Formal verification of a modern SAT solver by shallow embedding into Isabelle/HOL. Theor. Comput. Sci. 2010, 411, 4333–4356. [Google Scholar] [CrossRef]
- Blanchette, J.C.; Fleury, M.; Lammich, P.; Weidenbach, C. A Verified SAT Solver Framework with Learn, Forget, Restart, and Incrementality. J. Autom. Reason. 2018, 61, 333–365. [Google Scholar] [CrossRef] [PubMed]
- Fleury, M. Optimizing a Verified SAT Solver. In Proceedings of the 11th NASA Formal Methods Symposium, NFM 2019, Houston, TX, USA, 7–9 May 2019; pp. 148–165. [Google Scholar] [CrossRef]
- Lescuyer, S. Formalizing and Implementing a Reflexive Tactic for Automated Deduction in Coq. Ph.D. Thesis, Université Paris Sud-Paris XI, Bures-sur-Yvette, France, 2011. [Google Scholar]
- Shankar, N.; Vaucher, M. The Mechanical Verification of a DPLL-Based Satisfiability Solver. Electron. Notes Theor. Comput. Sci. 2011, 269, 3–17. [Google Scholar] [CrossRef][Green Version]
- Lammich, P. Efficient Verified (UN)SAT Certificate Checking. J. Autom. Reason. 2020, 64, 513–532. [Google Scholar] [CrossRef]
- Wetzler, N.; Heule, M.; Hunt, W.A.H., Jr. DRAT-trim: Efficient Checking and Trimming Using Expressive Clausal Proofs. In Proceedings of the 17th International Conference on Theory and Applications of Satisfiability Testing, SAT 2014, Vienna, Austria, 14–17 July 2014; Volume 8561, pp. 422–429. [Google Scholar] [CrossRef]
- Moskal, M. Programming with Triggers. In Proceedings of the 7th International Workshop on Satisfiability Modulo Theories, SMT ’09, Montreal, QC, Canada, 2–3 August 2009; pp. 20–29. [Google Scholar] [CrossRef]
- Becker, N.; Müller, P.; Summers, A.J. The Axiom Profiler: Understanding and Debugging SMT Quantifier Instantiations. In Proceedings of the 25th International Conference on Tools and Algorithms for the Construction and Analysis of Systems, TACAS 2019, Prague, Czech Republic, 6–11 April 2019; Volume 11427, pp. 99–116. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).