Abstract
Survival and reliability analyses deal with incomplete failure time data, such as censored and truncated data. Recently, the classical left-truncation scheme was generalized to analyze “field data”, defined as samples collected within a fixed period. However, existing competing risks models dealing with left-truncated field data are not flexible enough. We propose copula-based competing risks models for latent failure times, permitting a flexible parametric form. We formulate maximum likelihood estimation methods under the Weibull, lognormal, and gamma distributions for the latent failure times. We conduct simulations to check the performance of the proposed methods. We finally give a real data example. We provide the R code to reproduce the simulations and data analysis results.
Keywords:
censoring; competing risk; left-truncation; lognormal distribution; multivariate survival analysis; Weibull distribution; reliability MSC:
62H12; 62N01; 62N05; 62P30
1. Introduction
Survival analysis deals with incomplete failure time data, such as censored and truncated data [1,2,3,4,5]. Left-truncation arises if early failures occur before the data collection period and their failures are simply ignored. Right-censoring arises if late failures occur after the data collection period, where their exact times of failures are unascertainable. Competing risks arise if the failure event of interest becomes unavailable by the occurrence of other failure events.
Naïve statistical analyses of truncated, censored, and competing risks data lead to biased inference for the population of interest. Left-truncation, right-censoring, and competing risks are a classical topic in survival analysis that is widely recognized in both biostatistics [3] and reliability engineering [1,2,3,4,5].
Hong et al. [1] generalized the classical truncation scheme to a more complex scheme found in the “field data”, defined as samples collected within a fixed period (see Section 2). The well-known example is the failure time dataset for electric power transformers. Hong et al. [1] separated the samples into two parts: a truncated part (e.g., transformers installed before 1980) and an untruncated part (e.g., transformers installed after 1980), and then combined them into a single likelihood function. This type of truncated field data arises in many other practical applications, where there is a birth process (the installing process) of individuals and a certain data collection period of failure [6,7,8,9].
For left-truncated field reliability data, a variety of distributions have been considered for statistical inference. The inference methods for the lognormal and Weibull distributions were developed by [1,10,11,12]. The gamma and the generalized gamma distribution were considered in [13,14]. Comparison of the numerical methods for maximum likelihood estimator were considered by [12,15]. Bayesian approaches for the lognormal, Weibull, and gamma distributions were considered by [2,16]. The Lehmann family of distributions was considered by [17] and the log-location-scale family of distributions was considered by [18]. The spline model was proposed by [7]. In this research topic, the most up-to-date review paper is [2].
Competing risks could occur together with left-truncation. Competing risks means that there are latent failure times to events, and only one of the failure times is observable. As competing risks are dependent, copula-based dependent risks models have been extensively utilized [19,20,21,22,23,24,25], which formulate the joint distribution of latent failure times. However, in analysis of left-truncated field data, copula-based dependent risks models have not been proposed yet.
Existing competing risks analyses for left-truncated field data are limited to the following models: the independent Weibull model with the common shape parameter [26], the Marshall–Olkin bivariate Rayleigh model [27], and the Marshall–Olkin bivariate Weibull model [4]. While these three models provide an important starting point, their models are somewhat specific for modeling latent failure times of competing risks. Therefore, there is much room for proposing more flexible models.
In this paper, we will develop copula-based models for dependent competing risks under left-truncation, permitting more flexible models for dependence structure and failure time distributions than the existing three models of [4,26,27]. Due to our main interest in applications to reliability analyses, we adopt the standard parametric distributions, including the Weibull, lognormal, and gamma distributions. These failure time distributions are commonly used in reliability studies, and also found in recent engineering applications [28,29,30]. While the proposed copula models permit a variety of copulas, we nonetheless focus on the Clayton copula for modeling dependence among failure times to facilitate computation.
The remainder of the paper is structured as follows. Section 2 provides the backgrounds and key concepts, such as field failure data and competing risks. Section 3 introduces copula models and develops likelihood functions for the Weibull, lognormal, gamma marginal models. Section 4 reports simulation studies to check the performance of the proposed methods. In Section 5, we analyze a dataset for illustration. Section 6 concludes the paper with future directions.
2. Left-Truncation and Competing Risks
We review the structure of left-truncation and competing risks for data collected from field studies.
Suppose that there are two mutually exclusive events for failure, named Event 1 and Event 2. Let be a pair of failure times for Event 1 and Event 2, respectively. Under competing risks, the failure time is defined by , where only one of is observable. For instance, if , the observable failure time is , and the exact value of is unknown. The pair is called “latent failure times” since only one of and is observable.
Figure 1 explains left-truncation in the data collection scheme, where the individuals were born randomly over time. However, we cannot obtain samples of all the individuals since the data collection starts only after time s (the starting time). If individuals are born and then fail before time s, they are discarded and not observable; see “Not observed” in Figure 1. This leads to biased sampling.
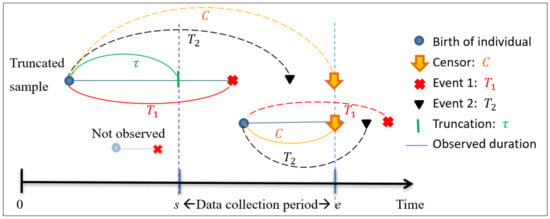
Figure 1.
Left-truncated and competing risks data from a field study. Event 1 and Event 2 are subject to competing risks. Solid curves show observable times, and dashed curves show unobservable times. One can observe Event 1, Event 2, or Censoring, whichever occurs first, between the starting time (s) and the ending time (e). One cannot observe anything if Event 1 or Event 2 occurs before time s.
To define left-truncation mathematically, we let be the time from birth to time s (Figure 1). For individuals to be included in our samples, their failure time must be greater than (Figure 1). Those who were born before s are defined as “truncated samples”, which are all conditional on . The individuals born after s are always included in our samples. Therefore, our samples are divided into truncated ones (born before s) and untruncated ones (born after s). For untruncated samples, the sample is observed without any condition, and is undefined.
To signify the difference between truncated and untruncated samples, we define the truncation indicator,
There could be a random censoring time that may censor the value of and , e.g., the duration of the data collection (Figure 1). If both Event 1 and Event 2 do not occur within the data collection period, one cannot exactly know and . One only knows that and are greater than the observed censoring time that is defined as time from birth to e (the ending time).
In this sense, what we actually observe is . The sample is censored if both and hold; otherwise, the sample is uncensored. We assume that two failures do not occur simultaneously, i.e., never occurs.
Under competing risks, there are three possible cases: The first case is where Event 1 is observable by and . The second case is where Event 2 is observable by and . The last case is where neither Event 1 nor Event 2 is observable by and . The first and last cases are shown in Figure 1.
In a dataset, there are n samples denoted as . In addition, as we know the event status of each individual, the samples are divided into three sets:
- ,
- ,
- .
Since each sample belongs to one of the three sets, it holds that .
3. Proposed Methods
In this section, we propose a copula-based model and a likelihood-based inference method.
3.1. Copula Model for Competing Risks
We use a copula model for bivariate competing risks as originally proposed by [19]. Let be a pair of failure times whose marginal survival functions are , . We assume that the failure times are continuous and hence have the density functions , . To model the dependence of and , we assume a survival copula model [21]
where is a parametric copula [31] with parameter .
Copulas are popular in statistical analyses for bivariate models involving competing risks [20,21,22,23,24,25,32,33,34]. There exist a number of copulas [31], and new copulas keep emerging [35,36]. Copulas are applied to a variety of fields, including reliability [37], ecology [38], meta-analysis [39,40], and econometrics [41]. However, to reduce the complexity of estimation, the copula has to be as simple as possible.
For computational simplicity, we particularly adopt the Clayton copula [31]
where specifies dependence between and , and is transformed to Kendall’s tau: . Hence, and are positively dependent whose strength increases as gets large. If , the Clayton copula reduces to , the independent risks model of [26]. The Clayton copula is one of the most frequently used copulas in competing risks models [22,24] and other models [33,40,41,42] due to its remarkable mathematical tractability.
Other copulas might be considered. However, we do not suggest fitting many copulas since the true one may not be identifiable from the data. We use the Clayton copula, and then focus on the selection of .
3.2. Likelihood Function
We extend the likelihood function for the independent risks models [26] to the copula-based models. Let be observed data as previously defined. Let be a pair of latent failure times for Event 1 and Event 2, respectively. In addition, let be independent and uninformative censoring times. Let , and be its observed value. For a sample without truncation (), the likelihood is divided into three cases:
- (i)
- if and ,
- (ii)
- if ,
- (iii)
- if ,
For a sample with truncation (), the likelihood is divided into other three cases:
- (iv)
- if and ,
- (v)
- if ,
- (vi)
- if .
In the last three cases, the “” can be dropped. Combining all the six cases and ignoring the constant factors for censoring, the likelihood function is
After some simplification, the likelihood function becomes
To estimate parameters in the model, the maximum likelihood estimator (MLE) is adopted under parametric models for and . We will consider commonly used parametric models for failure time distributions in reliability, including the Weibull, lognormal, and gamma distributions. Recent engineering applications of these distributions are found in [28,29,30]. The Weibull distribution will be detailed in Section 3.3 and the lognormal and gamma distributions in Appendix A and Appendix B.
3.3. Weibull Model
We set and . Under the independent risks model , the likelihood function is
If we set the common shape parameter , the above likelihood is equivalent to the one derived in Kundu et al. [26]. We do not impose this assumption, and let for generality.
Under the Clayton copula with parameter , the likelihood function is
where , , and . While the likelihood is undefined for , by letting , the likelihood function reduces to the one under the independent risks model.
There are a few different ways to estimate based on . The first one is the MLE under an “assumed” value of , which is defined as
The MLE under the independence copula is regarded as . The next one is the full MLE with the unknown , which is defined as
In either case, one can maximize by applying an iteration algorithm. In R (https://www.r-project.org/), there are a variety of optimization functions. We suggest the “optim(.)” function (https://stat.ethz.ch/R-manual/R-patched/library/stats/html/optim.html, accessed on 19 June 2022). This function has the option “hessian=TRUE” to yield the Hessian matrix of . The standard error (SE) of the estimates can be computed by the diagonal components of the inverse of the Hessian matrix. Details can be seen from the R code given in Supplementary Materials.
We generally recommend using the full MLE if one wishes to estimate . However, the full MLE gives large variance since data have little information for . In addition, the Hessian matrix could not be invertible, making the SE unavailable. We conjecture that the regularity conditions for the MLE hold with the unknown (as shown in [25]), but fail to hold for the full MLE.
An alternative approach to this problem is the pseudo-MLE (PMLE). We first obtain preliminary estimates under an assumed value of , and obtain that maximizes . The final estimates are then obtained. In our simulation studies, we set giving Kendall’s tau = 0.1. In practice, however, one may choose a few different values of , and then, choose the one that maximizes .
4. Simulation Studies
We conducted simulation studies to check the performance of the proposed methods of Section 3. To this end, we compared the performance of fitting (i) the independence copula, (ii) the Clayton copula with the known parameter, (iii) the Clayton copula with the parameter estimated by the MLE, and (iv) the Clayton copula with the parameter estimated by the PMLE.
4.1. Simulation Settings
We generated latent failure times from the Weibull model: and . Dependence structure for the two failure times is modeled by either the independence copula or the Clayton copula with (Kendall’s tau = 0.5).
Mimicking the sampling scheme of Figure 1, we generated , and , where is the birth time, s is the starting time, and e is the ending time. For truncated samples, we kept samples satisfying . This led to samples with for truncated samples and with for untruncated samples.
Based on the samples, the MLE was computed by fitting the independent model or the Clayton copula with being known. In addition, the MLE and PMLE were computed by fitting the Clayton copula with being unknown (the PMLE wasso computed under an assumed value of corresponding to Kendall’s tau = 0.1).
Based on 1000 repetitions, we calculated the mean, standard deviation (SD), and the mean squared error (MSE) of parameter estimates, and the average of the SEs. For instance, the MSE for is , where the expectation is taken by the average of 1000 repetitions.
The following parameter settings were considered to model different shapes of the hazard function (Figure 2):
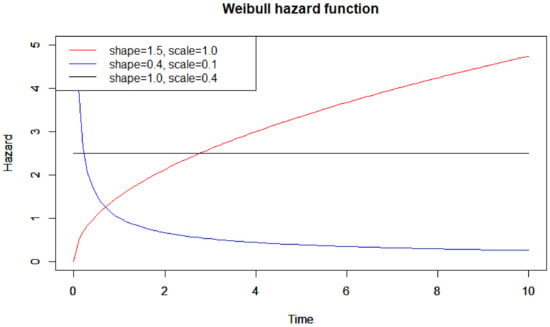
Figure 2.
The shape parameter and the scale parameter used in the simulation study for the Weibull model: and .
- (a)
- Decreasing hazard: ; ; ,
- (b)
- Constant hazard: ; ; ,
- (c)
- Increasing hazard: ; ; .
4.2. Simulation Results
Table 1 shows the means of parameter estimates. We see that the means of parameter estimates are nearly close to their true parameters when the copula is correctly specified. For instance, when the true copula is the Clayton copula with , accurate estimates are obtained by fitting the same copula. If the true copula is wrongly specified, the estimates are biased (e.g., by fitting the Clayton copula with under the independence copula). This implies the importance of selecting the correct value of to estimate the parameter. If is treated as unknown and estimated by data, the biases of estimates can often be large. These biases exist for both MLE and PMLE methods for dealing with the unknown . This unavoidable bias comes from the well-known difficulty of estimating under competing risks.

Table 1.
The means (biases) of parameter estimates based on 1000 simulation runs.
Table 2 shows the MSEs for the estimates. The smallest MSEs are attained when the true copula equals the fitted one. This agrees with the pattern of biases (Table 1), again implying the importance of selecting the correct value of . The MSEs remain large when estimating by the MLE or PMLE. Again, this problem comes from the difficulty of estimating under competing risks.

Table 2.
The MSEs of parameter estimates based on 1000 simulation runs.
Table 3 shows how the MSEs reduce as the sample size increases (only the results for estimating are shown as the results for other parameters exhibiting similar patterns). When the true copula’s parameter is correctly specified, the MSEs vanish toward zero with increased samples. This implies the consistency of the parameter estimates. When the copula parameter is wrongly chosen, the MSEs reduce very slowly or do not vanish toward zero. When the copula parameter is estimated, the MSEs do not always reduce with increased samples. This indicates the inconsistency of the parameter estimates when the copula parameter is wrongly specified or estimated.

Table 3.
The MSEs of the estimates of under various sample sizes based on 1000 runs.
Table 4 compares the SDs of the parameter estimates with the average of the SEs. The SDs and SEs are very close to each other, indicating that the SEs capture the true variations of the estimates. Hence, the SEs calculated by the proposed method (by the Hessian matrix from the “optim(.)” R function) are highly reliable. However, if is treated as unknown and estimated by data, there are some simulation runs where the SEs cannot be computed due to the calculation problem of the Hessian caused by some errors in the “optim(.)” function. Hence, we could not present the results in this case. We suspect that the regularity conditions for the Hessian matrix (to be negative definite) may not hold in this case.

Table 4.
The standard derivation (SD) and the average of SEs based on 1000 simulation runs.
5. Data Analysis
This section illustrates the proposed method by a data example.
Table 5 shows the artificial dataset created by Kundu et al. [26], who mimicked the setting of electric power transformers that were randomly installed from 1960 to 2008 [1]. The dataset consists of samples (electric power transformers) that are observed from the starting year (s = 1980) to the ending year (e = 2008). However, some transformers installed before 1980 are subject to left-truncation. The 30 transformers are truncated (; installed before 1980) and the other 70 transformers are untruncated (; installed after 1980). Observed events are three types of “Event” (=1 for Event 1; =2 for Event 2; =0 for censoring) in the 5th column of Table 5. The number of events is 14 for Event 1, 33 for Event 2, and 53 for censoring. The data seem to be a simulated dataset from the independent Weibull with the common shape parameter as considered in [26], though the details were not explained. We therefore will fit the Weibull failure time models.

Table 5.
Artificial data from Kundu et al. [26], which consist of power transformers observed from the starting year (s = 1980) to the ending year (e = 2008). is the installation year. is either failure year or censoring year (2008). The 30 transformers are truncated () and other 70 transformers are untruncated (). Observed events are shown in Event (=0 for censoring; =1 for Event 1; =2 for Event 2).
For the i-th transformer, let be a pair of latent failure times for Event 1 and Event 2, respectively, for . Following [26], we scaled the failure times (in days) by dividing them by 100 to avoid many decimal places in parameter estimates.
We postulate the model
where , and . We estimated the parameters , , , and under the assumed value of 0, 0.5, 2, or 8. We also estimated the parameters without giving the value of (all parameters were estimated together) by the MLE or the PMLE.
Table 6 compares the estimates for (, , , ) based on different values for . Under the assumed value of , the estimates are very close to the estimates obtained by Kundu et al. [26]. This is reasonable since the proposed model with and that of Kundu et al. [26] are both the independent Weibull models. Note that the model of Kundu et al. [26] imposed the common shape parameter while our proposed model did not. Estimates and show that the common shape parameter seems to be valid for these data. For the assumed values of , the estimates deviate from the results of Kundu et al. [26]. The results under should not be taken since their log-likelihood values are lower than the one under . The PMLE under the assumed values of improves the log-likelihood value, yet none of them reaches the log-likelihood value under . Indeed, the log-likelihood value under almost reaches the largest log-likelihood value under that comes from the MLE. In conclusion, our sensitivity analysis by the fixed values and estimated value of extremely confirms adequacy of the independent risks model for this dataset.

Table 6.
The estimates (SEs in parenthesis) for the Clayton copula model with the Weibull failure times based on the dataset from Kundu et al. [26]. The Clayton copula with fixed or estimated are fitted.
6. Conclusions and Future Work
In this paper, we propose a copula-based model for dependent competing risks in the presence of left-truncation. The copula-based competing risks model permits more flexible failure time distributions and dependence structure than the existing competing risks model [4,26,27]. Parametric likelihood-based inference methods are then formulated, motivated by the practically important applications in field reliability analyses.
Below, we list several problems to be considered or resolved in the future.
First, different failure time models can be examined besides the Weibull, lognormal, and gamma models considered in this paper. The candidate distributions could be the extreme-value distributions [43], the generalized Pareto distribution [44], and the generalized Bilal distribution [45]. The Fréchet (type II) and Gumbel (type I) distributions are of particular interest in the extreme-value distributions [43]. In addition, the model may include a covariate (e.g., an acceleration factor) associated with failure time as in the Weibull regression [1]. In addition to this usual failure time regression model, a conditional copula regression model is of another interest [46]. Cure fractions and latent variables may also be considered to be incorporated into the failure time model [47].
Second, the prediction analysis and the test design may be explored in addition to the estimation method considered in this paper. The prediction of remaining lifetime was considered under left-truncated and right-censored field data without competing risks [1,17]. This risk prediction at a censored time point may be informative for engineers to make decisions on future maintenance plans. However, it is not trivial to extend this prediction method under competing risks. This risk prediction scheme is equivalent to dynamic prediction [48,49,50,51,52,53]. Moreover, the accelerated life test plans may be considered including the case of one-shot devices with competing risks [54,55].
Third, a goodness-of-fit test and/or graphical model-diagnostic method for the proposed model may be developed. A possible strategy is to apply a distance measure between the empirical sub-distribution function and the model-based one. This strategy was adopted for right-censored competing risks data analyses [23] without left-truncation. In order to handle left-truncation, further methodological and numerical works are necessary.
Fourth, Bayesian methods can be considered as a competitor to the MLE methods of this paper. The choice of the marginal prior distributions could follow [2,16], while the bounded uniform prior could be recommended for the copula prior [56]. It is of interest to see if the difficulty of estimating the copula parameter is resolved by Bayesian methods.
Finally, the limited availability of open datasets could be resolved by encouraging engineers to collect field failure data. Due to the difficulty of obtaining real datasets in the literature, we applied our methods to the artificial dataset created by Kundu et al. [26], who considered the setting of electric power transformers. Dataset can also be searched from other applications of survival analysis, such as those for medical research.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/math10132163/s1, Supplementary Materials of this paper include “R.code.zip”, including the R code to reproduce the simulations and data analysis results.
Author Contributions
Conceptualization, H.M. and T.E.; methodology, H.M. and T.E.; writing—original draft preparation, H.M. and T.E.; writing—review and editing, H.M. and T.E. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by JSPS KAKENHI (JP21K12127) and (JP22K11948).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the numerical results of the paper are reproduced by the R code in Supplementary Materials.
Acknowledgments
We thank the special issue editor and five reviewers for their helpful comments that improved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Likelihood for the Gamma Model
We set the marginal survival functions
Under the independent risks model , the likelihood function is
Under the Clayton copula, the likelihood function is
where
Appendix B. Likelihood for the Lognormal Model
We set the marginal survival functions
where Φ is the cdf of the standard normal distribution. Under the independent risks model , the likelihood function is
Under the Clayton copula, the likelihood function is
where
References
- Hong, Y.; Meeker, W.Q.; McCalley, J.D. Prediction of remaining life of power transformers based on left truncated and right censored lifetime data. Ann. Appl. Stat. 2009, 3, 857–879. [Google Scholar] [CrossRef] [Green Version]
- Emura, T.; Michimae, H. Left-truncated and right-censored field failure data: Review of parametric analysis for reliability. Qual. Reliab. Eng. Int. 2022. [Google Scholar] [CrossRef]
- Klein, J.P.; Moeschberger, M.L. Survival Analysis Techniques for Censored and Truncated Data; Springer: New York, NY, USA, 2003. [Google Scholar]
- Wang, L.; Lio, Y.; Tripathi, Y.M.; Dey, S.; Zhang, F. Inference of dependent left-truncated and right-censored competing risks data from a general bivariate class of inverse exponentiated distributions. Statistics 2022, 56, 347–374. [Google Scholar] [CrossRef]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data, 2nd ed.; Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Li, Q.; Li, D.; Huang, B.; Jiang, Z.E.M.; Ma, J. Failure analysis for truncated and fully censored lifetime data with a hierarchical grid algorithm. IEEE Access 2020, 8, 34468–34480. [Google Scholar] [CrossRef]
- Jiang, W.; Ye, Z.; Zhao, X. Reliability estimation from left-truncated and right-censored data using splines. Stat Sin. 2020, 30, 845–875. [Google Scholar]
- Dörre, A. Semiparametric likelihood inference for heterogeneous survival data under double truncation based on a Poisson birth process. Jpn. J. Stat. Data Sci. 2021, 4, 1203–1226. [Google Scholar] [CrossRef]
- Dörre, A.; Huang, C.Y.; Tseng, Y.K.; Emura, T. Likelihood-based analysis of doubly-truncated data under the location-scale and AFT model. Comp. Stat. 2021, 36, 375–408. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Mitra, D. Likelihood inference for lognormal data with left truncation and right censoring with an illustration. J. Stat. Plan Inf. 2011, 141, 3536–3553. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Mitra, D. Left truncated and right censored Weibull data and likelihood inference with an illustration. Comp. Stat. Data Anal. 2012, 56, 4011–4025. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Mitra, D. Some further issues concerning likelihood inference for left truncated and right censored lognormal data. Comm. Stat. Simul Comp. 2014, 43, 400–416. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Mitra, D. Likelihood inference based on left truncated and right censored data from a gamma distribution. IEEE Trans. Reliab. 2013, 62, 679–688. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Mitra, D. EM-based likelihood inference for some lifetime distributions based on left truncated and right censored data and associated model discrimination. S. Afr. Stat. J. 2014, 48, 125–171. [Google Scholar]
- Emura, T.; Shiu, S. Estimation and model selection for left-truncated and right-censored lifetime data with application to electric power transformers analysis. Commun. Stat. Simul. 2016, 45, 3171–3189. [Google Scholar]
- Ranjan, R.; Sen, R.; Upadhyay, S.K. Bayes analysis of some important lifetime models using MCMC based approaches when the observations are left truncated and right censored. Reliab. Eng. Syst. Saf. 2021, 214, 107747. [Google Scholar] [CrossRef]
- Mitra, D.; Kundu, D.; Balakrishnan, N. Likelihood analysis and stochastic EM algorithm for left truncated right censored data and associated model selection from the Lehmann family of life distributions. Jpn. J. Stat. Data Sci. 2021, 4, 1019–1048. [Google Scholar] [CrossRef]
- Mitra, D.; Balakrishnan, N. Statistical inference based on left truncated and interval censored data from log-location-scale family of distributions. Comm. Stat. Simul. Comp. 2021, 50, 1073–1093. [Google Scholar] [CrossRef]
- Zheng, M.; Klein, J.P. A self-consistent estimator of marginal survival functions based on dependent competing risk data and an assumed copula. Commun. Stat. Theory Methods 1994, 23, 2299–2311. [Google Scholar] [CrossRef]
- Zheng, M.; Klein, J.P. Estimates of marginal survival for dependent competing risks based on an assumed copula. Biometrika 1995, 82, 127–138. [Google Scholar] [CrossRef]
- Escarela, G.; Carriere, J.F. Fitting competing risks with an assumed copula. Stat. Methods Med. Res. 2003, 12, 333–349. [Google Scholar] [CrossRef]
- Emura, T.; Shih, J.H.; Ha, I.D.; Wilke, R.A. Comparison of the marginal hazard model and the sub-distribution hazard model for competing risks under an assumed copula. Stat. Methods Med. Res. 2020, 29, 2307–2327. [Google Scholar] [CrossRef]
- Wang, Y.C.; Emura, T.; Fan, T.H.; Lo, S.M.; Wilke, R.A. Likelihood-based inference for a frailty-copula model based on competing risks failure time data. Qual. Reliab. Eng. Int. 2020, 36, 1622–1638. [Google Scholar] [CrossRef]
- De Uña-Álvarez, J.; Veraverbeke, N. Copula-graphic estimation with left-truncated and right-censored data. Statistics 2017, 51, 387–403. [Google Scholar] [CrossRef]
- Shih, J.H.; Emura, T. Likelihood-based inference for bivariate latent failure time models with competing risks under the generalized FGM copula. Comput. Stat. 2018, 33, 1293–1323. [Google Scholar] [CrossRef]
- Kundu, D.; Mitra, D.; Ganguly, A. Analysis of left truncated and right censored competing risks data. Comp. Stat. Data Anal. 2017, 108, 12–26. [Google Scholar] [CrossRef]
- Wu, K.; Wang, L.; Yan, L.; Lio, Y. Statistical inference of left truncated and right censored data from Marshall–Olkin bivariate Rayleigh distribution. Mathematics 2021, 9, 2703. [Google Scholar] [CrossRef]
- Shuto, S.; Amemiya, T. Sequential Bayesian inference for Weibull distribution parameters with initial hyperparameter optimization for system reliability estimation. Reliab. Eng. Syst. Saf. 2022, 224, 108516. [Google Scholar] [CrossRef]
- Bouwmeester, J.; Menicucci, A.; Gill, E.K.A. Improving CubeSat reliability: Subsystem redundancy or improved testing? Reliab. Eng. Syst. Saf. 2022, 220, 108288. [Google Scholar] [CrossRef]
- Wu, C.W.; Lee, A.H.; Liu, S.W. A repetitive group sampling plan based on the lifetime performance index under gamma distribution. Qual. Reliab. Eng. Int. 2022, 38, 2049–2064. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Shih, J.H.; Emura, T. Bivariate dependence measures and bivariate competing risks models under the generalized FGM copula. Stat. Pap. 2019, 60, 1101–1118. [Google Scholar] [CrossRef]
- Peng, M.; Xiang, L.; Wang, S. Semiparametric regression analysis of clustered survival data with semi-competing risks. Comp. Stat. Data Anal. 2018, 124, 53–70. [Google Scholar] [CrossRef]
- Wu, M.; Shi, Y.; Zhang, C. Statistical analysis of dependent competing risks model in accelerated life testing under progressively hybrid censoring using copula function. Commun. Stat. Simul. Comput. 2017, 46, 4004–4017. [Google Scholar] [CrossRef]
- Chesneau, C. Theoretical study of some angle parameter trigonometric copulas. Modelling 2022, 3, 140–163. [Google Scholar] [CrossRef]
- Susam, S.O. A multi-parameter Generalized Farlie-Gumbel-Morgenstern bivariate copula family via Bernstein polynomial. Hacet. J. Math. Stat. 2022, 51, 618–631. [Google Scholar] [CrossRef]
- Ota, S.; Kimura, M. Effective estimation algorithm for parameters of multivariate Farlie–Gumbel–Morgenstern copula. Jpn. J. Stat. Data Sci. 2021, 4, 1049–1078. [Google Scholar] [CrossRef]
- Ghosh, S.; Sheppard, L.W.; Holder, M.T.; Loecke, T.D.; Reid, P.C.; Bever, J.D.; Reuman, D.C. Copulas and their potential for ecology. In Advances in Ecological Research; Academic Press: Cambridge, MA, USA, 2020; Volume 62, pp. 409–468. [Google Scholar]
- Shih, J.H.; Konno, Y.; Chang, Y.T.; Emura, T. Estimation of a common mean vector in bivariate meta-analysis under the FGM copula. Statistics 2019, 53, 673–695. [Google Scholar] [CrossRef]
- Shih, J.H.; Konno, Y.; Chang, Y.T.; Emura, T. Copula-based estimation methods for a common mean vector for bivariate meta-analyses. Symmetry 2022, 14, 186. [Google Scholar] [CrossRef]
- Zhuang, H.; Diao, L.; Grace, Y.Y. A Bayesian nonparametric mixture model for grouping dependence structures and selecting copula functions. Econom. Stat. 2022, 22, 172–189. [Google Scholar] [CrossRef]
- Emura, T.; Hsu, J.H. Estimation of the Mann–Whitney effect in the two-sample problem under dependent censoring. Comp. Stat. Data Anal. 2020, 150, 106990. [Google Scholar] [CrossRef]
- Alves, M.I.F.; Neves, C. Extreme Value Distributions. Int. Encycl. Stat. Sci. 2011, 2, 493–496. [Google Scholar]
- Grimshaw, S.D. Computing maximum likelihood estimates for the generalized Pareto distribution. Technometrics 1993, 35, 185–191. [Google Scholar] [CrossRef]
- Akhter, Z.; Almetwally, E.M.; Chesneau, C. On the Generalized Bilal Distribution: Some Properties and Estimation under Ranked Set Sampling. Axioms 2022, 11, 173. [Google Scholar] [CrossRef]
- Emura, T.; Sofeu, C.L.; Rondeau, V. Conditional copula models for correlated survival endpoints: Individual patient data meta-analysis of randomized controlled trials. Stat. Method Med. Res. 2021, 30, 2634–2650. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; He, H.; Lu, B.; Song, X. Mixture additive hazards cure model with latent variables: Application to corporate default data. Comp. Stat. Data Anal. 2022, 167, 107365. [Google Scholar] [CrossRef]
- Emura, T.; Nakatochi, M.; Matsui, S.; Michimae, H.; Rondeau, V. Personalized dynamic prediction of death according to tumour progression and high-dimensional genetic factors: Meta-analysis with a joint model. Stat. Method Med. Res. 2018, 27, 2842–2858. [Google Scholar] [CrossRef] [PubMed]
- Emura, T.; Michimae, H.; Matsui, S. Dynamic risk prediction via a joint frailty-copula model and IPD meta-analysis: Building web applications. Entropy 2022, 24, 589. [Google Scholar] [CrossRef] [PubMed]
- Kawakami, R.; Michimae, H.; Lin, Y.H. Assessing the numerical integration of dynamic prediction formulas using the exact expressions under the joint frailty-copula model. Jpn. J. Stat. Data Sci. 2021, 4, 1293–1321. [Google Scholar] [CrossRef]
- Noughabi, M.S.; Kayid, M. Bivariate quantile residual life: A characterization theorem and statistical properties. Stat. Pap. 2019, 60, 2001–2012. [Google Scholar] [CrossRef]
- Kayid, M.; Shafaei Noughabi, M.; Abouammoh, A.M. A nonparametric estimator of bivariate quantile residual life model with application to tumor recurrence data set. J. Classificat. 2020, 37, 237–253. [Google Scholar] [CrossRef]
- Zheng, R.; Najafi, S.; Zhang, Y. A recursive method for the health assessment of systems using the proportional hazards model. Reliab. Eng. Syst. Saf. 2022, 221, 108379. [Google Scholar] [CrossRef]
- Meeker, W.Q.; Hahn, G.J. A comparison of accelerated test plans to estimate the survival probability at a design stress. Technometrics 1978, 20, 245–247. [Google Scholar] [CrossRef]
- Ling, M.H. Optimal constant-stress accelerated life test plans for one-shot devices with components having exponential lifetimes under gamma frailty models. Mathematics 2022, 10, 840. [Google Scholar] [CrossRef]
- Michimae, H.; Emura, T. Bayesian ridge estimators based on copula-based joint prior distributions for regression coefficients. Comput. Stat. 2022. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).