Abstract
Homomorphic encryption with the ability to compute over encrypted data without access to the secret key provides benefits for the secure and powerful computation, storage, and communication of resources in the cloud. One of its important applications is fast-growing robot control systems for building lightweight, low-cost, smarter robots with intelligent brains consisting of data centers, knowledge bases, task planners, deep learning, information processing, environment models, communication support, synchronous map construction and positioning, etc. It enables robots to be endowed with secure, powerful capabilities while reducing sizes and costs. Processing encrypted information using homomorphic ciphers uses the sign function polynomial approximation, which is a widely studied research field with many practical results. State-of-the-art works are mainly focused on finding the polynomial of best approximation of the sign function (PBAS) with the improved errors on the union of the intervals . However, even though the existence of the single PBAS with the minimum deviation is well known, its construction method on the complete interval is still an open problem. In this paper, we provide the PBAS construction method on the interval , using as a norm the area between the sign function and the polynomial and showing that for a polynomial degree , there is (1) unique PBAS of the odd sign function, (2) no PBAS of the general form sign function if is odd, and (3) an uncountable set of PBAS, if is even.
Keywords:
minimax approximate polynomial; Chebyshev polynomials of the second kind; Bernstein polynomial; sign function MSC:
90C23; 12-08
1. Introduction
Comparing numbers in a homomorphic cipher causes the problem of finding the polynomial of best approximation of the sign function (PBAS). To approximate it, various approaches are used: rational functions [1], Bernstein polynomials [2], Chebyshev polynomials of the first kind [3,4], Fourier series expansions, artificial neural networks [5], least-squares [6,7,8,9], Newton–Raphson [10], etc. In these approaches, the noncontinuous sign function is replaced by a continuous function equal to:
The main issue is that the approximation is considered on the union of two intervals . The smallest deviation of a polynomial from the sign function is used as a measure of quality. However, this measure has a maximum error close to 0.5 in the zero neighborhood regardless of the degree of the polynomial, which makes it inapplicable for approximating a polynomial on the complete interval .
According to Chebyshev theory, there exists a single polynomial for continuous function with the minimum deviation [11], also known as minimax approximate polynomial or polynomial of best approximation.
The form of the minimax polynomial for the sign function approximation depends on . Various strategies for choosing for polynomial approximate are proposed. However, the problem of constructing PBAS remains open.
In this paper, we consider the classical definition of the sign function:
To construct the PBAS, we use the norm as the area between the sign function and the polynomial , determined by the following formula.
This norm allows us to avoid dramatically increasing the least deviation of the polynomial from the sign function as a result in the zero neighborhood.
Let us formulate the problem of the PBAS construction.
It is required to find the polynomial , where is the -th term, is a coefficient, is a variable, and .
It is formally defined as follows:
If exists, it is called the PBAS. In [11], p. 160, the theorem is proved that the PBAS exists. However, the number of PBAS and their form remains open. In this paper, we study these two problems.
The rest of the paper is organized as follows: Section 2 discusses the properties of the norm, which are then used in the proof. Section 3 discusses approximation of the sign function by Bernstein polynomials. It is shown that if and is the PBAS, then . Section 4 discusses the PBAS properties. Section 5 discusses the number of the PBAS odd functions. Section 6 investigates the problem of the existence of the PBAS of general form. Section 7 contains a conclusion.
2. Norm and Its Properties
The section discusses the main properties of the norm used for the proof.
Property 1.
Ifis an even function, then.
Proof.
considering that , then
Since is an even function, then ; therefore:
The property is proven. □
Let us consider an example of calculating the norm for .
Example 1.
- (a)
- Calculate; if, then.
- (b)
- Calculate; if, then.
From the data presented in Example 1, we can conclude that for, there is an uncountable number of PBAS, and they are given by, where.
Property 2.
Ifis an odd function, then.
Proof.
Since is an odd function, then ; therefore:
The property is proven. □
Property 3.
Ifis a general function, then
, whereis an even function andis an odd function.
Proof.
Let , then:
Therefore,
According to Property 2 , we find:
The property is proven. □
Property 4.
Proof.
By the definition,
According to the basic trigonometric identity , then
Therefore:
The property is proven. □
Corollary 1.
Proof.
According to Property 4 . Let us show that the inequality holds in the case , then in the case , then .
The corollary is proven. □
Corollary 2.
If , then
Proof.
According to Corollary 1, we get:
The corollary is proven. □
From Example 1, it follows that if then there are infinitely many PBAS of the zero degree. If and , then defines every PBAS of degree zero.
Let us investigate the problem of the number of PBAS of degrees greater than or equal to one.
3. Approximation of the Sign Function by Bernstein Polynomials
Let us apply the Bernstein polynomials for an approximation of the sign function .
Since the function is odd, using Property 2, we can calculate using . Let us calculate the value , proving the following statement.
Statement 1.
Proof.
Since the Bernstein polynomials on the interval have the property that ,
Substituting—instead of —expression (1), we find
We represent in the form , and we find:
Substitute
Hence,
The statement is proven. □
Corollary 3.
Proof.
Since is an odd function, according to Property 2:
Let
if , then ; therefore : .
The corollary is proven. □
From Property 1 and Corollary 3, we can conclude that if , the PBAS is not an even function.
4. Properties of the PBAS
Since the polynomial is a continuous function on the interval , according to the Weierstrass theorem, it is bounded by this in interval and reaches the minimum and maximum values—that is, there are such that . Let us denote and , and . Let us investigate the values of and for the PBAS . The result is presented in the form of the following lemma.
Lemma 1.
If n ≥ 1 and is the PBAS, then and .
Proof.
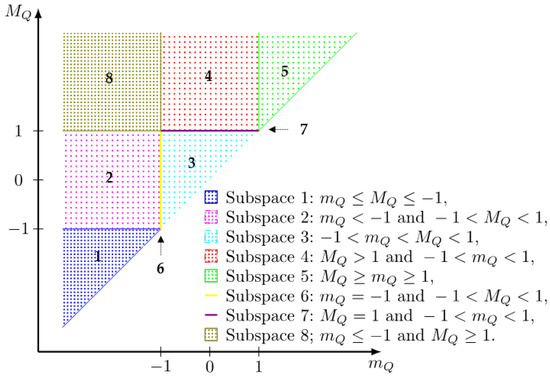
We split the two-dimensional space into subspaces using the curves and (see Figure 1).

Figure 1.
The set of possible values and .
In the following, we consider each subspace separately.
Subspace 1. Let us assume that PBAS satisfies the condition: (see Figure 1, Subspace 1), then , ; therefore:
From Corollary 3, it follows that for the PBAS has the property . Therefore, we came to a contradiction and our assumption is not correct.
Subspace 2. Let us assume that the PBAS satisfies the condition: and (see Figure 1, Subspace 2), then and :
We calculate and find
We subtract from the value and find:
Considering that
then
Therefore, . If , then is not a PBAS, so ; then, and
Let , then
Therefore,
since и , then
Therefore,
it means that is not a PBAS. We came to a contradiction.
Subspace 3. Let us assume that the PBAS satisfies the condition: (see Figure 1, Subspace 3), then , . Let . If , then and ; from the other side, . Therefore, we came to a contradiction and . Let and , . We calculate the value and find:
Since, according to the conditions of Theorem 1 and Corollary 3, and . Hence,
We calculate and find
Since и ,
Therefore,
and
Therefore, we came to a contradiction and our assumption is not correct.
Subspace 4. Let us assume that the PBAS satisfies the condition: and (see Figure 1, Subspace 4).
we calculate and get
we subtract from the value and get:
Considering that then ; therefore, . If , then is not a PBAS, so and and
let , then
Therefore,
since and , then
Therefore,
it means that is not a PBAS. We came to a contradiction.
Subspace 5. Let us assume that the PBAS satisfies the condition: (see Figure 1, Subspace 5); therefore, , means
From Corollary 3, it follows that for , the PBAS has the property . This means that we have come to a contradiction and our assumption is not correct.
Subspace 6. Let us assume that the PBAS satisfies the condition: and (see Figure 1, Subspace 6), then
Let , then
Therefore,
Since и ,
Therefore,
This means that is not a PBAS.
Subspace 7. Let us assume that satisfies the condition: and (see Figure 1, Subspace 7). Then,
Let , then
Therefore,
Since and ,
Therefore,
This means that is not a PBAS.
Subspace 8. Since in all seven cases we have come to a contradiction, if is a PBAS, it satisfies the boundary conditions defining Subspace 8 (See, Figure 1).
Lemma 1 is proven. □
Lemma 2.
For, there exists the PBAS odd function.
Proof.
The existence of the PBAS follows from Theorem [11] p. 160. Since for , the PBAS is not an even function, so is either a general function or an odd function.
Let us assume that is a general function; it can be represented in the form , where is an even function and is an odd function. It follows from Property 3 that . Considering that is the PBAS, , so the odd function is the PBAS. Therefore, for any , there is the PBAS , which is an odd function.
Lemma 2 is proven. □
Corollary 4.
Let,be a PBAS odd function, , and .
Proof.
We assume that PBAS is the odd function and .
Let us consider the function , where . Since is an odd function, is also an odd function. We calculate and using Property 2 and find:
Let us show that there exists , for which the inequality is satisfied.
We denote as a set of all for which the inequality holds and for which the inequality holds. We then find:
where is the length of the set .
We denote .
Since and , then and .
Let us consider two cases.
Case 1: If , then there is such a number for which holds. If , then ; therefore, so is not the PBAS. If , we choose as the value , for which the inequality holds, and is not a PBAS. Therefore, we came to a contradiction.
Case 2: If , then is an increasing function; that is, , for which the inequality holds. Therefore, for any , the following inequality holds:
Therefore, we came to a contradiction. If and , then , which is not the PBAS.
The corollary is proven. □
5. The Number of PBAS Odd Functions
In Lemma 2, it is proved that for , the PBAS is an odd function, but the question of their number remains open. The following theorem will answer this question.
Theorem 1.
If, then there is only one odd functionthat is the PBAS. Depending on the, the functionis determined as follows:
If is odd, then
and
If is even, then
and
Proof.
Let us consider two cases.
Case 1. is an odd number.
We consider the points such that . According to Corollary, 4 the value satisfies the condition . Considering that the function is an odd continuous function, then at least one point is such that exists.
Let us consider the question of the number of zeroes of the function . Since the function is an odd continuous function, then is an even function. The number of zeroes of is less or equal to , of which non-negative numbers are less than or equal to . Therefore, the number of solutions to the equation satisfying the question is less than or equal to . That is, .
Let us consider the points . In each of the points the value of the function changes its sign.
where .
We calculate the values of the partial derivatives :
Since by the definition, then:
We calculate the values of the partial derivatives :
The necessary condition for the value to be minimal is: ; therefore,
Solving the system [12], we find that
Considering that ; therefore, [12].
Using the Lagrange interpolation formula, we calculate the value , and we find , where
Then,
Let and , so is equal to
We calculate the value , and we obtain:
Considering that (2) holds, , then
and
If is even, then
Using the formula , where and , we have
Since and ([13] p. 2), where and , we have:
Therefore,
Using the basic trigonometric identities and , , where we obtain:
If is odd, then
Using the formula , where and , we have
Since [13] p. 2, where and we find:
According to the reduction formula , we have:
Using the formula [13] p. 2, where and we find:
According to the reduction formula , we obtain:
Since [13] p. 2, where and we find:
According to the reduction formula , we find:
Therefore,
Therefore, .
Since , then the smallest value at the maximum , considering that , then and .
Case 2. If is an even number, then the result is obtained similarly to case 1, except and .
The theorem is proved. □
From Theorem 1, it follows that for there is a unique odd function that is the PBAS, which is constructed using the Lagrange interpolation formula, and the interpolation nodes are an alternative to Chebyshev for Chebyshev polynomials of the second kind.
Example 2.
Construct the PBAS forand, which are odd functions.
Solution
If, then, according to Theorem 1, the PBAS is given by the following formula:
If, then, according to Theorem 1, the PBAS is given by the following formula:
Let us pay attention to the fact that. This fact can be generalized: ifis even and, then.
6. The Number of PBAS of the Neither Function
Let us investigate the problem of the existence of PBAS .
Theorem 2.
If n ≥ 1, then the following statements are true:
- 1.
- Ifis an odd number, then there is no PBAS.
- 2.
- Ifis an even number, then there is an infinite number of PBAS.
Proof.
From Theorem 1, it follows that there is a unique odd function that is a PBAS. Let us show that there exists an even function , such that: . For this, we calculate and find:
where , is an even function, and is an odd function.
is equal to zero only if the condition holds, equivalent to:
and
Therefore: .
Since is an odd-function PBAS, it follows from Theorem 1 that there are points such that . Since is an odd-function PBAS, it follows from the proof of Theorem 1 that if is an odd number, then . Otherwise, .
Substituting into the inequalities we find ; therefore, the necessary condition is . Since the function is an even function, ; therefore, is divisible by the polynomial and . Let us consider two cases.
Case 1. If is an odd number, then Therefore, there is no even polynomial satisfying the condition . Hence, if is an odd number, there is no PBAS that is a function of general form.
Case 2. If is an even number, then . From the other side, ; therefore, . To construct the polynomial we consider the polynomial of the form:
where .
We consider the equation , ; therefore, according to Rolle’s theorem, in each of the intervals , at least one point exists for which , where and . Since is an odd function, is an even function; therefore, . Considering that , then, according to the main theorem of algebra, the equation over the field of real numbers can have at most roots—considering their multiplicity—so are roots of multiplicity one. Since are roots of multiplicity one, the function passing through changes its sign; therefore, , ,…, ,, ,…,, are the intervals of the increase or decrease in the function . Therefore, the equation has at most one solution for each of the intervals. Taking into account that the intervals , ,…,, , solutions of the equation are respectively ; therefore, does not exist, and and .
Let us show that is a root of multiplicity one of the equation . We suppose that there exists , for which is a root of multiplicity greater than one of ; therefore, is also a root of the equation and .
Provided that , we have come to a contradiction. Therefore is a root of multiplicity one of the equation , so if there exists for which the condition is satisfied, then and one of the two conditions or hold.
Since , then if is an even number, then , otherwise .
Let us consider the function , given by the following formula:
The function is continuous on the interval . According to the Weierstrass theorem, it is bounded; that is, there exist such that . Considering that , we find that if is even number, then . Otherwise, . If is even number, ; otherwise, and we find the function satisfying . Since , it follows from Corollary 2 that , so is the PBAS and . It is also worth noting that is a PBAS, so is the PBAS.
The theorem is proven. □
Example 3.
Construct the general form PBAS for.
Solution follows from Example 2 that. Calculating, we have
We calculateand find:
We calculate the derivative of the functionand find:
Since there are no critical points on the segment, the functiontakes the maximum and minimum values at the ends of the segment. If we calculateand, respectively, we have:and
Therefore,and
whereis any number satisfying the condition, andis a Chebyshev polynomial of the second kind. Thus, the PBAShas the form.
Lemma 3.
Ifis an even number, then
Proof.
As , then
Consider two cases.
Case 1: If then
Because , we have
Case 2. If then
Because , we obtain
As , , and ,
Lemma 3 is proven. □
Theorem 3.
Ifis an even number, then PBAS is defined as
where,, and.
Proof.
Using the theorem on the expansion of rational functions in the case of different roots [14], we represent as partial fraction decomposition:
where . Therefore, we have
Calculating the values of at the point , we obtain:
On the other hand, , hence
Since , it follows that
Using Lemma 3, we find
Therefore,
Calculating , we have
Let us show that . Using the corollary of the Cauchy–Schwarz inequality we have
Therefore,
Let us add two inequalities:
As and then . Therefore, does not change sign on the interval [0, 1]. The minimum and maximum of the function will be reached at the ends of the interval. Let us calculate the value of the function at the points and :
Considering that
we have
As and , considering Theorem 2, we obtain
The theorem is proven. □
7. Conclusions
Homomorphic encryption enables the computing of encrypted data without access to the secret key. It has become a promising mechanism for the secure computation, storage, and communication of confidential data in cloud services [15]. Practical scenarios include robot control systems, machine learning models, image processing, and many others [6,7,8,9,10,16,17,18]. A challenge of processing encrypted information is finding a cryptographically compatible sign function approximation.
State-of-the-art works have mainly focused on constructing the polynomial of best approximation of the sign function (PBAS) on the union of the intervals . In this paper, we provide a construction of the PBAS on the complete interval and prove that:
If then PBAS has the form , where .
If then there is a unique PBAS odd function, which can be calculated using the zeros of the Chebyshev polynomial of the second kind.
If and is an odd number, then there are no PBAS of the general form.
If and is an even number, then there is an uncountable set of PBAS of the general form.
Future studies include assessing the accuracy and efficiency of PBAS on real systems, e.g., over privacy-preserving neural networks with homomorphic encryption, where the non-linear activation function is replaced with a PBAS to operate with encrypted data.
Author Contributions
Conceptualization, M.B., A.T., A.A. and F.G.; Data curation, B.P.-G. and F.G.; Formal analysis, M.B.; Investigation, M.B., A.T., B.P.-G., A.A., S.N., X.W. and F.G.; Methodology, A.A., S.N., X.W. and F.G.; Project administration, A.A.; Resources, S.N., X.W. and F.G.; Software, B.P.-G. and F.G.; Supervision, A.T. and A.A.; Validation, M.B., B.P.-G., S.N., X.W. and F.G.; Visualization, M.B. and B.P.-G.; Writing—original draft, M.B. and A.T.; Writing—review & editing, A.T. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Education and Science of the Russian Federation (Project 075-15-2020-915).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cheon, J.H.; Kim, D.; Kim, D.; Lee, H.H.; Lee, K. Numerical Method for Comparison on Homomorphically Encrypted Numbers. Lect. Notes Comput. Sci. 2019, 11922, 415–445. [Google Scholar] [CrossRef]
- Cheon, J.H.; Kim, D.; Kim, D. Efficient Homomorphic Comparison Methods with Optimal Complexity. Lect. Notes Comput. Sci. 2020, 12492, 221–256. [Google Scholar]
- Chen, H.; Chillotti, I.; Song, Y. Improved Bootstrapping for Approximate Homomorphic Encryption. Lect. Notes Comput. Sci. 2019, 11477, 34–54. [Google Scholar]
- Han, K.; Ki, D. Better bootstrapping for approximate homomorphic encryption. Lect. Notes Comput. Sci. 2020, 12006, 364–390. [Google Scholar] [CrossRef]
- Boura, C.; Gama, N.; Georgieva, M. Chimera: A unified framework for B/FV, TFHE and HEAAN fully homomorphic encryption and predictions for deep learning. IACR Cryptol. ePrint Arch. 2018, 2018, 758. [Google Scholar]
- Gilad-Bachrach, R.; Dowlin, N.; Laine, K.; Lauter, K.; Naehrig, M.; Wernsing, J. Cryptonets: Applying neural networks to encrypted data with high throughput and accuracy. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; Volume 48, pp. 201–210. Available online: http://proceedings.mlr.press/v48/gilad-bachrach16.pdf (accessed on 10 April 2022).
- Kim, M.; Song, Y.; Wang, S.; Xia, Y.; Jiang, X. Secure logistic regression based on homomorphic encryption: Design and evaluation. JMIR Med. Inform. 2018, 6, e19. [Google Scholar] [CrossRef] [PubMed]
- Bonte, C.; Vercauteren, F. Privacy-preserving logistic regression training. BMC Med. Genom. 2018, 11, 86. [Google Scholar] [CrossRef] [PubMed]
- Kim, A.; Song, Y.; Kim, M.; Lee, K.; Cheon, J.H. Logistic regression model training based on the approximate homomorphic encryption. BMC Med. Genom. 2018, 11, 83. [Google Scholar] [CrossRef] [PubMed]
- Bajard, J.-C.; Martins, P.; Sousa, L.; Zucca, V. Improving the Efficiency of SVM Classification with FHE. IEEE Trans. Inf. Forensics Secur. 2019, 15, 1709–1722. [Google Scholar] [CrossRef]
- Bakhvalov, N.S.; Zhidkov, N.P.; Kobelkov, G.M. Numerical Methods; Nauka: Moscow, Russia, 1987; p. 600. [Google Scholar]
- Korkine, A.; Zolotareff, G. Sur un certain minimum. Nouv. Ann. Mathématiques J. Candidats Écoles Polytech. Norm. 1873, 12, 337–355. Available online: http://www.numdam.org/item/NAM_1873_2_12__337_0/ (accessed on 7 November 2019).
- Zygmund, A. Trigonometric Series; Cambridge University Press: New York, NY, USA, 2002; Volume 1, p. 375. [Google Scholar]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics; Addison-Wesley Publishing Company: Reading, MA, USA, 1994; p. 625. [Google Scholar]
- Tchernykh, A.; Babenko, M.; Chervyakov, N.; Miranda-Lopez, V.; Avetisyan, A.; Drozdov, A.Y.; Rivera-Rodriguez, R.; Radchenko, G.; Du, Z. Scalable Data Storage Design for Nonstationary IoT Environment with Adaptive Security and Reliability. IEEE Internet Things J. 2020, 7, 10171–10188. [Google Scholar] [CrossRef]
- Pulido-Gaytan, B.; Tchernykh, A.; Cortés-Mendoza, J.M.; Babenko, M.; Radchenko, G.; Avetisyan, A.; Drozdov, A.Y. Privacy-preserving neural networks with Homomorphic encryption: Challenges and opportunities. Peer-to-Peer Netw. Appl. 2021, 14, 1666–1691. [Google Scholar] [CrossRef]
- Babenko, M.; Tchernykh, A.; Chervyakov, N.; Kuchukov, V.; Miranda-López, V.; Rivera-Rodriguez, R.; Du, Z.; Talbi, E.-G. Positional Characteristics for Efficient Number Comparison over the Homomorphic Encryption. Program. Comput. Softw. 2019, 45, 532–543. [Google Scholar] [CrossRef]
- Cortes-Mendoza, J.M.; Radchenko, G.; Tchernykh, A.; Pulido-Gaytan, B.; Babenko, M.; Avetisyan, A.; Bouvry, P.; Zomaya, A. LR-GD-RNS: Enhanced Privacy-Preserving Logistic Regression Algorithms for Secure Deployment in Untrusted Environments. In Proceedings of the 2021 IEEE/ACM 21st International Symposium on Cluster, Cloud and Internet Computing (CCGrid), Melbourne, Australia, 10–13 May 2021; IEEE: Melbourne, Australia, 2021; pp. 770–775. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).