Abstract
In this paper, we classify the complete regular orientable minimal surfaces in with total curvature and give a method to construct a series of complete non-holomorphic minimal surfaces with total curvature . Specially, we give a simplified classification in another method if the surfaces lie in .
MSC:
53A10; 53C42; 49Q05; 53C45; 53A07
1. Introduction
The classification of complete regular minimal surfaces in with finite total curvature is one of the most important problems in the theories of minimal surfaces. If M is a complete minimal surface in with finite total curvature, by using Huber’s theorem [1], Chern-Osserman [2] proved that M must be conformally equivalent to , where is a compact Riemann surface, and are ends of M. Furthermore, they [2] also proved that the the Gauss map of M can be extended to a meromorphic function on , and the total Gauss curvature of M is for some positive integer . The classical Gauss–Bonnet theorem [3], Equation (12) proved by Chern-Osserman [2] and the Jorge–Meek formula [4] all give the relation between the total Gauss curvature and the topological properties of such surfaces. Consequently, it is natural to look for the classification of such minimal surfaces with prescribed total curvature or genus or number of ends.
For minimal surfaces with a finite total curvature in , Osserman [5] proved that the total curvature of minimal surfaces in is equal to for some integer , and that catenoid and Enneper surface are the only complete orientable minimal surfaces of total curvature . Meeks [6] gave the classification of nonorientable complete minimal surfaces with total curvature greater than . The orientable case can also be characterized by López [7] under the work of Chen–Gackstatter [8] and Jorge–Meeks [4]. For the total curvature , Costa [9] obtained the classification of genus one embedded minimal surfaces in with finite total curvature . On the other hand, Chen and Gackstatter [8] constructed an example of genus two orientable minimal surface punctured in a point with total curvature .
For minimal surfaces in , Chen [10] gave the characterization of surfaces with total curvature . Then, Hoffman and Osserman gave a slightly different version of Chen’s theorem (see Theorem in [11]). They also gave a complete description of the complete minimal surfaces in with total curvature (see Theorem in [11]). Chen [12] gave some properties of complete minimal surfaces in with total curvature .
In this paper, we give the classification of complete minimal surfaces in with total curvature . Proposition 4 states that if S is a complete regular minimal surface in with total curvature , there are three possibilities: S is simply connected with , or S is doubly connected with , or S is a holomorphic curve in of genus 1. The last case can be excluded by Chen [12]; thus, we only have to consider the simply connected case and doubly connected case.
In Section 2, we give some basic results of minimal surfaces with finite total curvature. Propositions 2 and 3 give the representations of simply connectedness and k-connectedness, respectively, which are as devoted to the proof of our main theorems as what Hoffman and Osserman did in [11] for the total curvature . However, distinguished with the case, where a simple form of representation, especially in a doubly-connected case, is obtained by solving a system of equations, S may lie in an eight-dimensional affine subspace of (see corollary in [11], p. 82). Thus, there may be more equations to be solved and more coefficients to be determined, resulting in a highly complicated form of representation.
In Section 3, we give the transformation
Then
With these forms, if and only if . Thus, we get a system of Equation (22). By solving (22) and calculating the constraints condition in Propositions 2 and 3, we get the following theorems.
Theorem 1.
Suppose S is a complete regular simply connected minimal surface in with a total curvature ; then, S lies in some affine eight-dimensional space, and in terms of suitable coordinates, up to a constant factor, it may be represented by
where has the following form:
where
subject to the following constraints:
Theorem 2.
Let M be the plane minus a point 0, and up to a constant factor, let be defined by
Then, (7) defines a complete regular doubly connected minimal surface in with total curvature of genus 0, and Φ has the following forms:
where satisfies the same conditions as Φ in Theorem 1, in addition to
In Section 4, we give a universal method to construct a complete regular non-holomorphic minimal surface in with total curvature . In Equation (1), if all vanish, the surface S determined by is a complex analytic curve in . Thus, we can construct such minimal surfaces by deforming some specific complex analytic curve in .
Finally, in Section 5, a simplified classification of minimal surfaces in with total curvature is given from the viewpoint that the Gauss maps of such minimal surfaces have a fine representation about as follows:
Theorem 3.
Suppose S is a complete regular minimal surface in with total curvature . Then, in terms of suitable coordinates, it can be represented by one of the following forms:
- (a)
- S is a regular complex analytic curve in defined on with the maximal degree 4 at the pole ∞ of its components;
- (b)
- S is a regular complex analytic curve in defined on with the maximal degree at the poles respectively of its components;
- (c)
- Up to a constant factor,where Φ has the formwhere is polynomial of degree 2, is polynomial of degree less than 2, and they have no common factor.
- (d)
- Up to a constant factor,where has the formwhereor
Conversely, each form of (a)–(d) defines a complete regular minimal surface in with total curvature .
2. Preliminaries
Let S be an orientable surface in defined by a conformal map
where M is a Riemann surface. S is a minimal surface if and only if the mean curvature vector field vanishes everywhere. The generalized Gauss map of M is defined as
where is the Grassmannian manifold consisting of all two-dimensional oriented planes in . Let be an oriented pair of orthonormal vectors spanning ; then, the complex vector assigns a point of . A different choice of basis yields a point of the form , and if we pass to the complex projective space , the tangent plane corresponds to a unique point of . The orthogonality of the pair implies that the set of points obtained satisfies the equation
which defines the quadric . We may identify the quadric with the Grassmannian manifold . If , may be holomorpfic to [11].
If are locally isothermal parameters in a neighborhood of a point , then the pair of vectors
are orthogonal and equal in length. Then, we may represent the generalized Gauss map by
where
and
g is holomorphic if and only if is anti-holomorphic. From the lemma of Osserman [5], if M is a minimal surface in , then g is an anti-analytic function.
Denote , and the Euler characteristic of M; then, there are some properties of the corresponding minimal surface S.
Proposition 1
([2]). If the total curvature of S is finite, then
- (a).
- M is conformally to a compact Riemann surface with a finite number, say r, points deleted;
- (b).
- C is an even integer, and satisfieswhere g is the genus of M (=genus of );
- (c).
- The Gauss map of S extends to a map of whose image is an algebraic curve in lying in ; the total curvature of S is equal in absolute value to the area of , counting multiplicities;
- (d).
- intersects a fixed finite number m times (counting multiplicity) every hyperplane in except for those hyperplanes containing one or more of the (finite number of) points of .
There are representations for complete regular minimal surfaces in with finite total curvature:
Proposition 2
([11]). Let be defined by
where , and have the following properties:
- (i)
- Each is a polynomial;
- (ii)
- The maximal degree of the is m;
- (iii)
- The have no common factor;
- (iv)
- .
Then, defines a complete regular simply connected minimal surface S in with total curvature .
Conversely, every complete regular simply connected minimal surfaces in with total curvature is of the form given above.
Proposition 3
([11]). Let M denote the plane minus points, . Let be defined by
where the integral is taken from a fixed point to a variable point along any path in M. Assume that the complex vector is of the form
where is a meromorphic function of the form
and the satisfy
- (i)
- Each is a polynomial;
- (ii)
- The maximum degree of the is m;
- (iii)
- The have no common factor;
- (iv)
- .
Furthermore, the value satisfies
Finally, given any closed curve ,
Then, (13) defines a complete regular minimal surface in of genus 0, connectivity k and total curvature .
Remark 1.
Actually, the second condition of (16) in [11] can be stated as:
Here, could be excluded for the following reason. If it holds, similar to the proof of the simply connected case, we set
for some constant . Choose as the boundary of a sufficiently large disc so that for all j; then, the condition (17) implies
For , by the similar calculation, we have
Thus, holds, which leads to a contradiction.
We say a minimal surface S lies fully in if the image does not lie in any proper affine subspace of . If S is a complete regular minimal surface in with total curvature , then S has the following properties:
Proposition 4
([11]). Let S be a complete oriented minimal surface of total curvature lying fully in with genus g and number of boundary components r. Then, there are three possibilities:
- 1.
- S is simply-connected with ;
- 2.
- S is doubly-connected with
- 3.
- and S is a holomorphic curve in
3. Proof of the Main Theorems
As noted in Proposition 4, if S is a complete regular minimal surface in with finite total curvature , there are three possibilities. From Chen [12], the case can be ruled out. Then, we only consider the simply connected case and the doubly connected case of genus zreo. Thus, S must be conformally equivalent to the extended complex plane punctured finite number of points by Huber’s Theorem [1]. Combining the Propositions 2 and 4, S is given by
where , and are polynomials with maximal degree 3. Thus, we write
Note that the point is the image under the Gauss map of the point , i.e., it corresponds to the limit of the tangent plane to S as . By a rotation in , we may assume that the vector A is a non-zero multiple of the vector . The condition
means
If we choose
then yields . have the forms:
for some coefficients . Now, we introduce a new variable ; then, also has the form (18), but with
Next, we may consider the real and imaginary parts of as defining a pair of vectors in . Choosing an orthonormal pair of vectors in orthogonal to both those vectors, we may make an orthogonal transformation of , leaving the first two coordinates unchanged, but with
For the vector , we repeat the process and obtain .
Thus, by the trick of resetting the coordinates above, we obtain the representation of satisfying
where , for polynomial , is the degree of the polynomial, and the coefficients of the square terms for vanish.
Set
Then
We can assume that , otherwise changing the -th coordinate to the opposite. Then, together with condition (19), write and as follows:
where ; then, we have
Since the functions above are all polynomials, and the degree is at most 6, we assume
Consider , and directly, we get . Then, the following are left:
Given , ref. (22) can be considered as a system of linear equations about , L, R, T, K, M, N, , which must have solutions, since it is homogeneous. By solving these equations, we get the identities (5) and (6).
If any denominator in (5) and (6) is zero, it is easy to see the fact that the corresponding numerator vanishes. If any denominator vanishes in (5), the principle of resetting coordinates implies the fact that the left-hand side of the corresponding equality vanishes.
Notice that a common factor of is also common factor of . If such a common factor exists, must vanish; thus, so does P, which leads to (iii). Actually, if , then the constraint (iii) holds automatically.
So far, we give a complete proof of Theorem 1.
Now, we are going to consider the doubly connected case. From Proposition 3, it means , and has the form
Then, the condition (17) is non-trivial. We only need to consider the residue of at .
Case 1: .
From some direct calculation, the residue of at is
Thus, (17) is equal to:
Then
Case 2: . Consider
we can repeat the process similar to the case of and then lead to some conditions to meet. However, there is another viewpoint to show these two cases are actually the same.
Let M be the complex plane minus a point , which means indeed that M is a Riemann surface minus two points , and , and define a Möbius transformation
with , and . Let ; then, we have
where the components of are polynomials of degree at most 3. Thus, it is the same as Case 1 if there exists some component of of degree exactly 3. If not, we write
then
with coefficient of degree 3. If all the coefficients of degree 3 vanish, becomes a common root of all , which is a contradiction! Thus, we get the Theorem 2.
It seems that the description of the doubly connected case just adds one condition (9) compared to the simply connected case. However, we will see later that the condition (9) may play an important role in the doubly connected surfaces.
Remark 2.
From Proposition 4, we know that such surfaces in Theorem 2 are in some affine seven-dimensional space. In fact, restriction (9) implies this result. Since means
Here, notice that the coefficients of degree 2 are both real, so by the trick of resetting coordinates, we can set . Continue the process on , and then, we can get .
4. A Method to Give Some Families of Examples
In (22), there are two series of coefficients and . Notice that if the second ones all vanish, the surface corresponding to is a complex analytic curve. So, we can regard the second series of coefficients as the deformation upon some complex analytic curve. From this viewpoint and Theorem 1, there is a method to construct a series of complete non-holomorphic simply connected minimal surfaces with total curvature as follows:
- Step 1. Fix a series of data with . To simplify the next step, we could just choose and others arbitrarily.
In this method, there is a gap that the constraint (iii) holds naturally if choosing . This is for the reasons that has no factor; therefore, the terms in constraint (iii) have no common factor.
Example 1.
We can give a detailed example by using the method given above. Choose , other vanishing, and ; then, the Gauss map is
thus, is defined by
We can check easily that S lies fully in .
Similar to the simply connected case, Theorem 2 also gives a method to construct a series of complete non-holomorphic doubly connected minimal surfaces with total curvature as follows:
- Step 1. Fix a series of data with , , others arbitrarily.
Here, in Step 3, we say the surface is non-holomorphic since there is only exactly one component of of degree 2 from Remark 2, which cannot happen if S is holomorphic.
Comparing with the method to construct simply connected minimal surfaces, where we choose to simplify the process, here, works. In other words, if the condition in Step 1 is removed, the construction might be invalid. For example, we give as follows:
Then, combining (9), Equation (22) can be rewritten as:
which is overdetermined by some simple calculation. It means that the method given before cannot continue if such bad are given.
Example 2.
We also give a detailed example. Let , other vanish and ; then, the Gauss map is
thus, is defined by
where . In addition, it lies fully in .
Remark 3.
In our methods, to construct specific minimal surfaces, after giving a vector in
where , any decides such a simply connected minimal surface. In other words, any vector in decides such a simply connected minimal surface. In the other case, replacing by , any vector in decides such a doubly connected minimal surface.
There is a natural problem to check out which ones indeed result in the same surfaces up to an isometry. If solved, the expressions of such surfaces might be further simplified.
5. Complete Minimal Surfaces with Total Curvature in
Now, we consider the minimal surfaces with total curvature in lower dimensional Euclidean space. As seen in Section 1, complete minimal surfaces in have total curvature for some non-negative integer m. Thus, the surfaces discussed must lie in at least -dimensional Euclidean space. If it is exactly 4, the minimal surfaces need to be much more restricted. Therefore, we simplify the result of the classification in .
Naturally, we could set some coefficients given before vanishing to force the surface to lie in . However, in , there is another viewpoint on the Gauss maps of minimal surfaces given by Hoffman-Osserman [11]: may be biholomorphic to . The inverse is defined as
where regarding as and
5.1. Further Structure of
We know that an -action on gives a reselection of coordinates of the related minimal surfaces; thus, the orbit of the actions determines a unique surface. The following proposition describes the induced action on .
Proposition 5.
There is a corresponding pair of actions on and on so that the following diagram is commutated: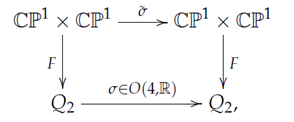 where has the form
with
where has the form
with
 where has the form
where has the formProof.
The inverse of F is given by
Then, it is easy to see that if
the induced action gives an exchange of and . Therefore, we only need to consider the -actions.
To consider the tangent map of , we choose a series of fine vectors in Lie algebra of as follows:
where is the matrix whose element of the i-th row and j-th column is 1 and elements in other positions are 0. Then, are linearly independent and . By calculating, the corresponding one-parameter transformations on are given respectively as:
Thus, it is obversed that any action for can be decomposed onto the two projections independently. Onto each one, the actions have forms
Thus, any action on induces an action on by F with (31).
Conversely, according to the well-known structure of ,
() generate . Thus, any acting on as (31) is related to an action on induced by F. □
5.2. Proof of Theorem 3
Since the induced metric on is
which is just the product metric of the standard metric defined on a sphere of radius . Each projection to defines holomorphic functions from to , so it will be a finite-sheeted covering of . Denote , then
The surfaces with total curvature have only two cases ([11], Sec. 2):
(i) One of the projections is constant, and the other is a three-sheeted covering. That is, is a three-sheeted covering of ;
(ii) One of the projections is single sheeted and the other is double sheeted. Thus, has genus 0 and is given by as before with one of expressed as a rational function of degree 2 in the other variable.
Then, write . For surfaces considered, we have (simply connected) or 2 (doubly connected) and .
Case 1. k = 1. Without loss of generality, assume and denote . We can choose an action to transform into . Up to a reselection of coordinates, the following assumption makes sense:
Case 1.1. is a three-sheeted covering of . Then, without loss of generality, we assume where is a constant and is a meromorphic function of degree 3. Write where and are polynomials with no common factor and . The assumption (32) implies and . Hence, the Gauss image can be represented as:
where is a polynomial with zero at some point if and only if is a pole of with the same order. Hence, with . Thus,
Then, up to conjugate, the determined surface M is complex analytic and expressed by polynomials of maximal degree 4, where the condition that P and Q have no common factor is equal to the regularization. It is form (a) in Theorem 3.
Case 1.2. is given by and, without loss of generality, with meromorphic G of degree 2. Then, the Gauss image can be represented as: , where is a holomorphic bijection on with . So, we can just say up to a constant factor. Then, . Write with and are polynomials with no common factor and . The assumption (32) implies , that is . Then
Similarly, we can assume with ; thus
which is form (c) in Theorem 3.
Case 2. k = 2. In addition, without loss of generality, assume Similar with Case 1, assume further
When choosing action in , we can let . In addition, cannot be both ∞, so we further assume .
Case 2.1. is a three-sheeted covering of . Then, where is a meromorphic function of degree 3, where C is a constant in , which forces . Write like Case 1.1. Thus, we have and . Then, the Gauss image can be represented as:
where is an analytic function in with zero at some point if and only if is a pole of with the same order. Combining the discussion in the proof of Theorem 2, is the pole of with order three. Hence, we can assume with . Thus,
and assume detailedly
where and are complex constants with . The residue condition
implies
Then, , and combining the condition that and have no common factor, we obtain
Then, up to conjugate and a constant factor, the determined surface M is expressed by
where additional condition (36) guarantees the order at 0 and regularization. It is form (b) in Theorem 3.
Case 2.2. is given by and (or similarly) with meromorphic G of degree 2. Then, . Write like Case 1.2. Thus, we have and . Then, assume detailedly
then, the Gauss image can be represented as:
Similarly, we can assume , thus
In addition, considering the residue condition (17) leads to . Then, .
Case 2.2.1.. implies . No common factor of and gives .
Case 2.2.2.. hold similarly.
Combining Case 2.2.1 and Case 2.2.2 results in form (d) in Theorem 3.
So far, we complete the proof of Theorem 3.
Remark 4.
In accord with Theorems 1 and 2, the surfaces of forms (a) and (c) in Theorem 3 are related to simply connected cases, while (b) and (d) are doubly connected.
Author Contributions
Conceptualization, M.L. and S.Z.; Methodology, M.L.; Visualization, L.O. and S.Z.; Writing—original draft, L.O.; Writing—review & editing, M.L. and L.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (11622103).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to express our gratitude to our supervisor, Ling Yang, for his instructive advice and useful suggestions on this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huber, A. On subharmonic functions and differential geometry in the large. Comm. Math. Helv. 1957, 32, 13–72. [Google Scholar] [CrossRef]
- Chern, S.S.; Osserman, R. Complete minimal surfaces in euclidean n-space. J. Analyse Math. 1967, 19, 15–34. [Google Scholar] [CrossRef]
- Struik, D.J. Lectures on Classical Differential Geometry; Addison-Wesley Press, Inc.: Cambridge, MA, USA, 1950; p. 156. [Google Scholar]
- Jorge, L.P.; Meeks, W.H., III. The topology of complete minimal surfaces of finite total Gaussian curvature. Topology 1983, 2, 203–221. [Google Scholar] [CrossRef] [Green Version]
- Osserman, R. A Survey of Minimal Surfaces; Van Nostrand: New York, NY, USA, 1969; Reprinted by Dover Publications: Dover, NY, USA, 1986. [Google Scholar]
- Meeks, W.H., III. The classification of complete minimal surfaces in ℝ3 with total curvature greater than −8π. Duke Math. J. 1981, 48, 523–535. [Google Scholar]
- López, F.J. The classification of complete minimal surfaces with total curvature greater than −12π. Trans. Am. Math. Soc. 1992, 334, 49–74. [Google Scholar]
- Chen, C.C.; Gackstatter, F. Elliptic and hyperelliptic functions and complete minimal surfaces with handles. IME-USP 1981, 27. [Google Scholar]
- Costa, C.J. Complete minimal surfaces embedded in ℝ3 with total curvature 12π. VIIth Sch. Differ. Geom. (Port.) (Camp. 1990). Mat. Contemp. 1991, 1, 25–33. [Google Scholar] [CrossRef]
- Chen, C.C. Complete minimal surfaces with total curvature −2π. Bol. Soc. Brasil. Mat. 1979, 10, 71–76. [Google Scholar] [CrossRef]
- Hoffman, D.A.; Osserman, R. The Geometry of the Generalized Gauss Map; American Mathematical Society: Providence, RI, USA, 1980; Volume 28. [Google Scholar]
- Chen, C.C. Total curvature and topological structure of complete minimal surfaces. Chin. J. Math. 1981, 9, 23–38. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).