Abstract
In this article, we propose a simplified radial basis function (RBF) method with exterior fictitious sources for solving elliptic boundary value problems (BVPs). Three simplified RBFs, including Gaussian, multiquadric (MQ), and inverse multiquadric (IMQ) without the shape parameter, are adopted in this study. With the consideration of many exterior fictitious sources outside the domain, the radial distance of the RBF is always greater than zero, such that we can remove the shape parameter from RBFs. Additionally, simplified Gaussian, MQ, and IMQ RBFs and their derivatives in the governing equation are always smooth and nonsingular. Comparative analysis is conducted for three different collocation types, including conventional uniform centers, randomly fictitious centers, and exterior fictitious sources. Numerical examples of elliptic BVPs in two and three dimensions are carried out. The results demonstrate that the proposed simplified RBFs with exterior fictitious sources can significantly improve the accuracy, especially for the Laplace equation. Furthermore, the proposed simplified RBFs exhibit the simplicity of solving elliptic BVPs without finding the optimum shape parameter.
MSC:
65D12
1. Introduction
Meshfree methods have been applied to solve problems with complicated and irregular geometry because of the advantages of their meshfree characteristics [1,2,3,4]. With the capability to deal with different kinds of partial differential equations (PDEs), the radial basis function collocation method (RBFCM) is one of the prominent methods for solving PDEs, where the variables are expressed by the function approximation [5,6,7,8]. Proposed by Hardy in 1971 [9], the multiquadric (MQ) radial basis function (RBF) was used for scattered data interpolation. The first attempt to extend the MQ RBF to the solution of PDEs was presented by Kansa in the early 1990s [10]. In addition to the MQ RBF, several RBFs have been presented, such as the inverse multiquadric (IMQ), Gaussian, and polyharmonic spline (PS) functions [11,12,13,14]. Among them, PS and MQ RBFs have received more attention for interpolation due to their high accuracy [15,16,17]. These RBFs are usually categorized into piecewise and infinite smooth functions. For example, the PS is piecewise smooth. On the other hand, the MQ is infinite smooth. In order to remain smooth, the shape parameter is introduced in the MQ [18]. Many RBF methods often contain the shape parameter, which has been proven to have a significant influence on the accuracy of RBF interpolation [19,20,21].
In the Kansa method, the centers are uniformly scattered within the domain, where the positions of the interior and center points are exactly the same [22]. The centers are often regarded as fictitious sources, which are randomly scattered within the domain [23]. On the other hand, the fictitious sources can also be simultaneously scattered within and outside the closure of the domain [24]. Recently, Ku et al. proposed the MQ RBF without the shape parameter using fictitious sources collocated outside the domain [25]. Because the fictitious sources are situated on the exterior domain, the radial distance always has a non-zero value, such that the RBFs and their derivatives are always smooth and globally infinitely differentiable [26]. The fictitious sources used for the collocation method have received significant attention due to their superior properties and wide utilization for solving PDEs. Accordingly, the accuracy of different RBFs when using fictitious sources in the collocation method to solve PDEs is of significant interest and needs to be investigated.
Identification of the shape parameter is often very challenging and tedious in the original RBFs when solving partial differential equations. In this study, we attempt to remove the shape parameter in conventional RBFs to solve partial differential equations. We propose three simplified Gaussian, MQ, and IMQ RBFs without using the shape parameter. The simplified RBFs have the advantages of a simple mathematical expression, high precision, and easy implementation. Furthermore, we demonstrate that the simplified RBFs, with the consideration of many exterior fictitious sources outside the domain, can achieve highly accurate results to solve elliptic boundary value problems.
In this article, the accuracy of three RBFs in the collocation method for solving stationary convention diffusion equations is investigated. Three RBFs, including the Gaussian, MQ, and IMQ, are adopted. Additionally, three different collocation types are considered in the collocation method. Accuracy analysis of the collocation types of each RBF is carried out. Numerical solutions are approximated by utilizing the RBFs to solve the elliptic boundary value equations. Comparisons of the accuracy of three RBFs are made. The remainder of this article is organized as follows: in Section 2, the mathematical formulations, including the governing equation, the RBFs, the discretization of the governing equation, and the location of fictitious sources, are introduced. Section 3 describes the convergence analysis conducted to evaluate the robustness and effectiveness of the three RBFs in the collocation method. Three different collocation types are considered in the collocation method. Accuracy analysis of the three collocation types of each RBF is also carried out. In Section 4, several investigations of the elliptic boundary value problems are conducted to examine the robustness of the RBFs. Finally, the conclusions of this study are presented in Section 5.
2. Methodology
2.1. Elliptic Boundary Value Problems
The equation of the elliptic boundary value problem is expressed as follows:
where defines the gradient operator; denotes the variable of interest, which is usually the concentration; x is the Cartesian coordinate, defined as ; A is the velocity, defined as ; is the given function; is the given function value; defines the given boundary conditions; and is the domain with the boundary .
2.2. Simplified Radial Basis Functions
Three simplified Gaussian, MQ, and IMQ RBFs without the shape parameter are proposed for solving elliptic boundary value problems, as listed in Table 1. The simplified RBF simply removes the shape parameter from its original one. For example, the simplified Gaussian RBF can be expressed as:
where denotes the simplified Gaussian RBF; r denotes the radial distance, ; x denotes the interior point; denotes the source point, defined as ; and R denotes the characteristic length, which is the maximum radial distance. We can easily obtain the simplified MQ RBF as follows:
where denotes the simplified MQ RBF. Similarly, the simplified IMQ RBF is expressed as:
where denotes the simplified IMQ RBF. In this study, three simplified MQ, IMQ, and Gaussian RBFs are developed without assigning any shape parameter. Table 1 lists a comparison of the original RBFs and the simplified RBFs. From Table 1, the original Gaussian, MQ, and IMQ RBFs in the RBFCM are defined by the shape parameter. The accuracy of these RBFs is strongly affected by the shape parameter. Accordingly, optimization techniques are required to determine the optimal shape parameter for these RBFs [19,20,21]. As for the proposed simplified RBFs, it is clear that the shape parameter has been completely eliminated in the RBFs.

Table 1.
RBFs adopted in this study.
2.3. Discretization
Utilizing the RBFCM, the unknown can be approximated as:
where M denotes the total number of source points; denotes the coefficient to be solved; denotes the RBF; denotes the radial distance at the jth source point, defined as ; and denotes the jth source point, defined as .
2.3.1. Discretization in Two Dimensions
The two-dimensional elliptic boundary value equation is expressed as:
Utilizing the simplified Gaussian RBF, the derivative of Equation (7) with respect to x is as follows:
Taking the derivative of Equation (7) with respect to y also gives:
Again, the derivative of Equation (8) with respect to x is as follows:
Similarly, we take the derivative of Equation (9) with respect to y:
Substituting the aforementioned Equations (8)–(11) into Equation (7), the approximation of the two-dimensional governing equation is as follows:
Equation (12) describes the discretization of the governing equation in two dimensions using the simplified Gaussian RBF. In the same way, we substitute the simplified MQ RBF into Equation (7):
Substituting the simplified IMQ RBF into Equation (7) also obtains:
Equations (13) and (14) describe the discretization of the governing equation in two dimensions using the simplified MQ and IMQ RBFs, respectively.
2.3.2. Discretization in Three Dimensions
The three-dimensional elliptic boundary value equation is:
Considering the three-dimensional problem depicted in Equation (15), the derivative of the simplified Gaussian RBF interpolation is as follows:
Using the same perspective, we obtain the derivative of Equation (15) by the simplified MQ RBF as:
Identifying the derivative of Equation (15) with the simplified IMQ interpolation results in the following equation:
From the above equations, the shape parameter has been eliminated from the original Gaussian, MQ, and IMQ RBFs. Considering the boundary conditions, the following system of linear equations is finally acquired:
where is an matrix for the interior points; is an matrix for the boundary points; is an vector of undetermined coefficients containing the unknown coefficients; f is an vector of the function values for the interior points, written as ; g is an vector of boundary data, written as ; is the number of interior points; and is the number of boundary points. Once the unknown coefficients are determined, we can collocate the validation points uniformly placed inside the domain to obtain the computed results.
To investigate the effectiveness and accuracy of the simplified RBFs in the collocation method, this study adopts the root mean square error (RMSE) as follows:
where denotes the number of validation points, denotes the ith validation point, and and are the analytical and numerical solutions evaluated at the ith validation point, respectively.
2.4. Location of Fictitious Sources
In the conventional RBF method, the interior, center, and boundary points must be placed where the positions of the interior and center points usually coincide at the same place. In this study, the center points in the conventional RBFs are regarded as the fictitious sources, where three different collocation types for locating the fictitious sources are considered in the collocation method as depicted in Figure 1. The implementation of the three different collocation types for solving the elliptic boundary value problems are described as follows.
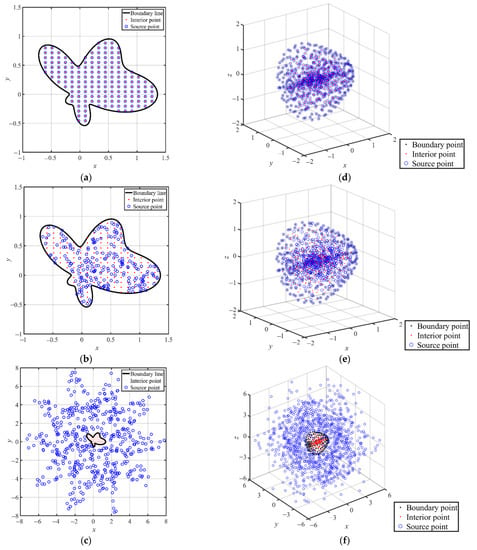
Figure 1.
Location of the fictitious sources for the two-dimensional and three-dimensional domain. (a) A two-dimensional domain: Type A. (b) A two-dimensional domain: Type B. (c) A two-dimensional domain: Type C. (d) A three-dimensional domain: Type A. (e) A three-dimensional domain: Type B. (f) A three-dimensional domain: Type C.
2.4.1. Type A: Uniform Centers
In type A, the source points are uniformly scattered within the domain. Figure 1a,d illustrate the location of the fictitious sources for the two-dimensional and three-dimensional domains, respectively. In Figure 1a, the two-dimensional amoeba-like object is adopted. The boundary shape is defined as follows:
The fictitious sources are uniformly scattered within the two-dimensional amoeba-like domain, as depicted in Figure 1a. The interior, sources, and boundary points are placed such that the positions of the interior and fictitious sources are identical.
Considering the three-dimensional object, the boundary shape is given by the spherical parametric equation as follows:
2.4.2. Type B: Randomly Fictitious Centers
In type B, the boundary shapes in two and three dimensions are exactly the same as those in type A. However, the source points are regarded as the fictitious centers, which are randomly scattered within the domain [24], as depicted in Figure 1b,e.
2.4.3. Type C: Exterior Fictitious Sources
In type C, the fictitious sources are randomly collocated in the exterior domain, as shown in Figure 1c,f. In Figure 1c, the two-dimensional amoeba-like object is adopted. The fictitious sources are randomly scattered within the range between the domain boundary and the fictitious boundary, as depicted in Figure 1c. The boundary shape of the problem domain is defined as Equation (21). The fictitious boundary is defined by the following parametric equation:
where denotes the fictitious boundary; denotes the x-coordinate of the jth source point; denotes the y-coordinate of the jth source point; denotes the dilation factor, which is used to adjust the size of the fictitious boundary; denotes the angle of the fictitious sources; and denotes the radius of the fictitious sources, defined as .
Considering a three-dimensional object, the boundary shape is given by the spherical parametric equation as shown in Equation (22). The fictitious sources are randomly scattered within the three-dimensional space between the domain boundary and the fictitious boundary, as depicted in Figure 1f. The boundary shape of the problem domain is defined as Equation (22). The three-dimensional fictitious boundary is defined by the following parametric equations:
where denotes the z-coordinate of the jth source point; represents the radius of the fictitious sources, defined as ; is the polar angle used to describe the location of the fictitious sources in cylindrical coordinates; and is the azimuth angle of the fictitious sources.
The fictitious sources are randomly collocated in the exterior domain, as shown in Figure 1c,f. Since the radial distance for RBFs remains greater than zero, the shape parameter for the original Gaussian, MQ, and IMQ RBFs can be completely eliminated. The three simplified Gaussian, MQ, and IMQ RBFs with exterior fictitious sources (type C) are utilized to solve elliptic boundary value problems.
3. Validation of the Methodology
3.1. Example 1
To investigate the accuracy, a comparison of the three collocation types is performed. The Laplace equation in two dimensions is described as Equation (1), where , , and . The domain boundary is defined as Equation (21). Boundary data for the boundary conditions are assigned to the boundaries by adopting the following exact solution:
Three simplified RBFs, including Gaussian, MQ, and IMQ, are adopted to solve this problem. Three collocation types for locating the sources are considered. In type A, the fictitious sources are uniformly scattered within the domain, as depicted in Figure 1a. The interior, sources, and boundary points are placed such that the positions of the interior and fictitious sources are identical. In type B, the fictitious sources are randomly scattered within the domain, as depicted in Figure 1b. In type C, the fictitious sources are simultaneously scattered outside the closure of the domain, as depicted in Figure 1c. The location of the exterior fictitious sources is defined as Equation (23). A total of 164 interior points, 315 source points, and 200 boundary points are used. The dilation factor is 3.
For comparison purposes, the original Gaussian, MQ, and IMQ RBFs with various shape parameters for type A and type B are also considered in the analysis. Particularly, for type C, the above RBFs without a shape parameter are utilized. The RMSE is used to examine the accuracy of the computed results. Comparisons of the accuracy for the three RBFs are then conducted.
3.1.1. The Gaussian RBF
The Gaussian RBF with three different collocation types with various shape parameters is first investigated, as shown in Figure 2a. From Figure 2a, it appears that the simplified Gaussian RBF without the shape parameter utilizing the exterior fictitious sources of type C provides the most accurate solution. The results obtained demonstrate that the RMSE of the simplified Gaussian RBF without a shape parameter for type C is in the order of 10−12. It seems that the simplified Gaussian RBFs utilizing the exterior fictitious sources of type C have the best accuracy among those Gaussian RBFs for type A and type B even when different values of the shape parameter are considered.
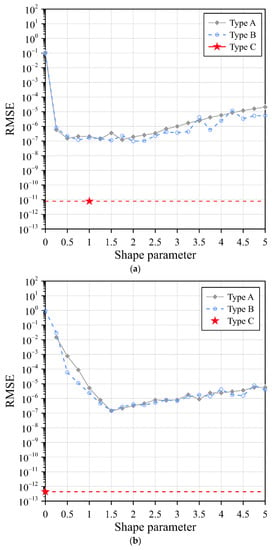
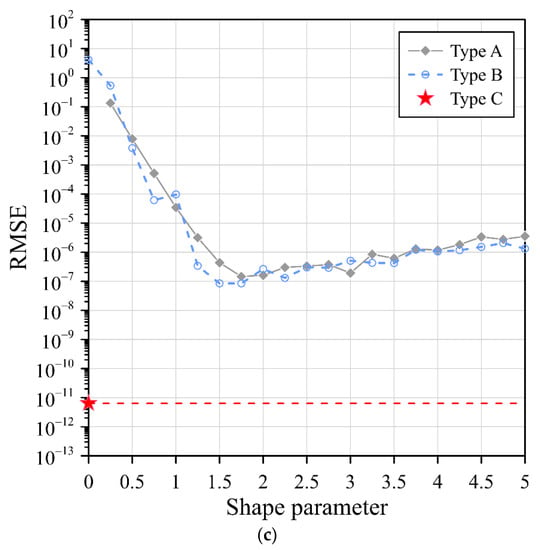
Figure 2.
The RMSE of the three RBFs with three different collocation types: (a) Gaussian RBF, (b) MQ RBF, and (c) IMQ RBF.
3.1.2. The MQ RBF
The MQ RBF with various shape parameters for type A and type B is considered. For type C, the simplified MQ RBF is utilized. Figure 2b illustrates the accuracy of the MQ RBFs for the three collocation types. According to Figure 2b, the RMSE of the MQ RBF in type A and type B are in the order of 10−2 to 10−7 as the shape parameter ranges from 0.2 to 5. However, the RMSE of the simplified MQ RBF in type C is 10–13. It was found that the RMSE of the simplified MQ RBF without a shape parameter in type C has the best accuracy among the MQ RBFs for type A and type B for different values of the shape parameter.
3.1.3. The IMQ RBF
The IMQ RBF is analyzed by adopting the same perspective. Figure 2c illustrates the accuracy of the IMQ RBF for the three collocation types. Similar to the results obtained in Figure 2b, we also found that the simplified IMQ RBF for type C acquires more accurate results than the other IMQ RBFs for type A and type B with the best shape parameter, as illustrated in Figure 2c. It is obvious that the simplified IMQ RBFs without a shape parameter that utilize the exterior fictitious sources of type C provide the most accurate solution.
Table 2 lists the results of the RMSE using the three RBFs with the three different collocation types. The processor used was an AMD Ryzen 7 5800X 8-Core @ 3.80 GHz. As depicted in Table 2, all the simplified Gaussian, MQ, and IMQ RBFs utilizing the exterior fictitious sources of type C provided more accurate results than the other two fictitious source collocation types, even when the best shape parameter was adopted. The simplified Gaussian, MQ, and IMQ RBFs utilizing the exterior fictitious sources of type C provided the most accurate results, with an RMSE of the order of 10−12, 10−13, and 10−12, respectively. From the results, we also demonstrated that the above simplified RBFs with exterior fictitious sources can be used to solve this two-dimensional Laplace problem with very high accuracy. From Table 2, the comparison of the computing time also illustrates the efficiency of the proposed method.

Table 2.
Comparison of the results for example 1.
To further clarify the possible influences of the positions of the exterior fictitious sources for type C on the accuracy, a sensitivity analysis was further conducted. Three RBFs considering the MQ, IMQ, and Gaussian RBFs were adopted to solve the two-dimensional Laplace problem. The MQ, IMQ, and Gaussian RBFs without the shape parameter were used.
In this example, the values of the dilation factor ranged from 0.5 to 5. A plot of the RMSE versus the dilation factor is depicted in Figure 3. From Figure 3, the RMSE of the MQ, IMQ, and Gaussian RBFs utilizing the exterior fictitious sources for type C fluctuates between 10–11 and 10–13 while the dilation factor ranges from 2.5 to 5. The results obtained show that the dilation factor has low sensitivity regarding the numerical accuracy while the dilation factor is greater than 2.5. Accordingly, the following numerical implementations of type C were solved using .
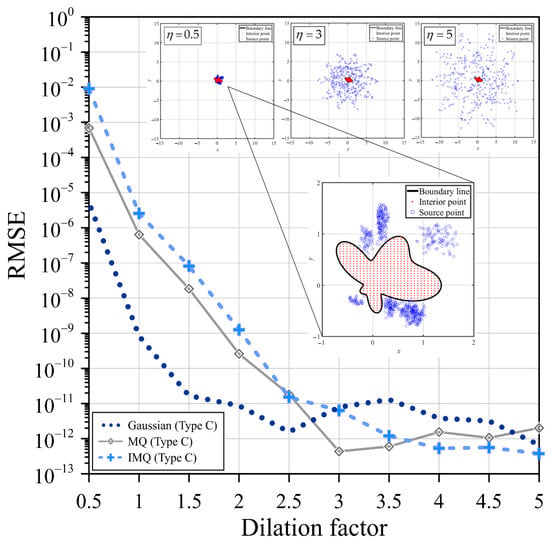
Figure 3.
RMSE versus the dilation factor.
3.2. Example 2
A three-dimensional problem is enclosed by a sophisticated irregular domain boundary, as shown in Figure 4a. The governing equation in three dimensions is expressed as Equation (1), where , , and are 0. The object boundary is given by the spherical parametric equation as follows:
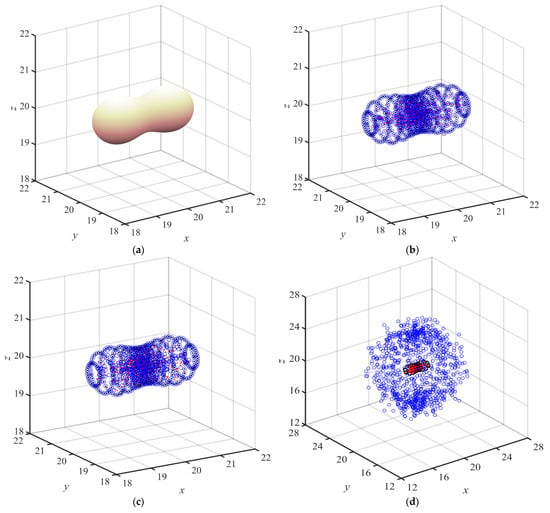
Figure 4.
Problem domain and location of the fictitious sources for example 2. (a) Problem domain. (b) Type A. (c) Type B. (d) Type C (blue and red circles denote the source and interior points, respectively).
The Dirichlet data are imposed using the following exact solution for this three-dimensional problem as:
The Gaussian, MQ, and IMQ RBFs were utilized in the analysis. Additionally, three collocation types were considered. As depicted in Figure 4b–d, there were 2461 source points, 1600 interior points, and 861 boundary points.
Figure 5 illustrates the RMSE of the Gaussian, MQ, and IMQ RBFs with three different collocation types. The RMSE of the simplified Gaussian, MQ, and IMQ RBFs (type C) was 10−14, 10−15, and 10−13, respectively. It is significant that excellent agreement was achieved, and highly accurate results were acquired using the simplified RBFs. From these results, it is demonstrated that the simplified RBFs with exterior fictitious sources can be used to solve the three-dimensional stationary Laplace equation with very high accuracy.
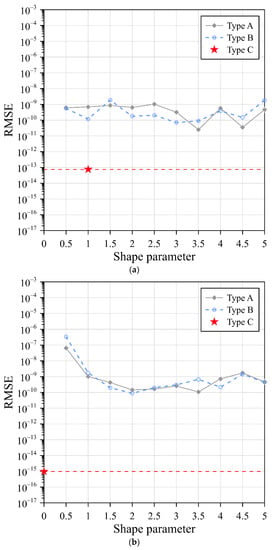
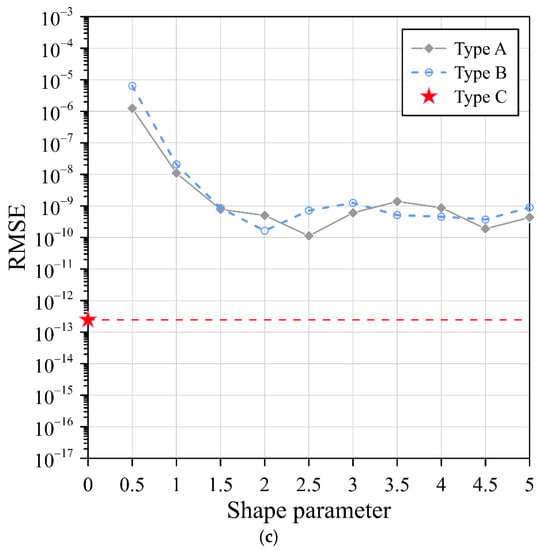
Figure 5.
RMSEs of three RBFs using three different collocation types: (a) Gaussian RBF, (b) MQ RBF, and (c) IMQ RBF.
4. Application Examples
4.1. Application Example 1
The governing equation for the first application example is depicted in Equation (1), where , , and . The boundary is defined as follows:
The Dirichlet data are assigned from the analytical solution:
Three RBFs, including the Gaussian, MQ, and IMQ, were used in the collocation method. Three collocation types for locating the sources as illustrated in Figure 6 were considered in the above RBFs to solve this problem. There were 342 source points, 151 interior points, and 200 boundary points. In type A, the fictitious sources are uniformly scattered within the domain, as depicted in Figure 6a. The interior, sources, and boundary points are placed such that the positions of the interior and fictitious sources are identical. In type B, the fictitious sources are randomly scattered within the domain, as depicted in Figure 6b. In type C, the fictitious sources are randomly scattered outside the closure of the domain, as depicted in Figure 6c. The collocation of the exterior fictitious sources is defined by the following parametric equations:
where . In this example, the dilation factor for type C is 3.
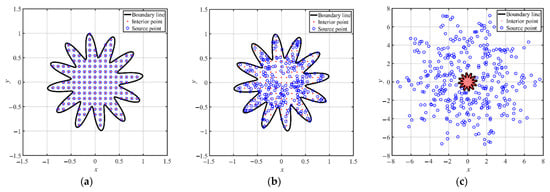
Figure 6.
Collocation points for application example 1. (a) Type A. (b) Type B. (c) Type C.
The Gaussian, MQ, and IMQ RBFs with various shape parameters for type A and type B were considered. For type C, the above RBFs without a shape parameter were utilized. The accuracy of the Gaussian, MQ, and IMQ RBFs for the three collocation types are illustrated in Figure 7. According to Figure 7a, the Gaussian RBF utilizing the exterior fictitious sources for type C obtained more accurate results, where the RMSE of the Gaussian RBF without a shape parameter in type C reached the order of 10–13. Figure 7b demonstrates the RMSE of the MQ RBF for the three collocation types. According to Figure 7b, the RMSE of the MQ RBF in type A and type B was in the order of 10−2 to 10−7 as the shape parameter ranged from 0 to 5. The RMSE of the MQ RBF without a shape parameter in type C was in the order of 10–10. The IMQ RBFs was analyzed by adopting the same perspective. The RMSE values of the IMQ for the three collocation types are illustrated in Figure 7c. Similar to the results obtained in Figure 7b, we also found the IMQ without the shape parameter for type C reached the order of 10–8. From the results, it is significant that the Gaussian RBF without the shape parameter for type C showed a high-accuracy performance.
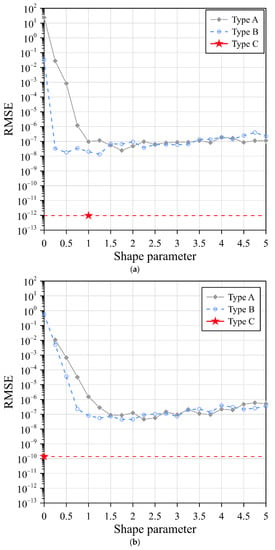
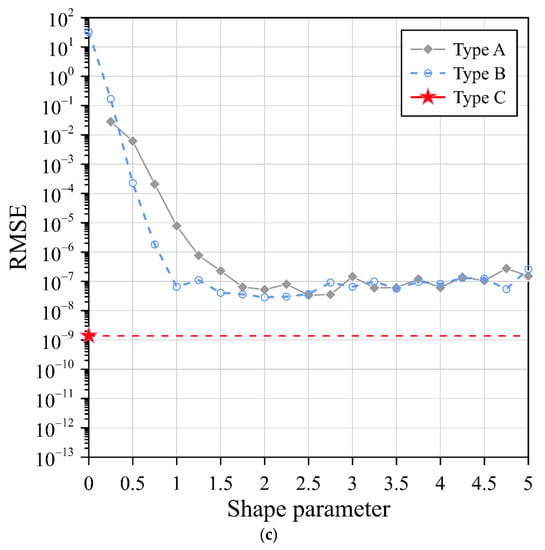
Figure 7.
RMSEs of three RBFs with three different collocation types: (a) Gaussian RBF, (b) MQ RBF, and (c) IMQ RBF.
Table 3 presents a comparison of the results for the application example 1. For type A and type B, the Gaussian, MQ, and IMQ RBFs with the optimal shape parameter were utilized. For type C, the above RBFs without a shape parameter were adopted. As depicted in Table 3, all the RBFs, including the Gaussian, MQ, and IMQ RBFs, utilizing the fictitious sources of type C provided more accurate results than the other two source collocation types even with the optimum shape parameter. From the results, it is clear that numerical solutions with a very high accuracy can be obtained by utilizing the proposed simplified Gaussian, MQ, and IMQ RBFs with exterior fictitious sources.

Table 3.
Comparison of the results for the application example 1.
4.2. Application Example 2
The governing equation for the second application example is expressed as Equation (1) [25], where , , , and . The object boundary is defined as:
The Dirichlet data are assigned to the boundaries utilizing the exact solution as follows:
Three RBFs, including the Gaussian, MQ, and IMQ, are were in the collocation method. Three collocation types for locating the sources, as illustrated in Figure 8, were considered in the above RBFs to solve this problem. There were 355 source points, 210 interior points, and 200 boundary points. In type A, the fictitious sources are uniformly scattered within the domain, as depicted in Figure 8a. The interior, sources, and boundary points are placed such that the positions of the interior and fictitious sources are identical. In type B, the fictitious sources are randomly scattered within the domain, as depicted in Figure 8b. In type C, the fictitious sources are randomly scattered outside the closure of the domain, as depicted in Figure 8c. The collocation of the exterior fictitious sources is defined by the following parametric equations:
where . In this example, the dilation factor for type C is 3.
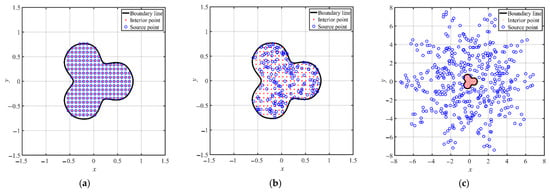
Figure 8.
Collocation points of the three types in the application example 2. (a) Type A. (b) Type B. (c) Type C.
Figure 9a demonstrates the RMSE of the Gaussian RBF for the three collocation types. From Figure 9a, the RMSE of the Gaussian RBF in type A and type B was in the order of 10−1 to 10−6 as the shape parameter ranged from 0.5 to 5. However, the RMSE of the Gaussian RBF without a shape parameter in type C reached the order of 10–11. The MQ and IMQ RBFs were analyzed by adopting the same perspective. The RMSE of the MQ and IMQ RBFs for the three collocation types are illustrated in Figure 9b,c, respectively. Similar to the results shown in Figure 9a, we also found that the MQ and IMQ RBFs without the shape parameter for type C reached the order of 10–9 and 10–8, respectively.
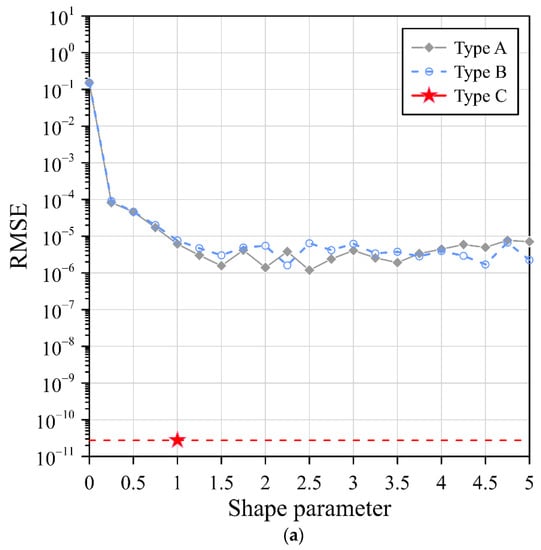
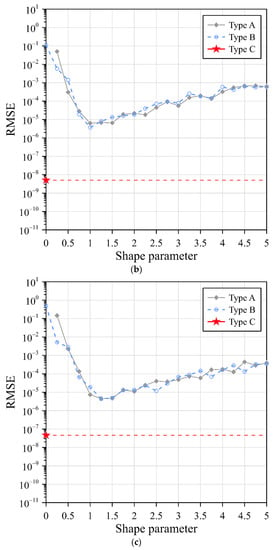
Figure 9.
RMSEs of RBFs with three different collocation types: (a) Gaussian RBF, (b) MQ RBF, and (c) IMQ RBF.
Table 4 presents a comparison of the results for the application example 2. For type A and type B, the Gaussian, MQ, and IMQ RBFs with the optimal shape parameter were utilized. For type C, the above RBFs without a shape parameter were adopted. As depicted in Table 4, all the RBFs, including the Gaussian, MQ, and IMQ RBFs utilizing the fictitious sources of type C, provided more accurate results than the other two source collocation types, even when the best shape parameter was adopted. The obtained results demonstrate that numerical solutions with a very high accuracy can be obtained by utilizing the proposed simplified Gaussian, MQ, and IMQ RBFs with exterior fictitious sources.

Table 4.
Comparison of the results for the application example 2.
4.3. Application Example 3
The three-dimensional problem is enclosed by a sophisticated irregular domain boundary, as shown in Figure 10a. The three-dimensional elliptic boundary value problems is expressed as Equation (1), where , , and . The object boundary is given by the spherical parametric equation as Equation (22). The Dirichlet data are imposed using the following exact solution for this three-dimensional problem as:
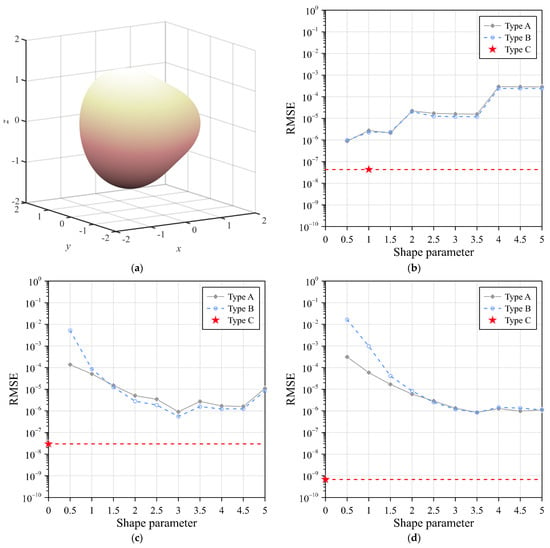
Figure 10.
Problem domain and RMSEs of RBFs using three different collocation types: (a) problem domain, (b) Gaussian RBF, (c) MQ RBF, and (d) IMQ RBF.
Three RBFs, including the Gaussian, MQ, and IMQ, were used in the collocation method. Three collocation types for locating the sources were considered in the above RBFs to solve this three-dimensional problem. There were 2500 source points, 1600 interior points, and 861 boundary points. The three collocation types of this three-dimensional problem are illustrated in Figure 1. In type A, the fictitious sources are uniformly scattered within the domain, as depicted in Figure 1d. The interior, sources, and boundary points are placed such that the positions of the interior and fictitious sources are identical. In type B, the fictitious sources are randomly scattered within the domain, as depicted in Figure 1e. In type C, the fictitious sources are randomly scattered outside the closure of the domain, as depicted in Figure 1f.
Figure 10 illustrates the RMSE of the Gaussian, MQ, and IMQ RBFs with the three different collocation types. From Figure 10, it appears that the RMSE of the above RBFs for type A and type B fluctuated between 10−2 to 10−6 as the shape parameter ranged from 0.5 to 5. However, the RMSE of the simplified Gaussian, MQ, and IMQ RBFs (type C) without a shape parameter reached the order of 10−8, 10−8, and 10−10, respectively.
5. Conclusions
In this study, a novel concept of using exterior fictitious sources to solve elliptic boundary value problems with the simplified radial basis function method was proposed. The concept of the proposed approach was addressed in detail. The significant findings are concluded as follows.
- (1)
- In this study, we demonstrated that the simplified RBFs, which consider many exterior fictitious sources outside the domain, can achieve accurate results to solve elliptic boundary value problems. The obtained results demonstrate that the simplified RBFs obtain a better accuracy than the original RBFs with the optimum shape parameter when solving elliptic boundary value problems.
- (2)
- Identification of the shape parameter is often very challenging and tedious in the original RBFs when solving partial differential equations. In this study, we proposed three simplified Gaussian, MQ, and IMQ RBFs without the shape parameter. The simplified RBFs have the advantages of a simple mathematical expression, high precision, and easy implementation.
- (3)
- With the consideration of many exterior fictitious sources outside the domain, we found that the radial distance is always greater than zero. The simplified Gaussian, MQ, and IMQ RBFs and their derivatives in the governing equation are always smooth and nonsingular.
- (4)
- Comparative analysis was conducted on the three different collocation types considering conventional uniform centers, randomly fictitious centers, and exterior fictitious sources. It was found that the exterior fictitious sources proposed in this study significantly improved the accuracy when solving problems.
- (5)
- Numerical examples, including elliptic BVPs in two and three dimensions, were carried out. The simplified radial basis function method with exterior fictitious sources can be applied to three-dimensional problems with ease and high accuracy.
- (6)
- In this study, we attempted to remove the shape parameter in conventional RBFs to solve partial differential equations. We achieved a promising result for three simplified Gaussian, MQ, and IMQ RBFs, especially for solving Laplace-type equations in two and three dimensions. Further studies to investigate the characteristics of the proposed method to solve different kinds of PDEs are suggested.
Author Contributions
Designing the study, C.-Y.K. and C.-Y.L.; formulation, C.-Y.L.; performing the analysis, C.-Y.L.; writing and editing, C.-Y.K. and C.-Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Research data are available on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sanyasiraju, Y.V.S.S.; Chandhini, G. A note on two upwind strategies for RBF-based grid-free schemes to solve steady convection–diffusion equations. Int. J. Numer. Methods Fluids 2009, 61, 1053–1062. [Google Scholar] [CrossRef]
- Stevens, D.; Power, H.; Lees, M.; Morvan, H. The use of PDE centres in the local RBF Hermitian method for 3D convective-diffusion problems. J. Comput. Phys. 2009, 228, 4606–4624. [Google Scholar] [CrossRef]
- Wang, F.; Wang, C.; Chen, Z. Local knot method for 2D and 3D convection–diffusion–reaction equations in arbitrary domains. Appl. Math. Lett. 2020, 105, 106308. [Google Scholar] [CrossRef]
- Gu, Y. Meshfree methods and their comparisons. Int. J. Comput. Methods 2005, 2, 477–515. [Google Scholar] [CrossRef]
- Grabski, J.K. On the sources placement in the method of fundamental solutions for time-dependent heat conduction problems. Comput. Math. Appl. 2021, 88, 33–51. [Google Scholar] [CrossRef]
- Ku, C.Y.; Liu, C.Y.; Xiao, J.E.; Hsu, S.M.; Yeih, W. A collocation method with space–time radial polynomials for inverse heat conduction problems. Eng. Anal. Bound. Elem. 2020, 122, 117–131. [Google Scholar] [CrossRef]
- Cheng, A.H.-D. Particular solutions of Laplacian, Helmholtz-type, and polyharmonic operators involving higher order radial basis functions. Eng. Anal. Bound. Elem. 2000, 24, 531–538. [Google Scholar] [CrossRef]
- Hu, H.Y.; Li, Z.C.; Cheng, A.H.-D. Radial basis collocation methods for elliptic boundary value problems. Comput. Math. Appl. 2005, 50, 289–320. [Google Scholar] [CrossRef] [Green Version]
- Hardy, R.L. Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 1971, 76, 1905–1915. [Google Scholar] [CrossRef]
- Kansa, E.J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid-dynamics. II Solutions to parabolic, hyperbolic and elliptic partial-differential equations. Comput. Math. Appl. 1990, 19, 147–161. [Google Scholar] [CrossRef] [Green Version]
- Beatson, R.K.; Light, W.A. Fast evaluation of radial basis functions: Methods for two-dimensional polyharmonic splines. IMA J. Numer. Anal. 1997, 17, 343–372. [Google Scholar] [CrossRef]
- Santos, L.G.C.; Manzanares-Filho, N.; Menon, G.J.; Abreu, E. Comparing RBF-FD approximations based on stabilized Gaussians and on polyharmonic splines with polynomials. Int. J. Numer. Methods Eng. 2018, 115, 462–500. [Google Scholar] [CrossRef]
- Soleymani, F.; Barfeie, M.; Haghani, F.K. Inverse multiquadric RBF for computing the weights of FD method: Application to American options. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 74–88. [Google Scholar] [CrossRef]
- Liu, G. An overview on meshfree methods: For computational solid mechanics. Int. J. Comput. Methods 2016, 13, 1630001. [Google Scholar] [CrossRef]
- Uddin, M. RBF-PS scheme for solving the equal width equation. Appl. Math. Comput. 2013, 222, 619–631. [Google Scholar] [CrossRef]
- Liu, C.S.; Chang, C.W. An energy regularization of the MQ-RBF method for solving the Cauchy problems of diffusion-convection-reaction equations. Commun. Nonlinear Sci. Numer. Simul. 2019, 67, 375–390. [Google Scholar] [CrossRef]
- Ku, C.Y.; Hong, L.D.; Liu, C.Y.; Xiao, J.E. Space–time polyharmonic radial polynomial basis functions for modeling saturated and unsaturated flows. Eng. Comput. 2021, 1–14. [Google Scholar] [CrossRef]
- Fornberg, B.; Wright, G. Stable computation of multiquadric interpolants for all values of the shape parameter. Comput. Math. Appl. 2004, 48, 853–867. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Hong, Y.; Lin, J. The sample solution approach for determination of the optimal shape parameter in the Multiquadric function of the Kansa method. Comput. Math. Appl. 2018, 75, 2942–2954. [Google Scholar] [CrossRef]
- Cavoretto, R.; De Rossi, A. Adaptive procedures for meshfree RBF unsymmetric and symmetric collocation methods. Appl. Math. Comput. 2020, 382, 125354. [Google Scholar] [CrossRef]
- Issa, K.; Humbali, K.M.; Biazar, J. An algorithm for choosing best shape parameter for numerical solution of partial differential equation via inverse multiquadric radial basis function. Open J. Math. Sci. 2020, 4, 147–157. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, F.Z.; Hou, E.R. The conical radial basis function for partial differential equations. J. Math. 2020, 2020, 6664071. [Google Scholar] [CrossRef]
- Katsiamis, A.; Karageorghis, A. Kansa radial basis function method with fictitious centres for solving nonlinear boundary value problems. Eng. Anal. Bound. Elem. 2020, 119, 293–301. [Google Scholar] [CrossRef]
- Liu, C.Y.; Ku, C.Y.; Hong, L.D.; Hsu, S.M. Infinitely smooth polyharmonic RBF collocation method for numerical solution of elliptic PDEs. Mathematics 2021, 9, 1535. [Google Scholar] [CrossRef]
- Ku, C.Y.; Liu, C.Y.; Xiao, J.E.; Hsu, S.M. Multiquadrics without the shape parameter for solving partial differential equations. Symmetry 2020, 12, 1813. [Google Scholar] [CrossRef]
- Yue, X.; Jiang, B.; Xue, X.; Yang, C. A Simple, Accurate and Semi-Analytical Meshless Method for Solving Laplace and Helmholtz Equations in Complex Two-Dimensional Geometries. Mathematics 2022, 10, 833. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).