Approximations of Fuzzy Numbers by Using r-s Piecewise Linear Fuzzy Numbers Based on Weighted Metric

Abstract

Using simple fuzzy numbers to approximate general fuzzy numbers is an important research aspect of fuzzy number theory and application. The existing results in this field are basically based on the unweighted metric to establish the best approximation method for solving general fuzzy numbers. In order to obtain more objective and reasonable best approximation, in this paper, we use the weighted distance as the evaluation standard to establish a method to solve the best approximation of general fuzzy numbers. Firstly, the conceptions of I-nearest r-s piecewise linear approximation (in short, PLA) and the II-nearest r-s piecewise linear approximation (in short, PLA) are introduced for a general fuzzy number. Then, most importantly, taking weighted metric as a criterion, we obtain a group of formulas to get the I-nearest r-s PLA and the II-nearest r-s PLA. Finally, we also present specific examples to show the effectiveness and usability of the methods proposed in this paper.

1. Introduction

Due to the complexity of the environment and the limitations of human inherent cognition, daily life is full of uncertain information. There are various approaches used to express and process this uncertain information, such as interval analysis [1,2], stochastic process [3] and fuzzy set theory [4]. In fuzzy set theory, a fuzzy number, which the notion was proposed by Zadeh in [5,6,7], has a good application in dealing with uncertain information. In recent years, a fuzzy number is very popular in the fields of cluster analysis, image recognition, system evaluation, automatic control, artificial intelligence and so on. Among them, multi-attribute decision making (MADM) with fuzzy information is the focus of scholars’ research [8,9].

In fact, when describing the characteristics of some fuzzy events, some fuzzy numbers are too complex. Therefore, the approximation of fuzzy numbers using regular fuzzy numbers to approximate complex fuzzy numbers has been deeply studied in fuzzy multi-attribute decision making. In the past few years, many scholars have obtained relevant important conclusions in this research field. For example, in [10], Ibrahim, Al-shami and Elbarbary defined the concept of (3,2)-fuzzy sets and establish the idea of relation in a (3,2)-fuzzy set and applied it to decision-making problems. In [11], with the aid of fuzzy soft β-neighborhoods, Atef, Ali and Al-shami introduced fuzzy soft covering-based multi-granulation fuzzy rough set models, which have a good application in solving multi-attribute group decision making (MAGDM) problems. In [12], Wang, Wan and Zhang further studied topological structures induced by L-fuzzifying approximation operators, where L denotes a completely distributive De Morgan algebra. In [13], Coroianu and Stefanini approximated fuzzy numbers by using the extended F-transform which always preserves the quasi-concavity property of a fuzzy number. In [14], by using the convolution method with useful properties for a general fuzzy number, Huang, Wu and Xie et al. constructed approximations comprising fuzzy number sequences. In [15], the approximation of fuzzy numbers by LR fuzzy numbers without constraints in the Euclidean class was studied by Yeh and Chu.

In addition, due to the simplification of calculation, data processing and management of uncertainty, the interval, triangular and trapezoidal approximation are very popularly studied and applied. In [16], Chanas proposed the notion of an approximation interval of a fuzzy number, and in [17,18], Grzegorzewski suggested two kinds of interval approximation operators successively to solve the problem of the interval approximation of fuzzy numbers. In [19], Ban and Coroianu found there exists at least a symmetric triangular fuzzy number which preserves a fixed parameter $p\in P$, which is a real parameter set related to fuzzy numbers. In [20], Abbasbandy and Hajjari suggested a weighted trapezoidal approximation of an arbitrary fuzzy number which preserves that the core is always a fuzzy number. In [21], Khastan and Moradi considered the width invariant trapezoidal and triangular approximations of fuzzy numbers, and its present methods avoid the effortful computation of Karush–Kuhn–Tucker theorem.

However, in some application situations, the trapezoidal approximation may be too restrictive and idealistic. Hence, in order to avoid the limitation of trapezoidal approximation and improve the accuracy, in [22], Coroianu, Gagolewski and Grzegorzewski defined the so-called piecewise linear 1-knot fuzzy numbers, which is simple enough and flexible to reconstruct the input fuzzy concepts, and further investigated some properties of the piecewise linear approximation of fuzzy numbers in [23]. Then, Wang and Shen proposed methods of approximating general fuzzy number by using a multi-knots piecewise linear fuzzy number in [24].

For a fuzzy number, it is known that the greater the value of the membership degree, the greater the contribution of the point to the fuzzy number, that is, the more important the point with the membership degree is. Therefore, compared with unweighted metric $d(u,v) = \sqrt{{\int }_0^1{(\underline{u}\left(r\right)-\underline{v}\left(r\right))}^{2}dr+{\int }_0^1{(\overline{u}\left(r\right)-\overline{v}\left(r\right))}^{2}dr}$, weighted metric $d^{*}(u,v) = \sqrt{{\int }_0^{1}2r{(\underline{u}\left(r\right)-\underline{v}\left(r\right))}^{2}dr+{\int }_0^{1}2r{(\overline{u}\left(r\right)-\overline{v}\left(r\right))}^{2}dr}$ is more reasonable and objective in describing the degree of difference between two fuzzy numbers.

In the study of approximating general fuzzy numbers with simple fuzzy numbers, for the convenience and simplicity of calculation, the methods established by predecessors (for example, see [22,23,24]) are basically based on unweighted metric. In order to establish a method to obtain a more objective and reasonable approximation solution, in this paper, we are going to use the weighted metric as the evaluation standard to explore the problem of using simple fuzzy numbers to approximate general fuzzy numbers. Of course, from the structure of the two metrics, the establishing of a method of solving the best approximation fuzzy numbers based on weighted metric is much more complex to calculate than that based on unweighted metric. This will bring some difficulties to the work we will do. However, from the structure of fuzzy numbers, the method we will establish will be able to obtain more reasonable and objective approximate solutions of general fuzzy numbers.

The specific arrangement of this paper is as follows: In Section 2, we briefly review some basic definitions, notations and results about fuzzy numbers. In Section 3, we give the conceptions of I-nearest r-s piecewise linear approximation and II-nearest r-s piecewise linear approximation for a general fuzzy number. Then, for a general fuzzy number, we obtain a group of calculation formulas of the I-nearest r-s piecewise linear approximation and the II-nearest r-s piecewise linear approximation. In Section 4, we give specific examples to show the effectiveness and usability of the methods in this paper, and compare some approximation methods of fuzzy numbers of the piecewise linear type. In Section 5, we make a brief summary to this paper and identify future research directions.

2. Basic Definitions and Notations

A fuzzy subset (in short, a fuzzy set) of the real line R is a function $u:R\to [0,1]$. For each such fuzzy set u, we denote by ${\left[u\right]}^r = \{x\in R:u\left(x\right)\ge r\}$ for any $r\in (0,1]$, its r-level set. By supp u, we denote the support of u, i.e., the $\{x\in R:u(x)>0\}$. By ${\left[u\right]}^0$, we denote the closure (according to the usual Euclidean topology on R) of the supp u, i.e., ${\left[u\right]}^0 = \overline{\{x\in R:u(x)>0\}}$.

If u is a normal and fuzzy convex fuzzy set of R, $u\left(x\right)$ is upper semi-continuous, and ${\left[u\right]}^0$ is compact (according to the usual Euclidean topology on R), then we call u a fuzzy number, and denote the collection of all fuzzy numbers by E.

It is known that if $u\in E$, then for each $r\in [0,1]$, ${\left[u\right]}^r$ is a convex compact set in R, i.e., a closed interval. For $u\in E$, we denote the closed interval as ${\left[u\right]}^r = [\underline{u}\left(r\right),\overline{u}\left(r\right)]$ for any $r\in [0,1]$.

For any $u,v\in E$, define $u \le v$ if and only if $\underline{u}\left(r\right) \le \underline{v}\left(r\right)$ and $\overline{u}\left(r\right) \le \overline{v}\left(r\right)$ for any $r\in [0,1]$.

The unweighted metric d on fuzzy numbers space E is defined [25] as

$$\begin{array}{c}\hfill d(u,v) = \sqrt{{\int }_0^1{(\underline{u}\left(r\right)-\underline{v}\left(r\right))}^{2}dr+{\int }_0^1{(\overline{u}\left(r\right)-\overline{v}\left(r\right))}^{2}dr}\end{array}$$

(1)

for any $u,v\in E$.

The weighted metric $d^{*}$ on fuzzy numbers space E is defined [26] as

$$\begin{array}{c}\hfill d^{*}(u,v) = \sqrt{{\int }_0^{1}2r{(\underline{u}\left(r\right)-\underline{v}\left(r\right))}^{2}dr+{\int }_0^{1}2r{(\overline{u}\left(r\right)-\overline{v}\left(r\right))}^{2}dr}\end{array}$$

(2)

for any $u,v\in E$.

Let $\mathit{r} = (r_0,r_1,r_2,\cdots ,r_m,r_{m+1})$, $\mathit{s} = (s_0,s_1,s_2,\cdots ,s_n,s_{n+1})$ with $0= r_0<r_1<r_2<\cdots <r_m<r_{m+1} =1= s_{n+1}>s_n>\cdots >s_2>s_1>s_0 =0$. For any $A = (a_0,a_1,\cdots ,a_{m+1})$ and $B = (b_0,b_1,\cdots ,b_{n+1})$ with $a_0 \le a_1 \le a_2 \le \cdots \le a_m \le a_{m+1} \le b_{n+1} \le b_n \le \cdots b_2 \le b_1 \le b_0$, then we call the fuzzy number u defined as

$$\begin{array}{c}\hfill u\left(x\right) =\left\{\begin{array}{cc}0,\hfill & x < a_0\hfill \\ r_1\frac{x-a_0}{a_1-a_0},\hfill & x\in [a_0,a_1)\hfill \\ r_1 + (r_2-r_1)\frac{x-a_1}{a_2-a_1},\hfill & x\in [a_1,a_2)\hfill \\ ⋮\hfill \\ r_{m-1} + (r_m-r_{m-1})\frac{x-a_{m-1}}{a_m-a_{m-1}},\hfill & x\in [a_{m-1},a_m)\hfill \\ r_m + (1-r_m)\frac{x-a_m}{a_{m+1}-a_m},\hfill & x\in [a_m,a_{m+1})\hfill \\ 1,\hfill & x\in [a_{m+1},b_{n+1}]\hfill \\ s_n + (1-s_n)\frac{b_n-x}{b_n-b_{n+1}},\hfill & x\in (b_{n+1},b_n]\hfill \\ s_{n-1} + (s_n-s_{n-1})\frac{b_{n-1}-x}{b_{n-1}-b_n},\hfill & x\in (b_n,b_{n-1}]\hfill \\ ⋮\hfill \\ s_1 + (s_2-s_1)\frac{b_1-x}{b_1-b_2},\hfill & x\in (b_2,b_1]\hfill \\ s_1\frac{b_0-x}{b_0-b_1},\hfill & x\in (b_1,b_0]\hfill \\ 0,\hfill & x > b_0\hfill \end{array}\right.\end{array}$$

(3)

is a r-s piecewise linear fuzzy number, and denote it as

$$\begin{array}{c}\hfill u_{pl} = PL\left(A^T,{\mathit{r}}^T;B^T,{\mathit{s}}^T\right) = PL\left[\left(\begin{array}{cc}{a}_0& r_0\\ a_1& r_1\\ ⋮& ⋮\\ a_m& r_m\\ a_{m+1}& r_{m+1}\end{array}\right);\left(\begin{array}{cc}{b}_0& s_0\\ b_1& s_1\\ ⋮& ⋮\\ b_m& s_m\\ b_{m+1}& s_{m+1}\end{array}\right)\right]\end{array}$$

(4)

and call $\mathit{r}$ and $\mathit{s}$ the left threshold value set and the right threshold value set of $u_{pl}$, respectively. Specially, as $\mathit{r} = \mathit{s}$, we call the fuzzy number $u_{pl}$ a r-knots (i.e., r-knots) piecewise linear fuzzy number, and call $\mathit{r}$ (i.e., $\mathit{s}$) the threshold value set of $u_{pl}$.

For example, as $\mathit{r} = (0,0.3,0.6,0.9,1)$, $\mathit{s}=(0,0.2,0.5,0.8,1)$, $A = (-1,-0.7,-0.6,$$-0.2,-0.1)$ and $B = (1,0.6,0.4,0.1,0)$, the membership function of $\tilde{u} = PL(A^T,{\mathit{r}}^T;B^T,{\mathit{s}}^T)$ (see Figure 1), i.e.,

$$\tilde{u} = PL\left[\left(\begin{array}{cc}-1& 0\\ -0.7& 0.3\\ -0.6& 0.6\\ -0.2& 0.9\\ -0.1& 1\end{array}\right);\left(\begin{array}{cc}1& 0\\ 0.6& 0.2\\ 0.4& 0.5\\ 0.1& 0.8\\ 0& 1\end{array}\right)\right]$$

is as follows:

$$\tilde{u}\left(x\right) =\left\{\begin{array}{cc}0,\hfill & x < -1\hfill \\ 0.3\frac{x-(-1)}{-0.7-(-1)},\hfill & x\in [-1,-0.7)\hfill \\ 0.3 + (0.6-0.3)\frac{x-(-0.7)}{-0.6-(-0.7)},\hfill & x\in [-0.7,-0.6)\hfill \\ 0.6 + (0.9-0.6)\frac{x-(-0.6)}{-0.2-(-0.6)},\hfill & x\in [-0.6,-0.2)\hfill \\ 0.9 + (1-0.9)\frac{x-(-0.2)}{-0.1-(-0.2)},\hfill & x\in [-0.2,-0.1)\hfill \\ 1,\hfill & x\in [-0.1,0]\hfill \\ 0.8 + (1-0.8)\frac{0.1-x}{0.1-0},\hfill & x\in (0,0.1]\hfill \\ 0.5 + (0.8-0.5)\frac{0.4-x}{0.4-0.1},\hfill & x\in (0.1,0.4]\hfill \\ 0.2 + (0.5-0.2)\frac{0.6-x}{0.6-0.4},\hfill & x\in (0.4,0.6]\hfill \\ 0.2\frac{1-x}{1-0.6},\hfill & x\in (0.6,1]\hfill \\ 0,\hfill & x > 1\hfill \end{array}\right.$$

i.e.,

$$\tilde{u}\left(x\right) =\left\{\begin{array}{cc}0,\hfill & x < -1\hfill \\ x + 1,\hfill & x\in [-1,-0.7)\hfill \\ 3x + 2.4,\hfill & x\in [-0.7,-0.6)\hfill \\ 0.75x + 1.05,\hfill & x\in [-0.6,-0.2)\hfill \\ x + 1.1,\hfill & x\in [-0.2,-0.1)\hfill \\ 1,\hfill & x\in [-0.1,0]\hfill \\ 1 - x,\hfill & x\in (0,0.1]\hfill \\ 0.9 - x,\hfill & x\in (0.1,0.4]\hfill \\ 1.1 - x,\hfill & x\in (0.4,0.6]\hfill \\ \frac{1-x}{2},\hfill & x\in (0.6,1]\hfill \\ 0,\hfill & x > 1\hfill \end{array}\right.$$

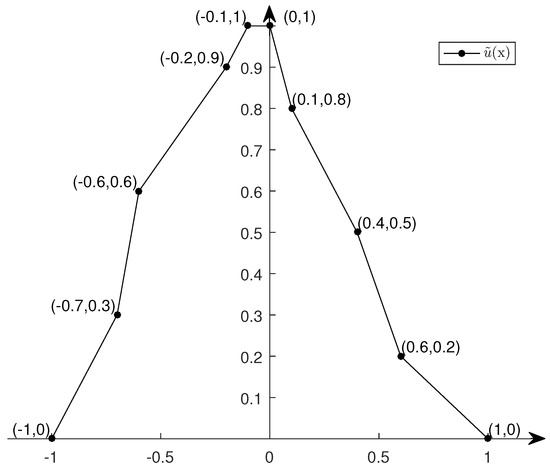
Figure 1. (0,0.3,0.6,0.9,1)–(0,0.2,0.5,0.8,1) piecewise linear fuzzy number $\tilde{u}$.

For fixed $r_i,s_j\in [0,1]$ with $0= r_0<r_1<r_2<\cdots <r_m<r_{m+1} =1= s_{n+1}>s_n>\cdots >s_2>s_1>s_0 =0$, we denote the collection r-s piecewise linear fuzzy numbers by ${}^{r}P{L}^s\left(E\right)$, and denote the collection of all r-knots (s-knots) piecewise linear fuzzy numbers by $P{L}^r\left(E\right)$ (i.e., $P{L}^s\left(E\right)$).

Let $u = u_{pl}\in {}^{r}P{L}^s\left(E\right)$. Then,

$$\begin{array}{c}\hfill \underline{u}\left(r\right) =\left\{\begin{array}{cc}{a}_0 + (a_1-a_0)\frac{r}{r_1},\hfill & r\in [r_0,r_1]=[0,r_1]\hfill \\ a_1 + (a_2-a_1)\frac{r-r_1}{r_2-r_1},\hfill & r\in (r_1,r_2]\hfill \\ ⋮\hfill \\ a_{m-1} + (a_m-a_{m-1})\frac{r-r_{m-1}}{r_m-r_{m-1}},\hfill & r\in (r_{m-1},r_m]\hfill \\ a_m + (a_{m+1}-a_m)\frac{r-r_m}{1-r_m},\hfill & r\in (r_m,r_{m+1}]=(r_m,1]\hfill \end{array}\right.\end{array}$$

(5)

and

$$\begin{array}{c}\hfill \overline{u}\left(r\right) =\left\{\begin{array}{cc}{b}_0 + (b_1-b_0)\frac{r}{s_1},\hfill & r\in [s_0,s_1]=[0,s_1]\hfill \\ b_1 + (b_2-b_1)\frac{r-s_1}{s_2-s_1},\hfill & r\in (s_1,s_2]\hfill \\ ⋮\hfill \\ b_{n-1} + (b_n-b_{n-1})\frac{r-s_{n-1}}{s_n-s_{n-1}},\hfill & r\in (s_{n-1},s_n]\hfill \\ b_n + (b_{n+1}-b_n)\frac{r-s_n}{1-s_n},\hfill & r\in (s_n,s_{n+1}]=(s_n,1]\hfill \end{array}\right.\end{array}$$

(6)

for $r\in [0,1]$.

Let $R^{n\times n}$ be the collection of all $n \times n$ real matrices (i.e., the matrices with all real number elements). If matrix $A = {\left(a_{ij}\right)}_{n\times n}\in R^{n\times n}$ satisfies

$$|a_{ii}| > \sum _{j=1,j\ne i}^n\left|a_{ij}\right|, i = 1, 2, \cdots , n$$

then A is a strictly diagonally dominant matrix (see Theorem I in [27]).

If $A = {\left(a_{ij}\right)}_{n\times n}\in R^{n\times n}$ is a strictly diagonally dominant matrix with positive diagonal entries (i.e., $a_{ii} > 0$, $i = 1, 2, \cdots , n$), then

$${\lambda }_i > 0$$

for any $i = 1, 2, \cdots , n$, where ${\lambda }_i(i=1,2,\cdots ,n)$ is the eigenvalues of A (see Theorem VII in [27]).

3. The Approximations of Membership Functions

In [18], Coroianu, Gagolewski and Grzegorzewski give a method of approximating general fuzzy numbers by using piecewise linear 1-knot fuzzy numbers with respect to the metric d. In this section, we are going to establish a recursion formula to obtain the r-s piecewise linear fuzzy number which is the nearest (with respect to metric $d^{*}$) approximation with the left threshold value set $\mathit{r}$ and the right threshold value set $\mathit{s}$. To do this, we first give the following definitions and theorems.

Definition 1.

Let $r_i,s_j\in [0,1]$ with $0= r_0<r_1<r_2<\cdots <r_m<r_{m+1} =1= s_{n+1}>s_n>\cdots >s_2>s_1>s_0 =0$. If there exists $u_{pl}\in {}^{r}P{L}^s\left(E\right)$ with $\underline{u_{pl}}\left(0\right) = \underline{u}\left(0\right)$, $\overline{u_{pl}}\left(0\right) = \overline{u}\left(0\right)$, $\underline{u_{pl}}\left(1\right) = \underline{u}\left(1\right)$, $\overline{u_{pl}}\left(1\right) = \overline{u}\left(1\right)$ (i.e., ${\left[u_{pl}\right]}^0 = {\left[u\right]}^0$ and ${\left[u_{pl}\right]}^1 = {\left[u\right]}^1$) such that

$$d^{*}(u,u_{pl}) = min\{d^{*}(u,v):v\in {}^{r}P{L}^s\left(E\right)\mathrm{with}{\left[v\right]}^0 = {\left[u\right]}^0,{\left[v\right]}^1 = {\left[u\right]}^1\}$$

then we say $u_{pl}$ to be the I-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation (in short, PLA) of fuzzy number u. Specially, as $\mathit{r} = \mathit{s}$, we say $u_{pl}$ to be the I-nearest (with respect to metric $d^{*}$) r-knots (i.e., s-knots) piecewise linear approximation (in short, PLA) of fuzzy number u.

Definition 2.

Let $r_i,s_j\in [0,1]$ with $0= r_0<r_1<r_2<\cdots <r_m<r_{m+1} =1= s_{n+1}>s_n>\cdots >s_2>s_1>s_0 =0$. If there exists $u_{pl}\in {}^{r}P{L}^s\left(E\right)$ such that

$$d^{*}(u,u_{pl}) = min\{d^{*}(u,v):v\in {}^{r}P{L}^s\left(E\right)\}$$

then we say $u_{pl}$ to be the II-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation (in short, PLA) of fuzzy number u. Specially, as $\mathit{r} = \mathit{s}$, we say $u_{pl}$ to be the II-nearest (with respect to metric $d^{*}$) r-knots (i.e., s-knots) piecewise linear approximation (in short, PLA) of fuzzy number u.

By the definitions of the I-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation and the II-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation of a fuzzy number, we can directly get the following result:

Proposition 1.

Let $u\in E$ and $r_i,s_j\in [0,1]$ with $0 = r_0<r_1<r_2<\cdots <r_m<r_{m+1} =1$$= s_{n+1}>s_n>\cdots >s_2>s_1>s_0 =0$ to be the I-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation of fuzzy number u, and $v_{pl}$ to be the II-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation of fuzzy number u. Then,

$$d^{*}(u,v_{pl}) \le d^{*}(u,u_{pl})$$

i.e., $v_{pl}$ is a better approximation of fuzzy number u than $u_{pl}$.

Proof. 

From

$$\{d^{*}(u,v):v\in {}^{r}P{L}^s\left(E\right)\mathrm{with}{\left[v\right]}^0 = {\left[u\right]}^0,{\left[v\right]}^1 = {\left[u\right]}^1\}\subset \{d^{*}(u,v):v\in {}^{r}P{L}^s\left(E\right)\}$$

We see that

$$\begin{array}{cc}\hfill d^{*}(u,u_{pl})& =min\{d^{*}(u,v):v\in {}^{r}P{L}^s\left(E\right)\mathrm{with}{\left[v\right]}^0 = {\left[u\right]}^0,{\left[v\right]}^1 = {\left[u\right]}^1\}\hfill \\ \hfill & \ge min\{d^{*}(u,v):v\in {}^{r}P{L}^s\left(E\right)\}\hfill \\ \hfill & = d^{*}(u,v_{pl})\hfill \end{array}$$

The proof of the proposition can be completed. □

For convenience, we give the following notations:

Let $\mathit{r} = (r_0,r_1,r_2,\cdots ,r_m,r_{m+1})$, $\mathit{s} = (s_0,s_1,s_2,\cdots ,s_n,s_{n+1})$ with $0= r_0<r_1<r_2<\cdots <r_m<r_{m+1} =1= s_{n+1}>s_n>\cdots >s_2>s_1>s_0 =0$. We give the following notations:

$$\begin{array}{c}\hfill \underline{{\alpha }_i} =\left\{\begin{array}{cc}\frac{\Delta r_2^2}{{\Sigma r_2}^2-{\Sigma r_1}^2},\hfill & i = 1\hfill \\ \frac{\Delta r_{i+1}^2}{{\Sigma r_{i+1}}^2-{\Sigma r_i}^2-\Delta r_i^2\underline{{\alpha }_{i-1}}},\hfill & i = 2 ,3 , \cdots , m-1\hfill \end{array}\right.\end{array}$$

(7)

$$\begin{array}{c}\hfill \underline{{\beta }_i} =\left\{\begin{array}{cc}\frac{\underline{{\gamma }_1}+\underline{{\lambda }_1}-r_1^2\underline{u}\left(0\right)}{{\Sigma r_2}^2-{\Sigma r_1}^2},\hfill & i = 1\hfill \\ \frac{\underline{{\gamma }_i}+\underline{{\lambda }_i}-\Delta r_i^2\underline{{\beta }_{i-1}}}{{\Sigma r_{i+1}}^2-{\Sigma r_i}^2-\Delta r_i^2\underline{{\alpha }_{i-1}}},\hfill & i = 2 ,3 , \cdots , m-1\hfill \end{array}\right.\end{array}$$

(8)

where, $\Sigma r_i = r_i + r_{i-1}$, $\Delta r_i^2 = r_i^2 - r_{i-1}^2$, $\underline{{\gamma }_i} = \frac{12}{r_i-r_{i-1}}{\int }_{r_{i-1}}^{r_i}\underline{u}\left(r\right)(r-r_{i-1})rdr$ and $\underline{{\lambda }_i} = \frac{12}{r_{i+1}-r_i}{\int }_{r_i}^{r_{i+1}}\underline{u}\left(r\right)(r_{i+1}-r)rdr$.

$$\begin{array}{c}\hfill \overline{{\alpha }_j} =\left\{\begin{array}{cc}\frac{\Delta s_2^2}{{\Sigma s_2}^2-{\Sigma s_1}^2},\hfill & j = 1\hfill \\ \frac{\Delta s_{j+1}^2}{{\Sigma s_{j+1}}^2-{\Sigma s_j}^2-\Delta s_j^2\overline{{\alpha }_{j-1}}},\hfill & j = 2 ,3 , \cdots , n-1\hfill \end{array}\right.\end{array}$$

(9)

$$\begin{array}{c}\hfill \overline{{\beta }_j} =\left\{\begin{array}{cc}\frac{\overline{{\gamma }_1}+\overline{{\lambda }_1}-s_1^2\overline{u}\left(0\right)}{{\Sigma s_2}^2-{\Sigma s_1}^2},\hfill & j = 1\hfill \\ \frac{\overline{{\gamma }_j}+\overline{{\lambda }_j}-\Delta s_j^2\overline{{\beta }_{j-1}}}{{\Sigma s_{j+1}}^2-{\Sigma s_j}^2-\Delta s_j^2\overline{{\alpha }_{j-1}}},\hfill & j = 2 ,3 , \cdots , n-1\hfill \end{array}\right.\end{array}$$

(10)

where, $\Sigma s_j = s_j + s_{j-1}$, $\Delta s_j^2 = s_j^2-s_{j-1}^2$, $\overline{{\gamma }_j} = \frac{12}{s_j-s_{j-1}}{\int }_{s_{j-1}}^{s_j}\overline{u}\left(r\right)(r-s_{j-1})rdr$ and $\overline{{\lambda }_j} = \frac{12}{s_{j+1}-s_j}{\int }_{s_j}^{s_{j+1}}\overline{u}\left(r\right)(s_{j+1}-r)rdr$.

Theorem 1.

Let $\mathit{r} = (r_0,r_1,r_2,\cdots ,r_m,r_{m+1})$, $\mathit{s} = (s_0,s_1,s_2,\cdots ,s_n,s_{n+1})$ with $0= r_0<r_1<r_2<\cdots <r_m<r_{m+1} =1= s_{n+1}>s_n>\cdots >s_2>s_1>s_0 =0$. If $a_i,b_j\in R(i=1,2,\cdots ,m,j=1,2,\cdots ,n)$ are respectively determined by following recursion formulas:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{a}_m = \frac{\underline{{\gamma }_m}+\underline{{\lambda }_m}-(1-r_m^2)\underline{u}\left(1\right)-\Delta r_m^2\underline{{\beta }_{m-1}}}{{\Sigma r_{m+1}}^2-{\Sigma r_m}^2-\Delta r_m^2\underline{{\alpha }_{m-1}}}\hfill \\ a_i = \underline{{\beta }_i}-\underline{{\alpha }_i}·a_{i+1}, i = m-1, m-2 , \cdots , 1\hfill \end{array}\right.\end{array}$$

(11)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{b}_n = \frac{\overline{{\gamma }_n}+\overline{{\lambda }_n}-(1-s_n^2)\overline{u}\left(1\right)-\Delta s_n^2\overline{{\beta }_{n-1}}}{{\Sigma s_{n+1}}^2-{\Sigma s_n}^2-\Delta s_n^2\overline{{\alpha }_{n-1}}}\hfill \\ b_j = \overline{{\beta }_j}-\overline{{\alpha }_j}·b_{j+1}, j = n-1, n-2, \cdots , 1\hfill \end{array}\right.\end{array}$$

(12)

and satisfy $\underline{u}\left(0\right)= a_0\le a_1\le a_2\le \cdots \le a_m\le a_{m+1} =\underline{u}\left(1\right)\le \overline{u}\left(1\right)= b_{n+1}\le b_n\le \cdots b_2\le b_1\le b_0 =\overline{u}\left(0\right)$, then

$$u_{pl} = PL\left(A^T,{\mathit{r}}^T;B^T,{\mathit{s}}^T\right) = PL\left[\left(\begin{array}{cc}{a}_0& r_0\\ a_1& r_1\\ ⋮& ⋮\\ a_m& r_m\\ a_{m+1}& r_{m+1}\end{array}\right),\left(\begin{array}{cc}{b}_0& s_0\\ b_1& s_1\\ ⋮& ⋮\\ b_m& s_m\\ b_{m+1}& s_{m+1}\end{array}\right)\right]$$

is the I-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation of fuzzy number u, where $A = (a_0,a_1,\cdots a_{m+1}) = (\underline{u}\left(0\right),a_1,\cdots ,\underline{u}\left(1\right))$ and $B = (b_0,b_1,\cdots b_{n+1}) = (\overline{u}\left(0\right),b_1,\cdots ,\overline{u}\left(1\right))$, and $\underline{{\alpha }_i}$, $\underline{{\beta }_i}$, $\overline{{\alpha }_j}$, $\overline{{\beta }_j}$ ($i = 1,2,\cdots ,m,j = 1,2,\cdots ,n$) are respectively determined by Formulas (7)–(10).

Proof. 

We denote the n-dimensional Euclidean space as $R^n$ for positive integer n. For any $x = (x_1,\cdots ,x_m)\in R^m,y = (y_1,\cdots ,y_n)\in R^n$ with $x_1 \le x_2 \le \cdots \le x_m \le y_n \le \cdots y_2 \le y_1$, we denote $X = (\underline{u}\left(0\right),x_1,x_2,\cdots ,x_m,\underline{u}\left(1\right)), Y = (\overline{u}\left(0\right),y_1,y_2,\cdots ,y_n,\overline{u}\left(1\right))$ and $u_{x,y} = PL(X,r;Y,s)$.

We define $D:R^{m+n}\to R$ as

$$D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n) = D(x,y) = {\left(d^{*}(u,u_{x,y})\right)}^2$$

for any $(x,y) = (x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)\in R^{m+n}$. By the definition of weighted metric $d^{*}$ (i.e, Equation (2)), we see that

$$D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n) = {\int }_0^{1}2r{(\underline{u}\left(r\right)-\underline{u_{x,y}}\left(r\right))}^{2}dr + {\int }_0^{1}2r{(\overline{u}\left(r\right)-\overline{u_{x,y}}\left(r\right))}^{2}dr$$

By the definition of $\underline{u}\left(r\right)$ and $\overline{u}\left(r\right)$ (see Formulas (5) and (6)), let $r_0 = 0, r_{m+1} = 1, x_0 = \underline{u}\left(0\right), x_{m+1} = \underline{u}\left(1\right), s_0 = 0, s_{n+1}=1, y_0 = \overline{u}\left(0\right)$ and $y_{n+1} = \overline{u}\left(1\right)$, we have that

$$\begin{array}{cc}\hfill & {\int }_0^{1}2r{(\underline{u}\left(r\right)-\underline{u_{x,y}}\left(r\right))}^{2}dr\hfill \\ \hfill =& {\int }_0^{r_1}2r{(\underline{u}\left(r\right)-\underline{u}\left(0\right)-(x_1-\underline{u}\left(0\right))\frac{r}{r_1})}^{2}dr + {\int }_{r_1}^{r_2}2r{(\underline{u}\left(r\right)-x_1-(x_2-x_1)\frac{r-r_1}{r_2-r_1})}^{2}dr\hfill \\ \hfill & + \sum _{k=2}^{i-2}{\int }_{r_k}^{r_{k+1}}2r{(\underline{u}\left(r\right)-x_k-(x_{k+1}-x_k)\frac{r-r_k}{r_{k+1}-r_k})}^{2}dr\hfill \\ \hfill & +{\int }_{r_{i-1}}^{r_i}2r{(\underline{u}\left(r\right)-x_{i-1}-(x_i-x_{i-1})\frac{r-r_{i-1}}{r_i-r_{i-1}})}^{2}dr+{\int }_{r_i}^{r_{i+1}}2r{(\underline{u}\left(r\right)-x_i-(x_{i+1}-x_i)\frac{r-r_i}{r_{i+1}-r_i})}^{2}dr\hfill \\ \hfill & + \sum _{k=i+1}^{m-2}{\int }_{r_k}^{r_{k+1}}2r{(\underline{u}\left(r\right)-x_k-(x_{k+1}-x_k)\frac{r-r_k}{r_{k+1}-r_k})}^{2}dr\hfill \\ \hfill & +{\int }_{r_{m-1}}^{r_m}2r{(\underline{u}\left(r\right)-x_{m-1}-(x_m-x_{m-1})\frac{r-r_{m-1}}{r_m-r_{m-1}})}^{2}dr+{\int }_{r_m}^{1}2r{(\underline{u}\left(r\right)-x_m-(\underline{u}\left(1\right)-x_m)\frac{r-r_m}{1-r_m})}^{2}dr\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\int }_0^{1}2r{(\overline{u}\left(r\right)-\overline{u_{x,y}}\left(r\right))}^{2}dr\hfill \\ \hfill =& {\int }_0^{s_1}2r{(\overline{u}\left(r\right)-\overline{u}\left(0\right)-(y_1-\overline{u}\left(0\right))\frac{r}{s_1})}^{2}dr + {\int }_{s_1}^{s_2}2r{(\overline{u}\left(r\right)-y_1-(y_2-y_1)\frac{r-s_1}{s_2-s_1})}^{2}dr\hfill \\ \hfill & +\sum _{k=2}^{j-2}{\int }_{s_k}^{s_{k+1}}2r{(\overline{u}\left(r\right)-y_k-(y_{k+1}-y_k)\frac{r-s_k}{s_{k+1}-s_k})}^{2}dr\hfill \\ \hfill & +{\int }_{s_{j-1}}^{s_j}2r{(\overline{u}\left(r\right)-y_{j-1}-(y_j-y_{j-1})\frac{r-s_{j-1}}{s_j-s_{j-1}})}^{2}dr+{\int }_{s_j}^{s_{j+1}}2r{(\overline{u}\left(r\right)-y_j-(y_{j+1}-y_j)\frac{r-s_j}{s_{j+1}-s_j})}^{2}dr\hfill \\ \hfill & + \sum _{k=j+1}^{n-2}{\int }_{s_k}^{s_{k+1}}2r{(\overline{u}\left(r\right)-y_k-(y_{k+1}-y_k)\frac{r-s_k}{s_{k+1}-s_k})}^{2}dr\hfill \\ \hfill & +{\int }_{s_{n-1}}^{s_n}2r{(\overline{u}\left(r\right)-y_{n-1}-(y_n-y_{n-1})\frac{r-s_{n-1}}{s_n-s_{n-1}})}^{2}dr+{\int }_{s_n}^{1}2r{(\overline{u}\left(r\right)-y_n-(\overline{u}\left(1\right)-y_n)\frac{r-s_n}{1-s_n})}^{2}dr\hfill \end{array}$$

Then, for any fixed $i = 1 , 2 , \cdots , m$, we have that

$$\begin{array}{cc}\hfill & \frac{\partial D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)}{\partial x_i}\hfill \\ \hfill =& \frac{\partial }{\partial x_i}[{\int }_{r_{i-1}}^{r_i}2r(\underline{u}\left(r\right)-x_{i-1}-{(x_i-x_{i-1}\frac{r-r_{i-1}}{r_i-r_{i-1}})}^2)dr+{\int }_{r_i}^{r_{i+1}}2r(\underline{u}\left(r\right)-x_i-{(x_{i+1}-x_i\frac{r-r_i}{r_{i+1}-r_i})}^2)dr]\hfill \\ \hfill =& \frac{\partial }{\partial x_i}[\frac{x_i^2}{{(r_i-r_{i-1})}^2}{\int }_{r_{i-1}}^{r_i}2r{(r-r_{i-1})}^{2}dr-\frac{2x_i}{r_i-r_{i-1}}{\int }_{r_{i-1}}^{r_i}2r(r-r_{i-1})(\underline{u}\left(r\right)-x_{i-1}\frac{r_i-r}{r_i-r_{i-1}})dr\hfill \\ \hfill & +{\int }_{r_{i-1}}^{r_i}2r{(\underline{u}\left(r\right)-x_{i-1}\frac{r_i-r}{r_i-r_{i-1}})}^{2}dr + \frac{x_i^2}{{(r_{i+1}-r_i)}^2}{\int }_{r_i}^{r_{i+1}}2r{(r_{i+1}-r)}^{2}dr\hfill \\ \hfill & -\frac{2x_i}{r_{i+1}-r_i}{\int }_{r_i}^{r_{i+1}}2r(r_{i+1}-r)(\underline{u}\left(r\right)-x_{i+1}\frac{r-r_i}{r_{i+1}-r_i})dr+{\int }_{r_i}^{r_{i+1}}2r{(\underline{u}\left(r\right)-x_{i+1}\frac{r-r_i}{r_{i+1}-r_i})}^{2}dr]\hfill \\ \hfill =& \frac{4x_i}{{(r_i-r_{i-1})}^2}{\int }_{r_{i-1}}^{r_i}r{(r-r_{i-1})}^{2}dr-\frac{4}{r_i-r_{i-1}}{\int }_{r_{i-1}}^{r_i}r(r-r_{i-1})(\underline{u}\left(r\right)-x_{i-1}\frac{r_i-r}{r_i-r_{i-1}})dr\hfill \\ \hfill & +\frac{4x_i}{{(r_{i+1}-r_i)}^2}{\int }_{r_i}^{r_{i+1}}r{(r_{i+1}-r)}^{2}dr-\frac{4}{r_{i+1}-r_i}{\int }_{r_i}^{r_{i+1}}r(r_{i+1}-r)(\underline{u}\left(r\right)-x_{i+1}\frac{r-r_i}{r_{i+1}-r_i})dr\hfill \\ \hfill =& \frac{1}{3}(r_i^2-r_{i-1}^2)x_{i-1} + \frac{1}{3}({(r_{i+1}+r_i)}^2-{(r_i+r_{i-1})}^2)x_i + \frac{1}{3}(r_{i+1}^2-r_i^2)x_{i+1}\hfill \\ \hfill & -\frac{4}{r_i-r_{i-1}}{\int }_{r_{i-1}}^{r_i}\underline{u}\left(r\right)(r-r_{i-1})rdr-\frac{4}{r_{i+1}-r_i}{\int }_{r_i}^{r_{i+1}}\underline{u}\left(r\right)(r_{i+1}-r)rdr\hfill \end{array}$$

Likewise, for any fixed $j = 1, 2, \cdots , n$, we have that

$$\begin{array}{cc}\hfill & \frac{\partial D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)}{\partial y_j}\hfill \\ \hfill =& \frac{\partial }{\partial y_j}[{\int }_{s_{j-1}}^{s_j}2r(\overline{u}\left(r\right)-y_{j-1}-{(y_j-y_{j-1}\frac{r-s_{j-1}}{s_j-s_{j-1}})}^2)dr+{\int }_{s_j}^{s_{j+1}}2r(\overline{u}\left(r\right)-y_j-{(y_{j+1}-y_j\frac{r-s_j}{s_{j+1}-s_j})}^2)dr]\hfill \\ \hfill =& \frac{\partial }{\partial y_j}[\frac{y_j^2}{{(s_j-s_{j-1})}^2}{\int }_{s_{j-1}}^{s_j}2r{(r-s_{j-1})}^{2}dr-\frac{2y_j}{s_j-s_{j-1}}{\int }_{s_{j-1}}^{s_j}2r(r-s_{j-1})(\overline{u}\left(r\right)-y_{j-1}\frac{s_j-r}{s_j-s_{j-1}})dr\hfill \\ \hfill & +{\int }_{s_{j-1}}^{s_j}2r{(\overline{u}\left(r\right)-y_{j-1}\frac{s_j-r}{s_j-s_{j-1}})}^{2}dr+\frac{y_j^2}{{(s_{j+1}-s_j)}^2}{\int }_{s_j}^{s_{j+1}}2r{(s_{j+1}-r)}^{2}dr\hfill \\ \hfill & -\frac{2y_j}{s_{j+1}-s_j}{\int }_{s_j}^{s_{j+1}}2r(s_{j+1}-r)(\overline{u}\left(r\right)-y_{j+1}\frac{r-s_j}{s_{j+1}-s_j})dr+{\int }_{s_j}^{s_{j+1}}2r{(\overline{u}\left(r\right)-y_{j+1}\frac{r-s_j}{s_{j+1}-s_j})}^{2}dr]\hfill \\ \hfill =& \frac{4y_j}{{(s_j-s_{j-1})}^2}{\int }_{s_{j-1}}^{s_j}r{(r-s_{j-1})}^{2}dr-\frac{4}{s_j-s_{j-1}}{\int }_{s_{j-1}}^{s_j}r(r-s_{j-1})(\overline{u}\left(r\right)-y_{j-1}\frac{s_j-r}{s_j-s_{j-1}})dr\hfill \\ \hfill & +\frac{4y_j}{{(s_{j+1}-s_j)}^2}{\int }_{s_j}^{s_{j+1}}r{(s_{j+1}-r)}^{2}dr-\frac{4}{s_{j+1}-s_j}{\int }_{s_j}^{s_{j+1}}r(s_{j+1}-r)(\overline{u}\left(r\right)-y_{j+1}\frac{r-s_j}{s_{j+1}-s_j})dr\hfill \\ \hfill =& \frac{1}{3}(s_j^2-s_{j-1}^2)y_{j-1}+\frac{1}{3}({(s_{j+1}+s_j)}^2-{(s_j+s_{j-1})}^2)y_j+\frac{1}{3}(s_{j+1}^2-s_j^2)y_{j+1}\hfill \\ \hfill & -\frac{4}{s_j-s_{j-1}}{\int }_{s_{j-1}}^{s_j}\overline{u}\left(r\right)(r-s_{j-1})rdr-\frac{4}{s_{j+1}-s_j}{\int }_{s_j}^{s_{j+1}}\overline{u}\left(r\right)(s_{j+1}-r)rdr\hfill \end{array}$$

Let

$$\frac{\partial D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)}{\partial x_i} = 0, i = 1, 2, \cdots , m$$

and

$$\frac{\partial D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)}{\partial y_j} = 0, j = 1, 2, \cdots , n$$

Then, we can obtain that

$$\begin{array}{c}\hfill C_1{x}^T =\left(\begin{array}{c}\underline{{\gamma }_1}+\underline{{\lambda }_1}-r_1^2\underline{u}\left(0\right)\\ \underline{{\gamma }_2}+\underline{{\lambda }_2}\\ ⋮\\ \underline{{\gamma }_i}+\underline{{\lambda }_i}\\ ⋮\\ \underline{{\gamma }_m}+\underline{{\lambda }_m}-(1-r_m^2)\underline{u}\left(1\right)\end{array}\right)\end{array}$$

(13)

and

$$\begin{array}{c}\hfill C_2{y}^T =\left(\begin{array}{c}\overline{{\gamma }_1}+\overline{{\lambda }_1}-r_1^2\overline{u}\left(0\right)\\ \overline{{\gamma }_2}+\overline{{\lambda }_2}\\ ⋮\\ \overline{{\gamma }_j}+\overline{{\lambda }_j}\\ ⋮\\ \overline{{\gamma }_n}+\overline{{\lambda }_n}-(1-s_n^2)\overline{u}\left(1\right)\end{array}\right)\end{array}$$

(14)

where, $x^T$ is the transposition of $x = (x_1,x_2\cdots ,x_m)$, $y^T$ is the transposition of $y = (y_1,y_2\cdots ,y_n)$, and

$$C_1 =\left(\begin{array}{ccccccc}{\Sigma r_2}^2-{\Sigma r_1}^2& \Delta r_2^2& 0& \cdots & 0& 0& 0\\ \Delta r_2^2& {\Sigma r_3}^2-{\Sigma r_2}^2& \Delta r_3^2& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & \Delta r_{m-1}^2& {\Sigma r_m}^2-{\Sigma r_{m-1}}^2& \Delta r_m^2\\ 0& 0& 0& \cdots & 0& \Delta r_m^2& {\Sigma r_{m+1}}^2-{\Sigma r_m}^2\end{array}\right)$$

and

$$C_2 =\left(\begin{array}{ccccccc}{\Sigma s_2}^2-{\Sigma s_1}^2& \Delta s_2^2& 0& \cdots & 0& 0& 0\\ \Delta s_2^2& {\Sigma s_3}^2-{\Sigma s_2}^2& \Delta s_3^2& \cdots & 0& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& ⋮\\ 0& 0& 0& \cdots & \Delta s_{n-1}^2& {\Sigma s_n}^2-{\Sigma s_{n-1}}^2& \Delta s_n^2\\ 0& 0& 0& \cdots & 0& \Delta s_n^2& {\Sigma s_{n+1}}^2-{\Sigma s_n}^2\end{array}\right)$$

From $0 = r_0<r_1<r_2<\cdots <r_m<r_{m+1} = 1= s_{n+1}>s_n>\cdots >s_2>s_1>s_0 =0$, we see that $\Delta r_{i+1}^2 > 0 ,i = 1, 2, \cdots , m$ and $\Delta s_{j+1}^2 > 0, j = 1, 2, \cdots , n$, so

$$\left\{\begin{array}{c}|{\Sigma r_2}^2-{\Sigma r_1}^2| > |\Delta r_2^2|\hfill \\ |{\Sigma r_{i+1}}^2-{\Sigma r_i}^2| > |\Delta r_i^2|+|\Delta r_{i+1}^2|, i = 2, 3, \cdots , m-1\hfill \\ |{\Sigma r_{m+1}}^2-{\Sigma r_m}^2| > |\Delta r_m^2|\hfill \end{array}\right.$$

and

$$\left\{\begin{array}{c}|{\Sigma s_2}^2-{\Sigma s_1}^2| > |\Delta s_2^2|\hfill \\ |{\Sigma s_{j+1}}^2-{\Sigma s_j}^2| > |\Delta s_j^2|+|\Delta s_{j+1}^2|,i = 2, 3, \cdots , n-1\hfill \\ |{\Sigma s_{n+1}}^2-{\Sigma s_n}^2| > |\Delta s_n^2|\hfill \end{array}\right.$$

Therefore, $C_1$ and $C_2$ are both a strictly diagonally dominant matrix. Thus, by Thomas algorithm in [27], we know that there is a unique set of solutions for the two equations for linear Equation (13) of unknown quantities $x_1,x_2\cdots ,x_m$ and linear Equation (14) of unknown quantities $y_1,y_2\cdots ,y_n$ (denote the solutions set of (13) as $(a_1,a_2,\cdots ,a_m)$ and the solutions set of (14) as $(b_1,b_2,\cdots ,b_n)$), and the solutions sets $(a_1,a_2,\cdots ,a_m)$ and $(b_1,b_2,\cdots ,b_n)$ are determined by recursion formulas (11) and (12).

Denoting $A= (a_0,a_1,a_2,\cdots ,a_m,a_{m+1}) = (\underline{u}\left(0\right),a_1,a_2,\cdots ,a_m,\underline{u}\left(1\right)), B= (b_0,b_1,b_2,$$\cdots ,b_n,b_{n+1}) = (\overline{u}\left(0\right),b_1,b_2,\cdots ,b_n,\overline{u}\left(1\right))$, by $\underline{u}\left(0\right)= a_0\le a_1\le a_2\le \cdots \le a_m\le a_{m+1} =\underline{u}\left(1\right)\le \overline{u}\left(1\right)= b_{n+1}\le b_n\le \cdots b_2\le b_1\le b_0 =\overline{u}\left(0\right)$, we can define the r-s piecewise linear fuzzy number as $u_{pl} = PL(A^T,{\mathit{r}}^T;B^T,{\mathit{s}}^T$).

In the following, in order to show that the r-s piecewise linear fuzzy number $u_{pl}$ is the I-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation of fuzzy number u, we only show that the Hessian matrix of the function $D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)$ of $m + n$ variables is a positive definite matrix as $(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)=(a_1,a_2,\cdots ,$$a_m,b_1,b_2,\cdots ,b_n)$.

From the expressions of $\frac{\partial D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)}{\partial x_i}(i = 1, 2, \cdots , m)$, which we obtained before, we have that

$$\frac{\partial D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)}{\partial x_1\partial x_k}=\left\{\begin{array}{cc}\frac{1}{3}({\Sigma r_2}^2-{\Sigma r_1}^2),\hfill & k = 1\hfill \\ \frac{1}{3}\Delta r_2^2,\hfill & k = 2\hfill \\ 0,\hfill & k = 3, 4, \cdots , m\hfill \end{array}\right.$$

$$\frac{\partial D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)}{\partial x_i\partial x_k}=\left\{\begin{array}{cc}\frac{1}{3}\Delta r_i^2,\hfill & k = i-1\hfill \\ \frac{1}{3}({\Sigma r_{i+1}}^2-{\Sigma r_i}^2),\hfill & k = i\hfill \\ \frac{1}{3}\Delta r_{i+1}^2,\hfill & k=i+1\hfill \\ 0,\hfill & k = 1, 2, \cdots , i-2, i+2, \cdots , m\hfill \end{array}\right.$$

for $i = 2, 3, \cdots , m-1$, and

$$\frac{\partial D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)}{\partial x_m\partial x_k} =\left\{\begin{array}{cc}\frac{1}{3}\Delta r_m^2,\hfill & k = m-1\hfill \\ \frac{1}{3}({\Sigma r_{m+1}}^2-{\Sigma r_m}^2),\hfill & k = m\hfill \\ 0,\hfill & k = 1, 2, \cdots , m-2\hfill \end{array}\right.$$

From the expressions of $\frac{\partial D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)}{\partial y_j}(j = 1, 2, \cdots , n)$, which we obtained before, we have that

$$\frac{\partial D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)}{\partial y_1\partial y_k} =\left\{\begin{array}{cc}\frac{1}{3}({\Sigma s_2}^2-{\Sigma s_1}^2),\hfill & k = 1\hfill \\ \frac{1}{3}\Delta s_2^2,\hfill & k = 2\hfill \\ 0,\hfill & k = 3, 4, \cdots , n\hfill \end{array}\right.$$

$$\frac{\partial D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)}{\partial y_j\partial y_k} =\left\{\begin{array}{cc}\frac{1}{3}\Delta s_j^2,\hfill & k = j-1\hfill \\ \frac{1}{3}({\Sigma s_{j+1}}^2-{\Sigma s_j}^2),\hfill & k = j\hfill \\ \frac{1}{3}\Delta s_{j+1}^2,\hfill & k = j+1\hfill \\ 0,\hfill & k = 1, 2, \cdots , j-2, j+2, \cdots , n\hfill \end{array}\right.$$

for $j = 2, 3, \cdots , n-1$, and

$$\frac{\partial D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)}{\partial y_n\partial y_k} =\left\{\begin{array}{cc}\frac{1}{3}\Delta s_n^2,\hfill & k = n-1\hfill \\ \frac{1}{3}({\Sigma s_{n+1}}^2-{\Sigma s_n}^2),\hfill & k = n\hfill \\ 0,\hfill & k = 1, 2, \cdots ,n-2\hfill \end{array}\right.$$

Therefore, we can obtain the Hessian matrix of the function $D(x_1,x_2,\cdots ,x_m,y_1,$$y_2,\cdots ,y_n)$ at $(a_1,a_2,\cdots ,a_m,b_1,b_2,\cdots ,b_n)$ as follow:

$$C = \frac{1}{3}\left(\begin{array}{cc}{C}_1& 0\\ 0& C_2\end{array}\right)$$

Since $C_1$ and $C_2$ are all strictly diagonally dominant and real symmetric, C is strictly diagonally dominant and real symmetric. It implies that the eigenvalues of C are all positive values, so C is a positive matrix. Therefore, $(a_1,a_2,\cdots ,a_m,b_1,b_2,\cdots ,b_n)$ is the minimum point of $D(x_1,x_2,\cdots ,x_m,y_1,y_2,\cdots ,y_n)$. Thus, we see that $u_{pl} = PL\left(A^T,{\mathit{r}}^T;B^T,{\mathit{s}}^T\right)$ is the I-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation of fuzzy number u. □

By Proposition 1, we see that for $u\in E$ and $\mathit{r} = (r_0,r_1,r_2,\cdots ,r_m,r_{m+1})$, $\mathit{s} = (s_0,s_1,s_2,\cdots ,s_n,s_{n+1})$ with $0= r_0<r_1<r_2<\cdots <r_m<r_{m+1} =1= s_{n+1}>s_n>\cdots >s_2>s_1>s_0 =0$, the II-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation $v_{pl}$ of fuzzy number u is better than the I-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation $u_{pl}$ of fuzzy number u. In the following, we are going to give the recursion formulas to calculate II-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation. For this purpose, we first give the following notations:

Let $u\in E$ and $0= r_0<r_1<r_2<\cdots <r_m<r_{m+1} =1= s_{n+1}>s_n>\cdots >s_2>s_1>s_0 =0$. We denote

$$\begin{array}{c}\hfill \underline{{\zeta }_i} =\left\{\begin{array}{cc}1,\hfill & i = 0\hfill \\ \frac{\Delta r_{i+1}^2}{{\Sigma r_{i+1}}^2-{\Sigma r_i}^2-\Delta r_i^2\underline{{\zeta }_{i-1}}},\hfill & i = 1, 2, \cdots , m\hfill \end{array}\right.\end{array}$$

(15)

$$\begin{array}{c}\hfill \underline{{\eta }_i} =\left\{\begin{array}{cc}\frac{\underline{{\lambda }_0}}{r_1^2},\hfill & i = 0\hfill \\ \frac{\underline{{\gamma }_i}+\underline{{\lambda }_i}-\Delta r_i^2\underline{{\eta }_{i-1}}}{{\Sigma r_{i+1}}^2-{\Sigma r_i}^2-\Delta r_i^2\underline{{\zeta }_{i-1}}},\hfill & i = 1, 2, \cdots , m\hfill \end{array}\right.\end{array}$$

(16)

where, $\Sigma r_i = r_i + r_{i-1}$, $\Delta r_i^2 = r_i^2 - r_{i-1}^2$, $\underline{{\gamma }_i} = \frac{12}{r_i-r_{i-1}}{\int }_{r_{i-1}}^{r_i}\underline{u}\left(r\right)(r-r_{i-1})rdr$ and $\underline{{\lambda }_i} = \frac{12}{r_{i+1}-r_i}{\int }_{r_i}^{r_{i+1}}\underline{u}\left(r\right)(r_{i+1}-r)rdr$.

$$\begin{array}{c}\hfill \overline{{\zeta }_j} =\left\{\begin{array}{cc}1,\hfill & j = 0\hfill \\ \frac{\Delta s_{j+1}^2}{{\Sigma s_{j+1}}^2-{\Sigma s_j}^2-\Delta s_j^2\overline{{\alpha }_{j-1}}},\hfill & j = 1, 2, \cdots , n\hfill \end{array}\right.\end{array}$$

(17)

$$\begin{array}{c}\hfill \overline{{\eta }_j} =\left\{\begin{array}{cc}\frac{\overline{{\lambda }_0}}{s_1^2},\hfill & j = 0\hfill \\ \frac{\overline{{\gamma }_j}+\overline{{\lambda }_j}-\Delta s_j^2\overline{{\beta }_{j-1}}}{{\Sigma s_{j+1}}^2-{\Sigma s_j}^2-\Delta s_j^2\overline{{\alpha }_{j-1}}},\hfill & j = 1 ,2, \cdots , n\hfill \end{array}\right.\end{array}$$

(18)

where, $\Sigma s_j = s_j + s_{j-1}$, $\Delta s_j^2 = s_j^2 - s_{j-1}^2$, $\overline{{\gamma }_j} = \frac{12}{s_j-s_{j-1}}{\int }_{s_{j-1}}^{s_j}\overline{u}\left(r\right)(r-s_{j-1})rdr$ and $\overline{{\lambda }_j} = \frac{12}{s_{j+1}-s_j}{\int }_{s_j}^{s_{j+1}}\overline{u}\left(r\right)(s_{j+1}-r)rdr$.

Theorem 2.

Let $u\in E$ and $\mathit{r} = (r_0,r_1,r_2,\cdots ,r_m,r_{m+1})$, $\mathit{s} = (s_0,s_1,s_2,\cdots ,s_n,s_{n+1})$ with $0= r_0<r_1<r_2<\cdots <r_m<r_{m+1} =1= s_{n+1}>s_n>\cdots >s_2>s_1>s_0 =0$. If $a_i,b_j\in R(i=0,1,2,\cdots ,m+1,j=0,1,2,\cdots ,n+1)$ are respectively determined by following recursion formulas:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{a}_{m+1} = \frac{\underline{{\gamma }_{m+1}}-\Delta r_{m+1}^2\underline{{\eta }_m}}{(3r_{m+1}+r_m)(r_{m+1}-r_m)-\Delta r_{m+1}^2\underline{{\zeta }_m}}\hfill \\ a_i = \underline{{\eta }_i}-\underline{{\zeta }_i}·a_{i+1}, i = m, m-1, \cdots ,1, 0\hfill \end{array}\right.\end{array}$$

(19)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{b}_{n+1} = \frac{\overline{{\gamma }_{n+1}}-\Delta s_{n+1}^2\overline{{\eta }_n}}{(3s_{n+1}+s_n)(s_{n+1}-s_n)-\Delta s_{n+1}^2\overline{{\zeta }_n}}\hfill \\ b_j = \overline{{\eta }_j} - \overline{{\zeta }_j}·b_{j+1}, j = n-1, n-2, \cdots , 1\hfill \end{array}\right.\end{array}$$

(20)

and satisfy $a_0\le a_1\le a_2\le \cdots \le a_m\le a_{m+1}\le b_n\le b_{n+1}\le \cdots b_2\le b_1\le b_0$, then

$$u_{pl} = PL\left(A^T,{\mathit{r}}^T;B^T,{\mathit{s}}^T\right) = PL\left[\left(\begin{array}{cc}{a}_0& r_0\\ a_1& r_1\\ ⋮& ⋮\\ a_m& r_m\\ a_{m+1}& r_{m+1}\end{array}\right),\left(\begin{array}{cc}{b}_0& s_0\\ b_1& s_1\\ ⋮& ⋮\\ b_m& s_m\\ b_{m+1}& s_{m+1}\end{array}\right)\right]$$

is the II-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation of fuzzy number u, where $A = (a_0,a_1,\cdots a_{m+1})$ and $B = (b_0,b_1,\cdots b_{n+1})$, and $\underline{{\zeta }_i}$, $\underline{{\eta }_i}$, $\overline{{\zeta }_j}$, $\overline{{\eta }_j}$ ($i=0,1,2,\cdots ,m,j=0,1,2,\cdots ,n$) are respectively determined by Formulas (15)–(18).

Proof. 

The Theorem 2 can be proved by the similar method as in Theorem 1. We omit the proof process. □

4. Examples and Comparisons of Some Approximation Methods

In this section, firstly, we compare the new methods with approximation algorithms in [24] by an example. In addition, then, we are going to give a specific example to show the effectiveness and usability of the methods proposed by us in this paper.

Example 1.

Let fuzzy number u be defined as

$$u\left(x\right) =\left\{\begin{array}{cc}\frac{2}{x^2+1} - 1,\hfill & x\in [-1,1]\hfill \\ 0,\hfill & x\notin [-1,1]\hfill \end{array}\right.$$

By the definition of $\underline{u}\left(r\right)$ and $\overline{u}\left(r\right)$, we have that $\underline{u}\left(r\right) = -\sqrt{\frac{2}{r+1}-1}$ and $\overline{u}\left(r\right) = \sqrt{\frac{2}{r+1}-1}$ and $\underline{u}\left(0\right) = -1 ,\underline{u}\left(1\right) = 0, \overline{u}\left(0\right) = 0, \overline{u}\left(1\right) = 1$.

It should be noted that the membership function is left–right symmetric, so for the convenience of observation, we give that the left threshold value set $\mathit{r}$ and the right threshold value set $\mathit{s}$ are equal.

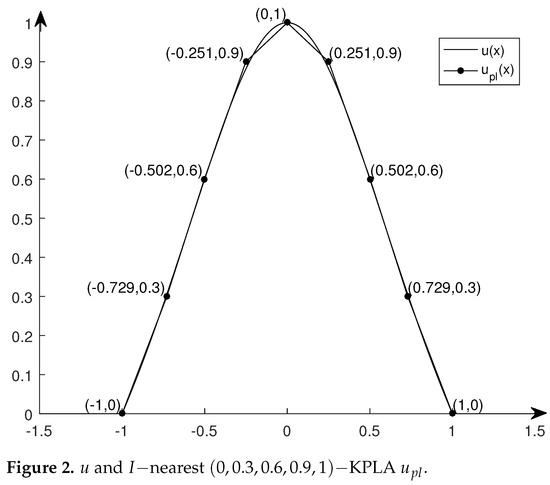
In [24], the authors demonstrated how to approximate the given fuzzy number u by using a multi-knots piecewise linear fuzzy number with respect to metric d. If we take $\mathit{r} = \mathit{s} = (0,0.3,0.6,0.9,1)$, then by the theorem in [24], we have that $A = (-1,-0.729,-0.502,-0.251,0)$ and $B=(1,0.729,0.502,0.251,0)$. Therefore, we know that the piecewise linear fuzzy number (see Figure 2)

$$u_{pl} = PL\left[\left(\begin{array}{cc}-1& 0\\ -0.729& 0.3\\ -0.502& 0.6\\ -0.251& 0.9\\ 0& 1\end{array}\right);\left(\begin{array}{cc}1& 0\\ 0.729& 0.3\\ 0.502& 0.6\\ 0.251& 0.9\\ 0& 1\end{array}\right)\right]$$

is the I-nearest $(0,0.3,0.6,0.9,1)$-knots piecewise linear approximation of fuzzy number u, where $A = (-1,-0.729,-0.502,-0.251,0)$ and $B = (1,0.729,0.502,0.251,0)$.

Figure 2. u and I-nearest $(0,0.3,0.6,0.9,1)$-KPLA $u_{pl}$.

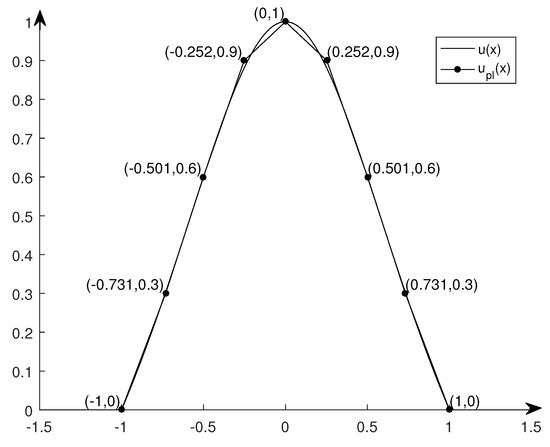
On the other hand, if we apply the methods (Formulas (11) and (12)) proposed in this paper, we can obtain that $A = (-1,-0.731,-0.501,-0.252,0)$ and $B = (1,0.731,$$0.501,0.252,0)$. Therefore, by Theorem 1, we know that the piecewise linear fuzzy number (see Figure 3)

$$u_{pl} = PL\left[\left(\begin{array}{cc}-1& 0\\ -0.731& 0.3\\ -0.501& 0.6\\ -0.252& 0.9\\ 0& 1\end{array}\right);\left(\begin{array}{cc}1& 0\\ 0.731& 0.3\\ 0.501& 0.6\\ 0.252& 0.9\\ 0& 1\end{array}\right)\right]$$

is the I-nearest $(0,0.3,0.6,0.9,1)$ piecewise linear approximation of fuzzy number u, where $A = (-1,-0.731,-0.501,-0.252,0)$ and $B = (1,0.731,0.501,0.252,0)$.

Figure 3. u and I-nearest $(0,0.3,0.6,0.9,1)$ PLA $u_{pl}$.

Remark 1.

Although the approximation effects of the two methods are not significantly different from Figure 2 and Figure 3, it should be admitted that, theoretically, the approximation method using weighted metric $d^{*}$ is better than that using unweighted metric d, and the approximation effect is better with the increase of the level threshold.

Example 2.

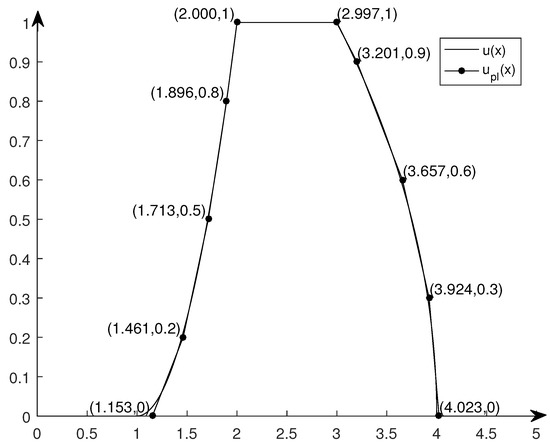
Let fuzzy number u be defined as

$$u\left(x\right) =\left\{\begin{array}{cc}{(x-1)}^2,\hfill & x\in [1,2)\hfill \\ 1,\hfill & x\in [2,3]\hfill \\ \sqrt{4-x},\hfill & x\in (3,4]\hfill \\ 0,\hfill & x\notin [1,4]\hfill \end{array}\right.$$

By the definition of $\underline{u}\left(r\right)$ and $\overline{u}\left(r\right)$, we have that $\underline{u}\left(r\right) = 1 + \sqrt{r}$ and $\overline{u}\left(r\right) = 4-r^2$ and $\underline{u}\left(0\right) = 1, \underline{u}\left(1\right)=2, \overline{u}\left(0\right) = 4, \overline{u}\left(1\right) = 3$.

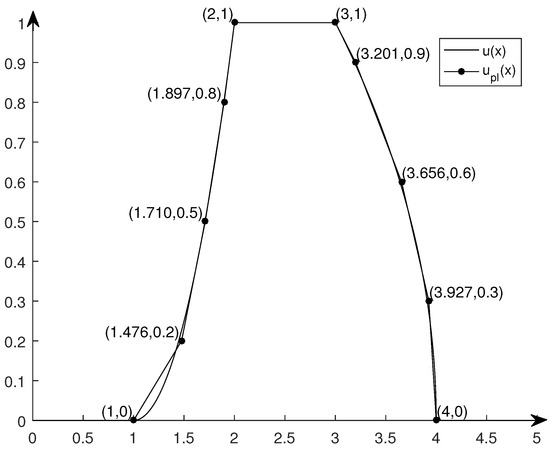
If we take $\mathit{r} = (0,0.2,0.5,0.8,1)$ and $\mathit{s} = (0,0.3,0.6,0.9,1)$, then by Formulas (11) and (12), we have that $A = (1,1.476,1.710,1.897,2)$ and $B = (4,3.927,3.656,3.201,3)$. Therefore, by Theorem 1, we know that the piecewise linear fuzzy number (see Figure 4)

$$u_{pl} = PL\left[\left(\begin{array}{cc}1& 0\\ 1.476& 0.2\\ 1.710& 0.5\\ 1.897& 0.8\\ 2& 1\end{array}\right),\left(\begin{array}{cc}4& 0\\ 3.927& 0.3\\ 3.656& 0.6\\ 3.201& 0.9\\ 3& 1\end{array}\right)\right]$$

is the I-nearest $(0,0.2,0.5,0.8,1)$–$(0,0.3,0.6,0.9,1)$ piecewise linear approximation of fuzzy number u.

Figure 4. u and I-nearest (0,0.2,0.5,0.8,1)–(0,0.3,0.6,0.9,1) PLA $u_{pl}$.

Likewise, by Formulas (19) and (20), we have that $A = (1.153,1.461,1.713,1.896,2.000)$ and $B = (4.023,3.924,3.657,3.201,2.997)$. Therefore, by Theorem 2, we know that the piecewise linear fuzzy number (see Figure 5)

$$u_{pl} = PL\left[\left(\begin{array}{cc}1.153& 0\\ 1.460& 0.2\\ 1.713& 0.5\\ 1.896& 0.8\\ 2.000& 1\end{array}\right),\left(\begin{array}{cc}4.023& 0\\ 3.924& 0.3\\ 3.657& 0.6\\ 3.201& 0.9\\ 2.997& 1\end{array}\right)\right]$$

is the II-nearest $(0,0.2,0.5,0.8,1)$–$(0,0.3,0.6,0.9,1)$ piecewise linear approximation of fuzzy number u.

Figure 5. u and II-nearest (0,0.2,0.5,0.8,1)–(0.3,0.6,0.9,1) PLA $u_{pl}$.

Remark 2.

The difference between the I-nearest r-s piecewise linear approximation (Definition 1) and the II-nearest r-s piecewise linear approximation (Definition 2) is that I-nearest r-s piecewise linear approximation remains the same as the kernel of the original fuzzy number to be approximated, however, the II-nearest r-s piecewise linear approximation re-optimizes the kernel of the approximate solution. Through the comparison of Figure 4 and Figure 5 in Example 2, we know again that the method given in Theorem 2 is better than the method given in Theorem 1 for approximating a general fuzzy number by using piecewise linear fuzzy number.

5. Conclusions and Future Research Directions

In this paper, based on weighted metric $d^{*}$, we give the definition (Definition 1) of I-nearest r-s (with respect to metric $d^{*}$) piecewise linear approximation and II-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation (Definition 2) for a general fuzzy number, and obtain the theorem (Proposition 1) of the relation between the two kinds of r-s piecewise linear approximations. Then, we obtain the method to get the I-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation (Theorem 1) and the II-nearest (with respect to metric $d^{*}$) r-s piecewise linear approximation (Theorem 2) for a general fuzzy number. Finally, we give a specific example to compare the new methods with approximation algorithms with respect to unweighted metric d (Example 1) and another example to show the effectiveness and usability of the methods proposed by us using weighted metric $d^{*}$(Example 2).

In this paper, we establish a method to solve the best approximation when $\mathit{r}$ and $\mathit{s}$ are known. In the future, we can consider establishing a method to approximate a general fuzzy number with a simple fuzzy number when $\mathit{r}$ and $\mathit{s}$ are unknown. In addition, we can also discuss the approximation of high-dimensional fuzzy numbers.