Stochastic Approximate Algorithms for Uncertain Constrained K-Means Problem

Abstract

The k-means problem has been paid much attention for many applications. In this paper, we define the uncertain constrained k-means problem and propose a $(1+ϵ)$-approximate algorithm for the problem. First, a general mathematical model of the uncertain constrained k-means problem is proposed. Second, the random sampling properties of the uncertain constrained k-means problem are studied. This paper mainly studies the gap between the center of random sampling and the real center, which should be controlled within a given range with a large probability, so as to obtain the important sampling properties to solve this kind of problem. Finally, using mathematical induction, we assume that the first $j-1$ cluster centers are obtained, so we only need to solve the j-th center. The algorithm has the elapsed time $O({(\frac{1891ek}{{ϵ}^2})}^{8k/ϵ}nd)$, and outputs a collection of size $O({(\frac{1891ek}{{ϵ}^2})}^{8k/ϵ}n)$ of candidate sets including approximation centers.

1. Introduction

The k-means problem has received much attention in the past several decades. The k-means problems consists of partitioning a set P of points in d-dimensional space ${\mathbb{R}}^d$ into k subsets $P_1,\dots ,P_k$ such that ${\sum }_{i=1}^k{\sum }_{p\in P_i}\left|\right|p-c_i{\left|\right|}^2$ is minimized, where $c_i$ is the center of $P_i$, and $\left|\right|p-q\left|\right|$ is the distance between two points of p and q. The k-means problem is one of the classical NP-hard problems, and has been paid much attention in the literature [1,2,3].

For many applications, each cluster of the point set may satisfy some additional constraints, such as chromatic clustering [4], r-capacity clustering [5], r-gather clustering [6], fault tolerant clustering [7], uncertain data clustering [8], semi-supervised clustering [9], and l-diversity clustering [10]. The constrained clustering problems was studied by Ding and Xu, who presented the first unified framework in [11]. Given a point set $P\subseteq {\mathbb{R}}^d$, and a positive integer k, a list of constraints $\mathbb{L}$, the constrained k-means problem is to partition P into k clusters $\mathbb{P}=\{P_1,\dots ,P_k\}$, such that all constraints in $\mathbb{L}$ are satisfied and ${\sum }_{P_i\in \mathbb{P}}{\sum }_{x\in P_i}\left|\right|x-c(P_i){\left|\right|}^2$ is minimized, where $c(P_i)=\frac{1}{|P_i|}{\sum }_{x\in P_i}x$ denotes the centroid of $P_i$.

In recent years, particular research has been focused on the constrained k-means problem. Ding and Xu [11] showed the first polynomial time approximation scheme with running time $O(2^{poly(k/ϵ)}{(logn)}^{k}nd)$ for the constrained k-means problem, and obtained a collection of size $O(2^{poly(k/ϵ)}{(logn)}^{k+1})$ of candidate approximate centers. The existing fastest approximation schemes for the constrained k-means problem takes $O(2^{O(k/ϵ)}nd)$ time [12,13], which was first shown by Bhattacharya, Jaiswai, and Kumar [12]. Their algorithm gives a collection of size $O(2^{O(k/ϵ)})$ of candidate approximate centers. In this paper, we propose the uncertain constrained k-means problem, which supposes that all points are random variables with probabilistic distributions. We present a stochastic approximate algorithm for the uncertain constrained k-means problem. The uncertain constrained k-means problem can be regarded as a generalization of the constrained k-means problem. We prove the random sampling properties of the uncertain constrained k-means problem, which are fundamental for our proposed algorithm. By applying random sampling and mathematical induction, we propose a stochastic approximate algorithm with lower complexity for the uncertain constrained k-means problem.

This paper is organized as follows. Some basic notations are given in Section 2. Section 3 provides an overview of the new algorithm for the uncertain constrained k-means problem. In Section 4, we discuss the detailed algorithm for the uncertain constrained k-means problem. In Section 5, we investigate the correctness, success probability, and running time analysis of the algorithm. Section 6 concludes this paper and gives possible directions for future research.

2. Preliminaries

Definition 1

(Uncertain constrained k-means problem). Given a random variable set $\mathcal{X}\subseteq {\mathbb{R}}^d$, the probability density function $f_X(s)$ for every random variable $X\in \mathcal{X}$, a list of constraints $\mathbb{L}$, and a positive integer k, the uncertain constrained k-means problem is to partition $\mathcal{X}$ into k clusters $\mathbb{X}=\{{\mathcal{X}}_1,\dots ,{\mathcal{X}}_k\}$, such that all constraints in $\mathbb{L}$ are satisfied and ${\sum }_{{\mathcal{X}}_i\in \mathbb{X}}{\sum }_{X\in {\mathcal{X}}_i}{\int }^{{\mathbb{R}}^d}\left|\right|s-c({\mathcal{X}}_i){\left|\right|}^2{f}_X(s)ds$ is minimized, where $c({\mathcal{X}}_i)=\frac{1}{|{\mathcal{X}}_i|}{\sum }_{X\in {\mathcal{X}}_i}{\int }^{{\mathbb{R}}^d}s{f}_X(s)ds$ denotes the centroid of ${\mathcal{X}}_i$.

Definition 2

([13]). Let $\mathcal{X}$ be a set of random variables in ${\mathbb{R}}^d$, $f_X(s)$ be probability density function for every random variable $X\in \mathcal{X}$, and $q\in {\mathbb{R}}^d$ and P be a set of points in ${\mathbb{R}}^d$, $p\in P$.

• Define $f_2(q,\mathcal{X})={\sum }_{X\in \mathcal{X}}{\int }^{{\mathbb{R}}^d}\left|\right|s-{q\left|\right|}^2{f}_X(s)ds$.
• Define $c(\mathcal{X})=\frac{1}{\left|\mathcal{X}\right|}{\sum }_{X\in \mathcal{X}}{\int }^{{\mathbb{R}}^d}s{f}_X(s)ds$.
• Define $dist(X,P)=mi{n}_{p\in P}{\int }^{{\mathbb{R}}^d}\left|\right|s-p\left|\right|f_X(s)ds$.

Definition 3

([13]). Let $\mathcal{X}$ be a set of random variables in ${\mathbb{R}}^d$, $f_X(s)$ be the probability density function for every random variable $X\in \mathcal{X}$, and ${\mathcal{X}}_1,\dots ,{\mathcal{X}}_k$ be a partition of $\mathcal{X}$.

• Define $m_j=c({\mathcal{X}}_j)$.
• ${\beta }_j=\frac{|{\mathcal{X}}_j|}{\left|\mathcal{X}\right|}$.
• Define ${\sigma }_j=\sqrt{\frac{f_2(m_j,{\mathcal{X}}_j)}{|{\mathcal{X}}_j|}}$.
• Define
  $OP{T}_k(\mathcal{X})={\sum }_{j=1}^k{\sum }_{X\in {\mathcal{X}}_j}{\int }^{{\mathbb{R}}^d}\left|\right|s-c({\mathcal{X}}_j){\left|\right|}^2{f}_X(s)ds={\sum }_{j=1}^k{f}_2(m_j,{\mathcal{X}}_j)$.
• Define ${\sigma }_{opt}=\sqrt{\frac{OP{T}_k(\mathcal{X})}{\left|\mathcal{X}\right|}}=\sqrt{{\sum }_{i=1}^k{\beta }_i{\sigma }_i^2}$.

Lemma 1.

For any point $x\in {\mathbb{R}}^d$ and a random variable set $\mathcal{X}\subseteq {\mathbb{R}}^d$, $f_2(x,\mathcal{X})=f_2(c(\mathcal{X}),\mathcal{X})+\left|\mathcal{X}\right|\left|\right|c(\mathcal{X})-{x\left|\right|}^2$.

Proof. 

Let $f_X(s)$ be the probability density function for every random variable $X\in \mathcal{X}$.

$$\begin{array}{}\mathrm{(1)}& f_2(x,\mathcal{X})\hfill & =\sum _{X\in \mathcal{X}}{\int }^{{\mathbb{R}}^d}\left|\right|s-{x\left|\right|}^2{f}_X(s)ds\hfill \mathrm{(2)}& \hfill & =\sum _{X\in \mathcal{X}}{\int }^{{\mathbb{R}}^d}\left|\right|s-c(\mathcal{X})+c(\mathcal{X})-{x\left|\right|}^2{f}_X(s)ds\hfill \mathrm{(3)}& \hfill & =\sum _{X\in \mathcal{X}}{\int }^{{\mathbb{R}}^d}\left|\right|s-{c(\mathcal{X})\left|\right|}^2{f}_X(s)ds+\sum _{X\in \mathcal{X}}{\int }^{{\mathbb{R}}^d}\left|\right|c(\mathcal{X})-{x\left|\right|}^2{f}_X(s)ds\hfill \mathrm{(4)}& \hfill & =f_2(c(\mathcal{X}),\mathcal{X})+\left|\right|c(\mathcal{X})-{x\left|\right|}^2\sum _{X\in \mathcal{X}}{\int }^{{\mathbb{R}}^d}{f}_X(s)ds\hfill \mathrm{(5)}& \hfill & =f_2(c(\mathcal{X}),\mathcal{X})+\left|\mathcal{X}\right|\left|\right|c(\mathcal{X})-{x\left|\right|}^2.\hfill \end{array}$$

The (3) equality follows from the fact that ${\sum }_{X\in \mathcal{X}}{\int }^{{\mathbb{R}}^d}(s-c(\mathcal{X}))f_X(s)ds=0$.    □

Lemma 2.

Let $\mathcal{X}$ be a set of random variables in ${\mathbb{R}}^d$ and $f_X(s)$ be the probability density function for every random variable $X\in \mathcal{X}$. Assume that $\mathcal{T}$ is a set of random variables obtained by sampling random variables from $\mathcal{X}$ uniformly and independently. For ∀$\mathsf{\delta }>0$, we have:

$$Pr(||c(\mathcal{T})-c(\mathcal{X})|{|}^2>\frac{1}{\mathsf{\delta }|\mathcal{T}|}{\sigma }^2)<\mathsf{\delta },$$

(6)

where ${\sigma }^2=\frac{1}{\left|\mathcal{X}\right|}{\sum }_{X\in \mathcal{X}}{\int }^{{\mathbb{R}}^d}\left|\right|s-{c(\mathcal{X})\left|\right|}^2{f}_X(s)ds$.

Proof. 

First, observe that

$$E(c(\mathcal{T}))=c(\mathcal{X}),E(||c(\mathcal{T})-{c(\mathcal{X})\left|\right|}^2)=\frac{1}{\left|\mathcal{T}\right|}{\sigma }^2$$

(7)

where ${\sigma }^2=\frac{1}{\left|\mathcal{X}\right|}{\sum }_{X\in \mathcal{X}}{\int }^{{\mathbb{R}}^d}\left|\right|s-{c(\mathcal{X})\left|\right|}^2{f}_X(s)ds$. Then apply the Markov inequality to obtain the following.

$$Pr(||c(\mathcal{T})-c(\mathcal{X})|{|}^2>\frac{1}{\mathsf{\delta }|\mathcal{T}|}{\sigma }^2)<\mathsf{\delta }.$$

(8)

   □

Lemma 3.

Let $\mathcal{Q}$ be a set of random variables in ${\mathbb{R}}^d$, $f_X(s)$ be the probability density function for every random variable $X\in \mathcal{Q}$, and ${\mathcal{Q}}_1$ be an arbitrary subset of $\mathcal{Q}$ with $\alpha \left|\mathcal{Q}\right|$ random variables for some $0<\alpha \le 1$. Then $\left|\right|c(\mathcal{Q})-c({\mathcal{Q}}_1)\left|\right|\le \sqrt{\frac{1-\alpha }{\alpha }}\sigma$, where ${\sigma }^2=\frac{1}{\left|\mathcal{Q}\right|}{\sum }_{X\in \mathcal{Q}}{\int }^{{\mathbb{R}}^d}\left|\right|s-{c(\mathcal{Q})\left|\right|}^2{f}_X(s)ds$.

Proof. 

Let ${\mathcal{Q}}_2=\mathcal{Q}\backslash {\mathcal{Q}}_1$. By Lemma 1, we have the following two equalities.

$$f_2(c(\mathcal{Q}),{\mathcal{Q}}_1)=f_2(c({\mathcal{Q}}_1),{\mathcal{Q}}_1)+|{\mathcal{Q}}_1\left|\right||c({\mathcal{Q}}_1)-{c(\mathcal{Q}||}^2,$$

(9)

$$f_2(c(\mathcal{Q}),{\mathcal{Q}}_2)=f_2(c({\mathcal{Q}}_2),{\mathcal{Q}}_2)+|{\mathcal{Q}}_2\left|\right||c({\mathcal{Q}}_2)-{c(\mathcal{Q}||}^2.$$

(10)

Let $L=\left|\right|c({\mathcal{Q}}_1)-c({\mathcal{Q}}_2)\left|\right|$. By the definition of the mean point, we have:

$$c(\mathcal{Q})=\frac{1}{\left|\mathcal{Q}\right|}\sum _{X\in \mathcal{Q}}{\int }^{{\mathbb{R}}^d}s{f}_X(s)ds=\frac{1}{\left|\mathcal{Q}\right|}(|{\mathcal{Q}}_1|c({\mathcal{Q}}_1)+|{\mathcal{Q}}_2|c({\mathcal{Q}}_2)).$$

(11)

Thus, the three points $\{c(\mathcal{Q}),c({\mathcal{Q}}_1),c({\mathcal{Q}}_2)\}$ are collinear, while $\left|\right|c({\mathcal{Q}}_1)-c(\mathcal{Q})\left|\right|=(1-\alpha )L$ and $\left|\right|c({\mathcal{Q}}_2)-c(\mathcal{Q})\left|\right|=\alpha L$. Meanwhile, by the definition of $\sigma$, we have ${\sigma }^2=\frac{1}{\left|\mathcal{Q}\right|}({\sum }_{X\in {\mathcal{Q}}_1}{\int }^{{\mathbb{R}}^d}\left|\right|s-{c(\mathcal{Q})\left|\right|}^2{f}_X(s)ds+{\sum }_{X\in {\mathcal{Q}}_2}{\int }^{{\mathbb{R}}^d}\left|\right|s-{c(\mathcal{Q})\left|\right|}^2{f}_X(s)ds)$. Combining Equality (9) and Equality (10), we have:

$$\begin{array}{}\mathrm{(12)}\hfill & {\sigma }^2\hfill & \ge \frac{1}{\left|\mathcal{Q}\right|}(|{\mathcal{Q}}_1\left|\right||c({\mathcal{Q}}_1)-{c(\mathcal{Q}||}^2+|{\mathcal{Q}}_2\left|\right||c({\mathcal{Q}}_2)-{c(\mathcal{Q}||}^2)\hfill \mathrm{(13)}\hfill & \hfill & =\alpha {((1-\alpha )L)}^2+(1-\alpha ){(\alpha L)}^2\hfill \mathrm{(14)}\hfill & \hfill & =\alpha (1-\alpha )L^2.\hfill \end{array}$$

Thus, we have $L\le \frac{\sigma }{\sqrt{\alpha (1-\alpha )}}$, which means that $\left|\right|c(\mathcal{Q})-c({\mathcal{Q}}_1)\left|\right|=(1-\alpha )L\le \sqrt{\frac{1-\alpha }{\alpha }}\sigma$.    □

Lemma 4

([12]). For any $x,y,z\in {\mathbb{R}}^d$, then $\left|\right|x-{z\left|\right|}^2\le 2\left|\right|x-{y\left|\right|}^2+2\left|\right|y-{z\left|\right|}^2$.

Theorem 1

([14]). Let $X_1,\dots ,X_s$ be s, an independent random $0-1$ variable, where $X_i$ takes 1 with a probability of at least p for $i=1,\dots ,s$. Let $X={\sum }_{i=1}^s{X}_i$. Then, for any $\mathsf{\delta }>0$, $Pr(X<(1-\mathsf{\delta })ps)<e^{-\frac{1}{2}{\mathsf{\delta }}^{2}ps}$.

3. Overview of Our Method

In this section, we first introduce the main idea of our methodology to solve the uncertain constrained k-means problem.

Considering the optimal partition $\mathbb{X}=\{{\mathcal{X}}_1,\dots ,{\mathcal{X}}_k\}(|{\mathcal{X}}_1|\ge \dots \ge |{\mathcal{X}}_k|)$ of $\mathcal{X}$, since $|{\mathcal{X}}_1|/|\mathcal{X}|\ge 1/k$, if we could sample a set $\mathcal{S}$ of size $O(k/ϵ)$ from $\mathcal{X}$ uniformly and independently, then at least $O(1/ϵ)$ random variables in $\mathcal{S}$ are from ${\mathcal{X}}_1$ with a certain probability. All subsets of $\mathcal{S}$ of size $O(1/ϵ)$ could be enumerated to discover the approximate center of ${\mathcal{X}}_1$.

We assume that $C_{j-1}=\{c_1,\dots ,c_{j-1}\}$ is the set including approximate centers of the ${\mathcal{X}}_1,\dots ,{\mathcal{X}}_j$. Let ${\mathcal{B}}_j=\{X\in \mathcal{X}|dist(X,C_{j-1})=mi{n}_{c\in C_{j-1}}{\int }^{{\mathbb{R}}^d}\left|\right|s-c\left|\right|f_X(s)ds\le r_j\}$, where $r_j=\sqrt{\frac{ϵ}{40{\beta }_{j}k}}{\sigma }_{opt}$. The set ${\mathcal{X}}_j$ is divided into two parts: ${\mathcal{X}}_j^{out}$ and ${\mathcal{X}}_j^{in}$, where ${\mathcal{X}}_j^{out}={\mathcal{X}}_j\backslash {\mathcal{B}}_j$ and ${\mathcal{X}}_j^{in}={\mathcal{X}}_j\cap {\mathcal{B}}_j$. For each random variable X, let $\tilde{X}$ be the nearest point (particular random variable) in $C_{j-1}$ to X. Let ${\tilde{\mathcal{X}}}_j^{in}=\left\{\tilde{X}\right|X\in {\mathcal{X}}_j^{in}\}$, and ${\tilde{\mathcal{X}}}_j={\tilde{\mathcal{X}}}_j^{in}\cup {\mathcal{X}}_j^{out}$.

If most of the random variables of ${\mathcal{X}}_j$ are in ${\mathcal{X}}_j^{in}$, our idea is to use the center of ${\tilde{\mathcal{X}}}_j^{in}$ to approximate the center of ${\mathcal{X}}_j$. The center of ${\tilde{\mathcal{X}}}_j^{in}$ is found based on $C_{j-1}$. If most of the random variables of ${\mathcal{X}}_j$ are in ${\mathcal{X}}_j^{out}$, our ideal is to replace the center of ${\mathcal{X}}_j$ with the center of ${\tilde{\mathcal{X}}}_j$. For seeking out the approximate center of ${\tilde{\mathcal{X}}}_j$, we should find out a subset ${\mathcal{S}}^{\prime }$ by uniformly sampling from ${\tilde{\mathcal{X}}}_j$. However, the set ${\mathcal{X}}_j^{out}$ is unknown. We need to find the set ${\mathcal{S}}^{\prime }\cap {\mathcal{X}}_j^{out}$. We apply a branching strategy to find a set $\mathcal{Q}$ such that $\mathcal{X}\backslash {\mathcal{B}}_j\subseteq \mathcal{Q}$, and $\left|\mathcal{Q}\right|<2|\mathcal{X}\backslash {\mathcal{B}}_j|$. Then, a random variables set $\mathcal{S}$ is obtained by sampling random variables from $\mathcal{Q}$ independently and uniformly. And the set $\mathcal{X}\backslash {\mathcal{B}}_j\subseteq \mathcal{Q}$ can be replaced by a subset ${\mathcal{S}}^{*}$ of $\mathcal{S}$ from ${\mathcal{X}}_j^{out}$. Based on ${\mathcal{S}}^{*}$ and ${\tilde{\mathcal{X}}}_j^{in}$, the approximation center of ${\tilde{\mathcal{X}}}_j$ could be obtained. Therefore, the algorithm presented in this paper outputs a collection of size $O({(\frac{1891ek}{{ϵ}^2})}^{8k/ϵ}n)$ of candidate sets containing approximation centers, and has the running time $O({(\frac{1891ek}{{ϵ}^2})}^{8k/ϵ}nd)$.

4. Our Algorithm cMeans

Given an instance $(\mathcal{X},k,\mathbb{L})$ of the uncertain constrained k-means problem, $\mathbb{X}=\{{\mathcal{X}}_1,\dots ,{\mathcal{X}}_k\}$ denotes an optimal partition of $(\mathcal{X},k,\mathbb{L})$. There exist six parameters ($ϵ$, $\mathcal{Q}$, g, k, C, U) in our $\mathbf{cMeans}$, where $ϵ\in (0,1]$ is the approximate factor, $\mathcal{Q}$ is the input random variable set, g is the number of centers, k is the number of the clusters, C is the set of approximate cluster centers, and U is a collection of candidate sets including the approximate center. Let $M=\frac{6}{ϵ},N=\frac{79,380k}{{ϵ}^3}$, where M is the size of subsets of the sampling set and N is the size of the sampling set. Without loss of generality, assume that values of M and N are integers.

We use the branching strategy to seek out the approximate centers of clusters in $\mathbb{X}$. There exist two branches in our algorithm $\mathbf{cMeans}$, which can be seen in Figure 1. On one branch, a size N set ${\mathcal{S}}_1$ is obtained by sampling from $\mathcal{Q}$ uniformly and independently; ${\mathcal{S}}_2$ is constructed by ${\mathcal{S}}_1$ and M copies of each point in C. Moreover, we consider each subset ${\mathcal{S}}^{\prime }$ of size M of ${\mathcal{S}}_2$, and the centroid c of ${\mathcal{S}}^{\prime }$ is solved to represent the approximate center of ${\mathcal{X}}_{k-g+1}$, and our algorithm $\mathbf{cMeans}$($ϵ,\mathcal{Q},g-1,k,C\cup \left\{c\right\},U$) is used to obtain the remaining $g-1$ cluster centers.

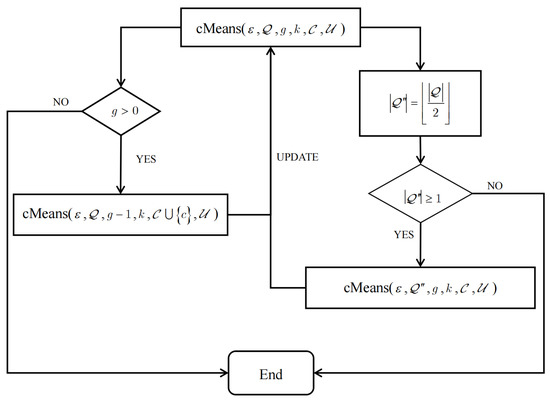
Figure 1. Flow chart of our algorithm $\mathbf{cMeans}$.

On the other branch, for each random variable $X\in \mathcal{Q}$, we calculate the distance between X and C first. H denotes the set of all distances of random variables in $\mathcal{X}$ to C, where H is a multi-set. We should obtain the median value m for all values in H, which is the $\lfloor \left|H\right|/2\rfloor$-th element if all of the values in H are sorted. In the second branch, $\mathcal{Q}$ is divided into two parts, ${\mathcal{Q}}^{\prime }$ and ${\mathcal{Q}}^{″}$, based on m such that for $\forall X^{\prime }\in {\mathcal{Q}}^{\prime }$, $X^{″}\in {\mathcal{Q}}^{″}$, $dist(X^{\prime },C)\le dist(X^{″},C)$, where $|{\mathcal{Q}}^{\prime }|=\lceil \frac{|\mathcal{Q}|}{2}\rceil$, $|{\mathcal{Q}}^{″}|=\lfloor \frac{|\mathcal{Q}|}{2}\rfloor$. Subroutine $\mathbf{cMeans}$($ϵ,{\mathcal{Q}}^{″},g,k,C,U$) is used to obtain the remaining g cluster centers. Therefore, we present the specific algorithm for seeking out a collection of candidate sets in the Algorithm 1.

Algorithm 1:$\mathbf{cMeans}$($ϵ,\mathcal{Q},g,k,C,U$)

5. Analysis of Our Algorithm $\mathbf{cMeans}$

We investigate the success probability, correctness, and time complexity analysis of the algorithm $\mathbf{cMeans}$ in this section.

Lemma 5.

There exists a candidate set, with a probability of at least $1/{12}^k$, including the approximate center $C_k=\{c_1,\dots ,c_k\}$ in U satisfying $\left|\right|m_j-c_j{\left|\right|}^2\le \frac{9}{10}ϵ{\sigma }_j^2+\frac{1}{10{\beta }_{j}k}ϵ{\sigma }_{opt}^2(1\le j\le k)$.

The following Lemmas from Lemma 6 to 16 are used to prove Lemma 5. We prove Lemma 5 via induction on j. For $j=1$, we can obtain ${\beta }_1\ge 1/k$ easily, and prove the success probability first.

Lemma 6.

In the process of finding $c_1$ in our algorithm $\mathit{cMeans}$, by sampling a set of $\mathrm{79,380}k/{ϵ}^3$ random variables from $\mathcal{X}$ independently and uniformly, denoted by ${\mathcal{S}}_1$, the probability that at least $6/ϵ$ random variables in ${\mathcal{S}}_2$ are from ${\mathcal{X}}_1$ is at least $1/2$.

Proof. 

In our algorithm $\mathbf{cMeans}$, we assume that ${\mathcal{S}}_1=S_1,\dots ,S_N$, where $N=\mathrm{79,380}k/{ϵ}^3$. Let $x_1^{{}^{\prime }},\dots ,x_N^{{}^{\prime }}$ be the corresponding random variables of elements in ${\mathcal{S}}_1$. If $S_i\in {\mathcal{X}}_1$, then $x_i^{{}^{\prime }}=1$. Otherwise $x_i^{{}^{\prime }}=0$. It is known easily that $Pr[S_i\in {\mathcal{X}}_1]\ge \frac{1}{k}$. Let $x={\sum }_{i=1}^N{x}_i^{{}^{\prime }},u={\sum }_{i=1}^{N}E(x_i^{{}^{\prime }})$. We obtain that $u\ge \mathrm{79,380}k/{ϵ}^3$. Then,

$$\begin{array}{}\mathrm{(15)}& \hfill Pr[x>\frac{6}{ϵ}]& =1-Pr[x\le \frac{6}{ϵ}]\hfill \mathrm{(16)}& \hfill & =1-Pr[x\le \frac{6{ϵ}^2}{\mathrm{79,380}}\frac{\mathrm{79,380}}{{ϵ}^3}]\hfill \mathrm{(17)}& \hfill & \ge 1-Pr[x\le \frac{{ϵ}^2}{\mathrm{13,230}}u]\hfill \mathrm{(18)}& \hfill & \ge 1-e^{-\frac{{(1-\frac{{ϵ}^2}{\mathrm{13,230}})}^{2}u}{2}}\hfill \mathrm{(19)}& \hfill & \ge 1-e^{-\frac{{(1-\frac{{ϵ}^2}{\mathrm{13,230}})}^2\frac{\mathrm{79,380}}{{ϵ}^3}}{2}}\hfill \mathrm{(20)}& \hfill & \ge 1-e^{-\frac{{(1-\frac{1}{\mathrm{13,230}})}^2·\mathrm{79,380}}{2}}\hfill \mathrm{(21)}& \hfill & \ge \frac{1}{2}.\hfill \end{array}$$

□

From Lemma 6, an ${\mathcal{S}}^{*}$ with size $6/ϵ$ of ${\mathcal{S}}_2$ can be obtained, and the probability that all points in ${\mathcal{S}}^{*}$ are from ${\mathcal{X}}_1$ is at least $1/2$. Let $c_1$ denote the centroid of ${\mathcal{S}}^{*}$, and $\mathsf{\delta }=5/6$. For $|{\mathcal{S}}^{*}|=6/ϵ$, by Lemma 2, we conclude that $\left|\right|m_1-c_1{\left|\right|}^2\le \frac{1}{5}ϵ{\sigma }_1^2$ holds with a probability of at least $1/6$. Then, the probability that a subset ${\mathcal{S}}^{*}$ of size $6/ϵ$ of ${\mathcal{S}}_2$ can be found such that $\left|\right|m_1-c_1{\left|\right|}^2\le \frac{1}{5}ϵ{\sigma }_1^2\le \frac{9}{10}ϵ{\sigma }_1^2+\frac{1}{10{\beta }_{1}k}ϵ{\sigma }_{opt}^2$ holds is at least $1/12$. Therefore, we conclude that Lemma 5 holds for $j=1$.

Moreover, we assume that for $j\le j_0(1\le j_0)$, Lemma 5 holds with a probability of at least $1/{12}^j$. Considering the case $j=j_0+1$, we prove Lemma 5 by the following two cases: (1)$|{\mathcal{X}}_j^{out}|\le \frac{ϵ}{49}{\beta }_{j}n$; (2)$|{\mathcal{X}}_j^{out}|>\frac{ϵ}{49}{\beta }_{j}n$.

5.1. Analysis for Case 1: $|{\mathcal{X}}_j^{out}|\le \frac{ϵ}{49}{\beta }_{j}n$

Since $|{\mathcal{X}}_j^{out}|\le \frac{ϵ}{49}{\beta }_{j}n$, most of the random variables of ${\mathcal{X}}_j$ are in ${\mathcal{B}}_j$. Our idea is to replace the center of ${\mathcal{X}}_j$ with the center of ${\tilde{\mathcal{X}}}_j^{in}$. Thus, we need to find the approximate center $c_j$ of ${\tilde{\mathcal{X}}}_j^{in}$ and the bound distance $\left|\right|m_j-c_j\left|\right|$. We divide the distance $\left|\right|m_j-c_j\left|\right|$ into the following three parts: $\left|\right|m_j-m_j^{in}\left|\right|$, $\left|\right|m_j^{in}-{\tilde{m}}_j^{in}\left|\right|$, and $\left|\right|{\tilde{m}}_j^{in}-c_j\left|\right|$. We first study the distance between $m_j$ and $m_j^{in}$.

Lemma 7.

$\left|\right|m_j-m_j^{in}\left|\right|\le \sqrt{\frac{ϵ}{48}}{\sigma }_j$.

Proof. 

Since $|{\mathcal{X}}_j|={\beta }_{j}n$ and $|{\mathcal{X}}_j^{out}|\le \frac{ϵ}{49}{\beta }_{j}n$, the proportion of ${\mathcal{X}}_j^{in}$ in ${\mathcal{X}}_j$ is at least $1-\frac{ϵ}{49}$. By Lemma 3, $\left|\right|m_j-m_j^{in}\left|\right|\le \sqrt{\frac{ϵ/49}{1-ϵ/49}}{\sigma }_j\le \sqrt{\frac{ϵ}{48}}{\sigma }_j$. □

Lemma 8.

$\left|\right|m_j^{in}-{\tilde{m}}_j^{in}\left|\right|\le r_j$.

Proof. 

Since $m_j^{in}=\frac{1}{|{\mathcal{X}}_j^{in}|}{\sum }_{X\in {\mathcal{X}}_j^{in}}{\int }^{{\mathbb{R}}^d}s{f}_X(s)ds$, and ${\tilde{m}}_j^{in}=\frac{1}{|{\mathcal{X}}_j^{in}|}{\sum }_{X\in {\mathcal{X}}_j^{in}}\tilde{X}$, we can obtain the following:

$$\begin{array}{}\mathrm{(22)}& \left|\right|m_j^{in}-{\tilde{m}}_j^{in}\left|\right|\hfill & =\left|\right|\frac{1}{|{\mathcal{X}}_j^{in}|}\sum _{X\in {\mathcal{X}}_j^{in}}{\int }^{{\mathbb{R}}^d}s{f}_X(s)ds-\frac{1}{|{\mathcal{X}}_j^{in}|}\sum _{X\in {\mathcal{X}}_j^{in}}\tilde{X}\left|\right|\hfill \mathrm{(23)}& \hfill & =\frac{1}{|{\mathcal{X}}_j^{in}|}\left|\right|\sum _{X\in {\mathcal{X}}_j^{in}}{\int }^{{\mathbb{R}}^d}(s-\tilde{X})f_X(s)ds\left|\right|\hfill \mathrm{(24)}& \hfill & \le \frac{1}{|{\mathcal{X}}_j^{in}|}\sum _{X\in {\mathcal{X}}_j^{in}}{\int }^{{\mathbb{R}}^d}\left|\right|s-\tilde{X}\left|\right|f_X(s)ds\hfill \mathrm{(25)}& \hfill & \le \frac{1}{|{\mathcal{X}}_j^{in}|}\sum _{X\in {\mathcal{X}}_j^{in}}{r}_j\hfill \mathrm{(26)}& \hfill & =r_j.\hfill \end{array}$$

□

Lemma 9.

$f_2({\tilde{m}}_j^{in},{\tilde{\mathcal{X}}}_j^{in})\le 2|{\mathcal{X}}_j^{in}|r_j^2+2f_2(m_j,{\mathcal{X}}_j^{in})-|{\mathcal{X}}_j^{in}\left|\right||m_j-{\tilde{m}}_j^{in}{\left|\right|}^2$.

Proof. 

Since $|{\tilde{\mathcal{X}}}_j^{in}|=|{\mathcal{X}}_j^{in}|$, by 1, we have $f_2(m_j,{\tilde{\mathcal{X}}}_j^{in})=f_2({\tilde{m}}_j^{in},{\tilde{\mathcal{X}}}_j^{in})+|{\mathcal{X}}_j^{in}\left|\right||{\tilde{m}}_j^{in}-m_j\left|\right|$. Then,

$$\begin{array}{}\mathrm{(27)}& f_2({\tilde{m}}_j^{in},{\tilde{\mathcal{X}}}_j^{in})\hfill & =f_2(m_j,{\tilde{\mathcal{X}}}_j^{in})-|{\mathcal{X}}_j^{in}\left|\right||{\tilde{m}}_j^{in}-m_j{\left|\right|}^2\hfill \mathrm{(28)}& \hfill & =\sum _{X\in {\mathcal{X}}_j^{in}}\left|\right|\tilde{X}-m_j{\left|\right|}^2-|{\mathcal{X}}_j^{in}\left|\right||m_j-{\tilde{m}}_j^{in}{\left|\right|}^2\hfill \mathrm{(29)}& \hfill & =\sum _{X\in {\mathcal{X}}_j^{in}}{\int }^{{\mathbb{R}}^d}\left|\right|\tilde{X}-m_j{\left|\right|}^2{f}_X(s)ds-|{\mathcal{X}}_j^{in}\left|\right||m_j-{\tilde{m}}_j^{in}{\left|\right|}^2\hfill \mathrm{(30)}& \hfill & =\sum _{X\in {\mathcal{X}}_j^{in}}{\int }^{{\mathbb{R}}^d}\left|\right|\tilde{X}-s+s-m_j{\left|\right|}^2{f}_X(s)ds-|{\mathcal{X}}_j^{in}\left|\right||m_j-{\tilde{m}}_j^{in}{\left|\right|}^2\hfill \mathrm{(31)}& \hfill & \le \sum _{X\in {\mathcal{X}}_j^{in}}{\int }^{{\mathbb{R}}^d}(2||\tilde{X}-{s\left|\right|}^2+2\left|\right|s-m_j{\left|\right|}^2)f_X(s)ds-|{\mathcal{X}}_j^{in}\left|\right||m_j-{\tilde{m}}_j^{in}{\left|\right|}^2\hfill \mathrm{(32)}& \hfill & \le 2|{\mathcal{X}}_j^{in}|r_j^2+2\sum _{X\in {\mathcal{X}}_j^{in}}{\int }^{{\mathbb{R}}^d}\left|\right|s-m_j{\left|\right|}^2{f}_X(s)ds-|{\mathcal{X}}_j^{in}\left|\right||m_j-{\tilde{m}}_j^{in}{\left|\right|}^2\hfill \mathrm{(33)}& \hfill & =2|{\mathcal{X}}_j^{in}|r_j^2+2f_2(m_j,{\mathcal{X}}_j^{in})-|{\mathcal{X}}_j^{in}\left|\right||m_j-{\tilde{m}}_j^{in}{\left|\right|}^2\hfill \end{array}$$

□

Lemma 10.

In the process of finding $c_j$ in our algorithm $\mathit{cMeans}$, for the set ${\mathcal{S}}_2$ in step 5, a subset ${\mathcal{S}}^{*}$ of size $6/ϵ$ of ${\mathcal{S}}_2$ can be obtained such that all random variables in ${\mathcal{S}}^{*}$ are from ${\tilde{\mathcal{X}}}_j^{in}$. Let $c_j$ be the centroid of ${\mathcal{S}}^{*}$. Then, the inequality $\left|\right|{\tilde{m}}_j^{in}-c_j{\left|\right|}^2\le \frac{2}{5}ϵr_j^2+\frac{49}{120}ϵ{\sigma }_j^2-\frac{1}{5}ϵ\left|\right|m_j-{\tilde{m}}_j^{in}{\left|\right|}^2$ holds with a probability of at least $1/6$.

Proof. 

For each point $p\in C_{j-1}$, $6/ϵ$ copies of p are added to ${\mathcal{S}}_2$ in step 9 in our algorithm $\mathbf{cMeans}$. Thus, a subset ${\mathcal{S}}^{*}$ of size $6/ϵ$ of ${\mathcal{S}}_2$ can be obtained such that all random variables in ${\mathcal{S}}^{*}$ are from ${\tilde{\mathcal{X}}}_j^{in}$. Let $\mathsf{\delta }=5/6$. Since $|{\mathcal{S}}^{*}|=6/ϵ$, by Lemma 2, $\left|\right|{\tilde{m}}_j^{in}-c_j{\left|\right|}^2\le \frac{ϵ}{5}\frac{f_2({\tilde{m}}_j^{in},{\tilde{\mathcal{X}}}_j^{in})}{|{\mathcal{X}}_j^{in}|}$ holds with a probability of at least $1/6$. Assume that $\left|\right|{\tilde{m}}_j^{in}-c_j{\left|\right|}^2\le \frac{ϵ}{5}\frac{f_2({\tilde{m}}_j^{in},{\tilde{\mathcal{X}}}_j^{in})}{|{\mathcal{X}}_j^{in}|}$. Then,

$$\begin{array}{}\mathrm{(34)}& \left|\right|{\tilde{m}}_j^{in}-c_j{\left|\right|}^2\hfill & \le \frac{ϵ}{5}\frac{f_2({\tilde{m}}_j^{in},{\tilde{\mathcal{X}}}_j^{in})}{|{\mathcal{X}}_j^{in}|}\hfill \mathrm{(35)}& \hfill & \le \frac{1}{5}ϵ\frac{2|{\mathcal{X}}_j^{in}|r_j^2+2f_2(m_j,{\mathcal{X}}_j^{in})-|{\mathcal{X}}_j^{in}\left|\right||m_j-{\tilde{m}}_j^{in}{\left|\right|}^2}{|{\mathcal{X}}_j^{in}|}\hfill \mathrm{(36)}& \hfill & =\frac{2}{5}ϵr_j^2+\frac{2}{5}ϵ\frac{f_2(m_j,{\mathcal{X}}_j^{in})}{|{\mathcal{X}}_j^{in}|}-\frac{1}{5}ϵ\left|\right|m_j-{\tilde{m}}_j^{in}{\left|\right|}^2\hfill \mathrm{(37)}& \hfill & \le \frac{2}{5}ϵr_j^2+\frac{2}{5}ϵ\frac{f_2(m_j,{\mathcal{X}}_j)}{|{\mathcal{X}}_j|-|{\mathcal{X}}_j^{out}|}-\frac{1}{5}ϵ\left|\right|m_j-{\tilde{m}}_j^{in}{\left|\right|}^2\hfill \mathrm{(38)}& \hfill & \le \frac{2}{5}ϵr_j^2+\frac{2}{5}ϵ\frac{{\beta }_{j}n{\sigma }_j^2}{(1-ϵ/49){\beta }_{j}n}-\frac{1}{5}ϵ\left|\right|m_j-{\tilde{m}}_j^{in}{\left|\right|}^2\hfill \mathrm{(39)}& \hfill & \le \frac{2}{5}ϵr_j^2+\frac{49}{120}ϵ{\sigma }_j^2-\frac{1}{5}ϵ\left|\right|m_j-{\tilde{m}}_j^{in}{\left|\right|}^2.\hfill \end{array}$$

□

Lemma 11.

If $c_j$ satisfies $\left|\right|{\tilde{m}}_j^{in}-c_j{\left|\right|}^2\le \frac{2}{5}ϵr_j^2+\frac{49}{120}ϵ{\sigma }_j^2-\frac{1}{5}ϵ\left|\right|m_j-{\tilde{m}}_j^{in}{\left|\right|}^2$, then $\left|\right|m_j-c_j{\left|\right|}^2\le \frac{9}{10}ϵ{\sigma }_j^2+\frac{1}{10{\beta }_{j}k}ϵ{\sigma }_{opt}^2$.

Proof. 

Assume that $c_j$ satisfies $\left|\right|{\tilde{m}}_j^{in}-c_j{\left|\right|}^2\le \frac{2}{5}ϵr_j^2+\frac{49}{120}ϵ{\sigma }_j^2-\frac{1}{5}ϵ\left|\right|m_j-{\tilde{m}}_j^{in}{\left|\right|}^2$. Then,

$$\begin{array}{}\mathrm{(40)}& \left|\right|m_j-c_j{\left|\right|}^2\hfill & =\left|\right|m_j-{\tilde{m}}_j^{in}+{\tilde{m}}_j^{in}-c_j{\left|\right|}^2\hfill \mathrm{(41)}& \hfill & \le 2\left|\right|m_j-{\tilde{m}}_j^{in}{\left|\right|}^2+2\left|\right|{\tilde{m}}_j^{in}-c_j{\left|\right|}^2\hfill \mathrm{(42)}& \hfill & \le (2-\frac{2}{5}ϵ)\left|\right|m_j-{\tilde{m}}_j^{in}{\left|\right|}^2+\frac{4}{5}ϵr_j^2+\frac{49}{60}ϵ{\sigma }_j^2\hfill \mathrm{(43)}& \hfill & \le (2-\frac{2}{5}ϵ)\left|\right|m_j-m_j^{in}+m_j^{in}-{\tilde{m}}_j^{in}{\left|\right|}^2+\frac{4}{5}ϵr_j^2+\frac{49}{60}ϵ{\sigma }_j^2\hfill \mathrm{(44)}& \hfill & \le (2-\frac{2}{5}ϵ)(2||m_j-m_j^{in}{\left|\right|}^2+2\left|\right|m_j^{in}-{\tilde{m}}_j^{in}{\left|\right|}^2)+\frac{4}{5}ϵr_j^2+\frac{49}{60}ϵ{\sigma }_j^2\hfill \mathrm{(45)}& \hfill & \le (2-\frac{2}{5}ϵ)(\frac{1}{24}ϵ{\sigma }_j^2+2r_j^2)+\frac{4}{5}ϵr_j^2+\frac{49}{60}ϵ{\sigma }_j^2\hfill \mathrm{(46)}& \hfill & \le \frac{9}{10}ϵ{\sigma }_j^2+4r_j^2\hfill \mathrm{(47)}& \hfill & =\frac{9}{10}ϵ{\sigma }_j^2+\frac{1}{10{\beta }_{j}k}ϵ{\sigma }_{opt}^2.\hfill \end{array}$$

□

5.2. Analysis for Case 2: $|{\mathcal{X}}_j^{out}|>\frac{ϵ}{49}{\beta }_{j}n$

Let ${\tilde{\mathcal{X}}}_j={\tilde{\mathcal{X}}}_j^{in}\cup {\mathcal{X}}_j^{out}$, and ${\tilde{m}}_j$ denote the centroid of ${\tilde{\mathcal{X}}}_j$. Our idea is to replace the center of ${\mathcal{X}}_j$ with the center of ${\tilde{\mathcal{X}}}_j$. But it is difficult to seek out the center of ${\tilde{\mathcal{X}}}_j$. Thus, we try to find an approximate center $c_j$ of ${\tilde{\mathcal{X}}}_j$.

Lemma 12.

$\frac{|{\mathcal{X}}_j^{out}|}{|\mathcal{X}\backslash {\mathcal{B}}_j|}\ge \frac{{ϵ}^2}{3969k}$.

Proof. 

$$\begin{array}{}\mathrm{(48)}& \frac{|{\mathcal{X}}_j^{out}|}{|\mathcal{X}\backslash {\mathcal{B}}_j|}\hfill & =\frac{|{\mathcal{X}}_j^{out}|}{{\sum }_{i=1}^{j-1}|{\mathcal{X}}_i\backslash {\mathcal{B}}_j|+|{\mathcal{X}}_j^{out}|+{\sum }_{i=j+1}^k|{\mathcal{X}}_i\backslash {\mathcal{B}}_j|}\hfill \mathrm{(49)}& \hfill & \ge \frac{|{\mathcal{X}}_j^{out}|}{{\sum }_{i=1}^{j-1}\frac{f_2(c_i,{\mathcal{X}}_i)}{r_j^2}+|{\mathcal{X}}_j^{out}|+{\sum }_{i=j+1}^k\left|{\mathcal{X}}_i\right|}\hfill \mathrm{(50)}& \hfill & \ge \frac{|{\mathcal{X}}_j^{out}|}{{\sum }_{i=1}^{j-1}\frac{f_2(m_i,{\mathcal{X}}_i)+|{\mathcal{X}}_i\left|\right||m_i-c_i{\left|\right|}^2}{r_j^2}+|{\mathcal{X}}_j^{out}|+{\sum }_{i=j+1}^k\left|{\mathcal{X}}_i\right|}\hfill \mathrm{(51)}& \hfill & \ge \frac{|{\mathcal{X}}_j^{out}|}{\frac{(1+ϵ)n{\sigma }_{opt}^2}{r_j^2}+|{\mathcal{X}}_j^{out}|+{\sum }_{i=j+1}^k\left|{\mathcal{X}}_i\right|}\hfill \mathrm{(52)}& \hfill & \ge \frac{|{\mathcal{X}}_j^{out}|}{\frac{40(1+ϵ)k{\beta }_{j}n}{ϵ}+\left|{\mathcal{X}}_j^{out}\right|+(k-j){\beta }_{j}n}\hfill \mathrm{(53)}& \hfill & \ge \frac{\frac{ϵ}{49}{\beta }_{j}n}{\frac{40(1+ϵ)k{\beta }_{j}n}{ϵ}+\frac{ϵ}{49}{\beta }_{j}n+(k-j){\beta }_{j}n}\hfill \mathrm{(54)}& \hfill & \ge \frac{{ϵ}^2}{(80k+k)49+(ϵ-49j)ϵ}\hfill \mathrm{(55)}& \hfill & \ge \frac{{ϵ}^2}{3969k}\hfill \end{array}$$

□

Lemma 13.

$\left|\right|m_j-{\tilde{m}}_j\left|\right|\le r_j$.

Proof. 

$$\begin{array}{}\mathrm{(56)}& \left|\right|m_j-{\tilde{m}}_j\left|\right|\hfill & =\left|\right|\frac{1}{|{\mathcal{X}}_j|}\sum _{X\in {\mathcal{X}}_j}{\int }^{{\mathbb{R}}^d}s{f}_X(s)ds-\frac{1}{|{\mathcal{X}}_j|}(\sum _{X\in {\mathcal{X}}_j^{in}}\tilde{X}+\sum _{X\in {\mathcal{X}}_j^{out}}{\int }^{{\mathbb{R}}^d}s{f}_X(s)ds)\left|\right|\hfill \mathrm{(57)}& \hfill & =\frac{1}{|{\mathcal{X}}_j|}\left|\right|\sum _{X\in {\mathcal{X}}_j^{in}}{\int }^{{\mathbb{R}}^d}(s-\tilde{X})f_X(s)ds\left|\right|\hfill \mathrm{(58)}& \hfill & =\frac{1}{|{\mathcal{X}}_j|}\sum _{X\in {\mathcal{X}}_j^{in}}{\int }^{{\mathbb{R}}^d}\left|\right|s-\tilde{X}\left|\right|f_X(s)ds\hfill \mathrm{(59)}& \hfill & \le \frac{1}{|{\mathcal{X}}_j|}\sum _{X\in {\mathcal{X}}_j^{in}}{r}_j\hfill \mathrm{(60)}& \hfill & =\frac{|{\mathcal{X}}_j^{in}|}{|{\mathcal{X}}_j|}{r}_j\hfill \mathrm{(61)}& \hfill & \le r_j\hfill \end{array}$$

□

Lemma 14.

$f_2({\tilde{m}}_j,{\tilde{\mathcal{X}}}_j)\le 2f_2(m_j,{\mathcal{X}}_j)+4{\beta }_{j}n{r}_j^2$.

Proof. 

$$\begin{array}{}\mathrm{(62)}& f_2({\tilde{m}}_j,{\tilde{\mathcal{X}}}_j)\hfill & =\sum _{X\in {\mathcal{X}}_j^{in}}\left|\right|\tilde{X}-{\tilde{m}}_j{\left|\right|}^2+\sum _{X\in {\mathcal{X}}_j^{out}}{\int }^{{\mathbb{R}}^d}\left|\right|s-{\tilde{m}}_j{\left|\right|}^2{f}_X(s)ds\hfill \mathrm{(63)}& \hfill & =\sum _{X\in {\mathcal{X}}_j^{in}}{\int }^{{\mathbb{R}}^d}\left|\right|\tilde{X}-{\tilde{m}}_j{\left|\right|}^2{f}_X(s)ds+\sum _{X\in {\mathcal{X}}_j^{out}}{\int }^{{\mathbb{R}}^d}\left|\right|s-{\tilde{m}}_j{\left|\right|}^2{f}_X(s)ds\hfill \mathrm{(64)}& \hfill & =\sum _{X\in {\mathcal{X}}_j^{in}}{\int }^{{\mathbb{R}}^d}\left|\right|\tilde{X}-s+s-{\tilde{m}}_j{\left|\right|}^2{f}_X(s)ds+\sum _{X\in {\mathcal{X}}_j^{out}}{\int }^{{\mathbb{R}}^d}\left|\right|s-{\tilde{m}}_j{\left|\right|}^2{f}_X(s)ds\hfill \mathrm{(65)}& \hfill & \le \sum _{X\in {\mathcal{X}}_j^{in}}{\int }^{{\mathbb{R}}^d}(2||\tilde{X}-{s\left|\right|}^2+2\left|\right|s-{\tilde{m}}_j{\left|\right|}^2)f_X(s)ds+\sum _{X\in {\mathcal{X}}_j^{out}}{\int }^{{\mathbb{R}}^d}\left|\right|s-{\tilde{m}}_j{\left|\right|}^2{f}_X(s)ds\hfill \mathrm{(66)}& \hfill & \le 2\sum _{X\in {\mathcal{X}}_j^{in}}{\int }^{{\mathbb{R}}^d}\left|\right|\tilde{X}-{s\left|\right|}^2{f}_X(s)ds+2\sum _{X\in {\mathcal{X}}_j^{out}}{\int }^{{\mathbb{R}}^d}\left|\right|s-{\tilde{m}}_j{\left|\right|}^2{f}_X(s)ds\hfill \mathrm{(67)}& \hfill & \le 2|{\mathcal{X}}_j^{in}|r_j^2+2f_2({\tilde{m}}_j,{\mathcal{X}}_j)\hfill \mathrm{(68)}& \hfill & =2|{\mathcal{X}}_j^{in}|r_j^2+2f_2(m_j,{\mathcal{X}}_j)+2|{\mathcal{X}}_j\left|\right||m_j-{\tilde{m}}_j{\left|\right|}^2\hfill \mathrm{(69)}& \hfill & \le 2f_2(m_j,{\mathcal{X}}_j)+4{\beta }_{j}n{r}_j^2\hfill \end{array}$$

□

Lemma 15.

In the process of finding $c_j$ in our algorithm $\mathit{cMeans}$, we assume that $\mathcal{Q}$ satisfies $\mathcal{X}\backslash {\mathcal{B}}_j\subseteq \mathcal{Q}$ and $\left|\mathcal{Q}\right|<2|\mathcal{X}\backslash {\mathcal{B}}_j|$. For the set ${\mathcal{S}}_2$ in step 5, a subset ${\mathcal{S}}^{*}$ of size $6/ϵ$ of ${\mathcal{S}}_2$ can be obtained such that all random variables in ${\mathcal{S}}^{*}$ are from ${\tilde{\mathcal{X}}}_j^{in}$ with a probability of $1/2$. Let $c_j$ denotes the centroid of ${\mathcal{S}}^{*}$. Then, the inequality $\left|\right|{\tilde{m}}_j-c_j{\left|\right|}^2\le \frac{4}{5}ϵr_j^2+\frac{2}{5}ϵ{\sigma }_j^2$ holds with a probability of at least $1/6$.

Proof. 

In our algorithm $\mathbf{cMeans}$, we assume that ${\mathcal{S}}_1=S_1,\dots ,S_N$, where $N=\mathrm{79,380}k/{ϵ}^3$. Let $x_1^{{}^{\prime }},\dots ,x_N^{{}^{\prime }}$ be the corresponding random variables of elements in ${\mathcal{S}}_1$. If $S_i\in {\mathcal{X}}_j^{out}$, obtain $x_i^{{}^{\prime }}=1$, or else $x_i^{{}^{\prime }}=0$. It is known easily that $Pr[S_i\in {\mathcal{X}}_j^{out}]\ge \frac{{ϵ}^2}{7938k}$ by Lemma 12. Let $x={\sum }_{i=1}^N{x}_i^{{}^{\prime }},u={\sum }_{i=1}^{N}E(x_i^{{}^{\prime }})$. We obtain that $u\ge 10/ϵ$, and

$$\begin{array}{}\mathrm{(70)}& Pr[x>\frac{6}{ϵ}]\hfill & =1-Pr[x\le \frac{6}{ϵ}]\hfill \mathrm{(71)}& \hfill & \ge 1-Pr[x\le \frac{3}{5}u]\hfill \mathrm{(72)}& \hfill & \ge 1-e^{-\frac{{(1-\frac{3}{5})}^{2}u}{2}}\hfill \mathrm{(73)}& \hfill & \ge 1-e^{-\frac{{(1-\frac{3}{5})}^2\frac{10}{ϵ}}{2}}\hfill \mathrm{(74)}& \hfill & \ge 1-e^{-\frac{4}{5}}\hfill \mathrm{(75)}& \hfill & \ge \frac{1}{2}.\hfill \end{array}$$

Then, the probability that at least $6/ϵ$ random variables in ${\mathcal{S}}_1$ are from ${\mathcal{X}}_j^{out}$ is at least $1/2$. Since ${\mathcal{S}}_2={\mathcal{S}}_1\cup \{6/ϵ$ copies of each point in $C\}$, a subset ${\mathcal{S}}^{*}$ of size $6/ϵ$ of ${\mathcal{S}}_2$ can be obtained, and the probability that all random variables in ${\mathcal{S}}^{*}$ are from ${\tilde{\mathcal{X}}}_j^{in}$ is at least $1/2$. Let $c_j$ denote the centroid of ${\mathcal{S}}^{*}$ and $\mathsf{\delta }=5/6$. For $|{\mathcal{S}}^{*}|=6/ϵ$ and $|widetilde{\mathcal{X}}_j|=|{\mathcal{X}}_j|$, by Lemma 2, $\left|\right|{\tilde{m}}_j-c_j{\left|\right|}^2\le \frac{ϵ}{5}\frac{f_2({\tilde{m}}_j,{\tilde{\mathcal{X}}}_j)}{|{\tilde{\mathcal{X}}}_j|}=\frac{ϵ}{5}\frac{f_2({\tilde{m}}_j,{\tilde{\mathcal{X}}}_j)}{|{\mathcal{X}}_j|}$ holds with a probability of at least $1/6$. Assume that $\left|\right|{\tilde{m}}_j-c_j{\left|\right|}^2\le \frac{ϵ}{5}\frac{f_2({\tilde{m}}_j,{\tilde{\mathcal{X}}}_j)}{|{\mathcal{X}}_j|}$. Then,

$$\left|\right|{\tilde{m}}_j-c_j{\left|\right|}^2\le \frac{ϵ}{5}\frac{f_2({\tilde{m}}_j,{\tilde{\mathcal{X}}}_j)}{|{\mathcal{X}}_j|}\le \frac{ϵ}{5}\frac{2f_2(m_j,{\mathcal{X}}_j)+4{\beta }_{j}n{r}_j^2}{|{\mathcal{X}}_j|}\le \frac{4}{5}ϵr_j^2+\frac{2}{5}ϵ{\sigma }_j^2.$$

(76)

□

Lemma 16.

If $c_j$ satisfies $\left|\right|{\tilde{m}}_j-c_j{\left|\right|}^2\le \frac{4}{5}ϵr_j^2+\frac{2}{5}ϵ{\sigma }_j^2$, then $\left|\right|m_j-c_j{\left|\right|}^2\le \frac{9}{10}ϵ{\sigma }_j^2+\frac{1}{10{\beta }_{j}k}ϵ{\sigma }_{opt}^2$.

Proof. 

Assume that $c_j$ satisfies $\left|\right|{\tilde{m}}_j-c_j{\left|\right|}^2\le \frac{4}{5}ϵr_j^2+\frac{2}{5}ϵ{\sigma }_j^2$. Then,

$$\begin{array}{}\mathrm{(77)}& \left|\right|m_j-c_j{\left|\right|}^2\hfill & =\left|\right|m_j-{\tilde{m}}_j+{\tilde{m}}_j-c_j{\left|\right|}^2\hfill \mathrm{(78)}& \hfill & \le 2\left|\right|m_j-{\tilde{m}}_j{\left|\right|}^2+2\left|\right|{\tilde{m}}_j-c_j{\left|\right|}^2\hfill \mathrm{(79)}& \hfill & \le 2r_j^2+\frac{8}{5}ϵr_j^2+\frac{4}{5}ϵ{\sigma }_j^2\hfill \mathrm{(80)}& \hfill & =\frac{4}{5}ϵ{\sigma }_j^2+(2+\frac{8}{5}ϵ)r_j^2\hfill \mathrm{(81)}& \hfill & \le \frac{9}{10}ϵ{\sigma }_j^2+\frac{1}{10{\beta }_{j}k}ϵ{\sigma }_{opt}^2.\hfill \end{array}$$

□

Lemma 17.

Given an instance $(\mathcal{X},k,\mathbb{L})$ of the uncertain constrained k-means problem, where the size of $\mathcal{X}$ is n, for $\forall ϵ\in (0,1],k\ge 2$, we assume that by using our algorithm $\mathit{cMeans}$(ϵ, $\mathcal{X}$, k, C, U) (C and U are initialized as empty sets), a collection U of candidate sets including approximate centers is obtained. If there exists a set $C_k=\{c_1,\dots ,c_k\}$ in U satisfying that $\left|\right|m_j-c_j{\left|\right|}^2\le \frac{9}{10}ϵ{\sigma }_j^2+\frac{1}{10{\beta }_{j}k}ϵ{\sigma }_{opt}^2(1\le j\le k)$, then $C_k$ is a $(1+ϵ)$-approximation for the uncertain constrained k-means problem.

Proof. 

Assume that $C_k=c_1,\dots ,c_k$ is a set in U satisfying that $\left|\right|m_j-c_j{\left|\right|}^2\le \frac{9}{10}ϵ{\sigma }_j^2+\frac{1}{10{\beta }_{j}k}ϵ{\sigma }_{opt}^2(1\le j\le k)$. Then,

$$\begin{array}{}\mathrm{(82)}& \sum _{j=1}^k{f}_2(c_j,{\mathcal{X}}_j)\hfill & =\sum _{j=1}^k(f_2(m_j,{\mathcal{X}}_j)+|{\mathcal{X}}_j\left|\right||m_j-c_j{\left|\right|}^2)\hfill \mathrm{(83)}& \hfill & \le \sum _{j=1}^k(f_2(m_j,{\mathcal{X}}_j)+{\beta }_{j}n(\frac{9}{10}ϵ{\sigma }_j^2+\frac{1}{10{\beta }_{j}k}ϵ{\sigma }_{opt}^2))\hfill \mathrm{(84)}& \hfill & \le \sum _{j=1}^k(f_2(m_j,{\mathcal{X}}_j)+\frac{9}{10}ϵn\sum _{j=1}^k{\beta }_j{\sigma }_j^2+\frac{1}{10}ϵn{\sigma }_{opt}^2\hfill \mathrm{(85)}& \hfill & \le \sum _{j=1}^k(f_2(m_j,{\mathcal{X}}_j)+\frac{9}{10}ϵn{\sigma }_{opt}^2+\frac{1}{10}ϵn{\sigma }_{opt}^2\hfill \mathrm{(86)}& \hfill & =(1+ϵ)·OP{T}_k(P).\hfill \end{array}$$

□

5.3. Time Complexity Analysis

We analyze the time complexity for our algorithm $\mathbf{cMeans}$ in this section.

Lemma 18.

The time complexity of our algorithm $\mathit{cMeans}$ is $O(4^k{(\frac{\mathrm{13,231}ek}{{ϵ}^2})}^{6k/ϵ}\frac{1}{ϵ}nd)$.

Proof. 

Let $a=C_{N+kM}^M$, which $N=\frac{\mathrm{79,380}k}{{ϵ}^3}$, $M=\frac{6}{ϵ}$. By the Stirling formula,

$$C_{N+kM}^M\le \frac{{(N+kM)}^M}{M!}\approx O({(e\frac{N+kM}{M})}^M)=O({(\frac{\mathrm{13,231}ek}{{ϵ}^2})}^{\frac{6}{ϵ}}).$$

In our algorithm $\mathbf{cMeans}$, steps 5–9 have a run time of $O(k/{ϵ}^3)$, step 11 have a run time of $O(d/ϵ)$, and steps 13–16 have a run time of $O(knd)$. Let $T(n,g)$ denote the time complexity of algorithm $\mathbf{cMeans}$, where g is the number of cluster centers, and n is the size of $\mathcal{Q}$.

If $g=0$, $T(n,0)=O(1)$. When $n=1$, $T(1,g)=a(T(1,g-1)+O(d/ϵ))+O(k/{ϵ}^3)$. Because $a>k/{ϵ}^3$, $T(1,g)=a(T(1,g-1)+O(d/ϵ))\le a^g·T(1,0)+g·a^g·O(d/ϵ)=O(g·a^g·d/ϵ)$. Therefore, $T(1,g)\le O(4^g{(\frac{\mathrm{13,231}ek}{{ϵ}^2})}^{6g/ϵ})\frac{1}{ϵ}d$, where $e=2.7183$.

For $\forall n\ge 2$ and $g\ge 1$, the recurrence of $T(n,g)$ could be obtained as follows:

$$T(n,g)=a·T(n,g-1)+T(\lfloor \frac{n}{2}\rfloor ,g)+a·O(\frac{d}{ϵ})+O(\frac{k}{{ϵ}^3})+O(knd).$$

Because $a>k/{ϵ}^3$, two constants $b_1$ and $b_2$ with $b_1\ge 1$ and $b_2\ge 1$ could be obtained to arrive at the following recurrence.

$$T(n,g)\le a·T(n,g-1)+T(\lfloor \frac{n}{2}\rfloor ,g)+a·b_1·\frac{d}{ϵ}+b_2·knd.$$

Now we claim that $T(n,g)\le b_1·b_2·\frac{1}{ϵ}·a^g·2^{2g}·nd-b_1·\frac{d}{ϵ}$. If $g=0$, then $T(n,0)=O(1)$. If $g\ge 1,n=1$, then $T(1,g)\le O(4^g{(\frac{\mathrm{13,231}ek}{{ϵ}^2})}^{6g/ϵ})\frac{1}{ϵ}d$, and the claim holds. Suppose that if $\forall n_1\ge 0,\forall g>g_1$, the claim holds for $T(n_1,g_1)$, and if $\forall 0<n_2<n,\forall g_2$, the claim holds for $T(n_2,g_2)$. We need to prove that:

$$\begin{array}{c}\hfill b_1·b_2·\frac{1}{ϵ}·a^g·2^{2g}·nd-b_1·\frac{d}{ϵ}\ge a(b_1·b_2·\frac{1}{ϵ}·a^{(}g-1)·2^{2(g-1)}·nd-b_1·\frac{d}{ϵ})\\ \hfill +b_1·b_2·\frac{1}{ϵ}·a^g·2^{2g}·\lfloor \frac{n}{2}\rfloor d-b_1·\frac{d}{ϵ}+a·b_1·\frac{d}{ϵ}+b_2·knd.\end{array}$$

The above formula can be simplified as $\frac{1}{4ϵ}·b_1·a^g{2}^{2g}\ge k$, which holds for $\forall g\ge 1$. For $a={(\frac{\mathrm{13,231}ek}{{ϵ}^2})}^{6/ϵ}$, $T(n,k)=O(4^k{(\frac{\mathrm{13,231}ek}{{ϵ}^2})}^{6k/ϵ}\frac{1}{ϵ}nd)$. □

Thus, we can obtain the following Theorem 2.

Theorem 2.

Given an instance $(\mathcal{X},k,\mathbb{L})$ of the uncertain constrained k-means problem, where the size of $\mathcal{X}$ is n, for $\forall ϵ\in (0,1],k\ge 2$, by using our algorithm $\mathit{cMeans}(ϵ,\mathcal{X},k,C,U)$, a collection U of candidate sets including approximate centers can be obtained with a probability of at least $1/{12}^2$ such that U includes at least one candidate set including approximate centers that is a $(1+ϵ)$-approximation for the uncertain constrained k-means problem, and the time complexity of our algorithm $\mathit{cMeans}$ is $O(4^k{(\frac{\mathrm{13,231}ek}{{ϵ}^2})}^{6k/ϵ}\frac{1}{ϵ}nd)$.

6. Conclusions

In this paper, we defined the uncertain constrained k-means problem first, and then presented a stochastic approximate algorithm for the problem in detail. We proposed a general mathematical model of the uncertain constrained k-means problem, and studied the random sampling properties, which are very important to deal with the uncertain constrained k-means problem. By applying a random sampling technique, we obtained a $(1+ϵ)$-approximate algorithm for the problem. Then, we investigated the success probability, correctness and time complexity analysis of our algorithm $\mathbf{cMeans}$, whose running time is $O(4^k{(\frac{\mathrm{13,231}ek}{{ϵ}^2})}^{6k/ϵ}\frac{1}{ϵ}nd)$. However, there also exists a big gap between the current algorithms for the uncertain constrained k-means problem and the practical algorithms for the problem, which has been mentioned in [13] similarly.

We will try to explore a much more practical algorithm for the uncertain constrained k-means problem in future. It is known that the 2-means problem is the smallest version of the k-means problem, and remains NP-hard. The approximation schemes for the 2-means problem can be generalized to solve the k-means problem. Due to the particularity of the uncertain constrained 2-means problem, we will study approximation schemes for the uncertain constrained 2-means problem and reduce the algorithm complexity of approximation schemes for the uncertain constrained k-means problem through approximation schemes of the uncertain constrained 2-means problem. Additionally, we will apply the proposed algorithm to some practical problems in the future.