Multi-Objective Bee Swarm Optimization Algorithm with Minimum Manhattan Distance for Passive Power Filter Optimization Problems

Abstract

Harmonic distortion in power systems is a significant problem, and it is thus necessary to mitigate critical harmonics. This study proposes an optimal method for designing passive power filters (PPFs) to suppress these harmonics. The design of a PPF involves multi-objective optimization. A multi-objective bee swarm optimization (MOBSO) with Pareto optimality is implemented, and an external archive is used to store the non-dominated solutions obtained. The minimum Manhattan distance strategy was used to select the most balanced solution in the Pareto solution set. A series of case studies are presented to demonstrate the efficiency and superiority of the proposed method. Therefore, the proposed method has a very promising future not only in filter design but also in solving other multi-objective optimization problems.

1. Introduction

1.1. Background

In a power system, nonlinear loads are commonly used by consumers [1], and the current drawn by these nonlinear loads is not sinusoidal, even though they are connected to a sinusoidal supply. Distortions in the waveform occur owing to the nonlinear nature of loads. The growth of nonlinear loads causes distortions in the current and voltage waveform [2,3,4], which are represented as harmonics. These harmonics may have several adverse effects on power systems, including power loss, power factor reduction, equipment malfunctioning, deterioration, and damage [5,6,7,8,9,10,11]. Several techniques, utilizing components such as reactors and chokes, active power filters (APFs), passive power filters (PPFs), different transformer connections, and a higher pulse number converter, have been developed to solve these problems. PPFs are the most effective and commonly used because they are simple and economical [12]. Several studies have shown the effectiveness of PPFs in reducing harmonics from nonlinear systems [13,14,15,16,17,18,19].

1.2. Literature Review

Several studies have calculated the parameters of PPFs and evaluated the sizing, sitting, type, and number of PPFs [13,20], minimizing the initial investment costs [19], minimizing the harmonic distortion [18], and maximizing the reactive power compensation [21]. In [13], power loss and investment costs were used to evaluate the PPF design and limitations, including the number of PPFs, limited buses for installation of PPFs, and total harmonic distortion in all buses. Therefore, the optimal PPF design has been used in various applications, as discussed above. A practical graph search algorithm was proposed to reduce the cost, power loss, and total harmonic voltage distortion in [17]. The number, size, and position of the PPFs were also determined. In [22], Hong and Liao proposed a cumulant and adaptive dynamic clone selection algorithm (ADCSA) for the PPF design, where the harmonic voltages were determined using a cumulant. In [22], the design of single-tuned PPFs were considered as an optimization problem to reduce the cost, time-varying harmonics, size, and location. In [15], the sitting and sizing planning of the PPFs using a bacterial foraging algorithm for a radial distribution system is discussed. Three objectives, namely harmonic distortion, power loss, and the initial cost of PPFs and distribution generation (DG) in the distribution system, were considered for the PPF optimization problem. In [23], the PPF was used to help the cables and transformers work more effectively in the power system by mitigating unwanted harmonics. In this study, an ideal PPF design approach was proposed to improve the power factor and line losses (depending on frequency).

Several methods have been proposed for the design of PPFs. Das developed a conventional trial-and-error-based method for designing PPFs [12]. However, obtaining optimal solutions is a time-consuming trial-and-error process. In recent years, heuristic optimization algorithms have been used in PPF design for their effective and optimal results. A genetic algorithm (GA) [24,25], particle swarm optimization (PSO) [18], and simulated annealing (SA) [26] were used for PPF designs. In [18], the PSO method was used to optimize the design of PPFs for aircraft starter/generator system applications. The main objective was to reduce the weight and volume of the filter, instead of mitigating harmonics. The optimal design of the PPF in an asymmetric system based on the GA was discussed in [25].

Other recent methods for PPF design have also been explored extensively in [27,28,29,30,31,32]. In [27], a class topper optimization (CTO) was developed. However, the deployment of the CTO requires careful effort in detuning mechanisms that can hinder an optimal solution. Wang Y. et al. achieved good results via the tuning filtering method [28]. However, the same problem emerges as this method requires careful tuning. A dynamic tuning passive filter (DTPF) was proposed in [29]. Although harmonic suppression effectiveness can be achieved, the range setting value of harmonic current coefficient is highly demanded. In [30,31], PSO was employed to reduce harmonics. However, the utility of the weight sum method can trigger unbalanced conditions in a power system. A more recent study was conducted in [32], employing a teaching–learning-based optimization (TLBO) with Pareto optimality. However, the study is heavily dependent on an external archive and fuzzy decision making to achieve the desired PPF design for both TLBO and Pareto.

In addition, a chaotic accelerated PSO (CAPSO) algorithm was used to determine the feasible optimal solutions of electromagnetic cloaking problems [33]. In [34], a brain storm optimization algorithm was used to optimize electromagnetic designs to obtain different performance characteristics such as antenna far-field radiation patterns and improved performance at the desired operating frequencies. Bee swarm optimization (BSO) [35,36] is an algorithm based on the search process of bees. It is a combination of two algorithms: the bee algorithm (BeA) [37] and PSO algorithms. Some studies have demonstrated the application of BSO in solving multi-objective optimization problems. In [38], Niknam and Franak proposed an improved BSO method based on dynamic economic dispatch optimization problems. The transmission losses, valve point effect, and ramp rate were considered for optimization. In [39], the BSO method was used in the field of cloud computing. An improved BSO method was proposed in the cloud (IBSO-C) to allow users to share virtual resources more efficiently by minimizing the total costs, including transfer and execution time. An improved ripple BSO (IRBSO) algorithm was used to solve the economic dispatch of the chiller plant optimization problem to save energy in [40]. BSO was also used in the field of data mining to solve document retrieval problems [41].

Pareto optimality is introduced with the multi-objective bee swarm optimization (MOBSO) to make the design of PPFs more efficient. Pareto optimality has been used to solve multi-objective problems in several studies [42,43,44,45,46]. In [46], Pareto optimality approaches were integrated with the harmony search algorithm to address the design of energy-efficient shading devices as an optimization problem. Kamila et al. [42] used the Pareto approach to classify data-mining optimization problems. In [43], a GA with the Pareto approach was also applied to solve the design of the fiber Bragg grating (FBG) sensor network optimization problem. In [44,45], the Pareto optimality approach was used with the bat algorithm (BA) to optimize the PPF design. In [44], different types of weight coefficients were used to make the PPF design more efficient.

1.3. Aim and Contributions

In this study, a multi-objective optimization method based on BSO and Pareto optimality was proposed for solving PPF design problems. An external archive was used to store all nondominated solutions in the Pareto optimality. A fuzzy decision-making method was used to evaluate the nominal membership of the non-dominated solutions. The roulette selection method was used to select a non-dominated solution from the external archive in the experienced forager bee phase. A series of case studies was conducted to verify the performance of the proposed method. First, the proposed method was compared with the SA for three different cases. Second, the proposed method was compared with two other established algorithms, PSO and BA, in terms of the minimum Manhattan distance (MMD) results [47]. In each case, the results demonstrate the superior performance of the proposed method.

1.4. Paper Organization

This paper is divided into the following sections: 2. Passive Power Filter Models; 3. Passive Power Filter Design: 4. Proposed Algorithm; 5. Results and Discussion; and 6. Conclusion.

2. Passive Power Filter Models

Power filters including passive, active, and hybrid filters can eliminate harmonics and are widely used in industry because of their low cost and simple configuration. PPFs typically consist of various combinations of resistors, inductors, and capacitors. The impedance of PPFs depends strongly on the frequency considered. In addition to mitigating harmonics, PPFs can also provide power-factor correction. The PPFs commonly used in power systems can be categorized as single-tuned filters, second-order damped filters, third-order damped filters, and C-type damped filters, as shown in Figure 1.

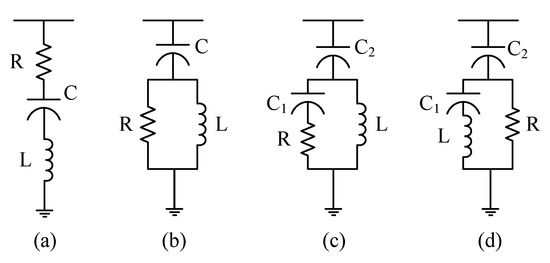
Figure 1. Types of passive power filters: (a) single-tuned filter, (b) second-order damped filter, (c) third-order damped filter, and (d) C-type damped filter.

2.1. Single-Tuned Filters

The configuration of the single-tuned filters is shown in Figure 1a. The impedance of the single-tuned filters at the h-th order harmonic frequency is calculated as follows:

$$h_n=\frac{1}{{\omega }_1\sqrt{LC}}$$

(1)

$$Z_{Fh}=R+j\left(h{X}_L-\frac{X_C}{h}\right)$$

(2)

where R is the internal resistance of the reactor, which may be neglected. $X_C=1/(\omega C)$, and $X_L=\omega L$.

2.2. Second-Order Damped Filters

The configuration of the second-order damped filters is shown in Figure 1b. The impedance of the second-order damped filters at the h-th order harmonic frequency is calculated as follows:

$$Z_{Fh}=\frac{R{(h{X}_L)}^2}{R^2+{(h{X}_L)}^2}+j\left(\frac{R^{2}h{X}_L}{R^2+{(h{X}_L)}^2}-\frac{X_C}{h}\right)$$

(3)

where $X_C=1/(\omega C)$ and $X_L=\omega L$.

2.3. Third-Order Damped Filters

The configuration of the third-order damped filters is shown in Figure 1c. The impedance of the third-order damped filters at the h-th order harmonic frequency is calculated as follows:

$$Z_{Fh}=\frac{R{(h{X}_L)}^2}{R^2+{\left(h{X}_L-\frac{X_C}{h}\right)}^2}+j\left[\frac{R^{2}h{X}_L-h{X}_L^2{X}_C+\frac{X_L{X}_C^2}{h}}{R^2+{\left(h{X}_L-\frac{X_C}{h}\right)}^2}-\frac{X_C}{h}\right]$$

(4)

where $X_C=1/(\omega C_2)$, $X_L=\omega L$, and $C_1=C_2$.

2.4. C-Type Damped Filters

The configuration of the C-type damped filters is shown in Figure 1d. The impedance of the C-type damped filters at the h-th order harmonic frequency is calculated as follows:

$$Z_{Fh}=\frac{R{\left(h{X}_L-\frac{X_L}{h}\right)}^2}{R^2+{\left(h{X}_L-\frac{X_L}{h}\right)}^2}+j\left[\frac{R^2\left(h{X}_L-\frac{X_L}{h}\right)}{R^2+{\left(h{X}_L-\frac{X_L}{h}\right)}^2}-\frac{X_C}{h}\right]$$

(5)

where $X_C=1/(\omega C_2)$, $X_L=\omega L$ and $C_1=1/({\omega }_1^{2}L)$.

3. Problem Formulation

PPFs can be roughly divided into single-pass and damped band-pass filters. Damped band-pass filters can be further categorized as second-order damped filters, third-order damped filters, and C-type damped filters. The design of PPFs is a complicated multi-objective engineering problem. The main considerations in a PPF design are cost and performance. The objective functions and constraints used in this study are as follows:

3.1. Objective Functions

The objective functions used in this study are minimizing the total harmonic distortion of the current, minimizing the total distortion of the voltage, minimizing the investment cost, and maximizing the total fundamental reactive power compensation.

3.1.1. Minimizing Total Harmonic Distortion of Current

The total harmonic distortion of current is defined as

$$F_1={\mathrm{THD}}_I=\frac{\sqrt{\left({\displaystyle \sum _{h=2}^H{\left|I_h\right|}^2}\right)}}{\left|I_1\right|}$$

(6)

where $h$ is the harmonic order; $H$ is the highest harmonic order considered, |I₁| is the rms of the fundamental current; and |I_k| is the rms of the harmonic current.

3.1.2. Minimizing Total Harmonic Distortion of Voltage

The total harmonic distortion of voltage is defined as

$$F_2={\mathrm{THD}}_V=\frac{\sqrt{\left({\displaystyle \sum _{h=2}^H{\left|V_h\right|}^2}\right)}}{\left|V_1\right|}$$

(7)

where h is the harmonic order; H is the highest harmonic order considered; |V₁| indicates the rms value of the fundamental part of the voltage; and |V_k| is the rms value of the harmonic voltage.

3.1.3. Minimizing Initial Investment Cost

The cost of a passive power filter may include passive component cost, fundamental power loss, and installation and maintenance costs. In engineering problems, the investment cost may be expressed as a linear combination of these costs, as shown in (8).

$$F_3=IC=\sum _{m=1}^4{\alpha }_m\sum _{n=1}^{X_m}(k_1{R}_{mn}+k_2{L}_{mn}+k_3{C}_{mn})$$

(8)

where m is the type of filter, and X_m is the number of filters of type $m$; $R_{mn}$, $L_{mn}$, and $C_{mn}$ are the resistance, inductance, and capacitance of the n-th filter of type $m$, respectively; $k_1$, $k_2$, and $k_3$ are considered cost weighting coefficients; and ${\alpha }_m$ is considered as the set number coefficient for the m-type filter.

3.1.4. Maximizing Total Fundamental Reactive Power Compensation

PPFs are not only used to solve the problem of harmonic noise but are also used to compensate for the power factor. The total fundamental reactive power produced by the filters is

$$F_4=Q_F={\displaystyle \sum _{m=1}^4{\displaystyle \sum _{n=1}^{X_m}{Q}_{Fmn}}}$$

(9)

where $Q_{Fmn}$ is the fundamental reactive power produced by the n-th filter of the m-th type.

3.2. Constraints

The constraints considered in this study are (1) total harmonic distortion, (2) individual harmonic distortion, and (3) total fundamental reactive power compensation.

3.2.1. Total Harmonic Distortion

The total harmonic distortions of currents and voltages are constrained by

$$g_1={\mathrm{THD}}_I\le {\mathrm{THD}}_{I,\max }$$

(10)

$$g_2={\mathrm{THD}}_V\le {\mathrm{THD}}_{V,\max }$$

(11)

where ${\mathrm{THD}}_{I,\max }$ and ${\mathrm{THD}}_{V,\max }$ are the maximum restriction values for the total harmonic distortions of the currents and voltages, respectively.

3.2.2. Individual Harmonic Distortion

The individual harmonic distortions for the harmonic components of each order are constrained by

$$g_3={\mathrm{HD}}_{Ih}\stackrel{\Delta }{=}\frac{\left|I_{Sh}\right|}{\left|I_{S1}\right|}\le {\mathrm{HD}}_{Ih,max}$$

(12)

$$g_4={\mathrm{HD}}_{Vh}\stackrel{\Delta }{=}\frac{\left|V_{Sh}\right|}{\left|V_{S1}\right|}\le {\mathrm{HD}}_{Vh,max}$$

(13)

where ${\mathrm{HD}}_{Ih,max}$ and ${\mathrm{HD}}_{Vh,max}$ are the maximum restriction values for the harmonic current and voltage at the h-th order, respectively.

3.2.3. Total Fundamental Reactive Power Compensation

The PPFs can effectively improve the power factor (PF) of the system. However, overcompensation may cause voltage instability and increase power loss. In this context, the constraint for the total fundamental reactive power can be expressed as

$$g_5=Q_{\min }\le Q_F\le Q_{\max }$$

(14)

where $Q_{\min }$ and $Q_{\max }$ are the minimum and maximum values of reactive power compensation, respectively.

4. Proposed Multi-Objective BSO Algorithm

4.1. Bee Swarm Optimization Algorithm

Akbari et al. developed a new method based on honey bee food searching intelligence approach called BSO in 2009 [35]. BSO is a combination of two algorithms: BeA and PSO algorithms; the search pattern is based on BeA, while the velocity vector and the collective memories are based on PSO. Three classes of bees are used to solve optimization problems, which are the experienced forager bee, onlooker bee, and scout bee classes. Each bee has a different flying pattern as well as different responsibilities, and flies in a $D$-dimensional search space $S(S\subset R^D)$ to seek the optimal solution. The quality of the food source is regarded as fitness.

BSO can be divided into four phases: (1) population initialization phase, (2) parameter initialization phase, (3) fitness function creation phase, and (4) updating the bee phase [35,38].

1.

Population Initialization Phase: The first step is to manually determine the number of bees (population). The entire group of bees is represented by (15):

$$\beta =\xi \cup \kappa \cup \vartheta$$

(15)

where ξ, $\kappa$, and $\vartheta$ represent the sets of onlooker bees, experienced forager bees, and scout bees, respectively. The percentage of experienced foragers, onlookers, and scout bees was determined manually. In general, the number of experienced forager bees is considered equal to that of onlooker bees, and the number of Scout bees are small. Here, each bee m is connected to a particular position vector, given by (16):

$$\overline{x}(\beta ,m)=\left(x(\beta ,m_1),x(\beta ,m_2),\dots ,x(\beta ,m_D)\right)$$

(16)

where $\overline{x}(\beta ,m)$ represents a feasible solution for the optimization problem in a $D$-dimensional search space $S$ $(S\subset R^D)$.

2.

Parameter Initialization Phase: In this phase, some parameters need to be initialized, such as the number of bees $\left(n(\beta )\right)$, the maximum number of iterations $\left(Ite{r}_{\max }\right)$, and the initialization function, as shown in (17):

$${\overline{x}}_0(\beta ,m)=In(m,S)\forall m\in \beta$$

(17)

where $In(m,S)$ refers to the initialization function in the search space of $S$, which is associated with a random position of the m-th bee.

3.

Fitness Function Creation: In this study, a multi-objective BSO algorithm was developed to search for potential global solutions. The fuzzy decision-making method is used to select one solution in the Pareto-optimal solutions as the compromise solution. The membership $fi{t}_i$ of the ith objective function $f_i$ is shown as follows:

$$fi{t}_i\left(x\right)=\{\begin{array}{cc}1& ,f_i\left(x\right)\le f_i^{\min }\\ \frac{f_i^{\max }-f_i\left(x\right)}{f_i^{\max }-f_i^{\min }}& ,f_i^{\max }<f_i\left(x\right)<f_i^{\min }\\ 0& ,f_i\left(x\right)\ge f_i^{\max }\end{array}$$

(18)

where $f_i{}^{\max }$ and $f_i^{\min }$ are the maximum and minimum of the ith objective function, respectively.

Furthermore, the nominal membership $fi{t}_{}^k$ of the non-dominated solution k is evaluated using (19):

$$fi{t}_{}^k={\displaystyle {\sum }_{i=1}^{n_F}fi{t}_i^k}$$

(19)

4.

Updating Bee Phase: In this phase, first, the position of an experienced forager bee is updated, followed by the onlooker bee, and then the scout bee.

• The position of an experienced forager bee $(\xi )$ is updated using (20):

  $${\overline{x}}_{new}(\xi ,m)=\underset{\mathrm{I}}{\underbrace{{\overline{x}}_{old}(\xi ,m)}}+\underset{\mathrm{II}}{\underbrace{w_b{r}_b\left(\overline{b}(\xi ,m)-{\overline{x}}_{old}(\xi ,m)\right)}}+\underset{\mathrm{III}}{\underbrace{w_e{r}_e\left(\overline{e}(\xi ,m)-{\overline{x}}_{old}(\xi ,m)\right)}}$$

  (20)

  where ${\overline{x}}_{new}(\xi ,m)$ is the new food source position found by the experienced forager bee, $r_b,r_e$ are the random variables distributed uniformly in the range of [0, 1]; $w_b,w_e$ represents the parameters that control the best food source found by the m-th bee and the elite bee, respectively.
  Equation (20) in the BSO algorithm can be explained by dividing the right-hand side into three parts. The first part, ${\stackrel{\rightharpoonup }{x}}_{old}(\xi ,m)$, denotes the old food position found by the experienced bee, whereas the second part represents the complete knowledge $w_b{r}_b\left(\overline{b}(\xi ,m)-{\overline{x}}_{old}(\xi ,m)\right)$ that draws the experienced bee to the best food position. The third part represents the social knowledge that attracts the experienced forager bee to the best position $\overline{e}(\xi ,m)$ found by the elite bee.
• The experienced forager bee shares social knowledge with the onlooker bees $(\kappa )$ to adjust their moving trajectories in the next iteration. The positions are updated using (21):

  $${\stackrel{\rightharpoonup }{x}}_{new}(\kappa ,m)={\stackrel{\rightharpoonup }{x}}_{old}(\kappa ,m)+w_e{r}_e\left(\stackrel{\rightharpoonup }{e}(\xi ,m)-{\stackrel{\rightharpoonup }{x}}_{old}(\kappa ,m)\right)$$

  (21)

  where ${\stackrel{\rightharpoonup }{x}}_{new}(\kappa ,m)$ denotes the new food source position selected by the onlooker bee $(m)$, $w_e,r_e$ are the parameters used to control the attraction of the bees to their interesting food source area, and $\stackrel{\rightharpoonup }{e}(\xi ,m)$ represents the position vector of the elite bee for the onlooker bees $(p_n)$ evaluated by (22):

  $$p_n=\frac{fit\left(\stackrel{\rightharpoonup }{x}(\xi ,n)\right)}{{\displaystyle \sum _{c=1}^{N_{\xi }}fit\left(\stackrel{\rightharpoonup }{x}(\xi ,c)\right)}}$$

  (22)

  where $fit\left(\stackrel{\rightharpoonup }{x}(\xi ,n)\right)$ is the nominal membership of the food source found by the experienced forager bee $(n)$, and $N_{\xi }$ is the number of experienced forager bees.
• The position of the scout bees $(\vartheta )$ is updated using (23):

  $${\stackrel{\rightharpoonup }{x}}_{new}(\vartheta ,m)={\stackrel{\rightharpoonup }{x}}_{old}(\vartheta ,m)+Rw\left(\tau ,x_{old}(\vartheta ,m)\right)$$

  (23)

  where ${\stackrel{\rightharpoonup }{x}}_{old}(\vartheta ,m)$ represents the position of the abandoned food source and $Rw$ is a random walk function that controls the current position of the scout bee within the radius search $\tau$. Typically, the initial value of radius $\tau \in ({\tau }_{\min }<\tau <{\tau }_{\max })$ is defined as a percentage of $\left|X_{\max }-X_{\min }\right|$, where $X_{\max }$ and $X_{\min }$ are the maximum and minimum values of the search space along a dimension.

5.

Information selecting: This is determined via (24):

$$\{\begin{array}{c}\mathrm{if}fit\left(\stackrel{\rightharpoonup }{x}(\xi ,m)\right)>fit\left(\stackrel{\rightharpoonup }{b}(\xi ,m)\right)\mathrm{then}\stackrel{\rightharpoonup }{b}(\xi ,m)=\stackrel{\rightharpoonup }{x}(\xi ,m)\\ \mathrm{if}fit\left(\stackrel{\rightharpoonup }{b}(\xi ,m)\right)>fit\left(\stackrel{\rightharpoonup }{e}(\xi ,•)\right)\mathrm{then}\stackrel{\rightharpoonup }{e}(\xi ,•)=\stackrel{\rightharpoonup }{b}(\xi ,m)\end{array}$$

(24)

where $\stackrel{\rightharpoonup }{b}(\xi ,m)$ marks the best food source recalled by an experienced forager $(m)$, and $\stackrel{\rightharpoonup }{e}(\xi ,m)$ indicates the best food source position found by an elite bee.

4.2. Pareto Optimality

A multi-objective optimization problem is a complex problem with more than one objective. In this type of problem, the probability of the solutions conflicting with each other is high. In several studies, researchers have chosen a combinatorial function to convert the multi-objective into a single objective. However, this also causes an imbalance between solutions. To avoid these possibilities, the Pareto optimality approach is the best method for handling the multi-objective optimization.

Suppose the multi-objective optimization problem involves minimization, i.e.,

$$\begin{gathered} \mathrm{Minimize} \\ {F}_j(\overline{x})(j=1,2,\dots ,n_F) \end{gathered}$$

(25)

subject to

$$g_k(\overline{x})\le 0(k=1,2,\dots n_g)$$

(26)

$$h_l(\overline{x})=0(l=1,2,\dots n_h)$$

(27)

where $\overline{x}$ and $F_j(\overline{x})$ are the vectors of the decision variables and an objective function, respectively. $n_F$ is the number of objective functions, while $g_p(\overline{x})$ and $h_q(\overline{x})$ represent the inequality and equality constraints, respectively. $n_g$ and $n_h$ represent the number of inequalities and the number of equality constraints, respectively.

$$\overline{x}={[x_1,x_2,\dots ,x_n]}^t,\overline{x}\in \Omega \subseteq S$$

(28)

A region where a decision variable $\overline{x}$ satisfies all the constraints called a feasible region denoted by set $\Omega$, and $S$ is assumed as a search space.

Suppose $F_1({\overline{x}}_1)$ and $F_2({\overline{x}}_2)$ are two objective functions:

$$F_m({\overline{x}}_2)\le F_m({\overline{x}}_1)\forall m\in \{1,2,3,\dots ,k\}$$

(29)

$$\mathrm{and}{F}_m({\overline{x}}_2)<F_m({\overline{x}}_1)\exists m\in \{1,2,3,\dots ,k\}$$

(30)

If a decision variable $\overline{x}\in \Omega$ and its function $F_m({\overline{x}}_2)$ dominate over all other $F_m(\overline{x})$ functions for each $\overline{x}\in \Omega$, then the vector decision variable ${\overline{x}}_2$ belonging to $F_m$ is known as the non-dominated solution.

4.3. External Archive

A non-dominated solution is the best solution for the PPF design. Several non-dominated solutions are produced in each iteration; therefore, it is necessary to store these solutions. Several studies have considered external archives. In 2016, an improved PSO method was proposed in which an external archive was used for storing purposes. In [48], an external archive was used to store the feasible solution obtained by the grey wolf method.

Practically, a well-suited size for the external archive is 100 bees. Figure 2 shows the concept of the selection and removal of the solution from the external archive, graphically explained in [44]. An objective space is divided into several hypercubes. If the external archive is full and a new nondominated solution is obtained, then the nondominated solution from the overcrowded hypercubes is randomly selected and deleted, as shown in Figure 2.

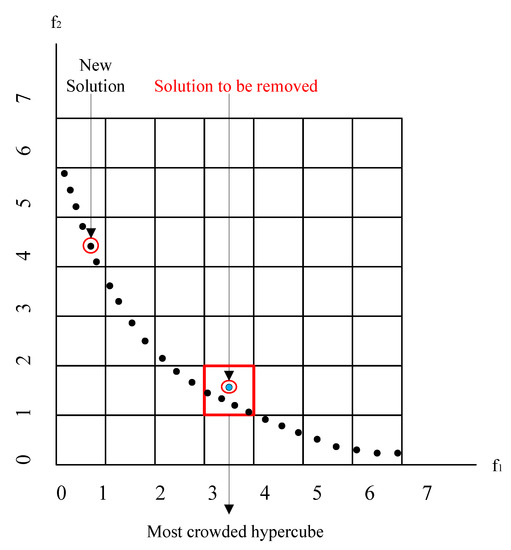
Figure 2. Graphical representation of inserting a new non-dominated solution when the external archive is full.

4.4. Minimum Manhattan Distance

Multiple criteria decision-making (MCDM) in multi-objective optimization problems implies the selection of the final non-dominated solution from all non-dominated solutions found, that is, choosing the balance solution among all non-dominated solutions. For this purpose, a minimum Manhattan distance (MMD) method is proposed to select the final solutions among all the non-dominated solutions to verify the superiority of the proposed MOBSO method. The Manhattan distance is the distance between two points. The solution having the minimum distance from the normalized ideal vector is called the MMD, as shown in Figure 3.

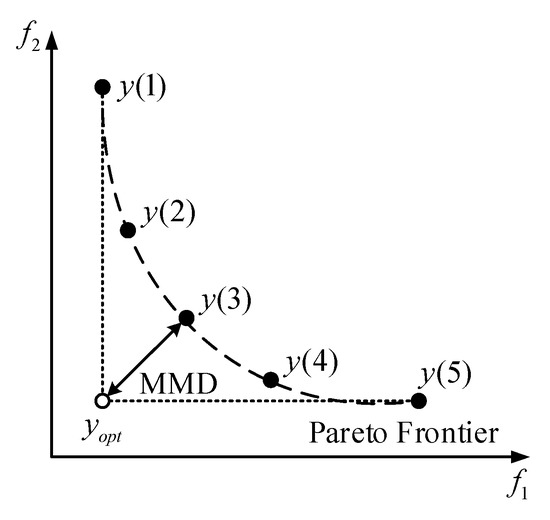
Figure 3. Interpretation of the MMD.

After normalization, the ideal vector $y_{opt}$ is denoted as

$$y_{opt}={\left[\begin{array}{cccc}\frac{{\ell }_1}{L_1}& \frac{{\ell }_2}{L_2}& \cdots & \frac{{\ell }_n}{L_n}\end{array}\right]}^t$$

(31)

$${\ell }_n=\underset{x\in N}{\min }{y}_n\left(x\right)N=\left\{x_1,x_2,\dots ,x_M\right\}$$

(32)

$$L_n=\underset{x\in N}{\max }{y}_n\left(x\right)-\underset{x\in N}{\min }{y}_n\left(x\right)$$

(33)

In the set of all feasible solutions, the minimum distance sum between the ideal vector $y_{opt}$ and the selected solution is defined as

$$\underset{x\in N}{\min }\Vert y_n\left(x\right)-y_{opt}\Vert =\underset{x\in N}{\min }{\displaystyle \sum _{n=1}^M\Vert \frac{y_n\left(x\right)}{L_n}-\frac{{\ell }_n}{L_n}\Vert }$$

(34)

The main steps of the MOBSO algorithm are listed below:

• Initialization Phase
  • Determine the $\beta$, which involves $\beta =\xi \cup \kappa \cup \vartheta$.
  • Initialize the food source position $\overline{x}(\beta ,m)$ that is associated with a particular bee m.
  • Generate the first non-dominated solution and update the archive.
  • Initialize the parameters: $n(\beta )$, $Ite{r}_{\max }$.
  • Sort the positions of food sources based on a fuzzy decision-making method.
  • Assign the food sources to the experienced forager bee.
• Experienced Forager Bee Phase
  For each experienced bee,
  • Select a non-dominated bee at the previous iteration as an experienced bee ${\overline{x}}_{old}(\xi ,m)$
  • Select the best bee from the archive using roulette wheel selection for an experienced forager bee $\overline{b}(\xi ,m)$.

    $$\{\begin{array}{l}\mathrm{if}fit\left(\stackrel{\rightharpoonup }{x}(\xi ,m)\right)>fit\left(\stackrel{\rightharpoonup }{b}(\xi ,m)\right)\mathrm{then}\stackrel{\rightharpoonup }{b}(\xi ,m)=\stackrel{\rightharpoonup }{x}(\xi ,m)\\ \mathrm{if}fit\left(\stackrel{\rightharpoonup }{b}(\xi ,m)\right)>fit\left(\stackrel{\rightharpoonup }{e}(\xi ,•)\right)\mathrm{then}\stackrel{\rightharpoonup }{e}(\xi ,•)=\stackrel{\rightharpoonup }{b}(\xi ,m)\end{array}$$
  • Produce a new position ${\overline{x}}_{new}(\xi ,m)$.
• Onlooker Bee Phase
  For each onlooker bee,
  • Select an elite bee from the experienced bees for onlooker bee m.
  • The position vector of the elite bee $\stackrel{\rightharpoonup }{e}(\xi ,m)$ for onlooker bees $(p_{jd})$ was determined using the probability approach.
  • Produce a new food source position ${\stackrel{\rightharpoonup }{x}}_{new}(\kappa ,m)$.
  • Save the most effective solution obtained so far.
• Scout Bee Phase
  For each scout bee
  • To improve the local search, a scout bee occurs and performs a random walk.
  • Produce a new random food position source ${\stackrel{\rightharpoonup }{x}}_{new}(\vartheta ,m)$.

If a termination condition is reached, then reports the final best solution and updates the archive by adding all non-dominated solutions, and else goes to the experienced forager bee phase. A flowchart of the proposed MOBSO algorithm is shown in Figure 4.

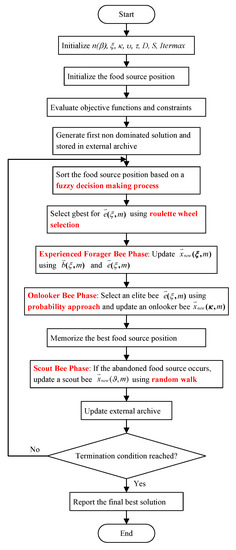
Figure 4. Flowchart of the proposed MOBSO algorithm.

5. Results and Discussion

5.1. Sample System

A system of 11.4 kV, 60 Hz is considered. This system consists of nonlinear loads considered as a harmonic source, and the PPFs are shown in Figure 5. Linear loads can be ignored owing to their enormous impedance value. A balanced system with three cases of different loads and ratings was used for the experiments, where all tolerances were based on IEEE standards 519–1992 [49]. Case 1 has a fundamental active power (load demand) of 14,590 kW with a PF of 0.892 (lagging). A load demand of 20 MW with a PF of 0.65 (lagging) is considered for both Case 2 and Case 3. The harmonic values of the systems for all three cases without using filters are listed in Table 1. From Table 1, it is clear that some harmonics in each case exceed the maximum permissible limits based on the IEEE standard, that is, the 5th harmonic current and the total harmonic current (THDI) exceed their tolerance value in Case 1. This means that they need to be mitigated. In Case 2, the 2nd order and 5th order harmonic current along with the 5th order harmonic voltage exceeded the maximum permissible limits, which proceeded with the THDI and THDV values exceeding the maximum tolerance values. They all need to be overcome. However, in Case 3, the situation was different. The 5th order harmonic current and the 5th, 17th, and 19th harmonic voltages exceed the maximum permissible limits, raising the THDI and THDV above the tolerances.

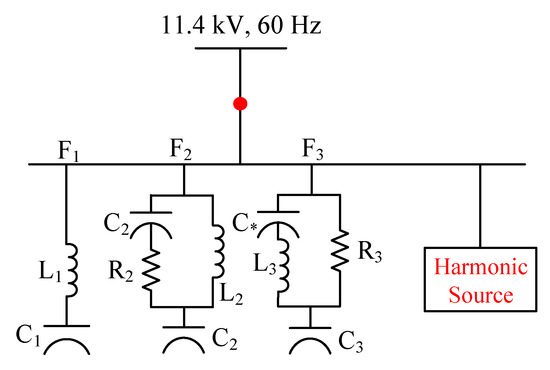
Figure 5. Schematic diagram of system with PPFs and nonlinear loads.

Table 1. Distributions of harmonic current and voltage without passive power filters.

Cases	Harmonic Orders	Current, A	Voltage, V	IEEE Standard 519
				Current, A	Current, %	Voltage, V	Voltage, %
Case 1	1	828.37	6581.79	-	-	-	-
	2	7.02	11.18	8.28	1	197.5	3
	3	8.64	20.63	33.1	4	197.5	3
	4	5.92	18.85	8.28	1	197.5	3
	5	45.8	182.3	33.1	4	197.5	3
	7	19.0	105.9	33.1	4	197.5	3
	11	15.4	134.9	16.6	2	197.5	3
	13	9.4	97.28	16.6	2	197.5	3
	THD (%)	6.55	4.11	-	5	-	5
Case 2	1	1558.3	6581.79	-	-	-	-
	2	19.2	30.57	15.58	1	197.5	3
	3	36.8	87.88	62.33	4	197.5	3
	4	5.41	17.23	15.58	1	197.5	3
	5	98.0	390.1	62.33	4	197.5	3
	7	18.0	100.3	62.33	4	197.5	3
	11	13.2	124.3	31.17	2	197.5	3
	13	12.6	130.4	31.17	2	197.5	3
	THD (%)	7.04	6.86	-	5	-	5
Case 3	1	1558.3	6581.79	-	-	-	-
	2	9.45	15.05	15.58	1	197.5	3
	3	15.6	37.26	62.33	4	197.5	3
	4	3.77	12.0	15.58	1	197.5	3
	5	62.7	249.6	62.33	4	197.5	3
	7	21.0	117.0	62.33	4	197.5	3
	11	19.4	166.9	31.17	2	197.5	3
	13	17.0	175.9	31.17	2	197.5	3
	17	16.0	216.5	23.38	1.5	197.5	3
	19	15.5	234.4	23.38	1.5	197.5	3
	THD (%)	4.92	7.42	-	5	-	5

5.2. Setting Parameters

To handle all these harmonics, the maximum number filter set used is a set of three, and the investment cost is set to 4000 pu. The short-circuit currents of the system are in the range of 8268 to 19,695A. Twenty bees consist of nine foragers, eight onlookers, and three scout bees distributed. A 100 size archive was chosen. Two hundred maximum iterations are taken, $w_b$, $w_e$ are in the range of [0.75, 1.5], and $r_b$, $r_e$ are in the range of [0, 1] are used for the proposed MOBSO. To confirm the efficiency of the proposed method, a solution obtained by the proposed method was selected and compared with that obtained by the SA proposed in [12]. Furthermore, popular optimization algorithms, such as PSO and BA, were used as benchmarks for comparison. The parameters of the MOBSO and other optimization algorithms are listed in Table 2.

Table 2. Parameters of MOBSO and other optimization algorithms.

Parameter	MOBSO	MOPSO	MOBA
Number of iterations	200	200	200
Population size	20	20	20
Other related parameters	$\mathrm{Foragerzise}=9$ $\mathrm{Onlookersize}=8$ $\mathrm{Scoutsize}=3$. Control parameters, $w_b\in \left[751.5\right]$$w_e\in \left[751.5\right]$	Cognitive parameter, $c_1=2.0$. Social parameter, $c_2=2.0$.	Maximum frequency, $F_{max}=2.0$ Minimum frequency, $F_{min}=2.0$ Constants, $\mathsf{\alpha }=0.9$ $\mathsf{\gamma }=0.9$

For Case 3, the decision variables used for the optimal design of the PPFs are as follows:

$${\overline{x}}_i={[L_1,C_1,R_2,L_2,C_2,R_3,L_3,C_3]}^t$$

Table 3 shows the planning results of the PPFs for each case determined by the proposed MOBSO method. In terms of cost considerations, THDI and THDV suppression, the results show that the PPF design by the MOBSO is more balanced than the PPF design determined by SA [12]. In other words, the performance of MOBSO was better than that of SA. Moreover, all the harmonics corresponding to each case were under the maximum permissible limit, as shown in Table 4.

Table 3. Comparisons of passive filter design results of MOBSO with SA.

Cases	Types of Filters	MOBSO	SA
Case 1 (PF = 0.95)	Single-tuned (F1)	$L_1=14.27$ $C_1=21.85$	$L_1=15.37$ $C_1=20.27$
	Single-tuned (F2)	$L_2=17.35$ $C_2=28.08$	$L_2=16.45$ $C_2=29.61$
	THDI (%)	4.74	4.79
	THDV (%)	1.29	1.30
	Cost(pu)	233.66	234.26
Case 2 (PF = 0.97)	Single-tuned (F1)	$L_1=3.61$ $C_1=86.46$	$L_1=4.32$ $C_1=72.24$
	C-type (F2)	$R_2=75.37$ $L_2=9.25$ $C_2=281.31$ $C*=760.67$	$R_2=51.84$ $L_2=8.21$ $C_2=302.40$ $C*=857.03$
	THDI (%)	4.89	4.95
	THDV (%)	1.30	1.35
	Cost(pu)	3170.02	3280.66
Case 3 (PF = 0.95)	Single-tuned (F1)	$L_1=4.03$ $C_1=77.46$	$L_1=3.67$ $C_1=105.42$
	3rd–order (F2)	$R_2=44.44$ $L_2=36.73$ $C_2=31.23$	$R_2=15.37$ $L_2=4.30$ $C_2=35.68$
	C-type (${\mathrm{F}}_3$)	$R_3=15.11$ $L_3=52.24$ $C_3=252.68$ $C*=134.69$	$R_3=40.44$ $L_3=15.25$ $C_3=218.95$ $C*=461.39$
	THD, (%)	3.99	4.81
	THDV, (%)	2.08	2.11
	Cost(pu)	1924.19	2431.17

In C-type PPFs, $C^{*}=1/\left({\omega }_1^{2}L\right).$

Table 4. Harmonic distortion of the solution obtained by MOBSO.

Cases	Harmonic Orders	Current, A	Current %	Voltage, V	Voltage %	IEEE Standard 519
						Current, A	Current, %	Voltage, V	Voltage, %
Case 1 $(PF=0.95)$	2	7.26		4.85		8.28	1	197.5	3
	3	9.88	0.93	9.91	0.07	33.1	4	197.5	3
	4	4.31	1.27	5.76	0.15	8.28	1	197.5	3
	5	26.04	0.55	43.50	0.09	33.1	4	197.5	3
	7	16.00	3.35	37.43	0.66	33.1	4	197.5	3
	11	13.58	2.06	49.90	0.57	16.6	2	197.5	3
	13	8.34	1.75	36.22	0.76	16.6	2	197.5	3
			1.07		0.55
	THD (%)	4.74		1.29		-	5	-	5
Case 2 $(PF=0.97)$	2	9.89		6.61		15.58	1	197.5	3
	3	36.87	0.94	36.96	0.10	62.33	4	197.5	3
	4	10.33	3.52	13.80	0.56	15.58	1	197.5	3
	5	27.14	0.99	45.35	0.21	62.33	4	197.5	3
	7	11.55	2.59	27.02	0.69	62.33	4	197.5	3
	11	10.14	1.10	37.26	0.41	31.17	2	197.5	3
	13	9.12	0.97	39.61	0.57	31.17	2	197.5	3
			0.87		0.60
	THD (%)	4.89		1.30		-	5	-	5
Case 3 $(PF=0.97)$	2	10.04		6.71		15.58	1	197.5	3
	3	18.05	0.96	18.10	0.10	62.33	4	197.5	3
	4	7.84	1.73	10.49	0.27	15.58	1	197.5	3
	5	19.35	0.75	32.33	0.16	62.33	4	197.5	3
	7	14.77	1.85	34.55	0.49	62.33	4	197.5	3
	11	14.81	1.41	54.46	0.52	31.17	2	197.5	3
	13	12.98	1.42	56.40	0.83	31.17	2	197.5	3
	17	11.99	1.24	68.10	0.86	23.38	1.5	197.5	3
	19	11.44	1.15	72.66	1.03	23.38	1.5	197.5	3
			1.09		1.10
	THD (%)	3.99		2.08		-	5	-	5

In Case 1, two single-tuned filters were used to eliminate harmonics because only the 5th harmonic and THDI exceeded the limit. According to the feasible combinations, all types of filters can be candidates for evaluation, and two single-tuned filters are most suitable in terms of cost and configuration. In Case 2, the 2nd order and 5th order harmonics exceed the limit. Therefore, for the 5th order, a single-tuned PPF was used. However, the 2nd order harmonic was enlarged. To eliminate the 2nd order harmonic, the combination of single-tuned and C-type filters is an evaluation candidate according to the selection strategy. In Case 3, the number of harmonics is higher than the above two cases, that is, the 5th order harmonic current and the 17th and 19th order harmonic voltages violate the limit tolerances of the IEEE standard. A single-tuned filter is used to suppress the 5th harmonic current. For the 17th and 19th harmonic orders, the 2nd order damped and the 3rd order damped filters are the evaluation candidates. A 2nd order damped filter can also be used. A 3rd order damped filter can be used to eliminate high-order harmonics, but it enlarges the lower-order harmonics such as the 2nd, 3rd, and 4th order harmonic current. Instead of a 3rd order damper filter, a C-type damped order is used.

5.3. Accuracy Test

The accuracy of the proposed MOBSO method was determined using the generational distance (GD) method. Veldhuizen and Lamont first proposed this method in 1998 [50]. The GD can be used to check the closeness of the estimated solutions with the true Pareto optimal set solution. The Monte Carlo Pareto optimal set is considered to be the true Pareto optimal set. The GD is given by

$$\mathrm{GD}=\frac{\sqrt{{\displaystyle \sum _m^n{d}_m^2}}}{n}$$

(35)

where $d_m$ represents the Euclidean distance between the estimated solutions and the nearest member of the true Pareto optimal set, and $n$ indicates the number of final solutions.

The GD value is inversely proportional to the closeness of the estimated solutions with the solutions of the true Pareto optimal set. That is, the lower the GD, the closer the solutions are to the true Pareto front. If the ideal case has zero GD, all solutions are in the true Pareto optimal set.

To verify the accuracy and reliability, the proposed MOBSO method was compared with the MOPSO method. Both methods were run 50 times with 500 iterations each time. Table 5 shows the GD obtained by the MOBSO and MOPSO methods. The GD obtained by MOBSO was lower than that obtained by MOPSO. That is, the solutions determined by MOBSO are closer to the solutions of the true Pareto optimal set than the solutions determined by the MOPSO method. Therefore, the accuracy of the proposed MOBSO method was higher than that of the MOPSO method. In addition, the 100 solutions are inserted in the external archive by the MOPSO method in 77 iterations, whereas MOBSO requires 42 iterations, as shown in Figure 6. The MOBSO method is, thus, faster than the MOPSO method.

Table 5. Generational distance determines by MOBSO and MOPSO (50 running times–25,000 iterations).

Algorithm	Generational Distance
	Best	Worst	Average	Median	Std. dev
MOBSO	0.00000150	0.0249	0.0002234	0.0001612	0.000722
MOPSO	0.00000196	0.0258	0.0002459	0.0001707	0.000854

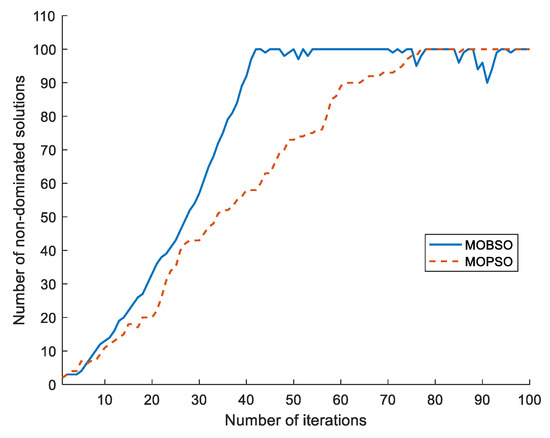
Figure 6. Number of non-dominated solutions inserted into the external archive of MOBSO and MOPSO.

5.4. Performance Test

In terms of MMD, Table 6 shows the most balanced or the best PPF design solution within the 400 solutions from all four types of filters. The sequence of solutions related to the types of filters for all cases is as follows:

Table 6. Most balanced types of PPFs determined by MOBSO among four different types of filters.

Case	Type of Filters	Sol. No.	Parameter										Cost	THDI	THDV	PF
			${\mathit{L}}_1$	${\mathit{C}}_1$	${\mathit{R}}_2$	${\mathit{L}}_2$	${\mathit{C}}_2$	$\mathit{C}*$	${\mathit{R}}_3$	${\mathit{L}}_3$	${\mathit{C}}_3$	$\mathit{C}*$
1	1	197	3.96	78.69									339.90	3.70	1.02	0.99
	1					25.01	19.48
2	1	15	3.45	90.34									3539.03	4.78	1.26	0.99
	4				59.52	7.65	314.96	919.76
3	1	63	3.12	100.0									906.47	4.41	1.18	0.98
	1				9.16	53.22
	2								24.17	17.88	160.02

• Case 1: Type 1 (1–100), Type 1-1 (101–200), Type 1-2 (201–300), and Type 1-3 (301–400).
• Case 2: Type 1-4 (1–100), Type 1-1-4 (101–200), Type 1-2-4 (201–300), and Type 1-3-4 (301–400).
• Case 3: Type 1-1-2 (1–100), Type 1-1-3 (101–200), Type 1-2-4 (201–300), and Type 1-3-4 (301–400).

For Case 1, the balanced type of PPF obtained by MOBSO is Type 1-1. For Case 2, the balanced type of PPFs obtained by MOBSO is Type 1-4. For Case 3, the balanced type of PPFs obtained by MOBSO is Type 1-1-2.

Table 7 shows the MMD results of MOBSO with two other algorithms: MOPSO and MOBA for Case 1 Type 1-1, Case 2 Type 1-4, and Case 3 Type 1-1-2. The topology mentioned above for each case can provide the most balanced solutions in the respective cases, as shown in Table 6.

Table 7. MMD results by merging all three algorithms: MOBSO (1–100), MOPSO (101–200), and MOBA (201–300) for Case 1, 2, and 3.

Case	Type of Filters	Sol. No.	Parameter										Cost	THDI	THDV	PF
			${\mathit{L}}_1$	${\mathit{C}}_1$	${\mathit{R}}_2$	${\mathit{L}}_2$	${\mathit{C}}_2$	$\mathit{C}*$	${\mathit{R}}_3$	${\mathit{L}}_3$	${\mathit{C}}_3$
1	1	53	4.50	69.24									312.22	3.75	1.04	0.99
	1					17.46	27.91
2	1	36	3.48	89.71									3377.88	4.79	1.27	0.98
	4				65.40	8.18	292.40	860.17
3	1	63	3.12	100.0									906.47	4.41	1.18	0.98
	1				9.16	53.22
	2								24.17	17.88	160.02

The MMD results select the final best solution among all the non-dominated solutions. Each method provides 100 solutions and merges them to select the balanced one out of 300 non-dominated solutions. The solution sequence was as follows: 1–100 (MOBSO), 100–200 (MOPSO), and 200–300 (MOBA). In each case, the sequence of the most balanced solutions obtained by the MMD lies between 1–100. The set of solutions was obtained using MOBSO, that is, the MMD results of MOBSO are better than those of MOPSO and MOBA. The Pareto front is obtained by the three algorithms (MOBSO, MOPSO, and MOBA) for each case with their respective topologies (see Figure 7, Figure 8 and Figure 9).

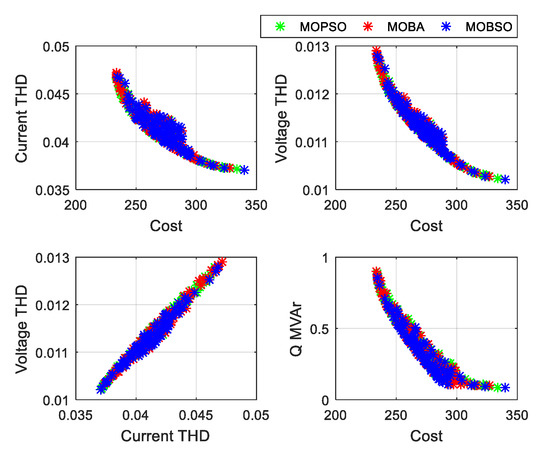
Figure 7. Pareto front obtained by MOPSO, MOBA, and MOBSO for Case 1 with PPF Type 1-1.

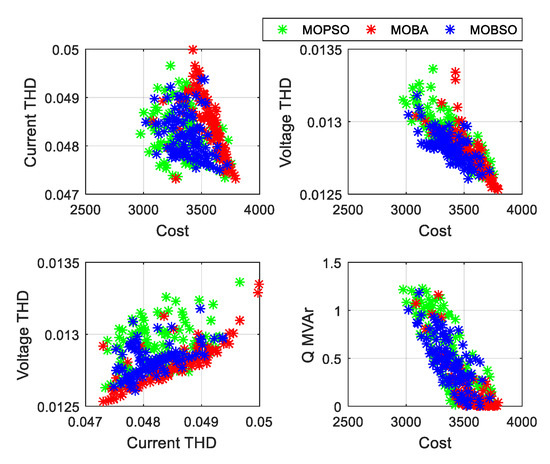
Figure 8. Pareto front obtained by MOPSO, MOBA, and MOBSO for Case 2 with PPF Type 1-4.

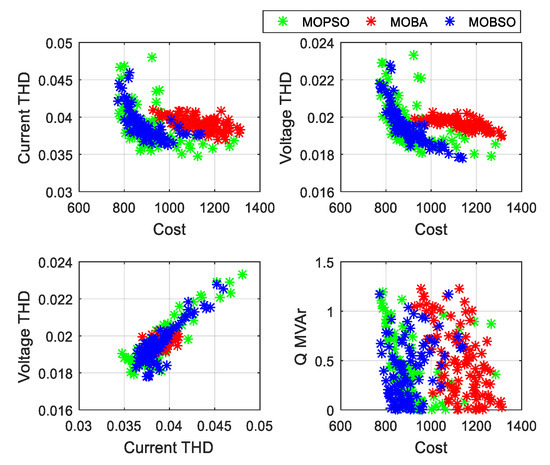
Figure 9. Pareto front obtained by MOPSO, MOBA, and MOBSO for Case 3 with PPF Type 1-1-2.

6. Conclusions

A MOBSO method was proposed to optimize the design of PPFs. An MMD approach was used to select the final balanced solution. In this study, four types of PPFs were considered, and a series of case studies is presented. First, three cases were considered to prove the performance of the proposed method and compare it with the well-known SA method. The results show that MOBSO performs better than SA in each case. Second, the GD method was used to verify the accuracy of the proposed method by comparing the results with those of the previous MOPSO method. The GD results indicate that the MOBSO method has a higher accuracy than the MOPSO method. Finally, the MMD results are presented to prove the superiority of the proposed method in two ways. First, the MMD results for three different cases under four different filter topologies were used to choose the most balanced combination of filters in each case. Second, compared with the two established algorithms, MOPSO and MOBA, the MMD results were selected from the set of solutions obtained by the MOBSO method. The proposed method has high accuracy, easy implementation, better performance, and the ability to create an optimal PPF design. Therefore, the proposed method has a very promising future not only in filter design but also in solving other multi-objective optimization problems.