Abstract
E-commerce sales have led to a considerable increase in the demand for last-mile delivery companies, revealing several problems in their logistics processes. Among these problems, are not meeting delivery deadlines. For example, in Chile, the national consumer service (SERNAC) indicated that in 2018, late deliveries represented 23% of complaints in retail online sales and were the second most common reason for complaints. Some of the causes are incorrectly designed delivery zones because in many cases, these delivery zones do not account for the demographic growth of cities. The result is an imbalanced workload between different zones, which leads to some resources being idle while others fail to meet their workload in satisfactory conditions. The present work proposes a hybrid method for designing delivery zones with an objective based on improving the quality of express delivery services. The proposed method combines a preprocess based on the grouping of demand in areas according to the structure of the territory, a heuristic that generates multiple candidates for the distribution zones, and a mathematical model that combines the different distribution zones generated to obtain a final territorial design. To verify the applicability of the proposed method, a case study is considered based on the real situation of a Chilean courier company with low service fulfillment in its express deliveries. The results obtained from the computational experiments show the applicability of the method, highlighting the validity of the aggregation procedure and improvements in the results obtained using the hybrid method compared to the initial heuristic. The final solution improves the ability to meet the conditions associated with express deliveries, compared with the current situation, by 12 percentage points. The results also allow an indicative sample of the critical service factors of a company to be obtained, identifying the effects of possible changes in demand or service conditions.
1. Introduction
A supply chain is the set of elements that allows the development and delivery of a product or service to its customers. Among the stages that can be found in a chain, one of the most important is the final stage, which is usually known as the last-mile service.
The last mile is the process by which a product is transported from the closest distribution center to the final customer [1]. This last-mile concept has been gaining increasing importance due to the enormous growth of e-commerce as well as the current COVID-19 pandemic situation, which limits people’s mobility. This is demonstrated, for example, by statistical data from Statista, where one can see that in mid-2014, online sales generated 1.3 trillion dollars worldwide, reaching 4.2 trillion dollars in 2020 [2].
Currently, the last-mile logistics process is considered one of the most crucial in the supply chain, not only because of the current importance of e-commerce but also because of how decisive it is and the impact it has in terms of customer satisfaction. It is also one of the points along the chain experiencing the most problems and that generates the most costs in the entire chain [3].
These problems can be structured in several groups. On the one hand, there are environmental problems that have to do with the ecological vision and commitment of each company. On the other hand, there are transportation problems caused, among other causes, by road congestion in densely packed areas, which prevents the efficient distribution of products. There are also problems associated with the relationship between the service and the customer with respect to the delivery of the product, such as not meeting delivery deadlines, failed delivery attempts due to the recipient not being present at the destination address, deliveries rejected by the customer given the poor condition of the packaging, and even deliveries not fulfilled due to lost packages. In summary, this final distribution phase presents several problems that need to be specifically addressed for an efficient operation.
The process of distribution to the final customer is usually carried out in two different ways: either by the workers of the company itself that sells the product or by outsourcing it to a logistics and transport company that performs the service of transfer of documents, parcels, or luggage of various customers from one origin to a destination (courier). This outsourcing is known as third-party logistics (3PL), is frequently used internationally, and is the most widespread in the Chilean market, since 3PLs have more experience, which leads them to having sustainable competitive advantages over time [4].
The courier market in Chile has experienced considerable changes in demand due to e-commerce, resulting in lower customer service metrics since it has been difficult for distribution companies to adapt to the increase in demand. This can be observed in the statistical data of customer satisfaction in the 2019 semiannual report of the ProCalidad de Chile organization and by the data provided by the website of the National Consumer Service (Servicio Nacional del Consumidor—SERNAC). In the ProCalidad data, the Couriers sector is classified into a group of many problems [5].
On the other hand, the National Consumer Service in 2018 received a total of 330,000 complaints, of which 33% were associated with retail. The online retail sales complaints were broken down into 53% due to noncompliance with the contracted conditions, 23% due to delays in the delivery of what was purchased, and 11.7% due to poor quality of service [6]. In addition, in 2020 and only during the first semester (during the period of pandemic caused by COVID-19), 72,000 complaints were received related to the delay of deliveries of products sold through e-commerce [7].
These statistics shows the relevance of proper on-time delivery as an integral part of any Customer Relationship Management (CRM) [8] strategy of a successful courier company. A CRM strategy should lead to improved customer satisfaction metrics, that helps to ensure loyal customers [9,10]. In order to achieve these results, a delivery company requires an effective logistic strategy, in which last-mile logistics play an important role. In fact, last-mile logistic were identified as a critical step with successful logistic strategies in early e-commerce literature, see [11] for an example, being delivery speed and delivery reliability two of the required capabilities of any successful last-mile logistics implementation [4].
This research originates from and studies a case observed in a courier company operating in the city of Antofagasta (Chile). Antofagasta is the mining capital of the country, and due to being isolated, suffers from a situation in which the distribution problems mentioned above are exacerbated. The company currently works with a distribution model that divides the city into 10 delivery zones, each of them assigned to a third-party delivery person who works with a long-term contract, freely organizing their operations within the assigned zone. The company offers various products that basically depend on the agreed delivery time. The most important service with the greatest number of problems is the Overnight (ON) service. Overnight service requires delivery before 11:00 a.m., with noncompliance of that deadline leading to the highest number of customer complaints and the highest noncompliance with internal service quality metrics. As an indicator, the initial service situation at the time this study was conducted showed that only 83% of deliveries met this condition, with the company’s short-term goal being to reach a level of service quality equal to 90%.
To alleviate the problems identified, the company needs to reevaluate its last-mile operations, moving from a cost-saving to a customer-based operational focus. Among the different changes that the company has to implement, this work focuses on the redesign of the delivery zones geared towards the fulfillment of the express delivery service needs.
Note that while the design of delivery areas falls within a broader class of problems known as districting in the scientific literature, see Section 2 for a review, our proposal differs from previous work on the metric used to evaluate the candidate districting plans. While the districting literature usually focuses on finding districts with a “fair” (i.e., even) distribution among them, our goal is to optimize a quality of service associated to the total expected number of late deliveries. This change modifies the structure of the problem, as the proposed method focuses on an overall metric built from the contributions of the selected delivery zones rather than on a similarity operational metric among delivery zones.
To solve this novel problem, a multi-stage hybrid optimization method is proposed that will be able to design new zones considering the critical factors of service. These delivery zones are defined by keeping in mind the quality of overnight service considering the time available for delivery and an estimate of the expected number of on-time deliveries according to the characteristics of the proposed delivery areas. The proposed procedure performs a preprocessing of the zone based on practical recommendations to add the deliveries in basic units assignable to the delivery zones, which allows maintaining some of the current practices’ territorial boundaries between distributors. Subsequently, a procedure is used that combines a random territory generator and a local improvement procedure, which generates alternative territorial configurations. Finally, these alternative configurations are combined through an integer linear program to obtain a final proposal. This procedure is tested in instances derived from the daily operations of the company, as well as in a case study situation, showing significant improvements with respect to current operations. Specifically, it is possible to achieve a level of quality of service greater than 95%, which illustrates the improvement obtained by the proposed process. Our experiments show the advantages of the different elements of our solution methodology. First, the aggregation approach balances computational requirements with solution quality, as more fine-grained aggregation schemes increase computational times without leading to better solutions in terms of quality. Second, the proposed constructive procedure followed by a local search method is able to provide high-quality delivery areas. Moreover, the generated areas are sufficiently diverse to provide a pool of partial solutions, which the combination procedure is able to use to obtain new and better districting plans.
The rest of the work is structured as follows. Section 2 performs a study of the available literature associated with the design of territories. Section 3 describes the problem addressed and the data processing performed. Section 4 describes the proposed resolution procedure, while Section 5 details the results of the experiments performed. Finally, Section 6 describes the conclusions reached and the possible extensions to be made in the work.
2. Literature Review
The problem of territory design or district design is a problem that consists of grouping small geographic areas, called basic units, into larger geographic groups called districts or territories in such a way that these territories are acceptable according to the planning criteria considered [12]. In the 1960s, Hess et al. [13] proposed the first works on the design of territories in an electoral context. In his research, the authors use a mathematical model and a heuristic to create electoral districts. The intention was to find territories with a similar number of voters (i.e., following the premise of “one man, one vote”) while avoiding the manipulation of electoral constituencies to favor certain candidates or parties (a defect known as “gerrymandering” in the literature). Subsequently [14] extended the same approach to a problem of the design of sales territories. In this case, the objective is to achieve equitable territories with respect to the associated workload between different vendors.
These investigations served as a starting point for the area, which was later expanded to a wide range of applications and resolution methods, both exact and heuristic or metaheuristic. Within the different applications, we can find both in the areas already mentioned, that is, the design of political territories [15,16,17] and that of sales territories [18,19,20], as in other areas, such as the design of service areas, in settings as diverse as home health care [21,22], police patrolling [23,24], the design of school districts [25], the design of energy distribution networks [26], or waste collection [27,28]. Finally, and of special interest for this work are the applications related to the design of distribution territories [29,30], which is the area in which this work is focused. The design of distribution territories consists of designing zones for the pick up and/or delivery of products to customers residing in the zone. Each of these areas is assigned one or more carriers, which will establish one or more service routes each day, starting from a warehouse where the products are stored.
Regardless of how the territories obtained are applied, there are a series of requirements and attributes that all the problems of territory design share and that serve as a point of comparison between the different studies [31]. Within the requirements, there is a unique assignment that implies that each basic unit, that is, each geometric object associated with customers or users, must be assigned to a single territory. Another criterion is the balance between different territories according to some measure. For example, in the distribution of goods, the measure is usually the workload, whose balance seeks to avoid comparative differences between workers. This workload can be represented, for example, by the number of customers in each zone [30].
The compactness of the generated territories is another of the typical requirements for this type of problem. The geometric interpretation of compactness corresponds to a preference for territories with rounded or rectangular shapes that do not have distortions or holes. This helps, for example, that the districts include customers that are close to each other, favoring efficient operations (for example, delivery routes). Finally, another typical requirement is that of contiguity, which is defined as the ability to travel between basic units of the same territory without having to leave it. Although these last two criteria have specific definitions, there is no single representation of the concepts of compactness and contiguity since they depend largely on the problem and its attributes.
Among the attributes of the problem, we highlight those linked to the type and characteristics of the basic units (the representation of the units or customers to be grouped) and of the districts (the groups to be created). For example, the type of basic unit indicates how customers are represented in space and may correspond to coordinates [29], lines, or geometric figures that define urban blocks [32], while the characteristics of the districts, such as the number of territories to be created, are usually fixed according to the characteristics of the system being designed (for example, it can be equal to the number of carriers that the distribution service provider has) or the variables that are to be optimized [29,33,34].
Considering that the territory design problem corresponds to an optimization problem in which one tries to optimize some objective function that indicates the quality of the solution offered by an optimization method, it is necessary to review the resolution methods that have been used in the literature for the problem of territory design and specifically for the design of territories in the area of logistics and distribution.
Among the methods that can be found are the exact methods based on mathematical programming techniques, which seek to obtain a global optimum as a solution to the problem. Optimality has only been achieved in cases with few customers due to the computational complexity of the territory design problem, which is a computationally NP-hard problem [35]. Among the different exact methods are [21,26,36].
Another type of available procedure is one that combines heuristics or metaheuristics with mathematical programming techniques, usually called matheuristics [37]. In [29] a large-scale design of territories is performed using data from up to 45,000 delivery points, in which the objective is to divide a set of customers into the minimum possible number of territories that satisfy the geometric condition of having a rectangular shape, as well as considerations of vehicle capacity and the time limit of the distribution service. To do this, ref. [29] apply a column generation procedure based on an extension of the capacitated clustering problem with which they search for candidate territories that meet the conditions and considerations described above, combining it with a metaheuristic based on the tabu search to select the best candidates.
Another type of research that also combines a heuristic method with another based on an exact method is that by [38]. In this work, territories are designed by partitioning concentric rings around the distribution center with the objective of minimizing transportation costs. These costs include vehicle operating expenses, such as the cost per mileage and delivery time, as well as an extra cost in case of exceeding the service time limit. It is important to mention that to reduce the computational effort, the Beardwood approximation [39] is used to calculate the service time and the distance traveled in each territory. The method used to solve this problem is an extension of a gradient method combined with a genetic algorithm. The procedure differs from a previous version by the same researchers [34] in that the formulation of the variables is continuous, which avoids cumbersome data preparation and the creation of disjointed concentric cell partitions.
In [33] a hybrid approach is also carried out in the design of territories for a meat distribution company. In this case, two K-means algorithms are used to partition the area and create candidate territories, which are then combined with a mathematical model based on formulations of a set covering model, which seeks to minimize the number of territories needed to perform the distribution service. It is important to mention that in this research, the level of service is represented, approximating the time it takes for the distribution service with the formula proposed in [40] since it allows an approximation with differently shaped territories without assuming a distribution of the customers in the zone.
A different resolution method consists of using tools derived from computational geometry. Generally, these methods are based on Voronoi diagrams to define territories. A Voronoi diagram consists of partitioning a plane from the intersection of the bisectors of a set of points. Through the intersection of these bisectors, polygons are formed that represent the area that contains the positions closest to the points of the set. In [41] the use of a weighted multiplicative version of these diagrams to define territories was studied. The weighted multiplicative version allows greater flexibility to create territories with a balanced number of customers. In this research, the balance criterion approximates the time it takes for vehicles to deliver to customers in each territory using the Beardwood formula, adding the round-trip distance to the warehouse and considering the service time for each customer.
Finally, there are heuristic methods that are ad hoc procedures for solving the problem. Within these are the metaheuristics that can be classified into three groups according to the basic ideas they represent: constructive procedures, neighbor exploration procedures, and population procedures. The constructive procedures yield a final solution through small steps in which simple decisions are made (for example, the inclusion of a basic unit in a district) and, generally, they take the one that seems the best choice in each step. On the other hand, metaheuristics based on neighbor exploration begin from an initial solution of the problem that is progressively improved through small modifications.
Finally, population-based metaheuristics procedures imitate the process of biological evolution, which consists of constructing new solutions from the combination of others. Among the numerous metaheuristics available for this type of problem, the most common are the Greedy Randomized Adaptive Search procedure, GRASP, metaheuristic [30,42,43,44], genetic algorithms [45], simulated annealing [23] and the tabu search [46].
Finally, it should be noted that although the bulk of the literature considers problems with a single objective, there are several studies that try to optimize two or more functions together in the field of service territories [47], political territories [48], or sales territories [32].
3. Problem Description
This section describes the problem addressed in this work, indicating the requirements and attributes of the problem, the starting data, and the objective sought in it.
As a starting point, there is a historical log of addresses with deliveries made in a delivery zone—in our case a city. The basic demarcations of the city are known (geographic limits, streets, and main avenues). These demarcations constitute the set of geographical characteristics that the company and the distributors use to designate the boundaries of the distribution territories. For each customer, their spatial coordinates are available (that is, their latitude and longitude) as well as the days in which a delivery was made to the customer (so the frequency of deliveries for each customer can be obtained, that is, the percentage of days in which the customer has had one or more scheduled deliveries). We also know the spatial location of the warehouse from which the deliveries begin, the traffic speed on expressways (such as “beltways” and highways) and within the city (through the streets), as well as the number, k, of territories to be designed.
In the first phase of preprocessing, basic demarcations are used to group customers into basic units. To do this, the city is divided using these demarcations, which are the same ones that the distributors use to delimit their areas in a logical way (that is, through avenues, main streets, and other physical divisions of the territory). The use of these demarcations has two benefits: first, it allows creating logical territorial groupings with the daily operations observed in practice; and second, it ensures that the territories (distribution zones) are better adopted by the workers and the managers of the company. This is an important step to ensure the applicability of the solutions provided by our solution method. Due to the particularities of the operations considered in our case study, see Section 5.2, the aggregation into basic units helps stakeholders to voice their opinion on how clients should be grouped into small areas that are to be serviced together.
Figure 1 shows an example of the divisions created in one zone of the city.
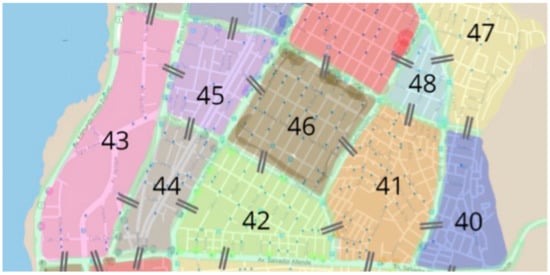
Figure 1.
Divisions created in a zone of the city studied in the case study. The different groupings are shown in different colors, while the roads used to delimit the territories are highlighted in green. Additionally, the adjacency among basic units are shown through the inclusion of two lines between adjacent territories.
Two basic units are said to be adjacent if they share a boundary. Figure 1 indicates these adjacency relationships through two lines. Computationally, the adjacency relations are coded through a graph G(V, E), where the vertices, V, are equivalent to the basic units and the edges, E, correspond to the adjacency relations between the basic units associated with both ends of the edges.
Each basic unit also has two associated labels that correspond to its equivalent workload and its center of mass. The equivalent workload of a basic unit is equivalent to the sum of the delivery frequencies of its addresses, the blue dots that can be seen in Figure 1, that is, the expected number of daily deliveries associated with customers located in that basic unit. The center of mass of each basic unit corresponds to the average of the coordinates of the customers weighted by their delivery frequency.
The basic units should be grouped into k territories under conditions of contiguity and quality of service. The quality of service plays the role of balance in other problems of territory design, although it does not necessarily imply that a regular distribution of deliveries is generated. Note that compactness, as described in Section 2 is not considered explicitly, but the blocks used to design the basic units inherently include an aspect of compactness, and the quality of service function that will be shown below penalizes the creation of unbalanced territories or odd structures in terms of their shape or size.
The condition of contiguity is established as a hard condition, that is, as a constraint that all solutions must meet to be considered valid and that forces the vertices of the basic units making up a territory to be connected in graph G(V, E). This condition can be verified by checking whether the subgraph induced by the subset of vertices associated with the basic units making up the territory constitutes a connected graph. This operation is easy to evaluate through an algorithm such as that of Hopcroft and Tarjan [49].
The quality of service will be the objective criterion used to evaluate the different territorial proposals and corresponds to an approximation of the expected number of late deliveries based on the proposed territorial design. Note that these characteristics makes our work depart from other works, as we focus on a service objective and estimate number of deliveries and not the cost of performing the delivery. The approach adopted in this work is constructed through an estimation of the time required by three components: (1) the time required to reach the territory from the logistics center (the warehouse) and (2) the service time required to deliver to each of the customers in the territory, and (3) the travel time in the territory between the various customers. The time to return to the warehouse is not taken into account since after making express deliveries, other deliveries will continue to be distributed throughout the day. The estimation of the service time allows the calculation of the number of maximum deliveries that can be made within the delivery window set by the service, and the difference between the expected number of deliveries and the maximum number of possible deliveries—in case such a difference is positive, it will be our estimate of the quality of service.
Each of the three time estimates is determined as follows.
The time it takes for the carrier to go from the distribution center to a territory, which we call , is calculated as the minimum distance between the distribution center and the territory multiplied by the average speed of travel on expressways. The calculation of this distance is performed by looking up the minimum distance between each basic unit that makes up the territory and the distribution center and selecting the minimum between them.
To determine the expected route time within the territory, the tour length to visit the customers is estimated. Generally, this step would correspond to the resolution of a traveling salesman problem (TSP) in case of knowing the specific customers that must be served. Given that the exact customers of each workday are unknown and the TSP is a complex problem in itself [50], it is decided to estimate the tour length using a “distribution-free” approximation as proposed in [40] and then multiply the length of the route by the average speed of travel observed within the urban center, which we denote as .
- () is the average of the distances between the delivery points and the central horizontal axis (central vertical axis);
- () is the standard deviation of Tpoints;
- () is the standard deviation of the absolute distance of the delivery points with the central horizontal axis (central vertical axis);
- is the area of the territory on which the approximation will be made;
- n is the number of delivery points within the territory.
As in [40], the central horizontal axis and the central vertical axis are defined as the midpoint of the space in which the distributions are made.
Finally, the service time per delivery, which we call , corresponds to an estimate of the time it takes for the recipient of the package to open the door, receive the package and sign the document that proves receipt of the delivery. This time must be multiplied by the number of deliveries to be made.
By combining the three factors, Equation (2), an estimate of the total time required to serve a territory, T, is obtained:
Given that it is intended to determine the maximum number of customers to serve in the time available for deliveries and that all the parameters of (2) are known except the number of customers n, the procedure to determine the quality of the service will obtain the value maximum of n such that (2) is less than the available time window for deliveries, and then this number will be compared with the number of deliveries within the territory. If the maximum number is less than the number of deliveries that must be made, then the difference between both will correspond to the number of late deliveries of the territory; otherwise, it is estimated that all deliveries can be made on time so the quality of service would be 100%, i.e., no late deliveries. Note that the description and the implementation aim to minimize the expected number of late deliveries, a measure of “disservice”, rather than to maximize the number of deliveries on-time. For all intents and purposes, both objectives are identical and, while the code internally minimizes disservice, solutions are reported in terms of quality of service.
In summary, the problem can be formulated as the assignment of the basic units to k groups in such a way that:
- Each basic unit belongs to a single grouping (i.e., to a single territory);
- The basic units of each grouping generate a related subgraph;
- The sum of the average number of late deliveries in the set of territories is minimized.
As mentioned above, the model does not verify the compactness of the solution, but the function that determines the length of the delivery route, Equation (1), favors the construction of compact districts when evaluating the deviations of the coordinates of the deliveries. Another important aspect of the model described is that when estimating the load of each basic unit as the value observed for the deliveries made during a period of time in that geographical area, the model does not work directly with customer history. This avoids the biases that could be created by assigning the past locations of customers as the only existing basic units. Furthermore, it is no longer assumed that historical delivery locations will be the same as future deliveries, nor will the distribution of deliveries in the future be similar to the historical distribution.
4. Proposed Solution Methodology
This section details the hybrid procedure proposed to solve the problem. This procedure is divided into two parts. The first part, which is described in Section 4.1 and Section 4.2, corresponds to a multi-start procedure that generates alternative solutions to the problem through a constructive procedure followed by a local improvement procedure. Although the multi-boot procedure has certain requests with a GRASP metaheuristic, it differs from it in the use of a completely random constructive strategy against GRASP in that the constructive phase limits the selection made at each step to a subset of candidates. This part does not use the quality of service function shown in Section 3 but rather optimizes an alternative function with less computational calculations, which significantly reduces the total time required by the algorithm.
In the second part, the level of service of each territory generated in the first part is evaluated, and a mathematical model is solved that attempts to combine the territories constructed by the multi-boot procedure looking for new and better combinations of territories that configure the final territory design. The evaluation of the quality of the proposed method, as well as the contribution of the second phase to the quality of the final procedure, is shown in Section 5.
4.1. Constructive Heuristic
The constructive phase is responsible for forming feasible territories, which will act as initial solutions for local improvement. The constructive method is detailed in Algorithm 1.
| Algorithm 1 Description of the constructive algorithm |
| Input: Number of territories k; Graph G(V, E); Coordinates of each basic unit. Output: Solution of the problem with k territories. 1: Select k different basic units at random and assign to each territory. 2: repeat 3: for each territory and basic unit v do 4: if v is not part of a territory but is adjacent to the territory then 5: Add the pair to the list of iteration candidates. 6: Select a candidate pair according to (3) and assign the basic unit v to the territory. 7: until Base units remain unassigned |
The first step of the constructive phase is to generate an amount of “seeds” for the territories equal to the number of clusters to be constructed. Each of these seeds corresponds to a different basic unit and will serve as a point from which the different territories will “grow”.
The next step is to find the basic units that can be assigned to the clusters under construction. Initially, the basic assignable units are those that are adjacent to the seeds of the clusters and that do not yet form a territory. Subsequently, they will correspond to any basic unit that is not part of a territory and that is adjacent to another basic unit that is part of a territory. Note that by restricting the search for candidates to basic units adjacent to basic units that are part of a territory, the connectivity condition of the resulting groupings is ensured.
After determining the candidates, we proceeded to calculate the distance between each of the candidates and the “seed” of its adjacent territory, considering as the distance between two basic units the Euclidean distance between the centers of mass of both basic units and a candidate-seed pair whose probability is proportional to the inverse of the distance between the “seed” and the district is chosen (that is, the shorter the distance of the basic unit with the seed, the greater the probability of being chosen). Let be the distance between a candidate basic unit v and a territory and let be the set of all candidates to be assigned to district . Then, (3) indicates the probability that the basic unit v is selected during this phase and is assigned to territory ,
Equation (3) gives each pair of candidate basic unit and territory a probability proportional to its distance between the basic unit and the “seed” of the district, the numerator of the equation. The denominator ensures that the sum of probabilities of all candidates equals 1, by dividing each numerator by the total sum among all numerators of the pairs of candidate basic units and territories.
This approach, in which a probability is assigned to any candidate instead of limiting the decision to the best candidate or a subset of candidates, allows increasing the diversity of solutions facing the subsequent steps of local improvement and solution combinations.
This process of candidate identification and the assignment of a candidate to a grouping is repeated until all basic units are part of a territory. These solutions do not take into account the objective of the problem directly but do try to obtain compact territories by assigning basic units, seeking to minimize distances with respect to a central unit.
4.2. Local Search Procedure
With the initial solution constructed, a local search is performed to “improve” this solution with respect to a metric that describes the balance of deliveries between different districts. The development of the local search phase is summarized in Algorithm 2.
| Algorithm 2 Description of the local search phase |
| Input: Initial solution; Number of territories k; Graph G(V, E); Workload of each basic unit. Output: Solution of the problem with k territories. 1: repeat 2: Initialize better change to null change 3: for each basic unit v do 4: for each territory do 5: if the assignment of v to is feasible then 6: Evaluate balance load, , according to Equation (4) 7: if the solution is improved and better change is improved then 8: Save v and as better change 9: if better change is not null change then 10: Implement change 11: until better change is null change |
The neighborhood used in the improvement process is defined by changing the assignment of a basic unit. Such change corresponds to extracting a basic unit (other than the seed of a territory) from some grouping and adding it to another grouping, maintaining the condition of contiguity (connectivity of territories). After moving, it is verified if the movement is feasible, that is, the two territories affected by the change continue to define related subgraphs in G(V, E), and it is evaluated whether there were improvements with respect to an auxiliary function that allows us to analyze the balance in the workload of the resulting territories. For this (4) is evaluated where v is the basic unit that leaves district and becomes part of district , is the workload of the basic unit and and are the current workloads of districts and respectively. In the case that , Equation (4), is positive, the move is considered an improvement since it reduces the load of the most loaded district associated with the change.
Equation (4) evaluates the effect on the workload balance between the districts involved in the change. By comparing the workloads among the most loaded districts, Equation (4) helps to identify candidate districting plans in which the workload differences among districts are small.
Note that the verification performed in (4) does not correspond directly with the objective function of the problem, but the calculation time of (4) is less, and preliminary computational experiments showed that territories with similar workloads had better quality of service values. The logic behind this result is that distributing deliveries equitably between delivery zones helps to obtain territories with similar workloads and avoids concentrating many deliveries in some districts, while others do not have enough; see Section 5.2 for an analysis of the associated importance to balance the number of deliveries for each district. In addition, seeing the equal distribution of work between the different distribution zones is easily interpreted within the operations of the company.
The local search is organized as a “best-improvement” procedure; that is, all possible feasible insertions are considered, of which the one that generates the greatest impact on the balance is kept. When all the changes have been reviewed, the change that leads to the greatest improvement in the auxiliary function is applied, and then all possible changes are checked again. The algorithm ends when there is no feasible change that improves the value of the auxiliary function. The implementation chooses to organize the search as “first improvement” since the second option showed biases in the order in which the basic units were considered within the procedure. In the case of using a “best-improvement” type move, it is observed that the algorithm tends to vary the districts and basic units involved in the changes made more frequently than in the “first-improvement” type search.
4.3. Combination of Solutions through Integer Programming
As the aforementioned heuristic generates many feasible solutions and the territories that comprise it have not been directly evaluated with the quality of service metric that is sought to be optimized, it is important to carry out a process that evaluates the territories according to the final metric and selects the best combination of territories according to this criterion. For this reason, the third step of the proposed method proposes a mathematical model that selects the best subset of territories among those found by the feasible solutions of the heuristic to reduce the average number of expected late deliveries. This third step also contributes to a better use of the solutions found during the first phase and can be seen as a phase of search intensification similar to a common “path relinking” in many implementations of the GRASP metaheuristic [51].
Let I be the set of feasible territories obtained as a result of the first phase. Each territory has an associate number of late deliveries obtained as indicated in Section 3 and a vector of length which has value 1, , if the territory i includes the basic unit j () and value 0, , if not. For each territory a binary variable is defined that will take value 1 if the territory is selected and 0 if not.
With these data and variables, Formulations (5)–(8) constitute a valid formulation for the problem of selecting territories among those available.
Equation (5) represents the objective function, which seeks to find a design of territories that has the least number of late deliveries. This objective is achieved by adding the number of late deliveries, , of the districts selected by the solution to the formulation, those districts whose variable take value 1. Constraint (6) indicates that the set of territories chosen must be composed of a number of k territories by enforcing that the number of districts whose variable take cvalue equal to 1 is exactly equal to a predetermined constant k which is a parameter of the problem. Constraint set (7) indicates that all urban blocks have to be assigned to a territory, by ensuring that exactly one district is selected, its variable takes value equal to 1, if it includes the urban block, that is, if . Finally, the decision variable is defined as a binary variable, as observed in condition (8). The resolution of the mathematical model is performed through a standard integer linear programming solver; see details in the next section. The model corresponds to a set partitioning problem with the additional condition that exactly k districts must be chosen among the available.
Given that each of the territories of the set of territories meets the conditions of connectivity, that the model ensures unique assignment of each basic unit to a territory and that the number of districts to be constructed is chosen, the resulting solution of optimizing (5)–(8) is a valid solution for the design of territories analyzed. In addition, this model always has a feasible solution since each solution obtained during the local search procedure is a feasible solution to the problem. Note that this step can be generalized to any other districting problem in which the combination of different districting solutions can be seen as a partition problem and the objective function can be obtained through the summation of the aggregation of each district.
Finally, it is important to comment that sometimes the proposal presented can generate solutions that do not meet some additional conditions of service that are useful in practice. In practice, these conditions are presented in such a way that two basic units cannot be assigned to the same territory. In this case, the model can be adapted to the requirement by eliminating those territories that do not meet the indicated condition without needing to change the model. Although this characteristic is not discussed in the computational results shown in Section 5, it does contribute to the practical applicability of the resolution procedure described.
5. Computational Experiments
This section presents the results of the computational experiments and the analysis of the results obtained by the procedures shown under different conditions and parameters.
The procedures described in the document were programmed in C language using IBM ILOG CPLEX version 12.10 to solve the integer linear program described in Section 4.3. The experiments were performed on a computer running an Intel i5 8600K processor at 3.6 GHz, 16 GB of RAM under the Windows 10 professional operating system.
The instances used in the experiments come from the delivery database of a courier company that operates in the city of Antofagasta (Chile). This database includes 21,025 deliveries made over 19 business days. Of the described deliveries, 4768 correspond to express parcel service, while the rest correspond to regular service. The delivery schedule begins at 9 a.m., and the limit imposed for express deliveries set by service conditions is 11 a.m., so 2 h are available for express deliveries. The number of territories (delivery zones) to be created is set at 10 since this is the value currently used and corresponds to hiring 10 independent distributors who work exclusively for the company. Finally, the time associated with each delivery is equal to 2 min, and the speeds within the city are at 14 km/h, while the speed on the main roads is 31 km/h. These values come from a study conducted by the traffic control operational unit in Chile. Note that while the instances and constants specifically refer to a particular situation, there is no reason to think that there is a bias introduced within the results due to this decision.
The set of instances was obtained by sampling for three demand scenarios: low demand (half of that observed in the data collection period), medium demand (that observed in that period), and high demand (double that observed) which are equivalent to 2384, 4768, and 9536 deliveries over 19 days. For the medium demand, those registered in the database are used as deliveries, while for the low demand, half of them are randomly chosen. For the scenario with high demand, an identical number of new deliveries chosen at random from the locations of the regular service deliveries are added to the deliveries considered in the medium-demand case. Although they are services performed at different times, they have similar demand behaviors, so this option is chosen to generate instances with higher demand.
During the preprocessing, three levels of granularity are considered in the definition of basic units, that is, different amounts of urban blocks (basic units) into which the city is divided during the preprocessing. These levels correspond to 43, 85, and 128 urban blocks.
For each of these combinations of demand levels and number of basic units, the territorial distribution is designed with different numbers of territories (for the low demand level, 5 and 7 districts are designed, for the medium level 5, 7, 10, and 12 districts and for high demand 5, 7, 10, 12, 15, 20, 22l and 25 districts).
Finally, a limit is imposed on the number of solutions proposed by the constructive heuristic equal to 50, 100, 200, 500, 1000, 5000, and 10,000 solutions, and the resolution time of the mathematical model is limited to 600 s. Given the reduced computation times of the proposed heuristic, which uses a simplified evaluation function to speed up the calculations, the total calculation times never reached 1200 s, a time that is considered reasonable in the practical environment analyzed since the design of territories is carried out every several years. The computation times of the heuristic solutions and of the integer programming procedure are also considered separately since it is possible to reuse the solutions constructed by the heuristic to obtain alternative solutions with the mathematical model if required.
5.1. Results from the Experiments
The results of Table 1, Table 2 and Table 3 show the detailed results for each instance, identified by the number of basic units (column ‘BUs’), the number of districts to build (column ‘#’), and the number of solutions generated by the first phase of the procedure (columns ‘50’ to ‘10,000’). The number reported is the estimated number of late deliveries, so the level of service would correspond to 1 minus the fraction between the number of late deliveries and the total number of deliveries to be made as indicated in the description of each table.

Table 1.
Average of late deliveries on the worst day by the number of solutions generated during the first phase of the algorithm, Columns ‘50’, ‘100’, ‘200’, ‘500’, ‘1000’, ‘5000’, and ‘10,000’ and instance parameters (number of basic units in column ‘BU’, and number of generated districts in column ‘#’) for instances with low demand.

Table 2.
Average of late deliveries on the worst day by number of solutions generated during the first phase of the algorithm, Columns ‘50’, ‘100’, ‘200’, ‘500’, ‘1000’, ‘5000’, and ‘10,000’ and instance parameters (number of basic units, column ‘BU’, and number of districts generated, column ‘#’) for instances with medium demand.

Table 3.
Average of late deliveries on the worst day by number of solutions generated during the first phase of the algorithm, Columns ‘50’, ‘100’, ‘200’, ‘500’, ‘1000’, ‘5000’, and ‘10,000’ and instance parameters (number of basic units, column ‘BU’, and number of districts generated, column ‘#’) for instances with high demand.
In the three scenarios, it can be observed that when the number of territories (or delivery zones) increases, the number of late deliveries decreases considerably, which shows that increasing the number of districts positively influences the level of service. This conclusion is logical and shows that there is a possibility of improving the quality of service through an increase in current subcontracted services, although there comes a time when increasing the number of districts does not generate great benefits. Specifically, for the current demand scenario, with a medium level of demand and 10 districts, an increase of 20% in the number of districts (going from 10 to 12 districts) would lead to substantial improvements and an expected fulfillment of almost 100% of the on time deliveries. If the results associated with changes in demand are compared, it can be seen that the current delivery service would not be able to cope with a significant increase in demand (a high number of deliveries scenario), requiring a significant growth in the number of districts to be able to adapt to this change.
With respect to the procedure of aggregating urban blocks, it can be seen that in the scenarios with low and medium demand, there are no appreciable differences in the results, which indicates that the grouping factor applied does not influence the results obtained. On the other hand, in the high demand scenario, it can be observed that increasing the granularity (a greater number of basic units) has a positive effect on the results obtained using this method. From this result, it can be inferred that the correct level of granularity depends on the number of deliveries to be analyzed and that if the level of aggregation is correct, the effect on the results is minimal. It should be emphasized that greater granularity implies a greater computational effort with respect to the resolution method, so it is important to define a degree of grouping consistent with the practical needs of the problem (for example, maintaining assigned distribution zones that make sense for the distributor) and the possible improvements derived from subdividing the territory into zones that are increasingly difficult to operate from a day-to-day operations point of view.
Regarding the number of independent executions of the first phase of the procedure, it is observed that when increasing their number, there is a small decrease in the number of late deliveries in the three respective scenarios. However, these increases are sometimes lower and imply an increase in computational effort, so it is necessary to know to what extent these changes are significant and thus reduce the run time of the procedure.
To measure how significant the use of different initial solutions is, a parametric ANOVA with blocking factors test is performed. In this case, the comparison element is the number of independent runs of the first phase of the procedure, that is, 50, 100, 200, 500, 1000, 5000, and 10,000 independent runs. A block design is chosen so that the test considers that part of the variations are caused by the different instances used (number of districts, granularity). The test performed takes as a null hypothesis that the treatments are equal, which leads to a negative outcome since the treatments show significance with a p-value of . Additionally, a nonparametric test, the Page test [52], is performed to avoid possible problems of the nonnormality of the residuals. This test also rejects the null hypothesis with a p-value of , which leads us to conclude that the number of independent runs of the metaheuristic impacts the results obtained by the algorithm.
To identify which treatments are significantly different, a nonparametric hypothesis test called the “Distribution free Two-Sided all-treatments multiple comparisons based on Friedman rank sums” (Wilcoxon, Nemenyi, McDonald, and Thompson) is applied, which performs multiple comparisons between pairs of treatments. The results of the test are shown in Table 4.

Table 4.
Results of the Wilcoxon, Nemenyi, McDonald, and Thompson test to identify possible improvements associated with the generation of a greater number of solutions during the first phase of the analyzed procedure.
The results of the nonparametric pairwise comparison test show that each increase in the multi-boot level implies a significant difference between the medians with a significance level of 95%. However, the comparison between 5000 and 10,000 has low significance and may not justify the additional computational cost.
In the previous tables of the 3 scenarios, when going from 5000 to 10,000 executions of the heuristic, it can be observed that the average change is smaller compared to the other increases in the number of executions of the heuristic.
Finally, Table 5 evaluates the effect of adding the second phase of the method, that is, the resolution of the mathematical model on the performance of the proposed procedure. For this, the percentage decrease in the number of late deliveries recorded by using the mathematical model is evaluated. This value results from dividing the difference between the expected number of late deliveries of the best solution of the first phase and the second phase by the expected number of late deliveries of the first phase. In this case, a different behavior can be observed according to the levels of grouping (number of basic units), number of solutions generated, and number of territories to be constructed. Specifically, it is observed that as the number of territories and alternative solutions increases, the differences are very significant, especially when a greater number of districts are constructed.

Table 5.
Percentage of improvement obtained by the use of the second phase of the proposed procedure (number of districts generated, column ‘#’).
5.2. Results from the Case Study
Considering the analysis performed in Section 5.1 with respect to the solutions obtained, it is decided to offer a solution to the new territorial design using the original conditions considered by the company (10 districts, medium demand) using a configuration of the procedure that uses 5000 iterations of the constructive heuristic followed by the combination of territories following the mathematical model.
In addition, given that the differences between the medium and high granularity levels were not significant for the scenarios with current demand, a medium granularity was chosen to offer solutions. This combination of characteristics of the procedure allows generating the number of initial solutions indicated and offering an optimal solution for the resulting mathematical model in a total of less than two minutes of run time.
The final solution proposal is shown in Figure 2. It should be noted that some territories have a reduced number of basic units; for example, there is a territory with a single basic unit that corresponds to a zone with a strong presence of industries and offices, while other zones include a large number of basic units (zones with less population and/or economic activity). This disparity is logical and is due to the structure of the city considered in the case study.
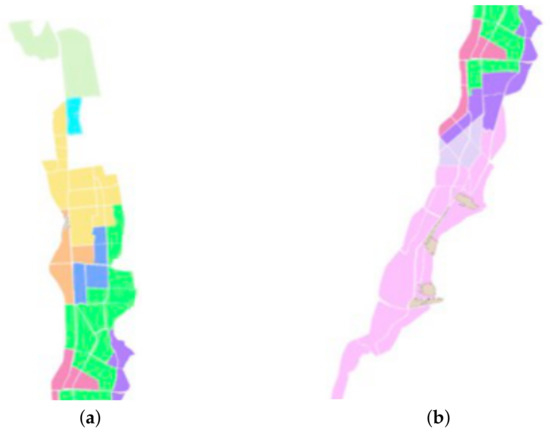
Figure 2.
Divisions created in a zone of the city studied in the case study (figure (a) shows the north and central area, while figure (b) shows the central and south area). The territories are shown in different colors with the basic units delimited by white lines.
The final solution is capable of obtaining an average quality of service of 95.7%, which represents an improvement of 12 points compared to the current service level, which is 83% and allows a certain buffer with respect to the company’s goal to reach a service level of 90%.
For a more detailed analysis of the behavior for each of the 19 days available in the study, see Table 6, shows a disparity of service levels throughout the different days, showing that on the day of greatest demand (Day 8) the service index worsens significantly.

Table 6.
Level of service reached by the proposed solution for each of the 19 days where which information is available.
Analyzing the individual results of each day, it is observed that one of the causes of greater service delays corresponds to a strong variability in the demand depending on the day. In addition, there is no pattern based on the day of the week or the month that justifies this variability. While an increase in the number of delivery zones would improve the level of service on those critical days, the change would lead to an oversized delivery service in most days since optimal levels, 100% of deliveries, are reached in most days of service.
Another important analysis to perform is the effect of service time on the quality of the solution. The service time is defined as the time it takes the carrier to stop the vehicle at the delivery destination, deliver the package, and resume the route. The company assumes that this time is two minutes per delivery, but the variability is high, and given the reduced time available to make all the express deliveries, even small variations can significantly vary the results. To respond to this problem, it was checked what the result would be if the service time were increased to 2 min and 15 s and to 2 min and 30 s.
The results of this change indicate that the quality of service decreases to 93.6% when the increase is only 15 s and to 90.3% when service time is increased by 30 s. These results translate into large variations on the worst day, in which the quality of service drops to 70.4% and 64.1%, respectively. Therefore, one of the improvements available to be made in the daily operation of the system corresponds to maintaining and/or improving that delivery time, which is of vital importance for managing a large number of shipments in smaller time windows.
6. Conclusions and Future Work
In the present work, a procedure and a case study are proposed for the design of delivery zones subject to quality of service conditions in express deliveries. The procedure considers a preprocess of grouping customers into basic units that, on the one hand, helps to generate solutions with the characteristics expected by both the management of the company and by the carriers and, on the other hand, reduces the computational needs of the design method.
The method for designing territories consists of an initial phase in which a set of alternatives are generated that are subsequently combined through a mathematical model to obtain a final territorial design. The mathematical model is general and can be used in other districting problems that feature similar characteristics in terms of the objective function and districts interactions. Moreover, and to minimize computation times, an alternative objective function is used in the initial search phase and to evaluate a more detailed estimate of the level of service offered by each territory considered only in the last phase of the algorithm. This procedure yields quality solutions in shorter times.
Our results show that while a very coarse granularity when grouping clients may hinder the quality of the solution, increasing granularity impacts algorithmic performance but may not directly translate into better solutions. Consequently, there is a “sweet spot” in which a proper degree of aggregation has a positive impact on the algorithmic performance and the properties expected from the proposed districting plans. While this result makes intuitive sense, previous literature on districting problems has not given much attention to it, focusing its attention on other issues, such as defining compactness metrics to try to reach similar results to those than can be obtained through aggregation.
If the results of the case study are examined, it is clear that the proposed territorial design leads to evident and achievable improvements in the company’s service indices. The redesigned delivery zones allow reaching a level of service equivalent to 95.7% without internal operational changes. Moreover, the districting plan make sense from a practical point of view as the borders between districts are defined by major roads and streets as in manually generated districts. It is also observed that given the sensitivity of the average service time, it is essential that there is a correct functioning in this process. This point is critical in overall system performance, and incorrect functioning of the system could lead to significant deterioration of the system.
Note that the conclusions reached within the case study may vary in different countries or even in different areas within a country. While the proposed methodology is agnostic to the area under study, data availability, or cultural particularities, the application of this research results to other countries or situations may or may not be possible. For instance, our methodology considers that the old territorial design can be ignored, while there are cases in which changes between the previous and the new territorial design should be minimal or units that need to be assigned to specific territories for some particular reasons. We also consider that all overnight deliveries are identical and no preference must be given to some of them. Other operational features, such as the existence of multiple product offerings with different express delivery deadlines would also impact the methodology and require changes to our approach, even if the overall methodological scheme would still be valid.
Among the possibilities for improvement and study, we highlight the inclusion of standard service or pickup operations, such as returns, within the express service in the same territorial design process. This work did not take this combined approach because the view of the company in the case study is that the standard service does not entail major problems and can be performed without taking its limiting factors into account, but this condition may not be true for other scenarios or settings. In this case, it would be necessary to approach the problem from a multicriteria perspective, evaluating the trade-off between the different needs and objectives of each type of service offered by the company.
Similarly, this study does not consider other side constraints that may impact the operational viability of the territories, such as the physical capacity of the vehicle or the size of the items delivered. While these conditions need to be considered in some applications and require additional study within the districting literature, they were not considered necessary in this study because most overnight deliveries are small parcels and letters that represent a small fraction of the total capacity of the vehicles used for delivery.
Finally, it would also be interesting to study the case where the number of districts is not specified as an input. Such a situation is less frequent in delivery companies as changes in their operations should take previous decisions (i.e., the number of territories) into account, but it is a problem of practical relevance that deserves proper attention. However, in some circumstances it may be interesting to reduce operational costs and given the structure of the delivery service, where territories are handed out to independent contractors to actually perform delivery operations, “district minimization” translates into “cost minimization”. While the proposed solution method does not provide a direct solution approach for such a problem, it does provide a tool to evaluate the effect on the quality of service metric when a different number of districts, parameter k, are used, and thus it can be seen as a possible decision-aiding tool to manually evaluate the pros and cons of alternative plans.
Author Contributions
Conceptualization, E.Á.-M. and J.P.; methodology, E.Á.-M. and J.P.; software, J.P.; validation, E.Á.-M. and J.P.; formal analysis, E.Á.-M. and J.P.; investigation, E.Á.-M. and J.P.; resources, E.Á.-M. and J.P.; data curation, J.P.; writing—original draft preparation, J.P.; writing—review and editing, E.Á.-M.; visualization, J.P.; supervision, E.Á.-M. and J.P.; funding acquisition, E.Á.-M. and J.P. All authors have read and agreed to the published version of the manuscript.
Funding
E. Álvarez-Miranda acknowledges the support of the National Agency of Research and Development (ANID), Chile, through the grant FONDECYT N.1180670 and through the Complex Engineering Systems Institute ANID PIA/BASAL AFB180003. J. Pereira acknowledges the support of ANID through the grant FONDECYT N.1180670.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Due to non disclosure agreements, the data used in this work cannot be provided. More detailed aggregated results are available upon request to the authors.
Acknowledgments
Both authors acknowledge to Benjamín Conejeros for his involvement in early stages of this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gevaers, R.; Van de Voorde, E.; Vanelslander, T. Characteristics and Typology of Last-mile Logistics from an Innovation Perspective in an Urban Context. In City Distribution and Urban Freight Transport; Macharis, C., Melo, S., Eds.; Edward Elgar Publishing: Cheltenham, UK, 2011; pp. 56–71. [Google Scholar]
- Retail e-Commerce Sales Worldwide from 2014 to 2024. Available online: https://www.statista.com/statistics/379046/worldwide-retail-e-commerce-sales/ (accessed on 18 August 2021).
- Chopra, S. Designing the Distribution Network in a Supply Chain. Transp. Res. Part E 2003, 39, 123–140. [Google Scholar] [CrossRef]
- Cho, J.; Ozment, J.; Sink, H. Logistics Capability, Logistics Outsourcing and Firm Performance in an E-commerce Market. Int. J. Phys. Distrib. Logist Manag. 2008, 38, 336–359. [Google Scholar]
- Índice Nacional de Satisfacción de Clientes: Informe de Resultados Generales. Available online: Https://procalidad.cl/indice-procalidad/ (accessed on 18 August 2021).
- Servicio Nacional del Consumidor: Un 88% de los Reclamos Recibidos por el SERNAC Fueron en Contra de Grandes Empresas. Available online: Https://www.sernac.cl/portal/604/w3-article-55432.html (accessed on 18 August 2021).
- Servicio Nacional del Consumidor: SERNAC Analiza Reclamos por Compras Online y Exige Compensaciones. Available online: Https://www.sernac.cl/portal/604/w3-article-58698.html (accessed on 18 August 2021).
- Kumar, V.; Reinartz, W. Customer Relationship Management, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Gajewska, T.; Zimon, D.; Kaczor, G.; Madzík, P. The impact of the level of customer satisfaction on the quality of e-commerce services. Int. J. Product. Perform. Manag. 2019, 69, 666–684. [Google Scholar] [CrossRef]
- Madzík, P.; Hrnčiar, M. Accuracy in measuring customer satisfaction. Int. J. Serv. Ind. Manag. 2021, 38, 161–187. [Google Scholar] [CrossRef]
- Kotzab, H.; Madlberger, M. European retailing in e-transition? An empirical evaluation of Web-based retailing—Indications from Austria. Int. J. Phys. Distrib. Logist Manag. 2001, 31, 440–462. [Google Scholar] [CrossRef]
- Kalcsics, J. Districting Problems. In Location Science; Laporte, G., Nickel, S., Saldanha da Gama, F., Eds.; Springer: New York, NY, USA, 2015; pp. 585–622. [Google Scholar]
- Hess, S.; Weaver, J.; Siegfeldt, H.; Whelan, J.; Zitlau, P. Nonpartisan political redistricting by computer. Oper. Res. 1965, 13, 998–1008. [Google Scholar] [CrossRef]
- Hess, S.; Samuels, S. Experiences with a sales districting model: Criteria and implementation. Manag. Sci. 1971, 18, 41–54. [Google Scholar] [CrossRef]
- Ricca, F.; Scozzari, A.; Simeone, B. Political Districting: From classical models to recent approaches. Ann. Oper. Res. 2013, 204, 271–299. [Google Scholar] [CrossRef]
- Bucarey, V.; Ordóñez, F.; Bassaletti, E. Shape and balance in police districting. In Applications of Location Analysis; Eiselt, H., Marianov, V., Eds.; Springer: New York, NY, USA, 2015; pp. 329–347. [Google Scholar]
- Dugošija, D.; Savić, A.; Maksimović, Z. A new integer linear programming formulation for the problem of political districting. Ann. Oper. Res. 2020, 288, 247–263. [Google Scholar] [CrossRef]
- Fleischmann, B.; Paraschis, J.N. Solving a Large-Scale districting problem: A case report. Comput. Oper. Res. 1988, 15, 521–533. [Google Scholar] [CrossRef]
- Zoltners, A.; Sinha, P. Sales territory design: Thirty years of modeling and implementation. Mark Sci. 2005, 24, 313–331. [Google Scholar] [CrossRef][Green Version]
- Salazar-Aguilar, M.A.; Ríos-Mercado, R.Z.; Cabrera-Ríos, M. New Models for Commercial Territory Design. Netw. Spat. Econ. 2011, 11, 487–507. [Google Scholar] [CrossRef]
- Benzarti, E.; Sahin, E.; Dallery, Y. Operations management applied to home care services: Analysis of the districting problem. Decis. Support. Syst. 2013, 55, 587–598. [Google Scholar] [CrossRef]
- Lin, M.; Chin, K.; Fu, C.; Tsui, K. An effective greedy method for the Meals-On-Wheels service districting problema. Comput. Ind. Eng. 2017, 106, 1–19. [Google Scholar] [CrossRef]
- D’Amico, S.; Wang, S.; Batta, R.; Rump, C. A simulated annealing approach to police district design. Comput. Oper. Res. 2002, 29, 667–684. [Google Scholar] [CrossRef]
- Chen, H.; Cheng, T.; Ye, X. Designing efficient and balanced police patrol districts on an urban street network. Int. J. Geogr. Inf. Sci. 2019, 33, 269–290. [Google Scholar] [CrossRef]
- Caro, F.; Shirabe, T.; Guignard, M.; Weintraub, A. School redistricting: Embedding GIS tools with integer programming. J. Oper. Res. Soc. 2004, 55, 836–849. [Google Scholar] [CrossRef]
- Ríos-Mercado, R.; Bard, J. An exact algorithm for designing optimal districts in the collection of waste electric and electronic equipment through an improved reformulation. Eur. J. Oper. Res. 2019, 276, 259–271. [Google Scholar] [CrossRef]
- Lin, H.; Kao, J. Subregion districting analysis for municipal solid waste collection privatization. J. Air Waste Manag. Assoc. 2008, 58, 104–111. [Google Scholar] [CrossRef]
- Cortinhal, M.; Mourão, M.; Nunes, A. Local search heuristics for sectoring routing in a household waste collection context. Eur. J. Oper. Res. 2016, 255, 68–79. [Google Scholar] [CrossRef]
- Jarrah, A.; Bard, J. Large-scale pickup and delivery work area design. Comput. Oper. Res. 2012, 39, 3102–3118. [Google Scholar] [CrossRef]
- González-Ramírez, R.; Smith, N.; Askin, R.; Camacho-Vallejo, J.; González-Velarde, J. A GRASP-Tabu Heuristic Approach to Territory Design for Pickup and Delivery Operations for Large-Scale Instances. Math. Probl. Eng. 2017, 2017, 4708135. [Google Scholar] [CrossRef]
- Kalcsics, J.; Nickel, S.; Schröder, M. Towards a unified territorial design approach—Applications, algorithms and GIS integration. TOP 2005, 13, 1–56. [Google Scholar] [CrossRef]
- Salazar-Aguilar, M.; Ríos-Mercado, R.; González-Velarde, J. GRASP strategies for a bi-objective commercial territory design problem. J. Heuristics 2013, 19, 179–200. [Google Scholar] [CrossRef]
- Moreno, S.; Pereira, J.; Yushimito, W. A hybrid K-means and integer programming method for commercial territory design: A case study in meat distribution. Ann. Oper. Res. 2020, 286, 87–117. [Google Scholar] [CrossRef]
- Novaes, A.; Graciolli, O. Designing multi-vehicle delivery tours in a grid-cell format. Eur. J. Oper. Res. 1999, 119, 613–634. [Google Scholar] [CrossRef]
- Altman, M. Is automation the answer: The computational complexity of automated redistricting. Rutgers K Comput. Technol. Law 1997, 23, 81–141. [Google Scholar]
- Sandoval, M.; Díaz, J.; Ríos-Mercado, R. An Improved Exact Algorithm for a Territory Design Problem with p-Center-Based Dispersion Minimization. Expert Sys. Appl. 2020, 146, 113150. [Google Scholar] [CrossRef]
- Maniezzo, V.; Boschetti, M.; Stützle, T. Matheuristics. Algorithms and Implementations, 1st ed.; Springer: New York, NY, USA, 2021. [Google Scholar]
- Novaes, A.; Souza De Cursi, J.; Graciolli, O. A continuous approach to the design of physical distribution systems. Comput. Oper. Res. 2000, 27, 877–893. [Google Scholar] [CrossRef]
- Beardwood, J.; Halton, J.; Hammersley, J. The shortest path through many points. Math. Proc. Camb. Philos. Soc. 1959, 55, 299–327. [Google Scholar] [CrossRef]
- Çavdar, B.; Sokol, J. A distribution-free tsp tour length estimation model for random graphs. Eur. J. Oper. Res. 2015, 243, 588–598. [Google Scholar] [CrossRef]
- Galvao, L.; Novaes, A.; Cursi, E.; Souza, J. A multiplicatively-weighted Voronoi diagram approach to logistics districting. Comput. Oper. Res. 2006, 33, 93–114. [Google Scholar] [CrossRef]
- Ríos-Mercado, R.; Fernández, E. A reactive GRASP for a commercial territory design problem with multiple balancing requirements. Comput. Oper. Res. 2009, 36, 755–776. [Google Scholar] [CrossRef]
- Fernández, E.; Kalcsics, J.; Nickel, S. A novel maximum dispersion territory design model arising in the implementation of the WEEE-directive. J. Oper. Res. Soc. 2010, 61, 503–514. [Google Scholar] [CrossRef]
- Gonzalez-Ramírez, R.; Smith, N.; Askin, R.; Kalashnikov, V. A heuristic approach for a logistics districting problem. Int. J. Innov. Comput. Inf. Control 2010, 6, 3551–3562. [Google Scholar]
- Lei, H.; Wang, R.; Laporte, G. Solving a multi-objective dynamic stochastic districting and routing problem with a co-evolutionary algorithm. Comput. Oper. Res. 2016, 67, 12–24. [Google Scholar] [CrossRef]
- Bozkaya, B.; Erkut, E.; Laporte, G. A tabu search heuristic and adaptive memory procedure for political districting. Eur. J. Oper. Res. 2003, 144, 12–26. [Google Scholar] [CrossRef]
- Tavares-Pereira, F.; Figueira, J.; Mousseau, V.; Roy, B. Multiple criteria districting problems: The public transportation network pricing system of the Paris region. Ann. Oper. Res. 2007, 154, 69–92. [Google Scholar] [CrossRef]
- Ricca, F.; Scozzari, A.; Simeone, B. Weighted Voronoi region algorithms for political districting. Math. Comput. Model. 2007, 48, 1468–1477. [Google Scholar] [CrossRef]
- Hopcroft, J.; Tarjan, R. Algorithm 447: Efficient algorithms for graph manipulation. Commun. ACM 1973, 16, 372–378. [Google Scholar] [CrossRef]
- Garey, M.; Johnson, D. Computers and Intractability: A Guide to the Theory of NP-Completeness (Series of Books in the Mathematical Sciences), 1st ed.; W. H. Freeman: New York, NY, USA, 1979. [Google Scholar]
- Resende, M.; Ribeiro, C. Path-relinking. In Optimization by GRASP; Springer: New York, NY, USA, 2016; pp. 167–188. [Google Scholar]
- Hollander, M.; Wolfe, D.; Chicken, E. Nonparametric Statistical Methods, 3rd ed.; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).