Abstract
This study aims to understand the functional thinking of 10th-grade students while studying functions. Specifically, we intend to answer the following research questions: what are the functional thinking processes used by 10th-grade students when studying functions? What difficulties do students present while learning functions? In view of the nature of this research objective, we adopted a qualitative and interpretative approach. In order to answer these questions, data were collected from the written records produced by the students while solving the proposed tasks, from records of the oral interactions during discussions and from a questionnaire. The results show that functional thinking processes were implicit in the resolution of the tasks proposed to the students. The students expressed an understanding of how the variables were related, presenting evidence of their functional thinking while working on the new concepts represented by the functions addressed in the proposed tasks. Some students expressed difficulties in interpreting the different types of representations associated with the functions, in retaining the necessary information from a graphical representation that would help them to draw conclusions and establish correspondences, in explaining functional relationships, and in interpreting the information provided by algebraic expressions. These difficulties can reduce the recognition of the relationships between variables and their behavior in the different representations, becoming an obstacle to learning for some students.
1. Introduction
One of the main objectives of teaching mathematics is to foster the development of the students’ reasoning skills [1]. It is through these skills that students acquire and articulate knowledge based on an evolutionary process that involves conjecturing, generalizing, investigating why, and developing and evaluating arguments about mathematical facts and procedures [2,3]. Throughout schooling, the reasoning that students are expected to develop evolves and advances from the reasoning associated with the concrete, at the most elementary levels, to the abstract reasoning in the more advanced years [4]. In the transition between these types of reasoning, which accompanies students’ cognitive development, the study of functions is prominent. Functions represent one of the most important concepts in mathematics [5,6] and one of the most complex concepts in school mathematics, not only in basic and secondary education, but also in higher education [7]. In Portugal, the notion of functions is introduced for the first time in the seventh grade as a relationship that is established between two non-empty sets, A and B, where each element x of A is associated with a unique element B. In this study, terms emerge such as ‘object’, ‘image’, ‘domain’, ‘arrival set’, and ‘variables’. The notion of function, the specificity of its language, and the study of linear and quadratic functions provide students with the requisite knowledge for a broader study of functions in high school. At this level, the study of polynomial, rational, trigonometric, exponential, and logarithmic functions is addressed. As proposed by Lichti and Roth [3], students are confronted with functional relationships from an early age, namely, when identifying the differences between linear and quadratic functions or when recognizing and working with numerical and geometric patterns. Along this route, solving problems, noticing the relationships between variables, and realizing how one depends upon the other (in the same way as the distance traveled by a car is a function of the speed at which it was driven) is highlighted. The study of the relationships between the values of the variables appears in the literature, in the context of mathematics education, as the focal point in the effort to describe, understand [8], and promote functional thinking [3,9,10,11].
Functional thinking is a reasoning process that is used, in the early years of schooling, for the construction and generalization of patterns and relationships [2,12]. Various linguistic and representational tools are used to promote this thinking. Functional thinking is one of the main components of algebraic reasoning [13]. The development of this type of thinking involves the exploration of the relationships, correspondences, and variations between two variables, taking a particular case as a starting point and a generalization as a conclusion [3]. Smith [13] advocates the idea that functional thinking implies the use of relational thinking, focusing on the relationship between two variables, starting from particular relationships and concluding with generalization.
Several researchers, such as Blanton [2,10], have highlighted the fact that students can use a variety of tools to develop their reasoning about functions. From the earliest elementary school levels, students can use tables, drawings, graphs, words, or symbols of recursive relationships, covariation, and correspondence. During schooling, students develop an understanding of the relationships between the elements of any two non-empty sets. The notion of a function is extended by exploring different representations during middle school, situations that contemplate linear or quadratic relationships. In high school, students’ knowledge of functions becomes more comprehensive, and they learn the different characteristics of different types of functions. As they work with different representations, i.e., numerical, graphical, and algebraic, students develop their knowledge and understanding of functions. However, some students find it difficult to establish connections between different representations of functions, to interpret graphs, manipulate symbols [6,14,15], establish relationships between tables of discrete values and continuous Cartesian graphs, describe the behavior of functions, think of functions as objects [16], and decipher the terminology intrinsic to functions, such as, for example, the terms ‘image’, ‘inverse image’, ‘ordered pair’, ‘domain’, ‘range’, and ‘arrival set’ [17].
The literature suggests that the development of functional thinking is not easy to achieve. In order to promote functional thinking, it is important to provide experiences that challenge students to recognize and articulate structures and relationships. Studying these experiences is particularly relevant in order to better understand the problems associated with the development of functional thinking. Taking these assumptions into account, this study aims to understand the functional thinking of 10th-grade students while studying functions. Specifically, it intends to answer the following research questions: (1) What are the functional thinking processes used by 10th-grade students during the study of functions? (2) What difficulties do students exhibit when learning functions?
2. Functional Thinking
Functional thinking is one component of algebraic reasoning and is part of students’ mathematical reasoning. In this section, we will start by discussing the meaning of the construct within mathematical reasoning and, more specifically, algebraic reasoning, before moving on to a discussion of its meaning in the context of students learning about functions.
2.1. Functional Thinking as Part of Algebraic Reasoning
Mathematical reasoning is associated with different ways of thinking, such as: predicting essential results for formulating conjectures; questioning the solutions, even the correct ones; looking for patterns; resorting to different representations in problem solving; and analyzing and synthesizing [18]. Solving problems or demonstrating the veracity of a conjecture is impossible to accomplish without the use of mathematical reasoning. In both, solving problems and demonstrating conjectures are ways of developing mathematical reasoning [18,19,20,21]. The connections between different contents, the communication and representations used by the students are the basis of the developed mathematical reasoning, leading to decision-making in the learning process of each student. Mathematical reasoning is a particular ‘intellectual activity’, and there are different types of reasoning. Algebraic reasoning is associated with the domain of Algebra, which includes the ability to manipulate symbols. According to NCTM [1], algebraic reasoning deals with the study of structures, symbols, modeling, and the study of variation. Kaput [22] associates algebraic reasoning with two central aspects: (i) formulating and expressing generalizations, and (ii) reason by manipulating the symbolism of generalizations. These aspects are part of three domains: (i) algebra as the study of structures and generalizations of calculations and numerical relationships (generalized arithmetic); (ii) algebra as the study of functions, relationships, and variations (functional relationships); and (iii) algebra as the application in mathematical modeling situations in order to express and formalize generalizations.
Blanton and Kaput [23] consider algebraic reasoning as “a process in which students generalize mathematical ideas from a set of particular instances, establish those generalizations through the discourse of argumentation, and express them in increasingly formal and age-appropriate ways” (p. 413). Functional thinking is one of the main components of algebraic reasoning [22], directed towards two essential aspects: (i) learning focused on generalized arithmetic, and (ii) functional thinking. In the early years of schooling, functional thinking can be defined as a reasoning process used in the construction and generalization of patterns and relationships, based on the use of different linguistic tools and different representations, exploring the generalizations of relationships or functions [2]. For Blanton [2], functional thinking is the relationship between two quantities, using the law of correspondence between two particular quantities. According to Blanton and Kaput [24], the ability to recognize patterns, relate data, and represent their correspondences through well-defined functional rules is crucial for the development of functional thinking. The generalization of patterns is a central activity in mathematics [24]. Kieran et al. [25] and Radford [26] argue that experience with patterns can naturally lead students to develop the ability to generalize. This activity can facilitate a better understanding of relationships between the quantities implicit in mathematical functions and contribute to establishing functional-type relationships [23,24,27]. Smith [13] advocated that functional thinking focuses especially on the relationship between two variables, starting from particular relationships to generalization. Blanton and Kaput [24] considered three different ways to analyze the kinds of functional thinking found in the classroom, which they described as follows:
(1) recursive patterning involves finding variation within a sequence of values; (2) covariational thinking is based on analyzing how two quantities vary simultaneously and keeping that change as an explicit, dynamic part of a function’s description (e.g., “as increases by one, increases by three”); and (3) a correspondence relationship is based on identifying a correlation between variables (e.g., “ is 3 times plus 2”). (p. 8)
2.2. Functional Thinking and Students Learning about Functions
In the transition from middle to high school, students’ knowledge about functions is a prerequisite to continue their study. At this stage, the variables advance from discrete to continuous, requiring an increase in the abstraction capacity, which for some authors has implications in determining the characteristics that integrate functional thinking. Functional thinking is central when relating two or more variable quantities, as, for example, the dependence between speed, distance, and time, or when modeling the spread of a virus. It is also relevant for studying other subjects and for understanding everyday situations. Pittalis et al. [11] described functional thinking as a process of construction, description, and reasoning with and about functions. For Lichti and Roth [3], functional thinking incorporates three fundamental characteristics: mapping, covariation, and function as an object:
- Mapping: for each element x of the domain, there is a single element y of the range. This is a level of functional thinking that translates functions as a requirement to perform calculations.
- Covariation: the variation in the independent variable x and the resulting covariation of the dependent variable y. This describes the change in y if x changes uniformly.
- Function as object: this includes the recognition that functions offer the possibility of understanding the described process as a whole.
Another way of describing functional thinking refers to the different ways of representing functions (by formulas, verbal descriptions, graphs, and tables) [10]. According to the aforesaid authors, students’ ability to think functionally is present in the way they deal with these different forms of representation, namely, in the interpretation they make, the change between representations, and, especially, the conversion from one representation to another. By using different forms of representation, students develop their functional thinking and learn about functional relationships as they are challenged to consider functions from different points of view, which can lead to a greater understanding of functional relationships.
Ursini and Trigueros [28] (pp. 328–329) understand that the functional relationships of variables involve a set of skills that students must work on, such as being able to:
- -
- Recognize the correspondence between related variables independently of the representation used;
- -
- Determine the values of the dependent variable given the value of the independent one and vice versa;
- -
- Recognize the joint variation in the variables involved in a relation independently of the representation used;
- -
- Determine the interval of variation in one variable given the interval of variation in the other one;
- -
- Symbolize a functional relationship based on the analysis of the data of a problem.
In general, functional thinking is defined as thinking used to study the relationships and correspondences between two or more quantities that vary and lead to generalization. In the study of functions, it is essential that students understand how the variables are related so that they can explain the functional relationship between them [29,30].
Different authors claim that a good way to develop and analyze students’ functional thinking is through the application of tasks, in which it is possible to use the different representations of functions (e.g., [31,32]). By analyzing how each representation is made, the progress between the different representations, and the relationships between variables, it is possible to infer the reasoning that the student has developed [1,4,32,33]. For Kieran [32], functional relationships can be represented in three different ways: (i) geometrically (using schemes, diagrams, graphs, among others); (ii) arithmetically (using numbers, tables, or ordered pairs); and (iii) algebraically (using literal symbols, formulas, and correspondences).
Smith [34] presented two distinct ways of analyzing a function and functional relationships. One way of analyzing refers to understanding the correspondence relationship between the existing values of each variable and the relationship that is associated with each value it takes. This analysis sometimes leads to students being able to represent functions through an algebraic expression or another type of representation possible for functions. On the other hand, the author says that the analysis can focus on how the variation in the value of a variable implies the variation in the other variable, being identified as covariation [34]. Regarding covariation in the study of a function, the author considers that students perform it more intuitively as a first approach to solving problems presented to them. The study of covariation allows students to understand the ‘behavior’ of a function through the patterns associated with each of the variables. An initial approach based on understanding the existing regularities can lead to the development of the correspondence relation, and thus be represented algebraically. According to Smith [34], the study of the covariation of a function is important because the change that is observed and what is retained about the presented problem is, consequently, what is most important to consider in the presented situation. These modes of the analysis of a function presented by Smith [35] lead us to the three different ways of analyzing functional thinking, previously presented by Blanton and Kaput [24].
Students’ understanding of the function concept begins to develop before the formal introduction of functions, and the teacher can help students develop functional thinking [1] by facilitating the construction and understanding of the function concept from the early years of schooling. Blanton and Kaput [23] share the same opinion and stress the importance of working on functional thinking from the earliest school years, based on the development of algebraic reasoning in students, since functional thinking leads to algebraic reasoning, being one of the main drivers for its development [22,23,24].
3. Method
This study aims to understand the functional thinking of 10th-grade students while studying functions. Specifically, it intends to answer the following research questions: (1) What are the functional thinking processes developed by 10th-grade students during the study of functions? (2) What difficulties do students reveal in learning functions? Difficulties show the cognitive actions that students did not perform adequately in solving the tasks proposed to them, or that give rise to erroneous resolutions [35].
The teaching experience that is the focus of this study took place during ten lessons, promoted by one of the authors of this paper as part of her pedagogical internship in the final year of her master’s degree in teacher training. This teaching experience outlined strategies that valued student activity through an exploratory teaching format [36]. In the first part of each lesson, the task was presented to the class, and the teacher checked if the students understood the task and its objective. In the second part, the students worked individually and autonomously on the task with the support of a graphing calculator. At this stage of the lesson, the teacher supported the students, but without interfering with their resolution strategies. After the completion of the students’ autonomous work, their resolutions were collected. In the third part, the teacher orchestrated the discussion, taking care to manage the students’ interventions and compare different resolutions. In the last part, based on what the students did or said, new concepts or procedures were institutionalized as a result of exploring and discussing the task.
The characteristics of the tasks proposed to the students are very important to make the students’ learning experience more dynamic. In addition to creating opportunities to make students more active in class, there was an intention to create opportunities for students to reason mathematically. This involvement of the students in the tasks is important for the discovery and construction of their knowledge. The diversity and the mathematics potential for learning or the mathematical richness of the tasks are very important [37]. A particular task can be more challenging or more accessible and can be structured in a more open or more closed way. Ponte [38] classified tasks according to their degree of challenge and their degree of structure. The degree of mathematical challenge is related to the difficulty of the questions, which varies from a low to high challenge, while the degree of structure varies from open to closed. A closed task (exercise or problem) is one where it is clearly stated what is given and what is asked, and an open task (exploration or investigation) is one where there is a certain degree of indetermination of what is given and/or what is asked. In the construction of the tasks that were part of this teaching experience, the degree of mathematical challenge and the degree of structure were benchmarked to the mathematical contents of the 10th grade syllabus (Table 1). This resulted in the development of a set of tasks which were applied over 10 lessons. Due to space constrains, only three of the tasks are analyzed here. The decision as to which tasks should be presented here is related to the relevance of the information provided about the process of functional thinking used by the students. This decision also considered the moment of implementation, intending to include tasks implemented at the beginning and at the end of the study.

Table 1.
Tasks proposed to the students.
The experiment was carried out in a 10th grade class of 27 students (20 boys and 7 girls aged between 15 and 16 years). Most of the students considered mathematics their favorite subject (52%), and functions the least appreciated topic (61%).
Given the nature and the focus of the study, we adopted a qualitative and interpretative methodology to understand the students’ activity [39]. The data were collected through the written records produced by the students while solving the tasks and by records of the oral interactions during discussions. At the beginning of this study, a questionnaire was used to collect information about the students, such as their preferred disciplines and mathematical themes.
Data analysis was based on the content of the students’ resolutions, focusing on the functional thinking processes: (i) mapping; (ii) correspondence; (iii) covariation; and (iv) function as object. The analysis of the students’ resolutions offers opportunities to identify the activities they carried out and also the difficulties they faced in their resolutions.
| Requested abilities | |
| Mapping | Calculate variable values. |
| Correspondence | Establish relationships between domain and range values. |
| Covariation | Relate the variation in the dependent variable as a function of the variation in the independent variable. |
| Function as object | Elaborate definitions.Operate with functions. |
These different processes of functional thinking derive from the literature, offering a more specific analysis of the characteristics of functional thinking evidenced by the students. Taking the research questions of this study as a reference, the focus on each of the processes (mapping, correspondence, covariation, and function as object) allows an understanding about which processes are carried out by the students and how are they carried, simultaneously offering information regarding the characteristics of their functional thinking and the difficulties manifested.
4. Results
In this section, we analyze the data collected in relation to: (i) the classification of injective, surjective, and bijective functions; (ii) the composite function; and (iii) transformations of the graph of a function.
4.1. Task 1: Classification of Functions—Injectivity, Subjectivity, and Bijectivity
In the study on the classification of functions, the students were challenged to solve Task 1, which asked them to analyze examples and non-examples of different types of functions (e.g., injective), to define the concept, as exemplified in the first question (Figure 1).
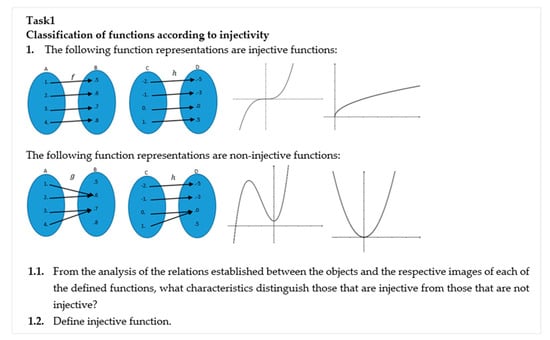
Figure 1.
Question 1—Task 1.
To solve this question, the students mainly used thinking by correspondence and function as object. Sometimes, they developed a functional relationship in geometric form (arrow diagram), as highlighted by Kieran [32], from which they emphasized the relevant points to define the type of function being worked on. The resolution proposed by student S10 (Figure 2) is an example of the use of functional thinking in question 1 of Task 1.

Figure 2.
Resolution of student S10 to question 1—Task 1.
Although student S10 identified the essential characteristic of an injective function using common language, he uses an arrow diagram to express his thoughts, restricting his reason to just a few values of the function domain. During the discussion of the tasks, it was possible to conclude that he was not attentive to what was happening with the remaining elements of the domain, which suggests difficulty in the use of symbolic language to generalize the identified characteristic to a domain.
Another student, S5, focused his work exclusively on the discrete examples (Figure 3). He separately analyzed the representation of each of the functions presented in the examples and in the non-examples of the injective functions, showing the ability to interpret and compare the information provided by arrow diagrams.

Figure 3.
Resolution of student S5 to question 1—Task 1.
When considering that in injective functions, each object corresponds to a single and unique image, the student correlates the variables, objects, and images of a function. However, in general, the students approach the question considering the isolated points of the function, which happens in the representations of functions by arrow diagrams. Regarding the graphical representations, where the identification of the injective functions could be conducted based on an overall analysis—function as object—the analysis is not completed by the students. This form of functional thinking is present in the definition elaborated by the students, and it assumes the form of a classification of any function, in an overall way.
After studying injectivity, the students focused on the concept of a surjective function by solving the second question of Task 1 (Figure 4).
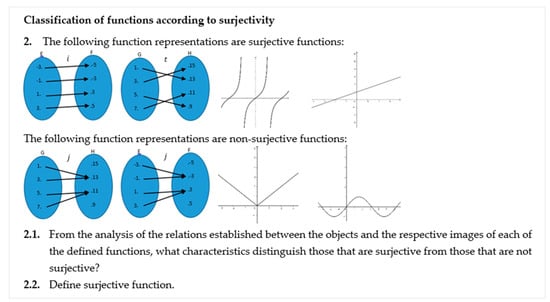
Figure 4.
Question 2—Task 1.
To solve this question, student S5 developed a similar thought to the one he completed in the study of injective functions, considering that the surjective functions have the arrival set equal to the range, a characteristic identified from the analysis of the examples expressed by arrow diagrams (Figure 5).

Figure 5.
Resolution of student S5 to question 2—Task 1.
The absence of a reference to the examples presented as Cartesian graphs and the comments made by the student during the class suggest that he found it difficult to compare the information from the analysis of the arrow diagrams with that from the graphical representations [16]. Despite this restriction, the student identified the characteristics of a surjective function. He did not present a generalization using symbolic language. On the contrary, the student presented his definition using common language, saying that all elements of the arrival set of a given function are images of at least one object in the function’s domain. This lack of generalization in the definition of a surjective function was common to the remaining students who answered the question. Student S5 presents a thinking by correspondence, and by function as object. These types of thinking are present in the students’ resolutions when they reveal the ability to recognize correspondences between variables [28] and establish the definition of a surjective function.
In the study of the bijective function, the students were asked to solve the third question of Task 1 (Figure 6).
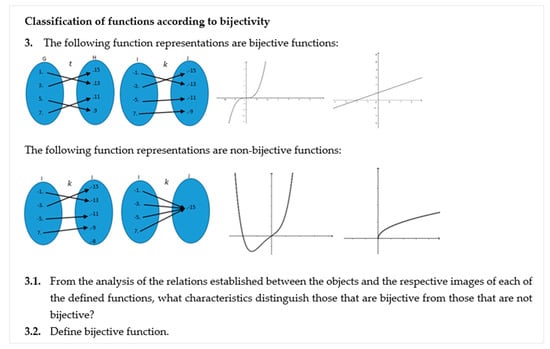
Figure 6.
Question 3—Task 1.
Student S2 considered it to be “a function in which each image corresponds to only one object and D’ is equal to the arrival set”, which ensures that the function is both injective and surjective (Figure 7).

Figure 7.
Resolution of student S2 to question 3—Task 1.
The student started by analyzing the characteristics of each representation to present the definition of a bijective function, although it is not presented in a generalized way using symbolic language. This resolution indicates that the student can connect the information he takes from different representations of functions and identify the existing relationships between the variables of the functions.
To solve Task 1, the students successfully analyzed arrow diagrams. However, that was not the case in relation to Cartesian graphs. While solving this task, they mobilized two of the three kinds of functional thinking, those related to correspondence and function as object (Table 2).

Table 2.
Summary of functional thinking processes used in Task 1.
The students distinguished the relationships that exist between the objects and images and the difference between the arrival set and range. In identifying the characteristics of the studied functions, most students (74%) revealed an understanding of the difference between injectivity and subjectivity. While in the first relation there is a correspondence that makes different objects correspond to different images, in the second type of relation, the correspondence between the variables requires that all elements of the arrival set are images of at least one object in the domain. Most students (59%) also identified the characteristics of a bijective function. The study of these three features of functions illustrates the use of correspondence and function as object as a form of functional thinking by the students.
4.2. Task 2: Composite Function
Task 2 was proposed to the students to introduce the composite function (Figure 8).

Figure 8.
Task 2.
Regarding the domains of functions f and g, most students appropriately determined the domain of the polynomial function g (95%), which was not the case with the irrational function f (30%). However, this was not the case for all students, as exemplified by student S20’s resolution (Figure 9).

Figure 9.
Resolution of student S20 to question 1—Task 2.
From the analysis of student S20’s resolution, it can be seen that the student took a mechanical approach guided by the approach used in the last functions studied, the irrational functions. When attempting to answer the question, the student relies on some kind of function as object reasoning by mixing aspects of the function’s domain and range.
In question 2 of Task 2, the students had to determine and and then infer another function that would allow them to determine the image of 5. This new function offers the opportunity to discover characteristics of composite functions, mobilizing aspects of functional thinking. The students S16 and S8 used mapping to discover the intended values, or to discover relevant values to reach the final conclusion:
- S16: We first find g(5); that is 25.
- S8: And f(25) is .
These were the only two students who, during the task discussion, managed to find the function that enables determining the image of five from the given functions, which he considered to be . The clarification of the answer by these students helped their colleagues to understand the possible relationship between the two functions to define a new function and determine the image of five, which translates the way in which the variables are related. The students also reveal the ability to determine the images of a given object from the analytical expression that represents the function, whether a polynomial or irrational one, associating the correspondence between an object and an image to each of the functions.
In question 3 of Task 2, student S25 (Figure 10) used function as object to relate the two functions, first considering the function and then transforming this function using the function.
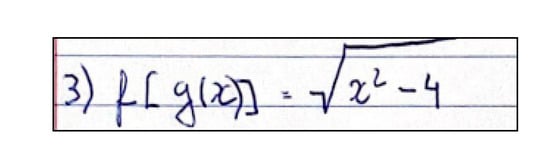
Figure 10.
Resolution of student S25 when calculating in question 3—Task 2.
The student understands the relationship between the variables, developing correspondence thinking. Based on this student’s answer, the definition and respective characterization of the composite function of two real functions of a real variable was instituted in the class group.
To solve the four questions of Task 2, the students presented the different processes of functional thinking (Table 3).

Table 3.
Summary of functional thinking processes used in Task 2.
The students had some difficulty in recognizing the values that the variable (independent variable) could take and, consequently, in defining the domain of the two functions. However, it was easier in the case of the second functions. In the process, it is possible to identify the emergence of functional thinking—function as object—related to the discovery of the value of the dependent variable. Mapping and correspondence thinking are reflected in the relationship that the students make between the coordination (link) of the variables (dependent and independent variable) to a specific function. Subsequently, this thinking was supposed to be involved in the presentation of the composite function that the students were expected to present. Determining the expression of that function also comprises the function as object thinking, which allows the students to check which variable (x—objects or y—images) differs from those previously found.
4.3. Task 3: Transformations of Functions’ Graphs
In the study of transformations of the graph of a function (translations and reflections), the students solved Task 3, which focuses on the vertical transformation (Question 1.1), the horizontal transformation (Question 1.2), and the transformation of the graph of a function according to the two directions (Question 1.3).
To complete the table in Question 1.1—task 3 (Figure 11), the students sketched the graph of each of the transformations of the graph of the function i and determined the domain, range, and zeros of each function obtained. Then, they established relationships between the obtained graphs and the starting one to generalize the study of the function defined by .
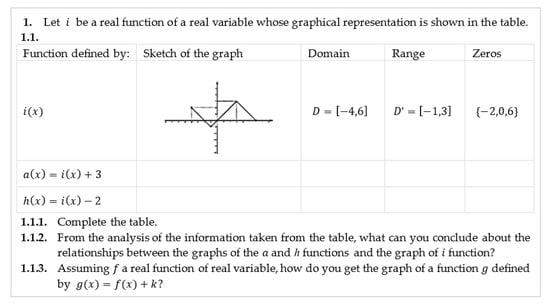
Figure 11.
Question 1.1—Task 3.
In general, the students observed and analyzed how the variables change and, consequently, how two functions vary simultaneously. Student S15 developed the expected answer to question 1.1. of Task 3 (Figure 12).
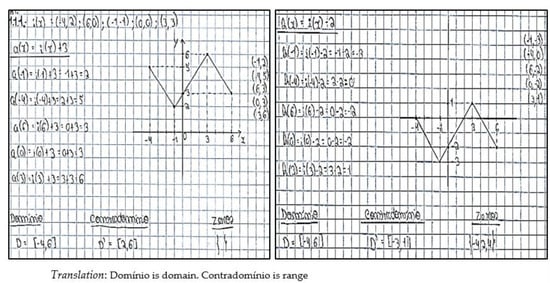
Figure 12.
Resolution of student S15 to question 1.1—Task 3.
The student’s resolution offers evidence about his recognition of the symbology normally used, denoting the ability to transform graphs of functions based on his interpretation of the invariance of objects and the alteration of the ordinate of each of the points that belong to the function domain. Such an interpretation suggests that the student relates the values of the variables and analyzes the behavior of a function in an explicit and dynamic way, recognizing the functional relationships.
Some of the students did not answer questions 1.1.2 and 1.1.3 (approximately, on average, 24%). Additionally, in the case of question 1.1.2, only eight students (30%) presented an acceptable answer, one being student S15 (Figure 13).

Figure 13.
Resolution of student S15 to questions 1.1.2 and 1.1.3—Task 3.
After studying the transformation of the graphs of a real function of a real variable through translations associated with a vector with a vertical direction, the study of the transformation of the graphs associated with horizontal translations followed, guided by question 1.2 of Task 3 (Figure 14).
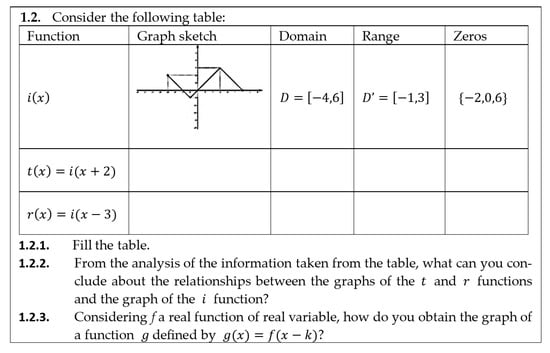
Figure 14.
Question 1.2—Task 3.
Only eleven students (41%) responded to item 1.2.1, with student S15 being one of them (Figure 15).

Figure 15.
Resolution of student S15 to questions 1.2.1, 1.2.2, and 1.2.3—Task 3.
The student reveals covariational thinking when realizing that translating the graph of the function i according to a horizontal direction changes the values of the independent variable, while the values of the dependent variable are invariant. The student shows a recognition of the behavior of the variation in the variables and, consequently, analyzes the relationship between the graph of function i and the graphs of functions and . Additionally, in question 1.2.3, the student generalizes the conclusion and is able to explain the impact of the change in the expression on the graph of the function.
This is not the case for all the students. Some students (44%) recognized the relationship between the variable and the parameter , but they faced difficulties in finding the suitable expressions to express their reason, failing to distinguish between the graph transformation and the function. For example, student S21 (Figure 16) analyzed how two quantities vary simultaneously, considering functions as having two parts, one explicit part (function ) that does not change, and a dynamic one (related to parameter ). The student found it difficult to explain the relationship generically in question 1.2.3. He mentioned that the parameter represents the variation, but he was unable to clarify the conclusion.

Figure 16.
Resolution of student S21 to questions 1.2.2 and 1.2.3—Task 3.
After studying the horizontal and vertical transformations of the graph of a function (i.e., according to a vector with one of its coordinates null), the transformation of the graphs associated with vectors with non-zero coordinates followed (question 1.3—Task 3) (Figure 17).
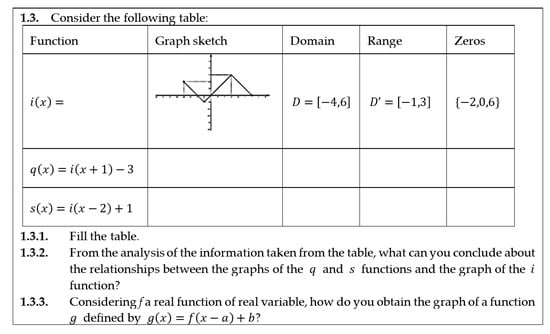
Figure 17.
Question 1.3—Task 3.
Student S13 (Figure 18) found that the domains, ranges, and zeros differ, but did not mention whether there was any change in the graph. Student S9 mentioned that there was a translation associated with the x-axis and the y-axis. This interpretation indicates that student S9 understood the information provided by the graphic representations and recognized the relationships between the variables and how the quantities of the two variables change.

Figure 18.
Resolution of students S13 and S9 to question 1.3.2—Task 3.
Question 1.4 of Task 3 (Figure 19) addresses the transformation of graphs through a reflection along the Cartesian axes.
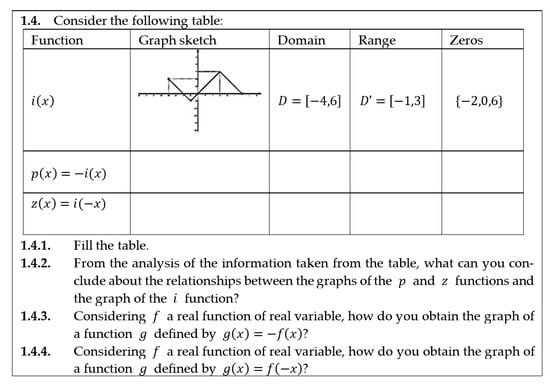
Figure 19.
Question 1.4—Task 3.
Student S3 recognized the relationship between the graph of function and the graphs of functions and , identifying the transformation of the graph (Figure 20).

Figure 20.
Resolution of students S3 to questions 1.4.2, 1.4.3, and 1.4.4—Task 3.
The student expresses an abductive thinking ability in the transition from the particular example to the generalization. From the resolution presented, it is clear that the student has the ability to translate and understand the existing relationships between the variables, extracting the information provided by the graphs and crosschecking it to elaborate the conclusions.
In Task 3, the students draft the requested graphic representation, revealing that they recognize the methods and conventions used to construct graphic representations. They also determine domains, ranges, and zeros, mobilizing knowledge about the associated concepts, terminologies, and symbology. The ability to understand the correspondence between the variables emerges along the way, which explains this process of the students’ functional thinking. Covariational thinking arises in the recognition and description of the relationship between the graph of the function i and the graphs of the functions that result from the transformations of this function. This process is also evident in the comparison between the graphs, which makes the students describe this variation through the analysis of how the functions vary simultaneously.
The students experienced difficulty in generalizing the transformations under study. Despite this difficulty, they gradually developed skills that enabled them to engage and apply functional thinking processes.
In general, ‘covariational thinking’ (reflected in the description of the behavior of the graph of the functions), ‘correspondence thinking’, and ‘function as object thinking’ (Table 4) are the main functional thinking processes present in the students’ resolutions to the questions in Task 3.

Table 4.
Summary of functional thinking processes used in Task 3.
The students developed a set of skills that lead them to understand the functional relationship of variables, such as how to: (i) recognize correspondences between quantities, regardless of the representation used; (ii) determine the value of the independent variable and the respective dependent variable, and vice versa; (iii) recognize the joint variation in the variables in the relationship, regardless of the representation used; (iv) determine the domain of variation in one of the variables when the values assumed by the other variable are already known; and (v) express the functional relationship presented, based on the data of the proposed problem, through different forms of representation. This set of skills was worked on and developed by the students during the teaching experience presented here, providing evidence about how 10th-grade students developed functional thinking.
5. Conclusions
With the objective of understanding the functional thinking of 10th-grade students while studying functions, we aimed to identify the processes mobilized and unveil any difficulties. This goal was addressed based on the analysis of the students’ resolutions to a set of tasks.
5.1. Characteristics of the Students Functional Thinking
During this study, the students relied on their functional thinking in different situations. Following the work developed by Smith [13] and Lichti and Roth [3], we can conclude that the students managed to understand the relationship between the independent variable and the dependent variable, i.e., they developed correspondence thinking; that they were also able to deal with the variation in variable values (object and image) and calculate new values for the variables, i.e., they developed mapping thinking; and that they understood the effect on a variable of varying the other, i.e., they developed covariational thinking. The combination of these three processes with the process of function as object helped the students to grasp the relationship between two variables, advancing from particular relationships to generalizations. This last process (function as object) is related to working with the function as a whole.
The correspondence process is evident in the students’ resolutions in the task on ‘injective, surjective, and bijective functions’, as well as in the resolutions of the remaining tasks. Sometimes, students present this form of functional thinking highlighted by Lichti and Roth [3], namely, in the geometric form [32], when the arrow diagrams are mentioned in the justifications and/or examples presented by the students. This result was also demonstrated in the study carried out by Rodrigues [40] with 10th-grade students. Despite the difficulties they had in solving the tasks, it was found that the students were able to recognize the correspondences between the variables, a process of functional thinking also presented by Ursini and Triguenos [28].
Mapping is present in the students’ resolutions of Tasks 2 and 3 through the determination of object images based on a graphic or an analytical expression of the function. This process was mobilized by the students when they discovered the requested values, or when they discovered important values that guide the achievement of the final conclusion.
Allusive to covariational thinking, according to Lichti and Roth [3], are the cognitive activities involved in the coordination of two quantities that vary when paying attention to the ways in which each of them changes with reference to the other. The uninterruptedness of this process of functional thinking during the resolutions presented by the students was extremely evident when they worked on tasks related to the transformation of functions’ graphs (Task 3). This process was mobilized by some students when they created a representation of the functions and when they identified that the variation in one variable’s values implies the variation in the other variable’s values [3,34].
Function as object appears in the resolutions of Tasks 1, 2, and 3. It appears in Task 1 in the elaboration of the requested definitions. These definitions gather the characteristics of the presented functions, characteristics that are then transposed to any function.
This functional thinking process is also contemplated in the students’ resolutions of Task 2, when determining the composite function of two real functions of a real variable. It is an operation between functions, which results in a new function with characteristics that translate it as a whole. This feature is also implicit in the transformation of graphs of functions (Task 3), which gives rise to a new function that transcends the entities observed in the graphs of the given functions.
As a whole, this study points to the relevance of the four processes of functional thinking considered, emphasizing the need to offer students the opportunity to experience them in the classroom, in order to develop their functional thinking in an overall way. This conclusion draws attention to the teacher’s role and to the tasks proposed to the students.
Sometimes, students revealed difficulties in developing functional thinking in their resolutions, but, gradually, they evolved as they deepened their study of functions.
5.2. Difficulties Revealed by the Students
The students experienced different difficulties in the study of functions. When working on the task about ‘injective, surjective, and bijective functions’, difficulties soon began to emerge when learning new concepts. The students easily established correspondences between independent and dependent variables in the arrow diagrams, but they experienced more difficulties in extracting the necessary information from a graphical representation, which would have helped them draw conclusions to establish correspondences and relationships between objects and images. Ponte [41] argued that the work with graphs associated with abstract thinking is not easy for students. Additionally, this was one of the difficulties identified in the present study.
The students experienced difficulty in interpreting the information provided by algebraic expressions [42]. This difficulty was evident in the incorrect domains given to functions when presented using this type of representation. When the function was represented through a graph, some students were able to overcome this difficulty. However, in the tasks related to the transformations of a graph of a function, the students also struggled. They had difficulty collecting and manipulating the correct and necessary information to use in order to obtain solutions for the proposed task [43]. Another difficulty revealed by the students refers to the description of the variation in the behavior of the variables, as well as the change in and interpretation of the graphical representation of a function.
In general, although the difficulties faced by the students differ depending on the processes of functional thinking involved, a very relevant point identified by this study is the way in which they differ depending on the representations used. Additionally, this is an aspect which requires the teacher’s attention when designing the tasks. The difficulties associated with the use of algebraic representations are well known, as is, likewise, the students’ preference for the use of graphical representations. This study revealed that the use of a graph is more difficult than the use of an arrow diagram, putting a strong emphasis on the different processes of functional thinking, but also on the representations used.
5.3. Final Remarks
This study presented evidence of how different processes of functional thinking are mobilized and worked by students during the study of functions. It also pointed to some difficulties, namely, those related to functions without discrete domains. It would be interesting to deepen this study, addressing the characteristics of the tasks that can contribute to strengthen the functional thinking of the students and the role of the four dimensions considered here: mapping, correspondence, covariational, and function as object thinking.
Author Contributions
Conceptualization, R.M. and F.V.; literature review, R.M. and F.V.; methodology, R.M. and F.V.; data collection, R.M.; data analysis presented, R.M., F.V. and H.R.; writing—original draft, R.M. and F.V.; writing—original first version, F.V. and H.R.; writing—review and editing, F.V. and H.R.; writing—review and translation, H.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work is funded by CIEd – Research Centre on Education, Institute of Education, University of Minho, projects UIDB/01661/2020 and UIDP/01661/2020, through national funds of FCT/MCTES-PT.
Institutional Review Board Statement
Ethical review and approval were waived for this study, due to data protection being assured by following the institutional protocol in place that regulates the practice component of PST training, including data collection procedures.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data analyzed during this study are available from the first author on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- NCTM. Principles and Standards for School Mathematics; National Council of Teachers of Mathematics: Reston, VA, USA, 2002; ISBN 0-87353-480-8. [Google Scholar]
- Blanton, M. Algebra and the Elementary Classroom: Transforming Thinking, Transforming Practice; Heinemann: Portsmouth, UK, 2008. [Google Scholar]
- Lichti, M.; Roth, J. Functional Thinking—A Three-Dimensional Construct? J. Für Math. Didakt. 2019, 40, 169–195. [Google Scholar] [CrossRef]
- Mata-Pereira, J.; Ponte, J.P. Enhancing students’ mathematical reasoning in the classroom: Teacher actions facilitating generalization and justification. Educ. Stud. Math. 2017, 96, 169–186. [Google Scholar] [CrossRef]
- Akkus, R.; Hand, B.; Seymour, J. Understanding students’ understanding of functions. Math. Teach. 2008, 207, 10–13. [Google Scholar]
- Elia, I.; Panoura, A.; Eracleous, A.; Gagatsis, A. Relations between secondary pupils’ conceptions about functions and problem solving in different representations. Int. J. Sci. Math. Educ. 2007, 5, 533–556. [Google Scholar] [CrossRef]
- Rocha, H. Graphical representation of functions using technology: A window to teacher knowledge. Teach. Math. Its Appl. 2020, 39, 105–126. [Google Scholar] [CrossRef]
- Vollrath, H.J. Search strategies as indicators of functional thinking. Educ. Stud. Math. 1986, 17, 387–400. [Google Scholar] [CrossRef]
- Lichti, M.; Roth, J. How to foster functional thinking in learning environments using computer based simulations or real materials. J. STEM Educ. Res. 2018, 1, 148–172. [Google Scholar] [CrossRef]
- Doorman, M.; Drijvers, P.; Gravemeijer, K.; Boon, P.; Reed, H. Tool use and the development of the function concept: From repeated calculations to functional thinking. Int. J. Sci. Math. Educ. 2012, 10, 1243–1267. [Google Scholar] [CrossRef]
- Pittalis, M.; Pitta-Pantazi, D.; Christou, C. Young students’ functional thinking modes: The relation between recursive patterning, covariational thinking, and correspondence relations. J. Res. Math. Educ. 2020, 51, 631–674. [Google Scholar] [CrossRef]
- Wilkie, K.J.; Clarke, D.M. Developing students’ functional thinking in algebra through different visualisations of a growing pattern’s structure. Math. Educ. Res. J. 2016, 28, 223–243. [Google Scholar] [CrossRef]
- Smith, E. Representational thinking as a framework for introducing functions in the elementary curriculum. In Algebra in the Early Grades, 1st ed.; Kaput, J.J., Carraher, D.W., Blanton, M., Eds.; Routledge: New York, NY, USA, 2008; pp. 133–160. [Google Scholar] [CrossRef]
- Leinhardt, G.; Zaslavsky, O.; Stein, M.K. Functions, Graphs, and Graphing: Tasks, Learning, and Teaching. Rev. Educ. Res. 1990, 60, 1–64. [Google Scholar] [CrossRef]
- Viseu, F.; Silva, A.; Rocha, H.; Martins, P.M. A representação gráfica na aprendizagem de funções por alunos do 10.º ano de escolaridade. Educ. Mat. 2022, 34, 186–213. [Google Scholar] [CrossRef]
- Steketee, S.; Scher, D. Using multiple representations to teach composition of functions. Math. Teach. 2012, 106, 260–268. [Google Scholar] [CrossRef]
- Markovits, Z.; Eylon, B.; Bruckheimer, M. Difficulties students have with the function concept. In The Ideas of Algebra, K-12; Coxford, A.F., Shulte, A.P., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 1988; pp. 43–60. [Google Scholar]
- Jeannotte, D.; Kieran, C. A conceptual model of mathematical reasoning for school mathematics. Educ. Stud. Math. 2017, 96, 1–16. [Google Scholar] [CrossRef]
- Carraher, D.W.; Schliemann, A.D. Early algebraic thinking and the US mathematics standards for grades K to 5. Infanc. Y Aprendiz. 2019, 42, 479–522. [Google Scholar] [CrossRef]
- Kusumaningsih, W.; Darhim, D.; Herman, T.; Turmudi, T. Improvement algebraic thinking ability using multiple representation strategy on realistic mathematics education. J. Math. Educ. 2018, 9, 281–290. [Google Scholar] [CrossRef]
- Stephens, A.C.; Ellis, A.B.; Blanton, M.; Brizuela, B.M. Algebraic thinking in the elementary and middle grades. In Compendium for Research in Mathematics Education; Cai, J., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, USA, 2017; pp. 386–410. [Google Scholar]
- Kaput, J.J. What is algebra? What is algebraic reasoning. In Algebra in the Early Grades, 1st ed.; Kaput, J.J., Carraher, D.W., Blanton, M., Eds.; Routledge: New York, NY, USA, 2008; pp. 5–17. [Google Scholar] [CrossRef]
- Blanton, M.; Kaput, J.J. Characterizing a classroom practice that promotes algebraic reasoning. J. Res. Math. Educ. 2005, 36, 412–446. [Google Scholar]
- Blanton, M.; Kaput, J.J. Functional thinking as a route into algebra in the elementary grades. In Early Algebraization, Advances in Mathematics Education; Cai, J., Knuth, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 5–23. [Google Scholar] [CrossRef]
- Kieran, C.; Pang, J.; Schifter, D.; Ng, S.F. Early Algebra. Research into Its Nature, Its Learning, Its Teaching; Springer Nature: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Radford, L. Iconicity and contraction: A semiotic investigation of forms of algebraic generalizations of patterns in different contexts. ZDM 2008, 40, 83–96. [Google Scholar] [CrossRef]
- Warren, E. Generalising the pattern rule for visual growth patterns: Actions that support 8 year olds’ thinking. Educ. Stud. Math. 2008, 67, 171–185. [Google Scholar] [CrossRef]
- Ursini, S.; Trigueros, M. A model for the uses of variable in elementary algebra. In Proceedings of the 25th Conference of the International Group for the Psychology of Mathematics Education, Utrecht, The Netherlands, 12–17 July 2001; van den Heuvel-Panhuizen, M., Ed.; Utrecht University: Utrecht, The Netherlands, 2001; Volume 4, pp. 327–334. [Google Scholar]
- Apsari, R.A.; Putri, R.I.I.; Sariyasa, S.; Abels, M.; Prayitno, S. Geometry representation to develop algebraic thinking: A recommendation for a pattern investigation in pre-algebra class. J. Math. Educ. 2019, 11, 45–58. [Google Scholar] [CrossRef]
- Blanton, M.; Levi, L.; Crites, T.; Dougherty, B. Developing Essential Understanding of Algebraic Thinking for Teaching Mathematics in Grades 3–5; Essential Understanding Series; Zbiek, R.M., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 2011. [Google Scholar]
- Cyrino, M.C.C.T.; Oliveira, H.M. Pensamento algébrico ao longo do ensino básico em Portugal. Bolema 2011, 24, 97–126. [Google Scholar]
- Kieran, C. The learning and teaching of school algebra. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D.A., Ed.; Macmillan Publishing Co., Inc.: New York, NY, USA, 1992; pp. 390–419. [Google Scholar]
- Kaput, J.J. Teaching and learning a new algebra. In Mathematics Classrooms That Promote Understanding; Fennema, E., Romberg, T., Eds.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1999; pp. 133–135. [Google Scholar]
- Smith, E. Stasis and change: Integrating patterns, functions, and algebra throughout the K-12 curriculum. In A Research Companion to Principles and Standards for School Mathematics; Kilpatrick, J., Martin, W.G., Schifter, D., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 2003; pp. 136–150. [Google Scholar]
- Heyd-Metzuyanim, E. The co-construction of learning difficulties in mathematics—Teacher–student interactions and their role in the development of a disabled mathematical identity. Educ. Stud. Math. 2013, 83, 341–368. [Google Scholar] [CrossRef]
- Rocha, H. Pre-service teachers’ knowledge and the use of different technologies to teach Mathematics. In Perspectives and Trends in Education and Technology; Mesquita, A., Abreu, A., Carvalho, J., Eds.; Springer: Singapore, 2022; pp. 505–515. [Google Scholar] [CrossRef]
- Stein, M.K.; Smith, M.S. Mathematical tasks as a framework for reflection: From research to practice. Math. Teach. Middle Sch. 1998, 3, 268–275. [Google Scholar] [CrossRef]
- Ponte, J.P. Gestão curricular em Matemática. In O Professor e o Desenvolvimento Curricular; GTI, Ed.; Associação de Professores de Matemática: Lisbon, Portugal, 2005; pp. 11–34. [Google Scholar]
- McMillan, J.H.; Schumacher, S. Research in Education Evidence-Based Inquiry, 7th ed.; Pearson Education Limited: London, UK, 2014. [Google Scholar]
- Rodrigues, A. O Raciocínio Funcional de Alunos de 8.º ano na Resolução de Tarefas. Master’s Thesis, Universidade de Lisboa, Lisbon, Portugal, 2016. [Google Scholar]
- Ponte, J.P. The history of concept of function and some educational implications. Math. Educ. 1992, 3, 3–8. [Google Scholar]
- Panasuk, R.M. Three phase ranking framework for assessing conceptual understanding in algebra using multiple representations. Education 2010, 13, 235–257. [Google Scholar]
- Ponte, J.P.; Branco, N.; Matos, A. Álgebra no Ensino Básico; Ministério da Educação—Direção Geral de Inovação e de Desenvolvimento Curricular: Lisbon, Portugal, 2009.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).