Abstract
This study examines the impact that fat-tailed distributions of the spread residuals have on the optimal orders for pairs trading of stocks and cryptocurrencies. Using daily data from selected pairs, the spread dynamics has been modeled through a mean-reverting Ornstein–Uhlenbeck process and investigates how deviations from normality affect strategy design and profitability. Specifically, we compared four fat-tailed distributions—Lévy stable, generalized hyperbolic, Johnson’s SU, and non-centered Student’s t—and showed how they modify optimal entry and exit thresholds, and performance metrics. The main findings reveal that the proposed pairs trading strategy correctly captures some key stylized facts of residual spreads such as large jumps, skewness, and excess Kurtosis. Interestingly, we considered regime-switching behaviors to account for structural changes in market dynamics, providing empirical evidence that optimal trading rules are regime-dependent and significantly influenced by the residual distribution’s tail behavior. Unlike conventional approaches, we optimized the entry signal and link heavy tails not only to volatility clustering but also to the nonlinearity in switching regimes. These findings suggest the need to account for distributional properties and dynamic regimes when designing robust pairs trading strategies, providing a more realistic and effective framework of these strategies in highly volatile and non-normal markets.
1. Introduction
Pairs trading is a widely used trading strategy (Bağcı & Soylu, 2024, 2025; Bergmann & de Oliveira, 2025; Liou et al., 2024; Tadi & Witzany, 2025; H. Yang & Malik, 2024; Wilkens, 2025), which relies on the assumption that a known function (i.e., the spread) of the portfolio price is a stationary, mean-reverting process (Krauss, 2016; Endres, 2020). The normality assumption when fitting probability distribution to spreads’ residuals has been neglected by previous research. In this context, fat-tailed distributions may overcome the restrictions of normal spreads in the context of pairs trading performance (Göncü & Akyildirim, 2016; Guang, 2021). Though there is an abundance in the literature on pairs trading modeled by the Ornstein–Uhlenbeck equation, there is very little research that evaluates optimal trading rules using non-normal probability distributions (Endres & Stübinger, 2019a).
In this way, a couple of studies (Stübinger & Endres, 2018; Endres & Stübinger, 2019b), which focus on S&P500 oil stocks, have modelled the central-involved random process as a Wiener process plus a Poisson process with variable size (amplitude) each time. They concluded that the proposed pairs trading strategy achieves a higher performance than traditional approaches (i.e., based on traditional distance and time-series models). However, they focused on high-frequency data, which is often, unfortunately, only accessible to a minority of investors due to the onerous costs of the required infrastructure. Larsson et al. (2013) used a similar approach—but the sizes of the changes in the case of a Poisson event had distributions given by truncated Gaussians—and concluded that there is an optimal stopping boundary that may help investors to obtain superior performance in pairs trading strategies in the presence of jumps. Wu et al. (2020) analyzed a pair of Chinese stocks, calculating optimal trading rules for pairs trading; they modeled returns using Poisson processes with constant jump intensity. They concluded that excess jumps in the spread have a significant impact on strategy profitability and the optimal timing for opening and closing positions. Guang (2021) analyzed optimal trading rules using the t-student distribution for modeling the noise of the spread. It showed the results of a few pairs of stocks (e.g., Pepsi/Coca–cola, American banks, etc.) and concluded that in almost all cases, the aforementioned approach significantly improved investment performance. Vergara and Kristjanpoller (2024) found optimal thresholds for pairs trading of cryptocurrencies, modeling returns (rather than residuals of a spread that follows an Ornstein–Uhlenbeck equation) with a generalized hyperbolic distribution. Rad et al. (2016) pointed out the fact that the spreads have fat tails. They applied the copula method using t-student copulas but did not focus on optimal trading rules systematically.
Interestingly, Göncü and Akyildirim (2016), which is the work more closely related to this study, focused on optimizing average profits in pairs related to commodity futures. They considered dollar-neutral pairs (instead of beta-neutral pairs) and modeled spreads using generalized hyperbolic probability density functions and subclasses of them (NIG and VG density functions). Unfortunately, they neither optimized the enter value and stop-loss nor compared the effects of normal and non-normal distributions on trading rules, and they considered no regime switching (this is, they considered no change in the parameters which characterize the random variables throughout the simulation). All these features separate their work from ours. Based on the previous research findings and to the best of our knowledge, the present article is the first study of optimal trading rules for Ornstein–Uhlenbeck-based pairs trading of stocks using fat-tailed distributions whose conclusions can be applied by most investors. In this way, this paper contributes to the existing literature in several ways. Firstly, we considered four different fat-tailed distributions (i.e., Lévy stable, generalized hyperbolic, Johnson’s SU, and non-centered t-student) as well as normal distribution, and we analyzed how well they suited the empirical spreads (note that nearly all research analyzing fat tails considers only one fat-tailed distribution). We have chosen the referred fat-tailed distributions because of their popularity; they have successfully been applied to financial problems (Carneiro et al., 2025; Göncü & Akyildirim, 2016; Simonato, 2012; Plerou et al., 2001) and because of the fact that they are easily usable within Python. The comparison between normal and fat-tailed distributions provides insights into the (low) quality of the nearly ubiquitous normality assumption. Secondly, we thoroughly analyzed optimal trading rules for all thresholds (enter value, profit-taking, and stop-loss), which is seldom found in the literature. Our analysis of regime-switching is central to these optimal rules (this analysis is also rare in the literature on optimal trading rules for pairs trading). Thirdly, we performed calculations for cryptocurrencies, which have seldom been analyzed in this context due to their relative novelty. Fourthly, we provided means (open-source code) to replicate our results and to extend our analysis to arbitrary stocks and cryptocurrencies. In summary, the work that we present is expected to overcome the limitations of previous studies, whose scope was narrower and less easily applicable.
Regime-switching is often ignored in the literature. However, recent research on pairs trading considers regime-switching models and reveals their superior performance in different markets. Chodchuangnirun et al. (2018) focuses on the US market and show that a Markov-switching model with generalized conditional heteroskedasticity effects (MS-GARCH) performs better than other conventional methods, such as kink and threshold models. Similarly, Namwong et al. (2019) focus on the stocks of the SET100 index to construct the pairs and apply a MS-GARCH model, and they conclude that this approach generates positive returns, which are higher than the return from trading in individual stocks. Focusing on the SP500 shares, Endres and Stübinger (2019b) implement a Lévy-driven Ornstein–Uhlenbeck MS approach and find significant results with Sharpe ratios of 3.92 after transaction costs. Chen et al. (2014) focus on the Dow Jones Industrial Average Index stock and propose a three-regime threshold autoregressive model with GARCH effects (TAR-GARCH) and conclude that this strategy generates positive excess returns.
This paper is structured as follows. In the next section, we present the time series used in the empirical calculations. Section 3 briefly presents our calculation methods, including stochastic modeling and trading strategies, measures of performance and risk of the analyzed strategies, and assumptions underlying this work. In Section 4, we present the main results. In the interest of thoroughness, we also analyze the out-of-sample profits of the trading strategies and the effects of Poisson events. Finally, Section 5 outlines our main conclusions. Additional information on the methods and results can be found in the Supplementary Material, which also presents an analysis of single-product trading as well as theoretical explanations to provide deeper insights.
2. Data Description
The details of the time series used in this study are shown in Table 1. We focused on 23 stocks that correspond to well-known large capitalization enterprises traded in efficient markets–North America and Europe–during the 2017/2025 period (20 February 2017 to 20 February 2025). For representativity purposes, stocks for all 11 GICS sectors were analyzed. We also considered four among the most traded cryptocurrencies for robustness purposes, because their properties strongly differ from conventional stocks. Data for the four analyzed cryptocurrencies were collected from 2021 to 2025 (20 February 2021 to 20 February 2025). The risk-free rates considered correspond to yields of either 1-year T-bills (US) or German 1-year govies (Ger). With the aim of making the calculation replicable, we focus on the daily time series (weekdays).

Table 1.
Analyzed stocks and cryptocurrencies.
Note that in our approach the trader can only buy or sell immediately before the closing time of each day; that is, in our framework, time is a discrete variable. It might be argued that by proceeding in this way we are making an error in the Ornstein–Uhlenbeck equation due to the non-infinitesimal size of the time step, which for us is one day (and, e.g., that a correction term proportional to must be added to correctly reproduce the variance of the process). However, we deemed that such an interpretation would be mistaken. For stocks, most of the trading activity takes place near the opening and closing times, hence properties like liquidity do strongly depend on the time of the day. If we were using time steps lower than one day in our modeling of the time series, we should give an account of such time of the day-dependent properties, which would make our model much more complex. That would be analogous to considering seasonality when modeling time series, which can be avoided if the time separation between measurements is exactly one year.
There exist two main methods for choosing candidates to form a pair (i.e., a traded long–short portfolio). The first one is to take a large set of (N) products, calculate the spreads of all (N·(N − 1)/2) pairs within this set, and choose the pairs to trade depending on their properties, like stationarity, variance of the residuals, etc. The second is based on fundamental information, i.e., on selecting candidates which have common features, like sector, country, currency, market capitalization, etc. In this paper, we followed the second method, because we found it more robust. If two stocks have similar features, it is more justified that the spread of the pair reverts to a mean. We deemed that following the first method would be prone to selecting pairs which behaved well in the past by mere coincidence (data snooping), which will less likely behave so in the future. Therefore, we constructed pairs as follows. For every GICS sector, we selected those with largest market cap which are traded either in the US or in Europe. We took between 10 and 20 stocks for each sector, as well as the 11 cryptocurrencies with highest market value. We then randomly chose the two constituents of the pair among those whose spreads presented the best stationarity properties (subject to the condition that at least one of the two stocks–or cryptocurrencies–is widely known).
Table 2 shows the main descriptive statistics, normality tests, and stationarity tests for the residuals of the pairs’ spreads (the way these spreads are calculated is explained in Section 3.1.1 below). The average Kurtosis for stocks is 19.7, much higher than the value obtained by Göncü and Akyildirim (2016) for futures of commodities (11.8); the Kurtosis of cryptocurrencies is still higher. As shown in Table 2, the normality assumption is clearly rejected for all the spread residuals, which also agrees with the results of Göncü and Akyildirim (2016), and strongly supports the usage of fat-tailed distributions. Though not explicitly presented in Table 2, three different normality tests (Anderson–Darling, Shapiro–Wilk, and Kolmogorov–Smirnov) support that the spreads do not follow a normal distribution (the p-values were below 10−19 for all normality tests for all the analyzed pairs). Accordingly, empirical features of the spreads suggest the use of several fat-tailed distributions to better capture the empirical properties of stocks’ returns and spreads. The values of the skewness and Kurtosis displayed in Table 2 also support the non-normality, making it clear that the model used in the vast majority of the literature (normality of the spread residuals) fails to appropriately suit to the observed data. Table 2 also shows the test statistics of Augmented Dickey–Fuller (ADF) tests, which support the stationarity of the spread residuals. Finally, the test statistics of the Brock, Dechert, y Scheinkman (BDS) tests (shown in the last column, in which there is a p-value of zero in all cases) confirm nonlinearity of the dynamics. Graphical representations of the pairs’ spreads vs. time are included in the Supplementary Materials.

Table 2.
Descriptive statistics of pairs’ spread residuals.
3. Methodology
3.1. Stochastic Models
In this section, we briefly present the mathematical methods behind the calculations of this paper. Detailed explanations of our methods for pairs trading can be found in the Supplementary Materials.
3.1.1. Pairs Trading Modeling
Pairs trading is a trading method aimed at reducing market risk where the investor builds a portfolio consisting of just two financial products, one being of long position and the other being of short position. The pair, however, must be appropriately selected, so that a known function of the portfolio price is a stationary, mean-reverting process. One of the most popular models to account for mean-reverting processes is the Ornstein–Uhlenbeck equation (Shreve, 2004), whose continuous time form is given by the following:
where is a mean-reverting stochastic process (for us, it is the spread of a long–short portfolio, i.e., ) and , , and are real numbers. For simplicity reasons, we assumed that and were constant and that the probability distribution of remained unchanged in certain periods. represents the mean towards tends, the mean-reversion parameter —which is positive–represents the speed of such trend, and is the multiplicative factor of the random variable , sometimes called the volatility of the process (Göncü & Akyildirim, 2016). Such as was used in previous research, this paper considers the stochastic process representing fat-tailed random variables (Göncü & Akyildirim, 2016; Yu et al., 2017; Endres, 2020). In this way, is called a generalized Ornstein–Uhlenbeck process or a Lévy-driven Ornstein–Uhlenbeck process.
Our pairs trading strategy defines the spread of a long–short portfolio formed by two financial products which presents the mean-reverting property. Such as was used in existing research (Vidyamurthy, 2004; Zeng & Lee, 2014; Göncü & Akyildirim, 2016), we defined the spread as the following:
where indicates the price of a financial product and and are indices of the two stocks. The weights of both stocks forming a pair are and , thus assuming that they are infinitely divisible. Dividends are assumed to be immediately reinvested. Although some authors (Huck & Afawubo, 2014; Elliott et al., 2005) prefer defining the spread by avoiding logarithms (), or using standardized prices (Carrasco-Blázquez et al., 2018), this paper defines the spread such as shown in Equation (2). This definition implies that the absolute return of the spread is approximately equal to the absolute return of our portfolio (see proof in Section S.2 of the Supplementary Materials). The coefficient has a strong impact on the mean-reversion property of the spread (an inappropriate choice may make the spread non-stationary). Notwithstanding, there is no unified criterion in the literature to assign a value to . Among the possible methods to do so, we shall mention three widely used approaches: (i) dollar-neutrality; (ii) Vidyamurthy’s cointegration approach (which is often beta-neutral), and (iii) the Vector Error Correction Model (VECM). The most straightforward calculation is to define dollar-neutral pairs, where the initial values of the long and short positions fully offset each other (). If the prices () are divided by their initial values, then this is equivalent to setting . Using dollar-neutral pairs is a popular approach (Elliott et al., 2005; Galenko et al., 2012; Göncü & Akyildirim, 2016) because it requires little funding. However, the investor is exposed to noise because the prices at just one time () are used to calculate . This can be avoided through variations of the dollar-neutral method which uses information on prices at several different times. Between them, we cite the definition of as the slope of the ordinary least squares linear regression of vs. (Huck & Afawubo, 2014). A third approach to calculating cointegration coefficients is the VECM (Engle & Granger, 1987). Under this approach, is computed as a two-stage least squares procedure, regressing expressions that involve both prices and returns of A and B (Carrasco-Blázquez et al., 2018; Nair, 2021).
A further way to calculate is Vidyamurthy’s cointegration approach (Vidyamurthy, 2004). This method provides high, stable, and robust returns (alpha) (Huck & Afawubo, 2014), also in pairs trading of cryptocurrencies. It has also been stated that returns from cointegration tend to present less extreme values (i.e., a lower Kurtosis coefficient) than other methods, like distance or copula methods (Rad et al., 2016). Given the aforementioned advantages, this paper focuses on this approach to calculate the value of .
Pairs trading relies on the hope that the spread reverts to a mean. To avoid a drift that shatters mean-reversion, the spread is defined so that it is stationary. This value of in Equation (2) is chosen so that, even if the time series , are not stationary, their linear combination is stationary. This is the definition of cointegration: two non-stationary time series are said to be cointegrated if there is a linear combination of them that is stationary (Vidyamurthy, 2004). Stocks prices , are frequently non-stationary because stock markets tend to be bullish in the long term; therefore, the choice of is central to the profitability of pairs trading. A common way to find an appropriate value for is from the regression of common trends. This is based on the assumption that each of the log-prices of Equation (2) can be deconstructed into two terms: (i) a common trend , which is non-stationary and is most often related to the evolution of markets and (ii) a random walk term , which is stationary and idiosyncratic (that is, it is unrelated to the general behavior of markets):
To guarantee cointegration, we needed the common trends to be proportional (). Indeed, their proportionality constant is (this is ), which is called the cointegration coefficient. In the simplest case, the common trends are proportional to a single observable quantity that accounts for the market behavior (e.g., an index like the S&P 500 or the price of a share of an ETF which tracks it). Let us call (for ) to the log-returns of the stock prices (), to the market returns (e.g., , where is the price of the aforementioned share of an ETF that tracks the S&P 500 index), and to a risk-free rate (e.g., the yield of the T-bills with maturity in one year). corresponds to the returns of the indices displayed in the fourth column of the table presented in Section S.2 of the Supplementary Materials (for the cases with one single risk factor). We can then express the returns of stocks , as follows:
where are the slopes of the linear regression of vs. (as given by the well-known Capital Asset Pricing Model, CAPM) and indicate returns which are specific (idiosyncratic) of the corresponding time series. Here we have considered a risk-free rate following the procedure indicated by Do et al. (2006), yet many authors simply assume that . Imposing in Equation (2) implies that the absolute returns of the spread () will be the following:
where the first term of the right-hand side is expected to have a low size because frequently ; this is the absolute returns of the spread lack market (non-stationary) components and will hence depend on idiosyncratic components, which are assumed to be stationary. Note that this does not mean that our portfolio is perfectly beta-neutral: When we enter our position, we are long (short) one dollar in stock and short (long) dollars (or other currency) in stock . Since is the quotient of betas, at inception our portfolio is beta-neutral; however, after the first day the values of our two positions have varied, and their quotient will most likely not remain equal to . Hence, our portfolio will have a non-zero exposure to the market, even if the spread is perfectly beta-neutral (beta-neutral portfolios would require continuous rebalancing).
Since there is no guarantee that , are indeed stationary, we performed stationarity tests of the spreads (see Table 2), and those pairs whose spreads fail to pass the test are discarded.
If we considered several risk factors instead of only one, that is, if we rely on the Arbitrage Pricing Theory (APT instead of CAPM), then Equation (4) becomes the following:
where is the number of considered risk factors (e.g., stocks, cryptocurrencies, or commodities indexes) and are their respective returns (see the returns of the indices displayed in the fourth column of the table presented in Section S.2 of the Supplementary Materials). In this case, would be the slope of the linear regression (-vs.-) of the cloud of points where and .
Note that for simplicity’s sake we consider a constant value for the betas in Equations (4) and (6); an interesting discussion about the stationarity of the betas can be found in Agrrawal and Clark (2007).
In order to obtain the parameters of the Ornstein–Uhlenbeck equation (, , and from Equation (1)), we performed a discretization such as indicated by Göncü and Akyildirim (2016). We made and , and we renamed as . Equation (1) hence becomes the following:
where are the residuals, being their scaling parameter. We will later fit these residuals to different fat-tailed distributions. The ordinary least squares linear regression of (i.e., ) vs. (i.e., ) provides the and parameters. The residuals of the regression () can be fit to any probability distribution which is deemed appropriate. If the analyzed data present the appropriate properties (i.e., stationarity of the spread and low autocorrelation of residuals), then the selected pair can be traded with profit expectations. To evaluate the optimal rules for such trading, we set a maximum horizon, which is defined as the maximum number of days that a portfolio is held before selling. We then performed a Monte Carlo (MC) analysis for different values of the thresholds (trading rules) that determine the strategy. These are the following: (i) the enter threshold, which determines the minimum absolute value of the spread to build a position (i.e., to enter the trade); (ii) the profit-taking threshold, which determines the value of the spread to unwind (finish) the portfolio making a profit; and (iii) the stop-loss threshold, which determines the value at which the portfolio is unwound having a loss.
The products which form the chosen long–short pairs have important features in common: they belong to the same GICS sector and to the same region, are traded in the same market with the same currency, as well as similar regulations, and both have large market capitalizations. Hence, they are expected to depend on the same economic forces. This supports the expectation that, when the spread (X in Equation (1)) moves far away from the mean (), such market forces will move it again towards this mean.
3.1.2. Probability Distributions
Each pair spread is fitted to five different distributions: (i) normal, (ii) Lévy stable, (iii) generalized hyperbolic, (iv) Johnson’s , and (v) non-centered t-student. All distributions have a loc and a scale parameter, which account for the location and scale (size) of the residuals. The four fat-tailed distributions also have two parameters each to account for the skewness and fatness of the tail. The generalized hyperbolic distributions that we have considered also have a fifth parameter (p-parameter) which accounts for the form. We called the set of two, four, or five parameters of the distribution plus the parameters of the Ornstein–Uhlenbeck equation1. For the normal distributions, the loc and scale parameters are the mean and standard deviation of the spread residuals. The former is always zero (by consequence of the definition of ordinary least squares linear regression), and hence the only actual parameter of the distribution is the scale ( and are found by simple ordinary least squares linear regression of vs. ). The parameters of the four fat-tailed distributions are calculated by maximum likelihood (ML), which is the standard method to this end (Borak et al., 2011). The calculation of the parameters through ML is made by minimizing the loss function:
where stands for the number of residuals and pdf is the probability density function. We calculated the optimal parameters of the distribution (i.e., those minimizing the loss function), by using the gradient descent method (Barzilai & Borwein, 1988). This method guarantees that a local minimum of the loss function is eventually reached. Apart from performing gradient descent iterations that involve all parameters, in order to minimize the loss function we performed a series of iterations that involved only the skewness parameter or the tail parameter. This was because the gradient with respect to the scale parameter is often much higher than the rest, which can make the skewness and tail parameters move very little away from their initial values unless such individual iterations are performed. In addition, to find appropriate solutions we included some randomness in the evolution, and we tried different random and deterministic starting values for the gradient descent method, except with the Lévy stable distribution This was because calculations of the pdf of the stable distribution are much slower than for non-centered t-student and generalized hyperbolic, which precluded promptly, performing many calculations using the stable distribution. The slowness of maximum likelihood fittings to Lévy stable distributions has already been pointed out by other authors (Kawai, 2012).
3.2. Trading Strategies
We searched for optimal trading strategies using synthetic data, due to their advantages (López de Prado, 2018). That is, for a given value of the set of trading rules, we generated numerous (200,000) time series. Each of these synthetic time series is one path of our Monte Carlo simulations and corresponds to the evolution of of Equation (7). The time series of are generated with up to five different probability distributions for : normal, Lévy stable, generalized hyperbolic, Johnson’s SU, and non-centered t-student. The trading rules consist of four numbers, which determine the thresholds for entering and exiting (unwinding) our positions. The enter value is the value of the spread at which we built our long–short portfolio (i.e., we bought product A and sold product B or vice versa). The limit orders are the profit-taking and stop-loss thresholds. If our position is long in spread, i.e., if the enter value is negative (we define it by subtracting ) because we bet that the spread will increase, then the profit-taking is a value of the spread which is above the enter value, and the stop-loss is a value of the spread which is below the enter value. The converse happens if our position is short in spread (i.e., if the enter value is positive because we bet that the spread will decrease); in this case the profit-taking is below the enter value, and the stop-loss is above the enter value. As soon as either the profit-taking or the stop-loss threshold is exceeded, we determined that the portfolio is unwound, obtaining a profit (if the profit-taking was surpassed) or a loss (if the stop-loss was exceeded). The last trading rule is the maximum horizon, which determines the uppermost time for holding a pair. If after such a period holding our pair we have reached neither the profit-taking nor the stop-loss thresholds, then the position is unwound anyway (at a profit or a loss). We did not make calculations to optimize the maximum horizon because we assumed that the trader may have had exogenous limitations for it. Therefore, each of the (e.g., 200,000) synthetic paths provides a profit (or loss), which is defined as the difference between the spread when unwinding the position minus the spread when the position was built (times −1 if we were short in spread). We considered transaction costs equal to 0.5% per year for shorted stocks and 1.2% for shorted cryptocurrencies. This is a proxy for fees and commissions and slippage and market impact (see the Supplementary Materials for a discussion about this choice).
When we tested each set of parameters corresponding to a given trading strategy (horizon and enter, profit-taking, and stop-loss thresholds), we used the same set of generated random variables which account for the evolution of prices. This is aimed at avoiding statistical error (Bouchaud & Potters, 2003; Göncü & Akyildirim, 2016). Otherwise, the differences between the synthetic price time series may lead to distorted results. For simplicity’s sake, we assumed that, at the initial time () of each MC path, the spread lies exactly at . The generation of synthetic time series allows mitigating the backtest overfitting, which is a major common drawback of quantitative investing modeling (López de Prado, 2023). Making an analysis based solely on the observed price time series would give excessive weight to the realized values of the random variable, altogether neglecting other values, that were equally likely, but not realized.
3.3. Performance Measures
For each set of trading rules (enter value, profit-taking, stop-loss, and maximum horizon), our software calculates eight measures of performance and risk: the Sharpe ratio of profits (), the rescaled Sharpe ratio calculated from semi-deviation (), standard deviation, semi-deviation, profit average, probability of loss, Value-at-Risk (VaR), and Expected Shortfall (ES). In this paper, we focused on the first two to account for the risk-adjusted returns, but choosing other criteria is a matter of taste. For example, the hierarchical risk-parity method (López de Prado, 2016) focuses on standard deviations of returns, and other authors prefer to simply use the expected profit to measure performance (Göncü & Akyildirim, 2016).
We define the profit average, the profit standard deviation, and the Sharpe ratio as the following:
where stands for the annualized cumulative return of the -th Monte Carlo path (note that a path can contain several enter and exit points; the cumulative return is the addition of all of them) and is the number of paths. For a given Monte Carlo path, we annualize its total return () by multiplying it by the number of trading days of a year and dividing it by the time span of the path. In the analysis of pairs trading, we define each individual return as , where is the time of closing (unwinding) our position and is the time of building it. In the analysis of trading a single product (presented in the Supplementary Materials), we define the return as for calculations of a single product ().
We define the semi-deviation and its corresponding Sharpe ratio as follows:
where only the returns that are below average are counted measuring the variability. The rescaling factor () is included to provide a more understandable comparison between and ; this term would make both Sharpe ratios equal if the returns were fully symmetric. We deem the rescaled Sharpe ratio from semi-deviation () a more reliable measure of performance than the bare Sharpe ratio () because it penalizes the variability of below-average profits, which better suits the loss aversion of investors (Thaler, 2015). Therefore, we present in most of the plots (heatmaps) of this article. Note that is conceptually similar to the Sortino ratio because its denominator is also a semi-deviation.
We define the ES, such as indicated by the European Banking Authority, though keeping a negative sign for losses; that is the following:
where the signs indicate the integer part (floor) of and the indices () of are ordered so that are monotonically increasing. For both VaR and ES, we set (1%). Note that Equation (14) is based on Historical Simulation, which makes that formula potentially inaccurate (García-Risueño, 2025); however, we used it because its usage is widely extended due to regulatory requirements. An interesting discussion about the properties of the ES can be found in Gribkova et al. (2025).
In the Supplementary Materials, we also provide examples of the VaR and the probability of loss. We define the VaR using the historical method (Choudhry, 2013), that is as the -th worst return. We define the probability of loss as the number of Monte Carlo paths whose return is negatively divided by the total number of paths; this is .
4. Results and Discussion
In this section, we present the calculated features of pairs trading. Complementary remarks on single-product trading can be viewed in the Supplementary Materials.
4.1. Fitting of Probability Distributions
We calculated spreads using the method presented in Section 3.1.1 (see Equation (2)), using pairs of the products listed in Table 1; the list of pairs is displayed in Table S1 in the Supplementary Materials. The spreads of the 13 analyzed pairs pass the stationarity test (see Table 2). The normality of the spread residuals was checked through the three normality tests, including Anderson–Darling’s (see Table 2). The results reveal that all the analyzed spreads are non-normally distributed. Then, the analyzed spreads were fitted to the normal and to four fat-tailed distributions. As an example, Figure 1 presents the histograms of the spreads (blue bars) for an example spread (pair of energy stocks, PSX/TTE). In each subplot, the curve represents the best fit found for a given distribution. As expected, the normal distribution fits much worse to the histogram than the fat-tailed distributions. This property holds for all the analyzed pairs (see the rest of the figures in the Supplementary Material). The subplots of our Figure 1 that correspond to normal and to generalized hyperbolic distributions present the same behaviors reported by Figures 2 and 4–6 of Göncü and Akyildirim (2016).
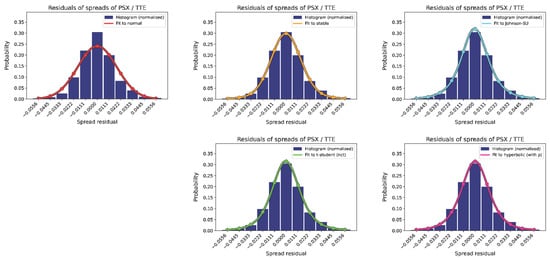
Figure 1.
Fitted spreads to the probability distributions (TTE/PSX example). The blue bars present the histogram of the spread residuals. The curves in each subplot correspond to the best-found fitting to it for each of the five analyzed probability distributions. The normal probability density function (red curve) fits to the histogram much worse than the fat-tailed density functions (yellow, blue, green, and pink curves).
Note that, for the analyzed periods, all the spreads listed in Table 2 (except BP/TTE) qualitatively display oscillation around one single value of the mean (see Figures S1–S3 in the Supplemental Materials), while the BP/TTE spread displays several different values around which the spread oscillates (see Figure 4 below in this document). Therefore, we fitted the spread residuals of every pair (except BP/TTE) to a unimodal distribution. Concerning BP/TTE, we fitted the spreads of different time windows to different unimodal distributions.
In Table 3, Table 4, Table 5, Table 6 and Table 7, we showed the fitting parameters of the spread residuals. These values clearly reveal that the tails of the residuals’ distribution are notably fat; for example, the average value of the number of degrees of freedom () of t-student distributions is 3.84 for stocks and 2.06 for cryptocurrencies (note that the heavy-tailed Cauchy distribution has , and the normal distribution has ), the average a-param of the generalized hyperbolic distribution is 0.141 for stocks, and the average value of the parameter of the stable distribution is 1.70 for stocks (note that the Cauchy distribution has , and the normal distribution has ). Table 3, Table 4, Table 5, Table 6 and Table 7 also show the loss function, which takes similar values for the four fat-tailed distributions, though among them the stable is the worst in most cases. Specifically, in six cases the generalized hyperbolic distribution provides the best fitting (i.e., lowest loss function) among all five analyzed distributions; in five cases, the non-centered, t-student function presents the best fitting; in two cases the Johnson fits best, in all cases considering the minimum loss function as the decision for determining the quality of the distribution. In Table 8, we displayed a comparison using the Akaike information criterion (AIC), which includes a penalty depending on the number of parameters of the distribution (which are two for the normal, four for non-centered t-Student, Johnson’s SU, and Lévy stable, and are five for the generalized hyperbolic distribution). The number displayed in Table 8 (the AIC) is the following:
where is the number of parameters of the distribution, n is the number of points of the time series (spread), and is the loss function as defined in Equation (8). Interestingly, the Akaike criterion relegates the generalized hyperbolic distribution for all stocks: for them, the best choice according to AIC would be the non-centered t-student distribution in all cases except one, where Johnson’s SU should be preferred.

Table 3.
Spreads fitting to normal distribution.

Table 4.
Spreads fitting to non-centered t-student distribution.

Table 5.
Spreads fitting to Johnson-SU distribution.

Table 6.
Spreads fitting to generalized hyperbolic distribution.

Table 7.
Spreads fitting to Lévy stable distribution.

Table 8.
Akaike information criterion for the analyzed distributions.
4.2. Trading Rules
In this section, we presented the performance of different trading strategies. We first (Section 4.2.1) displayed the case that is commonly assumed in the literature, which corresponds to the Ornstein–Uhlenbeck equation with constant parameters. Section 4.2.2 presents an attempt to overcome such limitations of the model, considering discrete changes in the mean () through Poisson events.
4.2.1. Mean Reversion with Constant Parameters
Figure 2 shows the heatmaps indicating profitability of the trading strategies. Each subplot corresponds to calculations made using synthetic data to generate time series of the spreads. A different distribution was used to generate the residuals of the spreads in each case; all were carried out using 200,000 Monte Carlo paths. They present the rescaled Sharpe ratio from semi-deviation (), which measures risk-adjusted profitability (see the Supplementary Materials for other performance metrics). The maximum horizon of all figures corresponds to one year. The (enter value) and (profit-taking) axes of Figure 2 represent the value of the spread when the position is built and unwound, respectively. Note that the heatmaps of this paper present values of the profit-taking and stop-loss thresholds which correspond to additive values with respect to the enter value, and the enter values correspond to additive values with respect to the corresponding .
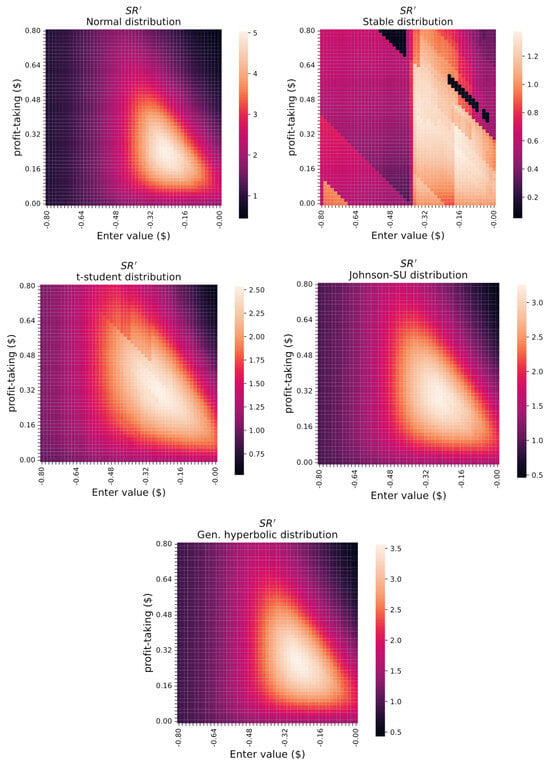
Figure 2.
Sharpe ratios’ heatmaps from fitting to each probability distribution (TTE/PSX example): heatmaps which present the Sharpe ratio as a function of different values of the trading rules (enter value and profit-taking thresholds). Each point of the heatmaps was calculated using synthetic data (200,000 Monte Carlo paths) for the time series of the residuals of the spread. Each subplot corresponds to the synthetic data being generated with a different probability density function (in all cases, using the parameters of the optimal fitting of the observed residuals to the corresponding distribution).
As can be noted in Figure 2, different distributions lead to differences in the maximum value of the Sharpe ratios (). Hence, the choice of distribution to fit the spread residuals has non-trivial consequences on the trading strategy. This is more clearly seen in Figure 3 (see Supplementary Materials for examples corresponding to other pairs). Each point of the curve of the left subplot corresponds to the maximum value sweeping all profit-taking thresholds and a given enter value. The right subplot corresponds to the maximum value sweeping all enter values for a given profit-taking threshold (measured with respect to the enter value). These plots inform us about several interesting findings: (i) The value of the maximum strongly depends on the distribution chosen to model the residuals of the spread (it is nearly six for the normal distribution, and four for the t-student and generalized hyperbolic distributions). (ii) The optimal profit-taking threshold also strongly differs for different distributions (it is 0.064 for the normal distribution and 0.048 for the t-student distribution). Accordingly, this will probably have an impact on the number of times a trade is entered. These results correspond to an analysis where no stop-loss orders are in force (i.e., the stop-loss parameter is set to ). Our analyses indicate that farther (higher size) stop-loss parameters lead to higher values of the Sharpe ratios, and thus the optimal trading rules consist of setting them to (if the bet is long in spread) or to (if the bet is short in spread).
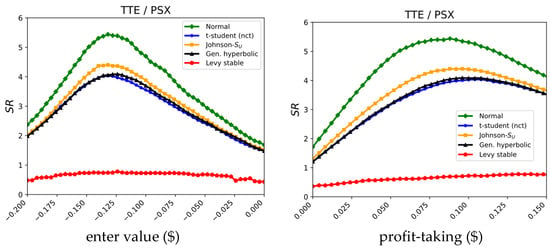
Figure 3.
Trading rules performance (XRP-USD/DOGE-USD example). (Left): Sharpe ratios vs. enter value (maximum for all profit-taking thresholds) for the five analyzed distributions; (Right): Sharpe ratios vs. profit-taking threshold (maximum for all enter values).
Although the analysis shown in Figure 2 and Figure 3 is based on static parameters of the Ornstein–Uhlenbeck equation (, ), in a real-life trading action, the investor would probably set a finite stop-loss threshold. In the next section, we overcome this drawback, allowing a regime switching process for the parameter.
4.2.2. Regime Switching and Stop-Loss Orders
This section comprises the analysis of optimal trading rules with regime switching, modeling the switch as a Poisson process and the noise using the previously considered fat-tailed distributions. This analysis complements previous research (Bai & Wu, 2017; Y. Yang et al., 2017; Altay et al., 2018), which considers optimal trading rules in the presence of regime switching, but not the effect of fat-tailed distributions. This analysis also extends the work of Endres and Stübinger (2019b), which does so through jump components (rather than fat-tailed distributions), but it does not optimize the trading rules as we do (their enter value is (E0 ± σ(t)/2), and the profit-taking threshold is the opposite of the enter value around E0).
Figure 4 shows the BP/TTE spread calculated from 2008 to 2024. As can be seen, different regions where the spread oscillates around distinct values exist (approximately indicated with red horizontal lines). Recalculating the spread for the period from 2010 to 2020 indicates that it is stationary, and hence it could be considered a candidate for pairs trading before March 2020. However, the regime switching it then undergoes advises against it. The change of the long-term mean level of the spread () has a dramatic effect on the optimal trading rules. As stated above, if one generates synthetic data naively, ignoring changes in , then the most profitable strategies omit a stop-loss order. They involve holding your portfolio until the spread finally reverts to the mean, no matter how large your temporary loss is.
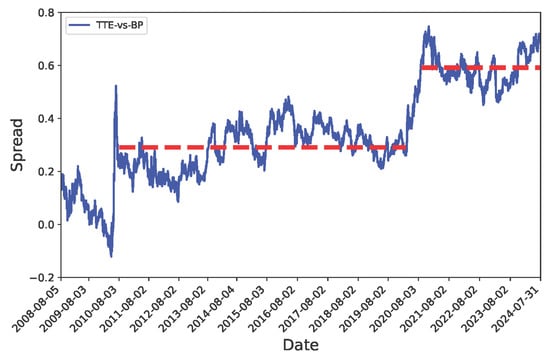
Figure 4.
BPE/TTE spread in the presence of regime switching. The blue line represents the observed spread (calculated using all the data of the period between 2008 and 2024). The dashed red lines present the approximate values of E0 the spread oscillates around. The clear difference between both dashed lines indicates that a regime switching happened.
Nevertheless, a more realistic approach which includes regime switching for synthetic data leads to optimal trading rules with a non-infinite stop-loss threshold, as we will see below. Let us assume that the long-term mean level of the spread () can change. We modeled the transition as a Poisson event. Results can be seen in Figure 5. The intermediate period is a time window from August 2010 to February 2020, which corresponds to 2310 trading days. Hence, we set a daily probability of the Poisson event of 0.0004329. We also assume that, if such an event takes place, there is a 50% probability of increasing or dropping; we set the size of the variation of equal to 0.62 because that is the difference between the values of the long-term mean level separately calculated using data from the two time stretches marked with red lines in Figure 4 (the set of residuals of each time window is fitted to a different unimodal distribution). Accordingly, Figure 5 shows the heatmaps ignoring (left graph) and considering (right graph) Poisson events (it corresponds to the t-student distribution, see Supplementary Materials for other distributions). The optimal thresholds are those which maximize the . This figure shows that for a given enter value the optimal stop-loss in the absence of changes in (Poisson events) has an infinite size (stop-loss ), while in the presence of changes in it has a finite value. It can be stated that regime switching reduces the maximum attainable , though the value with regime switching is still relatively high (about 0.5).
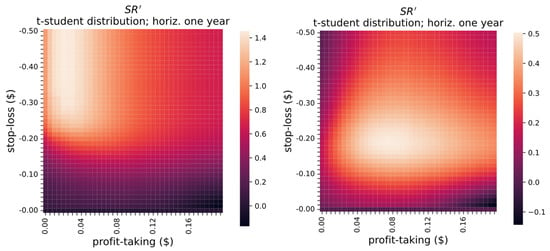
Figure 5.
Effect of the regime switching in the context of Poisson events: heatmaps which present the Sharpe ratio obtained from synthetic data of the spread residuals modeled with a t-student distribution. Each point corresponds to a given pair of thresholds (profit-taking and stop-loss). The (left) graph shows the without Poisson events for changes in the long-term mean level (E0) of the Ornstein–Uhlenbeck equation; the (right) considers changes in the long-term mean level. In the former case, the stop-loss which maximizes the Sharpe ratio is infinite; in the latter case, it is finite.
The result of Figure 5-left agrees with previous research (López de Prado, 2018), which states that the optimal rules for pairs trading consist of unwinding the position as soon as a small profit is realized and waiting (eventually for long periods) until your position is in-the-money, in case it is temporarily out-of-the-money (in practice, this is equivalent to setting a stop-loss threshold of infinite size, i.e., never to make an stop-loss order). However, such a bogus conclusion is due to naïve modeling, i.e., to the unrealistic assumption that the must forcedly remain unchanged. Note that in practice the price of a given stock can abruptly change for many reasons, like the company launching a new product, its board choosing a mistaken strategy, etc. This phenomenon can easily cause that takes a new value or even make both prices no longer cointegrated. The results displayed in Figure 5-right show that when the naïve modeling is avoided, i.e., when we consider regime switching, the optimal stop-loss order is no longer an infinite size. Figure 5-right also reveals that considering regime switching severely reduces the maximum . This indicates that spreads that are expected to be especially prone to changes in should be discarded in actual pairs trading.
4.3. Out-of-Sample Calculations
For the sake of completeness, we also present the out-of-sample profits of trading rules calculated using the methods presented in this paper. These results correspond to the actual profits that would have been obtained if an investor had traded the spreads of the analyzed pairs following optimal trading rules calculated using different probability density functions to fit the spread residuals. For every pair of stocks, we considered carrying out pairs trading between 20 February 2021 and 20 February 2025; for pairs of cryptocurrencies, we have considered carrying out pairs trading between 20 February 2023 and 20 February 2025. For every 3 months, we took the data of the spreads in the 5 years immediately before the beginning of that period. We fitted the residuals of the spreads of that 5-year period to each chosen probability density function and used the found probability density function to calculate optimal trading rules (heatmaps), calculated using 20,000 Monte Carlo paths. In each case, we set an arbitrary stop-loss parameter depending on the size of the past variations of the spread. Our trading rules cover both the positions short in spread (positive spread) and long in spread (negative spread). The trading rules specify when we enter and when we unwind the pair; the profit is calculated as the difference between the observed prices on both dates (note that, if the spread reaches a profit-taking threshold but unwinding the position results in a loss, then we do not unwind the position, because that would be contradictory to the concept of profit-taking). Whenever we enter a trade, we buy one dollar (or euro) of the long stock, and we sell short dollars (or euros) of the short stock (or the converse). Therefore, the cost of entering our position can be either positive or negative (if the size, measured in currency units, of the shorted position is higher than the size of the long position). We set a maximum horizon of 2 years; in all cases we consider transaction costs of 0.5%.
The results are shown in Table 9 (for stocks) and Table 10 (for cryptocurrencies). Columns with label “#” indicate the number of times that a trade was entered; columns with label Cost indicate the average cost of entering our position. The column with label Profit is the profit corresponding to the whole considered period measured in currency units (USD or euros). For example, if the price of a given entered long position is 1 dollar (it can be either 1 or γ, which is usually approximately 1) then a total profit of, for example, 0.16 implies that the profit was 16% of the cost of entering the long position.

Table 9.
Stocks’ out-of-sample pairs trading profitability.

Table 10.
Cryptocurrencies’ out-of-sample pairs trading profitability.
The results displayed in Table 9 and Table 10 indicate that the cointegration method produces consistent positive returns, as indicated by previous research (see e.g., Göncü & Akyildirim, 2016; Rad et al., 2016). Table 9 and Table 10 also indicate that the out-of-sample profits obtained usually differ for trading rules derived using fittings of the spread residuals to different probability density functions. This is reasonable because different functions lead to different trading rules, which lead to results that can clearly differ for one single set of historical prices. Nevertheless, for a given pair the total profits are usually positive and are usually the same order of magnitude.
5. Conclusions
This study determines optimal trading rules for Ornstein–Uhlenbeck-based pairs trading strategies applied to stocks and cryptocurrencies. The spread residuals are modeled by using fat-tailed distributions (i.e., Lévy stable, generalized hyperbolic, Johnson’s , and non-centered t-student), covering a gap in existing research where such distributional assumptions are narrowly considered in the context of trading thresholds. The model determines efficient entry, profit-taking, and stop-loss levels, addressing more realistic statistical properties of the spread residuals than the naïve normality and non-regime switching assumptions, which are widely present in the literature.
The empirical model assesses the adequacy of the selected fat-tailed distributions to account for heavy tails and skewness. After that, we extended existing frameworks by introducing regime-switching dynamics in trade rules optimization. Specifically, we used a Poisson-based, Markov-switching process that can capture structural breaks and changing market conditions, thereby increasing the strategy’s practical relevance.
The main findings reveal that the choice of distribution to model the spread residuals has a significant effect on optimal trading thresholds, especially profit-taking levels. Under the mean reversion model with constant parameters, larger stop-loss thresholds improve profitability. However, the need to shorten the finite stop-loss thresholds in real trading highlights the need to add regime-switching processes to pairs trading rules optimization. When a Poisson process accounting for regime-switching is considered, the trading thresholds are more conservative but better reflect real market constraints. Although the introduction of regime shifts reduces expected profitability, it confirms that optimal pairs trading strategies require unwinding positions with reduced performance.
Future research can benefit from the results of this study by focusing on more precisely addressing the magnitude and persistence of regime shifts when modeling residual spreads with fat-tailed distributions. Therefore, it could consider time-varying parameters or higher-frequency data to better address transitions and tail behavior, as well as more sophisticated models, like GARCH (to give account of volatility clustering) or copulas, which were omitted from this paper for the sake of simplicity. We will also consider tweaking the fitting to Lévy stable distributions. Another planned research line is to apply the knowledge from fat tails presented in this paper in more sophisticated trading strategies, e.g., using further market data, like Value Line ranks, as made in Waggle et al. (2001). The present research is not free from limitations. The assumption of specific parametric fat-tailed distributions and Poisson-based regime switching processes may not capture all the features and complexities of real market dynamics. Furthermore, while transaction costs are considered in the form of explicit fees, other parameters such as slippage, bid-ask spreads, and liquidity constraints are not explicitly addressed and should be considered by further research.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/ijfs13020096/s1.
Author Contributions
Conceptualization, P.G.-R.; methodology, P.G.-R.; software, P.G.-R.; validation, P.G.-R.; formal analysis, P.G.-R. and E.O.; investigation, P.G.-R., E.O. and J.M.M.; resources, P.G.-R.; data curation, P.G.-R.; writing—original draft preparation, P.G.-R. and E.O.; writing—review and editing, P.G.-R., E.O. and J.M.M.; visualization, P.G.-R. and E.O.; supervision, E.O. and J.M.M.; project administration, E.O. and J.M.M.; funding acquisition, E.O. and J.M.M. All authors have read and agreed to the published version of the manuscript.
Funding
Eduardo Ortas and José M. Moneva are grateful for the financial help from the Spanish Ministry of Science, Innovation and Universities (research project PID2023-146084OB-I00) and from the Government of Aragon, Spain (grant number S33_20R).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The Python code used in this paper is freely available in https://github.com/pablogr/FIN_optimal_trading_rules_fat_tails (accessed on 27 May 2025). This code can be used to download the raw input data from Yahoo Finance and to make every single calculation whose results are displayed in this paper. The corresponding author is at the disposal of the readers for discussion. Further data are contained within the article and Supplementary Materials.
Acknowledgments
We are grateful to Lorién López-Villellas for useful technical support and to Jo Robinson for proofreading.
Conflicts of Interest
Pablo García-Risueño discloses that all work corresponding to this article has been carried out in his non-working (free) time and using his own resources (books, internet searches, etc.), i.e., it is totally independent from his labor and paid activities in financial companies. The authors report that there are no competing interests to declare.
Note
| 1 | For all distributions, we used the implementations present in the scipy.stats v. 1.10.1 Python module. |
References
- Agrrawal, P., & Clark, J. M. (2007). ETF betas: A study of their estimation sensitivity to varying time intervals. Institutional Investor New York, 41(10), 96. [Google Scholar]
- Altay, S., Colaneri, K., & Eksi, Z. (2018). Pairs trading under drift uncertainty and risk penalization. International Journal of Theoretical and Applied Finance, 21(7), 1850046. [Google Scholar] [CrossRef]
- Bağcı, M., & Soylu, P. K. (2024). Classification of the optimal rebalancing frequency for pairs trading using machine learning techniques. Borsa Istanbul Review, 24, 83–90. [Google Scholar] [CrossRef]
- Bağcı, M., & Soylu, P. K. (2025). The optimal threshold selection for high-frequency pairs trading via supervised machine learning algorithms. Computational Economics. online first. [Google Scholar] [CrossRef]
- Bai, Y., & Wu, L. (2017). Analytic value function for optimal regime-switching pairs trading rules. Quantitative Finance, 18(4), 637–654. [Google Scholar] [CrossRef]
- Barzilai, J., & Borwein, J. M. (1988). Two-point step size gradient methods. IMA Journal of Numerical Analysis, 8(1), 141–148. [Google Scholar] [CrossRef]
- Bergmann, D., & de Oliveira, M. A. (2025). Tail dependence and equilibrium reversion in brazilian pairs trading: A copula-based analysis. Preprint. [Google Scholar] [CrossRef]
- Borak, S., Misiorek, A., & Weron, R. (2011). Models for heavy-tailed asset returns. Statistical Tools for Finance and Insurance, 2, 21–55. [Google Scholar]
- Bouchaud, J. P., & Potters, M. (2003). Theory of financial risk and derivative pricing: From statistical physics to risk management. Cambridge University Press. [Google Scholar]
- Carneiro, L., Gomes, L., Lopes, C., & Pereira, C. (2025). Spillovers between euronext stock indices: The COVID-19 effect. International Journal of Financial Studies, 13(2), 66. [Google Scholar] [CrossRef]
- Carrasco-Blázquez, M., De la Orden De la Cruz, C., & Prado-Román, C. (2018). Pairs trading techniques: An empirical contrast. European Research on Management and Business Economics, 24(3), 160–167. [Google Scholar] [CrossRef]
- Chen, C. W. S., Chen, M., & Chen, S. Y. (2014). Pairs trading via three-regime threshold autoregressive GARCH models. In V. N. Huynh, V. Kreinovich, & S. Sriboonchitta (Eds.), Modeling dependence in econometrics. Advances in intelligent systems and computing (Vol. 251). Springer. [Google Scholar] [CrossRef]
- Chodchuangnirun, B., Zhu, K., & Yamaka, W. (2018). Pairs trading via nonlinear autoregressive GARCH models. In V. N. Huynh, M. Inuiguchi, D. Tran, & T. Denoeux (Eds.), Integrated uncertainty in knowledge modelling and decision making. IUKM 2018 (Vol. 10758). Lecture Notes in Computer Science. Springer. [Google Scholar] [CrossRef]
- Choudhry, M. (2013). An introduction to value-at-risk. John Wiley & Sons. [Google Scholar]
- Do, B., Faff, R., & Hamza, K. (2006, June 28–July 1). A new approach to modeling and estimation for pairs trading. 2006 Financial Management Association European Conference, Madrid, Spain. [Google Scholar]
- Elliott, R. J., van der Hoek, J., & Malcolm, W. P. (2005). Pairs trading. Quantitative Finance, 5(3), 271–276. [Google Scholar] [CrossRef]
- Endres, S. (2020). Review of stochastic differential equations in statistical arbitrage pairs trading. Managerial Economics, 20(2), 71–118. [Google Scholar] [CrossRef]
- Endres, S., & Stübinger, J. (2019a). A flexible regime switching model with pairs trading application to the S&P 500 high-frequency stock returns. Quantitative Finance, 19(10), 1727–1740. [Google Scholar] [CrossRef]
- Endres, S., & Stübinger, J. (2019b). Optimal trading strategies for Lévy-driven Ornstein–Uhlenbeck processes. Applied Economics, 51(29), 3153–3169. [Google Scholar] [CrossRef]
- Engle, R. F., & Granger, C. W. J. (1987). Co-integration and error correction: Representation, estimation, and testing. Econometrica, 55(2), 251–276. [Google Scholar] [CrossRef]
- Galenko, A., Popova, E., & Popova, I. (2012). Trading in the presence of cointegration. Journal of Alternative Investments, 15(1), 85–97. [Google Scholar] [CrossRef]
- García-Risueño, P. (2025). Historical simulation systematically underestimates the expected shortfall. Journal of Risk and Financial Management, 18(1), 34. [Google Scholar] [CrossRef]
- Göncü, A., & Akyildirim, E. (2016). A stochastic model for commodity pairs trading. Quantitative Finance, 16(12), 1843–1857. [Google Scholar] [CrossRef]
- Gribkova, N., Wang, M., & Zitikis, R. (2025). Fundamentals of non-parametric statistical inference for integrated quantiles. Preprint. [Google Scholar] [CrossRef]
- Guang, Z. (2021). Pairs trading with general state space models. Quantitative Finance, 21(9), 1567–1587. [Google Scholar] [CrossRef]
- Huck, N., & Afawubo, K. (2014). Pairs trading and selection methods: Is cointegration superior? Applied Economics, 47(6), 599–613. [Google Scholar] [CrossRef]
- Kawai, R. (2012). Continuous-time modeling of random searches: Statistical properties inference. Journal of Physics A: Mathematical and Theoretical, 45(23), 235004. [Google Scholar] [CrossRef]
- Krauss, C. (2016). Statistical arbitrage pairs trading strategies: Review and outlook. Journal of Economic Surveys, 31(2), 513–545. [Google Scholar] [CrossRef]
- Larsson, S., Lindberg, C., & Warfheimer, M. (2013). Optimal closing of a pair trade with a model containing jumps. Applications of Mathematics, 58(3), 249–268. [Google Scholar] [CrossRef]
- Liou, J. H., Liu, Y. T., & Cheng, L. C. (2024). Price spread prediction in high-frequency pairs trading using deep learning architectures. International Review of Financial Analysis, 96, 103793. [Google Scholar] [CrossRef]
- López de Prado, M. (2016). Building diversified portfolios that outperform out of sample. The Journal of Portfolio Management, 42(4), 59–69. [Google Scholar] [CrossRef]
- López de Prado, M. (2018). Advances in financial machine learning. Wiley. [Google Scholar]
- López de Prado, M. (2023). Causal factor investing. Cambridge University Press. [Google Scholar]
- Nair, S. T. G. (2021). Pairs trading in cryptocurrency market: A long-short story. Investment Management and Financial Innovations, 18(3), 127–141. [Google Scholar] [CrossRef]
- Namwong, N., Yamaka, W., & Tansuchat, R. (2019). Trading signal analysis with Pairs trading strategy in the stock exchange of Thailand. In V. Kreinovich, & S. Sriboonchitta (Eds.), Structural changes and their econometric modeling. TES 2019 (Vol. 808). Studies in Computational Intelligence. Springer. [Google Scholar] [CrossRef]
- Plerou, V., Gopikrishnan, P., Gabaix, X., Amaral, L. A. N., & Stanley, H. E. (2001). Price fluctuations, market activity and trading volume. Quantitative Finance, 1(2), 262. [Google Scholar] [CrossRef]
- Rad, H., Low, R. K. Y., & Faff, R. (2016). The profitability of pairs trading strategies: Distance, cointegration and copula methods. Quantitative Finance, 16(10), 1541–1558. [Google Scholar] [CrossRef]
- Shreve, S. E. (2004). Stochastic calculus for finance II: Continuous-time models. Springer. [Google Scholar]
- Simonato, J. G. (2012). GARCH processes with skewed and leptokurtic innovations: Revisiting the Johnson Su case. Finance Research Letters, 9(4), 213–219. [Google Scholar] [CrossRef]
- Stübinger, J., & Endres, S. (2018). Pairs trading with a mean-reverting jump–diffusion model on high-frequency data. Quantitative Finance, 18(10), 1735–1751. [Google Scholar] [CrossRef]
- Tadi, M., & Witzany, J. (2025). Copula-based trading of cointegrated cryptocurrency Pairs. Financial Innovation, 11(1), 40. [Google Scholar] [CrossRef]
- Thaler, R. H. (2015). Misbehaving. The making of behavioral economics. W. W. Norton and Company. [Google Scholar]
- Vergara, G., & Kristjanpoller, W. (2024). Deep reinforcement learning applied to statistical arbitrage investment strategy on cryptomarket. Applied Soft Computing, 153, 111255. [Google Scholar] [CrossRef]
- Vidyamurthy, G. (2004). Pairs trading: Quantitative methods and analysis (Vol. 217). Wiley. [Google Scholar]
- Waggle, D., Agrrawal, P., & Johnson, D. (2001). Interaction between value line’s timeliness and safety ranks. Journal of Investing, 10(1), 53–62. [Google Scholar] [CrossRef]
- Wilkens, S. (2025). Pairs trading in the German stock market: Is there still life in the old dog? Financial Markets and Portfolio Management. online first. [Google Scholar] [CrossRef]
- Wu, L., Zang, X., & Zhao, H. (2020). Analytic value function for a pairs trading strategy with a Lévy-driven Ornstein–Uhlenbeck process. Quantitative Finance, 20(8), 1285–1306. [Google Scholar] [CrossRef]
- Yang, H., & Malik, A. (2024). Optimal market-neutral multivariate pair trading on the cryptocurrency platform. International Journal of Financial Studies, 12(3), 77. [Google Scholar] [CrossRef]
- Yang, Y., Göncü, A., & Pantelous, A. (2017). Pairs trading with commodity futures: Evidence from the Chinese market. China Finance Review International, 7(3), 274–294. [Google Scholar] [CrossRef]
- Yu, Q., Shen, G., & Cao, M. (2017). Parameter estimation for Ornstein–Uhlenbeck processes of the second kind driven by α-stable Lévy motions. Communications in Statistics-Theory and Methods, 46(21), 10864–10878. [Google Scholar] [CrossRef]
- Zeng, Z., & Lee, C. G. (2014). Pairs trading: Optimal thresholds and profitability. Quantitative Finance, 14(11), 1881–1893. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).