Abstract
The Halloween effect predicts that stock markets in the winter months (November through April) generate significantly higher returns than in the summer months (May through October). This paper examines the time-varying behavior of the Halloween effect within a new historical dataset that covers about 120 years of Portuguese stock market history. We combine subsample analysis with rolling window analysis to show that the performance of the anomaly has varied in an adaptive fashion over time. The anomaly existed during the first four decades of the 20th century. Afterward, it vanished for 60 years, reappearing only at the beginning of the 21st century. However, in the first two decades of the new century, the effect seems to be a mere reflection of the excess return generated in January. Overall, the time-varying performance of the Halloween effect supports the adaptive market hypothesis for the Portuguese stock market.
Keywords:
calendar anomalies; adaptive market hypothesis; Halloween effect; market efficiency; Portugal JEL Codes:
G12; G14; G15
1. Introduction
According to the efficient market hypothesis (EMH), the efficient nature of markets should imply that stock returns do not follow any observable patterns (Fama 1970). However, the empirical literature has identified several calendar anomalies, such as the January effect or the Halloween effect, which are usually considered to pose a challenge to the EMH (Sun and Tong 2010; Beyer et al. 2013; Zhang and Jacobsen 2021).
Recently, Lo (2004) proposed the adaptive market hypothesis (AMH), suggesting that the performance of calendar anomalies is expected to vary over time. The AMH applies the evolutionary principles of competition, adaptation, and natural selection to the interpretation of price dynamics. Whereas, in the context of the EMH, markets are thought to follow the consistent movement to a higher degree of efficiency; the AMH emphasizes the dynamics of change from the predictability of returns to nonpredictability of returns and vice versa. The advent of the AMH has led to a revision of calendar anomalies in the recent literature, and the results are, in most cases, at odds with the EMH (e.g., Xiong et al. 2019; Plastun et al. 2020; Rosini and Shenai 2020; Alekneviciene et al. 2022).
Following the insights of the AMH, this paper examines the time-varying behavior of the Halloween effect within a new historical dataset that covers the period 1900–2020 in the Portuguese stock market. The Halloween effect predicts that the winter months (November through April) generate higher returns than the summer months (May through October). The analysis is conducted in two stages: in the first stage, the efficiency of the market is investigated for the whole sample period under the classic EMH approach; in the second stage, the anomaly is studied using a combination of the subsample and rolling window analyses.
The results indicate that the Halloween effect existed in the first four decades of the 20th century and was independent of the January effect. Afterward, the effect vanished for 60 years, reappearing only at the beginning of the 21st century. However, in the first two decades of the new century, the Halloween effect seems to be a mere reflection of the excess return generated. Overall, the time-varying performance of the Halloween effect supports the AMH in the Portuguese stock market.
Our study contributes to the literature in several ways. Firstly, we are the first to use the historical database recently collected by Mata et al. (2017) to test the AMH. This new database covers nearly 120 years of Portuguese stock market history. Analyzing calendar anomalies in new historical databases is crucial for carrying out out-of-sample tests and avoiding data mining problems (Lakonishok and Smidt 1988; Brock et al. 1992). Second, we adopt a number of diverse statistical techniques to increase the robustness of our results. Thus, we combine subsample and moving windows analyses to capture the dynamics of anomalous returns over time. Furthermore, in addition to the standard regressions usually used to study the topic, we estimate a GARCH model to eliminate the heteroscedasticity of the data and apply Kruskal–Wallis tests, a nonparametric statistic that allows for the possibility of nonnormal stock returns.
2. Related Literature
2.1. Halloween Effect
The Halloween effect is a seasonal anomaly, according to which the winter months (November through April) generate higher returns than the summer months (May through October).
In their seminal paper, Bouman and Jacobsen (2002) observed this calendar anomaly in 36 out of the 37 national markets under scrutiny, including both developed and emerging markets. The effect was found to be particularly strong in European countries; it does not appear to be caused by data mining, and it does not seem to be driven by the January effect (except in the US).
Since then, several studies have confirmed the existence of the Halloween effect. For instance, Jacobsen and Visaltanachoti (2009) found that the Halloween effect impacted almost all companies from different industries in the US between 1926 and 2006. Carrazedo et al. (2016) also document a strong and economically significant Halloween effect in 8 out of the 10 European sector indices under study in 1992–2010. Andrade et al. (2013) confirmed the persistence of the anomaly after re-examining Bouman and Jacobsen’s (2002) findings and adding new data.
However, some doubts about the existence of the anomaly have also been reported (Maberly and Pierce 2004; Lucey and Zhao 2008; Dichtl and Drobetz 2014, 2015). For example, Lucey and Zhao (2008) argue that the Halloween effect in the US is a mere reflection of the January effect. It has also been claimed that the results obtained by Bouman and Jacobsen (2002) may be attributed to data outliers (Maberly and Pierce 2004). Notwithstanding, these critiques have been refuted as the anomaly is found to be robust when the outliers and January effects are excluded from the analysis (Haggard and Witte 2010).
The Halloween anomaly has been attributed to changes in risk aversion and liquidity effects (Bouman and Jacobsen 2002) and variations in investors’ sentiment (Kamstra et al. 2003; Cao and Wei 2005).
The debate about the significance of the anomaly in contemporaneous markets continues today. Dichtl and Drobetz (2014) analyzed six return stock indexes (S&P 500, euro Stoxx 50, Dax 30, CAC 40, and the FTSE 100) with a data-snooping-resistant “Superior Predictive Ability” test. Their results indicate that the Halloween effect has weakened or has even disappeared in the last years of the sample period, which ends in 2012. In a follow-up study, Dichtl and Drobetz (2015) reported similar results for both developed and emerging markets. On the other hand, Swinkels and Van Vliet (2012) find that the Halloween effect is profitable in a US sample covering the period 1963–2008. Moreover, Lloyd et al. (2017) conclude that the anomaly is significant in 34 out of the 35 stock markets during the period 2007–2015. In addition, they report that the Halloween effect has strengthened rather than weakened in recent years.
Zhang and Jacobsen (2013) studied more than 300 years of UK stock returns and found a positive Halloween effect, but the magnitude of the effect shifted over time and depended on the sample subperiod. More recently, Zhang and Jacobsen (2021) conducted a worldwide study to conclude that the Halloween effect was robust and provided profitable opportunities to investors.
Zhang and Jacobsen (2021) included data from the Portuguese stock market from 1934–2017 in their analysis and found that the effect was statistically significant. In our study, we expand by 37 years the sample period considered by the authors and examine, for the first time, the dynamics of the effect in the Portuguese stock market by using a subsample analysis and a rolling window analysis.
2.2. Calendar Anomalies and the Adaptive Market Hypothesis
According to the efficient market hypothesis posited by Fama (1970), financial prices can fully reflect the available information in the market. The EMH has been criticized on theoretical grounds. For example, Grossman and Stiglitz (1980) showed that if prices were to incorporate all the available information instantly, investors would not have the necessary incentives to search for new pieces of information, which would eventually undermine the efficiency of financial markets. Other authors have argued that contrary to the EMH, the concept of market efficiency should be treated as something different than an all-or-nothing case. For example, Gilson and Kraakman (1984) argue that efficiency is best understood as a relative concept and that the efficiency level in a particular financial market depends on the market’s cost structure for information.
More recently, Lo (2004) proposed the adaptive market hypothesis (AMH), highlighting the time-varying nature of market efficiency. The AMH applies the principles of species evolution—competition, adaptation, and natural selection—to the interpretation of price dynamics. If there are many “species” (groups of market participants) competing for scarce resources (profit opportunities) in a given market, then the market is expected to be very efficient. In this case, some investors are expected to suffer losses and exit the market, which, ceteris paribus, should decrease the intensity of competition and make profit opportunities more abundant. These new profit opportunities, in turn, should attract new investors and increase market efficiency again. In consequence, the AMH predicts that markets do not follow a consistent trend toward ever-increasing efficiency as indicated by the supporters of the EMH, but instead efficiency will vary in a cyclical fashion. This means that the performance of trading strategies based on patterns of predictability in price behavior (i.e., calendar anomalies) is also expected to vary over time.
In the last decade, several studies have been examining the topic of calendar anomalies within the framework of the AMH. For example, Urquhart and McGroarty (2014) employed subsample and rolling window analyses to study the evolution of four calendar anomalies (the January, Halloween, Monday, and turn-of-the-month effects) in the Dow Jones Industrial Average from 1900 to 2013. The results show that the performance of all anomalies varies over time, supporting the AMH. Further, Al-Khazali and Mirzaei (2017) used stochastic dominance and mean-variance analysis to examine the evolution over time of three calendar anomalies (the January, Monday, and weekly effects) in a number of Dow Jones Islamic Indices over the period 1996–2015. Although the results are not inconsistent with the EMH, the main conclusion is that the AMH offers a better explanation for the evidence. Xiong et al. (2019) studied the AMH through four calendar effects (the January, Monday, turn-of-the-month, and Chinese lunar new year effects) in the Chinese stock market. Referring to the subsample and rolling window analyses, the authors conclude that the AMH provides a better explanation for the dynamics of that market. More recently, Plastun et al. (2020) conducted a comprehensive investigation of the evolution of various monthly anomalies (the January, December, and Mark Twain effects) in the US stock market for its entire history. The results show that the January effect was the only prevalent anomaly, providing exploitable profit opportunities and that the behavior of the market is consistent with the AMH. Rosini and Shenai (2020) analyzed the evolution of the London Stock Exchange over the period 2007–2016, applying techniques such as GARCH regressions and Kruskal–Wallis tests. The anomalies under scrutiny (the January, Halloween, Monday, and turn-of-the-month effects) were shown to vary over time, supporting the AMH. Finally, Alekneviciene et al. (2022) tested the AMH regarding calendar anomalies in the Baltic stock markets using GARCH regressions, Kruskal–Wallis statistics, and rolling windows. The authors found three significant anomalies (the monthly, turn-of-the-month, and Friday effects), concluding that the behavior of the market is consistent with the AMH.
Although the literature includes some studies devoted to analyzing seasonal anomalies in the context of the Portuguese stock market (e.g., Silva 2010; Gama and Vieira 2013; Lobão and Lobo 2018), the evidence of the performance of the Halloween effect in this market is scarce. Our study adds to the knowledge of this important seasonal effect. Moreover, we contribute the AMH to the literature by testing this hypothesis in a new historical financial dataset, using subsample analysis and rolling window analysis.
3. Data and Methodology
3.1. Sources and Data Collection
The data used in this study include the continuous monthly returns observed for the period 1900–2020, except for the three years following the April 1974 military coup, during which the Portuguese stock exchange was closed.
We further split the data into several subperiods to explore the anomaly’s evolution over time. Additionally, we consider the subperiods in the data to be important for obtaining robust statistical testing (Zhang and Jacobsen 2013).
Monthly prices were gathered from different sources. For the period 1900–2015, we used the database created by Mata et al. (2017). Mata et al. (2017) developed a share index with weekly frequency, utilizing a methodology that makes the index comparable to common international indices. The estimated capitalization-weighted index comprises three different segments: (i) from the end of December 1899 until 24 April 1974, (ii) from January 1978 until December 1987, and (iii) from January 1988 to April 2015. The primary source of the numerical data for periods (i) and (ii) was the collection of daily bulletins published by the Lisbon Stock Exchange, which are available in the Documentation Centre of Euronext Lisbon. The information regarding period (iii) refers to the main Portuguese stock indexes in this period: the BVL Geral (BVLG) until 1992 and the PSI-Geral afterward. We completed the database of Mata et al. (2017), with more recent observations referring to the period from May 2015 to December 2020 collected from the Refinitiv Datastream. Then, weekly data were converted into monthly data using the method described by Martinovića et al. (2016), and stock returns were calculated the following way:
where and are the natural logarithms of the closing price of the stock market index at time t and t 1, respectively.
We also used the database of risk-free rates created by Mata et al. (2017), which comprises short-term interest rates. Once again, we completed the database for the most recent period (2015–2020) using the Euro interbank overnight index average (EONIA), as suggested by Da Costa et al. (2012). EONIA was obtained from the EURIBOR online statistics database.
3.2. Methodology
Our empirical work was developed over two different stages. In the first stage, we investigated the presence of the Halloween effect in our full sample. The second stage examined the evolution of the anomaly over time.
Thus, regarding the first stage, we adopted the standard econometric approach, where returns are regressed on a series of dummy variables representing the period of interest (e.g., Darrat et al. 2011; Zhang and Jacobsen 2013; Lobão 2018). Following the literature on the topic, the regressions are computed with the ordinary least squares (OLS) methodology considering the Newey-West estimator.
The existence of the anomaly is tested through the estimation of the following regression:
where denotes the natural logarithmic monthly return of the total index over the period t − 1 to t. is the dummy variable equal ro 1 if month t falls from November through April and is 0 otherwise.
is the constant, and is the error term. shows the magnitude of the difference between the mean return of the summer months and the mean return generated in the winter months. If is positive (negative) and statistically significant, then there is evidence that the returns in the summer months were significantly higher (lower) than in the remaining months.
Several studies suggest that the Halloween effect can be attributed to the above-average returns observed in January (Maberly and Pierce 2004; Lucey and Zhao 2008; Haggard and Witte 2010). We examine whether the difference in the average returns between the summer and winter months is due to the high performance in that month by running the following regression:
where is a dummy variable that takes the value 1 if month t falls into the time interval from November to April, excluding January. The additional dummy variable, , captures a potential January effect since it takes the value of 1 in January and is 0 otherwise.
If the Halloween effect is robust to the existence of the January anomaly, we should obtain a significant coefficient, , even in the presence of the January effect. If, on the contrary, only is significant, then it will be possible to conclude that the effect initially described by Bouman and Jacobsen (2002) is simply the January effect in disguise.
In the second stage of the empirical work, we examine how the Halloween effect evolves over time. For this purpose, we recur to a subsample analysis and a rolling window analysis. We divide the data into six subperiods for the subsample analysis: 1900–1920, 1921–1940, 1941–1960, 1961–1974, 1978–2000, and 2001–2020. Additionally, and given the paramount importance of the event in the history of the Portuguese stock market (Mata et al. 2017), we also split the data into a subperiod that includes the years that preceded the Carnation Revolution (1900–1974) and the subperiod that followed it (1978–2020). Then, we estimate the regression model (2) for each of these subperiods.
Since it is plausible to admit that the volatility of returns may vary across time, we also used the generalized conditional heteroscedastic (GARCH) model to estimate (2) for the subperiods mentioned above (Zhang and Jacobsen 2013, 2021). Adopting this estimation technique also allowed us to draw conclusions regarding the impact of clustering volatility on the results obtained previously (Caporale and Zakirova 2017). Engle (2001) argues that the GARCH (1, 1) model is the most robust and simplest of the family of volatility models and enables researchers to model return volatility as being conditional on past volatility through the series. The GARCH (1,1) regression equation can be presented as follows:
where and are the conditional variances in market returns at time t and t − 1, respectively; is the squared unexpected returns for the previous periods, and , , and are the GARCH (1, 1) model coefficients.
Since the models we have addressed so far cannot capture the non-normality of the data, we also apply the nonparametric Kruskal–Wallis (KW) test to the subsamples. The KW test examines if the populations from which the samples were drawn follow identical distributions. The test is particularly sensitive to differences in the means (Urquhart and McGroarty 2014). In our study, we examine the difference between market returns on calendar effect days and noncalendar effect days through the use of the KW test as
where is the average rank of observations in group j, nj is the total number of observations in group j, k is the number of groups, and N is the total number of observations. The KW estimates follow a distribution with K − 1 degrees of freedom.
The subsample analysis provides information regarding the behavior of the Halloween effect over time by examining the effects in each subsample. However, as the choice of the size of each subsample is subjective, and some of the dynamics of the behavior of calendar anomalies may not be observed with this approach, we also employed a rolling window analysis.
The use of the rolling windows technique in estimating model coefficients is relatively recent in the study of calendar anomalies (Zhang and Jacobsen 2013; Urquhart and McGroarty 2014; Zhang and Jacobsen 2021). For the rolling window analysis, we recurred to a fixed-length 20-year moving subsample window that rolls forward one year at a time. Then, we investigated how the coefficients generated by model (2) evolved over time, considering rolling windows for the Halloween effect.
3.3. Descriptive Statistics
Table 1 shows the descriptive statistics in the summer and winter months related to the Halloween effect.

Table 1.
Descriptive statistics for summer and winter months.
The mean monthly returns observed from November–April (1.4%) are higher than in May–October (0.6%), which suggests the possibility of a Halloween effect. The difference in the standard deviation between the two periods is rather low, with the volatility being higher in the winter months (5.6%) than in the summer months (4.9%). Both return series exhibit positive skewness and leptokurtic distributions.
4. Empirical Findings
This section investigates the presence of the Halloween effect in our sample (Section 4.1) and examines the behavior of the effect over time (Section 4.2).
4.1. The Halloween Effect in the Full Sample
We examine the Halloween effect and its relationship with the January effect. Table 2 reports the results of the estimation of regression models (2) and (3).

Table 2.
Controlling the impact of the January Effect on the Halloween effect (1900–2020).
The returns observed in the months from November to April were significantly higher than those generated from May to October, thus indicating the existence of a significant Halloween effect during the full sample. We also report that the Halloween effect detected with the regression model (2) vanishes when the results are controlled for the January effect. In fact, the variable that captures the Halloween effect ceases to be statistically significant at the conventional levels of significance when the January effect is introduced into the model. On the other hand, the variable that reflects the January effect is positive and statistically significant at the 1 percent level. This indicates that the Halloween effect may be attributed to the above-average returns observed in January.
4.2. Time-Varying Behavior of the Halloween Effect
The study of the Halloween anomaly in the whole sample period does not allow us to examine the potential time-varying nature of that effect. In order to analyze how the effect evolves over time, we start by employing a subsample analysis. Table 3 shows the results of the estimation of the regression model (2) for the Halloween effect observed in several subsamples, with and without controlling for the January effect.

Table 3.
Halloween effect in several subsamples, regression models (2) and (3) with OLS estimation.
The results show that the Halloween effect was present at the beginning of our sample period (the 1900–1920 and 1921–1940 subsamples). It is interesting to note that, during these periods, the effect existed independently of the January effect. From the 1940s onwards, the Halloween effect ceased to be observed, but it resurfaced at a statistically significant level in the 21st century. However, in this more recent subperiod, the Halloween effect seems to be a mere reflection of the higher returns observed in January.
Table 4 shows the Halloween effect in the same subsamples according to the KW statistics and the results of the GARCH (1, 1) estimation of the regression model (2).

Table 4.
Halloween effect in several subsamples, regression model (2) with GARCH (1, 1) estimation, and Kruskal–Wallis statistics.
In general, the evidence confirms the previously obtained conclusions: the Halloween effect was very significant from 1900 to 1940. Afterward, the effect vanished until it resurfaced with significant strength in the 21st century. The KW statistic provides further attestation of the time-varying nature of the effect, with some subperiods generating significant statistics and some generating nonsignificant statistics.
Continuing with our empirical investigation, we now resort to a rolling window approach to capture the dynamism of the Halloween effect. Figure 1 depicts the evolution of the coefficients generated by the regression model (2) in a fixed-length 20-year moving subsample window that rolls forward one year at a time.
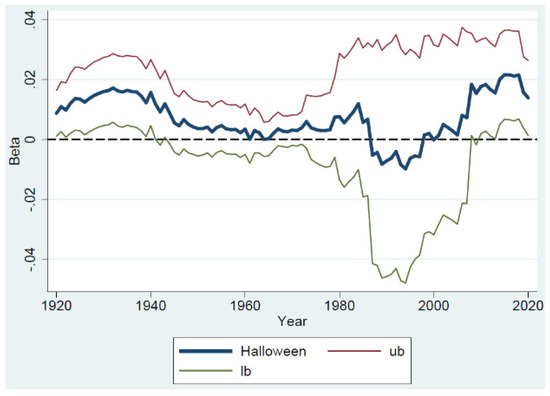
Figure 1.
Time-varying nature of the Halloween effect using rolling windows.
Figure 1 plots the estimates of the coefficients generated by the regression model (2) in a fixed 20-year rolling window that rolls forward one year at a time. The thicker line represents the coefficient estimates of the effect, and the upper and lower lines represent the 95% bounds calculated based on the Newey-West standard errors. Source: own elaboration.
The figure shows that the betas fluctuated above zero during most of the sample period. The effect started to be statistically significant in the initial period of our sample, up until the 1940s. Afterward, it lost significance until it reappeared in the 21st century.
5. Discussion and Conclusions
This paper examined the time-varying performance of the Halloween effect within a new historical dataset covering about 120 years of Portuguese stock market history. We employed a variety of approaches, including subsample analysis and rolling window analysis.
Our results reveal that the Halloween effect existed in the first two subperiods of our sample, then disappeared in the following subperiods, and reappeared in the new century. Moreover, while the Halloween effect existed independently of the January effect at the beginning of the sample, the results for the most recent period indicate that the Halloween effect is just a reflection of the January effect. The rolling window analysis confirms the fluctuation in the performance of the anomaly.
Overall, our findings suggest that the level of predictability of the market, captured by the performance of the Halloween effect, has been changing over time. The market exhibited periods of significant predictability and periods where no significant predictability was found. This time-varying market behavior is consistent with the AMH and suggests that market efficiency is not an all-or-nothing condition. The realization that a strategy based on the Halloween effect would provide gains from 1900–1940 must have attracted investors, which contributed to increased market efficiency and the disappearance of the anomaly in the following decades. The exit of investors with these strategies paved the way for the reappearance of the anomaly in recent decades.
Thus, our results are in line with the contributions of Urquhart and McGroarty (2014), Xiong et al. (2019), and Alekneviciene et al. (2022), among others, which conclude that the AMH provides a valuable explanation for the dynamics of the stock market. By showing that the Halloween effect is a mere reflection of the January effect in the most recent subperiod, our paper corroborates the findings of Lucey and Zhao (2008).
All in all, our findings concerning the cyclical nature of market behavior resulting from the combination of the subsample and the rolling window analyses described above support the AMH.
Our findings also interest practitioners, as they indicate that these agents should be flexible in exploiting calendar effects. The belief that a specific calendar effect is a persistent phenomenon will likely hurt investors’ performance.
The tests of the AMH are still in their infancy. Further avenues of research on this topic may include examining how the performance of calendar anomalies responds to different market regimes (market trends, extremely positive and negative returns, crashes, etc.) and economic conditions (economic uncertainty, economic growth, inflation levels, etc.) by studying the reasons for the variation observed in the performance of the Halloween effect over time (e.g., shifts in investors’ sentiment, changes in risk aversion, and liquidity effects) and analyzing how trading costs can impact the profitability of strategies based on calendar anomalies such as the Halloween effect.
Author Contributions
Conceptualization, J.L.; Methodology, A.C.C.; Software, A.C.C.; Validation, A.C.C.; Formal analysis, A.C.C.; Investigation, A.C.C.; Resources, A.C.C.; Writing—review & editing, J.L.; Supervision, J.L.; Project administration, J.L.; Funding acquisition, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been financed by Portuguese public funds through FCT—Fundação para a Ciência e a Tecnologia, I.P., in the framework of the project with reference UIDB/04105/2020.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alekneviciene, Vilija, Vaida Klasauskaitė, and Eglė Aleknevičiūtė. 2022. Behavior of calendar anomalies and the adaptive market hypothesis: Evidence from the Baltic stock markets. Journal of Baltic Studies 53: 187–210. [Google Scholar] [CrossRef]
- Al-Khazali, Osamah, and Ali Mirzaei. 2017. Stock market anomalies, market efficiency and the adaptive market hypothesis: Evidence from Islamic stock indices. Journal of International Financial Markets, Institutions and Money 51: 190–208. [Google Scholar] [CrossRef]
- Andrade, Sandro C., Vidhi Chhaochharia, and Michael E. Fuerst. 2013. “Sell in May and Go Away” Just Won’t Go Away. CFA Institute Magazine 69: 94–105. [Google Scholar] [CrossRef]
- Beyer, S., L. Garcia-Feijoo, and G. R. Jensen. 2013. Can you capitalize on the turn-of-the-year effect? Applied Financial Economics 23: 1457–68. [Google Scholar] [CrossRef]
- Bouman, Sven, and Ben Jacobsen. 2002. The Halloween Indicator, “Sell in May and Go Away”: Another Puzzle. The American Economic Review 92: 1618–35. [Google Scholar] [CrossRef]
- Brock, William, Josef Lakonishok, and Blake LeBARON. 1992. Simple Technical Trading Rules and the Stochastic Properties of Stock Returns. The Journal of Finance 47: 1731–64. [Google Scholar] [CrossRef]
- Cao, Melanie, and Jason Wei. 2005. Stock market returns: A note on temperature anomaly. Journal of Banking & Finance 29: 1559–73. [Google Scholar] [CrossRef]
- Caporale, Guglielmo Maria, and Valentina Zakirova. 2017. Calendar anomalies in the Russian stock market. Russian Journal of Economics 3: 101–8. [Google Scholar] [CrossRef]
- Carrazedo, Tiago, José Dias Curto, and Luís Oliveira. 2016. The Halloween effect in European sectors. Research in International Business and Finance 37: 489–500. [Google Scholar] [CrossRef]
- Da Costa, José Rodrigues, Maria Eugénia Mata, and David Justino. 2012. Estimating the Portuguese average cost of capital. Historical Social Research/Historische Sozialforschung 37: 326–61. [Google Scholar]
- Darrat, Ali F., Bin Li, Benjamin Liu, and Jen Je Su. 2011. A fresh look at seasonal anomalies: An international perspective. International Journal of Business & Economics 10: 93–116. [Google Scholar]
- Dichtl, Hubert, and Wolfgang Drobetz. 2014. Are stock markets really so inefficient? The case of the “Halloween Indicator”. Finance Research Letters 11: 112–21. [Google Scholar] [CrossRef]
- Dichtl, Hubert, and Wolfgang Drobetz. 2015. Sell in May and Go Away: Still good advice for investors? International Review of Financial Analysis 38: 29–43. [Google Scholar] [CrossRef]
- Engle, Robert. 2001. GARCH 101: The Use of ARCH/GARCH Models in Applied Econometrics. Journal of Economic Perspectives 15: 157–68. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1970. Efficient Capital Markets: A Review of Theory and Empirical Work. The Journal of Finance 25: 383. [Google Scholar] [CrossRef]
- Gama, Paulo M., and Elisabete F. S. Vieira. 2013. Another look at the holiday effect. Applied Financial Economics 23: 1623–33. [Google Scholar] [CrossRef]
- Gilson, Ronald J., and Reinier H. Kraakman. 1984. The Mechanisms of Market Efficiency. Virginia Law Review 70: 549. [Google Scholar] [CrossRef]
- Grossman, Sanford J., and Joseph E. Stiglitz. 1980. On the Impossibility of Informationally Efficient Markets. The American Economic Review 70: 393–408. [Google Scholar]
- Haggard, K. Stephen, and H. Douglas Witte. 2010. The Halloween effect: Trick or treat? International Review of Financial Analysis 19: 379–87. [Google Scholar] [CrossRef]
- Jacobsen, Ben, and Nuttawat Visaltanachoti. 2009. The Halloween Effect in U.S. Sectors. The Financial Review 44: 437–59. [Google Scholar] [CrossRef]
- Kamstra, Mark J., Lisa A. Kramer, and Maurice D. Levi. 2003. Winter Blues: A SAD Stock Market Cycle. The American Economic Review 93: 324–43. [Google Scholar] [CrossRef]
- Lakonishok, Josef, and Seymour Smidt. 1988. Are Seasonal Anomalies Real? A Ninety-Year Perspective. The Review of Financial Studies 1: 403–25. [Google Scholar] [CrossRef]
- Lloyd, Robert, Chengping Zhang, and Stevin Rydin. 2017. The Halloween Indicator is more a treat than a trick. Journal of Accounting and Finance 17: 96–108. [Google Scholar]
- Lo, Andrew W. 2004. The Adaptive Markets Hypothesis. The Journal of Portfolio Management 30: 15–29. [Google Scholar] [CrossRef]
- Lobão, Júlio, and Carlos Lobo. 2018. Sazonalidade Mensal e o Efeito Passagem de Ano: Nova Evidência da Euronext Lisbon. Portuguese Journal of Finance, Management and Accounting 4: 3–25. [Google Scholar]
- Lobão, Júlio. 2018. Seasonal anomalies in the market for American depository receipts. Journal of Economics Finance and Administrative Science 24: 241–65. [Google Scholar] [CrossRef]
- Lucey, Brian, and Shelly Zhao. 2008. Halloween or January? Yet another puzzle. International Review of Financial Analysis 17: 1055–69. [Google Scholar] [CrossRef]
- Maberly, Edwin D., and Raylene M. Pierce. 2004. Stock market efficiency withstands another challenge: Solving the sell in May/buy after Halloween puzzle. Econ Journal Watch 1: 29–46. [Google Scholar]
- Mata, Eugénia Maria, José Rodrigues da Costa, and David Justino. 2017. The Lisbon Stock Exchange in the Twentieth Century. Coimbra: Coimbra University Press. [Google Scholar]
- Martinovića, Marko, Marija Stoić, Miroslav Duspara, Ivan Samardžić, and Antun Stoić. 2016. Algorithmic Conversion of Data Displayed on a Weekly Basis to the Monthly Level Using the Spreadsheet. Procedia Engineering 149: 288–96. [Google Scholar] [CrossRef][Green Version]
- Plastun, Alex, Xolani Sibande, Rangan Gupta, and Mark E. Wohar. 2020. Historical evolution of monthly anomalies in international stock markets. Research in International Business and Finance 52: 101127. [Google Scholar] [CrossRef]
- Rosini, Lucrezia, and Vijay Shenai. 2020. Stock returns and calendar anomalies on the London Stock Exchange in the dynamic perspective of the Adaptive Market Hypothesis: A study of FTSE100 & FTSE250 indices over a ten year period. Quantitative Finance and Economics 4: 121–47. [Google Scholar] [CrossRef]
- Silva, Pm. 2010. Calendar “anomalies” in the Portuguese stock market. Investment Analysts Journal 39: 37–50. [Google Scholar] [CrossRef]
- Sun, Qian, and Wilson H. S. Tong. 2010. Risk and the January effect. Journal of Banking & Finance 34: 965–74. [Google Scholar] [CrossRef]
- Swinkels, Laurens, and Pim Van Vliet. 2012. An anatomy of calendar effects. Journal of Asset Management 13: 271–86. [Google Scholar] [CrossRef]
- Urquhart, Andrew, and Frank McGroarty. 2014. Calendar effects, market conditions and the Adaptive Market Hypothesis: Evidence from long-run U.S. data. International Review of Financial Analysis 35: 154–66. [Google Scholar] [CrossRef]
- Xiong, Xiong, Yongqiang Meng, Xiao Li, and Dehua Shen. 2019. An empirical analysis of the Adaptive Market Hypothesis with calendar effects:Evidence from China. Finance Research Letters 31. [Google Scholar] [CrossRef]
- Zhang, Cherry Y., and Ben Jacobsen. 2013. Are Monthly Seasonals Real? A Three Century Perspective. European Finance Review 17: 1743–85. [Google Scholar] [CrossRef]
- Zhang, Cherry Y., and Ben Jacobsen. 2021. The Halloween indicator, “Sell in May and Go Away”: Everywhere and all the time. Journal of International Money and Finance 110: 102268. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).