UQ4CFD: An Uncertainty Quantification Platform for CFD Simulation

Abstract

The credibility of Computational Fluid Dynamics (CFD) has been a topic of debate due to the significant uncertainties inherent in its modeling processes and numerical implementations. Uncertainty Quantification (UQ) offers a scientific framework for quantitatively assessing and mitigating uncertainties in CFD simulations. However, this procedure typically requires numerous CFD simulations and considerable manual effort for both simulation management and data analysis. To overcome these challenges, this work develops a platform called UQ4CFD, a browser–server software that provides automated and customized uncertainty quantification capabilities for CFD studies. The UQ4CFD platform integrates different kinds of methodologies to perform comprehensive uncertainty analysis, including uncertainty propagation, sensitivity analysis, surrogate modeling, numerical discretization uncertainty analysis, model validation, model calibration, etc. A tightly coupled CFD-UQ workflow is built to automate the complete analytical process, encompassing parameter sampling, simulation execution, and results analysis, which significantly improves computational efficiency while reducing risks associated with data processing errors. Comprehensive validation employing both analytical benchmark functions and practical CFD cases has been conducted to demonstrate the platform’s effectiveness and adaptability in diverse UQ scenarios.

1. Introduction

With the continuous development of numerical algorithms and high-performance computing, Computational Fluid Dynamics (CFD) has emerged as an indispensable tool for equipment design and evaluation in various critical engineering fields, including aerospace, energy and power, transportation, and more. However, due to the stochastic nature of fluid flows and limitations in human knowledge, CFD simulation inevitably involves multiple sources of uncertainties. Specifically, the primary sources of uncertainty in CFD arise from model formulation, parametric coefficients, boundary condition specification, geometric parameter variability, and numerical discretization. Such uncertainties can substantially compromise the reliability of CFD predictions, potentially leading to inaccurate engineering evaluations and scientifically unsound decision-making processes.

Uncertainty Quantification (UQ) is the science of quantitative characterization and reduction in uncertainties in computer simulation-based scientific applications. More specifically, the scope of uncertainty quantification may vary depending on research objectives, such as quantifying output variability resulting from uncertain input parameters, ranking parameters by significance to identify dominant sources of uncertainty, and reducing uncertainty through the calibration of model parameters. Considerable efforts have been devoted to uncertainty quantification in the aerospace domain, aiming to enhance the reliability of CFD simulations. The European Union’s Non-Deterministic Simulation for CFD-Based Design Methodologies project has developed advanced probabilistic CFD simulation techniques to enhance the reliability of aircraft design tools [1]. NASA implemented multiple aerospace-focused uncertainty analysis initiatives and identified comprehensive uncertainty management as a fundamental capability required for future CFD development [2,3]. Airbus has further emphasized the crucial role of CFD uncertainty quantification throughout aircraft design processes, as highlighted in the ERCOFTAC workshop discussions [4]. Lu et al. investigated the uncertainty in heat transfer and pressure within aircraft fin panel structures subjected to shock wave/turbulent boundary layer interaction, and identified the main contributors [5]. Carter et al. evaluated the effects of uncertainties in chemical kinetics and vibrational–electron–electronic source term parameters on plasma formation around a 2D axisymmetric sphere-cone. Their analysis provides valuable insight into the predictive uncertainty of plasma formation in nonequilibrium, weakly ionized hypersonic flows conditions [6]. Gao et al. investigated the effects of fouling thickness distribution and roughness on compressor blade aerodynamic performance via uncertainty quantification. The work underscores that blade fouling cannot be adequately characterized by considering roughness alone; a holistic assessment must also incorporate the consequences of the fouling structure on performance [7]. Tang et al. analyzed the impact of geometric manufacturing deviations of high-pressure compressor blades on the performance of an aircraft engine [8]. Focusing on transonic flows over airfoils, Schaefer et al. [9] and Chen et al. [10] analyzed how uncertainties in the coefficients of the SA turbulence model propagate to affect the aerodynamic characteristics of airfoils in transonic flow regimes. For further details on recent advances in uncertainty quantification for aerodynamics, readers are referred to the literature [11,12].

The development of robust and high-fidelity software tools is essential for the accurate execution of uncertainty quantification. Several software tools are available to facilitate uncertainty quantification problems to different degrees. Sandia National Laboratories’ DAKOTA software offers an extensive suite of optimization algorithms and surrogate models, enabling comprehensive parameter sensitivity analysis and uncertainty-based optimization design [13]. Lawrence Livermore National Laboratory’s PSUADE platform specializes in uncertainty analysis for large-scale dynamic systems, providing capabilities for sensitivity analysis, uncertainty propagation, and numerical optimization [14]. ETH Zurich developed the MATLAB-based UQLab framework [15]. Beijing Normal University created the Python-based UQ-PyL platform [16], which integrates common uncertainty propagation methods and features a graphical user interface for batch script execution. Additional UQ software that provide relevant capabilities include the NSSUR probabilistic analysis program [17], SIMLAB [18], OpenTURNS [19], UCODE [20], and Uranie [21].

However, to the best of our knowledge, no currently available software is specifically designed for UQ in CFD engineering. Despite the considerable advancements, existing tools exhibit significant limitations when applied to CFD applications. First, selecting and learning to use these tools requires substantial time and effort, especially for researchers unfamiliar with UQ methodologies and not good at programming. Second, contemporary UQ software predominantly focuses on parametric uncertainty propagation and quantification, while lacking comprehensive functionality for full CFD uncertainty quantification. Important aspects such as the assessment of numerical discretization errors—a critical source of uncertainty in CFD simulations—are often neglected. Third, the most significant limitation of current UQ tools lies in their lack of integration and capacity for automated operation among UQ software, CFD solvers, and high-performance computing clusters. Since uncertainty quantification in CFD typically involves executing a large number of simulations, manual handling of such analyses would require considerable human intervention, which severely hinders the wider application of UQ methodologies in CFD research.

In an attempt to overcome these limitations, this study introduces UQ4CFD, a software designed to provide a powerful, easy-to-use, and highly automated solution for uncertainty quantification in CFD applications. First, we conceived a novel UQ framework that integrates general theory with the specific practicalities of CFD, enabling the concurrent treatment of both parametric and numerical discretization uncertainties. This framework was subsequently implemented as a modular software platform featuring seamless integration with various CFD solvers. The platform’s main functionalities include uncertainty propagation, sensitivity analysis, surrogate modeling, numerical discretization uncertainty analysis, model validation, and model calibration. By incorporating UQ algorithms, CFD simulation management, and automated workflows, the platform abstracts away inherent complexities and tedious procedures. Consequently, the platform significantly lowers the barrier to entry, enabling a broader spectrum of users to conduct rigorous UQ analysis with ease. This paper is organized as follows. In Section 1, we introduce the theoretical framework of uncertainty quantification in CFD; Section 2 details the architecture and implementation of the UQ4CFD platform; Section 3 demonstrates the platform’s performance on analytical test cases and practical engineering applications.

2. CFD Uncertainty Quantification Framework

Important dimensions of uncertainty quantification relevant to analysis initiatives have been outlined by NASA [22], as illustrated in Figure 1. Key aspects of UQ—including uncertainty categorization, characterization and representation, propagation, solution bias estimation, and model prediction-bias uncertainty—are now well-established and practically applicable in the CFD domain. In contrast, uncertainty extrapolation and aggregation remain active areas of research, and no widely accepted methodologies have yet been established for these aspects. Motivated by the practical needs of UQ in CFD and the current landscape of methodologies, a dedicated UQ framework is proposed herein, as illustrated in Figure 2. The key elements of this framework are briefly introduced in the remainder of this section.

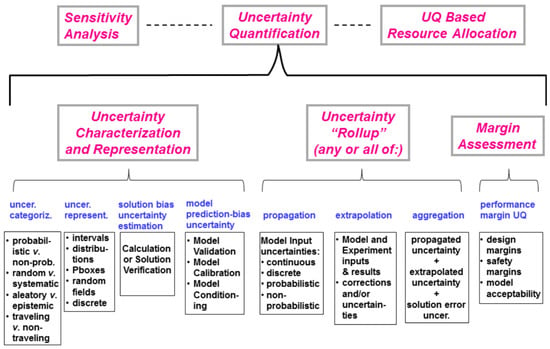
Figure 1. Key aspects in Uncertainty Quantification [22].

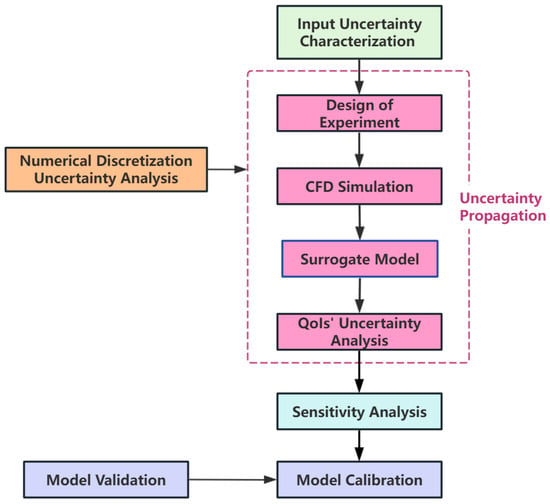
Figure 2. Framework of Uncertainty Quantification.

2.1. Input Uncertainty Characterization

The foundational step of uncertainty quantification involves systematically identifying uncertain input parameters aligned with the analysis objectives, mathematically characterizing their uncertainties using appropriate probabilistic or non-probabilistic representations, and defining the quantities of interests (QoIs) to be analyzed during uncertainty propagation.

From a mathematical perspective, uncertainty is broadly classified into two primary types: aleatory uncertainty (stemming from inherent system variability) and epistemic uncertainty (arising from a lack of knowledge). These fundamentally different natures dictate distinct implications and treatments in analysis. Aleatory uncertainty is irreducible and is conventionally modeled using probability theory. In contrast, epistemic uncertainty is reducible with increased information and often necessitates specialized frameworks like interval analysis or evidence theory. If a specific uncertain factor involves both aleatory and epistemic uncertainties, it is termed mixed uncertainty. In such cases, imprecise probability methods can be employed for characterization, among which probability box (p-box) is widely used.

2.2. Uncertainty Propagation

This process quantifies how input parameter uncertainties affect model outputs. The primary methods for propagating aleatory uncertainty include Monte Carlo (MC) simulation, Polynomial Chaos Expansion (PCE) [23], and surrogate model-based Monte Carlo methods. The standard MC approach involves generating numerous input samples, evaluating them using the CFD model, and performing a statistical analysis on the resulting outputs. While valued for its flexibility and conceptual simplicity, the MC method becomes computationally prohibitive for complex CFD applications, where a single simulation may take days. To mitigate this cost, surrogate model-based MC methods replace the CFD solver with an efficient approximation model. Alternatively, PCE represents the model response as a series of orthogonal polynomials of the input random variables. The coefficients of this expansion are determined through numerical integration or regression based on a limited set of sample points. A key advantage of PCE is its ability to directly compute statistical moments (e.g., mean and variance) from the PCE coefficients, bypassing the need for the extensive sampling required by MC. For propagating epistemic uncertainty, suitable methods such as interval analysis [24] and evidence theory can be employed, depending on the available information [25]. In cases of mixed uncertainty, a common strategy employs a double-loop sampling scheme to separately address each type, ultimately constructing a probability box (p-box) from the resulting model outputs [26].

A general workflow for parametric uncertainty propagation typically encompasses key steps: Design of Experiments (DoE), CFD simulation, surrogate model construction, and finally, uncertainty analysis for the Quantities of Interests. A further introduction to them follows.

2.2.1. DoE

DoE is a discipline concerned with the efficient planning of experiments. It employs structured sampling strategies to explore the parameter space, thereby generating data that captures the underlying model’s behavior. Common sampling techniques encompass Central Composite Design [27], Full-Factorial Design [28], Monte Carlo Sampling [29], Latin Hypercube Sampling (LHS) [30], the Sobol Sequence [31], among others. MC, LHS, and the Sobol sequence represent three distinct classes of sampling strategies. MC Sampling is a fundamental random sampling method that generates independent points randomly across the parameter space. Although statistically robust, its purely random nature can result in point clustering and uncovered gaps, leading to slower convergence in uncertainty analysis. LHS is a stratified sampling technique designed to improve efficiency over crude Monte Carlo. It divides the range of each input parameter into intervals of equal probability and ensures that each interval is sampled exactly once. This forces a more uniform projection over each parameter’s distribution, providing better space-filling properties. The Sobol Sequence is a deterministic, low-discrepancy sequence. It generates points that are highly uniform in space, effectively minimizing gaps and clusters. Compared to LHS, it achieves faster convergence rates in uncertainty quantification, particularly for high-dimensional problems.

2.2.2. Propagation with CFD Solver or Surrogate Model

Input parameter uncertainties propagate via the CFD simulation to the QoIs. Nonetheless, the prohibitive computational demands of high-fidelity CFD simulations render direct uncertainty propagation analysis impractical. Consequently, the construction of surrogate models to replace the CFD solver has emerged as a standard practice for efficient uncertainty propagation, as well as sensitivity analysis and parameter calibration. A range of surrogate models have been developed, such as Radial Basis Functions (RBF) [32], Kriging [33], and Neural Networks [34]. RBF provides a simple interpolation framework via a weighted sum of basis functions. Kriging, also known as Gaussian Process Regression, can provide not only predictions but also quantifies the associated uncertainty at any point within the parameter space, making it a widely favored technique in uncertainty quantification [35,36,37]. Recently, Neural Networks, as versatile non-linear approximators, have accordingly seen broad application in UQ [38,39,40], particularly in high-dimensional scenarios where traditional methods like Kriging become limited. Alternatively, PCE can be regarded as a specific surrogate model that can directly deliver analytical uncertainty estimates [41].

2.2.3. Uncertainty Analysis

The statistics of QoIs, including the mean, standard deviation, confidence intervals, and correlations between input parameters and output variables, can be assessed through the surrogate model-based MC analysis.

2.3. Sensitivity Analysis

Sensitivity Analysis addresses a central question in uncertainty quantification: which input parameters contribute most significantly to the output uncertainty? In problems involving high-dimensional uncertain factors, performing precise UQ analysis for all parameters is often computationally prohibitive. Sensitivity analysis helps rapidly identify parameters with negligible influence on the output, thus reducing the complexity of surrogate modeling and subsequent UQ analyses. Global sensitivity analysis methods are widely used to evaluate the overall impact of input parameters on QoIs. The primary techniques include the elementary effect methods [42], derivative-based methods [43], variance-based methods [44], and moment-independent methods [45].

2.4. Model Calibration

This process involves adjusting model parameters using high-confidence benchmark data to minimize discrepancies between simulation results and experimental or reference values. Fundamentally, calibration constitutes an inverse problem that can be formulated as an optimization task. Established approaches for solving optimization problems include Quasi-Newton [46], Conjugate Gradient [47], Genetic Algorithm [48], Shuffled Complex Evolution [49], Simulated Annealing [50], surrogate model-based optimization methods [51], as well as Bayesian inference methods [52].

2.5. Model Validation

Model validation quantifies discrepancies between computational predictions and experimental observations (or theoretical solutions) to evaluate whether a computational model satisfies application-specific requirements. The validation outcomes provide critical evidence for determining if model parameter calibration is required. A comprehensive validation process must account for uncertainties inherent in both numerical simulations and physical experiments. For random uncertainty, the primary methodologies for model validation encompass hypothesis testing, Bayesian factor analysis, frequency metrics, and area metrics. The area metric approach measures the alignment between simulation results and experimental data by determining the area discrepancy between the cumulative distribution function of the simulation output and the empirical distribution function of the experimental observations. This approach has been extended from the framework of random uncertainty to encompass epistemic and mixed uncertainty frameworks, thereby advancing interval area metric methods [53], probability box metric methods [54], and the U-pooling method [55] for multi-input state assessment.

2.6. Numerical Discretization Uncertainty Analysis

This process accesses uncertainties arising from the numerical solution process.

It is widely recognized in CFD practice, as demonstrated by research from the Drag Prediction Workshop and High-Lift Prediction Workshop [56,57], that variations in mesh discretization significantly affect results and are a major source of solution bias. Given this, performing numerical discretization uncertainty analysis prior to parametric uncertainty studies is crucial to isolate the effects of parameter variations from numerical errors. Classical methods for analyzing discretization errors in grids encompass Grid Convergence Index (GCI) estimation [58] and Richardson Extrapolation [59]. Another promising strategy for addressing this issue is the utilization of grid adaptation techniques [60,61].

It should be noted that Figure 2 outlines a general framework, and the elements within it can be flexibly tailored or expanded to suit specific UQ problems.

3. The UQ4CFD Platform

3.1. Software Architecture

The UQ4CFD platform is designed as an integrated solution for comprehensive uncertainty quantification in computational fluid dynamics. Embracing a cloud-native service model, it employs a Browser/Server architecture to provide users with on-demand access to essential UQ resources—including data, algorithms, and computational infrastructure—through integrated services. This approach allows users to perform CFD-based uncertainty quantification tasks directly via a web browser, eliminating complex local setup and significantly reducing the hardware requirements on end-user devices.

As illustrated in Figure 3, the platform follows a layered architectural pattern to ensure clarity and modularity. The front end is built using Vue2 and the ElementUI component library, while the backend leverages the Spring Boot framework with MyBatis-Plus. Although the platform is primarily developed in Java, core uncertainty quantification algorithms are developed in C++ to optimize computational performance. Docker containerization technology is used for streamlined deployment and portability. Figure 4 further outlines the physical architecture, which comprises two main components: the platform server and the high-performance computing (HPC) cluster. The platform server hosts frontend and backend services, UQ programs, and operational data storage. The HPC cluster is dedicated to running CFD solvers and data processing tools, delivering the computational power and job scheduling capabilities required for large-scale UQ analysis. Communication between the server and the cluster is efficiently managed through the SSH protocol, enabling secure and coordinated execution of distributed computational tasks.

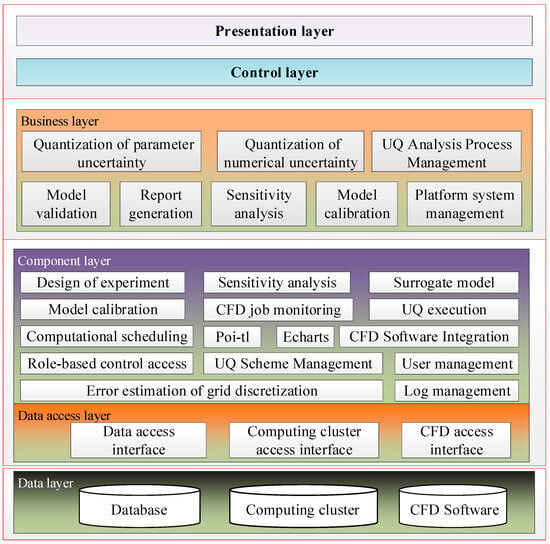
Figure 3. Logical architecture.

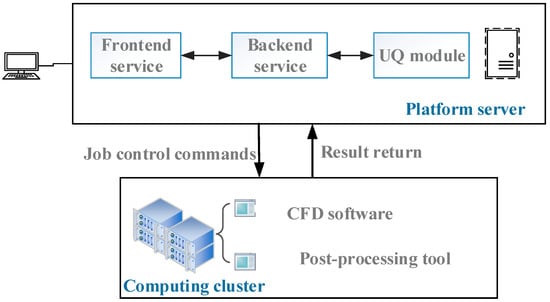
Figure 4. Physical architecture.

3.2. Software Module

The UQ platform consists of six core modules, which are as follows: UQ algorithm module, CFD software integration module, CFD job management module, UQ workflow customization module, chart and report generation module, and system management module. This subsection provides an overview of each module.

3.2.1. UQ Algorithm Module

The UQ algorithm module is encapsulated into different sub-modules according to its functions. For each sub-module, we have developed and integrated multiple classical algorithms into the platform. However, conducting in-depth algorithmic research or developing new algorithmic improvements is not the platform’s core objective. Instead, the platform aims to abstract away many complexities through algorithm testing and sound software engineering practices, thereby enabling a broader community to conduct UQ work with ease. The specific algorithms and corresponding functions are systematically presented in Table 1. As these methods are widely recognized and documented, this paper is not going to elaborate on their theoretical details.

Table 1. Overview of integrated UQ algorithms.

Sub-Module	Function	Algorithms
Design of experiment	Generate input sample data which can accurately reflect the characteristics of the model in the design space	Central-Composite [27], Full-Factorial [28], Monte Carlo [29], Latin Hypercube Sampling [30], Sobol [31], MOAT [42]
Uncertainty analysis	Quantify the uncertainty of model outputs	Statistical Analysis, Interval Analysis [24], Probability Box [26]
Sensitivity analysis	Qualitative or quantitative analysis of the influence of uncertain input factors on model outputs	Morris [42], Sobol [44], PCE-Sobol
Surrogate model	Construct a high-precision surrogate model to replace CFD solver for uncertainty analysis	Polynomial Chaos Expansion [23], Radial Basis Function [32], Kriging [33], Neural Network [34]
Model calibration	Calibrate model parameters to reduce the deviation between the simulation and experimental results	Quasi-Newton [46], Conjugate Gradient [47], Genetic Algorithm [48], MCMC [52]
Model validation metric	Quantitatively evaluate the coincidence degree between simulation results and experimental results	Area Metric [53], Interval Area Metric [53], Probability Box Metric [54], U-pooling [55]
Numerical discretization uncertainty analysis	Evaluate the influence of grid discretization on model outputs	GCI [58], Richardson Extrapolation [59]

3.2.2. CFD Software Integration Module

The CFD Software Integration Module is responsible for integrating various CFD software into the UQ4CFD platform by providing all necessary configurations. To this end, a generalized integration framework was built to address the heterogeneous computational workflows and input/output file structures of different programs, thus enabling the platform to correctly drive them to perform simulations. The framework performs three essential functions: First, it establishes software execution protocols by defining the required programs and their sequential workflow, thereby guaranteeing proper execution of all simulation phases including pre-processing, numerical solving, and post-processing. Second, it defines which files and parameters must be read from or written to during the CFD solution process. Third, it implements parameter mapping to maintain consistency between the platform’s parameter nomenclature and the CFD software’s native naming conventions, thereby preventing computational errors caused by terminology discrepancies.

3.2.3. CFD Job Management Module

The CFD Job Management Module is a core component of the UQ4CFD platform, responsible for submitting, monitoring, and managing large volumes of CFD computational jobs. Its main functions include: (1) Responding to computation requests -Processing CFD calculation tasks initiated by UQ sub-modules such as DoE and model calibration; (2) Batch job generation—Automatically generating control files required for CFD simulations and submitting batches of CFD jobs to the HPC cluster; (3) Job monitoring and management—Continuously tracking the convergence status of jobs and automatically identifying those requiring continuation, restart, or early termination; and (4) Results processing—Automatically extracting CFD results upon job completion and returning them to the UQ algorithm module for subsequent analyses.

3.2.4. UQ Workflow Customization Module

The UQ Workflow Customization Module allows for the configuration of differentiated UQ functionalities. On one hand, administrator users can publish standardized UQ workflows for all platform users. These well-established workflows are carefully designed and validated to meet the demands of most common UQ analyses. On the other hand, regular users can build upon administrator-provided templates to create personalized extensions. They can freely combine modules—such as additional experimental design, surrogate modeling, and parameter optimization—to develop customized UQ solutions for complex scenarios.

3.2.5. Chart and Report Generation Module

The Chart and Report Generation Module automatically generates data visualizations and detailed reports for UQ analysis. Built on open-source technologies, the module leverages the widely adopted ECharts library for chart rendering and incorporates the poi-tl template engine for report generation.

3.2.6. System Management Module

The System Management Module serves as the foundational component of the platform, providing essential support for security management and operational maintenance. It encompasses critical functions such as user management, role management, role-based access control, log management, and so on.

3.3. Software Features

3.3.1. Automation

By integrating algorithms, data management, and workflow orchestration into a unified platform, a high degree of automation is achieved throughout the UQ process. As illustrated in Figure 4, the process operates as follows: First, the user defines key information such as the probability distribution type and range of input parameters through the front-end interface; Then, the back-end of the platform invokes the UQ module to automatically perform parameter sampling and generate a sample dataset; Based on the sampling results, the platform automatically generates corresponding CFD calculation files for each sample, submits them to the HPC cluster to launch CFD tasks, and performs real-time monitoring and intelligent management of task status. Once all CFD simulations are detected as converged, the platform automatically extracts the computational results and returns them to the UQ algorithm module. Finally, UQ algorithms are called to perform uncertainty analysis on the CFD results, and visualization charts along with analysis reports are automatically generated.

3.3.2. Flexibility

The platform’s primary UQ functionalities include parametric uncertainty propagation, numerical discretization uncertainty quantification, sensitivity analysis, model validation, and calibration of model parameters. In addition to providing predefined workflows for these functions, the platform allows users to flexibly combine different algorithms to construct customized functional processes. For instance, for parametric uncertainty propagation, users can customize the following three typical analysis workflows (as shown in Figure 5A–C). Workflow A represents the most straightforward approach, suitable for low computational-cost CFD scenarios; Workflow B incorporates surrogate modeling prior to uncertainty propagation, optimizing efficiency for computationally intensive cases; and Workflow C extends Workflow B by integrating sensitivity analysis, making it particularly effective for high-dimensional input problems.

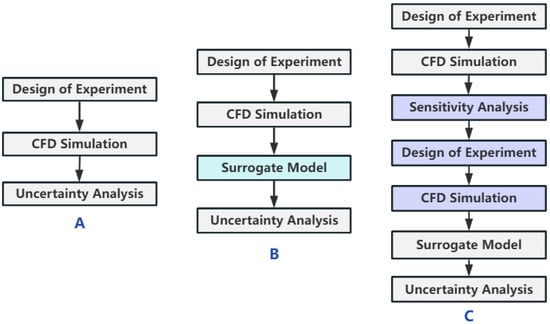
Figure 5. Schematic of customized uncertainty propagation workflows. (A) Workflow for low computational-cost scenarios; (B) Workflow with surrogate models for high computational-cost scenarios; (C) Workflow with sensitivity analysis for high-dimensional input problems.

Furthermore, UQ4CFD supports a solver-decoupled operational mode, which is particularly suited for scenarios where datasets have been pre-generated. This capability allows users to directly upload existing data for uncertainty quantification without requiring real-time CFD simulations. Such architectural flexibility substantially broadens the platform’s applicability across diverse computational domains, such as computational solid mechanics, ablation simulation for materials, and so on.

3.3.3. User-Friendly

The UQ4CFD platform features an intuitive graphical user interface, designed to deliver a clear, concise, and user-friendly interactive experience while enabling real-time visualization, monitoring, and management of the analysis workflow. Figure 6 illustrates the layout of the UQ task execution interface. The left side of the interface displays the various modules of the UQ analysis workflow in a tab-based format, while the right side dynamically presents the execution panel corresponding to the active tab. A key distinguishing feature of the platform is its dedicated CFD job monitoring interface, which allows users to track task progress and inspect computational status, as illustrated in Figure 7.

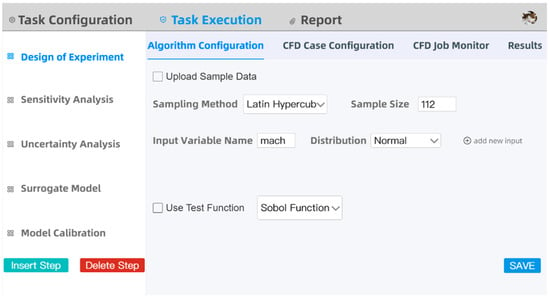
Figure 6. GUI schematic.

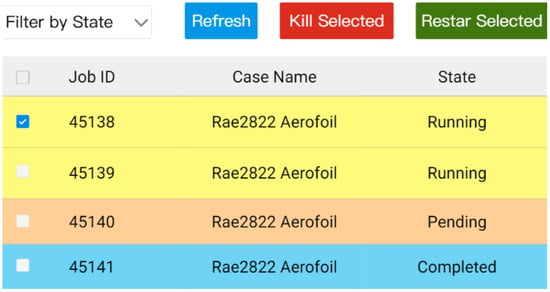
Figure 7. Job monitoring interface.

4. Test and Application

4.1. Algorithm Test

4.1.1. Sensitivity Analysis Algorithms Test

This subsection presents the evaluation of two sensitivity analysis algorithms: the Sobol method and the PCE-Sobol method. The Sobol method is a global sensitivity analysis technique based on variance decomposition. It quantifies the contribution of input variables to the total output variance through the first-order index (main effect) and the total effect index. The first-order index measures the proportion of variance attributable solely to an individual input variable, whereas the total effect index accounts for both its individual effect and all interactions with other variables. A notable limitation of the standard Sobol method is its computational cost, often requiring a large number of samples to achieve convergence. PCE-Sobol is a powerful global sensitivity analysis technique that combines Polynomial Chaos Expansion with Sobol method. Once the PCE model is built, the Sobol indices can be derived directly from its coefficients, thereby eliminating the need for extensive additional sampling.

The Ishigami function is employed as a benchmark to validate the correctness and performance of the implemented algorithms, and is defined as follows:

$$y=\sin (x_1)+7{\sin }^2(x_2)+0.1x_3^4\sin (x_1)$$

(1)

When the input variables $x_i$ follow a uniform distribution on $[-\pi ,\pi ]$, the Sobol index have exact solutions.

In this study, the Sobol method utilized 8192 samples to compute Sobol indices, whereas PCE-Sobol utilized 440 samples. Table 2 shows the theoretical and calculated values of the Sobol indices, where $S_i$ and $S{T}_i$ represent the main effect and total effect index of the variable $x_i$, respectively. The tests demonstrated a strong agreement between the UQ4CFD platform’s results, theoretical solutions, and SALib software outputs [62], accurately ranking the parameter sensitivities. A key finding was that PCE-Sobol achieved slightly higher accuracy than the standard Sobol method while using significantly fewer samples, underscoring its superior efficiency for sensitivity analysis.

Table 2. Theoretical and calculated Sobol indices for Ishigami function.

Method	S1	S2	S3	ST1	ST2	ST3
Theoretical solutions	0.3138	0.4424	0.0000	0.5574	0.4424	0.2436
Sobol (SALib software)	0.3168	0.4437	0.0122	0.5558	0.4418	0.2446
Sobol (UQ4CFD)	0.3185	0.4432	0.0013	0.5513	0.4327	0.2360
PCE-Sobol (UQ4CFD)	0.3147	0.4414	0.0000	0.5586	0.4414	0.2439

4.1.2. Model Calibration Algorithms Test

This subsection tests the algorithms of the model calibration, specifically the calibration methods based on Bayesian inference. Unlike deterministic optimization methods, Bayesian inference does not yield a single set of optimal parameters; instead, it provides the posterior distribution of the parameters. The Markov Chain Monte Carlo (MCMC) method provides an efficient approach for approximately sampling from complex probability distributions. Its core idea is to construct a Markov chain—a sequence of random samples in which each sample depends only on the previous one—such that its stationary distribution matches the target distribution from which we wish to sample. Various specific MCMC algorithms have been developed, among which the widely used Metropolis–Hastings algorithm is adopted in UQ4CFD.

The analytical pollutant dispersion model, so-called MDL, is employed as a benchmark case. The model computes the pollutant concentration at a given spatiotemporal point (x, t) using Equation (2).

$$f(x)=\sqrt{4\pi }\{{\displaystyle \frac{M}{\sqrt{4\pi Dt}}}{e}^{{\displaystyle \frac{-x^2}{4Dt}}}+{\displaystyle \frac{M}{\sqrt{4\pi D(t-\tau )}}}{e}^{{\displaystyle \frac{-{(x-L)}^2}{4D(t-\tau )}}}\}$$

(2)

where $\tau , M, D, L$ are model parameters, with true values 30.1225, 10, 0.07, and 1.505, respectively. We treat parameter $\tau$ as known and calibrate the unknown parameter $M, D, L$ against a set of five data points ($t = 33, x = 0.5, 1.0, 1.5, 2.0, 2.5$).

Table 3 summarizes the uncertainty characterization of MDL’s input parameters, where uniform distributions were adopted as priors. Using the MCMC algorithm, we generated 100,000 samples to approximate the posterior distributions of the parameters, from which the posterior means and maximum a posteriori (MAP) estimates were computed. As shown in Table 4, the MAP estimates align perfectly with the true values, while the posterior means exhibit a relative error of less than 1.5% compared to the true values. These results validate the efficacy and precision of the platform for uncertainty parameter calibration.

Table 3. Intervals of uncertain parameters in the MDL model.

Parameters	Probability Distribution	Min	Max
M	Uniform	7	13
D	Uniform	0.02	0.12
L	Uniform	0.01	3

Table 4. Bayesian inference results for the MDL model.

Parameters	Exact Value	MAP	Posterior Mean
M	10.000	10.000	10.041
D	0.070	0.070	0.071
L	1.505	1.505	1.505

4.2. Numerical Discretization Uncertainty Quantification

This section demonstrates the generalized Richardson extrapolation and the Grid Convergence Index (GCI) method to evaluate simulation uncertainties arising from grid resolution. The Richardson extrapolation approach, as shown in Equation (3), expresses the numerical solution as a Taylor series expansion with respect to the grid discretization scale.

$$u_h=u_{h=0}+g_p{h}^p+o(h^{p+1})$$

(3)

where $h$ is the grid discretization scale, $u_h$ is the numerical solution at grid scale $h$, $p$ is the observed order of accuracy, and $u_{h=0}$ is the estimated exact solution. Since computational grids are typically non-uniform, $h$ is generally defined as a certain average of the volumes of all grid cells.

By applying this equation to multiple grids with different resolutions and formulating the corresponding Taylor expansion equations, the observed order and an estimate of the exact solution can be determined. However, Richardson’s method for estimating the observed order may yield values that significantly deviate from the theoretical convergence rate, potentially compromising the reliability of Richardson estimation. To address this limitation, Roache presented the GCI method, which utilizes numerical solutions obtained from systematically refined grids to quantify discretization-induced uncertainties. The GCI is formally defined as

$$GCI={\displaystyle \frac{Fs}{r^p-1}}|u_h-u_{rh}|$$

(4)

where $Fs$ is the safety factor, and $r$ is the discretization scale ratio of coarse grid to fine grid. The uncertainty interval is believed to be within $u_h\pm GCI$. The safety factor $Fs$ is set to 1.25 if $\left|p-p_f\right|/p_f\le 0.1$, and to 3.0 otherwise, where $p_f$ denotes the theoretical order of accuracy.

In this study, the Common Research Model (CRM) from the AIAA Drag Prediction Workshop was selected as the demonstration case [56]. The CRM represents a modern wide-body airliner configuration, and its geometry is illustrated in Figure 8. Four sequentially refined unstructured grids were used to compute the drag coefficient at a Mach number of 0.85, a lift coefficient of 0.5, and a Reynolds number of 5 million. For the four grids, there are roughly 17.3 million, 26.3 million, 40.3 million, and 61.3 million grid cells in total. The simulations were conducted using our in-house solver, FlowStar [63,64], which is based on a second-order finite volume method for unstructured grids. The Roe scheme was employed for flux discretization, and turbulence was modeled using the Spalart–Allmaras model with Quadratic Constitutive Relation correction. The solver was integrated into our developed UQ4CFD platform to automate processes involved in the CFD simulation and GCI analysis workflow.

Figure 8. Overall configuration of NASA CRM.

As the grid was refined, the drag coefficient computed by FlowStar decreased progressively, converging to values of 0.02642, 0.02627, 0.02612, and finally 0.02601. The subsequent GCI analysis yielded the observed order of accuracy, an estimate of the exact solution via Richardson extrapolation, and the corresponding GCI values (Table 5). The observed order of accuracy shows excellent agreement with the theoretical value, validating the correctness of the solver’s numerical discretization and implementation. Furthermore, the small GCI value indicates that the numerical uncertainty interval for the drag coefficient is narrow, ranging from 0.02559 to 0.02643. This confirms that the discretization error has been effectively minimized through grid refinement, implying that the finest grid is sufficiently resolved for grid-induced uncertainty to be considered negligible.

Table 5. Uncertainty quantification results for grid discretization.

Observed Order	Richardson Extrapolation Solution	GCI
2.00002	0.02570	0.00042

4.3. Parametric Uncertainty Quantification

4.3.1. Problem Definition

Turbulence models pose a significant source of uncertainty in CFD, largely due to the closure coefficients introduced during their development. These coefficients are calibrated against limited experimental data, raising questions about their validity across diverse flow conditions. Variations in these coefficients may lead to deviations in CFD results. This study utilizes the UQ4CFD platform to evaluate the influence of Spalart–Allmaras (SA) coefficients’ uncertainty on the predicted aerodynamic characteristics of the RAE 2822 airfoil. It also provides a sensitivity ranking of the model parameters and demonstrates the ability to calibrate them.

The SA model has been extensively utilized in aerospace [65]. The analysis assumed fully turbulent flow and omitted the transition term from the original model. Under these conditions, nine closure coefficients ($c_{b1}, \sigma , c_{b2}, \kappa , c_{w2}, c_{w3}, c_{v1}, c_{t3}, c_{t4}$) were considered as uncertain inputs. These parameters were assumed to follow uniform distributions with the intervals specified in Table 6, with parameter ranges referenced from pertinent literature [9]. Detailed explanations of these parameters can also be found in this reference. It should be noted that the mathematical representation of model uncertainty parameters, including distribution types and parameters, requires thorough consultation with model developers. This subsection focuses on demonstrating the functionalities of the UQ4CFD platform, rather than presenting a rigorous aerodynamic investigation.

Table 6. SA closure coefficients and associated epistemic intervals.

Parameter	Minimum Value	Maximum Value	Standard Value
cb1	0.12893	0.137	0.1355
σ	0.6	1.0	2/3
cb2	0.60983	0.6875	0.622
κ	0.38	0.42	0.41
cw2	0.055	0.3525	0.3
cw3	1.75	2.5	2.0
cv1	6.9	7.3	7.1
ct3	1.0	2.0	1.2
ct4	0.3	0.7	0.5

The RAE 2822 is a classic transonic airfoil whose flow field poses considerable challenges for CFD simulation, primarily due to complex shock wave/boundary layer interaction. The computational mesh is shown in Figure 9, with a total grid cell of 98,550. The computational conditions were set at $Ma=0.729,Re=6.5\times {10}^6,\alpha =2.31$. All simulations were performed using the in-house solver FlowStar.

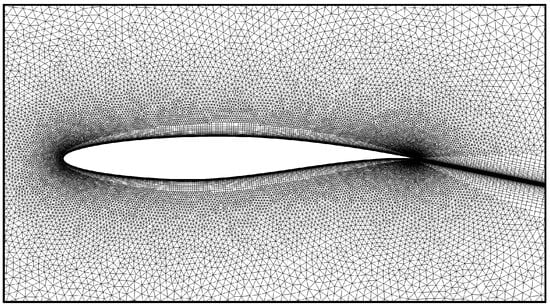
Figure 9. Computational mesh of RAE2822 airfoil.

4.3.2. Uncertainty Propagation

DoE was carried out first. A total of 112 samples were generated from the parameter space of the nine SA closure coefficients, defined in Table 6, by employing the Latin Hypercube Sampling technique. The QoIs were the lift coefficient ($C_L$) and drag coefficient ($C_D$). Then, CFD simulation process was executed automatically on the UQ4CFD platform and monitored in real-time. Upon completion of the computation, the platform automatically proceeds to extract the QoIs from the resultant files. Figure 10 shows the variation in the computed lift coefficient $C_L$ with the von Kármán constant κ, indicating a strong linear correlation between them.

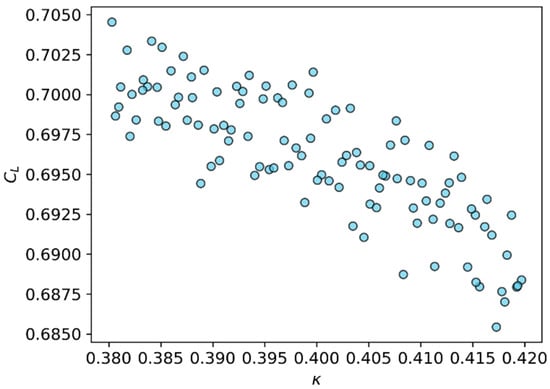
Figure 10. Correlation between input κ and output C_L.

Finally, polynomial chaos expansion was employed for uncertainty propagation. Although the mean and variance can be directly computed from the PCE coefficients, we treated the PCE as a conventional surrogate model and performed Monte Carlo sampling with 100,000 samples to obtain the output probability density statistics, shown in Figure 11. The results demonstrate a clear influence of turbulence model coefficient uncertainty on the output. It is noteworthy that although the input variables followed a uniform distribution, the resulting output uncertainty distribution closely resembles a normal distribution. In terms of computational efficiency, predicting lift and drag coefficients with the PCE model requires negligible time, whereas a single CFD simulation demands approximately 8 core hours on the same hardware. Performing 100,000 Monte Carlo simulations via CFD would thus be computationally prohibitive, underscoring the substantial efficiency advantage of the surrogate approach for uncertainty propagation.

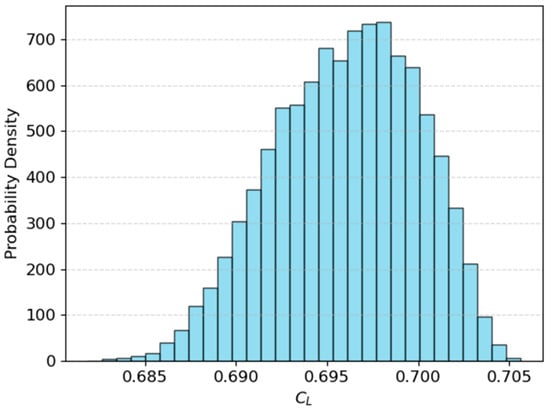
Figure 11. Probability density histogram of C_L.

4.3.3. Sensitivity Analysis

To quantify the influence of key SA closure coefficients on RAE2822 transonic flow, a sensitivity analysis was performed using the PCE-Sobol method. Figure 12 presents the sensitivity results. For the lift coefficient, coefficients κ, c_v1 exerts the most significant influence, followed by coefficients σ, c_b1, which is basically consistent with the conclusions of Schaefer [9]. For the drag coefficient, the most influential coefficients are κ, σ and c_w2. It is advisable to prioritize the calibration of these highly sensitive closure coefficients when incorporating higher-fidelity observational data (e.g., from DNS or experiments).

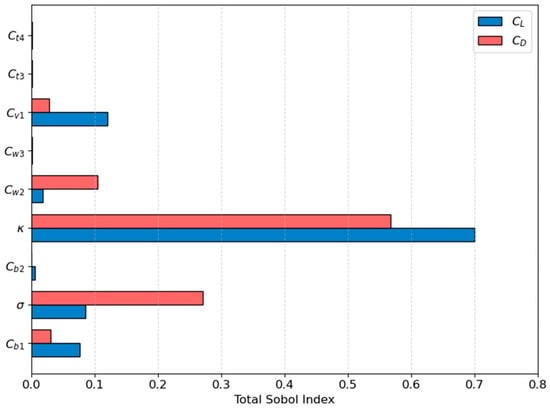
Figure 12. Sobol indices for SA coefficients.

4.3.4. Model Calibration

This subsection presents the calibration of the model parameters. Based on the sensitivity analysis results from the previous section, the parameters κ and c_v1 were selected for this process. The lift coefficient simulated with the standard values (Table 6) was used as the calibration target, with the expectation that the calibrated values would be close to their standard values.

The calibration was conducted using the MCMC method within the UQ4CFD platform. The prior distributions of the calibrated parameters remained consistent with those specified in Table 6. To address the computational expense of CFD simulations, a Kriging surrogate model was constructed based on the 110 samples from Section 4.3.2 to predict the lift coefficient for new parameter sets. A total of 500,000 samples were generated using MCMC to obtain their posterior distribution. The mean of the posterior distribution for each parameter was selected as the final calibrated value, as summarized in Table 7. The results demonstrated that the calibrated values were in remarkable agreement with the standard values, exhibiting a maximum relative error below 1%.

Table 7. Standard and calibrated values.

Parameter	Standard Value	Calibrated Value	Relative Error
κ	0.41	0.406	0.976%
cv1	7.1	7.102	−0.028%

4.4. Application Beyond CFD

This section showcases the application of the UQ4CFD platform to a non-aerodynamic case: a one-dimensional carbonizing material ablation problem from the 4th Ablation Workshop. This example serves to highlight the platform’s versatility and its potential utility for a wider range of scientific computing disciplines. The selected benchmark case involves the TACOT material (see Figure 13). Nine key material properties, listed below, were treated as uncertain inputs: thermal conductivity, specific heat, density, and enthalpy of formation for both the virgin and charred material states, as well as the enthalpy of pyrolysis gas, permeability, and porosity. The analysis focuses on quantifying the collective impact of these parameter uncertainties on the temperature at the specific location of 25 mm in height, where the top temperature is 1644 K and the bottom is adiabatic. Further details regarding the parameters’ definitions and distributions can be found in References [66,67].

Figure 13. Schematic of the ablation model for the TACOT material.

A total of 530 sample points were generated in the 9-dimensional stochastic parameter space using Latin Hypercube Sampling. The corresponding temperature responses were computed using a finite-element-based ablation simulation code [68]. Although the ablation code could not directly integrate into the UQ4CFD platform, the simulation results were imported into the platform for subsequent uncertainty quantification analysis. Radial Basis Function, Kriging, and Neural Network methods were employed to construct surrogate models, using a training set of 30 samples. The accuracy of each model was evaluated through ten-fold cross-validation. Table 8 presents the corresponding root mean square error (RMSE) results from the cross-validation. It can be observed that the Kriging model outperforms the other two methods. Furthermore, an additional set of 500 test samples was predicted using the trained Kriging model. A comparison between the predicted and simulated results is presented in Figure 14, showing a strong linear correlation with an R² value of 0.994. This result demonstrates that the Kriging model achieves high predictive accuracy and efficiency even in small-sample scenarios, which is consistent with the results reported in the literature [69,70].

Table 8. RMSE of different surrogate models’ predictions.

Radial Basis Function	Kriging	Neural Network
4.039	1.484	4.040

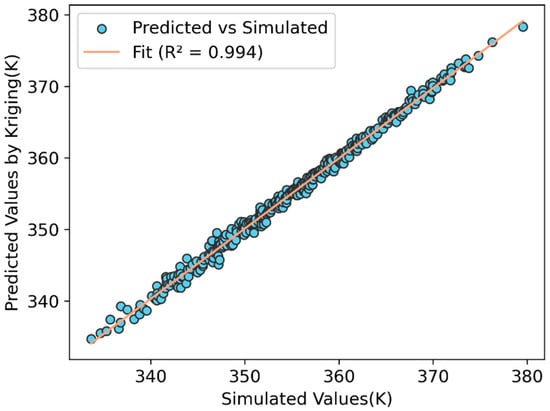
Figure 14. Predicted vs. simulated results.

The Kriging surrogate model was then employed for input parameters’ uncertainty propagation. A total of 100,000 input samples were generated using Latin Hypercube Sampling. These samples were subsequently processed through the established Kriging model to compute corresponding output responses. Finally, uncertainty analysis was performed for the resulting outputs, yielding a mean value of 355.99 K and a standard deviation of 8.42 K.

5. Summary

In this paper, we present UQ4CFD, a flexible, browser–server architecture-based software platform designed to streamline uncertainty quantification analysis in computational fluid dynamics. Equipped with a suite of well-established algorithms, the platform is capable of conducting comprehensive uncertainty analysis, encompassing key areas such as uncertainty propagation, sensitivity analysis, surrogate modeling, numerical discretization uncertainty analysis, model validation, and calibration. These algorithms feature standardized interfaces, allowing users to customize UQ analysis workflows to meet diverse application scenarios. The development target of UQ4CFD is not on further advancing algorithms but on ensuring rigorous algorithm testing and sound software engineering practices, enabling users across varying expertise levels to apply these techniques to CFD problems with ease. A most distinctive feature of the UQ4CFD platform, setting it apart from existing similar tools, is its seamless integration of CFD simulation workflow management and UQ analysis workflow management, coupled with automated data processing between these processes. This integration significantly reduces the complexities associated with UQ tasks, allowing users to effortlessly manage large-scale CFD simulations and data processing in UQ analysis, thereby encouraging the adoption and practical use of UQ in CFD. Enabling support for a wide range of CFD software presents a paramount challenge in the platform development process, primarily due to the disparate computational workflows and the distinct logic underpinning the read/write their input/output files. To overcome this, we have constructed a generalized integration framework. Within this framework, various CFD software can be configured and subsequently orchestrated to run correctly by the platform.

The capabilities of the platform have been validated through a series of analytical functions and CFD benchmark cases, confirming its reliable performance and effectiveness in handling different types of uncertainty quantification problems. UQ4CFD is currently under active development. Future efforts will focus on enhancing its capability to quantify epistemic and mixed uncertainties, as well as extending its support for UQ analysis of high-dimensional field data.