Abstract
Acoustic instabilities in solid rocket motors (SRMs) can lead to severe performance deterioration and structural damage. Nozzle damping accounts for the main acoustic dissipation source, and it is highly dependent on geometric parameters and operating conditions. This study experimentally investigated the acoustic damping characteristics of submerged nozzles in SRMs, focusing on the effects of submerged cavity dimensions, nozzle convergent angle, throat-to-port area ratio, and mean pressure variations on the longitudinal instability. The steady-state wave decay method was used to quantify the acoustic damping, and a designed rotary valve system was employed to introduce periodic pressure oscillations in the high-pressure combustion chamber. The results revealed that a larger submerged cavity would reduce the nozzle damping efficiency, with the elimination of the submerged cavity enhancing the nozzle decay coefficient magnitude by 41.9%. Furthermore, increasing the nozzle convergent angle was found to amplify acoustic wave reflection, thereby diminishing damping performance. A linear inverse relationship was observed between the throat-to-port area ratio and the decay coefficient, with a 125% increase in the ratio resulting in a 24.3% reduction in the decay coefficient. Interestingly, despite the formation of complex vortices in the submerged cavity, the mean pressure variation presented negligible effects on acoustic damping characteristics, and its damping performance is similar to a simple nozzle without a cavity. These findings provide valuable experimental data for predicting the stability of a solid rocket motor with a submerged nozzle and offer insights into the optimization of submerged nozzle designs for higher acoustic damping in SRMs.
1. Introduction
Combustion instability is a critical phenomenon that often occurs in many solid rocket motors, such as in RVA-10, Slufae, Sidewinder and Maverich [1,2]. It is characterized by large-amplitude pressure/heat oscillations, which may lead to several detrimental outcomes, including structure vibrations, severe erosions, significant trajectory deviation, and in extreme cases, catastrophic failure. To prevent the onset of or suppress severe thermoacoustic oscillations, a profound understanding of underlying mechanisms is mandatory.
During the early 1940s, Load Rayleigh [3] proposed a general and clear description of combustion instability: “if heat be given to the air at the moment of greatest condensation, or be taken from it at the moment of greatest rarefaction, the vibration is encouraged”. Later Culick [4], Price [5] and Hart [6] conducted extensive research efforts on solid rocket motors and confirmed that this destructive issue stemmed from the interaction among the solid propellant combustion dynamics, turbulent flows and acoustic wave propagation within the combustion chamber [7,8,9]. To predict the onset of combustion instability [10,11,12,13,14,15,16], a linear stability analysis revealed that the stability of the motor was determined by the net balance between acoustic energy gain and the damping mechanism [17,18,19,20,21]. The acoustic energy gains [22,23,24] primarily originated from two sources: the interaction between the unsteady heat release from the solid propellant combustion and acoustic oscillations and the coupling between the vortex shedding and the acoustic waves. As for the acoustic damping mechanism, there were many damping sources, including nozzle damping, particle damping, wall losses, and structural damping. Nozzle damping was generally caused through the acoustic wave radiation and convection [25,26]. It was found that if the acoustic energy gain was larger than the acoustic damping, the solid rocket motor was unstable; otherwise, the system was stable. Therefore, either decreasing the acoustic energy gain or increasing the acoustic damping can increase the stability of the solid rocket motor.
In solid rocket motors with large length-to-diameter ratios, combustion instability was predominantly characterized by low-frequency longitudinal acoustic modes [27]. In these configurations, nozzle damping played a crucial role in axial instability, which accounted for over 50% of the total acoustic energy dissipation within the combustor. Consequently, a comprehensive understanding of nozzle damping characteristics is essential for accurately predicting the stability of solid rocket motors and developing effective strategies to mitigate combustion instability.
Early investigations into nozzle damping characteristics employed a combination of theoretical analysis and experimental measurements [28,29]. To quantify the damping intensity, four primary methods have been utilized: direct measurement, steady-state wave decay, frequency response analysis, and the modified impedance tube method [30,31]. The direct measurement method involved a hotwire anemometer probe and a pressure transducer. Crocco [32] employed this method to directly measure the amplitudes and phases of the axial flow velocity and pressure oscillations, enabling the determination of the nozzle admittance. However, the quality of the nozzle admittances was diminished by the uncertainties associated with measuring velocity perturbations. Zinn and Bell [26,33] introduced a modification to the traditional impedance tube to incorporate the effect of mean flow. They measured the nozzle admittance for various nozzle convergent angles and inlet Mach numbers, and their experimental results exhibited good agreement with theoretical calculations. Janardan [34] used the similar modified impedance tube method to reveal that the cavity depth near the nozzle significantly influenced the nozzle admittance. Buffum [35] conducted acoustic dissipation experiments on a subscale rocket motor model to assess the impact of nozzle geometric variables on the acoustic performance and indicated that the transmission of acoustic energy through the nozzle was the primary source of loss for the axial mode, and these losses increased with the throat-to-port area ratio of the nozzle. Sattelmayer and Kathan [36] developed a transonic cold flow test facility for acoustic measurements, employing a siren to generate continuous harmonic excitation. They measured the first-order tangential mode nozzle damping of a liquid rocket motor using the wave decay method. Based on Sattelmayer’s siren, Price [37] designed a gate valve to excite pressure oscillations and measured the first-order axial, radial and tangential mode nozzle damping for various nozzle profiles. A lack of experimental evaluation of the submerged nozzle structure on the acoustic damping motivated the present work.
In this work, the effects of submerged nozzle geometry and the flow conditions on the nozzle damping characteristics were experimentally evaluated. A rotary valve was designed and employed to excite periodic pressure oscillations, and the steady-state wave decay method was utilized. The primary objective of this work was to provide valuable data that can contribute to the improvement of passive control strategies for solid rocket motors with submerged nozzles.
2. Experiment Equipment
In this paper, the experimental apparatus for nozzle damping measurements mainly comprised four main components: the air supply system, the rotary valve system, a rocket motor model and a data acquisition system, as illustrated in Figure 1.
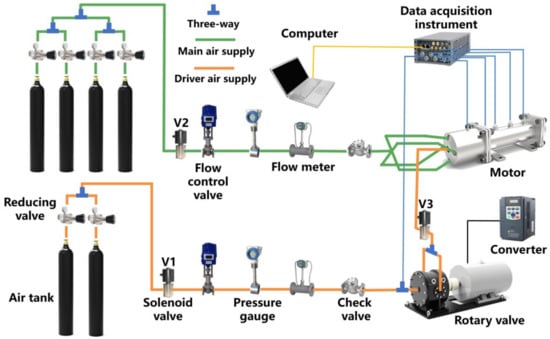
Figure 1.
Schematic of experimental setup for the nozzle damping measurement.
The air supply system consisted of two lines: a main air supply maintaining the mean pressure and a driver air supply for introducing pressure fluctuations. This dual-line configuration allowed for precise control over both steady-state and dynamic flow conditions. To generate periodic flow oscillations, a rotary valve system was designed, and it consisted of a stator, a rotor and an asynchronous motor (Siemens 1TL0001-1DA33-3, Yi’zheng, China). The asynchronous motor was used to drive the rotor to spin, allowing the air flow from upstream pipes to pass periodically through circumferential holes in the rotator. The frequency of the mass flow rate was directly controlled by the rotational speed of the rotary valve. In this work, the asynchronous motor has a maximum rotation speed of 3000 rpm, corresponding to a pressure oscillation frequency of 800 Hz. Therefore, the damping of the submerged nozzle can be only evaluated within 800 Hz here. The modulated flow was then directed to the solid rocket system via outlet pipes.
The rocket motor system, as illustrated in Figure 2, consisted of three main sections: a pre-chamber, a combustion combustor, and a submerged nozzle. The pre-chamber was mainly a cylindrical section with a diameter of 50 mm and a length of 40 mm, and it served as a mixing zone for the main and driver air flow before entering the combustion chamber. An acoustic admittance wall was placed between the combustion chamber and pre-chamber to prevent acoustic waves propagating upstream. This wall was a composite structure that included porous metal, perforated steel and wire mesh, as detailed in Figure 2c. The left three meshed structures were installed at the head of the pre-chamber before the main air entered the pre-chamber. The right meshed structures were installed between the pre-chamber and the combustion chamber, as shown in Figure 2b. This design isolated the acoustic waves in the combustion chamber from propagating upstream. The combustion chamber and the submerged nozzle formed the primary test section.

Figure 2.
(a) Assembled rocket motor system unit; (b) The axial cut-away view of the rocket motor corresponding to the model in reality. Five pressure transducers are located in the chamber (marked as P1-5); (c) The combined porous plate for experiment.
The structure of the solid rocket motor was based on the model proposed in ref. [38], featuring a sub-scaled combustion chamber with a length of 225 mm and a diameter of 50 mm. With the submerged nozzle, the total acoustic chamber length extended to 240 mm. To capture the system’s acoustic response, six CYG41000 pressure transducers (Xi’an Jiecheng Sensor & Control Technology Co., Ltd., Xi’an, China) were strategically installed with a range of 0–1 MPa and a natural frequency of 200 kHz. The pressure transducers were distributed as follows: the transducer P1 was mounted on the pre-chamber’s side wall, while four additional transducers (P2–P5) were positioned along the combustor’s side wall. This arrangement facilitated the identification of the first two eigen-modes of thermoacoustic oscillations. Using the inlet boundary of the combustor as the reference point (x = 0), the precise coordinates for the monitoring points P2, P3, P4 and P5 are detailed in Table 1. The final sensor P6 was installed at the rotary valve’s inlet to evaluate the performance of the rotary valve system. All measured signals were recorded simultaneously at a sampling rate of 10 kHz, ensuring high temporal resolution for subsequent analysis. This comprehensive data acquisition setup allowed for precise pressure measurement across the motor’s sections, providing essential information for analyzing the system’s acoustic behaviors under various operating conditions.

Table 1.
Coordinates of pressure monitoring points.
3. Results and Discussion
Firstly, the influence of the submerged nozzle geometry on the acoustic damping characteristics of solid rocket motors was investigated. Figure 3 displays the structure of the submerged nozzle. To shorten the length of the motor, the main body of the submerged nozzle extended into the combustion chamber, forming a cavity structure with the propellant. This study investigated three critical parameters: the inner diameter (), the convergent angle () and the ratio of throat-to-port area (). A series of nozzle configurations were designed and fabricated, with their specifications meticulously detailed in Table 2. This comprehensive set of nozzle designs enabled a thorough exploration of these parameters.
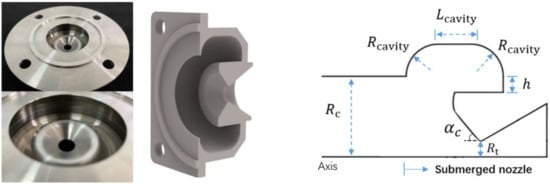
Figure 3.
The structure of the submerged nozzle.

Table 2.
The values of the submerged nozzle geometry parameters.
3.1. Data Analysis Method
To evaluate the nozzle damping characteristics, the steady-state decay method was employed. The experimental procedure mainly included two sequential phases: the forced oscillation and the free decay. During the forced oscillation phase, the flow within the combustion chamber was subjected to periodic disturbances generated by the rotary valve system, establishing a steady-state oscillatory condition. Subsequently, in the free decay phase, upon cessation of the periodic disturbance, the pressure oscillations within the chamber decayed exponentially, allowing for determination of the nozzle decay coefficient through analysis of the decay profile. Figure 4 illustrates a typical cold-flow test time sequence. The total duration of the cold flow operation extended to approximately 50 s, ensuring sufficient data acquisition for both forced oscillation and free decay analysis. The pressure drop across the acoustic admittance wall was maintained at approximately Pa, while the minimum absolute pressure in the combustion chamber was consistently maintained above Pa. This latter condition was crucial for ensuring sonic conditions at the nozzle throat throughout the experiment, a prerequisite for accurate modeling of the nozzle’s acoustic behavior.
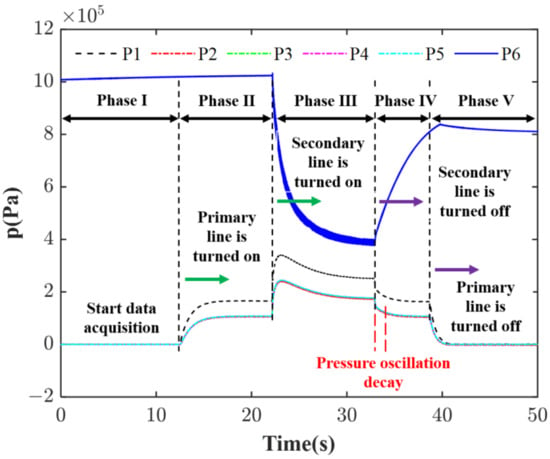
Figure 4.
Typical cold flow test sequence recorded at different monitoring points.
To isolate the acoustic pressure fluctuations from background noise and the mean pressure component, a second-order Butterworth filter with a bandwidth of 15 Hz was applied to the raw pressure signals. Figure 5 presents the temporal evolution of the filtered pressure fluctuations in the combustion chamber and the corresponding pressure spectra under steady-state conditions. The time-domain representation in Figure 5a reveals the generation of consistent sinusoidal signals within the combustion chamber, indicative of well-established acoustic modes. The spectral analysis, as depicted in Figure 5b, demonstrated a single dominant peak in the frequency domain at all four monitoring points. The peak frequency, approximately 625 Hz, corresponded precisely to the excitation frequency induced by the rotary valve system operating at 2325 rpm. This spectral uniformity across the multiple measurement locations confirmed the successful establishment of a coherent acoustic field within the combustion chamber.
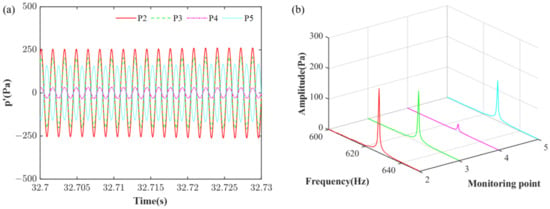
Figure 5.
Times series of the filtered pressure and the corresponding spectra from the four different monitoring points. (a) Pressure oscillation of the four monitoring points after filtering; (b) Fast Fourier transform of the four pressure signals corresponding to the figure a.
Figure 6 illustrates the measured pressure distribution along the axial direction of the combustion chamber, which was derived from different sensors. To provide a comprehensive representation of the acoustic field, we incorporated numerical simulation results from ref. [38] near the boundary regions. To ensure comparable acoustic behaviors, the referenced study employed the solid rocket motor model, which is scaled up by a factor of four relative to our experimental setup. The measured pressure distribution demonstrated remarkable consistency with the numerical predictions within the combustion chamber domain. Characteristically, the pressure profile exhibited a minimum near the chamber’s center and maxima at both ends, indicative of the first-order acoustic mode. This mode shape elucidated the observed response patterns across the monitoring points, with the minimal pressure fluctuation at monitoring point 4 and the maximum amplitudes at monitoring point 2. For comparative analysis, we superimposed the classic acoustic mode shape with no mean flow (represented by the blue circled curve) onto the experimental and numerical data. The close correspondence among these three profiles indicated that the mean flow within the combustion chamber exerted negligible influence on the acoustic pressure distributions under the studied conditions.
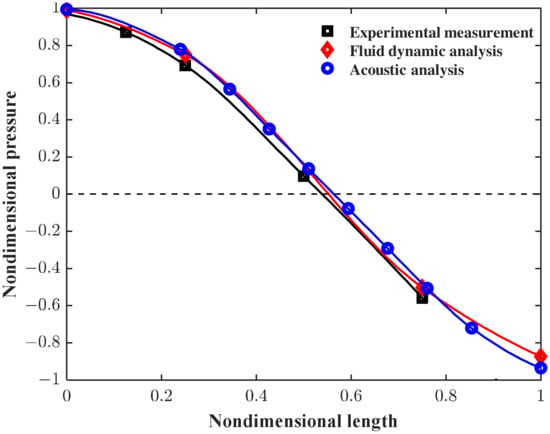
Figure 6.
The non-dimensional pressure distribution along the axial direction of solid rocket motor. In this experiment, Pa, = 0.24 m.
Figure 7 illustrates the decay curves of pressure oscillations after the band-pass filtration. Once the flow disturbances from the rotary valve were stopped, the pressure within the combustor exhibited characteristic exponential decay. The decay patterns observed at monitoring points 2, 3 and 5 demonstrated remarkable adherences to the theoretical exponential decay model. This consistency across multiple spatial locations indicated a uniform attenuation of the damped oscillations throughout the combustion chamber. Such spatial uniformity in damping behavior is highly desirable in solid rocket motor applications, as it suggests a consistent energy dissipation mechanism that is less prone to localize acoustic hot spots or regions of ineffective damping. In contrast, the data from monitoring point 4 deviated from the clear exponential decay trend observed at other monitoring points. This anomaly was due to the sensor’s proximity to a pressure nodal point of the first-order acoustic mode, where pressure fluctuations were inherently minimal. Consequently, the signal-to-noise ratio at this location was significantly reduced, compromising the accuracy of decay rate measurements. Therefore, to ensure the acquisition of precise damping characteristics, it was imperative to place the sensors away from the nodal points.
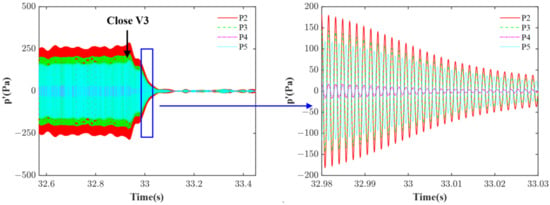
Figure 7.
Pressure oscillation decay curves after filtration.
To obtain the nozzle decay coefficient, the signal envelope was first extracted from the filtered pressure signal. Subsequently, the natural logarithm of this envelope was calculated, revealing a linear relationship between time and the natural logarithm of the pressure, as illustrated in Figure 8. This linearity in the decay process indicates that the pressure oscillations decrease exponentially. The nozzle decay coefficient can be determined from the slope of the linear fit curve. The decay coefficients at monitoring points 2, 3 and 5 were found to be −37.5, −37.4 and −40.3, respectively, with a mean value of −38.4 and a variance of 2.71. It was important to note that the negative sign of the decay coefficient indicated that acoustic energy was dissipated, while its magnitude represented the intensity of the damping. Consequently, a small decay coefficient corresponded to a large acoustic damping performance. As monitoring point 2 exhibited the highest pressure amplitude and effectively captured the main pressure oscillations, the decay coefficient from this point was selected for subsequent studies.
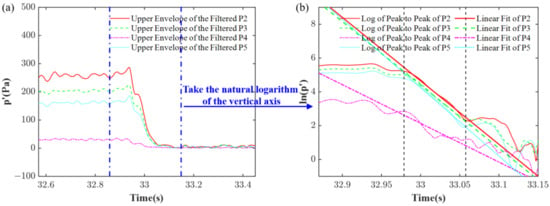
Figure 8.
(a) Envelope of the four filtered signal; (b) Log of four filtered signal and linear fit of the decay coefficient.
3.2. The Effect of the Submerged Nozzle Structure on the Damping Performance
Firstly, the influence of submerged cavity size on the damping performance of submerged nozzles was evaluated. Experiments were conducted using three nozzles with different cavity sizes, as specified in Table 2 and illustrated in Figure 9. The main air supply pressure was maintained at 2.2 MPa to ensure a consistent combustor pressure of 0.1 MPa (gauge pressure) across all test cases. Similarly, the secondary air supply pressure was fixed at 1 MPa. This consistent pressure setting allowed for an accurate evaluation of the effect of cavity size on damping without the inference of pressure variations.

Figure 9.
Experimental nozzles with different submerged cavity radius.
Figure 10 presents acoustic pressure evolutions and the decay coefficients evaluated at three different cavity radii. The corresponding numerical results in ref. [38] were adjusted by a factor of four, due to the scaling of the solid rocket motor structure. It can be seen that, as the submerged cavity size increased (from case 0 to 2), the decay coefficients increased monotonically too in both the experimental and numerical data, indicating that the corresponding acoustic damping was decreased. Furthermore, the experimental data were closely aligned with the adjusted numerical results, with discrepancies of 8.3%, 7.8% and 3.0% for cases 0, 1 and 2, respectively. In addition, under the same condition, the experimental value was smaller than the numerical prediction, which may be attributed to the fact that the experimental decay coefficients also accounted for the viscous wall losses.
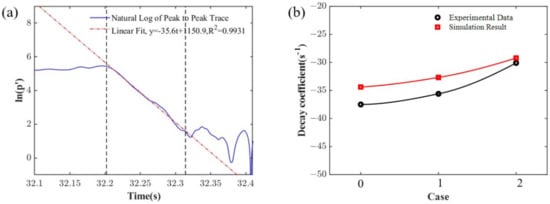
Figure 10.
The decay coefficient under different submerged cavity sizes. (a) 11.25 mm; (b) a comparison between the experimental and numerical data in ref. [36].
To further investigate the impact of a submerged cavity on nozzle damping, the nozzle with no submerged cavity (i.e., case 7) was also calculated. The pressure decay curve and the decay coefficient fitting line are depicted in Figure 11. Under identical nozzle geometric parameters and operating conditions, the decay coefficient of the simple nozzle in case 7 was obtained as −53.2, which was significantly smaller than the submerged nozzle. In another words, the removal of the submerged cavity resulted in an approximate 41.9% increase in the damping terms. This increase highlighted the detrimental effect of the submerged cavity on the damping capabilities.
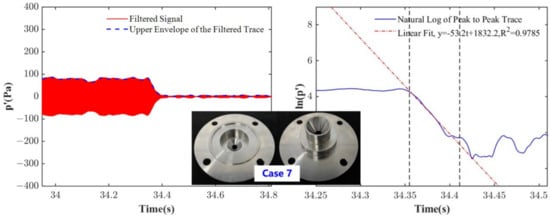
Figure 11.
Time series of acoustic pressure and the decay coefficient fitting line for case 7 nozzle with no submerged cavity.
Then, the effect of convergent angles on the submerged nozzle damping was evaluated experimentally. Three submerged nozzles with distinct convergent angles were considered: 40° (case 9), 50° (case 0) and 60° (case 4). The detailed structures are depicted in Figure 12.

Figure 12.
The submerged nozzles with different convergent angles.
The nozzle decay coefficients under different convergent angles are illustrated in Figure 13. The results revealed a monotonic increase in the nozzle decay coefficient with increasing convergent angle. This finding suggested that a larger convergent angle enhanced the reflection of acoustic waves within the nozzle, thereby reducing its damping effectiveness. As the convergent angle increased, the acoustic waves were more likely to be reflected back towards the combustion chamber, rather than being dissipated through the nozzle. Conversely, a small convergent angle promoted the transmission and dissipation of acoustic waves through the nozzle, resulting in a large damping performance.
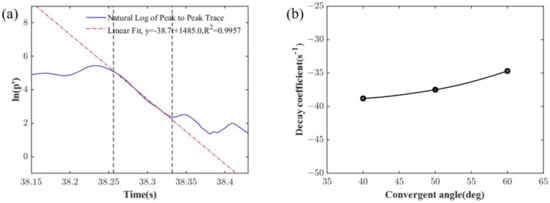
Figure 13.
The decay coefficient under different convergent angles. (a) = 40°; (b) The variation in the decay coefficient.
Figure 14 and Figure 15 investigate the influence of throat-to-port area ratio on the nozzle damping performance. With a constant grain port area (a diameter of 50 mm), the nozzle throat diameter varied, as illustrated in Figure 14. Three different nozzle throat diameters were considered: 5 mm, 7.5 mm and 10 mm. The corresponding throat-to-port area ratios were 0.01, 0.0225 and 0.04, respectively. Based on the steady-state decay method, the measured decay coefficients are presented in Figure 15. It can be seen that the throat-to-port area ratio was related to the decay coefficient in an inversely linear manner, and a 125% increase in the throat-to-port area ratio led to a decrease in the nozzle decay coefficient by approximately 24.3%.This finding suggested that, as the throat-to-port area ratio increased, both the acoustic energy radiation loss and the acoustic energy convection loss through the nozzle increased. Therefore, the submerged nozzle with a large throat-to-port area ratio exhibited stronger damping capability for combustion instability.

Figure 14.
Submerged nozzles with different throat-to-port area ratios.
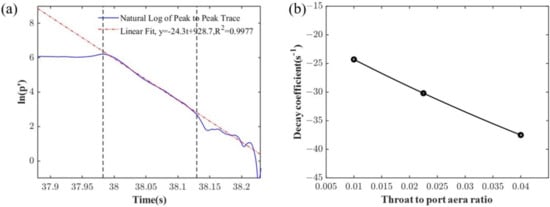
Figure 15.
The acoustic pressure under different throat-to-port area ratios. (a) = 5 mm; (b) The variation in the decay coefficient.
3.3. The Effect of Pressure on the Submerged Nozzle Damping
Finally, the impact of operating conditions on submerged nozzle damping performance was investigated. In the experiments, the combustor pressure was controlled by adjusting the main air supply flow rate. Increasing the main air supply pressure resulted in a corresponding increase in the pressure inside the combustor. The pressure of the secondary air supply was also adjusted to maintain the ratio of pressure oscillations to the average pressure of the combustion chamber constant. To elucidate the effect of mean pressure on submerged nozzle damping, three distinct cases (case 8, case 9 and case 10) were considered, with the relevant parameters outlined in Table 3. This systematic approach allows for a detailed analysis of the relationship between combustor pressure and damping characteristics.

Table 3.
Experimental setting parameters under different pressures.
Figure 16 illustrates the pressure variation in the combustion chamber at monitoring point 2. It was evident that an increase in the air supply pressure resulted in a high combustor pressure across cases 8 to 10.
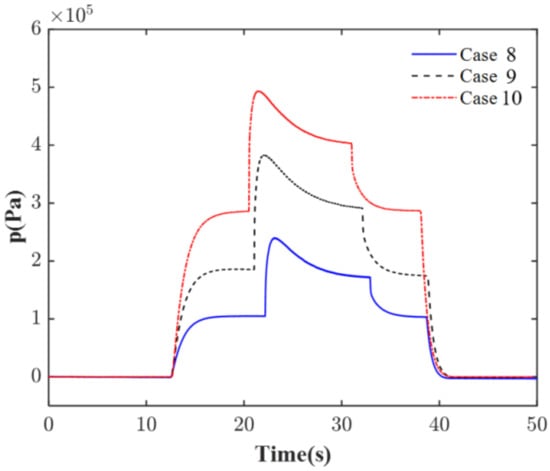
Figure 16.
Time evolution of the instantaneous pressure in the combustion chamber at monitoring point 2 under different mean pressures.
Figure 17a presents the temporal evolution of the acoustic pressure in the log scale for case 9. It can be seen that, at the initial stage when the rotary valves were turned off, the amplitude of the acoustic pressure exhibited distinct linear variations and we obtained good curve fitting to the decay of the acoustic pressure. The corresponding decay coefficients of case 9 and case 10 were obtained as −38.1 and −36.9. The results in Figure 17b indicate that the influence of mean pressure on acoustic damping was minimal and can be disregarded, even in the context of complex submerged nozzle configurations.
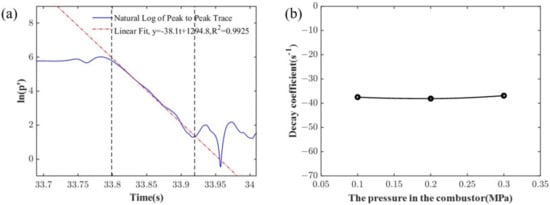
Figure 17.
The decay coefficient under different pressures. (a) Pressure of case 9; (b) The variation in the decay coefficient.
4. Conclusions
In the present work, the acoustic damping performance of submerged nozzles in solid rocket motors was studied experimentally, focusing on the effects of submerged nozzle geometry and operating conditions on the longitudinal combustion instability. The steady-state wave decay method was utilized to quantify the acoustic damping, and a rotary valve system was specifically designed to introduce periodic pressure oscillations in the high-pressure combustion chamber. The key findings were as follows:
- The submerged cavity dimensions exhibited an inverse relationship with nozzle damping efficiency. Enlarging the submerged cavity diminished the nozzle damping capability. Furthermore, it was found that eliminating the submerged cavity (relative to case S0) enhanced the nozzle decay coefficient magnitude by 41.9%.
- The nozzle convergent angle demonstrated a positive correlation with the nozzle decay coefficient. Increasing the convergent angle amplified acoustic wave reflection and consequently reduced the nozzle damping performance.
- A linear inverse relationship was observed between the throat-to-port area ratio and the decay coefficient. Quantitatively, a 125% increase in the throat-to-port area ratio resulted in a 24.3% reduction in the nozzle decay coefficient.
- Mean pressure variations within the operational range exhibited a negligible influence on the acoustic damping characteristics, even in complex submerged nozzle configurations. This suggests that the acoustic damping behavior remained consistent across typical operating pressures.
These results provided valuable experimental data for accurate evaluation of submerged nozzle damping and offered useful insights into the optimization of submerged nozzle designs for enhanced acoustic damping in solid rocket motors.
Author Contributions
Conceptualization, S.W.; Methodology, B.X.; Investigation, X.L. (Xiaosi Li); Resources, X.L. (Xiaosi Li); Data curation, Z.C.; Writing—original draft, X.L. (Xinyan Li) and Z.C.; Supervision, X.L. (Xinyan Li) and S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
Author Shengnan Wang was employed by the company China Academy of Aerospace Aerodynamics. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Casalis, G.; Boyer, G.; Radenac, E. Some recent advances in the instabilities occurring in long solid rocket motors. In Proceedings of the 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference Exhibit, San Diego, CA, USA, 3 August 2011. [Google Scholar]
- Hyun, W.; Kim, J.; Chae, H.; Lee, C. Passive Control of Low-Frequency Instability in Hybrid Rocket Combustion. Aerospace 2021, 8, 204. [Google Scholar] [CrossRef]
- Rayleigh, J.W.S.B. The Theory of Sound; MacMillan: London, UK, 1896. [Google Scholar]
- Culick, F.E.C. Combustion instabilities in solid propellant rocket motors. In Proceedings of the TO/VKI Special Course on “Internal Aerodynamics in Solid Rocket Propulsion”, Rhode-Saint-Genèse, Belgium, 27–31 May 2002. [Google Scholar]
- Price, E.W. Experimental solid rocket combustion instability. In Proceedings of the Symposium (International) on Combustion, Cambridge, UK, 17–21 August 1965; Volume 10, pp. 1067–1082. [Google Scholar]
- Hart, R.W.; McClure, F.T. Combustion instability: Acoustic interaction with a burning propellant surface. J. Chem. Phys. 1959, 30, 1501–1514. [Google Scholar] [CrossRef]
- Li, L.; Bao, F.; Wei, R.; Hou, K.; Shi, X. Research on oscillation response of Pressure-Combustion-Thrust System in Solid Rocket Motor. J. Aerosp. Eng. 2024, 37, 04024036. [Google Scholar] [CrossRef]
- O’Connor, J.; Acharya, V.; Lieuwen, T. Transverse combustion instabilities: Acoustic, fluid mechanic, and flame processes. Prog. Energy Combust. Sci. 2015, 49, 1–39. [Google Scholar] [CrossRef]
- Almayas, A.; Yaakob, M.S.; Aziz, F.A.; Yidris, N.; Ahmad, K.A. CFD application for solid propellant rocket simulation: A review. CFD Lett. 2021, 13, 84–95. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, P.; Ao, W. A reduced-order model of thermoacoustic instability in solid rocket motors. Aerosp. Sci. Technol. 2020, 97, 105615. [Google Scholar] [CrossRef]
- Xu, G.; Wang, B.; Guan, Y.; Wang, Z.; Liu, P. Early detection of thermoacoustic instability in a solid rocket motor: A generative adversarial network approach with limited data. Appl. Energy 2024, 373, 123776. [Google Scholar]
- Liu, J.; Wang, N.F.; Wang, J.; Li, Z.Y. Optimizing combustion performance in a solid rocket scramjet engine. Aerosp. Sci. Technol. 2020, 99, 105560. [Google Scholar] [CrossRef]
- Emelyanov, V.N.; Teterina, I.V.; Volkov, K.N.; Garkushev, A.U. Pressure oscillations and instability of working processes in the combustion chambers of solid rocket motors. Acta Astronaut. 2017, 135, 161–171. [Google Scholar]
- Poinsot, T. Prediction and control of combustion instabilities in real engines. Proc. Combust. Inst. 2017, 36, 1–28. [Google Scholar] [CrossRef]
- Lou, Y.; Ji, X.; Liu, P.; Yin, S.; Cao, Q.L. Critical Parametric Studies of Combustion Instability in Solid Rocket Motors. In Proceedings of the 2023 14th International Conference on Mechanical and Aerospace Engineering (ICMAE), Porto, Portugal, 18–21 July 2023; pp. 272–277. [Google Scholar]
- Li, X.; Zhao, D. Feedback control of self-sustained nonlinear combustion oscillations. J. Eng. Gas Turbines Power 2016, 138, 061505. [Google Scholar] [CrossRef]
- Li, X.; Zhao, D.; Yang, X.; Wen, H.; Jin, X.; Li, S.; Zhao, H.; Xie, C.; Liu, H. Transient growth of acoustical energy associated with mitigating thermoacoustic oscillations. Appl. Energy 2016, 169, 481–490. [Google Scholar] [CrossRef]
- Li, X.; Zhao, D.; Yang, X.; Wang, S. Unity maximum transient energy growth of heat-driven acoustic oscillations. Energy Convers. Manag. 2016, 116, 1–10. [Google Scholar] [CrossRef]
- Ji, S.; Wang, B.; Zhao, D. Numerical analysis on combustion instabilities in end-burning-grain solid rocket motors utilizing pressure-coupled response functions. Aerosp. Sci. Technol. 2020, 98, 105701. [Google Scholar] [CrossRef]
- Han, L.; Li, J.; Zhao, D.; Gu, X.; Ma, B.; Wang, N. Effects of baffle designs on damping acoustic oscillations in a solid rocket motor. Aerosp. Sci. Technol. 2021, 115, 106827. [Google Scholar] [CrossRef]
- Silva, C.F. Intrinsic thermoacoustic instabilities. Prog. Energy Combust. Sci. 2023, 95, 101065. [Google Scholar] [CrossRef]
- Mariappan, S.; Sujith, R.I. Thermoacoustic instability in a solid rocket motor: Non-normality and nonlinear instabilities. J. Fluid Mech. 2010, 653, 1–33. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, P.; Jin, B.; Ao, W. Nonlinear characteristics of the triggering combustion instabilities in solid rocket motors. Acta Astronaut. 2020, 176, 371–382. [Google Scholar] [CrossRef]
- Staschus, C.; Frederick, R.A. An Overview of Combustion Instabilities and Rocket Engine Injector Design. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016; p. 4724. [Google Scholar]
- Blomshield, F. Lessons learned in solid rocket combustion instability. In Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference Exhibit, Cincinnati, OH, USA, 8–11 July 2007; p. 5803. [Google Scholar]
- Zinn, B.T. Longitudinal mode acoustic losses in short nozzles. J. Sound Vib. 1972, 22, 93–105. [Google Scholar] [CrossRef]
- Kalyana Chakravarthy, V.; Iyer, A.S.; Chakraborty, D. Quasi-one-dimensional modeling of internal ballistics and axial acoustics in solid rocket Motors. J. Propuls. Power 2016, 32, 882–891. [Google Scholar] [CrossRef]
- Zhang, Q.; Wei, Z.J.; Su, W.X.; Li, J.W.; Wang, N.F. Theoretical modeling and numerical study for thrust-oscillation characteristicsin solid rocket motors. J. Propuls. Power 2012, 28, 312–322. [Google Scholar] [CrossRef]
- Anthoine, J.; Buchlin, J.M.; Hirschberg, A. Effect of nozzle cavity on resonance in large SRM: Theoretical modeling. J. Propuls. Power 2002, 18, 304–311. [Google Scholar] [CrossRef]
- Sun, B.B.; Li, S.P.; Su, W.X.; Li, J.W.; Wang, N.F. Effects of gas temperature on nozzle damping experiments on cold-flow rocket motors. Acta Astronaut. 2016, 126, 18–26. [Google Scholar] [CrossRef]
- Janardan, B.A.; Zinn, B.T. Rocket nozzle damping characteristics measured using different experimental techniques. AIAA J. 1977, 15, 442–444. [Google Scholar] [CrossRef]
- Crocco, L.; Monti, R.; Grey, J. Verification of nozzle admittance theory by direct measurement of the admittance parameter. ARS J. 1961, 31, 771–775. [Google Scholar] [CrossRef]
- Zinn, B.T.; Bell, W.A.; Daniel, B.R.; Smith, A., Jr. Experimental determination of three-dimensional liquid rocket nozzleadmittances. AIAA J. 1973, 11, 267–272. [Google Scholar] [CrossRef]
- Janardan, B.A.; Daniel, B.R.; Zinn, B.T. Damping of axial instabilities by small-scale nozzles under cold-flow conditions. J. Spacecr. Rocket. 1974, 11, 812–820. [Google Scholar] [CrossRef]
- Buffum, F.G., Jr.; Dehority, G.L.; Slates, R.O.; Price, E.W. Acoustic attenuation experiments on subscale, cold-flow rocket motors. AIAA J. 1967, 5, 272–280. [Google Scholar] [CrossRef]
- Sattelmayer, T.; Kathan, R.; Köglmeier, S.; Kaess, R.; Nicole, A. Validation of transverse instability damping computations for rocket engines. J. Propuls. Power 2015, 31, 1148–1158. [Google Scholar] [CrossRef]
- Price, T.J. Experimental Investigation of Transverse Mode Nozzle Damping. Master’s Thesis, University of Tennessee, Tennessee, TN, USA, 2017. [Google Scholar]
- Li, X.; Pang, K.; Li, X. The Submerged Nozzle Damping Characteristics in Solid Rocket Motor. Aerospace 2023, 10, 191. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).