Abstract
In this article, five feedback magnetic attitude control algorithms are compared in terms of stabilization accuracy and implementation problems. The control strategies are classic Lyapunov control with scalar gain; the same control strategy with matrix gain and a specific gain-tuning procedure; sliding control with a variable surface; a linear quadratic regulator constructed for a special time-invariant system of a higher degree than the initial time-varying system; and a special controllable trajectory developed using particle swarm optimization. A new sliding surface construction method is proposed in this paper. Surface parameters were changed in every control iteration to ensure that the required control torque component along the geomagnetic induction vector was small. The advantages and drawbacks of the considered methods and their applicability for different target attitudes are discussed.
1. Introduction
Magnetic attitude control systems significantly reduce satellite resource usage compared to reaction wheels. As such, their implementation in CubeSats is a long-sought goal. Three-axis stabilization suffers from low terminal accuracy both in the orbital (local vertical) and inertial reference frames. Magnetic control systems excel at certain specific tasks. Angular velocity damping can be effectively performed after a satellite’s separation from the launch vehicle [1,2]. Likewise, it is used for the unloading of the reaction wheels’ angular momentum. Magnetic damping may be used to achieve semi-passive stabilization along the local vertical frame, together with gravitational [3] torque; along the velocity of the satellite, together with aerodynamic torque [4,5]; and along the geomagnetic induction vector [6]. Spin-stabilized satellites [7,8,9], including stabilization towards the sun [10,11,12] for battery charging, provide high-accuracy solutions but only for one axis of a satellite.
Three-axis magnetic control is technically not restricted at terminal attitude, and this system is theoretically controllable [13,14,15]. In practice, achieving an arbitrary—far from the gravitational equilibrium—attitude in the orbital reference frame is challenging, and overall pointing accuracy is very low. The present paper compares five different control approaches for the three-axis stabilization of a satellite in the orbital reference frame. Although different, all control strategies essentially implement a feedback law.
The first considered control system is the simplest feedback law based on the Lyapunov function (Lyapunov control, denoted as LC throughout the text). Originally, this type of control was developed in both the inertial [16,17] and orbital [18,19] reference frames. The original Lyapunov control ensures asymptotic stability of the required attitude. Its magnetic counterpart, which is essentially the projection of the required torque on the plane perpendicular to the geomagnetic induction vector, does not benefit from global asymptotic stability properties. Careful control gain selection provides an asymptotically stable position [20]. However, the gain values and the resulting control torque are relatively low [21]. Stability is extremely sensitive to uncertainties in inertia tensor knowledge [22]. The gain can be found if the inertia moments and uncertainty are bounded [23]. Significant problems are encountered by satellites with elongated or disk-shaped ellipsoids of inertia. Among these are 3U CubeSats. This problem is leveraged using matrix control gain, distinguishing it from the second feedback control scheme considered in this paper (matrix Lyapunov control—MLC). This approach was first introduced in [18]. The gain selection procedure elaborated in [24] is utilized in the present paper.
The third control scheme is the sliding mode with special surface construction. Sliding control (SC) was first proposed for a magnetically actuated satellite in [25,26]. In [27,28], the respective authors introduce a sliding surface with an integral term representing control torque projection on the induction vector direction. This term is designed to minimize the inaccessible control component. This idea was directly investigated in [29] with varying sliding surface parameters. The sliding surface changes so that the resulting stabilizing torque lies almost within the plane perpendicular to the induction vector. However, terminal stabilization cannot be maintained with the developed procedure, which amplifies the typical chattering problem of sliding control. Therefore, the control is switched to the simple feedback law near the required attitude. The present paper introduces a new procedure for sliding surface construction. Compared to that reported in [29], this procedure minimizes the torque projection on the induction vector instead of directly restricting it so that it is equal to zero, thus leading to more robust behavior.
The fourth feedback method is based on the control construction procedure elaborated in [14]. The equations of motion are linearized in the vicinity of the required attitude. Linear equations of motion with periodic coefficients are transformed into time-invariant equations by changing the variables with larger state vectors. A linear quadratic regulator (LQR) is constructed for the time-invariant system. This directly provides the control dipole moment, not the control torque. It is then converted into initial variables to obtain the feedback for the time-varying system.
The fifth method generalizes the sliding surface construction idea into a direct search for the angular trajectory of the satellite near the required attitude. Each specific trajectory implies the need to account for specific control torque to satisfy the equations of motion. This torque projection on the induction vector is minimized using the particle swarm optimization method [30,31] to find the “most controllable” trajectory (particle swarm optimization control—PSO). Furthermore, simple feedback control is additionally introduced to settle on this trajectory. The trajectory near the required attitude has an inherent attitude error. However, the resulting error (the specific trajectory difference from the required attitude and the error in this trajectory maintenance) may be lower than the error of direct stabilization for the required attitude.
Each of the discussed feedback methods has its own advantages in different situations and inherent disadvantages. Simulation results are compared below to summarize the features of the five control methods and provide conclusions regarding the favorable application conditions of each method.
2. Equations of Motion and Environment Models
The satellite is stabilized in the orbital reference frame OX1X2X3. Its first axis lies in the orbital plane, and it is directed toward the satellite’s velocity vector in a near circular orbit. The second axis is positioned along the satellite’s normal orbit. The third axis is the radius vector of the satellite. The satellite reference frame OX1X2X3 is characterized by the principal central axes of inertia.
Euler’s equations of motion are shown below
where the symbol denotes a cross product; denotes the satellite inertia tensor; , , and are the gravitational, aerodynamic, and disturbing torque of an unknown nature; and is the control torque from the magnetic control system. Absolute angular velocity is related to the velocity relative to the orbital reference frame as represented below
where is the orbital angular velocity and is the orbital rate, while is the transition matrix from the orbital to the satellite reference frame. Note that throughout the text, bold letters correspond to matrices and vectors, while normal letters correspond to scalar values. The kinematics of the satellite are described in terms of the attitude quaternion derivative:
The control torque is expressed as
where is the control dipole moment. The geomagnetic induction vector was calculated using the IGRF model [32] in the numerical examples. The dipole model [33] was utilized in the feedback control gain adjustment procedure.
Gravitational torque is expressed as
where is the unit radius vector in the satellite reference frame.
Aerodynamic torque is calculated as the net torque acting on satellite surfaces facing the incoming flow. Atmospheric rotation with respect to the Earth is not considered. For the side with the normal vector , the force magnitude is expressed as
where is the drag coefficient, is surface area, is atmospheric density, and is the satellite’s velocity relative to the incoming flow. The torque acting on the side is expressed as follows:
The direction of the force is calculated according to the satellite’s attitude. Vector is the center-of-mass displacement relative to the center of pressure.
Other disturbing effects of a lower magnitude—solar radiation pressure, gravitational torque modification due to the Earth’s oblateness, etc.—are modelled as periodic torque of orbital and double orbital frequencies
where is the argument regarding latitude. Coefficients and are uniformly distributed in the range −1, 1. The magnitude is fitted so that the unknown disturbance is approximately one order of magnitude less than the gravitational torque magnitude.
The final important disturbance source is the inertia tensor uncertainty at the level of approximately 5% of the principal inertia moment values.
3. New Sliding Surface Design (SC Construction)
Sliding control [34] was utilized by the authors to create a control torque that is almost perpendicular to the geomagnetic induction vector [29]. The proposed surface was derived from the abovementioned condition . Thus, the control torque and therefore the sliding surface are significantly restricted in their parameters. This, in turn, leads to the significant deterioration of the control performance near the required attitude and for some specific mutual attitudes of the satellite and geomagnetic induction vector. To address this problem, a new sliding surface was developed, as shown below.
First, the equation of the surface is considered in the classic form
where the attitude error is expressed as the vector part of quaternion in this paper. Coefficient is introduced to simplify the resulting expressions. The positive definite matrix is variable, which is the major property of the proposed methodology. It depends on the current satellite attitude and the geomagnetic induction vector attitude, which, in turn, depend on time. This variation is necessary to achieve a “controllable” angular trajectory of the satellite characterized by . Matrix is referred to as the surface parameter below. Equation (4) operates using the relative angular velocity . The satellite is stabilized in the orbital reference frame in specific numerical examples provided in the paper. The same procedure was established for stabilization in the inertial space, and no significant difference was observed. The surface equation should evolve according to
where is a positive definite matrix. Substituting the surface Equation (4) into (5) leads to
The first derivative in Equation (6) is defined by the Euler equations of motion (1). The second derivative is defined by the kinematic relations (3). Note, however, that Equation (1) was derived for the absolute angular velocity, whereas Equation (6) requires the relative velocity derivative. Utilizing the relationship between the absolute and relative velocity (2), the following equations were derived for the latter,
where , and is a skew symmetric (cross product) matrix. Substituting (7) into (6) leads to
where only gravitational torque is considered and compensated for during the control construction process. The attitude error derivative is calculated from (3) as . The surface parameter derivative is approximated as a simple difference from two consecutive control iterations
Equation (8) is then formulated in the following form:
The left side of the Equation (9) has one unknown—the surface parameter in the current iteration . Its value defines the control torque . Vector contains known parameters: current satellite attitude and angular velocity and the surface parameter in the previous iteration.
The sliding control scheme developed in [29] suffers from rapid growth in the surface parameter when the condition is difficult to achieve. To avoid this situation, an optimization problem is formulated in this paper. First, a vector of the surface parameter matrix elements is introduced as . This vector contains only six parameters since matrix is symmetric. The cost function is shown below:
The first term indicates that the surface parameter should change as slowly as possible. The second term indicates that its elements should possibly decrease. Coefficient equals 100 in the example below.
The optimization problem utilizes three conditions:
- —the surface parameter is a positive definite matrix (moreover, eigenvalues should be less than a predefined threshold);
- —the control torque deviates from the plane perpendicular to the geomagnetic induction vector by no more than 10 degrees;
- <0.1 A·m2—the dipole moments are bounded.
Due to the typical values of the matrix elements, its eigenvalues are multiplied by 105 to ensure that the expressions in conditions 1 and 2 have approximately the same order. After the surface parameter matrix in the current iteration is calculated, the control torque is also calculated according to (9). It is then used to find the control dipole moment as a projection on the plane perpendicular to the geomagnetic induction vector . The same procedure is used during the optimization process to find the dipole moment in condition 3. The resulting control torque slightly differs from the calculated one . According to condition 2, the angle between the calculated and defined torques does not exceed 10 degrees. If the optimization procedure fails to find a feasible surface parameter and therefore the control torque with the defined restrictions, the control scheme is not implemented.
4. Description of the Feedback Laws Utilized for Comparison
Below is a brief description of four (excluding the sliding control scheme described above) feedback control strategies that are utilized in the comparison of their performance.
4.1. Lyapunov Control—LC
The simplest feedback control scheme is
where , and denotes the direction cosine matrix elements. This control scheme is derived from the Lyapunov function candidate and represents the simplest possible solution for three-axis satellite stabilization. Control scheme (10) does not ensure asymptotic stability for any positive control gain values. Gain should be carefully selected for each tensor of inertia and satellite orbit (altitude and inclination). A relevant procedure developed by this paper’s authors in [35] is used to find the gain values in the next section. In essence, the equations of motion are linearized near the required attitude:
Here, , , , , and are the attitude angles (rotation sequence 2-3-1), while , 7.7245∙106 T∙km3, and are periodic components of the geomagnetic induction vector in the dipole model. The linearized equations with periodic coefficients are examined for stability using Floquet theory [36].
4.2. Matrix Lyapunov Control—MLC
The natural extension of the feedback law (10) MLC scheme utilizes matrix control gain:
The derivation of the control law (10) from the Lyapunov function allows for positive definite matrix control gain. A gain search procedure for diagonal matrices was developed by the authors in [24]. This procedure uses the periodic linear Equation (11) and Floquet theory. However, each equation for has its own gain and on the right side. Control scheme (10) allows for convenient stability area visualization for two types of gain, whereas control scheme (12) operates with six parameters. Characteristic multiplier visualization with respect to gain is impossible. Therefore, an automatic procedure was established to find gain values that ensure the minimum possible number of characteristic multipliers.
4.3. Linear Quadratic Regulator—LQR
Special change of variables is used in the next control approach to turn the time-varying linear equations into time-invariant ones [14]. The general strategy of this method is as follows. The initial time-varying linear equations are
State vector comprises the attitude angles and velocity components. The specific expressions for the matrices in (13) for a magnetically actuated satellite can be found in [14]. Control matrix is periodic. Through the change in variables from
time-invariant equations can be obtained. These equations have more dimensions: instead of six variables, there are eighteen. However, some of these variables are uncontrollable or do not affect the initial system. Finally, a time-invariant system can be obtained:
Here, and , so only two magnetorquers are required for stabilization. A linear quadratic regulator is constructed for this system, defined as , where the gain matrix is calculated via solving the classic Riccati equation. The vector of the initial variable is augmented with two auxiliary variables, and , so . This is necessary to construct a scheme for the proper univocal change in variables and the following final control scheme:
Note that this method retains two auxiliary variables, and , in the final form of the equations of motion with control. These two variables are in essence the control parameters. They are calculated for each control step according to specific equations.
4.4. Particle Swarm Optimization—PSO
Finally, a special angular trajectory construction procedure is considered. The required satellite motion is parametrized as
where coefficients , , and should be found according to two main rules. First, they must be small, a few degrees each, to allow for precise stabilization. Second, the control torque that stabilizes the satellite in this trajectory should be as close as possible to the plane perpendicular to the geomagnetic induction vector, so . This generally leads to the formulation of an optimization problem with constraints.
To solve this problem, a particle swarm optimization routine [37] was established. The cost function is
where is the number of control iterations, and the required control torque is calculated from (1) as
The gravitational
torque is calculated for the reference trajectory (15). The reference angular
velocity is essentially the
derivative of the trajectory. The attitude angles in (15) are used to calculate
the attitude quaternion and then calculate the relative reference velocity from the quaternion
kinematics (3). The relationship between the absolute and relative velocities
(2) is used to find . Aerodynamic torque is not included in the control scheme’s construction, as the examples below are presented for a 550 km orbit. Control scheme (16) only ensures the existence of the required trajectory (15). To settle on this trajectory, control scheme (10) is utilized in the form given below
where defines the difference between the actual angular velocity or attitude and the reference one. The control gain of the feedback law (17) is found using another particle swarm optimization routine. The optimization objective is to minimize the maximum characteristic multiplier.
5. Simulation Results for Different Control Strategies
Simulations of satellite motion were performed using the following parameters:
- Satellite inertia moments of 0.15 (Case 1) or 0.2 (Case 2), 0.13, and 0.11 kg·m2 (the satellite is stabilized in the unstable gravitational equilibrium position);
- Orbit altitude of 550 km, inclination of 57°, and eccentricity equal to 0.01;
- Aerodynamic torque calculation:
- ○
- Satellite size is 10 × 20 × 30 cm;
- ○
- Center-of-mass displacement is 1 cm along the second satellite axis (aerodynamic torque is essentially non zero in the required attitude);
- ○
- Atmospheric density is 1.8·10−13 kg/m3;
- Principal moments of inertia are subject to 5% error.
These parameters refer to a generic small satellite launched in a low Earth orbit. The results on the circumpolar (sun-synchronous) orbit are generally the same. Orbit altitude has a significant impact on the stabilization results. A 550 km orbit was chosen to impose a relatively strong aerodynamic torque influence. At the same time, it does not lead to the drastic deterioration in the control performance that is observed in a 350 km orbit. Two inertia tensors are considered to represent satellites with relatively uniform mass distributions and with significant unbalance, where the moment of inertia along the first axis is close to the sum of two other moments. First, the control gain for the LC feedback law (10) should be established. Characteristic multipliers of the linearized equations of motion are presented in Figure 1 for Case 2.
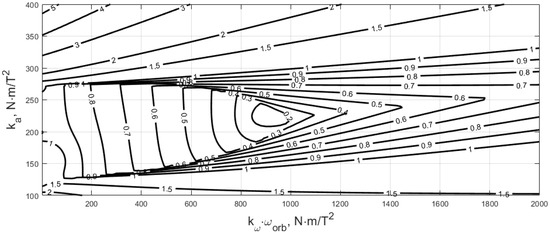
Figure 1.
Control gain of LC for the satellite with significantly uneven mass distribution, Case 2.
The simulations below utilize control gain values of = 460/ N·m/T2, = 150 N·m/T2 for Case 1 and = 360/ N·m/T2, = 220 N·m/T2 for Case 2. Damping gain is significantly shifted to the left compared to the theoretically best positions in terms of the degree of stability. The best characteristic multipliers are shown at ≈ 900/ N·m/T2 in Figure 1, whereas the manually adjusted “best” value is 360/ N·m/T2.
In Figure 2, the results for the LC (10) and SC are compared for the settling period, when the satellite approaches the required attitude. The brown line in Figure 2 represents the feedback law (10) results. The black line corresponds to the sliding control (9). The vertical, red, dotted line indicates the switching moment, when the satellite is close to the required attitude and SC is replaced with LC. Figure 2 reveals a decrease in the settling time duration for the sliding control. Lyapunov magnetic control is always characterized by a small control dipole moment. This is due to the fact that the designed control torque is not directly implemented—only its projection on the plane perpendicular to the geomagnetic induction vector. The sliding surface construction procedure ensures that (although no feasible point was found in approximately 10% of iterations in the considered example). The control torque (9) was implemented almost exactly as it was designed, with a difference of no more than 10 degrees. As a result, the control dipole moment was higher by a factor in the sliding control scheme presented in Section 3. However, it has its own disadvantages compared to the simple Lyapunov feedback law (10). The optimization routine requires extensive computational effort. The control scheme is significantly non-smooth, which can be examined by referring to the angular velocity curve in Figure 2. Most importantly, the developed sliding control cannot be used near the required attitude, so the final accuracy is the same as that for control scheme (10) or whichever control scheme is used near the required attitude.
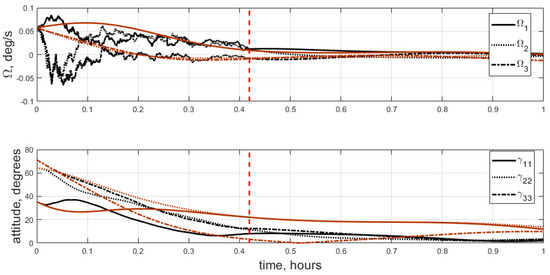
Figure 2.
Comparison of LC and SC, Case 1.
Figure 3 provides the results for the LC feedback law (10) for satellite Case 2 with a notable difference in inertia moments. Figure 4 shows the results for the same situation but also with uncertainty in inertia tensor knowledge.
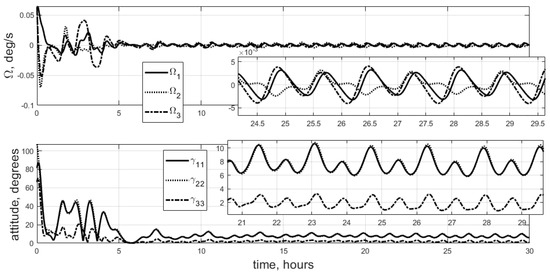
Figure 3.
Lyapunov control, Case 2.
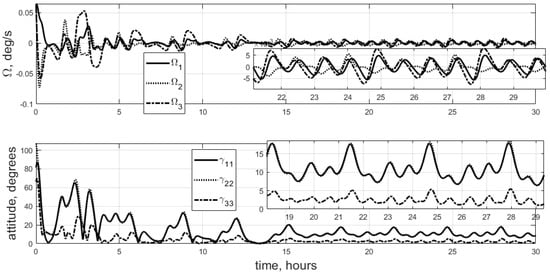
Figure 4.
Lyapunov control with inertia moment uncertainty, Case 2.
The stabilization accuracy for an uneven mass distribution is around 11–12 degrees, whereas Case 1 provides 7-degree accuracy. Final accuracy is significantly affected by the relations between the moments of inertia. In some specific situations, control scheme (10) may completely fail. For example, a 3U CubeSat with two large moments of inertia and one small moment of inertia quite often cannot be stabilized with simple Lyapunov control. A comparison of Figure 3 and Figure 4 highlights the influence of even small uncertainty in inertia tensor knowledge. The control gain in (10) is highly sensitive to satellite inertia, and Figure 1 may change significantly even after a small change in the inertia moment. Low accuracy, high sensitivity to inertia moment uncertainty, and low performance for satellites with highly uneven mass distributions are notable disadvantages of Lyapunov control scheme (10). However, it is very simple and transparent.
Its modification, MLC (12), shows lower stabilization accuracy.
The stabilization accuracy in Figure 5 is only 30 degrees. This is the main disadvantage of the considered control strategy. Theoretically, matrix control gain includes scalar gain as a special case. As such, control scheme (12) is capable of exhibiting at least the same performance as control scheme (10). However, the gain values utilized in Figure 2, Figure 3 and Figure 4 differ significantly from theoretically best gain in Figure 1. The lowest characteristic multiplier is characterized by the best degree of stability. This does not necessarily mean the best stabilization accuracy. Figure 1 provides the area of sensible control gain, which is then manually adjusted. This cannot be performed manually with matrix gain. However, control scheme (12) has distinct advantages over (10). Matrix gain is capable of handling significant differences in inertia moments. Also, this control scheme stabilizes the satellite not only in the gravitational equilibrium but in any predefined attitude in the orbital frame. Simple feedback law struggles with this task.
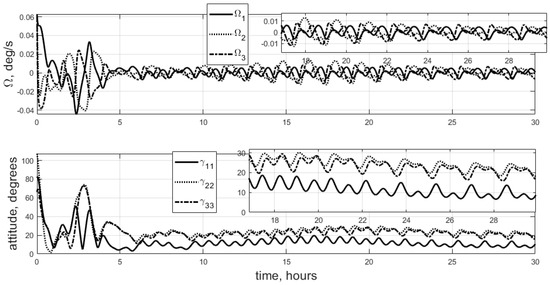
Figure 5.
MLC, Case 2.
LQR (14) performance is presented in Figure 6 for Case 1.
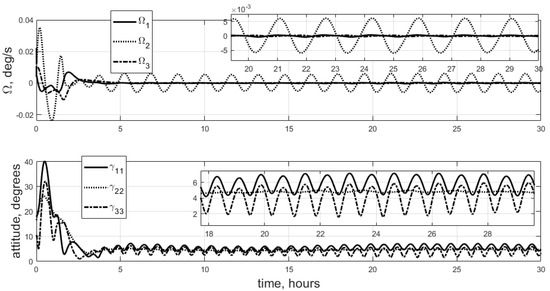
Figure 6.
LQR performance, Case 1.
The stabilization accuracy is the same as that for control scheme (10). The linear quadratic regulator with the change in variables described in Section 4 has one important advantage over simple feedback: it is possible to stabilize satellites with significantly uneven inertia moments. This control scheme operates with matrix control gain, so, similar to control scheme (12), it is possible to distinguish control channels with different “weights” represented by the inverse inertia moments. However, the described linear quadratic regulator only functions near the required attitude (although the neighborhood is slightly larger than the linear one), and it is sensitive to the uncertainty in inertia moment knowledge.
The last approach is a special “controllable” trajectory construction PSO strategy. The result is provided in Figure 7.
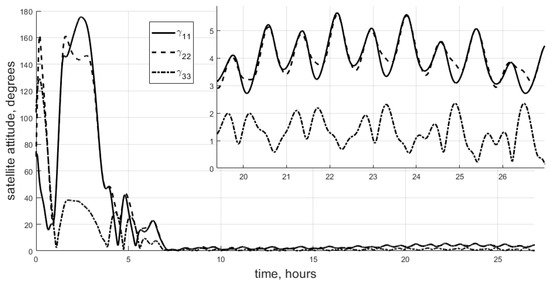
Figure 7.
Special trajectory construction with PSO, Case 2.
Figure 7 indicates approximately seven degrees accuracy for Case 2 with inertia tensor uncertainty. This control approach surpasses all others in terms of overall accuracy and does not suffer from problems with inertia moment relations. Due to the existence of a special trajectory construction procedure that incorporates gravitational torque, this approach can be used to stabilize a satellite in any attitude in the orbital frame. Although the gravitational torque is essentially non-zero in this case, the trajectory construction procedure ensures its successful rejection. The main disadvantage of this control strategy is its very-high computational demand.
6. Discussion and Conclusions
Five different strategies for three-axis magnetic attitude control are compared in this paper, including a new sliding control scheme with varying surface parameters. Feedback, or Lyapunov, control with scalar control gain shows moderate accuracy with a very simple structure and gain adjustment procedure. It suffers from inertia tensor uncertainty and an uneven mass distribution and struggles with stabilization when a satellite is not in the gravitational equilibrium position. The feedback law with matrix gain negates these disadvantages but requires specific computationally expensive optimization procedures to find proper gain matrixes and achieve the same accuracy as simple control with scalar gain. The linear quadratic regulator constructed for the time-invariant system in augmented space generally has the same properties as the feedback law with matrix gain but only operates in the vicinity of the required attitude. Sliding control provides faster convergence to the required attitude but fails to operate near it and requires an optimization problem solution. Being used together with any other approach, it has the corresponding control method accuracy. The best accuracy is achieved though the development of a special angular trajectory. Maintenance of this trajectory requires control torque that is almost perpendicular to the geomagnetic induction vector. This approach involves using a direct optimization method (particle swarm optimization) that cannot be run in real time onboard a satellite. Instead, it requires periodic (once every few orbits) uploading of the constructed trajectory and control parameters onboard, which significantly complicates mission maintenance.
Overall, the best control strategies are feedback with scalar gain due to its simplicity, feedback with matrix gain due to its ability to negate problems typical encountered with scalar gain (at the cost of a complicated and computationally demanding gain adjustment procedure), and special angular trajectory construction due to its high accuracy (at the cost of a complicated construction procedure and the necessity of periodically uploading new control parameters onboard).
These conclusions are based on the Figures provided in this paper. However, another important factor is control robustness toward variations in simulation conditions. One of the major and inherently varying factors is inertia tensor uncertainty. Different errors in inertia moment knowledge—even if they are on the same 5% level—can lead to the deterioration of t Lyapunov control performance (both with scalar and matrix gain). Different initial conditions affect sliding control schemes that strongly depend on the transient trajectory. On the contrary, particle swarm optimization is not sensitive to initial condition change. Despite this final note, the general conclusions regarding the best control strategies hold.
Author Contributions
Conceptualization, M.O. and D.R.; methodology, D.R.; software, D.R. and A.O.; formal analysis, D.R. and U.M.; writing—original draft preparation, D.R.; writing—review and editing, U.M. and M.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stickler, A.C.; Alfriend, K.T. Elementary Magnetic Attitude Control System. J. Spacecr. Rockets 1976, 13, 282–287. [Google Scholar] [CrossRef]
- Desouky, M.A.A.; Abdelkhalik, O. A new variant of the B-dot control for spacecraft magnetic detumbling. Acta Astronaut. 2020, 171, 14–22. [Google Scholar] [CrossRef]
- Ignatov, A.I.; Sazonov, V.V. Stabilization of the Gravitational Orientation Mode of an Artificial Earth Satellite (AES) by the Electromagnetic Control System. Cosm. Res. 2020, 58, 33–41. [Google Scholar] [CrossRef]
- Belokonov, I.V.; Timbai, I.A.; Nikolaev, P.N. Analysis and Synthesis of Motion of Aerodynamically Stabilized Nanosatellites of the CubeSat Design. Gyroscopy Navig. 2018, 9, 287–300. [Google Scholar] [CrossRef]
- Morozov, V.M.; Kalenova, V.I. Stabilization of Satellite Relative Equilibrium Using Magnetic Moments and Aerodynamic Forces. Cosm. Res. 2022, 60, 213–219. [Google Scholar] [CrossRef]
- Ignatov, A.I.; Sazonov, V.V. Investigation of Steady-State Motion of an Artificial Earth Satellite in the Uniaxial Magnetic Orientation Mode. Cosm. Res. 2021, 59, 112–125. [Google Scholar] [CrossRef]
- Avanzini, G.; de Angelis, E.L.; Giulietti, F. Spin-axis pointing of a magnetically actuated spacecraft. Acta Astronaut. 2014, 94, 493–501. [Google Scholar] [CrossRef]
- Slavinskis, A.; Kvell, U.; Kulu, E.; Sünter, I.; Kuuste, H.; Lätt, S.; Voormansik, K.; Noorma, M. High spin rate magnetic controller for nanosatellites. Acta Astronaut. 2014, 95, 218–226. [Google Scholar] [CrossRef]
- de Ruiter, A. A fault-tolerant magnetic spin stabilizing controller for the JC2Sat-FF mission. Acta Astronaut. 2011, 68, 160–171. [Google Scholar] [CrossRef]
- Roldugin, D.S. Stability of a Magnetically Actuated Satellite towards the Sun on a Sun-Synchronous Orbit. Cosm. Res. 2023, 61, 134–142. [Google Scholar] [CrossRef]
- Colagrossi, A.; Lavagna, M. A Spacecraft Attitude Determination and Control Algorithm for Solar Arrays Pointing Leveraging Sun Angle and Angular Rates Measurements. Algorithms 2022, 15, 29. [Google Scholar] [CrossRef]
- Roldugin, D.; Tkachev, S.; Ovchinnikov, M. Asymptotic Motion of a Satellite under the Action of Sdot Magnetic Attitude Control. Aerospace 2022, 9, 639. [Google Scholar] [CrossRef]
- Bhat, S.P. Controllability of nonlinear time-varying systems: Applications to spacecraft attitude control using magnetic actuation. IEEE Trans. Autom. Control 2005, 50, 1725–1735. [Google Scholar] [CrossRef]
- Morozov, V.M.; Kalenova, V.I. Satellite Control Using Magnetic Moments: Controllability and Stabilization Algorithms. Cosm. Res. 2020, 58, 158–166. [Google Scholar] [CrossRef]
- Liu, S.; Huang, Q. Controllability and observability of discretized satellite magnetic attitude control system. AIMS Math. 2023, 8, 7899–7916. [Google Scholar] [CrossRef]
- Lovera, M.; Astolfi, A. Spacecraft attitude control using magnetic actuators. Automatica 2004, 40, 1405–1414. [Google Scholar] [CrossRef]
- Lovera, M.; Astolfi, A. Global Magnetic Attitude Control of Inertially Pointing Spacecraft. J. Guid. Control Dyn. 2005, 28, 1065–1072. [Google Scholar] [CrossRef]
- Wisniewski, R.; Blanke, M. Fully magnetic attitude control for spacecraft subject to gravity gradient. Automatica 1999, 35, 1201–1214. [Google Scholar] [CrossRef]
- Damaren, C.J. Comments on “Fully magnetic attitude control for spacecraft subject to gravity gradient”. Automatica 2002, 38, 2189. [Google Scholar] [CrossRef]
- Celani, F. Gain Selection for Attitude Stabilization of Earth-Pointing Spacecraft Using Magnetorquers. Aerotec. Missili Spaz. 2021, 100, 15–24. [Google Scholar] [CrossRef]
- Rossa, F.D.; Bergamasco, M.; Lovera, M. Bifurcation analysis of the attitude dynamics for a magnetically controlled spacecraft. In Proceedings of the 51st IEEE Conference on Decision and Control, Maui, HI, USA, 10–13 December 2012; IEEE: Maui, HI, USA, 2012; pp. 1154–1159. [Google Scholar]
- Ivanov, D.S.; Ovchinnikov, M.Y.; Penkov, V.I.; Roldugin, D.S.; Doronin, D.M.; Ovchinnikov, A.V. Advanced numerical study of the three-axis magnetic attitude control and determination with uncertainties. Acta Astronaut. 2017, 132, 103–110. [Google Scholar] [CrossRef]
- Celani, F. Robust three-axis attitude stabilization for inertial pointing spacecraft using magnetorquers. Acta Astronaut. 2015, 107, 87–96. [Google Scholar] [CrossRef]
- Mashtakov, Y.V.; Ovchinnikov, M.Y.; Wöske, F.; Rievers, B.; List, M. Attitude determination & control system design for gravity recovery missions like GRACE. Acta Astronaut. 2020, 173, 172–182. [Google Scholar] [CrossRef]
- Wang, P.; Shtessel, Y.; Wang, Y.-Q. Satellite attitude control using only magnetorquers. In Proceedings of the 1998 American Control Conference, ACC, Philadelphia, PA, USA, 26–26 June 1998; pp. 500–504. [Google Scholar]
- Wisniewski, R. Sliding Mode Attitude Control for Magnetic Actuated Satellite. IFAC Proc. Vol. 1998, 31, 179–184. [Google Scholar] [CrossRef]
- Sofyalı, A.; Jafarov, E.M. Integral Sliding Mode Control of Small Satellite Attitude Motion by Purely Magnetic Actuation. IFAC Proc. Vol. 2014, 47, 7947–7953. [Google Scholar] [CrossRef]
- Sofyali, A.; Jafarov, E.M.; Wisniewski, R. Robust and global attitude stabilization of magnetically actuated spacecraft through sliding mode. Aerosp. Sci. Technol. 2018, 76, 91–104. [Google Scholar] [CrossRef]
- Ovchinnikov, M.Y.; Roldugin, D.S.; Penkov, V.I.; Tkachev, S.S.; Mashtakov, Y.V. Fully magnetic sliding mode control for acquiring three-axis attitude. Acta Astronaut. 2016, 121, 59–62. [Google Scholar] [CrossRef]
- Okhitina, A.; Roldugin, D.; Tkachev, S. Application of the PSO for the construction of a 3-axis stable magnetically actuated satellite angular motion. Acta Astronaut. 2022, 195, 86–97. [Google Scholar] [CrossRef]
- Okhitina, A.; Roldugin, D.; Tkachev, S.; Ovchinnikov, M. Academy transaction note “closed form solution for a minimum deviation magnetically controllable satellite angular trajectory”. Acta Astronaut. 2023, 203, 60–64. [Google Scholar] [CrossRef]
- Alken, P.; Thébault, E.; Beggan, C.D.; Amit, H.; Aubert, J.; Baerenzung, J.; Bondar, T.N.; Brown, W.J.; Califf, S.; Chambodut, A.; et al. International Geomagnetic Reference Field: The thirteenth generation. Earth Planets Space 2021, 73, 49. [Google Scholar] [CrossRef]
- Tikhonov, A.A.; Petrov, K.G. Multipole models of the earth’s magnetic field. Cosm. Res. 2002, 40, 203–212. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding Modes in Control and Optimization; Springer-Verlag: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Ovchinnikov, M.Y.; Roldugin, D.S.; Ivanov, D.S.; Penkov, V.I. Choosing control parameters for three axis magnetic stabilization in orbital frame. Acta Astronaut. 2015, 116, 74–77. [Google Scholar] [CrossRef]
- Malkin, I.G. Theory of Stability of Motion; U.S. Atomic Energy Commission, Technical Information Service: Oak Ridge, TN, USA, 1952. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).