Forecasting Inflation Uncertainty in the G7 Countries

Abstract

There is substantial evidence that inflation rates are characterized by long memory and nonlinearities. In this paper, we introduce a long-memory Smooth Transition AutoRegressive Fractionally Integrated Moving Average-Markov Switching Multifractal specification [$\mathrm{STARFIMA}(p,d,q)$-$\mathrm{MSM}\left(k\right)$] for modeling and forecasting inflation uncertainty. We first provide the statistical properties of the process and investigate the finite sample properties of the maximum likelihood estimators through simulation. Second, we evaluate the out-of-sample forecast performance of the model in forecasting inflation uncertainty in the G7 countries. Our empirical analysis demonstrates the superiority of the new model over the alternative $\mathrm{STARFIMA}(p,d,q)$-$\mathrm{GARCH}$-type models in forecasting inflation uncertainty.

1. Introduction

The financial crisis of 2007–2009 and the long-lasting economic recovery has renewed the interest in studying and measuring inflation uncertainty. Studies by Baker et al. (2015) and Jurado et al. (2015), for example, discuss new approaches to defining and measuring inflation and, more generally, macroeconomic uncertainty. Theoretical and empirical studies indicating that uncertainty negatively affects economic growth are well-documented in the literature (see Bernanke 1983; Bloom 2009, 2014; Stock and Watson 2012; Henzel and Rengel 2017). In this context, Stock and Watson (2012) find that liquidity risk and uncertainty shocks account for about two-thirds of the US GDP decline during the Great Recession. Bloom (2014) and Henzel and Rengel (2017) provide evidence for a countercyclical behavior of uncertainty. Gurkaynak and Wright (2012) and Wright (2011) argue that inflation uncertainty may explain the behavior of bond risk premia and thus plays a major role in understanding the different effects of monetary policy on short- and long-term interest rates. As stressed in Goodhart (1999) and Greenspan (2003), effective monetary policy purposes prevail as reliable, easy-to-update, and accurate measures of inflation uncertainty.

In spite of being inherently unobservable, inflation uncertainty can be estimated from econometric models. One of the most frequently used approaches to measuring inflation uncertainty consists of applying Engle’s (1982) AutoRegressive Conditional Heteroscedasticity (ARCH) processes and their generalized variants. These models are motivated by stylized facts on inflation uncertainty, in particular volatility clustering, high persistence, and asymmetry (see, among others, Baillie et al. 1996; Fountas et al. 2004; Karanasos and Schurer 2008; Caporale et al. 2012; Clements 2014; Makarova 2018). The popularity of GARCH-type models stems from their formal simplicity, flexibility, low computational costs, and their capacity to reproduce clustering effects. However, thorough investigations reveal that alternative inflation uncertainty measures (distinct absolute powers of inflation rates) typically exhibit structural dynamics and persistence patterns that GARCH-type models cannot reproduce. This leads to the question as to which econometric models may be appropriate for modeling (and producing accurate measures of) inflation uncertainty.

In this paper, we consider a new modeling approach by combining long-memory Smooth Transition AutoRegressive Fractionally Integrated Moving Average (STARFIMA) specifications with Markov Switching Multifractal (MSM) models, as recently developed by Calvet and Fisher (2004). MSM processes represent an alternative tool for modeling and forecasting volatility in financial and commodities markets, which regularly outperform GARCH-type models in out-of-sample forecasting evaluations (see Lux et al. 2016; Wang et al. 2016; Segnon et al. 2017). Owing to its formal construction, MSM models properly reproduce the structural dynamics observed in different absolute powers of inflation rates.1

The rest of the paper is organized as follows. Section 2 introduces the STARFIMA-MSM model. The statistical properties of the model are established in Section 3. Section 4 briefly outlines maximum likelihood estimation and optimal forecasting. Section 5 presents the data analysis for the G7 countries, forecasting methodologies, and the empirical results. Section 6 concludes.

2. The STARFIMA$(p,d,q)$-MSM$\left(k\right)$ Model

We define the STARFIMA$(p,d,q)$-MSM$\left(k\right)$ model to be a discrete-time stochastic process $\left\{x_t\right\}$ satisfying the equation

$${\Phi }_{s_t;\eta }\left(L\right){(1-L)}^d{x}_t=\Theta \left(L\right){ϵ}_t$$

(1)

where ${ϵ}_t|{\Omega }_{t-1}\sim N(0,h_t)$ and

$${\displaystyle h_t={\sigma }^2\prod _{j=1}^k{M}_t^{\left(j\right)}.}$$

(2)

In Equations (1) and (2), L denotes the lag operator and ${\Omega }_{t-1}$ is the $\sigma$-field generated by the information set $\{{ϵ}_{t-1},{ϵ}_{t-2},\dots \}$. The lag polynomials are defined as ${\Phi }_{s_t;\eta }\left(L\right)=1-{\varphi }_1(s_t;{\eta }_1)L-\cdots -{\varphi }_p(s_t;{\eta }_p)L^p$, where the p autoregressive coefficients ${\displaystyle {\varphi }_i\left(s_t,{\eta }_i\right)={\varphi }_{i0}+{\varphi }_{i1}G\left(s_t;\tau ,c\right)}$ are nonlinear functions of the state variable $s_t$. ${\eta }_i={\left({\varphi }_{i0},{\varphi }_{i1},\tau ,c\right)}^{\prime }$ is a vector of parameters, and $\Theta \left(L\right)=1+{\theta }_{1}L+\cdots +{\theta }_q{L}^q$. $d\in (-0.5,0.5)$ is a real number, and ${(1-L)}^d$ is the fractional differencing operator given by

$${\displaystyle {(1-L)}^d=\sum _{j=0}^{\infty }\frac{\Gamma (j-d)L^j}{\Gamma (-d)\Gamma (j+1)}}$$

(3)

where $\Gamma (·)$ denotes the gamma function.

In Equation (2), $M_t^{\left(1\right)},M_t^{\left(2\right)},\dots ,M_t^{\left(k\right)}$ denote the random volatility components (called multipliers). At date t, each multiplier $M_t^{\left(j\right)}$ is drawn from the base distribution M (to be specified) with positive support. Depending on its rank within the hierarchy of multipliers, $M_t^{\left(j\right)}$ changes from one period to the next with probability ${\gamma }_j$ and remains unchanged with probability $1-{\gamma }_j$. We specify these transition probabilities as

$${\displaystyle {\gamma }_j=2^{j-k},j=1,\dots ,k}$$

(4)

so that the transition matrix related to the jth multiplier is given by

$${\mathbf{P}}_j=\left(\begin{array}{cc}1-0.5{\gamma }_j& 0.5{\gamma }_j\\ 0.5{\gamma }_j& 1-0.5{\gamma }_j\end{array}\right).$$

In this paper, we draw each multiplier $M_t^{\left(j\right)}$ (in case of a change) from a binomial distribution with support $\{m_0,2-m_0\},1<m_0<2,$ and (binomial) probability $0.5$, implying the unconditional expectation $\mathbb{E}(M_t^{\left(j\right)})=1$. If we assume stochastic independence among the multipliers, the transition matrix of the vector ${\mathbf{M}}_t\equiv {(M_t^{\left(1\right)},\dots ,M_t^{\left(k\right)})}^{\prime }$ becomes the $2^k\times 2^k$ matrix $\mathbf{P}={\mathbf{P}}_1\otimes {\mathbf{P}}_2\otimes \cdots \otimes {\mathbf{P}}_k$, where ⊗ denotes the Kronecker product. Using the binomial base distribution for the single multipliers implies the finite support $\Gamma \equiv {\left\{m_0,2-m_0\right\}}^k$ for ${\mathbf{M}}_t$.

Remark 1.

The stochastic process in Equation (1) can be viewed as a special case of the model proposed by Hillebrand and Medeiros (2016) with constant conditional variance and multiple regimes. The process reduces to the linear AutoRegressive Fractionally Integrated Moving Average (ARFIMA) model, when setting ${\varphi }_i\left(s_t,{\eta }_i\right)={\varphi }_i$, $i=1,\dots ,p$. In this paper, we consider only two regimes, since this turns out to be sufficient in our empirical application below. We allow the conditional variance in Equation (2), which we model as the product of the time-varying multipliers and the positive scaling factor ${\sigma }^2$, to vary over time (see Calvet and Fisher 2004). As the transition function, we specify the first-order logistic function, $G(s_t;\tau ,c)={\left(1+exp\{-\tau (s_t-c)\}\right)}^{-1},\tau >0$, which is arbitrarily often differentiable and satisfies ${lim}_{s_t\to -\infty }G(s_t;\tau ,c)\to 0$ and ${lim}_{s_t\to +\infty }G(s_t;\tau ,c)\to 1$. For $\tau \to +\infty$ the function $G(s_t;\tau ,c)$ approaches the indicator function $\mathbf{1}(s_t>c)$. The parameter τ regulates the smoothness of the transition from one regime to another (cf. van Dijk et al. 2002).

Remark 2.

The transition probabilities defined in Equation (4) have been proposed by Lux (2008). This specification reduces the number of parameters to be estimated and enables us to obtain some statistical properties of the model. In Calvet and Fisher (2001), the k transition probabilities are specified as ${\gamma }_j=1-{(1-{\gamma }_1)}^{\left(b^{j-1}\right)}$ with ${\gamma }_1\in (0,1)$ and $b>1$, which guarantees the convergence of the discrete-time MSM model to the Poisson multifractal process in the continuous-time limit. Calvet and Fisher (2004) assume binomial and log-normal base distributions for the multipliers. Liu et al. (2007) find that assuming other base distributions, such as lognormal and gamma, makes little difference in empirical applications.

Our Markov-Switching Multifractal (MSM) volatility process as specified in Equations (2) and (4) could alternatively be specified as a GARCH-type process. In our out-of-sample forecasting analysis below, we compare the performance of our STARFIMA$(p,d,q)$-MSM$\left(k\right)$ model to that of a number of STARFIMA$(p,d,q)$-GARCH-type processes. He and Terasvirta (1999) propose a general class of GARCH$(1,1)$ models of the form

$$h_t^{\delta }=g\left(u_{t-1}\right)+c\left(u_{t-1}\right)h_{t-1}^{\delta }$$

(5)

with $\mathrm{Pr}(h_t^{\delta }>0)=1$, $\delta >0$, and where $\left\{u_t\right\}$ is a sequence of i.i.d. standard normal random variables, and $g\left(x\right),c\left(x\right)$ are nonnegative functions. This class of GARCH-type models includes, among others, the specifications of Bollerslev (1986) (standard GARCH), Glosten et al. (1993) (GJR-GARCH), Nelson (1991) (EGARCH), Sentana (1995) (QGARCH), and Ding et al. (1993) (APGARCH).

3. Statistical Properties

In this section, we consider statistical properties of the STARFIMA$(p,d,q)$-MSM$\left(k\right)$ and the general STARFIMA$(p,d,q)$-GARCH-type processes, as defined in Section 2.

Assumption .

The roots of the characteristic polynomials ${\Phi }_{s_t;\eta }\left(L\right)$ and $\Theta \left(L\right)$ lie outside the unit circle and the logistic transition function $G(s_t;\tau ,c)$ is well-defined.

Assumption 2.

The volatility components $M_t^{\left(1\right)},M_t^{\left(2\right)},\dots ,M_{\left(t\right)}^k$ with $\mathbb{E}(M_t^{\left(1\right)})=\dots \mathbb{E}(M_t^{\left(k\right)})=1$ are nonnegative and independent of each other for all t, and for the transition probabilities, we have ${\gamma }_1,\dots ,{\gamma }_k\in (0,1)$.

Proposition 1.

Under Assumptions 1 and 2, the STARFIMA$(p,d,q)$-MSM$\left(k\right)$ model defined in Equations (1)–(4) has a unique, second-order stationary solution. It follows that $\left\{x_t\right\},\left\{{ϵ}_t\right\},and\left\{h_t\right\}$ are strictly stationary, ergodic, and invertible.

Proof. 

Under Assumption 2, the conditions of Theorem 1 in (Shiryaev 1995, p. 118) are satisfied. It follows that the Markov chain underlying the dynamics of the multipliers $M_t^{\left(1\right)},\dots ,M_t^{\left(k\right)}$ is geometrically ergodic. The probabilities of the ergodic distribution are given by ${\pi }_l=1/2^k$, $l=1,\dots ,2^k$. Under Assumptions 1 and 2, $\left\{x_t\right\},\left\{{ϵ}_t\right\},and\left\{h_t\right\}$ are strictly stationary, ergodic, and invertible. ☐

Proposition 2.

Under Assumption 1, the STARFIMA(p,d,q)-GARCH model specified in Equations (1), (3), and (5) has a unique, $\alpha \delta$-order stationary solution (α a positive integer). It follows that $\left\{x_t\right\},\left\{{ϵ}_t\right\},and\left\{h_t\right\}$ are strictly stationary, ergodic, and invertible.

Proof. 

The proof follows from Assumption 1 and the conditions in Theorem 2.1 of Ling and McAleer (2002a), where we replace the constant mean process with our stationary STARFIMA$(p,d,q)$ process from Equations (1) and (3). ☐

Proposition 3.

Under Proposition 1 and with m denoting a positive integer, it follows that the $2m$-th moments of $\left\{x_t\right\}and\left\{{ϵ}_t\right\}$ are finite.

Proof. 

The proof follows from Proposition 1 and the conditions in Theorem 1 in Shiryaev (1995, p. 118). ☐

Proposition 4.

Under Proposition 2, it follows that the $m\delta$-th moments of $\left\{x_t\right\},\left\{{ϵ}_t\right\}$ exist.

Proof. 

The proof follows from Proposition 2 and Theorem $2.2$ in Ling and McAleer (2002a). ☐

Remark 3.

Second moments and autocovariances of the MSM$\left(k\right)$ process for binomial and lognormal base distributions of the multipliers are given in Lux (2008). As argued in Ling and McAleer (2002a), Proposition 4 cannot easily be extended to higher-order generalized GARCH processes, as specified in Equation (5). However, Ling (1999) provides a sufficient condition for the existence of $2m$-th moments for the standard GARCH$(p,q)$ process. Ling and McAleer (2002b) establish necessary and sufficient higher-order moment conditions for standard GARCH$(p,q)$ and APARCH$(p,q)$ processes.

Next, we present results for (i) the autocorrelation function of the process $\left\{x_t\right\}$ from Equation (1), which we denote by $\rho \left(n\right)=\mathrm{Cov}(x_t,x_{t-n})/\mathrm{Var}\left(x_t\right)$, and (ii) the q-order autocorrelation function of the process ${ϵ}_t$ denoted by ${\rho }_q\left(n\right)=\mathrm{Cov}\left(\right|{ϵ}_t{|}^q,|{ϵ}_{t-n}{|}^q)/\mathrm{Var}(|{ϵ}_t{|}^q)$, for every moment q and every integer n. For this purpose, we consider the two arbitrary numbers ${\kappa }_1,{\kappa }_2\in (0,1),{\kappa }_1<{\kappa }_2$, which we use to define the following set of integers (as before, k denotes the number of volatility multipliers in Equation (2)): $S_k=\left\{n:{\kappa }_{1}k\le {log}_2\left(n\right)\le {\kappa }_{2}k\right\}$. It is easy to check that $S_k$ contains a wide range of intermediate lags.

Proposition 5.

Under Assumption 1, we have $\rho \left(n\right)\sim {c\left|n\right|}^{2d-1}$ as $n\to \infty$, where c is a real constant.

Proof. 

The proof follows from Proposition 2 and Theorem $2.4$ in Hosking (1981). ☐

Proposition 6.

Under Assumption 2, it follows that $ln{\rho }_q\left(n\right)\sim -\psi \left(q\right)lnn$ as $k\to \infty$, where $\psi \left(q\right)={log}_2\left(\frac{\mathbb{E}\left(M^q\right)}{{\left[\mathbb{E}\left(M^{q/2}\right)\right]}^2}\right)$. (M is a random variable distributed as the base distribution of the multipliers $M_t^{\left(1\right)},\dots ,M_t^{\left(k\right)}$).

Proof. 

The proof follows from Proposition 2 and the proof of Proposition 1 in Calvet and Fisher (2004). ☐

Remark 4.

MSM processes only exhibit apparent long memory with asymptotic hyperbolic decay in the autocorrelation of absolute powers over a finite horizon. This does not coincide with the traditional definition of long memory with asymptotic power-law behavior of the autocorrelation function in the limit or divergence of the spectral density (see Beran 1994).

4. Maximum Likelihood Estimation and Optimal Forecasting

4.1. Maximum Likelihood Estimation

Hillebrand and Medeiros (2016) suggest using Nonlinear Least Squares (NLS) for parameter estimation of the STARFIMA model. We collect all parameters of the STARFIMA specification in the vector $\mathit{\chi }$ and denote (i) an appropriately defined subset of the parameter space by $\Xi$ and (ii) the true parameter vector by ${\mathit{\chi }}_0$. Then, for a sample of T observations, the NLS estimator is given by

$$\widehat{\mathit{\chi }}=arg\underset{\mathit{\chi }\in \Xi }{min}\sum _{t=1}^T{ϵ}_t^2.$$

(6)

In the case of normally distributed innovations ${ϵ}_t$, NLS is equivalent to Maximum Likelihood Estimation (MLE), whereas for non-normal innovations NLS can be interpreted as Quasi MLE (QMLE). Wooldridge (1994), Pötscher and Prucha (1997), and Hillebrand and Medeiros (2016) show that the NLS estimator is consistent and asymptotically normal under appropriate regularity conditions. Li and McLeod (1986) derive asymptotic properties of the MLE for the ARFIMA processes, and a portmanteau test for checking model adequacy.

Proposition 7.

Let $\widehat{\mathit{\chi }}$ be the solution to the minimization problem (6). Under Assumption 1, it follows that $\widehat{\mathit{\chi }}$ is (i) a consistent estimator of ${\mathit{\chi }}_0$ and (ii) asymptotically normal.

Proof. 

Under Assumption 1, the conditions of Theorems 1 and 2 in Hillebrand and Medeiros (2016) are satisfied, yielding the proof. ☐

Using a binomial base distribution for the k multipliers, Calvet and Fisher (2004) derive a closed-form solution for the log-likelihood and exact ML estimators of the parameters in the MSM(k) model. In fact, discrete base distributions with positive support for the multipliers imply a finite number of states for the hidden Markov process in the MSM model. This allows us to derive the exact likelihood function via Bayesian updating. For pre-specified k, it is known that the MLE is consistent and asymptotically efficient.

Since the off-diagonal blocks in the information matrix of a $\mathrm{STARFIMA}(p,d,q)$-$\mathrm{MSM}\left(k\right)$ model are zero, the parameters in the STARFIMA$(p,d,q)$ and MSM$\left(k\right)$ specifications can be estimated separately, without asymptotic efficiency loss (see Lundbergh and Terasvirta 1999). Therefore, in a first stage, we estimate the conditional mean via NLS, thus providing consistent estimates of the ${ϵ}_t$’s, which we use in the second stage to estimate the parameters of the conditional variance from the specification

$${\widehat{ϵ}}_t=u_t\sqrt{h_t}.$$

(7)

Denoting the parameter vector by $\mathit{\xi }={(m_0,\sigma )}^{\prime }$ (defined on a compact subset of the parameter space), we obtain the parameters in the second stage by maximizing the log-likelihood

$$\begin{array}{c}\widehat{\mathit{\xi }}=arg\underset{\mathit{\xi }}{max}\sum _{i=1}^{T}ln\left[\mathit{\omega }({\widehat{ϵ}}_t;\mathit{\xi })\left({\pi }_{t-1}\mathbf{P}\right)\right].\end{array}$$

(8)

In Equation (8), $\mathit{\omega }({\widehat{ϵ}}_t;\mathit{\xi })$ is a $1\times 2^k$ vector containing the conditional densities of any observation ${\widehat{ϵ}}_t$ given by

$$f\left({\widehat{ϵ}}_t\right|{\mathbf{M}}_t={\mathbf{m}}_j)=\frac{1}{h\left({\mathbf{m}}_j\right)}\varphi \left(\frac{{\widehat{ϵ}}_t}{h\left({\mathbf{m}}_j\right)}\right)$$

(9)

where $\varphi (·)$ denotes the standard normal density and $h\left({\mathbf{m}}_j\right)=\sigma \sqrt{{\prod }_{i=1}^k{m}_j^{\left(i\right)}}$ with $m_j^{\left(i\right)}$ being the i-th element of vector ${\mathbf{m}}_j$. The transition matrix $\mathbf{P}$ has the components ${\displaystyle p_{i,j}=\mathrm{Pr}({\mathbf{M}}_{t+1}={\mathbf{m}}^j|{\mathbf{M}}_t={\mathbf{m}}^i)}$. ${\mathbf{M}}_t$ is latent, but we can recursively compute the conditional probabilities ${\pi }_t^i=Pr({\mathbf{M}}_t={\mathbf{m}}^i|{\widehat{ϵ}}_t,\dots ,{\widehat{ϵ}}_1)$ through Bayesian updating as

$${\pi }_t=\frac{\mathit{\omega }({\widehat{ϵ}}_t;\mathit{\xi })·\left({\pi }_{t-1}\mathbf{P}\right)}{\sum \mathit{\omega }({\widehat{ϵ}}_t;\mathit{\xi })·\left({\pi }_{t-1}\mathbf{P}\right)}.$$

(10)

Proposition 8.

Let $\mathit{\vartheta }={({\mathit{\chi }}^{\prime },{\mathit{\xi }}^{\prime })}^{\prime }$ denote the complete parameter vector of the STARFIMA($p,d,q$)-MSM(k) model. Under Assumptions 1 and 2 and Propositions 3 and 4, there exists an MLE $\widehat{\mathit{\vartheta }}$ that is consistent and asymptotically efficient.

Proof. 

Under the given assumptions, the conditions of Theorem 1 in Hillebrand and Medeiros (2016) are met, yielding the proof. ☐

Remark 5.

The shortcoming of the exact MLE is that it becomes computationally demanding for a large number of multipliers $(k>10)$. Furthermore, a continuous base distribution with positive support for the multipliers implies an infinite state space of the hidden Markov chain, so that the MLE is not applicable. To circumvent these issues, Lux (2008) proposes a generalized method-of-moments estimator with linear forecasting. Recently, Žikeš et al. (2017) established the Whittle estimation approach.

In Section 4.3, we show that numerical optimization of the MSM(k) log-likelihood function produces satisfactory results for a moderate number of volatility components.

4.2. Optimal Forecasting

Using the maximum likelihood estimation approach, we easily obtain volatility forecasts in the MSM(k) model via Bayesian updating of the conditional probabilities. The h-step-ahead volatility forecasts of the MSM$\left(k\right)$ model are given by

$$\mathbb{E}\left(h_{t+h}\right|{\Omega }_t)={\widehat{\sigma }}^2\prod _{j=1}^k\mathbb{E}(M_{t+h}^{\left(j\right)}|{\Omega }_t).$$

(11)

In fact, to produce volatility forecasts over arbitrary, long-term horizons as given in Equation (11), we need the conditional probabilities of future multipliers. These conditional state probabilities can be iterated forward via the transition matrix $\mathbf{P}$ as follows:

$${\widehat{\pi }}_{t,t+h}={\pi }_t{\mathbf{P}}^h.$$

(12)

For GARCH-type models the formula for the h-step-ahead volatility forecasts are available in the literature (see, for example, Lux et al. 2016, Appendix A).

4.3. Monte Carlo Simulation

We assess the robustness of the MLE in small samples via Monte Carlo simulations. We choose the number of volatility components as $k=8$, which turns out to be optimal in our empirical application below.2 As the base distribution, we consider a binomial distribution taking on the values $m_0$ and 2 − $m_0$ each with probability $0.5$. Along with the switching probabilities from Equation (4), our simulation of the MSM model only requires two parameters: the binomial parameter $m_0$ and the scale factor (unconditional standard deviation) $\sigma$, which we normalize to unity. We simulate 500 independent sample paths of our restricted MSM model for (i) the three different binomial parameters $m_0\in \{1.1,1.2,1.3\}$ and (ii) the three different sample sizes $T\in \{250,500,1000\}$.

Table 1 reports the Monte Carlo maximum likelihood estimation results for small sample sizes. The first two rows provide the average bias and the mean squared error (MSE) of the parameter estimates, relative to the true parameters. The results of the ML estimation appear reasonable and exhibit a decrease in the MSEs with increasing sample size T. From $T_1=250$ to $T_2=500$, the MSEs decrease roughly with a factor of about 2. Overall, our Monte Carlo simulation demonstrates that ML estimation produces reliable results.

Table 1. Monte-Carlo maximum-likelihood-estimation results for small sample sizes.

	${\mathit{m}}_0=1.1$			${\mathit{m}}_0=1.2$			${\mathit{m}}_0=1.3$
	${\mathit{T}}_{\mathbf{1}}=\mathbf{250}$	${\mathit{T}}_{\mathbf{2}}=\mathbf{500}$	${\mathit{T}}_{\mathbf{3}}=\mathbf{1000}$	${\mathit{T}}_{\mathbf{1}}=\mathbf{250}$	${\mathit{T}}_{\mathbf{2}}=\mathbf{500}$	${\mathit{T}}_{\mathbf{3}}=\mathbf{1000}$	${\mathit{T}}_{\mathbf{1}}=\mathbf{250}$	${\mathit{T}}_{\mathbf{2}}=\mathbf{500}$	${\mathit{T}}_{\mathbf{3}}=\mathbf{1000}$
	Binomial parameter
Bias	−0.036	−0.028	−0.010	−0.025	−0.023	−0.036	−0.022	−0.027	−0.018
MSE	0.005	0.003	0.001	0.004	0.002	0.002	0.003	0.002	0.001
	Scaling factor
Bias	−0.108	−0.072	−0.061	−0.214	−0.150	−0.105	−0.315	−0.232	−0.187
MSE	0.013	0.006	0.004	0.048	0.024	0.012	0.101	0.055	0.036

Note: The table reports average biases and mean-squared errors (MSEs) of parameter estimates from 500 MSM(k) simulation paths for $k=8$.

Next, we analyze the capacity of the MSM model for reproducing the statistics of empirical data. We first estimate the binomial parameter $m_0$ and the scaling factor ${\sigma }^2$ for each G7 country and then use the parameter estimates to simulate 500 independent sample paths with country-specific sample sizes corresponding to those from the empirical data. The country-specific averaged means, standard deviations, skewness and kurtosis values, and the Hurst exponents are reported in Table 2. Overall, the results indicate that the MSM model reproduces the inflation-rate characteristics accurately. We note, however, that the MSM model is not able to capture the asymmetric properties observed in the data.

Table 2. Simulated moments and Hurst exponents via the binomial MSM(k) model.

	G7 Countries
	US	UK	France	Germany	Italy	Canada	Japan
Mean	1.659 × 10${}^{-4}$	9.152 × 10${}^{-4}$	−5.509 × 10${}^{-4}$	4.574 × 10${}^{-4}$	0.001	−1.472× 10${}^{-4}$	−6.959 × 10${}^{-4}$
Standard deviation	0.283	0.260	0.317	0.224	0.281	0.365	0.737
Skewness	−6.932 × 10${}^{-4}$	0.032	−0.003	0.021	0.006	0.006	−0.029
Kurtosis	4.369	7.130	5.627	5.775	8.202	4.686	8.380
	Hurst Exponent for the G7 Countries
${ϵ}_t$	0.499	0.491	0.508	0.504	0.515	0.499	0.508
${ϵ}_t^2$	0.673	0.814	0.780	0.772	0.867	0.694	0.901
$|{ϵ}_t|$	0.630	0.773	0.766	0.721	0.813	0.673	0.848

Note: For each country, we estimate the parameters in the binomial MSM$\left(8\right)$ specification and use the estimates to simulate data with country-specific sample sizes corresponding to those of the estimated residuals from the STARFIMA model. The moments and Hurst exponents are averaged over the number of replications.

5. Empirical Application

5.1. Data

Our data set consists of seasonally adjusted consumer-price-index (CPI)-based inflation rates for the G-7 countries (USA, UK, Germany, France, Italy, Canada and Japan). The monthly data were compiled from the International Financial Statistics (IFS). Our data cover the following country-specific time spans: (i) January 1985–December 2015 for the USA, France, and Italy; (ii) January 1985–November 2015 for Canada and Japan; (iii) January 1989–December 2015 for UK; (iv) January 1992–December 2015 for Germany.

The descriptive statistics of the inflation rates are reported in Table 3. The inflation-rate time series exhibit positive skewness and excess kurtosis (greater than 3) for all G7 countries. This indicates a deviation from the normal distribution that is confirmed by the Jarque-Bera test. To test for stationarity, we apply the Phillips-Perron unit-root test, which does not reject the null hypothesis of a unit root at the 1% level for any of G7 countries (see Table 4). We also apply the KPSS test for the stationarity, the results of which are also reported in Table 4. Here, the null hypothesis of stationarity is rejected for all G7 countries at any conventional significance level. In order to analyze the decay in the tails of the unconditional distributions, we also disclose the country-specific tail indices in Table 3, which range between 2 and 13. For the USA, UK, France, Germany, Italy, and Canada, the tail indices are substantially larger than 2, indicating convergence under time-aggregation towards the normal distribution. For Japan, the tail index is close to 2, indicating that the unconditional distribution exhibits tail behavior like the normal distribution. The results of the ARCH tests in Table 3 suggest the presence of heteroscedasticity in the G7 inflation-rate time series. Figure 1 displays the inflation-rate series.

Table 3. Descriptive statistics of the G7 inflation-rate time series.

	US	UK	France	Germany	Italy	Canada	Japan
No. of Obs	696	324	696	288	696	695	695
Mean	3.778	2.643	4.582	1.771	6.004	3.815	3.157
Standard deviation	2.864	1.802	3.980	1.171	5.739	3.082	4.264
Skewness	1.536	1.395	1.238	1.482	1.424	1.248	2.206
Kurtosis	5.428	4.624	3.728	5.993	4.105	3.687	10.080
Tail index	7.688	11.719	12.251	6.720	10.922	13.050	2.09
$Q\left(8\right)$	4.825 × 10${}^3$	2.056 × 10${}^3$	4.769 × 10${}^3$	1.359 × 10${}^3$	5.123 E× 10${}^3$	5.030 × 10${}^3$	4.712 × 10${}^3$
ARCH(1)	685.983	309.386	684.018	271.658	684.284	684.306	660.613
Jarque-Bera	444.528	140.674	193.272	213.002	207.722	194.039	2.095 × 10${}^3$

Note: $Q\left(8\right)$ denotes the Ljung-Box test for serial correlation out to lag 8. ARCH(1) denotes the Engle test for ARCH effects at lag 1.

Table 4. Unit root tests for inflation time series.

	${\mathit{H}}_0:\mathit{I}\left(1\right)$			${\mathit{H}}_0:\mathit{I}\left(0\right)$
Country	PP	PP *		ST	ST *
US	−2.044	−1.876		3.634	6.001
UK	−1.851	−1.669		2.101	3.963
France	−2.225	−2.243		2.753	13.571
Germany	−3.357	−3.363		1.148	3.495
Italy	−1.728	−1.324		4.549	8.382
Canada	−2.052	−1.798		4.356	8.033
Japan	−3.119	−2.345		1.704	13.913

Note: PP and PP* represent the Phillips-Perron adjusted t-statistics of the lagged dependent variable in a regression with (i) intercept and time trend and (ii) intercept only. The critical values at the 1% level are $-\mathbf{3.975}$ and $-\mathbf{3.441}$. ST and ST${}^{*}$ denote the KPSS test statistics using residuals from regressions with (i) intercept and time trend and (ii) intercept only. The critical values at the 1% level are $\mathbf{0.216}$ and $\mathbf{0.739}$.

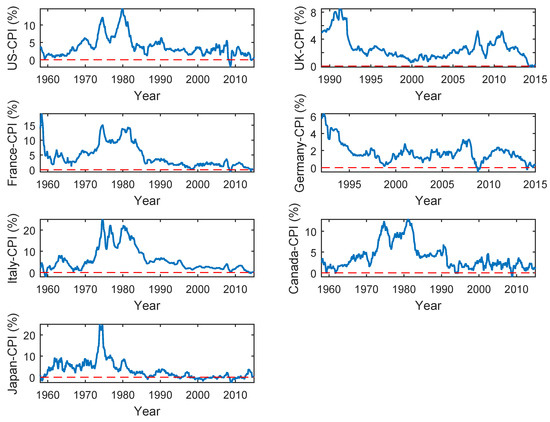
Figure 1. Consumer-price-index (CPI)-based inflation rates for the G7 countries.

5.2. Forecasting Methodology

To analyze the predictive ability of our proposed model in forecasting inflation uncertainty, we adopt a rolling forecasting scheme that keeps fixed the estimation sample size over the out-of-sample period and adds new (and removes old) observations on a monthly basis. We define the following in-sample (out-of-sample) periods: (i) January 1958–October 2009 (November 2009–November 2015) for the USA, Canada, and Japan; (ii) January 1989–November 2009 (December 2009–December 2015) for the UK; (iii) January 1958–November 2009 (December 2009–December 2015) for France and Italy; (iv) January 1992–November 2009 (December 2009–December 2015) for Germany. For each country and model specification, we consider inflation uncertainty forecasts for the horizons $h=1,2,3,4,5,6$ months. We consider the end of the global financial crisis 2007–2009 as the splitting point in our forecasting analysis.

In a first step, we first evaluate the forecasting performance of our specifications on the basis of two loss functions, (i) the mean squared error (MSE) and (ii) the mean absolute error (MAE), given by

$${\displaystyle \mathrm{MSE}=T^{-1}\sum _{i=1}^T{\left(h_{f,t}-{\sigma }_{a,t}^2\right)}^2}$$

(13)

$${\displaystyle \mathrm{MAE}=T^{-1}\sum _{i=1}^T\left|{\displaystyle h_{f,t}-{\sigma }_{a,t}^2}\right|}$$

(14)

with $h_{f,t}$ denoting the volatility forecast obtained from the binomial MSM or GARCH-type models, and ${\sigma }_{a,t}^2$ the monthly actual inflation uncertainty proxy obtained from the monthly squared residuals from suitably selected STARFIMA model specifications. (Here, T is the number of out-of-sample observations.)

Next, we use of the predictive ability tests of Hansen (2005) and Diebold and Mariano (1995) to test the relative forecasting performance of our proposed specification against competitor models. The Equal Predictive Ability (EPA) test of Diebold and Mariano (1995) enables us to directly compare the forecasting accuracy of two competing models (say, $M_1$ and $M_2$) under a predefined loss function. The null hypothesis of no difference in the forecasting accuracy between the competing models is stated as

$$\begin{array}{c}{H}_0:\mathbb{E}\left(d_t\right)=0\mathrm{for}\mathrm{all}t\end{array}$$

(15)

where $d_t=L\left({\epsilon }_{t,M_1}\right)-L\left({\epsilon }_{t,M_2}\right)$, with ${\epsilon }_{t,M_1}=h_{f,t,M_1}-{\sigma }_{a,t}^2$ and ${\epsilon }_{t,M_2}=h_{f,t,M_2}-{\sigma }_{a,t}^2$ denoting the forecast errors obtained from the models $M_1$ and $M_2$, respectively. The loss function $L(·)$ is either the squared error loss $L\left({\epsilon }_{t,M_i}\right)={\epsilon }_{t,M_i}^2$ or the absolute error loss $L\left({\epsilon }_{t,M_i}\right)=\left|{\epsilon }_{t,M_i}\right|$. The Diebold-Mariano test statistic is given by

$$\mathrm{EPA}=\overline{d}{\left[V\left(\overline{d}\right)\right]}^{-1/2}$$

(16)

where ${\displaystyle \overline{d}=T^{-1}\sum _{t=1}^T{d}_t}$, and $V\left(\overline{d}\right)=T^{-1}\left({\sum }_{j=-N}^N{\widehat{\gamma }}_j\right)$ is the heteroscedasticity and autocorrelation consistent (HAC) variance estimator. (${\widehat{\gamma }}_j$ is the estimate of the autocovariance function at lag j, N is the nearest integer larger than $T^{1/3}$.) Under the null hypothesis, the $EPA$ test statistic in Equation (16) is asymptotically standard normally distributed.

Based on the framework of the Reality Check (RC) proposed by White (2000), the Superior Predictive Ability (SPA) test of Hansen (2005) enables us to compare a benchmark forecast model, $M_0$, with K alternative competing models, $M_1,\dots ,M_K$, under predefined loss functions. The null hypothesis, stating that the benchmark model is not outperformed by any of the K competing models, is formalized as

$$\begin{array}{c}{H}_0:max\left\{\mathbb{E}\left(d_{t,M_1}\right),\dots ,\mathbb{E}\left(d_{t,M_K}\right)\right\}\le 0\mathrm{for}\mathrm{all}t\end{array}$$

(17)

where $d_{t,M_i}=L\left({\epsilon }_{t,M_0}\right)-L\left({\epsilon }_{t,M_i}\right)$ for $i=1,\dots ,K$ and $L(·)$ denotes either the squared-error or the absolute-error loss function, as defined above. To formally state the test statistic, we consider (i) the sample mean of the ith loss differential, ${\overline{d}}_{M_i}=1/T{\sum }_{t=1}^T{d}_{t,M_i}$, and (ii) the estimated variance $\widehat{Var}(\sqrt{T}·{\overline{d}}_{M_i})$ for $i=1,\dots ,K$. We refer the reader to Hansen (2005) for the technical details on how to estimate this latter variance by bootstrapping. To test the null hypothesis in Equation (17), we use the test statistic

$$\mathrm{SPA}=max\left\{\frac{\sqrt{T}{\overline{d}}_{M_1}}{\widehat{Var}\left(\sqrt{T}·{\overline{d}}_{M_1}\right)},\dots ,\frac{\sqrt{T}{\overline{d}}_{M_K}}{\widehat{Var}\left(\sqrt{T}·{\overline{d}}_{M_K}\right)}\right\},$$

(18)

the p-values of which can be obtained via a stationary bootstrap procedure.

5.3. Forecasting Results

The G7 country-specific root mean squared error (RMSE) and mean absolute error (MAE) values for alternative STARFIMA-MSM and STARFIMA-GARCH-type specifications at the forecasting horizons $h=1,2,3,4,5,6$ months are reported in Table 5, Table 6, Table 7 and Table 8. Instead of considering the general STARFIMA($p,d,q$) class in modeling our mean process, we restrict attention to two special cases, namely, the STARFI model (by setting $q=0$) and the ARFIMA model (by setting ${\varphi }_i(s_t,{\eta }_i)={\varphi }_i$ for $i=1,\dots ,p$ in the lag polynomial on the left side of Equation (1)).

Table 5. Root mean squared errors (RMSEs), mean process: AutoRegressive Fractionally Integrated Moving Average (ARFIMA).

Forecasting Horizons	1M		2M		3M		4M		5M		6M
Countries	GARCH
US	0.179		0.184		0.187		0.183		0.178		0.173
UK	0.110		0.115		0.120		0.123		0.124		0.126
France	0.065		0.065		0.066		0.067		0.068		0.069
Germany	0.078		0.077		0.076		0.069		0.068		0.066
Italy	0.076		0.078		0.078		0.078		0.078		0.078
Canada	0.213		0.210		0.210		0.211		0.209		0.209
Japan	0.512		0.510		0.509		0.508		0.505		0.506
	GJR
US	0.196		0.201		0.206		0.204		0.198		0.192
UK	0.117		0.119		0.121		0.125		0.128		0.130
France	0.063		0.064		0.065		0.067		0.067		0.069
Germany	0.082		0.081		0.079		0.073		0.072		0.071
Italy	0.076		0.077		0.077		0.078		0.078		0.078
Canada	0.213		0.210		0.210		0.211		0.210		0.209
Japan	0.513		0.511		0.509		0.507		0.504		0.504
	EGARCH
US	0.169		0.171		0.171		0.169		0.162		0.156
UK	0.117		0.115		0.116		0.116		0.116		0.117
France	0.078		0.083		0.079		0.082		0.080		0.081
Germany	0.085		0.084		0.082		0.077		0.075		0.073
Italy	0.078		0.078		0.079		0.080		0.080		0.080
Canada	0.215		0.210		0.210		0.210		0.211		0.211
Japan	0.505		0.503		0.502		0.500		0.498		0.497
	QGARCH
US	0.180		0.183		0.185		0.183		0.177		0.171
UK	0.103		0.104		0.106		0.107		0.108		0.110
France	0.061		0.063		0.064		0.065		0.067		0.066
Germany	0.083		0.082		0.080		0.072		0.071		0.069
Italy	0.077		0.078		0.078		0.079		0.079		0.078
Canada	0.213		0.210		0.210		0.211		0.209		0.208
Japan	0.509		0.508		0.507		0.505		0.503		0.503
	APGARCH
US	0.203		0.209		0.216		0.212		0.206		0.201
UK	0.120		0.123		0.123		0.128		0.128		0.125
France	0.057		0.057		0.058		0.058		0.058		0.059
Germany	0.086		0.086		0.086		0.078		0.076		0.075
Italy	0.075		0.077		0.078		0.079		0.078		0.078
Canada	0.214		0.212		0.213		0.214		0.212		0.211
Japan	0.509		0.506		0.505		0.504		0.410		0.500
	MSM
US	0.153		0.157		0.156		0.154		0.151		0.150
UK	0.104		0.104		0.103		0.105		0.106		0.106
France	0.060		0.061		0.061		0.062		0.062		0.062
Germany	0.082		0.081		0.080		0.075		0.074		0.073
Italy	0.082		0.086		0.089		0.091		0.092		0.093
Canada	0.219		0.215		0.215		0.216		0.214		0.214
Japan	0.518		0.514		0.513		0.511		0.508		0.511

Note: RMSEs are computed for the following out-of-sample periods: November 2009–November 2015 for Canada and Japan; December 2009–December 2015 for the US, UK, France, Germany, and Italy. The lag orders in the ARFIMA specification (not displayed here) were obtained from the Bayesian Information Criterion (BIC).

Table 6. Mean absolute errors (MAEs), mean process: ARFIMA.

Forecasting Horizons	1M		2M		3M		4M		5M		6M
Countries	GARCH
US	0.140		0.142		0.144		0.142		0.139		0.137
UK	0.083		0.088		0.091		0.094		0.093		0.096
France	0.059		0.060		0.061		0.062		0.063		0.064
Germany	0.063		0.064		0.064		0.060		0.060		0.060
Italy	0.049		0.049		0.050		0.050		0.049		0.050
Canada	0.151		0.148		0.150		0.151		0.150		0.149
Japan	0.199		0.199		0.200		0.199		0.198		0.199
	GJR
US	0.150		0.151		0.152		0.152		0.148		0.145
UK	0.091		0.093		0.092		0.093		0.096		0.098
France	0.056		0.058		0.059		0.061		0.061		0.063
Germany	0.066		0.066		0.066		0.063		0.062		0.061
Italy	0.048		0.047		0.049		0.049		0.048		0.048
Canada	0.151		0.150		0.150		0.152		0.151		0.149
Japan	0.214		0.215		0.214		0.214		0.213		0.215
	EGARCH
US	0.133		0.133		0.132		0.132		0.128		0.125
UK	0.092		0.091		0.089		0.088		0.088		0.089
France	0.072		0.078		0.073		0.077		0.074		0.076
Germany	0.070		0.070		0.069		0.066		0.065		0.064
Italy	0.050		0.050		0.051		0.051		0.051		0.050
Canada	0.144		0.137		0.139		0.140		0.141		0.142
Japan	0.191		0.192		0.190		0.189		0.190		0.192
	QGARCH
US	0.140		0.140		0.140		0.140		0.136		0.133
UK	0.077		0.078		0.079		0.079		0.080		0.080
France	0.056		0.058		0.060		0.060		0.062		0.061
Germany	0.067		0.067		0.066		0.063		0.061		0.060
Italy	0.049		0.049		0.050		0.051		0.050		0.050
Canada	0.151		0.149		0.149		0.151		0.150		0.148
Japan	0.204		0.205		0.207		0.207		0.207		0.210
	APGARCH
US	0.154		0.155		0.158		0.156		0.152		0.150
UK	0.089		0.090		0.087		0.090		0.091		0.090
France	0.052		0.052		0.053		0.054		0.054		0.055
Germany	0.071		0.072		0.072		0.068		0.067		0.067
Italy	0.048		0.048		0.050		0.050		0.048		0.049
Canada	0.155		0.154		0.155		0.157		0.154		0.154
Japan	0.186		0.188		0.186		0.187		0.188		0.190
	MSM
US	0.123		0.126		0.127		0.126		0.123		0.122
UK	0.080		0.082		0.081		0.082		0.084		0.086
France	0.051		0.052		0.053		0.054		0.054		0.055
Germany	0.067		0.068		0.068		0.066		0.065		0.064
Italy	0.063		0.066		0.071		0.073		0.074		0.077
Canada	0.162		0.159		0.161		0.163		0.161		0.161
Japan	0.216		0.219		0.227		0.231		0.234		0.240

Note: MAEs are computed for the following out-of-sample periods: November 2009–November 2015 for Canada and Japan; December 2009–December 2015 for the US, UK, France, Germany, and Italy. The lag orders in the ARFIMA specification (not displayed here) were obtained from the Bayesian Information Criterion (BIC).

Table 7. Root mean squared errors (RMSEs), mean process: Smooth Transition AutoRegressive Fractionally Integrated (STARFI).

Forecasting Horizons	1M		2M		3M		4M		5M		6M
Countries	GARCH
US	0.176		0.181		0.184		0.179		0.173		0.169
UK	0.108		0.113		0.112		0.114		0.118		0.120
France	0.067		0.067		0.067		0.068		0.068		0.069
Germany	0.080		0.080		0.079		0.072		0.071		0.070
Italy	0.075		0.076		0.076		0.076		0.076		0.076
Canada	0.206		0.203		0.203		0.204		0.203		0.203
Japan	0.516		0.514		0.513		0.511		0.509		0.509
	GJR
US	0.192		0.197		0.203		0.202		0.195		0.190
UK	0.121		0.115		0.117		0.122		0.125		0.129
France	0.066		0.066		0.067		0.068		0.068		0.069
Germany	0.082		0.083		0.081		0.076		0.075		0.074
Italy	0.074		0.075		0.075		0.075		0.075		0.075
Canada	0.205		0.203		0.202		0.205		0.203		0.204
Japan	0.517		0.515		0.513		0.511		0.507		0.508
	EGARCH
US	0.169		0.171		0.172		0.170		0.163		0.157
UK	0.117		0.117		0.118		0.119		0.119		0.122
France	0.078		0.084		0.079		0.081		0.080		0.081
Germany	0.086		0.085		0.083		0.077		0.075		0.078
Italy	0.077		0.077		0.077		0.078		0.078		0.078
Canada	0.209		0.203		0.203		0.204		0.204		0.205
Japan	0.508		0.507		0.506		0.503		0.501		0.503
	QGARCH
US	0.176		0.179		0.181		0.180		0.173		0.167
UK	0.105		0.105		0.107		0.109		0.110		0.112
France	0.061		0.060		0.059		0.060		0.060		0.060
Germany	0.085		0.085		0.082		0.076		0.075		0.074
Italy	0.076		0.076		0.077		0.077		0.077		0.077
Canada	0.206		0.203		0.202		0.204		0.202		0.202
Japan	0.513		0.512		0.510		0.508		0.506		0.508
	APGARCH
US	0.193		0.202		0.210		0.204		0.198		0.194
UK	0.111		0.118		0.121		0.126		0.130		0.128
France	0.060		0.060		0.061		0.061		0.062		0.062
Germany	0.086		0.086		0.092		0.084		0.082		0.082
Italy	0.073		0.076		0.076		0.076		0.075		0.074
Canada	0.205		0.204		0.206		0.206		0.204		0.204
Japan	0.512		0.509		0.507		0.505		0.503		0.504
	MSM
US	0.155		0.158		0.158		0.155		0.152		0.151
UK	0.103		0.103		0.102		0.104		0.104		0.105
France	0.061		0.061		0.061		0.062		0.062		0.062
Germany	0.083		0.084		0.083		0.078		0.077		0.076
Italy	0.082		0.086		0.088		0.089		0.089		0.091
Canada	0.213		0.208		0.208		0.210		0.208		0.208
Japan	0.522		0.518		0.517		0.515		0.511		0.515

Note: RMSEs are computed for the following out-of-sample periods: November 2009–November 2015 for Canada and Japan; December 2009–December 2015 for the US, UK, France, Germany, and Italy. The lag orders in the STARFI specification (not displayed here) were obtained from the Bayesian Information Criterion (BIC).

Table 8. Mean absolute errors (MAEs), mean process: STARFI.

Forecasting Horizons	1M		2M		3M		4M		5M		6M
Countries	GARCH
US	0.136		0.138		0.138		0.136		0.133		0.131
UK	0.081		0.087		0.086		0.088		0.091		0.093
France	0.062		0.062		0.062		0.063		0.063		0.064
Germany	0.064		0.064		0.064		0.061		0.061		0.060
Italy	0.049		0.049		0.050		0.049		0.048		0.050
Canada	0.152		0.149		0.150		0.151		0.150		0.149
Japan	0.198		0.197		0.200		0.199		0.198		0.200
	GJR
US	0.142		0.144		0.146		0.145		0.142		0.141
UK	0.095		0.091		0.090		0.094		0.097		0.097
France	0.060		0.060		0.061		0.062		0.063		0.064
Germany	0.065		0.066		0.066		0.063		0.062		0.061
Italy	0.046		0.047		0.047		0.047		0.047		0.047
Canada	0.150		0.149		0.149		0.152		0.152		0.151
Japan	0.216		0.216		0.217		0.217		0.216		0.218
	EGARCH
US	0.128		0.129		0.129		0.128		0.123		0.121
UK	0.093		0.093		0.092		0.091		0.092		0.093
France	0.072		0.078		0.074		0.075		0.075		0.075
Germany	0.071		0.070		0.068		0.067		0.066		0.067
Italy	0.050		0.050		0.051		0.052		0.051		0.052
Canada	0.147		0.140		0.142		0.143		0.144		0.145
Japan	0.192		0.193		0.194		0.194		0.195		0.198
	QGARCH
US	0.132		0.132		0.134		0.134		0.130		0.127
UK	0.081		0.080		0.083		0.083		0.084		0.084
France	0.055		0.055		0.055		0.056		0.056		0.055
Germany	0.067		0.068		0.066		0.064		0.063		0.061
Italy	0.049		0.049		0.050		0.050		0.050		0.051
Canada	0.151		0.149		0.149		0.152		0.150		0.149
Japan	0.204		0.206		0.208		0.209		0.209		0.213
	APGARCH
US	0.144		0.149		0.151		0.146		0.143		0.143
UK	0.085		0.091		0.088		0.091		0.094		0.093
France	0.055		0.055		0.056		0.057		0.057		0.057
Germany	0.072		0.073		0.075		0.070		0.070		0.069
Italy	0.046		0.048		0.049		0.047		0.046		0.047
Canada	0.153		0.151		0.154		0.156		0.152		0.152
Japan	0.185		0.187		0.186		0.188		0.189		0.192
	MSM
US	0.123		0.126		0.126		0.124		0.122		0.122
UK	0.081		0.082		0.081		0.082		0.084		0.085
France	0.052		0.052		0.053		0.054		0.054		0.055
Germany	0.067		0.068		0.068		0.066		0.065		0.064
Italy	0.062		0.066		0.070		0.072		0.073		0.076
Canada	0.163		0.159		0.161		0.162		0.159		0.160
Japan	0.214		0.219		0.226		0.230		0.233		0.239

Note: MAEs are computed for the following out-of-sample periods: November 2009–November 2015 for Canada and Japan; December 2009–December 2015 for the US, UK, France, Germany, and Italy. The lag orders in the STARFI specification (not displayed here) were obtained from the Bayesian Information Criterion (BIC).

Based on the RMSEs and MAEs in Table 5 and Table 6, the ARFIMA-MSM specification appears to fit best the US and UK inflation rates. For France, Germany, Italy, Canada, and Japan, the ARFIMA-GARCH model yields relatively similar RMSEs and MAEs, that are superior to those of the ARFIMA-MSM model. In order to test whether the observed RMSE- and MAE-differences between the ARFIMA-MSM and -GARCH-type models are statistically significant, we apply the SPA test of Hansen (2005). The p-values obtained from 5000 bootstrap samples using both, the squared and absolute error loss functions, are reported in Table 9 and Table 10. While the null hypothesis (that the ARFIMA-MSM model is not outperformed by any of the ARFIMA-GARCH specifications) cannot be rejected for the US, UK, and France at the 10% level, we find rejection of the null hypothesis for Germany, Italy, Canada, and Japan. We also apply the EPA test in order to compare the ARFIMA-MSM specification with each of the ARFIMA-GARCH-type models (see Table 11 and Table 12). The null hypothesis (no difference in forecast accuracy) can only be rejected for the US, UK, and France (in most cases) at the 10% level. For Germany, Italy, Canada, and Japan, the ARFIMA-MSM and -GARCH models appear to exhibit similar forecasting performance.

Table 9. Superior Predictive Ability (SPA) test, squared error loss, mean process: ARFIMA.

Forecasting Horizons	1M		2M		3M		4M		5M		6M
Benchmark Models	US
GARCH	0.088		0.066		0.047		0.070		0.049		0.045
GJR	0.034		0.032		0.026		0.024		0.021		0.039
EGARCH	0.055		0.088		0.081		0.072		0.143		0.284
QGARCH	0.041		0.047		0.041		0.031		0.031		0.032
APGARCH	0.038		0.038		0.031		0.031		0.033		0.043
MSM	1.000		1.000		1.000		1.000		0.857		0.716
	UK
GARCH	0.110		0.255		0.094		0.031		0.164		0.109
GJR	0.017		0.028		0.036		0.034		0.033		0.031
EGARCH	0.046		0.122		0.086		0.134		0.161		0.100
QGARCH	0.621		0.748		0.259		0.328		0.287		0.208
APGARCH	0.070		0.051		0.058		0.061		0.057		0.109
MSM	0.379		0.735		0.741		0.672		0.713		0.792
	France
GARCH	0.006		0.002		0.001		0.001		0.000		0.000
GJR	0.053		0.026		0.020		0.010		0.002		0.001
EGARCH	0.000		0.000		0.000		0.000		0.000		0.000
QGARCH	0.080		0.006		0.004		0.001		0.000		0.000
APGARCH	0.780		0.856		0.821		0.859		0.839		1.000
MSM	0.274		0.172		0.224		0.179		0.161		0.145
	Germany
GARCH	1.000		1.000		1.000		1.000		1.000		1.000
GJR	0.020		0.049		0.076		0.016		0.034		0.037
EGARCH	0.009		0.018		0.022		0.005		0.008		0.007
QGARCH	0.012		0.021		0.064		0.037		0.075		0.091
APGARCH	0.013		0.006		0.002		0.005		0.005		0.004
MSM	0.055		0.049		0.101		0.010		0.011		0.016
	Italy
GARCH	0.240		0.367		0.232		0.474		0.553		0.476
GJR	0.245		0.717		0.898		0.926		0.599		0.559
EGARCH	0.092		0.202		0.144		0.151		0.061		0.109
QGARCH	0.099		0.180		0.141		0.160		0.053		0.134
APGARCH	0.781		0.770		0.312		0.387		0.765		0.785
MSM	0.018		0.012		0.003		0.001		0.000		0.000
	Canada
GARCH	0.953		0.869		0.582		0.840		0.803		0.791
GJR	0.727		0.521		0.630		0.450		0.431		0.416
EGARCH	0.383		0.558		0.549		0.598		0.437		0.347
QGARCH	0.802		0.838		0.951		0.870		0.993		0.998
APGARCH	0.468		0.116		0.048		0.139		0.154		0.125
MSM	0.004		0.059		0.025		0.041		0.033		0.005
	Japan
GARCH	0.210		0.267		0.217		0.238		0.114		0.172
GJR	0.130		0.188		0.267		0.268		0.379		0.148
EGARCH	0.749		0.733		0.993		0.993		0.853		0.764
QGARCH	0.047		0.037		0.031		0.017		0.018		0.015
APGARCH	0.373		0.492		0.451		0.400		0.541		0.350
MSM	0.063		0.060		0.052		0.014		0.029		0.013

Note: The displayed numbers are the p-values of the SPA test of Hansen (2005) using the squared error loss. We test the null hypothesis that the benchmark model is not outperformed by any of the other candidate models. The p-values are obtained for the following out-of-sample periods: November 2009–November 2015 for Canada and Japan; December 2009–December 2015 for the US, UK, France, Germany, and Italy. The inflation-rate mean process is ARFIMA.

Table 10. Superior Predictive Ability (SPA) test, absolute error loss, mean process: ARFIMA.

Forecasting Horizons	1M		2M		3M		4M		5M		6M
Benchmark Models	US
GARCH	0.075		0.032		0.014		0.026		0.025		0.018
GJR	0.024		0.014		0.0150		0.017		0.017		0.028
EGARCH	0.089		0.156		0.180		0.168		0.236		0.346
QGARCH	0.053		0.076		0.036		0.052		0.078		0.051
APGARCH	0.023		0.020		0.009		0.016		0.023		0.030
MSM	1.000		0.844		0.820		0.832		0.764		0.678
	UK
GARCH	0.136		0.130		0.057		0.016		0.098		0.058
GJR	0.007		0.004		0.014		0.012		0.003		0.002
EGARCH	0.0122		0.020		0.051		0.073		0.050		0.036
QGARCH	0.814		1.000		0.742		0.802		1.000		1.000
APGARCH	0.058		0.043		0.159		0.058		0.049		0.091
MSM	0.258		0.145		0.375		0.265		0.175		0.155
	France
GARCH	0.001		0.000		0.000		0.000		0.000		0.000
GJR	0.008		0.003		0.001		0.000		0.000		0.000
EGARCH	0.000		0.000		0.000		0.000		0.000		0.000
QGARCH	0.098		0.004		0.001		0.002		0.000		0.001
APGARCH	0.359		0.537		0.470		0.544		0.542		0.578
MSM	0.641		0.463		0.530		0.456		0.458		0.422
	Germany
GARCH	1.000		1.000		0.847		1.000		0.756		0.691
GJR	0.161		0.154		0.204		0.123		0.188		0.229
EGARCH	0.006		0.007		0.014		0.004		0.004		0.003
QGARCH	0.086		0.105		0.250		0.220		0.393		0.484
APGARCH	0.033		0.018		0.006		0.012		0.008		0.001
MSM	0.009		0.010		0.020		0.010		0.016		0.031
	Italy
GARCH	0.272		0.204		0.249		0.402		0.271		0.200
GJR	0.611		1.000		1.000		0.913		0.822		0.715
EGARCH	0.062		0.065		0.063		0.082		0.052		0.133
QGARCH	0.045		0.024		0.030		0.043		0.012		0.060
APGARCH	0.630		0.281		0.063		0.374		0.559		0.462
MSM	0.000		0.000		0.000		0.000		0.000		0.000
	Canada
GARCH	0.365		0.084		0.066		0.094		0.139		0.261
GJR	0.268		0.078		0.087		0.096		0.112		0.200
EGARCH	0.880		1.000		1.000		1.000		1.000		1.000
QGARCH	0.388		0.091		0.092		0.102		0.155		0.337
APGARCH	0.050		0.012		0.010		0.006		0.036		0.009
MSM	0.000		0.000		0.000		0.000		0.000		0.000
	Japan
GARCH	0.121		0.162		0.092		0.140		0.179		0.175
GJR	0.007		0.007		0.003		0.003		0.004		0.003
EGARCH	0.433		0.469		0.271		0.373		0.377		0.542
QGARCH	0.045		0.039		0.013		0.007		0.010		0.005
APGARCH	0.731		0.704		0.729		0.627		0.623		0.651
MSM	0.006		0.001		0.000		0.000		0.000		0.000

Note: The displayed numbers are the p-values of the SPA test of Hansen (2005) using the absolute error loss. We test the null hypothesis that the benchmark model is not outperformed by any of the other candidate models. The p-values are obtained for the following out-of-sample periods: November 2009–November 2015 for Canada and Japan; December 2009–December 2015 for the US, UK, France, Germany, and Italy. The inflation-rate mean process is ARFIMA.

Table 11. Equal Predictive Ability (EPA) test, squared error loss, mean process: ARFIMA.

		Forecasting Horizons
Model 1	Model 2	1M	2M	3M	4M	5M	6M
		US
GARCH	MSM	0.026	0.087	0.087	0.068	0.136	0.192
GJR		0.015	0.067	0.074	0.055	0.106	0.155
EGARCH		0.045	0.140	0.142	0.066	0.169	0.308
QGARCH		0.022	0.084	0.086	0.050	0.118	0.190
APGARCH		0.012	0.064	0.066	0.061	0.113	0.154
		UK
GARCH	MSM	0.057	0.163	0.034	0.021	0.120	0.067
GJR		0.018	0.059	0.092	0.135	0.148	0.162
EGARCH		0.054	0.089	0.079	0.158	0.194	0.167
QGARCH		0.633	0.549	0.317	0.397	0.382	0.334
APGARCH		0.037	0.073	0.107	0.144	0.168	0.204
		France
GARCH	MSM	0.011	0.020	0.010	0.023	0.002	0.002
GJR		0.009	0.020	0.012	0.004	0.000	0.000
EGARCH		0.000	0.000	0.000	0.000	0.000	0.000
QGARCH		0.395	0.349	0.278	0.322	0.192	0.251
APGARCH		0.777	0.800	0.728	0.745	0.718	0.706
		Germany
GARCH	MSM	0.965	0.969	0.930	0.958	0.940	0.919
GJR		0.464	0.633	0.670	0.806	0.825	0.791
EGARCH		0.040	0.136	0.225	0.360	0.403	0.402
QGARCH		0.284	0.382	0.558	0.760	0.776	0.751
APGARCH		0.127	0.126	0.083	0.343	0.380	0.363
		Italy
GARCH	MSM	0.947	0.968	0.979	0.985	0.987	0.9871
GJR		0.890	0.966	0.980	0.982	0.981	0.981
EGARCH		0.783	0.929	0.956	0.963	0.959	0.966
QGARCH		0.846	0.950	0.971	0.975	0.970	0.976
APGARCH		0.969	0.967	0.968	0.971	0.981	0.984
		Canada
GARCH	MSM	0.995	0.972	0.977	0.978	0.974	0.996
GJR		0.997	0.951	0.959	0.927	0.926	0.972
EGARCH		0.738	0.747	0.791	0.797	0.689	0.677
QGARCH		0.995	0.966	0.978	0.967	0.975	0.996
APGARCH		0.991	0.814	0.743	0.853	0.846	0.981
		Japan
GARCH	MSM	0.937	0.831	0.772	0.736	0.657	0.809
GJR		0.729	0.658	0.675	0.701	0.691	0.941
EGARCH		0.988	0.985	0.968	0.976	0.917	0.996
QGARCH		0.966	0.946	0.893	0.922	0.823	0.973
APGARCH		0.996	0.987	0.931	0.879	0.877	0.986

Note: The displayed number are p-values of the EPA test of Diebold and Mariano (1995) using the squared error loss. We test the null hypothesis that the forecasts at horizon h of Model 1 are equal to those of Model 2 against the one-sided alternative that forecasts of Model 1 are inferior to those of Model 2. The p-values are obtained for the following out-of-sample periods: November 2009–November 2015 for Canada and Japan; December 2009–December 2015 for the US, UK, France, Germany, and Italy. The inflation-rate mean process is ARFIMA.

Table 12. Equal Predictive Ability (EPA) test, absolute error loss, mean process: ARFIMA.

		Forecasting Horizons
Model 1	Model 2	1M	2M	3M	4M	5M	6M
		US
GARCH	MSM	0.015	0.085	0.099	0.128	0.185	0.225
GJR		0.010	0.064	0.089	0.108	0.158	0.206
EGARCH		0.057	0.216	0.256	0.254	0.330	0.416
QGARCH		0.021	0.126	0.159	0.173	0.237	0.293
APGARCH		0.007	0.056	0.063	0.093	0.151	0.189
		UK
GARCH	MSM	0.246	0.149	0.054	0.045	0.188	0.102
GJR		0.024	0.086	0.142	0.191	0.199	0.200
EGARCH		0.036	0.127	0.166	0.271	0.351	0.371
QGARCH		0.834	0.835	0.696	0.724	0.775	0.764
APGARCH		0.086	0.170	0.301	0.266	0.328	0.384
		France
GARCH	MSM	0.000	0.000	0.000	0.001	0.000	0.000
GJR		0.000	0.000	0.000	0.000	0.000	0.000
EGARCH		0.000	0.000	0.000	0.000	0.000	0.000
QGARCH		0.046	0.049	0.059	0.122	0.060	0.099
APGARCH		0.324	0.515	0.464	0.515	0.514	0.532
		Germany
GARCH	MSM	0.999	0.993	0.963	0.957	0.930	0.891
GJR		0.833	0.917	0.917	0.935	0.956	0.939
EGARCH		0.055	0.167	0.315	0.435	0.480	0.467
QGARCH		0.494	0.641	0.804	0.844	0.855	0.826
APGARCH		0.086	0.137	0.156	0.289	0.334	0.307
		Italy
GARCH	MSM	1.000	1.000	1.000	1.000	1.000	1.000
GJR		1.000	1.000	1.000	1.000	1.000	1.000
EGARCH		1.000	1.000	1.000	1.000	1.000	1.000
QGARCH		1.000	1.000	1.000	1.000	1.000	1.000
APGARCH		1.000	1.000	1.000	1.000	1.000	1.000
		Canada
GARCH	MSM	1.000	1.000	1.000	1.000	1.000	1.000
GJR		1.000	0.999	0.999	0.997	0.991	0.997
EGARCH		0.995	0.997	0.999	0.999	0.997	0.991
QGARCH		1.000	1.000	1.000	1.000	1.000	1.000
APGARCH		0.996	0.958	0.976	0.986	0.998	0.999
		Japan
GARCH	MSM	1.000	1.000	1.000	1.000	1.000	1.000
GJR		0.563	0.634	0.777	0.836	0.860	0.899
EGARCH		0.997	0.991	0.994	0.996	0.995	0.999
QGARCH		0.983	0.969	0.982	0.992	0.993	0.997
APGARCH		1.000	1.000	1.000	1.000	1.000	1.000

Note: The displayed number are p-values of the EPA test of Diebold and Mariano (1995) using the absolute error loss. We test the null hypothesis that the forecasts at horizon h of Model 1 are equal to those of Model 2 against the one-sided alternative that forecasts of Model 1 are inferior to those of Model 2. The p-values are obtained for the following out-of-sample periods: November 2009–November 2015 for Canada and Japan; December 2009–December 2015 for the US, UK, France, Germany, and Italy. The inflation-rate mean process is ARFIMA.

When modeling the inflation-rate mean process by the STARFI specification, we obtain substantial gains in forecast accuracy. The RMSEs and MAEs in Table 7 and Table 8 as well as the SPA and EPA tests in Table 13, Table 14, Table 15 and Table 16 indicate that the STARFI-MSM specification systematically outperforms the respective STARFI-GARCH specifications for all G7 countries, except for Japan. Our results suggest that the STARFI-MSM model fits the G7 inflation rates considerably well, thus producing accurate inflation uncertainty forecasts. For Japan, all models perform well, but it appears impossible to find a specific model systematically dominating the others.

Table 13. Superior Predictive Ability (SPA) test, squared error loss, mean process: STARFI.

Forecasting Horizons	1M		2M		3M		4M		5M		6M
Benchmark Models	US
GARCH	0.108		0.068		0.051		0.099		0.058		0.038
GJR	0.041		0.036		0.027		0.029		0.024		0.041
EGARCH	0.081		0.111		0.094		0.081		0.142		0.292
QGARCH	0.049		0.053		0.037		0.027		0.026		0.052
APGARCH	0.058		0.047		0.035		0.052		0.045		0.055
MSM	1.000		1.000		0.906		1.000		0.858		0.737
	UK
GARCH	0.197		0.099		0.088		0.044		0.080		0.063
GJR	0.004		0.045		0.077		0.048		0.040		0.034
EGARCH	0.026		0.046		0.066		0.080		0.092		0.062
QGARCH	0.542		0.280		0.101		0.145		0.142		0.120
APGARCH	0.217		0.080		0.050		0.068		0.055		0.101
MSM	0.715		0.720		1.000		1.000		1.000		1.000
	France
GARCH	0.001		0.001		0.000		0.000		0.000		0.000
GJR	0.029		0.012		0.006		0.003		0.001		0.000
EGARCH	0.000		0.000		0.000		0.000		0.000		0.000
QGARCH	0.623		0.817		0.719		0.776		0.758		0.833
APGARCH	0.798		0.685		0.058		0.145		0.028		0.022
MSM	0.422		0.360		0.318		0.254		0.283		0.195
	Germany
GARCH	1.000		0.901		1.000		1.000		1.000		1.000
GJR	0.094		0.050		0.090		0.034		0.049		0.034
EGARCH	0.023		0.056		0.095		0.040		0.090		0.005
QGARCH	0.036		0.030		0.068		0.038		0.044		0.026
APGARCH	0.150		0.171		0.007		0.007		0.001		0.004
MSM	0.092		0.036		0.030		0.008		0.007		0.010
	Italy
GARCH	0.052		0.108		0.103		0.318		0.341		0.188
GJR	0.263		1.000		1.000		0.942		0.542		0.397
EGARCH	0.004		0.021		0.013		0.005		0.006		0.022
QGARCH	0.044		0.023		0.019		0.013		0.004		0.019
APGARCH	0.801		0.271		0.177		0.368		0.849		0.775
MSM	0.007		0.006		0.003		0.000		0.001		0.000
	Canada
GARCH	0.638		0.801		0.350		0.914		0.875		0.722
GJR	0.743		0.796		0.653		0.657		0.517		0.352
EGARCH	0.356		0.612		0.510		0.622		0.447		0.381
QGARCH	0.824		0.978		0.918		0.939		0.988		0.999
APGARCH	0.795		0.453		0.108		0.529		0.419		0.512
MSM	0.006		0.077		0.033		0.076		0.028		0.002
	Japan
GARCH	0.217		0.266		0.219		0.224		0.1456		0.198
GJR	0.109		0.158		0.200		0.199		0.327		0.225
EGARCH	0.712		0.680		0.985		0.987		0.907		0.995
QGARCH	0.054		0.031		0.024		0.010		0.008		0.018
APGARCH	0.430		0.561		0.543		0.514		0.459		0.388
MSM	0.052		0.035		0.059		0.011		0.010		0.030

Note: The displayed numbers are the p-values of the SPA test of Hansen (2005) using the squared error loss. We test the null hypothesis that the benchmark model is not outperformed by any of the other candidate models. The p-values are obtained for the following out-of-sample periods: November 2009–November 2015 for Canada and Japan; December 2009–December 2015 for the US, UK, France, Germany, and Italy. The inflation-rate mean process is STARFI.

Table 14. Superior Predictive Ability (SPA) test, absolute error loss, mean process: STARFI.

Forecasting Horizons	1M		2M		3M		4M		5M		6M
Models	US
GARCH	0.000		0.000		0.000		0.000		0.000		0.000
GJR	0.000		0.000		0.000		0.000		0.000		0.000
EGARCH	0.000		0.000		0.000		0.000		0.000		0.000
QGARCH	0.000		0.000		0.000		0.000		0.000		0.000
APGARCH	0.000		0.000		0.000		0.000		0.000		0.000
MSM	1.000		1.000		1.000		1.000		1.000		1.000
	UK
GARCH	0.000		0.000		0.000		0.000		0.000		0.000
GJR	0.000		0.000		0.000		0.000		0.000		0.000
EGARCH	0.000		0.000		0.000		0.000		0.000		0.000
QGARCH	0.000		0.000		0.000		0.000		0.000		0.000
APGARCH	0.000		0.000		0.000		0.000		0.000		0.000
MSM	1.000		1.000		1.000		1.000		1.000		1.000
	France
GARCH	0.000		0.000		0.000		0.000		0.000		0.000
GJR	0.000		0.000		0.000		0.000		0.000		0.000
EGARCH	0.000		0.000		0.000		0.000		0.000		0.000
QGARCH	0.000		0.000		0.000		0.000		0.000		0.000
APGARCH	0.000		0.000		0.000		0.000		0.000		0.000
MSM	1.000		1.000		1.000		1.000		1.000		1.000
	Germany
GARCH	0.000		0.000		0.000		0.000		0.000		0.000
GJR	0.000		0.000		0.000		0.000		0.000		0.000
EGARCH	0.000		0.000		0.000		0.000		0.000		0.000
QGARCH	0.000		0.000		0.000		0.000		0.000		0.000
APGARCH	0.000		0.000		0.000		0.000		0.000		0.000
MSM	1.000		1.000		1.000		1.000		1.000		1.000
	Italy
GARCH	0.000		0.000		0.000		0.000		0.000		0.000
GJR	0.000		0.000		0.000		0.000		0.000		0.000
EGARCH	0.000		0.000		0.000		0.000		0.000		0.000
QGARCH	0.000		0.000		0.000		0.000		0.000		0.000
APGARCH	0.000		0.000		0.000		0.000		0.000		0.000
MSM	1.000		1.000		1.000		1.000		1.000		1.000
	Canada
GARCH	0.000		0.000		0.000		0.000		0.000		0.000
GJR	0.000		0.000		0.000		0.000		0.000		0.000
EGARCH	0.000		0.000		0.000		0.000		0.000		0.000
QGARCH	0.000		0.000		0.000		0.000		0.000		0.000
APGARCH	0.000		0.000		0.000		0.000		0.000		0.000
MSM	1.000		1.000		1.000		1.000		1.000		1.000
	Japan
GARCH	0.115		0.174		0.101		0.148		0.179		0.217
GJR	0.006		0.007		0.004		0.004		0.006		0.008
EGARCH	0.395		0.437		0.390		0.443		0.450		0.441
QGARCH	0.041		0.046		0.022		0.016		0.020		0.014
APGARCH	0.931		0.935		0.936		0.935		0.934		0.931
MSM	0.229		0.243		0.239		0.244		0.252		0.257

Note: The displayed numbers are the p-values of the SPA test of Hansen (2005) using the absolute error loss. We test the null hypothesis that the benchmark model is not outperformed by any of the other candidate models. The p-values are obtained for the following out-of-sample periods: November 2009–November 2015 for Canada and Japan; December 2009–December 2015 for the US, UK, France, Germany, and Italy. The inflation-rate mean process is STARFI.

Table 15. Equal Predictive Ability (EPA) test, squared error loss, mean process: STARFI.

		Forecasting Horizons
Model 1	Model 2	1M	2M	3M	4M	5M	6M
		US
GARCH	MSM	0.030	0.094	0.096	0.081	0.149	0.210
GJR		0.023	0.081	0.086	0.070	0.119	0.163
EGARCH		0.068	0.167	0.158	0.096	0.186	0.319
QGARCH		0.040	0.112	0.105	0.064	0.134	0.215
APGARCH		0.024	0.081	0.076	0.078	0.134	0.173
		UK
GARCH	MSM	0.093	0.056	0.045	0.069	0.073	0.086
GJR		0.001	0.072	0.118	0.136	0.152	0.161
EGARCH		0.015	0.057	0.088	0.147	0.183	0.170
QGARCH		0.277	0.306	0.153	0.233	0.264	0.262
APGARCH		0.099	0.077	0.081	0.130	0.155	0.187
		France
GARCH	MSM	0.003	0.006	0.008	0.018	0.004	0.003
GJR		0.005	0.005	0.003	0.004	0.000	0.000
EGARCH		0.000	0.000	0.000	0.000	0.000	0.000
QGARCH		0.553	0.610	0.634	0.674	0.650	0.690
APGARCH		0.587	0.600	0.493	0.587	0.493	0.554
		Germany
GARCH	MSM	0.970	0.981	0.963	0.968	0.953	0.934
GJR		0.651	0.700	0.771	0.866	0.864	0.823
EGARCH		0.212	0.371	0.500	0.573	0.674	0.389
QGARCH		0.245	0.357	0.577	0.727	0.740	0.706
APGARCH		0.265	0.301	0.038	0.098	0.115	0.044
		Italy
GARCH	MSM	0.976	0.983	0.984	0.989	0.987	0.988
GJR		0.960	0.981	0.981	0.980	0.976	0.980
EGARCH		0.899	0.964	0.965	0.957	0.955	0.968
QGARCH		0.920	0.967	0.965	0.960	0.953	0.970
APGARCH		0.988	0.973	0.966	0.973	0.977	0.985
		Canada
GARCH	MSM	0.994	0.966	0.971	0.970	0.969	0.995
GJR		0.994	0.935	0.951	0.878	0.876	0.902
EGARCH		0.775	0.783	0.779	0.792	0.693	0.714
QGARCH		0.995	0.958	0.974	0.947	0.974	0.996
APGARCH		0.993	0.886	0.703	0.907	0.855	0.983
		Japan
GARCH	MSM	0.931	0.833	0.766	0.741	0.677	0.813
GJR		0.696	0.637	0.649	0.684	0.716	0.935
EGARCH		0.980	0.986	0.972	0.989	0.959	0.988
QGARCH		0.954	0.949	0.905	0.945	0.881	0.944
APGARCH		0.997	0.994	0.964	0.947	0.897	0.969

Note: The displayed number are p-values of the EPA test of Diebold and Mariano (1995) using the squared error loss. We test the null hypothesis that the forecasts at horizon h of Model 1 are equal to those of Model 2 against the one-sided alternative that forecasts of Model 1 are inferior to those of Model 2. The p-values are obtained for the following out-of-sample periods: November 2009–November 2015 for Canada and Japan; December 2009–December 2015 for the US, UK, France, Germany, and Italy. The inflation-rate mean process is STARFI.

Table 16. Equal Predictive Ability (EPA) test, absolute error loss, mean-process: STARFI.

		Forecasting Horizons
Model 1	Model 2	1M	2M	3M	4M	5M	6M
		US
GARCH	MSM	0.000	0.000	0.000	0.000	0.000	0.000
GJR		0.000	0.000	0.000	0.000	0.000	0.000
EGARCH		0.000	0.000	0.000	0.000	0.000	0.000
QGARCH		0.000	0.000	0.000	0.000	0.000	0.000
APGARCH		0.000	0.000	0.000	0.000	0.000	0.001
		UK
GARCH	MSM	0.000	0.000	0.000	0.000	0.000	0.000
GJR		0.000	0.000	0.000	0.000	0.000	0.000
EGARCH		0.000	0.000	0.000	0.000	0.000	0.000
QGARCH		0.000	0.000	0.000	0.000	0.000	0.000
APGARCH		0.000	0.000	0.000	0.000	0.000	0.000
		France
GARCH	MSM	0.000	0.000	0.000	0.000	0.000	0.000
GJR		0.000	0.000	0.000	0.000	0.000	0.000
EGARCH		0.000	0.000	0.000	0.000	0.000	0.000
QGARCH		0.000	0.000	0.000	0.000	0.000	0.000
APGARCH		0.000	0.000	0.000	0.000	0.000	0.000
		Germany
GARCH	MSM	0.000	0.000	0.000	0.000	0.000	0.000
GJR		0.000	0.000	0.000	0.000	0.000	0.000
EGARCH		0.000	0.000	0.000	0.000	0.000	0.000
QGARCH		0.000	0.000	0.000	0.000	0.000	0.000
APGARCH		0.000	0.000	0.000	0.000	0.000	0.000
		Italy
GARCH	MSM	0.000	0.000	0.000	0.000	0.000	0.000
GJR		0.000	0.000	0.000	0.000	0.000	0.000
EGARCH		0.000	0.000	0.000	0.000	0.000	0.000
QGARCH		0.000	0.000	0.000	0.000	0.000	0.000
APGARCH		0.000	0.000	0.000	0.000	0.000	0.000
		Canada
GARCH	MSM	0.000	0.000	0.000	0.000	0.000	0.000
GJR		0.000	0.000	0.000	0.000	0.000	0.000
EGARCH		0.000	0.000	0.000	0.000	0.000	0.000
QGARCH		0.000	0.000	0.000	0.000	0.000	0.000
APGARCH		0.000	0.000	0.000	0.000	0.000	0.000
		Japan
GARCH	MSM	0.738	0.738	0.736	0.742	0.746	0.759
GJR		0.684	0.679	0.680	0.684	0.692	0.711
EGARCH		0.754	0.752	0.761	0.769	0.779	0.795
QGARCH		0.719	0.714	0.711	0.713	0.717	0.726
APGARCH		0.775	0.769	0.779	0.781	0.787	0.794

Note: The displayed number are p-values of the EPA test of Diebold and Mariano (1995) using the absolute error loss. We test the null hypothesis that the forecasts at horizon h of Model 1 are equal to those of Model 2 against the one-sided alternative that forecasts of Model 1 are inferior to those of Model 2. The p-values are obtained for the following out-of-sample periods: November 2009–November 2015 for Canada and Japan; December 2009–December 2015 for the US, UK, France, Germany, and Italy. The inflation-rate mean process is STARFI.

6. Conclusions

This paper proposes the ARFIMA- and STAR-MSM models for forecasting inflation uncertainty in the G7 countries. The specifications are found to model the dynamics of inflation uncertainty appropriately, since they are able to capture (i) dual long memory, (ii) clustering effects, (iii) non-linearities, and (iv) asymmetries observed in inflation rates. Our out-of-sample forecasting analysis confirms these capacities and the robustness of our models, which yield accurate forecasts of inflation uncertainty. In particular, the performance of the STARFI-MSM is interesting and should have major implications for monetary policy, which merit careful investigation in future research.