Comparing Estimation Methods for the Power–Pareto Distribution

Abstract

Non-negative distributions are important tools in various fields. Given the importance of achieving a good fit, the literature offers hundreds of different models, from the very simple to the highly flexible. In this paper, we consider the power–Pareto model, which is defined by its quantile function. This distribution has three parameters, allowing the model to take different shapes, including symmetrical and left- and right-skewed. We provide different distributional characteristics and discuss parameter estimation. In addition to the already-known Maximum Likelihood and Least Squares of the logarithm of the order statistics estimation methods, we propose several additional methods. A simulation study and an application to two datasets are conducted to illustrate the performance of the estimation methods.

1. Introduction

Univariate continuous distributions play a crucial role in modeling real-world phenomena. While well-known distributions like the normal, exponential, and Pareto distributions are commonly used, there is often a need for specialized distributions, to model specific data patterns. One established practice for defining more flexible distributions is through the quantile function (QF)

$$Q\left(p\right)=inf\{x:F(x)\ge p\},0\le p\le 1,$$

where $F\left(x\right)=P(X\le x)$ represents the cumulative distribution function (CDF) of the random variable X. Thus, if F is strictly increasing, Q and F are inverse functions of each other, and $F\left(Q\right(p\left)\right)=p$. QFs possess numerous distinct characteristics that are absent in CDFs. We highlight that new and more flexible QFs can be easily constructed from the combination of existing QFs. For example, the product of QFs is still a valid QF.

Since the QF provides all valuable information about the distribution’s shape, several QF models have been proposed in the literature. The symmetric Tukey lambda distribution (Tukey 1960) and its asymmetric version, known as the generalized lambda distribution (Ramberg and Schmeiser 1972), are both defined in terms of their QF. Similarly, the quantile-based skew logistic distribution introduced by Gilchrist (2000) is also defined through its QF. More recently, Sankaran et al. (2016) introduce a new QF resulting from the sum of the QFs of the generalized Pareto and Weibull distributions.

In some cases, the density and distribution functions for distributions expressed through QFs are not available in closed form, except for specific parameter values. However, those functions can be easily computed by numerically inverting the corresponding QF. One significant advantage of these distributions is the simplicity of their QF, which facilitates the generation of random values through the use of uniform random variables and the application of inference procedures based on quantiles.

In this article, we are interested in the power–Pareto distribution introduced in Gilchrist (2000) and further studied in Hankin and Lee (2006). This is a versatile family of distributions for a non-negative random variable, such as income and wealth. This model is formed through the product of the power and Pareto QFs as

$$Q(p\mid c,{\lambda }_1,{\lambda }_2)=c{p}^{{\lambda }_1}{(1-p)}^{-{\lambda }_2},0\le p\le 1,$$

(1)

where $c>0$,   $min\left({\lambda }_1,{\lambda }_2\right)\ge 0$, and $max\left({\lambda }_1,{\lambda }_2\right)>0$. We write $X\sim PP(c,{\lambda }_1,{\lambda }_2)$ whenever X has the QF in Equation (1). The parameter c is related to the scale, while ${\lambda }_1$ and ${\lambda }_2$ control the shape of the distribution. By fixing or restricting some of this distribution’s parameters, we obtain well-known reduced versions. More precisely, if ${\lambda }_1=0$ and ${\lambda }_2>0$, then X follows a Pareto (type I) distribution with the QF

$$Q\left(p\right)=c{p}^{{\lambda }_1},0\le p\le 1,$$

and if ${\lambda }_1>0$ and ${\lambda }_2=0$, X has a scaled power distribution with the QF

$$Q\left(p\right)=c{(1-p)}^{-{\lambda }_2},0\le p\le 1.$$

Furthermore, it can be observed that when ${\lambda }_1={\lambda }_2>0$, X has the well-known log-logistic distribution, which is a special case of Burr (1942) type XII and Dagum (1977) family of distributions (for further details, see Caeiro and Mateus 2024). The case ${\lambda }_1={\lambda }_2=0$ is not considered here, as it results in a degenerate distribution at c. In the literature, the power–Pareto model in Equation (1) is also known as the Davies distribution (Hankin and Lee 2006) or Hankin–Lee distribution (Nair and Vineshkumar 2010). Hankin and Lee (2006) proposed two inference procedures to estimate the parameters c, ${\lambda }_1$, and ${\lambda }_2$ in Equation (1), namely the maximum likelihood and the least squares method for the logged order statistics. Additionally, the authors compare the efficiency of those two estimation methods by comparing their variance. Since maximum likelihood estimators are often severely biased, for small sample sizes, we argue that solely considering the variance of the estimators may not provide a comprehensive assessment of their performance, and thus, it could lead to misleading conclusions. Therefore, the primary goal of this paper is to discuss a broader set of estimation techniques and consider alternative criteria for a more precise and unbiased comparison of the estimators.

The remainder of the paper is organized as follows. In Section 2, we describe various known properties of the power–Pareto model, like probability density and distribution functions, moments, and quantile-based measures. Several inferential procedures for the parameters of the power–Pareto distribution are discussed in Section 3. In Section 4, we conduct Monte Carlo simulations to analyze the performance of the different inferential procedures. In Section 5, we apply the inferential methods to two real datasets, and Section 6 concludes the article.

2. Statistical Properties of the Power–Pareto Distribution

2.1. Functions

From now on, we use $\mathit{\theta }=(c,{\lambda }_1,{\lambda }_2)$ to denote the three parameters of the power–Pareto model. The derivative of $Q(p\mid \mathit{\theta })$, denoted as $q(p\mid \mathit{\theta })=\partial Q(p\mid \mathit{\theta })/\partial p$, is known as the quantile density function. For the model in Equation (1), this function is given by

$$q(p\mid \mathit{\theta })=Q(p\mid \mathit{\theta })\left(\frac{{\lambda }_1}{p}+\frac{{\lambda }_2}{1-p}\right),0\le p\le 1.$$

(2)

Note that the quantile density function in Equation (2) satisfies the identity

$$f\left(Q\right(p\mid \mathit{\theta }\left)\right)q(p\mid \mathit{\theta })=1,$$

where $f(·)$ is the probability density function.

If we exclude the cases where the power–Pareto reduces to the power, the Pareto, or the log-logistic distributions, neither the distribution function nor the density function can be expressed in closed form. Thus, these functions have to be computed through numerical inversion of the QF. Suppose that $u=u(x\mid \mathit{\theta })$ is the solution of the equation $x=Q(u\mid \mathit{\theta })$. Then, the CDF can be expressed as $F(x\mid \mathit{\theta })=u$, and the density function can be derived from the inverse function rule as

$$\begin{array}{cc}\hfill f(x\mid \mathit{\theta })& =\frac{\partial F(x\mid \mathit{\theta })}{\partial x}\hfill \\ \hfill & ={\left(\frac{\partial Q(u\mid \mathit{\theta })}{\partial u}\right)}^{-1}\hfill \\ \hfill & ={\left(Q(u\mid \mathit{\theta })\left(\frac{{\lambda }_1}{u}+\frac{{\lambda }_2}{1-u}\right)\right)}^{-1}.\hfill \end{array}$$

(3)

The density at the left tail can be approximated by

$$f(x\mid \mathit{\theta })\sim \frac{1}{c{\lambda }_1}{\left(\frac{x}{c}\right)}^{\frac{1}{{\lambda }_1}-1};$$

(4)

Similarly, the right tail density can be approximated by

$$f(x\mid \mathit{\theta })\sim \frac{1}{c{\lambda }_2}{\left(\frac{c}{x}\right)}^{\frac{1}{{\lambda }_2}+1}.$$

(5)

In addition, we have

$$1-F(x\mid \mathit{\theta })\sim {\left(\frac{x}{c}\right)}^{-\alpha },$$

(6)

for large x, where $\alpha =1/{\lambda }_2$ is the upper tail index (Finkelstein et al. 2006; Schluter 2018). Hence, the power–Pareto model belongs to the class of heavy-tailed distributions. In numerous applications, it is crucial to estimate accurately the tail index $\alpha$ in Equation (6). We refer the reader to Beirlant et al. (2012, 2004); Mehta and Yang (2022); Ndlovu and Chikobvu (2023); Reiss and Thomas (2007), among others. As noted in Hankin and Lee (2006), Equations (4) and (5) show that ${\lambda }_1$ controls the behavior of the left-hand tail, while ${\lambda }_2$ governs the right-hand tail. A larger value of ${\lambda }_1$ results in a shorter left tail, whereas a larger value of ${\lambda }_2$ leads to a longer right tail. This relationship is illustrated in Figure 1, where different parameter values are used to depict the probability density function.

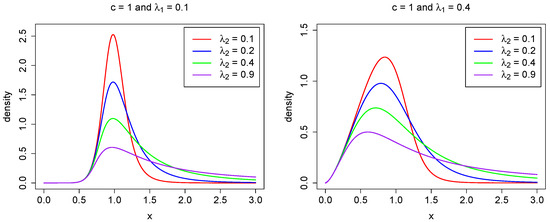
Figure 1. The density function in (3) for fixed parameters $c=1$, ${\lambda }_1=0.1$ (left), ${\lambda }_1=0.4$ (right), and selected values for ${\lambda }_2$.

2.2. Moments

The k-$\mathrm{th}$ moment can be expressed in an explicit form as follows:

$$\mathbb{E}\left(X^k\right)={\int }_0^1{\left(Q(p\mid \mathit{\theta })\right)}^{k}dp=c^{k}B(1+k{\lambda }_1,1-k{\lambda }_2),{\lambda }_2<\frac{1}{k},$$

(7)

where $B(a,b)={\int }_0^1{x}^{a-1}{(1-x)}^{b-1}dx$, with $a>0$ and $b>0$, represents the Beta function. Using the notation $b(k,{\lambda }_1,{\lambda }_2)=B(1+k{\lambda }_1,1-k{\lambda }_2)$, the mean ($\mu$) and the variance (${\sigma }^2$) are

$$\begin{array}{ccc}\hfill \mu & =& cb(1,{\lambda }_1,{\lambda }_2),\hfill \\ & & \\ \hfill {\sigma }^2& =& c^2\left(b(2,{\lambda }_1,{\lambda }_2)-b^2(1,{\lambda }_1,{\lambda }_2)\right),\hfill \end{array}$$

and exist if ${\lambda }_2<1$ and ${\lambda }_2<\frac{1}{2}$, respectively. Some other measures, like the coefficient of variation (CV), Pearson’s skewness (${\mathrm{S}}_p$), and kurtosis (${\mathrm{K}}_p$) can also be easily obtained in explicit forms,

$$\begin{array}{ccc}\hfill \mathrm{CV}& =& \frac{b(1,{\lambda }_1,{\lambda }_2)}{\sqrt{b(2,{\lambda }_1,{\lambda }_2)-b^2(1,{\lambda }_1,{\lambda }_2)}},{\lambda }_2<\frac{1}{2},\hfill \\ & & \\ & & \\ \hfill {\mathrm{S}}_p& =& \frac{b(3,{\lambda }_1,{\lambda }_2)-3b(1,{\lambda }_1,{\lambda }_2)b(2,{\lambda }_1,{\lambda }_2)+2b^3(1,{\lambda }_1,{\lambda }_2)}{{\left(b(2,{\lambda }_1,{\lambda }_2)-b^2(1,{\lambda }_1,{\lambda }_2)\right)}^{3/2}},{\lambda }_2<\frac{1}{3},\hfill \\ & & \\ & & \\ \hfill {\mathrm{K}}_p& =& \frac{b(4,{\lambda }_1,{\lambda }_2)-4b(1,{\lambda }_1,{\lambda }_2)b(3,{\lambda }_1,{\lambda }_2)+6b^2(1,{\lambda }_1,{\lambda }_2)b(2,{\lambda }_1,{\lambda }_2)-3b^4(1,{\lambda }_1,{\lambda }_2)}{{\left(b(2,{\lambda }_1,{\lambda }_2)-b^2(1,{\lambda }_1,{\lambda }_2)\right)}^2},{\lambda }_2<\frac{1}{4}.\hfill \end{array}$$

2.3. Quantile Measures

Quantile-based measures of distributional characteristics, including location, dispersion, skewness, and kurtosis, exhibit less sensitivity to outliers when compared to conventional moments. For the power–Pareto distribution, the median (M) and the interquartile range (IQR) are, respectively, given by

$$\begin{array}{ccc}\hfill \mathrm{M}& =& Q(1/2\mid \mathit{\theta })=c{2}^{{\lambda }_2-{\lambda }_1},\hfill \\ & & \\ \hfill \mathrm{IQR}& =& Q(3/4\mid \mathit{\theta })-Q(1/4\mid \mathit{\theta })=c{4}^{{\lambda }_2-{\lambda }_1}(3^{{\lambda }_1}-3^{-{\lambda }_2}).\hfill \end{array}$$

The asymmetry and peakedness of the distribution can be analyzed using Bowley (1901) Skewness ($S_B$) and Moors (1988) Kurtosis ($K_M$) quantile-based coefficients,

$$\begin{array}{ccc}\hfill {\mathrm{S}}_B& =& \frac{Q(3/4\mid \mathit{\theta })-2Q(1/2\mid \mathit{\theta })+Q(1/4\mid \mathit{\theta })}{\mathrm{IQR}}\hfill \\ & =& \frac{3^{{\lambda }_1}-2^{1+{\lambda }_1-{\lambda }_2}+3^{-{\lambda }_2}}{3^{{\lambda }_1}-3^{-{\lambda }_2}},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\mathrm{K}}_M& =& \frac{Q(7/8\mid \mathit{\theta })-Q(5/8\mid \mathit{\theta })+Q(3/8\mid \mathit{\theta })-Q(1/8\mid \mathit{\theta })}{\mathrm{IQR}}\hfill \\ & =& \frac{2^{{\lambda }_2-{\lambda }_1}(7^{{\lambda }_1}-5^{{\lambda }_1}{3}^{-{\lambda }_2}+3^{{\lambda }_1}{5}^{-{\lambda }_2}-7^{-{\lambda }_2})}{3^{{\lambda }_1}-3^{-{\lambda }_2}}.\hfill \end{array}$$

All the aforementioned quantile-based measures are more robust than moments, since they exist in the complete parameter space, in contrast to moments.

2.4. Order Statistics

Let $X_1,X_2,\dots ,X_n$ be a random sample of size n from a population with the QF defined in Equation (1), and let $X_{\left(1\right)}\le X_{\left(2\right)}\le \dots \le X_{\left(n\right)}$ be the corresponding ascending order statistics. Order statistics play a crucial role in statistical inference due to their ability to provide valuable insights into the distribution of X, as well as in estimation procedures for parameters of the model. The density function of $X_{\left(i\right)}$ is

$$f_{\left(i\right)}\left(x\right)=\frac{1}{B(i,n-i+1)}{\left(F\left(x\right)\right)}^{i-1}{(1-F\left(x\right))}^{n-i}f\left(x\right).$$

Note that $f_{\left(i\right)}\left(x\right)$ does not have a closed form, since neither the CDF nor the density function can be expressed in closed form. However, the single moments of the order statistics, ${\mu }_{\left(i\right)}=\mathbb{E}\left(X_{\left(i\right)}\right)$, can be easily obtained from the corresponding QF in Equation (1). For the class of distributions in Equation (1), ${\mu }_{\left(i\right)}$, can be expressed as follows:

$$\begin{array}{ccc}\hfill {\mu }_{\left(i\right)}& =& \frac{1}{B(i,n-i+1)}{\int }_0^{1}Q(p\mid \mathit{\theta })p^{i-1}{(1-p)}^{n-i}dp\hfill \\ & =& c\frac{B(i+{\lambda }_1,n-i+1-{\lambda }_2)}{B(i,n-i+1)},n-i+1-{\lambda }_2>0.\hfill \end{array}$$

(8)

Thus, as explicit formulas for moments of order statistics exist, several mathematical quantities associated with order statistics can be derived from Equation (8).

Additional properties can be found in Giorgi and Nadarajah (2010); Nair et al. (2013); Sunoj and Sankaran (2012).

3. Estimation Methods for the Power–Pareto Distribution

In this section, we discuss the parameter estimation methods employed in this paper. For the estimation of the parameters of the aforementioned reduced versions of the power–Pareto model, we refer to Bhatti et al. (2018); Caeiro et al. (2015); Caeiro and Mateus (2023); Lu and Tao (2007); Mateus and Caeiro (2022); Rytgaard (1990); Shakeel et al. (2016); Zaka et al. (2013). Concerning the three-parameter power–Pareto model, in Equation (1), Hankin and Lee (2006) proposed the estimation of the parameters by two methods: maximum likelihood and quantile least squares. The variance–covariance matrix of those two methods is also provided in Hankin and Lee (2006). The maximum likelihood estimators possess desirable asymptotic properties. However, in the case of small samples, this method may exhibit lower efficiency, when compared to other estimation methods. Therefore, in this paper, we consider not only the estimation methods in Hankin and Lee (2006), but also new estimation methods. In the following, let $x_1$, $x_2$, …, $x_n$ represent a sample of size n, from the power–Pareto distribution with all three parameters assumed unknown.

3.1. Maximum Likelihood (ML)

The maximum likelihood (ML) estimators of the three parameters are obtained by solving an optimization problem, which involves maximizing the likelihood function, or equivalently, minimizing the negative log-likelihood function. This can be expressed as follows:

$${\widehat{\mathit{\theta }}}^{\mathrm{ML}}=\underset{\mathit{\theta }}{argmin}\left\{-\sum _{i=1}^n\left(log\left(Q(u_i\mid \mathit{\theta })\right)+log\left(\frac{{\lambda }_1}{u_i}+\frac{{\lambda }_2}{1-u_i}\right)\right)\right\}.$$

(9)

where $u_i$ represents the solution of the equation $x_i=Q(u_i\mid \mathit{\theta })$. Here, ${\widehat{\mathit{\theta }}}^{\mathrm{ML}}=({\widehat{c}}^{\mathrm{ML}},{\widehat{\lambda }}_1^{\mathrm{ML}},{\widehat{\lambda }}_2^{\mathrm{ML}})$ denotes the ML estimate of $\mathit{\theta }=(c,{\lambda }_1,{\lambda }_2)$.

While the ML estimation method provides asymptotically unbiased estimators and efficiency for large sample sizes, the lack of a closed-form expression for the probability density function requires ${\widehat{\mathit{\theta }}}^{\mathrm{ML}}$ to be obtained through a three-dimensional numerical search. This makes the ML method computationally intensive, and convergence of the negative log-likelihood to the global minimum can be sensitive to the initial values. Thus, this estimation method for the parameters of the power–Pareto can be computationally complex and challenging, especially for large datasets. Additionally, the ML method can be impacted by model misspecification. Therefore, it is crucial to consider alternative methods, potentially with closed-form expressions for the estimators.

3.2. Log Quantile Least Squares (LQLS)

Hankin and Lee (2006) proposed a regression method for estimating the parameters of the power–Pareto distribution using order statistics. To achieve a simple linear relation involving the parameters, a log transformation is applied, yielding the sum of squares

$$\sum _{i=1}^n{\left[log{x}_{\left(i\right)}-\mathbb{E}\left(log\left(X_{\left(i\right)}\right)\right)\right]}^2$$

(10)

that needs to be minimized with respect to the vector parameters $\mathit{\theta }$. Since X is continuous, the inverse probability integral transform guarantees $X\stackrel{d}{=}Q(U\mid \mathit{\theta })$, where U denotes a uniform distribution on the interval $(0,1)$. Consequently,

$$X_{\left(i\right)}\stackrel{d}{=}Q(U_{\left(i\right)}\mid \mathit{\theta }),i=1,\dots ,n,$$

(11)

where $U_{\left(i\right)}$ denotes the $i^{\mathrm{th}}$-order statistic from a sample of size n from a uniform distribution on $(0,1)$. Note that $U_{\left(i\right)}$ has a Beta distribution with parameters i and $n-i+1$. Using Equation (11), we have

$$log\left(X_{\left(i\right)}\right)\stackrel{d}{=}{\lambda }_0+{\lambda }_{1}log\left(U_{\left(i\right)}\right)-{\lambda }_{2}log(1-U_{\left(i\right)}),i=1,\dots ,n,$$

with ${\lambda }_0=log\left(c\right)$. Thus,

$$\begin{array}{ccc}\hfill \mathbb{E}\left(log{U}_{\left(i\right)}\right)& =& \psi \left(i\right)-\psi (n+1)=-\sum _{k=i}^n\frac{1}{k},\hfill \\ \hfill \mathbb{E}\left(log(1-U_{\left(i\right)}\right)& =& \psi (n-i+1)-\psi (n+1)=-\sum _{k=n-i+1}^n\frac{1}{k},\hfill \end{array}$$

where $\psi$ is the digamma function, the derivative of the log gamma function. For n integer,

$$\psi \left(n\right)=-\gamma +\sum _{i=1}^{n-1}\frac{1}{i},$$

where $\gamma$ is Euler’s constant. Then, by introducing the notation $\mathit{\lambda }=({\lambda }_0,{\lambda }_1,{\lambda }_2)$, Equation (10) can be expressed in matrix form as

$$S\left(\mathit{\lambda }\right)={(\mathbf{Y}-\mathbf{X}\mathit{\lambda })}^{\top }(\mathbf{Y}-\mathbf{X}\mathit{\lambda })$$

where $\mathit{Y}$ is a column matrix with the logarithm of the order statistics from the sample, $log{X}_{\left(i\right)}$, and $\mathit{X}$ is an $n\times 3$ matrix where the $i^{\mathrm{th}}$ row is given by $(1,a_i,a_{n-i+1})$, with $a_i=-{\sum }_{k=i}^n\frac{1}{k}$. Applying the least squares method, the vector parameters are estimated by

$${\widehat{\mathit{\lambda }}}^{\mathrm{LQLS}}={\left({\mathbf{X}}^{\top }\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\top }\mathbf{Y};$$

Consequently,

$${\widehat{\mathit{\theta }}}^{\mathrm{LQLS}}=(exp\left({\widehat{\lambda }}_0^{\mathrm{LQLS}}\right),{\widehat{\lambda }}_1^{\mathrm{LQLS}},{\widehat{\lambda }}_2^{\mathrm{LQLS}}).$$

(12)

The LQLS method offers several advantages. Firstly, it is more robust against outliers, as the logarithmic transformation reduces the influence of those values. Secondly, unlike the ML method, estimates are based on the order statistics and require straightforward calculations, leading to computational efficiency. However, the LQLS method may exhibit lower efficiency when compared to the ML method and can be sensitive to small sample sizes.

3.3. Percentile (P)

Percentile points were first used for the determination of parameters of the Weibull model (Kao 1959). This method is nowadays popular due to its simplicity. Estimators are found from the relation, through the CDF or the QF, between probabilities and percentile values. To estimate the parameters, one must consider the same number of percentiles. Therefore, given three distinct cumulative probability levels $p_1$, $p_2$, and $p_3$ ($0<p_1<p_2<p_3<1$), the corresponding $100p_i\%$ percentiles, $i=1,2,3$, are the values $q_1$, $q_2$, and $q_3$ such that

$$F\left(q_i\mid \mathit{\theta }\right)=p_i\iff q_i=Q\left(p_i\mid \mathit{\theta }\right),i=1,2,3,$$

with Q the QF in Equation (1). Next, applying a log transformation to the ratio between two consecutive percentiles, we obtain

$$log\frac{q_2}{q_1}={\lambda }_{1}log\frac{p_2}{p_1}+{\lambda }_{2}log\frac{1-p_1}{1-p_2},$$

and

$$log\frac{q_3}{q_2}={\lambda }_{1}log\frac{p_3}{p_2}+{\lambda }_{2}log\frac{1-p_2}{1-p_3}.$$

Solving the above two equations for ${\lambda }_1$ and ${\lambda }_2$, we obtain

$${\lambda }_1=\frac{log\frac{1-p_2}{1-p_3}log\frac{q_2}{q_1}-log\frac{1-p_1}{1-p_2}log\frac{q_3}{q_2}}{log\frac{p_2}{p_1}log\frac{1-p_2}{1-p_3}-log\frac{p_3}{p_2}log\frac{1-p_1}{1-p_2}},$$

(13)

and

$${\lambda }_2=\frac{-log\frac{p_3}{p_2}log\frac{q_2}{q_1}+log\frac{p_2}{p_1}log\frac{q_3}{q_2}}{log\frac{p_2}{p_1}log\frac{1-p_2}{1-p_3}-log\frac{p_3}{p_2}log\frac{1-p_1}{1-p_2}}.$$

(14)

Next, we use the following equation for the second percentile:

$$q_2=c{p}_2^{{\lambda }_1}{\left(1-p_2\right)}^{-{\lambda }_2}\iff c=q_2{p}_2^{-{\lambda }_1}{\left(1-p_2\right)}^{{\lambda }_2}.$$

(15)

The estimators are obtained by replacing, in Equations (13)–(15), the percentiles $q_i$, by the corresponding sample percentiles. A possible choice for the probabilities is $\left(p_1,p_2,p_3\right)=(0.1,0.5,0.9)$. Equivalently, let I be a set of three distinct values from the first n positive integer values, $\{1,2,\dots ,n\}$, where n denotes the sample size. Another possible choice of percentiles is $q_i=x_{\left(i\right)}$, $i\in I$, associated to the cumulative probabilities $p_i=(i-a)/(n+b)$, where a and b are real constants. A popular choice of the constants is $a=0$ and $b=1$.

The P method offers simplicity in computation and robustness against outliers. This makes it straightforward to implement and suitable for exploratory analysis and initial estimation, providing a quick and effective way to estimate parameters. However, it may be less efficient and less accurate compared to other methods.

3.4. Least Squares (LS) and Weighted Least Squares (WLS)

Here we consider the difference between the empirical and the theoretical CDF. Then, the least squares (LS) estimator of $\mathit{\theta }$, denoted by ${\widehat{\mathit{\theta }}}^{\mathrm{LS}}=({\widehat{c}}^{\mathrm{LS}},{\widehat{\lambda }}_1^{\mathrm{LS}},{\widehat{\lambda }}_2^{\mathrm{LS}})$, can be obtained as

$${\widehat{\mathit{\theta }}}^{\mathrm{LS}}=\underset{\mathit{\theta }}{argmin}\left\{\sum _{i=1}^n{\left(F(x_{\left(i\right)}\mid \mathit{\theta })-\frac{i}{n+1}\right)}^2\right\}.$$

(16)

Furthermore, the estimation of parameters using the weighted least squares (WLS) method, symbolized as ${\widehat{\theta }}^{\mathrm{WLS}}=({\widehat{c}}^{\mathrm{WLS}},{\widehat{\lambda }}_1^{\mathrm{WLS}},{\widehat{\lambda }}_2^{\mathrm{WLS}})$, can be determined by

$${\widehat{\mathit{\theta }}}^{\mathrm{WLS}}=\underset{\mathit{\theta }}{argmin}\left\{\sum _{i=1}^n\frac{{(n+1)}^2(n+2)}{i(n-i+1)}{\left(F(x_{\left(i\right)}\mid \mathit{\theta })-\frac{i}{n+1}\right)}^2\right\}.$$

(17)

The LS method involves minimizing the squared difference between the empirical and theoretical CDFs. This method is straightforward to implement and interpret, making it accessible for various applications. However, LS assumes homoscedasticity, which is not valid, since the variance of $F(x_{\left(i\right)}\mid \mathit{\theta })$ depends on the index i. This violation does not affect the bias of the estimators, but may increase their variance. On the other hand, the weighting scheme used in the WLS method addresses heteroscedasticity by assigning larger weights to observations that are closer to the center of the sample and smaller weights to observations that are closer to the edges of the sample. Additionally, both the LS and WLS methods are computationally intensive, since both depend on the CDF, which needs to be computed numerically.

3.5. Quantile Least Squares (QLS)

The quantile least squares (QLS) estimator of distribution parameters, denoted by ${\widehat{\mathit{\theta }}}^{\mathrm{QLS}}=({\widehat{c}}^{\mathrm{QLS}},{\widehat{\lambda }}_1^{\mathrm{QLS}},{\widehat{\lambda }}_2^{\mathrm{QLS}})$, can be derived by

$${\widehat{\mathit{\theta }}}^{\mathrm{QLS}}=\underset{\mathit{\theta }}{argmin}\left\{\sum _{i=1}^n{\left(x_{\left(i\right)}-{\mu }_{\left(i\right)}\right)}^2\right\},$$

(18)

with ${\mu }_{\left(i\right)}$ defined in Equation (8).

The QLS estimator minimizes the squared difference between the order statistics and their expected value, which can be easily obtained from Equation (8). A limitation of this method is that ${\mu }_{\left(n\right)}$ only exists if ${\lambda }_2<1$; therefore, the QLS should only be considered if ${\lambda }_2$ is a small positive value. Furthermore, the accuracy of parameter estimates can be affected by the presence of large outliers.

A weighted version of this method was not considered because it would further restrict its domain of validity.

4. Comparison of the Estimation Methods by Monte Carlo Simulation

In this section, a Monte Carlo simulation study is carried out to compare the performance of the proposed P, LS, WLS, and QLS estimation methods, and to compare them with the ML and LQLS methods, proposed by Hankin and Lee (2006). Davies package was used for the ML method. Parameter estimation with the LS, WLS, and QLS was performed with the R optimization function optim of the R Software version 4.0.0 and using the starting values provided by the davies.start function in Davies package. The power–Pareto distribution was used to generate $r=1000$ samples with sizes $n=10$, 20, 50, 75, and 100. Sample values are generated using the inversion method. In the simulation study, the following parameter combinations were considered:

• Case 1: $(c,{\lambda }_1,{\lambda }_2)=(1,0.1,0.1)$;
• Case 2: $(c,{\lambda }_1,{\lambda }_2)=(1,0.1,0.4)$;
• Case 3: $(c,{\lambda }_1,{\lambda }_2)=(1,0.4,0.4)$;
• Case 4: $(c,{\lambda }_1,{\lambda }_2)=(1,0.4,0.9)$;
• Case 5: $(c,{\lambda }_1,{\lambda }_2)=(1,0.9,0.4)$.

All the parameter combinations provide a power–Pareto distribution with finite mean value and different levels of positive skewness and kurtosis. Both measures increase with respect to ${\lambda }_2$ and decrease with respect to ${\lambda }_1$. The corresponding densities, for all five cases, are presented in Figure 2.

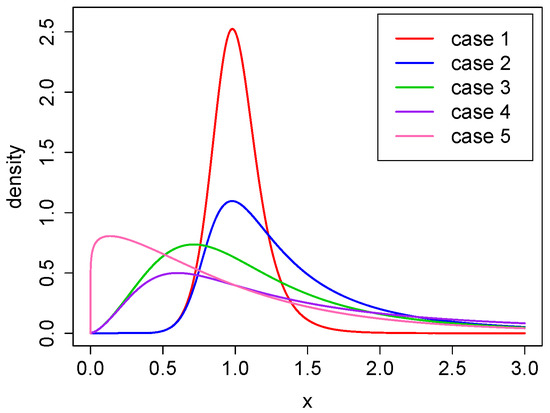
Figure 2. The density function for cases 1–5.

For each of the three parameters of $\mathit{\theta }$, denoted generically by $\theta$, we computed the simulated average bias (ABias), median bias (MBias), and root mean squared error (RMSE) of the corresponding estimator $\widehat{\theta }$. The statistics are defined by

$$\begin{array}{ccc}\hfill \mathrm{ABias}\left(\widehat{\theta }\right)& =& \frac{1}{r}\sum _{i=1}^r({\widehat{\theta }}_i-\theta ),\hfill \\ \hfill \mathrm{MBias}\left(\widehat{\theta }\right)& =& \mathrm{median}({\widehat{\theta }}_1,{\widehat{\theta }}_2,\dots ,{\widehat{\theta }}_r)-\theta ,\hfill \\ \hfill \mathrm{RMSE}\left(\widehat{\theta }\right)& =& \sqrt{\frac{1}{r}\sum _{i=1}^r{({\widehat{\theta }}_i-\theta )}^2},\hfill \end{array}$$

where ${\widehat{\theta }}_i$ is the estimate of $\theta$ computed using the $i^{\mathrm{th}}$ sample.

As a global criterion of comparison, we also computed the average absolute difference between the true and the estimated CDFs,

$${\mathrm{D}}_{\mathrm{abs}}=\frac{1}{r}\sum _{i=1}^r\left(\frac{1}{n}\sum _{j=1}^n|F\left(x_{ij}\right|\mathit{\theta })-F\left(x_{ij}\right|\widehat{\mathit{\theta }})|\right)$$

(19)

and the average of the maximum absolute difference between the true and estimated CDFs,

$${\mathrm{D}}_{\max }=\frac{1}{r}\sum _{i=1}^{r}max|F\left(x_{ij}\right|\mathit{\theta })-F\left(x_{ij}\right|\widehat{\mathit{\theta }})|,$$

(20)

where $x_{ij}$ represents the $j^{\mathrm{th}}$ observation in the $i^{\mathrm{th}}$ sample. The smaller the values of ${\mathrm{D}}_{\mathrm{abs}}$ and ${\mathrm{D}}_{max}$, the better the fit to the data.

The ABias, MBias, and RMSE are presented in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7, while the related Table A1, Table A2, Table A3, Table A4 and Table A5, with the corresponding values, are given in Appendix A. It is important to note that it was impossible to obtain estimates provided by the QLS method for a few samples. This was due to the non-convergence of the optimization method used to solve Equation (18). The number of cases where convergence was achieved is indicated beneath each table. This issue is not critical, as the QLS method generally demonstrates the poorest performance. Thus, we do not advise its use.

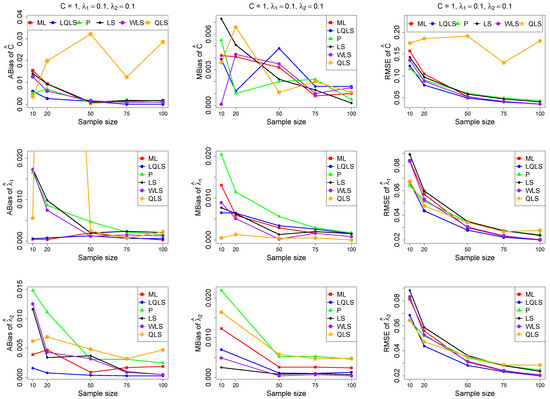
Figure 3. Monte Carlo simulated ABias, MBias, and RMSE from the power–Pareto distribution with $c=1$, ${\lambda }_1=0.1,{\lambda }_2=0.1$.

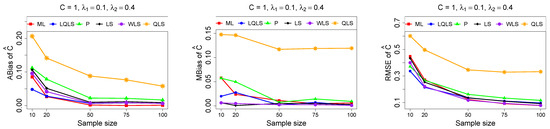
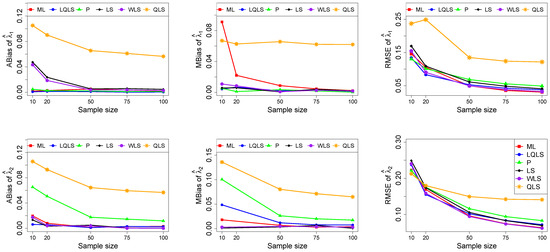
Figure 4. Monte Carlo simulated ABias, MBias, and RMSE from the power–Pareto distribution with $c=1$, ${\lambda }_1=0.1,{\lambda }_2=0.4$.

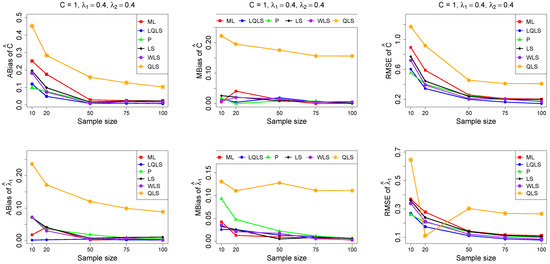
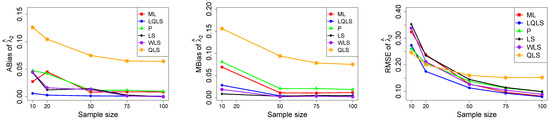
Figure 5. Monte Carlo simulated ABias, MBias, and RMSE from the power–Pareto distribution with $c=1$, ${\lambda }_1=0.4,{\lambda }_2=0.4$.

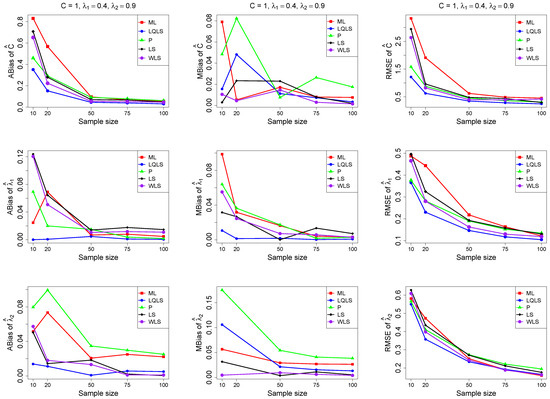
Figure 6. Monte Carlo simulated ABias, MBias, and RMSE from the power–Pareto distribution with $c=1$, ${\lambda }_1=0.4,{\lambda }_2=0.9$. Note that we remove the QLS methods because it is out of the range of plot.

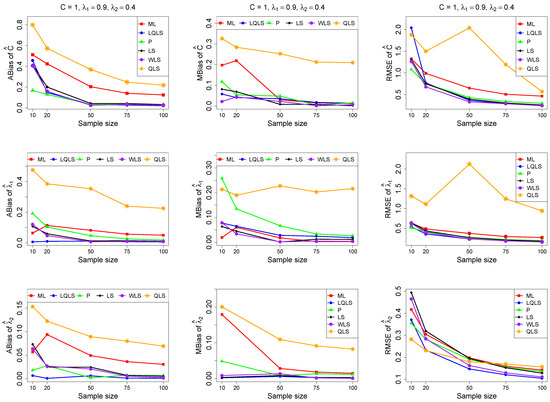
Figure 7. Monte Carlo simulated ABias, MBias, and RMSE from the power–Pareto distribution with $c=1$, ${\lambda }_1=0.9,{\lambda }_2=0.4$.

Moreover, since only small sample sizes were considered, it is difficult to assess the convergence of both median and mean simulated bias to zero, likely attributed to sampling error. However, it is evident that if $n=75$ or $n=100$, the simulated bias is usually closer to zero than if $n=10$ or $n=20$. In almost all cases, the RMSE of the estimators of the parameters c, ${\lambda }_1$, and ${\lambda }_2$ decreases toward zero, when the sample size increases.

Based on RMSE values in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7, it is evident that the performance of various estimation methods varies based on the values of ${\lambda }_1$ and ${\lambda }_2$, and also the sample size (n). Regarding the RMSE, we also have the following additional comments:

• For small sample sizes, such as $n=10$, the P method generally demonstrates the highest efficiency. Moreover, it is not a recommended method for larger sample sizes.
• The WLS method consistently outperforms the LS estimator in estimating each of the three parameters.
• The LQLS method always has a good performance for samples of size $n\ge 20$. The WLS has a similar performance to the LQLS method if ${\lambda }_1\ne {\lambda }_2$. If ${\lambda }_1={\lambda }_2$, LQLS and WLS methods have a similar performance for $n\ge 50$.
• The ML method shows strong performance when ${\lambda }_1=0.1$ and ${\lambda }_2\le 0.4$ and when the sample size is equal to or larger than 50. Thus, we do not recommend its use for samples of size smaller than $n=100$.

Table 1 and Table 2 provide a comparative analysis of Monte Carlo simulated mean absolute difference and mean maximum absolute difference between true and estimated CDFs. The best values are highlighted in bold. The insights derived from the analysis of these tables can be summarized as follows:

Table 1. Monte Carlo simulated average absolute difference ${\mathrm{D}}_{\mathrm{abs}}$ in Equation (19).

${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	n	ML	LQLS	P	LS	WLS	QLS*
0.10	0.10	10	$0.0996$	$0.0935$	$0.1041$	$0.0927$	$0.0912$	$\mathbf{0}.\mathbf{0877}$
		20	$0.0668$	$0.0633$	$0.0717$	$0.0656$	$0.0642$	$\mathbf{0}.\mathbf{0617}$
		50	$0.0405$	$0.0399$	$0.0437$	$0.0410$	$0.0399$	$\mathbf{0}.\mathbf{0395}$
		75	$0.0330$	$\mathbf{0}.\mathbf{0318}$	$0.0352$	$0.0329$	$0.0319$	$0.0319$
		100	$0.0290$	$0.0278$	$0.0307$	$0.0283$	$\mathbf{0}.\mathbf{0276}$	$0.0277$
	0.40	10	$0.0983$	$0.1176$	$0.1287$	$0.0921$	$\mathbf{0}.\mathbf{0905}$	$0.0965$
		20	$0.0675$	$0.0723$	$0.0841$	$0.0653$	$\mathbf{0}.\mathbf{0635}$	$0.0728$
		50	$0.0403$	$0.0430$	$0.0493$	$0.0409$	$\mathbf{0}.\mathbf{0395}$	$0.0538$
		75	$\mathbf{0}.\mathbf{0315}$	$0.0338$	$0.0373$	$0.0328$	$0.0316$	$0.0474$
		100	$\mathbf{0}.\mathbf{0271}$	$0.0292$	$0.0320$	$0.0282$	$0.0273$	$0.0456$
0.40	0.40	10	$0.1000$	$0.0935$	$0.1056$	$0.0926$	$\mathbf{0}.\mathbf{0912}$	$0.0954$
		20	$0.0686$	$\mathbf{0}.\mathbf{0633}$	$0.0717$	$0.0656$	$0.0642$	$0.0694$
		50	$0.0405$	$\mathbf{0}.\mathbf{0399}$	$0.0437$	$0.0410$	$\mathbf{0}.\mathbf{0399}$	$0.0483$
		75	$0.0320$	$\mathbf{0}.\mathbf{0318}$	$0.0352$	$0.0330$	$0.0320$	$0.0412$
		100	$0.0278$	$0.0278$	$0.0307$	$0.0284$	$\mathbf{0}.\mathbf{0276}$	$0.0383$
	0.90	10	$0.0991$	$0.1053$	$0.1237$	$0.0923$	$\mathbf{0}.\mathbf{0909}$	$0.1129$
		20	$0.0688$	$0.0663$	$0.0775$	$0.0655$	$\mathbf{0}.\mathbf{0640}$	$0.1199$
		50	$0.0406$	$0.0408$	$0.0451$	$0.0411$	$\mathbf{0}.\mathbf{0398}$	$0.1458$
		75	$0.0325$	$0.0325$	$0.0356$	$0.0329$	$\mathbf{0}.\mathbf{0318}$	$0.1612$
		100	$0.0276$	$0.0283$	$0.0310$	$0.0283$	$\mathbf{0}.\mathbf{0275}$	$0.1736$
0.9	0.4	10	$0.0996$	$0.0922$	$0.1015$	$0.0924$	$\mathbf{0}.\mathbf{0910}$	$0.0995$
		20	$0.0690$	$\mathbf{0}.\mathbf{0640}$	$0.0708$	$0.0654$	$0.0641$	$0.0749$
		50	$0.0440$	$0.0403$	$0.0440$	$0.0410$	$\mathbf{0}.\mathbf{0398}$	$0.0527$
		75	$0.0349$	$0.0321$	$0.0354$	$0.0329$	$\mathbf{0}.\mathbf{0318}$	$0.0441$
		100	$0.0296$	$0.0282$	$0.0310$	$0.0283$	$\mathbf{0}.\mathbf{0275}$	$0.0413$

* Convergence of this estimation method is not achieved in all cases.

Table 2. Monte Carlo simulated average of the maximum absolute difference ${\mathrm{D}}_{\max }$ in (20).

${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	n	ML	LQLS	P	LS	WLS	QLS*
0.10	0.10	10	$0.1876$	$0.1658$	$0.1961$	$0.1592$	$0.1559$	$\mathbf{0}.\mathbf{1535}$
		20	$0.1234$	$0.1115$	$0.1347$	$0.1157$	$0.1122$	$\mathbf{0}.\mathbf{1089}$
		50	$0.0723$	$0.0698$	$0.0802$	$0.0734$	$0.0705$	$\mathbf{0}.\mathbf{0693}$
		75	$0.0584$	$\mathbf{0}.\mathbf{0557}$	$0.0630$	$0.0587$	$0.0561$	$0.0562$
		100	$0.0515$	$0.0487$	$0.0554$	$0.0507$	$\mathbf{0}.\mathbf{0484}$	$0.0488$
	0.40	10	$0.1807$	$0.2246$	$0.2555$	$0.1562$	$\mathbf{0}.\mathbf{1528}$	$0.1682$
		20	$0.1239$	$0.1353$	$0.1722$	$0.1143$	$\mathbf{0}.\mathbf{1098}$	$0.1304$
		50	$0.0715$	$0.0786$	$0.0982$	$0.0727$	$\mathbf{0}.\mathbf{0692}$	$0.0982$
		75	$0.0552$	$0.0605$	$0.0712$	$0.0580$	$\mathbf{0}.\mathbf{0550}$	$0.0882$
		100	$0.0475$	$0.0519$	$0.0600$	$0.0500$	$\mathbf{0}.\mathbf{0473}$	$0.0855$
0.40	0.40	10	$0.1894$	$0.1656$	$0.1990$	$0.1592$	$\mathbf{0}.\mathbf{1561}$	$0.1654$
		20	$0.1278$	$\mathbf{0}.\mathbf{1115}$	$0.1348$	$0.1159$	$0.1122$	$0.1234$
		50	$0.0722$	$\mathbf{0}.\mathbf{0698}$	$0.0802$	$0.0734$	$0.0705$	$0.0878$
		75	$0.0567$	$\mathbf{0}.\mathbf{0557}$	$0.0630$	$0.0590$	$0.0567$	$0.0766$
		100	$0.0491$	$\mathbf{0}.\mathbf{0487}$	$0.0554$	$0.0511$	$0.0491$	$0.0714$
	0.90	10	$0.1855$	$0.1919$	$0.2394$	$0.1578$	$\mathbf{0}.\mathbf{1542}$	$0.2110$
		20	$0.1272$	$0.1179$	$0.1514$	$0.1156$	$\mathbf{0}.\mathbf{1115}$	$0.2456$
		50	$0.0727$	$0.0718$	$0.0845$	$0.0735$	$\mathbf{0}.\mathbf{0706}$	$0.3158$
		75	$0.0574$	$0.0572$	$0.0642$	$0.0586$	$\mathbf{0}.\mathbf{0558}$	$0.3550$
		100	$0.0488$	$0.0498$	$0.0561$	$0.0506$	$\mathbf{0}.\mathbf{0484}$	$0.3816$
0.90	0.40	10	$0.1860$	$0.1614$	$0.1896$	$0.1586$	$\mathbf{0}.\mathbf{1553}$	$0.1704$
		20	$0.1289$	$0.1126$	$0.1335$	$0.1152$	$\mathbf{0}.\mathbf{1119}$	$0.1323$
		50	$0.0809$	$0.0708$	$0.0817$	$0.0732$	$\mathbf{0}.\mathbf{0701}$	$0.0954$
		75	$0.0630$	$0.0565$	$0.0640$	$0.0590$	$\mathbf{0}.\mathbf{0563}$	$0.0815$
		100	$0.0527$	$0.0495$	$0.0561$	$0.0506$	$\mathbf{0}.\mathbf{0485}$	$0.0771$

* Convergence of this estimation method is not achieved in all cases.

• The performance rankings across different methods are consistent between the two tables.
• The WLS methods demonstrate a very good performance, typically yielding the smallest or second smallest values of ${\mathrm{D}}_{\mathrm{abs}}$ and ${\mathrm{D}}_{\max }$.
• The LS method consistently performs slightly worse than WLS, and LQLS shows similar performance to WLS when $n\le 50$, except when ${\lambda }_1=0.1$ and ${\lambda }_2=0.4$. The ML method is never the best performer, but it shows good performance if $n\ge 50$ and ${\lambda }_1<{\lambda }_2$ or ${\lambda }_1={\lambda }_2=0.4$.
• The remaining methods exhibit poor performance. Both P and WLS methods provide generally the largest absolute differences. The exception is the QLS method, for small sample sizes and ${\lambda }_1={\lambda }_2=0.1$.

5. Application

In this section, we use two real datasets to illustrate the behavior of the estimators, described in Section 3. To compare the fitted power–Pareto model we computed the Kolmogorov–Smirnov (K-S) statistic and associated p-value for each method. Since parameters are estimated, the p-value of the K-S test is obtained using Monte Carlo simulation. To measure the goodness-of-fit, we also computed the empirical correlation coefficient $r_{\mathrm{Q}}$, between empirical quantiles $x_i$ and the corresponding estimated quantiles $q_i=Q(x_i\mid \widehat{\mathit{\theta }})$, $i=1,2,\dots ,n$ (Beirlant et al. 2004). Since both vectors have monotonically increasing values, $r_{\mathrm{Q}}$ will be non-negative.

5.1. Household Income by State in USA

The U.S. Census Bureau defines “household income” as the gross income of all people aged 15 years or older who live in the same housing unit, regardless of their relationship. Household income reflects the standard of living in distinct households and is an important indicator of the local and national economies. Table 3 presents a dataset comprising the median household income in 2016 in the United States, in dollars, of $n=52$ states, as available on the website data.world.1

Table 3. Household income by state dataset.

60,309	48,237	77,351	58,328	46,894	68,070	72,084	77,556	59,294	72,508
52,277	54,678	73,684	57,780	62,706	57,300	60,365	58,032	46,345	43,103
51,950	75,346	73,820	58,319	71,728	41,983	56,199	58,302	60,651	56,623
77,900	69,940	49,493	62,758	54,920	61,478	55,146	52,039	60,407	62,290
62,851	55,505	58,685	52,448	59,396	68,932	62,145	67,880	71,822	45,308
61,103	59,073

The histogram and the boxplot of these observations, in Figure 8, are compatible with the power–Pareto distribution.

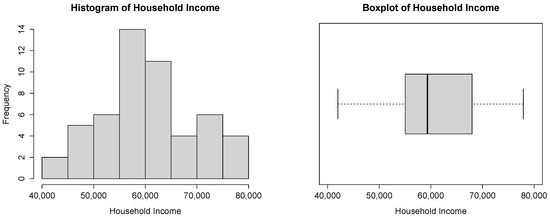
Figure 8. Histogram and boxplot for the household income dataset.

Table 4 summarizes the estimated parameters, K-S statistics, associated p-values, and the empirical correlation coefficient for various statistical methods applied to the household income dataset.

Table 4. Parameter estimates under all methods, K-S statistics, and the associated values for the household income data.

Method	$\widehat{\mathit{c}}$	${\widehat{\mathit{\lambda }}}_1$	${\widehat{\mathit{\lambda }}}_2$	K-S	p-Value	${\mathit{r}}_{\mathbf{Q}}$
ML	59,636.68	0.0855	0.0909	0.0965	0.6819	0.9838
LQLS	61,322.05	0.0981	0.0723	0.1064	0.5624	0.9868
P	58,936.56	0.0904	0.1004	0.0858	0.8067	0.9822
LS	59,604.21	0.0893	0.0937	0.0980	0.6639	0.9836
WLS	59,578.92	0.0890	0.0934	0.0965	0.6823	0.9837
QLS	62,520.99	0.1093	0.0635	0.1222	0.3880	0.9858

Regarding Table 4, it is shown that all estimation techniques produce p-values exceeding $0.05$, indicating a favorable fit of the power–Pareto distribution. Considering that a lower K-S statistic and a higher p-value signify a better fit, and a higher $r_{\mathrm{Q}}$ implies a stronger relationship between observed and expected quantiles, the P method stands out with notably high p-value and $r_{\mathrm{Q}}$, indicating a good fit. Moreover, the LQLS method achieves the highest $r_{\mathrm{Q}}$, further supporting its efficacy. Although the QLS method has a large $r_{\mathrm{Q}}$ value, the p-value is the lowest.

Figure 9 depicts Q-Q plots, comparing the observed data with the estimated quantiles provided from various methods. If the points in the Q-Q plots align closely along the diagonal line, it indicates that the estimated distribution provides an adequate statistical fit. Figure 10 provides the empirical CDF vs. the fitted CDF, for the six different estimation methods.

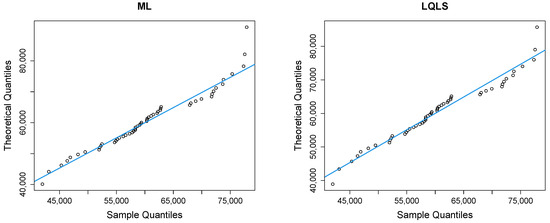
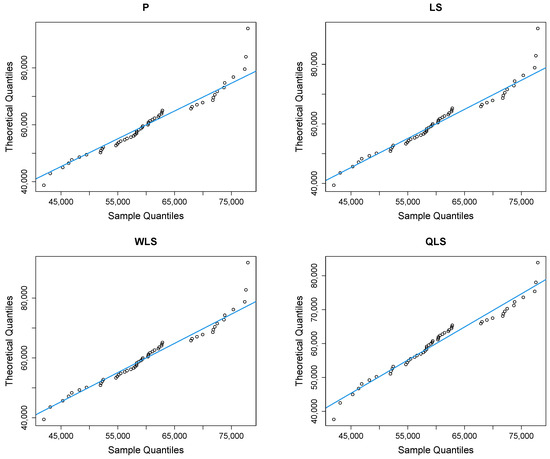
Figure 9. Q-Q plots of the household income dataset.

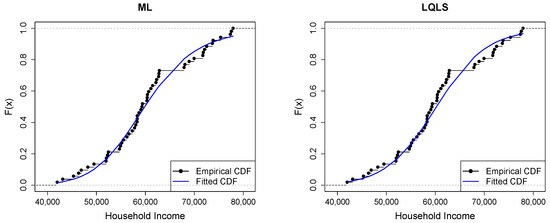
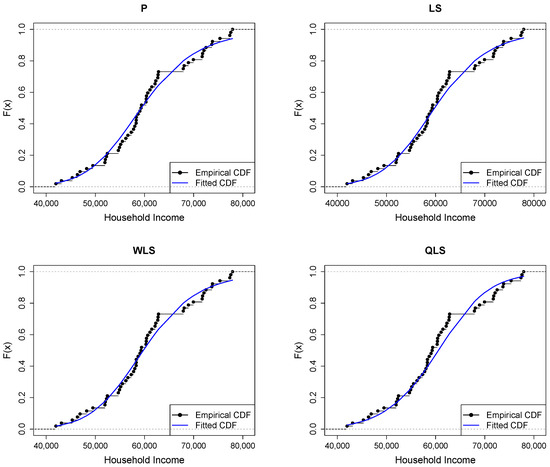
Figure 10. Empirical vs. fitted CDFs using different estimators for the household income dataset.

Figure 9 shows a good similarity between empirical and fitted quantiles in the body of the distribution, although there are discrepancies in the right tail. All methods provide a good correspondence in the body of the distribution. But the LQLS and QLS methods provide the best correspondence in the right tail. Similar conclusions can be drawn from Figure 10.

5.2. Peak Concentrations

For the examination of accidental releases of hazardous gases, a method commonly employed is the instantaneous release of a finite volume of gas into a surrounding flow field. Concentration measurements are then taken at a fixed location downwind. In a series of experiments conducted by Hall (1991) involving 100 repetitions, a key parameter for risk assessment was the peak concentrations achieved. The dataset, studied by Hankin and Lee (2006), is provided in Table 5.

Table 5. Peak concentration dataset.

12.100	1.701	9.074	7.056	7.025	4.777	8.870	7.656	10.920	6.806
$8.757$	$5.670$	$12.890$	$7.119$	$2.523$	$9.055$	$7.341$	$3.938$	$10.460$	$11.050$
$6.678$	$3.026$	$6.806$	$11.750$	$5.742$	$4.007$	$7.340$	$2.849$	$6.418$	$8.456$
$5.702$	$7.262$	$6.086$	$7.568$	$7.941$	$14.030$	$7.844$	$3.150$	$7.818$	$8.554$
$5.796$	$3.497$	$7.087$	$15.800$	$4.316$	$7.591$	$13.990$	$9.185$	$6.286$	$11.040$
$11.280$	$6.804$	$5.292$	$6.273$	$10.840$	$6.587$	$8.757$	$9.344$	$5.513$	$11.040$
$16.160$	$11.500$	$5.072$	$9.041$	$8.927$	$7.560$	$4.694$	$6.832$	$15.380$	$10.250$
$10.550$	$7.655$	$5.229$	$14.900$	$7.087$	$2.646$	$3.704$	$9.293$	$6.117$	$13.650$
$5.072$	$6.045$	$6.458$	$4.993$	$7.403$	$13.480$	$11.530$	$9.926$	$3.451$	$16.910$
$9.010$	$3.215$	$5.859$	$10.020$	$6.962$	$11.440$	$5.765$	$6.928$	$5.171$	$7.825$

In Figure 11, we present the histogram and the boxplot of the dataset. Both plots are compatible with the power–Pareto distribution.

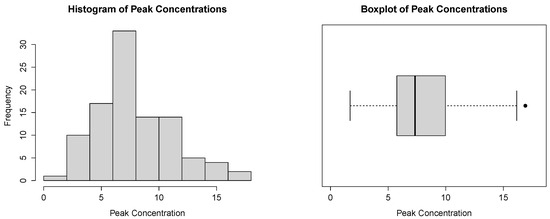
Figure 11. Histogram and boxplot for the peak concentration dataset.

Table 6 provides the estimated parameters, K-S statistics, the associated p-values, and the empirical correlation coefficient for various statistical methods for the peak concentration dataset.

Table 6. Parameter estimates under all methods, K-S statistics, and the associated values for the peak concentration dataset.

Method	$\widehat{\mathit{c}}$	${\widehat{\mathit{\lambda }}}_1$	${\widehat{\mathit{\lambda }}}_2$	K-S	p-Value	${\mathit{r}}_{\mathbf{Q}}$
ML	$8.3220$	$0.3189$	$0.1812$	$0.0634$	$0.7924$	$0.9928$
LQLS	$8.4020$	$0.3213$	$0.1729$	$0.0651$	$0.7649$	$0.9934$
P	$7.9760$	$0.3182$	$0.1984$	$0.0590$	$0.8565$	$0.9908$
LS	$7.7014$	$0.2740$	$0.2293$	$0.0509$	$0.9459$	$0.9834$
WLS	$8.1498$	$0.3142$	$0.1980$	$0.0584$	$0.8647$	$0.9908$
QLS	$9.1620$	$0.3842$	$0.1383$	$0.0854$	$0.4349$	$0.9930$

It is observed that the data conform well to the distribution for all estimation methods, with all associated p-values exceeding $0.05$ and empirical correlation coefficient close to 1. Results for the different estimation methods are similar, except for the QLS, which presents a much higher K-S value. Furthermore, the P, LS, and WLS methods demonstrate favorable outcomes, as indicated by the low K-S statistic, high p-value, and high empirical correlation coefficient, $r_{\mathrm{Q}}$.

Figure 12 presents Q-Q plots, contrasting the observed data with the estimated quantiles derived from the fitted power–Pareto distribution. Both the P and WLS methods demonstrate a good correspondence, with similar patterns and some discrepancies in the right tail. The QLS again evidences overfitting in the right tail.

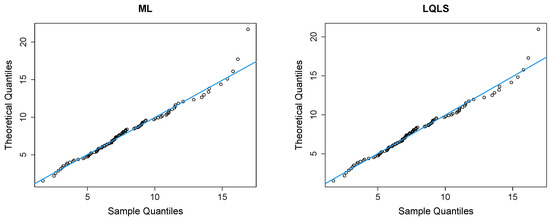
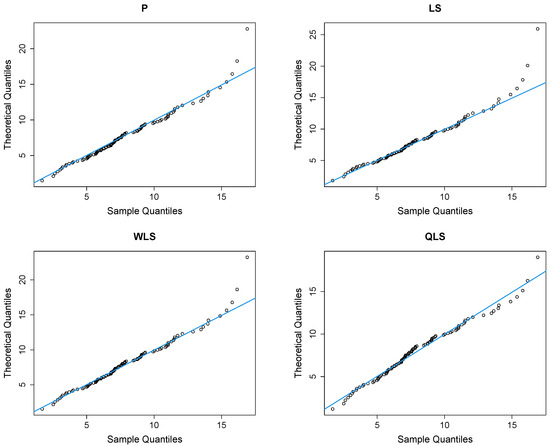
Figure 12. Q-Q plots of the peak concentration dataset.

Figure 13 displays the empirical and fitted CDFs. All methods work quite well for analyzing this dataset. However, the P and WLS are the ones that provide the best correspondence between CDFs.

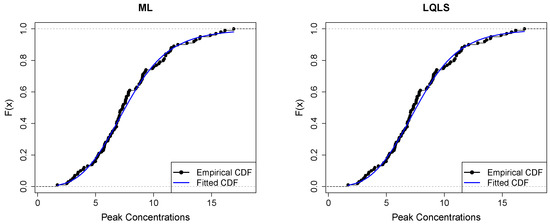
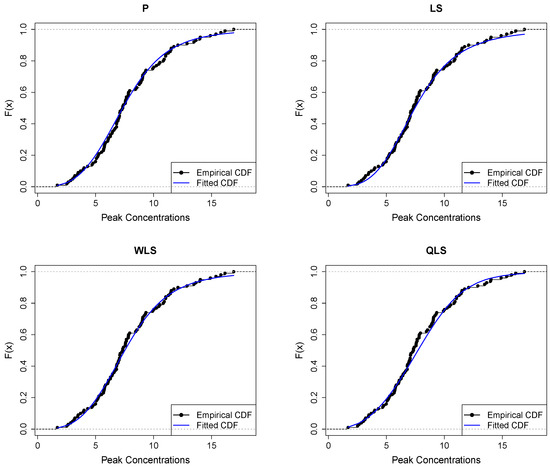
Figure 13. Empirical vs. fitted CDFs using different estimators for the peak concentration dataset.

6. Conclusions

This study examines the power–Pareto model for non-negative variables. The model has three parameters and can exhibit various shapes, making it suitable for modelling both symmetrical and skewed data. The paper explores distributional characteristics, with a particular focus on different parameter estimation techniques, some of them introduced in this work.

The numerical analysis reveals the importance of selecting an appropriate estimation method based on both sample size and the values of the power–Pareto distribution parameters. Our results indicate that for very small sample sizes, the P method performs well in terms of RMSE. However, for larger sample sizes, the LQLS and WLS methods emerge as adequate choices and are recommended for practical applications.

Additionally, it is worth noting that the ML method also exhibits good performance for larger sample sizes, typically with at least 100 observations. However, it is essential to consider the computational time associated with this method, which is longer when compared to other methods, a factor to weigh in the decision-making process.