Abstract
Traditional methods for predicting feeding amounts rely on historical data and experience but fail to account for non-linear fish growth and the influence of water quality and meteorological factors. This study presents a novel approach for sea bass feeding prediction based on Spearman + RF feature optimization and multi-scale feature fusion using a transformer model. A logistic growth curve model is used to analyze sea bass growth and establish the relationship between biomass and feeding amount. Spearman correlation analysis and random forest optimize the feature set for improved prediction accuracy. A dual-encoder structure incorporates historical feeding data and biomass along with water quality and meteorological information. Multi-scale feature fusion addresses time-scale inconsistencies between input variables The results showed that the MSE and MAE of the improved transformer model for sea bass feeding prediction were 0.42 and 0.31, respectively, which decreased by 43% in MSE and 33% in MAE compared to the traditional transformer model.
1. Introduction
According to the China Fisheries Statistical Yearbook, the production of sea bass in aquaculture has consistently exceeded 100,000 tons in recent years, with Guangdong, Fujian, and other regions accounting for over 80% of the national output [1]. Sea bass, as one of the key economic fish species and a leading variety in national marine aquaculture, requires precise feeding control to optimize aquaculture efficiency and economic returns. Overfeeding leads to feed wastage and an increase in harmful bacteria in the aquatic environment, raising maintenance costs. Conversely, insufficient feeding results in nutrient deficiencies and slowed growth. Therefore, determining the optimal feeding amount that ensures proper growth without waste is a pressing scientific challenge in aquaculture.
Traditional feeding prediction methods largely depend on historical data and expert experience, typically determining daily feed amounts based on feeding rate tables and the fish’s body weight [2]. However, fish growth is rarely a simple linear process and typically follows a specific growth curve. These curves provide a more accurate reflection of fish weight changes at different growth stages, allowing for better predictions of their feed requirements [3]. For example, Xiaoyan et al. [4] applied the logistic growth curve model to analyze the early growth of largemouth bass, demonstrating that the model accurately simulates the S-shaped growth curve. Similarly, Xiao Jun et al. [5] utilized the logistic model to examine Nile tilapia growth, showing that the model effectively fits the growth curve with a high R2 value (0.991), revealing dynamic growth patterns. Li Yuhu et al. [6] used the Gompertz curve to simulate the growth of the vannamei shrimp, capturing its rapid and stable growth phases. Li Jun et al. [7] employed the Von Bertalanffy model for lip fish growth in net-cage farming, which effectively described the log-growth and stable phases, providing valuable insights for aquaculture management. Therefore, establishing growth curves for sea bass and adjusting feeding amounts based on weight and growth stages allows for optimized feed delivery at each stage, improving feed conversion efficiency and reducing costs. Although growth curves are essential, they fail to account for the significant effects of water quality and meteorological factors on sea bass feeding and growth.
Real-time water quality monitoring is an indispensable practice in aquaculture. Adjusting feeding amounts based on measured water quality parameters can help reduce feed costs. Buentello et al. [8] identified that factors such as water temperature and dissolved oxygen influence daily feed demand and feed conversion efficiency. For example, peak feeding demand for spotted bass occurs at 27.1 °C with 100% dissolved oxygen saturation. Wu Qiangze [9] developed an intelligent feeding system using fuzzy logic control, incorporating dissolved oxygen, water temperature, and fish weight as input variables, with feeding amount as the output. Wu et al. [10] introduced an adaptive neural network fuzzy inference system to estimate feeding amounts based on dissolved oxygen levels, achieving a prediction accuracy of 97.89%, providing an efficient feeding decision-making tool. Chen et al. [11] combined backpropagation neural networks with evolutionary algorithms to predict fish food intake using variables such as group size, average weight, dissolved oxygen, and water temperature. Their model demonstrated a correlation coefficient of 0.96 between predicted and actual feeding amounts, offering a robust method for feed intake prediction. While meteorological factors, such as temperature, light, and wind speed, may not directly influence sea bass feeding, they can affect feeding behavior by altering the aquatic environment and sea bass physiology [12]. Extended cloudy weather and low light conditions can reduce dissolved oxygen levels, potentially impairing feeding and growth. Thus, accurate feeding prediction models must incorporate meteorological influences to improve feeding management. However, most existing models rely on linear regression or traditional machine learning techniques, which are unable to fully capture the complex nonlinear relationships in time-series data involving biomass, water quality, and meteorological factors. This limitation underscores the need for more advanced predictive models to enhance both forecast accuracy and management efficiency in aquaculture.
Recently, the transformer model has demonstrated significant success in natural language processing due to its powerful self-attention mechanism, which overcomes the inefficiencies, gradient explosion, and parallelization issues inherent in traditional models when processing long sequences [13]. The transformer excels at temporal modeling, enabling the capture of global dependencies in input data. Zhu et al. [14] developed a semi-supervised transformer network based on adaptive density proxies for fish density estimation in recirculating aquaculture systems, showcasing improved estimation performance and providing a novel tool for aquaculture management. Liu et al. [15] integrated the Swin transformer model with multi-scale feature fusion to propose an advanced underwater fish segmentation method. This approach leverages self-attention mechanisms to capture long-range dependencies and integrates multi-resolution features, enhancing performance in complex scenarios. Thus, applying transformer models to predict sea bass feeding amounts offers a promising solution to improve aquaculture management accuracy and efficiency. However, when dealing with long time-series data, transformer models face challenges in extracting complex nonlinear relationships among multiple features, limiting their ability to effectively integrate data from varying time scales in sea bass feeding prediction. Liu et al. [16] and Zhang et al. [17] addressed this limitation by using multi-scale feature extraction and sparse connections, significantly improving prediction accuracy in time-series data and compensating for the transformer model’s feature extraction shortcomings.
In summary, this study addresses the shortcomings of traditional feeding prediction methods that rely on historical data and experience, as well as the challenges posed by non-linear fish growth and the failure to account for water quality and meteorological influences. First, the logistic growth curve is applied to model the growth stages of sea bass and establish the relationship between biomass and feeding amount. Given the significant impact of water quality and meteorological factors on sea bass feeding behavior in real aquaculture settings, this study further explores the complex interactions between environmental parameters and feeding amounts to enhance model prediction accuracy. Additionally, the original feature set often contains highly correlated features that introduce redundancy, increasing model complexity and reducing generalization ability. To address this, a Spearman correlation analysis and random forest-based feature optimization method is proposed to construct a more precise and effective feature set. Since biomass, water quality, and meteorological data exhibit time-series characteristics, the transformer model is used to explore complex nonlinear relationships within time-series data. A dual-encoder architecture is proposed to handle inputs with different time scales for historical feeding amounts, biomass, water quality, and meteorological data. Furthermore, a multi-scale feature fusion approach is introduced to address inconsistencies across time scales, enhancing the model’s ability to capture temporal dependencies. This results in the development of an optimized transformer-based feeding prediction model for sea bass, which is compared with other models to validate its accuracy and reliability.
2. Materials and Methods
2.1. Data Acquisition
The experiment was conducted with sea bass as the study subject at a fish farming enterprise in a pond located in Rizhao, Shandong Province, from 19 July 2024 to 27 November 2024. The experimental setup is shown in Figure 1a. Feeding was administered twice daily at 7:00 a.m. and 4:00 p.m. Key water quality parameters—water temperature, dissolved oxygen, pH, and salinity—were measured using water quality sensors (Figure 1b). Additionally, a small meteorological station (Figure 1c) was deployed to collect relevant meteorological data, including temperature, humidity, air pressure, wind speed, wind direction, and precipitation. Both water quality and meteorological data were recorded every 5 min. To minimize stress on the sea bass, weight measurements were taken every 20 days to avoid frequent handling.

Figure 1.
(a) Pond culture environment. (b) Water quality sensor. (c) Small weather station.
2.2. Data Creation
2.2.1. Application of Growth Curves in Sea Bass
Sea bass weight does not follow a simple linear growth pattern, and to minimize the potential harm from frequent weighing, data collection was limited. Therefore, growth curve models were employed, as they effectively describe the growth patterns of individual fish across various developmental stages. Logistic growth models, which are commonly used for this purpose, are known to accurately predict growth changes. The logistic growth equation is an S-shaped curve that theoretically represents the different growth characteristics at various stages of life. The equation is as follows:
Using weight data from sea bass at different monthly ages, a growth curve was derived, and the goodness of fit was assessed using the coefficient of determination (R2). A higher R2 value indicates a better fit of the model to the observed data, as shown in Table 1.

Table 1.
Parameter estimates and fit of the growth curve.
Table 1 shows that the logistic model fits the data well, with an R2 value of 0.992. This indicates that the sea bass exhibit rapid weight gain during early development, which gradually slows, consistent with the characteristic S-shape of the logistic model. Based on this growth curve, daily weight estimates for the sea bass were generated, enabling the establishment of a relationship between biomass and feeding amount.
2.2.2. Relationship Between Biomass and Feed Intake in Sea Bass
Biomass, defined as the weight of the sea bass, is a critical factor influencing feed intake in aquaculture. Biomass directly correlates with the fish’s metabolic demands and growth potential. Previous research has shown that sea bass have varying energy requirements during different growth stages, necessitating adjustments in feeding strategies based on biomass. In the seedling period, the sea bass weight is small but grows rapidly, and the daily feeding rate should be controlled at 5% to 6% of the fish’s body weight. The sea bass’ metabolism is vigorous at this stage. The demand for protein and energy is high, and it needs high-protein and high-energy feeds to meet its growth needs. With growth, the fish’s body weight increases. In order to prevent health problems caused by overfeeding and to control the breeding cost, the daily feeding rate should be gradually reduced. In the early stage of aquaculture, the weight of the sea bass increases and the growth rate is still fast. The daily feeding rate can be 4% to 5% of the body weight of the fish. Entering the middle and late stage of aquaculture, the growth rate tends to stabilize. The daily feeding rate should be adjusted to 3% to 4% of the body weight of the fish. At this time, the sea bass have a higher body weight and improved ability to digest and absorb feed; however, overfeeding should still be avoided to prevent feed waste and water pollution. In the late stage of breeding, the growth rate further slows down, and the daily feeding rate can be reduced to 2% to 3% of the body weight of the fish [18]. The relationship between biomass and daily feeding rates is summarized in Table 2.

Table 2.
Relationship between biomass of sea bass and daily feeding rate.
However, the aquaculture environment is dynamic, and factors such as water quality and meteorological conditions can influence sea bass feeding behavior and physiological needs, resulting in discrepancies between theoretical and actual feeding amounts. Thus, in this study, both water quality and meteorological data, as well as fish weight data, were used to comprehensively analyze the daily feeding requirements of the sea bass.
Finally, the data set was divided into a training set, test set and verification set in a ratio of 7:2:1.
2.2.3. Data Cleaning
Prior to model training, the data underwent a cleaning process. Water quality and meteorological data were first merged. Missing values in the raw data were addressed using linear interpolation, as excessive missing data can significantly affect model performance. In time-series prediction tasks, missing values may distort the model’s understanding of temporal trends, ultimately diminishing the prediction accuracy. To ensure data integrity, duplicate entries resulting from data transmission errors were removed to avoid introducing bias into the model.
Additionally, to mitigate the impact of data with varying measurement scales, normalization was performed. Data with large ranges can diminish the influence of variables with smaller ranges. Therefore, min–max normalization was applied to rescale all data to a uniform range of [0, 1]. This approach improves the stability and predictive performance of the model.
2.3. Model Building
The initial feature set may include highly correlated features that introduce redundant information, thereby increasing the model’s complexity and reducing generalization performance. To address this, we employed a Spearman + random forest (Spear + RF) feature optimization method. Moreover, since sea bass biomass, water quality, and meteorological data exhibit time-series characteristics, a dual-encoder architecture was integrated into the transformer model. This architecture separately processes inputs at different time scales, specifically for historical feeding amounts, biomass, water quality, and meteorological data. A multi-scale feature fusion method was also incorporated to enhance the model’s ability to handle inconsistencies in time scales across different data types, effectively capturing multi-scale temporal dependencies. This approach led to the development of an optimized transformer-based feeding prediction model for sea bass, which was compared with other models to validate its performance.
2.3.1. Spear + RF Feature Optimization
In feeding amount prediction, high correlations between features can lead to multicollinearity, which undermines the accuracy of regression coefficients and reduces both model interpretability and predictive power. To mitigate this issue, we first conducted a Spearman correlation analysis to examine the nonlinear relationships between features and identify those most strongly associated with feeding amounts. The Spearman correlation coefficient is calculated as follows:
di is the rank difference between the -th pair of variables, and N is the total number of data points. The Spearman coefficient ranges from −1 to 1, where positive values indicate a positive correlation, negative values indicate a negative correlation, and larger absolute values represent stronger correlations. The correlation results between features and feeding amounts are presented in Table 3.

Table 3.
Correlation analysis of each characteristic factor and feeding amount Spearman.
When applying the random forest model to predict feed intake using multiple feature variables, it is possible to determine the importance of each feature in the modeling process without changing the data’s dimensionality. Consequently, assessing feature importance is a critical strategy in feature optimization for the random forest algorithm. The evaluation methodology is as follows: for each decision tree generated, predictions are made using out-of-bag (OOB) data with shuffled features. If a given feature significantly impacts the prediction results, the number of correct predictions will notably decrease when that feature is shuffled. This process is repeated multiple times, allowing the calculation of the feature’s importance score based on the correct prediction rates across all feature subsets. Once the importance scores for all features are obtained, they are ranked in descending order, as shown in Figure 2.
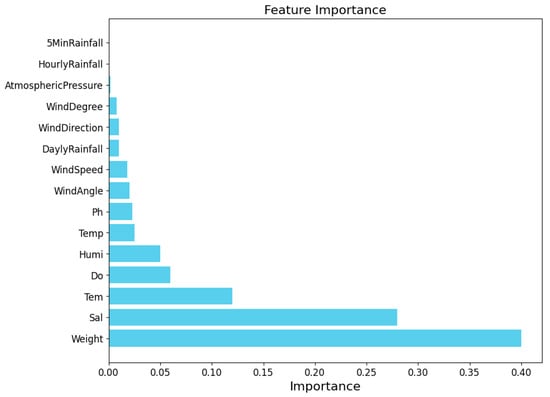
Figure 2.
Ranking of feature importance evaluation results.
As observed in Figure 2, weight is the most important feature, followed by salinity, water temperature, dissolved oxygen, humidity, air temperature, and pH. Features such as wind direction angle, wind speed, daily rainfall, wind direction, wind speed angle, air pressure, and hourly rainfall are of lower importance, with 5-min rainfall being the least important feature.
While Spearman correlation measures the monotonic relationship between features and the target variable, it only evaluates the correlation between individual features and feed intake and does not assess their actual contribution to the model’s predictive performance. To address this, after performing an initial Spearman analysis to evaluate the relationship between features and feed intake, the random forest algorithm is utilized to further analyze feature importance and optimize feature selection. Combining both methods allows for the identification of the optimal feature set for model input.
Root mean square error (RMSE) was chosen as the evaluation metric for the predictive accuracy of the random forest model. In the initial phase of random forest regression, all features are included in the model construction, after which the importance of each feature is evaluated. The feature selection process follows an iterative strategy: initially, the least important feature (e.g., 5-min rainfall) is removed, and the model is refitted with the remaining features. This iterative process continues, with the least important feature being removed at each step. The final optimal feature subset is determined based on the change in RMSE, as shown in Table 4.

Table 4.
Prediction accuracy after removing features.
Table 4 clearly indicates that after removing features such as 5-min rainfall, hourly rainfall, air pressure, wind speed angle, wind direction, daily rainfall, wind speed, and wind direction angle, the RMSE decreased to 0.0292. However, further removal of features caused an increase in RMSE. Therefore, the optimal feature subset for model input consists of weight, salinity, water temperature, dissolved oxygen, humidity, pH, and air temperature.
The selection of features such as water temperature and salinity through Spearman correlation analysis combined with random forest (Spearman + RF) accurately highlights their significant impact on sea bass growth and feeding behavior. In real-world aquaculture settings, these environmental parameters directly influence metabolic rates and overall fish health, thereby substantially affecting feed conversion efficiency and farming profitability. By optimizing these critical factors, not only is the accuracy of feeding prediction models enhanced, but more informed and effective farming management decisions can be reached. This research thus provides a robust foundation for precision and intelligent aquaculture practices, offering valuable practical guidance.
This approach strengthens the study’s relevance and persuasiveness in the field by demonstrating how scientifically selected environmental variables can improve both the efficiency and sustainability of aquaculture operations.
2.3.2. Dual-Encoder Multi-Scale Transformer Model
The transformer model is a neural network architecture built upon the attention mechanism, widely adopted in natural language processing (NLP) and sequence modeling tasks. Compared to traditional recurrent neural networks (RNNs) and convolutional neural networks (CNNs), the transformer demonstrates a significant advantage in processing long sequences and capturing long-range dependencies. In the context of complex time-series data that exhibit long-range dependencies and high-dimensional information, the transformer model can effectively capture intricate relationships between data points, thus enhancing predictive accuracy.
The key advantage of the transformer architecture is its ability to process all positions in the input sequence in parallel during both the encoding and decoding phases. This feature not only strengthens the model’s ability to capture global information but also enhances the efficiency of handling long sequences. The self-attention mechanism enables the model to assess the relevance of different elements within the sequence dynamically, based on their interrelationships, allowing it to excel in extracting contextual dependencies.
The transformer model comprises an encoder and a decoder. The encoder transforms the input sequence into a series of hidden representations, while the decoder converts these representations into the output sequence. Both the encoder and decoder consist of multiple layers of self-attention and feed-forward neural networks. These layers perform operations such as self-attention, positional encoding, and feed-forward mapping to encode the input sequence and decode the target sequence.
In this study, we propose the dual-encoder multi-scale transformer (DEMST) model, as depicted in Figure 3. This model utilizes dual encoders that separately input feed intake and weight data, as well as water quality and meteorological data, and employs a multi-scale feature fusion approach to process the input data for predicting the feed intake of sea bass. By handling input data with varying temporal resolutions, the DEMST model effectively captures multi-scale temporal dependencies, enabling precise predictions.
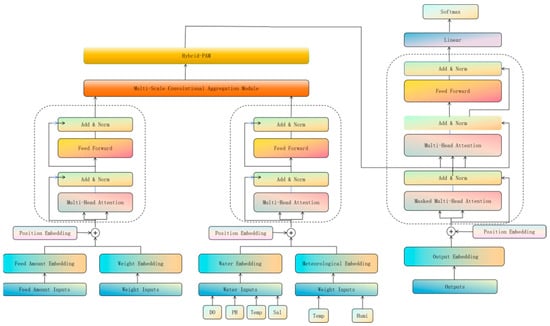
Figure 3.
Dual-encoder multi-scale transformer model structure.
A dual encoder structure is used in this study. By feeding different types of data into the two encoders separately, the dual encoder is able to extract and encode features independently for each type of data to better capture its different time-dependent features. The model input data are categorized into two types: historical feeding and body weight data, and water quality and meteorological data. The dual-encoder model is based on the transformer structure, which contains a multi-layer self-attention layer and a feed-forward neural network layer. The self-attention mechanism can dynamically adjust the weights according to the positional dependence of the input sequences to capture the temporal features, while the feed-forward neural network layer improves the expressive ability and explores the nonlinear relationships. Among them, the encoder processing historical feeding and body weight data focuses on short-term time dependence to recognize the short-term feeding trend, while the encoder processing water quality and meteorological data focuses on long-term time dependence to capture its long-term impact on the aquaculture environment. The two encoders extract features independently to obtain their respective feature representations.
The core components of the DEMST model are the hybrid pyramid attention mechanism (Hybrid-PAM) and the multi-scale convolutional aggregation module (MSCAM). The detailed structure is shown in Figure 4. Hybrid-PAM adopts a hierarchical feature extraction approach, constructing a pyramid structure to handle data at different time resolutions. In the lower layers, the model processes high-resolution data to capture short-term, fine-grained patterns, while the upper layers focus on low-resolution data to capture long-term trends. This design enables the model to process input data across various time steps, effectively capturing dependencies at different temporal granularities. The MSCAM, on the other hand, extends the feature dimension of the input sequence into a high-dimensional space through a linear layer. Convolutional layers with varying kernel sizes and strides are then used to extract features across different time scales. The MSCAM aggregates these features by concatenating the outputs of each convolutional layer along the time dimension, forming a comprehensive multi-resolution feature representation. By applying feature convolution, the DEMST model strengthens its ability to capture cross-temporal information.
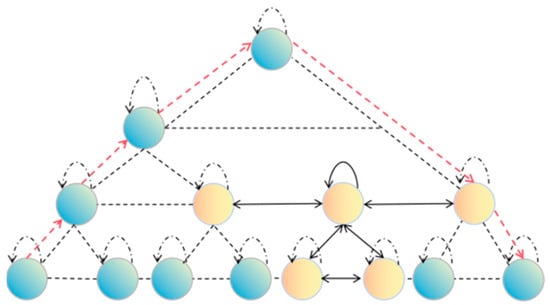
Figure 4.
Hybrid pyramid attention mechanism.
Convolutional layers progressively aggregate the detailed features from lower layers to higher layers, producing more abstract representations. The cross-step connection mechanism allows the model to skip a certain number of nodes within each layer and directly establish connections with more distant nodes, thus capturing dependencies over multiple time scales. The self-attention mechanism is then used to compute attention weights for the connections between each node and its adjacent nodes, child nodes, parent nodes, and cross-step nodes, dynamically adjusting the importance of each connection. The weighted features are subsequently aggregated to form the final representation of each node, which combines both local and global information across different temporal scales.
where denotes the neighboring nodes in the scale; A denotes the number of neighboring nodes in the scale; denotes the child nodes; denotes the parent nodes; denotes the nodes connected by hopping step; and is the total number of nodes that need to be computed for the attention mechanism [16]. In each layer of the pyramid, the self-attention mechanism is used to compute the attention weights between the nodes with the Formula [16]:
where is the query matrix corresponding to xi; and are the key and value matrices, respectively; is the length of the sequence; and is the output obtained by noting.
In the MSCAM [19], the input sequence is first mapped to a higher-dimensional space via a linear layer. The module then performs feature convolutions with convolutional layers of varying kernel sizes and strides to capture features at multiple temporal scales. To effectively combine these multi-scale features, MSCAM concatenates the outputs of each convolutional layer along the time dimension, resulting in a multi-resolution feature representation. To reduce the risk of overfitting and simplify the model, MSCAM reduces the number of parameters by adjusting the feature dimensions. Ultimately, all multi-scale features are concatenated to form a pyramid-like feature structure, as shown in Figure 5, which captures a broad range of multi-scale temporal dependencies for improved attention processing and feature fusion.
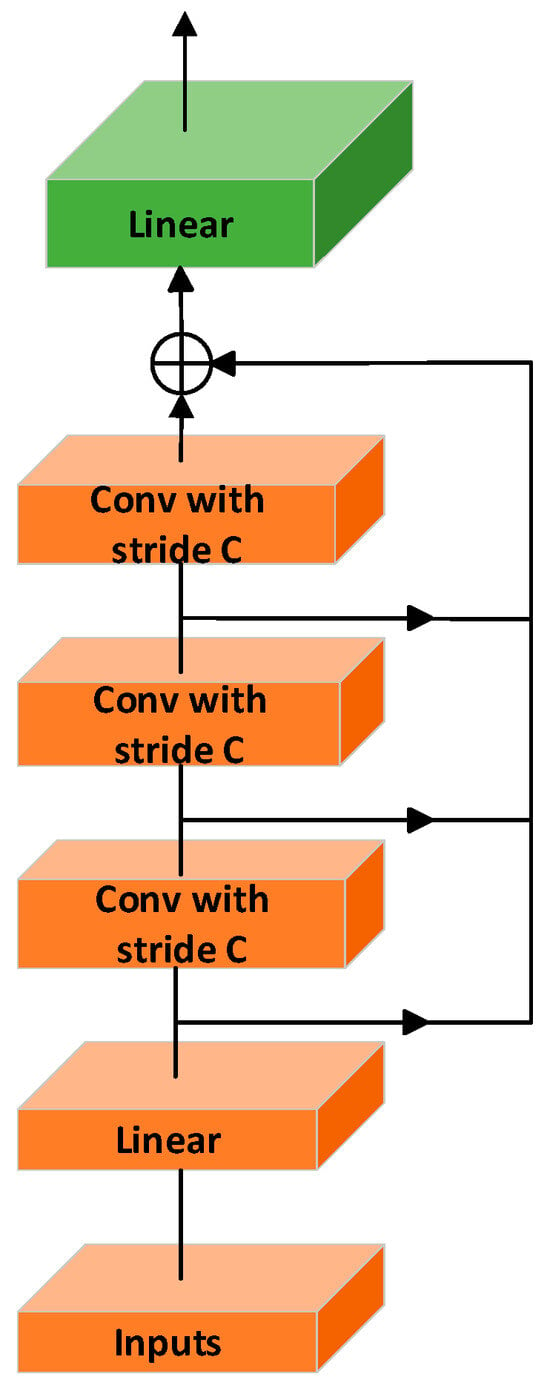
Figure 5.
Multi-scale convolution aggregation module, where B denotes the batch size, L denotes the length of the historical sequence, D denotes the dimension of each node, and DK denotes the size of the key matrix.
2.4. Model Evaluation Metrics
In order to assess the predictive accuracy of the model and facilitate comparisons with other models, we employed two widely-used evaluation metrics: mean absolute error (MAE) and mean squared error (MSE).
2.5. Experimental Environment
The hardware environment used for model development consists of a 12th Gen Intel (R) Core (TM) i7-12700H processor, an Nvidia RTX 3060 graphics card, and a Windows 11 64-bit operating system. The model was implemented using Python 3.8.2 and the PyTorch 1.12.0 framework, with PyCharm 2024.3.1.1 as the development platform. All comparison models were executed in the same environment to ensure fairness.
3. Results
3.1. Model Prediction Results
The preprocessed data were partitioned into training and test sets using a feature optimization algorithm. The features considered in the study include historical feeding amounts, weight, salinity, water temperature, dissolved oxygen, humidity, pH, and air temperature. The model was built and the parameters optimized using the training set, followed by validation of the model’s performance on the test set. The comparison between the predicted and actual feeding amounts is shown in the figure. The solid black line represents the actual feeding amounts, while the solid red line denotes the predicted values. It is evident from the Figure 6 that the predicted feeding amounts exhibit a strong fit with the actual values. One of the sample indexes is five minutes long.
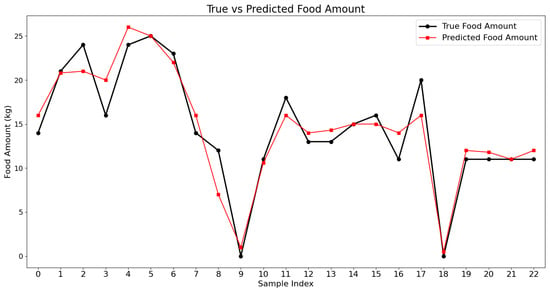
Figure 6.
Comparison of predicted feeding amount and actual feeding amount.
3.2. Ablation Study
To evaluate the impact of the individual components added to the model, an ablation study was conducted to assess the influence of each module on model performance. The evaluation was based on the metrics outlined in Section 2.4, and the results are summarized in Table 5.

Table 5.
Results of ablation experiments.
The findings suggest that the raw, unoptimized features were filtered using the Spearman correlation coefficient, eliminating weakly correlated features. By combining the Spearman correlation coefficient with the random forest (RF) feature optimization method, we derived the optimal input features for the model. The comparison of results demonstrates that, after feature optimization, the model’s predictive performance improved. Notably, the combination of Spearman correlation and RF feature optimization outperforms methods individually in both MSE and MAE, indicating that the presence of redundant features detracts from model performance. Moreover, the inclusion of a dual-encoder input and multi-scale feature fusion enhanced the model’s ability to capture patterns across different time scales. The DEMST model demonstrated superior performance compared to the transformer model, as evidenced by a significant improvement in predictive accuracy.
3.3. Comparison with Other Models
To further validate the proposed approach, the feature-optimized, multi-scale feature fusion transformer model was compared with three other models using the same dataset. The fitting performance of each model is illustrated in Figure 7.
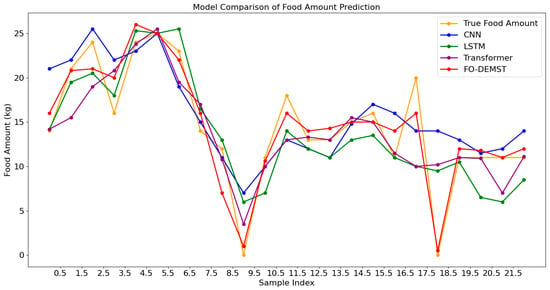
Figure 7.
Fitting effect of different models.
In Figure 7, the CNN model exhibits the poorest fitting performance, with considerable discrepancies between the predicted and actual values. The LSTM model struggles to fit most extreme values during periods of feeding reduction, resulting in suboptimal prediction performance. The transformer model performs reasonably well overall. However, the FO-DEMST model’s fitting curve is closest to the actual values.
For a more rigorous comparison, we applied the evaluation metrics from Section 2.4 to assess the accuracy of the models. The results are presented in Table 6.

Table 6.
Performance evaluation of different models.
As shown in Table 6, the multi-scale feature fusion transformer model outperforms the CNN, LSTM, and transformer models in terms of both MSE and MAE. Specifically, the MSE is 0.42, and the MAE is 0.31, indicating that the model achieves exceptional prediction accuracy on this dataset. These results demonstrate that the multi-scale feature fusion transformer model provides more accurate predictions than the other models evaluated in this study.
3.4. Model Timing Analysis
To further assess the computational complexity of the model, the time taken for computations on the same dataset was recorded. The details, as shown in Table 7, include the training time, testing time, and overall execution time for the model.

Table 7.
Time consumption statistics for different models.
Upon detailed analysis, it was observed that, despite the internal network structure of the proposed method being relatively complex, leading to longer runtimes for individual modules, the improved model accuracy justifies the increased computational cost. As a result, the model retains substantial predictive power and advantages, even with the higher computational demands.
4. Discussion
4.1. Relationship with Previous Studies and Hypothesis Verification
The results of this study are consistent with and supplement the existing research on aquaculture feeding prediction. The application of the logistic growth curve model in describing the growth of sea bass is in line with the research conclusions of Xiaoyan et al. [4] and Xiao Jun et al. [5], who also used the logistic model to effectively simulate the growth process of fish, which confirms that the growth curve model can better reflect the nonlinear growth characteristics of fish and provides a reasonable basis for establishing the relationship between biomass and feeding amount. This overcomes the defect that traditional methods only rely on historical data and experience to predict feeding amount and cannot adapt to the dynamic changes of fish growth [2].
In terms of feature optimization, the Spearman + RF method screens out key features that have a significant impact on the feeding amount, which is consistent with the research of Buentello et al. [9] that water quality factors such as water temperature and dissolved oxygen affect fish feeding behavior. At the same time, this method removes redundant features, reduces the complexity of the model, and improves the generalization ability, which is also supported by the view of Chen et al. [11] that optimizing the feature set is beneficial to improving the performance of the prediction model.
The excellent performance of the proposed FO-DEMST model in feeding amount prediction verifies the hypothesis that integrating multi-scale feature fusion and dual-encoder structure into the transformer model can improve the prediction accuracy. This is similar to the research results of Liu et al. [16] and Zhang et al. [17], who pointed out that processing time series data with multi-scale methods can better capture the temporal dependencies in the data. The dual-encoder structure in the model separately processes different types of data, which solves the problem that the traditional transformer model has difficulty in effectively handling data with different time scales in aquaculture scenarios [14], and further confirms the effectiveness of the model design.
4.2. Implications of the Findings
The improvement of the prediction accuracy of the FO-DEMST model has important practical significance for aquaculture production. Accurate feeding amount prediction can avoid the waste of feed caused by overfeeding and the slow growth of fish caused by underfeeding, thereby reducing aquaculture costs and improving economic benefits. At the same time, reducing feed waste can also reduce the pollution of the aquaculture environment caused by residual feed, which is conducive to the sustainable development of aquaculture.
The model is applicable to both open pond aquaculture and closed recirculating aquaculture systems, which expands its scope of application. In open ponds, where environmental factors such as meteorology and water quality are more variable, the model can comprehensively consider these factors to make more accurate predictions. In recirculating aquaculture systems with relatively stable environmental conditions, the model can also play a role in precise feeding by relying on key parameters, providing technical support for intelligent aquaculture.
4.3. Future Research Directions
Although the FO-DEMST model has achieved good results, there are still some aspects that can be improved in future research. Firstly, the research data comes from a single aquaculture site, and the model’s adaptability in different regions and aquaculture environments needs to be further verified. Expanding the sample range and including more diverse aquaculture scenarios can enhance the generalization ability of the model.
Secondly, the current model does not take into account some biological factors such as the health status of sea bass and the stocking density. Adding these factors into the model can make the prediction more in line with the actual situation of aquaculture. For example, combining with underwater monitoring technology to obtain the activity status and health information of fish in real time, and integrating them into the model as features.
In addition, the current model mainly focuses on short-term feeding amount prediction. In the future, we can explore the long-term prediction of feeding amount, considering the seasonal changes and long-term growth trends of fish, so as to provide more comprehensive decision-making support for aquaculture production planning and feed management.
Finally, the computational complexity of the FO-DEMST model is relatively high. Reducing the model’s complexity while ensuring prediction accuracy is also a direction worthy of research, and is conducive to the popularization and application of the model in actual aquaculture production.
5. Conclusions
This study presents a model that combines feature optimization with an enhanced transformer architecture for predicting the feeding amounts of European seabass (Dicentrarchus labrax). By using a logistic growth curve to model the varying growth characteristics of the seabass at different stages, the relationship between biomass and feeding amounts is established. Since feeding behavior in aquaculture is influenced by factors such as water quality and environmental conditions, the model incorporates the relationship between the farming environment and feeding amounts. Feature optimization was performed through Spearman correlation analysis and random forest-based feature selection, resulting in a refined and effective feature set.
Additionally, the FO-DEMST model processes input data at different temporal granularities, effectively capturing multi-scale temporal dependencies to achieve accurate predictions. Experimental results show that after feature optimization, the FO-DEMST model achieves an MSE of 0.42 and an MAE of 0.31 for feeding amount prediction. These results demonstrate a significant improvement in prediction accuracy over the transformer model. Furthermore, the FO-DEMST model outperforms CNN, LSTM, and transformer models in terms of both accuracy and efficiency, confirming the superiority and effectiveness of the FO-DEMST model.
The improved prediction accuracy of the FO-DEMST model, as evidenced by reductions in MSE and MAE, translates into tangible benefits for aquaculture operations. Specifically, more precise feeding predictions can lead to significant savings in feed costs—by minimizing waste—and reduce management time through optimized feeding schedules, ultimately enhancing overall farm efficiency and sustainability.
This model is particularly suited for both open pond systems and closed-loop recirculating aquaculture systems (RAS). In open pond settings, where environmental factors like water temperature, dissolved oxygen, and weather conditions can fluctuate widely, the inclusion of these variables in the model allows for more accurate feeding predictions. Similarly, in RAS, where precise control over water quality parameters is possible, the model’s ability to integrate detailed environmental data enhances its predictive accuracy. However, the implementation may require adjustments depending on the specific monitoring capabilities and operational scales of different facilities.
Author Contributions
H.W.: Investigation, Methodology, Project administration, Software, Supervision, Validation, Writing—original draft, Writing—review and editing, Conceptualization, Data curation, Formal Analysis. Q.Z.: Writing—review and editing, Writing—original draft. H.Z.: Data curation, Formal Analysis, Funding acquisition, Investigation, Project administration, Resources, Supervision, Visualization, Writing—review and editing, Methodology. Y.T.: Formal Analysis, Methodology, Supervision, Writing—review and editing. Y.J.: Writing—review and editing. J.Q.: Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Open Fund Project 2024 of the Key Laboratory of Smart Farming (2024-TJAULSBF-2404), The Key Technologies R & D Program of Tianjin: 24YFZCSN00200, 2024 Gannan Prefecture Science and Technology Plan Project: 2024ZY1NC004, National Key Research and Development Program of China (2020YFD0900600), and Supported by the earmarked fund for CARS (CARS-47), Tianjin Mariculture Industry Technology System Innovation Team Construction Project (ITTMRS2021000), The Key Technologies R&D Program of Tianjin (23YFZCSN00310), Scientific Developing Foundation of Tianjin Education Commission (2023KJ004).
Data Availability Statement
The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors wish to extend their gratitude to ChuGuang aquaculture Co., Ltd. for providing a venue for conducting their experiment. They also thank Tianjin Agricultural University for its invaluable technical support during the research process.
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Ministry of Agriculture and Rural Affairs of the People’s Republic of China; Fisheries and Fishery Administration; National Station of Aquatic Technology Promotion; Chinese Society of Fisheries. China Fishery Statistical Yearbook 2023; China Agriculture Press: Beijing, China, 2023. [Google Scholar]
- De Verdal, H.; Komen, H.; Quillet, E.; Chatain, B.; Allal, F.; Benzie, J.A.H.; Vandeputte, M. Improving feed efficiency in fish using selective breeding: A review. Rev. Aquac. 2018, 10, 833–851. [Google Scholar] [CrossRef]
- Wang, Z.; Lian, J. Analysis of factors affecting the growth of fish in offshore cage farming—Application of Interpretive Structural Modeling Method. J. Fish. Sci. 1999, 300–303. [Google Scholar]
- He, X.Y.; Bai, J.J.; Fan, J.J.; Li, S.J.; Liu, X.L. A study on the early growth and development of largemouth bass. J. Dalian Ocean Univ. 2011, 26, 23–29. [Google Scholar]
- Xiao, J.; Ling, Z.B.; Tang, Z.Y.; Luo, Y.J.; Guo, Z.B.; Guo, E.Y.; Yan, X.; Zhang, M.; Gan, X. Growth—Related analysis and model construction of Nile tilapia. Oceanol. Et Limnol. Sin. 2012, 43, 72–78. [Google Scholar]
- Li, Y.H.; Song, Q.Q.; Zhang, Z.H.; Huang, H.; Zhou, H.l.; Xiang, J.H. Analysis of growth and development rules and growth curve fitting of Litopenaeus vannamei. South China Fish. Sci. 2015, 11, 89–95. [Google Scholar] [CrossRef]
- Li, J.; Luo, X.N.; Jin, G.H.; Wei, H.X. Growth performance and growth model of cage—Reared lipfish bones. J. Guangdong Ocean Univ. 2015, 35, 99–103. [Google Scholar]
- Buentello, J.; Gatlin, M.D.; Neill, H.W. Effects of water temperature and dissolved oxygen on daily feed consumption, feed utilization and growth of channel catfish (Ictalurus punctatus). Aquaculture 2000, 182, 339–352. [Google Scholar] [CrossRef]
- Qiangze, W. A Study on Intelligent Feeding System for Pond Culture; Nanjing University Agricultural: Nanjing, China, 2016. [Google Scholar]
- Wu, T.; Huang, Y.; Chen, J. Development of an adaptive neural-based fuzzy inference system for feeding decision-making assessment in silver perch (Bidyanus bidyanus) culture. Aquac. Eng. 2015, 66, 41–51. [Google Scholar] [CrossRef]
- Chen, L.; Yang, X.; Sun, C.; Wang, Y.; Xu, D.; Zhou, C. Feed intake prediction model for group fish using the MEA-BP neuralnetwork in intensive aquaculture. Inf. Process. Agric. 2020, 7, 261–271. [Google Scholar] [CrossRef]
- Volkoff, H.; Rønnestad, I. Effects of temperature on feeding and digestive processes in fish. Temperature 2020, 7, 307–320. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inform. Process. Syst. 2017, 30, 5998–6008. [Google Scholar] [CrossRef]
- Zhu, K.; Yang, X.; Yang, C.; Fu, T.; Ma, P.; Hu, W.; Zhou, C. Semi-supervised fish school density estimation and counting network in recirculating aquaculture systems based on adaptive density proxy. Comput. Electron. Agric. 2025, 230, 109874. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, S.; Wang, Y.; Xin, J.; Li, D. An enhanced underwater fish segmentation method in complex scenes using Swin transformer with cross-scale feature fusion. Vis. Comput. 2024, 41, 5189–5203. [Google Scholar] [CrossRef]
- Liu, S.; Yu, H.; Liao, C.; Li, J.; Lin, W.; Liu, A.X.; Dustdar, S. Pyraformer: Lowcomplexity pyramidal attention for long-range time series modeling and forecasting. In Proceedings of the Tenth International Conference on Learning Representations, Virtual, 25–29 April 2022; pp. 1–20. [Google Scholar] [CrossRef]
- Zhang, R.; Hao, Y. Time Series Prediction Based on Multi-Scale Feature Extraction. Mathematics 2024, 12, 973. [Google Scholar] [CrossRef]
- Lin, G.B.; Lin, J.H. Sea bass culture technology i healthy pond culture technology of sea bass. China Fish. 2005, 8, 42–44. [Google Scholar]
- Dai, Y.; Gieseke, F.; Oehmcke, S.; Wu, Y.; Barnard, K. Attentional Feature Fusion. Comput. Vis. Pattern Recognit. 2020, 9, 29. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).