Abstract
Negative binomial (NB) regression model has been used to analyze crime in previous studies. The disadvantage of the NB model is that it cannot deal with spatial effects. Therefore, spatial regression models, such as the geographically weighted Poisson regression (GWPR) model, were introduced to address spatial heterogeneity in crime analysis. However, GWPR could not account for overdispersion, which is commonly observed in crime data. The geographically weighted negative binomial model (GWNBR) was adopted to address spatial heterogeneity and overdispersion simultaneously in crime analysis, based on a 3-year data set collected from ZG city, China, in this study. The count of residential burglaries was used as the dependent variable to calibrate the above models, and the results revealed that the GWPR and GWNBR models performed better than NB for reducing spatial dependency in the model residuals. GWNBR outperformed GWPR for incorporating overdispersion. Therefore, GWNBR was proven to be a promising tool for crime modeling.
1. Introduction
Due to the disparities of built environments and socio-demographic factors, the uneven distribution of crime across different neighborhoods has long been confirmed by many studies [1,2,3,4]. Previous researchers have found that the vast majority of crimes are committed in a few specific locations [5]. Among the many theories of crime geography, routine activity theory, and crime pattern theory are usually employed to explain the spatial agglomeration of criminal activity.
Routine activity theory proposed by Cohen and Felson is a theoretical framework commonly used in crime analysis [6], which states that the convergence of a motivated offender, a vulnerable victim, and a crime-prone place will lead to criminal offenses. Routine activity theory suggests that certain places are more likely to be criminal victimizations, such as bars, schools, and gas stations. Proposed by Brantingham and Brantingham [7], crime pattern theory argues that crime is not randomly distributed over space and time, but presents a specific pattern of places where the intersection of offenders and victims are more vulnerable to crime. The above two theories effectively explain why crime is spatially concentrated and form ‘hot spots’ of criminal offenses.
Social disorganization theory has been widely used to explore the relationship between crime and related neighborhood characteristics [8]. One of the premises of social disorganization theory is that the crime rate of disadvantageous communities is higher than others, which has been supported by many empirical studies [9]. Statistical techniques have been used to quantitatively investigate the relationship between crime and influencing factors, such as ordinary least squares (OLS) [10,11]. Crime research usually takes the number of crimes as a dependent variable, which is discrete, whereas the OLS model assumes that the dependent variable should be continuous. Therefore, the Poisson and negative binomial regression models have been adopted for crime modeling [12,13,14,15].
The above-mentioned techniques are all global regression methods, which assume that the connections between crime and related factors are constant across the space, whereas this is not always true [16]. Due to the inherently stochastic nature of crimes and the complex environments in which they occur, it is unrealistic to describe the influence of the risk factors on crime with a constant relationship. Many methodologies have been proposed to analyze the spatially varying relationships between crime and its related risk factors, such as geographically weighted regression models [17,18], the eigenvector spatial filtering model [19,20,21], and the Bayesian spatially varying coefficients model, etc. [22,23].
Among these models, the geographically weighted regression (GWR) has been widely applied due to its simple conceptual framework and convenience of interpretation when it comes to spatial heterogeneity modeling for crime [17]. According to the type of response variable, GWR has evolved into different versions, such as geographic weight Gaussian regression, geographic weight Poisson regression (GWPR), and geographic weight logistic regression (GWLR). Crime data are usually reported in the form of the number of criminal cases, which can be used as the response variable without any transformation in the GWPR model [24,25].
Crime rate and the number of crimes is usually used as a dependent variable in crime analysis due to the complexity of crime patterns. Overdispersion is another issue to be resolved in crime modeling when the dependent variable is a count [26,27]. Statistically speaking, overdispersion means that there are more variations in the data than predicted. Count data are very popular in crime research, while overdispersion is a difficulty in analyzing such data. Failure to address the overdispersion properly will lead to the underestimation of standard errors and misleading inference for the coefficients [28]. Although the negative binomial model (NB) has been adopted to address overdispersion as an alternative to the Poisson regression model in crime analysis [29,30,31], it fails to deal with spatial heterogeneity.
Although there are some studies that have indicated that it is necessary to model spatial heterogeneity and overdispersion simultaneously [32,33], empirical research integrating overdispersion into spatial heterogeneity has not been fully explored in crime analysis. This study is intended to fill this gap by modeling spatial heterogeneity in crimes incorporating overdispersion. As in the rest of the world, residential burglary is the most frequent crime in China, which is perhaps the most analyzed crime spatially across the globe. Therefore, residential burglary was selected as an example in this study.
2. Data and Methods
2.1. Study Area
With the development of the economy, the crime situation in China is becoming increasingly serious. Residential burglary is the largest crime type in China, and there are more than 1 million burglaries each year [34]. This research was carried out in, Z.G.; which is the largest city in the southeast of China. It is one of the most crowded cities in China and the population of ZG is about 14.9 million in 2018, which is a 3rd of the whole country. Since the reform and open policy changes in the 1980s, the economy of ZG city has made rapid developments due to the advantages of geographical location. In 2018, the per capita GDP (Gross Domestic Product) of ZG was 22,167 US dollars, and it has become one of the 5 richest cities in China.
2.2. Data
The data used in this research were collected from, Z.G.; China. The crime data were provided by the ZG Municipal Public Security Bureau. There were more than 150,000 residential burglary records during the period of 2013–2015. The demographic and socioeconomic data were obtained from the ZG Statistical Yearbook published by the ZG Statistics Bureau. The number of bus stops was collected from the geographical information system of ZG city.
Different zone systems have been used in crime analysis, such as states, counties, cities, block groups, and census tracts. A police station is the most grass-roots law enforcement agency in China. The whole city was divided into many areas that were called police station management areas (PSMA) according to the location of each police station. All policing policies are carried out through the police stations in China. Compared with other units, PSMA can be easily integrated with the safety planning process. Therefore, PSMA was selected as the spatial unit in this study, and all data were aggregated at the PSMA-level. There were 215 PSMAs in ZG city. The number of residential burglaries in each PSMA varied from 9 to 3547, as shown in Figure 1.
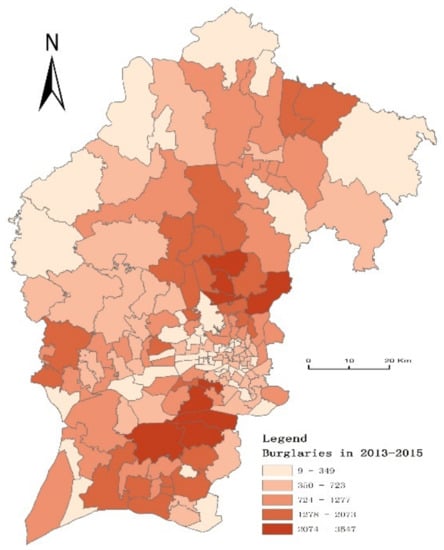
Figure 1.
Spatial distribution of residential burglary in 2013–2015.
Following previous studies [24,25,35,36,37], the variables selected for this research are shown in Table 1, as well as their descriptive statistics. The number of burglaries was adopted as the dependent variable in this study. The number of household units was selected as the exposure variable. The explanatory variables, which were commonly used in previous crime research, were selected according to the literature [38,39,40,41]. In order to prevent multi-collinearity between variables, to ensure a significant impact on the results of the model, a bivariate correlation test should be conducted before further analyses. The results are shown in Table 2. All the correlation coefficients were less than 0.7, which indicated that there was no strong correlation between explanatory variables.

Table 1.
Summary of variable and descriptive statistics.

Table 2.
The results of the bivariate correlation test.
2.3. Methodology
Although there are different methodologies to deal with spatial heterogeneity, GWR has been widely used for its convenience. The methodology adopted in this research was based on GWR. In order to compare the model performance, 4 models were developed in this study and are described briefly in this section.
2.3.1. Negative Binomial Model (NB)
The normal distribution of dependent variables is one of the basic assumptions of traditional linear regression models; however, this hypothesis is usually not met in practice. For example, when the number of crimes was adopted as the dependent variable, the distribution no longer presented as a normal distribution but as a Poisson or negative binomial distribution [42,43]. Then the generalized linear models, such as the Poisson regression model, were employed alternatively. The Poisson regression model is usually employed when the dependent variable is count data. However, the assumption of the Poisson model is that the mean is equal to the variance, which is often violated in crime data. Therefore, the negative binomial model is often used instead, to account for the overdispersion.
where stands for negative binominal, is the number of residential burglaries in the th () PSMA, is the th explanatory variable for PSMA , () are the coefficients, is the number of household units in PSMA , which is the offset variable, and is the parameter of overdispersion.
2.3.2. Geographically Weighted Poisson Model (GWPR)
The Poisson regression model was extended to geographically weighted Poisson regression (GWPR) when the geographical coordinates of observations were incorporated into the modeling process. The geographically weighted Poisson model was an extension of GWR under the context of generalized linear models, while the dependent variable was count data. The framework of GWPR is described as follows:
where are the geographical coordinates of the centroid of PSMA , and is the function of the centroid of PSMA , which could be calculated by:
where is the vector of the local parameters in PSMA , and is the spatial weight matrix, which can be presented as:
where is the weight given to PSMA during the calibrating procedure for PSMA .
2.3.3. Geographically Weighted Negative Binomial Model (GWNBR)
GWPR has been employed to explore the relationship between crime and related risk factors when the response variable was the number of crimes [24]. As Xu and Huang indicated, using GWPR to model count data was only a temporary solution, which was mainly restricted by the available software GWR4 [44]. GWR4 was developed by Nakaya et al. [45] to model spatial heterogeneity, which did not provide the calibration of GWR with a negative binomial structure. In order to overcome this disadvantage, the geographically weighted negative binomial regression model (GWNBR) should be used, which can model spatial heterogeneity and overdispersion simultaneously [33]. The GWNBR model can be described as follows:
where is an offset variable, which is the number of house units, is the coefficient for the explanatory variable , for , is the number of residential burglaries in the PSMA, and is the parameter of overdispersion.
A modified iteratively reweighted least squares (IRLS) method and a Newton–Raphson (NR) algorithm were used alternately to estimate and according to Silva and Rodrigues [33].
The basic idea of GWR was derived from the first law of geography [46], which indicates that observations near location have more influence on the estimation of than observations located further away. A kernel function can effectively represent the magnitude of the influence, and bi-square is one of the most frequently used kernel functions and is used in this study:
Bi-square:
where is the distance between PSMA and PSMA , and is the adaptive bandwidth.
Bandwidth has an important influence on parameter estimation. Corrected Akaike information criterion (AICc) and cross-validation (CV) are two commonly used methods to determine the optimal bandwidth, which are described as follows:
where is the log-likelihood of GWNBR and is the effective number of parameters. The of GWNBR should be recorded as , where and are the effective number of parameters of and . Depending on whether the overdispersion parameter varies over space, the GWNBR model can evolve into 2 models. The one with spatially various α is called local GWNBR, and the other, with the same α across the whole research area, is called global GWNBR. The for the global GWNBR is 1 and for the local GWNBR has been difficult to estimate until today. Therefore, the optimal bandwidth of local GWNBR should be estimated by CV:
where is the bandwidth and is the estimation for point .
The root mean squared error (RMSE) is another criterion to evaluate the performance of models, which can be presented as:
where is the observed number of residential burglaries, is the predicted number of residential burglaries, and is the number of PSMAs.
3. Results and Discussion
The count data models were selected in this study since the dependent variable was the number of crimes, which usually presents a skew distribution. Furthermore, this study tries to incorporate overdispersion into a geographically weighted regression model in order to analyze the effect of overdispersion on the non-stationary modeling of crime. Four models were developed to investigate the effect of overdispersion on crime analyses based on the above-mentioned methodology, including the negative binomial model (NB), geographically weighted Poisson regression model (GWPR), geographically weighted negative binomial regression model with local alpha (local GWNBR), and geographically weighted negative binomial regression model with global alpha (global GWNBR).
The above-mentioned models were calibrated using SAS® software macros developed by Silva and Rodrigues [33]. The optimum bandwidth for GWPR and global GWNBR were obtained by minimizing the AICc. Since it was impossible to estimate the AICc for local GWNBR, the CV was chosen to determine the optimum bandwidth.
3.1. Model Performance Comparison
Three criteria were adopted to compare the performance of the aforementioned four models, including root mean squared error (RMSE), log-likelihood (LL), and correct Akaike information criterion (AICc). The lower the RMSE and AICc of the model, the better the performance of the model. Models with higher LL values are advantageous over others. The results are shown in Table 3. The NB model had the highest RMSE, followed by the global GWNBR, local GWNBR, and GWPR models. It is obvious that the three spatial models outperform the non-spatial model. For the three spatial models, one possible reason to explain why the GWPR outperforms the two GWNBR models, with lower RMSE and higher, L.L.; is that the former had the smallest bandwidth. With regard to the AICc, The GWPR had the worst adjustment, followed by NB and the global GWNBR model. The possible reason is that the two later models incorporate overdispersion.

Table 3.
Adjustment measurements for models.
Table 4 presents the Moran’s I statistics and the corresponding p-value for the four models’ residuals. First of all, the Moran’s I value decreased considerably after incorporating spatial effects and overdispersion in the data. Second, it should be noted that the spatial dependency becomes insignificant in the two GWNBR models, which indicates that the spatial autocorrelation between the models’ residuals can be effectively explained by the overdispersion and spatial heterogeneity.

Table 4.
Moran’s I statistics for model residuals.
With the combination of Table 3 and Table 4, we can assess the relationship between model fit and spatial autocorrelation in the model residuals. The two GWNBR models yielded insignificant Moran’s I statistics with a moderate RMSE, which was lower than for NB. While the GWPR had the lowest RMSE, it could not solve the spatial dependency efficiently. This indicated that the spatial effect, especially spatial dependency, may not be directly related to the predictive ability of a model. A model with strong predictive power does not guarantee that it is unbiased spatially. A spatial model that produces a spatial non-biased estimate may be at the expense of its predictive power.
3.2. Parameters Estimation
The results of the coefficient estimate are presented in Table 5. The means of the coefficients in the global model (NB) are provided, as well as the descriptive statistics of coefficients estimated by local models (GWPR, global GWNBR, and local GWNBR) including the minimum and maximum of values, the lower quartile, the upper quartile, and the median values.

Table 5.
The estimated results of the different models.
The coefficients of GWPR, local GWNBR, and global GWNBR models vary spatially, while the parameters of the NB model are unique in the study area. With regard to the sign of the coefficients’ mean value, there is only one variable, Over60 (percent of people over 60 years of age (%)), that has a negative impact on residential burglary in the NB model, as well as the local GWNBR and global GWNBR models, whereas there are three variables that have a negative impact in GWPR.
With regard to the magnitude of coefficients, the parameters estimated by local GWNBR and global GWNBR models were closer to NB than GWPR. The range of coefficient variation was considerably wider for the GWPR model than for the local GWNBR and global GWNBR models, which may be partly explained by the fact that the GWPR model did not take into account the overdispersion of the data.
There are several local parameters varying from negative to positive in the local models, which is not in conformity with our common sense. For example, the floating population has been reported to have a significantly positive impact on residential burglaries in previous studies [25,47,48], which means that PSMAs with fewer floating populations were safer. Nevertheless, the coefficients of the floating population in some PSMAs are negative in this research. The counterintuitive sign problem was very popular in modeling with local models, such as GWR and GWPR [24,44,49]. One possible reason for this problem was the multi-collinearity among the explanatory variables. In order to quantify the extent of multicollinearity, a bivariate correlation test was conducted, and the results are presented in Table 2. The maximum value of the correlation coefficient was 0.667 between the floating populations and renters, which implied that there were no highly correlated explanatory variables in the models.
On the other hand, overdispersion in the data may be an important explanation for the unexpected parameter signs, as previous researchers reported [32,44]. For instance, the bus stop density was proven to have a positive impact on residential burglaries [50,51,52], as well in our local GWNBR and global GWNBR models, while the same coefficient estimated by GWPR varied from negative to positive. Not considering overdispersion in GWPR may be the reason for this phenomenon.
3.3. Spatial Analyses of the Coefficients
The spatial distribution of all coefficients estimated by the above local models is presented in Figure 2, Figure 3 and Figure 4, respectively, and the spatial patterns corresponding to them were investigated subsequently.
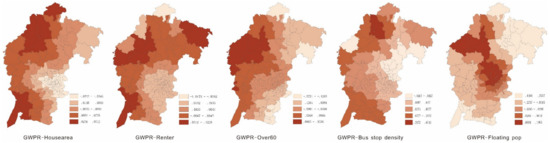
Figure 2.
The spatial distribution of geographically weighted Poisson (GWPR) coefficients.
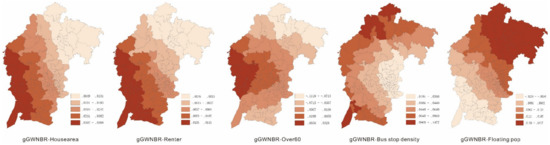
Figure 3.
The spatial distribution of global geographically weighted negative binomial regression model (GWNBR) coefficients.
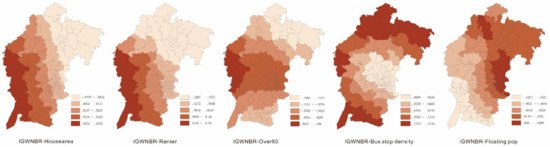
Figure 4.
The spatial distribution of local GWNBR coefficients.
There are several spatial patterns that should be noted here. First, given the fact that GWPR was the model with the smallest bandwidth, the coefficients of local GWNBR and global GWNBR were more smooth than GWPR. Second, it seems that the magnitudes of the local coefficients estimated in local GWNBR and global GWNBR shrank towards the range of coefficients of the same variable in the GWPR.
The spatial distribution of the overdispersion parameter for the local GWNBR model is presented in Figure 5. It can be found that the lower values of α are located in the downtown areas, and these values increased from the urban areas to the suburbs. The overdispersion parameters are significant at a 90% level in more than eighty percent of PSMAs, which indicates the necessity of using the local GWNBR model.
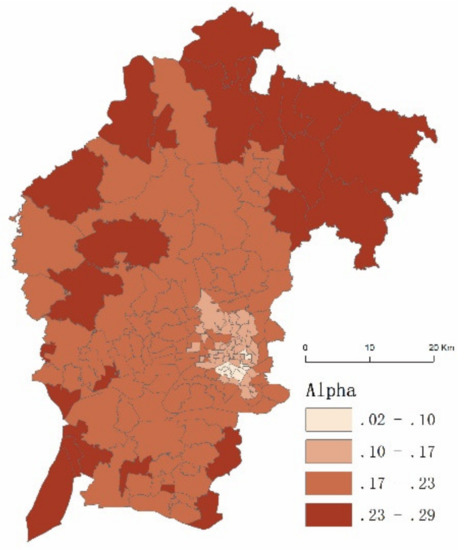
Figure 5.
The spatial distribution of overdispersion parameter alpha.
Given the fact that the two GWNBR models are similar, and outperform the NB and GWPR model, we selected the global GWNBR model to interpret our results. The developed model can also be effectively justified by a good interpretation of the parameter estimation.
The house area was adopted as attractiveness for offenders in this research. A higher frequency of large houses resulted in more targets for criminals to choose from. The house area was identified as a significant positive factor in residential burglaries in previous studies [24]. The coefficient signs of the house area in most PSMAs were positive, which indicated that the increase of big houses increased the residential burglary frequency. There were only 9 PSMAs with negative signs in GWPR followed by 4 in the local GWNBR, and 0 in the global GWNBR. The west of the city is an economic and technological development zone, where the house area has the greatest impact on crime. However, we know that this is a trade-off as larger houses may have better security and be harder to burgle. Burglars may give up stealing from big houses at the risk of being arrested according to rational choice theory. Additional variables should be added in future research to capture the variations.
The number of renters was positively related to the number of residential burglaries in the NB model, which suggested that more renters in a PSMA could result in more residential burglaries. The coefficients of the three local models were positive except for a few PSMAs. Renters have been reported as an important risk factor related to crime in previous studies due to high mobility [25]. According to the social disorganization theory, the increase of resident mobility will lead to more crimes [8]. This may be explained by the fact that house owners were more concerned about the security of the community than renters. When there was a potential security risk, house owners were more likely to try to solve the problem, while renters often moved away instead.
Elderly people are well-known as an important informal guardianship in crime literature [53], which meant that an area with more people over the age of 60 was expected to have fewer residential burglaries. In this research, Over60 was found to be associated with residential burglaries negatively in most of the PSMAs, except for 12. After checking the local t-statistics, we found that none of the 12 were significant at the 95% confidence level. As shown in Figure 2, Figure 3 and Figure 4, from a spatial perspective, the impact of Over60 on residential burglaries was greater in the suburbs compared to the urban areas. This may be due to the difference between the physical features of urban and rural areas. In the city center, people live in high buildings that are excluded from monitoring activities, which reduce natural surveillance.
Bus stop density is positively related to the residential burglary frequency in global GWNBR, as in the NB model, suggesting that more bus stops in a PSMA could lead to more residential burglaries. There was no consensus on the impact of accessibility on burglary. Some studies indicated that accessibility was negatively associated with burglary [54,55], while some others found that areas with better accessibility could result in more burglaries [56,57], which was similar to this study. As shown in Figure 2, Figure 3 and Figure 4, the bus stop density had a greater impact in the suburbs. Public transit is the major travel method in China and also for the offenders. There are many options for public transportation in urban areas, such as subway, bus, taxi, tramcar, shared bicycle, etc., while buses are almost the only means of public transport in the suburbs. Routine activity theory claimed that “illegal activities feed upon the legal activities of everyday life”. Public transport is an important way to travel in China, thus bus stops are an important node of daily activities. Therefore, it is not surprising that bus stops have a positive impact on residential burglary.
Floating populations were special groups in the process of social development in China. Previous studies found that floating populations were positively related to crime [47,48]. The coefficient of the floating population was negative in 7 out of 215 PSMAs. The investigation of the local t-statistics indicated that these 7 PSMAs with negative parameters were not significant. According to the social disorganization theory, informal social control helped to prevent crime, while excessive residential mobility was not conducive to informal social regulation. A high proportion of floating populations would lead to more crimes, which has been confirmed in this study.
3.4. Limitations
Although the results of the current study support that GWNBR is a promising tool for crime analysis, we cannot forget that this methodology is only applicable to modeling spatial count data with significant overdispersion. One limitation of this study is that only residential burglary was examined. However, overdispersion has been found in different types of crime, thus this method should be applicable to other crime types. Additionally, only a single Chinese city was investigated. There were great disparities in geographical context between cities or countries. Therefore, further studies should be conducted in different cities and countries and with multiple types of crime to justify the benefit of the proposed models. Nonetheless, previous studies have confirmed that models based the crime pattern theories and routine activity theories were generally applicable in Chinese cities. Furthermore, any research based on spatial units could not avoid the modifiable area unit problem (MAUP), which has also attracted the attention of criminologists [58,59]. Multi-scale analysis is considered to be an effective method to solve the MAUP [60,61]. However, limited by the data, this study cannot carry out sensitivity analysis for the scale effect and zoning effect, which should be implemented in the future.
4. Conclusions
Models for crime analysis have been widely applied. Geographically weighted regression has been proven to be a powerful methodology for crime modeling, which could capture spatial heterogeneity in crime data. However, there are many issues that have remained unresolved to date, one of which is overdispersion. Therefore, this study mainly focused on the possibility of the integration of spatial heterogeneity and overdispersion in crime modeling. For this purpose, the geographically weighted negative binomial model (GWNBR) was introduced to accommodate spatial heterogeneity and overdispersion simultaneously. A comparison was conducted between four models including the negative binomial model (NB), geographically weighted Poisson model (GWPR), local geographically weighted negative binomial model (local GWNBR), and global geographically weighted negative binomial model (global GWNBR), based on a case study in, Z.G.; China.
In conclusion, the results of this study proved that incorporating overdispersion into spatial heterogeneity could improve the performance of crime modeling. Compared with local GWNBR and global GWNBR, the coefficients of GWPR are more heterogeneous, which may be due to the fact that it does not incorporate the overdispersion of crime data. Another consequence is that the bandwidth of GWPR is the smallest of the three local models, which makes its coefficient surface appear to be sharp. Although GWPR has achieved the best performance for RMSE, it could not eliminate spatial autocorrelation in the model residuals. In addition, the two GWNBR models can resolve spatial heterogeneity and spatial dependence at the same time by incorporating overdispersion.
The coefficients were estimated by the GWNBR model for each PSMA. Then, the crime prediction model could be developed for each PSMA. These crime prediction models can be used to evaluate the daily safety situation and forecast the number of crimes in the future. These models can also be used to assess the effectiveness of current policing policies or countermeasures applied in particular PSMAs.
Author Contributions
Conceptualization, Jianguo Chen and Lin Liu; methodology, Jianguo Chen; software, Luzi Xiao, Chong Xu; formal analysis, Jianguo Chen, Luzi Xiao and Lin Liu; writing—original draft preparation, Jianguo Chen, Luzi Xiao, Chong Xu, and Dongping Long; writing—review and editing, Dongping Long; supervision, Lin Liu; project administration, Lin Liu; funding acquisition, Lin Liu. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key RandD Program of China (Grant No. 2018YFB0505500, 2018YFB0505505), National Natural Science Foundation of China (Grant No. 41531178, 41901172, 41601138).
Acknowledgments
The authors would like to thank three anonymous reviewers for their valuable suggestions and comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Uittenbogaard, A.; Ceccato, V. Space-time Clusters of Crime in Stockholm, Sweden. Rev. Eur. Stud. 2012, 4, 148–156. [Google Scholar] [CrossRef]
- Zhang, C.; Peterson, M. A spatial analysis of neighborhood crime in Omaha, Nebraska using alternative measures of crime rates. Int. J. Criminol. 2007, 31, 1–28. [Google Scholar]
- Breetzke, G.D. Modeling violent crime rates: A test of social disorganization in the city of Tshwane, South Africa. J Crim. Justice 2010, 38, 446–452. [Google Scholar] [CrossRef]
- Melo, S.N.D.; Andresen, M.A.; Matias, L.F. Geography of crime in a Brazilian context: An application of social disorganization theory. Urban Geogr. 2017, 38, 1550–1572. [Google Scholar] [CrossRef]
- Shi, S.; Dong, Y.; Song, L. A spatio-temporal analysis of urban crime in Beijing: Based on data for property crime. Urban Stud. 2015, 53, 3223–3245. [Google Scholar]
- Cohen, L.E.; Felson, M. Social change and crime rate trends: A routine activity approach. Am. Sociol. Rev. 1979, 44, 588–608. [Google Scholar] [CrossRef]
- Brantingham, P.; Brantingham, P. Crime pattern theory. Environ. Criminol. Crime Anal. 2013, 78–93. [Google Scholar] [CrossRef]
- Shaw, C.R.; Mckay, H.D. Juvenile delinquency and urban areas. Soc. Serv. Rev. 1942, 35, 394. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, X. Exploring the Influence of Neighborhood Characteristics on Burglary Risks: A Bayesian Random Effects Modeling Approach. ISPRS Int. J. Geo Inf. 2016, 5, 102. [Google Scholar] [CrossRef]
- Warner, B.D.; Pierce, G.L. Reexamining Social Disorganization Theory Using Calls to the Police as a measure of crime*. Criminology 1993, 31, 493–517. [Google Scholar] [CrossRef]
- Grubesic, T.H.; Mack, E.A.; Kaylen, M.T. Comparative modeling approaches for understanding urban violence. Soc. Sci. Res. 2012, 41, 92–109. [Google Scholar] [CrossRef] [PubMed]
- Paternoster, R.; Brame, R.; Bachman, R.; Sherman, L.W. Do fair procedures matter? The effect of procedural justice on spouse assault. Law Soc. Rev. 1997, 31, 163–204. [Google Scholar] [CrossRef]
- Song, G.; Liu, L.; Bernasco, W.; Zhou, S.; Xiao, L.; Long, D. Theft from the person in urban China: Assessing the diurnal effects of opportunity and social ecology. Habitat Int. 2018, 78, 13–20. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, L.; Lan, M.; Yang, B.; Wang, Z. Assessing the Impact of Nightlight Gradients on Street Robbery and Burglary in Cincinnati of Ohio State, USA. Remote Sens. 2019, 11, 1958. [Google Scholar] [CrossRef]
- Lan, M.; Liu, L.; Hernandez, A.; Liu, W.; Zhou, H.; Wang, Z. The Spillover Effect of Geotagged Tweets as a Measure of Ambient Population for Theft Crime. Sustainability 2019, 11, 6748. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Murillo, F.H.S.; Chica-Olmo, J. The spatial heterogeneity of factors of feminicide: The case of Antioquia-Colombia. Appl. Geogr. 2018, 92, 63–73. [Google Scholar] [CrossRef]
- Zhang, H.; Mccord, E.S. A spatial analysis of the impact of housing foreclosures on residential burglary. Appl. Geogr. 2014, 54, 27–34. [Google Scholar] [CrossRef]
- Mburu, L.W.; Helbich, M. Crime Risk Estimation with a Commuter-Harmonized Ambient Population. Ann. Assoc. Am. Geogr. 2016, 106, 804–818. [Google Scholar] [CrossRef]
- Helbich, M.; Arsanjani, J.J. Spatial eigenvector filtering for spatiotemporal crime mapping and spatial crime analysis. Cartogr. Geogr. Inf. Sci. 2015, 42, 134–148. [Google Scholar] [CrossRef]
- Chun, Y. Analyzing space–time crime incidents using eigenvector spatial filtering: An application to vehicle burglary. Geogr. Anal. 2014, 46, 165–184. [Google Scholar] [CrossRef]
- Law, J.; Quick, M. Exploring links between juvenile offenders and social disorganization at a large map scale: A Bayesian spatial modeling approach. J. Geogr. Syst. 2013, 15, 89–113. [Google Scholar] [CrossRef]
- Law, J. Bayesian Spatial Random Effect Modelling for Analysing Burglary Risks Controlling for Offender, Socioeconomic, and Unknown Risk Factors. Appl. Spat. Anal. Policy 2012, 5, 73–96. [Google Scholar] [CrossRef]
- Chen, J.; Liu, L.; Zhou, S.; Xiao, L.; Jiang, C. Spatial variation relationship between floating population and residential burglary: A case study from, Z.G.; China. ISPRS Int. J. Geo Inf. 2017, 6, 246. [Google Scholar] [CrossRef]
- Chen, J.; Liu, L.; Zhou, S.; Xiao, L.; Song, G.; Ren, F. Modeling spatial effect in residential burglary: A case study from ZG city, China. ISPRS Int. J. Geo Inf. 2017, 6, 138. [Google Scholar] [CrossRef]
- Park, S.M.; Tark, J.; Cho, Y.I. Victimization immunity and lifestyle: A comparative study of over-dispersed burglary victimizations in South Korea and, U.S. Int. J. Law Crime Justice 2016, 45, 44–58. [Google Scholar] [CrossRef]
- Hope, T.; Norris, P.A. Heterogeneity in the Frequency Distribution of Crime Victimization. J. Quant. Criminol. 2013, 29, 543–578. [Google Scholar] [CrossRef][Green Version]
- Yang, Z.; Hardin, J.W.; Addy, C.L. A score test for overdispersion in Poisson regression based on the generalized Poisson-2 model. J. Stat. Plan. Inference 2009, 139, 1514–1521. [Google Scholar] [CrossRef]
- Song, G.; Lin, L.; Bernasco, W.; Xiao, L.; Zhou, S.; Liao, W. Testing Indicators of Risk Populations for Theft from the Person across Space and Time: The Significance of Mobility and Outdoor Activity. Ann. Am. Assoc. Geogr. 2018, 108, 1370–1388. [Google Scholar] [CrossRef]
- Berk, R.; MacDonald, J.M. Overdispersion and Poisson regression. J. Quant. Criminol. 2008, 24, 269–284. [Google Scholar] [CrossRef]
- Bottcher, J.; Ezell, M.E. Examining the effectiveness of boot camps: A randomized experiment with a long-term follow up. J Res Crime Delinq 2005, 42, 309–332. [Google Scholar] [CrossRef]
- Gomes, M.J.T.L.; Cunto, F.; Silva, A.R. Geographically weighted negative binomial regression applied to zonal level safety performance models. Accid. Anal. Prev. 2017, 106, 254. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, A.R.; Rodrigues, T.C.V. Geographically weighted negative binomial regression—Incorporating overdispersion. Stat. Comput. 2014, 24, 769–783. [Google Scholar] [CrossRef]
- CSY. China Statistical Yearbook; China Statistical Publishing House: Beijing, China, 2016. [Google Scholar]
- Sohn, D.W. Residential crimes and neighbourhood built environment: Assessing the effectiveness of crime prevention through environmental design (CPTED). Cities 2016, 52, 86–93. [Google Scholar] [CrossRef]
- Katz, C.M.; Wallace, D.; Hedberg, E.C. A Longitudinal Assessment of the Impact of Foreclosure on Neighborhood Crime. J. Res. Crime Delinq. 2011, 50, 359–389. [Google Scholar] [CrossRef]
- Malczewski, J.; Poetz, A. Residential Burglaries and Neighborhood Socioeconomic Context in London, Ontario: Global and Local Regression Analysis*. Prof. Geogr. 2005, 57, 516–529. [Google Scholar] [CrossRef]
- Ariel, B.; Partridge, H. Predictable Policing: Measuring the Crime Control Benefits of Hotspots Policing at Bus Stops. J. Quant. Criminol. 2016, 33, 809–833. [Google Scholar] [CrossRef]
- Hunter, J.; Tseloni, A. Equity, justice and the crime drop: The case of burglary in England and Wales. Crime Sci. 2016, 5, 1–13. [Google Scholar] [CrossRef]
- Lee, J.; Park, S.; Jung, S. Effect of Crime Prevention through Environmental Design (CPTED) Measures on Active Living and Fear of Crime. Sustainability 2016, 8, 872. [Google Scholar] [CrossRef]
- Nobles, M.R.; Ward, J.T.; Tillyer, R. The Impact of Neighborhood Context on Spatiotemporal Patterns of Burglary. J. Res. Crime Delinq. 2016, 53, 711–740. [Google Scholar] [CrossRef]
- Osgood, D.W.; Chambers, J.M. Social Disorganization outside the Metropolis: An analysis of rural youth violence*. Criminology 2000, 38, 81–116. [Google Scholar] [CrossRef]
- Nagin, D.S.; Land, K.C. Age, Criminal Careers, and Population Heterogeneity: Specification and Estimation of a Nonparametric, Mixed Poisson Model*. Criminology 1993, 31, 327–362. [Google Scholar] [CrossRef]
- Xu, P.; Huang, H. Modeling crash spatial heterogeneity: Random parameter versus geographically weighting. Accid. Anal. Prev. 2015, 75, 16–25. [Google Scholar] [CrossRef] [PubMed]
- Nakaya, T.; Charlton, M.; Lewis, P.; Fortheringham, S.; Brunsdon, C. Windows Application for Geographically Weighted Regression Modelling; Ritsumeikan University: Kyoto, Japan, 2012. [Google Scholar]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Curran, D.J. Economic reform, the floating population, and crime: The transformation of social control in China. J. Contemp. Crim. Justice 1998, 14, 262–280. [Google Scholar] [CrossRef]
- Situ, Y.; Liu, W. Transient population, crime, and solution: The Chinese experience. Int. J. Offender Ther. 1996, 40, 293–299. [Google Scholar] [CrossRef]
- Hadayeghi, A.; Shalaby, A.S.; Persaud, B.N. Development of planning level transportation safety tools using Geographically Weighted Poisson Regression. Accid. Anal. Prev. 2010, 42, 676–688. [Google Scholar] [CrossRef]
- Kooi, B.R. Assessing the correlation between bus stop densities and residential crime typologies. Crime Prev. Commun. Saf. 2013, 15, 81–105. [Google Scholar] [CrossRef]
- Beavon, D.J.; Brantingham, P.L.; Brantingham, P.J. The influence of street networks on the patterning of property offenses. Crime Prev. Stud. 1994, 2, 115–148. [Google Scholar]
- White, G.F. Neighborhood permeability and burglary rates. Justice Q. 1990, 7, 57–67. [Google Scholar] [CrossRef]
- Lee, S. Spatial Analyses of Installation Patterns and Characteristics of Residential Burglar Alarms. J. Appl. Secur. Res. 2011, 6, 82–109. [Google Scholar] [CrossRef]
- Hillier, B. Can streets be made safe? Urban Des. Int. 2004, 9, 31–45. [Google Scholar] [CrossRef]
- Shu, C.F. Housing layout and crime vulnerability. Urban Des. Int. 2000, 5, 177–188. [Google Scholar]
- Lin, L.; Chao, J.; Zhou, S.; Kai, L.; Du, F. Impact of public bus system on spatial burglary patterns in a Chinese urban context. Appl. Geogr. 2017, 89, 142–149. [Google Scholar]
- Chang, D. Social crime or spatial crime? Exploring the effects of social, economical, and spatial factors on burglary rates. Environ. Behav. 2011, 43, 26–52. [Google Scholar] [CrossRef]
- Ratcliffe, J.H.; McCullagh, M.J. Hotbeds of crime and the search for spatial accuracy. J. Geogr. Syst. 1999, 1, 385–398. [Google Scholar] [CrossRef]
- Ratcliffe, J.H. Detecting Spatial Movement of Intra-Region Crime Patterns Over Time. J. Quant. Criminol. 2005, 21, 103–123. [Google Scholar] [CrossRef]
- Hay, G.; Marceau, D.; Dube, P.; Bouchard, A. A multiscale framework for landscape analysis: Object-specific analysis and upscaling. Landsc. Ecol. 2001, 16, 471–490. [Google Scholar] [CrossRef]
- Lechner, A.M.; Langford, W.T.; Jones, S.D.; Bekessy, S.A.; Gordon, A. Investigating species–environment relationships at multiple scales: Differentiating between intrinsic scale and the modifiable areal unit problem. Ecol. Complex. 2012, 11, 91–102. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).