Abstract
In map generalization, scale reduction and feature symbolization inevitably generate problems of overlapping objects or map congestion. To solve the legibility problem with respect to the generalization of dispersed rural buildings, selection of buildings is necessary and can be transformed into an optimization problem. In this paper, an improved genetic algorithm for building selection is designed to be able to incorporate cartographic constraints related to the building selection problem. Part of the local constraints for building selection is used to constrain the encoding and genetic operation. To satisfy other local constraints, a preparation phase is necessary before building selection, which includes building enlargement, local displacement, conflict detection, and attribute enrichment. The contextual constraints are used to ascertain a fitness function. The experimental results indicate that the algorithm proposed in this article can obtain good results for building selection whilst preserving the spatial distribution characteristics of buildings.
1. Introduction
Map generalization aims to represent geographic information in an abstract way when deriving small-scale maps from larger-scale ones. It has long been a core issue in automated map production and multi-scale spatial representation [1,2,3]. Among the various data themes, the building features have attracted much research attention in the field of map generalization because of their man-made shape and complex spatial distribution.
Scale reduction and feature symbolization in building generalization inevitably generate spatial conflicts of proximity and overlap, which reduce the readability of maps. To solve such conflicts, cartographers have conducted a great deal of research [4,5,6,7,8,9,10,11,12]. In these approaches, displacement has been the major generalization operator [4,5,6,7,8,9]. However, displacement itself does not guarantee that all conflicts are resolved, especially when the map space available is insufficient.
As one of the contextual operators, building selection, which can also be referred to as building elimination, is aimed at reducing the number of buildings under specific cartographic rules. When the density is too high to displace buildings while not high enough to aggregate them, selection should be used to eliminate the conflicts. At present, most selection algorithms have been developed for point set [13,14,15,16,17,18,19]. In terms of building selection, existing studies have focused either on local elimination [20,21] or on elimination of buildings with a regular distribution such as linear-structured buildings [11,22,23,24]. Therefore, it is necessary to find effective building selection approaches for irregularly distributed buildings, especially when their overall density is high.
Instead of the generalization of urban buildings, which has already been studied [25,26], the focus here is on the generalization of rural buildings. The main objective is to transform groups of buildings into a readable form at the target scales by extracting a new representative set of buildings. The major challenge facing the selection problem is that a set of cartographic constraints should be satisfied. For example, the result should contain as few conflicts as possible, preferably none; the spatial relationships and patterns of the original building set should be preserved as much as possible after the selection process. This implies that selection can be considered as an optimization problem, where different goals have to be satisfied simultaneously.
The genetic algorithm (GA) is a well-known optimization approach. The algorithm was first proposed by Holland [27] and then developed by Goldberg [28] in the field of artificial intelligence. Through simulation of biological evolutionary strategy, the algorithm is able to find the optimal or sub-optimal solution for a difficult problem from a host of feasible solutions. It has proven to be effective in building cluster displacement [29,30,31] and in other generalization problems such as map labeling [32] and line simplification [33]. Compared to other optimization algorithms (such as the steepest descent method and the simulated annealing algorithm), the GA has better performance under many constraints. The GA is therefore proven to be suitable for solving the building selection problem in this paper.
To make the generalization solutions more attractive to cartographers, the GA has been improved to satisfy a set of cartographic constraints. First, the concept of conflicting block is introduced in the encoding and genetic operation, making all solutions free of conflicts. Then, important buildings and identified alignments are preserved in the form of fixing the corresponding genes. Finally, spatial distribution and density constraints are specified in a fitness function. By incorporating these constraints into the GA design, it can be ensured that no conflict exists among the retained buildings and that the spatial distribution characteristics are preserved to the greatest extent possible.
The remainder of this paper is organized as follows. Section 2 reviews previous work on building generalization. Section 3 focuses on how to design the GA in three main compositions considering the related constraints that act on buildings. Section 4 describes the implementation of the method for the problem considered. To validate the algorithm, Section 5 presents experiments on two topographic datasets and discusses the experimental results. Finally, Section 6 concludes this study and suggests future works.
2. Related Work
Over the past few decades, many research studies have been carried out on building generalization. Some of these studies have focused on the overall process of generalization. Examples include agent modeling techniques based on constraints and the Multi-Agent System (MAS) paradigm [21,34,35]; a method for building groupings and then generalizations utilizing Gestalt principles and urban morphology [25]; and a multi-parameter approach to building grouping and generalization based on three principles of Gestalt theories and six parameters [12]. Other studies have focused mainly on developing new algorithms for specific generalization operators. These algorithms can be roughly categorized into two types: non-contextual operators for an individual building like simplification [24,36], and contextual operators for building groups such as displacement, selection or typification [4,5,6,7,8,9,22,23,24].
Compared with other generalization operators, the specificity of selection implies the need to determine the number of objects retained in the target map according to the scale and the purposes. Töpfer and Pillewizer [37] proposed a law, known as the radical law, which allows making such a decision. Another challenge facing selection is to decide which buildings should be retained and which ones should be removed. This decision needs to take into consideration not only the characteristics of the building such as its shape and size, but also contextual information such as the relationships among the building and the road or other features, all of which add to the complexity of selection.
Bjørke [20] proposed an entropy-based method for feature elimination. In an example of area elimination, house symbols were set to be of equal size. The grade of similarity of any two neighboring symbols could be evaluated according to their proximity to each other. After mapping, the grade of similarity to transition probabilities, the local equivocation for each symbol, was computed. At each step, the symbol with the greatest equivocation was eliminated from the map. This process was terminated when a map index received its maximum value.
Ruas [21] presented another iterative elimination algorithm. Unlike the entropy-based method, which can only consider one criterion in the process of elimination, this algorithm can consider numerous constraints simultaneously. These constraints were combined to define a cost function for each building. At each step, the elimination cost of the building was calculated, and the building with the highest value eliminated. These steps were repeated until the result satisfied a predefined criterion.
As elimination algorithms can only delete one building in one iteration step, they are most suitable for situations where the local density of buildings is high. When the overall density of buildings is high, these algorithms become inapplicable.
Building typification can be termed as selection with building relocation [38]. There is no clear distinction between selection and typification in some holistic process. Regnauld [11] presented a method for selection based on the typification principle. Buildings were grouped into homogeneous clusters, making use of graph theory and Gestalt principles, then the buildings in each group were analyzed, and the representation of new buildings according to each group’s information (e.g., size, orientation, length, width, etc.) were determined. This algorithm was mainly suitable for buildings with linear structures.
Sester [24] adopted a neural network technique in generalization, and presented a typification algorithm based on self-organizing maps. In the algorithm, the original building point set served as the input space. A subset of the point set represented the map space. The number of points in the subset could be determined using Töpfer’s radical law [37]. Each point was a neuron, and these neurons were linked to form a network by constructing a Delaunay triangulation. The points and their neighborhoods were iteratively adjusted according to the stimuli until they approximated the distribution of the original dataset. The prominent advantage of this algorithm is that the density characteristic can be well maintained after typification. The disadvantage is that the algorithm does not take into account other constraints such as the minimum distance constraint.
Burghardt and Cecconi [22] adopted a mesh simplification technique to develop a typification algorithm for buildings. The algorithm could be basically divided into two phases: positioning and representation. In the positioning phase, the target number and position of buildings were determined based on Töpfer’s radical law and Delaunay triangulation. The representation phase elaborated how to construct new buildings to replace the ones they represented in the determined position. Typification of buildings for any scale between two source scales (e.g., 1:25,000 and 1:200,000) can be achieved using this algorithm. One limitation is that no consideration was given to alignment.
Gong and Wu [23] identified a linear pattern utilizing Gestalt visual perception, computational geometry, and graph theory, and then developed a typification algorithm for linear pattern buildings. They divided the typification process into three parts: elimination of buildings with minimum overall effect, exaggeration of the remaining buildings according to their relative location in the linear pattern and displacement of buildings along the linear pattern trajectory direction. By iteratively executing the above three parts, the maintenance of linear patterns could be guaranteed after typification.
Building generalization is challenging because it needs to take into account spatial structure knowledge. Such knowledge is often implicit in datasets, and specific methods, such as cluster analysis and pattern recognition, should be used to make it explicit. For example, Jones et al. [36] used Delaunay triangulation for neighborhood analysis. Regnauld [39] extracted linear building clusters by constructing and segmenting a minimum spanning tree. Anders and Sester [40] proposed a parameter-free grouping method based on graph theory. Christophe and Ruas [38] identified straight-line building alignments and preserved the regular ones for typification. Li et al. [25] adopted a neighborhood model form urban morphology for global partitioning and then applied Gestalt principles to group buildings locally. Basaraner and Selcuk [41] developed a structure recognition technique using of Voronoi diagrams and spatial analysis methods. Zhang et al. [42] developed two algorithms to recognize collinear and curvilinear alignments in buildings. The knowledge gained from all these studies provides useful information for successful generalization.
3. Cartographic Selection from a GA Perspective
3.1. GA Summary
This section outlines the process of how to use a GA to solve an optimization problem. The core idea of the GA is to mimic Darwin’s idea of finding the optimal individual through selective reproduction in a given environment. When the GA is applied in generalization, a solution to the problem is represented using a chromosome. Each chromosome is composed of a number of genes and modeled by a string of values. A gene has two or more different versions called alleles. A certain number of chromosomal individuals make up a population. The evolutionary process is conducted on the basis of the population. The GA uses a fitness function to determine which individuals in the population can better solve a problem. Appropriate individuals are selected to generate a new generation by crossover and mutation. This process is iterated until a stop criterion is reached. The individual with the highest fitness value is considered as the best solution.
The main components of a typical GA include:
- Encoding: transforming solutions of a problem into gene representations.
- Initialization: generating a set of chromosomes that represent optional solutions to the problem.
- Selection: selecting individuals from the current population as parents for reproduction, based on their fitness values.
- Crossover: producing children by recombining the genes of two parents.
- Mutation: randomly selecting genes in an individual and replacing them by their allele to ensure diversity.
- Termination criterion: stopping the algorithm when the algorithm converges or when the number of iterations reaches a pre-specified value.
When using a GA to solve generalization problems, the following three key issues must be made clear in the algorithm design:
- Definition and expression of the solution to the problem, namely how to design the genes of an individual in the GA.
- Choice of appropriate genetic operators, such as selection, crossover, mutation, etc., to evolve the population of solutions.
- Definition of a fitness function to evaluate the quality of the solution with respect to a practical problem.
The next two subsections will propose solutions for these three issues.
3.2. Selection Constraints
Successful generalization needs to meet the requirements derived from the map specifications. These requirements are usually defined as a set of constraints. The constraint-based approach has been actively researched in generalization [11,25,26]. In these studies, constraints have mainly been used to control the process and evaluate the results.
As one of the contextual operations, selection is applied to a set of buildings in this paper. In addition to individual characteristics, contextual characteristics should be considered in the selection process. Therefore, the constraints required for a successful selection can be divided into two kinds: local constraints with respect to a single building (see Figure 1) and contextual constraints with respect to groups of buildings (see Figure 2). Each of them will be discussed in detail below.
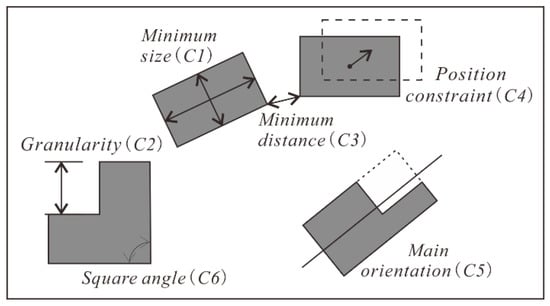
Figure 1.
Local constraints acting on buildings.
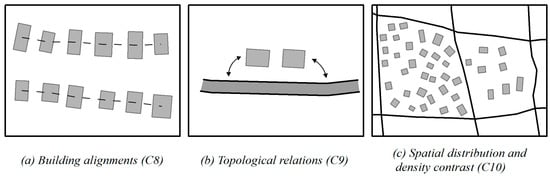
Figure 2.
Contextual constraints acting on buildings.
• Local constraints
Size constraint (C1). Buildings should have a minimum size to be interpretable. This size is set depending on the scale and visual interpretation thresholds. In terms of the scales involved in this paper (1:25,000 and 1: 50,000), the value can be specified as 0.35 m2 [43].
Granularity constraint (C2). The length of an edge of a building boundary should be large enough (0.3 mm) to avoid visual confusion [11].
Separation constraint (C3). The minimum distance between two buildings should be greater than a specific threshold. For instance, the human eye has a resolution power of approximately 0.2 mm at a reading distance of 30 cm [44].
Position constraint (C4). A building should be as close to its original position as possible. If it is to be displaced, the displacement distance should not exceed a specified value (e.g., 0.5 mm) [45].
Orientation constraint (C5). A building should preserve its initial main orientation.
Squareness constraint (C6). The square angles of the buildings should be maintained to make them recognizable.
Functionality constraint (C7). Important buildings should be preserved. How to define the importance of a building depends on the purpose of the map.
• Contextual constraints
Alignment constraint (C8). Particular building arrangements should be maintained.
Topology constraints (C9). The topological relationships among the buildings and other features should be retained as much as possible.
Spatial distribution and density constraints (C10). Spatial distribution patterns and density of settlement prior to and after generalization should be maintained.
3.3. An Improved GA
Having identified two main kinds of constraints, how to introduce them into the GA must now be addressed. When designing a GA, key tasks are to determine how a solution is to be modeled as a chromosome, how operators specific to the chromosome should behave, and how the fitness function should evaluate the solution. By considering the cartographic constraints, this subsection elaborates the decision-making process.
3.3.1. Encoding
When the GA is applied to building selection, a chromosome represents a selection solution. The number of buildings in a selection unit determines the chromosome length, and each building corresponds to a specific gene on the chromosome. The state of each building determines the value of its corresponding gene. In the selection process, each building has two states: being selected or being discarded. Therefore, a binary encoding can be adopted, composed of two binary characters (0 and 1), and which is convenient for encoding, decoding, and crossover. Figure 3 shows the binary encoding process for the selection of 10 buildings. The chromosome is a string composed of 1 s and 0 s, with 1 corresponding to the selected buildings (the gray buildings) and 0 corresponding to the discarded buildings (the white buildings).

Figure 3.
Binary encoding for the selection problem of 10 buildings.
According to constraint C3, there should be no conflict among the retained buildings. The encoding should be restricted by this constraint. Once a building is selected to be retained, then other buildings that conflict with this building should be discarded. Here, the concept of conflicting blocks is proposed to assist the constrained coding. The definition of a conflicting block for a building is a set of buildings that includes the building itself and all the others that are in conflict with this building. As shown in Figure 4, the building set {B1, B2, B3} is the conflicting block of building B2 (expressed as CB(B2)). Similarly, CB(B4) includes B3, B4 and B5. If B2 is included in a solution, then B1 and B3 should not be selected.
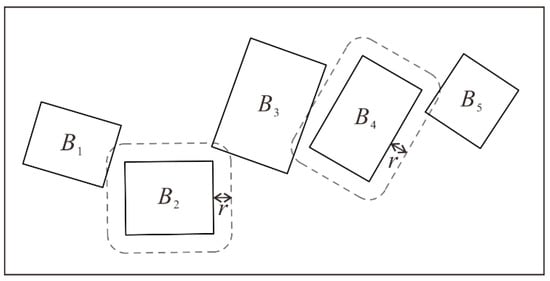
Figure 4.
Conflicting blocks. r is the minimum distance threshold for detecting conflicts.
According to constraint C7, important buildings must be selected. A building can be considered important either on the semantic level or on the structural level. For topographic map data, semantic information is often poor. Taking into account the scarcity of information, this paper attempts to identify and preserve the structurally important buildings. Three types of such buildings are involved (see Figure 5): (1) a building that is initially large enough to be represented without enlargement at the target scale (type I building), (2) a building that is located at a road intersection (type II building), and (3) a building that is a representative one on the borders of a settlement (type III building). These structural features are detected in the original scale by attribute enrichment (see Section 4.5).
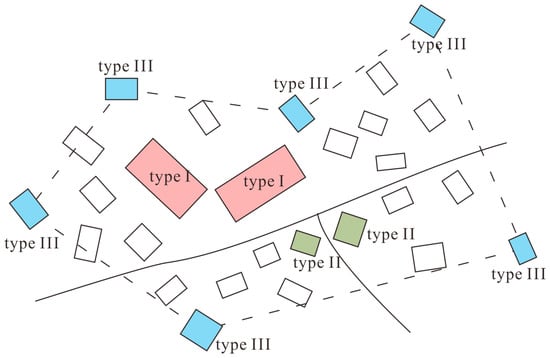
Figure 5.
Three types of structurally important buildings.
A must-be-selected building can be represented in the encoding process by the gene with a fixed value, namely 1. Similarly, the gene values corresponding to other buildings in its conflicting block are always set to be 0 s. There is a special case in which the conflicting block of an important building contains other important buildings. If these important buildings belong to different types, the priority to retain buildings is as follows: type I > type II > type III. If they are of the same type, the building with the largest size is preferred.
Constraint C8 is another constraint that needs to be considered during encoding. For each building alignment, the building located at either end is firstly selected. From the first selected building, the buildings that do not conflict with the previous one are selected in turn. Having determined which buildings should be retained and which buildings should be removed, the alignment pattern can be maintained by fixing their gene values in the GA. Figure 6 shows the selection configuration guided by the rules above and the corresponding gene representation for a group of aligned buildings. This gene segment remains unchanged throughout the GA process.
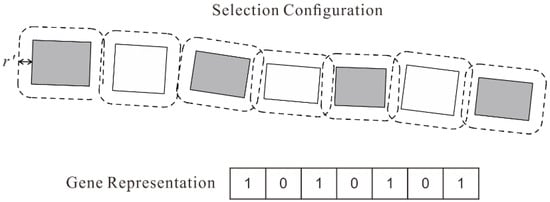
Figure 6.
Encoding for a group of aligned buildings. r’ is half the minimum distance threshold for detecting conflicts.
3.3.2. Crossover and Mutation by Considering Conflicting Blocks
There are two kinds of crossover operators commonly used in the GA: single point and uniform (Figure 7). In single-point crossover, a gene point is randomly selected on the parent chromosomes, and then the segments before or after the point in both chromosomes are swapped to generate two sub-chromosomes. Unlike single-point crossover, uniform crossover enables the children to inherit information at the gene level rather than at the segment level. With a probability of 0.5, each gene on both parent chromosomes is evaluated for exchange.
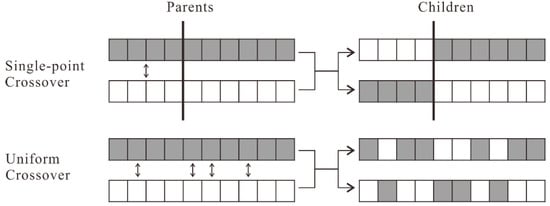
Figure 7.
Single-point crossover and uniform crossover.
Which crossover to use depends on the problem structure and the encoding. As pointed out by Van Dijk et al. [32], single-point crossover is unsuitable for two-dimensional problems. Uniform crossover has a better effect when the genes are independent of each other, as this crossover will cause too much disruption if there are linkages among genes. In the selection problem, linkages exist among genes belonging to the same conflicting block. Figure 8 shows uniform crossover performed on two chromosomes for the buildings in Figure 4. Initially, there is no conflict in the two parent chromosomes. After the genes (in gray) of B2 are swapped, the situation changes such that conflicts occur in one of the generated sub-chromosomes.
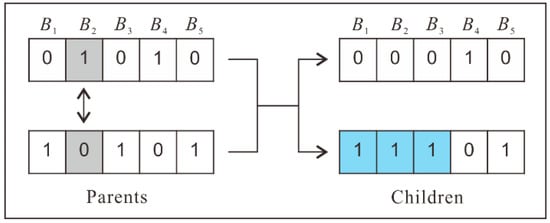
Figure 8.
Example of generic uniform crossover (conflicting genes are shown in blue).
To avoid the abovementioned situation, an enhanced uniform crossover considering conflicting blocks was constructed. When a gene bit in the chromosome is selected to cross, it is first checked to see if the values of the genes on the two parent chromosomes are the same. If they are inconsistent, the genes belonging to the same conflicting block are exchanged simultaneously.
Since there may be overlapping parts among different conflicting blocks, new conflicts may occur with a low probability after crossover. To remove the new conflicts, it is necessary to optimize the chromosome locally. For two buildings in a new conflict, if their conflicting blocks are of the same size, the larger building (at the original map scale) is preferred; otherwise, priority should be given to the one with a smaller conflicting block.
Figure 9 shows an example of the enhanced uniform crossover. As shown in Figure 4, B3 is the overlapping building of CB(B2) and CB(B4). Since the gene values of B2 on the two chromosomes are not the same, genes (drawn in gray) for CB(B2) in two parents are all exchanged. After that, a conflict arises between B3 and B4. The conflict is then removed through local optimizing. B4 is discarded because the size of the conflicting block of B4 is the same as that of B3, but its area is smaller.
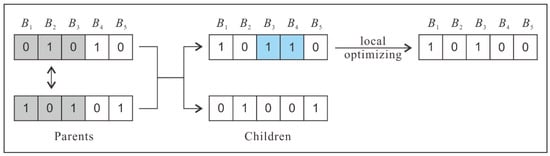
Figure 9.
Example of uniform crossover considering conflicting blocks.
After crossover, a single-bit flip mutation strategy is adopted. Mutation in the traditional sense randomly changes the gene value in a chromosome. To avoid destroying the assignment of genes for a conflicting block, the mutation is performed only on the non-fixed buildings without conflicting blocks.
3.3.3. Objective Function and Fitness Function
A fitness function is used to evaluate the relative quality of individuals and decide which individuals to evolve. How to set the fitness function is closely related to the problem to be solved, and will significantly affect the convergence speed. Generally, the fitness function can be derived from the objective function by scaling. The objectives from a global view of the current problem are defined below and the measures to describe these objectives determined.
Building selection is mainly for solving the spatial conflict caused by scale reduction whilst maintaining the spatial distribution as much as possible. Genetic operators such as encoding, crossover, and mutation ensure that there is no conflict among buildings in any selection configuration. Therefore, the objective function used here mainly focuses on whether the spatial distribution characteristics are maintained. There are two criteria in the objective function.
• Maintain distribution range
Clustered map features usually occupy a circumscribed area in a map space. The distribution range refers to the polygon that covers this area. After selection, the buildings retained should cover the original distribution range as much as possible. The goal can be achieved by minimizing the difference of the distribution range before and after selection.
The convex hull approach is a common method used for characterizing the distribution range of a group of objects. However, it is not suitable in this article as the distribution shape of some settlements may be concave. In addition, it does not take into account the impact area of the building. To be more realistic, the buffered building overlap technique is adopted here. The detailed method can be found in the selection unit extraction process (see Section 4.1). The distribution range of buildings before selection is fixed, while the distribution range of each individual in the selection process changes and requires immediate calculation.
The formula for the first objective can be expressed as follows:
where f1 represents the absolute value of range variation, Rng represents the area of the distribution range of buildings at the target scale when the selection is not performed, and r represents the area of the range polygon of any individual in the GA. Minimizing f1 produces a more attractive selection result.
• Maintain density difference
In settlement generalization, the difference in density of different units across a map should be preserved. That is, units with a greater density before selection should still possess a higher density after selection. Since the GA is applied to only one selection unit (see Section 4.1) at a time, the density contrast information among different selection units is not available during the selection process. Preservation of the density difference can be ensured by minimizing the density variation before and after the selection in each unit. If the building densities of the two units after selection are as close as possible to their initial densities, the density contrast between them can also be maintained to the greatest extent possible. To detect the variation, the first issue is to select the appropriate method for measuring the density. Traditionally, building density is measured by ink/paper area ratios [46]. As there is no partition available in rural settlements, distribution range can be used to estimate building density.
The formula for the second objective can be expressed as follows:
where f2 represents the absolute value of the building density variation, Den represents the building density before selection, and d represents the building density of any individual in the GA. Minimizing f2 produces a more attractive selection result.
These two criteria together constitute the objective function, and the mathematical description is as follows:
where w1 and w2 represent the weight values of f1 and f2, respectively. The larger the weight value, the greater the effect on the objective function. For different selection units, the magnitudes of f1 and f2 may be different, so fixed weights are not desirable. Here, the adaptive weights approach proposed by Cheng et al. [47] is adopted. This method assigns weights to each objective function adaptively according to the current population. The adaptive weight for objective i can be calculated by the following equation:
where and are the maximum and minimum values, respectively, for objective i in a certain generation. The adaptive weights approach can make the objective function better toward the ideal point. Then, the weighted-sum objective function for a given individual can be expressed as follows:
The objective function obtained is a minimal function, that is, the smaller the objective score, the better the selection configuration. However, in a GA, the individuals with higher fitness scores are better adapted and have a higher probability of surviving to the next generation. Therefore, the objective function of this problem can be transformed into a fitness function by the following formula:
where Fit (f) is the fitness function, cmax is the maximum estimate of the objective score, and f is the objective function value. The value of cmax is critical for ensuring that Fit (f) is non-negative; otherwise, the problem may appear in the selection stage of the GA. According to the estimation of Equation (5), the value of cmax is 2.
4. Implementation of the Proposed Method
Before the selection operation, operating units are extracted from the map dataset based on the “divide and conquer” principle. The selection is then carried out for each unit independently. Selection starts with the preprocessing procedure including building enlargement, local displacement, conflict detection, and attribute enrichment. Then, the GA is employed to obtain the best solution. A flowchart of the selection process is given in Figure 10.
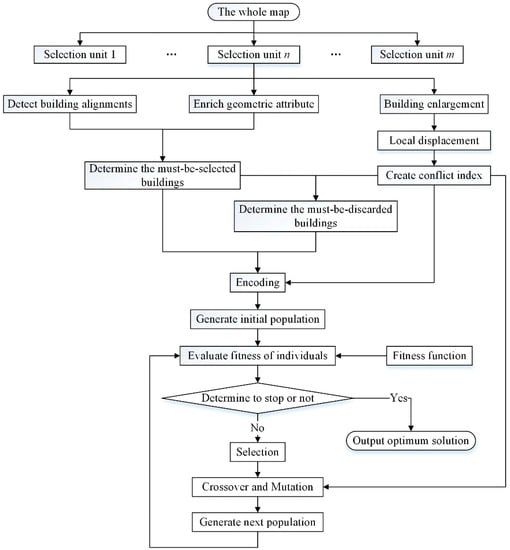
Figure 10.
Buildings selection procedure.
4.1. Extraction of Selection Units
First, selection units are extracted from the whole map. For this approach, a selection unit is a natural group including a set of buildings and roads. Buildings in a specific unit do not conflict with buildings in other units, and thus they can be treated together in the generalization. Similar ideas of data partitioning have been studied [8,25,30]. In these studies, the road network was used as a framework to define the partition. Since roads in rural areas are not always enclosed, a new method to extract selection units is necessary.
To derive suitable selection units, a polygon buffering approach is adopted based on the work of Boffet [48]. This method was originally used to identify different types of settlements such as major cities, towns, villages, and hamlets. The values of the parameters used below are set according to the experiments conducted by Boffet [48]. The main steps of the extraction process, as shown in Figure 11, are: (1) conducting a buffering operation with 25 m as the radius and assign a buffered area to each building; (2) merging overlapping buffer areas into several large polygons that cover all the buildings; (3) calculating the area of each polygon, and polygons with areas less than 20 ha can be termed as rural settlements; and (4) selecting polygons for rural settlements, and overlaying them with the building and road layers. Buildings and roads falling within the same polygon together form a selection unit.
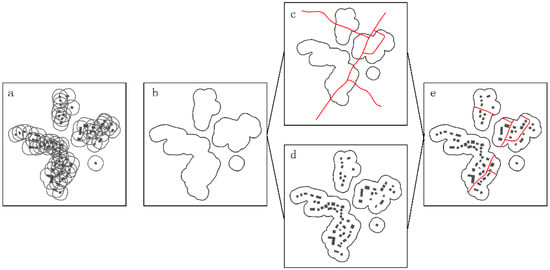
Figure 11.
Extraction of selection units: (a) building buffering; (b) merging of buffered polygons; (c) conducting an overlap with roads; (d) conducting an overlap with buildings; (e) assigning buildings and roads to form selection units.
Note that not all selection units need to use the GA to perform the selection. For a unit with 10 or fewer buildings, the selection can be carried out directly according to a sequencing rule such as the sizes of the buildings.
4.2. Building Enlargement
To enforce the constraints of minimum size, small buildings should be enlarged before selection. If enlargement occurs after selection, the expansion of building size may lead to new conflicts. According to the National Administration of Surveying [43], the rules for enlargement of individual buildings at scales of 1:25,000 and 1:50,000 can be determined as follows.
- Rule 1.
- If the graphic length and graphic width of a building are less than 0.7 mm and 0.5 mm, respectively, then replace the building with a predefined symbol of the appropriate size and orientation.
- Rule 2.
- If the graphic length of a building is larger than 0.7 mm, but its graphic width is less than 0.5 mm, then expand its symbol width to 0.5 mm. Similarly, if the graphic width of a building is larger than 0.5 mm, but its graphic length is less than 0.7 mm, then expand its symbol length to 0.7 mm.
- Rule 3.
- If the graphic length and graphic width of a building are larger than 0.7 mm and 0.5 mm, respectively, then represent them with their original outline.
A schematic of the three rules is shown in Figure 12. The prerequisite for the above rules is that the building is rectangular by default. However, not all buildings are represented as rectangles in the map. For non-rectangular buildings, in addition to expanding their size, shape simplification may also be required. Considering that rural buildings are usually relatively small, it is rarely worth simplifying their shapes. Therefore, an enlargement method is proposed that utilizes the smallest minimum bounding rectangle (SMBR). On the premise of expanding the size, this method can simplify the shape simultaneously. As the smallest rectangle that includes the whole building, the SMBR is fitted because it can maximally approximate the size and shape of the original building.
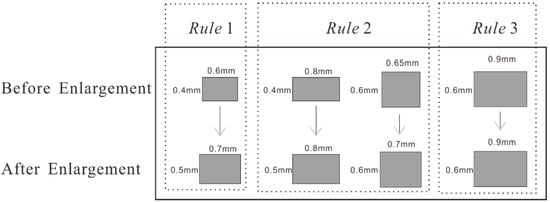
Figure 12.
Three rules for enlargement of individual buildings at scales of 1:25,000 and 1:50,000.
In the Cartesian coordinate system with the east–west direction as the horizontal axis, the enlargement begins by generating an SMBR for each building. Using the center of gravity as the anchor point, the SMBR is then rotated so that its long axis is horizontal. By comparing the length and width of the rotated graphic symbols with the predefined thresholds, a simple geometric expansion is performed in the horizontal and vertical directions. Finally, the rotation is implemented again for each enlarged SMBR to return the long axis to its original orientation. Then, the original buildings can be replaced by these enlarged graphic symbols. Figure 13 illustrates the process consisting of two rotations and one geometric change.
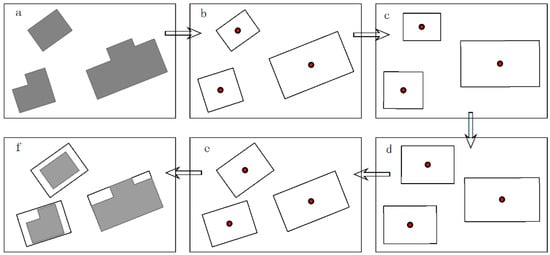
Figure 13.
Building enlargement process: (a) original buildings; (b) SMBRs; (c) first rotation; (d) simple geometric transformation; (e) second rotation; (f) buildings after enlargement compared to their initial states.
4.3. Local Displacement
After enlargement of the building size, the feature symbols that are originally separated from each other may overlap. To maintain the topological relationship among the buildings and their surrounding roads, the overlap needs to be removed. Since roads are more important than buildings in maps [49], the correct topological relationship is retained by displacing the overlapping buildings.
According to the positional relationship, overlapping buildings can be classified into two types: the corner type (C-type) and the edge type (E-type) (see Figure 14). Definitions for the buildings of these two types are as follows:
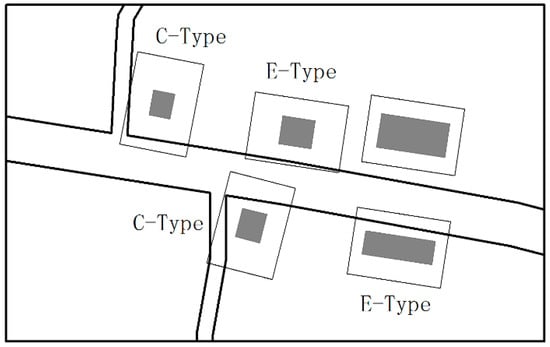
Figure 14.
Two types of buildings that overlap surrounding roads.
- A C-type building is one that is located at a road corner and overlaps at least one of the roads.
- An E-type building is one that is located on one side of the road and only overlaps one of the roads.
For a C-type building, buffering technology is used to determine its displacement vector. In Figure 15a, a buffering operation is conducted for the nearby road edges. The buffer radius is set to be half the larger diagonal length of the enlarged building. After that, the overlapping buffers will form an intersection (marked as a star) on the inside corner. The displacement vector can then be determined with the center of gravity of the building as the start point and the intersection as the end point. Figure 15b shows that, for an E-type building, the displacement direction is set to be perpendicular to the road. The displacement magnitude is the sum of d1 and d2, where d1 is the nearest distance from the original building to the road, and d2 is the maximum distance that the enlarged building covers the road. To avoid the violation of constraint C4, it is necessary to check the displacement magnitude before a building is displaced. Once the displacement magnitude exceeds 0.5 mm, the building should be removed instead of being displaced.
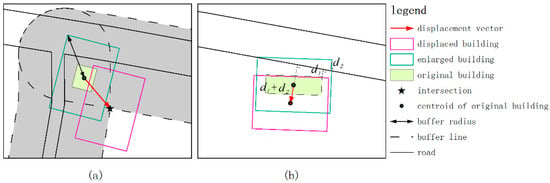
Figure 15.
Determination of the building displacement vector for: (a) a C-type building; (b) an E-type building.
4.4. Conflict Detection among Buildings
Spatial conflicts occur when the distance between two buildings is shorter than the minimum distance threshold, or when buildings overlap each other. This paper uses the buffer-based approach [6,49,50] to detect conflicts (see Figure 16). In this method, a buffer area is constructed for each building with half the minimum distance threshold as the radius. If the buffer of one building overlaps with that of another building, there is a conflict between the two buildings.
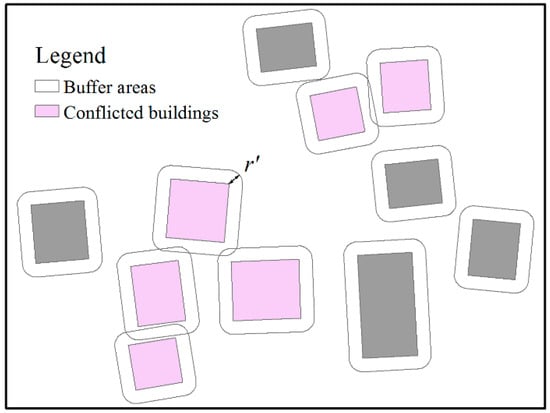
Figure 16.
The buffer-based approach for detecting conflicts. r’ is half the minimum distance threshold for detecting conflicts.
Conflicting blocks are taken into account in encoding, crossover, and mutation. To avoid repetitive detection of spatial conflicts and to speed up the running speed of the GA, a conflict index list after building enlargement and local displacement is generated. The conflict index mainly stores conflicting block information for each building. Therefore, in the selection process, once a building is processed, all buildings that conflict with it can be easily searched.
4.5. Enrichment of Geometric Attributes
This subsection aims to identify specific buildings on the source map that are important to retain. According to the previous description, it is necessary to identify three types of important buildings.
- (1)
- A type I building is determined by simple area calculation and comparison to the minimum size threshold. According to the National Administration of Surveying [43], buildings with an area of more than 0.35 mm2 are considered to be of this type.
- (2)
- A type II building is identified on the basis of detecting the proximity relationship among buildings and roads. Before performing the GA on a selection unit, a proximity graph is constructed using the method proposed by Liu et al. [51]. It is then possible to obtain information as to whether a building is adjacent to a road and how close it is. Utilizing the information, a building that is adjacent to two or more roads and whose proximity distance to each road is less than a certain threshold (e.g., 15 m) can be defined as a type II building.
- (3)
- To identify a type III building, the boundary of a settlement should be defined first. A boundary deriving method proposed by Yan and Weibel [17] is adopted after converting the building group to a point cluster. The buildings that overlap the generated boundary are called the boundary buildings. A type III building can be derived from these boundary buildings by performing a line reduction algorithm on the boundary line. The Douglas–Peucker algorithm [52] is preferred because it keeps all the key points that make up the basic shape of a line and removes the other points. The simplified tolerance in the algorithm is set to 25 m by experiment. The buildings corresponding to the points retained on the simplified line will be type III buildings.
4.6. Selection Based on the GA
Before running the GA, the must-be-selected buildings should be extracted from the three types of important buildings and the building alignment. Then, the must-be-discarded buildings can be easily determined using the generated conflict index.
4.6.1. Initialization
The GA begins with initialization, which generates the first population. The process of initializing a chromosome can be summarized as:
- (1)
- Mark all genes as ‘free’;
- (2)
- Assign the gene values corresponding with the must-be-selected buildings as 1 s and mark these genes as ‘fixed’;
- (3)
- Assign the gene values corresponding with the must-be-discarded buildings as 0 s and mark these genes as ‘fixed’;
- (4)
- Repeat the following steps until the number of genes assigned as 1 s reaches the target selection number or all the genes are marked as ‘fixed’;
- (4.1)
- Randomly select a ‘free’ building B and assign its gene as 1, then mark the gene as ‘fixed’;
- (4.2)
- Identify ‘free’ buildings from CB(B), assign the corresponding genes as 0 s and mark these genes as ‘fixed’;
To determine the target selection number, Töpfer’s radical law [37] can be applied:
where Nt is the number of buildings in the target map, Ns is the number of buildings in the source map, Ms is the denominator of the source scale, and Mt is the denominator of the target scale.
Through the above process, initialization of a chromosome is completed. A population often contains a set of chromosomes. In general, an initial population with a large size can handle more solutions at the same time, making it easier to find the global optimal solution. But the disadvantage is that it increases the time of each iteration. The general value of population size Psize ranges from 20 to 100. In this paper, the population sizes are set to 50 (at 1:25,000) and 150 (at 1:50,000), which have been determined through experimental testing.
4.6.2. Selection, Crossover, and Mutation
After the population is initialized, the GA makes use of crossover and mutation to evolve new solutions. The first step is to select appropriate individuals for the genetic operators. There are several selection operations available, and the one used here is the fitness proportionate selection, because it makes the GA robust. The basic idea is that the probability for each individual to be selected is proportional to its fitness value.
The way to perform crossover and mutation has been discussed in Section 3.3, but how to set the crossover probability Pc and mutation probability Pm remains a problem. The crossover probability indicates the probability that crossover operation will occur on two selected parents. If the value is set too high, individuals with high fitness can easily be destroyed. However, too small a crossover probability will slow down the search process. The mutation probability determines the probability that a gene value in an individual is altered. The GA becomes a random search algorithm when the mutation probability is set too high, since the gene information is easy to change. Too low a mutation probability will reduce the local search capability of the algorithm. In this paper, the crossover probability is set to 0.8, and the mutation probability is set to 0.1, which have been determined through experimental testing.
4.6.3. Iteration and the Elite Retention Strategy
After crossover and mutation, the children will replace the parent chromosomes in the initial population. To avoid destroying an excellent individual in the evolutionary process, the elite retention strategy [53] is introduced into the GA. The idea of the strategy in this paper is that the best individual of the previous generation can be directly copied to the next generation. This excellent individual, together with other children, produces a new population. The GA then starts the next evolution based on the new population. Through multiple iterations, the individual with the highest fitness value is obtained as the selection results. The iterative process terminates when the algorithm reaches the maximum generation Gm, where Gm is set using an experimentally determined threshold, namely 30 (at 1:25,000) and 50 (at 1:50,000).
5. Results and Analysis
5.1. Experimental Results
To validate the effectiveness of the approach, two selection units were chosen to carry out experiments on. They were extracted from the topographic dataset of Caidian District, Wuhan City, China. The original scale of the topographic map was 1:10,000, and the target scales were 1:25,000 and 1:50,000. For both selection units, the symbol width of roads was set to 0.2 mm and the outline width of buildings was set to 0.1 mm. The road was properly selected according to the scale changes. The proposed approach was programmed using C# and ArcGIS Engine, and the tests were implemented on a PC with Windows 7 OS and Intel® Core™ i5-4460 CPU (3.20 GHz).
Figure 17 shows the two selection units. Unit A contains 157 buildings and unit B contains 204 buildings. Figure 18 and Figure 19 demonstrate the results of unit A and a comparison of its states before and after selection. As shown in Figure 17, Figure 18 and Figure 19, there are two identified building alignments plotted with blue lines in selection unit A. The experimental results for unit B are shown in Figure 20 and Figure 21. A preliminary conclusion can be obtained through visual evaluation that the resultant map is more legible and the distribution characteristic is well maintained. Detailed statistical information is given in Table 1, Table 2 and Table 3 below.
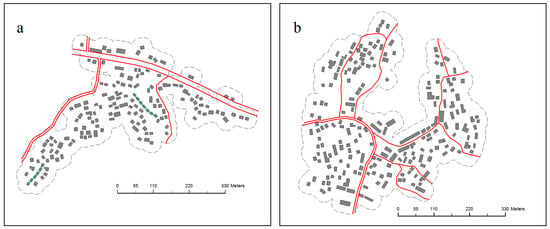
Figure 17.
Two test datasets: (a) selection unit A and (b) selection unit B.
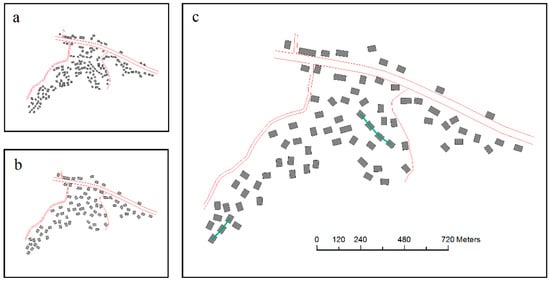
Figure 18.
Test results of selection unit A: (a) visual reduction without selection (1:25,000), (b) selection result using the GA (1:25,000), and (c) selection results enlarged to 1:10,000 from 1:25,000.
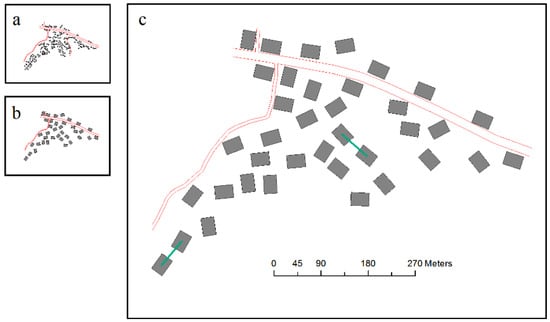
Figure 19.
Test results of selection unit A: (a) visual reduction without selection (1:50,000), (b) selection result using the GA (1:50,000), and (c) selection result enlarged to 1:10,000 from 1:50,000.
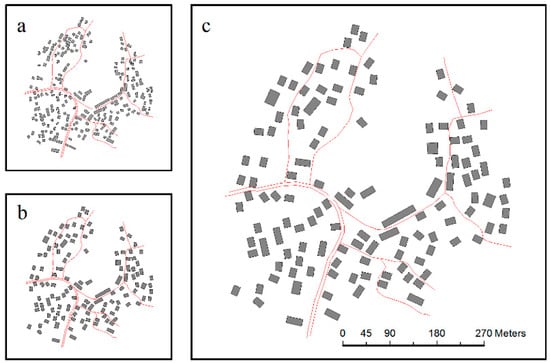
Figure 20.
Test results of selection unit B: (a) visual reduction without selection (1:25,000), (b) selection result using the GA (1:25,000), and (c) selection result enlarged to 1:10,000 from 1:25,000.
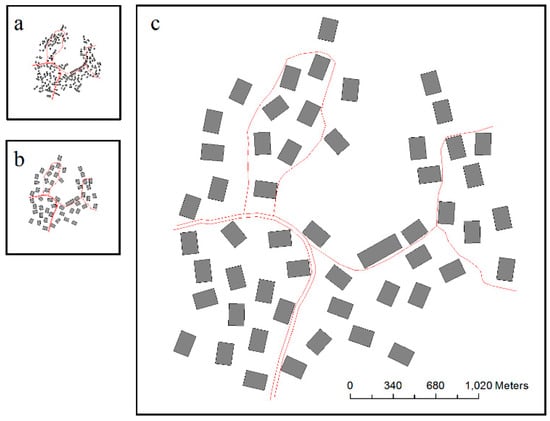
Figure 21.
Test results of selection unit B: (a) visual reduction without selection (1:50,000), (b) selection result using the GA (1:50,000), and (c) selection result enlarged to 1:10,000 from 1:50,000.

Table 1.
Statistical analysis of the GA results.

Table 2.
Magnitude of distribution range changes.

Table 3.
Density information at different scales.
5.2. Analysis
The goal of building selection is to remove spatial conflicts caused by scale reduction under related cartographic constraints. Therefore, the quality of the selection results can be assessed by determining whether these constraints have been satisfied.
5.2.1. Local Constraints
In this approach, the size constraint was enforced by building enlargement. It is advisable to give a higher priority to this constraint because it generally has an impact on other constraints. For example, the distance among the enlarged buildings will inevitably be reduced, which may cause violation of the separation constraint. Using the strategy that the enlargement comes first can avoid potential conflicts. The enlargement method used in this paper adopts the SMBR. Therefore, it has the beneficial effects of satisfying the constraints on granularity and squareness at the same time. In addition, the two rotations guarantee that the resultant buildings maintain their original main directions. Respecting these constraints ensures that the buildings retained in the target map are legible. After enlargement, to maintain the spatial relationship among the building and other features, the building symbols may need to be locally displaced during the selection process. To ensure positional accuracy, the displacements have been purposefully limited within a specific range (e.g., 0.5 mm).
The separation constraint is evaluated by measuring the number of spatial conflicts. As shown in Table 1, initial conflicts and final conflicts refer to the conflicts among the enlarged buildings at the target scale before and after selection. It can be seen that all the conflicts among the buildings have been completely resolved after selection. However, the number of selected buildings does not strictly correspond to the radical law, especially at the 1:50,000 scale. The reason is that the enlarged building is far from the initial geometry when the scale is reduced to 1:50,000. This greatly increases the size of the conflicting block of each building and further reduces the number of optional buildings when encoding. Taking this situation into account, the initialization of a chromosome has been set to be stopped as long as all the buildings are processed, even if the estimated building number has not been reached. In this way, building conflicts can be avoided as much as possible.
The current method satisfies the functionality constraint by enriching the geometry attributes and fixing important buildings when encoding. The identified must-be-selected buildings for two units are shown in Figure 22 and Figure 23. Among these buildings are the three types of important buildings, whilst others are the buildings that should be kept in the identified alignments. Some buildings may belong to more than one type at the same time. All these buildings are contained in the final solution. As shown, the must-be-selected buildings at 1:25,000 are more than those at 1:50,000. The main difference lies in the type I buildings. A building that can be recognized as type I on a 1:50,000 map requires an area of at least 875 m2 in the real world. Such a large building is very rare in rural areas. In this paper, the semantic attributes of buildings are lacking. As for a dataset with rich semantic attributes, the approach can be easily extended to include these semantically important buildings.

Figure 22.
Must-be-selected buildings in selection unit A when the target scale is: (a) 1:25,000, and (b) 1:50,000. The green dashed line is the simplified boundary line.
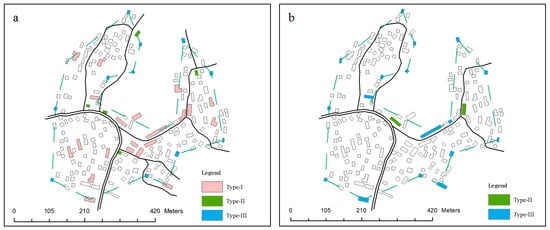
Figure 23.
Must-be-selected buildings in selection unit B when the target scale is: (a) 1:25,000, and (b) 1:50,000. The green dashed line is the simplified boundary line.
5.2.2. Contextual Constraint of Spatial Relationships and Patterns
An important indicator to assess the generalization results is whether building alignments are preserved. To satisfy this constraint, the building alignments must first be identified. Multiple studies have been undertaken by various researchers to detect buildings in alignment [11,25,38,42]. With the aid of these methods, these building alignments are extracted automatically and then handled in the algorithm.
The building alignments of selection unit A in Figure 17, Figure 18 and Figure 19 are magnified for closer observation in Figure 24. When the scale is reduced to 1:25,000, it is still possible to identify the alignments. In the 1:50,000 maps, the number of buildings in both alignments is reduced to 2. As the recognized alignment should contain at least three buildings, the alignments are unrecognizable at 1:50,000. It is found that whether the alignment constraint can be satisfied is highly correlated to two factors: the number of aligned buildings and the degree of scale change. When the number of aligned buildings is relatively small, it may be unrecognized at a scale of 1:25,000. On the contrary, alignments with a higher number of buildings may still be significant, even at 1:50,000.
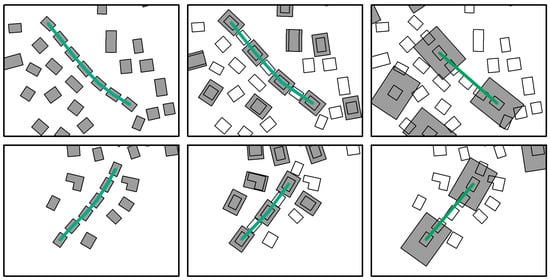
Figure 24.
Two alignments of selection unit A in detail. The pictures on the left are building alignments at the source map scale, the pictures in the middle are building alignments at 1:25,000, and the pictures on the right are building alignments at 1:50,000 (outlined shapes: original buildings, fully shaded shapes: selected buildings).
To evaluate the change of distribution range, the ratio between the area difference of the distribution range and the area of the initial distribution range was used. The smaller the ratio, the better the preservation of the distribution range. The results are shown in Table 2, where the maximum ratio of range changes is 11.24%. It can therefore be considered that the distribution range is well preserved.
According to Regnauld et al. [46], distribution density can be evaluated from the perspective of contrast of different units across a map. Table 3 illustrates the density information of the two selection units at different scales. As shown, the ordering of density values between the two units is consistent prior to and after selection. That is, unit B has a higher density than unit A at 1:10,000, and this situation still exists after selection. The conclusion can be drawn that the contrast among units of different density is well maintained.
6. Conclusions and Future Work
Building selection is a process in which various factors interact with and restrict each other. This study has proposed an improved GA for automated building selection. The proposed algorithm is highly efficient as it takes into account a wide range of constraints while producing very satisfactory results. On the one hand, spatial conflicts among buildings have all been resolved after selection by considering conflicting blocks when performing the encoding and genetic operations. On the other hand, the spatial distribution characteristics are well maintained, as the contextual constraints have been introduced into the fitness function. The improved algorithm was found to be feasible for conflict resolution for rural buildings, especially when their overall density was too high to perform displacement.
Future research will focus on collaborative generalization with other contextual operators, especially displacement. In this paper, the GA was mainly used to remove intra-feature conflicts. Inter-feature conflicts among buildings and their surrounding features, such as roads and rivers, have not been fully considered. These conflicts may be caused by scale reduction or the generalization operations of other features. For example, the symbolization, simplification, and displacement of roads may lead to spatial conflicts among roads and their adjacent buildings. Therefore, it is of great interest to collaborate the available generalization algorithms to resolve multiple cartographic conflicts.
Acknowledgments
This research was supported in part by the National Natural Science Foundation of China (Grant No. 41471384, No. 41071289, and No. 41701537).
Author Contributions
Lin Wang and Qingsheng Guo conceived and designed the experiments; Lin Wang and Yageng Sun performed the experiments; Lin Wang, Qingsheng Guo, and Zhiwei Wei analyzed the data; Yuangang Liu contributed reagents/materials/analysis tools; Lin Wang and Qingsheng Guo wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- McMaster, R.B.; Shea, K.S. Generalization in digital cartography. In Spatial Data Handling; Association of American Geographers: Washington, DC, USA, 1992; pp. 6.1–6.18. [Google Scholar]
- Ruas, A.; Plazanet, C. Strategies for automated generalization. In Proceedings of the 7th International Symposium on Spatial Data Handling, Delft, The Netherlands, 12–16 August 1996. [Google Scholar]
- Brassel, K.E.; Weibel, R. A review and conceptual framework of automated map generalization. Int. J. Geogr. Inf. Syst. 1988, 2, 229–244. [Google Scholar] [CrossRef]
- Mackaness, W.A. An algorithm for conflict identification and feature displacement in automated map generalization. Cartogr. Geogr. Inf. Syst. 1994, 21, 219–232. [Google Scholar] [CrossRef]
- Ruas, A. A method for building displacement in automated map generalisation. Int. J. Geogr. Inf. Syst. 1998, 12, 789–803. [Google Scholar] [CrossRef]
- Lonergan, M.; Jones, C.B. An iterative displacement method for conflict resolution in map generalization. Algorithmica 2001, 30, 287–301. [Google Scholar] [CrossRef]
- Harrie, L.; Sarjakoski, T. Simultaneous graphic generalization of vector data sets. GeoInformatica 2002, 6, 233–261. [Google Scholar] [CrossRef]
- Bader, M.; Barrault, M.; Weibel, R. Building displacement over a ductile truss. Int. J. Geogr. Inf. Sci. 2005, 19, 915–936. [Google Scholar] [CrossRef]
- Ai, T.; Zhang, X.; Zhou, Q.; Yang, M. A vector field model to handle the displacement of multiple conflicts in building generalization. Int. J. Geogr. Inf. Sci. 2015, 29, 1310–1331. [Google Scholar] [CrossRef]
- Ai, T.; Zhang, X. The aggregation of urban building clusters based on the skeleton partitioning of gap space. In The European Information Society; Fabrikant, S., Wachowicz, M., Eds.; Springer: Aalborg, Denmark, 2007; pp. 153–170. [Google Scholar]
- Regnauld, N. Contextual building typification in automated map generalization. Algorithmica 2001, 30, 312–333. [Google Scholar] [CrossRef]
- Yan, H.; Weibel, R.; Yang, B. A multi-parameter approach to automated building grouping and generalization. Geoinformatica 2008, 12, 73–89. [Google Scholar] [CrossRef]
- Kadmon, N. Automated selection of settlements in map generalisation. Cartogr. J. 1972, 9, 93–98. [Google Scholar] [CrossRef]
- Langran, G.E.; Poiker, T.K. Integration of name selection and name placement. In Proceedings of the 2nd International Symposium on Spatial Data Handling, Seattle, WA, USA, 5–10 July 1986; International Geographical Union and International Cartographic Association: Seattle, WA, USA, 1986; pp. 50–64. [Google Scholar]
- Ai, T.; Liu, Y. Analysis and simplification of point cluster based on delaunay triangulation model. In Advances in Spatial Analysis and Decision Making; Li, Z., Zhou, Q., Kainz, W., Eds.; Taylor & Francis: London, UK, 2003; pp. 9–18. [Google Scholar]
- Qian, H.; Meng, L. Polarization transformation as an algorithm for automatic generalization and quality assessment. In Proceedings of the SPIE 6751, Geoinformatics 2007: Cartographic Theory and Models, Nanjing, China, 25–27 May 2007; Li, M., Wang, J., Eds.; The International Society for Optical Engineering: Nanjing, China, 2007; Volume 67510Y. [Google Scholar]
- Yan, H.; Weibel, R. An algorithm for point cluster generalization based on the voronoi diagram. Comput. Geosci. 2008, 34, 939–954. [Google Scholar] [CrossRef]
- Peters, S. Quadtree-and octree-based approach for point data selection in 2D or 3D. Ann. GIS 2013, 19, 37–44. [Google Scholar] [CrossRef]
- Yan, H.; Li, J. An approach to simplifying point features on maps using the multiplicative weighted voronoi diagram. J. Spat. Sci. 2013, 58, 291–304. [Google Scholar] [CrossRef]
- Bjørke, J.T. Framework for entropy-based map evaluation. Cartogr. Geogr. Inf. Syst. 1996, 23, 78–95. [Google Scholar] [CrossRef]
- Ruas, A. Modèle de Généralisation de Données Géographiques à Base de Contraintes et D’autonomie. Ph.D. Thesis, Université de Marne la Vallée, Marne La Vallée, France, 1999. [Google Scholar]
- Burghardt, D.; Cecconi, A. Mesh simplification for building typification. Int. J. Geogr. Inf. Sci. 2007, 21, 283–298. [Google Scholar] [CrossRef]
- Gong, X.; Wu, F. A typification method for linear pattern in urban building generalisation. Geocarto Int. 2016, 1–19. [Google Scholar] [CrossRef]
- Sester, M. Optimization approaches for generalization and data abstraction. Int. J. Geogr. Inf. Sci. 2005, 19, 871–897. [Google Scholar] [CrossRef]
- Li, Z.; Yan, H.; Ai, T.; Chen, J. Automated building generalization based on urban morphology and gestalt theory. Int. J. Geogr. Inf. Sci. 2004, 18, 513–534. [Google Scholar] [CrossRef]
- Steiniger, S.; Taillandier, P.; Weibel, R. Utilising urban context recognition and machine learning to improve the generalisation of buildings. Int. J. Geogr. Inf. Sci. 2010, 24, 253–282. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Wilson, I.D.; Ware, J.M.; Ware, J.A. A genetic algorithm approach to cartographic map generalisation. Comput. Ind. 2003, 52, 291–304. [Google Scholar] [CrossRef]
- Ware, J.M.; Wilson, I.D.; Ware, J.A. A knowledge based genetic algorithm approach to automating cartographic generalisation. Knowl. Based Syst. 2003, 16, 295–303. [Google Scholar] [CrossRef]
- Sun, Y.; Guo, Q.; Liu, Y.; Ma, X.; Weng, J. An immune genetic algorithm to buildings displacement in cartographic generalization. Trans. GIS 2016, 20, 585–612. [Google Scholar] [CrossRef]
- Van Dijk, S.; Thierens, D.; De Berg, M. Using genetic algorithms for solving hard problems in GIS. GeoInformatica 2002, 6, 381–413. [Google Scholar] [CrossRef]
- Wu, F.; Deng, H.-Y. Using genetic algorithms for solving problems in automated line simplification. Acta Geodaetica Cartogr. Sin. 2003, 4, 013. [Google Scholar]
- Lamy, S.; Ruas, A.; Demazeau, Y.; Jackson, M.; Mackaness, W.; Weibel, R. The application of agents in automated map generalisation. In Proceedings of the 19th ICA Meeting, Ottawa, ON, Canada, 14–21 August 1999; Volume 14, pp. 1–8. [Google Scholar]
- Duchêne, C.; Ruas, A.; Cambier, C. The cartacom model: Transforming cartographic features into communicating agents for cartographic generalisation. Int. J. Geogr. Inf. Sci. 2012, 26, 1533–1562. [Google Scholar] [CrossRef]
- Jones, C.B.; Bundy, G.L.; Ware, M.J. Map generalization with a triangulated data structure. Cartogr. Geogr. Inform. 1995, 22, 317–331. [Google Scholar]
- Topfer, F.; Pillewizer, W. The principles of selection. Cartogr. J. 1966, 3, 10–16. [Google Scholar] [CrossRef]
- Christophe, S.; Ruas, A. Detecting building alignments for generalisation purposes. In Advances in Spatial Data Handling; Richardson, D.E., Oosterom, P.V., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 419–432. [Google Scholar]
- Regnauld, N. Recognition of building clusters for generalization. In Proceedings of the 7th International Symposium on Spatial Data Handling, Delft, The Netherlands, 12–16 August 1996; Kraak, M.-J.M.M., Ed.; Taylor & Francis: London, UK, 1996; Volume 1, pp. 185–198. [Google Scholar]
- Anders, K.-H.; Sester, M. Parameter-free cluster detection in spatial databases and its application to typification. Int. Arch. Photogramm. Remote Sens. 2000, 33, 75–83. [Google Scholar]
- Basaraner, M.; Selcuk, M. A structure recognition technique in contextual generalisation of buildings and built-up areas. Cartogr. J. 2008, 45, 274–285. [Google Scholar] [CrossRef]
- Zhang, X.; Ai, T.; Stoter, J.; Kraak, M.-J.; Molenaar, M. Building pattern recognition in topographic data: Examples on collinear and curvilinear alignments. Geoinformatica 2013, 17, 1–33. [Google Scholar] [CrossRef]
- National Administration of Surveying, Mapping and Geoinformation of China. Cartographic Symbols for National Fundamental Scale Map-Part3: Specifications for Cartographic Symbols 1:25,000, 1:50,000 & 1:100,000 Topographic Maps; China Zhijian Publishing House: Beijing, China, 2006.
- Swiss Society of Cartography. Topographic Maps: Map Graphics and Generalization; Federal Office of Topography: Berne, Switzerland, 2005.
- National Administration of Surveying, Mapping and Geoinformation of China. Compilation Specification for National Fundamental Scale Maps-Part1: Complilation Specifications for 1:25,000, 1:50,000 & 1:100,000 Topographic Maps; China Zhijian Publishing House: Beijing, China, 2008.
- Regnauld, N. Preserving density contrasts during cartographic generalization. In GIS and Geocomputation; Peter, M., David, M., Eds.; Taylor & Francis: London, UK, 2000; pp. 175–186. [Google Scholar]
- Cheng, R.; Gen, M.; Oren, S.S. An adaptive hyperplane approach for multiple objective optimization problems with complex constraints. In Proceedings of the 2nd Annual Conference on Genetic and Evolutionary Computation, Las Vegas, NV, USA, 10–12 July 2000; Whitley, L.D., Goldberg, D.E., Cantú-Paz, E., Spector, L., Parmee, I.C., Eds.; Morgan Kaufmann Publishers Inc.: Las Vegas, NV, USA, 2000; pp. 299–306. [Google Scholar]
- Boffet, A. Méthode de Création D’Informations Multi-Niveaux Pour la Généralisation Cartographique de L’urbain. Ph.D. Thesis, Université de Marne la Vallée, Marne La Vallée, France, 2001. [Google Scholar]
- Bader, M. Energy Minimization Methods for Feature Displacement in Map Generalization. Ph.D. Thesis, University of Zurich, Zurich, Switzerland, 2001. [Google Scholar]
- Nickerson, B.G. Automated cartographic generalization for linear features. Int. J. Geogr. Inf. Geovis. 1988, 25, 15–66. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, Q.; Sun, Y.; Ma, X. A combined approach to cartographic displacement for buildings based on skeleton and improved elastic beam algorithm. PLoS ONE 2014, 9, e113953. [Google Scholar] [CrossRef] [PubMed]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Int. J. Geogr. Inf. Geovis. 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Jong, K.A.D. An Analysis of the Behavior of a Class of Genetic Adaptive Systems. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1975. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).