Abstract
Geographic information systems (GIS) can be effectively utilized to carry out spatio-temporal analysis of spatial accessibility to primary healthcare services. Spatial accessibility to primary healthcare services is commonly measured using floating catchment area models which are generally defined with three variables; namely, an attractiveness component of the service centre, travel time or distance between the locations of the service centre and the population, and population demand for healthcare services. The nearest-neighbour modified two-step floating catchment area (NN-M2SFCA) model is proposed for computing spatial accessibility indices for the entire country. Accessibility values from 2010 to 2013 for Bhutan were analysed both spatially and temporally by producing accessibility ranking maps, plotting Lorenz curves, and conducting spatial clustering analysis. The spatial accessibility indices of the 205 sub-districts show great disparities in healthcare accessibility in the country. The mean- and median-based classification results indicate that, in 2013, 24 percent of Bhutan’s population have poor access to primary healthcare services, 66 percent of the population have medium-level access, and 10 percent have good access.
1. Introduction
Primary health care (PHC) “…is the first level of contact of individuals, the family and community with the national health system bringing health care as close as possible to where people live and work...” which has to be “scientifically sound and socially acceptable methods made universally accessible” provided by the well-trained health professionals ([1], p.1). Therefore, spatial (potential) accessibility that integrates availability of well-trained health care providers, potential demand from population for health care services, and geographic accessibility due to distance separation between location of the residents and providers is an important component of PHC. Spatial accessibility has widely been used to evaluate the equity of spatial access to PHC services [2,3,4,5,6,7].
Generally, a spatial accessibility measurement system is defined by a gravity model or a floating catchment area (FCA) model. Recent research on spatial accessibility indicate that the FCA models are more widely used than the gravity model because they are intuitively interpretable and use variable-sized population catchment areas for each of the service centres instead of using a single catchment area for all the service centres, as used in the gravity model [2,6,8]. However, it is important to note that the FCA models are a specialized variant of the gravity model [4]. There are three major issues to deal with the FCA measurement system. The first issue is with respect to the availability of a number of FCA models, such as the 2SFCA (Two-Step Floating Catchment Area) [4], KD2SFCA (Kernel Density Two-Step Floating Catchment Area) [9], E2SFCA (Enhanced Two-Step Floating Catchment Area) [3], 3SFCA (Three-Step Floating Catchment Area) [6], and M2SFCA (Modified Two-Step Floating Catchment Area) [2] models that have been successfully tested for measuring spatial accessibility to primary healthcare services. Delamater [2] has carried out an extensive analysis of the aforementioned FCA models and proposed the M2SFCA model, which has been formulated based on a sound mathematical framework. The second issue of any spatial accessibility model is concerning the selection of a distance decay function, which is generally used to derive relative distance weights for the distance impedance parameter in the spatial accessibility model. Five different distance decay functions have been reported in the literature—inverse power [5], linear [10], exponential [2], Epanechnikov kernel [9], and Butterworth filter functions [10]; however, none of those studies has exclusively analysed the effect of a distance decay function on spatial accessibility measures. The third issue deals with the method of delineation of population catchment areas for each service centre. Past studies have delineated population catchment areas by defining concentric circles with certain radii of travel-time values from the location of each population cluster [2,3,4,6,9]. This method is termed as the buffer-ring (BR) method in order to distinguish it from the proposed nearest-neighbour (NN) method. The NN method delineates catchment area by identifying a finite number of nearest service centres for each population cluster instead of identifying variable number of service centres falling within a finite-size buffer ring around each cluster. All the FCA-based accessibility studies so far, save for Jamtsho and Corner [11], have used the BR method of delineating population catchment areas. Wang has noted that the choice of distance weighting functions and delineation of population catchment areas can only be resolved by conducting actual surveys on health care utilization behaviour [12]. However, it is very expensive to conduct individual surveys of the whole country to collect travel diaries, so these uncertainties should be practically resolved by developing accessibility models with sound theoretical frameworks.
The majority of the spatial accessibility studies were conducted in either urban or rural regions in developed countries using travel-time-based computational methods where road access is the main form of transportation, and road network data are comprehensive and readily available. Travel-time-based methods are ideally suited to regions where travel time can be accurately derived from route network data. In the absence of route network data, an alternative approach of measuring spatial accessibility is necessary. This paper proposes the NN method of delineating population catchment areas within the M2SFCA model, using straight-line distance measures instead of travel-time measures, to compute the spatial accessibility indices of population clusters. The novelty of the proposed method is that it uses a nearest-neighbour method of defining catchment areas rather than the commonly used buffer-ring method, which is founded on a weak theoretical framework. Bhutan has been used as a case study to test the proposed computational approach. This country has been chosen as the case study area due to its small size and population, which facilitates the computation of spatial accessibility indices for the whole country. The importance of developing spatial accessibility indices for the whole country is that these indices can be used to assess the equity of spatial access to health care services for different sub-districts and districts in the country, which in turn can be used to conduct evidence-based spatial planning for allocation or re-allocation of health resources equitably across the country. It is important to note that there are very few accessibility modelling trials conducted for the entire country, such as by McGrail and Humphreys [8], where accessibility for the whole of Australia was modelled using travel-time-based variable-sized catchment areas using the 2SFCA model. The proposed computational method will be specifically significant for developing countries where road access is limited and road network data are scarce.
This paper has been structured as follows. Section 2 presents the review and evaluation of different FCA models. Section 3 describes data sources and outlines the methodology for computing spatial potential accessibility indices using the proposed straight line based method. Section 4 presents the spatial accessibility results. The spatial and temporal changes in spatial accessibility to primary health care services between 2010 and 2013 were assessed using accessibility values of population clusters, and composite accessibility indices of sub-districts and districts. Section 5 and Section 6 present a discussion and conclusions, respectively.
2. Review of Floating Catchment Area (FCA) Models
A modification to the original 2SFCA method was proposed by Delamater [2], and named it as the M2SFCA method. An adapted version of the M2SFCA model is given by Equation (1),
where Ai is the spatial accessibility index of population cluster i, n is the total number of healthcare service provider locations associated with population cluster i, Sj is the number of healthcare providers available at location j, Wij and Wkj are distance weights computed using a distance decay function, m is the total number of population clusters associated to the health facility j, and Pk is the population at the population cluster location k.
FCA-based accessibility indices are usually computed in two-steps due to the two summations involved in the model (Equation (1)), thus the prefix “two-step” is used in the nomenclature of FCA models. The variants of the FCA model differ only by their weighting mechanism. If all the weighting variables in Equation (1) are excluded, then it represents the 2SFCA model and if only one Wij variable is excluded then it represents the E2SFCA and KD2SFCA models. The E2SFCA and KD2SFCA models differ only by their use of a different distance decay function, in that the former model uses a step function, whereas the latter model employs a continuous decay function [2]. Figure 1 shows two different distance decay functions which define the aforementioned FCA methods. The 3SFCA model is the original E2SFCA model augmented by incorporating additional weighting function, Dij, on both the numerator and denominator components. Dij can be defined using Equation (2), which is a ratio of the distance weight of the population cluster location i and associated health facility j and the sum of all the distance weights for the population cluster i and its associated health facilities.
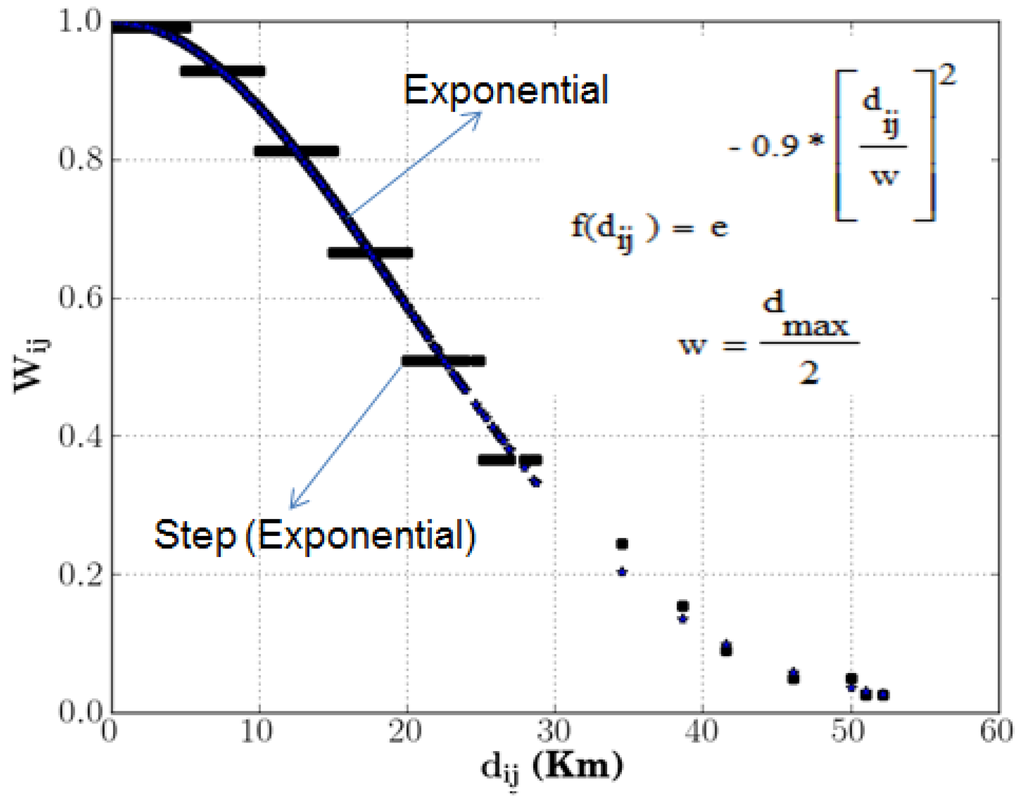
Figure 1.
Step (E2SFCA) and continuous (KD2SFCA) decay functions.
In order to understand the computational framework of different FCA models, following [2], a simulated system of service providers and population clusters was designed to evaluate these models. Figure 2 shows the design of a simulated system with two service centres and six population clusters. The entities A and B represent service providers and p, q, r, x, y, and z represent the locations of population clusters. For the sake of computation, the number of service providers in both service centres are assumed to be 10 and the number of people in each population clusters is assumed to be 100. The result of the computation of spatial accessibility values using three different FCA methods are shown in Table 1. The unit of the spatial accessibility value (Ai) is opportunities per person. As expected, Ai values of q and y clusters are lower than the values of p, r, x, and z clusters for the E2SFCA and M2SFCA models. KD2SFCA model was not tested as its mathematical formulation is similar to that of the E2SFCA model. However, Ai values of q and y clusters are larger than the corresponding values of p, r, x and z clusters for the 3SFCA model, which is logically incorrect. The results of the 3SFCA model obtained in this study agree with the results obtained by Delamater [2], who has conducted an extensive comparison between FCA measurement systems using a simple simulated system. Hence, it is evident from these computational experiments that the 3SFCA method is mathematically inconsistent and inferior to the other FCA measurement systems.
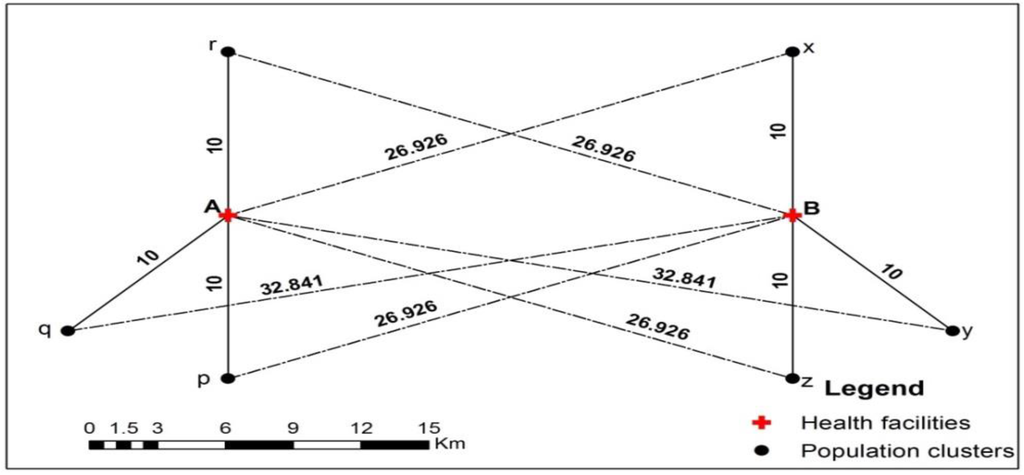
Figure 2.
A simulated system.

Table 1.
Accessibility results from simulated system.
| Methods | Ai Values (Opportunities per Person) | Estimated Total Opportunities of a System | |||||
| p | q | r | x | y | z | ||
| E2SFCA | 0.03464 | 0.03073 | 0.03464 | 0.03464 | 0.03073 | 0.03464 | |
| 3SFCA | 0.03317 | 0.03366 | 0.03317 | 0.03317 | 0.03366 | 0.03317 | |
| M2SFCA | 0.02527 | 0.02274 | 0.02527 | 0.02527 | 0.02274 | 0.02527 | |
| Total opportunities for a population unit | |||||||
| E2SFCA | 3.46365 | 3.07270 | 3.46365 | 3.46365 | 3.07270 | 3.46365 | 20 |
| 3SFCA | 3.31721 | 3.36558 | 3.31721 | 3.31721 | 3.36558 | 3.31721 | 20 |
| M2SFCA | 2.52676 | 2.27425 | 2.52676 | 2.52676 | 2.27425 | 2.52676 | 14.66 |
Both the E2SFCA and M2SFCA produce mathematically-consistent accessibility values. However, as pointed out by Delamater [2], the difference between these two models is that the M2SFCA model is more accurate when dealing with systems with sub-optimal configuration because it takes into account the absolute distance separation between the population and provider locations, unlike the E2SFCA model, which only considers the relative distance separation. Theoretically, an optimal configuration system is realized when both the population and provider locations are collocated. Any other configuration system is defined as sub-optimal. Following [2], for instance, the E2SFCA method produces the same accessibility values for all three population clusters, irrespective of the absolute distance separation between the population and provider locations in the following two configuration systems: first, a system with three population clusters located in different directions at the same distance of 2 km from the sole provider, and second, a system with three population clusters located in different directions at the same distance of 5 km from the sole provider. This limitation of the E2SFCA model can potentially bias the accessibility outcome of the disadvantaged regions by over-estimating their accessibility values as illustrated in the aforementioned scenario where three population clusters that are located 5 km away from the provider location have the same accessibility values as the population clusters that are located 2 km away. Such bias in the accessibility values is often referred to as the problem of over-estimation [2,6].
In addition, the M2SFCA model also produces lower accessibility values than the other FCA models. A conservative estimate of spatial accessibility values also results in estimating lower total opportunities than the actual total opportunities available in the complete system. The total opportunities available to a population unit is equal to the product of its spatial accessibility value (opportunities per person) and population, and an estimated total opportunity available in a system is equal to the sum of total opportunities of all population units within the system. Table 1 also shows that all 20 providers available in the simulated system have been distributed relatively between six population units by the E2SFCA and 3SFCA computational approach, whereas only 14.66 providers have been distributed by the M2SFCA approach. For any distance separation between provider and population locations, the E2SFCA and 3SFCA models will compute accessibility values of population units such that the estimated total opportunities in the system is always equal to the actual total opportunities available in the system. On the contrary, the M2SFCA model will compute spatial accessibility values of population units such that the estimated total opportunities available in the system progressively decrease with the increase in the absolute distance separation between the provider and population locations. This computational characteristic of the M2SFCA model makes more sense because the total opportunities available for a population unit must decrease with the increase in distance from the provider location because of the distance impedance costs incurred for accessing the services. Therefore, the M2SFCA model appears to be the most reliable computational model for measuring spatial accessibility to primary health care services, which has been adopted in this study.
3. Methodology
In the FCA measurement system, each health centre has a population catchment area and each population cluster has a service catchment area, which is generally finite and overlapping with the neighbouring catchment areas. The actual delineation of population catchment areas is supposed to be performed by modelling the spatial relationships between the service centre and the residents living within the vicinity of the service centre [4]. However, it is not practically feasible to accurately model the provider-population interaction since this would require extensive and costly surveys throughout the country. Therefore, the service and population catchment areas should be defined by developing a sound theoretical framework underpinning the spatial accessibility model. One such method can be developed on the basis of Tobler’s first law of geography, which states that the nearest entities interact each other more than the farther ones [13]. The proposed NN method assumes that people tend to seek healthcare services from the nearest facilities rather than from the farther ones.
The population catchment area of each service centre is defined by the number of population clusters associated with each service centre and the service catchment area is defined by the number of service centres associated with each population cluster. The existing method of delineation of service and population catchment areas are based on a BR method where catchment areas are modelled by associating service centres and population units falling within a specified travel-time or distance units. For instance, in a travel-time based computation approach, the service catchment area of each population cluster is defined by identifying potential service centres falling with a buffer ring of 30 [3], 45 [2], or 60 min [6] from the location of the population clusters. Similarly, a population catchment area of each service centre is defined by associating all population clusters falling within the specified buffer ring from the location of the respective service centres. This method of delineating catchment areas is flawed due to both theoretical and practical limitations. First, any real value is theoretically possible to define a buffer ring, for instance 5 min, 11 min, or 15.56 min can be used equally. Even the most commonly used time measure of 30 min is, at best, arbitrarily defined. The availability of infinite real values creates uncertainty in identifying a single accurate measure to define the buffer ring. On the contrary, the NN method eliminates or minimizes this real value ambiguity by directly associating each population cluster with a whole number of nearest neighbours, service centres. Second, the BR method produces a biased accessibility scores between different population clusters because population clusters are associated with variable number of service centres ranging from few to hundreds. For instance, McGrail and Humphreys have used a maximum of 100 nearest service centres found within a 60 min search radius to compute a 2SFCA-based accessibility measure [14]. Obviously, people would not access these many service centres, so the majority of those potential service centres are practically redundant, which only contribute accessibility bias by largely measuring “choice” in urban areas rather than actual accessibility, as correctly pointed by McGrail ([15], p. 6). The accessibility bias due to differences in associated service centres between population clusters will be referred as choice bias, henceforth. Recall that accessibility score of a given population cluster is computed as an additive component due to all the associated service centres (see Equation (1)). On the other hand, the NN method has the potential to completely eliminate the aforementioned accessibility bias by associating same number of service centres with each population clusters. Even with the use of variable number of nearest neighbours in order to segregate between rural and urban regions, for practical purpose, there is no need whatsoever to associate hundreds of service centres with any population cluster because it is unrealistic to assume that people would associate with such a large number of service centres, especially health centres. Third, the health planning and allocation of GP services should be done with an objective to provide few services as close as possible to the location of all population clusters. So the evaluation of accessibility should be done by comparing the service availability at few closest locations rather than by including redundant number of service centres located within 30, 45, or 60 min.
The NN method was originally developed to accommodate large variation in distances between some population clusters from their nearest health facilities while evaluating spatial accessibility of the entire nation [11]. For Bhutan, no particular distance cut-off value can be used since it has been observed from the health centres and population clusters network data that some of the population clusters (located in Lunana sub-district of Gas district) are located 53 kilometres away from their nearest health facilities. If this largest distance is chosen as the threshold value then the urban population would be associated with the population catchment areas of the health centres located in farther rural regions, and vice versa which, in practice, is not true. If a threshold distance smaller than the largest distance is chosen then some population clusters in rural regions will have no health facilities assigned to them as all the health facilities would fall outside the threshold distance. In order to associate all population clusters to some health facilities, each population cluster was associated to their two nearest health centres. It was decided to use the two closest health facilities by considering two criteria. Firstly, it was observed from the health system network data that most of the urban regions have more than one health facility located in a close proximity to another. Even in the rural regions, there are many population clusters that have almost equidistant health facilities located within their vicinity. In such instances, it is quite inaccurate to choose just one health facility as the only likely target facility. Secondly, the third-nearest health facility for the majority of the population clusters are located relatively much further away as the majority of sub-districts have only one or two health facilities. To choose more than two nearest health facilities is quite redundant and impractical because it is unlikely that people would travel to the third-nearest health facilities if there are two nearer health facilities located within their vicinity. Even in a densely populated region, such as Thimphu city, there are only five health centres available. Considering two nearest neighbours accommodates about half of the available opportunities. Therefore, the choice of two nearest health facilities was considered as optimal to define a realistic configuration of the healthcare delivery system for Bhutan. So the value of parameter n in Equation (1) is 2 for all population clusters. However, the value 2 is not absolute in the NN method because it can be adapted uniformly or variably in accordance with the health network data of a particular region.
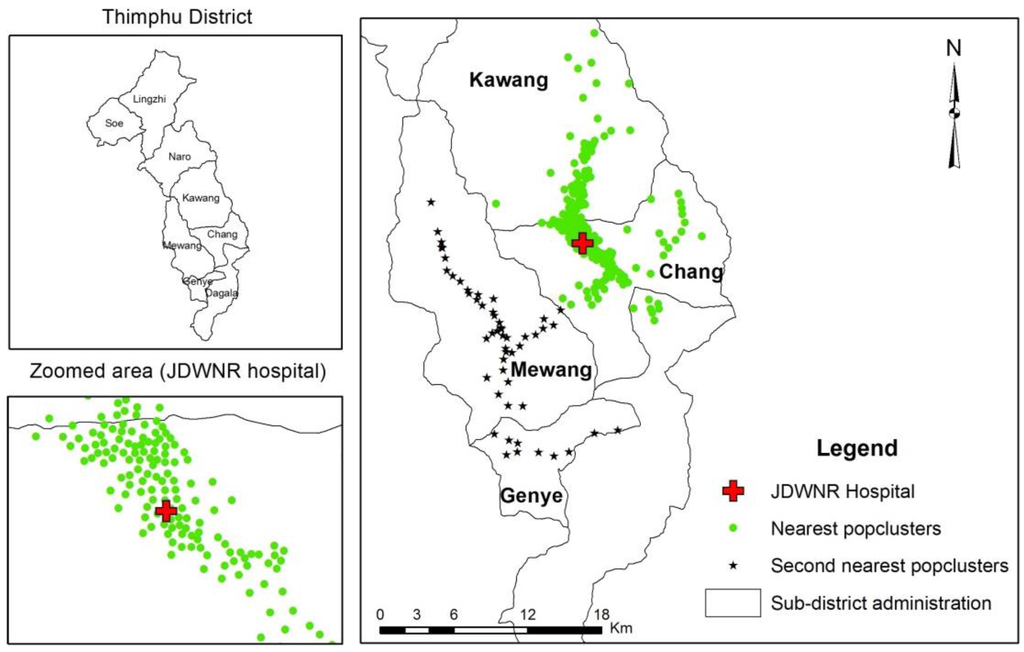
Figure 3.
Population catchment area of JDWNRH.
In order to delineate the population catchment areas of every health centre, firstly, each population cluster was associated with its two nearest health centres based on distance proximity, and secondly, the population catchment area of the health centres were delineated by including all the population clusters (both first- and second-nearest clusters) that were associated with the respective health centre. Figure 3 shows the distribution of the first- and second-nearest population clusters that were associated with Jigme Dorji Wangchuck National Referral Hospital (JDWNRH). The population clusters represented by circular markers are the clusters for which JDWNRH is the first-nearest facility, and the population clusters represented by star markers are those clusters for which JDWNRH is the second-closest health facility. Thus, the population catchment area of JDWNRH is formed by combining all first- and second-nearest population clusters associated to this health centre.
4. Data Sources and Modelling
Bhutan, a developing country located between China and India, with a population of about 730,000 people, has been chosen as the case study area. The administrative region of this country is divided into 20 districts and each district is further divided into sub-districts. There are 205 sub-districts in the country. Owing to the small size of the country, it is possible to compute spatial accessibility to primary health care services for the entire country, unlike the majority of previous work [3,4,6,7,9,14] in which only small region of a country was used. About 60 percent of the population of Bhutan live in rural areas where road transportation is sparsely available. The health care system in this country is completely owned by the government and provided free to all residents. Primary health care services are delivered to far-flung regions of the country through the establishment of subsidiary health centres such as Basic Health Units, Outreach Clinics, and Sub-posts. The distribution of various health facilities are shown in Figure 4
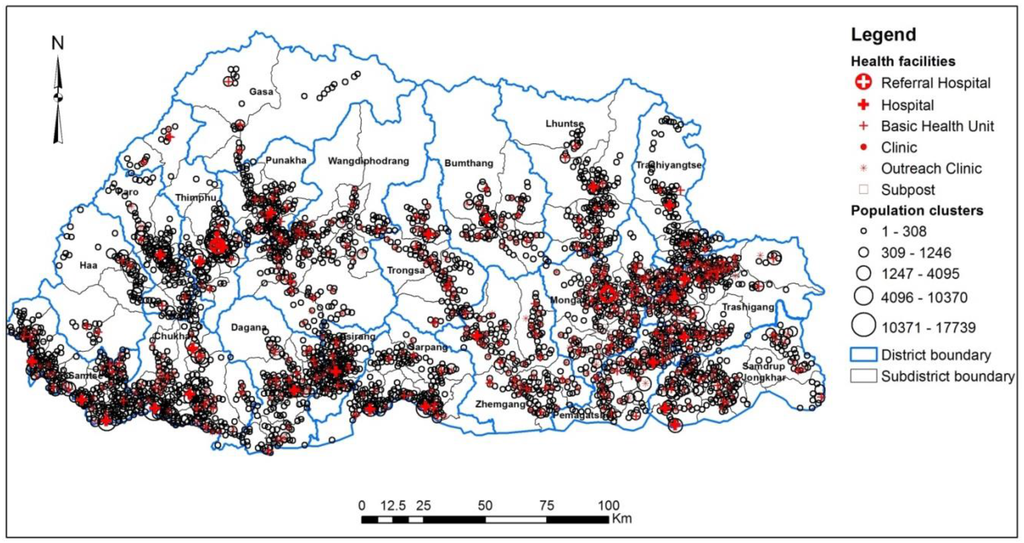
Figure 4.
Distribution of population clusters and health facilities.
Two primary spatial datasets required for computing spatial accessibility are population cluster data at the village level and the location of each health facility with its attractiveness attribute, such as the number of health care providers in each health centre. Two different primary health care providers, namely, doctors (general practitioners) and health assistants (HA), were used to define the attractiveness variable. Due to the acute shortage of doctors in the country, the health assistants are specially trained to provide primary level diagnostic services. Most of the health data was obtained from the Ministry of Health with only the location of some of the health centres being derived using rural cadastral data from the National Land Commission (NLC), the national mapping agency of Bhutan. Population cluster data at the village level are not available so it was necessary to model this data using aggregated population data. Housing data and aggregated population data were obtained from the National Statistical Bureau, the custodian of the Population and Housing Census of Bhutan (PHCB) 2005 database. PHCB 2005 is the first nationwide population and housing census ever undertaken in Bhutan. Locations of villages throughout the whole country were obtained from the NLC, and these locations have been used to define population cluster points.
The population data of Bhutan is published for sub-districts and town enumeration blocks, at a level that is too aggregated to be used reliably for the computation of spatial accessibility due to the modifiable areal unit problem (MAUP). MAUP introduces a statistical bias because of the use of actual point data as aggregated data [16]. For instance, it influences statistical results when point-based surveyed population data are represented at the aggregated sub-district or district level. There are a number of different statistical and non-statistical methods available to disaggregate population census data to smaller areal units. One commonly used method is the dasymetric mapping technique which uses some ancillary data to distribute a population from source areal unit to target units [17,18,19].
A simple model of dasymetric mapping technique using housing data to distribute a population of source units to target units is proposed in this study. It is a grid-based population distribution method where relative population distribution weights of the target cells were computed using the variation in density of the housing features located within each target cells. The proposed method was tested using the population and housing census data of Bhutan and compared with the results obtained from the traditional dasymetric method [18], which uses land use data to aid the interpolation process. The internal accuracy of these two dasymetric methods was evaluated by comparing population estimates of sixty-six town enumeration blocks. The truth value is the actual population of each disaggregated block obtained from a population survey. In order to crudely find out the accuracy of the dasymetric models, the population estimation was done at the higher aggregation level (aggregated town block in Figure 5). Then, the population estimates for each disaggregated block (disaggregated town block in Figure 5) was obtained by adding up the individual population estimates falling within its boundary. This estimate was compared with the truth value.
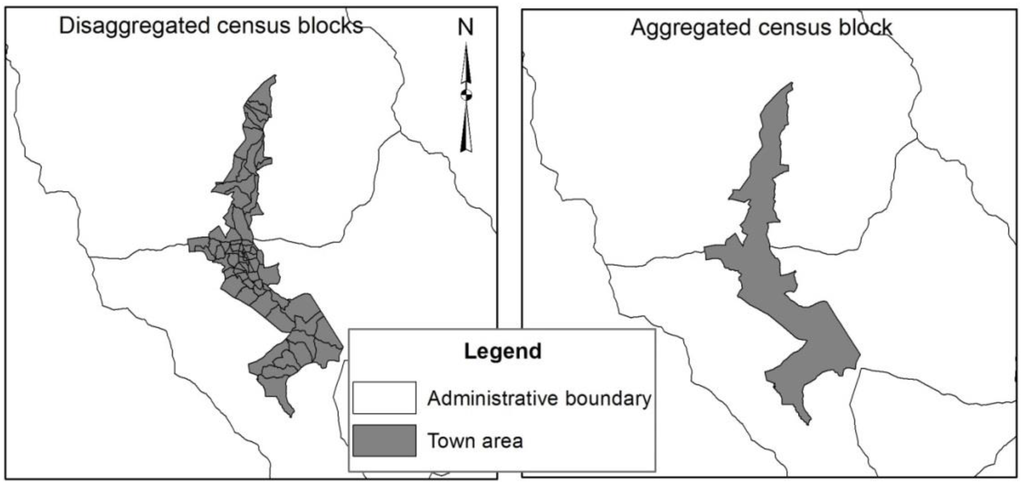
Figure 5.
Test area (Thimphu urban area).
Table 2 shows the error statistics of the proposed and traditional dasymetric methods. The mean absolute percent error (MAPE) and root mean squared error (RMSE) statistics are commonly used to assess the accuracy of dasymetric techniques [17,18]. MAPE is the percentage error computed using the absolute differences between the actual and estimated population values. The lower MAPE and RMSE values of the proposed dasymetric method than the traditional dasymetric method indicates that the proposed method is more accurate than the traditional method. The traditional model is only 34 (100–66) percent accurate, whereas the proposed dasymetric model is about 55 (100−45) percent accurate.

Table 2.
Error statistics.
| Statistics | Traditional Dasymetric Method | Proposed Method |
|---|---|---|
| MAPE | 66.10% | 44.84% |
| RMSE | 852 | 618 |
Population point features were generated at the individual grid locations bearing the population estimates, which were obtained from the dasymetric mapping process. Each of the population point features were associated to a nearby village-level population cluster point, which serve as an anchor point to collect the population estimates within that vicinity. The population value of each of the cluster points is equal to the sum of the values of its associated population point features. Figure 4 also shows the distribution of the population cluster data across the country.
5. Processing Steps
The general processing steps for the computation of spatial accessibility to primary healthcare service in Bhutan are shown in Figure 6. In Step 1, the origin-destination distances for all possible combinations between the health facilities and the population clusters within the national boundary were computed and then first- and second-nearest health centres of each population clusters were identified. Step 2 deals with the computation of spatial accessibility indices of the population clusters using the NN-M2SFCA model. In this study the continuous distance decay function defined with an exponential function was used to compute the distance weighting values. Firstly, the population catchment area of each health facility was determined by including all the first- and second-nearest population clusters associated with the given health facility, and then the denominator component of Equation (1) was computed. Secondly, the spatial accessibility indices of the given population cluster were computed as an additive components due to its associated health centres. Step 3 deals with the computation of sub-district accessibility index (Sk) and its relative accessibility index (RAk) using Equations (3) and (4), respectively,
where Ai is the spatial accessibility of the population cluster at location i, p is the number of population clusters within the sub-district k, and q is the number of sub-districts within the country. The sub-district accessibility index is simply computed by averaging the accessibility indices of all the population clusters falling within that sub-district. The relative accessibility index is computed using the minimum and maximum values of all the sub-district accessibility indices to rescale the given accessibility value to be within 0 and 1, where 1 refers to the highest accessibility and 0 refers to the lowest accessibility within the country. The accessibility ranking of the sub-districts can be obtained by re-arranging the relative accessibility values in ascending order. Using similar computational methods to Step 3, districts’ accessibility indices and their relative accessibility indices were computed in the final step (Step 4).
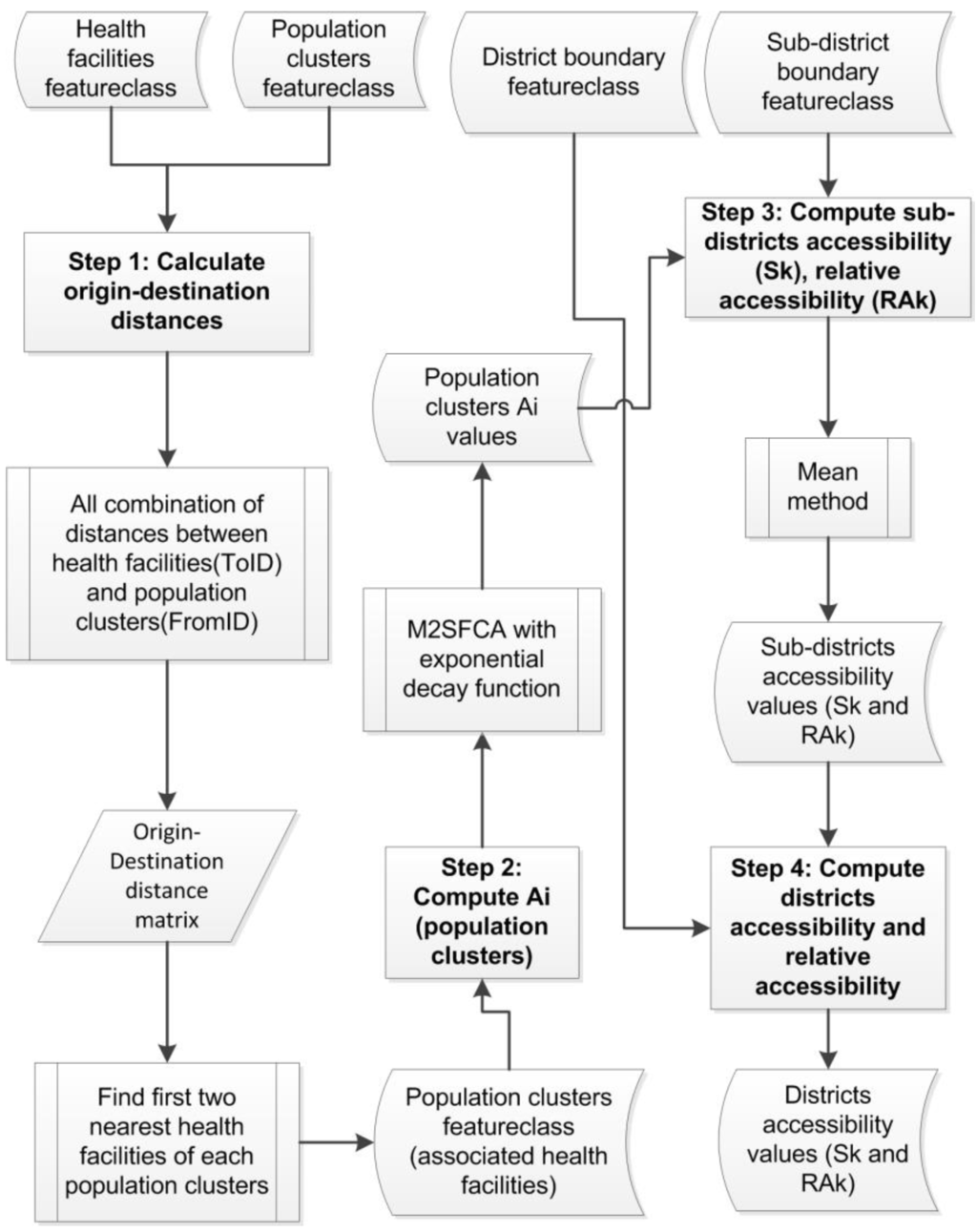
Figure 6.
Flowchart showing steps for computing spatial accessibility.
6. Results and Analysis
6.1. Analysis of Doctors’ Services
The population clusters’ accessibility values can be used to compare the spatial accessibility of different regions. Figure 7 shows the spatial accessibility of doctors’ services for all the population clusters of the four districts in 2013. This plot clearly indicates the variation of spatial accessibility between four districts, with Thimphu district having better accessibility for doctors’ services than the other three districts. This is to be expected as Thimphu is the capital of the country.
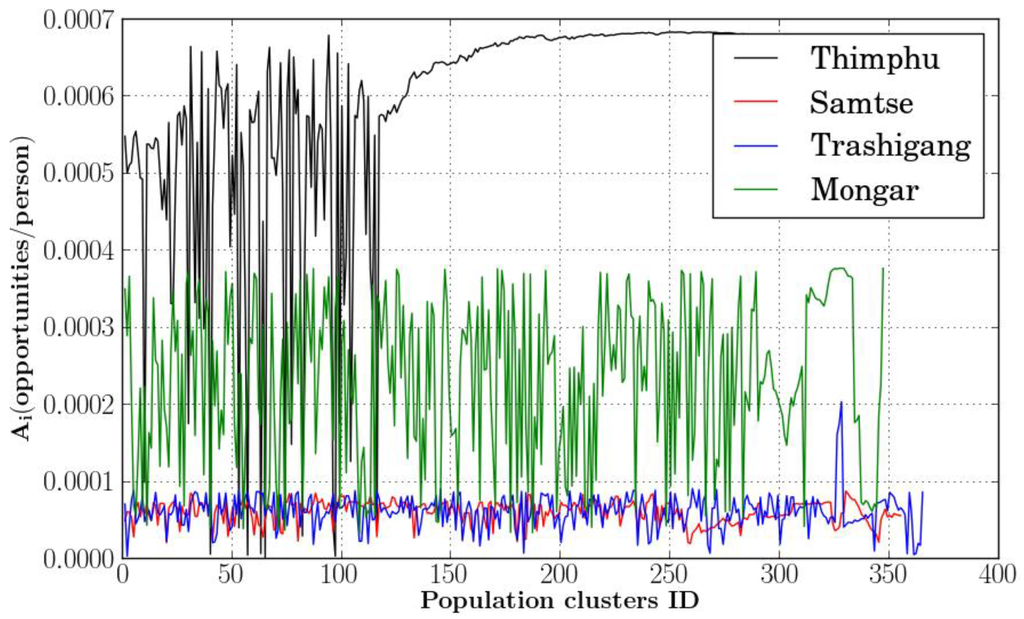
Figure 7.
Accessibility values for doctors’ services of the four districts.
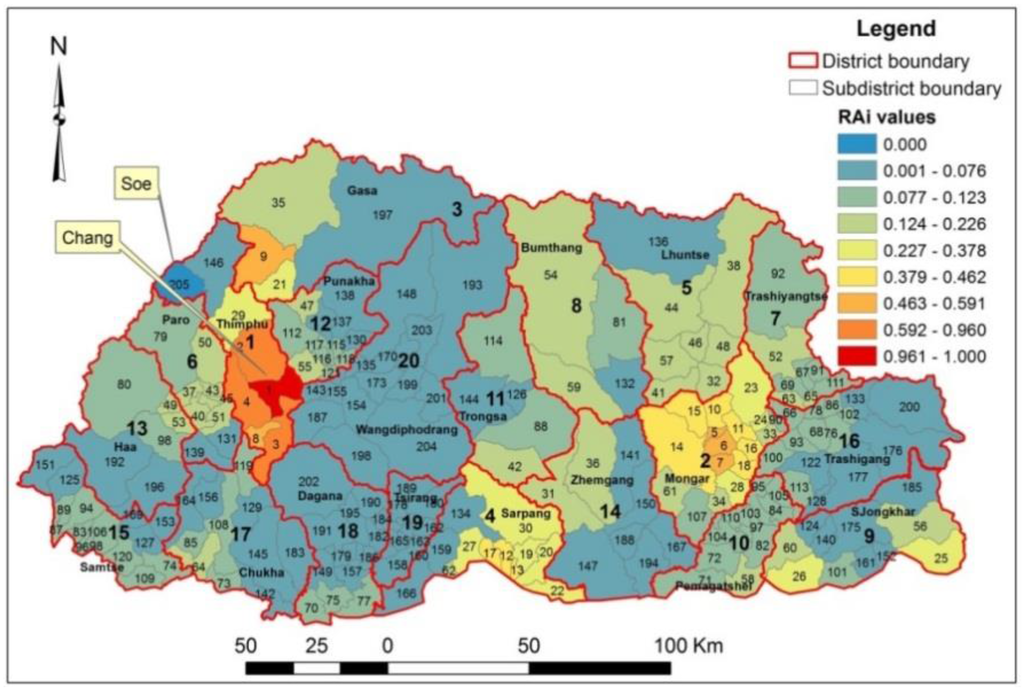
Figure 8.
Districts and sub-districts accessibility ranking map for doctors’ services.
The relative accessibility values of sub-districts and districts can be used to produce choropleth accessibility ranking maps. Figure 8 shows the regional ranking map for doctors’ services in 2013. Bold face figures refer to the district’s rank, while the non-bold face figures represent the ranking of the sub-districts. Chang and Soe sub-districts of the Thimphu district are the highest (Rank 1) and lowest (Rank 205) ranking sub-districts, respectively. The spatial health accessibility of Chang sub-district is about 135 times better than the Soe sub-district, even though the population of the former sub-district is six times more than the latter sub-district. In this case, the two computational parameters, namely, distance and the number of healthcare providers, have subdued the negative impact of the population parameter on the computation of the spatial accessibility indices. In terms of provider-to-population ratio, the spatial accessibility of Chang and Soe sub-districts can be interpreted as having one doctor for every 1497 and 200,000 people, respectively. Thimphu district has the highest accessibility for doctors’ services while Wangdiphodrang has the lowest accessibility because of the presence of poorly-ranked sub-districts in the latter district.
The spatial accessibility indices of population clusters can also be used to assess the evenness of distribution of primary healthcare services within a region by computing the Gini coefficient (Gc). Generally, the Gini coefficient is calculated by plotting a Lorenz curve, which is a plot of two variables represented in cumulative percentages. Mathematically, Gc is defined as the ratio between the areas: the numerator component represents the area between the Lorenz curve and the Line of Equality, and the denominator component represents the area under the Line of Equality [20]. For the spatial accessibility case, a Lorenz curve can be obtained by plotting the cumulative percentage of spatial units (population clusters or sub-districts) against the cumulative percentage of spatial accessibility values of the corresponding spatial unit. The Gini coefficients of the twenty districts indicates that the Pemagatshel district has the best equality in the distribution of health resources with a Gini coefficient of 0.09, and Zhemgang district with a value of 0.46 has the worst inequality of distribution of the health resources for doctors’ services in 2013. Figure 9 shows the Lorenz curves and Gini coefficients of five selected districts of Bhutan for doctors’ services.
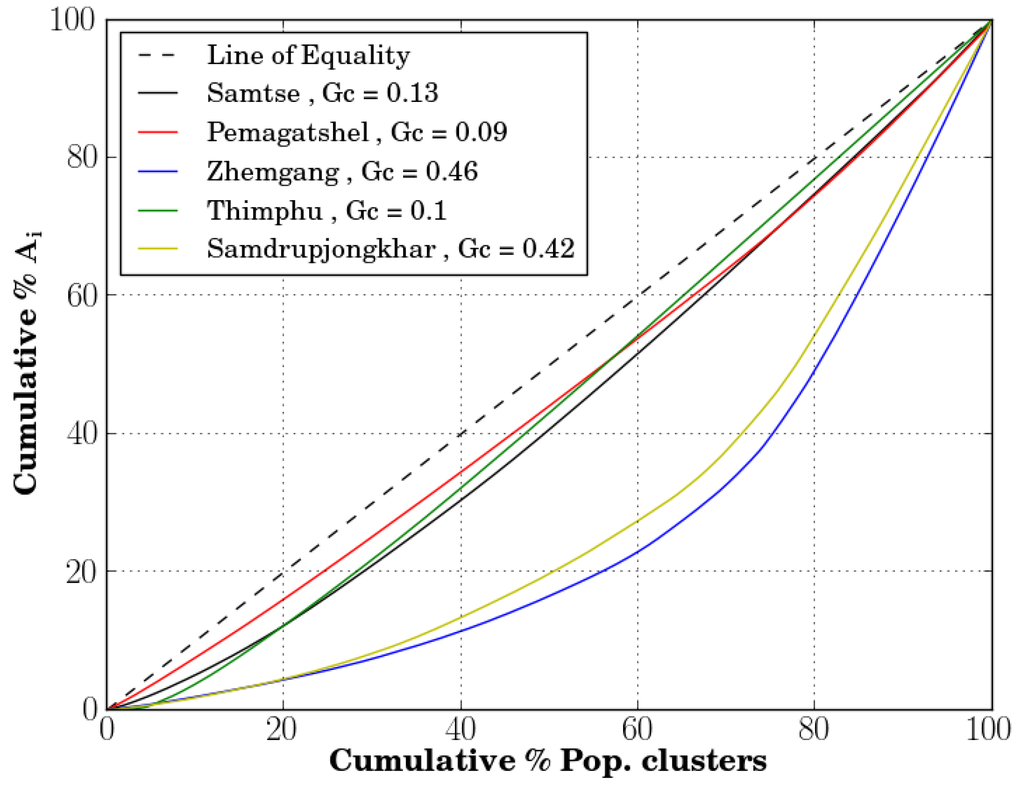
Figure 9.
Lorenz curves of five districts for doctors’ services.
6.2. Hot Spot Analysis
One of the important aspects of spatial data analysis is the ability to determine the existence of spatial patterns by using either location or both the location and attribute information of the incident data points [21]. In this study, the Getis-Ord Gi* local statistic was used to identify hot spots (high value clusters) and cold spots (low value clusters) using the spatial accessibility indices of the population clusters.
Figure 10 shows spatial clusters for doctors’ services in 2013. At the 95 percent confidence level, the clusters with z-score values greater than +1.96 with low p-values are categorised as hot spots and clusters with z-score values less than −1.96 with low p-values are categorised as cold spots. A spatial accessibility hot spot refers to a statistically significant feature with high accessibility values which are surrounded by other features with high accessibility values whereas a cold spot refers to statistically significant feature with low accessibility values surrounded by other features with low accessibility values. In general, the outcome from spatial pattern analysis can be used to investigate the underlying hidden spatial processes that have caused the rejection of the null hypothesis. In this study, the hot spots and cold spots can be used to identify the under-served or over-served regions in order to allocate or reallocate the limited healthcare resources towards achieving an equitable healthcare delivery system in the country.
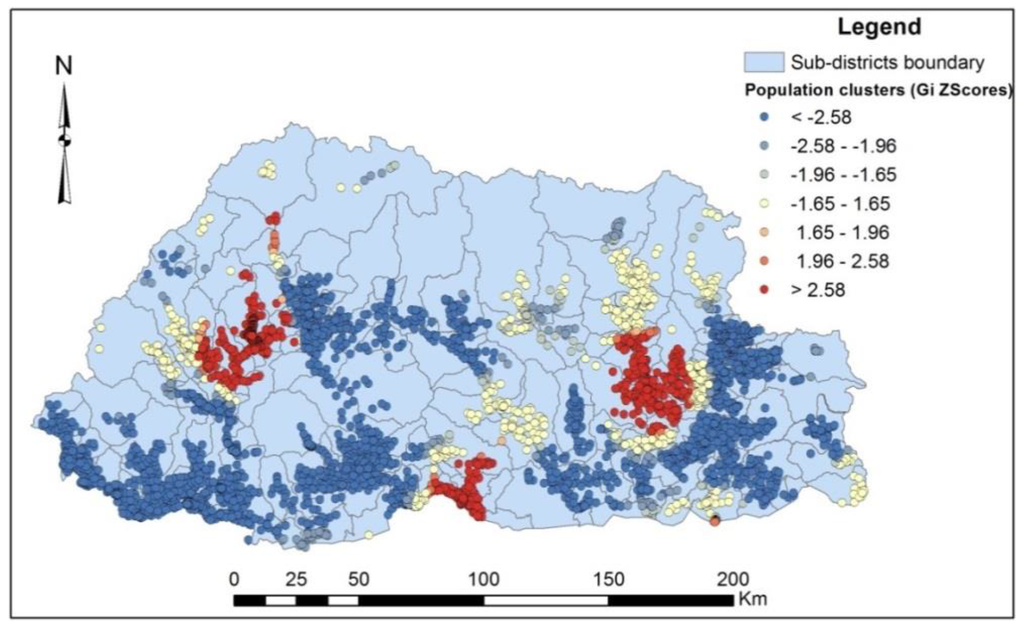
Figure 10.
Hot spot map for doctors’ services.
6.3. Combined Analysis of HA’s and Doctors’ Services
Sub-districts were classified into good, medium, and poor accessibility categories based on accessibility values of both the health care providers according to the classification method described by Unal et al. [5]. Median and average values of sub-districts’ accessibility indices for both the healthcare providers (doctors and HAs) were used to classify sub-districts into three classification categories. A poor status indicates that Gk value of a sub-district is lower than the national median value for both of the providers. A good status indicates that the Gk value of a sub-district is greater than the national average value for both the providers. All other Gk values are classified into the medium accessibility group. Figure 11 shows the classification of 205 sub-districts of Bhutan into three accessibility categories. There are 53 sub-districts with poor accessibility to both types of service providers, 121 sub-districts that have a medium level of accessibility, and 31 sub-districts with good accessibility to both types of providers. About 24 percent of the Bhutan’s predicted population in 2013 falls under the poor access category, 66 percent falls under the medium access category, and 10 percent under the good access category.
6.4. Temporal Analysis
The spatial accessibility indices at different levels were computed from 2010 to 2013 for both types of healthcare providers. Figure 12 shows the temporal variation in the districts spatial accessibility indices for doctors’ services from 2010 to 2013. For example, the accessibility to doctors’ services in Thimphu district decreased by 7 percent in 2011 and then increased by 8 and 0.3 percent in 2012 and 2013 respectively, which portrays a very similar trend to that observed for the districts’ population clusters’ accessibility indices shown in Figure 13.
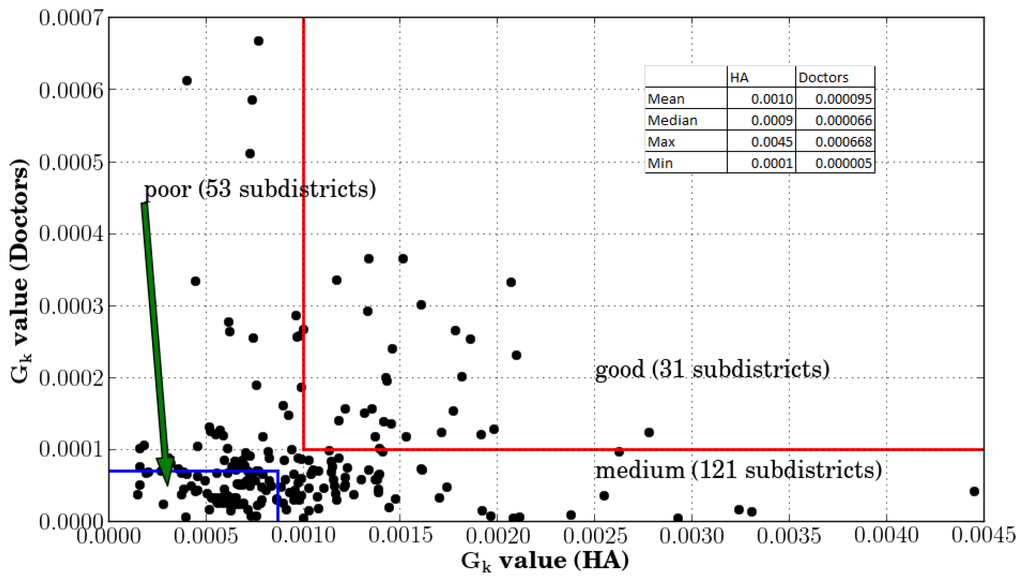
Figure 11.
Classification of sub-districts using Gk values of both the providers.
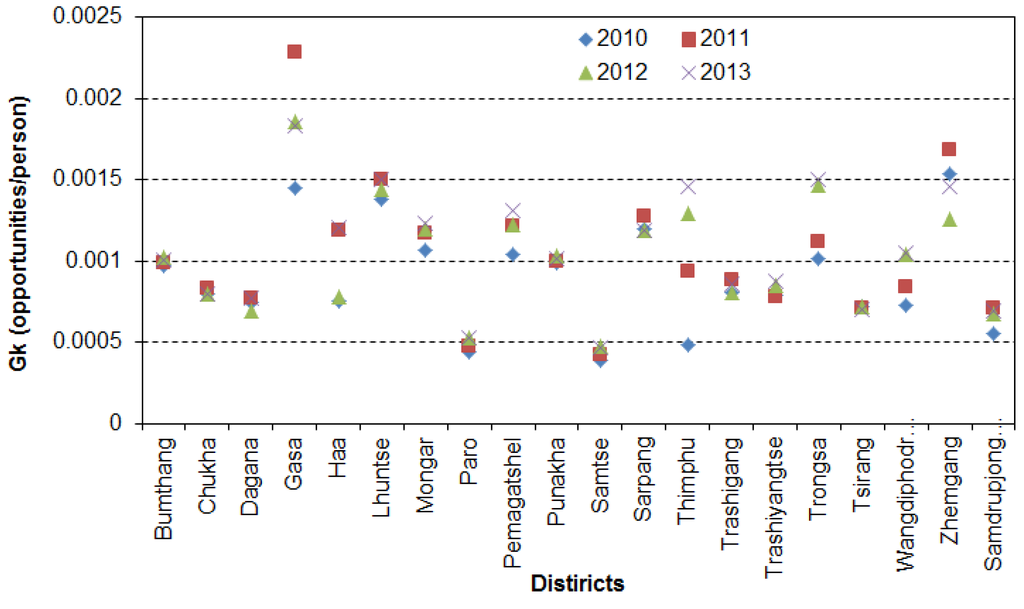
Figure 12.
Districts’ accessibility for doctors’ services from 2010 to 2013.
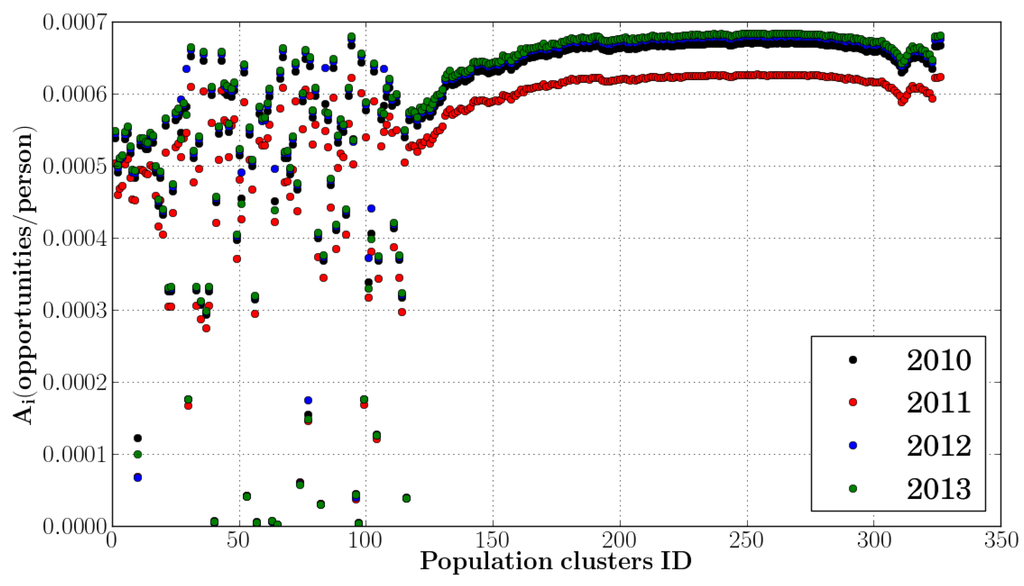
Figure 13.
Population clusters’ accessibility indices of Thimphu district from 2010 to 2013.
Thimphu district’s accessibility trend can be plausibly explained as follows. The computation of the spatial accessibility index for the population cluster depends on the distance, number of service providers, and population parameters. The average distance value for three years are the same, which indicates that the distances between the population clusters and the health facilities remained unaltered between 2010 and 2013; therefore, the distance parameter has not caused the variation of the Thimphu district’s accessibility indices within the study period. The population of the Thimphu district has gradually increased from 2010 to 2013 so the population parameter would decrease the accessibility values in the same order since this parameter is being used to normalize the accessibility index. On the other hand, the number of doctors available in these four years follow a similar trend in the order of their districts’ accessibility indices, which indicates that the number of providers parameter have impacted heavily for this district in the computation of its spatial accessibility indices.
7. Discussion
There are a number of uncertainties involved in the FCA-based accessibility model which would affect the accessibility outcome. These uncertainties are caused by the aggregation level of population cluster data because of the modifiable areal unit problem, travel distance or time measure because of the use of different metric measure, computational method because of the differences in weighting schemes, decay functions because of the differences in decaying patterns, and delineation of service and population catchment areas because of the differences in associating service centres to each population cluster. Despite there existing a number of uncertainties in the computation of spatial accessibility values, most or all of the variants of the FCA computational models are differentiated, based on their differences in the use of weighting scheme as described in Section 2.
In a theoretical sense, the actual potential accessibility can only be obtained by using the modified gravity model, as all the service centres are associated with each population cluster while defining the catchment areas. The modified gravity model has the same mathematical form as the E2SFCA model except that it uses only one catchment area to compute accessibility indices at all locations of population clusters. Such a model can certainly be employed for a small region where all service centres are accessible to all population units. However the modified gravity model cannot be reliably used for large study regions because it unrealistically considers only one service and population catchment area within a study region. In the real world, not all service centres are accessible to all population units [3]. That is why the development of the variable-sized buffer ring method using various FCA models has dominated the accessibility trials [2,3,6,7,8,14]. One of the important consequences to note about the buffer ring method is that the number of service centres associated to each population cluster varies from one cluster to the other. This consequence of the buffer ring method introduces accessibility differences between different population clusters because the spatial accessibility index of a population cluster is computed as the sum of accessibility components due to all service centres associated with the given cluster. If the variation in the number of associated service centres between population clusters is large then the difference in the accessibility outcome between respective clusters will also varied considerably due to the choice bias.
This study proposes a new variant of the FCA computational model based on the NN method of delineating the service and population catchment areas. In the NN method, the delineation of catchment areas are done by associating fixed or variable number of neighbouring service centres to each population cluster, unlike in the buffer ring method where number of service centres associated with population clusters vary from one cluster to the other. Since it uses the same number of nearest neighbours, or the range of variable number of nearest neighbours will be considerably smaller than the BR method, the choice bias in the NN method will be considerably less than the BR method. Therefore the accessibility scores from the NN method is expected to be less than the BR method. The actual comparison of accessibility scores between the two methods is unlikely to produce any sensible outcome because there are an infinite range of values of buffer-sizes and quite a lot of whole numbers of nearest neighbours to be compared. These two methods can be, at best, effectively resolved by assessing theoretical and practical aspects of their methodology. From our perspectives, the NN method is more theoretically sound than the BR method. In the real world, people generally tend to associate with few service centres which are closer to their location rather than unknown number of centres falling within certain travel-time or distance. A person can linguistically describe neighbouring spatial objects such as places “by less than 3000 miles” [22]. However, it is quite impracticable for people to spatially relate to the unknown number of similar places or service centres available within a specified distance, as computed by the buffer ring method. On the other hand, it is very much practicable to spatially relate to few closest service centres available within the vicinity, as computed by the NN method. Therefore, the NN method is practically more realistic in delineating the population catchment areas than the buffer ring method. However, there is one major uncertainty involved in the proposed method. It deals with the ambiguity in the selection of an optimal number of nearest health centres for each population cluster. Nonetheless, even the range of this whole number ambiguity is smaller compared to the buffer ring method where selection range is theoretically defined by an infinite number of real values. For Bhutan, two nearest neighbours were found optimal based on the general availability of only few health centres in each sub-district. Two neighbours are not the absolute number of associations to be used for all countries because the decision to choose any finite number of neighbours depend on the local density of service centres within the study region.
There is no exact solution to all of the uncertainties involved in the computation of spatial accessibility indices. The accommodation of these uncertainties in the spatial accessibility model depends on the nature of the data availability and the method of defining population catchment areas. In the context of Bhutan, the proposed NN-M2SFCA spatial accessibility model was developed to minimize the burden of these uncertainties by using an exponential decay function, where a variable-sized population catchment area of each service centre was defined by assigning the first- and second-nearest health facilities to each population cluster. The absolute accuracy of the accessibility values may not be known because of the unavailability of the perfect accessibility model as the aforementioned uncertainties cannot be completely eliminated through modelling. Nonetheless, these uncertainties would fully or partially cancel out when accessibility values are relatively compared with each other. As long as the spatial accessibility model is consistently defined with same parameters and the same variable catchment areas, then such models can be effectively utilized for assessing the spatio-temporal changes of spatial accessibility to PHC in different regions across the country.
8. Conclusions
This study proposes the NN-M2SFCA computational method for computing indices of spatial accessibility to primary health care services. The proposed computational method uses the M2SFCA model with the distance weighting parameter defined by an exponential distance decay function and the population catchment areas of each health centres defined by associating first- and second-nearest health centres to each population cluster. The salient feature of this method is that it uses a fixed number of health service centres as target facilities for each population cluster in defining the service and population catchment areas, which has not been used in past studies for computing spatial accessibility indices. Furthermore, the proposed method was trialled on a small country, Bhutan, where accessibility values of population clusters, sub-districts, and districts were computed from 2010 to 2013.
This study has also demonstrated that spatial accessibility indices can be used for identifying medically under-served and over-served regions, for measuring the equality of distribution of health resources across the regions and for studying spatial and temporal changes in the distribution of the health resources in the country. The spatial accessibility results of Bhutan for 2013 show that there is a huge disparity in the distribution of the health resources in this country with the best-ranked Lingzhi sub-district of Thimphu district having 35 times better accessibility to health assistants’ services than the lowest-ranked Bara sub-district of Samtse district, and Chang sub-district having 135 times better accessibility to doctor’ services than the Soe sub-district of the Thimphu district. The Gini coefficients of the twenty districts indicates that the Pemagatshel and Zhemgang districts havd the best and worst equality of distribution of doctors’ services, respectively, in 2013.
The proposed NN method may be theoretically sound than the BR method, however, the efficacy of this model cannot be ascertained in this study because of the lack of absolute accessibility scores. It is also unreliable to compare the accessibility outcome between the NN and BR methods, unlike the comparative study done between different FCA models, where parameters remain the same except for the weighting parameter, because the parameters involved in both these methods can be ambiguously defined with a range of values. For instance, the NN method can be defined with a range of nearest neighbours (1, 2, 3, …) whereas the BR method can be defined with a range of radial values of buffer rings (5, 10, 15, 30, 60 min, …). Therefore, it is quite unrealistic to compare between one value of the NN method with another value of the BR method, as such comparative study cannot absolutely ascertain their differences in accessibility outcome. However, there is a scope to conduct a comparative study between these methods by including a number of values for both the methods, which will be pursued in future research. In addition, the Bhutanese health system does not have a systematic approach to conducting spatial planning for distribution of health resources in the country, which has possibly affected the decision-making process, as evidenced from this study where there are huge disparities in the equity of spatial access to primary health care services in the country. The proposed spatial accessibility measurement system can be used to develop a spatial decision support system to facilitate evidence-based spatial planning for equitable distribution of health resources across the country.
Acknowledgments
We would like to acknowledge that the lead author, Sonam Jamtsho, is the recipient of the Australian Government’s Endeavour Postgraduate Award that supports his ongoing PhD study in Geographic Information Science.
Author Contributions
Sonam Jamtsho is the lead author of this paper who has conducted data processing and analysis, and also wrote the draft paper. Both the secondary authors contributed by providing valuable feedbacks and guidance during the process of writing this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- World Health Organization. Declaration of Alma Ata. Available online: http://www.phcris.org.au/guides/about_phc.php (accessed on 11 February 2015).
- Delamater, P.L. Spatial accessibility in sub-optimally configured healthcare systems: A modified two-step floating catchment area (m2sfca) metric. Health Place 2013, 24, 30–43. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Qi, Y. An enhanced two-step floating catchment area (e2sfca) method for measuring spatial accessibility to primary care physician. Health Place 2009, 15, 1100–1107. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Wang, F. Measures of spatial accessibility to health care in a GIS environment: Synthesis and a case study in Chicago region. Environ. Plan. B 2003, 30, 865–884. [Google Scholar] [CrossRef]
- Unal, E.; Chen, S.E.; Waldorf, B.S. Spatial Accessibility of Health Care in Indiana. Available online: http://ageconsearch.umn.edu/bitstream/7329/2/wp070007.pdf (accessed on 10 February 2014).
- Wan, N.; Zou, B.; Sternberg, T. A three-step floating catchment area method for analyzing spatial access to health services. Int. J. Geogr. Inf. Sci. 2012, 26, 1073–1089. [Google Scholar] [CrossRef]
- Yang, D.H.; Goerge, R.; Mullner, R. Comparing GIS-based methods of measuring spatial accessibility to health services. J. Med. Syst. 2006, 30, 23–32. [Google Scholar] [CrossRef] [PubMed]
- McGrail, M.R.; Humphreys, J.S. Measuring spatial accessibility to primary health care services: Utilising dynamic catchment sizes. Appl. Geogr. 2014, 54, 182–188. [Google Scholar] [CrossRef]
- Dai, D.; Wang, F. Geographic disparities in accessibility to food stores in southwest Mississippi. Environ. Plan. B: Plan. Des. 2011, 38, 659–677. [Google Scholar] [CrossRef]
- Langford, M.; Fry, R.; Higgs, G. Measuring transit system accessibility using a modified two-step floating catchment technique. Int. J. Geogr. Inf. Sci. 2012, 26, 193–214. [Google Scholar] [CrossRef]
- Jamtsho, S.; Corner, R.J. Evaluation of spatial accessibility to primary healthcare using GIS. In ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Proceedings of the 2014 ISPRS Technical Commission II Symposium, Toronto, ON, Canada, 6–8 October 2014; pp. 79–86.
- Wang, F. Measurement, optimization, and impact of health care accessibility: A methodological review. Ann. Assoc. Am. Geogr. 2012, 102, 1104–1112. [Google Scholar] [CrossRef] [PubMed]
- Tobler, W. Smooth pycnophylactic interpolation for geographical regions. J. Am. Stat. Assoc. 1979, 74, 519–530. [Google Scholar] [CrossRef] [PubMed]
- McGrail, M.R.; Humphreys, J.S. The index of rural access: An innovative integrated approach for measuring primary care access. BMC Health Serv. Res. 2009, 9, 533–541. [Google Scholar] [CrossRef] [PubMed]
- McGrail, M.R. Spatial accessibility of primary health care utilising the two step floating catchment area method: An assessment of recent improvements. Int. J. Health Geogr. 2012, 25, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Openshaw, S. Ecological fallacies and the analysis of areal census data. Environ. Plan. A 1984, 16, 17–31. [Google Scholar] [CrossRef] [PubMed]
- Eicher, C.L.; Brewer, C.A. Dasymetric mapping and areal interpolation: Implementation and evaluation. Cartogr. Geogr. Inf. Sci. 2001, 28, 125–138. [Google Scholar] [CrossRef]
- Mennis, J. Generating surface models of population using dasymetric mapping. Prof. Geogr. 2003, 55, 31–42. [Google Scholar]
- Wright, J.K. A method of mapping densities of population with Cape Cod as an example. Geogr. Rev. 1936, 26, 103–110. [Google Scholar] [CrossRef]
- Yitzhaki, S. More than a dozen alternative ways of spelling Gini. Res. Econ. Inequal. 1998, 8, 13–30. [Google Scholar]
- Ord, J.K.; Getis, A. Local spatial autocorrelation statistics: Distributional issues and an application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Landau, B.; Jackendoff, R. “What” and “where” in spatial language and spatial cognition. Behav. Brain Sci. 1993, 16, 217–265. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).