Abstract
Increased affordability and deployment of advanced tracking technologies have led researchers from various domains to analyze the resulting spatio-temporal movement data sets for the purpose of knowledge discovery. Two different approaches can be considered in the analysis of moving objects: quantitative analysis and qualitative analysis. This research focuses on the latter and uses the qualitative trajectory calculus (QTC), a type of calculus that represents qualitative data on moving point objects (MPOs), and establishes a framework to analyze the relative movement of multiple MPOs. A visualization technique called sequence signature (SESI) is used, which enables to map QTC patterns in a 2D indexed rasterized space in order to evaluate the similarity of relative movement patterns of multiple MPOs. The applicability of the proposed methodology is illustrated by means of two practical examples of interacting MPOs: cars on a highway and body parts of a samba dancer. The results show that the proposed method can be effectively used to analyze interactions of multiple MPOs in different domains.
1. Introduction
The increasing deployment of location-aware devices has given rise to an unprecedented wealth of trajectory information, documenting the movements of various types of moving objects, including vehicles [1], animals [2], bank notes [3], sportspersons [4], visitors at mass events [5], and tourists [6]. During the past two decades, the increasing availability and affordability of these data sets have aroused a burgeoning interest among (geographical) information scientists, who have steadily begun to develop and implement tools to discover, aggregate and cluster meaningful patterns of individual or group behavior in space-time (e.g., [7,8,9,10,11,12,13]). One specific area of interest concerns the line of inquiry that has developed qualitative formalisms to reason about moving objects. Adopting a qualitative approach implies that continuous information is being discretized by landmarks that classify neighboring open intervals into discrete quantity spaces [14]. Key to this approach is that a distinction is introduced only if it is relevant to the research context at hand [15,16]. The impetus for developing qualitative formalisms is that qualitative information aligns better with human intuition, communication and decision making than quantitative information [17,18]. Much of the work in the area of qualitative reasoning concentrates on either the spatial or the temporal dimension of objects or phenomena and only a few studies, however, have systematically examined the qualitative properties of spatio-temporal information (e.g., [19,20]). One of these studies includes Qualitative Trajectory Calculus (QTC) proposed by Van de Weghe (2004) [21]. QTC is a powerful formalism for representing and reasoning about interactions between two moving point objects (MPOs). In QTC, the interactions are considered to be the changes in the Euclidean distance between two MPOs. While insightful QTC has, until recently, remained largely conceptual, and new methods for inferring meaningful knowledge from qualitative spatio-temporal information remain sorely needed [22,23].
Hence, this study seeks to extend previous accomplishments in this area by developing a novel methodology to compare relative movements of MPOs based on corresponding (repetitive) sequences of qualitative relationships between MPOs. Our focus is on the clustering of trajectory pairs. Trajectories define the movement of moving objects, and consequently, the clustering of trajectory pairs contributes to detecting groups of pairs of MPOs with similar relative movement behavior.
Trajectory clustering is primarily application dependent. Until now, many attempts have been conducted in the field of trajectory clustering. Kisilevich et al. (2010) have categorized trajectory clustering approaches into one of the following groups [24]: descriptive and generative model-based clustering (e.g., [25,26], distance-based clustering (e.g., [27]), density-based clustering (e.g., [27]), visual-aided clustering (e.g., [28]), micro clustering (e.g., [29]), flocks and convoy (e.g., [30]), important places to users such as workplace (e.g., [31]), and pattern-based clustering (e.g., [32]). The approach presented here could be classified into pattern-based clustering. Patterns that are extracted from trajectories are referred to as trajectory patterns and express interesting behaviors of individual or multiple moving objects [33]. Different approaches exist in the mining of trajectory patterns (e.g., [32,34,35]). We use QTC to extract relative movement patterns of pairs of MPOs for clustering purposes. Additionally, a visual approach is applied to recognize the extracted patterns and to facilitate the understanding of the nature of the relative movement patterns that occur.
The main contributions of this study are threefold. First, we examine the role of qualitative data in spatio-temporal data mining and knowledge discovery from movement data. Second, we propose a distance measure for clustering trajectory pairs of MPOs. Although this is an important spatio-temporal data mining problem with broad applications, only limited attention has been paid to it. Most of the previously developed trajectory data mining techniques with clustering aims do not consider relative movements of MPOs. Third, we develop a technique to visualize, index and compare relative movement patterns that result from interactions between MPOs.
The remainder of this study is organized as follows. In the next section, we briefly discuss related work, while in Section 3, we introduce the proposed methodology. This section is subdivided into three subsections, which correspond to the three major steps of the method: (i) description of relative movement patterns using QTC (Section 3.1), (ii) representation of relative movement patterns in a SESI (Section 3.2), and (iii) clustering trajectory pairs based on their relative movement patterns (Section 3.3). Section 4 then demonstrates the usefulness of our methodology in identifying and clustering the relative movement patterns of cars and body parts of a samba dancer. Section 5 presents a detailed discussion. Finally, Section 6 summarizes and reflects on the major findings and outlines avenues for future research.
2. Related Works
The focus of this paper is on the development of a method to support our understanding of relative movement patterns of MPOs; hence, three main issues are covered in this section: (i) relationships among MPOs (ii) visualization of MPOs, and (iii) clustering movements.
2.1. Relationships among MPOs
Movement patterns can be derived either from the movement of an individual object over time or from the interaction between two or more moving objects during a time interval of movement. A comprehensive classification of patterns in movement data, which is applicable for all common types of moving objects has been presented by Dodge [10]. It is obvious that movement patterns of an isolated individual can differ from movement patterns of an individual who is part of a group. These differences between individual and group movement behavior have been discussed extensively [36].
Our research seeks to contribute to the exploration of interactions of multiple MPOs. The key idea is to examine relative movement patterns of multiple objects over space and time. We are investigating the interaction between pairs of MPOs instead of looking at the movement of individuals over time, and then, we infer the collective behavior of multiple objects. Furthermore, this paper does not investigate the changes in the motion attributes of MPOs (i.e., the change in the speed or motion azimuth over space and time). Instead, we examine how the relative changes in the Euclidean distance between MPOs can reveal relative movement patterns.
2.2. Visualization of MPOs
Visual representation is used as an effective technique to represent and support the analysis of movement patterns of objects. A large body of research has been conducted to express the significance of visualization in understanding movements in different domains (e.g., [36,37,38,39,40,41]). Detecting, understanding, and visualizing movement patterns are not limited to certain applications. For example, in a prior study [42], a technique for identifying, visualizing and interpreting repetitive movement patterns within groups of moving point objects based on QTC information has been studied.
2.3. Clustering of Movements
Over the past decade, many studies have addressed knowledge discovery and data mining issues that are related to moving object data. Among them, some contributed to the clustering of moving objects (e.g., [27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]), the mining of movement patterns (e.g., [34,38,43,44,45]) and the exploration of similarity of moving objects (e.g., [41,46,47,48,49]). The idea behind the approach proposed in this paper is to contribute to all three classes of knowledge discovery, i.e., mining patterns, similarity assessment, and clustering. In addition to detecting and visualizing relative movement patterns, we measure the similarity in the relative movement behavior of moving objects. Our work intends to explore similarities of relative movement patterns using a visualization technique called SESI. From multiple SESIs, in addition to obtaining a visual synopsis of the relative movement patterns of MPOs, we can measure the distance between the relative movement patterns. The measurement leads toward a clustering of trajectory pairs, being the identification of groups of similar trajectory pairs.
3. Methodology
Based on concepts from geographic knowledge discovery (GKD) [50] for extracting meaningful information, discovering interesting patterns, and interpreting them in a plausible way, we propose a technique for analyzing the relative movements of multiple disjoint MPOs using QTC. Up to now, a number of qualitative calculi have been developed to reason about moving objects (e.g., [51]). In this paper, we focus on the usefulness of QTC in identifying relative movement patterns of pairs of MPOs. An innovative visualization technique called sequence signature (SESI) is used to transform the QTC movement patterns of MPOs (i.e., relative movement patterns formed based on QTC) into a structure that is suitable for being analyzed through traditional data mining techniques such as clustering algorithms. Using a distance measure between two SESIs, we can quantify the similarity of the movements of the MPOs.
The methodology comprises three major steps. First, raw trajectory data that stems from location-aware technologies is converted into qualitative relationships based on the Euclidean distance between two interacting MPOs. Second, drawing on the concept of an iterated function system, sequences of these qualitative relationships (i.e., relative movement patterns) are visually summarized in a sequence signature (SESI). Finally, multiple SESIs are compared using a distance measure, which in turn is used to identify hierarchical clusters of qualitatively distinct pairs of trajectories. Each of these steps is discussed in depth below.
3.1. Step 1: Converting Raw Trajectory Data into Qualitative Relationships
To summarize raw trajectory data in terms of qualitative relationships, we use the Qualitative Trajectory Calculus (QTC) [21]. In recent years, three types of QTC have been developed: QTC-Basic (QTCB) [52], QTC-Double Cross (QTCC) [53], and QTC for networks (QTCN) [54]. The first two types address MPOs in a two-dimensional Euclidean space, whereas the latter is employed to describe network-constrained phenomena. In this study, we focus on QTCB because it is the simplest type from which all of the other types are derived. QTCB provides a qualitative representation of the two-dimensional movement of a pair of MPOs. Binary relations between two MPOs are evaluated based on the Euclidean distance [21]. In QTCB, a qualitative relationship between a first object k and a second object l at a time stamp t is defined by a label that is composed of two characters. This label represents the following two relationships [21,55]:
| Assume: MPOs k and l, and time stamp t |
| k | t denotes the position of k at t |
| l | t denotes the position of l at t |
| d(u,v) denotes the Euclidean distance between two positions u and v |
| t1 < t2 denotes that t1 is temporally before t2 |
- A.
- Movement of k with respect to l at t (distance constraint):
- − : k is moving toward l:
- +: k is moving away from l:
- 0: k is stable with respect to l (all other cases)
- B.
- Movement of l with respect to k at t (distance constraint) can be described as in A with k and l interchanged, and hence:−: l is moving toward k+: l is moving away from k
- 0: l is stable with respect to k (all other cases)
The resulting syntax for QTCB is thus the tuple (A B) that considers the distance constraints described above (relationships A and B). In total, this approach yields 9 (32) base relations, which are represented in Figure 1. In each of the nine cases that are depicted in this figure, k is represented on the left side, and l is represented on the right. The dashed line segments and crescents delineate potential motion areas. The dots can be stationary only if a dot is filled. The nine represented relationships form a set of jointly exhaustive and pairwise disjoint base relations; meaning that any two intervals stand to each other in exactly one of these relations [56]. Consequently, at each time instant, there is one and only one QTBB relation for each pair of MPOs.
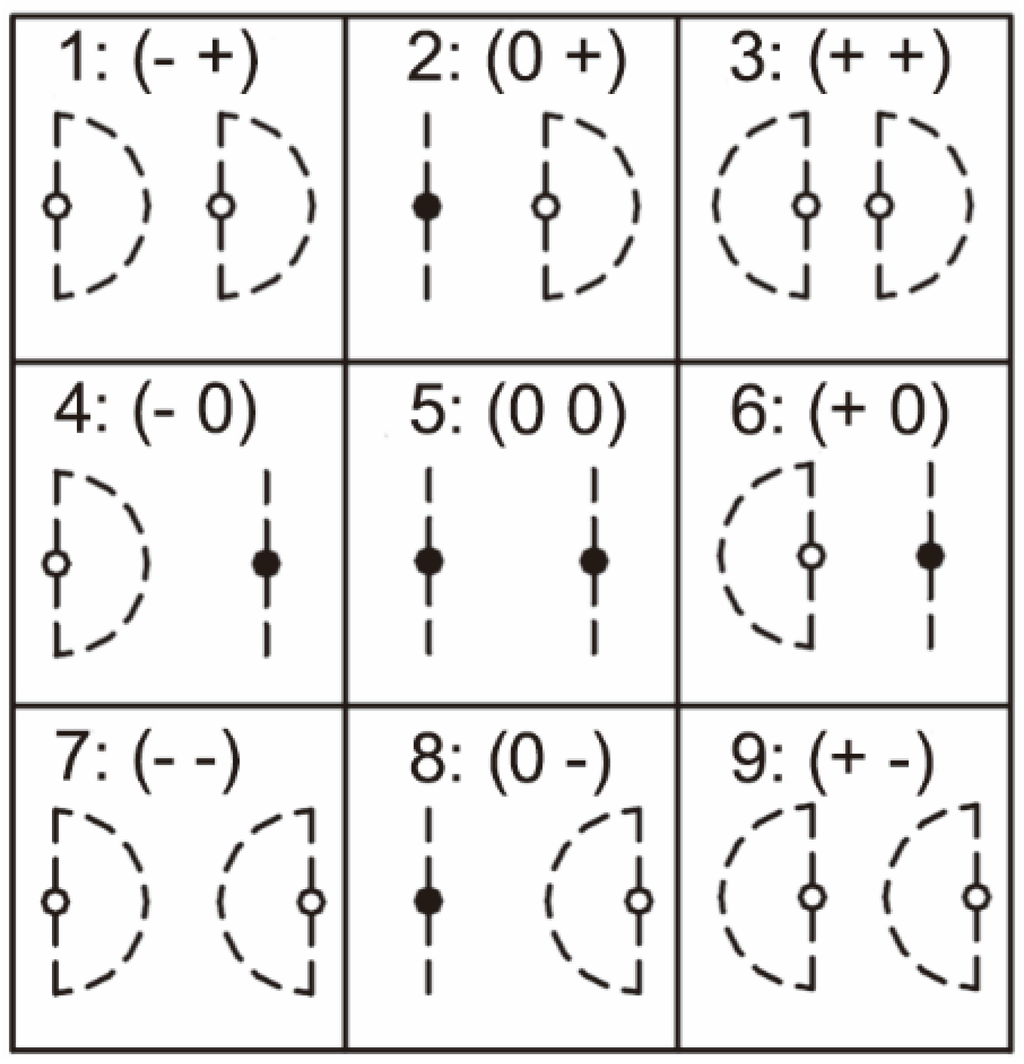
Figure 1.
Icons for QTCB in 2D [21].
To make this strategy clear, for example, QTCB relations , and are explained as follows.
- : k is stable with respect to l, and l is moving away from k
- : k is stable with respect to l, and l is moving toward k
- : k is moving away from l, and l is stable with respect to k
- : k is moving toward l, and l is stable with respect to k
A prototypical example of interaction between moving objects is the overtake event (see also [53]). Consider the interactions between two vehicles k and l during a time interval. The movements of these vehicles can be expressed by a conceptual animation, in other words, a chronological sequence of continuous transitions between the QTCB relations. Suppose that car k is going to overtake car l. This interaction can be expressed in terms of the QTCB relationships as follows. The video of the overtake event is available as supplementary information.
- State 1.
- car k and car l are both driving in the same traffic lane, and k is driving behind l:
- State 2.
- car k is heading out to the second lane:
- State 3.
- car k is driving in the second lane and is driving behind l, which is driving in the first lane: (see Figure 2).
- State 4.
- car k is driving in the second lane and is driving in front of car l, which is driving in the first lane:
- State 5.
- car k is heading back to the first lane:
- State 6.
- car k and car l are both driving in the first lane, and l is driving behind k:
It is noted that, following Galton’s theory of dominance (2001) [57] and Forbus' equality change law (1984) [58], a direct change from – to + and vice versa is impossible, because such a change must pass the qualitative value 0. This landmark value 0 needs to hold only for an instant. Therefore, there must be another relationship between State 3 and 4, namely (see also [59]). Lastly, the above overtake event is represented by the following movement pattern:
We use our earlier implementation prototype called QTCAnalyzt [23] to identify the QTCB movement patterns of MPOs. The next subsection presents a method to transform these patterns into a fractal-based representation.
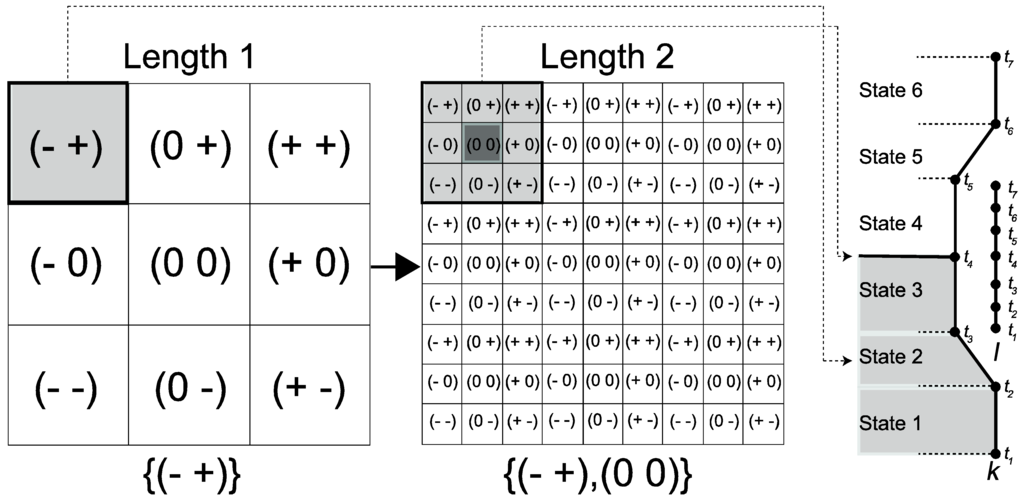
Figure 2.
SESIs of lengths 1 and 2.
3.2. Step 2: Summarizing QTCB Movement Patterns in a Sequence Signature
A sequence signature (SESI) is a fractal way of mapping patterns of the interactions between two MPOs in an indexed raster space. It is based on an iterated function system, as discussed in detail in Barnsley (1988) [59]. In a SESI, each sequence of n consecutive qualitative relationships is represented by a cell of length n (i.e., the number of subsequent QTCB relationships that constitute a movement pattern). Thus, a SESI of length 1 represents movement patterns that are composed of one QTCB relation, while, for example, a SESI of length 5 represents movement patterns that are composed of five consecutive QTCB relations. The resolution of these cells depends on the length of that SESI.
Figure 2 shows SESIs of lengths 1 and 2. The SESI of length 1 shows the nine base QTCB relationships. For higher lengths, each cell is further subdivided into nine cells, allowing each cell in a SESI of length n to correspond with a unique sequence of n qualitative QTCB relationships. In this way, each sequence of QTCB relationships has a specific location in the SESI. For example, the highlighted cells in the SESIs of lengths 1 and 2 in Figure 2 represent the movement patterns and of the above described overtake, respectively. In QTCB, a SESI of length n contains 9n cells.
However, not all sequences of QTCB relationships are possible or significant. First, based on the laws of continuity (see Section 3.1), we can exclude chronologically impossible combinations of QTCB relationships in SESIs of length 2 or more. Figure 3a demonstrates SESIs of length 2 after imposing the continuity constraint.
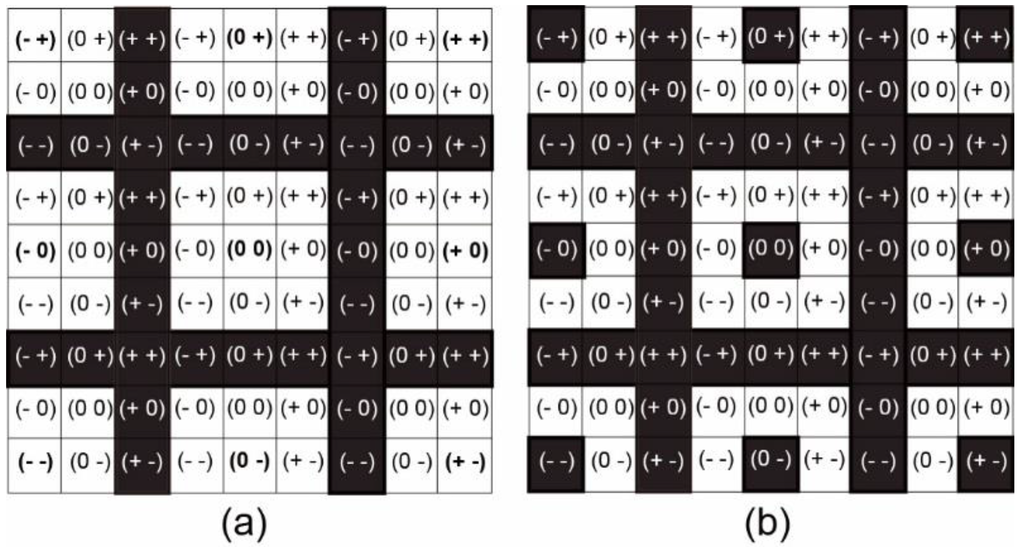
Figure 3.
(a) Continuity and (b) event-based constraints imposed on a SESI of length 2.
The black cells indicate discontinuous (and thus impossible) sequences of qualitative relationships between two MPOs. For example, it is not possible to have a direct transition from to relationships , and . Second, because we are typically interested in the changes in the relative motion between the MPOs over time (i.e., events), some sequences of qualitative relationships are not significant. This arrangement is the case when a QTCB relationship is invariant over time. For example, a transition from into itself is not very meaningful from a qualitative perspective. Figure 3b shows the result of imposing both of the above restrictions on a SESI of length two. For illustrative purposes, we also provide the representations of SESIs of lengths 1 to 3 in Figure 4a along with the SESI representation of the overtake event given in Equation (5) (Figure 4b). The fractal approach outlined above offers an insightful way to address repetitive movement patterns of any length.
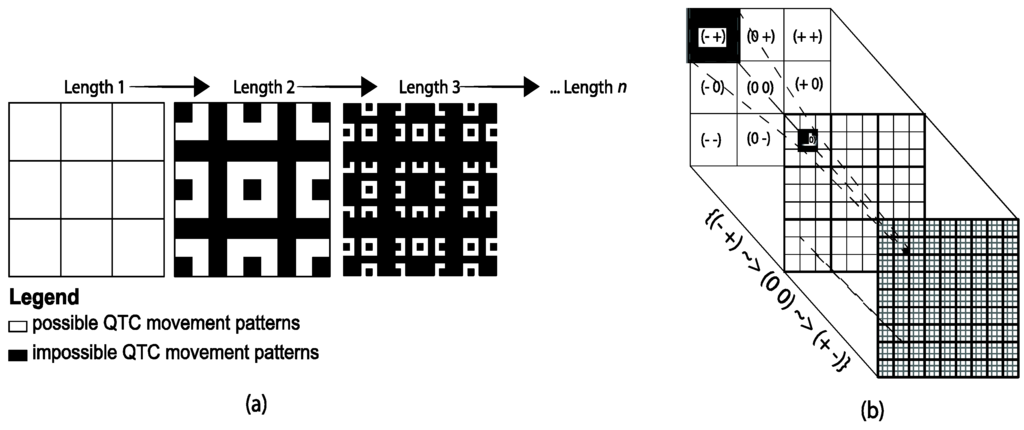
Figure 4.
(a) SESIs of lengths 1 to 3 and (b) the overtake event mapped on a SESI of length 3.
3.3. Step 3: Clustering Trajectory Pairs Based on Their Relative Movement Patterns.
In order to cluster pairs of trajectories of MPOs based on their relative movements, we need a function to express to what extent two SESIs are different. To that end, most clustering techniques use a distance measure [60]. Here, we used a distance measure taking into account the structure of the SESIs. More specifically, the distance between two SESIs S1 and S2 of length n is defined as:
where
denote the normalized frequencies S1,ij and S2,ij of the mapped QTCB movement patterns in the ijth cell of S1 and S2, respectively; denotes the number of impossible or insignificant cells in a SESI of length n; and Uij denotes the value of the highest frequency of the ijth cell among all of the SESIs on which the distance measure is applied.
Normalization is used to scale heterogeneous frequencies of QTCB movement patterns, to make it possible to compare them. As a result, the normalized frequency of each cell of a SESI is confined to the interval [0, 1]. To calculate the distance between two SESIs, we start from the top left cells in both SESIs to subtract their normalized frequencies from each other. The distance measure in Equation (6) runs over all of the cells in the SESIs. The denominator in Equation (6) represents the number of feasible sequences of QTC relationships in that SESI. By definition, infeasible sequences are assigned a frequency of 0. For example, there are 529 impossible cells in a SESI of length 3. The distance function in Equation (6) ranges from 0 to 1, where 0 indicates that the SESIs are identical and 1 indicates that there is no correspondence at all between the SESIs. In fact, dn is an indicator expressing to what extent QTC movement patterns of a pair of MPOs (with length n) are different from the QTCB movement patterns of another pair. As an illustration, Figure 5 depicts two arbitrary trajectory pairs of two objects during two different time intervals. The SESIs of length 3 for both trajectory pairs are shown in Figure 6. The black cells indicate impossible cells, whereas the green cells display the frequency of the movement patterns. In this simple example, the frequency of occurrence of a movement pattern is either 0 or 1. The distance between these two SESIs can be calculated based on Equation (6):
The low distance value indicates that the interaction patterns between the two MPOs are, according to QTCB, qualitatively similar across both time intervals.
In the case of multiple pairs of trajectories, we can apply a hierarchical clustering algorithm on the basis of the distance between every two SESIs, to identify pairs of trajectories that have similar interaction patterns.
The idea behind hierarchical clustering is to build a binary tree of the data that successively merges similar groups of objects. This binary tree provides a visualization of a useful summary of the data. In this study, we use an agglomerative hierarchical clustering method, which yields a dendrogram that represents a nested grouping of objects (in casu, trajectory pairs). The horizontal axis in the dendrogram represents the clustered objects, while the vertical axis shows the distance between clusters. We use average-linkage to compute distances between the new cluster and each of the old clusters (see for more explanation of average-linkage in clustering [61]). The distance between two clusters is computed as the average distance between objects from the first cluster and objects from the second cluster. We will illustrate the three major steps outlined above in the next section.
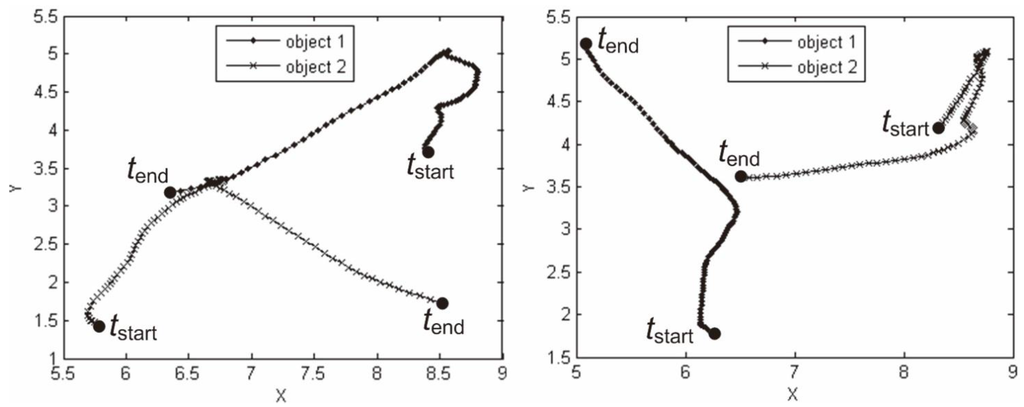
Figure 5.
Two trajectory pairs during two different time intervals.

Figure 6.
Movement patterns and SESIs for the trajectory pairs shown in Figure 5.
4. Illustration
In this section, we will apply our methodology in two examples: a simple overtake event and samba dance.
4.1. Example 1: Overtake Event on a Highway
Figure 7 illustrates five different traffic situations with two cars (k and l), where each situation lasts 7 s (time steps of 1 s). The first three situations are simple overtake events. Table 1 shows the QTCB movement patterns for all five trajectory pairs. Following our methodology, we must first transform the pairs of trajectories into sequences of qualitative relationships. These sequences are depicted in Table 1. We next convert the sequences into SESIs of lengths 2 and 3 (Figure 8). We then measure the distance between all of the pairs of SESIs of a specific length. These distance measurements are then placed in a (symmetric) distance matrix for each SESI length (Figure 9). We lastly group the trajectory pairs using a hierarchical clustering method (Figure 9). As presented in Table 1, the movement patterns of the first three situations (1, 2, and 3) are similar to each other, and the movement patterns of the last two situations (4 and 5) are the same. In fact, the distance matrix shows that the first three trajectory pairs are identical in terms of qualitative relationships (see Table 1).
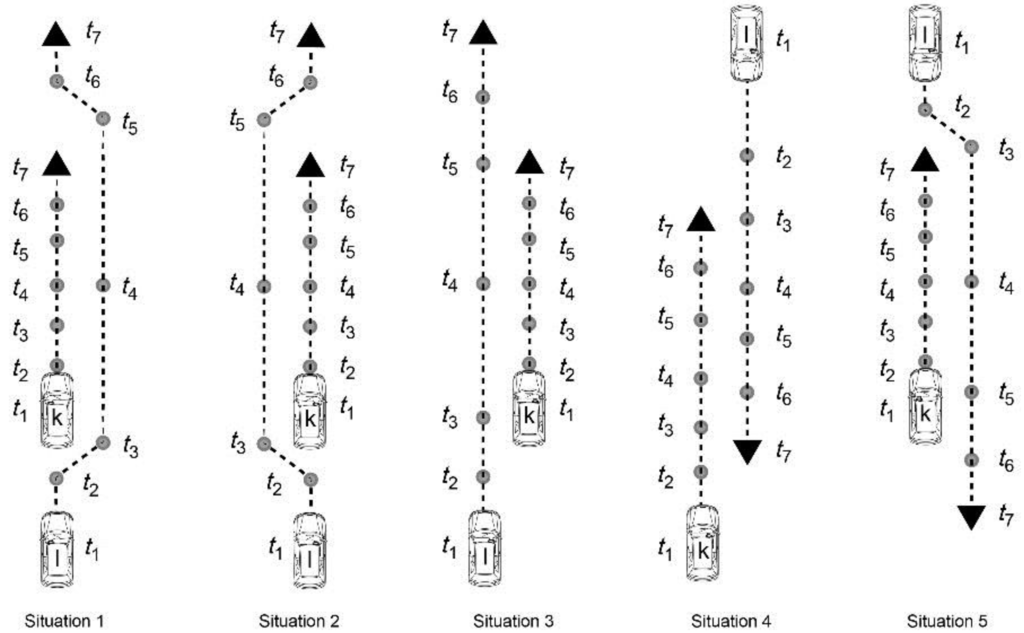
Figure 7.
Five traffic situations.

Figure 8.
SESIs of lengths 2 and 3 for all of the situations.
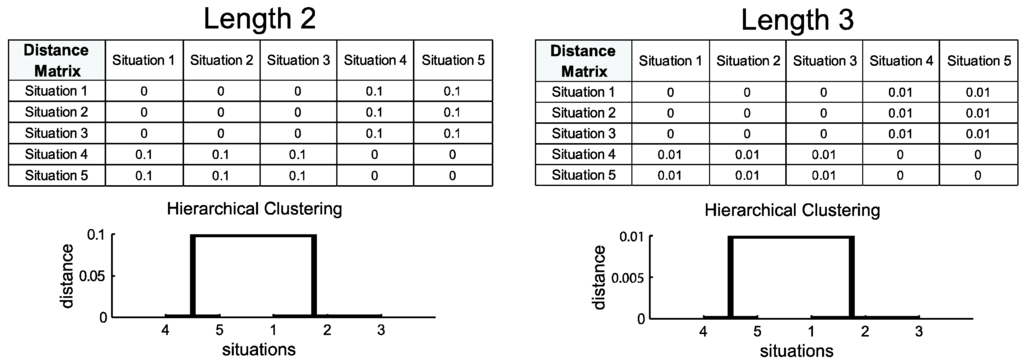
Figure 9.
Distance matrices and hierarchical clustering of five traffic situations (five trajectory pairs) for SESIs of lengths 2 and 3 based on the distance function in Equation (6).

Table 1.
QTC Movement patterns of the above five trajectory pairs between two cars, k and l.
| Situation 1 | Situation 2 | Situation 3 | Situation 4 | Situation 5 |
|---|---|---|---|---|
| { (+ -) ==> (00)} | { (+ -) ==> (00)} | { (+ -) ==> (00)} | { (- -) ==> (00)} | { (- -) ==> (00)} |
| {(0 0) ==> (- +)} | {(0 0) ==> (- +)} | {(0 0) ==> (- +)} | { (0 0) ==> (+ +)} | { (0 0) ==> (+ +)} |
| {(+ -) ==> (0 0) ==> (- +)} | {(+ -) ==> (0 0) ==> (- +)} | {(+ -) ==> (0 0) ==> (- +)} | {(- -) ==> (0 0) ==> (+ +)} | {(- -) ==> (0 0) ==> (+ +)} |
The trajectory pairs with similar QTCB movement patterns are then placed in the same clusters. Thus, trajectory pairs 1, 2 and 3 are taken together in the same cluster, while trajectory pairs 4 and 5 are grouped into another cluster. Here, cluster analysis allows a comparison of the movements of MPOs based on the QTCB movement patterns extracted from the trajectory pairs. The distance value at each branching in the dendrogram represents the average distance between the SESIs in the branches. Figure 9 represents only the hierarchical clustering of SESIs of lengths 2 and 3, respectively. The reason is that the maximum length of the considered sequences equals 3 in all of the situations presented in Table 1.
4.2. Example 2: Samba Dance
The interaction among MPOs could be much more complex in reality. In this subsection, we will specifically examine the movement of multiple MPOs. We use a data set of movements of a samba dancer during four different time intervals, each lasting 0.8 s. The time intervals have been deliberately considered short to be able to easily recognize the similarity between trajectories of movements. The movements of four parts of the body of the dancer, including the right finger (the right hand), the left finger (the left hand), the right toe (the right foot), and the left toe (the left foot), are captured at each time stamp of the movement with a temporal granularity of 0.04 s (Figure 10). The main reason for considering only four body parts to investigate the dance movement is their higher number of interactions compared to other parts of the body of the dancer.
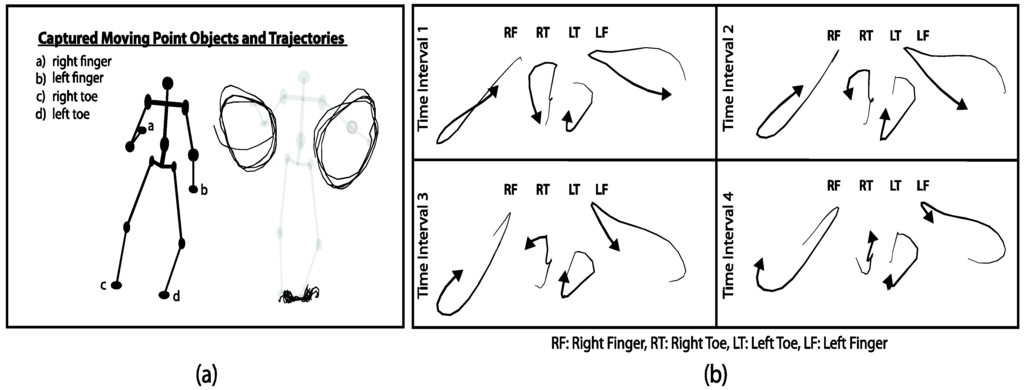
Figure 10.
(a) An abstracted movement of a samba dancer based on four parts of the body (right finger, left finger, right toe, and left toe), and (b) top view of movements of the samba dancer during four different time intervals, each lasting 0.8 s.
The positional information has been captured by an infrared motion capture system that yields the position of the markers attached to the body in three-dimensional space (Figure 10b). The data have been normalized with respect to one reference point and the orientation of the dancer’s body (that point is defined as the centroid of the body, called the root).
As each SESI represents the interaction between two MPOs, the interaction of multiple MPOs can be visualized simultaneously on a newly formed SESI called hyper-SESI, which is tessellated into all sub-SESIs. Based on the successive QTCB relations of all possible pairs of MPOs during each time interval, we create hyper-SESIs for four equal time intervals based on the frequency of the QTCB movement patterns (Figure 11). To enhance the visibility of the transformed QTCB movement patterns, impossible and insignificant QTCB movement patterns are not represented.
Due to the fact that in this subsection only the movement of four parts of the body of a dancer has been studied, there are six possible pairs of interactions. The pairs of movement interactions between different body parts are shown in terms of hyper-SESIs for each time interval of movement in Figure 11. In each hyper-SESI, the leftmost cell expresses the interaction between the right finger and right toe of the dancer, and the lowest cell represents the interaction, or in fact QTCB movement pattern, between the left toe and left finger. Note that only the upper parts of the main diagonal of the hyper-SESIs must be considered because the interactions of the moving parts are symmetrical. We attempt to discover whether there is a degree of closeness/similarity between the QTCB movement patterns of different pairs of body parts during different time intervals of movement. Based on the context of the movement data, we can interpret the hyper-SESIs. For example, we know that samba dance is a rhythmical dance that has regularity in the movements. The regularities in the movements can be distinguished on the hyper-SESIs’ cells. In Figure 11, the upper left cell of the hyper-SESIs shows the interactions between the right finger and right toe at four different time intervals. One can observe that there are more repetitive QTCB movement patterns during the time interval 4 because more frequent patterns are visualized on its hyper-SESI. This means that periodicity or frequency of patterns can be different in time in such fast rhythmical dance.
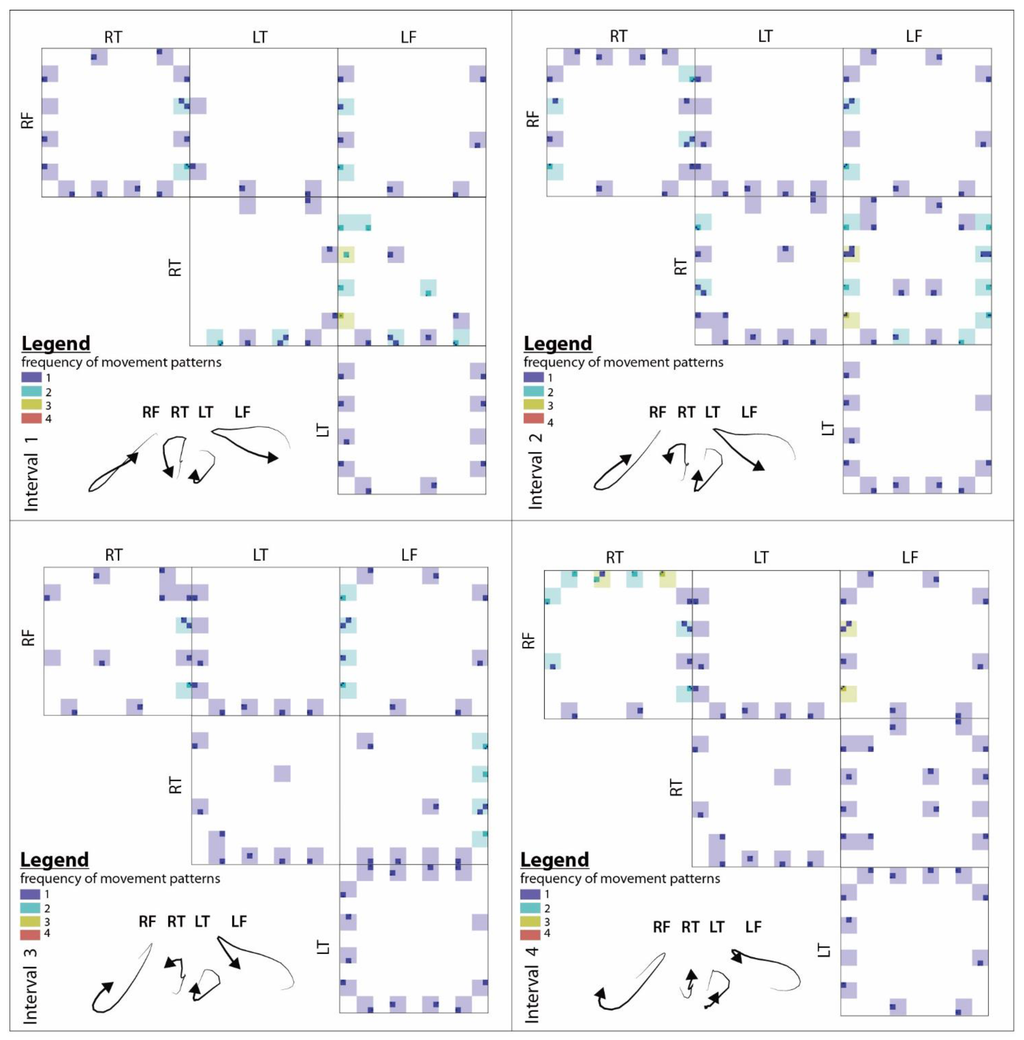
Figure 11.
Hyper-SESIs of four equal time intervals of movements based on the frequency of QTCB movement patterns.
From the perspective of visual assessment, many differences are found when we look more closely at the hyper-SESIs. For example, the SESIs of right toe-left toe at the first time interval of movement are slightly different from the SESIs at other time intervals. QTCB movement patterns and of length two and and of length three are observed in the first time interval of movement but not in the other intervals. It makes more sense when we expect certain patterns with a specific frequency. For example, in our case study, a dance tutor can ask the dance amateur to perform some movements. The requested movement patterns should be observed in the corresponding SESIs unless the dance amateur has failed to perform successfully.
In addition to frequency, each cell in a SESI may store other properties such as duration of QTCB movement patterns (Figure 12). Unlike the frequency, the duration of the QTCB movement patterns are different, and some of the QTCB movement patterns have lasted longer while others are shorter. As mentioned earlier, the temporal granularity of capturing dance movement is 0.04 s. For the sake of simplicity, we assume every 0.04 s to be a single time unit. For example, the pattern lasting 10 time units is equivalent to.
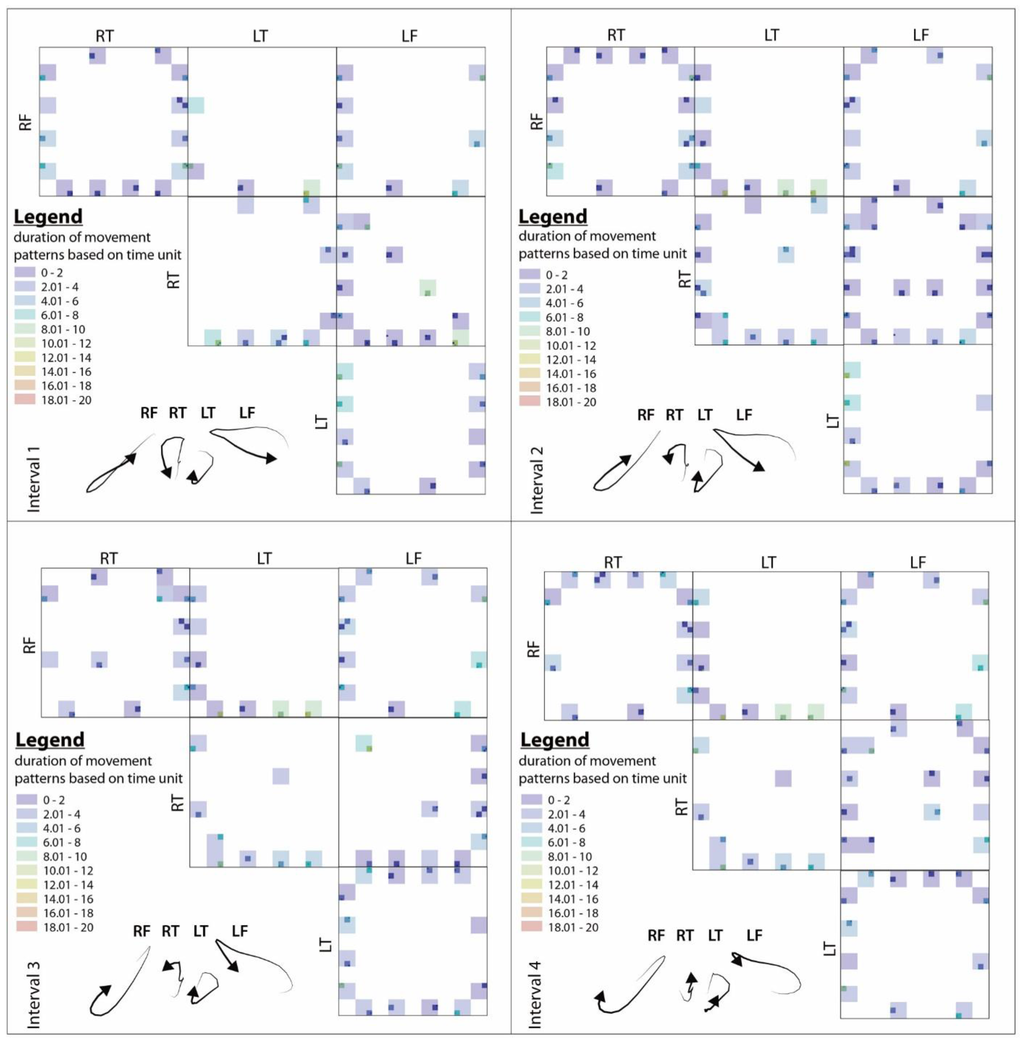
Figure 12.
Hyper-SESIs of four equal time intervals of movements based on the duration of QTCB movement patterns.
In addition to a visual judgment of SESIs or hyper-SESIs, the quality of the dance performances can be measured. One might compare the performances of a dancer (taken as a benchmark) and those of other dancers. For this purpose, we measure the distance between corresponding hyper-SESIs. In fact, we can investigate not only the movements of each individual pair, such as the left finger-right finger at different time intervals of movement, but also the overall distance of whole body part interactions. To calculate the overall distance between two hyper-SESIs, an average distance is taken into account. This approach means that an average is taken of all of the distance measures that were obtained from the comparison of all of the SESIs (i.e., right finger-right toe, right finger-left toe, right finger-left finger, right toe-left toe, right toe-left finger, and left toe-left finger) at each time interval of movement. The results are shown in Figure 13, where the overall performance of the samba dancer at time interval 1 is more similar to that at time interval 3 considering the frequency values (Figure 13a), while the results of comparing duration-based SESIs (Figure 13b) confirms the higher similarity between time intervals 3 and 4.
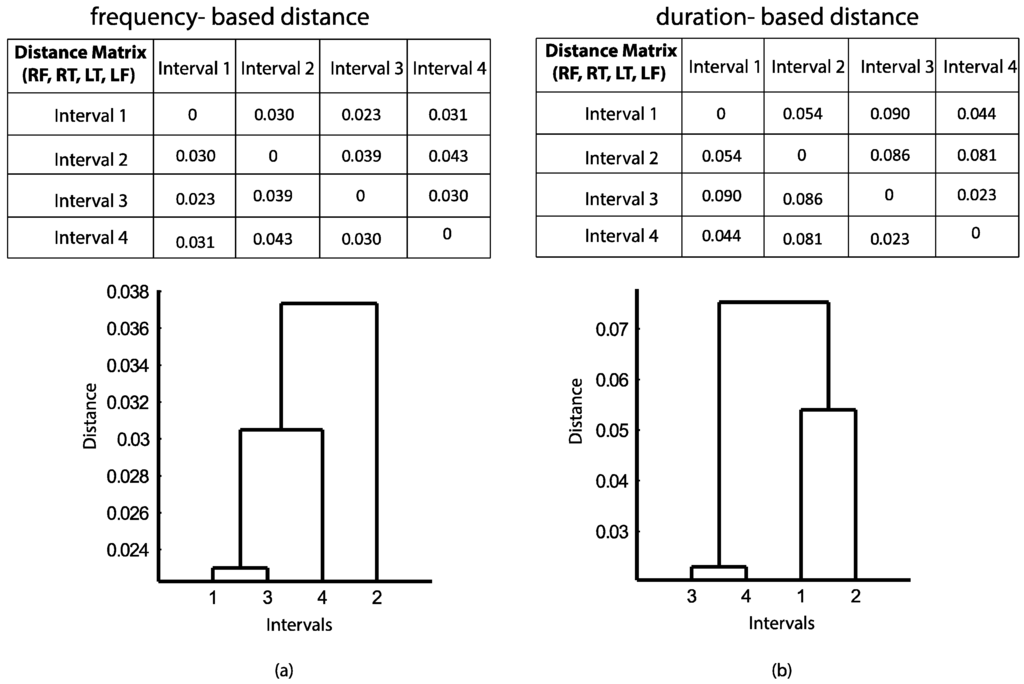
Figure 13.
Distance between hyper-SESIs at four time intervals of movement both for (a) frequency and (b) duration alongside the dendrograms that represent the agglomerative hierarchical clustering of pairs of trajectories.
5. Discussion
In this study, we contributed to the exploration of relative movement patterns of a pair of MPOs (e.g., two cars) or multiple MPOs (e.g., body parts of dancers). First, we contributed of how we could involve qualitative data in the procedure of knowledge discovery from movement data. In this regard, we made extensive use of QTC which has been studied to formulate interrelations between moving objects. We employed the concept of this calculus to show its usefulness, applicability, and power in reasoning about the movement of objects. We described relative movement patterns in terms of sequences of QTC relations. Second, we proposed a distance measure for clustering movement patterns. For this purpose, we defined a spatio-temporal data structure, i.e., sequence signature (SESI), to index sequences of QTC relationships. In addition to indexing movement patterns, SESIs provided us a context to visually analyze movement patterns that result from interactions between MPOs.
The scattering of QTCB movement patterns that have occurred is visible in SESIs. The availability of fine-grained movement data at small temporal sampling intervals increases the difficulty of detecting QTCB movement patterns in SESIs. That is, SESIs are used as a visual-aided approach to perceive the dispersion of QTCB movement patterns. However, we see the SESI mathematically as a rectangular array of numbers, symbols, or expressions, which are arranged in rows and columns. The individual items in this matrix are referred to as its elements or entries (e.g., the frequency of QTCB movement patterns). From a computational perspective, the longer the length of a SESI is, the more time is needed to compute the distance between two SESIs. In short, it is possible to calculate distances for any length of SESI, but visually detecting long-movement patterns in SESIs will become challenging.
The movement data used in our approach should be pre-processed and free of any shifting errors. Unlike many other similarity measures such as the edit distance, shifting greatly influences the QTC patterns, and, consequently, the SESIs and the values of the distance measure. Incomplete knowledge can be handled with QTC. Such incomplete knowledge in terms of QTC relations can then be transferred to the SESI representations and consequently be used to reason about interactions among MPOs. Obviously, in these situations, the available information could be insufficient to provide complete answers to queries. However, “a partial answer may be better than no answer at all.” as Freksa [62] argues.
In addition to the errors/noises/shifts, and imperfection associated with data, choosing the right spatial and temporal granularity of tracking data is important issue to be considered, in particular in the relatively young field of movement analysis. This is what has been termed granularity grief in [34]. Although this issue has less effect on the results of the proposed method, a complete study should be conducted to precisely investigate its impact on QTC patterns.
Throughout this study, two different examples are analyzed. In the first example, the movement patterns of two cars at five different traffic scenarios are evaluated. In the second example, more complicated movements are examined. Unlike a traffic scenario, the samba dancers are moving freely and made complex trajectories. Although the proposed approach is applied to two small-scale datasets, it has potentiality to be used for more large and complex datasets difficult to process using traditional data processing techniques. In this context, the required accuracy of the results of the analysis usually depends on the type of application at hand. Representing the movement interactions with a qualitative representation such as QTCB (our approach) significantly reduces the accuracy of the result. However, other types of QTC, such as QTC-Double Cross (QTCC), can incorporate more relevant information about the movement. In addition to the Euclidean distance considered in QTCB, in QTCC, directional information between two moving objects is included. Consequently, to visualize the QTCC movement patterns, a new high resolution SESI is needed because each QTCC relation is represented by a four-tuple (for more explanation about QTCC, see ([53]).
At the end of this section, we compare the proposed methodology with the one presented in [63] where the same case study (i.e., dance) was studied. We describe the strengths and weaknesses of the methodology compared to the one in [63] from data modeling point of view. In our previous work [63], we identified similarities in the movement behavior between pairs of interacting moving objects over time by cross-pollinating QTC with sequence alignment methods (SAMs). There, sequence alignment was used to calculate the similarity between movement sequences of QTC relations for some reasons. Above all, from the visual analysis viewpoint, the SAM approach supports better the human intuition in order to interpret the visual results. Therefore, the high dependency on expert knowledge can be counted as a weakness of the SESI approach and this is especially the case when multidimensional data are represented.
Different from our previous study where movement data were only investigated in the form of sequences, in this paper we demonstrated the usefulness of qualitative information integrated with SESI in the analysis of and reasoning about multi-dimensional data. We showed that hyper-SESIs not only cover the interactions of multiple objects (more than two objects) but also include the associated movement pattern attributes of interacting objects such as frequency and duration.
6. Conclusions and Future Work
Knowledge discovery of moving objects’ trajectories is an important and challenging issue in many research domains. This study presented a new technique for clustering pairs of trajectories, which is based on three major steps. In the first step, we described relative movement patterns of MPOs using qualitative trajectory calculus (QTC). QTC enables us to express the interactions between moving objects qualitatively. In the next step, QTCB movement patterns were represented in a sequence signature (SESI), which is a fractal way of mapping patterns of interactions between MPOs in an indexed raster space. Then, in the third step, a distance function was used to cluster SESIs and aims to improve the understanding of the movement patterns.
Unlike many trajectory similarity measures that are restricted to geometric abstractions of the trajectories, we were able to measure the distance between the trajectory pairs based on the QTCB movement patterns. The proposed methodology could be used in a wide range of research applications. Movement patterns such as walking, running, jumping, lifting, striking and swimming can be investigated for different purposes. For example, the proposed approach can be used in sports sciences to analyze the movement of athletes with the purpose of rehabilitation, physical education and practice. The emphasis of the therapy can be diverse, ranging from upper limb rehabilitation and balance rehabilitation, to the rehabilitation of specific body parts [64].
The proposed clustering approach can cluster pairs of interactions and assess whether body interactions are sufficiently improved relative to a ‘normal’ body interaction. In the case of swimming, for example, the investigation of movement patterns of lower/upper limbs of swimmers identifies common features of novice swimmers and how these features change with increasing skill during an instructional period. The proposed approach can be applied in dance analysis, where an examination of the movement patterns of the body parts of dancers is important to assist instructors for educational purposes.
We could also exploit the proposed approach as a complementary analysis technique to support coaching in certain sports, such as football. For example, movement behaviors of certain players (e.g., strikers) in different temporal periods of the game could be examined to discover techniques or strategies that lead to frequent QTC movement patterns on SESI. It would be an interesting step toward the visual analysis of the movement behavior of players by using SESIs.
Supplementary Files
Supplementary File 1Acknowledgments
The authors would like to thank the Special Research Fund of Ghent University (BOF) and the Research Foundation Flanders for supporting the research. We are grateful to IPEM, Department of Musicology, Ghent University for providing the samba dance data.
Author Contributions
All six authors have contributed to the work presented in this paper. They worked collaboratively on different topics that were presented in this paper, and all contributed to the writing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Haghani, A.; Hamedi, M.; Sadabadi, K.F.; Young, S.; Tarnoff, P. Data collection of freeway travel time ground truth with Bluetooth sensors. Transp. Res. Rec. J. Transp. Res. Board 2009. [Google Scholar] [CrossRef]
- Cagnacci, F.; Boitani, L.; Powell, R.A.; Boyce, M.S. Animal ecology meets GPS-based radiotelemetry: A perfect storm of opportunities and challenges. Philos. Trans. R. Soc. B Biol. Sci. 2010. [Google Scholar] [CrossRef] [PubMed]
- Brockmann, D.; Hufnagel, L.; Geisel, T. The scaling laws of human travel. Nature 2006, 439, 462–465. [Google Scholar] [CrossRef] [PubMed]
- Wisbey, B.; Montgomery, P.G.; Pyne, D.B.; Rattray, B. Quantifying movement demands of AFL football using GPS tracking. J. Sci. Med. Sport 2010, 13, 531–536. [Google Scholar] [CrossRef] [PubMed]
- Versichele, M.; Neutens, T.; Delafontaine, M.; Van de Weghe, N. The use of Bluetooth for analysing spatiotemporal dynamics of human movement at mass events: A case study of the Ghent Festivities. Appl. Geogr. 2012, 32, 208–220. [Google Scholar] [CrossRef]
- Tiru, M.; Saluveer, E.; Ahas, R.; Aasa, A. Web-based monitoring tool for assessing space-time mobility of tourists using mobile positioning data: Positium Barometer. J. Urban Technol. 2010, 17, 71–89. [Google Scholar] [CrossRef]
- Ahlqvist, O.; Ban, H.; Cressie, N.; Shaw, N.Z. Statistical counterpoint: Knowledge discovery of choreographic information using spatio-temporal analysis and visualization. Appl. Geogr. 2010, 30, 548–560. [Google Scholar] [CrossRef]
- Chavoshi, S.H.; De Baets, B.; Neutens, T.; Ban, H.; Ahlqvist, O.; De Tre, G.; Van de Weghe, N. Knowledge discovery in choreographic data using relative motion matrices and dnamic time warping. Appl. Geogr. 2014, 47, 111–124. [Google Scholar] [CrossRef]
- Delafontaine, M.; Versichele, M.; Neutens, T.; Van de Weghe, N. Analysing spatiotemporal sequences in Bluetooth tracking data. Appl. Geogr. 2012, 34, 659–668. [Google Scholar] [CrossRef]
- Dodge, S.; Weibel, R.; Lautenschutz, A.K. Towards a taxonomy of movement patterns. Inf. Vis. 2008, 7, 240–252. [Google Scholar] [CrossRef]
- Shoval, N.; Isaacson, M. Sequence alignment as a method for human activity analysis in space and time. Ann. Assoc. Am. Geogr. 2007, 97, 282–297. [Google Scholar] [CrossRef]
- Wang, C.; De, D.; Song, W.Z. Trajectory mining from anonymous binary motion sensors in Smart Environment. Knowl. Sys. 2013, 37, 346–356. [Google Scholar] [CrossRef]
- Gudmundsson, J.; Wolle, T. Football analysis using spatio-temporal tools. Comput. Environ. Urban Sys. 2014, 47, 16–27. [Google Scholar] [CrossRef]
- Weld, D.S.; Kleer, J.D. Readings in Qualitative Reasoning about Physical Systems; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1989. [Google Scholar]
- Clementini, E.; Felice, P.D.; Hernández, D. Qualitative representation of positional information. Artif. Intell. 1997, 95, 317–356. [Google Scholar] [CrossRef]
- Cohn, A.G. Calculi for qualitative spatial reasoning. In Artificial Intelligence and Symbolic Mathematical Computation; Springer Berlin Heidelberg: Berlin, Germany, 1996; pp. 124–143. [Google Scholar]
- Monferrer, M.T.E.; Lobo, F.T. Qualitative velocity. In Topics in Artificial Intelligence; Springer Berlin Heidelberg: Berlin, Germany, 2002; pp. 29–39. [Google Scholar]
- Renz, J.; Rauh, R.; Knauff, M. Towards cognitive adequacy of topological spatial relations. Spat. Cogn. II 2000, 1849, 184–197. [Google Scholar]
- Muller, P. Topological spatio-temporal reasoning and representation. Comput. Intell. 2002, 18, 420–450. [Google Scholar] [CrossRef]
- Wolter, F.; Zakharyaschev, M. Qualitative spatio-temporal representation and reasoning: A computational perspective. Explor. Artif. Intell. New Millen. 2002, 175–216. [Google Scholar]
- Van de Weghe, N. Representing and Reasoning about Moving Objects: A Qualitative Approach. PhD Thesis, University of Ghent, Kortrijk, Belgium, 2004. [Google Scholar]
- Bellotto, N.; Hanheide, M.; Van de Weghe, N. Qualitative design and implementation of human-robot spatial interactions. In Social Robotics; Herrmann, G., Pearson, M., Lenz, A., Bremner, P., Spiers, A., Leonards, U., Eds.; Springer International Publishing: Berlin, Germany, 2013; pp. 331–340. [Google Scholar]
- Delafontaine, M.; Cohn, A.G.; Van de Weghe, N. Implementing a qualitative calculus to analyse moving point objects. Expert Sys. Appl. 2011, 38, 5187–5196. [Google Scholar] [CrossRef]
- Kisilevich, S.; Mansmann, F.; Nanni, M.; Rinzivillo, S. Spatio-temporal clustering. In Data Mining and Knowledge Discovery Handbook; Maimon, O., Rokach, L., Eds.; Springer US: NY, US, 2010; pp. 855–874. [Google Scholar]
- Alon, J.; Sclaroff, S.; Kollios, G.; Pavlovic, V. Discovering clusters in motion time-series data. IEEE Comput. Vis. Pattern Recognit. 2003, 1, 375–381. [Google Scholar]
- Chudova, D.; Gaffney, S.; Mjolsness, E.; Smyth, P. Translation-invariant mixture models for curve clustering. In Proceedings of the 9th International Conference on Knowledge Discovery and Data mining (ACM SIGKDD), New York, NY, USA, 24–27 August 2003; pp. 79–88.
- Nanni, M.; Pedreschi, D. Time-focused clustering of trajectories of moving objects. J. Intell. Inf. Sys. 2006, 27, 267–289. [Google Scholar] [CrossRef]
- Andrienko, N.; Andrienko, G. Exploratory Analysis of Spatial and Temporal Data; Springer: Berlin, Germany, 2006. [Google Scholar]
- Hwang, S.Y.; Liu, Y.H.; Chiu, J.K.; Lim, E.P. Mining mobile group patterns: A trajectory-based approach. In Advances in Knowledge Discovery and Data Mining; Springer: Berlin, Germany, 2005; pp. 145–146. [Google Scholar]
- Gudmundsson, J.; van Kreveld, M. Computing longest duration flocks in trajectory data. In Proceedings of the 14th Annual ACM International Symposium on Advances in Geographic Information Systems, New York, NY, USA, 5–11 November 2006; pp. 35–42.
- Kang, J.H.; Welbourne, W.; Stewart, B.; Borriello, G. Extracting places from traces of locations. In Proceedings of the 2nd ACM International Workshop on Wireless Mobile Applications and Services on WLAN Hotspots, ACM, New York, NY, USA, 1 October 2004; pp. 110–118.
- Giannotti, F.; Nanni, M.; Pinelli, F.; Pedreschi, D. Trajectory pattern mining. In Proceedings of the 13th International Conference on Knowledge Discovery and Data Mining (ACM SIGKDD), ACM, San Jose, CA, USA, 12–15 August 2007; pp. 330–339.
- Giannotti, F.; Pedreschi, D. Mobility, Data Mining and Privacy: Geographic Knowledge Discovery; Springer: Berlin, Germany, 2008. [Google Scholar]
- Laube, P.; Purves, R.S. How fast is a cow? cross-scale analysis of movement data. Trans. GIS 2011, 15, 401–418. [Google Scholar] [CrossRef]
- Long, J.A.; Nelson, T.A. Measuring dynamic interaction in movement data. Trans. GIS 2013, 17, 62–77. [Google Scholar] [CrossRef]
- Andrienko, N.; Andrienko, G. Designing visual analytics methods for massive collections of movement data. Cartographica 2007, 42, 117–138. [Google Scholar] [CrossRef]
- Andrienko, N.; Andrienko, G.; Wachowicz, M.; Orellana, D. Uncovering interactions between moving objects. In Proceedings of 5th international conference on GIScience, Park City, UT, USA, 23–26 September 2008; pp. 16–26.
- Laube, P.; Imfeld, S.; Weibel, R. Discovering relative motion patterns in groups of moving point objects. Int. J. of Geogr. Inf. Sci. 2005, 19, 639–668. [Google Scholar] [CrossRef]
- Ooms, K.; Andrienko, G.; Andrienko, N.; De Maeyer, P.; Fack, V. Analysing the spatial dimension of eye movement data using a visual analytic approach. Expert Sys. Appl. 2012, 39, 1324–1332. [Google Scholar] [CrossRef]
- Pelekis, N.; Andrienko, G.; Andrienko, N.; Kopanakis, I.; Marketos, G.; Theodoridis, Y. Visually exploring movement data via similarity-based analysis. J. Intell. Inf. Sys. 2012, 38, 343–391. [Google Scholar] [CrossRef]
- Rinzivillo, S.; Pedreschi, D.; Nanni, M.; Giannotti, F.; Andrienko, N.; Andrienko, G. Visually driven analysis of movement data by progressive clustering. Inf. Vis. 2008, 7, 225–239. [Google Scholar] [CrossRef]
- Chavoshi, S.H.; De Baets, B.; Qiang, Y.; De Tré, G.; Van de Weghe, N. A qualitative approach to the identification, visualization and interpretation of repetitive motion patterns within groups of moving point objects. Int. Arab J. Inf. Technol. 2015, in press. [Google Scholar]
- Demsar, U.; Virrantaus, K. Space-time density of trajectories: Exploring spatio-temporal patterns in movement data. Int. J. Geogr. Inf. Sci. 2010, 24, 1527–1542. [Google Scholar] [CrossRef]
- Gudmundsson, J.; van Kreveld, M.; Speckmann, B. Efficient detection of patterns in 2D trajectories of moving points. GeoInformatica 2007, 11, 195–215. [Google Scholar] [CrossRef]
- Wilson, C. Activity patterns in space and time: Calculating representative Hagerstrand trajectories. Transportation 2008, 35, 485–499. [Google Scholar] [CrossRef]
- Buchin, K.; Buchin, M.; Van Kreveld, M.; Luo, J. Finding long and similar parts of trajectories. In Proceedings of 17th international conference on advances in geographic information systems (ACM SIGSPATIAL GIS 2009), ACM, Seattle, WA, USA, 4–6 November 2009; pp. 296–305.
- Dodge, S.; Weibel, R.; Forootan, E. Revealing the physics of movement: Comparing the similarity of movement characteristics of different types of moving objects. Comput. Environ. Urban Sys. 2009, 33, 419–434. [Google Scholar] [CrossRef]
- Lin, B.; Su, J.W. One way distance: For shape based similarity search of moving object trajectories. Geoinformatica 2008, 12, 117–142. [Google Scholar] [CrossRef]
- Dodge, S. Exploring movement using similarity analysis. PhD Thesis, University of Zurich, 2011. [Google Scholar]
- Giannotti, F.; Pedreschi, D. Mobility, data mining and privacy: A vision of convergence. In Mobility, data mining and privacy-geographic knowledge discovery; Giannotti, F., Pedreschi, D., Eds.; Springer: Berlin, Germany, 2008; pp. 1–11. [Google Scholar]
- Glez-Cabrera, F.J.; Álvarez-Bravo, J.V.; Díaz, F. Representing motion patterns with the qualitative rectilinear projection calculus. In Distributed Computing and Artificial Intelligence; Springer: Berlin, Germany, 2013; pp. 251–258. [Google Scholar]
- Van de Weghe, N.; Cohn, A.G.; De Tré, G.; De Maeyer, P. A qualitative trajectory calculus as a basis for representing moving objects in geographical information systems. Control Cybern. 2006, 35, 97–119. [Google Scholar]
- Van de Weghe, N.; Cohn, A.G.; De Maeyer, P.; Witlox, F. Representing moving objects in computer-based expert systems: The overtake event example. Expert Sys. Appl. 2005, 29, 977–983. [Google Scholar] [CrossRef]
- Delafontaine, M.; Van de Weghe, N.; Bogaert, P.; De Maeyer, P. Qualitative relations between moving objects in a network changing its topological relations. Inf. Sci. 2008, 178, 1997–2006. [Google Scholar] [CrossRef]
- Delafontaine, M.; Chavoshi, S.H.; Cohn, A.G.; Van de Weghe, N. A qualitative trajectory calculus to reason about moving point objects. In Qualitative Spatio-Temporal Representation and Reasoning: Trends and Future Directions; Hazarika, S.M., Ed.; IGI Global: Hershey, PA, USA, 2012; pp. 147–167. [Google Scholar]
- Cohn, A.G.; Hazarika, S.M. Qualitative spatial representation and reasoning: An overview. Fundam. Inf. 2001, 46, 1–29. [Google Scholar]
- Galton, A. Dominance diagrams: A tool for qualitative reasoning about continuous systems. Fundam. Inf. 2001, 46, 55–70. [Google Scholar]
- Forbus, K.D. Qualitative process theory. Artif. Intell. 1984, 24, 85–168. [Google Scholar] [CrossRef]
- Barnsley, M.F. Fractals Everywhere; Academic Press: New York, NY, USA, 1988. [Google Scholar]
- Rokach, L.; Maimon, O. A survey of clustering algorithms. In Data Mining and Knowledge Discovery Handbook; Rokach, L., Maimon, O., Eds.; Springer: Berlin, Germany, 2010; pp. 269–298. [Google Scholar]
- Dawyndt, P.; De Meyer, H.; De Baets, B. The complete linkage clustering algorithm revisited. Soft Comput. 2005, 9, 385–392. [Google Scholar] [CrossRef]
- Freksa, C. Temporal reasoning based on semi-intervals. Artif. Intell. 1992, 54, 199–227. [Google Scholar] [CrossRef]
- Chavoshi, S.H.; De Baets, B.; Neutens, T.; De Tre, G.; Van de Weghe, N. Exploring dance movement data using sequence alignment methods. PLoS ONE 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Schönauer, C.; Pintaric, T.; Kaufmann, H. Full body interaction for serious games in motor rehabilitation. In Proceedings of the 2nd Augmented Human International Conference, Tokyo, Japan, 13 March 2011; p. 4.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).