4SIM: A Novel Description Model for the Ternary Spatial Relation “Between” of Buildings

Abstract

Natural language spatial relations are often ambiguous and polysemic. They are also pluralistic and subjective in nature. Their descriptive methods are crucial but difficult in cartography, geographic information science, and map generalization. “Between” is a context-concerned spatial concept which is widely used to describe the arrangement of spatial objects. It involves the spatial distribution of at least three spatial objects and describes a scenario in which one (or more) object(s) is surrounded by objects on both sides. Existing models based on RCC and the n-intersection model are mainly used to describe binary spatial logic and are inadequate in describing the “between” ternary relation effectively. At present, although existing models can describe and reason about such ternary spatial relations, their limitations still exist. The description capability of ternary spatial relations is unspecific and polysemic, and certain results are inconsistent with spatial cognition and perception and application requirements. Therefore, this paper proposes a 4 Sides Intersection Model (4SIM) to express the spatial relation among ternary buildings in detail. Theoretically, 4SIM can effectively describe 45 spatial relations among ternary objects through the topological distances among the four boundaries of the region formed by the intermediate object and the two adjacent objects. The 4SIM has been demonstrated to offer a superior degree of accuracy in the depiction of spatial relations in comparison to the extant RIM method, thus providing new possibilities for map generalization.

1. Introduction

Spatial relation theory is crucial in geographic information science and serves as the foundation for applications in computer science and artificial intelligence [1], spatial analysis, spatial data matching, spatial data query, and spatial reasoning [2], among others. Additionally, it serves as a theoretical foundation in computer science, artificial intelligence, and other fields [3,4]. The first step in the research and application of spatial relations involves defining the formal set, which establishes a model for a specific spatial relation. This model is then applied to specific practical contexts. For instance, the nine-intersection model begins by creating a combined table of spatial relations and then establishes the reasoning mechanism for detecting the consistency of the topological relation.

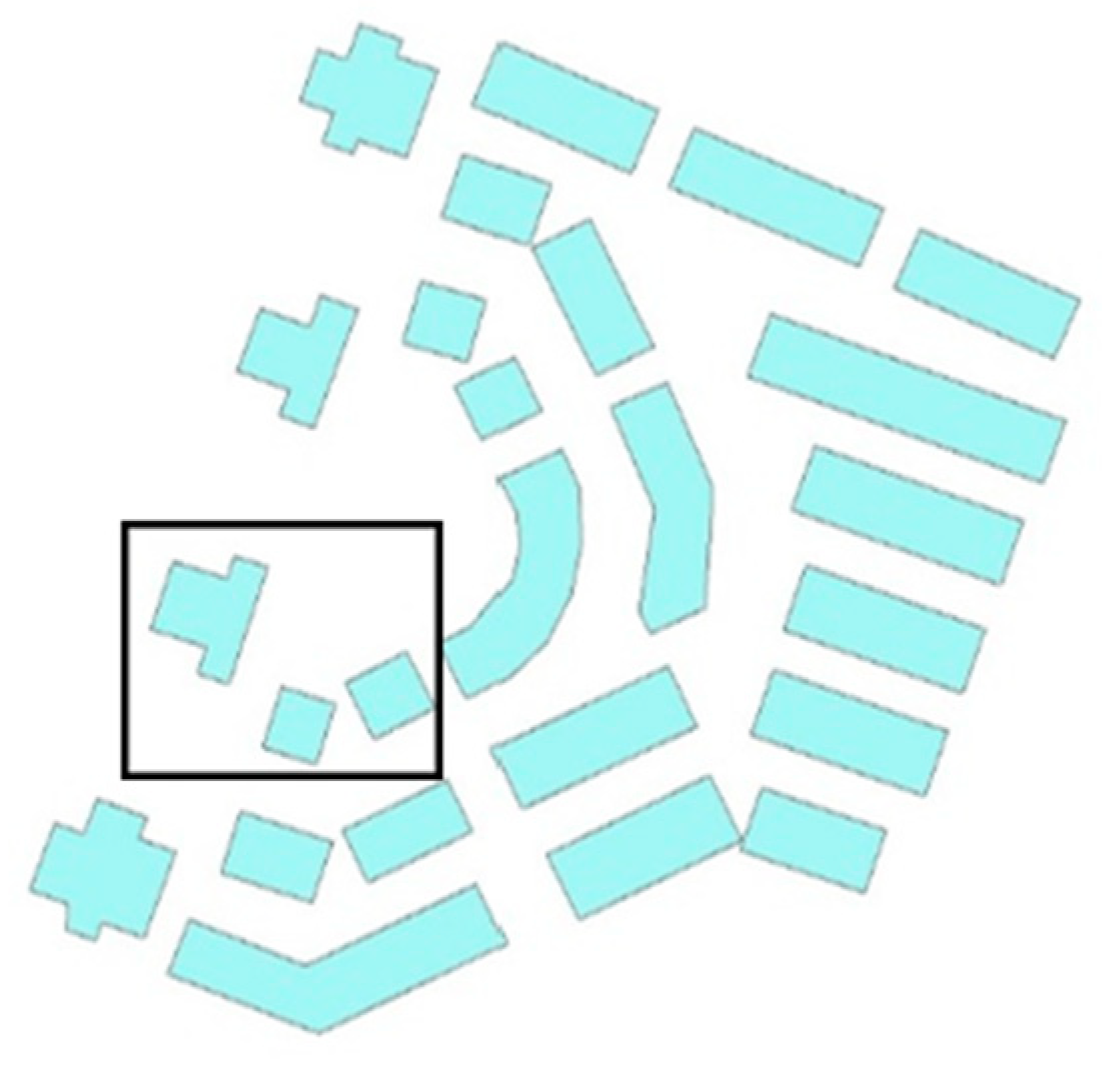
According to the perspective of map generalization, maintaining spatial structure is considered a fundamental requirement for both map generalization and multi-scale representation. Furthermore, spatial structure also serves as a key basis for selecting map generalization algorithms. The existing studies on the spatial structure of maps have focused on the pattern recognition of linear [5], curvilinear [6], grid [7], and typical letter-like patterns [8]. The irregular patterns (highlighted in the black box in Figure 1) refer to the spatial arrangement of geographic elements with no obvious regularity [9], which makes it difficult to characterize and express them, and have received less attention. While map generalization aims to preserve and enhance the readability of maps with fewer spatial elements [10], irregular patterns on maps are often constrained by traditional binary spatial relations, which fail to effectively express complex spatial relations between multiple objects and are not conducive to structured map generalization. Consequently, this limitation highlights the necessity for more robust models of spatial relations involving multiple objects. This paper focuses on the description of high-level spatial relations and explores methods for modeling and qualitatively describing methods for the “between” relation among buildings. The aim is to address the limitations of traditional binary spatial relations in expressing irregular patterns, especially for the effective expression of complex spatial relations between multiple objects. The irregular pattern formed by the three buildings shown in Figure 1 can be viewed as a “between” relation, where the middle building lies between the two buildings on either side. In this way, the ternary buildings can be treated as a unit to describe the map environment context, providing a technical foundation and favorable conditions for structured map generalization. As a result, the outcomes of map generalization might be enhanced in terms of logical consistency and readability.

Figure 1. Examples of irregular patterns of buildings.

In addition, a number of scholars have studied ternary and multivariate spatial relations. Michael Worboys [11] refers to these spatial relations as “higher-order spatial relations”, which are typically defined and described with terms such as “between” [12,13], “surround” [11], “along” [14], and “enter” [15]. These relations also have significant application prospects in structured map generalization.

The “between” relation is one of the basic spatial relations of high-level spatial relations. Although some scholars have proposed the Ray Intersection Model (RIM) to formalize the “between” relation, its ability to describe spatial relations among three objects is limited. The interchangeable positions of the objects on both sides create ambiguity in defining topological relations with the middle object, leading to imprecise descriptions of relative positions. This ambiguity makes the RIM inadequate in accurately characterizing ternary spatial relations, failing to fulfill the critical demands for precise spatial representation in map generalization [16]. For the above problems, this paper proposes a new model, the 4 Sides Intersection Model (4SIM), which differs from RIM in that the objects on both sides of this paper’s method are not exchangeable, and this clearly distinguishes between the objects and their spatial arrangement to ensure that it can more accurately describe the spatial structure relationship between ternary objects. In this paper, the algorithm is implemented using a building as an example, and the spatial structure of the ternary spatial objects is demonstrated and analyzed.

The rest of the paper is structured as follows: Section 2 summarizes related work. Section 3 presents the ternary spatial object cases in which 4SIM distinguishes spatial objects and discusses how 4SIM can be utilized to detect whether a spatial object is located between two other objects. Section 4 shows a concrete implementation of 4SIM. Section 5 demonstrates and analyzes a data set using 4SIM and conducts a comparison experiment with RIM. Finally, Section 6 concludes and looks forward to future work.

2. Related Works

This section is divided into three parts. Section 2.1 presents a concise review of existing spatial relation models. Section 2.2 reviews the spatial relations defined by natural language terms and their related spatial relation models. Section 2.3 is dedicated to the analysis and discussion of current studies on the “between” spatial relation model.

2.1. Spatial Relations

Existing studies on spatial relations have mainly concentrated on the formal expressions of topological relations on binary objects. The two most classical methods, among many, are the RCC models and the n-intersection models.

Based on the logical axiom of spatial calculus, Clarke, Randell [17] proposed the RCC model, which assumes that a primitive binary relation $C(x,y)$ denotes that region $x$ is connected to region $y$. A series of relations are defined through relation C. Among these, RCC5 and RCC8 are the two most typical and widely used methods.

The n-intersection model is another famous framework for modeling the interaction between two spatial objects. The relation is defined by a matrix that encodes the potential intersections between the interiors, boundaries, and exteriors of a pair of objects. The earliest significant n-intersection model is 4IM [18], which delineates the binary relation between the interiors and boundaries of two objects. Subsequently, Egenhofer introduced the concept of the exterior of an object, thereby extending the 4IM to 9IM [19]. This was then improved to become the Dimensionally Extended 9IM (DE-9IM), by extending the dimensions [20]. Since then, many other extensions of 9IM have been developed, including Voronoi-based 9IM (V9IM) [21]. The 9IM is particularly prevalent and serves as the theoretical foundation of several commercial and open-source GISs (e.g., ArcGIS, QIGIS), spatial databases (e.g., Oracle Spatial, PostGIS), and other software. This study employs the 9IM to describe the relation between the ternary objects. However, the n-intersection model, which is more advanced in describing the interactions between the interior, boundary, and exterior of two objects, lacks the ability to express higher-order relations.

2.2. Higher-Order Spatial Relations

The study of high-level spatial relations is actually part of the field of natural language spatial relations. In 1989, the National Center for Geographic Information and Analysis (NGGIA) conducted a study on natural language spatial relations. Du Shihong [22] proposed that the natural language used by individuals to describe spatial relations in everyday communication be referred to as natural language spatial relations. The most frequently occurring terms are “in”, “between”, “along”, and other spatial prepositions. At present, the majority of research is concentrated on the understanding of natural language spatial relations [23], with comparatively less research dedicated to the modeling and describing methodology.

With regard to binary spatial relations, Bloch et al. [12] proposed a mathematical definition of the extent of object A along object B, according to the region between A and B and the degree of extension of this region. Corcoran [15] argued that different concepts exist at different levels of the hierarchy. Consequently, he explored the “enter” relation between a road and a housing estate.

In terms of higher-order spatial relations, the higher-order spatial relation has been mentioned by Worboys and Duckham [11], but no explicit and clear definition has been provided. In this paper, we propose a definition of it as a ternary or higher-order spatial relation that extends beyond traditional binary spatial relations. Freska [24] formulated ternary relations between points to represent the qualitative orientation of a point with respect to a given line segment. Subsequently, he extended these relations in double-cross calculus [25]. Bloch [12] and Majic [13] explored the “between” relation with ternary objects. Clementini [26] defined and explored the expression of ternary projection relations involving three regions in the plane, based on tangents to two reference regions, and proposed 34 projection relations among the three regions, some of which agree with the explanation of “between”. Furthermore, Clementini [27] extended this approach to ternary region relations in the sphere. In addition, Worboys [11] explored a category of qualitative geometric relations between disjoint regions embedded in a sphere or plane. He defined the “surround” spatial relation, and demonstrated this relation for objects ranging from three to seven objects using the maptrees.

2.3. “Between” Spatial Relation Models

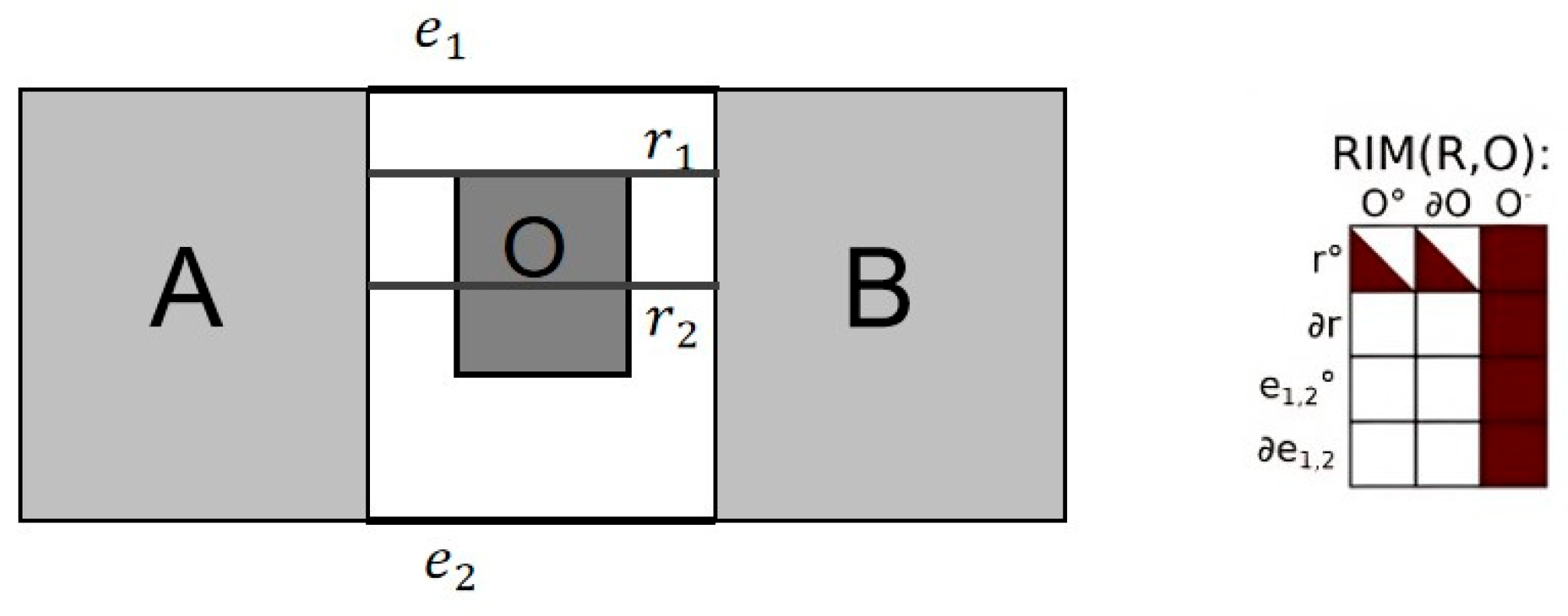
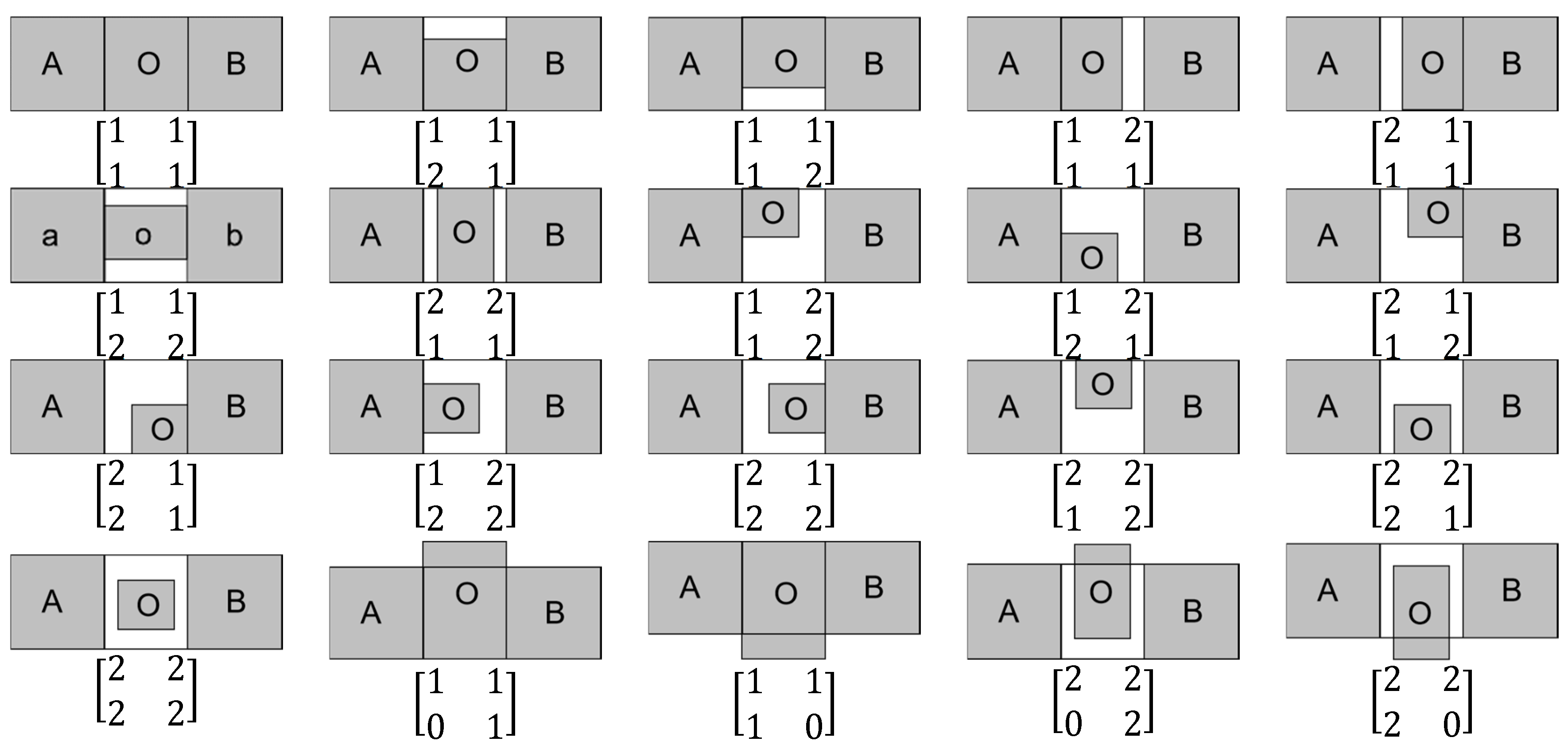
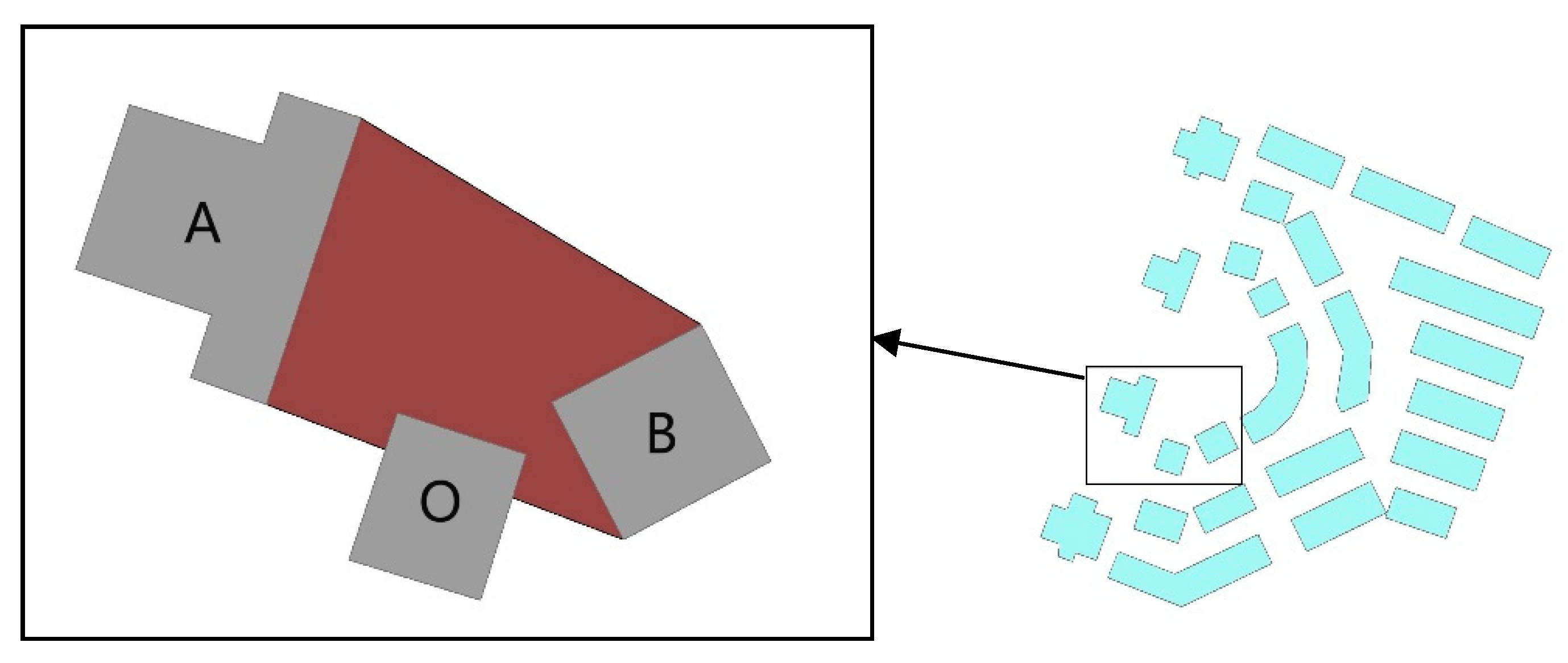
The “between” spatial relation serves as the foundation for numerous ternary spatial relations. The “between” relation plays a pivotal role in conceptualizing the spatial configuration and reasoning about the spatial arrangement of objects. Bloch [12] took into consideration the shape and the context of the object, and proposed a visibility concept for the effects of fuzzy object relations and relative sizes of objects. He also made a geometric definition of “between”. However, there is still no comprehensive model that can fully describe all the problems associated with this relation. Majic [13] proposed the RIM, which is a method for reasoning about ternary spatial relations through the intersection of the rays between the two objects on either side with the median object, and is able to describe and reason about ternary spatial relations relatively adequately. As shown in Figure 2, the RIM first divides the rays between A and B into extreme rays (denoted as $e_i$) and other rays (denoted as $r_i$), and then arranges the ray area $R$ with the RIM of the intermediate object into a matrix as shown in Table 1 to represent the spatial distribution of the distinguished ternary objects. To verify the validity of the method, experiments were also designed to verify the cognitive consistency between RIM and human spatial arrangement perception [28].

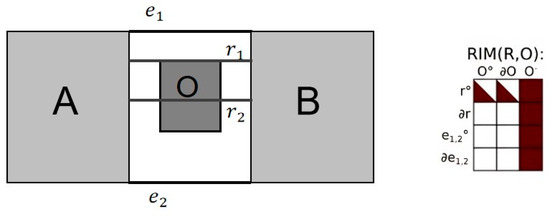
Figure 2. A case of spatial distribution of ternary objects A, B, and O and its RIM matrix representation of the ray area $R$ with the intermediate object O [13].

Table 1. The RIM between the ray set $R$, and object O.

	$O°$	$\partial O$	$O^{-}$
$r_i°\wedge e_i°$	${\displaystyle \frac{\sum _{i=1}^n{e}_i°\cap O°+\sum _{i=1}^n{r}_i°\cap O°}{N}}$	${\displaystyle \frac{\sum _{i=1}^n{e}_i°\cap \partial O+\sum _{i=1}^n{r}_i°\cap \partial O}{N}}$	${\displaystyle \frac{\sum _{i=1}^n{e}_i°\cap O^{-}+\sum _{i=1}^n{r}_i°\cap O^{-}}{N}}$
${\partial r}_i\wedge \partial e_i$	${\displaystyle \frac{\sum _{i=1}^n{\partial e}_i\cap O°+\sum _{i=1}^n{\partial r}_i\cap O°}{N}}$	${\displaystyle \frac{\sum _{i=1}^n{\partial e}_i\cap \partial O+\sum _{i=1}^n{\partial r}_i\cap \partial O}{N}}$	${\displaystyle \frac{\sum _{i=1}^n\partial e_i\cap O^{-}+\sum _{i=1}^n{\partial r}_i\cap O^{-}}{N}}$
$e_{\mathrm{1,2}}°$	${\displaystyle \frac{\sum _{i=1}^n{e}_i°\cap O°}{n}}$	${\displaystyle \frac{\sum _{i=1}^n{e}_i°\cap \partial O}{n}}$	${\displaystyle \frac{\sum _{i=1}^n{e}_i°\cap O^{-}}{n}}$
$\partial e_{\mathrm{1,2}}$	${\displaystyle \frac{\sum _{i=1}^n{\partial e}_i\cap O°}{n}}$	${\displaystyle \frac{\sum _{i=1}^n{\partial e}_i\cap \partial O}{n}}$	${\displaystyle \frac{\sum _{i=1}^n\partial e_i\cap O^{-}}{n}}$

To explore the “between” relation, it is first necessary to define the region between two objects before exploring whether the middle object is located between them, and to analyze the spatial relation among the three objects. In this study, a new perspective is proposed regarding the region between the two objects, which differs from previous approaches. Specifically, the region between two objects is calculated based on their geometric spatial relations, without considering the visibility of the two objects. Furthermore, in terms of the spatial relation among ternary objects, the two objects on either side are not exchangeable as RIM, and each group of ternary objects has a unique spatial relation. For example, in Figure 2, RIM presents the same result when describing object O as being connected to object A but separated from object B as it does when describing object O as being separated from object B. However, the method presented in this paper can provide a unique descriptive result that effectively distinguishes between these two different situations.

3. Description Method for the Ternary Spatial Relation “Between” of Buildings

This study needs to clarify two critical issues about the definition of “between”, in line with the fundamental ideas of this paper: firstly, to determine the region between two peripheral objects; secondly, to analyze the relation between the intermediate object and the region. For the first issue, this paper does not consider invisibility (a detailed explanation can be found in Section 4.1). Existing methods typically remove invisible regions when calculating the area between two peripheral objects. However, in the real world, such regions may hold significant importance. For instance, in applications like virtual reality or urban planning, invisible regions may contain critical obstacles, potential paths, or other essential spatial information. Removing these regions could lead to information loss or incorrect decision-making. In contrast, our method retains the invisible regions, making it more adaptable to real-world scenarios and providing a richer information foundation for spatial analysis and reasoning. This is described in detail in Section 4.1. The second issue, which builds upon the first, explores the core challenge of the descriptive model: when the intermediate object O is situated in a position of the region between A and B, it is possible to consider that O is between A and B. In this study, the geometric objects considered include lines and polygons. The method in this paper is applicable to these types of objects, but in some cases further extension may be required to handle more complex geometric shapes, such as islands, which involve curved surfaces.

3.1. The 4SIM Model

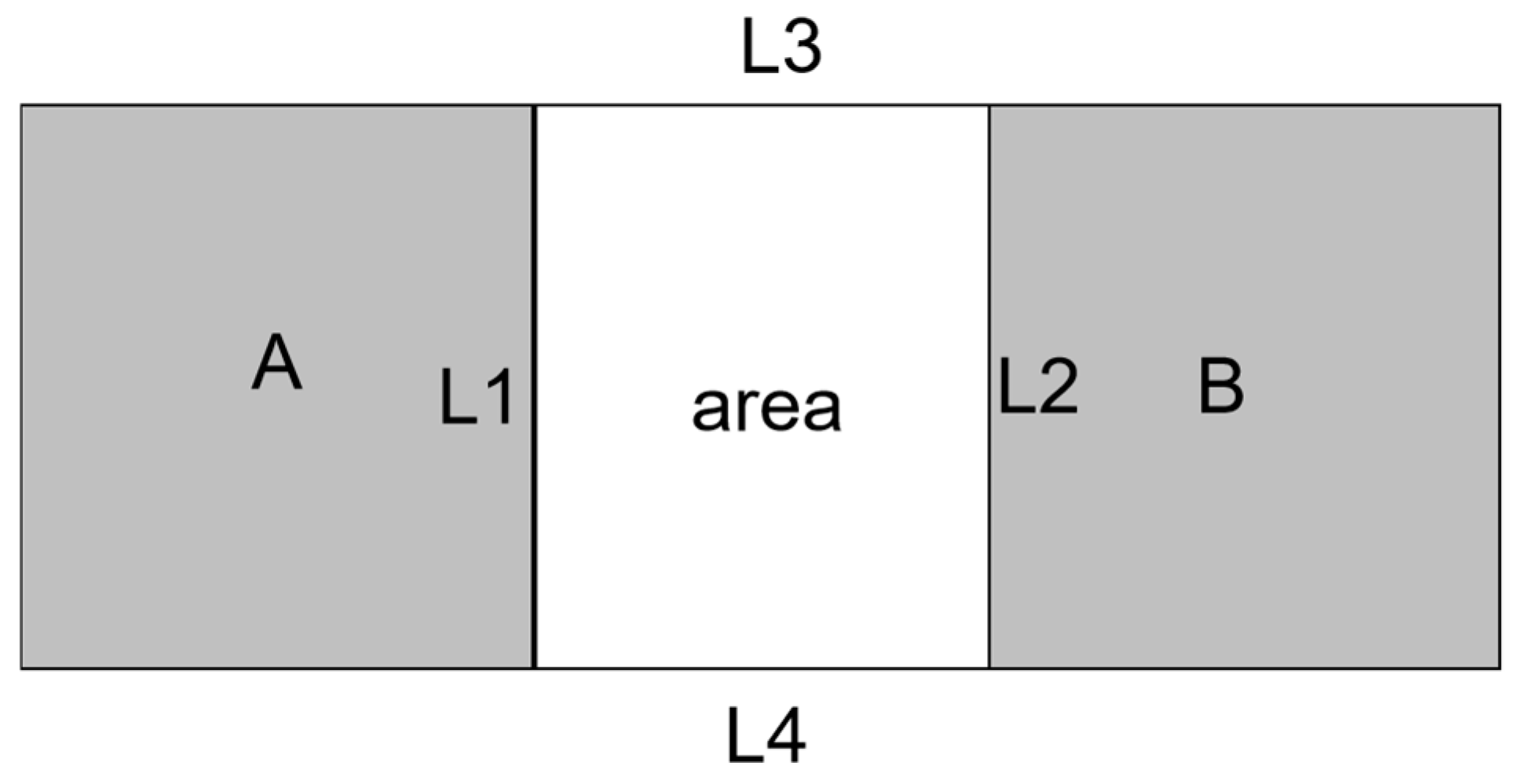
This section introduces the 4SIM model for describing ternary spatial relations. The model is defined on the basis of the intersection of the region between the objects A and B on both sides with the intermediate object O.

At first, the key parameters are delineated as follows. As illustrated in Figure 3, the area is the region between A and B. $L1$, $L2$, $L3$, and $L4$ form the boundaries of the $area$. Among them

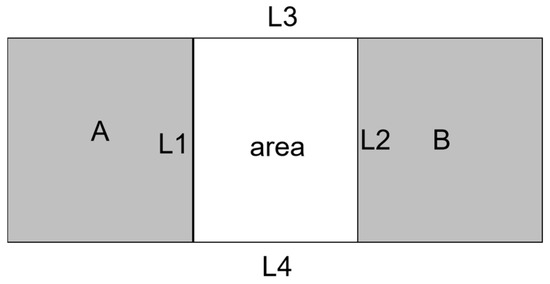
Figure 3. Diagram of the $area$ and its four boundaries: $L1$, $L2$, $L3$, $L4$.

• $L1$ is the intersection of object A with $area$, where $L1=area\cap A$;
• $L2$ is the intersection of object B with $area$, where $L2=area\cap B$;
• $L3$ and $L4$ are the boundaries of the $area$ that intersect with A and B, respectively. $L3$ is clockwise of $L1$ and $L4$ is clockwise of $L2$.

The 4SIM describes the spatial relation among ternary objects by creating a matrix $\left[\begin{array}{cc}{W}_{11}& W_{12}\\ W_{21}& W_{22}\end{array}\right]$, where $W_{ij}$ ($i$ represents row $i$ in the matrix and $j$ represents column $j$ in the matrix, $\forall i,j\in \left\{\mathrm{1,2}\right\}$) represents the intersection between the boundary $Li$ and the intermediate object O. The values of the matrix elements are determined based on the intersections between the intermediate object O and $L1$, $L2$, $L3$, $L4$, and $area$.

The general thought is that the $area$ is regarded as a constraint region, and $W_{ij}$ is positive if the object O is located inside the constraint region, while $W_{ij}$ is negative if the object O is located outside the constraint region. $L1$, $L2$, $L3$, and $L4$ are the constraint boundaries. The value of the matrix element $W_{ij}$ is determined according to the topological distance between O and the boundary line: if O intersects with the boundary line, then $W_{ij}$ is set to “$0$”; if it meets with the boundary line, then $W_{ij}$ is set to “$1$”; and if it is disjointed with regard to the boundary line, then $W_{ij}$ is set to “$2$”.

The detailed rules are as follows:

Rule 1: If $Li$ intersects with the interior of the intermediate object O, where $Li\cap O°\ne \varnothing$, then $W_{ij}=0$.

Rule 2: If $Li$ intersects with the boundary of the intermediate object O, where $Li\cap \partial O\ne \varnothing$, then determine whether the intermediate object O is completely outside the constraint region. If so, $W_{ij}=-1$; otherwise, $W_{ij}=1$.

Rule 3: If $Li$ intersects with the exterior of the intermediate object O, where $Li\cap O^{-}\ne \varnothing$, then determine whether the intermediate object O is completely outside the constraint region. If so, $W_{ij}=-2$; otherwise, $W_{ij}=2$.

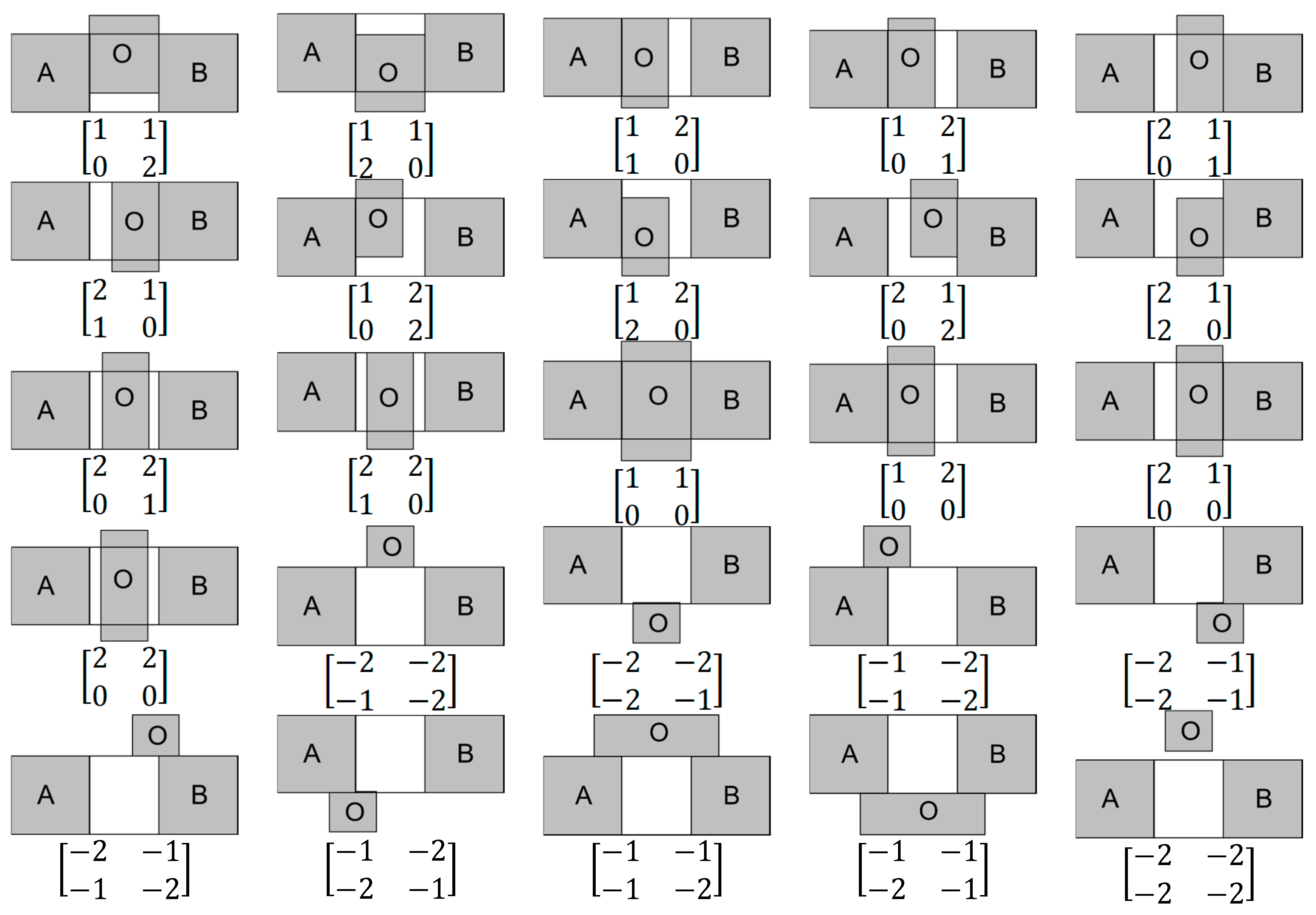
Figure 4 is a simple example of using 4SIM to describe ternary spatial relationships to illustrate these rules.

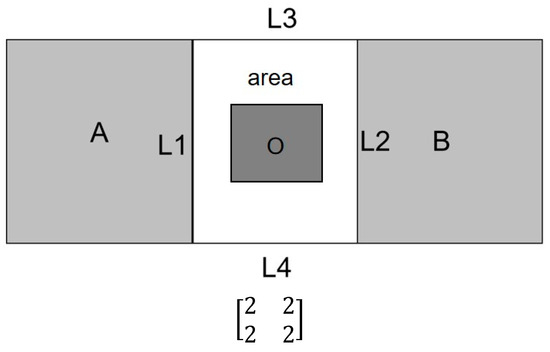
Figure 4. Spatial objects A, B, and O (Figure 2) where the middle object O intersects with the outside of $Li$ and is completely within the constraint region; therefore, $W_{ij}$ is two for all cases. The 4SIM matrix is analyzed according to the above rules.

i.

When object O is inside the constrained region or is covered by the constrained region or is equal to it, that is, if the 9IM of the spatial relations between O and the constrained region are $\left[\begin{array}{ccc}1& 0& 0\\ 1& 0& 0\\ 1& 1& 1\end{array}\right]$ or $\left[\begin{array}{ccc}1& 0& 0\\ 1& 1& 0\\ 1& 1& 1\end{array}\right]$ or $\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right],$ the topological relation between $Li$ and O is denoted as 1 or 2, namely, $\forall i,j\in \left\{\mathrm{1,2}\right\}, W_{ij}=1, 2$. There are in total $2\times 2\times 2\times 2=16$ cases.

ii.

When object O intersects with the constrained region, that is, if the 9IM of the spatial relation between O and the constrained region is $\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]$, $L1$ and $L2$ are topologically met or disjointed from O, denoted as $1$ or $2$. $L3$ or $L4$ are topologically connected to O, denoted as $0$, and another boundary line is topologically connected to O, denoted as $0$, $1$, or $2$. That is, $\forall i\in \left\{1\right\}, W_{ij}=1, 2; \exists i\in \left\{2\right\}, W_{ij}=0: \forall i\in \left\{2\right\},W_{ij}=0, 1, 2$. There are in total $2\times 2\times \left(2\times 3-1\right)=20$ cases.

iii.

When object O is separated from or in contact with the constrained region, the 9IM of spatial relations between O and the constrained region are $\left[\begin{array}{ccc}0& 0& 1\\ 0& 0& 1\\ 1& 1& 1\end{array}\right]$ or $\left[\begin{array}{ccc}0& 0& 1\\ 0& 1& 1\\ 1& 1& 1\end{array}\right]$, the topological relation between $L3$ and $L4$, and O is denoted as $-1$ or $-2$. When one of them is $-1$, the other must be $-2$. In this case, the topological relation between $L1$ and $L2$ and O is denoted as $-1$ or $-2$. When both of them are $-2$, the topological relation between $L1$ and $L2$ and O is denoted as $-2$. That is, $when \exists i\in \left\{2\right\}, W_{ij}=-1,-2: \forall i\in \left\{1\right\}, W_{ij}=-1,-2; when \forall i\in \left\{2\right\}, W_{ij}=-2: \forall i\in \left\{1\right\}, W_{ij}=-2$. There are in total $2\times 2\times 2+1=9$ cases.

Based on the above analysis, it can be seen that there are $16+20+9=45$ types of ternary relation that the 4SIM can distinguish, as shown in Figure 5.

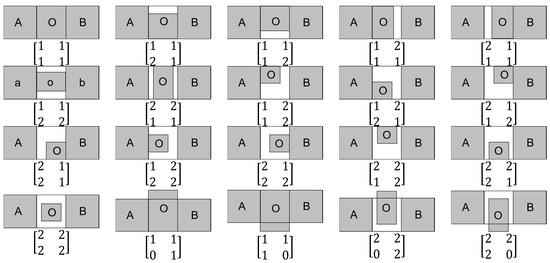
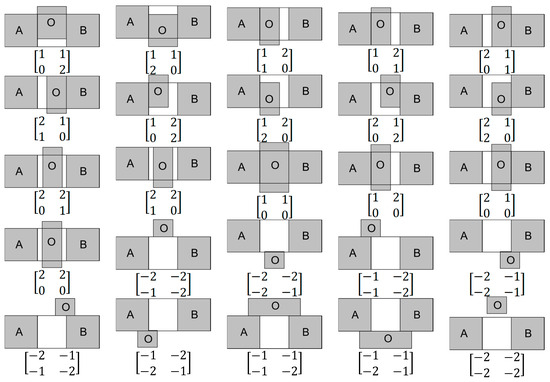
Figure 5. The 45 types of spatial relation “between” ternary objects expressed by 4SIM.

Here, two issues need to be noted.

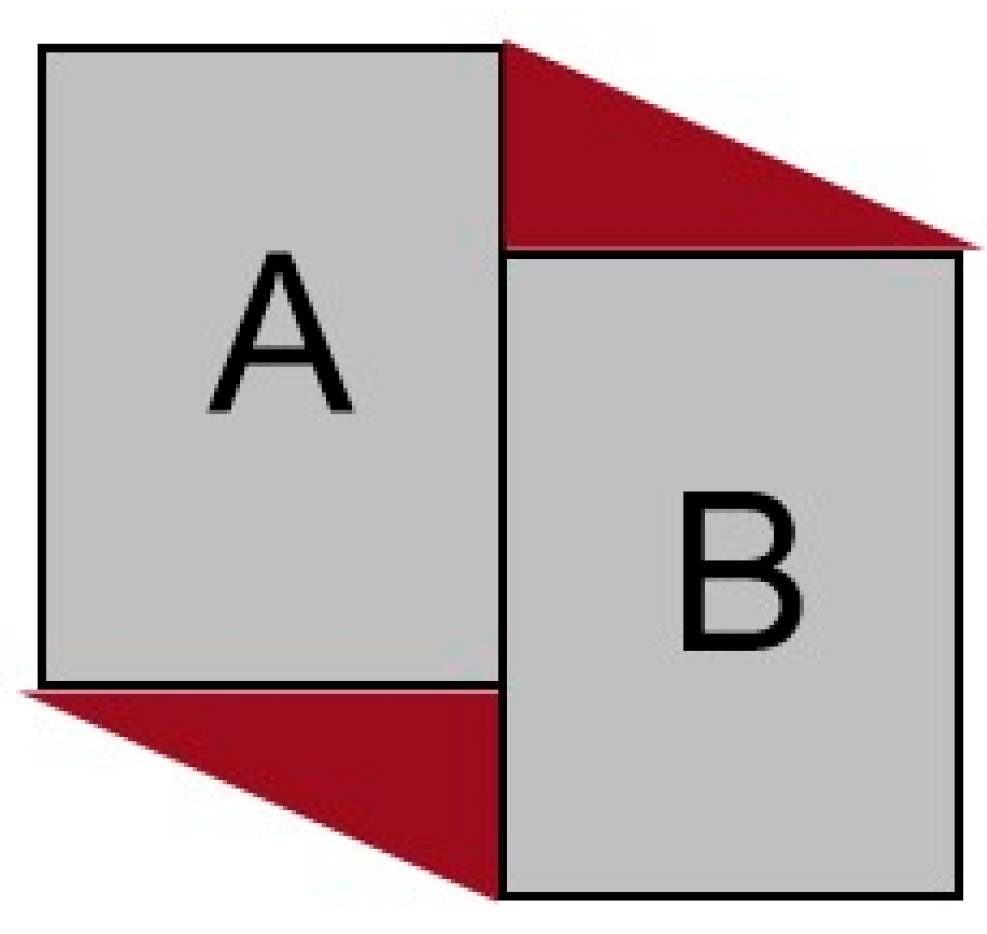
The first one is the precondition that the model holds. Here, 4SIM has a precondition that objects A and B on both sides are disjointed. If A and B meet, $L3$ and $L4$ cannot be determined. This is because when A and B meet, the $area$ will be a complex polygon (multipologon), as shown in Figure 6. Therefore, in this paper, the spatial relation result is denoted as “$null$” when objects A and B meet.

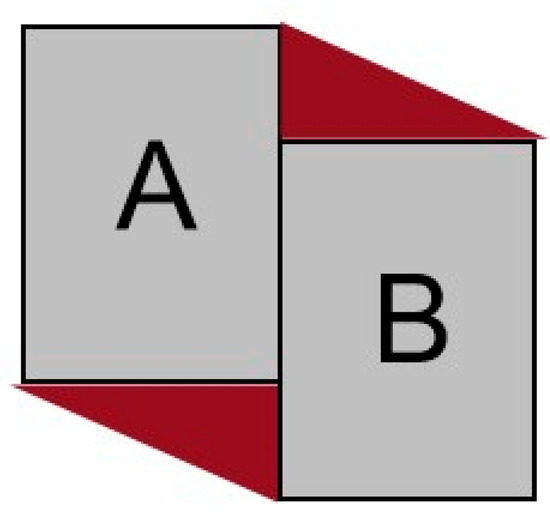
Figure 6. A and B meet, and the red parts are the resulting multipolygon areas.

The second issue is the order in which the objects are described. When given three objects, when the position (order) of A, B, and O is different, the results obtained by 4SIM may be different or may achieve the same result $\left[\begin{array}{cc}-2& -2\\ -2& -2\end{array}\right]$. However, these results are all correct and accurate descriptions of the relation among the three objects can help us understand the spatial pattern and configuration from different perspectives, and enable us to reason more accurately about the spatial distribution of ternary objects. Let us assume that there are three objects, numbered 1, 2, and 3, respectively. In this case, the 4SIM model will generate six expressions, as in Table 2, to describe the relation of these three objects separately.

Table 2. The same group of ternary objects in different orders.

A	B	O	A	B	O	A	B	O
1	2	3	1	3	2	2	3	1
2	1	3	3	1	2	3	2	1

3.2. 4SIM Performance Analysis

This section discusses the performance of 4SIM and its ability to distinguish between different cases of ternary objects. Based on the definitions from the previous section, it is intuitively clear that when $L3$ or $L4$ intersects with the interior of the intermediate object, the intermediate object is debatably between the two objects, and there must be a value of “$1$” in the matrix. When the intermediate object is not between the two objects, there are only negative values in the matrix, and when the intermediate object is between the two objects, there are only positive values in the matrix. Therefore, this paper adopts the idea of “whether object O is between objects A and B” to categorize the spatial relation of ternary objects into three major groups:

i.

The first is when O is completely between A and B, i.e., $\forall i,j\in \left\{1, 2\right\}, W_{ij}=\{1, 2\}$.

ii.

The second is when O is partially between A and B, i.e., $\exists i,j\in \left\{\mathrm{1,2}\right\}, W_{ij}=0$.

iii.

The third is that O is not between A and B, i.e., $\forall i,j\in \left\{\mathrm{1,2}\right\}, W_{ij}=\{-1,-2\}$.

First, the first scenario is discussed. When O is situated completely between A and B, whereby the $area$ contains, covers, or is equal to O, 4SIM is capable of distinguishing the ternary spatial relations by determining how O meets the four boundaries of the $area$ and a total of 16 cases can be distinguished.

Next, for the second situation, O is partially situated between A and B, meaning that O intersects the $area$. The 4SIM can distinguish the ternary spatial relations by determining whether O meets the boundaries of $L1$ and $L2$ and intersects the boundaries of $L3$ and $L4$ in the $area$, and a total of 20 cases can be distinguished.

Finally, in the third situation, where O is not between A and B, meaning that O has met or is disjointed from the $area$, 4SIM distinguishes the ternary spatial relations by determining whether O meets the four boundaries in the $area$. A total of nine cases can be distinguished.

This finding reveals that the 4SIM model exhibits a superior capacity for differentiating and delineating spatial relations with greater precision.

4. 4SIM Implementation Methodology

4.1. Calculation of the Region Between A and B

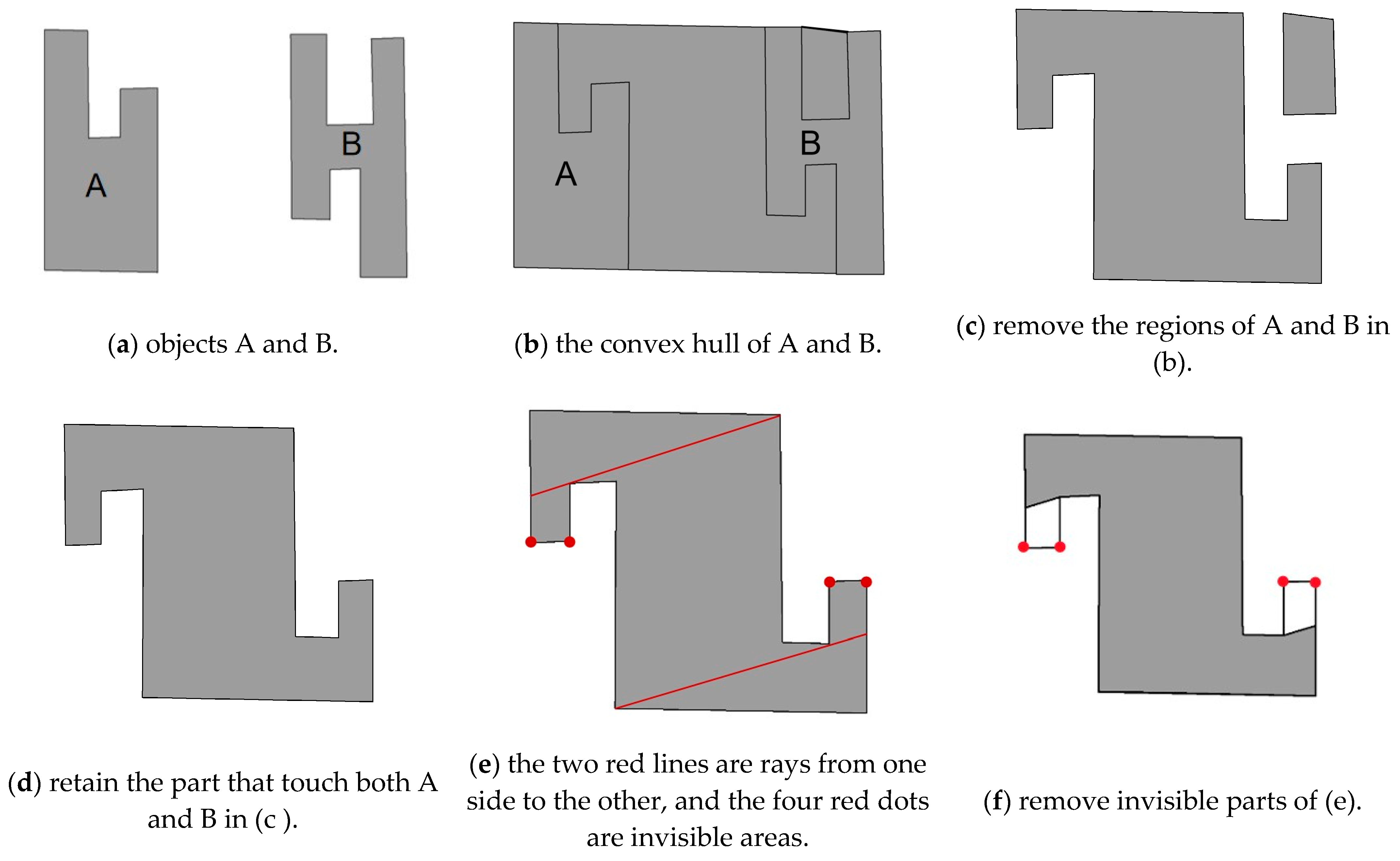
Determining the scope of the $area$ is a critical step in recognizing the ternary spatial relation “between”. The left and right objects in Figure 7a are denoted as A and B, respectively. The specific calculation process of the $area$ between them is as follows. First, find out the convex hull of A and B, as illustrated in Figure 7b. Subsequently, remove the regions of A and B themselves, as shown in Figure 7c. Finally, remove the parts that only touch A or only touch B, and retain the parts that touch both A and B. The area shown in Figure 7d is the $area$ between objects A and B that we are looking for. The calculation process can be found in Algorithm 1.

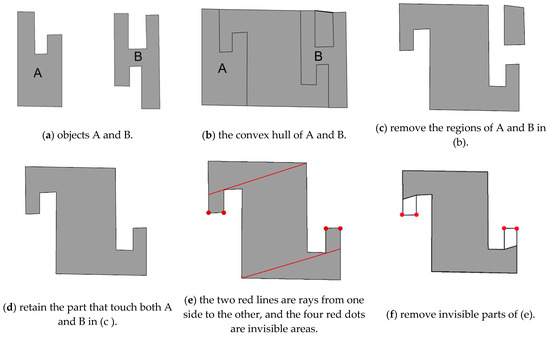
Figure 7. Specific steps for calculating the region between A and B.

As stated in Section 3, we do not consider the invisibility, which means that the invisible region remains. This is another difference between our solution and the existing research.

Section 2.3 explains the RIM principle, which mainly determines the region between two objects on both sides by emitting rays from one object to the other. The area where the rays cannot reach is the invisible region, as shown in Figure 7e. The four red dots are the invisible vertices. According to the literature [13], the invisible region is deleted, and Figure 7f shows the region between objects A and B retained after considering the visibility problem. However, in our opinion, the deleted region (the blank region in Figure 7e) is of great significance in practical applications such as map generalization and geographic simulation. For example, in map generalization, when performing merge operations, blank areas need to be filled to ensure the coherence and integrity of the map. In intelligent driving, the blank areas not only represent accessible areas, but may also contain potential parking areas, emergency avoidance areas, or temporary traffic diversion routes. These pieces of information are of great value for the path planning and decision-making systems of autonomous driving. Consequently, in this paper, the invisible region between A and B will be retained.

4.2. Identification of the Four Boundaries

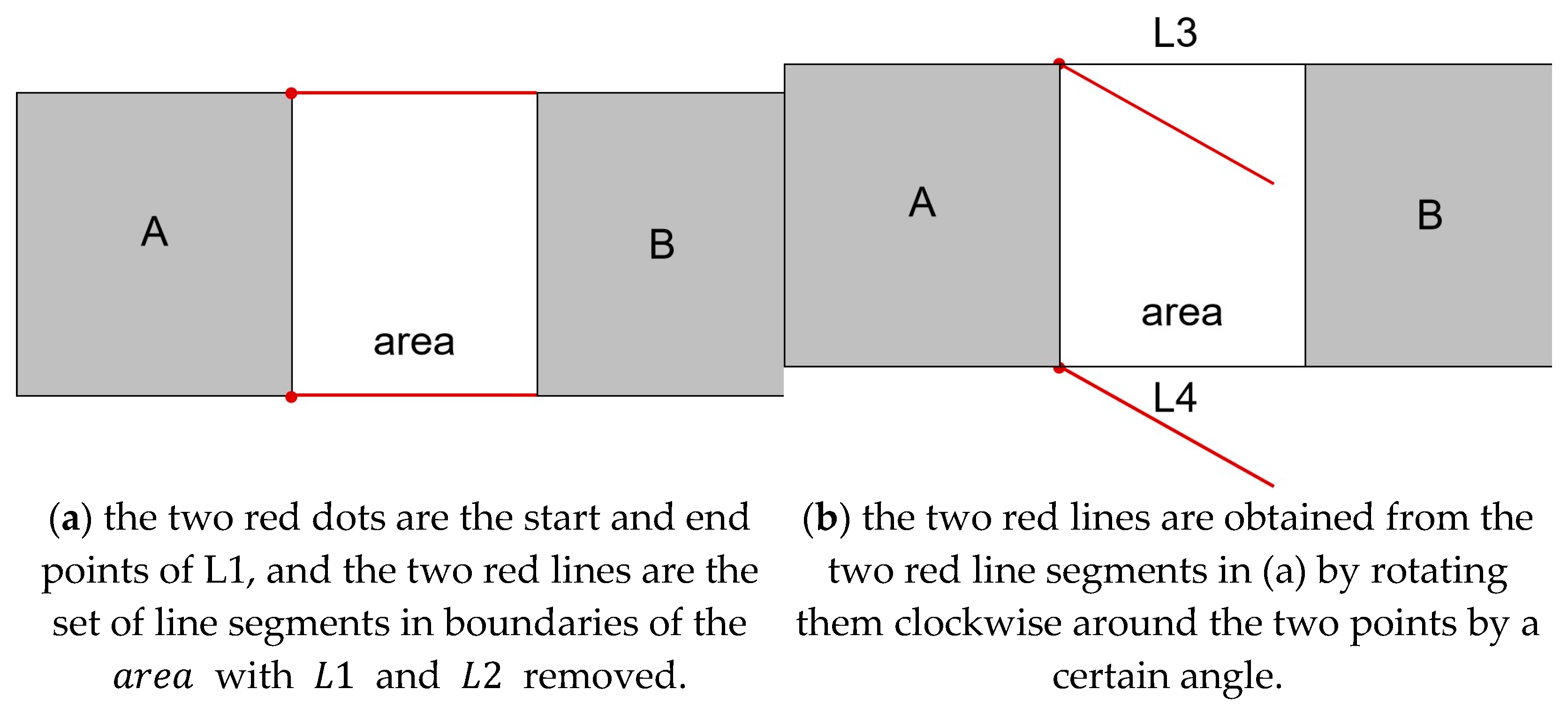
In the 4SIM matrix, the four boundaries of the $area$,$L1$, $L2$, $L3$, and $L4$, are of particular importance. According to the definition, $L1$ and $L2$ can be readily identified. $L1$ is the line segment that intersects A and $area$, and $L2$ is the line segment that intersects B and $area$. For $L3$ and $L4$, the following method is employed to ascertain their location: Firstly, find the starting and ending points of the $L1$ line segment, as shown in the two red endpoints in Figure 8a, and the line segment set of the $area$ region excluding $L1$ and $L2$, as shown in the two marked red line segments in Figure 8a. Secondly, rotate the set of line segments found in the previous step clockwise by an appropriate angle around the first and last points, respectively (in this paper, we only rotated them by $1°$), as shown in Figure 8b. Finally, judge whether the rotated line segment intersects with the $area$ or not. If it intersects with the $area$, this line segment is $L3$; otherwise, this line segment is $L4$. The calculation process can be found in Algorithm 1.

Algorithm 1. Calculation of the region between A and B, and L1, L2, L3, L4
# Step 1: Find the convex hull of A and B	1
convex_hull_ = convex_hull(A, B) ()	2
	3
# Step 2: Remove A and B’s regions	4
area = convex_hull_.difference(A).difference(B)	5
	6
# Step 3: Delete the part that touches only A or B, and keep the part that touches both A and B	7
for geom in list(area):	8
if geom.disjoint(A) or geom.disjoint(B):	9
area.remove(geom)	10
	11
# Step 4: Find L1 and L2	12
L1 = A.intersection(O)	13
L2 = B.intersection(O)	14
	15
# Step 5: Start and end of L1 line segment	16
start_point_L1, end_point_L1 = find_start_end_points(L1)	17
	18
# Step 6 Find the line segment set in area except L1 and L2	19
remaining_lines = area.boundary.difference(L1).difference(L2)	20
	21
# Step 7: Rotate the segment set clockwise around the starting point	22
rotated_lines = rotate_lines(remaining_lines, start_point_L1, 1)	23
	24
#Step 8: Determine whether the rotated line segment intersects the area	25
L3 = []	26
L4 = []	27
for line in rotated_lines:	28
if is_intersect(line, area):	29
L3.append(line)	30
else:	31
L4.append(line)	32

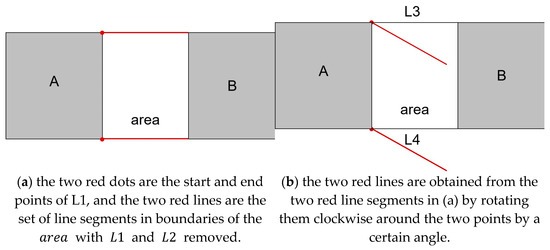
Figure 8. The steps to find the four boundaries of the $area$.

5. Comparative Experiment and Discussion

5.1. Combination of Ternary Buildings

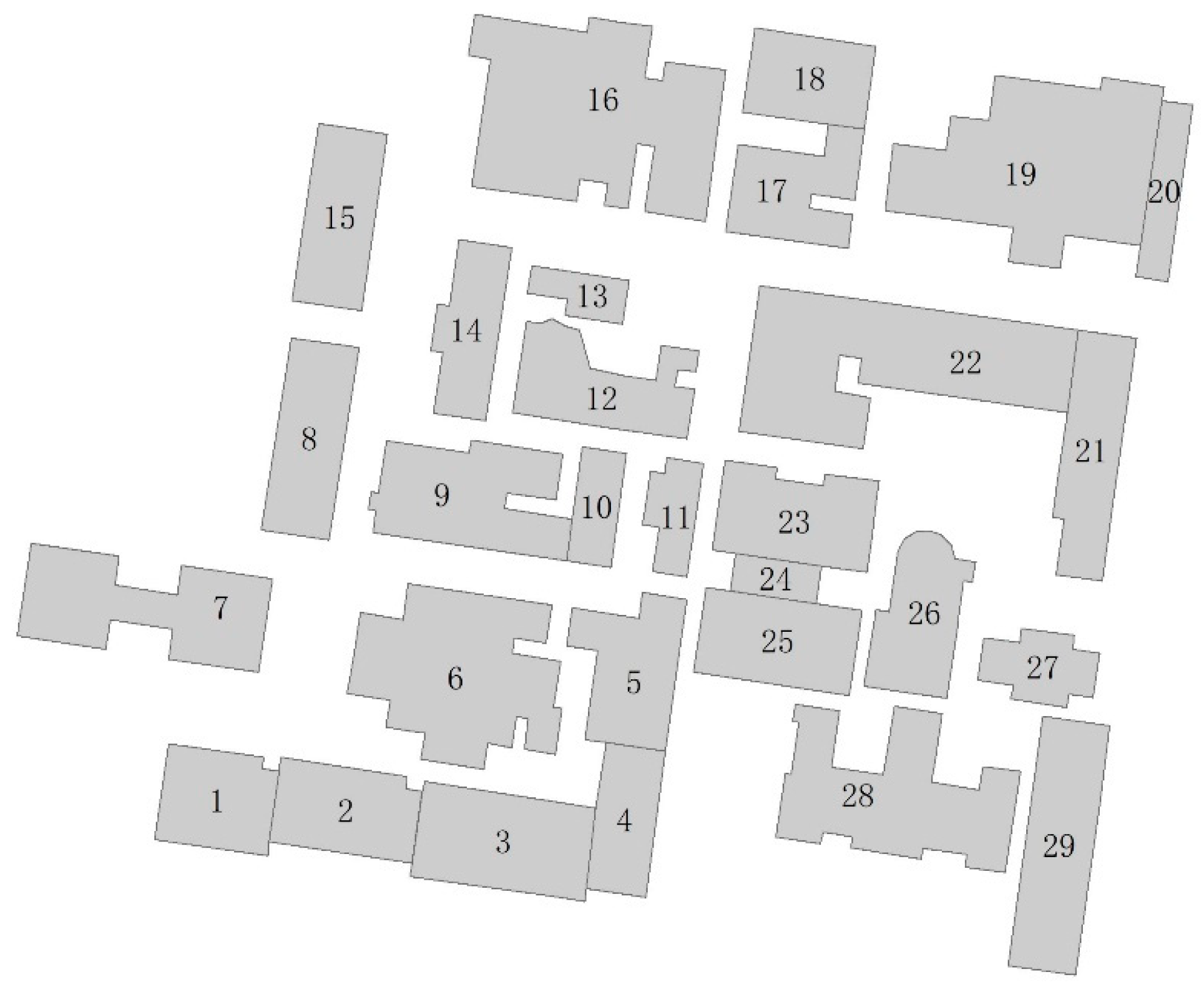
In this section, using the same data from RIM (e.g., Figure 9), the experimental data [13] are analyzed using the 4SIM method and compared with RIM. The experiment consists of 29 buildings, whose geometries are derived from OpenStreetMap (OSM) data. This group of buildings is located in the Parkville campus of the University of Melbourne, which is high densely and irregularly distributed and includes various types and functions of buildings, such as teaching buildings, libraries, laboratories, dormitories, etc.

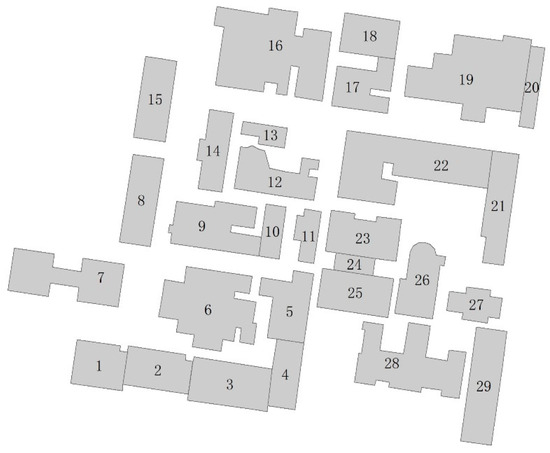
Figure 9. A set of 29 buildings belonging to the Parkville campus of the University of Melbourne for experimental data.

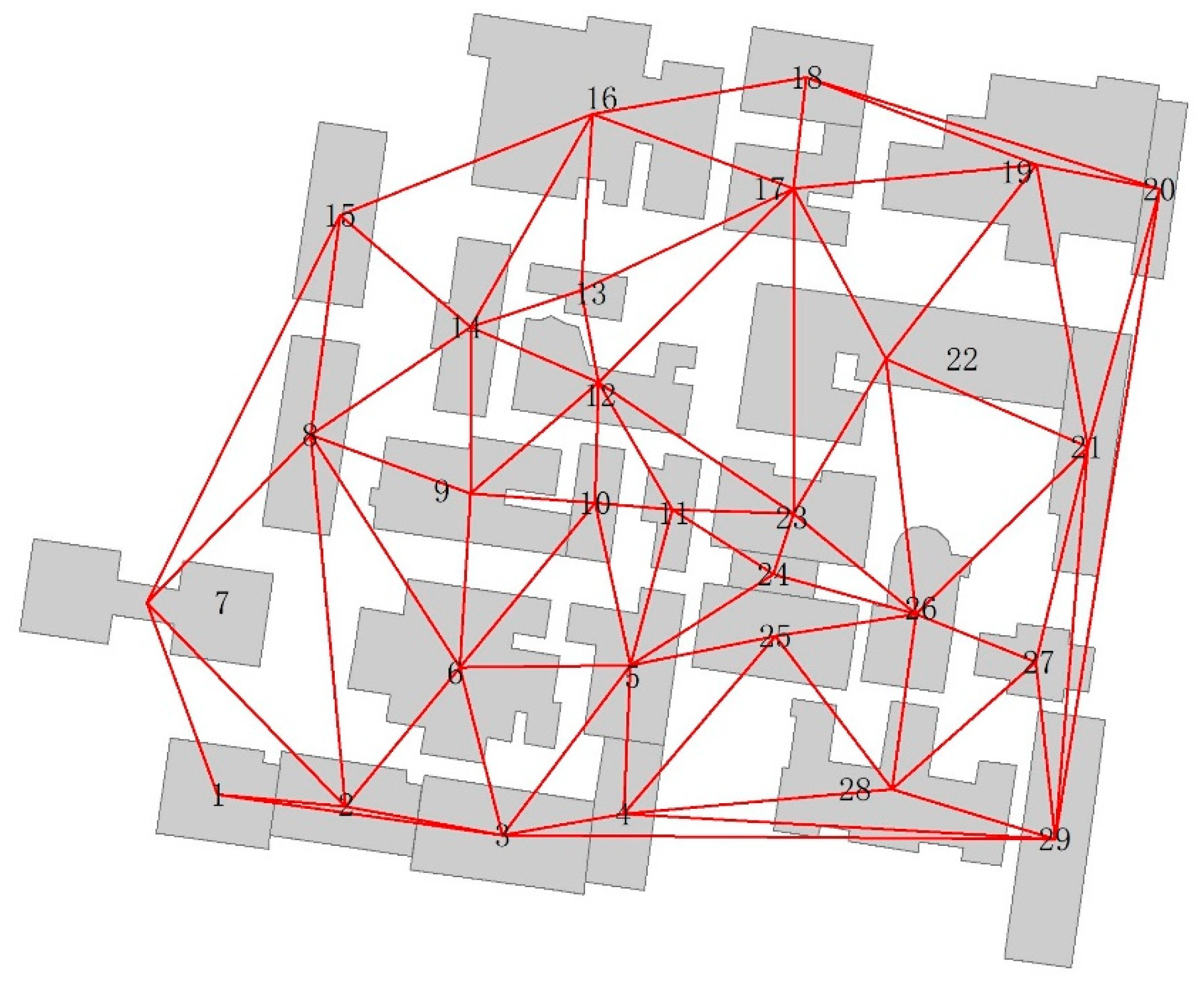
4SIM is a formal representation of a triplet of spatial objects. Therefore, the first step is to construct the triplet pairs. In this paper, the methodology employed is to pair buildings following the method in the literature [13], which first constructs a proximity graph of buildings using the Delaunay triangulation of building center points (see Figure 10). Subsequently, we selected a combination of three buildings that are connected by a path of length 2, where the direct connection path length between any two adjacent buildings is 1. The results in a total of 338 calculations.

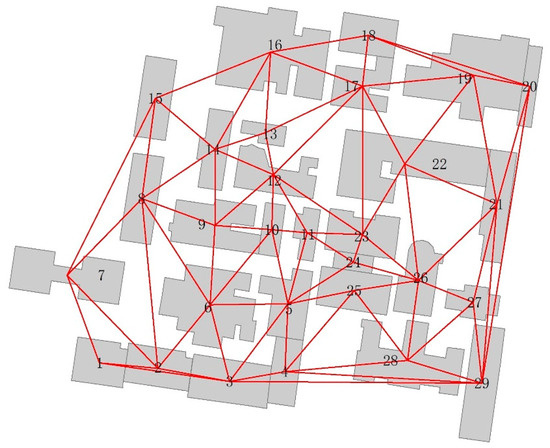
Figure 10. Delaunay triangles (red lines) between the centers of the 29 buildings from Figure 8.

5.2. Experiments

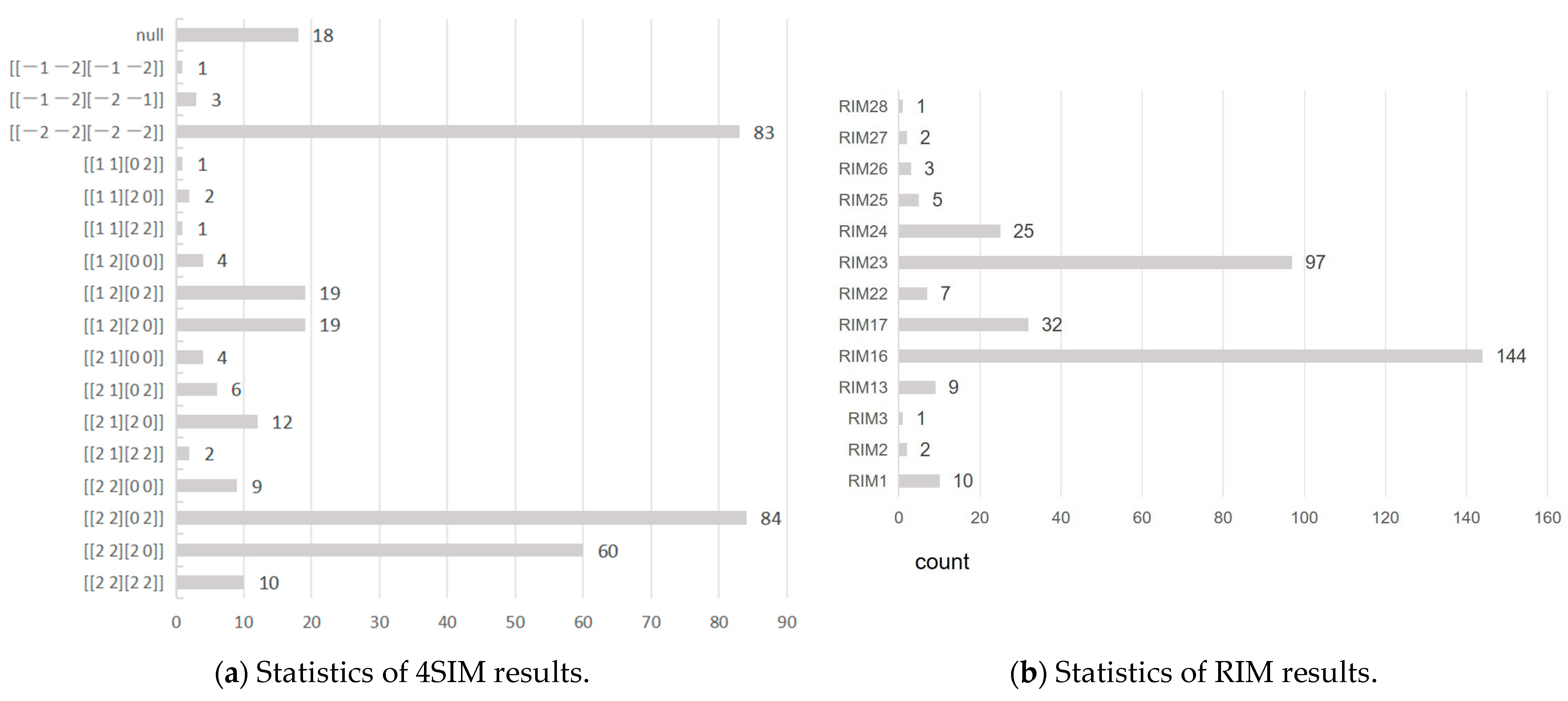
This section employs the ternary building pairs that were assembled in Section 5.1 as data and describes the spatial relations of the ternary buildings using 4SIM and RIM, respectively. The statistics of the results of the two methods are shown in Figure 11.

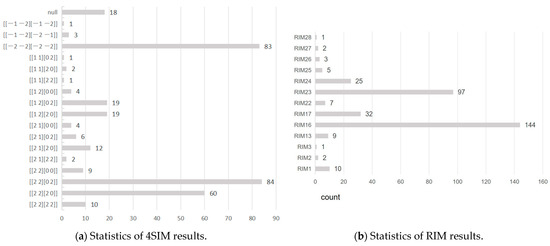
Figure 11. The 4SIM and RIM results statistics for 338 groups of ternary buildings.

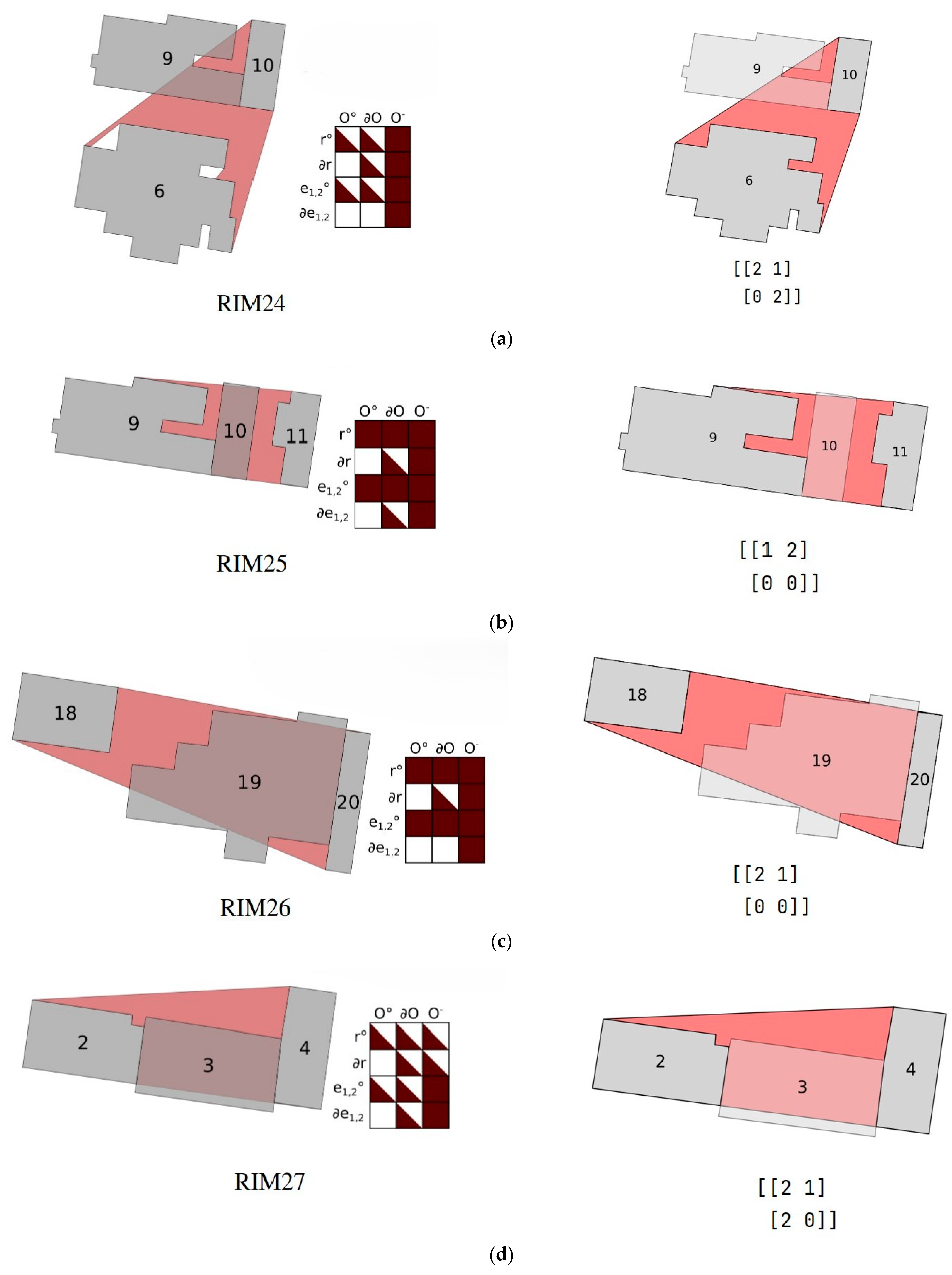
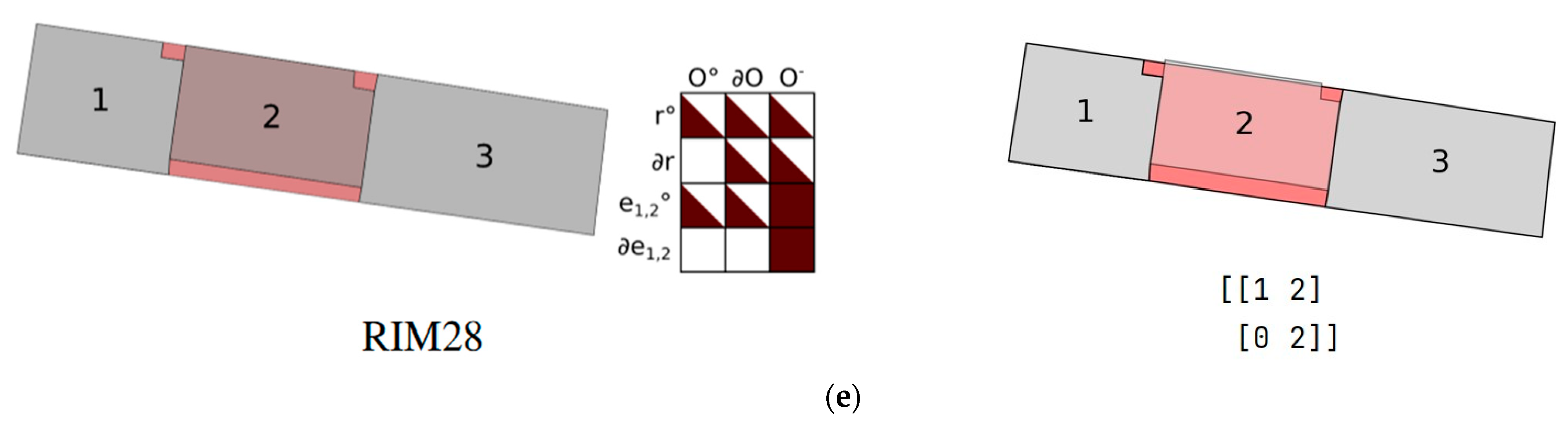
As illustrated in Figure 11a,b, the 4SIM recognition results total 18, whereas the RIM method identifies a total of 13, of which 8 are explicitly stated by RIM, while the remaining 5, including RIM24, RIM25, RIM26, RIM27, and RIM28, are forms not mentioned by RIM. Consequently, it is straightforward to see from the results that 4SIM is capable of describing any ternary buildings. In addition, a comparison of the 4SIM and RIM in Table 3 reveals that 4SIM, excluding the “$null$” value, exhibits a more specific and comprehensive descriptive ability than RIM. Additionally, 4SIM demonstrates slightly higher computing efficiency compared to RIM.

Table 3. Comparison of RIM and 4SIM results.

RIM	4SIM	338	$\mathrm{Excluding} \mathrm{“}null\mathrm{”}$
Runtime: 27.933 ms	Runtime: 23.925 ms
RIM1	$\left[\begin{array}{cc}2& 2\\ 2& 2\end{array}\right]$	10	O is completely between A and B
RIM2	$\left[\begin{array}{cc}2& 1\\ 2& 2\end{array}\right]$	2
RIM3	$\left[\begin{array}{cc}1& 1\\ 2& 2\end{array}\right]$	1
RIM13	$\left[\begin{array}{cc}2& 2\\ 0& 0\end{array}\right]$	9	O is partially between A and B
RIM16	$\left[\begin{array}{cc}2& 2\\ 0& 2\end{array}\right],\left[\begin{array}{cc}2& 2\\ 2& 0\end{array}\right]$	84 + 40 = 144
RIM17	$\left[\begin{array}{cc}1& 2\\ 0& 2\end{array}\right]$$,\left[\begin{array}{cc}1& 2\\ 2& 0\end{array}\right],\left[\begin{array}{cc}2& 1\\ 0& 2\end{array}\right],\left[\begin{array}{cc}2& 1\\ 2& 0\end{array}\right],null$	11 + 9 + 4 + 7 + 1 = 32
RIM22	$\left[\begin{array}{cc}-1& -2\\ -1& -2\end{array}\right],\left[\begin{array}{cc}-1& -2\\ -2& -1\end{array}\right],null$	3 + 1 + 3 = 7	O is not between A and B
RIM23	$\left[\begin{array}{cc}-2& -2\\ -2& -2\end{array}\right],null$	83 + 14 = 97
RIM24	$\left[\begin{array}{cc}1& 2\\ 0& 2\end{array}\right],\left[\begin{array}{cc}1& 2\\ 2& 0\end{array}\right],\left[\begin{array}{cc}2& 1\\ 0& 2\end{array}\right],\left[\begin{array}{cc}2& 1\\ 2& 0\end{array}\right]$	8 + 10 + 2 + 5 = 25	O is partially between A and B
RIM25	$\left[\begin{array}{cc}1& 2\\ 0& 0\end{array}\right]$$,\left[\begin{array}{cc}2& 1\\ 0& 0\end{array}\right]$	3 + 2 = 5
RIM26	$\left[\begin{array}{cc}1& 2\\ 0& 0\end{array}\right]$$,\left[\begin{array}{cc}2& 1\\ 0& 0\end{array}\right]$	1 + 2 = 3
RIM27	$\left[\begin{array}{cc}1& 1\\ 2& 0\end{array}\right]$	2
RIM28	$\left[\begin{array}{cc}1& 1\\ 0& 2\end{array}\right]$	1

5.3. Discussion and Analysis

(1)

Comparison of distinguishing ability with existing models

4SIM has been demonstrated to possess a superior capacity to RIMin the domain of ternary building description. Specifically, 4SIM was able to recognize 22 more situations than RIM in theory. Next, from the experimental results, when RIM recognizes buildings, it fails to recognize five situations not included in the theoretical mode. In contrast, 4SIM is able to describe them all, as illustrated in Figure 12. Finally, when describing ternary buildings, 4SIM results can directly show the topological relationship between two buildings in a ternary group, while RIM is described more vaguely in this aspect.

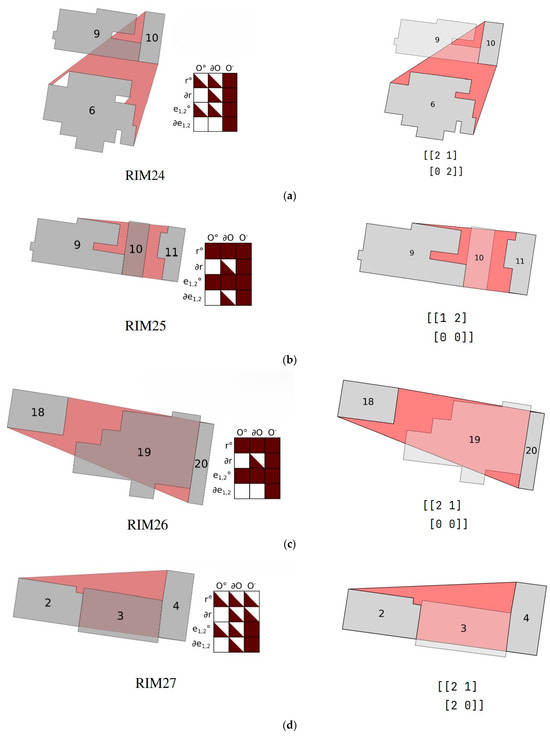
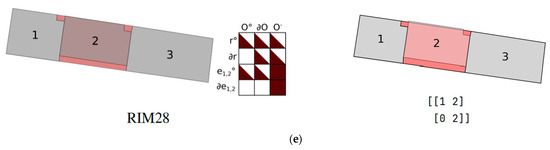
Figure 12. Five groups of cases not defined by RIM and the results of 4SIM representation of these cases.

(2)

Analysis of the “$null$” results

In Section 5.2, 4SIM has 18 sets of results with “$null$” values, indicating that building A is connected to building B in these sets. In accordance with the discussion in Section 3.1, the intermediate building can be replaced with either A or B to further analyze the spatial relations. Should the results persist in being “$null$”, then it means that these three buildings are connected two by two. For example, in Figure 10, buildings 1, 2, and 3 are labeled A, B, O and O, A, B, respectively, and 4SIM outputs the result as “$null$”, but when they are assumed to be A, O, B, respectively, as shown in the group of Figure 12e, the output result is $\left[\begin{array}{cc}1& 2\\ 0& 2\end{array}\right]$.

(3)

Description for spatial distribution of irregular buildings

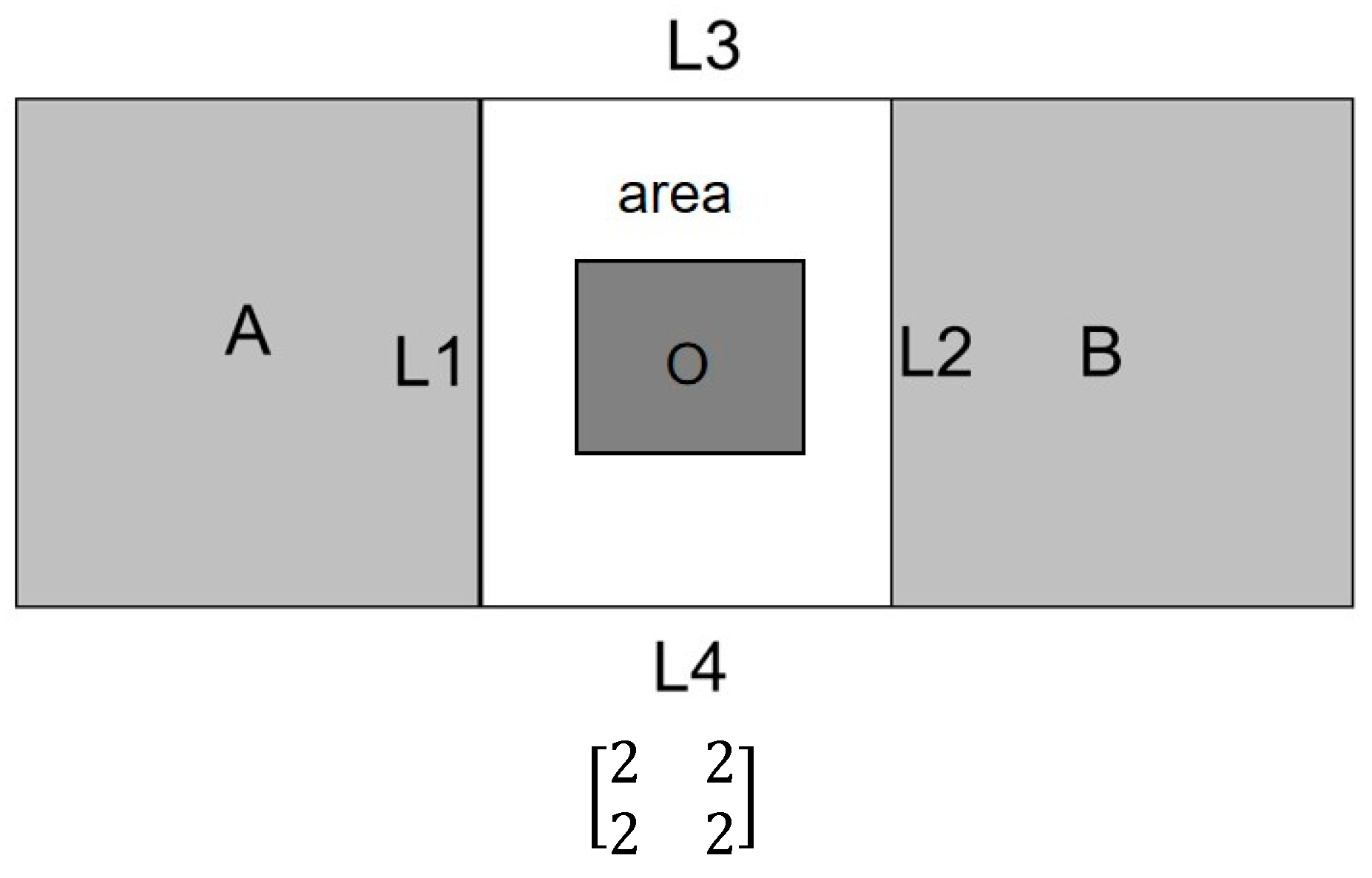
In the case of the irregular pattern buildings mentioned in Figure 1 in Section 1, the 4SIM formalizes the pattern as a matrix $\left[\begin{array}{cc}2& 2\\ 2& 0\end{array}\right]$. Thus, its spatial relation can be described as part O being between A and B (cf. Figure 13).

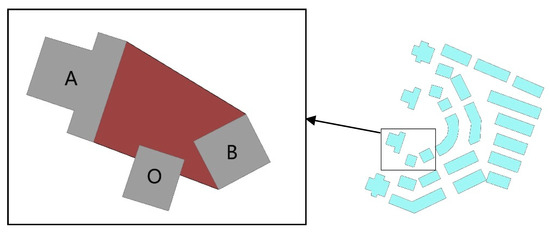
Figure 13. The 4SIM description for the irregular pattern buildings in Figure 1. The topological relations between O and $L1$, $L2$, $L3$ are separate, and the topological relation between O and $L4$ is intersected, to assist readers in understanding the matrix.

In summary, by comparing and analyzing the results of 4SIM and RIM in describing the relation between ternary buildings, we verified that 4SIM is better able to describe the spatial distribution between the vast majority of ternary buildings, and is able to describe the spatial relations between ternary objects in a more refined way.

6. Conclusions

This study explores the limitations of existing models in describing ternary spatial relations, providing a refined approach. RIM could not completely describe any ternary objects and lacks the detail required for accurate representation. Furthermore, certain ambiguities exist, such as the inability to discern the topological relation between the middle object and the objects on either side. In this paper, we propose a novel mode for spatial relations of ternary buildings, 4SIM, which models the spatial relations of ternary objects by describing the topological distances of the boundaries of the region between the middle object and the objects on both sides. The experimental results demonstrate that 4SIM is able to recognize the spatial relation of the vast majority of ternary building combinations. Moreover, the recognition outcomes vary from different viewpoints, which enhances spatial reasoning about ternary objects.

In the field of building pattern recognition, this paper aims to describe the combination of ternary buildings with irregular distribution patterns, and in the subsequent research, it is hoped that more irregularly distributed buildings can be combined into spatial relationships, thereby enabling their description and representation.

This paper demonstrates 4SIM with buildings (between regular faces), and the next step is to consider the use of 4SIM to describe the ternary spatial relationships between irregular faces and objects with fuzzy boundaries, such as islands. In addition, we discussed the robustness of the model in depth, and made a comprehensive comparison with other models, with a view to further expand its application potential in complex spatial relationship analysis. In addition, in future research, we hope to try to apply it to practical applications, such as considering the “between” relation in building map generalization, assisting in the calculation of spatial similarity relation in maps with the same scale, and in intelligent driving, where the model could be applied to represent vehicles in different lanes, helping autonomous vehicles monitor vehicles in adjacent lanes.