Adaptive Gaussian Mixture Models-Based Anomaly Detection for Under-Constrained Cable-Driven Parallel Robots

Abstract

Cable-driven parallel robots (CDPRs) are increasingly used for load manipulation tasks involving predefined toolpaths with intermediate stops. At each stop, where the platform maintains a fixed pose, and the motors keep the cables under tension, the system must evaluate whether it is safe to proceed by detecting anomalies that could compromise performance (e.g., wind gusts or cable impacts). This paper investigates whether anomalies can be detected using only motor torque data, without additional sensors. It introduces an adaptive unsupervised outlier detection algorithm based on Gaussian Mixture Models (GMMs) to identify anomalies from torque signals. The method starts with a brief calibration period—just a few seconds—during which a GMM is fit on known anomaly-free data. Real-time torque measurements are then evaluated using the Mahalanobis distance from the GMM, with statistically derived thresholds triggering anomaly flags. Model parameters are periodically updated using the latest segments identified as anomaly-free to adapt to changing conditions. Validation includes 14 long-duration test sessions simulating varied wind intensities. The proposed method achieves a 100% true positive rate and 95.4% average true negative rate, with 1-second detection latency. Comparative evaluation against power threshold and non-adaptive GMM methods indicates higher robustness to drift and environmental variation.

1. Introduction

Cable-driven parallel robots (CDPRs) are robotic systems where the end-effector’s position and orientation are controlled by adjusting the length of multiple cables, offering advantages in cost, performance, and adaptability [1]. Their structure, composed of cables and winches, enables larger workspaces and higher payload capacities compared to anthropomorphic robots [2]. Unlike other parallel robots like Delta or Stewart platforms, CDPRs are also more reconfigurable and capable of complex motions, making them ideal for applications that require extended workspaces and high load capacities [3,4].

However, their reliance on cables introduces a key limitation: cables can only operate under tension, not compression. As a result, stability depends on the specific setup of the systems. For instance, an eight-cable setup (four upper and four lower) provides precise control and robustness, while a four-cable configuration, though suitable for larger workspaces, is under-constrained and more prone to oscillations in the end-effector [5].

Research has explored CDPR applications in diverse fields such as 3D printing [6], rehabilitation [7], storage and retrieval systems [8], sports tracking devices [9], precision agriculture [10] and load manipulation [11,12]. Despite the aforementioned advantages, their industrial adoption remains limited [13,14]. The main barriers to widespread implementation are the scarcity of commercial solutions, with only a few available, such as RBOT9 and CRANEBOT [15,16], and challenges in meeting the industrial safety and operational standards required for seamless integration with industrial controllers.

Enhancing the safety could significantly boost CDPR adoption, but research has mainly focused on cable breakage and collisions. These kinds of solutions include adding passive auxiliary cables with clamping devices for redundancy [17] to reconfigurable architectures that actively relocate cable anchor points for task recovery after a cable failure [18,19], collision-management techniques that address external impacts with humans or the environment [20], and internal self-interference [21].

In addition, as stated, under-constrained CDPRs are more sensitive to external forces like wind, causing lateral disturbances that impact static positioning in pick-and-place tasks [22]. Accurate endpoint positioning is crucial, while trajectory errors during motion are more tolerable. Deviations of the end-effector due to external factors like wind or unintended operator contact are anomalies that do not lead to the expected and safe behavior [23]. These anomalies can compromise the grip quality or degrade outcomes in applications like laser inspection. Therefore, detecting these anomalies is the first step toward implementing actions to mitigate them.

Although machine learning, especially deep learning, has improved anomaly detection [24,25,26], many existing approaches remain highly specialized and still depend on extensive domain knowledge for effective deployment. Traditional methods like k-Nearest Neighbor, Decision Trees, or Discriminant Analysis have been applied to detect cable breakage or sensor failures in CDPRs [27], and Neural Networks have identified deviations from standard toolpaths [28]. Deep reinforcement learning has also been applied to improve position estimation in CDPRs under model uncertainty [29]. Despite recent advances, CDPRs still lack practical anomaly detection strategies that can learn on the fly, without pre-labeled anomalies, and remain robust to wind gusts.

We present an approach to detect unintended end-effector movements by analyzing anomalies in cable tensions without requiring additional external sensors or detailed environmental information. Our study focuses on conditions in which motion control maintains the robot’s pose while the motors remain powered and the motor brakes are switched off. These conditions occur, for instance, when the manipulator remains at rest while performing a picking or placing operation with its tool, as in typical pick-and-place tasks. We investigate whether disturbances from wind or other external forces can be detected solely through motor torque measurements based on servo amplifier current consumption. In this way, any detected anomalies can prompt the postponement of subsequent operations until the anomaly is resolved. This approach enhances safety and provides redundancy for critical decisions. From an implementation perspective, cable tension is inferred directly from motor torques, avoiding the extra hardware, wiring, and calibration effort required by cable-mounted load cells as proposed in [30]. Moreover, in this operating regime, the system is effectively static; therefore, we can treat cable-tension observations—estimated from motor torques—as samples from a stationary distribution and model this density with a Gaussian Mixture Model (GMM) —see details in Section 4.2. Compared with kernel or deep density estimators, a GMM captures multimodality with few parameters, yields interpretable likelihood-based anomaly scores, and retrains quickly with data-driven model order—advantages we examine empirically in Section 5.1.

The rest of this paper is organized as follows. Section 2 theoretically describes the stability of a CDPR. Section 3 details the experimental setup used and analyzes the stability conditions that allow the application of the anomaly detection method described in Section 4 for under-constrained CDPRs. Section 5 presents the results obtained from the various rounds of experiments. Finally, Section 6 summarizes the conclusions. All sources and CSV data files that support the findings of this study are openly available in the Data Availability section at the end of this article.

2. Static Stability of Under-Constrained Cable-Driven Parallel Robots

A mandatory condition to apply the outlier detection within our scope is verifying that the operating point is stable. Otherwise, an external perturbation may drive the system to new operation equilibria, making static-density models like GMM ill-posed: likelihood changes may confound genuine external anomalies with self-adjustments of the CDPR. In contrast, under a stable operating point, the nominal distribution is stationary (or at least slow-paced changing); so, deviations in likelihood can be attributed to external disturbances rather than internal readjustments, enabling consistent thresholds and low false positives/negatives.

Stability describes the response of a mechanical system to a disturbance and is a fundamental property in the design and operation of CDPRs, particularly for under-constrained systems like our four-cable experimental system (see Section 3), where gravity significantly influences performance [31]. A configuration is considered stable when a slight change in the cable forces does not permanently displace the platform or prevent it from returning to its original position once the disturbance disappears. Previous research has addressed the stability of CDPRs through analytical methods that involve the use of Lagrange multipliers and the computation of the Hessian matrix, as in [32,33], respectively. Specifically, following these works, stability is assured when the reduced Hessian ($H_{\mathrm{r}}$) is positive definite.

We define an equilibrium configuration as any pose in which the cable forces exactly counter-balance the external load (only gravity on the platform’s center of mass is considered) so that the resultant force and moment on the platform are both zero. When, in addition, the platform is at rest, the configuration becomes a static equilibrium. This study focuses exclusively on such static equilibrium and examines whether the CDPR remain stable under infinitesimal tension perturbations, a property hereafter referred to as static stability.

The CDPR model consists of a mobile platform connected to the base by n inelastic massless cables, as shown in Figure 1. $O_{\mathrm{xyz}}$ represents the system’s coordinate frame, and $P_{\mathrm{xyz}}$ is the mobile coordinate frame of the platform. The position of the platform is defined by the position vector p and the rotation matrix R, parameterized by Euler angles $\epsilon ={[\phi ,\psi ,\theta ]}^{\mathrm{T}}$, with generalized coordinates $q={[p^{\mathrm{T}},{\epsilon }^{\mathrm{T}}]}^{\mathrm{T}}$. $B_i$ denotes the distal anchor points where the cables originate, while $A_i$ represent the proximal anchor points where the cables attach to the mobile platform. The i-th cable is represented by vector $l_i$ (Equation (1)).

$$l_i=B_i-A_i=b_i-p-r_i=b_i-p-R{a}_i$$

(1)

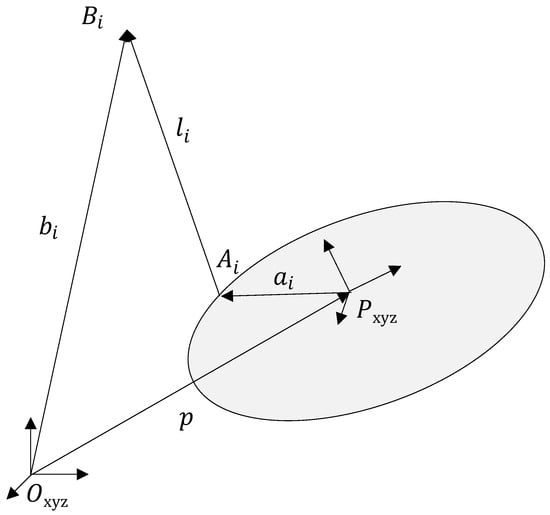
Figure 1. Closed loop diagram of a cable in a CDPR.

To simplify the model, we neglect the influence of pulley transmission on platform accelerations, cable tensions, and workspace boundaries. This assumption is supported by prior studies showing that omitting pulley effects reduces the workspace volume by approximately 1% when pulley radii are around 2.5% of the robot’s shortest edge [34]. Although pulley kinematics may temporarily amplify platform acceleration by up to 50% in worst-case scenarios [35], such transient effects are typically mitigated by the inner control loops of the drives and do not significantly impact the steady-state behavior under analysis.

Using the notation introduced by [32], the static stability condition reads

$$\sum _{i=1}^n{\displaystyle \frac{{\tau }_i}{\parallel l_i\parallel }}{\$}_i+Q{\$}_e=0,{\tau }_i\ge 0,i=1,\dots ,n,$$

(2)

where $({\tau }_i/\parallel l_i\parallel ){\$}_i$ is the force applied to the i-th cable, and $Q{\$}_e$ is the external wrench.

Under this static stability assumption, friction dissipates kinetic energy, leading the platform to a state of equilibrium over time. This result stems from the Lagrangian function $\mathcal{L}$, which relates the kinetic and potential energy to the system’s kinematics and dynamics. Following the criterion in [32], the reduced Hessian $H_r$ of $\mathcal{L}$ must be positive definite for the equilibrium defined in Equation (2). Its expression is

$$H_r=N_p^{\mathrm{T}}{H}_p{N}_p$$

(3)

$$H_p=\sum _{i=1}^n{\displaystyle \frac{{\tau }_i}{\parallel l_i\parallel }}\left[\begin{array}{cc}\mathrm{I}& -{\tilde{r}}_i\\ {\tilde{r}}_i& {\displaystyle \frac{1}{2}}\left({\tilde{r}}_i\tilde{p}-{\tilde{r}}_i{\tilde{b}}_i+\tilde{p}{\tilde{r}}_i-{\tilde{b}}_i{\tilde{r}}_i\right)\end{array}\right]$$

(4)

$$J_p=\left[\begin{array}{cc}{l}_1^{\mathrm{T}}& {(r_1\times l_1)}^{\mathrm{T}}\\ ⋮& ⋮\\ l_n^{\mathrm{T}}& {(r_n\times l_n)}^{\mathrm{T}}\end{array}\right],$$

(5)

where $N_p$ denotes the kernel (or null space) of the homomorphism $J_p$ (Equation (5)) and $\tilde{r}$ is the skew-symmetric matrix of dimension n. This methodology will be used in Section 3 to validate the static stability of the CDPR in the pose of the experiment.

3. Experimental Setup

An experimental setup was designed to evaluate the anomaly-detection system (detailed in Section 4) through controlled experiments in which disturbances simulate external forces and environmental interference similar to those in actual facilities. The setup, shown in Figure 2a, consists of a 4-cable CDPR and a fan with four adjustable strength levels (0 for off to 3 for maximum) to simulate external outliers (item 4 in Figure 2a). A tri-color beacon (item 6 in Figure 2a) provides visual feedback of the current fan setting in the recorded images, as shown in the center of Figure 2b.

Figure 2. Experimental setup for CDPR testing under wind disturbances. (a) Photograph of the experiment. (b) Capture of the video recorded during the tests with the timestamp data.

The mechanical prototype of the CDPR comprised several components. The dimensions of the structure are 860 × 1420 (length and width, respectively) at a height of 1600 mm and it utilizes aluminum profiles with a 40 × 40 mm cross section. At the extreme ends of this structure are the polyurethane pulleys with a 25 mm radius. The cables are made of Dyneema SK75 with a diameter of 1.5 mm, while the winches, fabricated from PLA material, have a radius of 45 mm. The aluminum end-effector measures $66\times 114\times 18$ mm and weighs $0.30$ kg. To increase its effective surface area and enhance its exposure to airflow, a $195\times 195\times 1$ mm aluminum sheet is attached as a “sail”, adding $0.12$ kg. In addition, a $1.00$ kg weight is suspended from the platform to ensure sufficient cable tension, and the coupling components between these elements contribute an additional $0.17$ kg. Overall, the end-effector assembly has a total mass of $1.59$ kg.

Inside the controller, kinematics, trajectory generation, and control structures are implemented in Structured Text (IEC 61131-3 [36]) under the TwinCAT 3 runtime [37], with motor control compliant with PLCopen Motion Control standards [38]. Torque and position data are forwarded over EtherCAT to a digital I/O card and then to four EL7211 servo drives. Each servo drive powers an AM8112 servomotor that reels the cables onto the winch (item 3 in Figure 2a).

The signal-and-data flow, used for the operation of the CDPR, is detailed in the architecture diagram of Figure 3. A script running on a PC launches each trial, issues starting commands to the Beckhoff CX5130 industrial controller (item 2 in Figure 2a), and receives a continuous stream of internal variables (cable tensions, platform position, and timestamps). The script also opens a data file for the incoming motor torque stream and starts recording video footage from the Intel RealSense depth camera (item 1 in Figure 2a). Both video and data file are timestamped for synchronization purposes. A view from the recorded video is provided in Figure 2b.

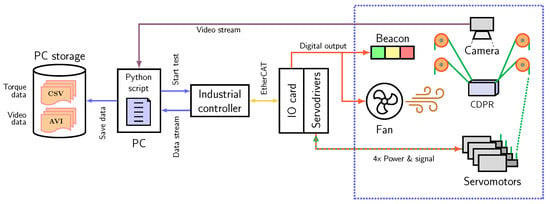
Figure 3. Signal schematic and component interaction for data acquisition and control of the CDPR under external disturbances.

Study of Static Stability for the 4-Cable CDPR

The stability study presented next for our CDPR is intended to confirm that the anomaly-detection system can be applied to this model.

The geometric configuration used in Equations (4) and (5) is defined by the distal anchor points $B_1={[-0.71,-0.43,1.60]}^{\mathrm{T}}$, $B_2={[0.71,-0.43,1.60]}^{\mathrm{T}}$, $B_3={[0.71,0.43,1.60]}^{\mathrm{T}}$, and $B_4={[-0.71,0.43,1.60]}^{\mathrm{T}}$ m, together with the proximal anchor points on the platform $A_1={[-0.06,-0.03,0]}^{\mathrm{T}}$, $A_2={[0.06,-0.03,0]}^{\mathrm{T}}$, $A_3={[0.06,0.03,0]}^{\mathrm{T}}$, and $A_4={[-0.06,0.03,0]}^{\mathrm{T}}$ m. The position and orientation of the end-effector are $\mathit{p}$ = ${\left[000.70\right]}^{\mathrm{T}}$ m and $\epsilon$ = ${\left[000\right]}^T$ rad, respectively. The cable vectors $l_i$ are $l_1$ = ${[-0.65-0.400.90]}^{\mathrm{T}}$, $l_2$ = ${[0.65-0.400.90]}^{\mathrm{T}}$, $l_3$ = ${\left[0.650.400.90\right]}^{\mathrm{T}}$, and $l_4$ = ${[-0.650.400.90]}^{\mathrm{T}}$ m. All cables have a length of 1.18 m. The cable tensions are $\tau$ = $\left[15.8911.1915.2012.57\right]$ N. All these data are obtained directly from the prototype, under the conditions of the experiments in Section 5. Evaluating $H_r$ in Equation (3) leads to

$$H_r=N_p^{\mathrm{T}}{H}_p{N}_p=\left[\begin{array}{cc}2.15& -0.15\\ -0.15& 0.91\end{array}\right].$$

(6)

Since $H_r$ is symmetric and has positive eigenvalues (2.17 and 0.89), it is positive definite, confirming that the CDPR is statically stable at the pose $q(p,\epsilon )$. Consequently, any small external disturbance produces only a temporary displacement: restoring forces bring the platform back to its equilibrium position as kinetic energy dissipates.

In addition to this experimental pose, three additional static configurations were evaluated within the workspace of the original prototype during the preliminary testing stage. These configurations were selected to represent different regions of the reachable volume, including non-symmetric postures. The corresponding cable lengths, cable tensions, and the projected stiffness matrix $H_r$ were computed for each case using data directly measured on the prototype. The numerical values are reported in Table 1. In all tests, $H_r$ resulted positive definite, confirming stable static equilibrium consistent with the theoretical stability analysis presented in Section 2.

In conclusion, an outlier discriminator should theoretically be able to identify anomalies, since the CDPR is in a statically stable condition. Since the additional tested poses were also confirmed to be statically stable, we selected the pose (p = ${\left[000.7\right]}^{\mathrm{T}}$ m) for the experiments in Section 5. The next section provides a detailed explanation of the anomaly detection algorithm developed in this study.

Table 1. Static stability measurements of the CDPR in three experimental positions. The table reports the cable lengths, cable tensions, the projected stiffness matrix $H_r$, and the corresponding eigenvalues.

Position (X,Y,Z) [m]	Cable Lengths l [m]	Cable Tensions $\mathit{\tau }$ [N]	${\mathit{H}}_{\mathit{r}}$	Eigenvalues
(0.02, −0.14, 0.73)	(1.10, 1.08, 1.24, 1.25)	(17.64, 15.93, 14.87, 8.82)	$\left[\begin{array}{cc}2.27& 0.17\\ 0.17& 0.91\end{array}\right]$	(2.29, 0.89)
(−0.05, −0.01, 0.82)	(1.07, 1.11, 1.11, 1.08)	(22.09, 6.70, 19.14, 10.21)	$\left[\begin{array}{cc}2.39& 0.53\\ 0.53& 0.98\end{array}\right]$	(2.56, 0.81)
(0.11, 0.12, 0.62)	(1.35, 1.28, 1.15, 1.22)	(9.62, 14.18, 19.50, 10.64)	$\left[\begin{array}{cc}1.99& -0.04\\ -0.04& 0.88\end{array}\right]$	(1.99, 0.88)

Table 1. Static stability measurements of the CDPR in three experimental positions. The table reports the cable lengths, cable tensions, the projected stiffness matrix $H_r$, and the corresponding eigenvalues.

Position (X,Y,Z) [m]	Cable Lengths l [m]	Cable Tensions $\mathit{\tau }$ [N]	${\mathit{H}}_{\mathit{r}}$	Eigenvalues
(0.02, −0.14, 0.73)	(1.10, 1.08, 1.24, 1.25)	(17.64, 15.93, 14.87, 8.82)	$\left[\begin{array}{cc}2.27& 0.17\\ 0.17& 0.91\end{array}\right]$	(2.29, 0.89)
(−0.05, −0.01, 0.82)	(1.07, 1.11, 1.11, 1.08)	(22.09, 6.70, 19.14, 10.21)	$\left[\begin{array}{cc}2.39& 0.53\\ 0.53& 0.98\end{array}\right]$	(2.56, 0.81)
(0.11, 0.12, 0.62)	(1.35, 1.28, 1.15, 1.22)	(9.62, 14.18, 19.50, 10.64)	$\left[\begin{array}{cc}1.99& -0.04\\ -0.04& 0.88\end{array}\right]$	(1.99, 0.88)

4. Anomaly Detection

The general goal of this research is to detect anomalies using the available CDPR state information. As discussed in Section 2, the state in an under-constrained CDPR comprises cable lengths and motor torques. When the platform is at rest, cable lengths define the position of the end-effector, but external forces can still alter the state of the CDPR without altering the lengths, instead modifying only the cable tensions. Consequently, our algorithm relies solely on motor torque data.

An initial approach to anomaly detection could be setting a threshold for the instantaneous detected power. However, this would underperform due to the noisy nature of the data. For example, in Figure 4, the moving-average 2-norm of the torque vector at each time instant is shown for two trials. The first one (Figure 4a) consisted of 10 h without wind gusts (anomalies), followed by 2 h with wind gusts every 10 min. The second one (Figure 4b) consisted of 12 h during which there were 10 min wind gust anomalies every 10 min.

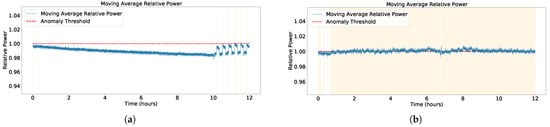
Figure 4. Relative power series for two experiments: (a) rest and gust cycle test; (b) gust test.

As can be seen, the anomalies can be hidden within the noise of the signal itself (Figure 4b). Even when more discernible, they may still fall below the detection threshold determined during calibration (Figure 4a), due to temporal drift and the small offset from the regular signal. This drift in the data is not attributable to a stability problem but to external changes such as temperature variations. Notably, these drifts are smooth over time, suggesting that it should be possible to detect and adapt to them.

Based on these observations, it is desirable to use a method that is less affected by noise, achieves a greater level of distinction when an outlier occurs, and is capable of correcting the model in the presence of temporal drifts. To this end, we have proposed a model based on the distance between new data and the CDPR model under stable conditions, using a multivariate GMM. The main stages in the operation of our algorithm are shown in Figure 5 and summarized as follows:

• Data acquisition. At the beginning of an operation with the CDPR, baseline data are gathered while the platform is at rest and are used to calibrate the model for subsequent idle periods.
• Model generation. A multivariate GMM is fit to the calibration data.
• Anomaly detection. New data are compared against the GMM model using the Mahalanobis distance to the cluster centroids. When this distance exceeds the threshold, an anomaly is declared.
• Model update. To handle observed data drifts, we update our model if a significant deviation from the data is found but it is still below the threshold.

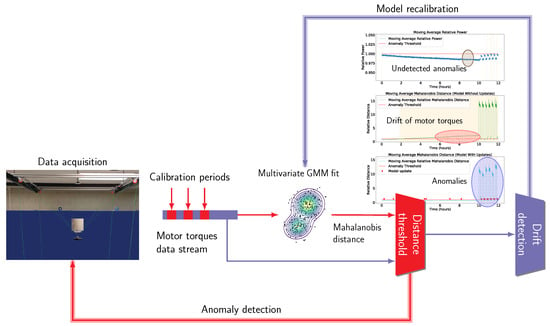
Figure 5. Model overview showing the main stages and the procedures involved in the data processing.

The next subsections describe these steps in depth.

4.1. Data Acquisition

Torque data are read sequentially from each of the n motors at each sampling instant j as an n-dimensional tuple ${\tau }^j$. At each processing step, these data are grouped into sets of M samples. That is, at processing instant j, the data $x^j$ are comprised of $x^j$=$\{{\tau }^j,\dots ,{\tau }^{j+M-1}\}$; thus, $x^j$ is $(n\times M)$ dimensional.

The first C points $\{x^1,\dots ,x^C\}$ are used for calibration. They correspond to the data recorded during the idle period at the beginning of the experimental session, after the motors have reached their steady temperature regime.

4.2. Model Generation

Given the C calibration points and setting the number of clusters to K, the GMM model parameters (means ${\mu }_k$ and covariances ${\Sigma }_k$, for k = $1,\dots ,K$) are fitted using the well-known Expectation-Maximization (EM) algorithm (e.g., see [39], Sect. 9.2.2) implemented in Python (version 3.7.9) using the scikit-learn library (version 0.23.2) through the GaussianMixture class. The number of clusters K is selected as the one minimizing the Bayesian Information Criterion (BIC) for the model fit, which is commonly used in models aimed at anomaly detection (see [39], Sects. 1.3 and 4.4.1).

4.3. Anomaly Detection

Once the model is fit, we can compute the distance from a new point x to the GMM model using the Mahalanobis distance. This is a common measure of the novelty of a point versus a (multi-)clustered dataset, which we assume to exist since the conditions are deemed as statically stable during the calibration phase (as studied in Section 3). Similar approaches for the analysis of outliers in data series have been successfully applied in other domains [40,41,42]. In a multi-clustered framework, the distance to the k-th cluster centroid is

$$d_k\left(x\right)={\left[{(x-{\mu }_k)}^{\mathrm{T}}\sum _k^{-1}(x-{\mu }_k)\right]}^{{\displaystyle \frac{1}{2}}};$$

(7)

thus, the distance from point x to the GMM is defined as the distance to the nearest cluster:

$$d\left(x\right)=\underset{k=1,\dots ,K}{min}{d}_k\left(x\right).$$

(8)

Once the distance criterion is defined, we can establish a threshold value for new data as the maximum distance reached during the calibration period, i.e.,

$$d_{\mathrm{th}}=\underset{j=1,\dots ,C-M}{max}d\left(x^j\right).$$

(9)

During data processing, the distance to new points is evaluated, and if it exceeds the established threshold $d_{\mathrm{th}}$ the region is considered as an outlier. To avoid false positives and areas where the anomaly is detected intermittently, moving-average distances are obtained over a sliding window of size S and compared to the threshold. Increasing S provides a more reliable criterion for declaring anomalies and avoiding false positives, although the detection of true positives may be slightly delayed. A balanced value for S is around 100 samples, which allows detection in approximately 1 s (for a data rate of 100 samples/s), suitable for real-time CDPR operation. All scripts used for the implementation of the outlier detector in the CDPR setup are accessible via GitHub at: https://github.com/javiervales/cdpr (accessed on 4 November 2025).

4.4. Model Update

During the experimental phase, data drift was observed in torque measurements in many of the long running tests. As previously mentioned, this may be due to external variations like temperature or humidity, as well as internal effects related to the motors. For example, this drift is clearly noticeable in Figure 6a and can cause, as it does in that case, normal regions to be erroneously treated as anomalies. Such misclassifications can be seen in the intermediate subplot of Figure 6a.

Figure 6. Relative power series and Mahalanobis distances for experiments (expanding Figure 4). (a) Experiment #12. (b) Experiment #4 (see Table 2).

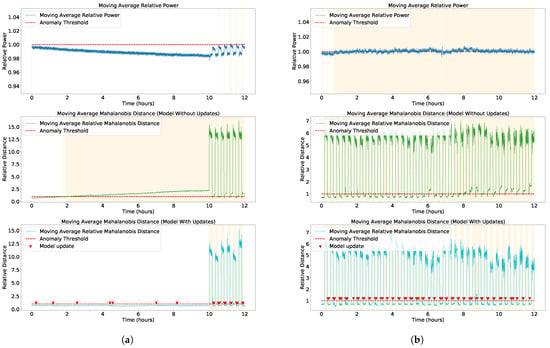
To avoid this problem, we introduced the following change: the algorithm recalculates the GMM model when the mean distance of the sliding window of new points exceeds $(1-\gamma )\times 100$% of the threshold but is less than 100% of it, being $\gamma$ a model hyperparameter with a nominal value of $0.25$. A distance in this range is strong evidence that the GMM model has changed slightly and should be readapted. The model is updated with the last C anomaly-free registered samples. The output of this method is shown in the bottom subfigures of Figure 6. Now, it correctly detects the zones with outliers through drift correction. The instances when there has been a model update are indicated with red inverted triangular marks in Figure 6.

5. Experimental Results and Discussion

During the tests, the CDPR remained in a stable position with consistent airflow always impacting it from the same direction when an anomaly takes place. The end-effector position was fixed at coordinates (0, 0, 700) mm. It is important to note that all tests were conducted only after the motors reached a stable operating temperature. The experiments were carried out in a laboratory testbed with the temperature and humidity controlled at approximately 20 ^oC and 75%, respectively. For each test, motor torques (as proxies for cable tensions) are timestamped and saved at a rate of 100 samples/s.

The tests conducted are as follows:

• Gust test (Type 1): The fan alternated between being off and operating at the selected wind strength for a given period of time (usually 10 min). These tests established a baseline for the anomaly detection algorithm, enabling it to accurately classify the presence or absence of wind.
• Rest and gust cycle test (Type 2): Following a prolonged resting period (fan off) of several hours, the system underwent 2 h of short gust sessions with 10 min on–off cycles. These tests evaluated the algorithm’s ability to handle motor torque drifts, defined as the gradual variation in delivered torque that arises when the motor current changes over time.
• Random wind disturbance test (Type 3): After an initial resting period, variable disturbances were applied, varying in strength (levels 0 to 3) and duration (1 to 20 min). These tests are aimed to assess the algorithm’s ability to detect outliers under dynamic wind conditions.

This section describes the results obtained from applying the anomaly detection method in the experimental testbeds. The primary objectives of the experimental phase were threefold:

• Validate improved strategies for anomaly detection.
• Study the phenomenon of temporal drift and how it affects anomaly detection.
• Establish parameterizations that provide robustness in decision-making while allowing the algorithms to operate in real time. A target detection time of 1 s has been considered.

A total of 14 experiments were performed. Table 2 summarizes the configuration and results of each experiment, and Figure 6 showcases the results for three different methods:

• Power method: a threshold procedure applied to the moving average of the torque power signal; as in the distance method, the threshold is determined as the maximum obtained during the calibration phase.
• Distance method without GMM updates: the distance method described in the previous section, applied without updating the GMM.
• Distance method with GMM updates: the same distance method, but with GMM model updates incorporated.

Table 2. Percentage of true positives (TP) and true negatives (TN). Tests last 12 h unless noted.

		Power Method		Distance Method (No Updates)		Distance Method (Updates)
Test	Description	TP [%]	TN [%]	TP [%]	TN [%]	TP [%]	TN [%]
#1	Type 1. 10/20 1 min on/off cycles, wind strength 3	0.0	99.7	100	98.6	100	98.6
#2	Steady conditions, no anomalies	100	5.0	100	15.1	100	100
#3	Type 2. 10/20 min on/off cycles in the last 2 h, wind strength 1	0.0	98.8	100	72.3	100	99.5
#4	Type 1. 10/20 min on/off cycle, wind strength 2	95.3	4.8	100	58.3	100	97.9
#5	Type 1. 1/2 h on/off cycle, wind strength 1	71.4	24.3	100	17.1	100	100
#6	Type 1. 1/2 h on/off cycle, wind strength 3	32.2	17.1	100	36.9	100	99.4
#7	Type 3. 6 h test, variable wind strength in the last 5 h	58.1	11.8	100	81.2	100	92.9
#8	Type 3. 45 min test, anomalies in the last 15 min, wind strength 3	0.0	90.0	100	100	100	100
#9	Type 1. 10/20 min on/off cycle, wind strength 1	4.7	95.2	100	85.2	100	100
#10	Type 2. 2 h test, 10/20 min on/off cycle in the last hour, wind strength 1	24.2	72.8	100	96.3	100	100
#11	Type 2. 10 h test, 10/20 min on/off cycle in the last 2 h, wind strength 1	27.3	68.1	100	0.2	100	99.7
#12	Type 2. 10/20 min on/off cycle in the last 2 h, wind strength 3	1.5	99.2	100	18.7	100	99.4
#13	Type 3. 20 h test, variable strength anomalies in the last 10 h	0.0	59.9	100	23.7	100	76.0
#14	Type 3. 3 h test, 20/30 min anomalies, alternate wind strengths 1 and 3	0.0	95.5	100	50.0	100	72.7
	Average	29.6	60.2	100	53.8	100	95.4

¹ Format A/B: anomaly duration (A) and total period (B: wind + rest).

Table 2. Percentage of true positives (TP) and true negatives (TN). Tests last 12 h unless noted.

		Power Method		Distance Method (No Updates)		Distance Method (Updates)
Test	Description	TP [%]	TN [%]	TP [%]	TN [%]	TP [%]	TN [%]
#1	Type 1. 10/20 1 min on/off cycles, wind strength 3	0.0	99.7	100	98.6	100	98.6
#2	Steady conditions, no anomalies	100	5.0	100	15.1	100	100
#3	Type 2. 10/20 min on/off cycles in the last 2 h, wind strength 1	0.0	98.8	100	72.3	100	99.5
#4	Type 1. 10/20 min on/off cycle, wind strength 2	95.3	4.8	100	58.3	100	97.9
#5	Type 1. 1/2 h on/off cycle, wind strength 1	71.4	24.3	100	17.1	100	100
#6	Type 1. 1/2 h on/off cycle, wind strength 3	32.2	17.1	100	36.9	100	99.4
#7	Type 3. 6 h test, variable wind strength in the last 5 h	58.1	11.8	100	81.2	100	92.9
#8	Type 3. 45 min test, anomalies in the last 15 min, wind strength 3	0.0	90.0	100	100	100	100
#9	Type 1. 10/20 min on/off cycle, wind strength 1	4.7	95.2	100	85.2	100	100
#10	Type 2. 2 h test, 10/20 min on/off cycle in the last hour, wind strength 1	24.2	72.8	100	96.3	100	100
#11	Type 2. 10 h test, 10/20 min on/off cycle in the last 2 h, wind strength 1	27.3	68.1	100	0.2	100	99.7
#12	Type 2. 10/20 min on/off cycle in the last 2 h, wind strength 3	1.5	99.2	100	18.7	100	99.4
#13	Type 3. 20 h test, variable strength anomalies in the last 10 h	0.0	59.9	100	23.7	100	76.0
#14	Type 3. 3 h test, 20/30 min anomalies, alternate wind strengths 1 and 3	0.0	95.5	100	50.0	100	72.7
	Average	29.6	60.2	100	53.8	100	95.4

¹ Format A/B: anomaly duration (A) and total period (B: wind + rest).

In all cases, the moving average is computed over the last S = 100 samples to meet the target detection time. For each of these methods, the percentages of true positives (TP) and true negatives (TN) are calculated: a TP occurs when an anomaly is correctly detected during the period when the fan is on; a TN occurs when no anomalies are detected during the period when the fan is off. These percentages are obtained by dividing the total time correctly classified as anomalous or non-anomalous by the actual total time with true anomalies (fan on) or without anomalies (fan off), respectively. Additionally, a guard period of 30 s is considered when the fan is turned off, since the CDPR should gradually return to the resting state. During this guard period, the detector’s output is not included in the TP and TN statistics, as the system may produce ambiguous results while settling. For safety reasons, the system must never run in hazardous conditions. Every anomaly has to be identified, even if this means accepting a small number of false positives (occasionally flagging normal situations as anomalies).

The experimental results demonstrate that the proposed distance method with GMM updates obtains consistent results across all experiments. Specifically, it achieved 100% TP rates across all tests, effectively detecting all anomalies. It also reached very high TN rates, with an average of 95.4%, indicating a low rate of false positives during normal operation. In contrast, the power threshold method showed poor performance, with an average TP rate of 29.6%. Regarding TN, the power and the distance model without updates only achieve rates in the order of 50%, due to their inability to correct from operational drifts, making them unreliable for practical anomaly detection purposes.

Figure 7 shows the results of the “method with GMM updates” on four additional experiments (#6, #7, #9, and #14). More specifically:

• Figure 7a shows the results of the experiment #6 in which the CDPR alternates between one-hour rest and one-hour steady wind periods. During each calm period (e.g., at 3 h, 5 h, and 9 h), the method is updated and corrects the drift. This figure also shows how the algorithm detects all anomalies above the threshold (yellow bands) and switches back to normal classification almost as soon as the anomaly ends, with a TN rate of 99.4%. The few false positives (0.6% of the samples) appear during the wind-to-rest transition.
• Figure 7b shows the system under winds of varying intensity, as reflected by the variations in the relative distance signal. Although the signal fluctuates, it remains above the threshold; so, the detector correctly identifies the whole period as anomalous. At about 3.5 h, the wind stops, but the algorithm waits for a minimum settling time before it considers the system back to normal; so, this brief interval is still labeled anomalous even when the distance suggests that it could be a nominal state. Additionally, there is a false positive at around 4.25 h, probably caused by the alterations in the model calculation. For safety reasons, the system flags an anomaly, and once the model is correctly updated, it returns to identifying the true negatives accurately.
• In Figure 7c, all anomaly regions are correctly detected (100% TP). When compared to the distance values in Figure 6, a direct correlation between wind intensity and increasing distance is observed, which supports the expected behavior of the system.
• In the test shown in Figure 7d, the algorithm perfectly identifies all outlier regions. However, because stability problems arise around 1.5 h, the model does not reach steady state until 1.64 h, which slightly delays accurate classification of the nominal states. This represents the most challenging scenario tested, yet the system still meets the required specifications. It successfully identifies all anomalous events and maintains an acceptable accuracy in detecting nominal conditions (Table 2). The delay in returning to normal classification is attributed to the temporary instability introduced by external winds, which delays model adjustments.

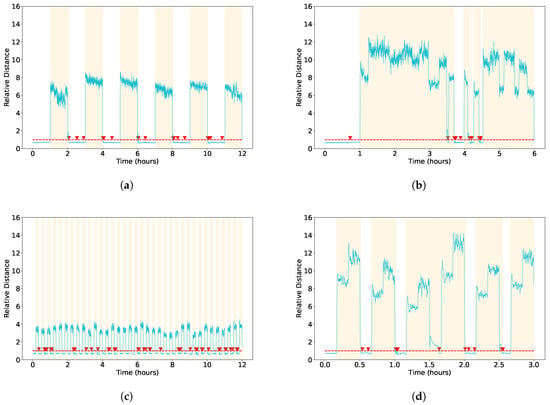
Figure 7. Moving average Mahalanobis distance (model with updates) for experiments. (a) Experiment #6, (b) Experiment #7, (c) Experiment #9, (d) Experiment #14. For additional information, see Table 2.

As an example of anomaly detection, Figure 8 illustrates the motion of the load when an anomaly was detected in test file #14. This anomaly was caused by a maximum-level (3) wind gust. Although the CDPR robot attempts to compensate for wind-induced motion, a slight displacement of the payload remains perceptible (highlighted by the left and right arrows in the figure to facilitate identification of the movement). In other anomaly examples, the oscillatory movements are less visually evident due to the CDPR’s rapid compensation, yet they are still readily detected by our proposed algorithm through the resulting changes in the torques.

Figure 8. Example of detected anomaly.

5.1. GMM Model Evaluation

This subsection presents an empirical evaluation of the chosen GMM methodology, covering the sensitivity to hyperparameters, calibration window, components, and fitting statistics.

5.1.1. Hyperparameter Study

First, the effect of the model’s configuration hyperparameters was investigated. Modifications were tested on the model updating threshold $1-\gamma$. The tests did not show significant variations when setting this parameter between $0.5$ and $0.95$. Regarding the hyperparameter M, which controls the dimensionality of the model and was set at M = 5 by default, various tests were conducted with values of M from 1 to 20. The results were mostly satisfactory across the entire range of values, although very low values result in a reduced distance dynamic range, which may, in rare occasions, lead to misclassifications. Conversely, when the dimensionality is too high, the model becomes unstable, and constant updates are necessary, which could affect the computational performance, as shown in Figure 9.

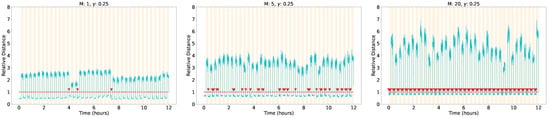
Figure 9. Effect of the model hyperparameter M on the outcome of experiment #9 (see Table 2).

5.1.2. Calibration Data

We evaluated calibration durations from 10 to 120 s and observed no material differences in the final outcomes. All experiments in Table 2 use a 10 s calibration window at a sampling rate of 100 Hz, yielding C = 1000 samples. As discussed in Section 4.1, these are grouped into M-sample multivariate data without gaps, producing $C-M$ training vectors (995 when M = 5). In the adaptive algorithm, each GMM fit uses the most recent C samples (10 s) that have been accepted as nominal (i.e., non-anomalous).

5.1.3. GMM Fitting Statistics

Across GMM fittings, the selected number of components was K = 1 in about 79.4% of cases, K = 2 in 13.7%, and K = 3 in 6.9%, indicating that a small number of components suffices in practice. The BIC information criterion used for component selection (see Section 4.2) is used solely to rank model orders for a given dataset; lower values indicate a better fit–complexity trade-off for that dataset and are not intended for comparison across datasets with different sizes or feature scales, which may happen in the context of CDPRs.

Finally, the average fitting time was $0.11$ s (median $0.10$ s) in a single-threaded implementation running on an Apple Mac mini M1. No engineering optimizations (e.g., multi-threaded execution or a native C++ implementation) were employed here, and such optimizations could further reduce training times in production environments, though even without these optimizations the algorithm is able to operate in real time.

6. Conclusions

In this paper, we presented an unsupervised anomaly detection algorithm for CDPRs while the platform is at rest, relying solely on motor-torque measurements and requiring no extra sensors. This anomaly detection is particularly relevant for CDPR operating modes in which the end-effector must hold a fixed pose while the motor torque remains active, as is commonly demanded during industrial operations and grip/release steps in pick-and-place tasks. The study presented in this article focuses on the phases immediately prior to performing the precision pick or place operations, with the tool in a static position, either alone or carrying the load, respectively. Both load conditions must be considered during the algorithm design. The proposed method does not automatically adapt to changes in payload; instead, it can be calibrated for any specific load condition, provided that the system operates at a static equilibrium point. When the payload is modified, a short calibration stage (on the order of 10 s) can be carried out to establish the corresponding nominal reference baseline. This ensures that the reference model accurately reflects the current operating condition, while deviations from it can still be reliably identified as anomalies.

The experimental results demonstrated that the proposed “method with GMM updates” efficiently detects anomalies and adapts to temporal drifts, maintaining high sensitivity while minimizing false positives. When compared to the relative power method and the GMM method without updates, our method consistently outperformed both in the face of drift and changing environments, all without requiring any labeled anomaly data. Across fourteen experiments the proposed method achieved an average 100% detection rate and correctly classified 95.4% of normal conditions, with every anomaly detected in one second.

These results indicate that the system will never operate under anomalous conditions, at the cost of accepting a small number of false positives. These false positives correspond to periods in which the machine remains idle without a clear cause (see Figure 7d around the 1.5 h mark), which can be interpreted as a loss of productivity. Nevertheless, introducing a redundant safety mechanism based on an additional detection method could help mitigate the impact of these idle periods, while still ensuring that the system never operates during an anomaly. In this context, the method presented in this work may also be considered as an additional redundant layer for anomaly detection, with redundancy being one of the fundamental principles of industrial safety [43].

Its simplicity and minimal parameter tuning make it well-suited for real-time applications, providing a practical solution to enhance the safety of CDPR operations. Future work will focus on extending the algorithm to other operational phases of CDPRs.