Concurrent Multi-Robot Search of Multiple Missing Persons in Urban Environments

Abstract

Coordinating robotic teams across multiple concurrent search tasks is a critical challenge in search and rescue operations. This work presents a new multi-agent framework designed to manage and optimize search efforts when several missing-person reports occur in parallel. The method extends iso-probability curve-based trajectory planning to the multi-target case and introduces a dynamic task allocation scheme that distributes search agents (e.g., UAVs) across tasks according to evolving probabilities of success. Overlapping search regions are explicitly resolved to eliminate duplicate coverage and to ensure balanced effort among tasks. The framework also extends the behavior-based motion prediction model for missing persons and the non-parametric estimator for iso-probability curves to capture more realistic search conditions. Extensive simulated experiments, with multiple concurrent tasks, demonstrate that the proposed method tangibly improves mean detection times compared with equal-allocation and individual static assignment strategies.

1. Introduction

In North America, over 700,000 persons go missing each year, with nearly 20% of cases remaining unresolved (e.g., [1]). This underscores the need for efficient search and rescue (SAR) operations. In urban/city contexts, when children or elderly individuals with cognitive impairments wander off, conventional ground-based searches are often slow and constrained by city infrastructure and traffic. In contrast, uncrewed aerial vehicles (UAVs) offer rapid deployment and provide broad aerial perspective.

City SAR involves several interrelated components: modeling the potential movement of missing persons (targets), dynamically allocating tasks to appropriate agents (e.g., UAVs), and managing resources for sustained, real-time operations. Researchers have addressed these challenges using heuristic optimization [2], multi-agent reinforcement learning [3], and hierarchical control frameworks [4], each offering distinct approaches to path planning, task allocation, and team coordination in multi-agent systems.

This paper, in particular, focuses on the centralized control of a multi-UAV team conducting concurrent searches for multiple missing persons in city settings. We propose a novel framework for dynamic task allocation and efficient management of overlapping search regions.

Below, we first provide a comprehensive review of the literature to contextualize our contributions, Section 1.1, and then highlight the specific research gaps our proposed method addresses, Section 1.2, respectively.

1.1. Literature Review

The review of the pertinent literature, herein, is organized as follows: Section 1.1.1 surveys major methodological approaches used in multi-UAV SAR (e.g., heuristic optimization, multi-agent reinforcement learning, and hierarchical control). Section 1.1.2 outlines common principles and architectures, including probabilistic belief maps, objective formulations, and coordination paradigms. Section 1.1.3 identifies differences among studies and remaining research gaps.

1.1.1. Common Search Methodologies

Most SAR methods focus on single targets, employing probabilistic models for target-motion estimation [5,6,7,8,9,10]. Extensions include dynamic clustering with static sensors [11], aerial-only probabilistic search [12], and particle swarm optimization (PSO)-based techniques [13,14]. Multi-target strategies, such as the semi-flocking algorithm in [15], integrate local search and tracking, but often lack active redeployment. Similarly, the region-based method in [16] is designed for indoor environments, while the grid-based optimal search in [17] assumes bounded domains, limiting open-area applicability.

Broader heuristic and classical optimization methods treat multi-UAV search and allocation as optimization problems solvable via genetic algorithms (GA) [18], ant colony optimization [19], and PSO [20]. Recent bio-inspired frameworks include the sparrow-enhanced African vulture optimization algorithm for trajectory planning [21], dream optimization for 3D path generation [22], and two-layer trajectory planning for multi-UAV coordination [23]. Simulated annealing, with destruction operators and backward learning, has also been applied to UAV path planning [24], while NSGA-II bilevel optimization has been shown to facilitate UAV dispatching [25]. A diameter–height model introduced in [26] enhances coverage path planning in mountainous terrains.

Deterministic methods complement the above heuristic methods, including multi-agent deep deterministic policy gradient (MADDPG) [27] and partially observable Markov decision processes (POMDPs) [28]. Building on these, behavior expression trees (BETs) [29] determine when to rely on heuristics versus learned policies, delegating trajectory generation to classical planners. Recent advances in sim-to-real multi-agent reinforcement learning (MARL) demonstrate safe UAV planning in cluttered, complex environments [30,31].

1.1.2. Common Principles and Architectures for SAR

Across methodologies, several common principles recur. Search areas are, typically, discretized into probabilistic belief maps updated in real time via Bayesian fusion of heterogeneous sensor data [18]. Objectives balance information gain (e.g., entropy reduction) against mission costs such as time, fuel, or collision risk, commonly via weighted-sum optimization rather than full constrained POMDPs. Task allocation either partitions the grid into non-overlapping regions [31] or promotes emergent division of labor through local interaction rules and penalty terms discouraging redundant coverage [19]. Probabilistic allocation strategies have also been shown to match specialized robots to deep-learning-based target detections [32]. Broader frameworks address coalition formation for scalable task allocation [33], cooperative optimization for UAV formation tracking [34], Voronoi-based coverage with attention mechanisms [35], and real-time mission planning in cluttered environments [36]. Additional studies consider 3D path and collision-risk management [37] and secure route planning in internet-of-drones contexts using enhanced SAR-inspired optimization [38].

1.1.3. Key Differences and Remaining Gaps

Differences in the pertinent literature stem from variations in target modeling, from static, planar assumptions to mobile models employing Kalman filters or diffusion processes for trajectory forecasting [39], and in path representation, ranging from discrete waypoints for combinatorial efficiency to continuous splines or Bézier curves requiring nonconvex optimization [40]. Coordination strategies vary from explicit map sharing with periodic consensus to leader-based or fully centralized task sequencing [41]. Despite these advances, major challenges remain. Scaling beyond small UAV teams requires hierarchical or districting frameworks, dynamic reallocation, and real-time task reprioritization. Capabilities such as mid-mission target insertion or UAV rerouting after early completion or failure remain limited [42]. Emerging areas, including UAV-enabled base-station deployment for emergency communication [43], UAV-based carbon-emission monitoring in ports [44], and multi-scene disaster response [26], illustrate expanding applications. Nonetheless, achieving scalable, adaptive, and dynamic multi-target SAR in dense city environments remains an open problem.

1.2. Motivation and Contribution

The literature review, as summarized above, reveals that most existing target-search research either emphasizes control strategies for robots with limited autonomy or employs static, weakly adaptive task allocation methods. Current multi-target search frameworks, typically, treat all targets as a single unified task, rather than decomposing them into distinct subtasks for individual targets. Consequently, there remains a lack of dynamic, reallocation-capable algorithms suited to multi-target search, particularly in complex city settings, where new tasks, such as newly reported missing persons, may emerge unpredictably during ongoing missions.

Concurrent multi-robot searches pose additional challenges, including inter-UAV coordination, avoidance of redundant coverage, and responsiveness to evolving task conditions. These challenges are intensified in city environments characterized by restricted airspace, frequent occlusions, and unpredictable target behavior, which demand robust and adaptive planning.

To address these gaps, this paper proposes a novel framework for concurrent search operations targeting multiple missing persons in city settings using aerial robots (UAVs). The framework introduces a dynamic task allocation strategy designed to efficiently manage overlapping search regions while balancing computational cost and search quality. By reducing pre-mission planning time and enabling rapid trajectory generation, the proposed approach enhances early mission responsiveness, an essential factor in improving search success rates and enabling practical real-world deployment.

2. Problem Statement

This section outlines the individual sub-problems that need to be addressed for multi-UAV concurrent city search for missing persons. Assumptions for the problem at hand are first outlined below in Section 2.1. The individual sub-problems are detailed next in Section 2.2. One, however, should note that the aerial agents’ sole responsibility is to search for and detect the targets, while subsequent verification tasks are to be handled by ground teams.

2.1. Search Assumptions

Several assumptions regarding target behavior and aerial search-agent capabilities are detailed below.

2.1.1. Target Motion

Assumptions regarding the target motion include the following: (i) The missing person is assumed to be in a known urban environment with a given map. (ii) The target would be traveling according to a mix of possible motion types, including occasional backtracking—starting at t = 0, at or near their last known position (LKP). (iii) As time progresses, the target’s motion is driven by both the road and pathway network and the presence of obstacles. (iv) When encountering ‘soft’ obstacles (different types of buildings), the target may enter these and spend some random amount of time in them, becoming undetectable to searchers. Entry probabilities need to be incorporated into the motion model to accurately capture realistic city-search scenarios. (v) A priority system is assumed for the targets, where more vulnerable individuals (such as children) receive higher search priority.

2.1.2. Search Agents and Environment

Assumptions regarding the search agents include the following: (i) Search agents are assumed to be all autonomous aerial units (i.e., UAVs) operating in a coordinated mode. (ii) They follow their assigned paths at a constant speed while being unaffected by urban obstacles. (iii) They are also assumed to have sufficient power reserves to complete their missions without requiring recharging. (iv) Each UAV is equipped with a binary sensing model that assumes detection with probability one if the target lies within its effective sensing radius, and zero otherwise. This assumption is consistent with established UAV-based SAR detection models [45,46]. While simplified, this formulation aligns with classical search theory and provides a tractable basis for our probability-of-detection (PoD) updates. (v) Throughout the search operation, all UAVs maintain accurate global positioning and remain in communication with a central controller that provides continuous trajectory updates. (vi) Communications are centralized; we assume reliable links in our experiments, and if a transient dropout occurs, a UAV continues along its last received waypoint sequence until the link is restored. (vii) The search scenario assumes the availability of a global fixed number of UAVs that can be deployed to locate an unknown number of targets, which may appear at various times.

Assumptions regarding the search environment include the following: The urban environment contains several predetermined search–response stations, where UAVs await task assignments. Initially, all UAVs are stationed at designated search–response stations. Each station has a fixed UAV capacity, and every UAV returns to its original station when idle.

2.2. Sub-Problems

In order to determine optimal search trajectories, this work will need to address three critical sub-problems: target-motion modeling, dynamic task allocation, and UAV search trajectory generation. These are detailed below, after the description of a search metric utilized.

2.2.1. Search Metric

An established approach to evaluating the search effectiveness in SAR operations is maximizing the probability of success (PoS) [47]. This metric is derived, herein, from the integration of two key probability distributions: the probability of area (PoA) and the probability of detection (PoD). The PoA quantifies the likelihood that the target is located at a specific position within the search region, while the PoD represents the likelihood of detecting the target, given that it is present at the location being searched.

In scenarios involving multiple targets, the optimal search trajectories are those that maximize the average rated probability of success (RPoS) across all targets, while accounting for the penalty of their relative priorities and following searcher constraints, such as not exceeding the rated speed. A higher RPoS corresponds to a greater overall likelihood of successfully locating all targets. The RPoS contains the average PoS part and penalty part. The average PoS is calculated by:

$$\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{P}\mathrm{o}\mathrm{S}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\mathrm{P}\mathrm{o}{\mathrm{S}}_i,$$

(1)

where $\mathrm{P}\mathrm{o}{\mathrm{S}}_i$ denotes the probability of success of finding Target $i$, and $N$ represents the total number of targets searched. To balance the PoS across all targets, according to their priorities, a penalty term needs to be employed:

$${\displaystyle \frac{2}{N\left(N-1\right)}}\sum _{a=1}^N\sum _{b=1}^{a-1}\left|\mathrm{P}\mathrm{o}{\mathrm{S}}_a\left(t\right)-\mathrm{P}\mathrm{o}{\mathrm{S}}_b\left(t\right)+g_a-g_b\right|,$$

(2)

where $\mathrm{P}\mathrm{o}{\mathrm{S}}_a\left(t\right)$ denotes the probability of success of finding Target $a$ after the start of its search at time $t$, $\mathrm{P}\mathrm{o}{\mathrm{S}}_b\left(t\right)$ denotes the probability of success of finding Target $b$ after the start of its search at time $t$, $g_a$ is the priority level for Target $a$, and $g_b$ is the priority level for Target $b$. The above penalty term compares the PoS values after the same search duration for each target. The penalty increases as the differences between the PoSs of the targets over the same search duration increases. Accordingly, the RPoS for determining the optimal search trajectories, obtained by combining Equations (1) and (2), is given by:

$$\mathrm{R}\mathrm{P}\mathrm{o}\mathrm{S}=\left({\displaystyle \frac{1}{\mathrm{N}}}\sum _{i=1}^N\mathrm{P}\mathrm{o}{\mathrm{S}}_i-{\displaystyle \frac{2}{N\left(N-1\right)}}\sum _{a=1}^N\sum _{b=1}^{a-1}\left|\mathrm{P}\mathrm{o}{\mathrm{S}}_a\left(t\right)-\mathrm{P}\mathrm{o}{\mathrm{S}}_b\left(t\right)+g_a-g_b\right|\right).$$

(3)

Thus, the optimal search trajectories should maximize the RPoS value.

2.2.2. Target-Motion Modeling

The target-motion model, to be used for a search, must predict potential trajectories of missing person(s) during the search period, generating a probability distribution of their locations. The model must incorporate the constraint that targets cannot traverse major urban obstacles (e.g., buildings or walls), reflecting realistic movement patterns in city environments.

2.2.3. Dynamic Task Allocation

In a multi-target scenario, the search problem decomposes into multiple concurrent tasks, each requiring a specific number of search agents to execute. An effective and efficient task-allocation strategy is therefore needed to distribute the available agents into distinct search teams, with each team assigned to a single task. As the conditions of the search environment may evolve over time, the initial allocation may become suboptimal or infeasible. Therefore, a mechanism is required to monitor the search process and update the agent allocation dynamically when necessary.

The evaluation of the allocation strategy should be based on the RPoS formulated in Equation (3) across all tasks. The optimal allocation would, thus, be defined as the one that maximizes the RPoS.

Furthermore, since search agents may be positioned at different locations, at the start of the search, the allocation strategy must also account for travel time. The final assignment should aim to minimize the average travel time required, for example, for UAVs to reach their designated search areas, while still maintaining the optimal number of UAVs per task.

2.2.4. Search Trajectories

Originally introduced in [12], iso-probability curves model the likely movement of a lost person over time, radiating outward from a known initial location. These curves, as chosen to be used herein, offer a probabilistic description of a target’s potential location within the search area at any given time. They are constructed using a one-dimensional probability distribution function that models the likely distance a missing person may have traveled along a single direction. Each curve in the set corresponds to a specific quantile $q$, representing the radial boundary within which the person is expected to remain with probability $q$. The complete set of curves, spanning quantiles from 0 to 1, collectively defines the spatial uncertainty of the target’s location. These curves are time-varying and are centered on the last known position (LKP) of the individual, expanding outward as time progresses.

In multi-target scenarios, separate search teams would be assigned to different targets, with each team generating its own iso-probability curves to guide trajectory planning. However, the original iso-probability approach does not account for coordination between different search teams. As a result, the areas enclosed by the curves, particularly at high quantiles, may overlap. When this happens, agents from different teams may redundantly search the same regions, leading to duplicated effort and reduced overall efficiency.

Therefore, a method is needed to resolve such overlaps in multi-target scenarios, ensuring that search responsibilities are properly partitioned and that search resources are used effectively and efficiently.

3. Proposed Methodology

This section describes the proposed methodology for addressing the problem outlined above. An overview of the workflow is illustrated in Figure 1. In Step 1, we assume that ‘humans’ send a missing report to the search team, who in turn initiate the search, Section 3.1. In Step 2, a closed-loop phase that periodically updates the robot/UAV trajectories for the next iteration is initiated, Section 3.2. If a new missing person is reported or any target is found, all current searches are temporarily paused. In such a case, Steps 3a and 3b are triggered to review the data at hand and re-allocate resources before resuming the search(es), Section 3.3.

Figure 1. Overview of the proposed methodology.

3.1. Search Initialization

Search initialization aims to collect the necessary data required to generate robot trajectories for the first missing-person case. Target-motion data is produced using the target-motion model, Section 3.1.1. Then, iso-probability curves are constructed to guide the trajectory generation process, Section 3.1.2. The goal of initialization is not to fully compute all possible data in advance, but rather to generate only the minimal data required to begin the first iteration of the trajectory generation loop, Section 3.2, thereby reducing precomputation time. The target-motion data and iso-probability curves are, then, updated and extended dynamically within the loop, Section 3.2.3.

3.1.1. Target-Motion Modeling for Urban Areas

The urban/city missing-person behavior, utilized herein, is based on an extension of the model first introduced in [17]. It incorporates five key behaviors: random_traveling, consistent_traveling, route_traveling, direction_traveling, and backtracking into a unified, Monte Carlo–driven motion-prediction framework. This model simulates a large ensemble of possible trajectories and represents each as an iterative sequence of open polygonal segments. For every segment, the target follows a locomotion strategy and a decision-making strategy to either travel along a consistent heading or move randomly. Probabilistic transitions between these locomotion and decision strategies, including occasional backtracking, are controlled by model parameters calibrated from prior behavioral studies, enabling the prediction to capture both structured and exploratory human movements in dense urban settings. Unlike in [17], herein, according to a building-entry model, every building footprint in our urban grid is treated as a “soft” obstacle that may temporarily shelter the missing person rather than merely deflect their path.

The target-motion model utilizes the following coefficients: $p_{rand}$, $p_{trav}$, $p_{back}$, $p_{dir}$, and $p_{route}$ for the probability of random_traveling, consistent_traveling, backtracking, direction_traveling, and route_traveling behaviors, respectively; ${\mu }_v$ and ${\sigma }_v$ are the mean and standard deviation of the target moving speed; $d_{route}$ is the linear distance for consistent_traveling behavior, which the target will move along before changing to other behaviors; $p_{private}$ and $p_{residence}$ are probabilities that the target may enter a private establishment or residence building, respectively, and, $t_{stop}$ represents the time the target would remain inside a structure.

3.1.2. Iso-Probability Curves and Partitioning

A kernel-based method is used to generate iso-probability curves for multi-target cases. This non-parametric estimation approach models the spatial uncertainty of a missing person’s location over time. Therefore, the iso-probability curve acts as the PoA described in Section 2.2.1. It operates on missing-person trajectory data represented in polar coordinates, using a product of two Epanechnikov kernels: one applied to the angular component with bandwidth $h_{\theta }$, and the other to the radial component with bandwidth $h_r$. This method avoids the limitations of histogram-based estimation by providing smoother and more accurate density estimates. The result is a cumulative distribution function $F(r\mid \theta ,t)$ that estimates the probability of the missing person being within distance $r$ in direction $\theta$ at time $t$. This function can be inverted to determine the radial position corresponding to a given quantile.

(i) 

Multi-Target Search Scenarios

A search region is defined, herein, by an area enclosed by the 100% quantile iso-probability curve, which implies target presence with near-absolute certainty. When multiple persons are reported missing, their respective search regions could overlap over time, leading to duplicated effort and reduced overall efficiency, Figure 2a below.

Figure 2. Adjustment of three iso-probability curves. (a) curves before adjustment and (b) curves after reassignment of overlapping regions.

To resolve duplicated efforts, we suggest a simple strategy: assign the intersection regions to the most recently reported target, based on the assumption that newer targets, typically, have smaller initial search regions. For this goal, we modify the iso-probability curves for all search tasks at hand, except for the latest task.

Let us assume that there are $N$ targets, each of which has an associated cumulative distribution function (CDF) that represents its set of iso-probability curves over time. For Target $i$, this function is denoted as $F_i\left(r∣\theta ,t\right)$, where $r$ is the radial distance, $\theta$ is the direction, and $t$ is the time elapsed since the target was reported missing. These CDFs are, first, sorted based on their corresponding reporting times in ascending order. For each target, its $F_i\left(r∣\theta ,t\right)$ is, then, modified to account for the previously assigned search regions of earlier Targets $1$ to $i-1$.

Let $R_i\left(t\right)$ denote the union of all search regions associated with Targets $1$ to $i-1$, enclosed by their 100% iso-probability curves at time $t$. Then, the value of $F_i\left(r∣\theta ,t\right)$ is modified based on the rule below:

$$F_i\left(r∣\theta ,t\right)=\left\{\begin{array}{c}\underset{r^{\prime }>r,(r^{\prime },\theta )\notin R_i\left(t\right)}{\min }{F}_i\left(r\prime ∣\theta ,t\right),if(r,\theta )\in R_i(t)\\ F_i\left(r∣\theta ,t\right),otherwise\end{array}\right.,$$

(4)

Equation (4), however, does not directly address the critical case, when the origin $(r=0,\theta )$, i.e., the center of the iso-probability curves (LKP), lies inside a previously assigned region $R_i\left(t\right)$. Thus, there exists a need to utilize the following equation:

$$F_i\left(r∣\theta ,t\right)=\left\{\begin{array}{c}0,if\left(r,\theta \right)\in R_i\left(t\right),and{F}_i\left(r∣\theta ,t\right)<1\\ F_i\left(r∣\theta ,t\right),otherwise\end{array}\right..$$

(5)

Equation (5) is invoked after Equation (4). This adjustment expands the 0% curve outward to exclude the overlapping area, while ensuring that it does not grow beyond the original 100% boundary.

Figure 2b illustrates the outcome of this adjustment process. On the left, overlapping 100% iso-probability curves result in duplicated search regions. On the right, after applying Equations (4) and (5), the curves are “redrawn” to avoid overlapping.

(ii) 

Partitioning

A partitioning strategy divides the workload among multiple robots/UAVs assigned to the same task, ensuring full coverage while avoiding redundant effort. Each robot is assigned a lower and upper bound of the cumulative probability range, denoted as $L{B}_i$ and $H{B}_i$, respectively. Namely, Robot $i$ is responsible for searching the area between the iso-probability curves corresponding to $L{B}_i$ and $H{B}_i$.

However, computing optimal partitions would be computationally expensive in case of multiple concurrent searches. Therefore, herein, we adopt a simple, uniform partitioning method, which divides the region between the 0% and 100% iso-curves equally among all assigned robots:

$$\begin{array}{c}L{B}_i=\max \left(0\%,\left(i-1\right)\times {\displaystyle \frac{100\%}{n_R}}\right)\\ H{B}_i=\min \left(100\%,i\times {\displaystyle \frac{100\%}{n_R}}\right)\end{array},$$

(6)

where $n_R$ is the total number of robots allocated to the task. The 0% and 100% bounds ensure that the partitions remain within the effective iso-probability search region.

Figure 3, below, illustrates the partition boundaries for three targets scenarios. In this example, each search team has its own partitioning scheme (denoted as Partitions $1_1,1_2,1_3$ for Target 1, Partitions $2_1,2_2,2_3$ for Target 2, and Partitions $3_1,3_2,3_3$ for Target 3, respectively).

Figure 3. Partitions for a three-target search.

3.2. Trajectory Generation Phase

The trajectory-generation phase, proposed herein, is responsible for generating search trajectories for all robots, Algorithm 1 below. It is executed until all targets are found or a predefined termination condition is met.

This phase begins by taking simulation data as input (Line 1 of Algorithm 1). Specifically, curves stores the iso-probability data for all missing targets, and target_ trajectories contains the simulated trajectories for those targets. robot_trajectories are, then, initialized to their current locations (Line 2).

Next, the task-allocation algorithm (Section 3.2.1) is executed to determine the robot-to-task assignments, regardless of how many targets are present (Line 3). The variable output_time is initialized to zero (Line 4). It serves as a counter to determine when to output the generated trajectories, carried out every t_update.

Lines 6–19 of the algorithm represent the core trajectory-generation phase. In Lines 7–9, trajectory generation (Section 3.2.2) is performed for a short horizon of t_check, where t_check is less than t_update. This allows the system to update the current task allocation more frequently. The task allocation method (Section 3.2.4) updates the current allocation to ensure its optimality, shown in Line 11.

If output_time exceeds t_update, the current robot_trajectories are sent to the robot control center, allowing robots to begin or continue searching along the planned paths (Line 14). After the trajectories are output, the simulation data is updated and extended (Section 3.2.3), which includes both iso-probability curves and simulated target trajectories.

Finally, the robot_trajectories and output_time are re-initialized to reflect the current robot locations and zero, respectively (Line 17–18), in preparation for the next iteration.

Algorithm 1. Proposed trajectory-generation algorithm pseudocode

1   curves, target_ trajectories $\leftarrow$ Input(n_task)

2   robot_trajectories $\leftarrow$ CurrentRobotLocations(n_robot)

3   allocation $\leftarrow$ TaskAllocation(curves, target_ trajectories, robot_trajectories)

4   output_time $\leftarrow$ 0

5

6   while not CheckTermination()

7   trajectory $\leftarrow$ TrajectoryGenerate(n_robot, allocation, t_check)

8   append trajectory to robot_trajectories

9   output_time $\leftarrow$ output_time + t_check

10

11    allocation $\leftarrow$ TaskAllocation(curves, target_ trajectories, robot_trajectories, allocation)

12

13    if output_time is larger than t_update

14   robot_trajectories $\to$ Output()

15   target_ trajectories $\leftarrow$ UpdateTarget(robot_trajectories)

16   curves $\leftarrow$ UpdateCurve(n_task)

17   robot_trajectories $\leftarrow$ CurrentRobotLocations(n_robot)

18   output_time $\leftarrow$ 0

19    end if

20 end while

3.2.1. Task Allocation

This sub-section describes the task-allocation algorithm, which is designed to handle any number of search tasks. The algorithm takes as input the iso-probability curves and simulated target trajectories for each task, along with the current positions of all robots. Its goal is to determine the optimal robot-to-task assignment that maximizes the RPoS described in Equation (3).

Since there exists no direct metric for evaluating a given robot-to-task assignment, the algorithm must first generate robot trajectories based on a proposed assignment. It then evaluates the overall performance of these trajectories using the RPoS.

The PoS for a given search task is estimated by dividing the number of simulated targets found by the total number of simulated targets:

$$\mathrm{P}\mathrm{o}\mathrm{S}={\displaystyle \frac{n_{found}}{n_{all}}},$$

(7)

where $n_{found}$ counts targets found on the current robot trajectories and $n_{all}$ is the total simulated target trajectories.

Task allocation begins with a random task-to-robot combination and relies on historical PoS values to calculate the RPoS. Thereafter, a gradient-descent–style update is performed. It adjusts one robot per step until either the maximum number of steps is reached or the allocation repeats (i.e., converges). Algorithm 2, shown below, illustrates the structure of this process. Line 1 generates a random task-to-robot combination under three main constraints. First, each task must be assigned at least one robot to ensure that no task is left unattended. Second, a user-defined parameter max_allocation is used to specify the maximum number of robots assigned to any single task. Third, a user-defined parameter min_reserved is used to specify the minimum number of robots that must remain unassigned and stay at search–response stations. The value of min_reserved can be dynamically adjusted based on the current number of active tasks.

This task-to-robot combination only specifies the number of robots assigned to each task, rather than assigning specific robots to specific tasks. However, since each robot may be located at a different position and has a different travel distance to each task area, it is necessary to determine the exact robot-to-task assignment.

It is intuitive that a robot located closer to a task is more suitable for that task. Therefore, RobotToTaskAssignment in Line 2 translates each task-to-robot combination into a concrete robot-to-task assignment by minimizing the total travel distance. To efficiently perform this assignment, the algorithm does not exhaustively search through all possible robot-to-task mappings. Instead, it uses a greedy approach based on proximity. First, tasks are sorted in ascending order according to the number of robots required. Then, for each task, starting with the one that requires the fewest robots, the algorithm iteratively assigns the nearest available robots to that task until its requirement is met. Once a robot is assigned, it is removed from the pool of available robots and cannot be assigned to another task in the current combination. This approach ensures that tasks are fulfilled efficiently, while prioritizing robots with the shortest travel distances.

The robot trajectories are generated based on the current_ allocation in Line 3. This method plans the paths for all robots over a short horizon of t_check. A short horizon is sufficient since the allocation will be re-evaluated and potentially updated after t_check.

Once the search trajectories are generated, Line 4 evaluates the effectiveness of the assignment. It determines the number of simulated targets found for each task based on the current robot trajectories and uses this to calculate the task’s PoS. Given the simulated target trajectories and robot trajectories, a simulated target is marked as found if, at any point in time, it comes within the sensing range of any robot moving along its planned trajectory. With the task’s PoS and the historical PoS data for all the targets, the RPoS value can be calculated. Line 4 also identifies the two targets that contribute the largest penalty in the RPoS evaluation. To reduce this penalty, Line 8 moves a single robot between those two tasks, applying one-robot adjustment to the current task-to-robot combination. Lines 7–19 iterate this one-robot update, tracking and returning the best allocation (highest RPoS) encountered.

Algorithm 2. Task Allocation Algorithm, Task Update Algorithm (Section 3.2.3)

1   current_ comb $\leftarrow$ RandomAssignment(n_robot, max_allocation, min_reserved)

2   current_assignment $\leftarrow$ RobotToTaskAssignment (current_ comb)

3   trajectories $\leftarrow$ TrajectoryGenerate(n_robot, current_ allocation, t_check)

4   best_RPoS, robot_give, robot_recieve $\leftarrow$ EvaluatePath(trajectories, target)

5   best_ assignment $\leftarrow$ current_ assignment

6

7   for step is 1 to stepmax

8  current_ comb $\leftarrow$ Update (current_comb, robot_give, robot_recieve)

9  current_ assignment $\leftarrow$ RobotToTaskAssignment(current_ comb)

10   trajectories $\leftarrow$ TrajectoryGenerate(n_robot, current_ assignment, t_check)

11   next_RPoS, robot_give, robot_recieve $\leftarrow$ EvaluatePath(trajectories, target)

12   if next_RPoS is larger than best_RPoS

13       best_RPoS $\leftarrow$ next_RPoS

14       best_ allocation $\leftarrow$ current_ assignment

15   end if 16   if current_ assignment appears before 17       break the loop 18   end if 19 end for

20 Output $\leftarrow$ best_ assignment

3.2.2. Search-Trajectory Generation

The trajectory-generation process determines the path that each robot will follow based on the given robot-to-task assignment. Each robot’s trajectory is represented as a sequence of $(x,y,t,r,\theta ,P)$ tuples, where $(x,y)$ denotes the robot’s position at time $t$ with respect to a global coordinate frame, $(r,\theta )$ represents the robot’s polar coordinates at time $t$ relative to the center (i.e., LKP) of the assigned search task, and $P$ is the probability value at that position, obtained from the corresponding iso-probability curve. This data can be directly used to guide real robots in practice, serving as a time-stamped navigation path. While this process generates efficient paths, it does not explicitly account for inter-UAV collisions. To address this, herein, a simple rule-based protocol handles potential collisions. If a collision is predicted, one of the UAVs involved reduces its speed for a short while, creating a minimum separation distance, effectively avoiding the collision. Such short-term interventions (in real time) are common in practice and would have a negligible impact on overall performance. Consequently, the UAV trajectory-generation algorithm does not need to incorporate collision avoidance into its planning.

The trajectory-generation approach could comprise two distinct phases: an outward trajectory and an inward return trajectory. Furthermore, this method, for single-target searches, could synchronize the inward and outward motions of each robot within the same search task. Herein, however, such synchronization would not be feasible due to the multi-target scenario since robots may be assigned to different search tasks, each with independent timing and spatial requirements. As a result, synchronization across all robots would impose unnecessary constraints and reduce flexibility. Therefore, in our work, the synchronization requirement is not invoked, and each robot generates its (spiral) trajectory independently based on its assigned task and partition. The inward and outward motions of the robot are generated in discrete steps, where each new position is calculated based on the current position and the structure of the iso-probability curves.

At Step $n$, let $P\left(n\right)$ be the cumulative probability value, $\theta \left(n\right)$ and $r\left(n\right)$ be the angular and radial coordinates in polar space, and $t\left(n\right)$ be the corresponding time stamp, where

$$P\left(n+1\right)=P\left(n\right)+c\times d\theta ,$$

(8)

$$c=\left\{\begin{array}{c}{c}_{in},ifP\left(n+1\right)>HB\\ c_{out},ifP\left(n+1\right)<LB\end{array}\right.,$$

(9)

$$P\left(n+1\right)=\left\{\begin{array}{c}HB,ifP\left(n+1\right)>HB\\ LB,ifP\left(n+1\right)<LB\end{array}\right.,$$

(10)

$$\theta \left(n+1\right)=\theta \left(n\right)+d\theta ,$$

(11)

$$r\left(n+1\right)=GetR\left(P\left(n+1\right),\theta \left(n+1\right),t(n+1)\right).$$

(12)

Above, $d\theta$ is the angular increment at each step, $GetR$ is a lookup function that returns the radial distance $r$, corresponding to a given cumulative probability $P$, angle $\theta$, and time $t$, based on iso-probability curve data, and the scalar $c$ controls the rate of change of the probability value. For inward motion, $c_{in}$ is negative, indicating that the robot is moving toward lower-probability contours. For outward motion, $c_{out}$ is set to a large positive value (e.g., 100), which effectively causes the robot to move directly toward the upper iso-probability curve bound in a straight line. By switching the value of $c$ in Equation (8), Equation (9) can represent both inward and outward motion in a unified framework.

After determining $\theta (n+1)$, $r(n+1)$, and $P(n+1)$, the Cartesian coordinates $(x,y)$ are obtained by converting from Polar to Cartesian space. The timestamp $t(n+1)$ is updated based on the Euclidean distance between steps divided by the robot’s rated speed.

In multi-target scenarios, an additional phase is required—transitioning to a new task area. When a robot is reassigned to a new task, its next trajectory begins at its current location and ends at the HB boundary of its newly assigned partition. Since the HB curve, typically, forms a closed shape (e.g., circular or elliptical), the transition trajectory is determined as the shortest path from the robot’s current position to the HB curve of the new partition.

3.2.3. Information Update

In the search initialization step above, only the information necessary for the first iteration of trajectory generation is determined. Specifically, the simulated target trajectories are generated using the target-motion model, and the iso-probability curves are constructed only for the time interval from the initial time to $t_{update}$. This limited scope helps reduce precomputation time. After the first iteration, both the target-motion data and iso-probability curves must be extended to cover the next $t_{update}$. Therefore, an information update step is required after each iteration to determine the data needed for the next one. This update consists of two components: the extension of the simulated target trajectories for each existing target and the extension of the iso-probability curves for each corresponding search task, respectively.

The target-trajectory update involves not only extending the existing trajectories but also removing any simulated targets that would have already been found. However, regions that have been previously searched should be excluded from future search iterations. This ensures that only possible positions that have not been detected in prior iterations are considered in the ongoing search. Following this principle, we exclude from the simulation data any target trajectory that would have been detected by the robot team during earlier iterations. A simulated target is marked as found if, at any point in time, it comes within the sensing range of any robot moving along its planned trajectory

Once found targets are removed, the remaining unfound trajectories are extended forward using the same target-motion model described in Section 3.2.1. The only difference is that the starting point for this extension is no longer the LKP, but rather the current position at the end of the previous simulation horizon, taken from the prior simulated trajectory.

After the target trajectories are extended, the iso-probability curves are updated using the same method described in Section 3.1.2, applied to the newly extended simulated trajectories. Since the iso-probability curves are equivalent to PoA, updating the iso-probability curves also updates the PoA.

3.2.4. Validating Allocations

The robot-to-task assignment determined by the task-allocation algorithm (Section 3.2.1) may become suboptimal over time, as targets continue to move away from their LKPs and as the corresponding iso-probability curves evolve. Therefore, periodic reallocation is required to ensure that the current assignment remains effective.

It is, thus, necessary to re-run the task-allocation algorithm, Algorithm 2, each $t_{check}$ period of time to update the current robot-to-task assignment. Here, the start assignment can be the current assignment instead of random assignment to save computation time.

Once the assignment is updated, it is used as input to the trajectory-generation module (Section 3.2.2) to yield robot trajectories for the next $t_{check}$. Moreover, since this periodic reallocation operates within the trajectory generation phase, it works on predicted future trajectories rather than those already executed by the real robots. As a result, periodic reallocation does not interrupt the ongoing search process in real operations.

3.3. Reallocation

In the multi-target scenario, as considered herein, there are two types of events that may interrupt the main trajectory-generation phase (Section 3.2): the appearance of a new missing target/person and/or the discovery of an existing target, respectively. Both events change the number of active search tasks and require an immediate reallocation of robot resources. In response, the proposed system triggers a full re-execution of the task-allocation algorithm (Section 3.2.1) to account for the updated task set.

In the case of a new missing target, a new search task is initiated. The first step is to generate the simulated target trajectories for the new target, using the target-motion model described in Section 3.1.1. These trajectories begin at the LKP of the target and are simulated from the time the target was reported missing until the next $t_{update}$, the time horizon required for the next iteration of trajectory generation. After this, iso-probability curves for all existing targets are redetermined using the method described in Section 3.1.2. This is necessary since the presence of a new target may affect the assignment of overlapping regions, and the iso-curves must be adjusted to avoid conflicts.

Once the simulation data is ready, it is passed to the task-allocation step in the trajectory generation phase (Section 3.2.1). At this point, all robots are paused at their current positions, since these positions are required as inputs to the allocation algorithm. The system, then, executes the full task-allocation procedure with one additional task. All robots are considered available and are reallocated across the updated set of tasks. The algorithm remains the same, except that the number of tasks is now incremented by one. After task allocation, the trajectory-generation phase resumes normally, generating the next iteration of robot trajectories based on the new assignment.

In the case of a found target, an existing search task is removed. Since there are no new simulated target trajectories to generate, the process begins by updating the iso-probability curves for all remaining tasks to reflect the removal of the found target. Then, similar to the new-task case, all robots are paused at their current positions, and the system proceeds to run the full task-allocation algorithm. This time, the number of tasks is decreased by one, but the rest of the procedure remains identical.

If the last remaining target is found, and no other missing targets remain, the system concludes that the search has been completed successfully. In this case, the entire search operation is terminated.

4. Simulated Experiments—Example Results

In this paper, three multi-target search examples are presented to demonstrate the full workings of the proposed method. To maintain clarity and focus, selected supporting simulations are provided in the appendices rather than, herein, in the main body of the paper. The first example provides a description of a simple two-target scenario—it is detailed in Appendix A. The second example introduces a slightly more complex case involving three targets—it is detailed below in Section 4.2. The third example addresses a more challenging scenario with six targets—it is detailed in Appendix B.

4.1. The Set-Up

“Coordinates are given in a local map-fixed Cartesian frame (in meters)—x axis is aligned with the map’s horizontal axis, and y with the vertical. Coordinates are continuous (i.e., no raster grid). Paths are executed as time-stamped waypoints derived from the iso-probability field.”

For all examples, the 20 × 20 km² urban environment shown in Figure 4 was used. It includes a high-density downtown core, medium-density suburban regions, and sparsely populated areas farther from the city center. The road network is shown as red lines. The blue areas in Figure 4 represent soft obstacles—structures that the target is allowed to enter and spend random periods of time, during which it would not be detectable by the search agents.

Figure 4. (a) 20 × 20 km² Urban environment used for all examples. (b) Zoom-in 6 × 6 km² City center.

Based on data provided in [48,49], we use the parameter values in Table 1. Priority settings may vary across different target types. The four target groups considered, herein, were based on simple demographics (Table 2).

Table 1. Parameters for the missing-person motion model used for all examples.

$\mathit{\sigma }$ (rad)	${\mathit{p}}_{\mathit{r}\mathit{a}\mathit{n}\mathit{d}}$	${\mathit{p}}_{\mathit{t}\mathit{r}\mathit{a}\mathit{v}}$	${\mathit{p}}_{\mathit{b}\mathit{a}\mathit{c}\mathit{k}}$	${\mathit{p}}_{\mathit{d}\mathit{i}\mathit{r}}$	${\mathit{p}}_{\mathit{r}\mathit{o}\mathit{u}\mathit{t}\mathit{e}}$
0.518	1	0.276	0	0.938	0.312
${\mathit{p}}_{\mathit{p}\mathit{r}\mathit{i}\mathit{v}\mathit{a}\mathit{t}\mathit{e}}$	${\mathit{p}}_{\mathit{r}\mathit{e}\mathit{s}\mathit{i}\mathit{d}\mathit{e}\mathit{n}\mathit{c}\mathit{e}}$	${\mathit{t}}_{\mathit{s}\mathit{t}\mathit{o}\mathit{p}}\mathsf{(}\mathit{s}\mathsf{)}$	${\mathit{\mu }}_{\mathit{v}}$  (m/s)	${\mathit{\sigma }}_{\mathit{v}}$  (m/s)	${\mathit{d}}_{\mathit{r}\mathit{o}\mathit{u}\mathit{t}\mathit{e}}$  (m)
0.05	0.01	50	0.8	0.0815	10

Table 2. Priority Setting for Four Different Target Types.

Target Type (Age Span)	Children (0–12)	Teenagers (13–19)	Adults (19–60)	Seniors (60+)
Priority	0.8	0.7	0.5	0.65

One should note that all parameters in our algorithms are tunable according to the demographics of the lost individuals, where these choices do not affect the performance of the proposed search method.

All potential target trajectories considered for the simulations originate from the last-known position (LKP) of the missing person. Figure 5 illustrates an example set of 100 such trajectories.

Figure 5. One hundred sample missing-person trajectories over a two-hour period.

The searches for missing persons were conducted using identical robots/UAVs. The UAVs were assumed to fly at an altitude high enough to clear all obstacles in the environment. These homogeneous robots were assumed to be capable of following arbitrary paths at speeds of up to 30 m/s and detecting a person within a 30 m ground radius, provided there is an unobstructed line of sight.

For all examples presented in this paper, it was assumed that, for the search of the missing persons, there were twelve identical robots/UAVs (initially) available, distributed amongst three ground search–response stations. All stations had a capacity of four robots. Station 1 was located at (8000 m, 8000 m), Station 2 was located at (12,000 m, 12,000 m), and Station 3 was located at (4000 m, 12,000 m), respectively.

Furthermore, it was assumed that (1) for targets with priority of 0.5, any search task can be assigned a maximum of four robots, (2) for targets with priority level of 0.65 and 0.7, any search task can be assigned a maximum of five robots, and (3) for targets with priority level of 0.8, any search task can be assigned a maximum of six robots. A total city-wide concurrent response capability of up to a maximum of six missing persons is enabled, and at least one robot per future target must be kept in reserve.

One should note that, at any time, if a target is detected (i.e., declared found), the search is paused, and robots are re-allocated. The optimization process may return some robots back to their bases/stations if determined to be part of the optimal solution.

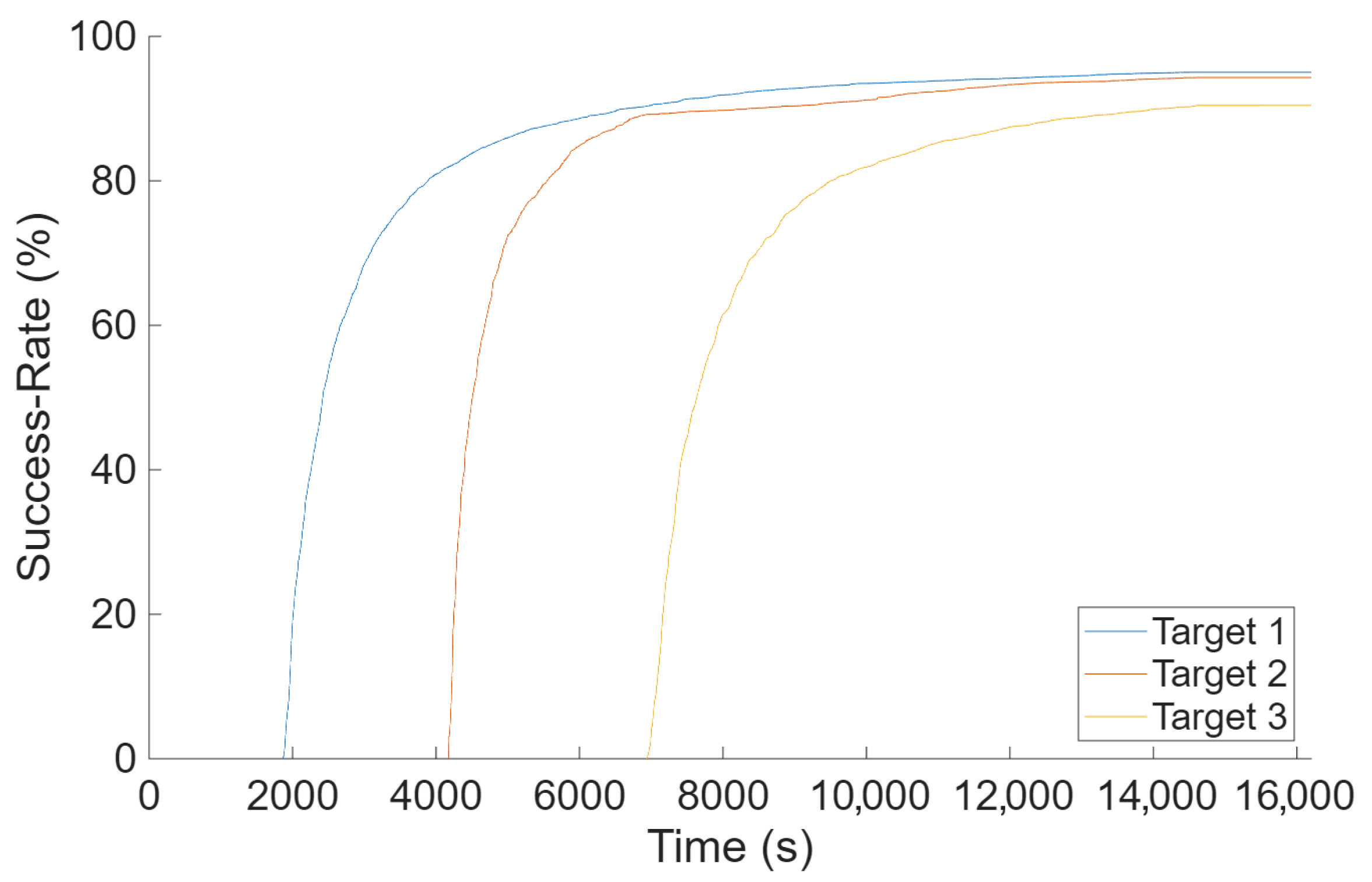
4.2. A Three-Target Search Example

In this example, Target 1 was assumed to go missing at LKP 1, (8768 m, 12,958 m) at t = 0 s but was reported missing at t = 1800 s. Target 2 was assumed to go missing at LKP 2 (13,613 m, 10,762 m) at t = 3000 s but was reported missing at t = 4000 s. Target 3 was assumed to go missing at LKP 3 (14,712 m, 16,061 m) at t = 5000 s but was reported missing at t = 6800 s. All targets were assigned a priority level of 0.5.

Figure 6a–d show the 100% iso-probability curves for this three-target scenario at four different time points. The curves were determined based on a simulation of 10,000 possible target motions emanating from their respective LKPs.

Figure 6. This three-target figure shows 100% iso-probability curves at (a) t = 2400 s, (b) t = 4800 s, (c) t = 7200 s, and (d) t = 9600 s, respectively.

Figure 7a–c illustrate an example case of successful detection for Targets 1, 2, and 3, respectively. The process is briefly summarized below:

Figure 7. Three successful detection examples: (a) Target 1 was detected at t = 7082 s, (b) Target 2 was detected at t = 10,094 s, and (c) Target 3 was detected at t = 7336 s, respectively.

1.

At t = 1800 s, when the first missing target was reported, Search Task 1 was created and optimally assigned four robots (#5, 6, 7, and 8). Eight robots were kept in reserve for future use.

2.

At t = 4000 s, when the second missing target was reported, Search Task 2 was created. Consequently, the search was paused for reallocation of all robots: four robots (#1, 2, 3, and 4) were assigned to Task 2, and four robots (#5, 6, 7, and 8) remained assigned to Task 1. Four robots were kept in reserve for future use.

3.

At t = 6800 s, when the third missing target was reported, Search Task 3 was created. Consequently, the search was paused, once again, for reallocation of all robots: four robots (#1, 2, 3, and 9) were assigned to Task 3, one robot (#4) remained assigned to Task 2, and four robots (#5, 6, 7, and 8) remained assigned to Task 1. Three robots were kept in reserve for future use.

4.

At t = 7082 s, Target 1 was found. Consequently, the search was paused for reallocation of all robots: four robots (#1, 2, 3, and 9) remained assigned to Task 3, four robots (#4, 5, 7, and 8) were assigned to Task 2, and one robot (#6) moved to Station 2.

5.

At t = 7336 s, Target 3 was found. Consequently, the search was paused for reallocation of all robots: four robots (#4, 5, 7, and 8) remained assigned to Task 2, three robots moved to Station 1 (#1, 2, and 3), and one robot (#9) moved to Station 3.

6.

At t = 10,094 s, the last target, Target 2, was found. All robots returned to their stations.

In order to evaluate the performance of the proposed search method for this scenario, 10,000 simulated target trajectories were used. Figure 8 shows the (detection) success rate versus search time for all three targets for a four-hour search window. After four hours of searching, a success rate of 95% was achieved for Target 1, 94% for Target 2, and 90% for Target 3.

Figure 8. Success rate versus search time for a four-hour search period for three targets with equal priorities.

For comparison, the simulations were re-run for targets with different priorities: Target 3 had a higher priority level of 0.65, while Targets 1 and 3 remained at a priority of 0.5. In this scenario, after four hours of searching, a success rate of 95% was achieved for Target 1, 93% for Target 2, and 95% for Target 3, respectively. Table 3 shows the mean detection times for the equal priority case, as well as the non-equal priority case.

Table 3. Mean Detection Times for The Three-target Scenario.

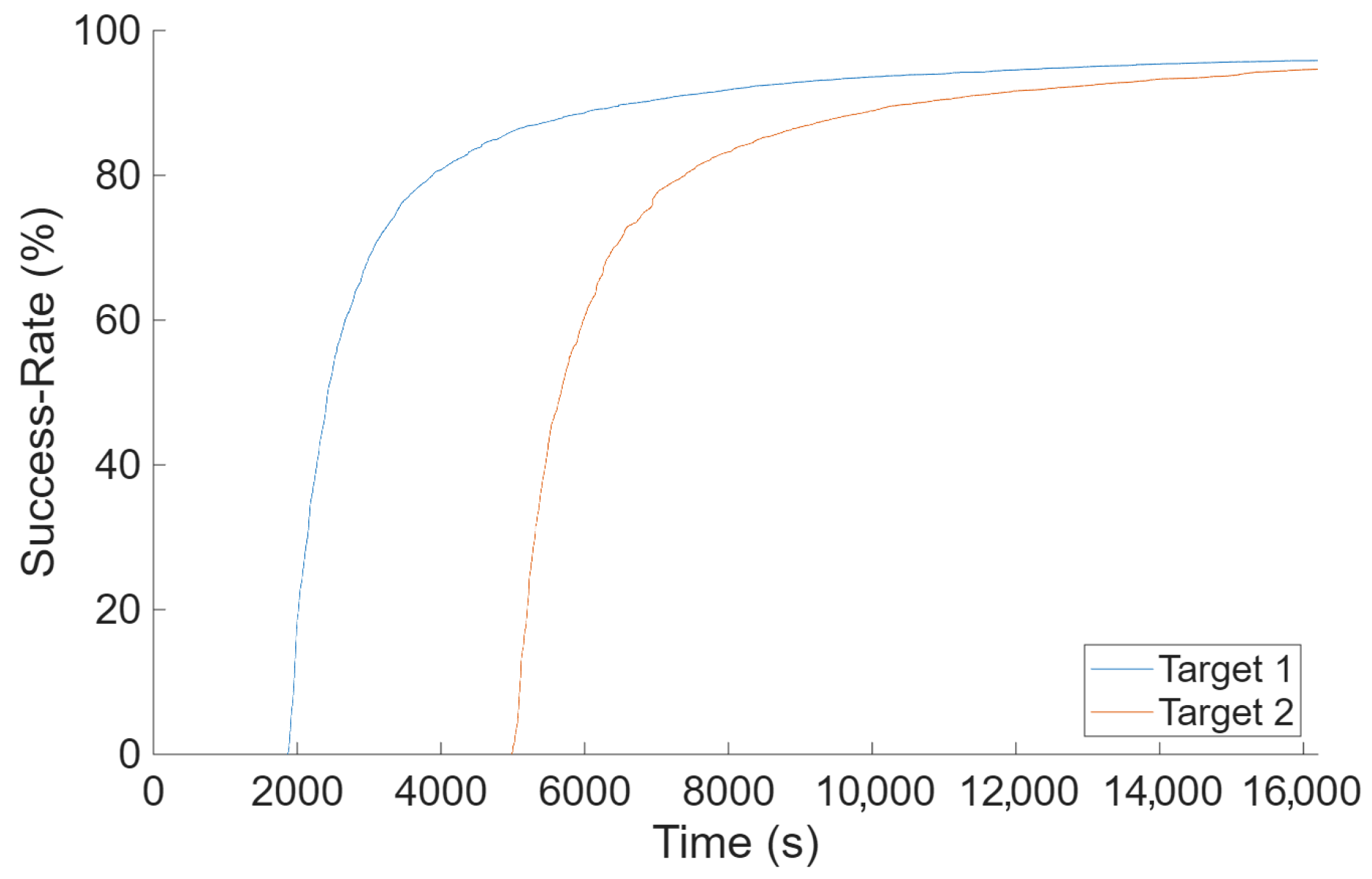
	Mean Detection Time (s)
Target Number	1	2	3
Equal Priority (All 0.5)	1175	808	1132
Non-Equal Priority (0.5, 0.5, 0.65, respectively)	1201	745	1011

5. Comparison Study

In order to evaluate the effectiveness of the proposed dynamic-allocation method, comparative simulations were conducted using an alternative approach, namely, the equal-allocation method. In this alternative comparison method, robots are distributed equally among the tasks while still satisfying the three constraints described in Section 3.2.1. Furthermore, for fairness of comparison, although search robots focus on their own respective targets, while using their own respective iso-probability curves, they are allowed to detect targets belonging to other tasks.

A set of 500 distinct/random simulation examples (each with a 10,000 target trajectories) were run for a six-target scenario under the same settings outlined in Section 4.1 and Appendix B. The targets’ missing and reporting times were also randomly generated. All targets had equal priority. Twelve UAVs were utilized for the searches.

The searches for the alternative method and the proposed method were compared by the mean detection times for the 500 distinct samples (averaged over 6 targets’ detection times). Table 4 shows the mean detection times for both methods. As shown, it was clearly validated that the proposed optimal resource-allocation and search method indeed enhances mean detection performance in multi-target scenarios. Statistical analysis confirmed that this improvement is significant with a confidence level of 99%. Our method reduced the mean detection time by an average of 23%, in a range of minimum 0% to maximum of 49% improvement for the 100 samples, Figure 9.

Table 4. Mean Detection Times and Standard Deviation for Two Methods of Comparison.

	Mean Detection Time (s)	Standard Deviation (s)
Proposed Method	1197	209
Alternative Method	1549	202

Figure 9. Histogram of percentage improvements in detection times as achieved by our proposed method.

6. Conclusions

In this work, we propose a novel dynamic resource-allocation method with overlapping-area handling. This method utilizes an efficient dynamic task allocation strategy to balance the search effort across all targets. The search trajectories are guided by continuously updated iso-probability curves while eliminating overlapping regions. Moreover, the framework incorporates full planning of robot deployment from search–response stations, enhancing the realism and practical applicability of the method.

Simulation results confirm that the proposed dynamic allocation method tangibly and positively reduces mean detection times compared with the equal-allocation method, demonstrating its effectiveness for multi-target search scenarios.

While the current equal partition method reduces computing time, it cannot ensure a fair distribution of work among robots after the duplicate regions of the iso-probability curve are eliminated. Looking ahead, future work may explore extending the proposed trajectory-generation algorithm to fixed-time control strategies, which provide faster convergence and improved robustness. In particular, the switching-topology coordination models presented in [50] offer promising directions for enhancing scalability and responsiveness. Integrating such approaches with our dynamic task allocation framework could further strengthen multi-robot search performance in dense urban environments.