Abstract
Kinematic redundancy of manipulators is a well-understood topic, and various methods were developed for the redundancy resolution in order to solve the inverse kinematics problem, at least for serial manipulators. An important question, with high practical relevance, is whether the inverse kinematics solution is cyclic, i.e., whether the redundancy solution leads to a closed path in joint space as a solution of a closed path in task space. This paper investigates the cyclicity property of two widely used redundancy resolution methods, namely the projected gradient method (PGM) and the augmented Jacobian method (AJM), by means of examples. Both methods determine solutions that minimize an objective function, and from an application point of view, the sensitivity of the methods on the initial configuration is crucial. Numerical results are reported for redundant serial robotic arms and for redundant parallel kinematic manipulators. While the AJM is known to be cyclic, it turns out that also the PGM exhibits cyclicity. However, only the PGM converges to the local optimum of the objective function when starting from an initial configuration of the cyclic trajectory.
1. Introduction
Kinematically redundant serial kinematic manipulators (SKM) are gaining importance for dedicated solution in flexible automation due their advantageous properties. Only a few kinematically redundant parallel kinematic manipulators (PKM) have been proposed, and they have not yet seen a similar application in industry. Kinematic redundancy offers various advantages, and it can in particular be exploited to improve dexterity, to avoid singularities, to circumvent obstacles, and eventually to increase the workspace. These advantages are accompanied with an increased complexity of the control and with increased costs, however. The complexity is due to the non-uniqueness of the solution to the geometric inverse kinematics problem (IKP), which consists of finding a vector of generalized coordinates (joint coordinates in SKM) for a given vector of end-effector (EE) coordinates satisfying the forward kinematics relation
where f is the forward kinematics mapping. The corresponding velocity IKP, in a given pose , is to find a vector of generalized coordinates for given EE-velocity satisfying the velocity forward kinematics
where is the forward kinematics Jacobian.
A manipulator is kinematically redundant if , where r is called the degree of redundancy, n is the degree of freedom (DOF), and m denotes the dimension of the task space. For a redundant manipulator, the Jacobian is not square, and the inverse kinematics has r-dimensional solution set.
A number of solution techniques for solving the geometric IKP problem for redundant manipulators have been introduced in the last three decades, almost exclusively focusing on SKM [1]. Most of them determine a solution of the geometric inverse kinematics problem from a solution of the velocity inverse kinematics problem with the aim to provide an online solution scheme that can be executed on the robot controller with a well-defined computation time. As a consequence, all these method yield a local solution rather than the global solution of the geometric inverse kinematics problem. The two most widely used local solution schemes are the following:
- Null space methods: A particular solution of (2) is determined by adding a vector in the null-space of the Jacobian. The latter is usually the gradient of a scalar objective function that is to be maximized (or minimized).
- Task augmentation methods: Redundancy is eliminated by adding r auxiliary tasks, in order to make the overall system non-redundant.
Most industrial use cases involve repetitive tasks. That is, the EE performs a cyclic motion. An obvious requirement for safe application of redundant robots is that the IK solution is well-determined in the sense that for given pose of the EE the IK solution scheme always yields the same pose of the robot. This property is called cyclicity, which means that for a closed EE-path the IK solution method gives a closed path in joint space. It is well-known that null-space methods cannot be guaranteed to be cyclic [2]. This is an important drawback of the null-space methods since the motion of the chain is unpredictable during the motion. The cyclicity problem was first analyzed in a differential geometric framework in [3] and then explored in [4,5] for the pseudoinverse solution. In [6] the authors were able to design a feedback control law to produce convergence of the joint motion towards a cyclic trajectory assuming the null space vector as a linear map of the EE trajectory.
While task augmentation methods are cyclic [6], they suffer from algorithmic singularities [7]. It must be mentioned that this topic was extensively used and studied for SKM (aiming to avoid collision and singularities). To the authors knowledge these same techniques have been applied very rarely to PKMs as in [8]. For the sake of the completeness, we must point out that recently these classical schemes have been applied to the hyper-redundant manipulators [9,10] as well as algorithms based on the machine learning have been applied to the redundancy resolution [11].
In this paper the projected gradient method (PGM) and the augmented Jacobian method (AJM) are compared by means of examples when applied to SKM and PKM. The methods are designed to minimize an objective function. In the following, and w.l.o.g., the objective function will be the sum of the squared joint variables. The comparison regards (1) the cyclicity of the joint trajectories, and (2) the dependency of the (cyclic) joint trajectory with respect to changes in the initial configuration. The sensitivity is an aspect that has not yet been addressed in the literature as well as the cyclicity of the solutions for PKMs. It will be shown that only the projected gradient method is capable of minimizing the objective function independently of the initial configurations. Results are reported for both SKM and PKM.
This is the first publication that addresses the cyclicity of PGM. The novel contribution is a numerical investigation and comparison of the cyclicity of PGM and AJM when applied to SKM as well as to PKM.
2. Redundancy Resolution Methods
Redundancy resolution of the differential kinematics of a manipulator is expressed as:
is the Moore–Penrose pseudoinverse of the manipulator Jacobian . In order to avoid integration drift, an algorithm solution (CLIK: closed-loop inverse kinematics) of Equation (3) is widely adopted and the geometric inverse kinematic problem expressed as:
where represents the error between the desired and actual EE location and is a positive–definite diagonal gain matrix. Numerical integration of the Equation (4) given the initial configuration followed by the solution of the forward position kinematic equations closes the feedback loop.
- PGMThe PGM exploits the fact that a general solution of the differential kinematics can be substituted to Equation (4) when a desired joint rate vector is projected into the null space of :with defined as the projector matrix. The added term generates self–motion of the kinematic chain without affecting the EE velocity. Vector can be chosen in order to make a scalar objective function stationary by using the gradient projection method, such that , with . may be any analytical differentiable function expressed in terms of the joint variables only.
- AJMA different approach is followed in the AJM. An additional constraint task is imposed to the original task of the EE. Following [7,12], the objective function is projected onto the null space of and imposed to be zero. Formally we can write:is an orthonormal basis for the null space of and is the gradient of with respect to the joint variables as in the previous method. Therefore, Equation (6) yields r independent constraints keeping at the extreme at each time of the trajectory starting from the initial configuration .The added Jacobian can simply obtained asthat leads to the CLIK kinematic resolution expressed as:
The two methods are, therefore, designed to reach the same goal in order to have a direct comparison between them.
As pointed out in [6] for SKM, the cyclicity of the joints trajectories for a closed EE path can be reached exactly, asymptotically or it cannot even be reached. Exact cyclicity is obtained whenever at the steady–state, i.e., . It has been shown in [6] that the augmented Jacobian can be expressed in this form thus proving its cyclicity. Furthermore, the cyclicity property may be verified on–line by calculating that the Lie brackets formed by any columns of the control matrix, , are linear combinations of the columns (involutive property) [13]. This calculation was indeed performed in this paper.
On the contrary, PGM cannot guarantee to lead to exact or even asymptotic cyclicity a priori. Indeed, it has been proved that control scheme in Equation (4) can only be asymptotic cyclic with , with representing the joint trajectory to converge to in order to reach repeatability.
3. Numerical Simulations
PGM and AJM are implemented for the serial manipulators 4R and the parallel 2RRP planar manipulators and for a 6R industrial UR10e robot. The planar manipulators have a degree of redundancy , while the 6DOF arm has . The end effectors of the manipulators can track a circle at a given constant speed.
For all the manipulators, the objective function to be minimized was chosen to be:
with for the SKMs and for the PKM. The simple nature of strongly simplifies the computations. In the PGM method, indeed, only the analytical calculation of the gradient of the objective function is required. Instead, AJM requires the analytical calculation of the gradient of in Equation (6) to obtain the added rows of the Jacobian. First, an analytical calculation of is needed. This can be avoided using an alternative procedure proposed in [14] to calculate only numerically.

Table 1.
4R. a: links length; (), R: coordinates of the centre and radius of the EE trajectory.

Table 2.
2RRP. a: links length; H: base width, (), R: coordinates of the centre and radius of the EE trajectory.

Table 3.
6R. (), R: coordinates of the centre and radius of the EE trajectory. EE trajectory on the plane m. : Denavit-Hartenberg geometrical parameters.
3.1. Serial 4R
The Jacobian of the manipulator in Figure 1a is trivial and it is not shown in the paper. Instead, Equation (10) shows used in the AJM:
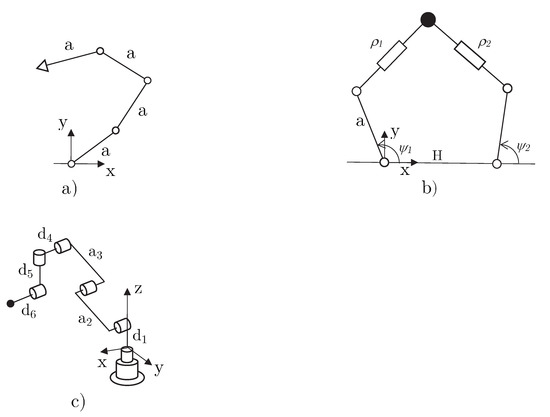
Figure 1.
The test cases: (a) Planar 4R, (b) Planar 2RRP, (c) UR10 industrial 6R robot.
is then differentiated with respect to the joint angles to obtain .
In Figure 2 we show from both the methods for the planar 4R. The initial configuration was calculated such to be a solution of the inverse position problem and that .
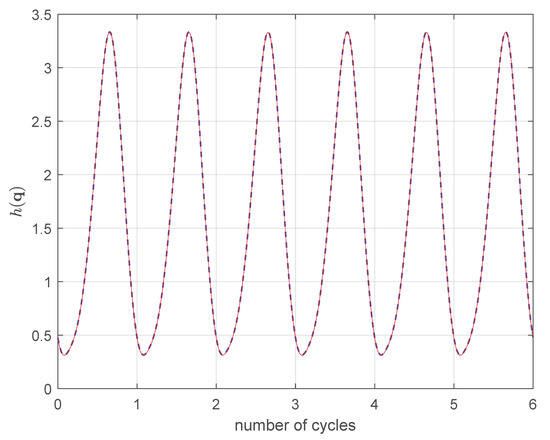
Figure 2.
in 4R. PGM: − (red line), AJM: (blue line).
From Figure 2 we see that from the methods are in very good agreement. Both can keep the objective function stationary. Accordingly, also the joint trajectories of the two methods, shown in Figure 3, only exhibit small differences.
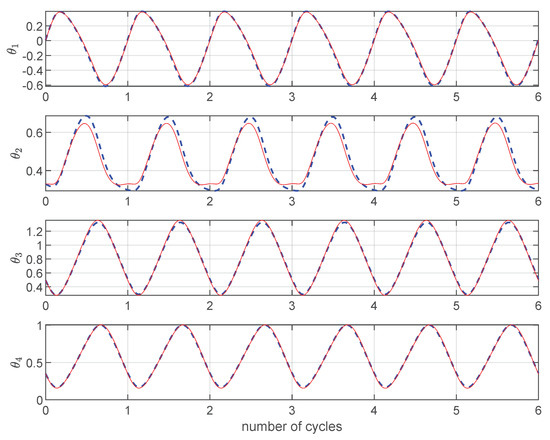
Figure 3.
in 4R. PGM: − (red line), AJM: (blue line).
From Figure 3 we also see that both methods produce cyclic joints trajectories. In the case of the PGM we can verify that only by inspection while for the AJM we performed the numerical calculations of the Lie brackets associated to the augmented Jacobian. To have cyclicity we need to have that for any two columns and of , their Lie bracket is a linear combination of the columns of the control matrix. In this case, for each step of calculation we obtain of the order of proving the cyclicity. Figure 4 shows the objective function whenever as with . As expected, the results show that AJM can only keep the constraint as it is, while PGM quickly reaches the minimum.
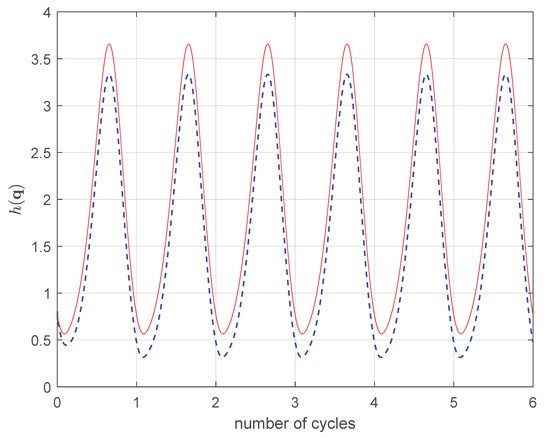
Figure 4.
in 4R with . PGM: − (red line), AJM: (blue line).
The inability of AJM to converge to the minimum is stressed in Figure 5 where is plotted with different initial conditions.

Figure 5.
AJM: in 4R. : (black line), : (red line), : − (blue line).
We then tested the robustness of PGM as the initial conditions varied. In Figure 6, is computed by PGM when starting from different initial configurations. The method allows reaching the minimum even when . In this case the method converges in cycles chosen as threshold. Similarly, the joints trajectories coincide quickly. This is a striking characteristic of this method that proves to be robust with respect to the initial configuration of the motion that can be inaccurate for some reasons. In this case the method can reach the minimum curve even when the gap from the correct initial configuration is about .
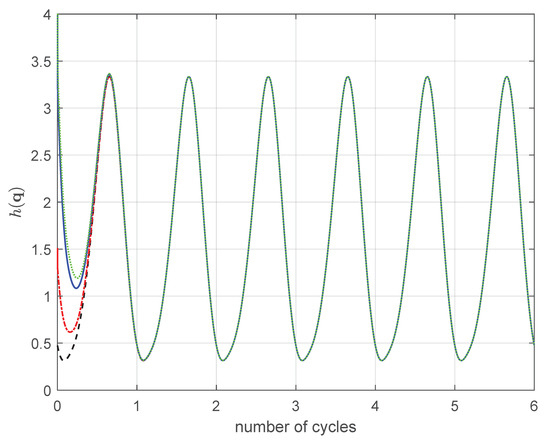
Figure 6.
PGM: in 4R. : (black line), : (red line), : − (blue line), : ⋯ (green line).
3.2. Parallel 2RRP
The kinematic relation of the PKM is [15]:
The forward kinematics Jacobian in (2) is thus . For the planar PKM in Figure 1b), the Jacobians and are
The term used in the AJM is
As with the planar serial case, Figure 7 shows from both the methods for the PKM. The initial configuration was calculated such to be a solution of the inverse position problem and that .
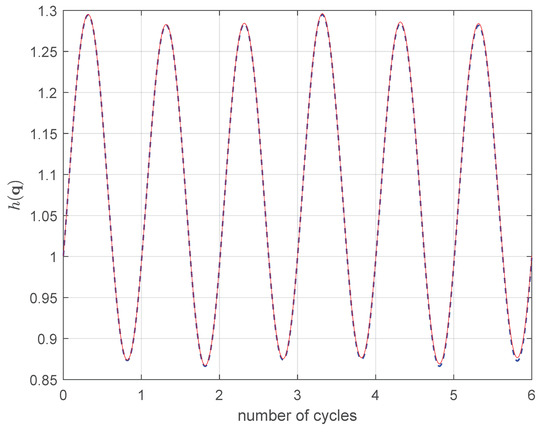
Figure 7.
in 2RRP. PGM: − (red line), AJM: (blue line).
Also in this case the methods coincide.
We repeat the tests considering . However, in this case because of the different types of joints we use with . The methods work consistently for the PKM as well. Only PGM can quickly reach the minimum of the objective function as shown in Figure 8.
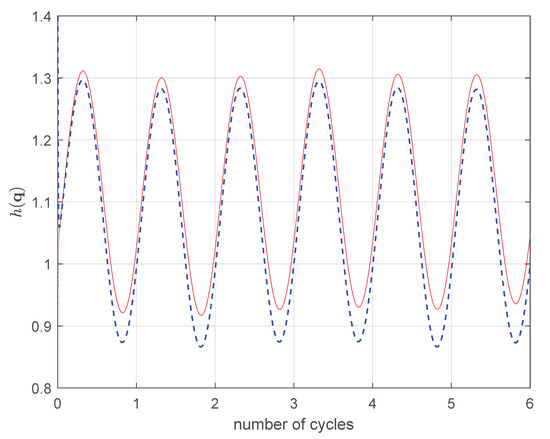
Figure 8.
in 2RRP with . PGM: − (red line), AJM: (blue line).
Therefore, AJM cannot reach the minimum as pointed out in Figure 9.
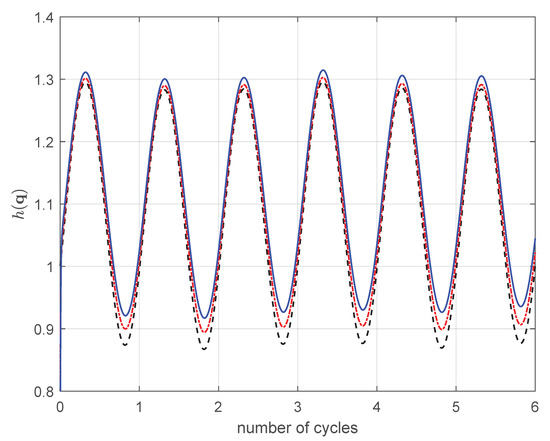
Figure 9.
AJM: in 2RRP. : (black line), : (red line), : − (blue line).
The robustness of PGM when varying the initial conditions for the PKM is essentially the same of that for the serial . The results of the test are shown in Figure 10. The convergence rate in terms of number of cycles was computed of .
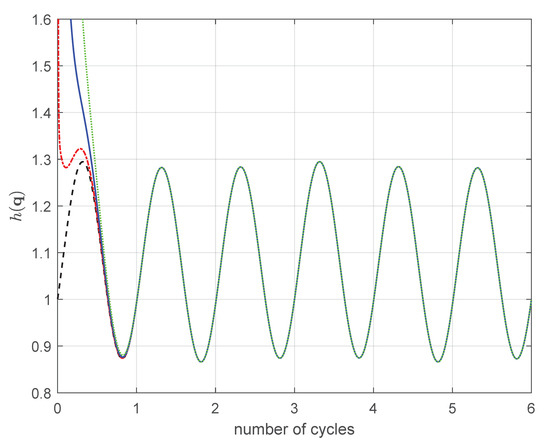
Figure 10.
PGM: in 2RRP. : (black line), : (red line), : − (blue line), : ⋯ (green line).
3.3. Serial 6R
Finally the AJM and PGM methods were tested for a 6DOF industrial robotic arm UR10e. In this case, due to their sizes, it is not possible to show explicitly the terms involved into calculations. Figure 11 shows that also in this case the methods coincide when , i.e., the objective function is at the minimum at the initial configuration.
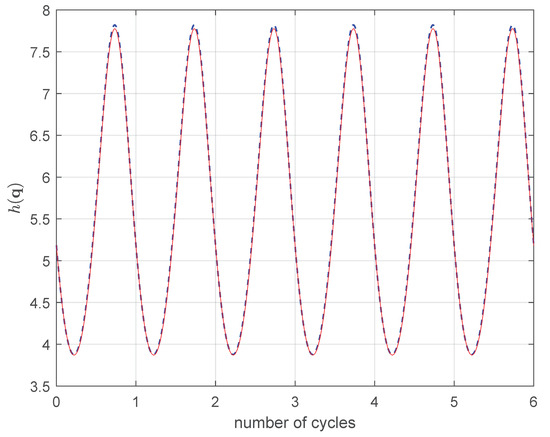
Figure 11.
in 6R. PGM: − (red line), AJM: (blue line).
Also, in the case of with , the methods work as in the other cases as shown in Figure 12.
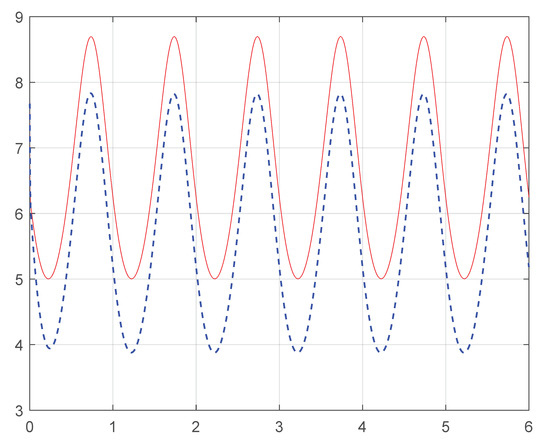
Figure 12.
in 6R with . PGM: − (red line), AJM: (blue line).
The response of the AJM in terms of variation of the initial conditions is shown in Figure 13.
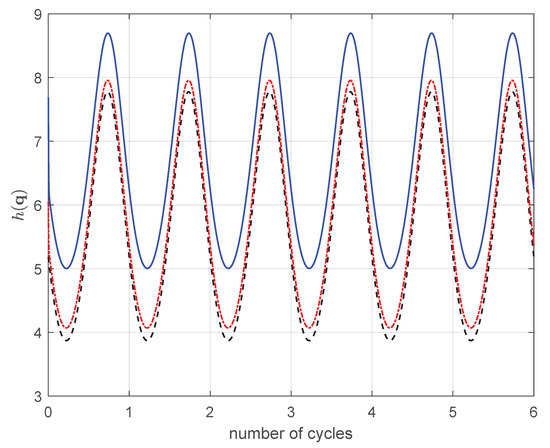
Figure 13.
AJM: in 6R. : (black line), : (red line), : − (blue line).
Sensitivity of the PGM method to the initial configuration is shown in Figure 14. The behavior is similar to the other cases.
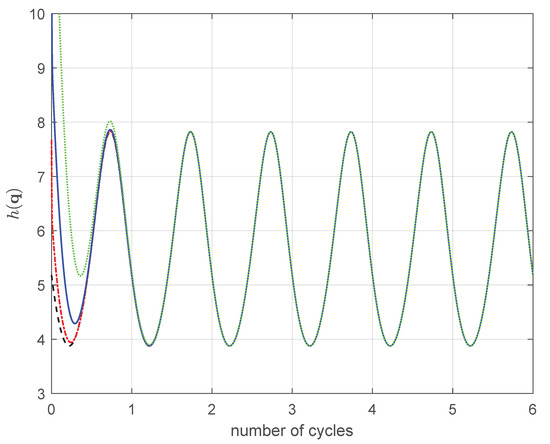
Figure 14.
PGM: in 6R. : (black line), : (red line), : − (blue line), : ⋯ (green line).
The convergence measure in terms of number of cycles is . In order to check the robustness of the methods, two further test were performed. First, the circular trajectory was tracked with a variable EE velocity obtained as with
Then, a test with a trajectory represented by Bernoulli’s Lemniscate (∞-like curve) tracked with an EE velocity . In this case, the angular velocity follows Equation (14) while the radial velocity is kept constant. The authors did not find discrepancies with respect to the case of the circle trajectory tracked at the constant velocity for all the manipulators. As an example, Figure 15 shows the robustness of the PGM for the PKM when the EE is tracking the ∞-like curve at the v velocity.
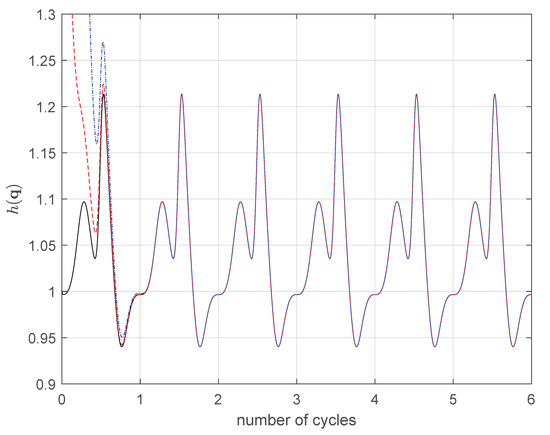
Figure 15.
PGM with v and ∞-trajectory: in 2RRP. : − (black line), : (red line), : (blue line).
4. Conclusions
This paper is the combination of two research directions pursued independently: investigation of the trajectories cyclicity and of the gradient-based algortihms for redundancy resolution. In the past, the augmented Jacobian method was shown to lead to cyclic trajectories while the projected gradient method for the inverse kinematics was only used to maximize an objective function. It was never attempted to use the projected gradient method to generate cyclic inverse kinematics solution. In this paper, the cyclicity property of the gradient-based and of the augmented Jacobian method for the redundancy resolution is investigated by means of numerical examples. This paper is the first presented in the literature in which a such comparison is performed.
Briefly, the main results of this paper are: (a) The PGM leads to cyclic trajectories at which the objective function attains a minimum, and converges to such cyclic trajectory even if the initial configuration is far from a point where the objective is minimized. The tests on the robustness with respect to the initial configurations showed similar behavior for all the manipulators investigated. On the contrary, as expected, the AJM can only keep the objective function at the value at the initial configuration. (b) The results are identical for serial and parallel manipulators since both kinematically characterized by a forward/inverse kinematic mapping. Both methods are cyclic either for the SKMs or for the PKM investigated. The cyclicity property of the AJM was confirmed by numerical calculation of the relevant Lie brackets, while the asymptotic cyclicity of the PGM was confirmed by numerical calculation. These results are novel and it remains to further investigate the properties of the PGM. Moreover, the analyses carried out in this paper are numeric and further research needs to address this topic from an analytical point of view.
Author Contributions
Conceptualization, M.R. and A.M.; software, M.R. and A.M.; investigation, M.R. and A.M.; writing—original draft preparation, M.R. and A.M.; writing—review and editing, M.R. and A.M.; Both authors have equally contributed to this paper. All authors have read and agreed to the published version of the manuscript.
Funding
The second author acknowledges support from the LCM K2 Center for Symbiotic Mechatronics within the framework of the Austrian COMET-K2 program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nenchev, D.N. Redundancy Resolution through Local Optimization: A Review. J. Robot. Syst. 1989, 6, 769–798. [Google Scholar] [CrossRef]
- Siciliano, B. Kinematic Control of Redundant Robot Manipulators: A Tutorial. J. Lntelligent Robot. Syst. 1990, 3, 201–212. [Google Scholar] [CrossRef]
- Shamir, T.; Yomdin, Y. Repeatability of Redundant Manipulators: Mathematical Solution of the Problem. IEEE Trans. Autom. Control 1988, 33, 1004–1009. [Google Scholar] [CrossRef]
- Klein, C.A.; Kee, K.B. The nature of drift in pseudo-inverse control of kinematically redundant manipulators. IEEE Trans. Robot. Automat. 1989, RA-5, 231–234. [Google Scholar] [CrossRef]
- Luo, S.; Ahmad, S. Predicting the Drift Motion for Kinematically Redundant Robots. IEEE Trans. Syst. Man Cybern. 1992, 22, 717–728. [Google Scholar] [CrossRef]
- De Luca, A.; Lanari, L.; Oriolo, G. Control of Redundat Robots on Cyclic Trajectories. In Proceedings of the IEEE International Conference on Robotics and Automation, Nice, France, 12–14 May 1992; pp. 500–506. [Google Scholar]
- Baillieul, J. Kinematic programming alternatives for redundant manipulators. In Proceedings of the IEEE International Conference on Robot and Automation, St. Louis, MO, USA, 25–28 March 1985; pp. 772–778. [Google Scholar]
- Simas, H.; Di Gregorio, R. A Technique Based on Adaptive Extended Jacobians for Improving the Robustness of the Inverse Numerical Kinematics of Redundant Robots. J. Mech. Robot. 2019, 11, 020913. [Google Scholar] [CrossRef]
- Chembuly, V.V.M.J.S.; Voruganti, H.K. An Efficient Approach for Inverse Kinematics and Redundancy Resolution Scheme of Hyper-Redundant Manipulators. AIP Conf. Proc. 2018, 1943, 020019. [Google Scholar]
- Yahya, S.; Moghavvemi, M.; Mohamed, H.A.F. Geometrical Approach of Planar Hyper-Redundant Manipulators: Inverse Kinematics, Path Planning and Workspace. Simul. Modell. Pract. Theory 2011, 19, 406–422. [Google Scholar] [CrossRef]
- Perrusquía, A.; Yu, W.; Li, X. Multi-agent reinforcement learning for redundant robot control in task-space. Int. J. Mach. Learn. Cybern. 2020. [Google Scholar] [CrossRef]
- Chang, P.H. A closed-form solution for inverse kinematics of robot manipulators. IEEE J. Robot. Automat. 1987, 3, 393–403. [Google Scholar] [CrossRef]
- Boothby, W.M. An Introduction to Differentiable Manifolds and Riemannian Geometry; Academic Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Klein, C.A.; Chu-Jenq, C.; Ahmed, S. A New Formulation of the Extended Jacobian Method and its Use in Mapping Algorithmic Singularities for Kinematically Redundant Manipulators. IEEE Trans. Robot. Autom. 1995, 11, 50–55. [Google Scholar] [CrossRef]
- Gosselin, C.; Angeles, J. Singularity Analysis of Closed-Loop Kinematic Chains. IEEE Trans. Robot. Autom. 1990, 6, 281–290. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).