Abstract
The spectrum of silver, excited in a vacuum spark, was recorded in the region 150–350 Å on a 3-m grazing incidence spectrograph. The resonance 4dk–(4dk−15p + 4dk−14f + 4p54dk+1) was studied in the Ag6+–Ag8+ spectra (Ag VII–Ag IX) with k = 5–3, respectively. Several hundred lines were identified with the aid of the Cowan code and orthogonal operator technique calculations. The energy levels were found and the transition probabilities were calculated.
1. Introduction
Six- through eight-times ionized silver atoms are the members of the isonuclear sequence of the silver ions with the unfilled 4dk (k = 5–3) ground-state configuration. The spectra of these ions have not been investigated previously. The excitation of the 4d electron leads to the lowest odd configurations 4dk−15p and 4dk−14f. The third odd configuration 4p54dk+1 is formed by the excitation of the inner shell 4p electron. The resonance transitions are represented by the transitions from these odd configurations to the ground-state configuration. Out of all resonance transitions only the 4dk–4dk−14p (k = 9–6) ones were previously studied in the silver spectra of the lower ionization stages: Ag III [1], Ag IV [2], Ag V [3] and Ag VI [4]. On the other hand, all three resonance transition arrays were investigated in rather simple spectra of ions having 4d and 4d2 ground-state configurations: Ag XI [5,6] and Ag X [7]. In this article we report the results of the study of the Ag VII, Ag VIII and Ag IX to fill the gap between the Ag VI and Ag X isonuclear spectra.
This study is part of a project to get atomic data for the ions of lighter than tin chemical elements isoelectronic with Sn IX–Sn XIV which are relevant to a development of bright source for projection lithography at the 135 Å wavelength. The results for the palladium isonuclear spectra were recently published (see [8] and references therein). Such isoelectronic data are necessary for validation of previously reported analyses of the corresponding tin ion spectra [9,10]. Research on these spectra is also of general interest to atomic physics for improving of theoretical methods of calculations of multi-electron heavy atom spectra.
2. Experiment
The experimental technique and the theoretical approaches for spectrum calculations were the same as in our previous publications [7,8]. Briefly, the light source was a low-inductance vacuum spark operated with an additional inductance up to 2.5 μH. A 150 or 12 μF capacitor was charged up to 4.5 kV resulting in the spark peak current in a range of ~10–20 kA. Ionization stages were distinguished by comparing the intensities of the lines at various peak currents. A 3 m grazing incidence spectrograph (85° angle of incidence) equipped with a gold coated holographic grating having 3600 lines/mm was used for taking the spectra. A plate factor of the spectrograph in the region 160–350 Å was 0.32–0.46 Å mm−1 respectively. The spectra were recorded on Kodak SWR photographic plates (Eastman Kodak Company, Rochester, NY, USA) and measured on an EPSON EXPRESSION 10000XL scanner (Seiko Epson Corporation, Suwa, Japan). Wavelengths were calibrated using titanium ion lines [11] as the standards. The titanium spectrum was superimposed on some silver exposures. The measured wavelength uncertainty is estimated as ±0.005 Å for the unperturbed lines of moderate intensity. General view of the silver spectrum in the region 150–350 Å is shown in Figure 1, where the lines identified in this work, previously identified, and remaining unidentified are marked by different colours depending on particular spectrum.
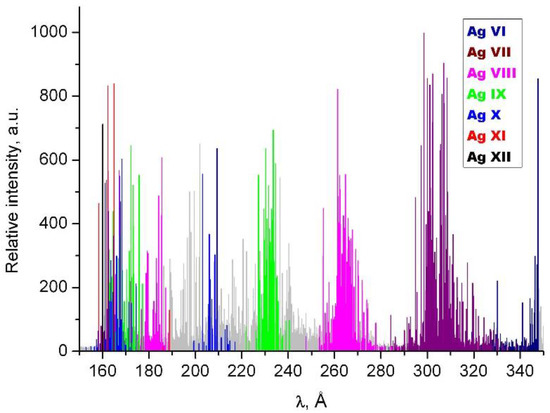
Figure 1.
Spectrum of silver in the region 150–350 Å excited in a vacuum spark. Lines of different ion spectra are marked by different colours: Ag VI—royal blue, Ag VII—wine, Ag VIII—magenta, Ag IX—green, Ag X—blue, Ag XI—red, Ag XII—black and unidentified lines—gray.
The relative line intensities were obtained as described in our previous article [8] “from the measured optical densities using an approximate photoplate response curve estimated from different experiments. They should be considered mostly as qualitative ones because of some uncertainty of used photoplate response curve and neglect of the wavelength dependence of the spectrograph efficiency and photoplate sensitivity. Also the saturation effects resulting from the photoplate response nonlinearity can significantly influence the intensity ratios of the weak to strong lines.” The intensity I = 1000 was attributed to the strongest line of the 4dk–4dk−15p transition array in each ion spectrum.
The program IDEN [12] was used for the spectrum identification. As in [8], ab initio calculations were performed with the use of the Dirac–Fock (DF) code of Parpia et al. [13], or by the Hartree–Fock method with relativistic corrections (HF) with the use of the Cowan code (Cowan programs RCN, RCN2, RCG, and RCE) [14]. Semiempirical correction of ab initio values of Slater parameters was made with the RCE Cowan code or by using a technique of orthogonal operators [15,16,17,18].
The energies derived after the identification of spectral lines were optimized using the program LOPT [19].
3. Results
In the following, the results of the analyses of silver ions in the charge states Ag6+, Ag7+ and Ag8+ are presented. Line identifications are summarized in Table A1, Table A2, Table A3 and Table A4 (see Appendix A at the end of the document) and energy levels are collected in Table A5, Table A6, Table A7, Table A8, Table A9, Table A10 and Table A11. The data were interpreted using semi-empirical orthogonal parameters and Cowan code calculations resulting in calculated values for the energy levels, wave-function composition, transition probabilities and energy parameters. The semi-empirical energy parameters and their comparison with the corresponding ab initio values are shown in Table A12, Table A13 and Table A14.
3.1. Ag VII
A diagram of the low lying configurations of Ag VII with the ground-state configuration 4d5 is shown in Figure 2. As in the case of silver ions in lower stages of ionization (Ag III–Ag VI) we were able to make the analysis of only the 4d5–4d45p transition array (Table A1). The lines of these transitions are represented by a compact group in the region 271–343 Å mostly isolated from the other transitions in Ag VII as well as in the neighboring ions (see Figure 1). Three hundred and seventy-eight lines were identified in this transition array, 47 of them were doubly and one trebly identified. Eight lines are probably blended with previously identified Ag VI transitions. Thirty-four levels out of 37 possible 4d5 ones were found (Table A5) and 142 levels of the 4d45p configurations were located out of 180 possible levels (Table A6). The relative uncertainty of the level energies given by least-squares optimization [19] ranges from 1 to 4 cm−1 for 4d5 levels and from 3 to 8 cm−1 for 4d45p depending on the number of lines used for the level optimization and on their wavelength uncertainties. Identification was performed with the help of the semi-empirical calculations based on the orthogonal operators. The initial orthogonal energy parameters were extrapolated along the sequence Ag IV–Ag V. Final energy parameters of Ag VII after a fitting of the calculated levels to the found levels are listed in Table A12 and Table A13. They are compared with the values from the Parpia et al. code [13]. Only the parameters of the 4d5 and 4d45p configurations are listed in the tables although the matrixes of the interacting 4d5 + 4d45s + 4d35s2 (even) and 4d45p + 4d35s5p + 4d25s25p (odd) configurations were used in the fittings. The parameters of the unknown configurations were fixed on extrapolated values; the interaction parameters were fixed on values obtained with scaling by 0.85 of the ab initio integrals.
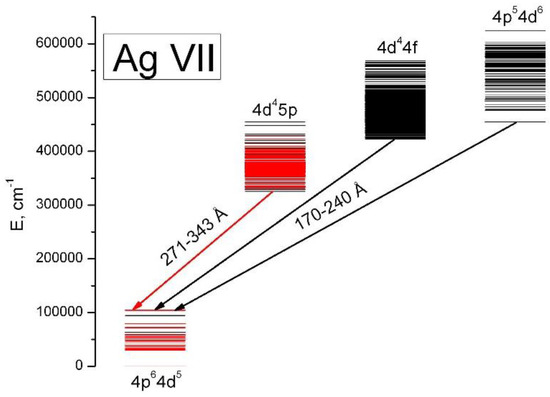
Figure 2.
Energy levels of Ag VII. The arrows show electric dipole transitions. The levels found in this work and studied transitions are marked by red color. Black color indicates unknown levels and transitions.
In a treatment of the 4d5 shell (as well as of the other 4dk shells) by the orthogonal parameter technique O2, O2′, Ea′ and Eb′ are the orthogonal counterparts of the traditional parameters F2(4d,4d,), F4(4d,4d), α and β. The one-electron magnetic (spin-orbit) operator ζ(4d) and the effective 3-particle electrostatic operators T1 and T2 are the same as in Cowan code and (Ac...A0) are additional 2-body magnetic parameters. The 4d45p configuration and the other 4dk−15p configurations contain additional parameters: C1dp–C3pd are the orthogonal counterparts of the Slater exchange integrals G1(4d,5p)–G3(4d,5p); S1dp, S2dp are the effective electrostatic 2-body dp-parameters; Sd.Lp…SS(dp)20 are magnetic 2-body dp-parameters [15], and T16 to T35 are the electrostatic 3-body ddp-parameters. In case of Ag VII 2-body magnetic parameters were varied at the fitting on one bunch keeping the ratios of the corresponding ab initio values. Root mean square deviations of the fitting σ were 14 and 19 cm−1 in even and odd configurations, respectively.
Almost all levels of the 4d5 configuration can be well designated with the leading member of their eigenvector composition. Only 48,086 cm−1 (J = 3/2) and 47119 cm−1 (J = 5/2) were designated with the second term. For 4d45p configuration, in many cases two wave functions have the same first component leading to non-unique labels for the energy levels. Therefore, the level energies are listed in Table A6 along with the level designations to avoid the ambiguities.
According to our predictions the most intense lines of the 4d5–(4d44f + 4p54d6) transitions are expected in the 170–240 Å wavelength range. As it is seen in Figure 1 there are many unknown lines in this region but we were not able to make reliable identification of these lines.
3.2. Ag VIII
The low lying configurations of Ag VIII are shown in Figure 3. The transitions from all low odd configurations decaying to the ground-state 4d4 configuration are identified in this spectrum. The 4d4–4d35p transitions are overlapped with some unknown lines of moderate intensity. But nevertheless, 118 lines were identified in this transition array (Table A2). Twenty-one lines were doubly and two lines trebly identified. Twenty-nine (out of 34 possible) 4d4 levels were found with the relative uncertainty from 3 to 7 cm−1 and collected in Table A7. The levels of the 4d35p configurations are contained in Table A8. It was possible to locate 83 out of 110 possible levels of this configuration. Their uncertainties are from 4 to 14 cm−1. As in Ag VII the identification of the 4d4 4d35p transitions was performed with by means of the semi-empirical calculations based on the orthogonal operators.
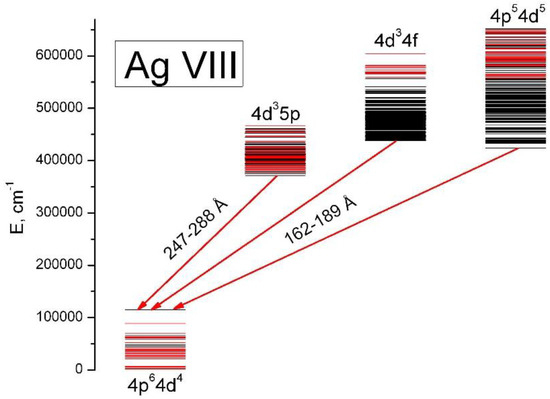
Figure 3.
Energy levels of Ag VIII. The arrows show electric dipole transitions studied in this article. The levels found in this work are marked by red color. Black color indicates unknown levels.
The energy parameters obtained in the final fitting are collected in Table A12 for 4d4 and Table A13 for 4d35p. For the meaning of the energy parameters and the procedure of the calculations see Section 3.1. Root mean square deviations of the fitting were 26 and 47 cm−1 in the 4d4 and 4d35p configurations, respectively. In case of the 4d35p configuration the fitting is affected by the interaction with the levels of the 4p54d5 configuration. The 4d35p levels above ~424,000 cm−1 overlap with the low lying 4p54d5 levels. Their interaction cannot be taken into account in the orthogonal operator code. The LS-coupling scheme is good approximation for the 4d4 levels. The value of the first component of the eigenvector composition for all levels is not less than 50%, thus a unique label by the name of the first component can be assigned to all energy levels. To differentiate 4d4 terms with the same LS values (recurring terms) the seniority numbers are used in the orthogonal operator code, whereas the Nielson and Koster sequential indices [20] are employed in the Cowan code [14]. Both labels are retained in Table A7 for the 4d4 levels because the 4d4–(4d35p + 4d34f + 4p54d5) transitions were analyzed with the aid of the Cowan code as described below. Contrary to 4d4, the percentage of the first component of the eigenvector composition is less than 50% for many of the 4d35p levels. It goes down to 16%. It makes LS-labeling of many levels meaningless in many cases. Therefore, the energy level values are listed in Table A2 along with the LSJ labels for the wavelength identification.
The identification of the 4d4–(4d35p + 4d34f + 4p54d5) transitions using the Cowan code resulted in 118 classified lines in the region 162–189 Å (Table A3). Seventeen lines were doubly classified. The wavelengths and intensities of 10 lines are affected by blending with the Ag IX lines. Table A9 contains the (4d34f + 4p54d5) levels above 556,000 cm−1. It was possible to find 58 levels of these configurations with the uncertainties from 7 to 19 cm−1. Cowan’s calculations of the odd level system were performed for a matrix of interacting configurations 4d35p + 4d36p + 4d25s5p + 4d5s25p + 4d3(4f-6f) + 4p54d5 + 4p54d45s. Starting energy parameters for the 4d35p, 4d34f and 4p54d5 configurations in Ag VIII were estimated by extrapolation of the scaling factors (the ratios of the fitted to the corresponding Hartree - Fock energy parameters) from Pd VII [21] and Pd VIII [8]. The ab initio electrostatic parameters in the unknown configurations were multiplied by 0.85 scaling factor. The configuration interaction parameters were scaled by 0.8 and the average energies along with the spin-orbit parameters were fixed at the corresponding HF values. Final energy parameters for the 4d35p, 4d34f and 4p54d5 configurations obtained in the fitting of the calculated energy levels to the experimental ones using the Cowan code are presented in Table A14. Standard deviation of the fitting σ was 213 cm−1. It should be noted, that for the 4d3 levels alone, the fitting by the Cowan code results in σ = 129 cm−1 what is 2.7 times larger than at the fitting using the orthogonal parameter code (see Table A13).
All found levels belong to the upper part of configurations (“emissive zone” [22]) from 557,000 to 669,000 cm−1. Only the levels for this energy range are listed in Table A9. According to our calculations full spread of the 4d34f + 4p54d5 levels cover the range up to 424,000 cm−1 overlapping with the 4d35p levels. Because of significant uncertainty in prediction of the low lying 4d34f + 4p54d5 levels they are omitted from Table A9.
Examination of Table A9 shows that the percentage contribution of the leading eigenvector component never exceeds 41% and can be as low as 9%. Moreover, the 4d34f wave function can be found as the leading component only at 13 levels with the largest contribution 31%, second component being mostly 4p54d5. Therefore, not only LS-assignment of many levels in Table A3, but also configuration attributions are arbitrary in many cases. Therefore, in Table A9, the upper levels of the transitions are designated by their energies and J values, whereas for convenience, a configuration name and LS-label are given according to the output files from the Cowan code in spite of possible ambiguity in many cases.
3.3. Ag IX
The scheme of the 4d3, 4d25p, 4d24f and 4p54d4 levels for Ag IX is shown in Figure 4. It shows that in comparison with Ag VII and Ag VIII the 4d25p levels are almost fully imbedded within the widely spread 4d24f + 4p54d4 levels. The levels of all odd configurations strongly interact. Their initial prediction in the framework of the Cowan code was performed by cross-extrapolation of the scaling factors and effective parameters from isonuclear Ag VIII (this work) and isoelectronic Pd VIII [8]. The 4d3 energies were calculated in the framework of the orthogonal parameters by extrapolation from Ag VII and Ag VIII (Table A12) and used as an input to Cowan’s calculations of the 4d3–(4d25p + 4d24f + 4p54d4) transition probabilities. Thus predicted energy levels and transition probabilities were then used for the spectrum analysis by the IDEN code [12].
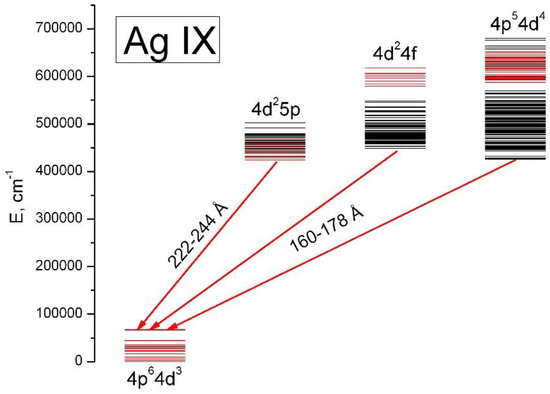
Figure 4.
Energy levels of Ag IX. The arrows show electric dipole transitions studied in this article. The levels found in this work are marked by red color. Black color indicates calculated positions of unknown levels.
As a result, 132 lines were identified in the 4d3–(4d25p + 4d24f + 4p54d4) transition array (Table A4). Nine lines were doubly classified and one line was trebly classified. The 4d3–4d25p part of this transition array lying in the 221–244 Å region is overlapped by unidentified lines (see Figure 1) discussed in Section 3.1. Nevertheless, it was possible to select the majority of the Ag IX lines by observation of their intensities with the change of the vacuum spark excitation conditions. The other 4d3–(4d24f + 4p54d4) part falls in the middle of the region where the spectrum consists of many overlapping lines in Ag VIII–Ag XII. Therefore 10 lines of Ag IX are found to be blended with Ag VIII and 8 with Ag X. In total, 17 levels of the 4d3 configuration and 78 levels of the 4d25p + 4d24f + 4p54d4 configurations were established and collected in Table A10 and Table A11, respectively. The uncertainty of relative positions of the levels after optimization by LOPT [19] ranges from 4 to 17 cm−1 for the ground-state configuration and from 6 to 19 cm−1 for the excited configurations.
As was mentioned above the energy levels of the 4d3 configuration were treated by orthogonal operator technique. As in Ag VII and Ag VIII calculated matrix consisted of three interacting configurations: 4d3 + 4d25s + 4d5s2 with similar scaling of the energy parameters for unknown configurations. The levels of the 4d3 configuration are presented in Table A10 along with the eigenvector compositions and deviations from the orthogonal parameter calculations. Standard deviation of the fitting was 27 cm−1. The resulting energy parameters of this configuration are collected in Table A12 in comparison with those of 4d4 (Ag VIII) and 4d5 (Ag VII). Table A12 shows regular behavior of the parameters and scaling factors along this part of the isonuclear sequence of silver ions. The labeling of the 4d3 energy levels by the fist component of their eigenvectors is unambiguous.
Table A11 contains all 306 levels of the 4d25p + 4d24f + 4p54d4 configurations. Because of the numerous blends only 78 levels were found. Similar to Ag VIII, a set of the interacting configurations (4d25p + 4d26p + 4d5s5p + 5s25p + 4d2(4f − 6f) + 4p54d4 + 4p55d35s) with the same treatment of the unknown configurations was used in the Cowan code calculations. The energy parameters for these configurations in Ag IX are listed in Table A14. The standard deviation of the fitting σ was 327 cm−1, to be compared with σ = 213 cm−1 in Ag VIII. It should be noted that in Ag IX more energy parameters than in Ag VIII were fixed on the estimated values for stability of the fitting. Similar considerations are applied to the eigenvector composition of the Ag IX odd levels. There are ambiguities in the LS- labeling and configuration assignment of the levels. Only the level energy and J value can serve as unique label, what is used in the list of the identified lines in Table A4.
4. Discussion
The spectra reported in this article are relevant to the verification of the identifications of the EUV spectra of Sn ions [9,10] which are used as a “fuel” in the radiation sources for the projection lithography at the 135 Å wavelength. The previous analyses in [9,10] were performed without any isoelectronic or isoionic support. The isoelectronic sequence Rh VIII–Cd XI was recently studied in [7]. It was found by extrapolation to Sn XIII that the identification of this spectrum should be revised. Similar conclusion was made after the identification of the M1 transitions between the levels of ground-state configurations in Sn XIII and other ions with open 4d- shell [23]. More data on the VUV spectra of the neighboring to Sn elements are needed. The analyses of Ag VII, Ag VIII and Ag IX were performed in this work for the first time and all Ag ion spectra with the 4dk (k = 1–10) ground-state configuration now became known. After the studies of spectra of the 4d- palladium ions ([8] and references therein) the present work on Ag ion spectra is the next step in the study of the ion spectra isoelectronic with Sn IX–Sn XIII. The work on Cd- and In- ion spectra is in progress at this laboratory.
Author Contributions
A.R. recorded the spectra, performed their analyses and wrote the paper; E.K. made spectrum measurements and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Identified lines of the 4d5−4d45p transitions in the spectrum of Ag6+.
| λ (Å) a | o-c, (Å) b | ν (cm−1) | I c | gA, (108 s−1) | 5d5 | 5d45p | ||
|---|---|---|---|---|---|---|---|---|
| Term e | E (cm−1) | Term e | E (cm−1) | |||||
| 271.910 | 0.000 | 367,768.8 | 36 | 31 | 54G11/2 | 30,662 | (23F)4F9/2 | 398,431 |
| 277.706 | 0.003 | 360,092.8 | 11 | 42 | 54G11/2 | 30,662 | (41F)2G9/2 | 390,759 |
| 277.852 | −0.001 | 359,904.2 | 19 | 37 | 54G5/2 | 29,390 | (23F)4F3/2 | 389,293 |
| 277.969 | 0.003 | 359,752.2 | 13 | 51 | 54D7/2 | 36,485 | (23P)4D7/2 | 396,241 |
| 280.155 | −0.002 | 356,944.6 | 12 | 11 | 54D5/2 | 39,299 | (23P)4D7/2 | 396,241 |
| 280.826 | 0.000 | 356,092.1 | 5 | 48 | 32H9/2 | 53,797 | (21G)2F7/2 | 409,889 |
| 281.791 | −0.003 | 354,872.4 | 13 | 47 | 56S5/2 | 0 | (45D)4D7/2 | 354,869 |
| 283.387 | 0.002 | 352,874.3 | 9 | 44 | 34F3/2 | 53,796 | (23F)4D1/2 | 406,673 |
| 284.236 | −0.003 | 351,820.2 | 62 | 518 | 32H11/2 | 57,962 | (21G)2G9/2 | 409,779 |
| 284.511 | −0.001 | 351,479.9 | 12 | 93 | 32H11/2 | 57,962 | (21G)2H11/2 | 409,441 |
| 285.168 | −0.003 | 350,670.3 | 30 | 276 | 52G9/2 | 59,223 | (21G)2F7/2 | 409,889 |
| 285.727 | 0.002 | 349,984.1 | 6 | 153 | 52F7/2 | 59,792 | (21G)2G9/2 | 409,779 |
| 285.785 | 0.004 | 349,912.9 | 5 | 55 | 34F9/2 | 49,104 | (23F)4G11/2 | 399,022 |
| 286.212 | 349,391.3 | 32 | 377 | 32G9/2 | 79,131 | (21D)2F7/2 | 428,522 | |
| 286.254 | −0.010 | 349,339.5 | 30 | 159 | 32H9/2 | 53,797 | (23F)4D7/2 | 403,133 |
| 286.276 | 0.011 | 349,313.3 | 23 | 76 | 34F9/2 | 49,104 | (23F)4F9/2 | 398,431 |
| 286.411 | −0.002 | 349,148.6 | 8 | 28 | 34F7/2 | 48,712 | (23F)4G7/2 | 397,858 |
| 286.744 | 0.009 | 348,743.4 | 15 | 132 | 34F9/2 | 49,104 | (23F)4G7/2 | 397,858 |
| 287.950 | 0.001 | 347,282.9 | 15 | 113 | 32F7/2 | 53,353 | (41F)2D5/2 | 400,637 |
| 288.074 | 0.003 | 347,133.0 | 10 | 88 | 34F9/2 | 49,104 | (23P)4D7/2 | 396,241 |
| 288.806 | 0.002 | 346,253.7 | 16 | 36 | 54G9/2 | 30,907 | (43D)4F7/2 | 377,163 |
| 288.970 | 0.003 | 346,057.0 | 12 | 33 | 56S5/2 | 0 | (45D)4F7/2 | 346,061 |
| 289.226 | 0.005 | 345,750.6 | 16 | 25 | 54G11/2 | 30,662 | (41I)2I13/2 | 376,419 |
| 289.431 | 0.001 | 345,506.0 | 5 | 36 | 54G9/2 | 30,907 | (43G)4G11/2 | 376,414 |
| 289.575 | 0.002 | 345,334.0 | 18 | 95 | 34F7/2 | 48,712 | (23F)4F5/2 | 394,049 |
| 289.665 | −0.001 | 345,225.9 | 7 | 28 | 32H9/2 | 53,797 | (23F)4G11/2 | 399,022 |
| 289.944 | 0.000 | 344,894.1 | 18 | 114 | 52G9/2 | 59,223 | (23F)2F7/2 | 404,117 |
| 290.169 | 0.006 | 344,626.6 | 47 | 326 | 32H9/2 | 53,797 | (23F)4F9/2 | 398,431 |
| 290.203 | −0.003 | 344,586.3 | 9 | 24 | 34F7/2 | 48,712 | (23F)4G7/2 | 393,295 |
| 290.265 | −0.006 | 344,512.5 | 12 | 72 | 32F7/2 | 53,353 | (23F)4G7/2 | 397,858 |
| 290.415 | 0.002 | 344,335.1 | 18 | 53 | 52D3/2 | 48,086 | (23P)4D1/2 | 392,424 |
| 291.263 | 0.003 | 343,332.2 | 52 | 39 | 56S5/2 | 0 | (45D)4F5/2 | 343,336 |
| 291.310 | 0.002 | 343,277.0 | 15 | 113 | 32G7/2 | 79,705 | (21D)2F5/2 | 422,985 |
| 291.817 | 0.003 | 342,680.2 | 14 | 79 | 34F7/2 | 48,712 | (23F)4G5/2 | 391,396 |
| 291.862 | −0.002 | 342,627.8 | 19 | 132 | 34F7/2 | 48,712 | (23F)4F7/2 | 391,338 |
| 291.915 | −0.004 | 342,565.6 | 32 | 138 | 34F5/2 | 51,049 | (41D)2P3/2 | 393,610 |
| 292.019 | 0.001 | 342,443.3 | 46 | 390 | 32H9/2 | 53,797 | (23P)4D7/2 | 396,241 |
| 292.260 | 0.000 | 342,160.6 | 44 | 235 | 54G11/2 | 30,662 | (43G)4H13/2 | 372,822 |
| 292.700 | 0.007 | 341,647.2 | 53 | 450 | 34F9/2 | 49,104 | (41F)2G9/2 | 390,759 |
| 292.860 | −0.002 | 341,460.2 | 37 | 80 | 56S5/2 | 0 | (45D)6D7/2 | 341,458 |
| 293.002 | 0.001 | 341,294.3 | 17 | 43 | 54G7/2 | 30,378 | (43G)4G7/2 | 371,673 |
| 293.077 | 0.000 | 341,206.8 | 31 | 89 | 52D3/2 | 48,086 | (23F)4F3/2 | 389,293 |
| 293.201 | −0.002 | 341,062.7 | 2 | 30 | 32H11/2 | 57,962 | (23F)4G11/2 | 399,022 |
| 293.388 | 0.000 | 340,845.3 | 17 | 225 | 52F7/2 | 59,792 | (41F)2D5/2 | 400,637 |
| 293.457 | 0.001 | 340,764.8 | 8 | 27 | 54G9/2 | 30,907 | (43G)4G7/2 | 371,673 |
| 293.516 | −0.001 | 340,696.8 | 32 | 201 | 32F7/2 | 53,353 | (23F)4F5/2 | 394,049 |
| 293.681 | −0.002 | 340,506.1 | 33 | 126 | 34F5/2 | 51,049 | (23P)4D3/2 | 391,553 |
| 293.711 | −0.001 | 340,470.6 | 14 | 178 | 32H11/2 | 57,962 | (23F)4F9/2 | 398,431 |
| 293.822 | 0.004 | 340,342.2 | 5 | 31 | 34F5/2 | 51,049 | (23F)4G5/2 | 391,396 |
| 293.865 | −0.003 | 340,292.7 | 4 | 101 | 34F5/2 | 51,049 | (23F)4F7/2 | 391,338 |
| 293.954 | −0.001 | 340,189.4 | 9 | 35 | 54G5/2 | 29,390 | (43F)2F5/2 | 369,578 |
| 294.467 | −0.002 | 339,596.6 | 24 | 43 | 54G9/2 | 30,907 | (43G)2H9/2 | 370,501 |
| 294.526 | −0.001 | 339,529.1 | 18 | 44 | 52I11/2 | 44,011 | (41I)2H11/2 | 383,539 |
| 294.551 | −0.001 | 339,499.6 | 13 | 109 | 32H9/2 | 53,797 | (23F)4G7/2 | 393,295 |
| 294.798 | −0.006 | 339,214.9 | 26 | 119 | 52G9/2 | 59,223 | (23F)4F9/2 | 398,431 |
| 294.834 | −0.002 | 339,174.3 | 197 | 342 | 56S5/2 | 0 | (45D)6D5/2 | 339,172 |
| 294.872 | 0.003 | 339,130.2 | 37 | 202 | 32F7/2 | 53,353 | (23F)4G9/2 | 392,486 |
| 294.932 | −0.002 | 339,061.6 | 23 | 117 | 34F9/2 | 49,104 | (41F)2G7/2 | 388,163 |
| 294.980 d | 0.004 | 339,006.0 | 43 | 199 | 34F5/2 | 51,049 | (23F)4F5/2 | 390,060 |
| 294.980 d | −0.006 | 339,006.0 | 43 | 134 | 54G11/2 | 30,662 | (41I)2I11/2 | 369,661 |
| 295.091 | 0.002 | 338,878.2 | 19 | 34 | 54D7/2 | 36,485 | (43G)2G7/2 | 375,365 |
| 295.253 | −0.003 | 338,692.6 | 22 | 61 | 32H9/2 | 53,797 | (23F)4G9/2 | 392,486 |
| 295.304 | 0.001 | 338,633.8 | 47 | 203 | 52G9/2 | 59,223 | (23F)4G7/2 | 397,858 |
| 295.304 | −0.005 | 338,633.8 | 47 | 159 | 34F3/2 | 53,796 | (23P)4D1/2 | 392,424 |
| 295.537 | −0.001 | 338,367.6 | 90 | 657 | 52I11/2 | 44,011 | (41I)2H9/2 | 382,377 |
| 295.648 | 0.004 | 338,240.1 | 12 | 32 | 34F5/2 | 51,049 | (23F)4F3/2 | 389,293 |
| 295.801 | 0.001 | 338,064.9 | 20 | 35 | 52F7/2 | 59,792 | (23F)4G7/2 | 397,858 |
| 295.944 | 0.002 | 337,901.3 | 22 | 85 | 34F7/2 | 48,712 | (41F)2G7/2 | 386,615 |
| 295.980 | 0.003 | 337,861.1 | 10 | 79 | 54D5/2 | 39,299 | (43D)4F7/2 | 377,163 |
| 296.056 | −0.006 | 337,773.4 | 22 | 55 | 54G11/2 | 30,662 | (43G)4H9/2 | 368,429 |
| 296.579 | 0.005 | 337,177.8 | 14 | 87 | 54G5/2 | 29,390 | (43F)4F3/2 | 366,573 |
| 296.716 d | 0.004 | 337,023.2 | 18 | 52 | 54D1/2 | 38,685 | (43D)4D3/2 | 375,706 |
| 296.716 d | −0.004 | 337,023.2 | 18 | 117 | 52G9/2 | 59,223 | (23P)4D7/2 | 396,241 |
| 296.779 | 0.003 | 336,950.9 | 12 | 116 | 32D5/2 | 72,934 | (21G)2F7/2 | 409,889 |
| 296.892 | −0.001 | 336,822.6 | 37 | 160 | 54G11/2 | 30,662 | (43F)4G11/2 | 367,483 |
| 296.910 | 0.001 | 336,802.8 | 17 | 103 | 54D1/2 | 38,685 | (43D)4P1/2 | 375,489 |
| 296.944 | −0.008 | 336,763.9 | 17 | 103 | 54D3/2 | 39,788 | (43D)4F5/2 | 376,543 |
| 297.106 | −0.004 | 336,580.1 | 22 | 55 | 54G9/2 | 30,907 | (43F)4G11/2 | 367,483 |
| 297.124 | 0.004 | 336,559.4 | 22 | 35 | 34P5/2 | 32,005 | (43F)4D3/2 | 368,569 |
| 297.216 | −0.002 | 336,456.2 | 29 | 174 | 34P3/2 | 32,994 | (43D)4P3/2 | 369,448 |
| 297.251 | −0.008 | 336,415.8 | 12 | 54 | 54D5/2 | 39,299 | (43D)4D3/2 | 375,706 |
| 297.324 | 336,333.8 | 307 | 565 | 56S5/2 | 0 | (45D)6P3/2 | 336,333 | |
| 297.504 | −0.004 | 336,130.1 | 8 | 44 | 54D1/2 | 38,685 | (43P)2P1/2 | 374,810 |
| 297.702 | −0.007 | 335,906.6 | 36 | 79 | 54G9/2 | 30,907 | (43F)4F7/2 | 366,806 |
| 297.882 | −0.002 | 335,702.9 | 16 | 188 | 54D3/2 | 39,788 | (43D)4P1/2 | 375,489 |
| 297.911 | −0.002 | 335,670.5 | 55 | 299 | 34F9/2 | 49,104 | (41D)2F7/2 | 384,772 |
| 297.951 | −0.003 | 335,625.9 | 18 | 143 | 52G7/2 | 55,773 | (23F)4G5/2 | 391,396 |
| 298.066 d | 0.001 | 335,495.9 | 40 | 272 | 34F3/2 | 53,796 | (23F)4F3/2 | 389,293 |
| 298.066 d | −0.008 | 335,495.9 | 41 | 68 | 54G5/2 | 29,390 | (43P)4P5/2 | 364,877 |
| 298.311 | −0.005 | 335,220.5 | 52 | 378 | 52I11/2 | 44,011 | (43G)2G9/2 | 379,226 |
| 298.367 | −0.001 | 335,157.4 | 35 | 58 | 32D3/2 | 71,517 | (23F)4D1/2 | 406,673 |
| 298.564 d | 334,936.4 | 660 | 266 | 54D5/2 | 39,299 | (43D)4P3/2 | 374,236 | |
| 298.564 d | −0.001 | 334,936.4 | 660 | 239 | 54G9/2 | 30,907 | (43F)2G7/2 | 365,842 |
| 298.591 d | 334,905.8 | 1000 | 1405 | 56S5/2 | 0 | (45D)6P7/2 | 334,906 | |
| 298.591 d | 0.001 | 334,905.8 | 1000 | 621 | 54G11/2 | 30,662 | (43F)4F9/2 | 365,569 |
| 298.651 | 0.003 | 334,839.3 | 23 | 100 | 34P1/2 | 34,605 | (43D)4P3/2 | 369,448 |
| 299.048 | 0.002 | 334,394.9 | 12 | 251 | 34F7/2 | 48,712 | (43D)2F5/2 | 383,109 |
| 299.073 | −0.011 | 334,367.0 | 79 | 244 | 54G11/2 | 30,662 | (43H)4H11/2 | 365,017 |
| 299.301 d | −0.002 | 334,111.7 | 82 | 115 | 54G11/2 | 30,662 | (43F)4G9/2 | 364,772 |
| 299.301 d | −0.001 | 334,111.7 | 82 | 221 | 54G9/2 | 30,907 | (43H)4H11/2 | 365,017 |
| 299.346 | 0.002 | 334,061.9 | 26 | 140 | 54G5/2 | 29,390 | (43D)4F3/2 | 363,454 |
| 299.396 | 0.002 | 334,006.1 | 12 | 97 | 34F7/2 | 48,712 | (41G)2G9/2 | 382,720 |
| 299.432 | −0.002 | 333,966.1 | 15 | 119 | 34P1/2 | 34,605 | (43F)4D3/2 | 368,569 |
| 299.526 | 0.004 | 333,861.1 | 127 | 498 | 54G9/2 | 30,907 | (43F)4G9/2 | 364,772 |
| 299.719 | 0.001 | 333,645.6 | 63 | 419 | 54G7/2 | 30,378 | (43D)2D5/2 | 364,025 |
| 299.740 | 0.001 | 333,622.6 | 32 | 180 | 34F9/2 | 49,104 | (41G)2G9/2 | 382,728 |
| 299.772 | −0.002 | 333,586.8 | 35 | 71 | 54G5/2 | 29,390 | (43P)4D5/2 | 362,975 |
| 299.803 | 0.000 | 333,551.8 | 15 | 72 | 54G5/2 | 29,390 | (43G)4H7/2 | 362,942 |
| 299.941 | −0.004 | 333,399.3 | 32 | 185 | 54D7/2 | 36,485 | (43P)4D7/2 | 369,879 |
| 299.954 | −0.003 | 333,384.9 | 32 | 46 | 52I11/2 | 44,011 | (43F)2G9/2 | 377,393 |
| 300.006 | 333,327.1 | 315 | 783 | 56S5/2 | 0 | (45D)6P5/2 | 333,327 | |
| 300.065 d | 0.001 | 333,261.5 | 41 | 193 | 52G9/2 | 59,223 | (23F)4G9/2 | 392,486 |
| 300.065 d | 0.001 | 333,261.5 | 41 | 114 | 32F7/2 | 53,353 | (41F)2G7/2 | 386,615 |
| 300.216 | −0.001 | 333,093.9 | 36 | 178 | 54D7/2 | 36,485 | (43F)2F5/2 | 369,578 |
| 300.224 | 0.000 | 333,084.2 | 36 | 113 | 34P3/2 | 32,993 | (43F)4F3/2 | 366,077 |
| 300.305 | −0.003 | 332,994.5 | 56 | 319 | 54G5/2 | 29,390 | (43H)4G5/2 | 362,381 |
| 300.342 | −0.001 | 332,953.5 | 74 | 267 | 54G11/2 | 30,662 | (43H)4I13/2 | 363,614 |
| 300.419 | 0.004 | 332,868.1 | 12 | 66 | 34P5/2 | 32,005 | (43P)4P5/2 | 364,877 |
| 300.473 d | 0.000 | 332,808.5 | 144 | 274 | 52I13/2 | 45,546 | (41I)2K15/2 | 378,355 |
| 300.473 d | −0.010 | 332,808.5 | 144 | 641 | 32H11/2 | 57,962 | (41F)2G9/2 | 390,759 |
| 300.693 | −0.001 | 332,564.7 | 39 | 203 | 54G7/2 | 30,378 | (43G)4H7/2 | 362,942 |
| 300.760 | −0.007 | 332,490.7 | 39 | 208 | 54D7/2 | 36,485 | (43P)4D7/2 | 368,968 |
| 300.833 | −0.006 | 332,410.1 | 26 | 57 | 52I11/2 | 44,011 | (43G)4G11/2 | 376,414 |
| 300.855 | 0.004 | 332,385.9 | 26 | 96 | 52G7/2 | 55,773 | (41F)2G7/2 | 388,163 |
| 301.047 | −0.003 | 332,174.2 | 342 | 1899 | 52I13/2 | 45,546 | (41G)2H11/2 | 377,717 |
| 301.098 | −0.003 | 332,118.1 | 16 | 95 | 52G9/2 | 59,223 | (23F)4F7/2 | 391,338 |
| 301.141 | −0.001 | 332,070.5 | 15 | 141 | 54G7/2 | 30,378 | (43G)4F9/2 | 362,447 |
| 301.178 d | 0.006 | 332,029.0 | 34 | 149 | 54G9/2 | 30,907 | (43G)4H7/2 | 362,942 |
| 301.178 d | −0.008 | 332,029.0 | 34 | 192 | 34P5/2 | 32,005 | (43D)2D5/2 | 364,025 |
| 301.262 | 0.007 | 331,936.7 | 16 | 143 | 54D7/2 | 36,485 | (43G)4H9/2 | 368,429 |
| 301.314 | −0.006 | 331,879.4 | 140 | 547 | 54G11/2 | 30,662 | (43H)2I11/2 | 362,535 |
| 301.404 d | 0.002 | 331,781.0 | 147 | 92 | 54G5/2 | 29,390 | (43F)4G7/2 | 361,173 |
| 301.404 d | 0.004 | 331,781.0 | 147 | 712 | 54G11/2 | 30,662 | (43G)4F9/2 | 362,447 |
| 301.585 | 0.001 | 331,581.0 | 9 | 152 | 52I11/2 | 44,011 | (43D)4F9/2 | 375,593 |
| 301.618 d | 0.001 | 331,545.3 | 73 | 415 | 52F7/2 | 59,792 | (23F)4F7/2 | 391,338 |
| 301.618 d | −0.008 | 331,545.3 | 73 | 58 | 52G9/2 | 59,223 | (41F)2G9/2 | 390,759 |
| 301.701 | −0.004 | 331,453.7 | 42 | 243 | 34P5/2 | 32,005 | (43D)4F3/2 | 363,454 |
| 301.720 | 0.001 | 331,433.2 | 89 | 388 | 54D7/2 | 36,485 | (43D)4P5/2 | 367,919 |
| 301.866 | −0.001 | 331,272.8 | 28 | 65 | 54G7/2 | 30,378 | (43H)4G9/2 | 361,650 |
| 301.920 | 0.001 | 331,213.5 | 60 | 333 | 54G7/2 | 30,378 | (43G)4F7/2 | 361,593 |
| 301.932 | 331,200.4 | 147 | 211 | 56S5/2 | 0 | (45D)4P3/2 | 331,200 | |
| 302.140 | −0.005 | 330,972.2 | 13 | 41 | 52F7/2 | 59,792 | (41F)2G9/2 | 390,759 |
| 302.191 | 0.002 | 330,916.4 | 155 | 680 | 54G7/2 | 30,378 | (43F)4F5/2 | 361,296 |
| 302.226 d | −0.009 | 330,878.0 | 351 | 441 | 52I13/2 | 45,546 | (43G)4G11/2 | 376,414 |
| 302.226 d | −0.005 | 330,878.0 | 351 | 768 | 52I13/2 | 45,546 | (41I)2I13/2 | 376,419 |
| 302.307 d | 0.005 | 330,789.4 | 146 | 453 | 54G7/2 | 30,378 | (43F)4G7/2 | 361,173 |
| 302.307 d | 0.001 | 330,789.4 | 146 | 248 | 52D5/2 | 47,119 | (41S)2P3/2 | 377,910 |
| 302.350 d | 0.001 | 330,742.4 | 565 | 1173 | 54G9/2 | 30,907 | (43H)4G9/2 | 361,650 |
| 302.350 d | 0.014 | 330,742.4 | 565 | 619 | 32G9/2 | 79,131 | (21G)2F7/2 | 409,889 |
| 302.401 | −0.001 | 330,687.0 | 192 | 881 | 54G9/2 | 30,907 | (43G)4F7/2 | 361,593 |
| 302.687 d | 0.002 | 330,374.0 | 21 | 108 | 34P5/2 | 32,005 | (43H)4G5/2 | 362,381 |
| 302.687 d | −0.008 | 330,374.0 | 21 | 186 | 34F7/2 | 48,712 | (41F)2F5/2 | 379,077 |
| 302.748 d | 0.002 | 330,307.5 | 57 | 208 | 32G9/2 | 79,131 | (21G)2H11/2 | 409,441 |
| 302.748 d | 0.012 | 330,307.5 | 57 | 154 | 54D7/2 | 36,485 | (43F)4F7/2 | 366,806 |
| 302.784 d | −0.001 | 330,268.8 | 49 | 87 | 52F7/2 | 59,792 | (23F)4F5/2 | 390,060 |
| 302.784 d | −0.003 | 330,268.8 | 49 | 84 | 54G9/2 | 30,907 | (43F)4G7/2 | 361,173 |
| 302.836 | −0.004 | 330,212.1 | 110 | 309 | 54D7/2 | 36,485 | (43D)4D5/2 | 366,693 |
| 302.865 | 0.008 | 330,180.0 | 26 | 413 | 52G7/2 | 55,773 | (43D)2F5/2 | 385,962 |
| 302.936 d | 0.001 | 330,103.2 | 34 | 150 | 54G7/2 | 30,378 | (43F)4G9/2 | 360,482 |
| 302.936 d | 0.003 | 330,103.2 | 34 | 225 | 32F5/2 | 59,954 | (23F)4F5/2 | 390,060 |
| 303.045 | −0.003 | 329,983.8 | 72 | 299 | 34P3/2 | 32,994 | (43P)4D5/2 | 362,975 |
| 303.063 | −0.007 | 329,964.7 | 29 | 442 | 34F9/2 | 49,104 | (41G)2G7/2 | 379,061 |
| 303.133 | −0.004 | 329,888.5 | 9 | 47 | 54D1/2 | 38,685 | (43F)4D3/2 | 368,569 |
| 303.191 d | −0.001 | 329,824.7 | 95 | 131 | 52D3/2 | 48,086 | (41S)2P3/2 | 377,910 |
| 303.191 d | −0.005 | 329,824.7 | 95 | 332 | 54G11/2 | 30,662 | (43H)4I11/2 | 360,481 |
| 303.252 | −0.003 | 329,758.8 | 20 | 60 | 32F7/2 | 53,353 | (43D)2F5/2 | 383,109 |
| 303.340 | −0.003 | 329,663.2 | 11 | 147 | 54D3/2 | 39,788 | (43D)4P3/2 | 369,448 |
| 303.421 | 0.000 | 329,575.0 | 46 | 170 | 54G9/2 | 30,907 | (43F)4G9/2 | 360,482 |
| 303.505 | −0.002 | 329,483.4 | 55 | 893 | 32G7/2 | 79,705 | (21G)2F5/2 | 409,186 |
| 303.557 | −0.003 | 329,427.2 | 12 | 64 | 52D5/2 | 47,119 | (43D)4F5/2 | 376,543 |
| 303.670 | 0.004 | 329,304.9 | 103 | 391 | 54G7/2 | 30,378 | (43G)4G7/2 | 359,687 |
| 303.791 | −0.004 | 329,173.5 | 46 | 331 | 52F5/2 | 57,413 | (41S)2P3/2 | 386,582 |
| 303.852 | 0.001 | 329,107.7 | 69 | 335 | 52I11/2 | 44,011 | (43G)4G9/2 | 373,120 |
| 303.950 d | −0.002 | 329,001.2 | 111 | 371 | 52G7/2 | 55,773 | (41D)2F7/2 | 384,772 |
| 303.950 d | 329,001.2 | 111 | 353 | 54G5/2 | 29,390 | (43F)4G5/2 | 358,392 | |
| 304.087 | 0.002 | 328,852.8 | 35 | 264 | 52F5/2 | 57,413 | (41D)2D5/2 | 386,268 |
| 304.087 | −0.004 | 328,852.8 | 35 | 61 | 34P1/2 | 34,605 | (43D)4F3/2 | 363,454 |
| 304.154 | −0.001 | 328,781.1 | 12 | 103 | 54G9/2 | 30,907 | (43G)4G7/2 | 359,687 |
| 304.261 | 0.000 | 328,665.6 | 41 | 348 | 52I11/2 | 44,011 | (43H)2H11/2 | 372,676 |
| 304.302 | −0.001 | 328,621.4 | 28 | 210 | 54D5/2 | 39,299 | (43D)4P5/2 | 367,919 |
| 304.338 | −0.002 | 328,582.2 | 53 | 421 | 32H9/2 | 53,797 | (41I)2H9/2 | 382,377 |
| 304.515 | 0.001 | 328,391.4 | 17 | 97 | 54D7/2 | 36,485 | (43P)4P5/2 | 364,877 |
| 304.568 | 328,334.2 | 12 | 215 | 32D3/2 | 71,517 | (41F)2D3/2 | 399,850 | |
| 304.608 d | −0.004 | 328,290.9 | 36 | 163 | 54D7/2 | 36,485 | (43F)4G9/2 | 364,772 |
| 304.608 d | −0.002 | 328,290.9 | 36 | 55 | 34F9/2 | 49,104 | (43F)2G9/2 | 377,393 |
| 304.684 | 0.000 | 328,208.5 | 12 | 112 | 32F5/2 | 59,954 | (41F)2G7/2 | 388,163 |
| 304.798 | 0.000 | 328,086.6 | 44 | 281 | 34P5/2 | 32,005 | (43P)4P3/2 | 360,092 |
| 304.831 | 0.008 | 328,050.5 | 8 | 50 | 34F9/2 | 49,104 | (43D)4F7/2 | 377,162 |
| 305.046 d | 0.000 | 327,819.4 | 18 | 121 | 52D5/2 | 47,119 | (43D)2P3/2 | 374,938 |
| 305.046 d | 0.011 | 327,819.4 | 18 | 101 | 34F7/2 | 48,712 | (43D)4F5/2 | 376,543 |
| 305.152 | −0.002 | 327,705.2 | 91 | 266 | 32D5/2 | 72,934 | (41F)2D5/2 | 400,637 |
| 305.172 | −0.002 | 327,684.1 | 91 | 223 | 34P5/2 | 32,005 | (43G)4G7/2 | 359,687 |
| 305.249 | 0.001 | 327,601.6 | 87 | 395 | 54G5/2 | 29,390 | (43F)2D3/2 | 356,993 |
| 305.305 | −0.003 | 327,541.3 | 32 | 49 | 32F7/2 | 53,353 | (41G)2F5/2 | 380,891 |
| 305.341 | 0.004 | 327,503.1 | 49 | 406 | 54D5/2 | 39,299 | (43F)4F7/2 | 366,806 |
| 305.441 t | −0.003 | 327,395.2 | 47 | 490 | 52G9/2 | 59,223 | (41F)2G7/2 | 386,615 |
| 305.441 t | −0.001 | 327,395.2 | 47 | 234 | 54D5/2 | 39,299 | (43D)4D5/2 | 366,693 |
| 305.441 t | −0.002 | 327,395.2 | 47 | 108 | 54D1/2 | 38,685 | (43F)4F3/2 | 366,078 |
| 305.469 | −0.002 | 327,365.7 | 58 | 111 | 32G9/2 | 79,131 | (23F)2G7/2 | 406,495 |
| 305.524 d | 0.000 | 327,306.8 | 54 | 145 | 52D5/2 | 47,119 | (43G)4F5/2 | 374,426 |
| 305.524 d | 0.003 | 327,306.8 | 54 | 154 | 34F9/2 | 49,104 | (43G)4G11/2 | 376,414 |
| 305.554 d | 0.001 | 327,274.8 | 262 | 868 | 52I13/2 | 45,546 | (43G)4H13/2 | 372,822 |
| 305.554 d | −0.001 | 327,274.8 | 262 | 92 | 54D5/2 | 39,299 | (43F)4F3/2 | 366,573 |
| 305.689 | 0.000 | 327,129.8 | 295 | 1616 | 52I13/2 | 45,546 | (43H)2H11/2 | 372,676 |
| 305.787 | 0.002 | 327,025.0 | 265 | 1038 | 54G11/2 | 30,662 | (43H)4G11/2 | 357,689 |
| 305.902 | 0.003 | 326,901.5 | 19 | 143 | 54D3/2 | 39,788 | (43D)4D5/2 | 366,693 |
| 305.961 | 0.004 | 326,838.8 | 107 | 133 | 54G5/2 | 29,390 | (43F)4D5/2 | 356,233 |
| 306.009 d | 0.002 | 326,787.6 | 173 | 936 | 32G7/2 | 79,705 | (23F)2G7/2 | 406,495 |
| 306.009 d | −0.002 | 326,787.6 | 173 | 266 | 54D3/2 | 39,788 | (43F)4F3/2 | 366,573 |
| 306.020 | 0.006 | 326,775.9 | 31 | 397 | 54G9/2 | 30,907 | (43H)4G11/2 | 357,689 |
| 306.072 | 0.004 | 326,720.1 | 21 | 146 | 52D3/2 | 48,086 | (43P)2P1/2 | 374,810 |
| 306.159 | 0.000 | 326,627.8 | 46 | 361 | 32F5/2 | 59,954 | (41S)2P3/2 | 386,582 |
| 306.288 d | −0.001 | 326,490.6 | 372 | 167 | 34F9/2 | 49,104 | (43D)4F9/2 | 375,593 |
| 306.288 d | −0.001 | 326,490.6 | 372 | 1477 | 52I11/2 | 44,011 | (43G)2H9/2 | 370,501 |
| 306.303 | 0.002 | 326,474.1 | 77 | 436 | 52F7/2 | 59,792 | (41D)2D5/2 | 386,268 |
| 306.425 | −0.004 | 326,344.3 | 16 | 55 | 52D3/2 | 48,086 | (43G)4F5/2 | 374,426 |
| 306.479 | 0.003 | 326,286.8 | 12 | 110 | 54D3/2 | 39,788 | (43F)4F3/2 | 366,078 |
| 306.712 | −0.001 | 326,039.2 | 12 | 46 | 54G7/2 | 30,378 | (43H)4I9/2 | 356,416 |
| 306.737 | −0.004 | 326,011.7 | 23 | 294 | 32F5/2 | 59,954 | (43D)2F5/2 | 385,962 |
| 306.781 | −0.003 | 325,965.8 | 62 | 360 | 54D7/2 | 36,485 | (43G)4F9/2 | 362,447 |
| 306.857 | 0.002 | 325,884.4 | 18 | 51 | 54D7/2 | 36,485 | (43H)4G5/2 | 362,381 |
| 306.876 | 0.002 | 325,864.4 | 34 | 417 | 52F5/2 | 57,413 | (43D)2D3/2 | 383,280 |
| 306.981 | 0.001 | 325,753.5 | 133 | 394 | 54G11/2 | 30,662 | (43H)4I9/2 | 356,416 |
| 307.013 | 0.004 | 325,719.5 | 131 | 656 | 32F7/2 | 53,353 | (41F)2F5/2 | 379,077 |
| 307.086 d | 0.008 | 325,641.9 | 505 | 1764 | 52I11/2 | 44,011 | (41I)2I11/2 | 369,661 |
| 307.086 d | 0.001 | 325,641.9 | 505 | 213 | 52I11/2 | 44,011 | (41I)2K13/2 | 369,654 |
| 307.147 d | 0.001 | 325,577.1 | 393 | 172 | 54D5/2 | 39,299 | (43P)4P5/2 | 364,877 |
| 307.147 d | 0.000 | 325,577.1 | 393 | 1711 | 32H11/2 | 57,962 | (41I)2H11/2 | 383,539 |
| 307.178 | 0.005 | 325,543.6 | 100 | 607 | 52G9/2 | 59,223 | (41D)2F7/2 | 384,772 |
| 307.230 | −0.002 | 325,488.8 | 31 | 185 | 34P1/2 | 34,605 | (43P)4P3/2 | 360,092 |
| 307.290 | 0.003 | 325,425.5 | 3 | 139 | 32H9/2 | 53,797 | (43G)2G9/2 | 379,226 |
| 307.448 | 0.006 | 325,257.7 | 70 | 609 | 32H9/2 | 53,797 | (41G)2G7/2 | 379,061 |
| 307.579 | −0.002 | 325,120.2 | 83 | 598 | 52G7/2 | 55,773 | (41G)2F5/2 | 380,891 |
| 307.608 | 0.000 | 325,088.7 | 14 | 74 | 54D3/2 | 39,788 | (43P)4P5/2 | 364,877 |
| 307.707 | 0.001 | 324,984.9 | 49 | 518 | 32G9/2 | 79,131 | (23F)2F7/2 | 404,117 |
| 307.871 | 324,811.2 | 111 | 987 | 32G9/2 | 79,131 | (23F)2G9/2 | 403,942 | |
| 307.918 d | 0.007 | 324,761.4 | 147 | 198 | 54D1/2 | 38,685 | (43D)4F3/2 | 363,454 |
| 307.918 d | −0.003 | 324,761.4 | 147 | 786 | 32H11/2 | 57,962 | (41G)2G9/2 | 382,720 |
| 307.981 | −0.001 | 324,695.8 | 53 | 394 | 52G7/2 | 55,773 | (41F)2F7/2 | 380,468 |
| 308.024 | 0.007 | 324,649.9 | 11 | 89 | 34F5/2 | 51,049 | (43D)4D3/2 | 375,706 |
| 308.114 | −0.001 | 324,555.0 | 16 | 110 | 52D5/2 | 47,119 | (43G)4G7/2 | 371,673 |
| 308.180 | 0.002 | 324,486.0 | 96 | 453 | 34P5/2 | 32,005 | (43F)4D7/2 | 356,493 |
| 308.247 d | 0.003 | 324,415.1 | 66 | 179 | 52I11/2 | 44,011 | (43G)4H9/2 | 368,429 |
| 308.247 d | −0.007 | 324,415.1 | 66 | 167 | 34F7/2 | 48,712 | (43G)4G9/2 | 373,120 |
| 308.538 d | 0.005 | 324,109.7 | 515 | 155 | 52I13/2 | 45,546 | (41I)2I11/2 | 369,661 |
| 308.538 d | −0.002 | 324,109.7 | 515 | 1122 | 52I13/2 | 45,546 | (41I)2K13/2 | 369,654 |
| 308.588 d | 324,056.3 | 220 | 408 | 54G11/2 | 30,662 | (43H)4H13/2 | 354,719 | |
| 308.588 d | 0.007 | 324,056.3 | 220 | 196 | 54G5/2 | 29,390 | (43G)4H7/2 | 353,454 |
| 308.640 | −0.004 | 324,001.7 | 62 | 284 | 54D7/2 | 36,485 | (43F)4G9/2 | 360,482 |
| 308.685 | 0.007 | 323,954.5 | 16 | 31 | 54G9/2 | 30,907 | (45D)4D7/2 | 354,869 |
| 308.820 | −0.003 | 323,813.2 | 58 | 157 | 32F7/2 | 53,353 | (43D)4F7/2 | 377,163 |
| 308.885 | −0.001 | 323,745.4 | 59 | 255 | 54G7/2 | 30,378 | (43H)4H9/2 | 354,122 |
| 308.922 | −0.002 | 323,706.6 | 20 | 195 | 52G7/2 | 55,773 | (43G)2F5/2 | 379,478 |
| 309.038 | 0.011 | 323,584.5 | 15 | 156 | 32H9/2 | 53,797 | (43F)2G9/2 | 377,393 |
| 309.123 | 0.001 | 323,496.0 | 9 | 163 | 52G9/2 | 59,223 | (41G)2G9/2 | 382,720 |
| 309.159 | 0.002 | 323,458.5 | 78 | 311 | 54G11/2 | 30,662 | (43H)4H9/2 | 354,122 |
| 309.190 | −0.005 | 323,426.0 | 12 | 86 | 32G7/2 | 79,705 | (23F)4D7/2 | 403,133 |
| 309.243 d | 0.007 | 323,370.1 | 45 | 219 | 34F5/2 | 51,049 | (43G)4F5/2 | 374,426 |
| 309.243 d | −0.004 | 323,370.1 | 45 | 165 | 32H9/2 | 53,797 | (43D)4F7/2 | 377,163 |
| 309.286 | 0.001 | 323,325.0 | 13 | 216 | 32F5/2 | 59,954 | (43D)2D3/2 | 383,280 |
| 309.318 | 0.002 | 323,292.4 | 17 | 67 | 54G5/2 | 29,390 | (43G)4G5/2 | 352,685 |
| 309.366 | −0.002 | 323,241.3 | 55 | 212 | 34P3/2 | 32,994 | (43F)4D5/2 | 356,233 |
| 309.426 | 0.008 | 323,178.8 | 90 | 168 | 54D3/2 | 39,788 | (43P)4D5/2 | 362,975 |
| 309.450 | 0.000 | 323,153.9 | 90 | 593 | 52G9/2 | 59,223 | (41I)2H9/2 | 382,377 |
| 309.633 | −0.002 | 322,963.2 | 107 | 582 | 34F7/2 | 48,712 | (43G)4G7/2 | 371,673 |
| 309.732 | 0.004 | 322,859.6 | 19 | 119 | 34P5/2 | 32,005 | (45D)4D7/2 | 354,869 |
| 309.793 | 322,796.5 | 32 | 192 | 34P3/2 | 32,994 | (43P)4P1/2 | 355,790 | |
| 309.976 | 0.011 | 322,605.2 | 23 | 148 | 32H9/2 | 53,797 | (43G)4G11/2 | 376,414 |
| 310.029 | −0.003 | 322,550.5 | 73 | 151 | 54G9/2 | 30,907 | (43G)4H7/2 | 353,454 |
| 310.140 | −0.005 | 322,434.9 | 52 | 310 | 32G9/2 | 79,131 | (21G)2H9/2 | 401,561 |
| 310.211 | −0.011 | 322,360.8 | 15 | 111 | 34F7/2 | 48,712 | (43H)2H9/2 | 371,061 |
| 310.259 | −0.005 | 322,311.8 | 37 | 90 | 54G7/2 | 30,378 | (43G)4G5/2 | 352,685 |
| 310.340 | 0.003 | 322,227.0 | 48 | 75 | 34P5/2 | 32,005 | (45D)4D5/2 | 354,235 |
| 310.604 | 0.004 | 321,953.2 | 51 | 303 | 34F9/2 | 49,104 | (43H)2H9/2 | 371,061 |
| 310.663 | −0.003 | 321,892.2 | 89 | 407 | 34F9/2 | 49,104 | (43F)2F7/2 | 370,993 |
| 310.707 d | 0.002 | 321,847.2 | 21 | 124 | 52D5/2 | 47,119 | (43P)4D7/2 | 368,968 |
| 310.707 d | 0.009 | 321,847.2 | 21 | 194 | 32G7/2 | 79,705 | (21G)2H9/2 | 401,561 |
| 310.885 | 0.002 | 321,662.3 | 5 | 165 | 52F5/2 | 57,412 | (41F)2F5/2 | 379,076 |
| 310.923 | −0.003 | 321,622.5 | 2 | 86 | 52G7/2 | 55,773 | (43F)2G9/2 | 377,393 |
| 310.985 d | 0.009 | 321,559.0 | 65 | 194 | 32H9/2 | 53,797 | (43G)2G7/2 | 375,365 |
| 310.985 d | −0.001 | 321,559.0 | 65 | 225 | 52I11/2 | 44,011 | (43F)4F9/2 | 365,569 |
| 311.058 | 0.003 | 321,483.3 | 122 | 687 | 32F7/2 | 53,353 | (43H)4G7/2 | 374,839 |
| 311.121 | 0.002 | 321,418.0 | 17 | 38 | 54G11/2 | 30,662 | (43H)4H11/2 | 352,082 |
| 311.161 | 0.007 | 321,376.6 | 43 | 223 | 34F9/2 | 49,104 | (43G)4H11/2 | 370,488 |
| 311.272 | 0.002 | 321,262.0 | 49 | 513 | 32H11/2 | 57,962 | (43G)2G9/2 | 379,226 |
| 311.355 | −0.002 | 321,177.0 | 66 | 185 | 54G9/2 | 30,907 | (43H)4H11/2 | 352,082 |
| 311.414 | −0.001 | 321,115.8 | 8 | 169 | 32D5/2 | 72,934 | (23F)4F5/2 | 394,049 |
| 311.453 | −0.003 | 321,076.2 | 18 | 81 | 32F7/2 | 53,353 | (43G)4F5/2 | 374,426 |
| 311.518 d | −0.006 | 321,008.4 | 60 | 381 | 34F5/2 | 51,049 | (43H)4G5/2 | 372,051 |
| 311.518 d | −0.002 | 321,008.4 | 60 | 59 | 52I11/2 | 44,011 | (43H)4H11/2 | 365,017 |
| 311.594 d | 0.006 | 320,930.4 | 36 | 412 | 32F5/2 | 59,954 | (41G)2F5/2 | 380,891 |
| 311.594 d | 0.002 | 320,930.4 | 36 | 154 | 32G7/2 | 79,705 | (41F)2D5/2 | 400,637 |
| 311.845 | 0.003 | 320,672.7 | 8 | 146 | 32D5/2 | 72,934 | (41D)2P3/2 | 393,610 |
| 311.891 | 0.005 | 320,624.5 | 20 | 135 | 34F3/2 | 53,796 | (43G)4F5/2 | 374,426 |
| 311.963 | 0.004 | 320,551.2 | 24 | 164 | 34P3/2 | 32,994 | (45D)4D3/2 | 353,549 |
| 312.007 | 0.001 | 320,505.8 | 9 | 78 | 52I11/2 | 44,011 | (43H)2I13/2 | 364,518 |
| 312.030 | 0.001 | 320,481.5 | 26 | 118 | 52D3/2 | 48,086 | (43F)4D3/2 | 368,569 |
| 312.465 | 0.000 | 320,035.6 | 29 | 140 | 32D3/2 | 71,517 | (23P)4D3/2 | 391,553 |
| 312.497 | 0.000 | 320,002.7 | 59 | 466 | 52G9/2 | 59,223 | (43G)2G9/2 | 379,226 |
| 312.716 | 0.001 | 319,779.1 | 36 | 152 | 32H9/2 | 53,797 | (43F)4D7/2 | 373,577 |
| 312.742 | 0.003 | 319,752.1 | 36 | 149 | 32H11/2 | 57,962 | (41G)2H11/2 | 377,717 |
| 312.807 | 0.000 | 319,685.6 | 39 | 345 | 52F7/2 | 59,792 | (43G)2F5/2 | 379,478 |
| 312.836 | 319,656.8 | 99 | 248 | 54G5/2 | 29,390 | (43H)4H7/2 | 349,047 | |
| 312.895 | −0.004 | 319,596.1 | 46 | 332 | 52G7/2 | 55,773 | (43G)2G7/2 | 375,365 |
| 312.966 | 0.000 | 319,523.7 | 12 | 123 | 32F5/2 | 59,954 | (43G)2F5/2 | 379,478 |
| 313.025 | 0.008 | 319,463.4 | 31 | 228 | 52I13/2 | 45,546 | (43H)4H11/2 | 365,017 |
| 313.058 | 0.002 | 319,429.4 | 59 | 513 | 32H11/2 | 57,962 | (43F)2G9/2 | 377,393 |
| 313.143 | 0.000 | 319,343.1 | 48 | 115 | 54G7/2 | 30,378 | (43H)4I9/2 | 349,721 |
| 313.164 | 0.001 | 319,321.8 | 48 | 199 | 32H9/2 | 53,797 | (43G)4G9/2 | 373,120 |
| 313.208 | 0.000 | 319,276.3 | 23 | 81 | 34P3/2 | 32,994 | (45D)4D1/2 | 352,270 |
| 313.375 | 0.000 | 319,106.8 | 21 | 191 | 32F5/2 | 59,954 | (41G)2G7/2 | 379,061 |
| 313.423 | 0.001 | 319,057.6 | 48 | 155 | 54G11/2 | 30,662 | (43H)4I9/2 | 349,721 |
| 313.522 | 318,957.4 | 32 | 150 | 32G7/2 | 79,705 | (23F)2F5/2 | 398,662 | |
| 313.599 | 0.000 | 318,879.0 | 9 | 82 | 32H9/2 | 53,797 | (43H)2H11/2 | 372,676 |
| 313.641 | −0.006 | 318,835.7 | 9 | 72 | 34F5/2 | 51,049 | (43P)4D7/2 | 369,878 |
| 313.957 | 0.009 | 318,514.8 | 17 | 92 | 52I11/2 | 44,011 | (43H)2I11/2 | 362,535 |
| 313.981 d | 0.003 | 318,490.5 | 17 | 147 | 52G9/2 | 59,223 | (41G)2H11/2 | 377,717 |
| 313.981 d | −0.003 | 318,490.5 | 17 | 165 | 52D3/2 | 48,086 | (43F)4F3/2 | 366,573 |
| 314.013 | −0.001 | 318,458.5 | 66 | 339 | 32H11/2 | 57,962 | (41I)2I13/2 | 376,419 |
| 314.152 | 0.003 | 318,316.8 | 7 | 60 | 32F7/2 | 53,353 | (43G)4G7/2 | 371,673 |
| 314.212 | −0.001 | 318,256.6 | 22 | 197 | 34F3/2 | 53,796 | (43H)4G5/2 | 372,051 |
| 314.298 d | −0.006 | 318,169.6 | 18 | 206 | 12D3/2 | 104,821 | (21D)2F5/2 | 422,985 |
| 314.298 d | 0.000 | 318,169.6 | 18 | 220 | 52G9/2 | 59,223 | (43F)2G9/2 | 377,393 |
| 314.370 | −0.003 | 318,096.9 | 19 | 75 | 34F7/2 | 48,712 | (43F)4F7/2 | 366,806 |
| 314.400 | 0.002 | 318,065.8 | 8 | 69 | 52I13/2 | 45,546 | (43H)4I13/2 | 363,614 |
| 314.545 | 0.000 | 317,919.3 | 19 | 184 | 34F5/2 | 51,049 | (43P)4D7/2 | 368,968 |
| 314.650 | −0.010 | 317,813.5 | 9 | 113 | 52G7/2 | 55,773 | (43F)4D7/2 | 373,577 |
| 314.712 | −0.001 | 317,750.9 | 23 | 81 | 54D7/2 | 36,485 | (45D)4D5/2 | 354,235 |
| 314.749 | 0.002 | 317,713.4 | 89 | 236 | 54G11/2 | 30,662 | (45D)6D9/2 | 348,377 |
| 314.797 | 0.000 | 317,665.5 | 23 | 109 | 34P1/2 | 34,605 | (45D)4D1/2 | 352,270 |
| 314.856 | −0.005 | 317,605.8 | 22 VI | 156 | 52F7/2 | 59,792 | (43F)2G9/2 | 377,393 |
| 315.100 | −0.012 | 317,359.3 | 14 | 145 | 52G7/2 | 55,773 | (43G)4G9/2 | 373,120 |
| 315.192 | −0.003 | 317,266.6 | 11 | 79 | 32H9/2 | 53,797 | (43H)2H9/2 | 371,061 |
| 315.264 d | 0.001 | 317,194.8 | 83 | 181 | 32H9/2 | 53,797 | (43F)2F7/2 | 370,993 |
| 315.264 d | −0.004 | 317,194.8 | 83 | 310 | 52G9/2 | 59,223 | (43G)4G11/2 | 376,414 |
| 315.327 d | −0.001 | 317,130.8 | 37 | 284 | 34F7/2 | 48,712 | (43F)2G7/2 | 365,842 |
| 315.327 d | −0.005 | 317,130.8 | 37 | 125 | 32D5/2 | 72,934 | (23F)4F5/2 | 390,060 |
| 315.552 | 0.001 | 316,905.2 | 16 | 119 | 52D5/2 | 47,119 | (43D)2D5/2 | 364,025 |
| 315.751 | −0.002 | 316,705.6 | 11 | 124 | 32H9/2 | 53,797 | (43G)2H9/2 | 370,501 |
| 315.758 | −0.007 | 316,698.2 | 18 | 97 | 32H9/2 | 53,797 | (43G)4H11/2 | 370,488 |
| 315.988 | 0.003 | 316,467.3 | 4 | 41 | 52I11/2 | 44,011 | (43H)4I11/2 | 360,481 |
| 316.291 | 0.000 | 316,164.3 | 18 | 148 | 52F5/2 | 57,413 | (43F)4D7/2 | 373,577 |
| 316.384 | 0.010 | 316,071.5 | 9 | 106 | 32H9/2 | 53,797 | (43P)4D7/2 | 369,878 |
| 316.548 | 0.006 | 315,907.6 | 44 | 248 | 34F9/2 | 49,104 | (43H)4H11/2 | 365,017 |
| 316.588 | −0.004 | 315,867.8 | 12 | 103 | 32H9/2 | 53,797 | (41I)2I11/2 | 369,661 |
| 316.780 | −0.009 | 315,676.9 | 21 | 149 | 34F9/2 | 49,104 | (43F)4G9/2 | 364,772 |
| 316.804 | −0.001 | 315,652.9 | 29 | 26 | 34F3/2 | 53,796 | (43D)4P3/2 | 369,448 |
| 316.843 | 0.002 | 315,613.8 | 83 | 249 | 52G9/2 | 59,223 | (43H)4G7/2 | 374,839 |
| 317.044 | −0.002 | 315,413.3 | 8 | 46 | 32F5/2 | 59,954 | (43G)2G7/2 | 375,365 |
| 317.146 | −0.008 | 315,312.5 | 4 | 18 | 54G5/2 | 29,389 | (45D)4F5/2 | 344,697 |
| 317.305 | −0.001 | 315,154.6 | 126 | 362 | 54G9/2 | 30,907 | (45D)4F7/2 | 346,061 |
| 317.408 | −0.005 | 315,051.9 | 14 | 200 | 52F7/2 | 59,792 | (43H)4G7/2 | 374,839 |
| 317.572 | 0.000 | 314,889.0 | 15 | 31 | 52D3/2 | 48,086 | (43P)4D5/2 | 362,975 |
| 317.594 | −0.003 | 314,867.0 | 26 | 65 | 54D1/2 | 38,685 | (45D)4D3/2 | 353,549 |
| 317.710 | −0.001 | 314,752.3 | 20 | 62 | 32D3/2 | 71,517 | (41D)2D5/2 | 386,268 |
| 317.735 | 0.000 | 314,728.1 | 24 | 91 | 52G7/2 | 55,773 | (43G)2H9/2 | 370,501 |
| 317.823 | −0.008 | 314,640.2 | 31 | 135 | 32H9/2 | 53,797 | (43G)4H9/2 | 368,429 |
| 318.013 | −0.005 | 314,452.3 | 30 VI | 156 | 54D3/2 | 39,788 | (45D)4D5/2 | 354,235 |
| 318.174 | 0.001 | 314,293.4 | 30 | 125 | 52D3/2 | 48,086 | (43H)4G5/2 | 362,381 |
| 318.202 | −0.003 | 314,265.9 | 19 | 92 | 34F7/2 | 48,712 | (43P)4D5/2 | 362,975 |
| 318.307 | 0.001 | 314,162.5 | 17 | 224 | 32G9/2 | 79,131 | (23F)4G7/2 | 393,295 |
| 318.411 | −0.004 | 314,059.9 | 11 | 37 | 34P5/2 | 32,005 | (45D)4F7/2 | 346,061 |
| 318.791 d | −0.004 | 313,685.3 | 9 | 200 | 32D5/2 | 72,934 | (41F)2G7/2 | 386,615 |
| 318.791 d | 0.001 | 313,685.3 | 9 | 53 | 32H9/2 | 53,797 | (43F)4G11/2 | 367,483 |
| 318.832 | 0.003 | 313,645.3 | 26 | 135 | 32D5/2 | 72,934 | (41S)2P3/2 | 386,582 |
| 319.143 d | −0.005 | 313,338.9 | 14 | 126 | 32D5/2 | 72,934 | (41D)2D5/2 | 386,268 |
| 319.143 d | 0.004 | 313,338.9 | 14 | 184 | 34F9/2 | 49,104 | (43G)4F9/2 | 362,447 |
| 319.273 | −0.002 | 313,211.9 | 14 | 46 | 52D3/2 | 48,086 | (43F)4F5/2 | 361,296 |
| 319.534 | 0.002 | 312,955.9 | 102 | 256 | 54G7/2 | 30,378 | (45D)4F5/2 | 343,336 |
| 319.902 | −0.003 | 312,595.6 | 65 | 194 | 54G5/2 | 29,390 | (45D)4F3/2 | 341,983 |
| 320.035 | −0.001 | 312,465.5 | 12 | 57 | 52F5/2 | 57,413 | (43P)4D7/2 | 369,878 |
| 320.251 | 0.004 | 312,255.5 | 14 | 30 | 52F7/2 | 59,792 | (43H)4G5/2 | 372,051 |
| 320.366 | 0.000 | 312,142.8 | 18 | 43 | 52I13/2 | 45,546 | (43H)4G11/2 | 357,689 |
| 320.625 | 0.001 | 311,891.2 | 28 | 89 | 54D7/2 | 36,485 | (45D)6D9/2 | 348,377 |
| 320.752 d | 0.003 | 311,767.4 | 14 | 62 | 52G9/2 | 59,223 | (43F)2F7/2 | 370,993 |
| 320.752 d | −0.005 | 311,767.4 | 9 | 248 | 32D3/2 | 71,517 | (43D)2D3/2 | 383,280 |
| 320.823 d | 0.000 | 311,698.5 | 25 | 82 | 32H11/2 | 57,962 | (41I)2I11/2 | 369,661 |
| 320.823 d | −0.008 | 311,698.5 | 25 | 216 | 32G7/2 | 79,705 | (23F)4G5/2 | 391,396 |
| 320.900 | 0.003 | 311,623.9 | 60 | 163 | 54G11/2 | 30,662 | (45D)6D9/2 | 342,289 |
| 321.154 | 0.001 | 311,377.5 | 15 VI | 66 | 34F9/2 | 49,104 | (43F)4G9/2 | 360,482 |
| 321.198 | −0.003 | 311,334.3 | 26 | 136 | 34P5/2 | 32,005 | (45D)4F5/2 | 343,336 |
| 321.257 | 0.001 | 311,277.1 | 17 | 19 | 52G9/2 | 59,223 | (43G)2H9/2 | 370,501 |
| 321.312 | −0.004 | 311,224.0 | 18 | 42 | 32H9/2 | 53,797 | (43H)4H11/2 | 365,017 |
| 322.007 | −0.001 | 310,552.4 | 41 | 91 | 54G9/2 | 30,907 | (45D)6D7/2 | 341,458 |
| 322.338 | 310,233.1 | 29 | 579 | 12D5/2 | 103,996 | (23F)2D5/2 | 414,230 | |
| 322.612 | 0.002 | 309,969.4 | 8 | 57 | 34P5/2 | 32,005 | (45D)4F3/2 | 341,976 |
| 322.852 | 0.006 | 309,739.4 | 13 | 74 | 52G9/2 | 59,223 | (43P)4D7/2 | 368,968 |
| 323.598 | 0.007 | 309,025.3 | 12 VI | 118 | 32G9/2 | 79,131 | (41F)2G7/2 | 388,163 |
| 323.626 | 0.000 | 308,998.8 | 11 | 5 | 52G7/2 | 55,773 | (43F)4G9/2 | 364,772 |
| 323.721 | −0.001 | 308,907.5 | 17 | 87 | 52D3/2 | 48,086 | (43F)2D3/2 | 356,993 |
| 323.897 | −0.002 | 308,740.0 | 22 | 204 | 32H9/2 | 53,797 | (43H)2I11/2 | 362,535 |
| 324.055 | −0.005 | 308,589.8 | 25 | 199 | 34F9/2 | 49,104 | (43H)4G11/2 | 357,689 |
| 324.404 | 0.003 | 308,257.6 | 26 VI | 79 | 52G9/2 | 59,223 | (43F)4G11/2 | 367,483 |
| 324.427 | −0.003 | 308,235.7 | 82 | 59 | 34P3/2 | 32,994 | (45D)6D1/2 | 341,227 |
| 324.458 | 0.003 | 308,206.7 | 38 | 87 | 54D7/2 | 36,485 | (45D)4F5/2 | 344,695 |
| 324.718 | 0.002 | 307,959.3 | 19 | 194 | 32D3/2 | 71,517 | (43G)2F5/2 | 379,478 |
| 325.135 | −0.005 | 307,564.4 | 5 | 92 | 32D3/2 | 71,516 | (41F)2F5/2 | 379,077 |
| 325.170 | 0.003 | 307,531.5 | 15 | 74 | 32D5/2 | 72,934 | (41F)2F7/2 | 380,468 |
| 325.319 | −0.001 | 307,390.2 | 32 | 161 | 34F9/2 | 49,104 | (43F)4D7/2 | 356,493 |
| 325.829 | 0.001 | 306,909.1 | 5 | 51 | 32G7/2 | 79,705 | (41F)2G7/2 | 386,615 |
| 325.943 | 0.008 | 306,802.0 | 13 | 4 | 32H11/2 | 57,962 | (43F)4G9/2 | 364,772 |
| 326.139 | 0.004 | 306,618.0 | 17 | 19 | 34P1/2 | 34,605 | (45D)6D1/2 | 341,227 |
| 326.204 | −0.001 | 306,556.6 | 26 VI | 122 | 32H11/2 | 57,962 | (43H)2I13/2 | 364,518 |
| 326.519 | −0.004 | 306,260.7 | 9 | 129 | 32G7/2 | 79,705 | (43D)2F5/2 | 385,962 |
| 326.609 | 0.002 | 306,176.4 | 13 | 12 | 34P3/2 | 32,994 | (45D)6D5/2 | 339,172 |
| 326.915 d | 0.000 | 305,890.1 | 24 | 41 | 32H9/2 | 53,797 | (43G)4G7/2 | 359,687 |
| 326.915 d | 0.003 | 305,890.1 | 24 | 318 | 12D5/2 | 103,996 | (21G)2F7/2 | 409,889 |
| 327.004 | −0.003 | 305,806.4 | 11 | 20 | 54D7/2 | 36,485 | (45D)6D9/2 | 342,289 |
| 327.048 | 0.000 | 305,765.2 | 39 | 219 | 34F9/2 | 49,104 | (45D)4D7/2 | 354,869 |
| 327.307 | −0.001 | 305,523.8 | 38 VI | 119 | 34F7/2 | 48,712 | (45D)4D5/2 | 354,235 |
| 327.438 | −0.002 | 305,401.0 | 31 | 133 | 54D5/2 | 39,299 | (45D)4F5/2 | 344,697 |
| 327.850 | 0.001 | 305,017.1 | 8 | 20 | 34F9/2 | 49,104 | (43H)4H9/2 | 354,122 |
| 328.555 | 0.002 | 304,362.8 | 31 VI | 228 | 12D3/2 | 104,821 | (21G)2F5/2 | 409,186 |
| 329.712 | 0.003 | 303,295.2 | 12 | 36 | 54D1/2 | 38,685 | (45D)4F3/2 | 341,983 |
| 329.830 | 0.000 | 303,186.1 | 21 | 94 | 34F5/2 | 51,049 | (45D)4D5/2 | 354,235 |
| 330.391 | 0.000 | 302,672.1 | 16 | 202 | 32G7/2 | 79,705 | (41I)2H9/2 | 382,377 |
| 330.560 | 0.004 | 302,516.8 | 15 | 50 | 32H11/2 | 57,962 | (43F)4G9/2 | 360,482 |
| 332.140 | −0.006 | 301,077.9 | 12 | 65 | 32H9/2 | 53,797 | (45D)4D7/2 | 354,869 |
| 332.353 | −0.003 | 300,885.1 | 11 | 69 | 32F7/2 | 53,353 | (45D)4D5/2 | 354,235 |
| 332.485 d | −0.003 | 300,765.3 | 12 | 133 | 32G7/2 | 79,705 | (41F)2F7/2 | 380,468 |
| 332.485 d | 0.004 | 300,765.3 | 12 | 76 | 32F7/2 | 53,353 | (43H)4H9/2 | 354,122 |
| 333.198 | −0.001 | 300,121.8 | 4 | 266 | 12D5/2 | 103,996 | (23F)2F7/2 | 404,117 |
| 334.140 | −0.003 | 299,275.8 | 12 | 52 | 34F9/2 | 49,104 | (45D)6D9/2 | 348,377 |
| 334.911 | −0.001 | 298,587.1 | 1 | 53 | 32G9/2 | 79,131 | (41G)2H11/2 | 377,717 |
| 338.225 | −0.001 | 295,661.2 | 15 | 92 | 32G7/2 | 79,705 | (43G)2G7/2 | 375,365 |
| 341.089 | 0.008 | 293,178.3 | 20 | 30 | 34F9/2 | 49,104 | (45D)6D9/2 | 342,289 |
| 342.628 | 0.000 | 291,861.7 | 30 | 9 | 32G9/2 | 79,131 | (43F)2F7/2 | 370,993 |
a Observed wavelengths, d—doubly identified, t—trebly identified; b Difference between the observed wavelength and the wavelength derived from the final level energies (Ritz wavelength). A blank value indicates that the upper level is derived only from that line; c Relative intensity; VI—line is also identified as Ag VI; e The number preceding the terms is seniority number.

Table A2.
Identified lines of the 4d4–4d35p transitions in the spectrum of Ag7+.
| λ (Å) a | o-c, (Å) b | ν (cm−1) | I c | gA, (108 s−1) | 5d4 | 5d35p | ||
|---|---|---|---|---|---|---|---|---|
| Term e | E (cm−1) | Term f | E (cm−1) | |||||
| 247.539 | −0.005 | 403,976.8 | 56 | 150 | 43H6 | 28,185 | (32F)3G5 | 432,154 |
| 253.534 | −0.002 | 394,424.4 | 54 | 114 | 43H4 | 23,302 | (32H)3G3 | 417,724 |
| 253.627 | 0.001 | 394,279.8 | 98 | 383 | 23F4 | 60,980 | (12D)3F4 | 455,261 |
| 253.737 | −0.001 | 394,108.9 | 60 | 284 | 45D3 | 5292 | (34P)5P3 | 399,399 |
| 254.226 | −0.003 | 393,350.8 | 20 | 174 | 41G4 | 43,104 | (32F)1F3 | 436,451 |
| 254.451 | 0.001 | 393,003.0 | 23 | 75 | 43H6 | 28,185 | (32H)1I6 | 421,189 |
| 254.641 | 0.000 | 392,709.8 | 17 | 41 | 23F3 | 62,552 | (12D)3F4 | 455,261 |
| 255.131 | 0.000 | 391,955.5 | 550 | 1307 | 45D4 | 7443 | (34P)5P3 | 399,399 |
| 255.214 | 391,828.0 | 140 | 596 | 23F4 | 60,980 | (12D)3D3 | 452,808 | |
| 255.570 | 0.001 | 391,282.2 | 28 | 99 | 45D0 | 0 | (34P)5P1 | 391,283 |
| 255.891 | 0.000 | 390,791.4 | 38 | 78 | 23F3 | 62,552 | (12D)1D2 | 453,343 |
| 255.891 | 390,791.4 | 38 | 210 | 43G3 | 26,967 | (32D)3D2 | 417,758 | |
| 255.919 | 390,748.6 | 115 | 455 | 45D3 | 5292 | (34P)5P2 | 396,041 | |
| 256.069 | 390,519.8 | 61 | 435 | 21G4 | 69,584 | (12D)1F3 | 460,104 | |
| 256.138 | 0.002 | 390,414.5 | 49 | 231 | 45D2 | 3212 | (34P)5P2 | 393,630 |
| 256.446 | −0.002 | 389,945.7 | 70 | 320 | 45D1 | 1,340 | (34P)5P1 | 391,283 |
| 256.757 | 389,473.3 | 180 | 347 | 43H6 | 28,185 | (32H)3I7 | 417,658 | |
| 257.391 | −0.001 | 388,514.0 | 110 | 354 | 45D4 | 7443 | (34F)5F5 | 395,955 |
| 257.505 | −0.003 | 388,342.0 | 57 | 314 | 45D3 | 5292 | (34P)5P2 | 393,630 |
| 257.603 | 0.003 | 388,194.3 | 35 | 194 | 43G3 | 26,967 | (34P)3D3 | 415,165 |
| 257.627 | 0.006 | 388,158.1 | 160d | 114 | 43H4 | 23,302 | (32D)3D3 | 411,469 |
| 257.627 | 0.007 | 388,158.1 | 160d | 567 | 43F4 | 29,555 | (32H)3G3 | 417,724 |
| 257.645 | −0.004 | 388,131.0 | 83 | 482 | 43G4 | 32,698 | (32H)3G4 | 420,822 |
| 257.685 | 0.000 | 388,070.7 | 260 | 437 | 45D2 | 3212 | (34P)5P1 | 391,283 |
| 257.740 | 0.001 | 387,987.9 | 33 | 230 | 43P2 | 32,134 | (32F)3F3 | 420,123 |
| 257.796 | −0.002 | 387,903.6 | 43 | 172 | 45D3 | 5292 | (34F)5F4 | 393,193 |
| 257.947 | −0.001 | 387,676.5 | 68 | 289 | 45D2 | 3212 | (34F)5F3 | 390,887 |
| 258.332 | 0.004 | 387,098.8 | 26 | 165 | 43F3 | 32926 | (32P)3P2 | 420,031 |
| 258.347 | 0.002 | 387,076.3 | 29 | 107 | 43H5 | 26,250 | (32G)1H5 | 413,329 |
| 258.583 | 0.003 | 386,723.0 | 120 | 492 | 43H5 | 26,250 | (32F)1G4 | 412,977 |
| 258.855 | 386,316.7 | 22 | 82 | 45D0 | 0 | (34F)5F1 | 386,317 | |
| 259.104 | −0.001 | 385,945.4 | 170 | 944 | 43G5 | 35,077 | (32H)3G5 | 421,021 |
| 259.192 | 0.000 | 385,814.4 | 130 | 320 | 43H6 | 28,185 | (32H)3I6 | 413,999 |
| 259.239 | 0.000 | 385,744.4 | 60d | 412 | 43G5 | 35,077 | (32H)3G4 | 420,822 |
| 259.239 | 0.004 | 385,744.4 | 60d | 259 | 45D4 | 7443 | (34F)5F4 | 393,193 |
| 259.283 | −0.001 | 385,679.0 | 56 | 106 | 21G4 | 69,584 | (12D)3F4 | 455,261 |
| 259.342 | 0.001 | 385,591.2 | 71d | 163 | 43P1 | 26,526 | (32D)3D1 | 412,118 |
| 259.342 | 0.011 | 385,591.2 | 71d | 125 | 43H4 | 23,302 | (32G)3H5 | 408,910 |
| 259.432 | 0.002 | 385,457.5 | 39 | 120 | 45D1 | 1340 | (34F)5F2 | 386,800 |
| 259.643 | 0.000 | 385,144.2 | 120 | 672 | 43H6 | 28,185 | (32G)1H5 | 413,329 |
| 259.878 | −0.001 | 384,795.9 | 110d | 155 | 43G4 | 32,698 | (32D)3F4 | 417,492 |
| 259.878 | 0.001 | 384,795.9 | 110d | 680 | 43F3 | 32,926 | (32H)3G3 | 417,724 |
| 259.978 | 0.003 | 384,647.9 | 130 | 554 | 45D3 | 5292 | (34F)3G3 | 389,944 |
| 260.115 | 0.001 | 384,445.3 | 37 | 337 | 41F3 | 52,004 | (32F)1F3 | 436,451 |
| 260.280 | 0.002 | 384,201.6 | 180 | 746 | 43H4 | 23,302 | (32G)3F3 | 407,506 |
| 260.376 | 0.005 | 384,060.0 | 32 | 172 | 43F2 | 28,051 | (32D)3D1 | 412,118 |
| 260.443 | 0.001 | 383,961.2 | 81 | 398 | 45D1 | 1340 | (34F)5D2 | 385,302 |
| 260.575 | 0.000 | 383,766.7 | 41 | 302 | 23F3 | 62,552 | (12D)3D3 | 446,318 |
| 260.695 | −0.001 | 383,590.0 | 170 | 198 | 45D2 | 3212 | (34F)5F2 | 386,800 |
| 260.709 | −0.001 | 383,569.4 | 130 | 319 | 45D0 | 0 | (34F)5D1 | 383,568 |
| 260.989 | −0.004 | 383,157.9 | 59 | 220 | 43D3 | 36,879 | (32P)3P2 | 420,031 |
| 261.086 | 0.000 | 383,015.6 | 290 | 561 | 45D4 | 7443 | (34F)5G5 | 390,458 |
| 261.173 | 0.000 | 382,888.0 | 32 | 207 | 23F2 | 61,644 | (12D)3D2 | 444,532 |
| 261.247 | 0.002 | 382,779.5 | 26 | 75 | 43G3 | 26,967 | (32G)1F3 | 409,750 |
| 261.323 | −0.001 | 382,668.2 | 1000 | 1735 | 43H6 | 28,185 | (32G)3H6 | 410,851 |
| 261.328 | 0.000 | 382,660.9 | 958 | 1568 | 43H5 | 26,250 | (32G)3H5 | 408,910 |
| 261.400 | 382,555.5 | 94 | 486 | 43G3 | 26,967 | (32D)3F2 | 409,522 | |
| 261.458 | −0.002 | 382,470.6 | 99 | 547 | 43G4 | 32,698 | (34P)3D3 | 415,165 |
| 261.496 | 0.000 | 382,415.0 | 590 | 1655 | 43G5 | 35,077 | (32D)3F4 | 417,492 |
| 261.625 | 0.001 | 382,226.5 | 37 | 267 | 45D1 | 1340 | (34F)5D1 | 383,568 |
| 261.718 | 0.000 | 382,090.7 | 250 | 720 | 45D2 | 3212 | (34F)5D2 | 385,302 |
| 261.752 | −0.003 | 382,041.0 | 490 | 1121 | 45D3 | 5292 | (34F)5F3 | 387,329 |
| 261.793 | 0.000 | 381,981.2 | 65d | 264 | 23F3 | 62,552 | (12D)3D2 | 444,532 |
| 261.793 | 0.003 | 381,981.2 | 65d | 399 | 43H5 | 26,250 | (34P)5D4 | 408,236 |
| 261.836 | −0.003 | 381,918.4 | 160 | 695 | 43F4 | 29,555 | (32D)3D3 | 411,469 |
| 262.106 | −0.003 | 381,525.0 | 420 | 950 | 45D4 | 7443 | (34F)5F4 | 388,964 |
| 262.160 | −0.001 | 381,446.4 | 670 | 1886 | 41I6 | 39,744 | (32H)1I6 | 421,189 |
| 262.276 | −0.001 | 381,277.8 | 620 | 2055 | 41I6 | 39,744 | (32H)3G5 | 421,021 |
| 262.323 | 0.000 | 381,209.4 | 110 | 397 | 43P2 | 32,134 | (32P)3P1 | 413,344 |
| 262.340 | 381,184.7 | 100 | 468 | 45D1 | 1340 | (34F)5D0 | 382,525 | |
| 262.520 | −0.004 | 380,923.3 | 280d | 359 | 43G5 | 35,077 | (32H)1H5 | 415,995 |
| 262.520 | 380,923.3 | 280d | 492 | 43H5 | 26,250 | (34P)5D4 | 407,173 | |
| 262.535 | 380,901.6 | 490 | 1502 | 41G4 | 43,104 | (32P)3D3 | 424,006 | |
| 262.653 | −0.004 | 380,730.5 | 27 | 162 | 43H6 | 28,185 | (32G)3H5 | 408,910 |
| 262.787 | 0.002 | 380,536.3 | 51 | 240 | 43G3 | 26,967 | (32G)3F3 | 407,506 |
| 262.910 | 380,358.3 | 250d | 553 | 43F2 | 28,051 | (32G)3F2 | 408,409 | |
| 262.910 | −0.002 | 380,358.3 | 250d | 688 | 45D2 | 3212 | (34F)5D1 | 383,568 |
| 262.966 | 0.001 | 380,277.3 | 50 | 392 | 43G4 | 32,698 | (32F)1G4 | 412,977 |
| 263.020 | −0.003 | 380,199.2 | 87 | 269 | 43F4 | 29,555 | (32G)1F3 | 409,750 |
| 263.150 | −0.001 | 380,011.4 | 130 | 687 | 45D3 | 5292 | (34F)5D2 | 385,302 |
| 263.212 | 0.003 | 379,921.9 | 370 | 1258 | 45D3 | 5292 | (34F)5D4 | 385,218 |
| 263.240 | 0.003 | 379,881.5 | 73 | 306 | 45D4 | 7443 | (34F)5F3 | 387,329 |
| 263.303 | 379,790.6 | 46 | 267 | 41G4 | 43,104 | (32F)3F3 | 422,895 | |
| 263.336 | 0.001 | 379,743.0 | 35 | 303 | 43P1 | 26,526 | (32D)3D2 | 406,270 |
| 263.510 | −0.004 | 379,492.3 | 250 | 1114 | 43F3 | 32,926 | (32P)3D2 | 412,412 |
| 263.811 | 0.001 | 379,059.3 | 520 | 1894 | 43H6 | 28,185 | (32H)3I5 | 407,246 |
| 263.914 | −0.012 | 378,911.3 | 500t | 372 | 43H5 | 26,250 | (32H)3H5 | 405,144 |
| 263.914 | 0.007 | 378,911.3 | 500 t | 279 | 43G5 | 35,077 | (32H)3I6 | 413,999 |
| 263.914 | 0.001 | 378,911.3 | 500 t | 1145 | 43H5 | 26,250 | (32G)3G4 | 405,162 |
| 264.072 | −0.003 | 378,684.6 | 84 | 627 | 43F4 | 29,555 | (34P)5D4 | 408,236 |
| 264.159 | 378,559.9 | 140 | 338 | 43P0 | 21,309 | (32P)3P1 | 399,869 | |
| 264.293 | 0.000 | 378,367.9 | 470 | 1252 | 45D2 | 3212 | (34F)5D3 | 381,580 |
| 264.374 | 0.000 | 378,252.0 | 50 | 384 | 43G5 | 35,077 | (32G)1H5 | 413,329 |
| 264.409 | −0.005 | 378,201.9 | 33 | 130 | 43G3 | 26,967 | (32G)3G4 | 405,162 |
| 264.546 | −0.001 | 378,006.1 | 23 | 208 | 43P1 | 26,526 | (32P)3D1 | 404,530 |
| 264.581 | −0.004 | 377,956.1 | 96 | 406 | 43F4 | 29,555 | (32G)3F3 | 407,506 |
| 264.705 | −0.003 | 377,779.0 | 680 | 2033 | 45D4 | 7443 | (34F)5D4 | 385,218 |
| 264.752 | 0.004 | 377,712.0 | 65 | 753 | 41G4 | 43,104 | (32H)3G4 | 420,822 |
| 264.769 | 0.002 | 377,687.7 | 180 | 415 | 43F4 | 29,555 | (32H)3I5 | 407,246 |
| 264.802 | 377,640.7 | 73 | 288 | 21D2 | 88,586 | (12D)1P1 | 466,227 | |
| 265.169 | −0.006 | 377,118.0 | 83 | 467 | 43H5 | 26,250 | (32H)3H6 | 403,359 |
| 265.283 | 0.002 | 376,955.9 | 340 | 936 | 43H6 | 28,185 | (32H)3H5 | 405,144 |
| 265.439 | 376,734.4 | 320d | 1405 | 43G4 | 32,698 | (32D)3F3 | 409,432 | |
| 265.439 | 0.000 | 376,734.4 | 320d | 317 | 21G4 | 69,584 | (12D)3D3 | 446,318 |
| 265.620 | 0.001 | 376,477.7 | 78 | 366 | 43F2 | 28,051 | (32P)3D1 | 404,530 |
| 265.728 | −0.002 | 376,324.7 | 390 | 725 | 45D1 | 1340 | (34F)3D2 | 377,661 |
| 265.782 | 0.002 | 376,248.2 | 500 | 1790 | 41I6 | 39,744 | (32H)1H5 | 415,995 |
| 265.948 | 0.001 | 376,013.3 | 260 | 394 | 43D3 | 36,879 | (34P)3D2 | 412,894 |
| 265.977 | −0.007 | 375,972.3 | 440d | 1413 | 43H4 | 23,302 | (32G)1G4 | 399,265 |
| 265.977 | 0.008 | 375,972.3 | 440d | 291 | 45D4 | 7443 | (34F)5G5 | 383,426 |
| 266.238 | 0.002 | 375,603.8 | 170 | 816 | 43F4 | 29,555 | (32G)3G4 | 405,162 |
| 266.285 | 0.001 | 375,537.5 | 140 | 292 | 43G4 | 32,698 | (34P)5D4 | 408,236 |
| 266.384 | 0.003 | 375,397.9 | 420 | 1410 | 43H4 | 23,302 | (32G)3G3 | 398,704 |
| 266.545 | 0.002 | 375,171.2 | 320 | 831 | 43H6 | 28,185 | (32H)3H6 | 403,359 |
| 266.744 | 374,891.3 | 77 | 345 | 45D0 | 0 | (34F)3D1 | 374,891 | |
| 266.964 | 0.006 | 374,582.3 | 430t | 921 | 43D3 | 36,879 | (32D)3D3 | 411,469 |
| 266.964 | 374,582.3 | 430t | 529 | 43D3 | 36,879 | (34P)5S2 | 411,461 | |
| 266.964 | −0.002 | 374,582.3 | 430t | 762 | 43F3 | 32,926 | (32G)3F3 | 407,506 |
| 267.197 | 0.000 | 374,255.7 | 120 | 277 | 41I6 | 39,744 | (32H)3I6 | 413,999 |
| 267.281 | −0.001 | 374,138.1 | 250d | 602 | 43P2 | 32,134 | (32D)3D2 | 406,270 |
| 267.281 | −0.001 | 374,138.1 | 250d | 326 | 45D4 | 7443 | (34F)5D3 | 381,580 |
| 267.426 | 0.001 | 373,935.2 | 130 | 462 | 43G3 | 26,967 | (34P)5D2 | 400,904 |
| 267.676 | −0.001 | 373,586.0 | 460d | 1579 | 41I6 | 39,744 | (32G)1H5 | 413,329 |
| 267.676 | −0.003 | 373,586.0 | 460d | 310 | 43H5 | 26,250 | (34F)3G5 | 399,831 |
| 267.942 | 0.004 | 373,215.1 | 28 | 222 | 43D1 | 39,191 | (32P)3D2 | 412,412 |
| 268.145 | −0.004 | 372,932.6 | 48 | 324 | 43D1 | 39,191 | (32D)3D1 | 412,118 |
| 268.201 | −0.001 | 372,854.7 | 81 | 412 | 43F2 | 28,051 | (34P)5D2 | 400,904 |
| 268.347 | 0.001 | 372,651.8 | 120 | 332 | 43H4 | 23,302 | (34F)5F5 | 395,955 |
| 268.362 | 372,631.0 | 250 | 1228 | 41F3 | 52,004 | (32D)1D2 | 424,635 | |
| 268.487 | −0.008 | 372,457.5 | 48d | 274 | 43G4 | 32,698 | (32H)3H5 | 405,144 |
| 268.487 | 0.005 | 372,457.5 | 48d | 205 | 43G4 | 32,698 | (32G)3G4 | 405,162 |
| 268.553 | 0.002 | 372,366.0 | 24 | 110 | 45D3 | 5292 | (34F)3D2 | 377,661 |
| 268.597 | −0.005 | 372,305.0 | 28 | 109 | 43G3 | 26,967 | (32G)1G4 | 399,265 |
| 268.648 | 0.001 | 372,234.3 | 29 | 308 | 43F3 | 32,926 | (32G)3G4 | 405,162 |
| 268.691 | −0.004 | 372,174.7 | 31 | 270 | 43G5 | 35,077 | (32H)3I5 | 407,246 |
| 269.009 | 0.002 | 371,734.8 | 71 | 618 | 43G3 | 26,967 | (32G)3G3 | 398,704 |
| 269.074 | 0.001 | 371,645.0 | 390 | 1249 | 43H6 | 28,185 | (34F)3G5 | 399,831 |
| 269.420 | 0.004 | 371,167.7 | 24 | 201 | 23F4 | 60,980 | (32F)3G5 | 432,154 |
| 269.465 | 0.001 | 371,105.7 | 41 | 164 | 41I6 | 39,744 | (32G)3H6 | 410,851 |
| 269.790 | −0.004 | 370,658.7 | 33 | 364 | 43F2 | 28,051 | (32G)3G3 | 398,704 |
| 270.102 | 0.001 | 370,230.5 | 350d | 995 | 43H5 | 26,250 | (34F)3G4 | 396,481 |
| 270.102 | −0.004 | 370,230.5 | 350d | 281 | 41G4 | 43,104 | (32G)1H5 | 413,329 |
| 270.227 | 0.006 | 370,059.3 | 50 | 255 | 43G5 | 35,077 | (32H)3H5 | 405,144 |
| 270.265 | 370,007.2 | 37 | 356 | 43D2 | 38,402 | (32G)3F2 | 408,409 | |
| 270.358 | 369,879.9 | 290d | 395 | 23F3 | 62,552 | (32F)3D2 | 432,431 | |
| 270.358 | −0.005 | 369,879.9 | 290d | 858 | 41G4 | 43,104 | (32F)1G4 | 412,977 |
| 270.518 | 369,661.2 | 32 | 330 | 23F4 | 60,980 | (32F)3D3 | 430,642 | |
| 270.958 | 369,060.9 | 110 | 382 | 23P1 | 63,371 | (32F)3D2 | 432,431 | |
| 271.536 | 0.005 | 368,275.3 | 37 | 205 | 43G5 | 35,077 | (32H)3H6 | 403,359 |
| 271.933 | 367,737.7 | 270 | 1089 | 21G4 | 69,584 | (32F)1G4 | 437,322 | |
| 272.381 | 0.000 | 367,132.8 | 50 | 336 | 43G4 | 32,698 | (34F)3G5 | 399,831 |
| 272.579 | 0.001 | 366,866.1 | 150 | 1131 | 21G4 | 69,584 | (32F)1F3 | 436,451 |
| 272.743 | −0.003 | 366,645.5 | 99 | 473 | 43H4 | 23,302 | (34F)3G3 | 389,944 |
| 272.808 | 0.007 | 366,558.2 | 81 | 500 | 43G4 | 32,698 | (32G)1G4 | 399,265 |
| 273.055 | 0.000 | 366,226.6 | 48 | 307 | 43G3 | 26,967 | (34F)5F4 | 393,193 |
| 273.866 | 0.000 | 365,142.1 | 200 | 595 | 43G5 | 35,077 | (34F)3F4 | 400,219 |
| 273.912 | 365,080.8 | 43 | 325 | 43G4 | 32,698 | (34F)3F3 | 397,779 | |
| 273.967 | 365,007.5 | 15 | 109 | 43P0 | 21,309 | (34F)5F1 | 386,317 | |
| 274.155 | −0.002 | 364,757.2 | 160 d | 415 | 43G5 | 35,077 | (34F)3G5 | 399,831 |
| 274.155 | 0.000 | 364,757.2 | 160 d | 663 | 21D2 | 88,586 | (12D)1D2 | 453,343 |
| 274.705 | 0.000 | 364,026.9 | 31 | 200 | 43H4 | 23,302 | (34F)5F3 | 387,329 |
| 275.061 | −0.001 | 363,555.7 | 27 | 292 | 43F3 | 32,926 | (34F)3G4 | 396,481 |
| 275.224 | 0.000 | 363,340.4 | 41 | 454 | 43D3 | 36,879 | (34F)3F4 | 400,219 |
| 275.408 | 363,097.7 | 24 | 301 | 23P1 | 63,371 | (34P)3S1 | 426,468 | |
| 275.702 | 0.003 | 362,710.5 | 35 | 243 | 43H5 | 26,250 | (34F)5F4 | 388,964 |
| 275.902 | 362,447.5 | 22 | 229 | 23F3 | 62,552 | (32F)3F4 | 424,999 | |
| 276.325 | 0.000 | 361,892.7 | 18 | 175 | 43F2 | 28,051 | (34F)3G3 | 389,944 |
| 276.754 | 0.000 | 361,331.7 | 22 | 251 | 43F4 | 29,555 | (34F)5F3 | 390,887 |
| 277.091 | −0.001 | 360,892.3 | 24 | 140 | 41F3 | 52,004 | (34P)3D2 | 412,894 |
| 277.749 | 0.003 | 360,037.3 | 110 d | 376 | 23F4 | 60,980 | (32H)3G5 | 421,021 |
| 277.749 | 360,037.3 | 110 d | 594 | 41F3 | 52,004 | (32H)1G4 | 412,041 | |
| 278.440 | 359,143.8 | 24 d | 390 | 21D2 | 88,586 | (12D)3F2 | 447,730 | |
| 278.440 | −0.001 | 359,143.8 | 20 d | 237 | 23F4 | 60,980 | (32F)3F3 | 420,123 |
| 279.517 | 0.000 | 357,760.0 | 17 | 34 | 43G4 | 32,698 | (34F)5G5 | 390,458 |
| 280.308 | −0.005 | 356,750.4 | 22 | 285 | 23F4 | 60,980 | (32H)3G3 | 417,724 |
| 280.775 | 0.003 | 356,157.1 | 17 | 188 | 41G4 | 43,104 | (32G)1G4 | 399,265 |
| 281.501 | 0.002 | 355,238.5 | 27 | 130 | 43H6 | 28,185 | (34F)5G5 | 383,426 |
| 284.333 | 0.000 | 351,700.3 | 12 | 73 | 23F2 | 61,644 | (32P)3P1 | 413,344 |
| 284.791 | 0.000 | 351,134.7 | 17 | 147 | 43P1 | 26,526 | (34F)3D2 | 377,661 |
| 287.065 | −0.003 | 348,353.2 | 18 | 73 | 43G5 | 35,077 | (34F)5G5 | 383,426 |
| 287.468 | 0.000 | 347,864.8 | 17 | 227 | 21D2 | 88,586 | (32F)1F3 | 436,451 |
a Observed wavelengths, d—doubly identified, t—trebly identified; b Difference between the observed wavelength and the wavelength derived from the final level energies (Ritz wavelength). A blank value indicates that the upper level is derived only from that line; c Relative intensity; e The number preceding the terms is seniority number; f Term attribution is arbitrary in a few cases (see text) for the level composition, see Table A8. The number preceding the terms of the 5d3 configuration is seniority number.

Table A3.
Identified lines of the 4d4–(4d34f + 4p54d5) transitions in the spectrum of Ag7+.
| λ, Å a | o-c, (Å) b | ν (cm−1) | I c | gA, (109 s−1) | 4d4 | (4d34f + 4p54d5) | |||
|---|---|---|---|---|---|---|---|---|---|
| Term e | E (cm−1) | Config. f | Term f | E (cm−1) | |||||
| 162.528 | 0.001 | 615,277 | 32 | 394 | 3G4 | 32,698 | 4p54d5 | (4F)3F3 | 647,982 |
| 162.554 | −0.001 | 615,182 | 26 | 564 | 3G5 | 35,078 | 4p54d5 | (4F)3F4 | 650,256 |
| 164.321 | −0.001 | 608,564 | 54 | 1260 | 3H5 | 26,249 | 4p54d5 | (4G)3G4 | 634,810 |
| 164.542 | 0.001 | 607,749 | 534 IX | 4247 | 3H6 | 28,185 | 4p54d5 | (4G)3G5 | 635,935 |
| 165.158 | 0.004 | 605,482 | 122 | 567 | 3F42 | 29,555 | 4p54d5 | (4G)3G3 | 635,050 |
| 165.481 | 604,300 | 294 | 5122 | 1I6 | 39,744 | 4p54d5 | (2H)1H5 | 644,043 | |
| 166.744 | 0.003 | 599,721 | 355 IX | 2821 | 3G5 | 35,078 | 4p54d5 | (4G)3G4 | 634,810 |
| 166.917 | 0.006 | 599,099 | 72 | 1966 | 1G41 | 69,585 | 4p54d5 | (2G1)1F3 | 668,708 |
| 167.156 | −0.005 | 598,244 | 693 | 1429 | 3F42 | 29,555 | 4p54d5 | (4P)3D3 | 627,779 |
| 167.460 | 597,158 | 190 IX | 2888 | 5D4 | 7,442 | 4p54d5 | (6S)5P3 | 604,600 | |
| 167.731 | 0.000 | 596,193 | 111 | 275 | 1I6 | 39,744 | 4p54d5 | (4G)3G5 | 635,935 |
| 167.835 | −0.003 | 595,824 | 83 | 1261 | 3H5 | 26,249 | 4p54d5 | (4D)3F4 | 622,060 |
| 168.436 | 0.000 | 593,698 | 254 IX | 827 | 3G3 | 26,968 | 4p54d5 | (4G)3F2 | 620,664 |
| 168.741 | −0.003 | 592,625 | 20 | 509 | 3F22 | 28,051 | 4p54d5 | (4G)3F2 | 620,664 |
| 168.932 | −0.002 | 591,953 | 109 IX | 2031 | 1G42 | 43,105 | 4p54d5 | (4G)3G3 | 635,050 |
| 169.010 | −0.003 | 591,683 | 24 | 591 | 5D2 | 3,212 | 4p54d5 | (6S)5P2 | 594,881 |
| 169.235 | 0.002 | 590,894 | 37 | 432 | 3D3 | 36,878 | 4p54d5 | (4P)3D3 | 627,779 |
| 169.613 | 0.003 | 589,578 | 72 IX | 831 | 5D3 | 5292 | 4p54d5 | (6S)5P2 | 594,881 |
| 169.676 | 0.001 | 589,357 | 49 | 597 | 3G4 | 32,698 | 4p54d5 | (4D)3F4 | 622,060 |
| 170.070 | 587,994 | 48 | 1080 | 3F31 | 62,552 | 4p54d5 | (4F)3D2 | 650,545 | |
| 170.271 | 587,298 | 39 | 513 | 1G42 | 43,105 | 4p54d5 | (2D3)1F3 | 630,389 | |
| 170.359d | 0.002 | 586,994 | 312 IX | 1490 | 3F41 | 60,981 | 4p54d5 | (4F)3F3 | 647,982 |
| 170.359d | −0.003 | 586,994 | 312 IX | 664 | 3G5 | 35,078 | 4p54d5 | (4D)3F4 | 622,060 |
| 170.595 | 0.002 | 586,184 | 57 | 628 | 3G5 | 35,078 | 4p54d5 | (2I)1I6 | 621,268 |
| 170.812 | −0.003 | 585,439 | 23 | 881 | 3F31 | 62,552 | 4p54d5 | (4F)3F3 | 647,982 |
| 171.075 | 0.001 | 584,539 | 35 | 643 | 3F21 | 61,645 | 4p54d5 | (4D)3P2 | 646,185 |
| 171.339 | −0.001 | 583,638 | 46 | 492 | 3F31 | 62,552 | 4p54d5 | (4D)3P2 | 646,185 |
| 171.512 | −0.001 | 583,050 | 34 | 337 | 1F3 | 52,004 | 4p54d5 | (4G)3G3 | 635,050 |
| 171.539 | 582,957 | 383 IX | 2207 | 3F41 | 60,981 | 4p54d5 | (2H)1G4 | 643,939 | |
| 171.587 | 0.003 | 582,795 | 27 | 211 | 1F3 | 52,004 | 4p54d5 | (4G)3G4 | 634,810 |
| 171.748 | 0.004 | 582,247 | 20 | 574 | 3D2 | 38,403 | 4p54d5 | (4G)3F2 | 620,664 |
| 171.960 | −0.002 | 581,530 | 267 | 6420 | 1I6 | 39,744 | 4p54d5 | (2I)1I6 | 621,268 |
| 172.171 | −0.001 | 580,818 | 66 | 606 | 5D1 | 1340 | 4p54d5 | (6S)5P1 | 582,154 |
| 172.215 | 0.000 | 580,671 | 787 | 2558 | 1G41 | 69,585 | 4p54d5 | (4F)3F4 | 650,256 |
| 172.372 | −0.006 | 580,140 | 61 | 1512 | 1D21 | 88,587 | 4p54d5 | (2G1)1F3 | 668,708 |
| 172.460 | 579,846 | 71 | 1498 | 3F21 | 61,645 | 4p54d5 | (4F)3F2 | 641,516 | |
| 172.730 | 0.001 | 578,937 | 92 | 549 | 5D2 | 3212 | 4p54d5 | (6S)5P1 | 582,154 |
| 172.968 | −0.002 | 578,143 | 20 | 1138 | 3H5 | 26,249 | 4p54d5 | (2G1)3G4 | 604,385 |
| 173.327 | 0.000 | 576,943 | 295 | 5775 | 3H6 | 28,185 | 4p54d5 | (2I)3H6 | 605,128 |
| 173.525 | 0.000 | 576,287 | 28 | 323 | 3D3 | 36,878 | 4p54d5 | (4G)3F4 | 613,166 |
| 173.682 | 0.003 | 575,766 | 45 | 1187 | 1F3 | 52,004 | 4p54d5 | (4P)3D3 | 627,779 |
| 174.487 | −0.004 | 573,110 | 104 IX | 2384 | 3H5 | 26,249 | 4p54d5 | (4F)3G5 | 599,345 |
| 174.558 | −0.002 | 572,875 | 16 | 605 | 3H4 | 23,304 | 4p54d5 | (2I)3H4 | 596,171 |
| 174.618 | −0.003 | 572,678 | 70 IX | 343 | 3F42 | 29,555 | 4p54d5 | (4F)3F4 | 602,225 |
| 174.742 | −0.004 | 572,271 | 40 | 486 | 3F31 | 62,552 | 4p54d5 | (4G)3G4 | 634,810 |
| 174.993 | 571,450 | 63 | 2290 | 3G5 | 35,078 | 4p54d5 | (4G)3G5 | 606,529 | |
| 175.054d | −0.004 | 571,253 | 48 | 464 | 3G3 | 26,968 | 4p54d5 | (4F)3G4 | 598,206 |
| 175.054d | 0.004 | 571,253 | 39 | 1651 | 1G42 | 43,105 | 4p54d5 | (2G1)1H5 | 614,370 |
| 175.086 | 0.004 | 571,149 | 31 | 1104 | 3H6 | 28,185 | 4p54d5 | (4F)3G5 | 599,345 |
| 175.419d | −0.001 | 570,063 | 30 | 2899 | 1G42 | 43,105 | 4p54d5 | (4G)3F4 | 613,166 |
| 175.419d | −0.004 | 570,063 | 37 | 946 | 3G5 | 35,078 | 4p54d5 | (2I)3H6 | 605,128 |
| 175.580 | −0.004 | 569,541 | 41 | 722 | 3G4 | 32,698 | 4p54d5 | (4F)3F4 | 602,225 |
| 175.652 | −0.001 | 569,306 | 29 | 470 | 5D4 | 7442 | 4d34f | (4F)3H5 | 576,746 |
| 175.855 | 0.000 | 568,651 | 46 | 1521 | 3F42 | 29,555 | 4p54d5 | (4F)3G4 | 598,206 |
| 176.130 | −0.006 | 567,761 | 20 | 350 | 5D3 | 5292 | 4d34f | (4F)3H4 | 573,036 |
| 176.489 | 0.002 | 566,609 | 40 | 1205 | 3F42 | 29,555 | 4p54d5 | (2I)3H4 | 596,171 |
| 176.526 | −0.002 | 566,490 | 18 | 162 | 3H4 | 23,304 | 4p54d5 | (2H)3G4 | 589,786 |
| 176.699d | −0.021 | 565,933 | 160 | 1440 | 3H5 | 26,249 | 4p54d5 | (2H)1H5 | 592,118 |
| 176.699d | −0.002 | 565,933 | 160 | 2788 | 3H4 | 23,304 | 4p54d5 | (2I)3H4 | 589,229 |
| 176.833 | 0.001 | 565,504 | 52 | 1171 | 3G4 | 32,698 | 4p54d5 | (4F)3G4 | 598,206 |
| 176.872 | 0.001 | 565,381 | 33 | 652 | 1I6 | 39,744 | 4p54d5 | (2I)3H6 | 605,128 |
| 177.156 | 0.000 | 564,474 | 33 | 906 | 3G3 | 26,968 | 4p54d5 | (4F)3G3 | 591,442 |
| 177.484 | 0.002 | 563,431 | 47 | 688 | 3P12 | 26,525 | 4p54d5 | (2D1)3P2 | 589,963 |
| 177.625 | −0.001 | 562,983 | 24 | 435 | 3H5 | 26,249 | 4p54d5 | (2I)3H4 | 589,229 |
| 177.674 | −0.003 | 562,827 | 15 | 151 | 3G3 | 26,968 | 4p54d5 | (2H)3G4 | 589,786 |
| 178.240w | 0.013 | 561,041 | 61 | 685 | 3F41 | 60,981 | 4p54d5 | (4D)3F4 | 622,060 |
| 178.280 | 0.004 | 560,916 | 60 | 1099 | 3P22 | 32,137 | 4p54d5 | (2F1)3D3 | 593,064 |
| 178.292 | −0.001 | 560,878 | 113 | 1859 | 5D4 | 7442 | 4d34f | (4F)3I5 | 568,319 |
| 178.695d | 559,614 | 299 | 2756 | 5D2 | 3212 | 4p54d5 | (4G)5F3 | 562,825 | |
| 178.695d | −0.001 | 559,614 | 299 | 3408 | 5D3 | 5292 | 4p54d5 | (4F)5D4 | 564,902 |
| 178.728 | 0.002 | 559,508 | 294 | 1956 | 5D1 | 1340 | 4p54d5 | (4G)5F2 | 560,857 |
| 178.765 | 0.008 | 559,394 | 50 | 870 | 3G4 | 32,698 | 4p54d5 | (2H)1H5 | 592,118 |
| 178.864d | 0.003 | 559,083 | 50 | 587 | 5D3 | 5292 | 4p54d5 | (4F)5D4 | 564,383 |
| 178.864d | 0.00 | 559,083 | 50 | 14 | 5D2 | 3212 | 4p54d5 | (4F)5D3 | 562,295 |
| 178.916 | −0.003 | 558,922 | 50 | 362 | 5D1 | 1340 | 4d34f | (4F)5D2 | 560,251 |
| 179.217 | 0.000 | 557,983 | 383 | 3390 | 5D4 | 7442 | 4p54d5 | (4G)5F5 | 565,427 |
| 179.296 | −0.002 | 557,738 | 68 | 1058 | 5D0 | 0 | 4d34f | (4F)5D1 | 557,732 |
| 179.323 | −0.003 | 557,653 | 22 | 752 | 5D2 | 3212 | 4p54d5 | (4G)5F2 | 560,857 |
| 179.383 | −0.003 | 557,468 | 17 | 268 | 5D4 | 7442 | 4p54d5 | (4F)5D4 | 564,902 |
| 179.431 | −0.001 | 557,319 | 135 | 903 | 5D1 | 1340 | 4p54d5 | (4G)5F1 | 558,654 |
| 179.531d | 0.010 | 557,007 | 260 | 958 | 5D2 | 3212 | 4d34f | (4F)5D2 | 560,251 |
| 179.531d | −0.001 | 557,007 | 260 | 2739 | 5D3 | 5292 | 4p54d5 | (4F)5D3 | 562,295 |
| 179.550 | −0.002 | 556,949 | 375 | 3857 | 5D4 | 7442 | 4p54d5 | (4F)5D4 | 564,383 |
| 179.574 | −0.005 | 556,872 | 111 | 2462 | 3F32 | 32,925 | 4p54d5 | (2H)3G4 | 589,786 |
| 179.642 | −0.009 | 556,663 | 35 | 525 | 3G3 | 26,968 | 4p54d5 | (2G1)3F3 | 583,603 |
| 179.795 | −0.002 | 556,190 | 18 | 479 | 3D3 | 36,878 | 4p54d5 | (2F1)3D3 | 593,064 |
| 180.038 | 0.001 | 555,437 | 60 | 527 | 5D2 | 3212 | 4p54d5 | (4G)5F1 | 558,654 |
| 180.194 | 0.001 | 554,959 | 60 | 1111 | 5D3 | 5292 | 4d34f | (4F)5D2 | 560,251 |
| 180.229 | 0.001 | 554,849 | 45 | 770 | 5D4 | 7442 | 4p54d5 | (4F)5D3 | 562,295 |
| 180.288 | −0.002 | 554,667 | 20 | 515 | 3D2 | 38,403 | 4p54d5 | (2F1)3D3 | 593,064 |
| 180.338 | 0.002 | 554,513 | 22 | 408 | 5D2 | 3212 | 4d34f | (4F)5D1 | 557,732 |
| 180.455 | 554,156 | 28 | 1276 | 3P12 | 26,525 | 4p54d5 | (2F2)3D2 | 580,680 | |
| 180.685 | −0.002 | 553,449 | 26 | 134 | 3H4 | 23,304 | 4d34f | (4F)3H5 | 576,746 |
| 180.819 | 0.000 | 553,038 | 31 | 748 | 3D2 | 38,403 | 4p54d5 | (4F)3G3 | 591,442 |
| 180.869 | 0.006 | 552,888 | 28 | 525 | 3D3 | 36,878 | 4p54d5 | (2H)3G4 | 589,786 |
| 180.919 | 0.001 | 552,735 | 55 | 936 | 3H6 | 28,185 | 4d34f | (4F)3H6 | 580,923 |
| 181.004 | −0.002 | 552,475 | 50 | 872 | 3F42 | 29,555 | 4d34f | (4P)3G5 | 582,024 |
| 181.047 | 0.003 | 552,343 | 33 | 826 | 3D3 | 36,878 | 4p54d5 | (2I)3H4 | 589,229 |
| 181.236 | −0.005 | 551,768 | 33 | 611 | 3F42 | 29,555 | 4p54d5 | (2G2)3G4 | 581,306 |
| 181.302 | −0.002 | 551,565 | 14 | 364 | 3D2 | 38,403 | 4p54d5 | (2D1)3P2 | 589,963 |
| 181.341 | 0.007 | 551,448 | 46 | 1007 | 3P22 | 32,137 | 4p54d5 | (2G1)3F3 | 583,603 |
| 181.563 | 0.002 | 550,772 | 60 | 867 | 3H6 | 28,185 | 4d34f | (2H)1K7 | 578,963 |
| 181.654 | 0.000 | 550,496 | 37 | 216 | 3H5 | 26,249 | 4d34f | (4F)3H5 | 576,746 |
| 181.752 | 0.007 | 550,200 | 159 | 2125 | 1F3 | 52,004 | 4p54d5 | (4F)3F4 | 602,225 |
| 181.781 | 0.001 | 550,114 | 17 | 256 | 3G3 | 26,968 | 4p54d5 | (2H)3G3 | 577,085 |
| 182.043 | 0.002 | 549,321 | 192 | 2799 | 3G4 | 32,698 | 4d34f | (4P)3G5 | 582,024 |
| 182.137d | −0.008 | 549,038 | 157 | 1393 | 1G42 | 43,105 | 4p54d5 | (2H)1H5 | 592,118 |
| 182.137d | −0.002 | 549,038 | 157 | 2609 | 3F22 | 28,051 | 4p54d5 | (2H)3G3 | 577,085 |
| 182.354 | −0.001 | 548,384 | 65 | 1175 | 3F32 | 32,925 | 4p54d5 | (2G2)3G4 | 581,306 |
| 182.749 | −0.003 | 547,199 | 145 | 2520 | 3F42 | 29,555 | 4d34f | (4F)3H5 | 576,746 |
| 183.131 | 0.004 | 546,058 | 234 | 3198 | 3G3 | 26,968 | 4d34f | (4F)3H4 | 573,036 |
| 183.202 | 0.000 | 545,845 | 355 | 4991 | 3G5 | 35,078 | 4d34f | (4F)3H6 | 580,923 |
| 183.421 | 0.002 | 545,194 | 27 | 454 | 3D2 | 38,403 | 4p54d5 | (2G1)3F3 | 583,603 |
| 183.482 | 0.001 | 545,014 | 260 | 2889 | 3H4 | 23,304 | 4d34f | (4F)3I5 | 568,319 |
| 183.503 | 0.000 | 544,949 | 62 | 115 | 3P22 | 32,137 | 4p54d5 | (2H)3G3 | 577,085 |
| 183.556 | −0.003 | 544,792 | 30 | 721 | 1G41 | 69,585 | 4p54d5 | (2G1)1H5 | 614,370 |
| 183.685 | 0.006 | 544,411 | 41 | 801 | 3D3 | 36,878 | 4p54d5 | (2G2)3G4 | 581,306 |
| 183.808 | 0.001 | 544,047 | 76 | 1418 | 3G4 | 32,698 | 4d34f | (4F)3H5 | 576,746 |
| 184.001 | 0.002 | 543,474 | 24 | 288 | 3F42 | 29,555 | 4d34f | (4F)3H4 | 573,036 |
| 184.113 | −0.003 | 543,144 | 594 | 6224 | 3H5 | 26,249 | 4d34f | (4F)3I6 | 569,385 |
| 184.456 | −0.003 | 542,133 | 102 | 2095 | 3H4 | 23,304 | 4p54d5 | (4G)5F5 | 565,427 |
| 184.481 | 0.003 | 542,061 | 29 | 403 | 3H5 | 26,249 | 4d34f | (4F)3I5 | 568,319 |
| 184.560 | 0.002 | 541,830 | 44 | 1623 | 3F31 | 62,552 | 4p54d5 | (2G1)3G4 | 604,385 |
| 184.620 | 0.005 | 541,655 | 32 | 545 | 3G5 | 35,078 | 4d34f | (4F)3H5 | 576,746 |
| 184.641 | 0.003 | 541,592 | 29 | 74 | 3H4 | 23,304 | 4p54d5 | (4F)5D4 | 564,902 |
| 184.780d | 0.006 | 541,184 | 34 | 264 | 3H6 | 28,185 | 4d34f | (4F)3I6 | 569,385 |
| 184.780d | −0.002 | 541,184 | 34 | 255 | 1I6 | 39,744 | 4d34f | (4F)3H6 | 580,923 |
| 185.452 | −0.001 | 539,223 | 520 | 6429 | 1I6 | 39,744 | 4d34f | (2H)1K7 | 578,963 |
| 185.553 | 538,930 | 741 | 6779 | 3H6 | 28,185 | 4d34f | (2H)1K7 | 567,115 | |
| 185.607 | −0.003 | 538,773 | 62 | 536 | 3F42 | 29,555 | 4d34f | (4F)3I5 | 568,319 |
| 185.897 | 0.001 | 537,931 | 31 | 306 | 3G3 | 26,968 | 4p54d5 | (4F)5D4 | 564,902 |
| 185.959 | 0.010 | 537,753 | 27 | 613 | 1F3 | 52,004 | 4p54d5 | (2H)3G4 | 589,786 |
| 186.615 | 0.003 | 535,862 | 24 | 121 | 3F42 | 29,555 | 4p54d5 | (4G)5F5 | 565,427 |
| 187.168 | 534,280 | 243 | 2386 | 1G41 | 69,585 | 4d34f | (2D1)1H5 | 603,864 | |
| 188.279 | 0.004 | 531,127 | 68 | 1100 | 3F41 | 60,981 | 4p54d5 | (2H)1H5 | 592,118 |
a Observed wavelengths: d—doubly identified, w—wide; b Difference between the observed wavelength and the wavelength derived from the final level energies (Ritz wavelength). A blank value indicates that the upper level is derived only from that line; c Relative intensity; IX—line is also identified as Ag IX; e Numbers following the term values display Nielson and Koster sequential indices [20]; f Designation and configuration attribution is arbitrary in a few cases (see text), for the level composition, see Table A9. Numbers following the term values of the 4d5 configuration display Nielson and Koster sequential indices [20].

Table A4.
Identified lines of the 4d3–(4d25p + 4d24f + 4p54d4) transitions in the spectrum of Ag8+.
| λ, Å a | o-c, (Å) b | ν (cm−1) | I c | gA, (109 s−1) | 4d3 | 4d25p + 4d24f + 4p54d4 | ||
|---|---|---|---|---|---|---|---|---|
| Term e | Config. f | Term f | E (cm−1) | |||||
| 160.837 | 0.005 | 621,749 | 100 X | 1092 | 4F7/2 | 4p54d4 | (5D)4D5/2 | 628,302 |
| 161.466 | −0.005 | 619,327 | 50 | 3141 | 4F9/2 | 4p54d4 | (5D)4D7/2 | 629,173 |
| 162.302 | 616,135 | 250 X | 1091 | 2D5/22 | 4p54d4 | (3P1)2P3/2 | 649,186 | |
| 162.411 | −0.002 | 615,723 | 190 | 1327 | 2F7/2 | 4p54d4 | (1G1)2F7/2 | 659,798 |
| 162.500 | 615,383 | 130 | 645 | 4F3/2 | 4p54d4 | (5D)4D1/2 | 615,385 | |
| 162.644 | 0.002 | 614,839 | 540 | 2516 | 2H9/2 | 4p54d4 | (3H)2G7/2 | 647,197 |
| 163.010 | −0.003 | 613,458 | 370 | 4684 | 2H11/2 | 4p54d4 | (3H)2G9/2 | 644,980 |
| 163.132 | 0.003 | 613,001 | 90 | 1863 | 2F5/2 | 4p54d4 | (3G)2F5/2 | 657,606 |
| 163.228 | −0.003 | 612,641 | 80 | 464 | 2H9/2 | 4p54d4 | (3H)2G9/2 | 644,980 |
| 163.267 | 0.001 | 612,494 | 70 | 577 | 2G7/2 | 4p54d4 | (3F2)2F7/2 | 634,657 |
| 163.416 | 0.003 | 611,937 | 180 | 356 | 2D5/21 | 4p54d4 | (3F1)2D3/2 | 680,196 |
| 163.532 | −0.004 | 611,503 | 220 | 2272 | 2D3/21 | 4p54d4 | (3F1)2D3/2 | 680,196 |
| 163.589 | 0.004 | 611,287 | 110 X | 1237 | 2G9/2 | 4p54d4 | (3F2)2F7/2 | 634,657 |
| 163.839 | 610,356 | 140 | 1254 | 2D3/22 | 4p54d4 | (5D)4P1/2 | 637,178 | |
| 163.949 | −0.003 | 609,947 | 400 | 1702 | 4P5/2 | 4p54d4 | (5D)4P5/2 | 632,322 |
| 164.099 | 609,387 | 110 | 668 | 4F5/2 | 4p54d4 | (5D)4D3/2 | 612,491 | |
| 164.397 | 608,284 | 310 | 2866 | 2D5/21 | 4p54d4 | (3F1)2D5/2 | 676,533 | |
| 164.493 | 607,930 | 80 | 578 | 4P5/2 | 4p54d4 | (5D)4P3/2 | 630,316 | |
| 164.542d | 0.013 | 607,749 | 740 VIII | 1677 | 2F7/2 | 4p54d4 | (3P2)2D5/2 | 651,880 |
| 164.542d | −0.005 | 607,749 | 740 | 7777 | 2H11/2 | 4p54d4 | (3H)2H11/2 | 639,262 |
| 164.772 | 0.004 | 606,900 | 170 | 576 | 2H9/2 | 4p54d4 | (3H)2H11/2 | 639,262 |
| 164.808 | 0.005 | 606,766 | 370 X | 1781 | 4P5/2 | 4p54d4 | (5D)4D7/2 | 629,173 |
| 164.952 | −0.000 | 606,239 | 70 | 725 | 4F7/2 | 4p54d4 | (5D)4D5/2 | 612,769 |
| 165.036 | −0.003 | 605,927 | 170 | 831 | 4P5/2 | 4p54d4 | (5D)4D5/2 | 628,302 |
| 165.418 | 0.001 | 604,531 | 100 | 1245 | 2G7/2 | 4p54d4 | (1D1)2F5/2 | 626,693 |
| 165.945 | −0.002 | 602,610 | 90 | 1679 | 2F5/2 | 4p54d4 | (3H)2G7/2 | 647,197 |
| 165.999 | 0.003 | 602,412 | 510 X | 1403 | 2P3/2 | 4p54d4 | (3P2)2P3/2 | 638,784 |
| 166.023 | −0.005 | 602,325 | 200 | 1348 | 2H9/2 | 4p54d4 | (3F2)2F7/2 | 634,657 |
| 166.423 | 0.005 | 600,880 | 90 | 1650 | 2F7/2 | 4p54d4 | (3H)2G9/2 | 644,980 |
| 166.518 | −0.000 | 600,537 | 60 | 509 | 2H11/2 | 4p54d4 | (3H)2H9/2 | 632,069 |
| 166.744 | 0.000 | 599,721 | 490 VIII | 5298 | 2H9/2 | 4p54d4 | (3H)2H9/2 | 632,069 |
| 166.872 | 0.002 | 599,262 | 50 | 862 | 2D5/22 | 4p54d4 | (5D)4P5/2 | 632,322 |
| 167.307 | 597,704 | 620 | 5028 | 2G9/2 | 4p54d4 | (1G2)2G9/2 | 621,061 | |
| 167.460 | −0.002 | 597,158 | 270 VIII | 2912 | 2F7/2 | 4p54d4 | (1G2)2F7/2 | 641,234 |
| 167.492 | −0.001 | 597,042 | 100 | 883 | 4F7/2 | 4p54d4 | (5D)4F9/2 | 603,570 |
| 167.814 | 595,896 | 120 | 1278 | 2G7/2 | 4p54d4 | (3D)2F5/2 | 618,058 | |
| 167.898 | −0.000 | 595,601 | 170 X | 1248 | 4P3/2 | 4p54d4 | (5D)4D5/2 | 612,769 |
| 168.022 | −0.004 | 595,162 | 160 | 1520 | 2D5/21 | 4p54d4 | (3P1)2P3/2 | 663,396 |
| 168.130 | 594,778 | 40 | 964 | 4P1/2 | 4p54d4 | (5D)4D3/2 | 612,491 | |
| 168.159 | 0.004 | 594,677 | 30 | 322 | 2D3/21 | 4p54d4 | (3P1)2P3/2 | 663,396 |
| 168.294 | −0.002 | 594,197 | 90 | 469 | 2F5/2 | 4p54d4 | (3P2)2P3/2 | 638,784 |
| 168.414 | −0.001 | 593,775 | 90 | 707 | 4F5/2 | 4p54d4 | (5D)4F7/2 | 596,876 |
| 168.436d | 0.007 | 593,698 | 430 VIII | 1955 | 2G7/2 | 4p54d4 | (1G2)2G7/2 | 615,884 |
| 168.436d | 0.001 | 593,698 | 430 VIII | 3827 | 4F9/2 | 4p54d4 | (5D)4F9/2 | 603,570 |
| 168.479 | −0.002 | 593,545 | 110 | 909 | 2F5/2 | 4p54d4 | (3F2)2F5/2 | 638,134 |
| 168.605 | 0.005 | 593,101 | 50 | 1153 | 2G9/2 | 4p54d4 | (3F2)2G9/2 | 616,475 |
| 168.766 | −0.003 | 592,537 | 80 | 1585 | 2G9/2 | 4p54d4 | (1G2)2G7/2 | 615,884 |
| 168.808 | 0.002 | 592,389 | 110 X | 759 | 4F7/2 | 4p54d4 | (3F1)4D7/2 | 598,929 |
| 168.932d | −0.003 | 591,953 | 150 VIII | 967 | 2P3/2 | 4p54d4 | (5D)4D5/2 | 628,302 |
| 168.932d | −0.000 | 591,953 | 150 VIII | 1267 | 2G9/2 | 4p54d4 | (3H)2H11/2 | 615,308 |
| 169.049 | 0.002 | 591,543 | 140 | 3139 | 2D5/21 | 4p54d4 | (1G1)2F7/2 | 659,798 |
| 169.392d | −0.004 | 590,346 | 270 | 1157 | 2P3/2 | 4p54d4 | (1D1)2F5/2 | 626,693 |
| 169.392d | −0.001 | 590,346 | 270 | 2701 | 4F7/2 | 4p54d4 | (5D)4F7/2 | 596,876 |
| 169.475 | 0.001 | 590,058 | 50 X | 548 | 2F5/2 | 4p54d4 | (3F2)2F7/2 | 634,657 |
| 169.595 | 0.001 | 589,642 | 50 | 428 | 4F3/2 | 4p54d4 | (5D)4F5/2 | 589,644 |
| 169.613 | 0.000 | 589,578 | 100 VIII | 765 | 4F9/2 | 4p54d4 | (1I)2H9/2 | 599,446 |
| 169.762 | 0.000 | 589,062 | 50 | 787 | 4F9/2 | 4p54d4 | (3F1)4D7/2 | 598,929 |
| 169.806 | −0.002 | 588,907 | 20 | 1462 | 2D3/21 | 4p54d4 | (3G)2F5/2 | 657,606 |
| 170.192 | 0.002 | 587,572 | 30 | 80 | 4F7/2 | 4p54d4 | (1D1)2F5/2 | 594,111 |
| 170.306 | −0.001 | 587,180 | 60 | 620 | 4F5/2 | 4d24f | (3P)4D3/2 | 590,280 |
| 170.359t | 0.007 | 586,994 | 440 VIII | 1882 | 4F9/2 | 4d24f | (3F)2I11/2 | 596,885 |
| 170.359t | 0.004 | 586,994 | 440 VIII | 769 | 4F9/2 | 4p54d4 | (5D)4F7/2 | 596,876 |
| 170.359t | −0.001 | 586,994 | 440 VIII | 1501 | 2G7/2 | 4p54d4 | (3G)2G7/2 | 609,152 |
| 170.490 | −0.001 | 586,545 | 280 | 2414 | 4F5/2 | 4p54d4 | (5D)4F5/2 | 589,644 |
| 170.933 | 585,026 | 120 | 2598 | 2D5/22 | 4d24f | (3P)2F7/2 | 618,075 | |
| 171.286 | 583,818 | 260 | 2018 | 4F3/2 | 4d24f | (3F)4F3/2 | 583,819 | |
| 171.339 | −0.002 | 583,638 | 60 | 848 | 2D5/21 | 4p54d4 | (3P2)2D5/2 | 651,880 |
| 171.493 | −0.000 | 583,114 | 40 | 409 | 4F7/2 | 4p54d4 | (5D)4F5/2 | 589,644 |
| 171.539 | 0.001 | 582,957 | 530 VIII | 5000 | 2H9/2 | 4p54d4 | (3H)2H11/2 | 615,308 |
| 171.996 | 0.001 | 581,408 | 40 | 482 | 2G7/2 | 4p54d4 | (5D)4F9/2 | 603,570 |
| 172.215d | −0.001 | 580,671 | 1100 | 4948 | 4F7/2 | 4p54d4 | (3H)4G9/21 | 587,200 |
| 172.215d | −0.001 | 580,671 | 1100 | 3951 | 4F5/2 | 4d24f | (3F)4G7/21 | 583,771 |
| 172.372 | 580,140 | 90 | 1120 | 2D3/22 | 4d24f | (1D)2D3/2 | 606,963 | |
| 172.556 | −0.005 | 579,521 | 390 | 3149 | 4F3/2 | 4d24f | (3F)4G5/2 | 579,505 |
| 173.077 | −0.001 | 577,778 | 890 | 5063 | 4F9/2 | 4p54d4 | (3H)4G11/2 | 587,642 |
| 173.224d | 0.014 | 577,288 | 670 | 765 | 4F9/2 | 4p54d4 | (3H)4G9/2 | 587,200 |
| 173.224d | −0.000 | 577,288 | 670 | 4944 | 2G7/2 | 4p54d4 | (1I)2H9/2 | 599,446 |
| 173.236 | −0.002 | 577,246 | 380 | 932 | 4F7/2 | 4d24f | (3F)4G7/2 | 583,771 |
| 173.445 | −0.003 | 576,551 | 150 | 1869 | 4P5/2 | 4p54d4 | (3F1)4D7/2 | 598,929 |
| 173.495 | 0.005 | 576,386 | 60 | 528 | 4F5/2 | 4d24f | (3F)4G5/2 | 579,505 |
| 173.578 | −0.003 | 576,110 | 110 | 1309 | 2D5/22 | 4p54d4 | (3G)2G7/2 | 609,152 |
| 174.248 | 0.003 | 573,895 | 30 | 20 | 4F9/2 | 4d24f | (3F)4G7/2 | 583,771 |
| 174.357 | −0.002 | 573,535 | 360 VIII | 3568 | 2G9/2 | 4d24f | (3F)2I11/2 | 596,885 |
| 174.487 | 0.000 | 573,110 | 140 | 1302 | 4P3/2 | 4d24f | (3P)4D3/2 | 590,280 |
| 174.526 | 0.002 | 572,979 | 40 | 690 | 2D5/21 | 4p54d4 | (1G2)2F7/2 | 641,234 |
| 174.618 | 572,678 | 100 VIII | 1088 | 4P5/2 | 4p54d4 | (3P1)4S3/2 | 595,066 | |
| 174.701 | −0.004 | 572,407 | 340 | 2551 | 2F7/2 | 4p54d4 | (3F2)2G9/2 | 616,475 |
| 174.908 | −0.002 | 571,730 | 60 | 94 | 4P5/2 | 4p54d4 | (1D1)2F5/2 | 594,111 |
| 175.617 | 0.001 | 569,422 | 30 | 1317 | 2D3/21 | 4p54d4 | (3F2)2F5/2 | 638,134 |
| 175.738 | 569,029 | 940 | 7991 | 2H11/ | 4d24f | (3F)2I13/2 | 600,561 | |
| 176.977 | −0.001 | 565,044 | 40 | 328 | 2G7/2 | 4p54d4 | (3H)4G9/2 | 587,200 |
| 177.136d | 0.006 | 564,539 | 100 | 1114 | 2F5/2 | 4p54d4 | (3G)2G7/2 | 609,152 |
| 177.216d | 0.000 | 564,283 | 360 | 2077 | 2G9/2 | 4p54d4 | (3H)4G11/2 | 587,642 |
| 221.880 | −0.001 | 450,694 | 80 | 22 | 4F9/2 | 4d25p | (3P)4D7/2 | 460,559 |
| 223.061 | 0.001 | 448,307 | 40 | 12 | 2G9/2 | 4d25p | (1G)2H11/2 | 471,667 |
| 226.030 | 0.003 | 442,420 | 120 | 17 | 4F9/2 | 4d25p | (1G)2G9/2 | 452,292 |
| 226.226 | 0.000 | 442,036 | 60 | 15 | 2G9/2 | 4d25p | (3P)4D7/2 | 465,394 |
| 227.202 | −0.001 | 440,137 | 700 | 144 | 2H11/2 | 4d25p | (1G)2H11/2 | 471,667 |
| 227.723 | −0.004 | 439,130 | 400 | 81 | 4F9/2 | 4d25p | (3F)2F7/2 | 448,989 |
| 228.487 | 437,662 | 320 | 67 | 4F3/2 | 4d25p | (3F)4D1/2 | 437,662 | |
| 228.963 | 0.004 | 436,751 | 140 | 45 | 4P5/2 | 4d25p | (3P)4P3/2 | 459,146 |
| 229.415 | 435,891 | 520 | 172 | 4F7/2 | 4d25p | (3F)4D5/2 | 442,423 | |
| 229.557 | 435,621 | 400 | 91 | 4F5/2 | 4d25p | (3F)4D3/2 | 438,725 | |
| 229.783 | 0.001 | 435,193 | 340 | 36 | 4F5/2 | 4d25p | (3F)4F5/2 | 438,297 |
| 229.820 | 435,124 | 200 | 32 | 2F5/2 | 4d25p | (1G)2F5/2 | 479,718 | |
| 229.877 | 435,015 | 100 | 20 | 2F5/2 | 4d25p | (1G)2F5/2 | 479,610 | |
| 230.176 | 0.004 | 434,450 | 230 | 61 | 2H11/2 | 4d25p | (1G)2H9/2 | 465,990 |
| 230.241 | 434,328 | 630 | 157 | 4F9/2 | 4d25p | (3F)4F9/2 | 444,195 | |
| 230.601 | −0.005 | 433,650 | 350 | 113 | 2H9/2 | 4d25p | (1G)2H9/2 | 465,990 |
| 230.922 | −0.001 | 433,047 | 500 | 89 | 2H9/2 | 4d25p | (3P)4D7/2 | 465,394 |
| 231.179 | 0.002 | 432,565 | 150 | 16 | 4F3/2 | 4d25p | (3F)4F5/2 | 432,569 |
| 231.545 | 431,882 | 620 | 106 | 2H9/2 | 4d25p | (1D)2F7/2 | 464,230 | |
| 231.602d | −0.005 | 431,774 | 580 | 19 | 4F7/2 | 4d25p | (3F)4F5/2 | 438,297 |
| 231.602d | −0.002 | 431,774 | 580 | 149 | 4F9/2 | 4d25p | (3F)4D7/2 | 441,637 |
| 231.819 | 431,370 | 300 | 32 | 2F7/2 | 4p54d4 | (3G)4G7/2 | 475,453 | |
| 231.946 | −0.003 | 431,135 | 450 | 154 | 4F7/2 | 4d25p | (3F)4F7/2 | 437,662 |
| 232.127 | 430,799 | 130 | 13 | 2D3/22 | 4d25p | (3P)4D5/2 | 457,621 | |
| 232.259 | −0.005 | 430,554 | 410 | 251 | 2G9/2 | 4d25p | (1G)2G7/2 | 453,902 |
| 232.337 | 430,410 | 330 | 159 | 2G7/2 | 4d25p | (1D)2F5/2 | 452,569 | |
| 232.845 | −0.002 | 429,470 | 550 | 102 | 4F5/2 | 4d25p | (3F)4F5/2 | 432,569 |
| 233.133 | −0.003 | 428,940 | 450 | 89 | 2G9/2 | 4d25p | (1G)2G9/2 | 452,292 |
| 233.206 | −0.005 | 428,806 | 50 | 16 | 4P5/2 | 4d25p | (3P)4S3/2 | 451,183 |
| 233.531 | 0.000 | 428,209 | 750 m | 103 | 2H9/2 | 4d25p | (3P)4D7/2 | 460,559 |
| 233.691 | 427,915 | 310 | 91 | 4F3/2 | 4d25p | (3F)4F3/2 | 427,916 | |
| 233.759 | 0.003 | 427,790 | 300 | 17 | 4F9/2 | 4d25p | (3F)4F7/2 | 437,662 |
| 233.877 | 427,576 | 170 | 64 | 4F9/2 | 4d25p | (3F)4G9/2 | 437,442 | |
| 234.539 | 426,368 | 1000 | 424 | 2H11/2 | 4d25p | (3F)2G9/2 | 457,900 | |
| 234.686 | −0.003 | 426,101 | 150 | 22 | 2D5/22 | 4d25p | (3P)4P3/2 | 459,146 |
| 234.945 | 0.001 | 425,631 | 350 | 36 | 2G9/2 | 4d25p | (3F)2F7/2 | 448,989 |
| 235.240 | −0.002 | 425,098 | 360 | 88 | 2G7/2 | 4d25p | (3F)2G7/2 | 447,255 |
| 235.532d | 424,570 | 200 | 19 | 4F3/2 | 4d25p | (3F)4G5/2 | 424,571 | |
| 235.532d | 424,570 | 200 | 17 | 2D5/22 | 4d25p | (3P)4D5/2 | 457,621 | |
| 235.581 | 424,482 | 190 | 51 | 2G7/2 | 4d25p | (3F)2F5/2 | 446,642 | |
| 235.649 | 424,360 | 200 | 71 | 2D3/22 | 4d25p | (3P)4S3/2 | 451,183 | |
| 235.726 | 424,222 | 230 | 101 | 2F5/2 | 4d25p | (3P)2D3/2 | 468,817 | |
| 235.907 | 0.002 | 423,895 | 100 | 21 | 2G9/2 | 4d25p | (3F)2G7/2 | 447,255 |
| 236.756 | 422,376 | 110 | 32 | 2F7/2 | 4d25p | (1D)2D5/2 | 466,458 | |
| 237.222 | 0.004 | 421,546 | 70 | 33 | 2H9/2 | 4d25p | (1G)2G7/2 | 453,902 |
| 237.458 | 0.001 | 421,127 | 80 | 15 | 4P3/2 | 4d25p | (3F)4F5/2 | 438,297 |
| 239.077 | 0.003 | 418,275 | 160 | 34 | 2G9/2 | 4d25p | (3F)4D7/2 | 441,637 |
| 239.161 | 0.002 | 418,129 | 60 | 19 | 2D5/22 | 4d25p | (3P)4S3/2 | 451,183 |
| 240.423 | 0.002 | 415,934 | 160 | 32 | 2D5/22 | 4d25p | (3F)2F7/2 | 448,989 |
| 243.734 | −0.001 | 410,284 | 160 | 30 | 2P3/2 | 4d25p | (3F)2F5/2 | 446,642 |
a Observed wavelengths: d—doubly identified, t—trebly identified; b Difference between the observed wavelength and the wavelength derived from the final level energies (Ritz wavelength). A blank value indicates that the upper level is derived only from that line; c Relative intensity: X, VIII—line is also identified as respectively Ag X or Ag VIII; m masked by O IV; e Numbers following the term values display Nielson and Koster sequential indices [20]; f Designation and configuration attribution is arbitrary in a few cases (see text), for the level composition, see Table A11. Numbers following the term values of the 4d4 configuration display Nielson and Koster sequential indices [20].

Table A5.
Energies (in cm−1) of the 4d5 configuration of Ag VII.
| E a | o-c b | Eigenvector Composition c | ||
|---|---|---|---|---|
| J = 1/2 | ||||
| 94,730 * | 98% 32P | 2% 52S | ||
| 63,467 * | 96% 52S | 2% 34P | 2% 32P | |
| 38,685 | 6 | 67% 54D | 32% 34P | 1% 52S |
| 34,605 | −20 | 66% 34P | 33% 54D | 1% 52S |
| J = 3/2 | ||||
| 104,821 | −27 | 74% 12D | 18% 52D | 6% 32P |
| 93,529 * | 94% 32P | 4% 12D | 1% 52D | |
| 71,517 | −2 | 97% 32D | 2% 12D | 1% 54D |
| 53,796 | 0 | 55% 34F | 37% 52D | 6% 12D |
| 48,086 | 2 | 42% 52D | 43% 34F | 13% 12D |
| 39,788 | −1 | 52% 54D | 44% 34P | 1% 34F |
| 32,994 | −4 | 53% 34P | 44% 54D | 1% 34F |
| J = 5/2 | ||||
| 103,996 | 34 | 80% 12D | 19% 52D | 1% 32D |
| 72,934 | −26 | 91% 32D | 6% 52F | 2% 54D |
| 59,954 | −5 | 30% 32F | 29% 52F | 19% 52D |
| 57,413 | 2 | 53% 52F | 18% 32F | 17% 52D |
| 51,049 | 11 | 74% 34F | 12% 32F | 8% 52F |
| 47,119 | 2 | 31% 52D | 32% 32F | 13% 34P |
| 39,299 | 10 | 54% 54D | 32% 34P | 7% 52D |
| 32,005 | −19 | 44% 34P | 35% 54D | 13% 54G |
| 29,390 | 27 | 79% 54G | 8% 32F | 4% 34P |
| 0 | 4 | 98% 56S | 2% 34P | |
| J = 7/2 | ||||
| 79,705 | 4 | 96% 32G | 2% 52F | 1% 52G |
| 59,792 | 11 | 75% 52F | 15% 34F | 6% 32F |
| 55,773 | 8 | 74% 52G | 17% 32F | 8% 52F |
| 53,353 | 2 | 47% 32F | 34% 34F | 8% 52G |
| 48,712 | 10 | 45% 34F | 26% 32F | 15% 52G |
| 36,485 | 9 | 92% 54D | 4% 34F | 3% 54G |
| 30,378 | 0 | 93% 54G | 3% 32F | 2% 34F |
| J = 9/2 | ||||
| 79,131 | −13 | 99% 32G | 1% 52G | |
| 59,223 | 2 | 47% 52G | 42% 32H | 10% 34F |
| 53,797 | −11 | 52% 32H | 30% 34F | 18% 52G |
| 49,104 | −11 | 59% 34F | 34% 52G | 6% 32H |
| 30,907 | −2 | 97% 54G | 1% 34F | 1% 32H |
| J = 11/2 | ||||
| 57,962 | 2 | 86% 32H | 11% 52I | 2% 54G |
| 44,011 | 1 | 88% 52I | 10% 32H | 1% 54G |
| 30,662 | −14 | 96% 54G | 3% 32H | |
| J = 13/2 | ||||
| 45,546 | 3 | 100% 52I | ||
a The star * indicates a calculated value for the level; b The difference between the observed and the calculated energies; c For the eigenvector composition, up to three components with the largest percentages in the LS-coupling scheme are listed. The number preceding the terms is the seniority number.

Table A6.
Energies (in cm−1) of the 4d45p configuration of Ag VII.
| E a | o-c b | Eigenvector Composition c | ||
|---|---|---|---|---|
| J = 1/2 | ||||
| 448,199 * | 68% (01S)2P | 15% (1S)2P | 14% (21D)2P | |
| 419,718 * | 64% (21D)2P | 12% (01S)2P | 11% (1D)2P | |
| 409,158 * | 47% (3P)2S | 27% (3P)2S | 12% (23P)2P | |
| 406,673 | 37 | 39% (23F)4D | 20% (3F)4D | 13% (23P)2P |
| 405,606 * | 28% (23P)2P | 13% (23F)4D | 10% (3P)2P | |
| 394,516 * | 41% (23P)4P | 11% (3P)4P | 9% (23P)4D | |
| 392,424 | −57 | 36% (23P)4D | 21% (23P)4D | 11% (23P)4P |
| 389,336 * | 59% (1D)2P | 9% (3P)4P | 7% (21D)2P | |
| 380,449 * | 48% (3D)2P | 23% (1S)2P | 9% (3D)4D | |
| 375,489 | 17 | 64% (3D)4P | 10% (23P)4P | 6% (3D)4D |
| 374,810 | −24 | 35% (3P)2P | 16% (1S)2P | 9% (3P)4P |
| 370,586 * | 22% (1S)2P | 19% (3P)2S | 15% (3P)2S | |
| 368,200 * | 32% (3F)4D | 30% (3D)4D | 11% (3D)2P | |
| 366,416 * | 32% (3D)4D | 31% (23F)4D | 13% (23F)4D | |
| 364,278 * | 19% (3P)4P | 19% (3P)2P | 11% (23P)2S | |
| 355,790 | −19 | 32% (3P)4P | 16% (3P)4P | 13% (23P)2S |
| 352,270 | 26 | 77% (5D)4D | 9% (3P)4D | 4% (3D)4D |
| 347,791 * | 32% (3P)4D | 23% (23P)4D | 10% (3P)2P | |
| 341,227 | −1 | 65% (5D)6D | 30% (5D)4P | 1% (23P)2S |
| 328,555 * | 54% (5D)4P | 33% (25D)6D | 5% (3P)4P | |
| 325,860 * | 89% (5D)6F | 3% (3P)4D | 3% (5D)4D | |
| J = 3/2 | ||||
| 455,917 * | 74% (01S)2P | 16% (1S)2P | 7% (21D)2P | |
| 429,981 * | 65% (21D)2D | 24% (1D)2D | 6% (21D)2P | |
| 416,277 * | 29% (23F)2D | 18% (3P)2D | 14% (3P)2D | |
| 415,087 * | 56% (21D)2P | 6% (3P)2D | 6% (1D)2P | |
| 406,960 * | 38% (23F)4D | 17% (23F)4D | 11% (23P)4D | |
| 404,310 * | 23% (23P)2P | 14% (23P)4S | 13% (23P)4S | |
| 403,643 * | 31% (23P)2P | 22% (3P)4S | 19% (3P)4S | |
| 399,850 | 2 | 41% (1F)2D | 13% (3F)2D | 8% (23P)2D |
| 395,638 * | 39% (1F)2D | 18% (23F)4F | 12% (23P)2D | |
| 393,610 | −2 | 22% (1D)2P | 15% (23P)4P | 8% (23F)4D |
| 391,553 | 7 | 19% (23P)4D | 14% (23P)4D | 14% (23F)2D |
| 389,293 | 26 | 45% (23F)4F | 7% (23P)4D | 7% (3D)2D |
| 387,806 * | 21% (23P)4P | 10% (3P)4P | 10% (1D)2P | |
| 386,582 | −38 | 31% (1S)2P | 10% (21D)2D | 8% (3D)2P |
| 383,280 | 4 | 46% (3D)2D | 19% (3F)2D | 9% (1D)2D |
| 377,910 | 34 | 19% (1S)2P | 18% (1D)2D | 17% (1D)2P |
| 375,706 | 21 | 30% (3D)4D | 13% (3D)2P | 11% (3D)4F |
| 374,938 | 0 | 22% (3D)2P | 11% (3P)2P | 11% (3D)4F |
| 374,236 | 31 | 24% (3D)4P | 18% (3G)4F | 9% (3D)4F |
| 371,218 * | 25% (3P)2D | 14% (23P)2P | 13% (23P)2D | |
| 369,448 | −4 | 27% (3D)4P | 18% (3D)4D | 15% (3P)2P |
| 368,569 | 0 | 22% (3F)4D | 10% (3D)4D | 8% (3D)4F |
| 366,573 | 3 | 25% (3F)4F | 14% (3F)4D | 9% (3F)2D |
| 366,078 | −4 | 17% (3F)4F | 16% (3P)4S | 14% (23P)4S |
| 363,454 | −23 | 31% (3D)4F | 29% (3G)4F | 12% (3P)4P |
| 361,846 * | 20% (3P)2P | 9% (3P)4S | 9% (5D)4D | |
| 360,092 | −51 | 34% (3P)4P | 14% (3P)4P | 11% (3D)4D |
| 356,993 | −2 | 20% (3F)2D | 18% (3F)4F | 10% (3P)4D |
| 353,549 | 22 | 44% (5D)4D | 22% (23P)4D | 8% (23P)4D |
| 351,904 * | 34% (5D)4D | 16% (3P)4D | 14% (23P)4D | |
| 342,965 * | 48% (5D)4F | 25% (5D)6D | 16% (5D)4P | |
| 341,983 | 4 | 31% (5D)4F | 27% (5D)4P | 26% (5D)6D |
| 336,333 | −24 | 72% (5D)6P | 16% (5D)6D | 6% (5D)4P |
| 331,200 | −4 | 41% (5D)4P | 31% (5D)6D | 22% (5D)6P |
| 327,322 * | 91% (5D)6F | 3% (5D)4D | 2% (23P)4D | |
| J = 5/2 | ||||
| 432,566 * | 64% (21D)2D | 23% (1D)2D | 8% (21D)2F | |
| 422,985 | −10 | 43% (21D)2F | 17% (1G)2F | 13% (1G)2F |
| 414,230 | 8 | 46% (23F)2D | 17% (3F)2D | 14% (23P)2D |
| 409,186 | 50 | 51% (21G)2F | 21% (21D)2F | 8% (23F)2F |
| 405,964 * | 45% (23F)4D | 16% (3F)4D | 12% (23P)4D | |
| 400,637 | 16 | 28% (1F)2D | 10% (23P)4D | 10% (23F)2F |
| 398,662 | −16 | 32% (23F)2F | 22% (3F)4G | 8% (3F)4G |
| 395,990 * | 44% (23P)4P | 15% (23P)4P | 10% (23P)2D | |
| 394,049 | 7 | 28% (23F)4F | 20% (21F)2D | 12% (23P)4D |
| 391,396 | 28 | 29% (23F)4G | 11% (3F)2F | 11% (3F)4G |
| 390,060 | −66 | 38% (23F)4F | 11% (3P)4D | 6% (23F)4D |
| 387,358 * | 20% (23P)2D | 12% (23F)2D | 11% (1F)2D | |
| 386,268 | −6 | 25% (1D)2D | 17% (21D)2F | 9% (23F)2F |
| 385,962 | 10 | 21% (3D)2F | 13% (23D)2D | 12% (1G)2F |
| 383,109 | 22 | 25% (3D)2F | 8% (1F)2F | 7% (3P)2D |
| 380,891 | −18 | 28% (1G)2F | 18% (3D)2D | 8% (3F)2F |
| 379,478 | −25 | 25% (3G)2F | 21% (1D)2F | 12% (3P)2D |
| 379,077 | −7 | 29% (1F)2F | 13% (3P)2D | 12% (23P)2D |
| 376,543 | 17 | 23% (3D)4F | 17% (3D)4D | 9% (3G)4F |
| 374,426 | −0 | 13% (3G)4F | 11% (1G)2F | 11% (3P)2D |
| 372,051 | −6 | 24% (3H)4G | 20% (3G)4G | 16% (3F)2F |
| 370,940 * | 16% (3D)4D | 15% (3F)4D | 12% (3F)4F | |
| 369,578 | 12 | 21% (3F)2F | 15% (3D)4P | 11% (3H)4G |
| 367,919 | 13 | 24% (3D)4P | 23% (3P)4P | 9% (3G)4G |
| 366,693 | −15 | 14% (3D)4D | 13% (3F)4F | 13% (3F)4D |
| 364,877 | −3 | 17% (3P)4P | 13% (3P)4P | 8% (3P)2D |
| 364,025 | −28 | 15% (3D)2D | 14% (3D)4P | 10% (3H)4G |
| 362,975 | 3 | 25% (3P)4D | 17% (23F)4F | 13% (3G)4F |
| 362,381 | 56 | 20% (3H)4G | 11% (3D)2F | 10% (3D)4F |
| 361,296 | −14 | 22% (3F)4F | 13% (3G)4F | 11% (3F)2D |
| 358,392 | 29 | 21% (3F)4G | 12% (3G)2F | 8% (3P)4D |
| 356,233 | 1 | 14% (3F)4D | 13% (3F)4G | 12% (3P)4D |
| 354,235 | 16 | 78% (5D)4D | 4% (3D)4D | 2% (3F)4F |
| 352,685 | 45 | 26% (3G)4G | 22% (3F)4G | 14% (23F)4G |
| 344,695 | 6 | 32% (5D)4F | 30% (5D)4P | 27% (5D)6D |
| 343,336 | −17 | 42% (5D)4F | 33% (5D)4P | 5% (5D)6P |
| 339,172 | 1 | 50% (5D)6D | 30% (5D)6P | 8% (5D)4P |
| 333,327 | 18 | 61% (5D)6P | 18% (5D)4P | 17% (5D)6D |
| 329,356 * | 89% (5D)6F | 4% (5D)4F | 2% (5D)4D | |
| J = 7/2 | ||||
| 428,522 | −6 | 70% (21D)2F | 15% (1D)2F | 7% (1G)2F |
| 409,889 | 5 | 39% (21G)2F | 14% (1G)2G | 10% (23F)2G |
| 406,495 | −4 | 46% (23F)2G | 17% (3F)2G | 12% (21G)2G |
| 404,117 | −8 | 27% (23F)2F | 19% (23F)4D | 9% (21G)2G |
| 403,133 | −5 | 25% (23F)4D | 17% (1G)2G | 10% (23P)4D |
| 397,858 | 12 | 26% (23F)4G | 22% (23F)4F | 9% (3F)4G |
| 396,241 | −22 | 32% (23P)4D | 21% (23F)2F | 15% (3P)4D |
| 393,295 | −10 | 20% (23F)4G | 15% (23F)4D | 13% (23F)2F |
| 391,338 | 32 | 43% (23F)4F | 12% (23F)4G | 12% (1D)2F |
| 388,163 | −3 | 23% (1F)2G | 14% (23D)2F | 13% (1D)2F |
| 386,615 | 15 | 26% (1F)2G | 21% (21F)2F | 7% (23F)4F |
| 384,772 | 25 | 24% (1D)2F | 16% (1G)2G | 11% (3F)2F |
| 380,468 | −6 | 20% (1F)2F | 19% (3G)2G | 10% (3D)2F |
| 379,061 | −3 | 21% (1G)2G | 18% (1F)2F | 15% (3D)2F |
| 377,163 | −3 | 27% (3D)4F | 17% (3D)4D | 17% (3G)4F |
| 375,365 | 3 | 37% (3G)2G | 9% (3D)2F | 8% (3D)4D |
| 374,839 | −5 | 14% (3H)4G | 13% (1G)2F | 11% (3G)4F |
| 373,577 | −30 | 13% (3F)4D | 10% (3D)4D | 10% (3G)2F |
| 371,673 | 0 | 25% (3G)4G | 24% (1G)2F | 7% (21G)2F |
| 370,993 | −50 | 33% (3F)2F | 25% (3G)2F | 10% (3D)4D |
| 369,879 | −23 | 28% (3P)4D | 13% (3D)4F | 11% (23P)4D |
| 368,968 | 3 | 15% (3P)4D | 10% (3H)4G | 10% (23P)4D |
| 366,806 | 21 | 29% (3F)4F | 11% (3G)4F | 8% (3H)4G |
| 365,842 | 3 | 16% (3F)2G | 15% (3F)4F | 14% (3D)2F |
| 362,942 | −4 | 25% (3G)4H | 25% (3H)4H | 10% (3H)2G |
| 361,593 | −18 | 25% (3G)4F | 18% (3D)4F | 9% (5D)4F |
| 361,173 | −0 | 39% (3F)4G | 12% (3H)4G | 11% (3G)4H |
| 359,687 | −10 | 16% (3G)4G | 12% (3F)4D | 12% (3H)4G |
| 356,493 | −0 | 17% (3F)4D | 11% (3G)4G | 10% (3H)4H |
| 354,869 | −9 | 68% (5D)4D | 6% (3D)4D | 5% (3F)4F |
| 353,454 | −22 | 19% (3G)4H | 18% (3H)2G | 9% (3F)4G |
| 349,047 | 10 | 47% (3H)4H | 23% (3G)4H | 9% (3H)2G |
| 346,061 | −1 | 55% (5D)4F | 28% (5D)6D | 3% (5D)6F |
| 341,458 | 1 | 59% (5D)6D | 18% (5D)4F | 12% (5D)6F |
| 334,906 | 25 | 85% (5D)6P | 6% (5D)6D | 4% (5D)4D |
| 331,831 * | 82% (5D)6F | 8% (5D)4F | 4% (5D)6D | |
| J = 9/2 | ||||
| 409,779 | 3 | 34% (21G)2G | 17% (1G)2G | 16% (21G)2H |
| 403,942 | −32 | 49% (23F)2G | 12% (3F)2G | 11% (23F)4G |
| 401,561 | −26 | 33% (21G)2H | 14% (1G)2H | 14% (21G)2G |
| 398,431 | 16 | 37% (23F)4F | 25% (3F)4G | 7% (21G)2H |
| 392,486 | 12 | 29% (23F)4G | 21% (1F)2G | 17% (23F)4F |
| 390,759 | 19 | 45% (1F)2G | 31% (23F)4F | 5% (23F)2G |
| 382,720 | 4 | 31% (1G)2G | 22% (1G)2G | 18% (3G)2G |
| 382,377 | −27 | 57% (1I)2H | 13% (23G)2H | 10% (21G)2H |
| 379,226 | 12 | 20% (3G)2G | 12% (23G)4F | 11% (1G)2H |
| 377,393 | 24 | 22% (3F)2G | 13% (3H)2G | 11% (3D)4F |
| 375,593 | 8 | 53% (3D)4F | 14% (3G)2G | 9% (3H)2G |
| 373,120 | 4 | 22% (3G)4G | 14% (3H)2H | 11% (3H)4G |
| 371,061 | −6 | 22% (3H)2H | 21% (3G)2H | 13% (3H)4G |
| 370,501 | 1 | 13% (3G)2H | 11% (3G)2G | 10% (3H)2H |
| 368,429 | −8 | 25% (3G)4H | 17% (3F)4G | 14% (3F)4F |
| 365,569 | −33 | 43% (3F)4F | 10% (3G)2H | 8% (3G)4H |
| 364,772 | −14 | 17% (3F)4G | 17% (3G)4F | 13% (3H)2G |
| 362,447 | −2 | 30% (3G)4F | 22% (3H)4H | 6% (3G)4H |
| 361,650 | 0 | 34% (3H)4G | 22% (3G)4G | 13% (3F)2G |
| 360,482 | 0 | 15% (3F)4G | 13% (3G)4F | 12% (1G)2H |
| 356,416 | −9 | 33% (3H)4I | 11% (3G)4H | 11% (3G)4G |
| 354,122 | −6 | 29% (3H)4H | 14% (3H)4I | 13% (3H)2G |
| 349,721 | −13 | 27% (3H)4I | 27% (3H)4H | 18% (3G)4H |
| 348,377 | −14 | 43% (5D)6D | 29% (5D)4F | 5% (3H)4I |
| 342,289 | −12 | 41% (5D)6D | 27% (5D)6F | 24% (5D)4F |
| 334,849 * | 69% (5D)6F | 15% (5D)4F | 9% (5D)6D | |
| J = 11/2 | ||||
| 409,441 | 8 | 64% (21G)2H | 26% (1G)2H | 5% (1I)2H |
| 399,022 | −1 | 78% (23F)4G | 14% (3F)4G | 4% (21G)2H |
| 383,539 | −14 | 24% (1I)2H | 20% (1G)2H | 17% (21G)2H |
| 377,717 | 14 | 38% (1G)2H | 24% (1I)2H | 14% (3G)2H |
| 376,414 | −1 | 32% (3G)4G | 23% (3G)2H | 18% (3H)4G |
| 372,676 | 6 | 45% (3H)2H | 14% (1I)2H | 14% (3G)4G |
| 370,488 | −1 | 20% (3G)4H | 18% (3G)2H | 15% (3G)4G |
| 369,661 | 6 | 33% (1I)2I | 21% (3H)2I | 15% (3H)2H |
| 367,483 | −2 | 41% (3F)4G | 21% (3H)2I | 9% (1I)2I |
| 365,017 | −2 | 28% (3H)4H | 23% (3G)4H | 17% (3G)2H |
| 362,535 | −1 | 35% (3H)2I | 14% (3F)4G | 13% (3G)2H |
| 360,481 | 1 | 52% (3H)4I | 14% (3G)4G | 14% (3H)4H |
| 357,689 | 2 | 45% (3H)4G | 12% (3H)2H | 12% (3G)4G |
| 352,082 | −7 | 39% (3H)4H | 30% (3H)4I | 17% (3G)4H |
| 340,947 * | 96% (5D)6F | 3% (3F)4G | 1% (23F)4G | |
| J = 13/2 | ||||
| 376,419 | 14 | 55% (1I)2I | 38% (1I)2K | 4% (3H)4H |
| 372,822 | −2 | 52% (3G)4H | 29% (3H)2I | 8% (3H)4H |
| 369,654 | 7 | 39% (1I)2K | 23% (1I)2I | 19% (3H)2I |
| 364,518 | 12 | 34% (3H)2I | 22% (3G)4H | 20% (3H)4I |
| 363,614 | −26 | 49% (3H)4I | 37% (3H)4H | 6% (1I)2K |
| 354,719 | 3 | 48% (3H)4H | 24% (3H)4I | 13% (3H)2I |
| J = 15/2 | ||||
| 378,355 | 9 | 94% (1I)2K | 6% (3H)4I | |
| 365,186 * | 94% (3H)4I | 6% (1I)2K | ||
a The star * indicates a calculated value for the level; b The difference between the observed and the calculated energies; c For the eigenvector composition, up to three components with the largest percentages in the LS-coupling scheme are listed. The number preceding the terms is the seniority number.

Table A7.
Energies (in cm−1) of the 4d4 configuration of Ag VIII.
| E a | o-c b | Eigenvector Composition c | ||
|---|---|---|---|---|
| J = 0 | ||||
| 114,851 * | 82% 01S1 | 17% 41S2 | 1% 23P1 | |
| 65,762 * | 62% 23P1 | 35% 43P2 | 3% 41S2 | |
| 45,338 * | 72% 41S2 | 16% 01S1 | 11% 43P2 | |
| 21,309 | −37 | 50% 43P2 | 32% 23P1 | 8% 45D |
| 0 | −26 | 92% 45D | 4% 23P1 | 4% 43P2 |
| J = 1 | ||||
| 63,371 | −50 | 63% 23P1 | 37% 43P2 | 0% 43D |
| 39,191 | −7 | 95% 43D | 3% 23P1 | 1% 43P2 |
| 26,526 | 19 | 60% 43P2 | 32% 23P1 | 4% 43D |
| 1,340 | −10 | 96% 45D | 2% 23P1 | 2% 43P2 |
| J = 2 | ||||
| 88,586 | 34 | 80% 21D1 | 19% 41D2 | 0% 43D |
| 61,644 | 6 | 68% 23F1 | 24% 43F2 | 5% 41D2 |
| 58,958 * | 64% 23P1 | 28% 43P2 | 3% 41D2 | |
| 48,505 * | 61% 41D2 | 13% 21D1 | 10% 43D | |
| 38,402 | 17 | 63% 43D | 12% 23P1 | 8% 43P2 |
| 32,134 | −19 | 55% 43P2 | 22% 43D | 21% 23P1 |
| 28,051 | 4 | 70% 43F2 | 21% 23F1 | 5% 41D2 |
| 3,212 | −7 | 98% 45D | 1% 23P1 | 1% 43D |
| J = 3 | ||||
| 62,552 | −10 | 72% 23F1 | 17% 43F2 | 10% 41F |
| 52,004 | 31 | 85% 41F | 7% 23F1 | 5% 43D |
| 36,879 | −39 | 92% 43D | 3% 41F | 1% 23F1 |
| 32,926 | 23 | 50% 43F2 | 42% 43G | 7% 23F1 |
| 26,967 | 11 | 55% 43G | 31% 43F2 | 12% 23F1 |
| 5,292 | 1 | 98% 45D | 1% 43F2 | 1% 43D |
| J = 4 | ||||
| 69,584 | −60 | 66% 21G1 | 28% 41G2 | 4% 23F1 |
| 60,980 | 42 | 83% 23F1 | 10% 43F2 | 6% 21G1 |
| 43,104 | −4 | 52% 41G2 | 18% 21G1 | 16% 43F2 |
| 32,698 | −11 | 56% 43G | 20% 43F2 | 16% 41G2 |
| 29,555 | 17 | 42% 43F2 | 25% 43H | 21% 43G |
| 23,302 | −4 | 68% 43H | 15% 43G | 6% 43F2 |
| 7,443 | −5 | 95% 45D | 3% 43F2 | 1% 23F1 |
| J = 5 | ||||
| 35,077 | 11 | 84% 43G | 16% 43H | |
| 26,250 | 12 | 84% 43H | 16% 43G | |
| J = 6 | ||||
| 39,744 | −4 | 91% 41I | 9% 43H | |
| 28,185 | −5 | 91% 43H | 9% 41I | |
a The star * indicates a calculated value for the level; b The difference between the observed and the calculated energies; c For the eigenvector composition, up to three components with the largest percentages in the LS-coupling scheme are listed. The number preceding the terms is the seniority number. The number following the terms displays Nielson and Koster sequential indices [20].

Table A8.
Energies (in cm−1) of the 4d35p configuration of Ag VIII.
| E a | o-c b | Eigenvector Composition c | ||
|---|---|---|---|---|
| J = 0 | ||||
| 460,564 * | 72% (12D)3P | 26% (32D)3P | 1% (32P)3P | |
| 422,372 * | 44% (32D)3P | 30% (32P)3P | 12% (32P)1S | |
| 410,445 * | 48% (34P)3P | 27% (32P)1S | 8% (32D)3P | |
| 400,473 * | 53% (32P)3P | 15% (34P)3P | 14% (32D)3P | |
| 398,971 * | 39% (32P)1S | 39% (34P)5D | 10% (34F)5D | |
| 391,021 * | 34% (34P)5D | 27% (34P)3P | 17% (32P)1S | |
| 382,525 | −78 | 73% (34F)5D | 20% (34P)5D | 2% (32D)3P |
| J = 1 | ||||
| 466,227 | −16 | 73% (12D)1P | 18% (32D)1P | 4% (12D)3P |
| 459,403 * | 64% (12D)3P | 22% (32D)3P | 6% (12D)3D | |
| 444,840 * | 53% (12D)3D | 19% (32F)3D | 15% (32D)3D | |
| 433,769 * | 60% (32F)3D | 26% (12D)3D | 8% (32D)1P | |
| 430,256 * | 45% (32P)1P | 13% (34P)3S | 10% (32D)1P | |
| 426,468 | 33 | 69% (34P)3S | 10% (32D)3P | 5% (34P)3P |
| 419,422 * | 33% (32D)3P | 22% (32D)1P | 11% (34P)3S | |
| 415,902 * | 47% (34P)3D | 27% (32P)3S | 9% (32P)3P | |
| 413,344 | 47 | 33% (32P)3P | 25% (34P)3D | 22% (32P)3S |
| 412,118 | −9 | 55% (32D)3D | 11% (32P)3S | 7% (12D)3D |
| 411,728 * | 35% (32P)1P | 13% (32D)1P | 10% (32P)3S | |
| 404,530 | 9 | 54% (32P)3D | 13% (34P)3P | 9% (32P)3S |
| 403,127 * | 44% (34P)3P | 30% (34P)5D | 8% (32P)3D | |
| 399,869 | 32 | 16% (32P)3P | 15% (32D)3P | 14% (34P)5P |
| 393,703 * | 37% (34P)5D | 23% (34P)3P | 19% (34F)5D | |
| 391,283 | 81 | 72% (34P)5P | 7% (32P)3S | 6% (32P)3P |
| 386,317 | −2 | 53% (34F)5F | 26% (34F)3D | 7% (34P)3D |
| 383,568 | −48 | 64% (34F)5D | 21% (34P)5D | 6% (34F)5F |
| 374,891 | 13 | 47% (34F)3D | 36% (34F)5F | 7% (34F)5D |
| J = 2 | ||||
| 457,523 * | 59% (12D)3P | 14% (32D)3P | 12% (12D)3D | |
| 453,343 | −75 | 36% (12D)1D | 23% (12D)3F | 12% (32F)1D |
| 447,730 | −20 | 31% (12D)3F | 21% (32F)1D | 10% (32D)3F |
| 444,532 | −36 | 44% (12D)3D | 12% (12D)3F | 12% (12D)3P |
| 432,431 | −90 | 54% (32F)3D | 16% (12D)3D | 11% (12D)1D |
| 431,074 * | 30% (12D)1D | 26% (32F)1D | 12% (32F)3D | |
| 424,635 | −19 | 33% (32D)1D | 26% (32P)1D | 17% (32F)3F |
| 421,941 * | 26% (32F)3F | 22% (32P)1D | 12% (32P)3P | |
| 420,031 | 58 | 25% (32P)3P | 22% (34P)3D | 14% (32D)3P |
| 417,758 | 31 | 26% (32D)3D | 16% (32F)3F | 16% (32P)3P |
| 412,894 | 30 | 28% (34P)3D | 21% (34P)5S | 16% (32D)3P |
| 412,412 | −44 | 50% (32P)3D | 18% (32G)3F | 11% (32D)3F |
| 411,461 | −29 | 48% (34P)5S | 20% (34P)3P | 11% (32D)3P |
| 409,522 | −14 | 19% (32D)3F | 15% (32F)1D | 14% (32D)1D |
| 408,409 | −16 | 52% (32G)3F | 12% (32P)3D | 9% (32P)1D |
| 406,270 | −12 | 25% (32D)3D | 23% (32P)3P | 22% (32D)3P |
| 402,086 * | 25% (34P)3P | 23% (34P)5D | 16% (34P)5P | |
| 400,904 | 31 | 23% (34P)5D | 21% (34F)3F | 16% (32D)3F |
| 396,041 | 59 | 36% (34P)5P | 18% (34P)5D | 15% (34F)5D |
| 394,552 * | 52% (34F)3F | 8% (32D)3F | 7% (34F)5G | |
| 393,630 | −4 | 34% (34P)5P | 27% (34P)3P | 13% (34F)3D |
| 386,800 | −9 | 55% (34F)5F | 12% (34F)3D | 5% (34P)3D |
| 385,302 | −69 | 55% (34F)5D | 22% (34P)5D | 5% (34F)5F |
| 377,661 | 4 | 38% (34F)3D | 33% (34F)5F | 17% (34F)5D |
| 371,899 * | 86% (34F)5G | 7% (34F)3F | 3% (32D)3F | |
| J = 3 | ||||
| 460,104 | 100 | 62% (12D)1F | 15% (32D)1F | 11% (12D)3F |
| 452,808 | 172 | 41% (12D)3D | 35% (12D)3F | 9% (32D)3F |
| 446,318 | −13 | 33% (12D)3D | 26% (12D)3F | 13% (12D)1F |
| 436,451 | −25 | 74% (32F)1F | 11% (32F)3D | 5% (32F)3G |
| 430,642 | 2 | 26% (32F)3D | 19% (32F)3F | 19% (32F)3G |
| 427,542 * | 21% (32H)3G | 19% (32F)3D | 18% (32F)3G | |
| 424,006 | −25 | 24% (32P)3D | 23% (32D)1F | 11% (32G)1F |
| 422,895 | 77 | 25% (32F)3F | 22% (32D)3D | 17% (32H)3G |
| 420,123 | 36 | 24% (32F)3F | 17% (34P)3D | 11% (32P)3D |
| 417,724 | 43 | 24% (32H)3G | 23% (32F)3G | 16% (34P)3D |
| 415,165 | 114 | 24% (34P)3D | 14% (32G)1F | 10% (32H)3G |
| 411,469 | −67 | 24% (32D)3D | 18% (32P)3D | 15% (32F)3D |
| 409,750 | −9 | 25% (32G)1F | 13% (32D)1F | 11% (32D)3F |
| 409,432 | −14 | 31% (32D)3F | 20% (32G)3F | 15% (32D)3D |
| 407,506 | 39 | 23% (32G)3F | 22% (32G)3G | 11% (34F)3F |
| 402,520 * | 62% (34P)5D | 11% (34F)5D | 8% (32P)3D | |
| 399,399 | 46 | 72% (34P)5P | 9% (34F)3D | 5% (32P)3D |
| 398,704 | 20 | 35% (32G)3G | 21% (32G)1F | 16% (34F)3G |
| 397,779 | 1 | 59% (34F)3F | 7% (32D)3F | 6% (34P)5P |
| 390,887 | −10 | 29% (34F)5F | 21% (34F)3D | 18% (34F)3G |
| 389,944 | −8 | 31% (34F)3G | 15% (34F)3D | 14% (34F)5D |
| 387,329 | −2 | 34% (34F)5F | 25% (34F)5D | 19% (34F)3G |
| 381,580 | −5 | 40% (34F)5D | 29% (34F)5F | 21% (34F)3D |
| 375,456 * | 87% (34F)5G | 5% (34F)3F | 2% (34F)3G | |
| J = 4 | ||||
| 455,261 | 29 | 77% (12D)3F | 15% (32D)3F | 3% (32F)1G |
| 437,322 | 112 | 61% (32F)1G | 28% (32H)1G | 6% (32F)3G |
| 431,659 * | 48% (32F)3G | 25% (32F)3F | 18% (32H)3G | |
| 424,999 | 1 | 47% (32F)3F | 13% (32H)3G | 11% (32F)3G |
| 420,822 | 37 | 35% (32H)3G | 16% (32F)3G | 14% (32G)3F |
| 417,492 | −62 | 67% (32D)3F | 10% (12D)3F | 7% (34F)3F |
| 412,977 | 6 | 22% (32F)1G | 17% (32G)1G | 13% (32F)3G |
| 412,041 | −47 | 33% (32H)1G | 28% (32G)1G | 13% (32H)3G |
| 408,236 | 37 | 30% (34P)5D | 14% (32H)3H | 13% (32G)3H |
| 407,173 | −50 | 57% (34P)5D | 14% (32G)3F | 9% (32H)3H |
| 405,162 | −21 | 52% (32G)3G | 16% (32G)3F | 13% (32H)3H |
| 400,219 | −10 | 58% (34F)3F | 18% (32G)3F | 3% (32H)3G |
| 399,265 | 14 | 34% (32G)1G | 18% (32G)3H | 13% (32H)3H |
| 396,481 | 18 | 43% (34F)3G | 19% (32H)3H | 18% (32G)3H |
| 393,193 | −2 | 34% (34F)5F | 32% (32G)3H | 11% (32H)3H |
| 388,964 | 4 | 33% (34F)5F | 23% (34F)3G | 16% (34F)5G |
| 385,218 | −11 | 67% (34F)5D | 15% (34F)5F | 6% (34F)3F |
| 379,386 * | 80% (34F)5G | 7% (34F)3G | 6% (34F)5F | |
| J = 5 | ||||
| 432,154 | 32 | 85% (32F)3G | 13% (32H)3G | 1% (32G)1H |
| 421,021 | 4 | 45% (32H)3G | 16% (32G)1H | 13% (32H)1H |
| 415,995 | −15 | 52% (32H)1H | 24% (32G)3G | 17% (32H)3I |
| 413,329 | 57 | 61% (32G)1H | 20% (32H)3G | 10% (32H)3I |
| 408,910 | 1 | 54% (32G)3H | 31% (32H)3H | 9% (32G)3G |
| 407,246 | −19 | 38% (32H)3I | 36% (32G)3G | 8% (32H)3G |
| 405,144 | 26 | 26% (32H)3H | 23% (32H)1H | 11% (32H)3I |
| 399,831 | −1 | 47% (34F)3G | 23% (34F)5F | 16% (32H)3H |
| 395,955 | −2 | 32% (34F)5F | 22% (32G)3H | 16% (32H)3I |
| 390,458 | −6 | 40% (34F)5G | 28% (34F)5F | 18% (34F)3G |
| 383,426 | −48 | 58% (34F)5G | 15% (34F)3G | 13% (34F)5F |
| J = 6 | ||||
| 421,189 | 52 | 67% (32H)1I | 19% (32G)3H | 7% (32H)3I |
| 413,999 | −7 | 66% (32H)3I | 24% (32H)3H | 5% (32H)1I |
| 410,851 | 20 | 57% (32G)3H | 25% (32H)1I | 14% (32H)3H |
| 403,359 | −13 | 55% (32H)3H | 25% (32H)3I | 14% (32G)3H |
| 391,512 * | 94% (34F)5G | 6% (32G)3H | ||
| J = 7 | ||||
| 417,658 | −35 | 100% (32H)3I | ||
a The star * indicates a calculated value for the level; b The difference between the observed and the calculated energies; c For the eigenvector composition, up to three components with the largest percentages in the LS-coupling scheme are listed. The number preceding the terms is the seniority number.

Table A9.
Energies (in cm−1) of the 4d34f + 4p54d5 configurations of Ag VIII.
| E a | o-c b | J | Eigenvector Composition c | ||
|---|---|---|---|---|---|
| 557,732 | 258 | 1 | 24% 4d34f (4F)5D | 20% 4p54d5 (4F)5D | 10% 4p54d5 (4D)5D |
| 557,962 * | 4 | 40% 4p54d5 (2G1)3H | 10% 4p54d5 (2D1)3F | 6% 4p54d5 (2F2)3G | |
| 558,654 | 182 | 1 | 22% 4p54d5 (4G)5F | 18% 4d34f (4F)5F | 17% 4d34f (4P)5F |
| 560,251 | 257 | 2 | 31% 4d34f (4F)5D | 27% 4p54d5 (4F)5D | 13% 4p54d5 (4D)5D |
| 560,857 | 186 | 2 | 27% 4p54d5 (4G)5F | 21% 4d34f (4F)5F | 20% 4d34f (4P)5F |
| 560,877 * | 4 | 24% 4p54d5 (2D1)3F | 13% 4p54d5 (2D3)3F | 11% 4p54d5 (2G1)3F | |
| 562,295 | 122 | 3 | 21% 4d34f (4F)5D | 21% 4p54d5 (4F)5D | 13% 4p54d5 (4G)5F |
| 562,825 | 92 | 3 | 14% 4p54d5 (4G)5F | 10% 4d34f (4P)5F | 10% 4d34f (4F)5F |
| 564,383 | −53 | 4 | 20% 4p54d5 (4F)5D | 17% 4d34f (4F)5D | 16% 4p54d5 (4G)5F |
| 565,233 * | 3 | 14% 4p54d5 (2D1)3F | 11% 4p54d5 (2D1)1F | 9% 4d34f (2D1)1F | |
| 564,902 | −365 | 4 | 14% 4p54d5 (4G)5F | 13% 4p54d5 (4F)5D | 10% 4d34f (4F)5F |
| 565,427 | −49 | 5 | 17% 4p54d5 (4G)5F | 10% 4d34f (4F)5F | 9% 4d34f (4P)5F |
| 567,115 | 119 | 7 | 21% 4d34f (2H)1K | 18% 4d34f (4F)3I | 15% 4d34f (2H)3I |
| 568,319 | 12 | 5 | 15% 4d34f (4F)3I | 13% 4p54d5 (2I)3I | 13% 4p54d5 (4G)5F |
| 568,352 * | 2 | 26% 4p54d5 (2P)3D | 14% 4p54d5 (2D1)3D | 10% 4p54d5 (2D1)3F | |
| 569,385 | 138 | 6 | 22% 4d34f (4F)3I | 18% 4p54d5 (2I)3I | 18% 4d34f (2H)3I |
| 571,903 * | 1 | 38% 4p54d5 (2P)3P | 20% 4p54d5 (2D1)3P | 18% 4p54d5 (2D3)3P | |
| 573,036 | −36 | 4 | 17% 4d34f (4F)3H | 11% 4p54d5 (2H)3H | 8% 4d34f (2G)3H |
| 576,375 * | 1 | 20% 4p54d5 (2F2)3D | 10% 4d34f (2P)3D | 10% 4d34f (2D2)3D | |
| 576,746 | −170 | 5 | 17% 4d34f (4F)3H | 10% 4p54d5 (2H)3H | 8% 4d34f (2G)3H |
| 577,085 | −795 | 3 | 14% 4p54d5 (2H)3G | 12% 4d34f (2G)3G | 11% 4p54d5 (2G2)3G |
| 578,963 | 209 | 7 | 29% 4d34f (2H)1K | 18% 4d34f (2G)1K | 14% 4p54d5 (2I)1K |
| 578,767 * | 2 | 21% 4p54d5 (2P)3P | 15% 4p54d5 (2D1)3P | 12% 4p54d5 (2D2)3P | |
| 579,661 * | 1 | 36% 4p54d5 (2P)3D | 11% 4p54d5 (2D1)3D | 7% 4d34f (2D1)3D | |
| 580,373 * | 3 | 15% 4p54d5 (2D2)1F | 15% 4p54d5 (2D1)3F | 8% 4d34f (2D2)1F | |
| 580,680 * | 2 | 13% 4p54d5 (2F2)3D | 9% 4d34f (2P)3D | 6% 4p54d5 (2F1)3D | |
| 580,568 * | 0 | 39% 4p54d5 (2P)3P | 20% 4p54d5 (2D3)3P | 12% 4p54d5 (2P)1S | |
| 581,094 * | 1 | 32% 4d34f (2D1)1P | 19% 4d34f (2D2)1P | 12% 4p54d5 (2P)1P | |
| 580,923 | −221 | 6 | 22% 4d34f (4F)3H | 14% 4p54d5 (4G)3H | 14% 4p54d5 (2H)3H |
| 581,306 | 22 | 4 | 11% 4p54d5 (2G2)3G | 11% 4d34f (4P)3G | 7% 4d34f (2G)3G |
| 582,024 | −42 | 5 | 13% 4d34f (4P)3G | 11% 4p54d5 (2G2)3G | 7% 4d34f (2G)3G |
| 582,154 | −19 | 1 | 30% 4p54d5 (6S)5P | 10% 4d34f (4F)5P | 10% 4p54d5 (4P)3S |
| 583,603 | 46 | 3 | 15% 4p54d5 (2G1)3F | 10% 4d34f (2D2)3F | 10% 4p54d5 (4F)3F |
| 585,291 * | 3 | 10% 4p54d5 (2D2)3D | 9% 4p54d5 (2F2)3D | 6% 4d34f (2G)3D | |
| 587,262 * | 2 | 10% 4p54d5 (2P)3D | 9% 4p54d5 (2D1)3F | 7% 4p54d5 (2G1)3F | |
| 589,229 | −70 | 4 | 12% 4p54d5 (2I)3H | 8% 4d34f (2H)3H | 5% 4p54d5 (4F)3G |
| 589,963 | 238 | 2 | 12% 4p54d5 (2D1)3F | 10% 4p54d5 (2D1)3P | 8% 4p54d5 (2D2)3D |
| 589,786 | −107 | 4 | 9% 4p54d5 (2H)3G | 4% 4p54d5 (2I)3H | 4% 4d34f (2D2)1G |
| 590,761 * | 1 | 9% 4p54d5 (2D2)3D | 8% 4p54d5 (2F1)3D | 8% 4p54d5 (2D2)1P | |
| 591,056 * | 2 | 13% 4p54d5 (2D1)3F | 11% 4p54d5 (2G2)3F | 8% 4p54d5 (2G1)3F | |
| 591,442 | 124 | 3 | 17% 4p54d5 (4F)3G | 6% 4d34f (4F)3G | 6% 4p54d5 (4G)3G |
| 591,781 * | 1 | 11% 4p54d5 (6S)5P | 11% 4p54d5 (2D1)3P | 7% 4p54d5 (4D)3P | |
| 592,118 | −49 | 5 | 9% 4p54d5 (2H)1H | 9% 4d34f (2G)1H | 8% 4d34f (2D1)3G |
| 593,449 * | 2 | 19% 4p54d5 (6S)5P | 6% 4p54d5 (2D2)3F | 6% 4p54d5 (2D1)3P | |
| 593,578 * | 0 | 17% 4p54d5 (4P)3P | 16% 4p54d5 (2D1)3P | 15% 4p54d5 (4D)3P | |
| 593,064 | −698 | 3 | 15% 4p54d5 (2F1)3D | 11% 4p54d5 (4D)3D | 11% 4d34f (2P)3D |
| 594,881 | −367 | 2 | 27% 4p54d5 (6S)5P | 8% 4p54d5 (4D)5P | 8% 4p54d5 (4P)5P |
| 596,171 | −15 | 4 | 9% 4p54d5 (2I)3H | 9% 4p54d5 (2G2)1G | 8% 4d34f (2H)3H |
| 598,210 | 207 | 4 | 16% 4p54d5 (4F)3G | 7% 4p54d5 (2G2)3G | 6% 4p54d5 (2F1)1G |
| 598,784 * | 3 | 17% 4p54d5 (2G1)3G | 15% 4d34f (2D1)3G | 5% 4p54d5 (2F2)3D | |
| 599,018 | 15 | 1 | 11% 4p54d5 (2P)3S | 10% 4d34f (2F)3P | 9% 4p54d5 (2S)3P |
| 599,345 | 109 | 5 | 15% 4p54d5 (4F)3G | 10% 4p54d5 (2I)3H | 8% 4p54d5 (2G2)3G |
| 602,225 | 723 | 4 | 8% 4p54d5 (4F)3F | 7% 4p54d5 (2G2)1G | 7% 4d34f (2F)1G |
| 601,789 * | 2 | 11% 4p54d5 (2D3)3P | 8% 4d34f (2F)3P | 7% 4p54d5 (4P)3P | |
| 602,116 * | 3 | 9% 4p54d5 (4F)3G | 8% 4d34f (2G)3F | 8% 4p54d5 (2G2)3F | |
| 603,864 | 132 | 5 | 20% 4d34f (2D1)1H | 11% 4p54d5 (2I)3H | 9% 4p54d5 (2G1)1H |
| 604,385 | −19 | 4 | 24% 4p54d5 (2G1)3G | 13% 4d34f (2D1)3G | 7% 4d34f (2H)3G |
| 604,600 | 3 | 3 | 43% 4p54d5 (6S)5P | 12% 4p54d5 (4D)5P | 9% 4p54d5 (4P)5P |
| 605,132 | −102 | 6 | 25% 4p54d5 (2I)3H | 14% 4p54d5 (2I)1I | 13% 4p54d5 (4G)3H |
| 606,529 | 91 | 5 | 17% 4p54d5 (4G)3G | 16% 4p54d5 (4F)3G | 8% 4d34f (4F)3G |
| 607,167 * | 1 | 16% 4p54d5 (2P)3S | 14% 4p54d5 (4P)3S | 6% 4p54d5 (2D3)1P | |
| 607,348 * | 2 | 16% 4p54d5 (4D)3P | 9% 4p54d5 (2D1)3P | 7% 4p54d5 (4P)3P | |
| 607,709 * | 0 | 27% 4p54d5 (2P)3P | 20% 4p54d5 (2S)3P | 19% 4d34f (2F)3P | |
| 608,132 * | 1 | 12% 4p54d5 (2D2)1P | 10% 4p54d5 (2D2)3D | 6% 4d34f (2G)3D | |
| 607,628 | −663 | 3 | 10% 4p54d5 (2F2)3D | 10% 4p54d5 (2F1)1F | 8% 4d34f (2F)1F |
| 613,166 | −109 | 4 | 12% 4p54d5 (4G )3F | 9% 4p54d5 (2F2)1G | 7% 4d34f (2G)1G |
| 614,370 | 76 | 5 | 19% 4p54d5 (2G1)1H | 13% 4p54d5 (2G1)3G | 6% 4p54d5 (2I)1H |
| 615,653 * | 3 | 11% 4p54d5 (2D1)3D | 8% 4p54d5 (4D)3D | 7% 4p54d5 (2F1)3D | |
| 615,971 * | 1 | 19% 4p54d5 (4D)3D | 16% 4p54d5 (2D3)3D | 11% 4p54d5 (4P)3D | |
| 616,249 * | 2 | 11% 4p54d5 (4D)3D | 11% 4p54d5 (2D2)1D | 11% 4p54d5 (2D3)3D | |
| 617,860 * | 1 | 34% 4p54d5 (2D1)3D | 7% 4d34f (2D1)3D | 6% 4d34f (2D2)1P | |
| 619,061 * | 2 | 26% 4p54d5 (2D1)3D | 11% 4p54d5 (4P)3D | 9% 4d34f (2D1)3D | |
| 620,379 * | 3 | 15% 4p54d5 (4G)3F | 13% 4p54d5 (4D)3F | 5% 4p54d5 (4G)3G | |
| 620,664 | 128 | 2 | 13% 4p54d5 (4G)3F | 10% 4p54d5 (2F1)1D | 9% 4p54d5 (2D3)1D |
| 621,268 | −115 | 6 | 41% 4p54d5 (2I)1I | 16% 4p54d5 (2I)3H | 11% 4d34f (2H)1I |
| 622,060 | −146 | 4 | 20% 4p54d5 (4D)3F | 12% 4p54d5 (4G)3G | 8% 4p54d5 (2G1)3F |
| 622,489 * | 3 | 15% 4p54d5 (4D)3D | 9% 4p54d5 (4P)3D | 7% 4p54d5 (4G)3G | |
| 624,693 * | 2 | 15% 4p54d5 (2D2)1D | 10% 4p54d5 (2P)1D | 8% 4p54d5 (4P)3D | |
| 627,779 | −430 | 3 | 12% 4p54d5 (4P)3D | 11% 4p54d5 (2G2)1F | 8% 4p54d5 (2F2)1F |
| 630,389 | 405 | 3 | 14% 4p54d5 (2D3)1F | 11% 4p54d5 (4G)3G | 11% 4p54d5 (2F1)1F |
| 630,848 * | 2 | 14% 4p54d5 (2P)1D | 10% 4p54d5 (2F2)1D | 7% 4p54d5 (4G)3F | |
| 634,810 | 230 | 4 | 33% 4p54d5 (4G)3G | 8% 4p54d5 (4F)3G | 8% 4p54d5 (4G)3F |
| 635,050 | −166 | 3 | 22% 4p54d5 (4G)3G | 11% 4p54d5 (2F2)1F | 7% 4p54d5 (2F1)1F |
| 635,935 | 510 | 5 | 41% 4p54d5 (4G)3G | 18% 4p54d5 (2H)3G | 13% 4p54d5 (4F)3G |
| 635,583 * | 1 | 29% 4p54d5 (2D3)1P | 15% 4p54d5 (2S)1P | 6% 4p54d5 (2D3)3D | |
| 636,245 * | 1 | 39% 4p54d5 (4P)3S | 21% 4p54d5 (2P)3S | 8% 4d34f (2F)3S | |
| 641,516 | 56 | 2 | 16% 4p54d5 (4F)3F | 7% 4p54d5 (4F)3D | 5% 4p54d5 (4D)3P |
| 643,491 * | 3 | 18% 4p54d5 (4F)3D | 11% 4p54d5 (2D1)3D | 9% 4p54d5 (2D1)1F | |
| 644,043 | 065 | 5 | 28% 4p54d5 (2H)1H | 26% 4p54d5 (2I)1H | 21% 4p54d5 (2G2)1H |
| 643,939 | −245 | 4 | 18% 4p54d5 (2H)1G | 15% 4p54d5 (4F)3F | 13% 4p54d5 (2G1)1G |
| 644,760 * | 1 | 25% 4p54d5 (4D)3P | 10% 4p54d5 (2D2)3P | 9% 4p54d5 (4F)3D | |
| 645,906 | 221 | 2 | 15% 4p54d5 (2D2)1D | 11% 4p54d5 (2D1)1D | 7% 4d34f (2D1)1D |
| 646,185 | 348 | 2 | 11% 4p54d5 (4D)3P | 9% 4p54d5 (4F)3F | 7% 4p54d5 (2D2)3P |
| 647,898 * | 0 | 40% 4p54d5 (4D)3P | 14% 4p54d5 (2D2)3P | 10% 4p54d5 (4P)3P | |
| 647,982 | 30 | 3 | 22% 4p54d5 (4F)3F | 12% 4p54d5 (4F)3D | 5% 4p54d5 (2G1)3F |
| 650,256 | 171 | 4 | 19% 4p54d5 (4F)3F | 13% 4p54d5 (2G1)1G | 11% 4p54d5 (2G1)3F |
| 650,545 | −375 | 2 | 23% 4p54d5 (4F)3D | 7% 4p54d5 (2P)3D | 5% 4p54d5 (4F)3F |
| 651,358 * | 3 | 18% 4p54d5 (2F1)1F | 15% 4p54d5 (2G2)1F | 14% 4p54d5 (2D1)1F | |
| 664,590 * | 1 | 40% 4p54d5 (2P)1P | 15% 4p54d5 (2D1)1P | 9% 4d34f (2D1)1P | |
| 668,708 | −344 | 3 | 32% 4p54d5 (2G1)1F | 15% 4p54d5 (2D2)1F | 13% 4p54d5 (2F2)1F |
a The star * indicates a calculated value for the level; b The difference between the observed and the calculated energies; c For the eigenvector composition, up to three components with the largest percentages in the LS-coupling scheme are listed. The number following the terms displays Nielson and Koster sequential indices [20].

Table A10.
Energies (in cm−1) of the 4d3 configuration of Ag IX.
| E a | o-c b | Eigenvector Composition c | ||
|---|---|---|---|---|
| J = 1/2 | ||||
| 28,502 * | 87% 2P | 13% 4P | ||
| 17,851 * | 87% 4P | 13% 2P | ||
| J = 3/2 | ||||
| 68,707 | 48 | 76% 2D1 | 24% 2D2 | |
| 36,360 | −6 | 57% 2P | 27% 2D2 | 10% 2D1 |
| 26,823 | 24 | 41% 2D2 | 25% 4P | 20% 2P |
| 17,169 | 56 | 69% 4P | 23% 2P | 5% 2D2 |
| 0 | 12 | 95% 4F | 3% 2D2 | 1% 2D1 |
| J = 5/2 | ||||
| 68,249 | −22 | 83% 2D1 | 12% 2D2 | 3% 2F |
| 44,595 | −41 | 96% 2F | 2% 2D1 | 2% 2D2 |
| 33,051 | 10 | 84% 2D2 | 12% 2D1 | 2% 4P |
| 22,387 | −10 | 97% 4P | 2% 2D1 | 1% 2D2 |
| 3103 | 0 | 98% 4F | 1% 2D2 | 0% 2D1 |
| J = 7/2 | ||||
| 44,082 | −3 | 98% 2F | 1% 2G | 0% 4F |
| 22,160 | −24 | 96% 2G | 2% 4F | 1% 2F |
| 6532 | 4 | 97% 4F | 2% 2G | 0% 2F |
| J = 9/2 | ||||
| 32,349 | 19 | 57% 2H | 41% 2G | 2% 4F |
| 23,357 | −22 | 50% 2G | 43% 2H | 7% 4F |
| 9867 | −13 | 91% 4F | 8% 2G | 1% 2H |
| J = 11/2 | ||||
| 31,532 | 15 | 100% 2H | ||
a The star * indicates a calculated value for the level; b The difference between the observed and the calculated by orthogonal parameter technique energies; c For the eigenvector composition, up to three components with the largest percentages in the LS-coupling scheme are listed. The number following the terms displays Nielson and Koster sequential indices [20].

Table A11.
Energies (in cm−1) of the 4d25p + 4d24f + 4p54d4 configurations of Ag IX.
| E a | o-c b | J | Config. c | Eigenvector Composition d | ||
|---|---|---|---|---|---|---|
| 424,571 | 90 | 5/2 | 4d25p | 71% 4d25p (3F)4G | 17% 4d25p (3F)2F | 7% 4d25p (1D)2F |
| 427,386 * | 7/2 | 4p54d4 | 81% 4p54d4 (5D)6D | 11% 4p54d4 (5D)6F | 6% 4p54d4 (5D)6P | |
| 427,916 | −112 | 3/2 | 4d25p | 61% 4d25p (3F)4F | 25% 4d25p (3F)2D | 7% 4d25p (3F)4D |
| 428,156 * | 5/2 | 4p54d4 | 78% 4p54d4 (5D)6D | 9% 4p54d4 (5D)6P | 8% 4p54d4 (5D)6F | |
| 428,306 * | 9/2 | 4p54d4 | 85% 4p54d4 (5D)6D | 12% 4p54d4 (5D)6F | 1% 4p54d4 (5D)4F | |
| 430,308 * | 3/2 | 4p54d4 | 76% 4p54d4 (5D)6D | 9% 4p54d4 (5D)6P | 5% 4p54d4 (5D)6F | |
| 431,109 * | 7/2 | 4d25p | 77% 4d25p (3F)4G | 9% 4d25p (3F)4F | 9% 4d25p (3F)2F | |
| 432,569 | 157 | 5/2 | 4d25p | 56% 4d25p (3F)4F | 16% 4d25p (3F)2D | 16% 4d25p (3F)4D |
| 433,690 * | 1/2 | 4p54d4 | 84% 4p54d4 (5D)6D | 6% 4p54d4 (5D)4P | 4% 4p54d4 (3D)4P | |
| 437,442 | 34 | 9/2 | 4d25p | 58% 4d25p (3F)4G | 25% 4d25p (3F)4F | 11% 4d25p (3F)2G |
| 437,662 | 68 | 1/2 | 4d25p | 49% 4d25p (3F)4D | 35% 4d25p (3P)4D | 6% 4d25p (3P)2S |
| 437,662 | −478 | 7/2 | 4d25p | 53% 4d25p (3F)4F | 27% 4d25p (3F)4D | 10% 4d25p (3F)2F |
| 438,297 | −107 | 5/2 | 4d25p | 29% 4d25p (3F)4F | 22% 4d25p (3F)4G | 22% 4d25p (3F)2F |
| 438,725 | −103 | 3/2 | 4d25p | 36% 4d25p (3F)4D | 28% 4d25p (3F)4F | 14% 4d25p (3F)2D |
| 440,957 * | 3/2 | 4d25p | 25% 4d25p (3P)4D | 25% 4d25p (3F)2D | 18% 4d25p (3P)2D | |
| 441,473 * | 1/2 | 4d25p | 73% 4d25p (3P)2S | 15% 4d25p (3P)4P | 6% 4d25p (3F)4D | |
| 441,637 | −122 | 7/2 | 4d25p | 26% 4d25p (3F)4D | 23% 4d25p (3F)2F | 20% 4d25p (3F)4F |
| 442,423 | 120 | 5/2 | 4d25p | 46% 4d25p (3F)4D | 25% 4d25p (3P)4D | 13% 4d25p (1D)2F |
| 444,195 | 220 | 9/2 | 4d25p | 43% 4d25p (3F)4F | 41% 4d25p (3F)4G | 10% 4d25p (3F)2G |
| 444,319 * | 11/2 | 4p54d4 | 92% 4p54d4 (5D)6F | 5% 4p54d4 (3F2)4G | 1% 4p54d4 (3F1)4G | |
| 444,355 * | 3/2 | 4d25p | 50% 4d25p (3P)4S | 15% 4d25p (1D)2P | 6% 4d25p (3F)4D | |
| 445,529 * | 5/2 | 4p54d4 | 41% 4p54d4 (3H)4G | 32% 4d24f (3F)4G | 10% 4p54d4 (3G)4G | |
| 446,642 | −4 | 5/2 | 4d25p | 41% 4d25p (3F)2F | 20% 4d25p (3F)2D | 18% 4d25p (3P)2D |
| 447,243 * | 7/2 | 4d25p | 43% 4d25p (3F)2G | 18% 4d25p (1G)2G | 10% 4d25p (3F)4F | |
| 447,255 | −279 | 7/2 | 4p54d4 | 33% 4p54d4 (3H)4G | 30% 4d24f (3F)4G | 11% 4p54d4 (3G)4G |
| 447,694 * | 11/2 | 4d25p | 97% 4d25p (3F)4G | 1% 4d25p (1G)2H | 1% 4d24f (3F)4G | |
| 448,369 * | 7/2 | 4d24f | 32% 4d24f (3F)2G | 10% 4p54d4 (3H)2G | 8% 4d25p (3F)2G | |
| 448,623 * | 3/2 | 4p54d4 | 28% 4p54d4 (3P2)4S | 11% 4d25p (1D)2P | 8% 4p54d4 (3P2)4P | |
| 448,989 | 232 | 7/2 | 4d25p | 31% 4d25p (3F)2F | 22% 4d25p (3F)4D | 12% 4d25p (3P)4D |
| 448,995 * | 1/2 | 4d25p | 54% 4d25p (3P)4D | 36% 4d25p (3F)4D | 3% 4d25p (3P)2P | |
| 449,006 * | 9/2 | 4p54d4 | 16% 4p54d4 (5D)6F | 16% 4d24f (3F)4G | 14% 4p54d4 (3H)4G | |
| 450,334 * | 3/2 | 4p54d4 | 16% 4p54d4 (3G)4F | 12% 4d24f (3F)4F | 10% 4p54d4 (3F2)4D | |
| 451,183 | −53 | 3/2 | 4d25p | 31% 4d25p (3P)4S | 23% 4d25p (1D)2P | 13% 4d25p (1D)2D |
| 451,424 * | 9/2 | 4p54d4 | 28% 4p54d4 (5D)6F | 14% 4p54d4 (3H)4G | 13% 4d24f (3F)4G | |
| 451,430 * | 5/2 | 4p54d4 | 17% 4p54d4 (5D)6F | 16% 4p54d4 (3F2)4D | 12% 4p54d4 (5D)6P | |
| 451,946 * | 1/2 | 4p54d4 | 41% 4p54d4 (3F2)4D | 12% 4p54d4 (5D)4D | 12% 4p54d4 (3D)4D | |
| 452,041 * | 7/2 | 4p54d4 | 28% 4p54d4 (5D)6F | 11% 4p54d4 (3F2)4D | 9% 4p54d4 (5D)6P | |
| 452,292 | 198 | 9/2 | 4d25p | 22% 4d25p (1G)2G | 21% 4d25p (3F)4F | 18% 4d25p (3F)2G |
| 452,569 | 249 | 5/2 | 4d25p | 59% 4d25p (1D)2F | 12% 4d25p (3F)2F | 11% 4d25p (3F)2D |
| 452,857 * | 3/2 | 4d25p | 28% 4d25p (3P)4D | 15% 4d25p (3F)4D | 11% 4p54d4 (5D)6P | |
| 452,951 * | 9/2 | 4p54d4 | 21% 4p54d4 (5D)6F | 20% 4d24f (3F)2G | 8% 4p54d4 (3H)2G | |
| 453,404 * | 3/2 | 4d25p | 24% 4d25p (3P)4D | 13% 4p54d4 (3G)4F | 11% 4d25p (3F)4D | |
| 453,632 * | 11/2 | 4p54d4 | 26% 4d24f (3F)4G | 22% 4p54d4 (3H)4G | 17% 4p54d4 (3F2)4G | |
| 453,902 | −209 | 7/2 | 4d25p | 52% 4d25p (1G)2G | 14% 4d25p (1D)2F | 11% 4d25p (3F)2G |
| 454,133 * | 5/2 | 4p54d4 | 27% 4p54d4 (3G)4F | 12% 4d24f (3F)4F | 10% 4p54d4 (3F2)4D | |
| 455,093 * | 7/2 | 4p54d4 | 13% 4p54d4 (3F2)4D | 13% 4p54d4 (5D)6F | 13% 4p54d4 (3G)4F | |
| 455,362 * | 3/2 | 4p54d4 | 31% 4p54d4 (5D)6P | 18% 4p54d4 (3D)4P | 15% 4p54d4 (3F2)4D | |
| 455,506 * | 5/2 | 4p54d4 | 20% 4p54d4 (3P1)4P | 15% 4d24f (3F)4P | 10% 4p54d4 (3P2)4D | |
| 457,009 * | 1/2 | 4d25p | 50% 4d25p (1D)2P | 39% 4d25p (3P)4P | 5% 4d25p (3F)4D | |
| 457,621 | 41 | 5/2 | 4d25p | 49% 4d25p (3P)4D | 19% 4d25p (3F)4D | 12% 4d25p (3F)2D |
| 457,734 * | 7/2 | 4d24f | 80% 4d24f (3F)4H | 3% 4p54d4 (3G)4H | 3% 4p54d4 (3H)4G | |
| 457,900 | 111 | 9/2 | 4d25p | 52% 4d25p (3F)2G | 33% 4d25p (1G)2G | 10% 4d25p (1G)2H |
| 457,882 * | 9/2 | 4p54d4 | 22% 4d24f (3F)4H | 9% 4d24f (3F)4I | 9% 4p54d4 (3H)4H | |
| 458,434 * | 1/2 | 4d24f | 26% 4d24f (3F)2S | 18% 4p54d4 (3D)4P | 16% 4d24f (3F)4P | |
| 458,503 * | 9/2 | 4d24f | 34% 4d24f (3F)4H | 33% 4d24f (3F)4I | 7% 4d24f (1D)2H | |
| 458,762 * | 11/2 | 4p54d4 | 39% 4d24f (3F)4H | 23% 4p54d4 (3H)4H | 15% 4p54d4 (3G)4H | |
| 459,044 * | 7/2 | 4p54d4 | 19% 4d24f (3F)4F | 16% 4p54d4 (5D)6F | 15% 4p54d4 (3P2)4D | |
| 459,146 | −45 | 3/2 | 4d25p | 59% 4d25p (3P)4P | 11% 4d25p (1D)2P | 9% 4d25p (1D)2D |
| 460,347 * | 13/2 | 4p54d4 | 31% 4d24f (3F)4H | 23% 4p54d4 (3H)4H | 22% 4p54d4 (3G)4H | |
| 460,559 | −65 | 7/2 | 4d25p | 37% 4d25p (3P)4D | 15% 4d25p (1D)2F | 12% 4d25p (3F)4D |
| 460,753 * | 5/2 | 4p54d4 | 11% 4p54d4 (3F2)4F | 11% 4d24f (3F)2F | 11% 4d24f (3F)4F | |
| 460,784 * | 9/2 | 4d24f | 25% 4p54d4 (3D)4F | 20% 4d24f (3F)4I | 13% 4d24f (3F)4H | |
| 460,974 * | 11/2 | 4d24f | 57% 4d24f (3F)4I | 13% 4d24f (3F)4H | 7% 4p54d4 (3H)4I | |
| 461,009 * | 1/2 | 4d25p | 29% 4d25p (3P)4P | 22% 4d25p (1D)2P | 10% 4d24f (3F)2S | |
| 461,370 * | 5/2 | 4p54d4 | 15% 4p54d4 (5D)6P | 12% 4d25p (3P)4P | 12% 4d25p (1D)2D | |
| 461,715 * | 3/2 | 4p54d4 | 15% 4d25p (1D)2D | 11% 4p54d4 (5D)6F | 9% 4d25p (3P)4P | |
| 461,846 * | 5/2 | 4d25p | 30% 4d25p (1D)2D | 22% 4d25p (3P)4P | 10% 4d25p (3P)4D | |
| 461,926 * | 3/2 | 4d25p | 21% 4d25p (1D)2D | 18% 4d25p (3P)4P | 8% 4d25p (1D)2P | |
| 462,202 * | 9/2 | 4d24f | 29% 4p54d4 (1I)2H | 18% 4d24f (3F)4I | 16% 4d24f (1G)2H | |
| 462,353 * | 1/2 | 4d25p | 17% 4d24f (3F)2S | 14% 4d25p (3P)4P | 11% 4d24f (3F)4P | |
| 462,396 * | 5/2 | 4p54d4 | 16% 4p54d4 (5D)6P | 15% 4p54d4 (3D)4P | 10% 4p54d4 (5D)4P | |
| 462,523 * | 7/2 | 4p54d4 | 20% 4p54d4 (3F2)4F | 12% 4p54d4 (3F1)4F | 7% 4p54d4 (3D)4F | |
| 462,635 * | 3/2 | 4p54d4 | 18% 4p54d4 (5D)6F | 7% 4p54d4 (3P2)4S | 7% 4d24f (3F)4F | |
| 463,146 * | 9/2 | 4p54d4 | 31% 4d24f (3F)4F | 20% 4p54d4 (3F2)4F | 13% 4p54d4 (3F1)4F | |
| 463,748 * | 13/2 | 4d24f | 53% 4d24f (3F)4I | 26% 4d24f (3F)4H | 16% 4p54d4 (3H)4I | |
| 464,491 * | 15/2 | 4p54d4 | 58% 4p54d4 (3H)4I | 40% 4d24f (3F)4I | 1% 4p54d4 (1I)2K | |
| 464,230 | −294 | 7/2 | 4d25p | 21% 4d25p (1D)2F | 16% 4d24f (3F)4D | 8% 4p54d4 (3P2)4D |
| 464,852 * | 11/2 | 4p54d4 | 21% 4p54d4 (1I)2H | 18% 4d24f (1D)2H | 16% 4d24f (1G)2H | |
| 465,027 * | 1/2 | 4d24f | 41% 4d24f (3F)4D | 13% 4p54d4 (5D)6F | 10% 4d24f (3F)2S | |
| 465,143 * | 3/2 | 4p54d4 | 19% 4d24f (3F)4D | 9% 4p54d4 (1F)2D | 7% 4d24f (1D)2D | |
| 465,394 | −335 | 7/2 | 4d25p | 28% 4d25p (3P)4D | 17% 4d25p (1D)2F | 11% 4p54d4 (3P2)4D |
| 465,872 * | 5/2 | 4d25p | 24% 4d25p (3P)4P | 17% 4d25p (1D)2D | 8% 4d25p (3P)2D | |
| 465,990 | 62 | 9/2 | 4d25p | 68% 4d25p (1G)2H | 28% 4d25p (1G)2G | 1% 4d25p (3F)4F |
| 466,458 | 26 | 5/2 | 4d25p | 19% 4d25p (1D)2D | 16% 4d25p (3P)4P | 7% 4p54d4 (3F2)4F |
| 467,537 * | 7/2 | 4p54d4 | 11% 4d24f (3F)2G | 10% 4p54d4 (3H)4H | 9% 4p54d4 (3G)4G | |
| 467,914 * | 3/2 | 4p54d4 | 15% 4d24f (3F)4D | 10% 4d25p (3P)2D | 6% 4d24f (3F)4P | |
| 467,929 * | 1/2 | 4p54d4 | 26% 4p54d4 (5D)6F | 17% 4p54d4 (3F2)4D | 14% 4d24f (3F)4D | |
| 468,817 | 138 | 3/2 | 4d25p | 46% 4d25p (3P)2D | 15% 4d25p (3P)2P | 11% 4d25p (3F)2D |
| 468,895 * | 11/2 | 4p54d4 | 34% 4p54d4 (3G)4G | 24% 4p54d4 (3F2)4G | 13% 4d24f (3F)4H | |
| 469,199 * | 5/2 | 4d24f | 45% 4d24f (3F)4D | 6% 4p54d4 (3P1)4P | 6% 4p54d4 (5D)6F | |
| 469,249 * | 11/2 | 4d24f | 23% 4d24f (3F)4H | 21% 4d24f (3F)4I | 10% 4p54d4 (3H)4H | |
| 469,387 * | 3/2 | 4p54d4 | 13% 4d24f (3P)4D | 10% 4p54d4 (3F2)4F | 6% 4d24f (3F)4D | |
| 469,401 * | 7/2 | 4p54d4 | 19% 4d24f (3P)4D | 14% 4p54d4 (5D)6P | 13% 4p54d4 (3P2)4D | |
| 470,136 * | 9/2 | 4p54d4 | 21% 4p54d4 (3H)4H | 18% 4p54d4 (3G)4G | 15% 4d24f (3F)4H | |
| 470,867 * | 7/2 | 4d24f | 14% 4d24f (3P)4D | 14% 4d24f (3F)2F | 13% 4p54d4 (3H)4H | |
| 471,042 * | 5/2 | 4p54d4 | 20% 4d24f (3P)4D | 11% 4d24f (1D)2D | 9% 4p54d4 (3D)4D | |
| 471,491 * | 1/2 | 4d25p | 46% 4d25p (3P)2P | 17% 4d24f (3F)2P | 8% 4d24f (1D)2P | |
| 471,667 | 31 | 11/2 | 4d25p | 92% 4d25p (1G)2H | 2% 4p54d4 (3F2)4G | 1% 4d25p (3F)4G |
| 471,960 * | 5/2 | 4d25p | 25% 4d25p (3P)2D | 13% 4d25p (3F)2D | 11% 4d25p (3P)4P | |
| 472,224 * | 3/2 | 4d24f | 23% 4d24f (3F)2P | 21% 4d24f (1D)2P | 6% 4d24f (3F)4D | |
| 472,431 * | 5/2 | 4p54d4 | 19% 4d25p (3P)2D | 12% 4d24f (1D)2D | 8% 4p54d4 (1F)2D | |
| 472,982 * | 9/2 | 4p54d4 | 15% 4p54d4 (3F2)4G | 12% 4p54d4 (3G)4G | 12% 4d24f (3F)2G | |
| 473,124 * | 3/2 | 4p54d4 | 16% 4p54d4 (1S2)2P | 14% 4d24f (1D)2P | 11% 4p54d4 (1F)2D | |
| 473,235 * | 13/2 | 4d24f | 33% 4d24f (3F)4H | 28% 4d24f (3F)4I | 26% 4p54d4 (3H)4H | |
| 474,478 * | 11/2 | 4d24f | 36% 4d24f (1G)2I | 28% 4d24f (3F)2I | 6% 4p54d4 (3F2)4G | |
| 474,797 * | 7/2 | 4d25p | 61% 4d25p (1G)2F | 7% 4d25p (1G)2G | 6% 4d25p (1D)2F | |
| 474,983 * | 1/2 | 4d24f | 31% 4d24f (1D)2P | 27% 4d25p (3P)2P | 10% 4p54d4 (1D2)2P | |
| 475,453 | 150 | 7/2 | 4p54d4 | 19% 4p54d4 (3G)4G | 13% 4d25p (1G)2F | 7% 4p54d4 (3D)4F |
| 475,428 * | 9/2 | 4p54d4 | 32% 4d24f (3P)4G | 18% 4p54d4 (3F2)4G | 12% 4p54d4 (1G2)2G | |
| 475,874 * | 3/2 | 4d25p | 23% 4d25p (3P)2P | 10% 4d24f (3P)4D | 8% 4d25p (3P)2D | |
| 476,126 * | 5/2 | 4d24f | 17% 4d24f (3P)4G | 12% 4d24f (3P)2D | 9% 4d24f (3F)4G | |
| 476,268 * | 1/2 | 4p54d4 | 14% 4d25p (3P)2P | 12% 4p54d4 (1D2)2P | 11% 4d24f (3F)2P | |
| 476,658 * | 13/2 | 4d24f | 39% 4d24f (1G)2I | 19% 4d24f (3F)2I | 12% 4p54d4 (1I)2I | |
| 476,896 * | 15/2 | 4d24f | 55% 4d24f (3F)4I | 33% 4p54d4 (3H)4I | 11% 4p54d4 (1I)2K | |
| 477,099 * | 7/2 | 4p54d4 | 13% 4d24f (3P)4G | 11% 4p54d4 (1D2)2F | 11% 4p54d4 (3F2)4G | |
| 477,494 * | 1/2 | 4p54d4 | 28% 4p54d4 (5D)6F | 24% 4d24f (3P)4D | 14% 4p54d4 (3F1)4D | |
| 477,525 * | 5/2 | 4p54d4 | 19% 4p54d4 (3G)4G | 17% 4d24f (1D)2F | 8% 4p54d4 (3H)4G | |
| 477,730 * | 3/2 | 4d25p | 35% 4d25p (3P)2P | 8% 4d24f (3P)4D | 6% 4d24f (1D)2D | |
| 478,297 * | 7/2 | 4d24f | 31% 4d24f (3P)4G | 10% 4p54d4 (1D2)2F | 9% 4d24f (1D)2F | |
| 478,563 * | 11/2 | 4p54d4 | 23% 4p54d4 (3H)4I | 16% 4d24f (3P)4G | 10% 4p54d4 (3F1)4G | |
| 478,577 * | 5/2 | 4d24f | 28% 4d25p (1G)2F | 14% 4d24f (3P)2D | 6% 4d24f (3F)2D | |
| 479,341 * | 9/2 | 4d24f | 21% 4d24f (3F)2H | 21% 4d24f (1D)2H | 10% 4p54d4 (3G)2H | |
| 479,610 | 45 | 5/2 | 4p54d4 | 22% 4d25p (1G)2F | 19% 4d24f (3P)4G | 6% 4p54d4 (1G1)2F |
| 479,719 * | 3/2 | 4p54d4 | 23% 4p54d4 (3P2)2D | 9% 4p54d4 (3P1)2D | 7% 4d24f (3F)2D | |
| 479,718 | −233 | 5/2 | 4d25p | 35% 4d25p (1G )2F | 14% 4d24f (3P)4G | 5% 4p54d4 (3F2)4G |
| 480,710 * | 13/2 | 4p54d4 | 39% 4p54d4 (3H )4I | 18% 4p54d4 (3H)2I | 13% 4p54d4 (3G)4H | |
| 570,288 * | 9/2 | 4p54d4 | 24% 4p54d4 (1G2)2H | 22% 4p54d4 (1G1)2H | 16% 4p54d4 (3F1)2G | |
| 570,992 * | 7/2 | 4p54d4 | 47% 4p54d4 (1D1)2F | 17% 4p54d4 (1G2)2F | 12% 4p54d4 (1D2)2F | |
| 579,505 | 472 | 5/2 | 4d24f | 32% 4d24f (3F)4G | 28% 4p54d4 (3H)4G | 15% 4d24f (3P)4G |
| 583,771 | 278 | 7/2 | 4p54d4 | 32% 4d24f (3F)4G | 31% 4p54d4 (3H)4G | 14% 4d24f (3P)4G |
| 583,819 | 21 | 3/2 | 4p54d4 | 22% 4d24f (3F)4F | 20% 4p54d4 (5D)4F | 18% 4p54d4 (3F1)4F |
| 587,200 | 100 | 9/2 | 4p54d4 | 29% 4p54d4 (3H)4G | 27% 4d24f (3F)4G | 12% 4d24f (3P)4G |
| 587,642 | 141 | 11/2 | 4d24f | 17% 4p54d4 (3H)4G | 15% 4d24f (3F)4G | 12% 4d24f (3F)2H |
| 589,644 | 137 | 5/2 | 4p54d4 | 24% 4p54d4 (5D)4F | 23% 4d24f (3F)4F | 18% 4p54d4 (3G)4F |
| 590,280 | 472 | 3/2 | 4p54d4 | 14% 4d24f (3P)4D | 10% 4p54d4 (3F1)4D | 10% 4p54d4 (3F2)4D |
| 590,209 * | 1/2 | 4p54d4 | 21% 4d24f (3P)4D | 16% 4p54d4 (3F1)4D | 15% 4d24f (3F)4D | |
| 594,111 | 557 | 5/2 | 4p54d4 | 38% 4p54d4 (1D1)2F | 16% 4p54d4 (1G2)2F | 14% 4p54d4 (1D2)2F |
| 594533 * | 5/2 | 4p54d4 | 17% 4p54d4 (3F1)4D | 14% 4d24f (3P)4D | 11% 4d24f (3F)4D | |
| 595,066 | −292 | 3/2 | 4p54d4 | 27% 4p54d4 (3P1)4S | 21% 4d24f (3F)4S | 15% 4p54d4 (3P2)4S |
| 596,876 | 171 | 7/2 | 4p54d4 | 25% 4p54d4 (5D)4F | 21% 4d24f (3F)4F | 19% 4p54d4 (3G)4F |
| 596,885 | −16 | 11/2 | 4d24f | 22% 4d24f (3F)2I | 20% 4d24f (1G)2I | 15% 4p54d4 (3H)4G |
| 598,929 | −85 | 7/2 | 4p54d4 | 20% 4p54d4 (3F1)4D | 11% 4d24f (3P)4D | 10% 4d24f (3F)4D |
| 599,446 | 190 | 9/2 | 4p54d4 | 18% 4p54d4 (1I)2H | 15% 4d24f (3F)2H | 13% 4d24f (1D)2H |
| 600,561 | −15 | 13/2 | 4d24f | 36% 4d24f (3F)2I | 29% 4d24f (1G)2I | 21% 4p54d4 (1I)2I |
| 601,905 * | 3/2 | 4p54d4 | 30% 4p54d4 (1S1)2P | 26% 4p54d4 (1D1)2P | 15% 4p54d4 (1S2)2P | |
| 603,570 | 205 | 9/2 | 4p54d4 | 22% 4p54d4 (5D)4F | 17% 4p54d4 (3G)4F | 15% 4d24f (3F)4F |
| 605,674 * | 5/2 | 4p54d4 | 11% 4d24f (1D)2F | 10% 4p54d4 (1G1)2F | 8% 4p54d4 (3F2)2D | |
| 606,963 | −39 | 3/2 | 4p54d4 | 22% 4d24f (1D)2D | 22% 4p54d4 (1F)2D | 6% 4p54d4 (3F2)2D |
| 609,152 | 153 | 7/2 | 4p54d4 | 14% 4p54d4 (3G)2G | 13% 4p54d4 (3F2)2G | 11% 4d24f (3F)2G |
| 612,491 | −463 | 3/2 | 4p54d4 | 21% 4p54d4 (5D)4D | 8% 4p54d4 (3F2)4D | 7% 4p54d4 (5D)4P |
| 612,769 | −650 | 5/2 | 4p54d4 | 17% 4p54d4 (5D)4D | 14% 4p54d4 (5D)4P | 7% 4p54d4 (3F2)4D |
| 613,700 * | 1/2 | 4p54d4 | 21% 4p54d4 (3P2)2P | 19% 4p54d4 (1D2)2P | 8% 4d24f (3F)2P | |
| 615,308 | −172 | 11/2 | 4p54d4 | 21% 4p54d4 (3H)2H | 14% 4d24f (3F)2H | 12% 4p54d4 (1I)2H |
| 615,385 | −297 | 1/2 | 4p54d4 | 40% 4p54d4 (5D)4D | 10% 4p54d4 (3F2)4D | 9% 4p54d4 (3P2)2S |
| 615,884 | −639 | 7/2 | 4p54d4 | 19% 4p54d4 (1G2)2G | 18% 4p54d4 (3F1)2G | 13% 4d24f (1G)2G |
| 616,475 | −614 | 9/2 | 4p54d4 | 15% 4p54d4 (3F2)2G | 14% 4p54d4 (3G)2G | 13% 4p54d4 (1G1)2G |
| 618,075 | 152 | 7/2 | 4p54d4 | 14% 4d24f (3P)2F | 12% 4d24f (1D)2F | 11% 4p54d4 (1G1)2F |
| 618,058 | −125 | 5/2 | 4p54d4 | 13% 4p54d4 (3D)2F | 12% 4p54d4 (1D1)2F | 11% 4p54d4 (1F)2D |
| 618,894 * | 1/2 | 4p54d4 | 20% 4p54d4 (1S1)2P | 15% 4p54d4 (1D1)2P | 12% 4p54d4 (3P2)2S | |
| 620,387 * | 3/2 | 4p54d4 | 20% 4p54d4 (5D)4D | 11% 4p54d4 (3D)2P | 6% 4d24f (3F)2P | |
| 621,061 | 107 | 9/2 | 4p54d4 | 17% 4p54d4 (1G2)2G | 17% 4p54d4 (3H)2H | 11% 4p54d4 (3H)2G |
| 622,698 * | 1/2 | 4p54d4 | 15% 4p54d4 (1S1)2P | 14% 4p54d4 (1D1)2P | 10% 4p54d4 (3D)2P | |
| 625,187 * | 3/2 | 4p54d4 | 12% 4p54d4 (3D)2P | 10% 4p54d4 (5D)4P | 8% 4p54d4 (5D)4D | |
| 626,693 | 543 | 5/2 | 4p54d4 | 10% 4p54d4 (1D1)2F | 10% 4p54d4 (3D)2F | 9% 4p54d4 (3F2)2F |
| 628,302 | 215 | 5/2 | 4p54d4 | 27% 4p54d4 (5D)4D | 10% 4p54d4 (3F2)4D | 8% 4p54d4 (3F2)2D |
| 629,173 | 363 | 7/2 | 4p54d4 | 56% 4p54d4 (5D)4D | 15% 4p54d4 (3F2)4D | 6% 4d24f (3P)4D |
| 630,316 | −277 | 3/2 | 4p54d4 | 26% 4p54d4 (5D)4P | 11% 4p54d4 (3D)4P | 7% 4d24f (3F)4P |
| 632,069 | −311 | 9/2 | 4p54d4 | 29% 4p54d4 (3H)2H | 12% 4p54d4 (3F1)2G | 10% 4p54d4 (3G)2G |
| 632,322 | −117 | 5/2 | 4p54d4 | 27% 4p54d4 (5D)4P | 14% 4p54d4 (3D)4P | 8% 4d24f (3F)4P |
| 634,657 | 4 | 7/2 | 4p54d4 | 24% 4p54d4 (3F2)2F | 19% 4p54d4 (3D)2F | 12% 4p54d4 (1G2)2F |
| 635,225 * | 1/2 | 4p54d4 | 24% 4p54d4 (3P1)2P | 17% 4p54d4 (3P2)2S | 14% 4p54d4 (1S2)2P | |
| 637,178 | 286 | 1/2 | 4p54d4 | 20% 4p54d4 (5D)4P | 17% 4p54d4 (3P2)2S | 9% 4p54d4 (3P1)2P |
| 638,134 | − 70 | 5/2 | 4p54d4 | 20% 4p54d4 (3F2)2F | 14% 4p54d4 (3F1)2F | 13% 4d24f (3P)2F |
| 638,784 | 81 | 3/2 | 4p54d4 | 18% 4p54d4 (3P2)2P | 12% 4p54d4 (1D2)2P | 11% 4p54d4 (3F2)2D |
| 639,262 | 308 | 11/2 | 4p54d4 | 36% 4p54d4 (3H)2H | 32% 4p54d4 (1I)2H | 12% 4d24f (1G)2H |
| 641,234 | − 78 | 7/2 | 4p54d4 | 16% 4p54d4 (3F1)2F | 16% 4p54d4 (1G2)2F | 13% 4p54d4 (3G)2F |
| 644,980 | −248 | 9/2 | 4p54d4 | 33% 4p54d4 (3H)2G | 17% 4p54d4 (3G)2G | 14% 4p54d4 (3F2)2G |
| 647,197 | −45 | 7/2 | 4p54d4 | 35% 4p54d4 (3H)2G | 15% 4p54d4 (3G)2G | 11% 4p54d4 (3F2)2G |
| 649,186 | 144 | 3/2 | 4p54d4 | 20% 4p54d4 (3P1)2P | 14% 4p54d4 (1D2)2P | 12% 4p54d4 (3P2)2P |
| 651,880 | 259 | 5/2 | 4p54d4 | 19% 4p54d4 (3P2)2D | 12% 4p54d4 (3F1)2D | 11% 4p54d4 (1D1)2D |
| 657,606 | 122 | 5/2 | 4p54d4 | 38% 4p54d4 (3G)2F | 11% 4p54d4 (3F1)2F | 10% 4p54d4 (1G1)2F |
| 659,798 | −619 | 7/2 | 4p54d4 | 24% 4p54d4 (1G1)2F | 20% 4p54d4 (3G)2F | 17% 4p54d4 (3F1)2F |
| 664,136 * | 1/2 | 4p54d4 | 37% 4p54d4 (1S1)2P | 16% 4p54d4 (3P1)2P | 13% 4p54d4 (1S2)2P | |
| 663,396 | −939 | 3/2 | 4p54d4 | 30% 4p54d4 (3P1)2P | 22% 4p54d4 (1D1)2P | 8% 4d24f (1G)2P |
| 676,533 | 735 | 5/2 | 4p54d4 | 36% 4p54d4 (3F1)2D | 13% 4p54d4 (3D)2D | 8% 4p54d4 (1F)2D |
| 680,196 | 360 | 3/2 | 4p54d4 | 42% 4p54d4 (3F1)2D | 13% 4p54d4 (3D)2D | 11% 4p54d4 (1D1)2D |
a The star * indicates a calculated value for the level; b The difference between the observed and the calculated energies; c Configuration attribution is arbitrary in a few cases (see text); d For the eigenvector composition, up to three components with the largest percentages in the LS-coupling scheme are listed. The number following the terms of the 4d4 configuration displays Nielson and Koster sequential indices [20].

Table A12.
Energy parameters (in cm−1) of the ground configuration in Ag VII, Ag VIII and Ag IX calculated by orthogonal parameter technique in comparison with the Dirac-Fock (DF) parameters.
| Name | AgVII (4d5) | AgVIII (4d4) | AgIX (4d3) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FIT | Error a | DF | FIT/DF | FIT | Error a | DF | FIT/DF | FIT | Error a | DF | FIT/DF | |
| Eav | 51914 | 3 | 60,863 | 0.853 | 37,710 | 6 | 42,776 | 0.882 | 27,795 | 8 | 31,440 | 0.884 |
| O2 | 8652 | 2 | 10,175 | 0.850 | 8978 | 6 | 10,515 | 0.854 | 9295 | 8 | 10,834 | 0.858 |
| O2’ | 5512 | 3 | 6923 | 0.796 | 5701 | 7 | 7128 | 0.800 | 5892 | 8 | 7323 | 0.805 |
| Ea’ | 213 | 2 | 223 | 3 | 251 | 6 | ||||||
| Eb’ | 38 | 2 | 45 | 6 | 50 | f | ||||||
| ζ | 2493 | 2 | 2428 | 1.027 | 2655 | 5 | 2603 | 1.020 | 2830 | 7 | 2782 | 1.017 |
| T1 | −4.62 | 0.08 | −4.62 | 0.19 | −4.85 | 0.36 | ||||||
| T2 | 0.40 | f | 0.50 | f | ||||||||
| Ac | 7.80 | 1.5 | 13.21 | 0.6 | 7.46 | f | 12.43 | 0.6 | 7.08 | f | 11.81 | 0.6 |
| A3 | 1.93 | r | 3.27 | 0.6 | 1.90 | f | 3.18 | 0.6 | 1.87 | f | 3.13 | 0.6 |
| A4 | 3.28 | r | 5.56 | 0.6 | 3.31 | f | 5.52 | 0.6 | 3.32 | f | 5.53 | 0.6 |
| A5 | 3.16 | r | 5.36 | 0.6 | 3.31 | f | 5.51 | 0.6 | 3.42 | f | 5.71 | 0.6 |
| A6 | 0.96 | r | 1.63 | 0.6 | 0.47 | f | 0.78 | 0.6 | 0.00 | f | −0.00 | 1.0 |
| A1 | −0.10 | r | −0.16 | 0.6 | −0.05 | f | −0.08 | 0.6 | 0 | f | 0 | 0.6 |
| A2 | −0.32 | r | −0.55 | 0.6 | −0.43 | f | −0.72 | 0.6 | −0.53 | f | −0.88 | 0.6 |
| A0 | −0.49 | r | 0.29 | 0.6 | −0.28 | f | −0.46 | 0.6 | −0.25 | f | −0.42 | 0.6 |
| σ | 14 | 26 | 27 | |||||||||
a r—parameters are fixed at DF ratio to Ac, f- fixed parameter.

Table A13.
Energy parameters (in cm−1) of the 4d45p configuration in Ag VII and 4d35p configuration in Ag VIII calculated by orthogonal parameter technique in comparison with the DF parameters.
| Name | Ag VII | Ag VIII | ||||||
|---|---|---|---|---|---|---|---|---|
| FIT | Error a | DF | FIT/DF | FIT | Error b | DF | FIT/DF | |
| Eav | 37,3862 | 2 | 384,168 | 0.973 | 41,1052 | 5 | 417,702 | 0.984 |
| O2dd | 8849 | 2 | 10,418 | 0.849 | 9147 | 8 | 10,738 | 0.852 |
| O2’dd | 5581 | 4 | 7070 | 0.789 | 5747 | 12 | 7265 | 0.791 |
| Ea’ | 216 | 1 | 221 | 6 | ||||
| Eb’ | 36 | 3 | 31 | 6 | ||||
| T1 | −4.86 | 0.09 | −5.08 | 0 | ||||
| T2 | 0.48 | 0.09 | 0.50 | f | ||||
| ζ(4d) | 2631 | 4 | 2572 | 1.023 | 2809 | 8 | 2747 | 1.022 |
| Ac | 8.01 | 1.8 | 12.68 | 0.63 | 11.76 | f | 11.76 | 1.0 |
| A3 | 1.97 | r1 | 3.12 | 0.63 | 3.44 | f | 3.44 | 1.0 |
| A4 | 3.25 | r1 | 5.15 | 0.63 | 5.40 | f | 5.40 | 1.0 |
| A5 | 3.46 | r1 | 5.48 | 0.63 | 5.68 | f | 5.68 | 1.0 |
| A6 | 0.64 | r1 | 1.02 | 0.62 | 0.18 | f | 0.18 | 1.0 |
| A1 | −0.17 | r1 | −0.28 | 0.63 | −0.23 | f | −0.23 | 1.0 |
| A2 | −0.63 | r1 | −1.00 | 0.63 | −0.35 | f | −0.35 | 1.0 |
| A0 | −0.69 | r1 | −1.10 | 0.63 | −0.18 | f | −0.19 | 1.0 |
| C1dp | 3702 | 4 | 4270 | 0.867 | 4012 | 11 | 4621 | 0.868 |
| C2dp | 2605 | 3 | 2998 | 0.869 | 2755 | 10 | 3176 | 0.867 |
| C3dp | 1258 | 4 | 1411 | 0.891 | 1321 | 10 | 1471 | 0.898 |
| S1dp | 67 | 3 | 63 | 8 | ||||
| S2dp | −118 | 3 | −129 | 8 | ||||
| ζ(5p) | 6317 | 5 | 5975 | 1.057 | 7268 | 14 | 6933 | 1.048 |
| Sd.Lp | −27.49 | 1.5 | −34.81 | 0.79 | −27.2 | f | −34.04 | 0.8 |
| Sp.Ld | −2.77 | r2 | −3.52 | 0.79 | −2.7 | f | −3.46 | 0.8 |
| Zp2ppa | −19.98 | r2 | −25.29 | 0.79 | −20.0 | f | −25.01 | 0.8 |
| Zp2dda | 13.74 | r2 | 17.42 | 0.79 | 13.5 | f | 16.93 | 0.8 |
| Zp1ppa | 41.56 | r2 | 52.62 | 0.79 | 41.2 | f | 51.56 | 0.8 |
| Zp1dda | −2.94 | r2 | −3.71 | 0.79 | −2.3 | f | −2.99 | 0.8 |
| Zp3ppa | 10.85 | r2 | 13.74 | 0.79 | 11.0 | f | 13.81 | 0.8 |
| Zp3dda | −2.22 | r2 | −2.82 | 0.79 | −2.3 | f | −2.95 | 0.8 |
| SS(dp)02 | −1.53 | r2 | −1.95 | 0.79 | −1.8 | f | −2.32 | 0.8 |
| SS(dp)20 | −0.52 | r2 | −0.66 | 0.79 | −0.3 | f | −0.40 | 0.8 |
| t16’ | −23.8 | 2.8 | −23.8 | f | ||||
| t17’ | 8.0 | 2.8 | 8.0 | f | ||||
| t18’ | −10.4 | 2.9 | −10.4 | f | ||||
| t19’ | −8.9 | 2.1 | −8.9 | f | ||||
| t20’ | −42.2 | 3.6 | −42.2 | f | ||||
| t21’ | −3.4 | 2.3 | −3.4 | f | ||||
| t22’ | −14.4 | 4.6 | −14.4 | f | ||||
| t23’ | −4.2 | 3.9 | −4.2 | f | ||||
| t24’ | −7.5 | 2.9 | −7.5 | f | ||||
| t25’ | 3.6 | 2.5 | 3.6 | f | ||||
| t26’ | −33.5 | 3.0 | −33.5 | f | ||||
| t27’ | 18.5 | 2.4 | 18.5 | f | ||||
| t28’ | 35.6 | 3.5 | 35.6 | f | ||||
| t29’ | −12.1 | 2.5 | −12.1 | f | ||||
| t30’ | −45.5 | 2.7 | −45.5 | f | ||||
| t31’ | −4.4 | 3.0 | −4.4 | f | ||||
| t32’ | −0.3 | 2.2 | −0.3 | f | ||||
| t33’ | 11.9 | 2.8 | 11.9 | f | ||||
| t34’ | −30.2 | 3.2 | −30.2 | f | ||||
| t35’ | −32.3 | 3.4 | −32.3 | f | ||||
| σ | 19 | 47 | ||||||
a r1—parameters are fixed at DF ratio to Ac, r1 parameters are fixed at DF ratio to Sd.Lp; b f—parameter is fixed on predetermined value.

Table A14.
Fitted (FIT) with their uncertainties (Unc.) and Hartree - Fock (HF) energy parameters in cm−1 of the odd 4d35p, 4d34f, and 4p54d4 configurations in Ag VIII and 4d25p, 4d24f and 4p54d3 configurations in Ag IX calculated with the Cowan code.
| Name a | Ag VIII | Ag IX | ||||||
|---|---|---|---|---|---|---|---|---|
| HF | FIT | Unc. b | FIT/HF c | HF | FIT | Unc. b | FIT/HF c | |
| Eav(5p) | 417,702 | 412,728 | 26 | −4974 | 459,300 | 455,716 | 88 | −3584 |
| F2(4d,4d) | 95,978 | 80,972 | 237 | 0.844 | 98,603 | 83,046 | 1159 | 0.842 |
| F4(4d,4d) | 64,366 | 56,750 | 484 | 0.882 | 66,314 | 54,364 | 3227 | 0.820 |
| α | 49 | 5 | 71 | 26 | ||||
| β | −627 | −99 | −600 | f | ||||
| T1 | −4 | −1 | ||||||
| ζ(4d) | 2702 | 2812 | 36 | 1.041 | 2870 | 2919 | 65 | 1.017 |
| ζ (5p) | 6510 | 7299 | 66 | 1.121 | 7426 | 8338 | 165 | 1.123 |
| F1(4d,5p) | −2072 | −265 | −2000 | f | ||||
| F2(4d,5p) | 39,205 | 32,005 | 275 | 0.816 | 41,777 | 35,950 | 898 | 0.861 |
| G1(4d,5p) | 12,359 | 10,505 | 137 | 0.850 d | 12,926 | 11,649 | 342 | 0.901 d |
| G3(4d,5p) | 12,110 | 10,293 | 134 | 0.850 d | 12,836 | 11,568 | 340 | 0.901 d |
| Eav(4f) | 508,665 | 496,302 | 569 | −12,363 | 522,389 | 507,990 | 380 | −14,399 |
| F2(4d,4d) | 95,126 | 80,381 | f | 0.845 | 97,640 | 80,359 | f | 0.823 |
| F4(4d,4d) | 63,728 | 55,443 | f | 0.87 | 65,594 | 54,443 | f | 0.83 |
| α | 48 | f | 62 | f | ||||
| β | −600 | f | ||||||
| T1 | −4 | f | ||||||
| ζ(4d) | 2652 | 2732 | f | 1.03 | 2808 | 2910 | f | 1.036 |
| ζ(4f) | 95 | 95 | f | 1.0 | 124 | 124 | f | 1.0 |
| F2(4d,4f) | 70,569 | 64,433 | 1452 | 0.913 d | 78,433 | 71,374 | f | 0.91 |
| F4(4d,4f) | 44,636 | 40,755 | 919 | 0.913 d | 50,344 | 45,814 | f | 0.91 |
| G1(4d,4f) | 83,516 | 72,648 | 572 | 0.87 | 93,840 | 85,394 | f | 0.91 |
| G3(4d,4f) | 51,477 | 47,876 | 377 | 0.930 d | 58,481 | 53,218 | f | 0.91 |
| G5(4d,4f) | 36,169 | 33,640 | 265 | 0.930 d | 41276 | 37,562 | f | 0.91 |
| Eav(pd) | 538,566 | 526,473 | 194 | −12,093 | 529,361 | 52,3487 | 344 | −5874 |
| F2(4d,4d) | 94,305 | 79,014 | 393 | 0.838 | 97,018 | 85,702 | 496 | 0.883 |
| F4(4d,4d) | 63,119 | 51,318 | 598 | 0.813 | 65,133 | 50,607 | 1080 | 0.777 |
| α | 48 | f | 60 | f | ||||
| β | −600 | f | −600 | f | ||||
| T1 | −4 | f | −4 | f | ||||
| ζ(4p) | 29,355 | 29,355 | f | 1 | 30,239 | 30,576 | 415 | 1.011 |
| ζ(4d) | 2602 | 2849 | f | 1.095 | 2767 | 2782 | 116 | 1.005 |
| F2(4p,4d) | 100,314 | 83,916 | 1065 | 0.837 | 102,723 | 79,518 | 973 | 0.774 |
| G1(4p,4d) | 127,225 | 101,162 | 192 | 0.795 d | 130,315 | 101,056 | 342 | 0.775 d |
| G3(4p,4d) | 79,353 | 63097 | 120 | 0.795 d | 81,523 | 63,219 | 214 | 0.775 d |
| σ | 213 | 327 | ||||||
a Eav(5p), Eav(4f) and Eav(pd) stand for Eav(4dk−15p), Eav(4dk−14f) and Eav(4p54dk+1) for Ag VIII and Ag IX where k = 4 and 3, respectively; b f- parameter is fixed on predetermined value; c For Eav the FIT-HF difference is listed; d Adjacent pairs of parameters are linked at their HF ratios.
References
- Benschop, H.; Joshi, Y.N.; Van Kleef, Th.A.M. The spectrum of doubly ionized silver: Ag III. Can. J. Phys. 1975, 53, 498–503. [Google Scholar] [CrossRef]
- Van Kleef, Th.A.M.; Joshi, Y.N. Analysis of 4d8–d75p transitions in trebly ionized silver: Ag IV. Can. J. Phys. 1981, 59, 1930–1939. [Google Scholar] [CrossRef]
- Van Kleef, Th.A.M.; Raassen, A.J.J.; Joshi, Y.N. Analysis of the 4d7–4d65p transitions in the fifth spectrum of silver (Ag V). Phys. Scr. 1987, 36, 140–148. [Google Scholar] [CrossRef]
- Joshi, Y.N.; Raassen, A.J.J.; Van Kleef, Th.A.M.; Van der Valk, A.A. The sixth spectrum of silver: Ag VI, and a study of the parameter values in 4d-spectra. Phys. Scr. 1988, 38, 677–698. [Google Scholar] [CrossRef]
- Sugar, J.; Kaufman, V.; Rowan, W.L. Rb-like spectra: Pd X to Nd XXIV. J. Opt. Soc. Am. B 1992, 9, 1959–1961. [Google Scholar] [CrossRef]
- Ryabtsev, A.N.; Kononov, E.Y.; Churilov, S.S. Spectra of rubidium-like Pd X-Sn XIV ions. Opt. Spectr. 2008, 105, 844–850. [Google Scholar] [CrossRef]
- Ryabtsev, A.N.; Kononov, E.Y. Resonance transitions in Rh VIII, Pd IX, Ag X and Cd XI spectra. Phys. Scr. 2011, 84, 015301. [Google Scholar] [CrossRef]
- Ryabtsev, A.N.; Kononov, E.Ya. Eighth spectrum of palladium: Pd VIII. Phys. Scr. 2016, 91, 025402. [Google Scholar] [CrossRef]
- Churilov, S.S.; Ryabtsev, A.N. Analysis of the spectra of In XII-XIV and Sn XIII-XV in the far-VUV region. Opt. Spectr. 2006, 101, 169–178. [Google Scholar] [CrossRef]
- Churilov, S.S.; Ryabtsev, A.N. Analyses of the Sn IX-Sn XII spectra in the EUV region. Phys. Scr. 2006, 73, 614–619. [Google Scholar] [CrossRef]
- Svensson, L.A.; Ekberg, J.O. The titanium vacuum-spark spectrum from 50 to 425 Å. Ark. Fys. 1969, 40, 145–164. [Google Scholar]
- Azarov, V.I. Formal approach to the solution of the complex-spectra identification problem. 2. Implementaton. Phys. Scr. 1993, 48, 656–667. [Google Scholar] [CrossRef]
- Parpia, F.A.; Froese Fischer, C.; Grant, I.P. GRASP92: A package for large-scale relativistic atomic structure calculations. Comput. Phys. Commun. 1996, 94, 249–271. [Google Scholar] [CrossRef]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Hansen, J.E.; Uylings, P.H.M.; Raassen, A.J.J. Parametric fitting with orthogonal operators. Phys. Scr. 1988, 37, 664–672. [Google Scholar] [CrossRef]
- Hansen, J.E.; Raassen, A.J.J.; Uylings, P.H.M.; Lister, G.M.S. Parametric fitting to dn configurations using ortogonal operators. Nucl. Instrum. Methods Phys. Res. B 1988, 31, 134–138. [Google Scholar] [CrossRef]
- Uylings, P.H.M.; Raassen, A.J.J.; Wyart, J.-F. Calculations of 5dN−16s systems using orthogonal operators: do orthogonal operators survive configuration interaction? J. Phys. B 1993, 26, 4683–4693. [Google Scholar] [CrossRef]
- Uylings, P.H.M.; Raassen, A.J.J. High precision calculation of odd iron-group systems with orthogonal operators. Phys. Scr. 1996, 54, 505–513. [Google Scholar] [CrossRef]
- Kramida, A.E. The program LOPT for least-squares optimization of energy levels. Comput. Phys. Commun. 2010, 182, 419–434. [Google Scholar] [CrossRef]
- Nielson, C.W.; Koster, G.F. Spectroscopic Coefficients for the pn, dn, and fn Configurations; The M.I.T. Press: Cambridge, MA, USA, 1963. [Google Scholar]
- Ryabtsev, A.N.; Kononov, E.Y. Resonance transitions in the Pd VII spectrum. Phys. Scr. 2012, 85, 025301. [Google Scholar] [CrossRef]
- Bauche, J.; Bauche-Arnoult, C.; Luc-Koenig, E.; Wyart, J.-F.; Klapisch, M. Emissive zones of complex atomic configurations in highly ionized atoms. Phys. Rev. A 1983, 28, 829–835. [Google Scholar] [CrossRef]
- Windberger, A.; Torretti, F.; Borschevsky, A.; Ryabtsev, A.; Dobrodey, S.; Bekker, H.; Eliav, E.; Kaldor, U.; Ubachs, W.; Hoekstra, R.; et al. Analysis of the fine structure of Sn11+...14+ ions by optical spectroscopy in an electron beam ion trap. Phys. Rev. A 2016, 94, 012506. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).