CO Dissociation Induced by 1 keV/u Ar²⁺ Ion

Abstract

CO is one of the important molecules in dense molecular clouds, and its dissociation induced by cosmic ray heavy ions is a fundamental process for molecular breaking up and rearrangement in astronomical networks. Extensive laboratory simulations are required to understand molecular evolution in astrophysical contexts. Here, we investigate the CO dissociation induced by 1 keV/u ${\mathrm{Ar}}^{2+}$ using cold target recoil ion momentum spectroscopy. Kinetic energy release for double electron capture ${\mathrm{Ar}}^{2+}+\mathrm{CO}\to {\mathrm{Ar}}^0+{\mathrm{C}}^{+}+{\mathrm{O}}^{+}$ and transfer ionization ${\mathrm{Ar}}^{2+}+\mathrm{CO}\to {\mathrm{Ar}}^{+}+{\mathrm{C}}^{+}+{\mathrm{O}}^{+}+{\mathrm{e}}^{-}$ was obtained. The dissociation mechanisms are attributed to different KER distributions. The autoionization process is identified below the ${\mathrm{CO}}^{2+}$ double ionization threshold.

1. Introduction

The structure of the excited states unveils the characteristics of ionization and radiation processes, with applications extending from interstellar space to investigations of the physical properties and evolution of giant molecular clouds [1]. Due to the large mass of the nucleus, its motion is several orders of magnitude slower than the electron in the self-consistent field. Therefore, according to the Born–Oppenheimer approximation, electron removal in the molecule induces the vertical transition in the potential energy curves (PECs) from the molecule to its multi-charged ion. Subsequently, the PECs determine the behavior of the molecular ion such as dissociation.

In the molecular dissociative ionization, the dissociation of doubly charged molecule ions, such as CO²⁺, ${\mathrm{N}}_2^{2+}$, ${\mathrm{O}}_2^{2+}$ [2,3,4,5], attracts a lot of interest, since the competition [2] between bonding and repulsive force results in a non-Coulombic potential curve [6]. In addition, PECs of diatomic molecules are relatively simple, only involving the internuclear distance, which offers an approach to probe the population of the molecular energy levels and the dissociation mechanism via measuring kinetic energy release (KER). Compared with direct dissociation following one specific PEC, indirect dissociation takes place due to the coupling of the electronic states through the avoided crossing (AC) [7]. The electronic states are altered during the dissociation; therefore, the indirect dissociation draws more attention because of the complexity of the dissociation mechanism.

Predissociation is a typical indirect dissociation observed in ${\mathrm{CO}}^{2+}$ photoionization and electron impact ionization [8,9,10,11]. The low-lying vibrational states are energy-insufficient to cross the potential barrier. However, they are close to or higher than the AC region with repulsive states. The coupling between electronic states enables these levels to dissociate via the resonance [5,7,12]. Lundqvist [11] measured the KER of ${\mathrm{CO}}^{2+}$ dissociation with vibrational level discrimination. All discrete states dissociate into ground ionic states ${\mathrm{C}}^{+}{(}^2\mathrm{P})+{\mathrm{O}}^{+}{(}^4\mathrm{S})$, indicating strong coupling with a ³${\Sigma }^{-}$ repulsive state. AC allows crossing the potential barrier, and the tunneling mechanism of these states becomes significant in molecular dissociation. Several studies [13,14,15,16,17,18,19] have reported the tunneling lifetime of metastable ${\mathrm{CO}}^{2+}$ for different vibrational states.

Below the double ionization threshold, autoionization (AI) [8,20,21,22] is another significant indirect process in CO dissociation. High-lying Rydberg and inner-valence vacancy states generate the highly excited ${\mathrm{CO}}^{+*}$. The potential curves of the states lies below the double ionization threshold, but above the dissociation asymptotic limit of ${\mathrm{C}}^{+}{(}^2\mathrm{P})+{\mathrm{O}}^{+}{(}^4\mathrm{S})$ [22]. They are unstable, and dissociate into ${\mathrm{C}}^{+}{(}^2\mathrm{P})+{\mathrm{O}}^{+}{(}^4\mathrm{S})$ with the ejection of AI electron. Experimental studies of CO AI have been enhanced by the development of coincidence techniques, which have led to the advancement of photoelectron–photoion coincidence spectroscopy [8] and (e,2e) experiments [23]. These techniques allow for the simultaneous observation of AI electron energy and KER. Lablanquie [8] first investigated CO photoionization in the range of 35 to 150 eV using the photoion–photoion coincidence technique. They measured the KER distribution for different photon energy and the absolute cross-section, observing highly excited ${\mathrm{CO}}^{+*}$ autoionizing into ${\mathrm{C}}^{+}+{\mathrm{O}}^{+}$. Osipov [22] reported a kinematically complete experiment of ${\mathrm{CO}}^{+*}$ AI states using cold target recoil ion momentum spectroscopy (COLTRIMS) [24,25,26]. AI states originate from Rydberg or inner valence electronic states, as confirmed by ab initio calculation. The measured angular distribution of AI electrons shows excellent agreement with the theoretical predictions.

The CO AI states have scarcely been investigated through heavy ion collision [27,28]. Unlike photoionization and electron impact ionization, where the vertical excitation energy can be determined or inferred from photo energy or electron energy loss, this information cannot be directly inferred in ion collisions. However, the configuration interaction plays an important role [29,30], especially in slow ion collisions. In this report, we present the dissociation of CO by collision with 1 keV/u ${\mathrm{Ar}}^{2+}$ ion using the COLTRIMS setup. The ${\mathrm{CO}}^{+*}$ AI in KER distribution was identified by distinguishing the scattered ion charge states. We report KER of CO AI by slow heavy ion collision, which contradicts the previous conclusions [28] that no AI occurs in the capture process. The KER distributions of double electron capture (DEC) and transfer ionization (TI) are compared, and dissociation mechanisms are discussed.

2. Experimental Setup

The experiment was conducted on the 320 kV highly charged ion multidisciplinary research platform at the Institute of Modern Physics, Chinese Academy of Science (IMP-CAS) in Lanzhou. An expanded beamline provided a 1 keV/u ${\mathrm{Ar}}^{2+}$ beam using a Dresden electron-beam ion source [31]. The ${\mathrm{Ar}}^{2+}$ beam is selected and compressed by a Wien filter and an einzel lens. Two sets of scanning electrodes guide the ion beam to collide with the orthogonal CO gas target. After charge exchange with ${\mathrm{Ar}}^{2+}$, unstable ${\mathrm{CO}}^{2+}$ dissociates into ${\mathrm{C}}^{+}$ and ${\mathrm{O}}^{+}$. The fragment ions were extracted by a time-of-flight (TOF) setup, as shown in Figure 1. TOF and position of ions are registered by the position-sensitive detector (PSD) at the end of the flight tube. The TOF setup comprises a 107.5 mm extraction region and a 215 mm field-free drift region with the electric field set as 100 V/cm, meeting with the Wiley–McLaren focusing condition [32].

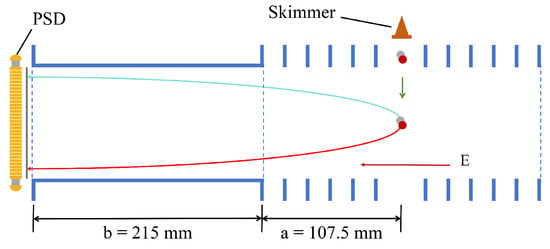
Figure 1. Sketch of COLTRIMS setup. The extraction and drift regions are 107.5 mm and 215 mm in length labeled by ‘a’ and ‘b’, respectively. The arrow labeled by ‘E’ points out the direction of the extraction field.

Charge states changed ${\mathrm{Ar}}^{+}$ and ${\mathrm{Ar}}^0$ scattered ions, which were collected on the PSD to provide the collision starting point, and unreacted ${\mathrm{Ar}}^{2+}$ ions were deflected into a Faraday cup. A high-performance time-to-digital converter recorded the signals from the multichannel plate (MCP) and delay line to deduce the TOF and position. Subsequently, three-dimensional momentum and KER were deduced from TOF and position by the formulas:

$$\begin{array}{cc}\hfill P_x& =m{\displaystyle \frac{x-x_0}{t}},\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill P_y& =m{\displaystyle \frac{y-y_0}{t}},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill P_z& ={\displaystyle \frac{Uq}{a}}(t_0-t),\hfill \end{array}$$

(3)

where $P_x$ and $P_y$ are the momentum perpendicular to the extraction field, and $P_z$ is the momentum along the extraction field. U and a are extraction voltage and extraction field length. $t_0$ is TOF of zero momentum ion. The KER can be obtained by summing all fragment ion i kinetic energy by the following formula:

$$KER=\sum _i{\displaystyle \frac{P_x^2+P_y^2+P_z^2}{2m}}.$$

(4)

3. Results and Discussion

3.1. One-Dimensional TOF Spectrum

Different ion species are separated in the one-dimensional TOF spectrum in Figure 2, according to the charge-to-mass ratio (q/m). The distribution of ${\mathrm{C}}^{+}$ and ${\mathrm{O}}^{+}$ is broadened due to the KER from the dissocaition of ${\mathrm{CO}}^{2+}$ into ${\mathrm{C}}^{+}+{\mathrm{O}}^{+}+\mathrm{KER}$. The flat top of the ${\mathrm{C}}^{+}$ and ${\mathrm{O}}^{+}$ peaks are caused by the incomplete collection of ${\mathrm{CO}}^{2+}$ dissociation events that occur perpendicular to the extraction field for KER values exceeding 12 eV. The peak intensity of ${\mathrm{O}}^{+}$ is lower than that of ${\mathrm{C}}^{+}$ due to the detection efficiency $\epsilon$. The MCP open area ratio is approximately 0.6, and ions fly across three grids from the collision point to the MCP surface with a penetration rate of about 0.9 for each grid. This results in an estimated detection efficiency of approximately 0.44. The detector efficiency can also be calculated from the intensity of the first hit one-dimensional TOF spectrum [33]. Assuming that ${\mathrm{C}}^{+}$ and ${\mathrm{O}}^{+}$ are detected by the MCP with the same efficiency, the intensity of the ${\mathrm{C}}^{+}$ peak, $I_{C^{+}}$, is proportional to $N·\epsilon$ (where N represent all dissociation events), while the intensity of the ${\mathrm{O}}^{+}$ peak, $I_{O^{+}}$, is proportional to the $N·\epsilon (1-\epsilon )$ (where $(1-\epsilon )$ is the probability that the ${\mathrm{C}}^{+}$ ion is not detected, hence the ${\mathrm{O}}^{+}$ ion is registered as first hit).

$${\displaystyle \frac{\epsilon }{\epsilon (1-\epsilon )}}={\displaystyle \frac{I_{C^{+}}}{I_{O^{+}}}}.$$

(5)

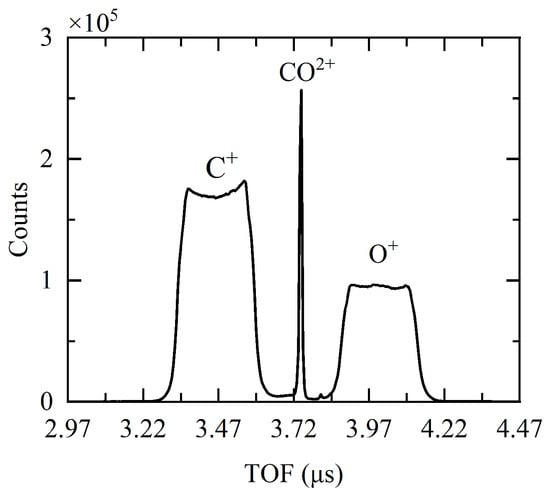
Figure 2. First hit registered one-dimensional TOF mass spectrum for 1 keV/u ${\mathrm{Ar}}^{2+}$ + CO.

The calculated detection efficiency is 0.45, consistent with the setup configuration.

3.2. Two-Dimensional TOF Spectrum

In the two-dimensional TOF correlation spectrum shown in Figure 3, the ${\mathrm{C}}^{+}$ and ${\mathrm{O}}^{+}$ TOF are recorded as the Hit1 and Hit2 signal. Three TOF correlation bands with negative slopes are observed. Two low-intensity bands correspond to the isotopes ¹³C⁺ and ¹⁸O⁺, with relative ratios of about $1.03\%$ and $0.20\%$, respectively, which are in agreement with their natural abundance. In addition to the high-intensity band, two tails with different slopes appear on the lower right side in ¹²C⁺ + ¹⁶O⁺ channel, labeled as ‘a’ and ‘b’. These are the long-lived metastable ${\mathrm{CO}}^{2+}$ dissociating in the extraction and drift region.

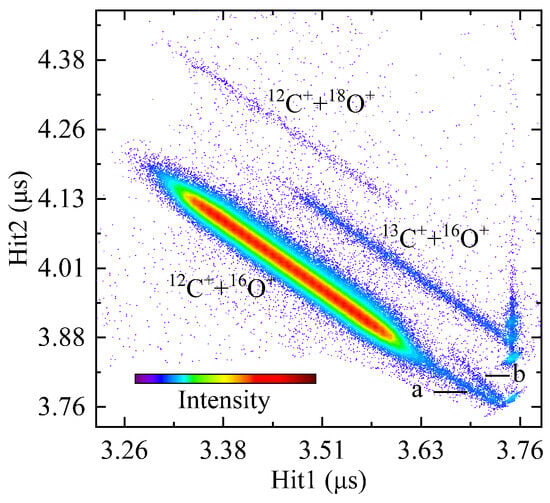
Figure 3. Correlation spectrum for TOF of ${\mathrm{CO}}^{2+}\to {\mathrm{C}}^{+}+{\mathrm{O}}^{+}$. TOF of ions, which firstly and secondly hit the detector, are registered as Hit1 and Hit2, where a and b labeled the metastable states dissociation.

3.3. Potential Curves

In Figure 4a, we present the potential curves of several low-lying states of ${\mathrm{CO}}^{2+}$, as previously detailed by Pandey et al. [2]. Among these, certain electronic states, such as $1^1{\Sigma }^{+}$, $1^1\Pi$, and $1^3\Pi$, exhibit deep potential barriers. These states intersect with the repulsive state $1^1{\Sigma }^{-}$, facilitating dissociation through predissociation. Asymptotic limits A, B, C, and D correspond to ${\mathrm{C}}^{+}{(}^2{\mathrm{P}}_{\mathrm{u}})+{\mathrm{O}}^{+}{(}^4{\mathrm{S}}_{\mathrm{u}})$, ${\mathrm{C}}^{+}{(}^2{\mathrm{P}}_{\mathrm{u}})+{\mathrm{O}}^{+}{(}^2{\mathrm{D}}_{\mathrm{u}})$, ${\mathrm{C}}^{+}{(}^2{\mathrm{P}}_{\mathrm{u}})+{\mathrm{O}}^{+}{(}^2{\mathrm{P}}_{\mathrm{u}})$ and ${\mathrm{C}}^{+}{(}^4{\mathrm{P}}_{\mathrm{g}})+{\mathrm{O}}^{+}{(}^4{\mathrm{S}}_{\mathrm{u}})$, respectively, with associated energies of 35.98, 39.3, 41, and 41.33 eV. Figure 4b provides a schematic diagram of the autoionization states of ${\mathrm{CO}}^{+*}$. These states, which may be either inner-valence or Rydberg states, have been explored by Osipov et al. [22]. At small internuclear distance, the potential of ${\mathrm{CO}}^{+*}$ lies below that of the ${\mathrm{CO}}^{2+}$ ground state. Due to the strong Coulomb repulsion between C⁺ and O⁺, as compared to C⁺ and O*, the potential curves of ${\mathrm{CO}}^{+}$ remain relatively flat, intersecting the steep potential curve of ${\mathrm{CO}}^{2+}$$(X^3\Pi )$ at internuclear distances greater than 25 $\mathring{\mathrm{A}}$ [22].

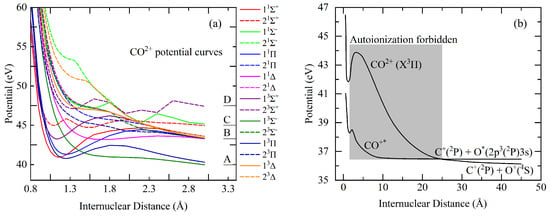
Figure 4. (a) Some low-lying potential curves of ${\mathrm{CO}}^{2+}$ [2]. (b) Schematic diagram of autoionization states of ${\mathrm{CO}}^{+*}$ [22].

3.4. KER

The KER distribution for ${\mathrm{Ar}}^{2+}+\mathrm{CO}\to {\mathrm{Ar}}^0+{\mathrm{C}}^{+}+{\mathrm{O}}^{+}$ channel is presented in Figure 5a. Three distinct peaks appear at 6.3, 8.2, and 9.7 eV. The first peak contains contributions from the $X^1\Pi$, $1^1{\Sigma }^{+}$, and $1^3\Pi$ electronic states. The FC factor [2] for $X^1\Pi$ and $1^1{\Sigma }^{+}$ decreases with an increasing vibrational quantum number; therefore, low-lying vibrational states mainly contribute to the KER. The deep potential well prevents dissociation for low-lying vibrational states of $1^1{\Sigma }^{+}$ and $1^1\Pi$. However, the AC with repulsive $1^3{\Sigma }^{-}$ enables these states to dissociate via predissociation mechanism to ${\mathrm{C}}^{+}{(}^2\mathrm{P})+{\mathrm{O}}^{+}{(}^4\mathrm{S})$ asymptotic limit. The vibrational energy discriminated KER [11] reports the contribution from $X^1\Pi (\nu =1-10)$ and $1^1{\Sigma }^{+}(\nu =0,1)$. For $X^3\Pi$, predissociation and tunneling mechanism contribute to the ${\mathrm{CO}}^{2+}$ dissociation. Since the high-lying vibrational states of $X^3\Pi$ have large FC factor [2], they also contribute to the KER distribution through tunneling. The second peak mainly arises from the high-lying vibrational states of $1^1\Pi$, $1^1{\Sigma }^{+}$, and low-lying vibrational states of $1^3{\Sigma }^{+}$. These states can also predissociate through AC with $1^3{\Sigma }^{-}$. The third peak contribute from $2^1{\Sigma }^{+}$ and repulsive $1^3{\Sigma }^{-}$. Only events with KER below 12 eV are entirely collected. Events from repulsive states contribute to high energy part of the distribution. The unscreening effect [28] of the electronic states leads to higher KER values.

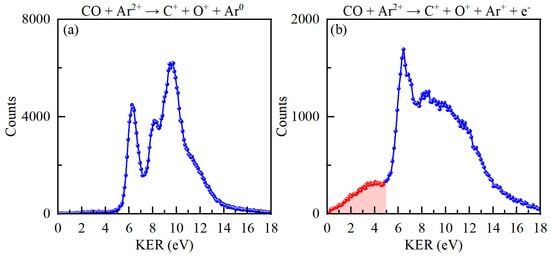
Figure 5. KER distribution for (a) ${\mathrm{Ar}}^{2+}+\mathrm{CO}\to {\mathrm{Ar}}^0+{\mathrm{C}}^{+}+{\mathrm{O}}^{+}$ channel, and (b) ${\mathrm{Ar}}^{2+}+\mathrm{CO}\to {\mathrm{Ar}}^{+}+{\mathrm{C}}^{+}+{\mathrm{O}}^{+}+{\mathrm{e}}^{-}$ channel where red line comes from ${\mathrm{CO}}^{+*}$ AI process.

The KER distribution of ${\mathrm{Ar}}^{2+}+\mathrm{CO}\to {\mathrm{Ar}}^{+}+{\mathrm{C}}^{+}+{\mathrm{O}}^{+}+{\mathrm{e}}^{-}$ channel is presented in Figure 5b, where the electron is not detected. The distribution exhibits less peak structure except for the peak at 6.3 eV. Notably different from Figure 5a,b, it shows the presence of contributions below 5 eV in KER. Taking into consideration the PECs, it reveals that the $X^3\Pi$ ($\nu =2$) vertical excitation energy is 41.6 eV, and the ground asymptotic limit ${\mathrm{C}}^{+}{(}^2\mathrm{P})+{\mathrm{O}}^{+}{(}^4\mathrm{S})$ is 36.0 eV. This corresponds to a KER of 5.6 eV, indicating that no dissociation to higher limits such as ${\mathrm{C}}^{+}{(}^2\mathrm{P})+{\mathrm{O}}^{+}{(}^2\mathrm{D})$ (39.3 eV), which may contribute to smaller KERs in Figure 5a, occurs.

Therefore, a KER below 5.5 eV originates from states below the double ionization threshold but above the ground asymptotic limit. These states correspond to highly excited ${\mathrm{CO}}^{+*}$, which undergo dissociation via AI. AI states can manifest as Rydberg states or involve inner-valence electron vacancies [22]. Given their potential energy lower than the double ionization threshold, AI electron emission is energetically not allowed until the internuclear distance reaches a sufficiently large distance [5,22]. At this stage, their potential energy surpasses that of the ground states ${\mathrm{C}}^{+}{(}^2\mathrm{P})+{\mathrm{O}}^{+}{(}^4\mathrm{S})$, enabling electron emission.

${\mathrm{CO}}^{+*}$ states can decay radiatively via photo radiation, while the autoionization electron emission is only energetically allowed at internuclear distance reaching tens of angstrom [5]. The intensity of AI distribution rises with KER, reflecting extended lifetimes of higher-level populated ${\mathrm{CO}}^{+*}$ states. Our findings diverge from the results of early measurements [28], where Tarisien investigated collisions of ${\mathrm{O}}^{7+}$ ions at energies of 4 keV/u and 11.4 MeV/u with CO. Tarisien reported no observation of KER distributions below 5 eV in slow ${\mathrm{O}}^{7+}$ collisions, and concluded that the capture process does not induce such excitations. In contrast, our measurement demonstrates that AI is a significant dissociation process during slow ion charge exchange with CO.

The KER above 5.5 eV shown in Figure 5b originates from the TI process. The relative cross-sections for the DEC, AI, and TI processes are 1, 0.046, and 0.37, respectively. This indicates that DEC has a larger cross-section than TI. Compared to the KER distributions of TI and DEC, we observed that the peak at 6.3 eV exhibits higher intensity in the TI process, whereas the peak at 9.7 eV shows greater intensity in the DEC process. This suggests that DEC transfers more excitation energy compared to TI, leading to a population of higher electronic states during collisions. This result is divergent from the idea [28] that electron capture can induce dissociation in a relatively gentle manner. In their report of CO²⁺ dissociation, ionization of CO by ${\mathrm{O}}^{7+}$ contributes to the higher part of KER distribution, and the first peak is dominant, whereas the third peak is dominant in our measurement. Similar results can also be found in other experiments [29,30,34], where the average KER increases with decreasing projectile velocity. Folker pointed out that electron correlation effects [29,30] may contribute to the formation of CO configurations at lower collision velocity. In conclusion, the present KER distribution of DEC and TI can not be well explained. The complex nature of the electronic state population needs more advanced quantum theories for comprehensive understanding.

4. Conclusions

We investigate the collision of 1 keV/u ${\mathrm{Ar}}^{2+}$ with CO using the COLTRIMS technique. KER distributions are obtained for the DEC channel ${\mathrm{Ar}}^{2+}+\mathrm{CO}\to {\mathrm{Ar}}^0+{\mathrm{C}}^{+}+{\mathrm{O}}^{+}$ and TI channel ${\mathrm{Ar}}^{2+}+\mathrm{CO}\to {\mathrm{Ar}}^{+}+{\mathrm{C}}^{+}+{\mathrm{O}}^{+}+{\mathrm{e}}^{-}$. The contributions of different electronic states to the KER are discussed for both the DEC and TI processes. AI of ${\mathrm{CO}}^{+*}$, not observed in previous publications, is identified in slow ion collisions, which is not observed in previous publications [28]. It was found that DEC transfers more excitation energy to CO than the TI process, leading to a higher contribution of repulsive state dissociation in KER distribution. This highlights the significant role of configuration interactions in slow ion collisions, as evidenced by the pronounced differences in KER distributions.