Abstract
This study explores the inelastic doubly differential transverse momentum spectra of the primary charged particles, , and , as a function of observables associated with underlying event (UE) at . The particle production is measured on the basis of different angular regions like toward, transverse and away, elucidated with respect to the direction of leading particle of an event. To study the thermal freeze-out parameters, the non-extensive Tsallis distribution function is used to extract the temperature and chemical potential , which provide a basis to explain the QCD matter. The Tsallis distribution function describes transverse momentum spectra in pseudorapidity region of . It is observed that effective temperature changes from away to towards and forward region.
1. Introduction
The identification of various stages of dense matter during the evolution of heavy-ion collisions [1] is a crucial task. At an extremely high energy or density, a state of matter exists in which quarks and gluons are deconfined, forming a Quark–Gluon Plasma (QGP) [2]. This state is also presumably present in the early universe, occurring microseconds ( s) after the Big Bang [3] before condensing into hadrons. Evaluating phase transitions [4] in finite systems has been a longstanding focus, studied for decades through various phenomenological applications.
The Relativistic Heavy-Ion Collider (RHIC) [5] and the Large Hadron Collider (LHC) [6] provide useful tools for identifying the phase structure and investigating the properties of Quantum Chromodynamics (QCD) matter.
According to statistical thermal models, the initial stage of nuclei collisions at RHIC and LHC generates high temperatures, creating a dense “fireball” with a large radius in a short period (about s). This fireball consists of QGP, which subsequently cools and expands the system. Partons recombine to form a cascade of hadronic matter, and these hadrons continue to interact until these interactions cease, freezing the particle momenta. The temperature at this point decreases to a specific value known as the chemical freeze-out temperature (). However, the rescattering process continues to occur, contributing to the ongoing development of collective (hydrodynamical) expansion. Consequently, the matter becomes more dilute, and the mean free path of the given hadrons in an elastic reaction processes becomes comparable to the size of the system. At this stage, the rescattering process ceases, resulting in the separation of hadrons from the rest of the system [7,8]. This phase is termed as kinetic or thermal freeze-out stage, and the temperature at this point is denoted as the kinetic or thermal freeze-out temperature (). Following this stage, the particle’s energy/momentum spectrum becomes fixed in time, marking the concluding phase of the system’s evolution. If flow effect is included at the stage of kinetic freeze-out along with the degree of excitation of the interacting system, then that temperature is called the effective temperature (), and it is generally greater than the [9].
As the purpose of heavy-ion collision is to study the QGP probed through its signatures. However, the small collision system like [10] shows similar features to those observed in heavy-ions like [11], [12], and [13] collisions. The signatures like anisotropic radial flow and strangeness enhancement are associated with the formation of quark gluon plasma (QGP) [2], is also observed in and systems.
In this paper, we have investigated the thermodynamic characteristics of interacting systems. For this purpose, several statistical models, including the Boltzmann–Gibbs distribution [14], have been employed. Notably, the Tsallis distribution function [15] has proven to be an excellent representation of particle spectra for values. By applying the non-extensive Tsallis distribution function for ALICE data fitting purposes [16], we have determined various thermodynamic parameters, such as effective temperature () [17], characterized as combined effect of thermal motion and collective flow in the system; chemical potential (), which indicates the balance between particle production and annihilation of given species; and radius and volume of the system [18]. The non-extensive Tsallis distribution function is utilized for combined minimum fits.
2. Methodology
The study of underlying events (UE) [16] is proposed to understand the effect observed in small collision system. The UE consists of the initial state radiation (ISR), final state radiation (FSR), beam remnant, and multiparticle interactions (MPIs). The particles produced as a function of UE activity allows to probe the properties in MPI suppressed environment. This experiment yields a similar signal to the radial flow, but with increased multiplicity due to jet hardening.
At LHC, an enormous number of particles are produced. We analyzed the primary charged particles, , and , as a function of UE at [11] in this work. The UE activity is probed through particle event topology, where leading charged particle carries the highest transverse momentum within in the pseudorapidity interval of . The lower threshold of guarantees the multiple soft scattering, while the upper threshold is used to reduce the effects of wide angle radiation which is significant for and associated with hard scattering.
The three different topological regions (away, towards, and transverse) are reported in this paper. These are determined by comparing the azimuthal angles of the leading and associated particles = . The associated particles lying in the kinematic range of and . The away, towards, and transverse regions are defined as , , and . The particles produced in away and toward region contain constituents from away-side and leading jets, whereas the transverse region is sensitive to ISR, FSR and MPIs.
The relative transverse activity classifier () is used to quantify the UE activity; it is defined as . Here, is the charged particle multiplicity per event in the transverse region, and is the average of all analyzed events. Regardless of the center-of-mass energy, precisely distinguishes between occurrences with “higher-than-average” UE and “lower-than-average” UE.
In this paper, we have used the non-extensive Tsallis distribution function [15] to extract the thermodynamic information for a primary charged particle , and produced as a function of over a wide range of transverse momentum for pseudorapidity region , at a center-of-mass energy . These primary charged particles have mean life time , larger than , which is produced in interactions or from the decay of particles with life time smaller than .
Particle Distribution in Tsallis Statistics
Various statistical models are used to extract the thermodynamic parameters like T and , e.g., Boltzmann–Gibbs statistics and Tsallis non-extensive statistics. Generally, two main processes, i.e., soft excitation (which contributes the soft component of the low region) and hard excitation (which contributes to the hard component in the region) are involved in the transverse momentum spectra [11]. For a soft excitation, one could possibly used the Boltzmann–Gibbs statistics, while if the reaches up to in the collision at collider, than one needs to use Tsallis statistics. In this study, the transverse momentum spectra of the final state particles produced in collision at high energy can be explored using Tsallis statistics [15]. The number of particles are given as
where g, , and T are degeneracy, chemical potential, and temperature, respectively, and and q is the fitting parameter, which tells us the deviation from the Boltzmann–Gibbs distribution. The particular form which satisfies the thermodynamic consistency is given as
where V is the volume, is the transverse mass, and y is rapidity.
3. Results
Figure 1a–c depicts the particle yield as a function of relative transverse momentum classifier , for primary charged particles like produced in high energy collisions at fitted with thermodynamically consistent Tsallis distribution function with chemical potential . The observations reported are measured in three different topological regions: away, towards, and transverse. The circles display the experimental data in the pseudorapidity range of used in this analysis at LHC by ALICE collaborations [2]. The curve represents the fitting of the data by using Equation (3); the values of extracted parameters, Tsallis temperature, radius, non-extensive parameter () and are presented in Table 1.
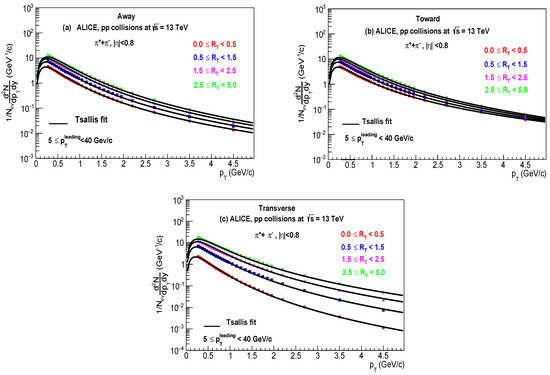
Figure 1.
Combined minimum fits (solid lines) of the transverse momentum distribution of using the Tsallis distribution function with at the center of mass energies for (a) away, (b) toward, and (c) transverse regions.

Table 1.
The thermodynamic parameters , R, q, and , for in collision.
It is seen clearly that the Tsallis distribution function describes the measured experimental data at the pseudorapidity region of in collisions very well. The best fit corresponds to minimum . It is observed that the is higher for the transverse region due to presence of more UE events, like contributions from ISR, FSR, and MPIs, while for the away and towards regions, the is lower because of the fragmentation particle production. Moreover, at low , the particle momentum is dominated by thermalized particle, while at high , due to hard scattering, the jets (mini jets) dominate. To justify the choice of fit range based on the expected physical processes (e.g., soft physics at low , hard physics at higher ) ensures that the analysis provides clear insights into the underlying dynamics of the system.
Figure 2a–c presents the particle yield as a function of relative transverse momentum classifier for strange particles like produced in high-energy collisions at fitted with a thermodynamically consistent Tsallis distribution function with chemical potential . The observables reported are measured in three different topological regions: away, towards, and transverse. The circles display the experimental data in the pseudorapidity range of used in this analysis at LHC by ALICE collaborations [2]. The curve represents the fitting of the data by using Equation (3); the values of extracted parameters, Tsallis temperature, radius, non-extensive parameter () and are presented in Table 2.
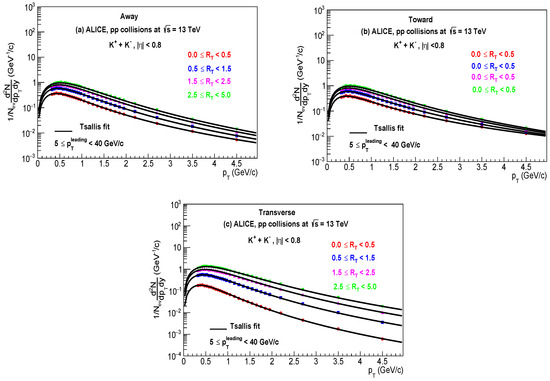
Figure 2.
Combined minimum fits (solid lines) of the transverse momentum distribution of using the Tsallis distribution function with at the center of mass energies for (a) away, (b) toward, and (c) transverse regions.

Table 2.
The thermodynamic parameters , R, q, and , for in collision.
Figure 3a–c shows the particle yield as a function of relative transverse momentum classifier for primary charged particles like produced in high energy collisions at fitted with a thermodynamically consistent Tsallis distribution function with chemical potential . The observables reported are measured in three different topological regions: away, towards, and transverse. The circles display the experimental data in the pseudorapidity range of used in this analysis at LHC by ALICE collaborations [2]. The curve represents the fitting of the data by using Equation (3); the values of extracted parameters, Tsallis temperature, radius, non-extensive parameter () and are presented in Table 3.
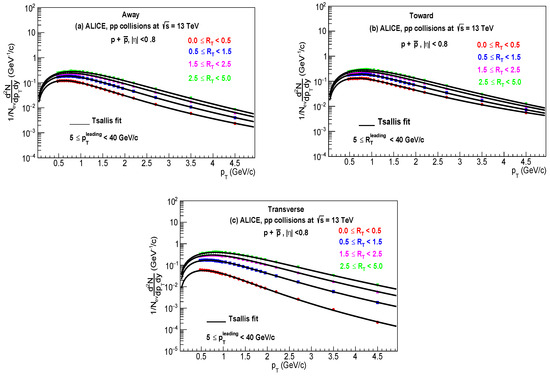
Figure 3.
Combined minimum fits (solid lines) of the transverse momentum distribution of using the Tsallis distribution function with at the center of mass energies for (a) away, (b) toward, and (c) transverse regions.

Table 3.
The thermodynamic parameters , R, q, and , for in collision.
It is clear from Table 1, Table 2 and Table 3 that the changes with the regions. The values for the non-extensive parameter q ranges between q = 1.137 and 1.158, which is acceptable within the high energy limit and matches to the values obtained in the literature [7,19,20]. Radius R and volume V are connected with the collective expansion of the system, and the relation between them is the part of parameterization used for fitting data, which is essential for understanding system size and dynamics.
Figure 4a–c depicts the variation in chemical potential , non-extensive parameter q, and effective temperature with for primary charged particles like produced in high energy collisions at .

Figure 4.
Dependence of , q and on in pp collision for at for (a) away, (b) toward, and (c) transverse regions.
Figure 5a–c depicts the variation in chemical potential , non-extensive parameter q and temperature with for strange particles like produced in high energy collisions at .
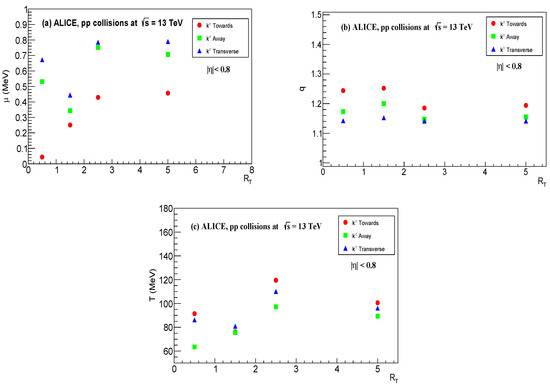
Figure 5.
Dependence of , q and on in pp collision for at for (a) away, (b) toward, and (c) transverse regions.
Figure 6a–c depicts the variation in chemical potential , non-extensive parameter q, and temperature with for the baryon-like produced in high energy collisions at . The dependence of chemical potential , non-extensive parameter q, and temperature on relative transverse activity classifier is critical when analyzing high energy collisions, as these parameters reveals the information about the collision dynamics and thermalization. Effective temperature , radius R, and chemical potential increased when increased, which indicates the stronger collective flow and more expansion due to the central collisions. It is obvious from results that extracted parameters for the transverse region show increasing trends compared to the towards and away regions.
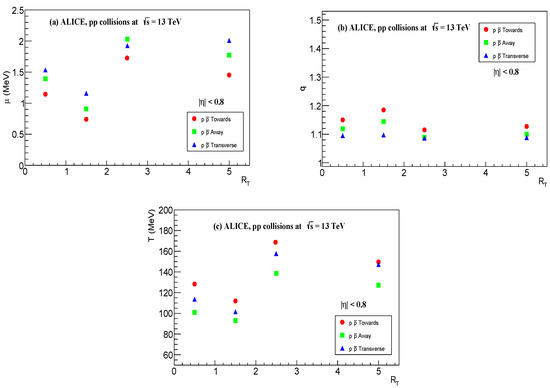
Figure 6.
Dependence of , q and on in pp collision for at for (a) away, (b) toward, and (c) transverse regions.
4. Conclusions
In this paper, we have presented the fitting of the non-extensive Tsallis distribution function to the transverse momentum spectra of primary charged particles like , and produced in high energy collision at center of mass energy of . The momentum spectra of particles are classified according to the classes. Two main parameters, i.e., and are extracted from the Tsallis distribution function, which are very important regarding the discussion of QCD matter. From the fitted spectra, we observed that the is higher for the transverse region. This region is very sensitive to the multiple parton interactions, and the initial and final state radiations.
Author Contributions
Conceptulization, U.T.; drafting, Z.U.A.; computing, K.G.; analysis, I.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Data Availability Statement
This manuscript has associated data in a data repository. All data included in this manuscript are available upon request by contacting the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Harris, J.W.; Müller, B. The search for the quark-gluon plasma. Annu. Rev. Nucl. Part. Sci. 1996, 46, 71–107. [Google Scholar] [CrossRef]
- McLerran, L. The physics of the quark-gluon plasma. Rev. Mod. Phys. 1986, 58, 1021–1064. [Google Scholar] [CrossRef]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A.; Yeh, T.H. Big Bang Nucleosynthesis: Present status. Rev. Mod. Phys. 2016, 88, 015004. [Google Scholar] [CrossRef]
- Spieles, C.; Stoecker, H.; Greiner, C. Phase transition of a finite quark-gluon plasma. Phys. Rev. C 1998, 57, 908. [Google Scholar] [CrossRef]
- Harrison, M.; Peggs, S.; Roser, T. The RHIC accelerator. Annu. Rev. Nucl. Part. Sci. 2002, 52, 425–469. [Google Scholar] [CrossRef]
- Ellis, J. Physics at the LHC. Eur. Phys. J. C 2004, 34, 51–56. [Google Scholar] [CrossRef]
- Tabassam, U.; Ali, Y.; Olimov, K.K. Study of multiplicity dependence in Charmed Hadrons production in pp collisions at LHC energies. Eur. Phys. J. Plus 2023, 138, 367. [Google Scholar] [CrossRef]
- Waqas, M.; Liu, F.H.; Wazir, Z. Dependence of Temperatures and Kinetic Freeze-Out Volume on Centrality in Au-Au and Pb-Pb Collisions at High Energy. Adv. High Energy Phys. 2020, 2020, 8198126. [Google Scholar] [CrossRef]
- Inghirami, G.; Hillmann, P.; Tomasik, B.; Bleicher, M. Temperatures and chemical potentials at kinetic freeze-out in relativistic heavy ion collisions from coarse grained transport simulations. J. Phys. G 2020, 47, 025104. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adamet, W.; Aşilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Ero, J.; et al. Evidence for collectivity in pp collisions at the LHC. Phys. Lett. B 2017, 765, 193–220. [Google Scholar] [CrossRef]
- Floris, M.; The ALICE Collaboration. Identified particles in pp and Pb-Pb collisions at LHC energies with the ALICE detector. J. Phys. G Nucl. Part. Phys. 2011, 38, 124025. [Google Scholar] [CrossRef]
- Muller, B.; Schukraft, J.; Wyslouch, B. First Results from Pb+Pb collisions at the LHC. Annu. Rev. Nucl. Part. Sci. 2012, 62, 361–386. [Google Scholar] [CrossRef]
- Abidin, Z.U.; Tabassam, U. PYTHIA8 and HIJING2 predictions for the Xe − Xe collisions at = 5.44 TeV. Eur. Phys. J. Plus 2022, 137, 115. [Google Scholar] [CrossRef]
- Rowlinson, J.S. The maxwell–boltzmann distribution. Mol. Phys. 2005, 103, 2821–2828. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. The Tsallis distribution in proton-proton collisions at = 0.9 TeV at the LHC. J. Phys. G 2012, 39, 025006. [Google Scholar] [CrossRef]
- ALICE Collaboration. Production of pions, kaons, and protons as a function of the relative transverse activity classifier in pp collisions at = 13 TeV. J. High Energy Phys. 2023, 2023, 27. [Google Scholar] [CrossRef]
- Berrehrah, H.; Bratkovskaya, E.; Steinert, T.; Cassing, W. A dynamical quasiparticle approach for the QGP bulk and transport properties. Int. J. Mod. Phys. E 2016, 25, 1642003. [Google Scholar] [CrossRef]
- Soloveva, O.; Moreau, P.; Bratkovskaya, E. QCD at finite chemical potential in and out-of equilibrium. Phys. Scr. 2021, 96, 124067. [Google Scholar] [CrossRef]
- Waqas, M.; Peng, G.X.; Khubrani, A.M.; Ajaz, M.; Tabassam, U.; Yang, P.P. Pseudorapidity, transverse momentum and multiplicity distributions of charged particles in pp collisions at 13 TeV. Eur. Phys. J. Plus 2023, 138, 450. [Google Scholar] [CrossRef]
- Tabassam, U.; Awais, M.; Olimov, K.K.; Majid, M. Analysis of properties of the charged-particle jets in pp collisions at 13 TeV using non-extensive Tsallis statistics. Eur. Phys. J. Plus 2023, 138, 394. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).