Abstract
This article discusses how the pattern of elastic scattering of an electron on a pair of identical atomic centers is modified if we abandon the assumption, standard in molecular physics, that outside of some molecular sphere surrounding the centers, the wave function of the molecular continuum is atomic-like, being a linear combination of the regular and irregular solutions of the wave equation. For this purpose, the elastic scattering of slow particles by a pair of non- overlapping short-range potentials has been studied. The continuum wave function of the particle is represented as a combination of a plane wave and two spherical s-waves propagating freely throughout space. The asymptotic behavior of this function determines the amplitude of elastic particle scattering in closed form. It is demonstrated that this amplitude can be represented as a partial expansion in a set of the orthonormal functions other than spherical harmonics . General formulas for these functions are obtained. The coefficients of the scattering amplitude expansion into a series of functions and determine the scattering phases for the considered two- atomic target. The special features of the S-matrix method for the case of arbitrary non-spherical potentials are discussed.
1. Introduction
In molecular collision physics, the idea that the molecular continuum electron functions are similar to those for electron-atom scattering [1] is considered as a matter-of-course, and, as far as we know, it is beyond any doubt. It cannot be asserted that this statement is obvious. In the muffin-tin model, a molecule is represented as a cluster of N non-overlapping atomic spheres. The classical physical picture of wave scattering on such a target is based on the Huygens–Fresnel principle. According to this principle, the initial wave interacts with each target center, which becomes a source of the secondary spherical scattered waves, and beyond the target, there are N spherical waves going out from each of the centers, rather than a set of partial spherical waves having the asymptotic form
as in the case of electron scattering by an atom. In Equation (1), is the position vector of the scattered electron relative to the center of mass of the molecule; is the electron wave vector; is the partial phase shift corresponding to the angular momentum l; and is the radial component of the electron wave function. Here and below, spherical harmonics , where and are the spherical angles of the vector . We use the atomic system of units.
Apparently, the statement above is related to the standard methods of calculation of the molecular continuum. According to the reviews [1,2,3], the configuration space describing the scattered or ejected electron and the molecule is divided into two regions: internal and external. Some sphere with radius defines the internal region, in which the main part of the charge distribution of the molecular states of interest is located. The electron continuum wave functions in the external region are represented as a linear combination of the regular and irregular solutions of the Schrödinger equation with the potential that, in this region, “is taken to be spherical … about the molecular center” [4]. A microscopic observer (Maxwell’s demon), located inside the sphere, sees the picture of the electron wave scattering from the separated centers. However, when he moves outside the sphere, he observes the pattern of the wave scattering on a single center located in the center of mass of the molecule. What is the scattering pattern if we abandon the assumption given in the first paragraph in italics?
The qualitative picture of the electron wave scattering by a diatomic target is shown in Figure 1a,b.
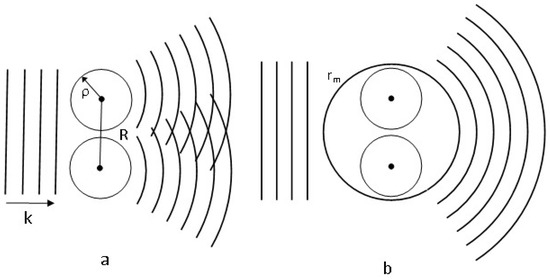
Figure 1.
The qualitative picture of the electron wave scattering by a diatomic target; (a) is the Huygens–Fresnel picture; (b) is the Dill and Dehmer picture [4].
The left part of Figure 1a depicts a plane wave. The right part shows two spherical waves according to the Huygens–Fresnel principle. The interference of these waves creates a diffraction scattering pattern whose properties depend periodically on the ratio of the inter-atomic distance to the electron wavelength. Figure 1b allows us to see how the electron wave scattering pattern is transformed after the introduction of the molecular sphere. Outside the molecular sphere, there is only a single spherical wave centered at the center of the molecular sphere. No interference pattern is observed as in Figure 1a.
A question related to Figure 1 arises: is it possible to adapt the method of partial waves for the case of a multicenter target keeping the Huygens–Fresnel picture of the scattering process? According to the picture, far from the target, there exists a system of secondary waves outgoing from each of the centers. Demkov and Rudakov gave a positive answer to this question in the paper [5], where it was demonstrated that the S-matrix method could also be applied to non-spherical potentials. In the present paper, we analyze the special features of the partial wave method for non-spherical targets. We consider the targets with fixed positions of atoms in space as a simple example of scattering of a slow particle by two short-range non-overlapping potentials.
The outline of our article is as follows. In Section 1, we calculate the scattering amplitude of a particle on a pair of short-range potentials, based on the scattering pattern presented in Figure 1a. It is shown that this amplitude can be written in a closed form, but not as an expansion in partial waves. In Section 2, we describe the partial wave method for the scattering pattern in Figure 1a. Expansion of the scattering amplitude in a series of functions is carried out in Section 3. Section 4 contains some numerical calculations. Section 5 presents the conclusion remarks.
2. Elastic Scattering of a Particle by Two Short-Range Potentials
Based on Brueckner’s paper [6], we trace how the problem of particle scattering by a pair of non-overlapping short-range potential wells with radii is solved. In the coordinate system with the origin at the center of mass of a pair of identical potential wells, the continuum wave function, according to Figure 1a, is represented as a combination of a plane wave and two spherical s-waves, generated by the short-range potentials with centers at the points
Function (2) is the general solution of the wave equation outside the scatterer’s spheres with radius [6].
The unknown coefficients and in (2) are of imposing boundary conditions on the trial wave function at the points and - . Let us find these boundary conditions. We consider the behavior of a particle in the s-state in the field of a short-range spherical potential well. Outside the well, at a distance larger than the range of the potential , the particle wave function satisfying the wave equation reads
Let us assume that we know the s-phase of the elastic scattering of a particle on an isolated potential well, which is the function over the entire range of the wave vector . Passing to the limit in Formula (3), we obtain the following boundary condition imposed on function (2) at the centers of the potential wells:
For wells centered at the points , we obtain the following boundary conditions for Function (2):
where and are some constants. Applying Formula (5) to Function (2), we obtain the exact general solution of the Schrödinger equation outside the scatterer’s spheres that describes the multiple scattering of a particle by a two-center target [6]. The amplitude of particle scattering by the target is obtained by considering the asymptotic behavior of the wave function (2). As result, we obtain the following exact amplitude of the particle multiple s-scattering by the two-center target [6,7]
We do not reproduce the details here but refer the reader to the original paper [7]. As in [7], we use here the following notation: and are the particle linear momenta before and after scattering, respectively; the functions and . Here, is the s-partial amplitude of particle elastic scattering by an isolated potential well. The scattering amplitude (6) includes the amplitudes of scattering on individual centers. It is seen that the result of a superposition of the scattered waves depends on vector defining the positions of the scattering centers. The total cross-section of particle scattering in [6] is obtained from the amplitude (6) using the optical theorem [8]
The case when a pair of non-identical atomic spheres forms the target was considered in [9]. The generalization of the formulas in this section to a larger number of scattering centers is not difficult. The coefficients for spherical s-waves are obtained in this case from the boundary conditions (5) imposed at the centers of all atomic spheres forming the target. The application of the Huang–Yang multipolar pseudopotential [10,11,12] for each of the scattering centers makes it possible to generalize the results presented here for the s-wave to spherical waves with nonzero orbital angular momenta.
3. Method of Partial Waves for Non-Spherical Targets
The molecular potential of a cluster of non-overlapping atomic potentials centered at the atomic sites is non-spherical. The solution of the Schrödinger equation with this potential is impossible to present at an arbitrary point of space as an expansion in spherical harmonics . However, according to Demkov and Rudakov’s paper [5], the continuum wave function of the scattered electron at great distances from the molecule can be presented as an expansion into a set of other than orthonormal functions and
with the partial wave function, as opposed to (1), determined by the following formula
Here, the index enumerates partial waves similar to the quantum numbers l and m for a central field; is the quantum number that is equal to the orbital momentum l for the spherical symmetry case; are the “proper molecular phases”. Functions , where and are the spherical angles of the vector as for spherical harmonics. The explicit form of the functions (in terminology [5], “characteristic amplitudes”) depends upon the specific type of the target field that is defined by the number of atoms forming the target and their spatial configuration. Functions , being similar to the spherical harmonics , create an orthonormal system, and for this reason
The elastic-scattering amplitude for a non-spherical target, according to [5], is given by the following expression:
The total elastic scattering cross-section, i.e., the cross-section integrated over all directions of the momentum of the scattered electron , is defined by the formula
Certainly, this cross-section depends on the mutual orientation of the incident electron momentum and molecule axis. The cross-section averaged over all the directions of the incident electron momentum is related to the molecular phases according to the formula
In the case of a spherically symmetric target, Formula (13) coincides with the known formula for the total scattering cross-section. Indeed, for a central field, the index is to be replaced by the quantum numbers l and m. However, the phase of scattering by a central field is independent of the magnetic number and, therefore, for a given value of the orbital momentum l, it is necessary to sum over all m. The summation leads to a factor under the summation sign in Formula (13).
The partial wave (9) and the molecular phases are classified, according to [5], by their behavior for low electron energies, i.e., for . In this limit, the particle wavelength is great as compared to the target size, and the function tends to some spherical harmonic . The corresponding phase is characterized in this limit by the following asymptotic behavior: .
For the molecular system that is created by two short-range potentials, each of which is a source of the scattered s-waves, the molecular phase shifts to , and the functions can be calculated in the explicit form (see [7,13] for low electron energies). This simplest multicenter system is a good example illustrating the method of partial waves for non-spherical targets formed by non-overlapping atomic potentials. It is important that the problem of slow particle scattering by this system of centers can be solved analytically.
4. Expansion of the Scattering Amplitude (6) in a Series of Functions
According to [5], the exact amplitude (6) can be represented as a partial expansion in a series of the functions . Following the papers [7,14], let us rewrite the scattering amplitude (6) in the following form
The amplitude (14) should be considered as a sum of two partial amplitudes. The first of them is written as
The second one is defined by the following expression:
After elementary transformations of (15) and (16), we obtain two molecular phases
where the wave number .
Comparing these expressions with the general Formula (9), we come to the following conclusions. If the electron states are characterized by the projection of the angular momentum on the axis and by the parity of the wave function relative to the reflection in the plane perpendicular to and going through the middle point of the inter-atomic distance, then the first partial wave (17) corresponds to the state , and the second one corresponds to .
The molecular phases in (17) can be classified by considering their behavior at [5]. In this limit, the electron wavelength is much greater than the target size and the picture of scattering should approach the case of spherical symmetry. Considering the transition to this limit in Formula (17), we obtain: and . Thus, the molecular phases behave similarly to the s- and p- phases in the spherically symmetrical potential. This explains the choice of their indexes.
In Ref. [13], formulas for molecular phases (17) were obtained in the limit of low electron energies, for which the electron scattering length A on the atom forming the target is related to the wave number as . Let us find a relation between the molecular electron scattering length and the atomic scattering length A. These scattering lengths are determined by the following formulas [14]:
Multiplying both parts of the zero phase (17) by and passing to the limit , we obtain the required relationship between the scattering lengths (compare with [15])
From Formulas (15) and (16), we obtain two “characteristic amplitudes”,
where . Function here is the spherical Bessel function [16]. It is easy to demonstrate that the functions , similarly to the spherical harmonics , create an orthonormal system. The functions (20) are defined by the geometrical target structure, i.e., by the direction of the molecular axis in an arbitrary coordinate system, in which the electron momentum vectors before and after scattering are and , respectively. The transition to the limit in Formula (17) gives the well-known spherical harmonics
where is the angle between the vector and axis . Therefore, only in the limit does it become correct to replace a non-spherical molecular field in an external region (beyond the molecular sphere) with a spherical one.
Let us summarize the results obtained with the method of partial waves for a target formed by non-overlapping atomic potentials. For two atomic targets, the molecular phases of scattering and the functions can be found explicitly. The phases of molecular scattering are functions of electron momentum only as well as the atomic phases. The form of the function is defined by the structure of the target and its orientation in space. The number of non-zero molecular phases, in this case, is equal to two. This is related to the fact that each of these two scattering centers is a source of s-spherical waves only. This situation is realized for low electron energy only. If the scattering by the centers leads to the generation of spherical waves with non-zero orbital momenta (this case was considered in paper [17]) then the number of non-zero molecular phases would be greater.
It should be noted that other generalizations of spherical harmonics are available in the literature. For example, prolate spheroidal and Coulomb spheroidal angular functions were used in [18] for the description of electron behavior in the field of diatomic molecular cations. So-called dipole functions were demonstrated [19] to be convenient for the description of target molecules with constant dipole moments.
5. Numerical Results
To illustrate the potentialities of the formulas obtained in Section 4, we calculate the functions (20) and the differential cross-sections for electron scattering (12) for a model quasi-molecule formed by a pair of identical atomic hard-spheres for which the s-wave phase shift is [20]
where is the radius of the scatterer spheres in (2). The hard-sphere radius can also be looked upon as the scattering length A (18). The distance between the centers of the atomic spheres is considered Å = 2.067 atomic units (au) (the bond length of N molecule); the radii of the atomic spheres au (a reasonable value). The behavior of the scattering phases as functions of the electron momentum k has been discussed by us (and before us) in a number of papers [5,7,9,13,14], while the special features of the functions have not been studied by anyone. It turned out that the behavior of the functions is nontrivial. In our next step, we focus on the study of these functions. Some numerical results necessary for their calculation are given in Table 1.

Table 1.
Evaluations of the molecular phases and related quantities. All parameters are given in atomic units.
The results of numerical calculations of “characteristic amplitudes” (20) [21,22] are presented in Figure 2.
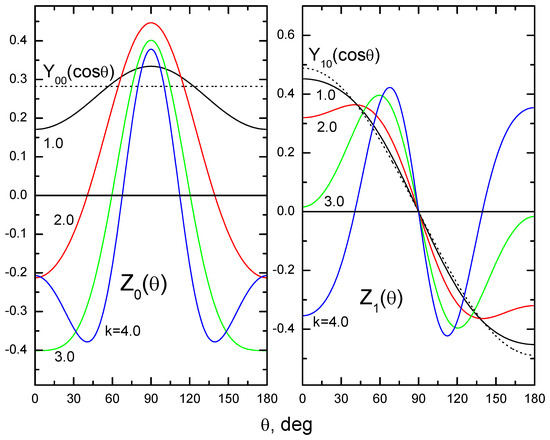
Figure 2.
The “characteristic amplitudes” (20) as functions of the angle .
The angle in this figure is the angle between the vectors and for the functions . For the functions , is the angle between the vectors and . Dotted lines are the spherical harmonics and , to which the calculated curves with indices tend to approach in the limit .
Figure 3 demonstrates the partial differential cross-sections (12)
and the sum of these partial sections (12) as functions of the angle between the vectors and .
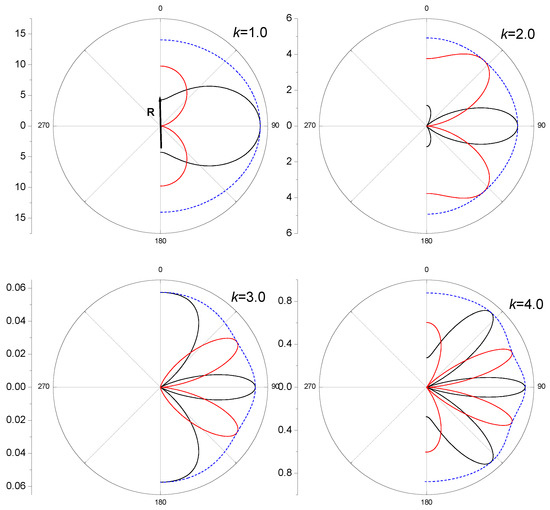
The axis of the molecule is the polar axis in these figures. The 3D pictures of the differential cross sections are figures of rotation of the curves around the -axis. The dotted lines, which represent the sums of the partial cross sections, are not circles, as they would be in the case of spherical waves (1). The passage of the curves through the center of the polar coordinate system is associated with the zeros of the curves in Figure 2. The more frequent these zeros are, the more lobes on the curves of the cross sections and appear. Numerical calculations of the cross-sections using the optical theorem (Equation (7)), as expected, coincide with the total cross sections presented in Figure 3 by dotted lines.
It is simple to calculate the functions and the scattering phases when one knows the exact wave function (2). On the other hand, if this function is known, as is the case for a system of non-overlapping potentials, the scattering amplitude can be obtained in the closed form (2), and the cross-section can be found using the optical theorem (7). Therefore, there is no need to resort to the method of partial waves. However, for non-spherical potentials, different from muffin-tin potentials, i.e., when the model of non-overlapping potential becomes inapplicable, the use of the partial wave method [5] makes it possible to separate the scattering dynamics contained in the molecular phases from the kinematics of the process defined by the functions into the explicit form.
6. Conclusions
In the studies of electron-molecule scattering, the continuum electron is usually treated [1,2,3,4] as moving in a spherically averaged molecular field (Figure 1b). The wave functions describing the scattering of an electron by a polyatomic molecule outside the so-called molecular sphere (in the external region) are considered a linear combination of the regular and irregular solutions of the wave equation. The phase shifts of the molecular wave function are defined from the matching condition for the solutions of the wave equation inside and beyond this sphere. Obviously, the introduction of the molecular sphere changes the scattering pattern (compare Figure 1a and Figure 1b). The diffraction pattern of the electron wave itself disappears since there is only one spherical wave far from the target. Due to the terms in Formula (17), obtained for the scattering pattern 1(a), there is a clear manifestation of the electron diffraction of a pair of spherical s-waves emitted by spatially separated sources. Apparently, the traditional approach based on Formulas (1) and (2) and Figure 1b allows one to obtain the scattering phases of a particle on an isolated molecular sphere rather than on a real two-center target. Thus, the statement that the molecular continuum electron functions are similar to those for electron-atom scattering should be supplemented with the words if we assume that in the external region the continuum wave function is atomic-like.
In the present article, we abandoned this assumption and allowed the spherical waves to propagate freely throughout space and came to a different result. Instead of partial spherical waves (1), obtained within the standard methods for calculating the molecular continuum, we have the following pair of wave functions (9)
Since the asymptotic expressions of the wave function contain the functions instead of the spherical harmonics , it becomes clear that: no matter how far we move away from a non-spherical target, we will never be able to consider the target as atomic-like or the wave function of the particle as spherical waves, except for the case when the particle wavelength significantly exceeds the target size .
Author Contributions
Conceptualization, A.S.B.; Investigation, A.S.B. and I.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are available upon request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gianturco, F.A.; Jain, A. The theory of electron scattering from polyatomic molecules. Phys. Rep. 1986, 143, 347–425. [Google Scholar] [CrossRef]
- Burke, P.G. R-matrix method—Advantages and applications. J. Phys. Colloq. 1978, 39, C4. [Google Scholar] [CrossRef]
- Burke, P.G.; Tennyson, J. R-matrix theory of electron molecule scattering. Mol. Phys. 2005, 103, 2537–2548. [Google Scholar] [CrossRef]
- Dill, D.; Dehmer, J.L. Electron-molecule scattering and molecular photoionization using the multiple-scattering method. J. Chem. Phys. 1974, 61, 692–699. [Google Scholar] [CrossRef]
- Demkov, Y.N.; Rudakov, V.S. The Method of Partial Waves for a Nonspherical Scatterer. Sov. Phys. JETP 1971, 32, 1103–1109. [Google Scholar]
- Brueckner, K.A. Multiple Scattering Corrections to the Impulse Approximation in the Two-Body System. Phys. Rev. A 1953, 89, 834–838. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Baltenkov, A.S. Time Delay of Slow Electrons by a Diatomic Molecule Described by Non-Overlapping Atomic Potentials Model. JETF 2020, 131, 707–713. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics, Non-Relativistic Theory, 3rd ed.; Pergamon Press: Oxford, UK, 1977. [Google Scholar]
- Baltenkov, A.S.; Woiciechowski, I. Slow electron elastic scattering by a target represented by different zero-range potentials. arXiv 2022, arXiv:2206.08693. [Google Scholar]
- Huang, K.; Yang, C.N. Quantum-Mechanical Many-Body Problem with Hard-Sphere Interaction. Phys. Rev. 1957, 105, 767–775. [Google Scholar] [CrossRef]
- Huang, K. Statistical Mechanics, 1st ed.; Wiley: New York, NY, USA, 1963. [Google Scholar]
- Derevianko, A. Revised Huang-Yang Multipolar Pseudopotential. Phys. Rev. A 2005, 72, 044701. [Google Scholar] [CrossRef]
- Drukarev, G.F.; Yurova, I.Y.M. Multiple-scattering approach to the vibrational-rotational excitation of molecules by slow electrons. J. Phys. B At. Mol. Phys. 1977, 10, 3551–3558. [Google Scholar] [CrossRef]
- Demkov, Y.N.; Ostrovskii, V.N. Zero-Range Potentials and Their Applications in Atomic Physics, 1st ed.; Plenum Press: New York, NY, USA, 1988. [Google Scholar]
- Seidel, E.P.; Arretche, F. Rovibrational excitation of rare-gas dimers by electron impact. Phys. Rev. A 2018, 98, 052707. [Google Scholar] [CrossRef]
- Abramovitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover: New York, NY, USA, 1965. [Google Scholar]
- Baltenkov, A.S.; Manson, S.T.; Msezane, A.Z. Interference in electron–molecule elastic scattering. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 205101. [Google Scholar] [CrossRef]
- Komarov, I.V.; Ponomarev, L.I.; Slavyanov, S.Y. Spheroidal and Coulomb Spheroidal Functions; Nauka: Moscow, Russia, 1976. [Google Scholar]
- Baryshnikov, F.F.; Zakharov, L.E.; Lisitsa, V.S. Electron bremsstruhlung in a dipole potential. Sov. Phys. JETP 1980, 42, 406–411. [Google Scholar]
- Schiff, L.I. Quantum Mechanics; McGraw-Hill Education: New York, NY, USA, 1968. [Google Scholar]
- Baltenkov, A.S.; Woiciechowski, I. About the standard methodology in electron-molecule collision physics. arXiv 2022, arXiv:2207.14501. [Google Scholar]
- Baltenkov, A.S.; Woiciechowski, I. Interference phenomenon in electron-molecule collisions. arXiv 2022, arXiv:2209.08302. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).