Neutrino Mixing Sum Rules and the Littlest Seesaw

Abstract

In this work, we study the neutrino mixing sum rules arising from discrete symmetries and the class of Littlest Seesaw (LS) neutrino models. These symmetry-based approaches all offer predictions for the cosine of the leptonic CP phase $cos\delta$ in terms of the mixing angles, ${\theta }_{13}$, ${\theta }_{12}$, ${\theta }_{23}$, while the LS models also predict the sine of the leptonic CP phase $sin\delta$, as well as making other predictions. In particular, we study the solar neutrino mixing sum rules, arising from charged lepton corrections to tri-bimaximal (TB), bimaximal (BM), golden ratio (GR) and hexagonal (HEX) neutrino mixing, and the atmospheric neutrino mixing sum rules, arising from preserving one of the columns of these types of mixing—for example, the first or second column of the TB mixing matrix (TM1 or TM2)—and we confront them with an up-to-date global fit of the neutrino oscillation data. We show that some mixing sum rules, such as an atmospheric neutrino mixing sum rule arising from a version of neutrino golden ratio mixing (GRa1), are already excluded at 3$\sigma$, and we determine the remaining models allowed by the data. We also consider the more predictive LS models (which obey the TM1 sum rules and offer further predictions) based on constrained sequential dominance CSD(n) with $n\approx 3$. We compare for the first time the three cases $n=2.5$, $n=3$ and $n=1+\sqrt{6}\approx 3.45$, which are favored by theoretical models, using a new type of analysis to accurately predict the observables ${\theta }_{12}$, ${\theta }_{23}$ and $\delta$. We study all the above approaches, solar and atmospheric mixing sum rules and LS models, together so that they may be compared and to give an up-to-date analysis of the predictions of all of these possibilities, when confronted with the most recent global fits.

1. Introduction

Neutrino mass and mixing represents the first and, so far, the only new physics beyond the standard model (SM) of particle physics. We know that it must be new physics because its origin is unknown and it is not predicted by the SM. Independently of whatever the new (or nu) SM is, we do know that the minimal paradigm involves three active neutrinos, the weak eigenstates ${\nu }_e,{\nu }_{\mu },{\nu }_{\tau }$ (the $SU{\left(2\right)}_L$ partners to the left-handed charged lepton mass eigenstates), which are related to the three mass eigenstates $m_{1,2,3}$ by a unitary PMNS mixing matrix [1].

The PMNS matrix is similar to the CKM matrix, which describes quark mixing, but involves three independent leptonic mixing angles ${\theta }_{23},{\theta }_{13},{\theta }_{12}$ (or $s_{23}=sin{\theta }_{23}$, $s_{13}=sin{\theta }_{13}$, $s_{12}=sin{\theta }_{12}$); one leptonic CP violating Dirac phase $\delta$, which affects neutrino oscillations; and possibly two Majorana phases, which do not enter into neutrino oscillation formulas. Furthermore, neutrino oscillations only depend on the two mass squared differences $\Delta m_{21}^2=m_2^2-m_1^2$, which is constrained by data to be positive, and $\Delta m_{31}^2=m_3^2-m_1^2$, which current data allow to take a positive (normal) or negative (inverted) value. In 1998, the angle ${\theta }_{23}$ was first measured to be roughly ${45}^{\circ }$ [2] (consistent with equal bimaximal ${\nu }_{\mu }-{\nu }_{\tau }$ mixing) by atmospheric neutrino oscillations, while ${\theta }_{12}$ was determined to be roughly ${35}^{\circ }$ (consistent with equal trimaximal ${\nu }_e-{\nu }_{\mu }-{\nu }_{\tau }$ mixing) in 2002 by solar neutrino oscillation experiments [3], while ${\theta }_{13}$ was first accurately found to be $8.5^{\circ }$ in 2012 by reactor oscillation experiments [4,5].

Various simple ansatzes for the PMNS matrix have been proposed, the most simple ones involving a zero reactor angle and bimaximal atmospheric mixing, $s_{13}=0$ and $s_{23}=c_{23}=1/\sqrt{2}$, leading to a PMNS matrix of the form

$$\begin{array}{c}\hfill U_0=\left(\begin{array}{ccc}{c}_{12}& s_{12}& 0\\ -\frac{s_{12}}{\sqrt{2}}& \frac{c_{12}}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ \frac{s_{12}}{\sqrt{2}}& -\frac{c_{12}}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right),\end{array}$$

(1)

where the zero subscript reminds us that this form has ${\theta }_{13}=0$ (and ${\theta }_{23}={45}^{\circ }$).

For golden ratio (GRa) mixing [6], the solar angle is given by $tan{\theta }_{12}=1/\varphi$, where $\varphi =(1+\sqrt{5})/2$ is the golden ratio, which implies ${\theta }_{12}=31.7^{\circ }$. There are two alternative versions where $cos{\theta }_{12}=\varphi /2$ and ${\theta }_{12}={36}^{\circ }$ [7], which we refer to as GRb mixing and GRc, where $cos{\theta }_{12}=\varphi /\sqrt{3}$ and ${\theta }_{12}\approx 20.9^{\circ }$.

For bimaximal (BM) mixing (see, e.g., [8,9,10] and references therein), we insert $s_{12}=c_{12}=1/\sqrt{2}$ (${\theta }_{12}={45}^{\circ }$) into Equation (1),

$$\begin{array}{c}\hfill U_{\mathrm{BM}}=\left(\begin{array}{ccc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& 0\\ -\frac{1}{2}& \frac{1}{2}& \frac{1}{\sqrt{2}}\\ \frac{1}{2}& -\frac{1}{2}& \frac{1}{\sqrt{2}}\end{array}\right).\end{array}$$

(2)

For tri-bimaximal (TB) mixing [11], alternatively, we use $s_{12}=1/\sqrt{3}$, $c_{12}=\sqrt{2/3}$ (${\theta }_{12}=35.{26}^{\circ }$) in Equation (1),

$$\begin{array}{c}\hfill U_{\mathrm{TB}}=\left(\begin{array}{ccc}\sqrt{\frac{2}{3}}& \frac{1}{\sqrt{3}}& 0\\ -\frac{1}{\sqrt{6}}& \frac{1}{\sqrt{3}}& \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{3}}& \frac{1}{\sqrt{2}}\end{array}\right).\end{array}$$

(3)

Finally, another pattern studied in the literature with ${\theta }_{13}=0$ (and ${\theta }_{23}={45}^{\circ }$) is the hexagonal mixing (HEX), where ${\theta }_{12}=\pi /6$.

These proposals are typically enforced by finite discrete symmetries such as $A_4,S_4,S_5$ (for a review, see, e.g., [12]). After the reactor angle was measured, which excluded all these ansatzes, there were various proposals to rescue them and to maintain the notion of the predictivity of the leptonic mixing parameters. Indeed, the measurement of the reactor angle opens up the possibility to predict the CP phase $\delta$, which has not been directly measured so far and remains poorly determined even indirectly. Two approaches have been developed, in which some finite symmetry (typically a subgroup of $A_4,S_4,S_5$) can enforce a particular structure of the PMNS matrix consistent with a non-zero reactor angle, leading to solar and atmospheric sum rules, as we now discuss.

The first approach, which leads to solar sum rules, is to assume that the above patterns of mixing still apply to the neutrino sector but receive charged lepton mixing corrections due to the PMNS matrix being the product of two unitary matrices, which, in our convention, is written as $V_{eL}{V}_{{\nu }_L}^{†}$, where $V_{{\nu }_L}^{†}$ is assumed to take the BM, TB or GR form, while $V_{eL}$ differs from the unit matrix. If $V_{eL}$ involves negligible 13 charged lepton mixing, then it is possible to generate a non-zero 13 PMNS mixing angle, while leading to correlations amongst the physical PMNS parameters, known as solar mixing sum rules [13,14,15,16]. This scenario may be enforced by a subgroup of $A_4,S_4,S_5$, which enforces the $V_{\nu }$ structure [12] while allowing charged lepton corrections.

In the second approach, which leads to atmospheric sum rules, it is assumed that the physical PMNS mixing matrix takes the BM, TB or GR form but only in its first or second column, while the third column necessarily departs from these structures due to the non-zero 13 angle. Such patterns again lead to correlations amongst the physical PMNS parameters, known as atmospheric mixing sum rules. This scenario may be enforced by a subgroup of $A_4,S_4,S_5$, which enforces the one column $V_{\nu }$ structure [12] while forbidding charged lepton corrections.

Apart from the large lepton mixing angles, another puzzle is the extreme lightness of neutrino masses. Although the type I seesaw mechanism can qualitatively explain the smallness of neutrino masses through the heavy right-handed neutrinos (RHNs), if one does not make other assumptions, it contains too many parameters to make any particular predictions for neutrino mass and mixing. The sequential dominance (SD) [17,18] of right-handed neutrinos proposes that the mass spectrum of heavy Majorana neutrinos is strongly hierarchical, i.e., $M_{\mathrm{atm}}\ll M_{\mathrm{sol}}\ll M_{\mathrm{dec}}$, where the lightest RHN with mass $M_{\mathrm{atm}}$ is responsible for the atmospheric neutrino mass that, with mass $M_{\mathrm{sol}}$, gives the solar neutrino mass, and a third largely decoupled RHN gives a suppressed lightest neutrino mass. It leads to an effective two right-handed neutrino (2RHN) model [19,20] with a natural explanation for the physical neutrino mass hierarchy, with normal ordering and the lightest neutrino being approximately massless, $m_1=0$.

A very predictive minimal seesaw model with two right-handed neutrinos and one texture zero is the so-called constrained sequential dominance (CSD) model [13,21,22,23,24,25,26,27,28,29]. The CSD(n) scheme, also known as the Littlest Seesaw, assumes that the two columns of the Dirac neutrino mass matrix are proportional to $(0,1,-1)$ and $(1,n,2-n)$ or $(1,2-n,n)$, respectively, in the RHN diagonal basis (or equivalently $(0,1,1)$ and $(1,n,n-2)$ or $(1,n-2,n)$), where the parameter n was initially assumed to be a positive integer but, in general, may be a real number. For example, the CSD(3) (also called the Littlest Seesaw model) [22,23,24,25,26], CSD(4) models [27,28] and CSD($2.5$) [30] can give rise to phenomenologically viable predictions for lepton mixing parameters and the two neutrino mass squared differences $\Delta m_{21}^2$ and $\Delta m_{31}^2$, corresponding to special constrained cases of lepton mixing that preserve the first column of the TB mixing matrix, namely TM1, and hence satisfy the atmospheric mixing sum rules. As has been observed, modular symmetry remarkably suggests CSD($1+\sqrt{6}$) ≈ CSD($3.45$) [31,32,33,34].

In this paper, we study neutrino solar and atmospheric mixing sum rules arising from discrete symmetries and also discuss the class of Littlest Seesaw (LS) models corresponding to CSD(n) with $n\approx 3$. The motivation is to study all the above symmetry-based approaches, namely solar and atmospheric mixing sum rules and LS models, together in one place so that they may be compared, and to give an up-to-date analysis of the predictions of all of these possibilities, when confronted with the most recent global fits. All these approaches offer predictions for the cosine of the leptonic CP phase $cos\delta$ in terms of the mixing angles, ${\theta }_{13}$, ${\theta }_{12}$, ${\theta }_{23}$, which can be tested in forthcoming high-precision neutrino experiments. In particular, we study the solar neutrino mixing sum rules, arising from charged lepton corrections to TB, BM and GR neutrino mixing, and atmospheric neutrino mixing sum rules, arising from preserving one of the columns of these types of mixing—for example, the first or second column of the TB mixing matrix (TM1 or TM2)—and we confront them with an up-to-date global fit of the neutrino oscillation data. We show that some mixing sum rules, e.g., all the atmospheric neutrino mixing sum rules arising from a golden ratio mixing, are already excluded at 3$\sigma$ apart from GRa2, and we determine the remaining models allowed by the data. We also give detailed comparative results for the highly predictive LS models (which are special cases of TM1). These models are highly predictive, with only two free real parameters fixing all the neutrino oscillation observables, making them candidates for being the most minimal predictive seesaw models of leptons still compatible with data. This is the first time that the three LS cases corresponding to CSD(n) with $n=2.5$, $n=3$ and $n=1+\sqrt{6}\approx 3.45$ have been studied together in one place, using the most up-to-date global fits. These three cases are predicted by theoretical models. In particular, $n=3$ is studied in a flavon model based on $S_4$  [22,23,24,25,26], $n=2.5$ is introduced in the tri-direct CP approach based on the flavor symmetry $S_4\times Z_5\times Z_8$ [30] and $n=1+\sqrt{6}\approx 3.45$ is derived in the modular symmetry framework with three $S_4$ groups [31,32,33,34]. We also propose a new means of analyzing these models, which allows accurate predictions for the least well-determined oscillation parameters ${\theta }_{12}$, ${\theta }_{23}$ and $\delta$ to be extracted.

The layout of the remainder of the paper is as follows. In Section 2, we introduce the notation for the PMNS matrix and discuss the symmetries of the leptonic Lagrangian. In Section 3 and Section 4, we introduce the atmospheric and solar sum rules for the different models that we study and confront them with the up-to-date neutrino data global fit. We proceed in Section 5 by discussing the CDS and the Littlest Seesaw model, showing its high predictivity and the viable parameter space given the experimental data and its fit. Finally, we conclude in Section 6.

2. Lepton Mixing and Symmetries

The mixing matrix in the lepton sector, the PMNS matrix $U_{\mathrm{PMNS}}$, is defined as the matrix that appears in the electroweak coupling to the W bosons expressed in terms of lepton mass eigenstates. With the mass matrices of charged leptons $M_e$ and neutrinos $M_{LL}^{\nu }$ written as1

$$\begin{array}{c}\hfill L=-\overline{e_L}{M}^e{e}_R-\frac{1}{2}\overline{{\nu }_L}{M}^{\nu }{\nu }_L^c+H.c.,\end{array}$$

(4)

and performing the transformation from flavor to mass basis by

$$\begin{array}{c}\hfill V_{e_L}{M}^e{V}_{e_R}^{†}=diag(m_e,m_{\mu },m_{\tau }),V_{{\nu }_L}{M}^{\nu }{V}_{{\nu }_L}^T=diag(m_1,m_2,m_3),\end{array}$$

(5)

the PMNS matrix is given by

$$\begin{array}{c}\hfill U_{\mathrm{PMNS}}=V_{e_L}{V}_{{\nu }_L}^{†}.\end{array}$$

(6)

Here, it is assumed implicitly that unphysical phases are removed by field redefinitions, and $U_{\mathrm{PMNS}}$ contains one Dirac phase and two Majorana phases. The latter are physical only in the case of Majorana neutrinos; for Dirac neutrinos, the two Majorana phases can be absorbed as well.

According to the above discussion, the neutrino mass and flavor bases are misaligned by the PMNS matrix as follows,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \left(\begin{array}{c}{\nu }_e\\ {\nu }_{\mu }\\ {\nu }_{\tau }\end{array}\right)=& \left(\begin{array}{ccc}{U}_{e1}& U_{e2}& U_{e3}\\ U_{\mu 1}& U_{\mu 2}& U_{\mu 3}\\ U_{\tau 1}& U_{\tau 2}& U_{\tau 3}\end{array}\right)\left(\begin{array}{c}{\nu }_1\\ {\nu }_2\\ {\nu }_3\end{array}\right)\equiv U_{\mathrm{PMNS}}\left(\begin{array}{c}{\nu }_1\\ {\nu }_2\\ {\nu }_3\end{array}\right),\hfill \end{array}\end{array}$$

(7)

where ${\nu }_e,{\nu }_{\mu },{\nu }_{\tau }$ are the $SU{\left(2\right)}_L$ partners to the left-handed charged lepton mass eigenstates and ${\nu }_{1,2,3}$ are the neutrinos in their mass basis. Following the standard convention, we can describe $U_{\mathrm{PMNS}}$ in terms of three angles, one CP violation phase and two Majorana phases,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill U_{\mathrm{PMNS}}=& \left(\begin{array}{ccc}1& 0& 0\\ 0& c_{23}& s_{23}\\ 0& -s_{23}& c_{23}\end{array}\right)\left(\begin{array}{ccc}{c}_{13}& 0& s_{13}{e}^{-\mathrm{i}\delta }\\ 0& 1& 0\\ -s_{13}{e}^{\mathrm{i}\delta }& 0& c_{13}\end{array}\right)\left(\begin{array}{ccc}{c}_{12}& s_{12}& 0\\ -s_{12}& c_{12}& 0\\ 0& 0& 1\end{array}\right)P,\hfill \end{array}\end{array}$$

(8)

$$\begin{array}{c}\hfill =\left(\begin{array}{ccc}{c}_{12}{c}_{13}& s_{12}{c}_{13}& s_{13}{e}^{-i\delta }\\ -s_{12}{c}_{23}-c_{12}{s}_{13}{s}_{23}{e}^{i\delta }& c_{12}{c}_{23}-s_{12}{s}_{13}{s}_{23}{e}^{i\delta }& c_{13}{s}_{23}\\ s_{12}{s}_{23}-c_{12}{s}_{13}{c}_{23}{e}^{i\delta }& -c_{12}{s}_{23}-s_{12}{s}_{13}{c}_{23}{e}^{i\delta }& c_{13}{c}_{23}\end{array}\right)P,\end{array}$$

(9)

where P contains the Majorana phases

$$\begin{array}{c}\hfill P=diag\left(1,e^{i{\alpha }_{21}/2},e^{i{\alpha }_{31}/2}\right),\end{array}$$

(10)

The current $3\sigma$ parameter intervals coming from the global fit of the neutrino oscillation data by the (nuFIT) http://www.nu-fit.org/ (accessed on 14 September 2023) collaboration [35] are

$$\begin{array}{c}\hfill {\theta }_{12}=[31.{31}^{\circ },35.{74}^{\circ }],{\theta }_{23}=[39.6^{\circ },51.9^{\circ }],{\theta }_{13}=[8.{19}^{\circ },8.{89}^{\circ }],\end{array}$$

(11)

$$\begin{array}{c}\delta =[0^{\circ },{44}^{\circ }]\&[{108}^{\circ },{360}^{\circ }],\frac{{\Delta }_{21}^2}{{10}^{-5}{\mathrm{eV}}^2}=[6.82,8.03],\\ \frac{{\Delta }_{3l}^2}{{10}^{-3}{\mathrm{eV}}^2}=[2.428,2.597].\end{array}$$

(12)

The PMNS matrix reads

$$\begin{array}{c}\hfill {\left|U\right|}_{3\sigma }^{\mathrm{w}/\mathrm{o}\mathrm{SK}-\mathrm{atm}}=\left(\begin{array}{ccc}0.803\to 0.845\hfill & 0.514\to 0.578\hfill & 0.142\to 0.155\hfill \\ 0.233\to 0.505\hfill & 0.460\to 0.693\hfill & 0.630\to 0.779\hfill \\ 0.262\to 0.525\hfill & 0.473\to 0.702\hfill & 0.610\to 0.762\hfill \end{array}\right).\end{array}$$

(13)

These results are obtained considering normal ordering, which is the current best fit, and without including the Super-Kamiokande (SK) data.

Simple mixing patterns such TB, BM or GR could explain the first neutrino oscillation data. These patterns can be enforced via symmetries of the mass matrices. Let us take a basis where the charged lepton $M_e$ mass matrix is diagonal, and we notice that, for three generations, we have that $Z_3^T$ is a symmetry of the Lagrangian

$$\begin{array}{c}\hfill T^{†}\left(M_e^{†}{M}_e\right)T=M_e^{†}{M}_e,\end{array}$$

(14)

where $T=diag\left(1,{\omega }^2,\omega \right)$ and $\omega =e^{i2\pi /3}$. The light Majorana neutrino mass matrix is invariant under the Klein symmetry: $Z_2^U\times Z_2^S$. This can be seen taking the diagonal neutrino mass matrix and performing the transformations

$$\begin{array}{c}\hfill M^{\nu }=S^T{M}^{\nu }S,M^{\nu }=U^T{M}^{\nu }U,\end{array}$$

(15)

and $M^{\nu }$ is left invariant with

$$\begin{array}{c}\hfill \begin{array}{c}S=U_{\mathrm{PMNS}}^{*}diag(+1,-1,-1)U_{\mathrm{PMNS}}^T\\ U=U_{\mathrm{PMNS}}^{*}diag(-1,+1,-1)U_{\mathrm{PMNS}}^T,\end{array}\end{array}$$

(16)

where this result follows from the fact that, in the charged lepton mass eigenstate basis, the neutrino mass matrix is diagonalized by $U_{\mathrm{PMNS}}$ as in Equation (5), where any two diagonal matrices commute. Then, Equation (16) shows that the matrices $S,U$ are both diagonalized by the same matrix $U_{\mathrm{PMNS}}$ that also diagonalizes the neutrino mass matrix. Given this result, we can always find the two matrices $S,U$ for any PMNS mixing matrix, and hence the Klein symmetry is present for any choice of the PMNS mixing. However, not all Klein symmetries may be identified with finite groups of low order.

This description is meaningful if the charged leptons are diagonal (T is conserved) or approximately diagonal (T is softly broken). We are therefore interested in finite groups that are supersets of $Z_2^U\times Z_2^S$ and $Z_3^T$ and have a triplet representation. Groups of low order that satisfy these constraints are given in Figure 1.

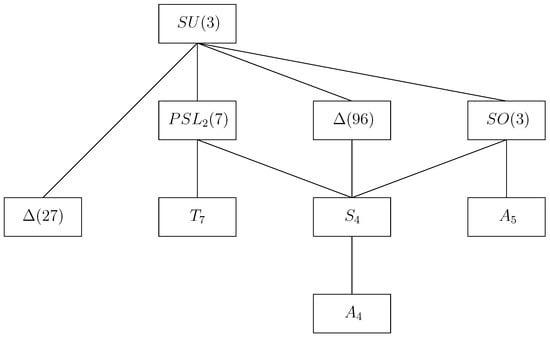
Figure 1. Subgroups of $SU\left(3\right)$ with triplet representations. The smaller of the two groups connected in the graph is a subset of the other. Figure from [12].

One simple example is the group $G=S_4$, of order 24, which is the group of permutation of four objects. The generators follow the presentation rules [12]

$$\begin{array}{c}\hfill S^2=T^3={\left(ST\right)}^3=U^2={\left(TU\right)}^2={\left(SU\right)}^2={\left(STU\right)}^4=1.\end{array}$$

(17)

The two possible $S_4$ triplet irreducible representations with a standard choice of basis [36] give the generators’ explicit expression

$$\begin{array}{c}\hfill S=\frac{1}{3}\left(\begin{array}{ccc}-1& 2& 2\\ 2& -1& 2\\ 2& 2& -1\end{array}\right),T=\left(\begin{array}{ccc}1& 0& 0\\ 0& {\omega }^2& 0\\ 0& 0& \omega \end{array}\right),U=\mp \left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right),\end{array}$$

(18)

where, again, $\omega =e^{i2\pi /3}$, and the sign of the U matrix corresponds to the two different triplet representations. The group $S_4$ predicts TB mixing [11]; see Figure 2. This can be checked by the fact that S and U are diagonalized by $U_{\mathrm{TB}}$; see Equation (16). Another commonly used group is $A_4$, which has two generators S and U that follow the same presentation rules as in Equation (17), and, in a standard basis [37], the generators have the same form as in Equation (18).

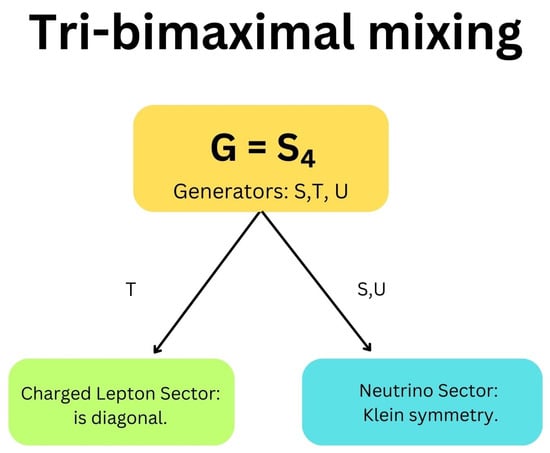
Figure 2. A schematic diagram that illustrates the way in which the two subgroups $Z_2^U\times Z_2^S$ and $Z_3^T$ of a finite group work in the charged lepton and neutrino sectors in order to enforce a particular pattern of PMNS mixing. In this example, the group $S_4$ leads to TB mixing.

In order to explain the experimental results, G needs to be broken down to generate a non-zero $\left(13\right)$ PMNS element. This will lead to corrections to the leading order PMNS predictions from the discrete group G. In Figure 3, we illustrate two possible directions by which we can proceed. The first one is to break the T generator while the Klein symmetry in the neutrino sector is exact (left-hand side). This means that the charged lepton matrix is approximately diagonal. In the mass basis, we will have then a correction to the neutrino mixing matrix by a unitary matrix $V_e$ and the PMNS is now $U_{\mathrm{PMNS}}=V_e^{†}{V}_{\nu }$. Applying this to a group G will lead to solar sum rules. The second direction is to preserve $Z_3^T$ but break $Z_2^U$ while keeping either $Z_2^{SU}$ or $Z_2^S$ unbroken (right-hand side). This leads to corrections to the prediction of G within the neutrino mixing and to atmospheric sum rules. It is convenient to introduce small parameters that can simplify the sum rule expressions and help us to understand their physical behavior since, both in solar and atmospheric sum rules, we implement a small deviation from the prediction of the exact finite discrete symmetries. We can consider the deviation parameters $s,r,a$ [38]

$$\begin{array}{c}\hfill sin{\theta }_{12}\equiv \frac{1+s}{\sqrt{3}},sin{\theta }_{13}\equiv \frac{r}{\sqrt{2}},sin{\theta }_{23}\equiv \frac{1+a}{\sqrt{2}},\end{array}$$

(19)

that highlight the differences from TB mixing. Given the latest fit, the $3\sigma$ allowed range for the solar, reactor and atmospheric deviation is, respectively,

$$\begin{array}{c}\hfill \begin{array}{c}-0.0999<s<0.0117,\\ 0.20146<r<0.21855,\\ -0.0985<a<0.1129.\end{array}\end{array}$$

(20)

This shows that the reactor angle differs from zero significantly ($r\ne 0$), but the solar and atmospheric angles remain consistent with TB mixing ($s=a=0$) at $3\sigma$. From a theoretical point of view, one of the goals of neutrino experiments would be to exclude the TB prediction $s=a=0$ [39], which is so far still allowed at $3\sigma$.

Figure 3. In order to generate a non-zero (13) PMNS element, one or more of the generators $S,T,U$ must be broken. In the left panel, we depict T breaking, leading to charged lepton mixing corrections and possible solar sum rules. In the right panel, U is broken, while either S or $SU$ is preserved, leading to neutrino mixing corrections and atmospheric sum rules.

3. Solar Mixing Sum Rules

The first possibility to generate a non-zero reactor angle, whilst maintaining some of the predictivity of the original mixing patterns, is to allow the the charged lepton sector to give a mixing correction to the leading order mixing matrix $U_{\nu }$. This will lead to the so-called solar sum rules, which are relations between the parameters that can be tested. This operation is equivalent to considering the T generator of the $S_4$ symmetry, which enforces the charged lepton mass matrix to be diagonal (in our basis) to be broken.

When the T generator is broken, the charged lepton matrix is not exactly diagonal and it will give a correction to the PMNS matrix predicted by the symmetry group G. For example, for the $S_4$, $U_{\mathrm{PMNS}}$ is not exactly $U_{\mathrm{TB}}$ but it receives a correction that we will compute. The fact that S and U are preserved leads to a set of correlations among the physical parameters, the solar sum rules, which are the predictions of the model. For the solar sum rules, we can obtain a prediction for $cos\delta$, as we shall now show.

For example, consider the case of TB neutrino mixing with the charged lepton mixing corrections involving only (1,2) mixing, so that the PMNS matrix in Equation (6) is given by

$$\begin{array}{c}{U}_{\mathrm{PMNS}}=\left(\begin{array}{ccc}{c}_{12}^e& s_{12}^e{e}^{-i{\delta }_{12}^e}& 0\\ -s_{12}^e{e}^{i{\delta }_{12}^e}& c_{12}^e& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{ccc}\sqrt{\frac{2}{3}}& \frac{1}{\sqrt{3}}& 0\\ -\frac{1}{\sqrt{6}}& \frac{1}{\sqrt{3}}& \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{3}}& \frac{1}{\sqrt{2}}\end{array}\right)\\ =\left(\begin{array}{ccc}\cdots & \cdots & \frac{s_{12}^e}{\sqrt{2}}{e}^{-i{\delta }_{12}^e}\\ \cdots & \cdots & \frac{c_{12}^e}{\sqrt{2}}\\ \frac{1}{\sqrt{6}}& -\frac{1}{\sqrt{3}}& \frac{1}{\sqrt{2}}\end{array}\right)\end{array}$$

(21)

The elements of the PMNS matrix are clearly related by [16,40]

$$\begin{array}{c}\hfill \frac{|U_{\tau 1}|}{|U_{\tau 2}|}=\frac{s_{12}^{\nu }}{c_{12}^{\nu }}=t_{12}^{\nu }=\frac{1}{\sqrt{2}}.\end{array}$$

(22)

This relation is easy to understand if we consider only one charged lepton angle to be non-zero, ${\theta }_{12}^e$, and the third row of the PMS matrix in Equation (21) is unchanged, so the elements $U_{\tau i}$ may be identified with the corresponding elements in the uncorrected mixing matrix in Equation (1). Interestingly, the above relation still holds even if both ${\theta }_{12}^e$ and ${\theta }_{23}^e$ are non-zero. However, it fails if ${\theta }_{13}^e\ne 0$ [41].

The above relation in Equation (22) can be translated into a prediction for $cos\delta$ as [40]2

$$\begin{array}{c}cos\delta =\\ \frac{tan{\theta }_{23}sin{\theta }_{12}^2+sin{\theta }_{13}^{2}cos{\theta }_{12}^2/tan{\theta }_{23}-{(sin{\theta }_{12}^{\nu })}^2\left(tan{\theta }_{23}+sin{\theta }_{13}^2/tan{\theta }_{23}\right)}{sin2{\theta }_{12}sin{\theta }_{13}},\end{array}$$

(23)

where only the parameter $sin{\theta }_{12}^{\nu }$ is model-dependent, and we have, respectively, $sin{\theta }_{12}^{\nu }=1/\sqrt{3}$, $sin{\theta }_{12}^{\nu }=1/\sqrt{2}$, $tan{\theta }_{12}^{\nu }=1/\phi$ and ${\theta }_{12}^{\nu }=\pi /5$, $cos{\theta }_{12}^{\nu }=\phi /\sqrt{3}$ and ${\theta }_{12}^{\nu }=\pi /6$ for mixing based on TB, BM, GRa, GRb, GRc and HEX, where $\phi =(1+\sqrt{5})/2$.

Let us discuss an approximation of the sum rules for the TB mixing as an example, where $sin{\theta }_{12}^{\nu }=1/\sqrt{3}$. We can re-write Equation (23) using the parameters s, a and r defined in Equation (19) and then expand them. The linearized sum rule reads [38]

$$\begin{array}{c}\hfill cos\delta =\frac{s}{r},\end{array}$$

(24)

but it does not describe adequately the exact sum rules as shown in the left panel of Figure 4.

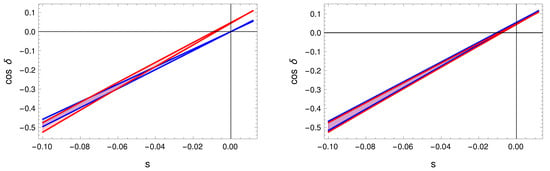
Figure 4. Solar mixing sum rule predictions for TB neutrino mixing. In both panels, the red band is the allowed region of the exact TB solar sum rules using the $3\sigma$ range of r (i.e., the deviation of $sin{\theta }_{13}$ from the TB value). It is plotted in the $3\sigma$ range of s (i.e., the deviation of $sin{\theta }_{12}$ from the TB value) and using the best fit value $a=0.071$. The exact sum rules correspond to Equation (23). Similarly, the blue band is the linearized sum rule allowed region, which is given in Equation (24). In the right panel, the blue band is the second-order expansion sum rule prediction (Equation (25)) and it matches the exact sum rule.

Therefore, we can proceed to the second-order expansion, which is

$$\begin{array}{c}\hfill cos\delta =\frac{s}{r}+\frac{r^2+8as}{4r},\end{array}$$

(25)

and it matches the exact sum rule behavior as seen in the right panel in Figure 4. Similarly, we can obtain higher-order expansion for the other cases and check them against the data, as for the BM case shown in Figure 5. In this case, we did not choose the best fit value for a because it would fall outside of the physical range of $cos\delta$, since BM is almost excluded by the data. The approximated expression for the sum rules can help us to understand its behavior and the dependence of $cos\delta$ on the other parameters that are, in general, non-linear and assess the deviation from the non-corrected PMNS mixing. We then expect, for the exact sum rules, a first-order linear dependence on s.

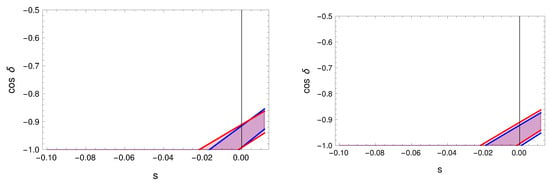
Figure 5. Solar sum rule predictions for BM neutrino mixing. In both panels, the red band is the allowed region of the exact BM solar sum rules using the $3\sigma$ range of r (i.e., the deviation of $sin{\theta }_{13}$ from the TB value). It is plotted in the $3\sigma$ range of s (i.e., the deviation of $sin{\theta }_{12}$ from the TB value) and using the value $a=-0.1$. The exact sum rules correspond to Equation (23). Similarly, the blue band is the linearized sum rule allowed region, which is given in Equation (24). In the right panel, the blue band is the second-order expansion sum rule prediction (Equation (25)) and it matches the exact sum rule.

In Figure 6, we present the exact sum rule prediction from Equation (23) for TB, BM, GRa, GRb, GRc and HEX and the constraints from the fit of the neutrino oscillation data [35]. We require $cos\delta$ to fall within the physical range $-1<cos\delta <1$ and we present it in the y-axis. In all panels, the x-axis is ${sin}^2{\theta }_{12}$ and the different color bands are sampled in the allowed $sin{\theta }_{23}$ region. The width of the band is given by allowing $sin{\theta }_{13}$ to vary in its $3\sigma$ range. We notice that the ${\theta }_{12}^{\nu }={45}^{\circ }$ BM mixing (top-right panel) is closed to be excluded at $3\sigma$ and only low values of ${sin}^2{\theta }_{12}$ and high values of ${sin}^2{\theta }_{12}$ are still viable. Similarly, for GRc mixing (bottom-left panel), with $cos{\theta }_{12}^{\nu }=\phi /3$, the viable parameter space is very tight; only for maximal values of $sin{\theta }_{13}$ and minimal values of $sin{\theta }_{12}$ and $sin{\theta }_{23}$ can we obtain physical results for the CP phase. For TB mixing (top-left panel) with $sin{\theta }_{12}^{\nu }=1/\sqrt{3}$ in the neutrino sector with charged lepton correction, we obtain consistent results in the whole parameter space, with a prediction for $cos\delta$ that shows an approximately linear dependence on ${sin}^2{\theta }_{12}$, as understood by the leading order term in the sum rules in Equation (24). The prediction for the CP phase lies in the $0.52\lesssim cos\delta \lesssim 0.12$ range. The yellow and green bands are the $1\sigma$ ranges, respectively, of ${sin}^2{\theta }_{12}$ and $cos\delta$, and we notice how these ranges favor GRa and GRb mixing. For both these models, we see that the predictions of $cos\delta$ are in the negative plane. For GRa (center-left panel), with $tan{\theta }_{12}^{\nu }=1/\phi$, the whole parameter space leads to a physical prediction of $cos\delta$. For GRb (center-right panel), with ${\theta }_{12}^{\nu }=\pi /5$ mixing, larger values $sin{\theta }_{23}$ are excluded for small values of ${sin}^2{\theta }_{12}$. We finally notice that TM and HEX are the only models predicting positive values of $cos\delta$ and HEX (bottom-right panel), with ${\theta }_{12}^{\nu }=\pi /6$ in particular being the only predicting values of $cos\delta \gtrsim 0.2$. Of the mixing patterns studied, GRa and GRb are favored by the current $1\sigma$ ranges and BM and GRc are much disfavored and only consistent with the far corners of the parameter space, with a prediction of $|cos\delta |\approx 1$.

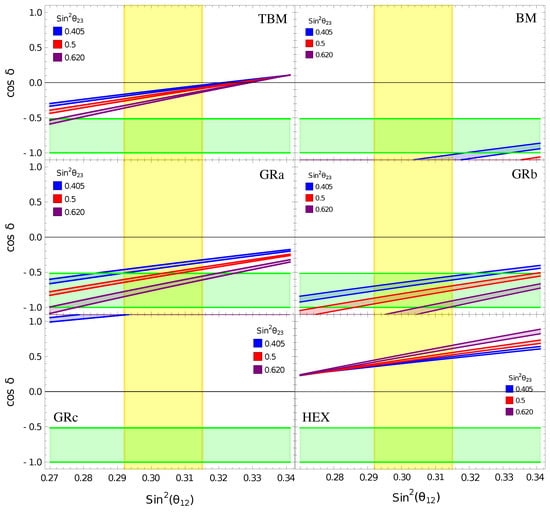
Figure 6. Summary of exact solar sum rule predictions for different types of neutrino mixing. In the top left-hand panel, we present, with the different colored bands, the sum rule predictions for TB for $cos\delta$, allowing $sin{\theta }_{12}$ to vary in its $3\sigma$ range; the different colors denote different choices of $sin{\theta }_{23}$ given in the legend, in its $3\sigma$ range, and the width of the band is given by the $3\sigma$ range in $sin{\theta }_{13}$. The green and yellow bands are the $1\sigma$ ranges for, respectively, $cos\delta$ and $sin{\theta }_{23}$. Similar plots for BM, GRa, GRb, GRc and HEX are presented, respectively, in the top-right, center-right, center-left, bottom-left and bottom-right panels. The exact sum rules for the different models are derived from Equation (23).

4. Atmospheric Mixing Sum Rules

In this section, we discuss the second possibility, which is to have the T generator unbroken; therefore, the charged lepton mixing matrix is exactly diagonal. In this case, the correction to the PMNS matrix predicted from the group G comes from the neutrino sector and it provides a non-zero reactor angle. For each group, there are two possible corrections achieved by either breaking U and preserving S or with S and U broken and SU preserved. Therefore, for each discrete symmetry, we study two mixing patterns [43,44,45].

Let us consider again $G=S_4$ and the TB mixing in Equation (3) as an example. If we break S and U but preserve $SU$, the first column of the TB matrix is preserved and we have the so-called TM1 mixing pattern [46,47]:

$$\begin{array}{c}\hfill U_{\mathrm{TM}1}\approx \left(\begin{array}{ccc}\sqrt{\frac{2}{3}}& -& -\\ -\frac{1}{\sqrt{6}}& -& -\\ \frac{1}{\sqrt{6}}& -& -\end{array}\right).\end{array}$$

(26)

If instead S is unbroken the second column is preserved, we have the second mixing pattern TM2:

$$\begin{array}{c}\hfill U_{\mathrm{TM}2}\approx \left(\begin{array}{ccc}-& \sqrt{\frac{1}{3}}& -\\ -& \sqrt{\frac{1}{3}}& -\\ -& -\sqrt{\frac{1}{3}}& -\end{array}\right).\end{array}$$

(27)

We can explicitly check this noticing that

$$\begin{array}{c}\hfill S\left(\begin{array}{c}\sqrt{\frac{1}{3}}\\ \sqrt{\frac{1}{3}}\\ \sqrt{\frac{1}{3}}\end{array}\right)=\left(\begin{array}{c}\sqrt{\frac{1}{3}}\\ \sqrt{\frac{1}{3}}\\ \sqrt{\frac{1}{3}}\end{array}\right),\end{array}$$

(28)

meaning that the second column of the TB mixing matrix is an eigenvector of the S matrix. This is similar for the first column with the $SU$ matrix.

In this second case, where the second column of the TB matrix is conserved, we have

$$\begin{array}{c}\hfill \left|U_{e2}\right|=\left|U_{\mu 2}\right|=\left|U_{\tau 2}\right|=\frac{1}{\sqrt{3}},\end{array}$$

(29)

and, given the parametrization in Equation (9), we have

$$\begin{array}{cc}\hfill \left|U_{e2}\right|=|s_{12}& c_{13}|,\left|U_{\mu 2}\right|=|c_{12}{c}_{23}-s_{12}{s}_{13}{s}_{23}{e}^{i\delta }|,\hfill \end{array}$$

(30)

$$\begin{array}{cc}& \left|U_{\tau 2}\right|=|-c_{12}{s}_{23}-s_{12}{s}_{13}{c}_{23}{e}^{i\delta }|.\hfill \end{array}$$

(31)

Using the first equation $\left|U_{e2}\right|=\left|s_{12}{c}_{13}\right|$, we have the first atmospheric sum rule

$$\begin{array}{c}\hfill s_{12}^2=\frac{1}{3c_{13}^2},\end{array}$$

(32)

which allows us to write ${\theta }_{12}$ in terms of ${\theta }_{13}$, and removing a parameter in our description gives a prediction that can be tested. Using Equation (32) and $|c_{12}{c}_{23}-s_{12}{s}_{13}{s}_{23}{e}^{i\delta }{|}^2=\frac{1}{3}$, we obtain the second atmospheric sum rule [46,47]:

$$\begin{array}{c}\hfill cos\delta =\frac{2c_{13}cot2{\theta }_{23}cot2{\theta }_{13}}{\sqrt{2-3s_{13}^2}}.\end{array}$$

(33)

For the other models, the discussion is similar, where we call $X_1$ and $X_2$ the atmospheric sum rules, respectively, derived by preserving the first and second columns of the unbroken group with mixing X. In terms of the deviation parameters for TM2, we have the sum rule

$$\begin{array}{c}\hfill cos\delta =\frac{2a(2+a)\left(-1+r^2\right)}{(1+a)\sqrt{1-2a-a^2}r\sqrt{4-3r^2}}.\end{array}$$

(34)

We can expand this expression for small deviation parameters and, at the zero-th order, we have [43]

$$\begin{array}{c}\hfill cos\delta =-\frac{2a}{r}\end{array}$$

(35)

In Figure 7, we test this approximation against the exact sum rules using the experimental constraint in (12). We can see that, given the updated data, the linear approximation is now insufficient to describe the exact expression as it was instead in previous studies [43]. This is similar for TM1, as seen in Figure 8. This is also true for the other model that we discuss later, and, therefore, we provide the higher-order expansions that agree with the exact sum rule in Equation (34) given the current data:

$$\begin{array}{c}\hfill cos\delta =-\frac{2a}{r}-\frac{a^2}{r}\end{array}$$

(36)

For the TM2 example, we see in Figure 7 that the second-order expansion is a good description of the exact sum rule. For TM1, instead, as shown in Figure 8, the third-order expansion is needed.

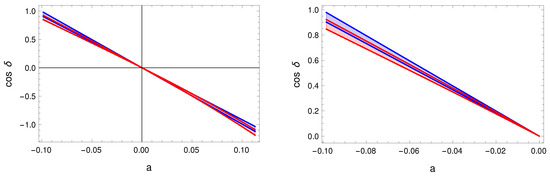
Figure 7. The red band is the allowed region of the exact TM2 sum rules using the 3$\sigma$ range of r and a (i.e., the deviation of $sin{\theta }_{13}$ and $sin{\theta }_{23}$ from the TB value), and it corresponds to Equation (33). The blue band is given by the linearized sum rule that is given in Equation (35). On the right, we zoom in on the region $-0.1<a<0$.

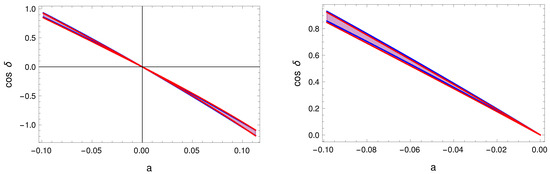
Figure 8. The red band is the allowed region of the exact TM2 sum rules using the 3$\sigma$ range of r and a (i.e., the deviation of $sin{\theta }_{13}$ and $sin{\theta }_{23}$ from the TB value), and it corresponds to Equation (33). The blue band is given by the second-order sum rule that is given in Equation (36). On the right, we zoom in on the region $-0.1<a<0$.

Since the second exact sum rules are quite involved, having an approximated expression is of help to understand the physical meaning of it and to understand the difference with respect to the TB model. We present in Table 1 the exact and approximated second sum rules for TM1, TM2 and GRa2, which, as we will see later, are the viable atmospheric mixing. Note that the approximated expression leads to simple results for TM1 and TM2 because the parameters a, r and s are built as deviation parameters from the TB mixing and, beyond the first-order expansion, they may not bring new insights for other types of mixing. We present in Table 2 the first atmospheric sum rules used in Figure 9. These results were derived using the normal ordered data without SK atmospheric results; the discussion regarding linearization is the same including SK or considering the inverted ordering since $sin{\theta }_{13}$ is very constrained and it does not change much in the different cases considered.

Table 1. Exact and approximated sum rules for the experimentally viable models, where $\theta =arctan\frac{1}{\varphi }$ and $\varphi =\frac{1+\sqrt{5}}{2}$.

	Exact Sum Rule	Approximated Sum Rule
TM1	$cos\delta =-\frac{cot2{\theta }_{23}\left(1-5sin{\theta }_{13}^2\right)}{2\sqrt{2}sin{\theta }_{13}\sqrt{1-3sin{\theta }_{13}^2}}$	$cos\delta =\frac{a}{r}+\frac{a^2}{2r}+\frac{2a^3}{r}-\frac{7ar}{4}$
TM2	$cos\delta =\frac{2cos{\theta }_{13}cot2{\theta }_{23}cot2{\theta }_{13}}{\sqrt{2-3sin{\theta }_{13}^2}}$	$cos\delta =-\frac{2a}{r}-\frac{a^2}{r}$
GRa2	$cos\delta =\frac{(1-{tan}^2{\theta }_{23})csc\theta (1-3{sin}^2{\theta }_{13}+(1+{sin}^2{\theta }_{13})cos2\theta )}{8sin{\theta }_{13}cos{\theta }_{23}\sqrt{{cos}^2{\theta }_{13}-{sin}^2\theta }}$	$cos\delta =a\frac{\sqrt{1+cos2\theta }csc\theta }{r}\left(1+\frac{a}{2}\right)$

Table 2. Exact sum rules plotted in Figure 9, where $\theta =arctan\frac{1}{\varphi }$ and $\varphi =\frac{1+\sqrt{5}}{2}$.

TM1	$cos{\theta }_{12}=\sqrt{\frac{2}{3}}\frac{1}{cos{\theta }_{13}}$	TM2	$sin{\theta }_{12}=\frac{1}{\sqrt{3}cos{\theta }_{13}}$
BM1	$cos{\theta }_{12}=\frac{1}{\sqrt{2}cos{\theta }_{13}}$	BM2	$cos{\theta }_{12}=\frac{1}{\sqrt{2}cos{\theta }_{13}}$
GRa1	$cos{\theta }_{12}=\frac{cos\theta }{cos{\theta }_{13}}$	GRa2	$cos{\theta }_{12}=\frac{sin\theta }{cos{\theta }_{13}}$
GRb1	$cos{\theta }_{12}=\frac{1+\sqrt{5}}{4cos{\theta }_{13}}$	GRb2	$sin{\theta }_{12}=\frac{\sqrt{5+\sqrt{5}}}{4cos{\theta }_{13}}$
GRc1	$cos{\theta }_{12}=\frac{1+\sqrt{5}}{2\sqrt{3}cos{\theta }_{13}}$	GRc2	$sin{\theta }_{12}=\frac{1+\sqrt{5}}{2\sqrt{3}cos{\theta }_{13}}$
HEX1	$cos{\theta }_{12}=\frac{\sqrt{3}}{2cos{\theta }_{13}}$	HEX2	$sin{\theta }_{12}=\frac{1}{2\sqrt{2}cos{\theta }_{13}}$

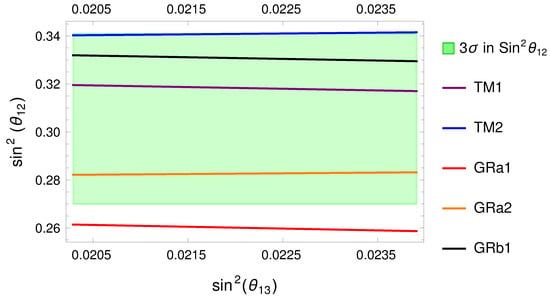
Figure 9. Summary of exact atmospheric sum rule predictions that predict the solar angle for different types of lepton mixing corresponding to a preserved column of the PMNS matrix, with only a mild dependence on the reactor angle. The corresponding Equations are collected in Table 2. The pink, blue, red, orange and black curves are, respectively, the predictions for TM1, TM2, GRa1, GRa2 and GRb1 mixing patterns. The $3\sigma$ allowed region is in green.

In Figure 9 and Figure 10, we study the exact atmospheric sum rules for models obtained modifying TB, BM, GRa, GRb, GRc and HEX. In Figure 9, we present the first atmospheric sum rule in Table 2, where the green band is the $3\sigma$ range for ${sin}^2{\theta }_{12}$. The models that do not appear are already excluded and far from the $3\sigma$ region. Therefore, BM1, BM2, GRa1, GRb2, GRc1, GRc2, HEX1 and HEX2 are already excluded. In red, we show GRa1, which is excluded at $3\sigma$; in blue, we show TM2, which is still not excluded but only in a narrow parameter space, for high values of the solar and atmospheric angle. TM1 is shown in purple, GRa2 in orange and GRb1 in black.

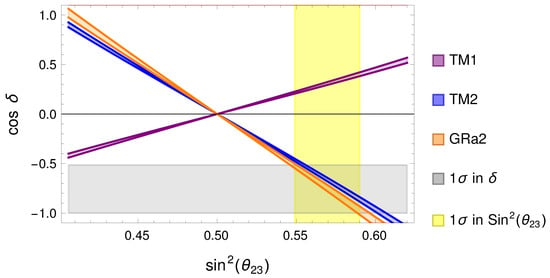
Figure 10. Summary of exact atmospheric sum rule predictions that predict $cos\delta$ in terms of the other mixing angles for different types of lepton mixing corresponding to a preserved column of the PMNS matrix. The corresponding Equations are collected in Table 1. We present with the blue band the exact sum rule prediction for TM2 for $cos\delta$, letting $sin{\theta }_{13}$ vary in its $3\sigma$ range. In orange and purple, we present the exact the sum rule predictions for GRa2 and TM1. The yellow and gray regions are, respectively, the $1\sigma$ ranges of $sin{\theta }_{23}$ and $cos\delta$, while the plot covers the whole $3\sigma$ range.

In Figure 10, we show the exact atmospheric sum rules (Table 1) and the corresponding equations for other models that are still allowed from Figure 9. We plot $cos\delta$ against $sin{\theta }_{23}$ and, letting $sin{\theta }_{13}$ vary in its $3\sigma$ range, this gives the width of the different bands. In yellow and gray, respectively, are the $1\sigma$ bands for ${sin}^2{\theta }_{23}$ and $cos\delta$. The GRb1 mixing does not appear in the plot because it lies within unphysical values of $cos\delta$. In purple, blue and orange, we present TM1, TM2 and GR12. We can see that, given the $1\sigma$ bands, the GRa2 mixing is favored when considering normal ordering and without the SK data, since TM2 is allowed only in a small portion of the parameter space, as shown in Figure 9.

5. Littlest Seesaw

There are many mechanisms proposed to explain the smallness of the neutrino masses and that remain consistent with the data. For example, the type I seesaw mechanism can address the problem through the introduction of heavy right-handed neutrinos. However, in general, it contains too many parameters to make any predictions for the neutrino mass and mixing. The constrained sequential dominance (CSD) model is a very predictive minimal seesaw model with two right-handed neutrinos and one texture zero [13,21,22,23,24,25,26,27,28,29]. As discussed in the Introduction, the CSD(n) scheme assumes that the two columns of the Dirac neutrino mass matrix are proportional to $(0,1,-1)$ and $(1,n,2-n)$ or $(1,2-n,n)$, respectively, in the RHN diagonal basis (or equivalently $(0,1,1)$ and $(1,n,n-2)$ or $(1,n-2,n)$), where the parameter n was initially assumed to be a positive integer but, in general, may be a real number. For example, the CSD(3) (also called the Littlest Seesaw model) [22,23,24,25,26] can give rise to phenomenologically viable predictions for lepton mixing parameters and the two neutrino mass squared differences $\Delta m_{21}^2$ and $\Delta m_{31}^2$, corresponding to special constrained cases of lepton mixing that preserve the first column of the TB mixing matrix, namely TM1, and hence satisfy the atmospheric mixing sum rules.

The Littlest Seesaw (LS) mechanism is one of the most economic neutrino mass generation mechanisms that is still consistent with the experimental neutrino data [22,23,24]. We will show that after the choice of a specific n value, all the neutrino observables are fixed by two free parameters. Different values of n can be realized by different discrete symmetry groups. The LS introduces two new Majorana right-handed (RH) neutrinos $N_R^{atm}$ and $N_R^{sol}$ that will be mostly responsible for providing the atmospheric and solar neutrino mass, respectively, and the lightest SM neutrino is approximately massless; this is the idea of the sequential dominance (SD) of RH neutrinos combined with the requirement for the $N_R^{atm}$-${\nu }_e$ interaction to be zero [48]. The Majorana neutrino mass matrix is given by the standard type I seesaw equation

$$\begin{array}{c}\hfill M^{\nu }=-m^D{M}_R^{-1}{m}^{D^T},\end{array}$$

(37)

where the RH neutrino mass matrix $M_R$ is a $2\times 2$ diagonal matrix,

$$\begin{array}{c}\hfill M_R=\left(\begin{array}{cc}{M}_{\mathrm{atm}}& 0\\ 0& M_{\mathrm{sol}}\end{array}\right),M_R^{-1}=\left(\begin{array}{cc}{M}_{\mathrm{atm}}^{-1}& 0\\ 0& M_{\mathrm{sol}}^{-1}\end{array}\right),\end{array}$$

(38)

where the convention for the heavy Majorana neutrino mass matrix corresponds to the Lagrangian term $-\frac{1}{2}\overline{{\nu }_R^c}{M}_R{\nu }_R$ (which is equivalent to $-\frac{1}{2}{\nu }_R^T{M}_R{\nu }_R$) and the convention for the light Majorana neutrino mass matrix corresponds to the Lagrangian term $-\frac{1}{2}\overline{{\nu }_L}{M}^{\nu }{\nu }_L^c$ as in Equation (5), which follows after performing the seesaw mechanism in Equation (37) [12]3.

The Dirac mass matrix in left-right (LR) convention is a $3\times 2$ matrix with arbitrary entries

$$\begin{array}{c}\hfill m^D=\left(\begin{array}{cc}d& a\\ e& b\\ f& c\end{array}\right),{\left(m^D\right)}^T=\left(\begin{array}{ccc}d& e& f\\ a& b& c\end{array}\right),\end{array}$$

(39)

where the entries are the coupling between the Majorana RH neutrinos and the SM neutrinos. The first column describes the interaction of the neutrinos in the flavor basis with the atmospheric RH neutrino and the second with the solar RH neutrino. The SD assumptions are that $d=0$, $d\ll e,f$ and

$$\begin{array}{c}\hfill \frac{{(e,f)}^2}{M_{\mathrm{atm}}}\gg \frac{{(a,b,c)}^2}{M_{\mathrm{sol}}}.\end{array}$$

(40)

These, together with the choice of the almost massless neutrino to be the first mass eigenstate $m_1$, leads to $m_3\gg m_2$ and therefore a normal mass hierarchy. This description can be further constrained choosing exactly $e=f$, $b=na$ and $c=(n-2)a$, giving a simplified Dirac matrix

$$\begin{array}{c}\hfill m^D=\left(\begin{array}{cc}0& a\\ e& na\\ e& (n-2)a\end{array}\right),\end{array}$$

(41)

which is called the constrained dominance sequence (CSD) for the real number n [13,21,22]. It has been shown that the reactor angle is [23]

$$\begin{array}{c}\hfill {\theta }_{13}\sim (n-1)\frac{\sqrt{2}}{3}\frac{m_2}{m_3}.\end{array}$$

(42)

Therefore, this can provide a non-zero and positive angle for $n>1$ and also excludes already models with $n\ge 5$ since they do not fit the experimental value. The choice $n\approx 3$ provides good fits to the data, as we shall discuss. Following the literature, we will refer to CSD(n) models with $n\approx 3$ as Littlest Seesaw (LS) models [23].

The LS Lagrangian unifies in one triplet of flavor symmetry the three families of electroweak lepton doublets, while the two extra right-handed neutrinos, $N_R^{\mathrm{atm}}$ and $N_R^{\mathrm{sol}}$, are singlets and read [23]

$$\begin{array}{c}\mathcal{L}=-y_{\mathrm{atm}}\overline{L}·{\varphi }_{\mathrm{atm}}{N}_R^{\mathrm{atm}}-y_{\mathrm{sol}}\overline{L}·{\varphi }_{\mathrm{sol}}{N}_R^{\mathrm{sol}}-\\ \frac{1}{2}{M}_{\mathrm{atm}}{N}_R^{\mathrm{atm}}{N}_R^{\mathrm{atm}}-\frac{1}{2}{M}_{\mathrm{sol}}{N}_R^{\mathrm{sol}}{N}_R^{\mathrm{sol}}+h.c.,\end{array}$$

(43)

which can be enforced by a $Z_3$ symmetry and where ${\varphi }_{\mathrm{atm}}$ and ${\varphi }_{\mathrm{sol}}$ can be either Higgs-like triplets under the flavor symmetry or a combination of Higgs electroweak doublets and flavons depending on the specific choice of symmetry to use. In both cases, the alignment should follow

$$\begin{array}{c}\hfill {\varphi }_{\mathrm{atm}}^T\propto (0,1,1),{\varphi }_{\mathrm{sol}}^T\propto (1,n,n-2),\end{array}$$

(44)

or

$$\begin{array}{c}\hfill {\varphi }_{\mathrm{atm}}^T\propto (0,1,1),{\varphi }_{\mathrm{sol}}^T\propto (1,n-2,n).\end{array}$$

(45)

We will refer to the first possibility in Equation (44) as the normal case [22,23] and the second in Equation (45) as the flipped case [24]. The predictions for n in the flipped case are related to the normal one by

$$\begin{array}{c}\hfill tan{\theta }_{23}\to cot{\theta }_{23}({\theta }_{23}\to \pi -{\theta }_{23})\&\delta \to \delta +\pi .\end{array}$$

(46)

Therefore, we will discuss them together as one single n case.

There is an equivalent convention that can be found in the literature [33], where the alignment is chosen to be

$$\begin{array}{c}\hfill {\varphi }_{\mathrm{atm}}^T\propto (0,1,-1),{\varphi }_{\mathrm{sol}}^T\propto (1,n,2-n).\end{array}$$

(47)

or

$$\begin{array}{c}\hfill {\varphi }_{\mathrm{atm}}^T\propto (0,1,-1),{\varphi }_{\mathrm{sol}}^T\propto (1,2-n,n).\end{array}$$

(48)

which leads to the same results as the previous two cases, respectively. In the neutrino mass matrix, there will appear a $(-1)$ factor that is only a non-physical phase, which can therefore be neglected. In particular, the case $n=1+\sqrt{6}$ that can be obtained with modular symmetry in [33]4 is still $n=1+\sqrt{6}$ in our convention using Equation (44). This means that the case $n=1-\sqrt{6}$ is merely the flipped version of $n=1+\sqrt{6}$ and not a new LS model. We will follow the derivation in [23] and, using Equation (44), derive the flipped result with Equation (46). We will consider LS models corresponding to CSD(n) models with $n\approx 3$, particularly $n=2.5$, 3 and $1+\sqrt{6}\approx 3.45$, together with their flipped cases.

For the normal cases of CSD(n), the mass matrix in the diagonal charged lepton basis is given by

$$\begin{array}{c}\hfill m^{\nu }=m_a\left(\begin{array}{ccc}0& 0& 0\\ 0& 1& 1\\ 0& 1& 1\end{array}\right)+m_b{e}^{i\eta }\left(\begin{array}{ccc}1& n& n-2\\ n& n^2& n(n-2)\\ n-2& n(n-2)& {(n-2)}^2\end{array}\right),\end{array}$$

(49)

where we used Equations (37), (38) and (41)

$$\begin{array}{c}\hfill m_a=\frac{{\left|e\right|}^2}{M_{\mathrm{atm}}}{m}_b=\frac{{\left|a\right|}^2}{M_{\mathrm{sol}}},\end{array}$$

(50)

and the only relevant phase is $\eta =arg(a/e)$. At this point, we notice that, in the diagonal charged lepton mass basis that we are using, the PMNS mixing matrix is fully specified by the choice of n and the parameters $m_b/m_a$ and $\eta$. Indeed, it is possible to derive exact analytic results for the masses and mixing angles [23] and hence obtain the LS prediction for the neutrino oscillation observables.

We first observe that

$$\begin{array}{c}\hfill m^{\nu }\left(\begin{array}{c}\sqrt{\frac{2}{3}}\\ -\sqrt{\frac{1}{6}}\\ \sqrt{\frac{1}{6}}\end{array}\right)=\left(\begin{array}{c}0\hfill \\ 0\hfill \\ 0\hfill \end{array}\right),\end{array}$$

(51)

where the vector ${(\sqrt{\frac{2}{3}},-\sqrt{\frac{1}{6}},\sqrt{\frac{1}{6}})}^T$ is the first column of the TB matrix in Equation (3) and is then an eigenvector of the neutrino mass matrix with eigenvalue 0, and it corresponds to the massless neutrino eigenstate. This means that for a generic n, we obtain a TM1 mixing, as in Equation (26), where the first column of the TB matrix is preserved and the other two can change. Therefore, we can think of the LS as a special case of the atmospheric sum rules for TB mixing. Since the atmospheric sum rules were derived only using the fact that the first column of the TB matrix is preserved, all LS implementations also follow the TM1 sum rules in Equation (26). Once we have noticed this, it is clear that $m_{\nu }$ can be block-diagonalized using the TB matrix

$$\begin{array}{c}\hfill m_{\mathrm{block}}^{\nu }=U_{\mathrm{TB}}^T{m}^{\nu }{U}_{\mathrm{TB}}=\left(\begin{array}{ccc}0& 0& 0\\ 0& x& y\\ 0& y& z\end{array}\right),\end{array}$$

(52)

with

$$\begin{array}{c}\hfill x=3m_b{e}^{i\eta },y=\sqrt{6}{m}_b{e}^{i\eta }(n-1),z=\left|z\right|e^{i{\varphi }_z}=2\left[m_a+m_b{e}^{i\eta }{(n-1)}^2\right].\end{array}$$

(53)

Finally, we diagonalize $m_{\mathrm{block}}^{\nu }$ to obtain a matrix of the form $diag\left(0,m_2,m_3\right)$

$$\begin{array}{c}\hfill U_{\mathrm{block}}^T{m}_{\mathrm{block}}^{\nu }{U}_{\mathrm{block}}=P_{3\nu }^{*}{R}_{23\nu }^T{P}_{2\nu }^{*}{m}_{\mathrm{block}}^{\nu }{P}_{2\nu }^{*}{R}_{23\nu }{P}_{3\nu }^{*}=m_{\mathrm{diag}}^{\nu }=diag\left(0,m_2,m_3\right),\end{array}$$

(54)

where the matrix including the phases is

$$\begin{array}{c}\hfill \begin{array}{c}{P}_{2\nu }=\left(\begin{array}{ccc}1& 0& 0\\ 0& e^{i{\varphi }_2^{\nu }}& 0\\ 0& 0& e^{i{\varphi }_3^{\nu }}\end{array}\right),\\ P_{3\nu }=\left(\begin{array}{ccc}{e}^{i{\omega }_1^{\nu }}& 0& 0\\ 0& e^{i{\omega }_2^{\nu }}& 0\\ 0& 0& e^{i{\omega }_3^{\nu }}\end{array}\right),\end{array}\end{array}$$

(55)

and the angle that we use to diagonalize is

$$\begin{array}{c}\hfill R_{23\nu }=\left(\begin{array}{ccc}1& 0& 0\\ 0& cos{\theta }_{23}^{\nu }& sin{\theta }_{23}^{\nu }\\ 0& -sin{\theta }_{23}^{\nu }& cos{\theta }_{23}^{\nu }\end{array}\right)\equiv \left(\begin{array}{ccc}1& 0& 0\\ 0& c_{23}^{\nu }& s_{23}^{\nu }\\ 0& -s_{23}^{\nu }& c_{23}^{\nu }\end{array}\right),\end{array}$$

(56)

with the angle being fully specified by the free parameters $m_b/m_a$ and $\eta$, given by

$$\begin{array}{c}\hfill t\equiv tan2{\theta }_{23}^{\nu }=\frac{2\left|y\right|}{\left|z\right|cos(A-B)-\left|x\right|cosB},\end{array}$$

(57)

where

$$\begin{array}{c}\hfill tanB=tan\left({\varphi }_3^{\nu }-{\varphi }_2^{\nu }\right)=\frac{\left|z\right|sinA}{\left|x\right|+\left|z\right|cosA},\end{array}$$

(58)

and

$$\begin{array}{c}\hfill A={\varphi }_z-\eta =arg\left[m_a+m_b{e}^{i\eta }{(n-1)}^2\right]-\eta .\end{array}$$

(59)

Recall that the PMNS matrix is the combination of the charged lepton and neutrino mixing matrices

$$\begin{array}{c}\hfill U_{\mathrm{PMNS}}=U_{E_L}{U}_{{\nu }_L}^{†},\end{array}$$

(60)

where the neutrino mixing matrix, as we have shown, is the product of the TB matrix and the $U_{\mathrm{block}}$ matrices

$$\begin{array}{c}\hfill U_{{\nu }_L}=U_{\mathrm{block}}^T{U}_{\mathrm{TB}}^T.\end{array}$$

(61)

Now we can compare the PMNS matrix for the LS model with the standard parametrization in Equation (9) to extract the mixing angles

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill sin{\theta }_{13}& =\frac{1}{\sqrt{3}}{s}_{23}^{\nu }=\frac{1}{\sqrt{6}}{\left(1-\sqrt{\frac{1}{1+t^2}}\right)}^{1/2},\hfill \\ \hfill tan{\theta }_{12}& =\frac{1}{\sqrt{2}}{c}_{23}^{\nu }=\frac{1}{\sqrt{2}}{\left(1-3{sin}^2{\theta }_{13}\right)}^{1/2},\hfill \\ \hfill tan{\theta }_{23}& =\frac{\left|\frac{e^{iB}}{\sqrt{2}}{c}_{23}^{\nu }+\frac{1}{\sqrt{3}}{s}_{23}^{\nu }\right|}{\left|\frac{e^{iB}}{\sqrt{2}}{c}_{23}^{\nu }-\frac{1}{\sqrt{3}}{s}_{23}^{\nu }\right|}=\frac{\left|1+{ϵ}_{23}^{\nu }\right|}{\left|1-{ϵ}_{23}^{\nu }\right|},\hfill \end{array}\end{array}$$

(62)

with

$$\begin{array}{c}\hfill {ϵ}_{23}^{\nu }\equiv \sqrt{\frac{2}{3}}tan{\theta }_{23}^{\nu }{e}^{-iB}=\sqrt{\frac{2}{3}}{t}^{-1}\left[\sqrt{1+t^2}-1\right]e^{-iB}.\end{array}$$

(63)

The neutrino masses can be computed from $m_{\mathrm{block}}^{\nu }$ and they are

$$\begin{array}{c}\hfill H_{\mathrm{block}}^{\nu }=m_{\mathrm{block}}^{\nu }{m}_{\mathrm{block}}^{\nu †}=\left(\begin{array}{ccc}0& 0& 0\\ 0& {\left|x\right|}^2+{\left|y\right|}^2& \left|x\right|\left|y\right|+\left|y\right|e^{i\eta }{z}^{*}\\ 0& \left|x\right|\left|y\right|+\left|y\right|e^{-i\eta }z& {\left|y\right|}^2+{\left|z\right|}^2\end{array}\right),\end{array}$$

(64)

and, after diagonalization, we can extract the eigenvalues as a function of the LS model parameters

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill m_2^2+m_3^2& =T\equiv {\left|x\right|}^2+{2\left|y\right|}^2+{\left|z\right|}^2,\hfill \\ \hfill m_2^2{m}_3^2& =D\equiv {\left|x\right|}^2{\left|z\right|}^2+{\left|y\right|}^4-{2\left|x\right|\left|y\right|}^2\left|z\right|cosA,\hfill \end{array}\end{array}$$

(65)

and finally

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill m_3^2& =\frac{1}{2}T+\frac{1}{2}\sqrt{T^2-4D},\hfill \\ \hfill m_2^2& =D/m_3^2,\hfill \\ \hfill m_1^2& =0,\hfill \end{array}\end{array}$$

(66)

For the CP phase $\delta$, we have the cosine sum rule

$$\begin{array}{c}\hfill cos\delta =-\frac{cot2{\theta }_{23}\left(1-5sin{\theta }_{13}^2\right)}{2\sqrt{2}sin{\theta }_{13}\sqrt{1-3sin{\theta }_{13}^2}},\end{array}$$

(67)

which is the same as for the TM1 mixing in Table 1. This can be understood since the LS is a subset of TM1, as noticed before when we showed that the first column of the TB matrix is an eigenvector of the LS neutrino’s mass matrix. Notice that, for the flipped case, $cos\delta$ changes sign (because ${\theta }_{23}\to \pi -{\theta }_{23}$). Further information on the CP phase can be extracted from the Jarlskog invariant, which has been computed for the LS models [23,24],

$$\begin{array}{c}\hfill J=s_{12}{c}_{12}{s}_{13}{c}_{13}^2{s}_{23}{c}_{23}sin\delta =\mp \frac{24m_a^3{m}_b^3(n-1)sin\eta }{m_3^2{m}_2^2\Delta m_{32}^2},\end{array}$$

(68)

where the negative sign corresponds to the normal case and the positive sign to the flipped. This leads to the sum rules for $sin\delta$ for the respective cases

$$\begin{array}{c}\hfill sin\delta =\mp \frac{24m_a^3{m}_b^3(n-1)sin\eta }{m_3^2{m}_2^2\Delta m_{32}^2{s}_{12}{c}_{12}{s}_{13}{c}_{13}^2{s}_{23}{c}_{23}}.\end{array}$$

(69)

Notice that, in this case, the model is more predictive than the discrete symmetries and it predicts both sine and cosine fixing unambiguously the CP phase $\delta$. Both $sin\delta$ and $cos\delta$ change sign when moving from the normal to the flipped cases, meaning that $\delta \to \pi +\delta$, as anticipated before.

The above analytic results emphasize the high predictivity of these models, which, for a given choice of n, successfully predict all nine neutrino oscillation observables (three angles, three masses, three phases) in terms of three input parameters, namely the effective real masses $m_a,m_b$ and the phase $\eta$, which are sufficient to determine the neutrino mass matrix in Equation (49), where these parameters appear in the above analytic formulas. However, one neutrino mass is predicted to be zero ($m_1=0$), corresponding to a predicted normal hierarchy, so one Majorana phase is irrelevant. For the remaining seven observables (three angles, two masses, two phases), the overall neutrino mass scale may be factored out, and the Majorana phase is difficult to measure, so that, in practice, we shall focus on the five observables, namely the three angles ${\theta }_{13},{\theta }_{12},{\theta }_{23}$, the mass squared ratio $\Delta m_{21}^2/\Delta m_{31}^2=m_2^2/m_3^2$ and the CP violating Dirac phase $\delta$, which are fixed by the two input parameters, the phase $\eta$ and the ratio of the masses $r=m_b/m_a$, In practice, we shall take the two most accurately determined observables, $\Delta m_{21}^2/\Delta m_{31}^2$ and ${\theta }_{13}$, to fix the input parameters $\eta$ and $r=m_b/m_a$ within a narrow range, resulting in accurate predictions for the remaining observables, ${\theta }_{12},{\theta }_{23}$ and the Dirac phase $\delta$. In addition, we could add the input parameter n as a free parameter, but this, together with the constrained form of the mass matrices, will eventually be determined by the flavor model. In particular, a successful LS model structure corresponding to CSD(n) can emerge from a theory of flavor, as has been discussed in the literature for $n=3$ [24], $n=2.5$ [50] and more recently $n=1+\sqrt{6}\approx 3.45$ [30,31,32,33,34].

In Figure 11, we consider the LS results for the above three cases with $n\approx 3$ and the corresponding flipped cases, which are all realized successfully via $S_4$ symmetry [23]. When we plot the experimental ranges of ${\theta }_{13}$ and the mass squared ratio $m_2^2/m_3^2$ in the $r-\eta$ plane, it is clear that only two small parameter regions are allowed, which determine the maximal and minimal values of r and $\eta$ as the intersection of the blue and orange bands. Once we have the ranges of r and $\eta$ for each value of n, thanks to the high predictivity of the model, we can derive all the physical parameters and we can test them against the observed values. We do this for each value of $n=3$, $1+\sqrt{6}\approx 3.45$ and $2.5$ in Table 3, Table 4 and Table 5. We do not present the plot for the flipped cases since they are exactly the same. In fact, they involve only the mass ratio and ${\theta }_{13}$.

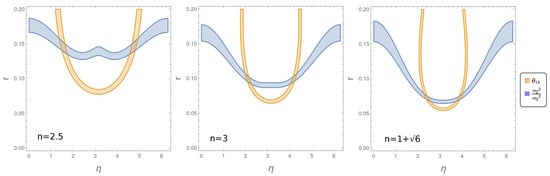
Figure 11. The results for the LS models with $n\approx 3$. The input parameters $\eta$ and $r=m_b/m_a$ are constrained to a good degree of accuracy by only two experimental observables, namely ${\theta }_{13}$ and the mass ratio $m_2^2/m_3^2$. The $3\sigma$ allowed region for ${\theta }_{13}$ and the mass ratio are, respectively, the blue and orange bands. The area of intersection is the allowed parameter space for $\eta$ and r. From the left to the right, we assume $n=2.5$, 3 and $1+\sqrt{6}\approx 3.45$.

Table 3. The LS predictions for $n=3$ where the two most accurately measured observables, ${\theta }_{13}$ and the mass squared ratio $m_2^2/m_3^2$, are used to accurately determine the two input parameters $r=m_b/m_a=0.100\pm 0.008$ for two $\eta$ ranges, as shown above, corresponding to the center panel of Figure 11. This then leads to highly constrained predictions for the less accurately determined observables ${\theta }_{12}$, ${\theta }_{23}$ and $\delta$, which may be compared to the current experimental ranges as shown in the table. All results are given to 3$\sigma$ accuracy.

	$\mathit{n}=3$	$\mathit{\eta }=2.11\pm 0.15$	$\mathit{\eta }=4.17\pm 0.15$	Exp. Range
	${\theta }_{12}{[}^{\circ }]$	$34.32{}_{-0.24}^{+0.20}$	$34.32{}_{-0.25}^{+0.20}$	31.31–35.74
normal	${\theta }_{23}{[}^{\circ }]$	$45.5{}_{-2.4}^{+2.3}$	$45.5{}_{-2.4}^{+2.3}$	39.6–51.9
normal	$\delta {[}^{\circ }]$	$272.2_{-11.0}^{+9.6}$	$87.9{}_{-9.6}^{+11.0}$	0–44 and 108–360
flipped	${\theta }_{23}{[}^{\circ }]$	$44.5{}_{-2.4}^{+2.3}$	$44.5{}_{-2.4}^{+2.3}$	39.6–51.9
flipped	$\delta {[}^{\circ }]$	$92.2_{-11.0}^{+9.6}$	$267.9{}_{-9.6}^{+11.0}$	0–44 and 108–360

Table 4. The LS predictions for $n=1+\sqrt{6}\approx 3.45$ where the two most accurately measured observables, ${\theta }_{13}$ and the mass squared ratio $m_2^2/m_3^2$, are used to accurately determine the two input parameters $r=m_b/m_a=0.072\pm 0.004$ for two $\eta$ ranges, as shown above, corresponding to the right panel of Figure 11. This then leads to highly constrained predictions for the less accurately determined observables ${\theta }_{12}$, ${\theta }_{23}$ and $\delta$, which may be compared to the current experimental ranges as shown in the table. All results are given to 3$\sigma$ accuracy.

	$\mathit{n}=1+\sqrt{6}$	$\mathit{\eta }=2.42\pm 0.16$	$\mathit{\eta }=3.87\pm 0.16$	Exp. Range
	${\theta }_{12}{[}^{\circ }]$	$34.{36}_{-0.21}^{+0.18}$	$34.{36}_{-0.21}^{+0.18}$	31.31–35.74
normal	${\theta }_{23}{[}^{\circ }]$	$41.4_{-2.6}^{+2.6}$	$41.5_{-2.6}^{+2.6}$	39.6–51.9
normal	$\delta {[}^{\circ }]$	$253.8{}_{-13.8}^{+11.7}$	$105.7{}_{-11.6}^{+13.7}$	0–44 and 108–360
flipped	${\theta }_{23}{[}^{\circ }]$	$48.6_{-2.6}^{+2.6}$	$48.5_{-2.6}^{+2.6}$	39.6–51.9
flipped	$\delta {[}^{\circ }]$	$74.8{}_{-13.8}^{+11.7}$	$285.8_{-11.6}^{+13.7}$	0–44 and 108–360

Table 5. The LS predictions for $n=2.5$ where the two most accurately measured observables, ${\theta }_{13}$ and the mass squared ratio $m_2^2/m_3^2$, are used to accurately determine the two input parameters $r=m_b/m_a=0.15\pm 0.01$ for two $\eta$ ranges, as shown above, corresponding to the left panel of Figure 11. This then leads to highly constrained predictions for the less accurately determined observables ${\theta }_{12}$, ${\theta }_{23}$ and $\delta$, which may be compared to the current experimental ranges as shown in the table. All results are given to 3$\sigma$ accuracy.

	$\mathit{n}=2.5$	$\mathit{\eta }=1.5\pm 0.2$	$\mathit{\eta }=4.7\pm 0.2$	Exp. Range without SK
	${\theta }_{12}{[}^{\circ }]$	$34.{31}_{-0.20}^{+0.16}$	$34.{28}_{-0.21}^{+0.17}$	31.31–35.74
normal	${\theta }_{23}{[}^{\circ }]$	$51.5_{-2.2}^{+1.9}$	$51.0_{-2.3}^{+2.0}$	39.6–51.9
normal	$\delta {[}^{\circ }]$	$299.9_{-9.9}^{+9.2}$	$63.6_{-9.3}^{+10.1}$	0–44 and 108–360
flipped	${\theta }_{23}{[}^{\circ }]$	$38.5_{-2.2}^{+1.9}$	$39.0_{-2.3}^{+2.0}$	39.6–51.9
flipped	$\delta {[}^{\circ }]$	$119.9_{-9.9}^{+9.2}$	$243.6_{-9.3}^{+10.1}$	0–44 and 108–360

In Table 3, we focus on the originally studied $n=3$ and its flipped case. We present the theoretical prediction and its uncertainty coming from the allowed region in Figure 11 (center panel) and the experimental bound. Since the theoretical prediction is exact given $\eta$ and r, we are allowing two significant figures for the theoretical errors. We notice that ${\theta }_{12}$ and ${\theta }_{23}$ fall well within the experimental range for all the cases and that, even if $\delta$ is still not measured very precisely, it allows us to exclude one of the two possible $\eta$ both in the normal and flipped case. In fact, only the $\eta =2.11$ normal case and $\eta =4.17$ flipped case are within the $3\sigma$ experimental range.

In Table 4, we focus on $n=1+\sqrt{6}\approx 3.45$, which can be realized with a modular symmetry [33]. We notice that for the normal case, both $\eta$ values are still allowed but with the $\delta$ prediction for $\eta =3.87$ that lies at the edge of the allowed experimental range. For the flipped case, instead, $\eta =2.42$ is excluded, thanks again to the bound on $\delta$. As before, moving from $n=1+\sqrt{6}$ to the flipped case only changes the sign of t in Equation (57). The predictions for the mass ratio, ${\theta }_{13}$ and ${\theta }_{12}$, are independent of this sign, while ${\theta }_{23}$ and $\delta$ are affected by it, as we can see in Equations (62) and as discussed above for $\delta$. The predictions are thus related by $tan{\theta }_{23}\to cot{\theta }_{23}$ (or ${\theta }_{23}\to \pi -{\theta }_{23}$) and $\delta \to \delta +\pi$.

In Table 5, we focus on $n=2.5$ and notice that, given the $\delta$ values, $\eta =4.7$ is excluded for the normal case, while, for the flipped, both $\eta$ values are allowed. Finally, ${\theta }_{23}$ lies in the higher and lower end of the experimental range, respectively, for the normal and flipped case, making the $n=2.5$ disfavored given the current data. This case is also known in the literature as $n=-1/2$ using the convention in Equation (48). However, it is more consistent to refer to it as $n=2.5$ in our notation.

In summary, we see that most of the LS models with $n\approx 3$ are still allowed by the current data. We have considered the cases $n=2.5$ and $n=1+\sqrt{6}\approx 3.45$ and compared the results to $n=3$, which was the originally proposed CSD(3). We emphasize the high predictivity of the LS models, which have three input parameters describing nine neutrino observables. We have presented a new method here to present the results, namely to use the two most accurately measured observables, ${\theta }_{13}$ and the mass squared ratio $\Delta m_2^2/\Delta m_3^2=m_2^2/m_3^2$, to accurately constrain the two input parameters $r=m_b/m_a$ and $\eta$. This then leads to highly constrained predictions for the less accurately determined observables ${\theta }_{12}$, ${\theta }_{23}$ and $\delta$, which can be tested by future neutrino oscillation experiments. Indeed, some of the possible LS cases are already excluded by the current data. In addition, all these LS cases predict the zero lightest neutrino mass $m_1=0$, with a normal neutrino mass hierarchy, and the neutrinoless double beta decay parameter $m_{\beta \beta }$ equal to $m_b$, which is merely the first element of the neutrino mass matrix in Equation (49). Indeed, $m_{\beta \beta }=m_b$ can be readily determined from $\Delta m_2^2=m_2^2$, but its value is too small to be measured in the near future, so we have not considered it here. On the other hand, a non-zero measurement of $m_1$ or $m_{\beta \beta }$ in the inverted mass squared ordering region would immediately exclude the LS models.

6. Conclusions

In the past few decades, many attempts have been made to explain the flavor structure of the PMNS matrix by imposing symmetry on the leptonic Lagrangian. These symmetries imply correlations among the parameters that are called sum rules. We have studied two types of sum rules: solar and atmospheric mixing sum rules. Then, we have studied the Littlest Seesaw (LS) models that obey the TM1 atmospheric mixing sum rule but are much more predictive. The goal of this paper has been to study all these approaches together in one place so that they may be compared, and to give an up-to-date analysis of the predictions of all of these possibilities, when confronted with the most recent global fits.

In the case of solar mixing sum rules, the T generator of a given symmetry group is broken in the charged lepton sector in order to generate a non-zero reactor angle ${\theta }_{13}$. This leads to a prediction for $cos\delta$ that can be tested against the experimental data. These in turn show a preference for GRa and GRb mixing, while BM and GRc are constrained to lie in a very small window of the parameter space of the current data. Future high-precision neutrino oscillation experiments will constrain the solar mixing sum rules, further as discussed elsewhere [40].

The atmospheric mixing sum rules instead come from either the breaking of both S and U in the neutrino sector while preserving $SU$, or from breaking S and preserving U. In this case, we have two relations among the parameters that can be tested. We noticed that only TM1, TM2 and GRa2 are still allowed by the neutrino oscillation data, with a preference for GRa2 and with TM2 very close to being excluded. Future high-precision neutrino oscillation experiments will constrain the atmospheric mixing sum rules further, as discussed elsewhere [43].

We have also considered the class of LS models that follow the constrained sequential dominance idea, CSD(n) with $n\approx 3$. The LS models obey the TM1 atmospheric mixing sum rule, but have other predictions as well. We have compared the cases $n=2.5$, $n=3$ and $n=1+\sqrt{6}\approx 3.45$, which are predicted by theoretical models. These models are highly predictive, with only two free real parameters fixing all the neutrino oscillation observables, making them candidates for being the most minimal predictive seesaw models of leptons still compatible with data. This is the first time that all three n values above, in both normal and flipped cases, have been studied together in one place, using the most up-to-date global fits. We have also proposed a new means of analyzing these models, which allows accurate predictions for the least well-determined oscillation parameters ${\theta }_{12}$, ${\theta }_{23}$ and $\delta$, which we have shown to lie in relatively narrow 3$\sigma$ ranges, much smaller than the current data ranges but (largely) consistent with them, allowing these models to be decisively tested in future neutrino oscillation experiments, as has been discussed elsewhere [25]. In our analysis, we have ignored the model-dependent renormalization group (RG) corrections to LS models, which have been shown to be generally quite small [51].

In conclusion, we have shown that the recent global fits to experimental data have provided significantly improved constraints on all these symmetry-based approaches, and future neutrino oscillation data will be able to significantly restrict the pool of viable models. In particular, improvements in the measurement of the leptonic CP violating Dirac phase $\delta$ will strongly constrain all these cases. This is particularly true in LS models, which provide very precise theoretical predictions for $\delta$, as well as ${\theta }_{12}$ and ${\theta }_{23}$, consistent with current global fits. Future high-precision neutrino experiments are of great importance to continue to narrow down the choice of possible PMNS flavor models based on symmetry and lead to a deeper understanding of the flavor puzzle of the SM.