Einstein Field Equation, Recursion Operators, Noether and Master Symmetries in Conformable Poisson Manifolds

Abstract

We show that a Minkowski phase space endowed with a bracket relatively to a conformable differential realizes a Poisson algebra, confering a bi-Hamiltonian structure to the resulting manifold. We infer that the related Hamiltonian vector field is an infinitesimal Noether symmetry, and compute the corresponding deformed recursion operator. Besides, using the Hamiltonian–Jacobi separability, we construct recursion operators for Hamiltonian vector fields in conformable Poisson–Schwarzschild and Friedmann–Lemaître–Robertson–Walker (FLRW) manifolds, and derive the related constants of motion, Christoffel symbols, components of Riemann and Ricci tensors, Ricci constant and components of Einstein tensor. We highlight the existence of a hierarchy of bi-Hamiltonian structures in both the manifolds, and compute a family of recursion operators and master symmetries generating the constants of motion.

1. Introduction

Conformable fractional calculus has a long and rich history. In 1695, Gottfried Leibniz asked Guillaume l’Hôspital if the (integer) order of derivatives and integrals could be extended [1]. Would it be possible if the order was some irrational, fractional or complex number? This idea motivated many mathematicians, physicists and engineers to develop the concept of fractional calculus in diverse fields of science and engineers (see, e.g., [2,3,4,5,6,7,8,9], and references therein). Over four centuries, many famous mathematicians contributed to this development. It is still nowadays one of the most intensively developing areas of mathematical analysis, including several definitions of fractional operators like Riemann–Liouville, Caputo, Grünwald–Letnikov, Riesz and Weyl definitions [5,10,11,12]. Two of these definitions, namely Riemann–Liouville and Caputo, are famous. Mathematicians prefer the Riemann–Liouville fractional derivative while physicists and engineers use the Caputo fractional one. Indeed, the Riemann–Liouville fractional derivative of a constant is not zero, and it requires fractional initial conditions that are not generally specified [5]. In contrast, the Caputo derivative of a constant is zero, and a fractional differential equation expressed in terms of a Caputo fractional derivative requires standard boundary conditions. Unfortunately, the Riemann–Liouville derivative and Caputo derivative do not obey the Leibniz rule and chain rule, which sometimes prevents us from applying these derivatives to ordinary physical systems with a standard Newton derivative. In 2014, Khalil et al. [13] introduced the new fractional derivative called the conformable fractional derivative and the integral obeying the Leibniz rule and chain rule. One year later, i.e., in 2015, Chung [5] used this conformable fractional derivative and integral to discuss the fractional version of the Newtonian mechanics. In that work, he constructed the fractional Euler–Lagrange equation from the fractional version of the calculus of variations and used this equation to discuss some mechanical problems such as fractional harmonic oscillator problem, the fractional damped oscillator problem and the forced oscillator problem. In 2017, Chung et al. [14] discussed the dynamics of a particle in a viscoelastic medium using the conformable fractional derivative of order $\alpha$ with respect to time. Further, in 2019, the same authors [15] discussed the fractional classical mechanics and applied it to the anomalous diffusion relation from the $\alpha$-deformed Langevin equation. During the same year, Kiskinov et al. [16] investigated the Cauchy problem for nonlinear systems with conformable derivatives and variable delays. Furthermore, Khalil et al. gave the geometric meaning of a conformable derivative via fractional cords in 2019 [17]. In 2020, Chung et al. [18] studied the deformed special relativity based on $\alpha$-deformed binary operations. In that work, they gave the $\alpha$-translation invariant distance ($\alpha$-distance) of infinitesimally close space-time based on the definition of $\alpha$-translation invariant infinitesimal displacement and $\alpha$-translation invariant infinitesimal time interval.

In addition, in the last few decades, there was a renewed interest in completely integrable Hamiltonian systems (IHS), the concept of which goes back to Liouville in 1897 [19] and Poincaré in 1899 [20]. In short, IHS are defined as nonlinear differential equations admitting a Hamiltonian description and possessing enough constants of motion so that they can be integrated by quadratures [21]. This Liouville formalism does not provide a method for obtaining the integrals of motion; it has therefore been necessary to elaborate different methods for obtaining constants of motion (Hamilton–Jacobi separability, Lax pairs formalism, Noether symmetries, Hidden symmetries, etc). A relevant progress in the analysis of the integrability was the important remark that many of these systems are Hamiltonian dynamics with respect to two compatible symplectic structures [22,23,24], permitting a geometrical interpretation of the so-called recursion operator [25,26,27]. A description of integrability working both for systems with finitely many degrees of freedom and for field theory can be given in terms of an invariant, diagonalizable mixed $(1,1)$-tensor field, having bidimensional eigenspaces and vanishing Nijenhuis torsion. One of the powerful methods of describing IHS with involutive Hamiltonian functions or constants of motion uses the recursion operator admitting a vanishing Nijenhuis torsion. In 2015, Takeuchi constructed recursion operators of Hamiltonian vector fields of geodesic flows for some Riemannian and Minkowski metrics [28], and obtained related constants of motion. In his work, Takeuchi used five particular solutions of the Einstein equation in the Schwarzschild, Reissner–Nordström, Kerr, Kerr–Newman, and FLRW metrics, and constructed recursion operators inducing the complete integrability of the Hamiltonian functions. Further, in 2019, we investigated the same problem in a noncommutative Minkowski phase space [29].

In the present work, we investigate Noether symmetry and recursion operators induced by a conformable Poisson algebra in a Minkowski phase space. We construct recursion operators using conformable Schwarzschild and Friedmann–Lemaître–Robertson–Walker (FLRW) metrics and discuss their relevant master symmetries.

The paper is organized as follows. In Section 2, we give the notion of conformable differential and related formulation of the wellknown Takeuchi Lemma [28]. In Section 3, we construct a conformable Poisson algebra and the Lie algebra of deformed vector fields, prove the existence of infinitesimal Noether symmetry and bi-Hamiltonian structure, and compute the corresponding recursion operator in a conformable Minkowski phase space. In Section 4, we construct recursion operators for Hamiltonian vector fields, related constants of motion, Christoffel symbols, components of Riemann and Ricci tensors, Ricci constant, and components of Einstein tensor in the framework of conformable Schwarzschild and FLRW metrics. In Section 5, we derive a hierarchy of master symmetries and compute the conserved quantities. In Section 6, we end with some concluding remarks.

2. Conformable Differential and Formulation of Takeuchi Lemma

A Hamiltonian system is a triple $(\mathcal{Q},\omega ,H)$, where $(\mathcal{Q},\omega )$ is a symplectic manifold and H is a smooth function on $\mathcal{Q}$, called Hamiltonianor Hamiltonian function [30].

Given a general dynamical system defined on the $2n$-dimensional manifold $\mathcal{Q}$ [31,32], its evolution can be described by the equation

$$\dot{x}\left(t\right)=X\left(x\right),x\in \mathcal{Q},X\in \mathcal{T}\mathcal{Q}.$$

(1)

If the system (1) admits two different Hamiltonian representations:

$$\dot{x}\left(t\right)=X_{H_1,H_2}={\mathcal{P}}_{1}d{H}_1={\mathcal{P}}_{2}d{H}_2,$$

(2)

its integrability as well as many other properties are subject to Magri’s approach. The bi-Hamiltonian vector field $X_{H_1,H_2}$ is defined by two pairs of Poisson bivectors ${\mathcal{P}}_1,{\mathcal{P}}_2$ and Hamiltonian functions $H_1,H_2.$ Such a manifold $\mathcal{Q}$ equipped with two Poisson bivectors is called a double Poisson manifold, and the quadruple $(\mathcal{Q},{\mathcal{P}}_1,{\mathcal{P}}_2,X_{H_1,H_2})$ is called a bi-Hamiltonian system. ${\mathcal{P}}_1$ and ${\mathcal{P}}_2$ are two compatible Poisson bivectors with a vanishing Schouten–Nijenhuis bracket [33]:

$${[{\mathcal{P}}_1,{\mathcal{P}}_2]}_{NS}=0.$$

(3)

A recursion operator $T:\mathcal{T}\mathcal{Q}⟶\mathcal{T}\mathcal{Q}$ is defined by

$$\begin{array}{c}\hfill T:={\mathcal{P}}_2\circ {\mathcal{P}}_1^{-1}.\end{array}$$

(4)

A Noether symmetry is a diffeomorphism $\mathsf{\Phi }:\mathcal{Q}⟶\mathcal{Q}$ such that [34]:

$${\mathsf{\Phi }}^{*}\omega =\omega ,{\mathsf{\Phi }}^{*}H=H.$$

(5)

An infinitesimal Noether symmetry is a vector field $Y\in \mathfrak{X}\left(\mathcal{Q}\right)$ (the set of all differentiable vector fields on $\mathcal{Q}$) such that:

$${\mathcal{L}}_Y\omega =0,{\mathcal{L}}_{Y}H=0.$$

(6)

Definition 1.

Consider the map g and its inverse $g^{-1}$:

$$\begin{array}{cc}\hfill & g:{\mathbb{R}}_{\alpha }^{2n}⟶{\mathbb{R}}^{2n}{g}^{-1}:{\mathbb{R}}^{2n}⟶{\mathbb{R}}_{\alpha }^{2n}\hfill \\ \hfill & z⟼g\left(z\right)={|z|}^{\alpha -1}z=\mathbf{Z}\mathbf{Z}⟼g^{-1}\left(\mathbf{Z}\right)={|\mathbf{Z}|}^{(1/\alpha )-1}\mathbf{Z}=z,\hfill \end{array}$$

(7)

where $g\left(0\right)=0,g\left(1\right)=1,$ and $g(\pm \infty )=\pm \infty .$ Then, for this map, the α-addition, α-subtraction, α-multiplication, and α-division are given by:

$$\begin{array}{cc}\hfill & a{\oplus }_{\alpha }b={|a|a|}^{\alpha -1}+{b|b|}^{\alpha -1}{|}^{(1/\alpha )-1}{(a|a|}^{\alpha -1}+{b|b|}^{\alpha -1}),\hfill \\ \hfill & a{\ominus }_{\alpha }b={|a|a|}^{\alpha -1}-{b|b|}^{\alpha -1}{|}^{(1/\alpha )-1}{(a|a|}^{\alpha -1}-{b|b|}^{\alpha -1}),\hfill \\ \hfill & a{\otimes }_{\alpha }b=ab,\hfill \\ \hfill & a{\oslash }_{\alpha }b={\displaystyle \frac{a}{b}},\hfill \end{array}$$

where $a,b\in {\mathbb{R}}_{\alpha }^{2n}$.

Definition 2.

Let h be a differentiable coordinates function on ${\mathbb{R}}_{\alpha }^{2n}$. The conformable differential, also called α-differential in the sequel, with respect to the position q and its associated momentum p is defined by:

$$\begin{array}{cc}\hfill d_{\alpha }:{\mathbb{R}}_{\alpha }^{2n}& ⟶{\mathbb{R}}^{2n}\hfill \\ \hfill h& ⟼d_{\alpha }h:=\sum _{\mu =1}^{2n}\alpha {|x_{\mu }|}^{\alpha -1}{\displaystyle \frac{\partial }{\partial x_{\mu }}}h,(x_{\nu }=q^{\nu },x_{\nu +n}=p_{\nu },n=4,\nu =1,2,3,4)\hfill \end{array}$$

(8)

satisfying the following properties:

(i) 

$d_{\alpha }(ah+bf)=a{d}_{\alpha }h+b{d}_{\alpha }f$ for all $a,b\in \mathbb{R}$;

(ii) 

$d_{\alpha }\left(h^m\right)=m{h}^{m-1}{d}_{\alpha }h,$ for all $m\in \mathbb{R}$;

(iii) 

$d_{\alpha }\left(c\right)=0,$ for all constant functions $h(q,p)=c$;

(iv) 

$d_{\alpha }\left(hf\right)=h{d}_{\alpha }f+f{d}_{\alpha }h$;

(iv) 

$d_{\alpha }\left({\displaystyle \frac{h}{f}}\right)={\displaystyle \frac{f{d}_{\alpha }h-h{d}_{\alpha }f}{f^2}}$, where f is also a differentiable coordinates function on ${\mathbb{R}}_{\alpha }^{2n}$.

The $\alpha$-differential produces a new deformed phase space called a conformable phase space. The ordinary differential is obtained for $\alpha =1$. Using the $\alpha$-addition and $\alpha$-subtraction, we obtain the following infinitesimal distance between two points of coordinates $(x_i,\dots ,x_n)$ and $(x_i{\oplus }_{\alpha }{d}_{\alpha }{x}_i,\dots ,x_n{\oplus }_{\alpha }{d}_{\alpha }{x}_n)$

$$\begin{array}{c}\hfill d_{\alpha }s={(d_{\alpha }^2{x}_i+\dots +d_{\alpha }^2{x}_n)}^{\frac{1}{2}}.\end{array}$$

(9)

In the ${\mathbb{R}}_{\alpha }^{2n}$, Takeuchi Lemma [28] takes the following form:

Lemma 1.

Consider the conformable vector fields

$$X_{{\alpha }_i}=-|x_i{|}^{(1-\alpha )}{|x_{n+i}|}^{(1-\alpha )}{\displaystyle \frac{\partial }{\partial x_{n+i}}},i=1,\dots ,n$$

(10)

on ${\mathbb{R}}_{\alpha }^{2n}$ and

$$T_{\alpha }=\sum _{i=1}^n|x_i{|}^{(\alpha -1)}|x_i\left({\displaystyle \frac{\partial }{\partial x_i}}\otimes d{x}_i+{\displaystyle \frac{\partial }{\partial x_{n+i}}}\otimes d{x}_{n+i}\right),$$

(11)

a $(1,1)$-tensor field on ${\mathbb{R}}_{\alpha }^{2n}$. Then, we have that the Nijenhuis torsion of $T_{\alpha }$ is vanishing, $i.e.,$ ${\mathcal{N}}_{T_{\alpha }}=0$ and ${\mathcal{L}}_{X_{{\alpha }_i}}{T}_{\alpha }=0,$ that is, the $(1,1)$-tensor field $T_{\alpha }$ is a conformable recursion operator of $X_{{\alpha }_i},(i=1,\dots ,n)$.

Proof of Lemma 1. 

We have:

$$\begin{array}{cc}\hfill {\mathcal{L}}_{X_{{\alpha }_i}}{T}_{\alpha }& ={\mathcal{L}}_{X_{{\alpha }_i}}\left\{\sum _{i=1}^n|x_i{|}^{(\alpha -1)}|x_i\left({\displaystyle \frac{\partial }{\partial x_i}}\otimes d{x}_i+{\displaystyle \frac{\partial }{\partial x_{n+i}}}\otimes d{x}_{n+i}\right)\right\}\hfill \\ \hfill & =\sum _{i=1}^n\{{\mathcal{L}}_{X_{{\alpha }_i}}(|x_i{|}^{(\alpha -1)}|x_i)\left({\displaystyle \frac{\partial }{\partial x_i}}\otimes d{x}_i+{\displaystyle \frac{\partial }{\partial x_{n+i}}}\otimes d{x}_{n+i}\right)\hfill \\ \hfill & +|x_i{|}^{(\alpha -1)}|x_i\left({\mathcal{L}}_{X_{{\alpha }_i}}\left[{\displaystyle \frac{\partial }{\partial x_i}}\otimes d{x}_i\right]+{\mathcal{L}}_{X_{{\alpha }_i}}\left[{\displaystyle \frac{\partial }{\partial x_{n+i}}}\otimes d{x}_{n+i}\right]\right)\}\hfill \\ \hfill {\mathcal{L}}_{X_{{\alpha }_i}}{T}_{\alpha }& =\sum _{i=1}^n|x_i{|}^{(\alpha -1)}|x_i\left({\mathcal{L}}_{X_{{\alpha }_i}}\left[{\displaystyle \frac{\partial }{\partial x_i}}\otimes d{x}_i\right]+{\mathcal{L}}_{X_{{\alpha }_i}}\left[{\displaystyle \frac{\partial }{\partial x_{n+i}}}\otimes d{x}_{n+i}\right]\right)\hfill \end{array}$$

because ${\mathcal{L}}_{X_{{\alpha }_i}}(|x_i{|}^{(\alpha -1)}|x_i)=0.$

Then,

$$\begin{array}{cc}\hfill {\mathcal{L}}_{X_{{\alpha }_i}}{T}_{\alpha }& =\sum _{i=1}^n|x_i{|}^{(\alpha -1)}|x_i({\mathcal{L}}_{X_{{\alpha }_i}}\left[{\displaystyle \frac{\partial }{\partial x_i}}\right]\otimes d{x}_i+{\displaystyle \frac{\partial }{\partial x_i}}\otimes {\mathcal{L}}_{X_{{\alpha }_i}}\left(d{x}_i\right)\hfill \\ & +{\mathcal{L}}_{X_{{\alpha }_i}}\left[{\displaystyle \frac{\partial }{\partial x_{n+i}}}\right]\otimes d{x}_{n+i}+{\displaystyle \frac{\partial }{\partial x_{n+i}}}\otimes {\mathcal{L}}_{X_{{\alpha }_i}}\left(d{x}_{n+i}\right))\hfill \\ \hfill {\mathcal{L}}_{X_{{\alpha }_i}}{T}_{\alpha }& =0.\hfill \end{array}$$

The components of the Nijenhuis torsion are as follows [28]:

$$\begin{array}{cc}\hfill {\left({\mathcal{N}}_{T_{\alpha }}\right)}_{ij}^h& ={\left(T_{\alpha }\right)}_i^k{\displaystyle \frac{\partial {\left(T_{\alpha }\right)}_j^h}{\partial x_k}}-{\left(T_{\alpha }\right)}_j^k{\displaystyle \frac{\partial {\left(T_{\alpha }\right)}_i^h}{\partial x_k}}+{\left(T_{\alpha }\right)}_k^h{\displaystyle \frac{\partial {\left(T_{\alpha }\right)}_i^k}{\partial x_j}}-{\left(T_{\alpha }\right)}_k^h{\displaystyle \frac{\partial {\left(T_{\alpha }\right)}_j^k}{\partial x_i}}\hfill \\ \hfill & =|x_i{|}^{(\alpha -1)}|x_i{\displaystyle \frac{\partial {\left(T_{\alpha }\right)}_j^h}{\partial x_i}}-|x_j{|}^{(\alpha -1)}|x_j{\displaystyle \frac{\partial {\left(T_{\alpha }\right)}_i^h}{\partial x_j}}+{\left(T_{\alpha }\right)}_i^h{\displaystyle \frac{\partial (|x_i{|}^{(\alpha -1)}|x_i)}{\partial x_j}}-{\left(T_{\alpha }\right)}_j^h{\displaystyle \frac{\partial (|x_j{|}^{(\alpha -1)}|x_j)}{\partial x_i}}\hfill \\ \hfill & =|x_i{|}^{(\alpha -1)}|x_i{\displaystyle \frac{\partial {\left(T_{\alpha }\right)}_j^h}{\partial x_i}}-|x_j{|}^{(\alpha -1)}|x_j{\displaystyle \frac{\partial {\left(T_{\alpha }\right)}_i^h}{\partial x_j}}+\alpha {\left(T_{\alpha }\right)}_i^h|x_i{|}^{(\alpha -1)}{\delta }_j^i-\alpha {\left(T_{\alpha }\right)}_j^h{|x_j|}^{(\alpha -1)}{\delta }_i^j.\hfill \end{array}$$

• If $i=j,$ we have ${\delta }_j^i={\delta }_i^j=1$ and we get

  $$\begin{array}{cc}\hfill {\left({\mathcal{N}}_{T_{\alpha }}\right)}_{ij}^h& =|x_i{|}^{(\alpha -1)}|x_i{\displaystyle \frac{\partial {\left(T_{\alpha }\right)}_i^h}{\partial x_i}}-|x_i{|}^{(\alpha -1)}|x_i{\displaystyle \frac{\partial {\left(T_{\alpha }\right)}_i^h}{\partial x_i}}+\alpha |x_i{|}^{(\alpha -1)}{\left(T_{\alpha }\right)}_i^h-\alpha {|x_i|}^{(\alpha -1)}{\left(T_{\alpha }\right)}_i^h=0;\hfill \end{array}$$

  (12)
• If $i\ne j,$ we have ${\delta }_j^i={\delta }_i^j=0$ and ${\displaystyle \frac{\partial {\left(T_{\alpha }\right)}_j^h}{\partial x_i}}={\displaystyle \frac{\partial {\left(T_{\alpha }\right)}_i^h}{\partial x_j}}=0.$ Then,

  $${\left({\mathcal{N}}_{T_{\alpha }}\right)}_{ij}^h=0$$

  (13)

  .

From (12) and (13), we get ${\mathcal{N}}_{T_{\alpha }}=0.$ □

3. Recursion Operator in Conformable Minkowski Phase Space

In this section, we derive the recursion operator of Hamiltonian vector fields of geodesic flow for a free particle in a conformable Minkowski phase space and obtain the associated constants of motion.

3.1. Symplectic Structure, Poisson Bracket and Lie Algebra

We consider our configuration space as a manifold $\mathcal{Q}={\mathbb{R}}_{\alpha }^4\setminus \left\{0\right\}$ that is, a four-dimensional real Euclidean vector space with the origin removed. The cotangent bundle ${\mathcal{T}}^{*}\mathcal{Q}=\mathcal{Q}\times {\mathbb{R}}_{\alpha }^4$ has a natural symplectic structure ${\omega }_{\alpha }:\mathcal{T}\mathcal{Q}⟶{\mathcal{T}}^{*}\mathcal{Q}$ which, in local coordinates $(q,p)$, is given by

$${\omega }_{\alpha }=\sum _{\mu =1}^4{d}_{\alpha }{p}_{\mu }\wedge d_{\alpha }{q}^{\mu }=\sum _{\mu =1}^4{\alpha }^2|p_{\mu }{|}^{\alpha -1}{|q^{\mu }|}^{\alpha -1}d{p}_{\mu }\wedge d{q}^{\mu }.$$

(14)

Since ${\omega }_{\alpha }$ is non-degenerate, it induces an inverse map, called bivector field ${\mathcal{P}}_{\alpha }$: ${\mathcal{T}}^{*}\mathcal{Q}⟶\mathcal{T}\mathcal{Q}$ (tangent bundle) defined by

$${\mathcal{P}}_{\alpha }=\sum _{\mu =1}^4{\alpha }^{-2}|p_{\mu }{|}^{1-\alpha }{|q^{\mu }|}^{1-\alpha }{\displaystyle \frac{\partial }{\partial p_{\mu }}}\wedge {\displaystyle \frac{\partial }{\partial q^{\mu }}},{\omega }_{\alpha }\circ {\mathcal{P}}_{\alpha }={\mathcal{P}}_{\alpha }\circ {\omega }_{\alpha }=1,$$

(15)

and is used to construct the Hamiltonian vector field $X_{{\alpha }_f}$ of a Hamiltonian function f by the relation

$$X_{{\alpha }_f}={\mathcal{P}}_{\alpha }df.$$

We consider now the next conformable Minkowski metric on the manifold $\mathcal{Q}$:

$$d_{\alpha }{s}^2=-{\alpha }^2|q^1{|}^{2(\alpha -1)}{\left(d{q}^1\right)}^2+{\alpha }^2|q^2{|}^{2(\alpha -1)}{\left(d{q}^2\right)}^2+{\alpha }^2|q^3{|}^{2(\alpha -1)}{\left(d{q}^3\right)}^2+{\alpha }^2{|q^4|}^{2(\alpha -1)}{\left(d{q}^4\right)}^2,$$

(16)

where $c=1$ for commodity yielding the tensor metric ${\left(g_{\mu \nu }\right)}_{\alpha }$ and its inverse ${\left(g^{\mu \nu }\right)}_{\alpha }$

$${\left(g_{\mu \nu }\right)}_{\alpha }={\alpha }^2\left(\begin{array}{cccc}-{\left(q^1\right)}^{2(\alpha -1)}& 0& 0& 0\\ 0& {\left(q^2\right)}^{2(\alpha -1)}& 0& 0\\ 0& 0& {\left(q^3\right)}^{2(\alpha -1)}& 0\\ 0& 0& 0& {\left(q^4\right)}^{2(\alpha -1)}\end{array}\right),$$

(17)

$${\left(g^{\mu \nu }\right)}_{\alpha }={\displaystyle \frac{1}{{\alpha }^2}}\left(\begin{array}{cccc}-{\left(q^1\right)}^{2(1-\alpha )}& 0& 0& 0\\ 0& {\left(q^2\right)}^{2(1-\alpha )}& 0& 0\\ 0& 0& {\left(q^3\right)}^{2(1-\alpha )}& 0\\ 0& 0& 0& {\left(q^4\right)}^{2(1-\alpha )}\end{array}\right).$$

(18)

In our framework, the equation of the geodesic on the manifold $\mathcal{Q}$ is given by

$${\displaystyle \frac{d^2{q}^{\mu }}{d{t}^2}}+{\left({\Gamma }_{\nu \lambda }^{\mu }\right)}_{\alpha }{\displaystyle \frac{d{q}^{\nu }}{dt}}{\displaystyle \frac{d{q}^{\lambda }}{dt}}=0,(\nu ,\mu ,\lambda =1,2,3,4),$$

(19)

where

$${\left({\Gamma }_{\nu \lambda }^{\mu }\right)}_{\alpha }={\displaystyle \frac{1}{2}}{\left(g^{\mu ϵ}\right)}_{\alpha }\left({\displaystyle \frac{\partial {\left(g_{ϵ\nu }\right)}_{\alpha }}{\partial q^{\lambda }}}+{\displaystyle \frac{\partial {\left(g_{ϵ\lambda }\right)}_{\alpha }}{\partial q^{\nu }}}-{\displaystyle \frac{\partial {\left(g_{\nu \lambda }\right)}_{\alpha }}{\partial q^{ϵ}}}\right)$$

(20)

are Christoffel symbols. From (20), we have

$${\left({\Gamma }_{11}^1\right)}_{\alpha }={\displaystyle \frac{\alpha -1}{q^1}};{\left({\Gamma }_{22}^2\right)}_{\alpha }={\displaystyle \frac{\alpha -1}{q^2}};{\left({\Gamma }_{33}^3\right)}_{\alpha }={\displaystyle \frac{\alpha -1}{q^3}};{\left({\Gamma }_{44}^4\right)}_{\alpha }={\displaystyle \frac{\alpha -1}{q^4}};{\left({\Gamma }_{\nu \lambda }^{\mu }\right)}_{\alpha }=0,\mathrm{otherwise},$$

(21)

and obtain that the Riemann tensor components are vanished, i.e., $R_{ijkl}=0,(i,j,k,l=1,2,3,4)$. Then, the Minkowski phase space endowed with the metric $d_{\alpha }{s}^2$ is a flat space. Thus, we notice that this result does not change the geometric structure of the ordinary Minkowski phase space. Further, the presence of the Christoffel symbols ${\left({\Gamma }_{ii}^i\right)}_{\alpha },(i=1,2,3,4)$ means that the parallel displacement of any basic vector of our considered manifold with respect to itself always remains parallel with this same basic vector. The ordinary Minkowski phase space is obtained for $\alpha =1.$

Since the quantities ${\left({\tilde{\Gamma }}_{\nu \lambda }^{\mu }\right)}_{\alpha }={\displaystyle \frac{1}{\alpha +1}}{\left({\Gamma }_{\nu \lambda }^{\mu }\right)}_{\alpha }$ do not change the geometric structure of the Minkowski phase space, we replace ${\left({\Gamma }_{\nu \lambda }^{\mu }\right)}_{\alpha }$ by ${\left({\tilde{\Gamma }}_{\nu \lambda }^{\mu }\right)}_{\alpha }$ in (19). Then, the equation of the geodesic becomes:

$${\displaystyle \frac{d^2{q}^{\mu }}{d{t}^2}}+{\left({\tilde{\Gamma }}_{\nu \lambda }^{\mu }\right)}_{\alpha }{\displaystyle \frac{d{q}^{\nu }}{dt}}{\displaystyle \frac{d{q}^{\lambda }}{dt}}=0,(\nu ,\mu ,\lambda =1,2,3,4).$$

(22)

If we put ${\upsilon }^{\mu }={\displaystyle \frac{d{q}^{\mu }}{dt}}$, we have a first order differential equation on the tangent bundle $\mathcal{T}\left(\mathcal{Q}\right)$ of the manifold $\mathcal{Q}$:

$$\dot{q^{\mu }}={\upsilon }^{\mu },\dot{{\upsilon }^{\mu }}=-{\displaystyle \frac{1}{\alpha +1}}{\left({\Gamma }_{\nu \lambda }^{\mu }\right)}_{\alpha }{\upsilon }^{\nu }{\upsilon }^{\lambda }.$$

(23)

From the above equations, we get the geodesic spray

$$X_{\alpha }:={\upsilon }^{\mu }{\displaystyle \frac{\partial }{\partial q^{\mu }}}-{\displaystyle \frac{1}{\alpha +1}}{\left({\Gamma }_{\nu \lambda }^{\mu }\right)}_{\alpha }{\upsilon }^{\nu }{\upsilon }^{\lambda }{\displaystyle \frac{\partial }{\partial {\upsilon }^{\mu }}}.$$

(24)

By setting $p_{\mu }={\epsilon }_{\mu ϵ}{\upsilon }^{ϵ},$ $\epsilon =sgn(-,+,+,+),$ the vector field $X_{\alpha }$ is equivalently transformed to the vector field $X_{\alpha }$ on the cotangent bundle ${\mathcal{T}}^{*}\left(\mathcal{Q}\right)$ such that

$$X_{\alpha }=-p_1{\displaystyle \frac{\partial }{\partial q^1}}+\sum _{k=2}^4{p}_k{\displaystyle \frac{\partial }{\partial q^k}}+\left({\displaystyle \frac{\alpha -1}{\alpha +1}}\right){\displaystyle \frac{p_1^2}{q^1}}{\displaystyle \frac{\partial }{\partial p_1}}-\sum _{k=2}^4\left({\displaystyle \frac{\alpha -1}{\alpha +1}}\right){\displaystyle \frac{p_k^2}{q^k}}{\displaystyle \frac{\partial }{\partial p_k}},$$

(25)

The vector field $X_{\alpha }$ is a Hamiltonian vector field of a certain Hamiltonian function $H_{\alpha }$.

Proposition 1.

The set $\mathfrak{F}$ of differentiable functions defined on ${\mathcal{T}}^{*}\left(\mathcal{Q}\right)$ endowed with the bracket

$${\{f,g\}}_{\alpha }:=\sum _{\mu =1}^4{\alpha }^{-2}|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left({\displaystyle \frac{\partial f}{\partial p_{\mu }}}{\displaystyle \frac{\partial g}{\partial q^{\mu }}}-{\displaystyle \frac{\partial f}{\partial q^{\mu }}}{\displaystyle \frac{\partial g}{\partial p_{\mu }}}\right)$$

(26)

is a conformable Poisson algebra.

Proof of Proposition 1. 

To prove this Proposition, we just have to prove that the bracket ${\{.,.\}}_{\alpha }$ is a conformable Poisson bracket.

Let us consider $f,g,$ and h as the three arbitrary elements of $\mathfrak{F}$.

• Antisymmetry

$$\begin{array}{cc}\hfill {\{f,g\}}_{\alpha }& =\sum _{\mu =1}^4{\alpha }^{-2}|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left({\displaystyle \frac{\partial f}{\partial p_{\mu }}}{\displaystyle \frac{\partial g}{\partial q^{\mu }}}-{\displaystyle \frac{\partial f}{\partial q^{\mu }}}{\displaystyle \frac{\partial g}{\partial p_{\mu }}}\right),\hfill \\ \hfill & =-\sum _{\mu =1}^4{\alpha }^{-2}|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left({\displaystyle \frac{\partial g}{\partial p_{\mu }}}{\displaystyle \frac{\partial f}{\partial q^{\mu }}}-{\displaystyle \frac{\partial g}{\partial q^{\mu }}}{\displaystyle \frac{\partial f}{\partial p_{\mu }}}\right),\hfill \\ \hfill & =-{\{g,f\}}_{\alpha }\hfill \end{array}$$

(27)

.

• Jacobi identity

$$\begin{array}{cc}\hfill {\{f,{\{g,h\}}_{\alpha }\}}_{\alpha }& ={\left\{f,\sum _{\mu =1}^4{\alpha }^{-2}|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left({\displaystyle \frac{\partial g}{\partial p_{\mu }}}{\displaystyle \frac{\partial h}{\partial q^{\mu }}}-{\displaystyle \frac{\partial g}{\partial q^{\mu }}}{\displaystyle \frac{\partial h}{\partial p_{\mu }}}\right)\right\}}_{\alpha }\hfill \\ \hfill & =\sum _{\mu ,\nu =1}^4{\alpha }^{-4}|p_{\nu }{|}^{(1-\alpha )}|q^{\nu }{|}^{(1-\alpha )}\left[{\displaystyle \frac{\partial f}{\partial p_{\nu }}}\right({\sigma }_1{|p_{\mu }|}^{(1-\alpha )}{\left(q^{\mu }\right)}^{-\alpha }\left({\displaystyle \frac{\partial g}{\partial p_{\mu }}}{\displaystyle \frac{\partial h}{\partial q^{\mu }}}-{\displaystyle \frac{\partial g}{\partial q^{\mu }}}{\displaystyle \frac{\partial h}{\partial p_{\mu }}}\right)\hfill \\ \hfill & +|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left({\displaystyle \frac{{\partial }^{2}g}{\partial q^{\nu }\partial p_{\mu }}}{\displaystyle \frac{\partial h}{\partial q^{\mu }}}+{\displaystyle \frac{\partial g}{\partial p_{\mu }}}{\displaystyle \frac{{\partial }^{2}h}{\partial q^{\nu }\partial q^{\mu }}}-{\displaystyle \frac{{\partial }^{2}g}{\partial q^{\nu }\partial q^{\mu }}}{\displaystyle \frac{\partial h}{\partial p_{\mu }}}-{\displaystyle \frac{\partial g}{\partial q^{\mu }}}{\displaystyle \frac{{\partial }^{2}h}{\partial q^{\nu }\partial p_{\mu }}}\right))\hfill \\ \hfill & -{\displaystyle \frac{\partial f}{\partial q^{\nu }}}({\sigma }_2|q^{\mu }{|}^{(1-\alpha )}{\left(p_{\mu }\right)}^{-\alpha }\left({\displaystyle \frac{\partial g}{\partial p_{\mu }}}{\displaystyle \frac{\partial h}{\partial q^{\mu }}}-{\displaystyle \frac{\partial g}{\partial q^{\mu }}}{\displaystyle \frac{\partial h}{\partial p_{\mu }}}\right)+|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\hfill \\ \hfill & \times \left({\displaystyle \frac{{\partial }^{2}g}{\partial p_{\nu }\partial p_{\mu }}}{\displaystyle \frac{\partial h}{\partial q^{\mu }}}+{\displaystyle \frac{\partial g}{\partial p_{\mu }}}{\displaystyle \frac{{\partial }^{2}h}{\partial p_{\nu }\partial q^{\mu }}}-{\displaystyle \frac{{\partial }^{2}g}{\partial p_{\nu }\partial q^{\mu }}}{\displaystyle \frac{\partial h}{\partial p_{\mu }}}-{\displaystyle \frac{\partial g}{\partial q^{\mu }}}{\displaystyle \frac{{\partial }^{2}h}{\partial p_{\nu }\partial p_{\mu }}}\right)\left)\right],\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill {\{h,{\{f,g\}}_{\alpha }\}}_{\alpha }& ={\left\{h,\sum _{\mu =1}^4{\alpha }^{-2}|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left({\displaystyle \frac{\partial f}{\partial p_{\mu }}}{\displaystyle \frac{\partial g}{\partial q^{\mu }}}-{\displaystyle \frac{\partial f}{\partial q^{\mu }}}{\displaystyle \frac{\partial g}{\partial p_{\mu }}}\right)\right\}}_{\alpha }\hfill \\ \hfill & =\sum _{\mu ,\nu =1}^4{\alpha }^{-4}|p_{\nu }{|}^{(1-\alpha )}|q^{\nu }{|}^{(1-\alpha )}\left[{\displaystyle \frac{\partial h}{\partial p_{\nu }}}\right({\sigma }_1{|p_{\mu }|}^{(1-\alpha )}{\left(q^{\mu }\right)}^{-\alpha }\left({\displaystyle \frac{\partial f}{\partial p_{\mu }}}{\displaystyle \frac{\partial g}{\partial q^{\mu }}}-{\displaystyle \frac{\partial f}{\partial q^{\mu }}}{\displaystyle \frac{\partial g}{\partial p_{\mu }}}\right)\hfill \\ \hfill & +|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left({\displaystyle \frac{{\partial }^{2}f}{\partial q^{\nu }\partial p_{\mu }}}{\displaystyle \frac{\partial g}{\partial q^{\mu }}}+{\displaystyle \frac{\partial f}{\partial p_{\mu }}}{\displaystyle \frac{{\partial }^{2}g}{\partial q^{\nu }\partial q^{\mu }}}-{\displaystyle \frac{{\partial }^{2}f}{\partial q^{\nu }\partial q^{\mu }}}{\displaystyle \frac{\partial g}{\partial p_{\mu }}}-{\displaystyle \frac{\partial f}{\partial q^{\mu }}}{\displaystyle \frac{{\partial }^{2}g}{\partial q^{\nu }\partial p_{\mu }}}\right))\hfill \\ \hfill & -{\displaystyle \frac{\partial h}{\partial q^{\nu }}}({\sigma }_2|q^{\mu }{|}^{(1-\alpha )}{\left(p_{\mu }\right)}^{-\alpha }\left({\displaystyle \frac{\partial f}{\partial p_{\mu }}}{\displaystyle \frac{\partial g}{\partial q^{\mu }}}-{\displaystyle \frac{\partial f}{\partial q^{\mu }}}{\displaystyle \frac{\partial g}{\partial p_{\mu }}}\right)+|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\hfill \\ \hfill & \times \left({\displaystyle \frac{{\partial }^{2}f}{\partial p_{\nu }\partial p_{\mu }}}{\displaystyle \frac{\partial g}{\partial q^{\mu }}}+{\displaystyle \frac{\partial f}{\partial p_{\mu }}}{\displaystyle \frac{{\partial }^{2}g}{\partial p_{\nu }\partial q^{\mu }}}-{\displaystyle \frac{{\partial }^{2}f}{\partial p_{\nu }\partial q^{\mu }}}{\displaystyle \frac{\partial g}{\partial p_{\mu }}}-{\displaystyle \frac{\partial f}{\partial q^{\mu }}}{\displaystyle \frac{{\partial }^{2}g}{\partial p_{\nu }\partial p_{\mu }}}\right)\left)\right],\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill {\{g,{\{h,f\}}_{\alpha }\}}_{\alpha }& ={\left\{g,\sum _{\mu =1}^4{\alpha }^{-2}|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left({\displaystyle \frac{\partial h}{\partial p_{\mu }}}{\displaystyle \frac{\partial f}{\partial q^{\mu }}}-{\displaystyle \frac{\partial h}{\partial q^{\mu }}}{\displaystyle \frac{\partial f}{\partial p_{\mu }}}\right)\right\}}_{\alpha }\hfill \\ \hfill & =\sum _{\mu ,\nu =1}^4{\alpha }^{-4}|p_{\nu }{|}^{(1-\alpha )}|q^{\nu }{|}^{(1-\alpha )}\left[{\displaystyle \frac{\partial g}{\partial p_{\nu }}}\right({\sigma }_1{|p_{\mu }|}^{(1-\alpha )}{\left(q^{\mu }\right)}^{-\alpha }\left({\displaystyle \frac{\partial h}{\partial p_{\mu }}}{\displaystyle \frac{\partial f}{\partial q^{\mu }}}-{\displaystyle \frac{\partial h}{\partial q^{\mu }}}{\displaystyle \frac{\partial f}{\partial p_{\mu }}}\right)\hfill \\ \hfill & +|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left({\displaystyle \frac{{\partial }^{2}h}{\partial q^{\nu }\partial p_{\mu }}}{\displaystyle \frac{\partial f}{\partial q^{\mu }}}+{\displaystyle \frac{\partial h}{\partial p_{\mu }}}{\displaystyle \frac{{\partial }^{2}f}{\partial q^{\nu }\partial q^{\mu }}}-{\displaystyle \frac{{\partial }^{2}h}{\partial q^{\nu }\partial q^{\mu }}}{\displaystyle \frac{\partial f}{\partial p_{\mu }}}-{\displaystyle \frac{\partial h}{\partial q^{\mu }}}{\displaystyle \frac{{\partial }^{2}f}{\partial q^{\nu }\partial p_{\mu }}}\right))\hfill \\ \hfill & -{\displaystyle \frac{\partial g}{\partial q^{\nu }}}({\sigma }_2|q^{\mu }{|}^{(1-\alpha )}{\left(p_{\mu }\right)}^{-\alpha }\left({\displaystyle \frac{\partial h}{\partial p_{\mu }}}{\displaystyle \frac{\partial f}{\partial q^{\mu }}}-{\displaystyle \frac{\partial h}{\partial q^{\mu }}}{\displaystyle \frac{\partial f}{\partial p_{\mu }}}\right)+|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\hfill \\ & \times \left({\displaystyle \frac{{\partial }^{2}h}{\partial p_{\nu }\partial p_{\mu }}}{\displaystyle \frac{\partial f}{\partial q^{\mu }}}+{\displaystyle \frac{\partial h}{\partial p_{\mu }}}{\displaystyle \frac{{\partial }^{2}f}{\partial p_{\nu }\partial q^{\mu }}}-{\displaystyle \frac{{\partial }^{2}h}{\partial p_{\nu }\partial q^{\mu }}}{\displaystyle \frac{\partial f}{\partial p_{\mu }}}-{\displaystyle \frac{\partial h}{\partial q^{\mu }}}{\displaystyle \frac{{\partial }^{2}f}{\partial p_{\nu }\partial p_{\mu }}}\right)\left)\right],\hfill \end{array}$$

(30)

where ${\sigma }_1=(1-\alpha ){\left(sgn\left(q^{\mu }\right)\right)}^{1-\alpha }$ and ${\sigma }_2=(1-\alpha ){\left(sgn\left(p_{\mu }\right)\right)}^{1-\alpha }.$

Summing (28)–(30), we get

$${\{f,{\{g,h\}}_{\alpha }\}}_{\alpha }+{\{g,{\{h,f\}}_{\alpha }\}}_{\alpha }+{\{h,{\{f,g\}}_{\alpha }\}}_{\alpha }=0,$$

(31)

which is the Jacobi identity.

• Derivation

$$\begin{array}{cc}\hfill {\{f,gh\}}_{\alpha }& =\sum _{\mu =1}^4{\alpha }^{-2}|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left({\displaystyle \frac{\partial f}{\partial p_{\mu }}}{\displaystyle \frac{\partial \left(gh\right)}{\partial q^{\mu }}}-{\displaystyle \frac{\partial f}{\partial q^{\mu }}}{\displaystyle \frac{\partial \left(gh\right)}{\partial p_{\mu }}}\right)\hfill \\ \hfill & =\sum _{\mu =1}^4{\alpha }^{-2}|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left[{\displaystyle \frac{\partial f}{\partial p_{\mu }}}\left({\displaystyle \frac{\partial g}{\partial q^{\mu }}}h+g{\displaystyle \frac{\partial h}{\partial q^{\mu }}}\right)-{\displaystyle \frac{\partial f}{\partial q^{\mu }}}\left({\displaystyle \frac{\partial g}{\partial p_{\mu }}}h+g{\displaystyle \frac{\partial h}{\partial p_{\mu }}}\right)\right]\hfill \\ \hfill & =\sum _{\mu =1}^4{\alpha }^{-2}|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left[g\left({\displaystyle \frac{\partial f}{\partial p_{\mu }}}{\displaystyle \frac{\partial h}{\partial q^{\mu }}}-{\displaystyle \frac{\partial f}{\partial q^{\mu }}}{\displaystyle \frac{\partial h}{\partial p_{\mu }}}\right)+\left({\displaystyle \frac{\partial f}{\partial p_{\mu }}}{\displaystyle \frac{\partial g}{\partial q^{\mu }}}-{\displaystyle \frac{\partial f}{\partial q^{\mu }}}{\displaystyle \frac{\partial g}{\partial p_{\mu }}}\right)h\right],\hfill \end{array}$$

(32)

which proves the derivative property: ${\{f,gh\}}_{\alpha }=g{\{f,h\}}_{\alpha }+{\{f,g\}}_{\alpha }h$.

Thus, the bracket ${\{.,.\}}_{\alpha }$ is antisymmetric and satisfies the Jacobi identity and the derivation property. Therefore, it is a Poisson bracket and $(\mathfrak{F},{\{.,.\}}_{\alpha })$ is a conformable Poisson algebra. □

Proposition 2.

The set of Hamiltonian vector fields ${\mathfrak{X}}_{{\alpha }_{\mathfrak{F}}}$ endowed with the Lie bracket given by the commutator $[.,.]$ is a conformable Lie algebra.

Proof of Proposition 2. 

Using the Jacoby identity, we have:

$$\begin{array}{c}\hfill {\{f,{\{g,h\}}_{\alpha }\}}_{\alpha }+{\{g,{\{h,f\}}_{\alpha }\}}_{\alpha }+{\{h,{\{f,g\}}_{\alpha }\}}_{\alpha }=0.\end{array}$$

(33)

The left hand side of this identity can be handled as:

$$\begin{array}{cc}\hfill & {\{f,{\{g,h\}}_{\alpha }\}}_{\alpha }+{\{g,{\{h,f\}}_{\alpha }\}}_{\alpha }+{\{h,{\{f,g\}}_{\alpha }\}}_{\alpha }\hfill \\ \hfill & ={\{f,{\{g,h\}}_{\alpha }\}}_{\alpha }-{\{g,{\{f,h\}}_{\alpha }\}}_{\alpha }-{\{{\{f,g\}}_{\alpha },h\}}_{\alpha }\hfill \\ \hfill & =X_{{\alpha }_f}{\{g,h\}}_{\alpha }-{\{g,X_{{\alpha }_f}h\}}_{\alpha }-{\{X_{{\alpha }_f}g,h\}}_{\alpha }\hfill \\ \hfill & =X_{{\alpha }_f}{X}_{{\alpha }_g}h-X_{{\alpha }_g}{X}_{{\alpha }_f}h-X_{{\alpha }_{{\{f,g\}}_{\alpha }}}h\hfill \\ \hfill & =[X_{{\alpha }_f},X_{{\alpha }_g}]h-X_{{\alpha }_{{\{f,g\}}_{\alpha }}}h\hfill \end{array}$$

leading to

$$\begin{array}{c}\hfill [X_{{\alpha }_f},X_{{\alpha }_g}]h=X_{{\alpha }_{{\{f,g\}}_{\alpha }}}h.\end{array}$$

(34)

Then, the map $f\mapsto X_{{\alpha }_f}={\{f,.\}}_{\alpha },{\{f,.g\}}_{\alpha }\mapsto X_{{\alpha }_{{\{f,g\}}_{\alpha }}}$ is a conformable Lie algebra morphism $(\mathfrak{F},{\{.,.\}}_{\alpha })\to ({\mathfrak{X}}_{{\alpha }_{\mathfrak{F}}},[.,.])$. Therefore, $({\mathfrak{X}}_{{\alpha }_{\mathfrak{F}}},[.,.])$ is a conformable Lie algebra. □

3.2. Noether Symmetry and Recursion Operator

By definition, we have

$$X_{\alpha }:={\{H_{\alpha },.\}}_{\alpha }=\sum _{\mu =1}^4{\alpha }^{-2}|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left({\displaystyle \frac{\partial H_{\alpha }}{\partial p_{\mu }}}{\displaystyle \frac{\partial }{\partial q^{\mu }}}-{\displaystyle \frac{\partial H_{\alpha }}{\partial q^{\mu }}}{\displaystyle \frac{\partial }{\partial p_{\mu }}}\right).$$

(35)

Using (25) and (35), we obtain the following set of equations:

$$\left\{\begin{array}{cc}{\alpha }^{-2}|p_1{|}^{(1-\alpha )}{|q^1|}^{(1-\alpha )}{\displaystyle \frac{\partial H_{\alpha }}{\partial p_1}}\hfill & =-p_1\hfill \\ {\alpha }^{-2}|p_1{|}^{(1-\alpha )}{|q^1|}^{(1-\alpha )}{\displaystyle \frac{\partial H_{\alpha }}{\partial q^1}}\hfill & =-\left({\displaystyle \frac{\alpha -1}{\alpha +1}}\right){\displaystyle \frac{p_1^2}{q^1}}\hfill \\ {\alpha }^{-2}|p_k{|}^{(1-\alpha )}{|q^k|}^{(1-\alpha )}{\displaystyle \frac{\partial H_{\alpha }}{\partial p_k}}\hfill & =p_k,k=2,3,4\hfill \\ {\alpha }^{-2}|p_k{|}^{(1-\alpha )}{|q^k|}^{(1-\alpha )}{\displaystyle \frac{\partial H_{\alpha }}{\partial q^k}}\hfill & =\left({\displaystyle \frac{\alpha -1}{\alpha +1}}\right){\displaystyle \frac{p_k^2}{q^k}},k=2,3,4\hfill \end{array}\right.$$

(36)

leading to

$$H_{\alpha }=-{\displaystyle \frac{{\alpha }^2}{\alpha +1}}|q^1{|}^{\alpha -1}|p_1{|}^{\alpha +1}+\sum _{k=2}^4{\displaystyle \frac{{\alpha }^2}{\alpha +1}}|q^k{|}^{\alpha -1}{|p_k|}^{\alpha +1}.$$

(37)

This function is called the Hamiltonian function. For $\alpha =1$, we naturally obtain the Hamiltonian function of a free particle on the ordinary Minkowski phase space.

The vector field

$$Y_{\alpha }=-{\displaystyle \frac{1}{2{\alpha }^2}}|p_1{|}^{1-\alpha }{p}_1^{-2}|q^1{|}^{1-\alpha }|q^1{|}^{\frac{1-\alpha }{1+\alpha }}{\displaystyle \frac{\partial }{\partial p_1}}+{\displaystyle \frac{1}{2{\alpha }^2}}\sum _{k=2}^4|p_k{|}^{1-\alpha }{p}_k^{-2}|q^k{|}^{1-\alpha }{|q^k|}^{\frac{1-\alpha }{1+\alpha }}{\displaystyle \frac{\partial }{\partial p_k}}$$

(38)

is a master symmetry, i.e.,

$$\left[\left[Y_{\alpha },X_{\alpha }\right],X_{\alpha }\right]=0,$$

(39)

and the following relations hold:

$$\begin{array}{cc}\hfill L_{\alpha }& :={\mathcal{L}}_{Y_{\alpha }}{H}_{\alpha }={\displaystyle \frac{1}{2}}\left(p_1^{-1}{\left(q^1\right)}^{\frac{1-\alpha }{1+\alpha }}+\sum _{k=2}^4{p}_k^{-1}{\left(q^k\right)}^{\frac{1-\alpha }{1+\alpha }}\right),\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill {\omega }_{{\alpha }_1}& :={\mathcal{L}}_{Y_{\alpha }}{\omega }_{\alpha }=d{\iota }_{Y_{\alpha }}{\omega }_{\alpha }+{\iota }_{Y_{\alpha }}d{\omega }_{\alpha }\hfill \\ \hfill & =p_1^{-3}|q^1{|}^{\frac{1-\alpha }{1+\alpha }}d{p}_1\wedge d{q}^1-\sum _{k=2}^4{p}_k^{-3}{|q^k|}^{\frac{1-\alpha }{1+\alpha }}d{p}_k\wedge d{q}^k,\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill X_{{\alpha }_1}& :=[X_{\alpha },Y_{\alpha }]\hfill \\ \hfill & =-{\displaystyle \frac{1}{2{\alpha }^2}}\left[{\displaystyle \frac{1-\alpha }{(1+\alpha )}}{G}_1|p_1{|}^{-\alpha }|q^1{|}^{\frac{1-2\alpha -{\alpha }^2}{1+\alpha }}{\displaystyle \frac{\partial }{\partial p_1}}+|p_1{|}^{1-\alpha }{p}_1^{-2}{|q^1|}^{\frac{2-\alpha -{\alpha }^2}{1+\alpha }}{\displaystyle \frac{\partial }{\partial q^1}}\right]\hfill \\ \hfill & -{\displaystyle \frac{1}{2{\alpha }^2}}\sum _{k=2}^4\left[{\displaystyle \frac{1-\alpha }{(1+\alpha )}}{G}_k{p}_k^{-\alpha }|q^k{|}^{\frac{1-2\alpha -{\alpha }^2}{1+\alpha }}{\displaystyle \frac{\partial }{\partial p_k}}+|p_k{|}^{1-\alpha }{p}_k^{-2}{|q^k|}^{\frac{2-\alpha -{\alpha }^2}{1+\alpha }}{\displaystyle \frac{\partial }{\partial q^k}}\right],\hfill \end{array}$$

(42)

where $G_i=sgn\left(p_i\right)sgn\left(q^i\right),i=1,2,3,4.$

We notice that $X_{{\alpha }_1}$ satisfies the relation

$${\iota }_{{}_{X_{{\alpha }_1}}}{\omega }_{\alpha }=-d{L}_{\alpha },$$

where ${\iota }_{{}_{X_{{\alpha }_1}}}{\omega }_{\alpha }$ is the interior product of ${\omega }_{\alpha }$ with respect to the vector field $X_{{\alpha }_1}.$ Since $X_{{\alpha }_1}$ is a dynamical symmetry, i.e., $[X_{\alpha },X_{{\alpha }_1}]=0,$ $L_{\alpha }$ is a first integral, also called a constant of motion. Thus, we arrive at the following property:

Proposition 3.

The vector field $X_{{\alpha }_1}$ is an infinitesimal Noether symmetry.

Proof of Proposition 3. 

We have:

$${\mathcal{L}}_{X_{{\alpha }_1}}{\omega }_{\alpha }=d{\iota }_{X_{{\alpha }_1}}{\omega }_{\alpha }+{\iota }_{X_{{\alpha }_1}}d{\omega }_{\alpha }=d{\iota }_{X_{{\alpha }_1}}{\omega }_{\alpha }=-d^2{L}_{\alpha }=0.$$

(43)

Since $X_{{\alpha }_1}$ is a dynamical symmetry, then

$${\mathcal{L}}_{X_{{\alpha }_1}}{H}_{\alpha }=X_{{\alpha }_1}\left(H_{\alpha }\right)=0.$$

(44)

Equations (43) and (44) show that $X_{{\alpha }_1}$ is both an infinitesimal geometric symmetry, i.e., leaving invariant the geometric structure (the symplectic form ${\omega }_{\alpha }$), and an infinitesimal Hamiltonian symmetry leaving invariant the dynamics (the Hamiltonian function $H_{\alpha }$). Hence, $X_{{\alpha }_1}$ is an infinitesimal Noether symmetry. □

In the sequel, we consider the following Poisson bivector

$${\mathcal{P}}_{{\alpha }_1}=p_1^3|q^1{|}^{\frac{\alpha -1}{1+\alpha }}{\displaystyle \frac{\partial }{\partial p_1}}\wedge {\displaystyle \frac{\partial }{\partial q^1}}-\sum _{k=2}^4{p}_k^3{|q^k|}^{\frac{\alpha -1}{1+\alpha }}{\displaystyle \frac{\partial }{\partial p_k}}\wedge {\displaystyle \frac{\partial }{\partial q^k}}$$

(45)

and define the conformable Poisson bracket

$${\{f,g\}}_{{\alpha }_1}:=p_1^3|q^1{|}^{\frac{\alpha -1}{1+\alpha }}\left({\displaystyle \frac{\partial f}{\partial p_1}}{\displaystyle \frac{\partial g}{\partial q^1}}-{\displaystyle \frac{\partial f}{\partial q^1}}{\displaystyle \frac{\partial g}{\partial p_1}}\right)-\sum _{k=2}^4{p}_k^3{|q^k|}^{\frac{\alpha -1}{1+\alpha }}\left({\displaystyle \frac{\partial f}{\partial p_k}}{\displaystyle \frac{\partial g}{\partial q^k}}-{\displaystyle \frac{\partial f}{\partial q^k}}{\displaystyle \frac{\partial g}{\partial p_k}}\right),$$

(46)

with respect to the symplectic form ${\omega }_{{\alpha }_1}$.

Thus, the vector field $X_{\alpha }$ is a bi-Hamiltonian vector field with respect to $({\omega }_{\alpha },{\omega }_{{\alpha }_1}),$ i.e.,

$${\iota }_{{}_{X_{\alpha }}}{\omega }_{\alpha }=-d{H}_{\alpha }\mathrm{and}{\iota }_{X_{\alpha }}{\omega }_{{\alpha }_1}=-d{\tilde{L}}_{\alpha },X_{\alpha }={\{H_{\alpha },.\}}_{\alpha }={\{{\tilde{L}}_{\alpha },.\}}_{{\alpha }_1},$$

(47)

where

$${\displaystyle {\tilde{L}}_{\alpha }=\sum _{\mu =1}^4{|q^{\mu }|}^{\frac{1-\alpha }{1+\alpha }}{p}_{\mu }^{-1}}$$

(48)

are first integrals for $X_{H_{\alpha }}.$

Therefore, the associated recursion operator $T_{\alpha }$ is given by:

$$\begin{array}{cc}\hfill T_{\alpha }& :={\mathcal{P}}_{{\alpha }_1}\circ {\mathcal{P}}_{\alpha }^{-1}\hfill \\ \hfill & =\left(p_1^3|q^1{|}^{\frac{\alpha -1}{1+\alpha }}{\displaystyle \frac{\partial }{\partial p_1}}\wedge {\displaystyle \frac{\partial }{\partial q^1}}-\sum _{k=2}^4{p}_k^3{|q^k|}^{\frac{\alpha -1}{1+\alpha }}{\displaystyle \frac{\partial }{\partial p_k}}\wedge {\displaystyle \frac{\partial }{\partial q^k}}\right)\circ \left(\sum _{\mu =1}^4{\alpha }^2|p_{\mu }{|}^{(\alpha -1)}{|q^{\mu }|}^{(\alpha -1)}d{p}_{\mu }\wedge d{q}^{\mu }\right)\hfill \\ \hfill & ={\alpha }^2{p}_1^3|p_1{|}^{(\alpha -1)}|q^1{|}^{\frac{-2+{\alpha }^2+\alpha }{1+\alpha }}{\displaystyle \frac{\partial }{\partial p_1}}\otimes d{p}_1-{\alpha }^2\sum _{k=2}^4{p}_k^3|p_k{|}^{(\alpha -1)}{|q^k|}^{\frac{-2+{\alpha }^2+\alpha }{1+\alpha }}{\displaystyle \frac{\partial }{\partial p_k}}\otimes d{p}_k\hfill \\ \hfill & +{\alpha }^2{p}_1^3|p_1{|}^{(\alpha -1)}|q^1{|}^{\frac{-2+{\alpha }^2+\alpha }{1+\alpha }}{\displaystyle \frac{\partial }{\partial q^1}}\otimes d{q}^1-{\alpha }^2\sum _{k=2}^4{p}_k^3|p_k{|}^{(\alpha -1)}{|q^k|}^{\frac{-2+{\alpha }^2+\alpha }{1+\alpha }}{\displaystyle \frac{\partial }{\partial q^k}}\otimes d{q}^k,\hfill \end{array}$$

(49)

providing the constants of motion

$$Tr\left(T_{\alpha }^h\right)=2^h{\alpha }^{2h}\left\{{\left(p_1^3|p_1{|}^{(\alpha -1)}{|q^1|}^{\frac{-2+{\alpha }^2+\alpha }{1+\alpha }}\right)}^h+{(-1)}^h{\left(\sum _{k=2}^4{p}_k^3|p_k{|}^{(\alpha -1)}{|q^k|}^{\frac{-2+{\alpha }^2+\alpha }{1+\alpha }}\right)}^h\right\},h\in \mathbb{N}.$$

(50)

This work can be considered as a conformable case of previous investigations [28,29]. The only difference resides in the fact that we here use the method of Noether symmetry to obtain the integrals of motion instead of the method of Hamilton–Jacobi separability, developed in [27,28,29].

4. Conformable Einstein Field Equation

In this section, we investigate the solutions of the Einstein field equation in the conformable Schwarzschild and Friedmann–Lemaître–Robertson–Walker (FLRW) metrics. We consider the Einstein field equation shortly written in the tensor form as:

$$G_{\alpha }+\Lambda g_{\alpha }=\kappa T_{\alpha },$$

(51)

where the tensor

$$G_{\alpha }=R_{\alpha }-{\displaystyle \frac{1}{2}}{g}_{\alpha }{\mathbf{R}}_{\alpha }$$

(52)

is the Einstein tensor, the constant $\Lambda$ is the cosmological constant, $\kappa$ is a constant; $T_{\alpha }$ and $R_{\alpha }$ are the tress-energy tensor and Ricci tensor measuring the geodesic deviation, respectively. $g_{\alpha }$ is the metric tensor, and ${\mathbf{R}}_{\alpha },$ is the scalar curvature. The energy-momentum tensor $T_{\alpha }$, determines how the geometry is.

4.1. Recursion Operator in Conformable Schwarzschild Metric

The Schwarzschild metric is the simplest one among the particular solutions of the Einstein field equation.

Here, we consider the following conformable Schwarzschild metric

$$\begin{array}{cc}\hfill d_{\alpha }{s}^2& =-\left(1-{\displaystyle \frac{2M}{q^2}}\right){\left(q^1\right)}^{2(\alpha -1)}{\left(d{q}^1\right)}^2+{\left(1-{\displaystyle \frac{2M}{q^2}}\right)}^{-1}{\left(q^2\right)}^{2(\alpha -1)}{\left(d{q}^2\right)}^2\hfill \\ \hfill & +{\left(q^2\right)}^2{\left(q^3\right)}^{2(\alpha -1)}{\left(d{q}^3\right)}^2+{\left(q^2\right)}^2{\left(q^4\right)}^{2(\alpha -1)}{sin}^2{q}^3{\left(d{q}^4\right)}^2,\hfill \end{array}$$

(53)

where $t=q^1,r=q^2,\theta =q^3,\varphi =q^4,$ M is a positive constant representing the mass of the black hole, $t\in (-\infty ,\infty ),$ $r\in (2M,\infty ),$ $\theta \in (0,\pi ),$ and $\varphi \in (0,2\pi )$.

The metric is defined on a manifold

$$\begin{array}{cc}\hfill \mathcal{Q}& =\{(q^1,q^2,q^3,q^4)|0\ne q^1\in (-\infty ,\infty ),q^2\in (2M,\infty ),\\ & 0\ne q^3\in (0,\pi ),\mathrm{and}0\ne q^4\in (0,2\pi )\}.\end{array}$$

(54)

For $\alpha =1,$ we recover the Karl Schwarzschild metric [35].

For our purpose, let us consider the phase space ${\mathcal{T}}^{*}\mathcal{Q}\ni (q,p),q\in \mathcal{Q},$ and the Hamiltonian function

$$\begin{array}{cc}\hfill H_{S\alpha }& =-{\displaystyle \frac{1}{2}}{\left(1-{\displaystyle \frac{2M}{q^2}}\right)}^{-1}{\left(q^1\right)}^{2(1-\alpha )}{p}_1^2+{\displaystyle \frac{1}{2}}\left(1-{\displaystyle \frac{2M}{q^2}}\right){\left(q^2\right)}^{2(1-\alpha )}{p}_2^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2{\left(q^2\right)}^2}}{\left(q^3\right)}^{2(1-\alpha )}{p}_3^2+{\displaystyle \frac{1}{2{\left(q^2\right)}^2{sin}^2{q}^3}}{\left(q^4\right)}^{2(1-\alpha )}{p}_4^2.\hfill \end{array}$$

(55)

The Hamiltonian vector field of $H_{S\alpha }$ in a conformable Schwarzschild metric with respect to the canonical symplectic structure ${\displaystyle {\omega }_{\alpha }=\sum _{\mu =1}^4{\alpha }^2|p_{\mu }{|}^{(\alpha -1)}{|q^{\mu }|}^{(\alpha -1)}d{p}_{\mu }\wedge d{q}^{\mu }}$ is given by

$$\begin{array}{cc}\hfill X_{S\alpha }& :={\{H_{S\alpha },.\}}_{\alpha }=\sum _{\mu =1}^4{\alpha }^{-2}|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left({\displaystyle \frac{\partial H_{\alpha }}{\partial p_{\mu }}}{\displaystyle \frac{\partial }{\partial q^{\mu }}}-{\displaystyle \frac{\partial H_{\alpha }}{\partial q^{\mu }}}{\displaystyle \frac{\partial }{\partial p_{\mu }}}\right)\hfill \\ \hfill & =\sum _{\mu =1}^4{\alpha }^{-2}|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left(V_{\mu }{\displaystyle \frac{\partial }{\partial q^{\mu }}}+U_{\mu }{\displaystyle \frac{\partial }{\partial p_{\mu }}}\right),\hfill \end{array}$$

(56)

where

$$\begin{array}{cc}\hfill V_1& =-{\left(1-{\displaystyle \frac{2M}{q^2}}\right)}^{-1}{\eta }_1,V_2=\left(1-{\displaystyle \frac{2M}{q^2}}\right){\eta }_2,V_3={\displaystyle \frac{1}{{\left(q^2\right)}^2}}{\eta }_3,V_4={\displaystyle \frac{1}{{\left(q^2\right)}^2{sin}^2{q}^3}}{\eta }_4,\hfill \\ \hfill U_1& =(1-\alpha ){\left(1-{\displaystyle \frac{2M}{q^2}}\right)}^{-1}{\zeta }_1,U_3=-\left({\displaystyle \frac{1-\alpha }{{\left(q^2\right)}^2}}{\zeta }_3-{\displaystyle \frac{cos{q}^3}{{\left(q^2\right)}^2{sin}^3{q}^3}}{\eta }_4{p}_4\right),U_4=-{\displaystyle \frac{1-\alpha }{{\left(q^2\right)}^2{sin}^2{q}^3}}{\zeta }_4,\hfill \\ \hfill U_2& =-\{{\displaystyle \frac{M}{{\left(q^2\right)}^2}}{\left(1-{\displaystyle \frac{2M}{q^2}}\right)}^{-2}{\eta }_1{p}_1+(1-\alpha )\left(1-{\displaystyle \frac{2M}{q^2}}\right){\zeta }_2+{\displaystyle \frac{M}{{\left(q^2\right)}^2}}{\eta }_2{p}_2-{\displaystyle \frac{1}{{\left(q^2\right)}^3}}{\eta }_3{p}_3\hfill \\ \hfill & -{\displaystyle \frac{1}{{\left(q^2\right)}^3{sin}^2{q}^3}}{\eta }_4{p}_4\},\hfill \end{array}$$

with ${\eta }_{\nu }={\left(q^{\nu }\right)}^{2(1-\alpha )}{p}_{\nu },$ and ${\zeta }_{\nu }={\left(q^{\nu }\right)}^{(1-2\alpha )}{p}_{\nu }^2,\nu =1,2,3,4.$

Then, we get in conformable Schwarzschild metric, the Christoffel symbols ${\left({\Gamma }_{ij}^k\right)}_{\alpha },$ the components of the Riemann and Ricci tensors ${\left(R_{ii}\right)}_{\alpha },$ the Ricci scalar $\mathbf{R},$ and the components of the Einstein tensor ${\left(G_{ij}\right)}_{\alpha }$, $i,j,k,l=1,2,3,4$, see Appendix A.

Note that the components of defined geometric objects are obtained in the usual undeformed Schwarzschild metric by setting $\alpha =1.$

Now, we consider the Hamilton–Jacobi equation for the Hamiltonian function $H_{S\alpha }$

$$\begin{array}{cc}\hfill E_S& =H_{S\alpha }\left(q,{\displaystyle \frac{\partial W}{\partial q}}\right)\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}{\left(1-{\displaystyle \frac{2M}{q^2}}\right)}^{-1}{\left(q^1\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{\partial W}{\partial q^1}}\right)}^2+{\displaystyle \frac{1}{2}}\left(1-{\displaystyle \frac{2M}{q^2}}\right){\left(q^2\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{\partial W}{\partial q^2}}\right)}^2\hfill \\ \hfill & +{\displaystyle \frac{1}{2{\left(q^2\right)}^2}}{\left(q^3\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{\partial W}{\partial q^3}}\right)}^2+{\displaystyle \frac{1}{2{\left(q^2\right)}^2{sin}^2{q}^3}}{\left(q^4\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{\partial W}{\partial q^4}}\right)}^2,\hfill \end{array}$$

(57)

where $E_S$ is a constant and ${\displaystyle W=\sum _{\mu =1}^4{W}_{\mu }\left(q_{\mu }\right)}$ is the generating function. In particular, we put $W_1={\displaystyle \frac{a}{\alpha }}{|q^1|}^{\alpha }$, where a is a constant. This equation is a type of separation of variables; then, the above Hamilton–Jacobi equation becomes

$$\begin{array}{cc}\hfill & 2E_S{\left(q^2\right)}^2+{\left(1-{\displaystyle \frac{2M}{q^2}}\right)}^{-1}{\left(q^2\right)}^2{a}^2-\left(1-{\displaystyle \frac{2M}{q^2}}\right){\left(q^2\right)}^{2(2-\alpha )}{\left({\displaystyle \frac{d{W}_2}{d{q}^2}}\right)}^2\hfill \\ \hfill & ={\left(q^3\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{d{W}_3}{d{q}^3}}\right)}^2+{\displaystyle \frac{1}{{sin}^2{q}^3}}{\left(q^4\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{d{W}_4}{d{q}^4}}\right)}^2,\hfill \end{array}$$

(58)

which can be rewritten through a constant K as:

$$\begin{array}{cc}\hfill K& =2E_S{\left(q^2\right)}^2+{\left(1-{\displaystyle \frac{2M}{q^2}}\right)}^{-1}{\left(q^2\right)}^2{a}^2-\left(1-{\displaystyle \frac{2M}{q^2}}\right){\left(q^2\right)}^{2(2-\alpha )}{\left({\displaystyle \frac{d{W}_2}{d{q}^2}}\right)}^2\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill K& ={\left(q^3\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{d{W}_3}{d{q}^3}}\right)}^2+{\displaystyle \frac{1}{{sin}^2{q}^3}}{\left(q^4\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{d{W}_4}{d{q}^4}}\right)}^2.\hfill \end{array}$$

(60)

From the above, we set:

$$\begin{array}{cc}\hfill \left(K-{\left(q^3\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{d{W}_3}{d{q}^3}}\right)}^2\right){sin}^2{q}^3& =G\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill {\left(q^4\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{d{W}_4}{d{q}^4}}\right)}^2& =G.\hfill \end{array}$$

(62)

and obtain

$$W_4={\displaystyle \frac{\sqrt{G}}{\alpha }}{|q^4|}^{\alpha -1}{q}^4+A,$$

(63)

where A is a constant.

We put the solutions of Equations (59) and (61) in the form:

$$W_2=W_2(q^2,E_S,a,K),W_3=W_3(q^3,K,G).$$

(64)

Then, a generating function W takes the form:

$$W={\displaystyle \frac{a}{\alpha }}|q^1{|}^{\alpha }+W_2(q^2,E_S,a,K)+W_3(q^3,K,G)+{\displaystyle \frac{\sqrt{G}}{\alpha }}{|q^4|}^{\alpha -1}{q}^4+A.$$

(65)

Now, we consider the canonical system $(Q,P)$, where

$$\begin{array}{cc}\hfill & Q^1=E_S,Q^2=a,Q^3=K,Q^4=\sqrt{G},\hfill \end{array}$$

(66)

$$\begin{array}{cc}\hfill & P_1:=-{\displaystyle \frac{\partial W}{\partial Q^1}}=-{\displaystyle \frac{\partial W_2}{\partial Q^1}},P_2:=-{\displaystyle \frac{\partial W}{\partial Q^2}}=-{\displaystyle \frac{a}{\alpha }}{\left(q^1\right)}^{\alpha }-{\displaystyle \frac{\partial W_2}{\partial Q^2}},\hfill \end{array}$$

(67)

$$\begin{array}{cc}\hfill & P_3:=-{\displaystyle \frac{\partial W}{\partial Q^3}}=-{\displaystyle \frac{\partial W_2}{\partial Q^3}}-{\displaystyle \frac{\partial W_3}{\partial Q^3}},\mathrm{and}{P}_4:=-{\displaystyle \frac{\partial W}{\partial Q^4}}=-{\displaystyle \frac{\partial W_4}{\partial Q^4}}-{\displaystyle \frac{\partial W_3}{\partial Q^4}}=-{\displaystyle \frac{1}{\alpha }}{|q^4|}^{\alpha -1}{q}^4-{\displaystyle \frac{\partial W_3}{\partial Q^4}}.\hfill \end{array}$$

(68)

In this new canonical system, we define the following Poisson bracket

$${\{f,g\}}_{\alpha }=\sum _{\mu =1}^4{\alpha }^{-2}|P_{\mu }{|}^{(1-\alpha )}{|Q^{\mu }|}^{(1-\alpha )}\left({\displaystyle \frac{\partial f}{\partial P_{\mu }}}{\displaystyle \frac{\partial g}{\partial Q^{\mu }}}-{\displaystyle \frac{\partial f}{\partial Q^{\mu }}}{\displaystyle \frac{\partial g}{\partial P_{\mu }}}\right),$$

(69)

with respect to the symplectic form

$${\omega }_{\alpha }=\sum _{\mu =1}^4{\alpha }^2|P_{\mu }{|}^{(\alpha -1)}{|Q^{\mu }|}^{(\alpha -1)}d{P}_{\mu }\wedge d{Q}^{\mu }.$$

(70)

Then, the Hamiltonian vector field takes the form:

$$X_{S\alpha }:={\{H_{S\alpha },.\}}_{\alpha }=-{\alpha }^{-2}|P_1{|}^{(1-\alpha )}{|Q^1|}^{(1-\alpha )}{\displaystyle \frac{\partial }{\partial P_1}}.$$

(71)

Now, we consider a $(1,1)$-tensor field $T_{S\alpha }$ as

$$T_{S\alpha }=\sum _{\mu =1}^4{|Q^{\mu }|}^{\alpha -1}{Q}^{\mu }\left({\displaystyle \frac{\partial }{\partial P_{\mu }}}\otimes d{P}_{\mu }+{\displaystyle \frac{\partial }{\partial Q^{\mu }}}\otimes d{Q}^{\mu }\right).$$

(72)

We can put $Q^{\mu }=x_{\mu }$ and $P_{\mu }=x_{\mu +n},$ where $n=4$ in this case and $\mu =1,2,3,4$. Then, by Lemma 1, $T_{S\alpha }$ satisfies ${\mathcal{L}}_{X_{S\alpha }}{T}_{S\alpha }=0$, ${\mathcal{N}}_{T_{S\alpha }}=0,$ and $deg{Q}^{\mu }=2$. Hence, $T_{S\alpha }$ is a recursion operator of $X_{S\alpha }$. The constants of motion $Tr\left(T_{\alpha }^l\right)(l\in \mathbb{N})$ of the Hamiltonian vector field $X_{S\alpha }$ for the conformable Schwarzschild metric are finally obtained as:

$$Tr\left(T_{F\alpha }^l\right)=2({\left(Q^1\right)}^l+{\left(Q^2\right)}^l+{\left(Q^3\right)}^l+{\left(Q^4\right)}^l),l\in \mathbb{N}.$$

(73)

4.2. Recursion Operator in Conformable FLRW Metric

Now, we consider the following conformable Friedmann–Lemaître–Robertson–Walker (FLRW) metric:

$$\begin{array}{cc}\hfill d_{\alpha }{s}^2& =-|q^1{|}^{2(\alpha -1)}{\left(d{q}^1\right)}^2+R^2\left(q^1\right)\{{\displaystyle \frac{|q^2{|}^{2(\alpha -1)}}{1-k{\left(q^2\right)}^2}}{\left(d{q}^2\right)}^2+{\left(q^2\right)}^2({|q^3|}^{2(\alpha -1)}{\left(d{q}^3\right)}^2\hfill \\ \hfill & +|q^4{|}^{2(\alpha -1)}{sin}^2{q}^3{\left(d{q}^4\right)}^2\left)\right\}\hfill \end{array}$$

(74)

defined on the same manifold $\mathcal{Q}$ (54), where $R\left(q^1\right)$ is a scale factor and k is a constant representing the curvature of the space. Considering the Hamiltonian function

$$\begin{array}{c}\hfill H_{F\alpha }=-{\displaystyle \frac{1}{2}}{\left(q^1\right)}^{2(1-\alpha )}{p}_1^2+{\displaystyle \frac{1-k{\left(q^2\right)}^2}{2R^2\left(q^1\right)}}{\left(q^2\right)}^{2(1-\alpha )}{p}_2^2+{\displaystyle \frac{{\left(q^3\right)}^{2(1-\alpha )}}{2{\left(q^2\right)}^2{R}^2\left(q^1\right)}}{p}_3^2+{\displaystyle \frac{{\left(q^4\right)}^{2(1-\alpha )}}{2{\left(q^2\right)}^2{R}^2\left(q^1\right){sin}^2\left(q^3\right)}}{p}_4^2,\end{array}$$

(75)

we obtain the following Hamiltonian vector field

$$\begin{array}{c}\hfill X_{F\alpha }=\sum _{\mu =1}^4{\alpha }^{-2}|p_{\mu }{|}^{(1-\alpha )}{|q^{\mu }|}^{(1-\alpha )}\left({\tilde{V}}_{\mu }{\displaystyle \frac{\partial }{\partial q^{\mu }}}+{\tilde{U}}_{\mu }{\displaystyle \frac{\partial }{\partial p_{\mu }}}\right),\end{array}$$

(76)

with respect to the symplectic structure

$${\displaystyle {\omega }_{\alpha }=\sum _{\mu =1}^4{\alpha }^2|p_{\mu }{|}^{(\alpha -1)}{|q^{\mu }|}^{(\alpha -1)}d{p}_{\mu }\wedge d{q}^{\mu },}$$

(77)

where

$$\begin{array}{cc}\hfill & {\tilde{V}}_1={\eta }_1,{\tilde{V}}_2={\displaystyle \frac{1-k{\left(q^2\right)}^2}{2R^2\left(q^1\right)}}{\eta }_2,{\tilde{V}}_3={\displaystyle \frac{1}{{\left(q^2\right)}^2{R}^2\left(q^1\right)}}{\eta }_3,{\tilde{V}}_4={\displaystyle \frac{1}{{\left(q^2\right)}^2{R}^2\left(q^1\right){sin}^2\left(q^3\right)}}{\eta }_4,\hfill \\ \hfill & {\tilde{U}}_1=(1-\alpha ){\zeta }_1+{\displaystyle \frac{1}{R^3\left(q^1\right)}}\left((1-k{\left(q^2\right)}^2){\eta }_2{p}_2+{\displaystyle \frac{1}{{\left(q^2\right)}^2}}{\eta }_3{p}_3+{\displaystyle \frac{1}{{sin}^2{q}^3}}{\eta }_4{p}_4\right){\displaystyle \frac{dR\left(q^1\right)}{d{q}^1}},\hfill \\ \hfill & {\tilde{U}}_2=-{\displaystyle \frac{p_2^2}{R^2\left(q^1\right)}}\left(-k{q}^2{\eta }_2{p}_2+(1-\alpha )(1-k{\left(q^2\right)}^2){\zeta }_2\right)+{\displaystyle \frac{1}{{\left(q^2\right)}^3{R}^2\left(q^1\right)}}{\eta }_3{p}_3+{\displaystyle \frac{1}{{\left(q^2\right)}^3{R}^2\left(q^1\right){sin}^2{q}^3}}{\eta }_4{p}_4,\hfill \\ \hfill & {\tilde{U}}_3=-{\displaystyle \frac{(1-\alpha )}{{\left(q^2\right)}^2{R}^2\left(q^1\right)}}{\zeta }_3+{\displaystyle \frac{cos{q}^3}{{\left(q^2\right)}^2{R}^2\left(q^1\right)si{n}^3{q}^3}}{\eta }_4{p}_4,{\tilde{U}}_4=-{\displaystyle \frac{(1-\alpha )}{{\left(q^2\right)}^2{R}^2\left(q^1\right)si{n}^2{q}^3}}{\zeta }_4,\hfill \end{array}$$

with ${\eta }_{\nu }={\left(q^{\nu }\right)}^{2(1-\alpha )}{p}_{\nu },$ ${\zeta }_{\nu }={\left(q^{\nu }\right)}^{(1-2\alpha )}{p}_{\nu }^2,$ and $\nu =1,2,3,4.$

Here, we perform in a conformable FLRW metric, the computation of the Christoffel symbols, the components of the Riemann and Ricci tensors, the Ricci scalar and the components of the Einstein tensor, see Appendix A.

Remark that for $\alpha =1,$ we recover the components of these geometric objects in the usual FLRW metric, as expected.

The Hamiltonian–Jacobi equation here takes the form:

$$\begin{array}{cc}\hfill 2E_F& =-{\left(q^1\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{\partial W}{\partial q^1}}\right)}^2+{\displaystyle \frac{1-k{\left(q^2\right)}^2}{R^2\left(q^1\right)}}{\left(q^2\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{\partial W}{\partial q^2}}\right)}^2\hfill \\ \hfill & +{\displaystyle \frac{{\left(q^3\right)}^{2(1-\alpha )}}{{\left(q^2\right)}^2{R}^2\left(q^1\right)}}{\left({\displaystyle \frac{\partial W}{\partial q^3}}\right)}^2+{\displaystyle \frac{{\left(q^4\right)}^{2(1-\alpha )}}{{\left(q^2\right)}^2{R}^2\left(q^1\right){sin}^2\left(q^3\right)}}{\left({\displaystyle \frac{\partial W}{\partial q^4}}\right)}^2,\hfill \end{array}$$

(78)

where $E_F$ is a constant and ${\displaystyle W=\sum _{\mu =1}^4{W}_{\mu }\left(q_{\mu }\right)}$ is the generating function. The above equation can be rewritten as

$$\begin{array}{cc}\hfill 2E_F{R}^2\left(q^1\right)+{\left(q^1\right)}^{2(1-\alpha )}{R}^2\left(q^1\right){\left({\displaystyle \frac{d{W}_1}{d{q}^1}}\right)}^2& =(1-k{\left(q^2\right)}^2){\left(q^2\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{d{W}_2}{d{q}^2}}\right)}^2+{\displaystyle \frac{{\left(q^3\right)}^{2(1-\alpha )}}{{\left(q^2\right)}^2}}{\left({\displaystyle \frac{d{W}_3}{d{q}^3}}\right)}^2\hfill \\ \hfill & +{\displaystyle \frac{{\left(q^4\right)}^{2(1-\alpha )}}{{\left(q^2\right)}^2{sin}^2\left(q^3\right)}}{\left({\displaystyle \frac{d{W}_4}{d{q}^4}}\right)}^2,\hfill \end{array}$$

which is of a type of separation of variables. Thus, we can also express them via a constant K as:

$$\begin{array}{cc}\hfill & K=2E_F{R}^2\left(q^1\right)+{\left(q^1\right)}^{2(1-\alpha )}{R}^2\left(q^1\right){\left({\displaystyle \frac{d{W}_1}{d{q}^1}}\right)}^2,\hfill \end{array}$$

(79)

$$\begin{array}{cc}\hfill & K=(1-k{\left(q^2\right)}^2){\left(q^2\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{d{W}_2}{d{q}^2}}\right)}^2+{\displaystyle \frac{{\left(q^3\right)}^{2(1-\alpha )}}{{\left(q^2\right)}^2}}{\left({\displaystyle \frac{d{W}_3}{d{q}^3}}\right)}^2+{\displaystyle \frac{{\left(q^4\right)}^{2(1-\alpha )}}{{\left(q^2\right)}^2{sin}^2\left(q^3\right)}}{\left({\displaystyle \frac{d{W}_4}{d{q}^4}}\right)}^2.\hfill \end{array}$$

(80)

Moreover, from Equation (80), we get

$$\begin{array}{c}\hfill (1-k{\left(q^2\right)}^2){\left(q^2\right)}^{2(2-\alpha )}{\left({\displaystyle \frac{d{W}_2}{d{q}^2}}\right)}^2-{\left(q^2\right)}^{2}K=-{\left(q^3\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{d{W}_3}{d{q}^3}}\right)}^2-{\displaystyle \frac{{\left(q^4\right)}^{2(1-\alpha )}}{{sin}^2\left(q^3\right)}}{\left({\displaystyle \frac{d{W}_4}{d{q}^4}}\right)}^2.\end{array}$$

(81)

Since Equation (81) is of a type of separation of variables, we can introduce a constant L, such that

$$\begin{array}{cc}\hfill L& ={\left(q^2\right)}^{2}K-(1-k{\left(q^2\right)}^2){\left(q^2\right)}^{2(2-\alpha )}{\left({\displaystyle \frac{d{W}_2}{d{q}^2}}\right)}^2,\hfill \end{array}$$

(82)

$$\begin{array}{cc}\hfill L& ={\left(q^3\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{d{W}_3}{d{q}^3}}\right)}^2+{\displaystyle \frac{{\left(q^4\right)}^{2(1-\alpha )}}{{sin}^2\left(q^3\right)}}{\left({\displaystyle \frac{d{W}_4}{d{q}^4}}\right)}^2,\hfill \end{array}$$

(83)

and the Equation (83) can be expressed as

$$\begin{array}{c}\hfill L{sin}^2\left(q^3\right)-{\left(q^3\right)}^{2(1-\alpha )}{sin}^2\left(q^3\right){\left({\displaystyle \frac{d{W}_3}{d{q}^3}}\right)}^2={\left(q^4\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{d{W}_4}{d{q}^4}}\right)}^2.\end{array}$$

(84)

Setting

$$\begin{array}{cc}\hfill G& =L{sin}^2\left(q^3\right)-{\left(q^3\right)}^{2(1-\alpha )}{sin}^2\left(q^3\right){\left({\displaystyle \frac{d{W}_3}{d{q}^3}}\right)}^2,\hfill \end{array}$$

(85)

$$\begin{array}{cc}\hfill G& ={\left(q^4\right)}^{2(1-\alpha )}{\left({\displaystyle \frac{d{W}_4}{d{q}^4}}\right)}^2,\hfill \end{array}$$

(86)

we can formulate the solutions of the Equations (79), (82), and (85) as:

$$\begin{array}{c}\hfill W_1=W_1(q^1;E_F,K),W_2=W_2(q^2;K,L),W_3=W_3(q^3;L,G).\end{array}$$

(87)

From (86), we obtain

$$\begin{array}{c}\hfill W_4={\displaystyle \frac{\sqrt{G}}{\alpha }}{|q^4|}^{\alpha -1}{q}^4+C,\end{array}$$

(88)

where C is a constant, and, hence,

$$\begin{array}{c}\hfill W=W_1(q^1;E_F,K)+W_2(q^2;K,L)+W_3(q^3;L,G)+{\displaystyle \frac{\sqrt{G}}{\alpha }}{|q^4|}^{\alpha -1}{q}^4+C.\end{array}$$

(89)

Considering now the canonical system $(Q,P)$, where

$$\begin{array}{cc}\hfill & Q^1=E_F,Q^2=K,Q^3=\sqrt{L},Q^4=\sqrt{G},\hfill \end{array}$$

(90)

$$\begin{array}{cc}\hfill & P_1:=-{\displaystyle \frac{\partial W}{\partial Q^1}}=-{\displaystyle \frac{\partial W_1}{\partial Q^1}},P_2:=-{\displaystyle \frac{\partial W}{\partial Q^2}}=-{\displaystyle \frac{\partial W_1}{\partial Q^2}}-{\displaystyle \frac{\partial W_2}{\partial Q^2}},\hfill \end{array}$$

(91)

$$\begin{array}{cc}\hfill & P_3:=-{\displaystyle \frac{\partial W}{\partial Q^3}}=-{\displaystyle \frac{\partial W_2}{\partial Q^3}}-{\displaystyle \frac{\partial W_3}{\partial Q^3}},\mathrm{and}{P}_4:=-{\displaystyle \frac{\partial W}{\partial Q^4}}=-{\displaystyle \frac{\partial W_3}{\partial Q^4}}-{\displaystyle \frac{\partial W_4}{\partial Q^4}}=-{\displaystyle \frac{1}{\alpha }}{|q^4|}^{\alpha -1}{q}^4-{\displaystyle \frac{\partial W_3}{\partial Q^4}},\hfill \end{array}$$

(92)

the Hamiltonian vector field $X_{F\alpha }$ and the $(1,1)$-tensor field $T_{F\alpha }$ are given by

$$X_{F\alpha }:={\{H_{F\alpha },.\}}_{\alpha }=-{\alpha }^{-2}|P_1{|}^{(1-\alpha )}|Q^1{|}^{(1-\alpha )}{\displaystyle \frac{\partial }{\partial P_1}},T_{F\alpha }=\sum _{\mu =1}^4{|Q^{\mu }|}^{\alpha -1}{Q}^{\mu }\left({\displaystyle \frac{\partial }{\partial P_{\mu }}}\otimes d{P}_{\mu }+{\displaystyle \frac{\partial }{\partial Q^{\mu }}}\otimes d{Q}^{\mu }\right),$$

(93)

respectively.

Similarly, by Lemma 1, $T_{F\alpha }$ satisfies ${\mathcal{L}}_{X_{F\alpha }}{T}_{F\alpha }=0$, ${\mathcal{N}}_{T_{F\alpha }}=0,$ and $deg{Q}^{\mu }=2$. Thus, $T_{F\alpha }$ is a recursion operator of $X_{F\alpha },$ and the constants of motion $Tr\left(T_{F\alpha }^l\right)(l\in \mathbb{N})$ of the vector field $X_{F\alpha }$ for the conformable FLRW metric are provided in the form

$$Tr\left(T_{F\alpha }^l\right)=2({\left(Q^1\right)}^l+{\left(Q^2\right)}^l+{\left(Q^3\right)}^l+{\left(Q^4\right)}^l),l\in \mathbb{N}.$$

(94)

5. Family of Conserved Quantities

In this section, we consider the Hamiltonian system $({\mathcal{T}}^{*}\mathcal{Q},\omega ,Q^1),$ for which the Hamiltonian function $H_{\alpha }$, the vector field $X_{\alpha }$, the symplectic form ${\omega }_{\alpha }$, the bivector field ${\mathcal{P}}_{\alpha }$, and the recursion operator $T_{\alpha }$ are given in both the conformable Schwarzschild and FLRW metrics by: $H_{\alpha }=Q^1>0,$

$$X_{\alpha }={\{H_{\alpha },.\}}_{\alpha }=-{\alpha }^{-2}|P_1{|}^{(1-\alpha )}|Q^1{|}^{(1-\alpha )}{\displaystyle \frac{\partial }{\partial P_1}},{\omega }_{\alpha }=\sum _{\mu =1}^4{\alpha }^2|P_{\mu }{|}^{(\alpha -1)}{|Q^{\mu }|}^{(\alpha -1)}d{P}_{\mu }\wedge d{Q}^{\mu },$$

$${\mathcal{P}}_{\alpha }=\sum _{\mu =1}^4{\alpha }^{-2}|P_{\mu }{|}^{(1-\alpha )}|Q^{\mu }{|}^{(1-\alpha )}{\displaystyle \frac{\partial }{\partial P_{\mu }}}\wedge {\displaystyle \frac{\partial }{\partial Q^{\mu }}},\mathrm{and}{T}_{\alpha }=\sum _{\mu =1}^4{|Q^{\mu }|}^{\alpha -1}{Q}^{\mu }\left({\displaystyle \frac{\partial }{\partial P_{\mu }}}\otimes d{P}_{\mu }+{\displaystyle \frac{\partial }{\partial Q^{\mu }}}\otimes d{Q}^{\mu }\right).$$

In the sequel, we introduce the functions

$$\begin{array}{c}\hfill {\tilde{H}}_{{\alpha }_j}=-\sum _{\mu =1}^4\alpha |Q^{\mu }{|}^{\alpha (1-j)-1}{Q}^{\mu }{|P_{\mu }|}^{\alpha -1}{P}_{\mu }\end{array}$$

(95)

and obtain the vector fields $Z_{{\alpha }_j}\in {\mathcal{T}}^{*}\mathcal{Q},$

$$\begin{array}{cc}\hfill Z_{{\alpha }_j}& :={\{{\tilde{H}}_{{\alpha }_j},.\}}_{\alpha }=\sum _{\mu =1}^4{|Q^{\mu }|}^{-\alpha j}\left((1-j)P_{\mu }{\displaystyle \frac{\partial }{\partial P_{\mu }}}-Q^{\mu }{\displaystyle \frac{\partial }{\partial Q^{\mu }}}\right).\hfill \end{array}$$

(96)

satisfying the relation

$${\iota }_{Z_{{\alpha }_j}}{\omega }_{\alpha }=-d{\tilde{H}}_{{\alpha }_j}.$$

(97)

Then, it is straightforward to notice that the symplectic structure ${\omega }_{\alpha }$ generates a set of Hamiltonian systems on the same manifold ${\mathcal{T}}^{*}\mathcal{Q}.$ The Lie bracket between the vector fields $X_{{}_{{\alpha }_i}}$ and $Z_{{\alpha }_j}$ obeys the relations

$$[X_{{}_{{\alpha }_i}},Z_{{\alpha }_j}]=X_{{}_{{\alpha }_{i+j}}},[X_{{}_{{\alpha }_i}},X_{{}_{{\alpha }_{i+j}}}]=0,i,j\in \mathbb{N},X_{{\alpha }_0}=X_{\alpha },$$

(98)

with

$$X_{{\alpha }_{i+j}}=-{\alpha }^{-2}(1-\alpha i)[1-(i+j)\alpha ]|Q^1{|}^{1-\alpha (i+j+1)}{|P_1|}^{(1-\alpha )}{\displaystyle \frac{\partial }{\partial P_1}}.$$

(99)

These relations are diagrammatically well represented in Figure 1. In terms of differential geometry, $Z_{{\alpha }_j}$ and ${\tilde{H}}_{{\alpha }_j}$ are called master symmetries for $X_{{\alpha }_i}$ and master integrals, respectively. For more details on these symmetries, see [36,37,38,39,40].

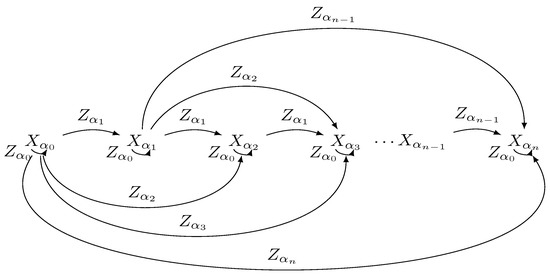
Figure 1. Diagrammatical illustration of Equation (98).

Thus, we can generate a family of Hamiltonian functions:

$$H_{{\alpha }_{i+j}}:=\{H_{{\alpha }_i},{\tilde{H}}_{{\alpha }_j}\}=(1-\alpha i){\left(Q^1\right)}^{1-\alpha (i+j)},\mathrm{with}{H}_{{\alpha }_0}=H_{\alpha },i,j\in \mathbb{N}.$$

(100)

The recursion operator $T_{\alpha }$ can be written as:

$$T_{\alpha }={\mathcal{P}}_{{\alpha }_1}\circ {\mathcal{P}}_{\alpha }^{-1},$$

(101)

where

$${\mathcal{P}}_{{\alpha }_1}=\sum _{\mu =1}^4{\alpha }^{-2}{Q}^{\mu }{|P_{\mu }|}^{(1-\alpha )}{\displaystyle \frac{\partial }{\partial P_{\mu }}}\wedge {\displaystyle \frac{\partial }{\partial Q^{\mu }}}$$

(102)

and ${\mathcal{P}}_{\alpha }$ are two compatible Poisson bivectors with the vanishing Schouten–Nijenhuis bracket ${[{\mathcal{P}}_{\alpha },{\mathcal{P}}_{{\alpha }_1}]}_{NS}=0.$

Furthermore, we put ${\displaystyle {\mathcal{P}}_{{\alpha }_1}^{k+1}=S_{k+1}{\mathcal{P}}_{{\alpha }_1}=S_{k+1}\sum _{\mu =1}^4{\alpha }^{-2}{Q}^{\mu }{|P_{\mu }|}^{(1-\alpha )}{\displaystyle \frac{\partial }{\partial P_{\mu }}}\wedge {\displaystyle \frac{\partial }{\partial Q^{\mu }}},}$ with $S_{k+1}={\displaystyle \frac{1-k\alpha }{1-(k+1)\alpha }},k=i+j\in \mathbb{N},(1-(k+1)\alpha )\ne 0,$ and introduce the following $\alpha$-Poisson bracket ${\{.,.\}}_{{\alpha }_1}^{k_1}$

$${\{f,g\}}_{{\alpha }_1}^{k+1}:=\sum _{\mu =1}^4{\alpha }^{-2}{S}_{k+1}{Q}^{\mu }{|P_{\mu }|}^{(1-\alpha )}\left({\displaystyle \frac{\partial f}{\partial P_{\mu }}}{\displaystyle \frac{\partial g}{\partial Q^{\mu }}}-{\displaystyle \frac{\partial f}{\partial Q^{\mu }}}{\displaystyle \frac{\partial g}{\partial P_{\mu }}}\right)$$

(103)

with respect to the symplectic form

$${\displaystyle {\omega }_{{\alpha }_1}^{k+1}=\sum _{\mu =1}^4{\alpha }^2{S}_{k+1}^{-1}{\left(Q^{\mu }\right)}^{-1}{|P_{\mu }|}^{(\alpha -1)}d{P}_{\mu }\wedge d{Q}^{\mu }}$$

(104)

and get

$$X_{{\alpha }_k}={\{H_{{\alpha }_k},.\}}_{\alpha }={\{H_{{\alpha }_{k+1}},.\}}_{{\alpha }_1}^{k+1},$$

(105)

proving that $X_{{\alpha }_k}$ are bi-Hamiltonian vector fields defined by the two Poisson bivectors ${\mathcal{P}}_{\alpha }$ and ${\mathcal{P}}_{{\alpha }_1}^{k+1}.$ Then, the quadruple $(\mathcal{Q},{\mathcal{P}}_{\alpha },{\mathcal{P}}_{{\alpha }_1}^{k+1},X_{{\alpha }_k})$ is a bi-Hamiltonian system for each k.

The associated recursion operators are given by

$$T_{(k+1)\alpha }:={\mathcal{P}}_{{\alpha }_1}^{k+1}\circ {\mathcal{P}}_{\alpha }^{-1}=\sum _{\mu =1}^4{S}_k{|Q^{\mu }|}^{\alpha -1}{Q}^{\mu }\left({\displaystyle \frac{\partial }{\partial P_{\mu }}}\otimes d{P}_{\mu }+{\displaystyle \frac{\partial }{\partial Q^{\mu }}}\otimes d{Q}^{\mu }\right).$$

(106)

In addition, we have

$$\begin{array}{ccc}& & {\displaystyle {\mathcal{L}}_{Z_{{\alpha }_0}}\left({\mathcal{P}}_{\alpha }\right)=0,(\tilde{\alpha }=0),{\mathcal{L}}_{Z_{{\alpha }_0}}\left({\mathcal{P}}_{{\alpha }_1}^{k+1}\right)=-\alpha \sum _{\mu =1}^4{\alpha }^{-2}{S}_{k+1}{Q}^{\mu }{|P_{\mu }|}^{(1-\alpha )}{\displaystyle \frac{\partial }{\partial P_{\mu }}}\wedge {\displaystyle \frac{\partial }{\partial Q^{\mu }}}=-\alpha {\mathcal{P}}_{{\alpha }_1}^{k+1},}\hfill \\ & & (\tilde{\beta }=-\alpha ),{\mathcal{L}}_{Z_{{\alpha }_0}}\left(H_{\alpha }\right)=-Q^1=-H_{\alpha },(\tilde{\gamma }=-1)\hfill \end{array}$$

permitting to conclude that the vector field

$$\begin{array}{cc}\hfill Z_{{\alpha }_0}& =\sum _{\mu =1}^4\left(P_{\mu }{\displaystyle \frac{\partial }{\partial P_{\mu }}}-Q^{\mu }{\displaystyle \frac{\partial }{\partial Q^{\mu }}}\right)\hfill \end{array}$$

(107)

is a conformal symmetry for ${\mathcal{P}}_{\alpha },{\mathcal{P}}_{{\alpha }_1}^{k+1}$ and $H_{\alpha }$ [39].

Defining now the families of quantities $X_{{\alpha }_l}^{k+1},Z_{{\alpha }_l}^{k+1},{\mathcal{P}}_{{\alpha }_l}^{k+1},{\omega }_{{\alpha }_l}^{k+1}$ and $d{H}_{{\alpha }_l}^{k+1}$ by $X_{{\alpha }_l}^{k+1}:=T_{(k+1)\alpha }^l{X}_{\alpha },Z_{{\alpha }_l}^{k+1}:=T_{(k+1)\alpha }^l{Z}_{{\alpha }_0},{\mathcal{P}}_{{\alpha }_l}^{k+1}:=T_{(k+1)\alpha }^l{\mathcal{P}}_{\alpha },{\omega }_{{\alpha }_l}^{k+1}:=\left({\left(T_{(k+1)\alpha }^l\right)}^{*}\right){\omega }_{\alpha },$ $d{H}_{{\alpha }_l}^{k+1}:={\left(T_{(k+1)\alpha }^l\right)}^{*}$$d{H}_{\alpha }$, where $l\in \mathbb{N},$ and $T_{(k+1)\alpha }^{*}:={\mathcal{P}}_{\alpha }^{-1}\circ {\mathcal{P}}_{{\alpha }_1}^{k+1}$ denoting the adjoint of $T_{(k+1)\alpha }:={\mathcal{P}}_{{\alpha }_1}^{k+1}\circ {\mathcal{P}}_{\alpha }^{-1},$ we obtain

$$\begin{array}{cc}\hfill X_{{\alpha }_l}^{k+1}& =-{\alpha }^{-2}{\left(S_{k+1}\right)}^l{\left(Q^1\right)}^{1+\alpha (l-1)}{|P_1|}^{(1-\alpha )}{\displaystyle \frac{\partial }{\partial P_1}};\hfill \end{array}$$

(108)

$$\begin{array}{cc}\hfill Z_{{\alpha }_l}^{k+1}& =\sum _{\mu =1}^4{\left(S_{k+1}\right)}^l{|Q^{\mu }|}^{l(\alpha -1)}{\left(Q^{\mu }\right)}^l\left(P_{\mu }{\displaystyle \frac{\partial }{\partial P_{\mu }}}-Q^{\mu }{\displaystyle \frac{\partial }{\partial Q^{\mu }}}\right);\hfill \end{array}$$

(109)

$$\begin{array}{cc}\hfill {\mathcal{P}}_{{\alpha }_l}^{k+1}& =\sum _{\mu =1}^4{\alpha }^{-2}{\left(S_{k+1}\right)}^l{\left(Q^{\mu }\right)}^l|P_{\mu }{|}^{(1-\alpha )}{|Q^{\mu }|}^{(1-\alpha )(1-l)}{\displaystyle \frac{\partial }{\partial P_{\mu }}}\wedge {\displaystyle \frac{\partial }{\partial Q^{\mu }}};\hfill \end{array}$$

(110)

$$\begin{array}{cc}\hfill {\omega }_{{\alpha }_l}^{k+1}& =\sum _{\mu =1}^4{\alpha }^2{\left(S_{k+1}\right)}^l{\left(Q^{\mu }\right)}^l|P_{\mu }{|}^{(\alpha -1)}{|Q^{\mu }|}^{(\alpha -1)(l+1)}d{P}_{\mu }\wedge d{Q}^{\mu };\hfill \end{array}$$

(111)

$$\begin{array}{cc}\hfill d{H}_{{\alpha }_l}^{k+1}& ={\left(S_{k+1}\right)}^l{\left(Q^1\right)}^{\alpha l}d{Q}^1;\mathrm{and}{H}_{{\alpha }_l}^{k+1}=\frac{1}{l\alpha +1}{\left(S_{k+1}\right)}^l{\left(Q^1\right)}^{\alpha l+1}\hfill \end{array}$$

(112)

and for each $l\in \mathbb{N}$, we derive the following plethora of conserved quantities:

$$\begin{array}{cc}\hfill {\mathcal{L}}_{Z_{{\alpha }_l}^{k+1}}\left(Z_{{\alpha }_h}^{k+1}\right)& =\alpha (l-h){\left(S_{k+1}\right)}^{l+h}\sum _{\mu =1}^4{|Q^{\mu }|}^{(l+h)(\alpha -1)}{\left(Q^{\mu }\right)}^{l+h}\left(P_{\mu }{\displaystyle \frac{\partial }{\partial P_{\mu }}}-Q^{\mu }{\displaystyle \frac{\partial }{\partial Q^{\mu }}}\right)\hfill \\ \hfill & =\alpha (l-h)Z_{{\alpha }_{l+h}}^{k+1};\hfill \end{array}$$

(113)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{Z_{{\alpha }_l}^{k+1}}\left(X_{{\alpha }_h}^{k+1}\right)& ={\alpha }^{-2}{\left(S_{k+1}\right)}^{l+h}(h\alpha +1){\left(Q^1\right)}^{1+\alpha \left(\right(l+h)-1)}{|P_1|}^{(1-\alpha )}{\displaystyle \frac{\partial }{\partial P_1}}\hfill \\ \hfill & =-(h\alpha +1)X_{{\alpha }_{l+h}}^{k+1};\hfill \end{array}$$

(114)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{Z_{{\alpha }_l}^{k+1}}\left({\mathcal{P}}_{{\alpha }_h}^{k+1}\right)& ={\alpha }^{-1}{\left(S_{k+1}\right)}^{l+h}(l-h){\left(Q^{\mu }\right)}^{l+h}|P_{\mu }{|}^{(1-\alpha )}{|Q^{\mu }|}^{(1-\alpha )(1-(l+h\left)\right)}{\displaystyle \frac{\partial }{\partial P_{\mu }}}\wedge {\displaystyle \frac{\partial }{\partial Q^{\mu }}}\hfill \\ \hfill & =\alpha (l-h){\mathcal{P}}_{{\alpha }_{l+h}}^{k+1};\hfill \end{array}$$

(115)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{Z_{{\alpha }_l}^{k+1}}\left({\omega }_{{\alpha }_h}^{k+1}\right)& =-{\alpha }^3{\left(S_{k+1}\right)}^{l+h}(l+h)\sum _{\mu =1}^4{\left(Q^{\mu }\right)}^{l+h}|P_{\mu }{|}^{(\alpha -1)}{|Q^{\mu }|}^{(\alpha -1)\left(\right(l+h)+1)}d{P}_{\mu }\wedge d{Q}^{\mu }\hfill \\ & =-\alpha (l+h){\omega }_{{\alpha }_{l+h}}^{k+1};\hfill \end{array}$$

(116)

$$\begin{array}{cc}\hfill <d{H}_{{\alpha }_l}^{k+1},Z_{{\alpha }_h}^{k+1}>& =-{\left(S_{k+1}\right)}^{l+h}{\displaystyle \frac{\alpha (l+h)+1}{\alpha (l+h)+1}}{\left(Q^1\right)}^{1+\alpha (l+h)}\hfill \\ \hfill & =-(\alpha (l+h)+1)H_{{\alpha }_{l+h}}^{k+1};\hfill \end{array}$$

(117)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{Z_{{\alpha }_l}^{k+1}}\left(T_{(k+1)\alpha }\right)& =-\alpha \sum _{\mu =1}^4{\left(S_{k+1}\right)}^{l+1}{|Q^{\mu }|}^{(\alpha -1)(l+1)}{\left(Q^{\mu }\right)}^{l+1}\left({\displaystyle \frac{\partial }{\partial P_{\mu }}}\otimes d{P}_{\mu }+{\displaystyle \frac{\partial }{\partial Q^{\mu }}}\otimes d{Q}^{\mu }\right)\hfill \\ \hfill & =-\alpha T_{(k+1)\alpha }^{l+1},\hfill \end{array}$$

(118)

satisfying the following relations linking the master symmetries $Z_{{\alpha }_j}$ to the conformal symmetry $Z_{{\alpha }_0}$ for ${\mathcal{P}}_{\alpha },{\mathcal{P}}_{{\alpha }_1}^{k+1}$ and $H_{\alpha }$, and to a set of conformal symmetries generated by successive applications of the recursion operator $T_{(k+1)\alpha }$ on $Z_{{\alpha }_0}$:

$$\begin{array}{cc}\hfill & {\mathcal{L}}_{Z_{{\alpha }_l}^{k+1}}\left(Z_{{\alpha }_h}^{k+1}\right)=(\tilde{\beta }-\tilde{\alpha })(h-l)Z_{{\alpha }_{l+h}}^{k+1},{\mathcal{L}}_{Z_{{\alpha }_l}^{k+1}}\left(X_{{\alpha }_h}^{k+1}\right)=(\tilde{\beta }+\tilde{\gamma }+(h-1)(\tilde{\beta }-\tilde{\alpha }))X_{{\alpha }_{l+h}}^{k+1},\hfill \\ & {\mathcal{L}}_{Z_{{\alpha }_l}^{k+1}}\left({\mathcal{P}}_{{\alpha }_h}^{k+1}\right)=(\tilde{\beta }+(h-l-1)(\tilde{\beta }-\tilde{\alpha })){\mathcal{P}}_{{\alpha }_{l+h}}^{k+1},{\mathcal{L}}_{Z_{{\alpha }_l}^{k+1}}\left({\omega }_{{\alpha }_h}^{k+1}\right)=(\tilde{\beta }+(l+h-1)(\tilde{\beta }-\tilde{\alpha })){\omega }_{{\alpha }_{l+h}}^{k+1},\hfill \\ \hfill & {\mathcal{L}}_{Z_{{\alpha }_l}^{k+1}}\left(T_{(k+1)\alpha }\right)=(\tilde{\beta }-\tilde{\alpha })T_{(k+1)\alpha }^{1+l},⟨d{H}_{{\alpha }_h}^{k+1},Z_{{\alpha }_l}^{k+1}⟩=(\tilde{\gamma }+(l+h)(\tilde{\beta }-\tilde{\alpha }))H_{{\alpha }_{l+h}}^{k+1}.\hfill \end{array}$$

This is reminiscent to the well-known Oevel formulas (see [26,31,32,39,41,42]).

Finally, it is worth mentioning a generalization of the conformable Poisson brackets (103), as follows:

$${\{f,g\}}_{{\alpha }_t}^{k+t}:=\sum _{\mu =1}^4{\alpha }^{-2}{S}_{k+t}|Q^{\mu }{|}^{1+\alpha (t-1)}{|P_{\mu }|}^{(1-\alpha )}\left({\displaystyle \frac{\partial f}{\partial P_{\mu }}}{\displaystyle \frac{\partial g}{\partial Q^{\mu }}}-{\displaystyle \frac{\partial f}{\partial Q^{\mu }}}{\displaystyle \frac{\partial g}{\partial P_{\mu }}}\right),$$

(119)

where $S_{k+t}={\displaystyle \frac{1-k\alpha }{1-(k+t)\alpha }},k,t\in \mathbb{N},(1-(k+t)\alpha )\ne 0,\mathrm{and}{\{f,g\}}_{{\alpha }_0}^0={\{f,g\}}_{\alpha },\mathrm{with}{S}_0=1,$ leading to a set of generalized bi-Hamiltonian vector fields

$$X_{{\alpha }_k}={\{H_{{\alpha }_k},.\}}_{\alpha }={\{H_{{\alpha }_{k+t}},.\}}_{{\alpha }_t}^{k+t},$$

(120)

the main ingredients governing the Hamiltonian dynamics and pertaining symmetries.

6. Concluding Remarks

In this work, we have proved that a Minkowski phase space endowed with a bracket relatively to a conformable differential realizes a conformable Poisson algebra, conferring a bi-Hamiltonian structure to the resulting manifold. We have deduced that the related conformable Hamiltonian vector field for a free particle is an infinitesimal Noether symmetry. We have computed the corresponding conformable recursion operator. Using the Hamiltonian–Jacobi separability, we have constructed recursion operators in the framework of conformable Schwarzschild and Friedmann–Lemaître–Robertson–Walker (FLRW) metrics, and obtained related constants of motion. We have highlighted the existence of a hierarchy of bi-Hamiltonian structures in both the metrics, and derived a family of conformable recursion operators and master symmetries generating the constants of motion. This study has also shown that Hamiltonian dynamics hint at a connection between the geometry of our physical system, (conformable symplectic manifolds and related Hamiltonian vector fields), and conservation laws. In this connection, the free particle positions on the conformable manifolds are viewed as states and vector fields as laws governing how those states evolve.

Further, we have calculated the conformable Christoffel symbols, Ricci scalar, components of the Riemann, Ricci, and Einstein tensors. This study has revealed that the Christoffel symbols (${\left({\Gamma }_{11}^1\right)}_{\alpha },{\left({\Gamma }_{22}^2\right)}_{\alpha },$ ${\left({\Gamma }_{33}^3\right)}_{\alpha },\mathrm{and}{\left({\Gamma }_{44}^4\right)}_{\alpha }$) in conformable Minkowski metric are no longer null, contrary to the ordinary case corresponding to $\alpha =1$. Similarly, the Christoffel symbols (${\left({\Gamma }_{11}^1\right)}_{\alpha },{\left({\Gamma }_{33}^3\right)}_{\alpha },\mathrm{and}{\left({\Gamma }_{44}^4\right)}_{\alpha }$) are not equal zero in conformable Schwarzschild and FLRW metrics. The existence of these symbols ${\left({\Gamma }_{ii}^i\right)}_{\alpha },(i=1,2,3,4)$ informs us about the way in which the parallel displacement of any basic vector on the conformable manifolds with respect to itself always remains parallel to the same basic vector.