Abstract
We propose the generalized multipomeron exchange model for multiparticle production in high-energy proton–proton, proton–nucleus and heavy-ion collisions. For all of these systems, we consider collectivity effects based on the quark–gluon string fusion concept, where new types of particle-emitting sources—strings with higher tension—are produced. We obtained the model parameters using the data on the multiplicity dependence of the mean transverse momentum of charged particles in and collisions over a wide energy range (from ISR to LHC). We calculated the yields of strange, multi-strange and charm particles as a function of multiplicity for , p- and - collisions at the LHC energy and compared the results with the experimental data.
1. Introduction
The existence of quark–gluon plasma (QGP), a unique state of strongly interacting matter composed of unconfined quarks and gluons, was predicted by quantum chromodynamics (QCD), a fundamental theory of strong interaction. The experiments at SPS and RHIC obtained indications of the QGP formation in the collisions of ultra-relativistic heavy nuclei, which were later proven at the LHC. They used various observables as characteristic signals of QGP formation in A-A collisions, such as an increased yield of strangeness, particle flow harmonics, suppression and jet quenching. Some selected signatures of the QGP observed at RHIC and the LHC are reviewed in the recently published paper [1]. The thermodynamics of extremely hot strongly interacting matter formed in ultra-relativistic nuclear collisions was considered in state-of-the-art hydrodynamic simulations in [2].
In the early works, the collective effects [3], including the intermittence analysis [4], can be related to the formation of a new form of a strongly interacting quark–gluon medium that happens only in the collisions of heavy nuclei.
However, new experimental data obtained in collider experiments during the last decade in proton–proton () and proton–nucleus (p-A) high-multiplicity collisions provided puzzling evidence that is forcing change in the initially accepted paradigm of relativistic heavy-ion interactions as the only source (as the only way) of the QGP formation. Contrary to the initial assumptions of “elementary”, sort-of-reference-type processes in high energy collisions, and of “cold nuclear matter” manifestations in the case [5], a set of experimental indications of the collective effects was obtained for all types of these light systems, which were quite similar to the QGP signals in AA collisions. Two striking phenomena were observed in collisions of small systems: (i) the long-range pseudorapidity correlations, including the “ridge” phenomenon—the azimuthally collimated, well-extended-in-pseudorapidity structure found in and p-A collisions in the distributions in two-particle correlations in CMS [6,7], ATLAS [8], ALICE [9] and LHCb [10] experiments at the LHC—and (ii) the enhanced yield of strange and multi-strange particles obtained by ALICE in high-multiplicity and p-A collisions [11]. Therefore, it is extremely interesting to investigate the common physics origin of these complex phenomena, including, in particular, the long-range correlations and the increased yield of strangeness observed in high-multiplicity -A events similar to the peripheral A-A collisions.
Two general approaches exist for the relativistic nucleus–nucleus collisions [12]. The widely used one is a parton-based consideration, where multiple scatterings of partons of colliding systems are accompanied by the emission and absorption of quarks and gluons producing intermittent parton cascades. The second one is a string picture, where primary interactions of hadron systems lead to the formation of color flux tubes (quark–gluon strings) that are stretched between partons of colliding systems and then broken via creation, producing particles. Discussion of the details of these two approaches and some useful references can be found in [12].
In our work, we follow the second, the quark–gluon string approach, and present further developments of the multipomeron exchange model worked out previously—see [13,14,15,16,17,18,19]—that already provided a reasonable description of collisions of the processes of mean -multiplicity correlations, multiplicity distributions, mean pt dependence on collision energy and KNO scaling violations. The focus in the present study is on the calculations, performed on the same platform, of the yield of strange and multi-strange particles measured by ALICE in the high-multiplicity collisions of both light (-) and heavy - systems [11].
Similar to [13], we do not consider in the framework of the multipomeron exchange model any scenario of string interaction. Instead, we introduce it effectively through a single parameter that controls the increase in string tension in case of string fusion.
Using data in a broad energy range from ISR to Fermilab, in the previous analysis of the mean -multiplicity correlation, we fixed the parameter and two other parameters (the mean number of particles produced per unit of rapidity (the charged rapidity density) per string, and the average string tension, t), as well as their dependence on the collision energy.
The paper is organized as follows: We give, in Section 2, an overview of experimental results on long-range correlations and motivation for studies of strangeness production in -A and A-A collisions in the string-based approach based on the extended multipomeron exchange model with collectivity.
In Section 3, we describe the effective multipomeron exchange model developed initially for or collisions.
This includes the procedure for the definition of values of the model parameters k (mean multiplicity per rapidity from one string), t (tension of a single quark–gluon string) and (parameter that considers the growth of the efficient string tension in case of n pomerons) (see in Section 3.1). Parameters are extracted by fitting to the available experimental data on multiplicity yields as a function of collision energy and -multiplicity (-) correlations in a wide energy range of () collisions. We also discuss here the string tension parameter and the contributions to the (-) correlation function from different multiple soft pomerons.
In Section 4, we present a more detailed analysis of the behavior of model parameters and predictions using ML-related methods.
Particularly, the multivariate Bayesian Gaussian process with principal component analysis is applied to the multipomeron exchange model data on the -multiplicity (-) correlation and multiplicity distribution in () collisions in a wide energy range.
An additional study of the behavior of the multipomeron model parameters (,t) on the collision energy has been performed.
We also constructed a model prediction for - correlation for collisions at 100 TeV energy.
Section 5 contains the description of different particle yields and calculations in the Schwinger approach.
In Section 6, the extension of the model to p-A and A-A collisions is presented for the description of strangeness and multi-strangeness production, and, in addition, of open charm production yields.
Section 7 discusses the results of the extended multipomeron model calculations. They include the energy dependence of the different particle yields in collisions, the multiplicity dependence of strangeness and multi-strangeness production in comparison with the experiment [11] and, in addition, the results of calculations of open charm production as the function of the multiplicity in - and - collisions.
Finally, we present our conclusions in Section 8.
2. Motivation for Extended Multipomeron Exchange Model
The main peculiarity of the long-range correlations found for all hadronic colliding systems between some observables measured as well-separated in rapidity windows is that they are relevant to the initial and not the final states of interaction. In line with the requirement of the principle of causality, these long-range correlations could originate only at the very early stages of the collisions [20,21].
Therefore, it appears that the most natural way, potentially capable of taking into account both two striking phenomena of the long-range correlations and the increased yield of strangeness in high-multiplicity events, is to consider, as the main particle production sources, the strong color fields that exist at the initial stages of hadronic collisions.
The color glass condensate (CGC) effective theory [22,23], which is the approach to the formation of the color flux tubes—longitudinal chromo-electric and chromo-magnetic fields—is capable of taking into account the origin of two-particle long-range azimuthal correlations and the gluon content of high-energy colliding hadrons at an early stage, preceding the formation of the QGP.
Another approach could be based on the concept of multiple exchanges of pomerons and the formation of quark–gluon strings (color flux tubes) between pairs of partons of colliding systems. It is these fluctuations of strong color fields, formed at the early stages of the collisions, that will produce the long-range correlations between observables in an event-by-event analysis in separate rapidity windows [24,25,26,27,28,29,30,31] and that are also capable of ensuring the production of strange and multi strange particles.
Therefore, both the long-range rapidity correlations (including the azimuthal harmonics of particle flows) observed in , and collisions and the production mechanism of strange and multi-strange particles could be relevant to multiple exchanges of pomerons and to the production of particles in the strong longitudinal color fields (quark–gluon strings) formed at the early stages of collisions.
In our approach, we are following this stringy picture based on the Regge–Gribov theory [32], which assumes that, in any nucleon–nucleon interaction, depending on the collision energy, several pomeron exchanges can occur. Each cut pomeron exchange [33] corresponds to a pair of quark–gluon strings in the process of fragmentation, during which, the observed charged particles are produced [34,35,36,37,38].
The hadronization of strings is achieved via the creation of quark–antiquark pairs, which is usually described via the Schwinger mechanism [39]. This mechanism satisfactorily describes the “soft” region of the spectrum of observed particles in a wide range of data produced in the high-energy hadronic collisions. This low- part of the particle spectra is relevant to the soft non-perturbative QCD physics. The detailed analysis of space–time dynamics and signatures of the soft fragmentation of the color flux tubes are discussed in [40,41,42], along with the contribution from the hard-scattering process.
Note that, in our study, we do not discuss hard collisions with a large momentum transfer, focusing instead on soft processes of string hadronization. We also consider the Schwinger mechanism [39] in an initial form, derived for a uniform and static system, without consideration of the effects of fluctuations in the string tension, capable of accounting for the “thermal” distribution of a transverse mass of particles created in the decay of a color string [43,44].
In the original string approach [34,35,36,37,38,45,46], the density of strings is small and they do not interact with each other. However, in the case of a high density of overlapping strings formed in hadron–hadron collisions, these color flux tubes cannot be considered as independent particle-emitting sources any more, and some kind of interaction between them might be expected. The pioneering hypothesis of string–string interaction is in two forms—repulsion or fusion, depending on the direction of the chromoelectric fields—which was formulated in [24]. It predicts that flux tubes with oppositely directed fields repel each other in the transverse direction, whereas they will attract each other in the case where the direction of the fields is the same.
In case of attraction, at some definite critical string density reached in A-A collisions or at sufficiently high-energy collisions, the percolation phase transition could be reached and new particle-emitting sources or clusters could appear [25,26,47,48,49,50,51,52,53].
In addition, we have to note, as was pointed out in [47], that we can also consider the percolation of strings as a smooth way to create quark–gluon plasma after cluster thermalization.
The critical string density effects in the hadronic collisions were investigated in [54]. The estimates of the string percolation parameter were conducted for A-A and collisions based on the experimental data on the onset of the ridge phenomenon observed by STAR in Au-Au collisions at RHIC energies of 62 and 200 GeV [55]. The authors found in [54] that the “critical” value of the string density parameter could be reached in central - collisions at SPS collisions at = 17.3 GeV, thus confirming the earlier estimate in [48]. At the same time, the string density reached in all centrality classes in - collisions at the LHC energies considerably exceeds the value of the percolation threshold. We could also expect a sufficiently high string density in collisions with a very high overlap of strings (approximately five) in collisions at the LHC. It was suggested in [25,26,56] that string–string interactions could cause the appearance of new strings with changed properties. One of the first notes on strangeness as a signal for QGP formation in relativistic nuclear collisions was presented in [57]. Further on, this subject of strangeness production in the hadronic collisions was the focus of many theoretical studies. In particular, they proposed the string fusion model [48,58,59,60], which was widely used for the analysis of data on multi-particle production and explanation of enhanced yields of strange and multi-strange particles in heavy-ion collisions in [27,28,29,30,51,61,62,63,64,65,66].
Strangeness and heavy flavor production and long-range correlations in collisions at LHC energies were considered in the string fusion approach in [16,67,68]. In the case of string fusion or percolation (see [48]), the yields of the particles with a higher transverse momentum and of particles containing strange or charm quarks are increased due to the formation of new types of color flux tubes with much stronger color fields (or strings with higher tension).
Investigations of the early stages of the hadronic collisions could be performed using the long-range correlations for various physical observables in multi-particle production. Studies of these long-range correlations require the minimization of trivial effects relevant to the trivial, so-called volume fluctuations. In order to eliminate their influence in the analysis of collisions, strongly intensive observables were proposed in [66,69,70,71] and, remarkably, strongly intensive observable , characterizing correlations between the number of particles produced in two observation windows separated by a rapidity interval, was found in [52,53,65,66,71,72,73] to be sensitive to the formation of strings of different types.
In [74], they proposed a model with a fusion of interacting strings and formation of a multi-string object, called “a rope”. Here, the Schwinger mechanism was implemented depending on the rope’s initial color charge. Several MC event-generators apply the effects of string interaction. The parton string fusion MC model (PSM) [75] was developed to consider the effects of the fusion of strings in A-A collisions. Some forms of collectivity, such as color reconnection and MPI, were included in the PYTHIA event generator [76].
The model of color ropes, DIPSY [77], considered the effects of long-range azimuthal correlations and of mass ordering observed for small systems, with results like those from a hydrodynamic expansion, but without assuming a thermalized medium.
In the paper [78], the attractive interaction between strings was considered as a result of meson exchange. In this case, the collective effect of the large number of strings produced in the collision area might proceed to a significant compression of the system in the transverse plane, leading to an implosion of such high-density “spaghetti-type” configurations of strings [78].
In the opposite case of repulsion between strings, due to the acquired transverse momentum for the whole color flux tube (string), the distorted azimuthal distribution of the produced hadrons will appear and the large azimuthal asymmetry may be observed, as was predicted in the pioneering work of string–string interactions [24]. In particular, it is this string–string repulsion that could be present in the microscopic origin of the elliptic flow and of higher flow harmonics observed in - collisions at the LHC [79] (and is also being studied in an p-A collisions). This repulsive interaction was successfully demonstrated in the MC calculations [80,81] with the toy model [82]. In this approach, the particle-emitting sources (strings) are boosted by the combined repulsion by neighbors. Thus, the initial space anisotropy is converted into anisotropic azimuthal distributions of charged particles. It was also shown in the Monte Carlo model calculations [81] that collective effects observed in the experiment on the azimuthal and rapidity topology of the two-particle correlations picture, including the harmonic decomposition, centrality dependence of flow coefficients and mass ordering [83], could be rather accurately reproduced due to some rather weak repulsive types of interactions between color flux tubes (strings).
The string repulsion model (PYTHIA 8 with shoving) [84] is being currently considered in the analysis of collectivity in hadronic interactions in collisions of small systems (see references elsewhere).
Recently, interacting color strings were considered [85], with small systems, as the origin of the liquid behavior of the quark–gluon plasma that might be formed in collision events. The investigation of the radial distribution function of the color strings, produced in hadronic collisions, was performed using a percolation-based string model that incorporates a repulsive interaction. Using the concept of three structures—ideal gas, non-ideal gas and liquid-like—results demonstrate the existence of states that simultaneously show a gas–liquid transition and the emergence of a spanning cluster.
These ideas [85] could be considered as a new explanation of the experimentally observed liquid behavior of the quark–gluon plasma above the confined–deconfined transition temperature.
In conclusion to this section, we have to note that the universal approach, which considers all effects of different possible string–string interaction scenarios and observables mentioned above, including string repulsion and string fusion, correlations and heavy flavor production and energy and system size dependence, does not exist today. However, in the present study, we show below, with an efficient account of collectivity and with the minimum number of parameters, that the common nature of multiparticle production in the case of small and large systems can be explained in the framework of the multipomeron exchange model.
3. Effective Multipomeron Exchange Model for or and - Collisions
According to the Regge–Gribov multi-pomeron exchange approach, in one nucleon–nucleon collision, several pomeron exchanges can occur.
Each pomeron exchange corresponds to a pair of quark–gluon strings in the process of fragmentation, during which, they produce the observed charged particles.
The multiplicity of charged particles in the collision with n pomeron exchanges can be obtained as:
where k is the proportionality coefficient, n is the number of pomerons and is the acceptance, i.e., width, of the (pseudo-)rapidity interval.
In the construction of the model for or collisions, we start from the probability of the event with n cut-pomeron exchanges [36,37]:
where is the cross section of n cut-pomeron exchanges:
The numerical values of the parameters used are the following [13,86,87]:
which allows for a description of inelastic and total cross-sections of the interaction in a wide energy range.
Using probabilities (2), we can calculate the mean and variance of the number of cut-pomerons:
The results are plotted in Figure 1 as a function of collision energy .
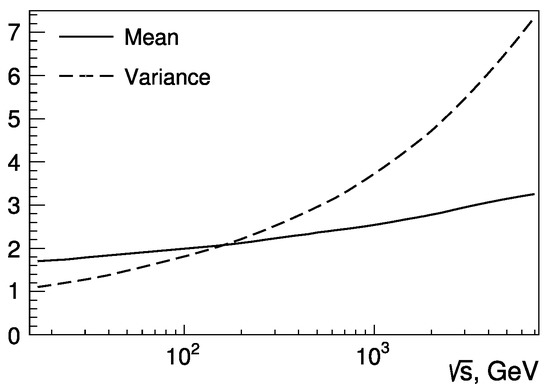
Figure 1.
Mean (solid line) and variance (dashed line) of the number of pomerons [14].
For the description of the charged multiplicity in mid-rapidity, we assume that each cut-pomeron corresponds to a pair of strings. Each of them emits particles into a given acceptance according to a Poisson distribution with a mean value proportional to this (pseudo)-rapidity interval. Therefore, the probability for n cut-pomerons to produce particles is given by:
where k is the mean multiplicity per rapidity unit from one string and is the acceptance, i.e., width, of the (pseudo-)rapidity interval.
Using (5), we obtain the probability of having particles in a given event:
and mean charged multiplicity:
For the description of the pseudorapidity density of charged particles, we can use Formula (6), substituting . Note that, in this case, we have only one parameter k to adjust for the description of experimental data.
In order to also cover the transverse momentum and its correlation with multiplicity, we perform the extension of the model as follows. We use the general idea of the Schwinger mechanism of particle production from one string [39], where the transverse momentum distribution of charged particles from a string has a Gaussian form:
where t corresponds to the string tension.
The assumptions that all strings are identical or that the string tension does not depend on multiplicity would give zero correlation between transverse momentum and multiplicity. In order to include collectivity in our model and to be able to describe non-trivial - correlations, we introduce, similar to [13], the new parameter , which is responsible in an effective way for string interaction (fusion), with corresponding to the absence of collective effects. Thus, the dependence of transverse momentum from one string on the number of cut-pomerons is introduced:
Note that the denominator in (8) gives effective string tension .
Due to the well-known dominance of pions observed in particle spectra, it is possible to simplify the Schwinger mechanism at this stage of analysis of experimental - correlations. We calculate this function in the present model as
where is the distribution of particles over :
Here, is a normalization factor:
The first multiplier in (10) corresponds to the probability of the production of n pomerons, the second one is the Poisson distribution of the charged particles from strings and the last reflects the modified Schwinger mechanism discussed above. We assume in (10), (11), as a first approximation, that all of the particles have the same mass. Therefore, the particle mass m is cancelled in the normalization. The treatment of the different particle masses will be considered in Section 5.
3.1. Parameter Determination
The first stage of the parameter fitting is the determination of the parameter k—the mean multiplicity per rapidity from one string. We extract this parameter from the data (Figure 2) on charged particles multiplicity vs. or collision energy:
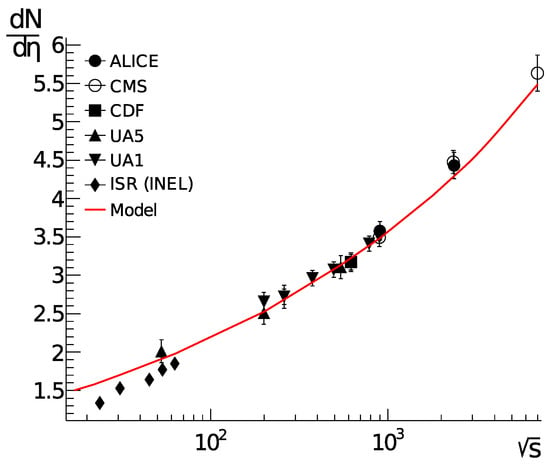
Figure 2.
Pseudorapidity density of multiplicity as a function on energy. Experimental data on charged particle pseudorapidity density at midrapidity vs. or collision energy (data are borrowed from [88]) and the modified multipomeron exchange model—solid line [14].
Note that it is possible to achieve the constant behavior of the parameter k, which is the mean multiplicity per rapidity from one string, while maintaining reasonable agreement with the experimental data, by applying non-standard Regge–Gribov parameters (4) [89,90,91,92].
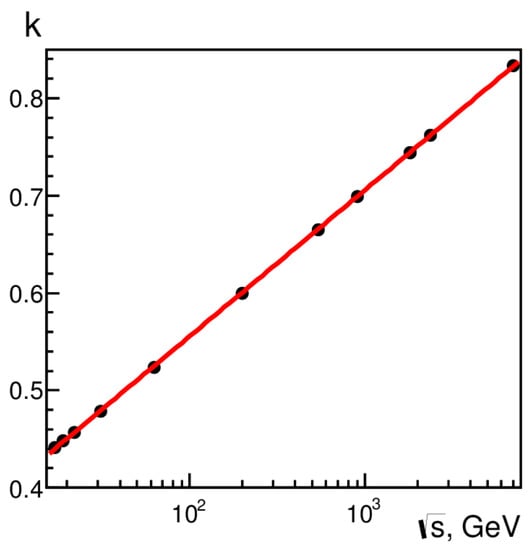
Figure 3.
Dependence of parameter k on energy, obtained in the present model [14].
We obtain the values of the parameters and t in our approach using the available data on - correlations from 17 GeV to 7 TeV. We show the results of fitting in Figure 4.
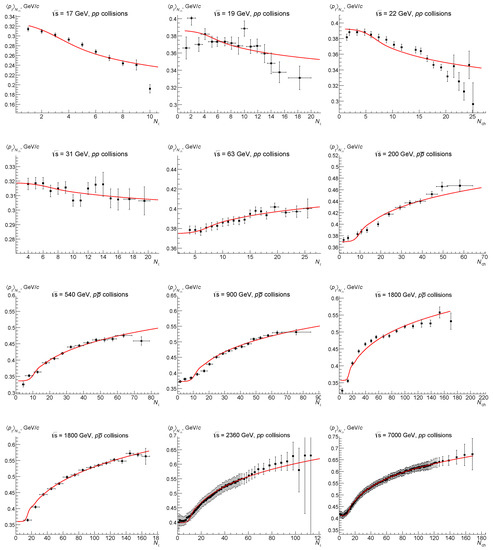
Figure 4.
Experimental data on the - correlation at several energies in and collisions fitted by the present model [14]. We took the experimental data from [93,94,95,96,97,98,99,100,101].
The results in Figure 5 show the dependencies of parameters and t as a function of energy. The smooth behavior of parameter with energy is obtained. We approximated this dependence in Figure 5 by
We found, similar to [13], the set of obtained variables t to split in the experimental data analysis into two subsets: one is around and the second is at . The discrepancy between these sets is related to the differences in data analysis procedures used in the experiments (in particular, in the interpolation to the softest part of the spectra). We use, for our analysis, the values belonging to the first subset because they provided the correct values of (see also in [13,15]).
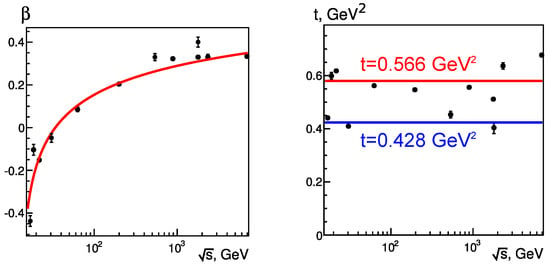
Figure 5.
Dependence of model parameters (left) and t (right) on energy [14].
3.2. Charged Particles Multiplicity Distribution
We show, in Figure 6, the example of the charged particle multiplicity distribution calculated in the multipomeron exchange model [14,15] using (15) for collisions at 2360 GeV. We compare it to the experimental data by CMS obtained in the pseudorapidity interval [101].
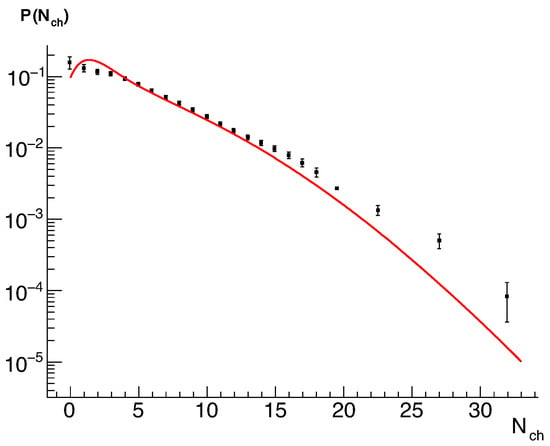
Figure 6.
Example of charged particles multiplicity distributions calculated using (15) in the multipomeron exchange model [14,15] for collisions at 2.36 TeV. Experimental data are from [101].
We have to note here that there was not any fitting to the data, so some small discrepancies observed at high multiplicity values for particle multiplicity distributions calculated in the multipomeron exchange model based on - correlation (15) results can be considered as quite reasonable for such an approach. We also note that, in our approach, no resonance decays are considered, and the contribution of diffractive events is also absent.
3.3. Contributions from Different Multiple Soft Pomerons and String Tension Parameter
We show, in the left part of Figure 7, the example of contributions to the - correlation function at 7 TeV from different exchanges of multiple soft pomerons. We obtained these results with a set of model parameters, as described above; in particular, with the value of a single string tension of . As we can see, the role of the multipomeron exchanges increases with the growing multiplicity in the collisions. In addition, both the number of pomerons and fluctuations in the number of pomerons grow with the energy (see the results in Figure 1), thus leading to the observed flattening of the - correlation function with the growing multiplicity.
We found that the value t = 0.566 GeV of the efficient string tension parameter obtained in our study is larger than the one in the Regge–Gribov theory, which is usually taken as 0.197 GeV. We note that, in our approach, in the procedure of fitting the experimental -multiplicity correlation functions, we considered t as a free parameter responsible for the values of the mean at low-multiplicity events (i.e., in the case of a single pomeron exchange). However, the contribution from both the soft hadronization of strings and from the semi-hard processes (such as jetty events) could be contained in the experimental spectra of charged particles produced at the midrapidity in pp and collisions in the case of events with small values of multiplicities. Therefore, the values of the efficient parameter t could be biased due to the jetty contributions.
It is found that this empirical effective value of string tension t = 0.566 GeV produces the qualitatively correct description of strange and charm particle yields relative to pions in the collisions of both small and large systems. Thus, it may be considered as some proof of the dominating Schwinger mechanism of different particle production, and relevant to the hadronization of both strings and jets.
Concerning the fixed value of the single string tension parameter used here, we note that, within the accuracy of the points in Figure 5 obtained in the fitting of the existing experimental data on the - correlation, we cannot make a strong conclusion on how t depends on energy. One may argue that there is a tendency for the data of parameter t in this Figure 5 to grow with the energy of the collision. We compared our calculations for the correlation between transverse momentum and multiplicity in collisions at a top LHC energy of 14 TeV with the data at 13 TeV (in the right panel of Figure 7).
As one can see, a better description of experimental data at 13 TeV is shown here with a higher value of parameter . This may point to some inefficiency of the too-simplified model used.
We took, in all of our calculations, the parameter of tension for a single string t to be a constant: t = . In addition, we used a smooth behavior with energy for parameter , as has been approximated by (14). The indications of a growth of single string tension with energy is supposed to be investigated in a separate study in the next Section 4.
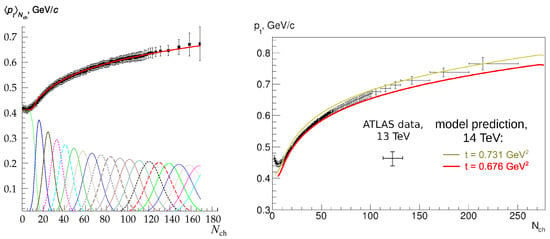
Figure 7.
Left: example of - correlation function calculated at = 7 TeV using (9). Pseudo-rapidity interval is < 2.4. The results are obtained with a set of model parameters as described above. Experimental data points are from [102]. We also show contributions of processes made via the exchange of n soft pomerons. Right: prediction obtained for 14 compared to experimental data at 13 TeV [102].
4. Bayesian Gaussian Process and Principal Component Decomposition
In this section, we present our application of the multivariate Bayesian Gaussian process and principal component analysis (PCA) to the data in the multipomeron model.
The main motivation for the Bayesian approach in the parameter estimation is the possibility of the determination of not only the most probable values of the model parameters but also the possible admissible regions based on available experimental data, with further propagation of errors to the model predictions. In addition, we can apply the Bayesian Gaussian process to study the energy dependence of the parameters with no assumption on the fitting function.
The parameter tuning performed as described above (Section 3.1) is based on the data on multiplicity and the - correlation function in () collisions at an energy of up to 7 TeV. However, as Figure 7 shows, the assumption of the constant behavior of the parameter t with seems to not hold at the higher LHC energy.
Considering the available experimental data, we perform an additional study of the behavior of the multipomeron model parameters in a wider energy range using the methods of the multivariate Bayesian approach and Gaussian process [103,104]. As an advantage, this method allows for a full treatment of the experimental errors in the analysis with the propagation into the model predictions.
We took the tension of a single string (t) and the parameter of string collectivity () as the parameters to be optimized. We used experimental data on the multiplicity dependence of the mean transverse momentum in the energy range of 17 GeV–13 TeV [93,94,95,96,97,98,99,100,101,102].
Due to the fact that the experimental data on the full - are quite correlated bin-by-bin, in order to reduce the dimension of the data, we applied principal component analysis (PCA).
We made the calculations using the SCIKIT-Learn Gaussian Process Regressor package (Python 2.7.12, Sklearn 0.18.1) [105,106]. We used a quadratic exhibitor as a correlation function and Gaussian likelihood function.
In the first stage, the parameter estimation was performed at a fixed energy. First, for each value of , using the Gaussian process, we obtained model predictions as a function of the model parameters in a sufficiently large range (the interpolation error did not exceed 1–2% in the entire range of parameter variations).
Before comparison of the model predictions with the experimental data, we applied the principal component analysis in order to deal with the existing correlation between different bins in - functions. The definition of the main components was made on the basis of model predictions. An example is shown in Figure 8. We obtained that, among the principal components, the two most important ones are related to the growth of the mean transverse momentum with , and the third one represents the correction for the shape of the - form correlation function. In all cases, three components are enough to recover the experimental data, as we show in the closure test in Figure 8, right.
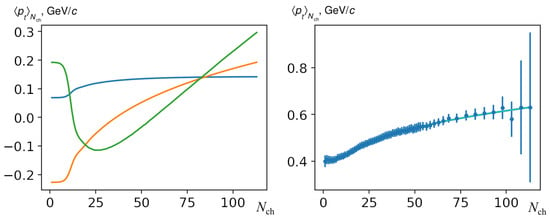
Figure 8.
An example of the application of the method of the main component for collisions at 2.36 The first three main components of the - correlation function obtained in the model are shown on the left. Right—decomposition of experimental data on these main components (closure test).
From a physical point of view, we can relate this to the two components in the transverse momentum spectrum—soft and hard ones [107]—that have different behavior. However, we note that they are explicitly absent in the multipomeron model.
On this basis, we used the three most important components to decompose both the model predictions and the experimental data. We obtained the posterior distribution using the distance between the model and data expansion coefficients, (see the example in Figure 9) and we extracted the most probable values of the parameters with the standard deviations for each collision energy.
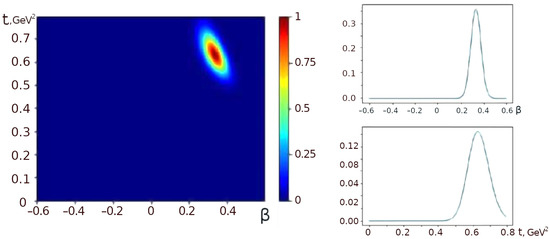
Figure 9.
A posterior distribution of model parameters (,t) for collisions at 2.36 TeV energy (left) and its projections (right).
Then, we investigated the dependence of the parameters and their errors on the energy . We again applied the Gaussian process approach in order to approximate this dependence. In addition, we increased the extrapolation into a higher energy region (up to 100 TeV), which corresponds to the planned maximum energy of the Future Circular Collider (FCC) [108,109]. We show the results for the energy dependence of the parameters (,t) in Figure 10. The results of the approximation show that the data are not enough to determine whether the growth of may occur in the limit of infinitely large energy approaching 0.5, with an energy reaching over 13 TeV in the string fusion [47,48]. However, we consider that the growth of the t parameter is proven, and we assume that it might be related to the increase in the hard process contribution (in the minimum bias collisions).
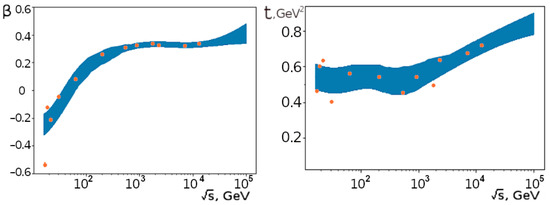
Figure 10.
Approximation of the dependence of the parameters of the model (,t) on the collision energy (, GeV) using the Gaussian process. Dots show the most probable values of the parameters extracted from the datasets at fixed energy. The shaded area shows the one standard deviation region.
Using the obtained posterior distributions, we constructed a prediction of the model for the - correlation at a 100 TeV energy (Figure 11). We can see that, in the large multiplicity events, the average transverse momentum reaches 1 GeV/c, which is close to the region of perturbative QCD.
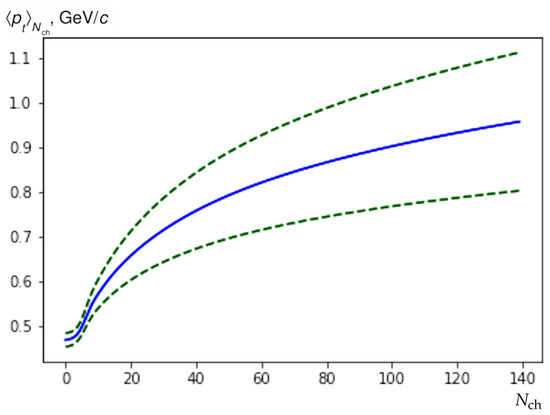
Figure 11.
Prediction for - correlation function for collisions at 100 TeV (the width of the pseudorapidity interval = 2.0). Dotted lines show the area of one standard deviation.
We have also applied the same method to the charged multiplicity distribution at the LHC energy.
The example of the principle component decomposition of the multiplicity distribution is shown in Figure 12. The meaning of the different components, in this case, indicates the contribution from the sources at a different number of pomerons n. We compared the model predictions with the experimental data [101] and we obtained the posterior distribution of the parameter k (Figure 13).
The most probable value of the parameter is slightly different from the one obtained in Section 3.2 describing only the mean . The value of at TeV allows us to better describe the multiplicity distribution (Figure 14), including the large . The higher value of the parameter k may be because of the normalization of events with a low multiplicity and the contribution of diffraction events.
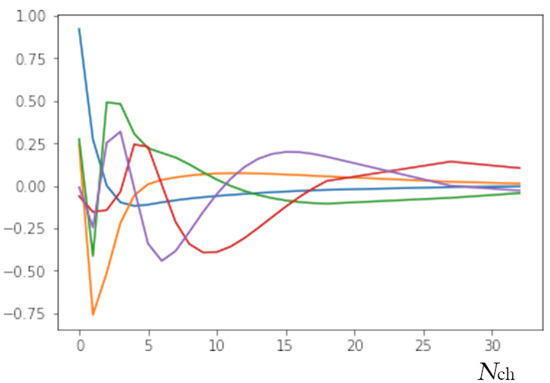
Figure 12.
Example of a principal component decomposition of charged multiplicity distribution in collisions at 2.36 .
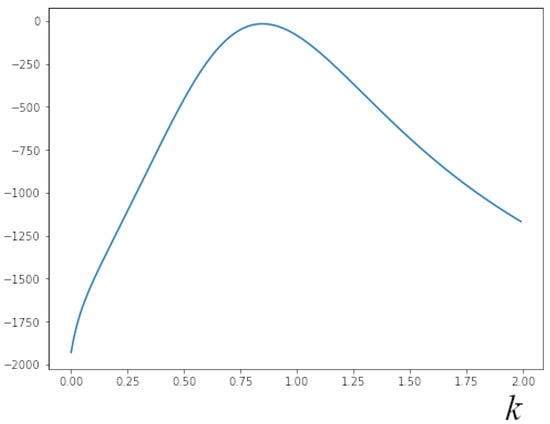
Figure 13.
An example of logarithm posterior distribution for model parameter k in describing the multiplicity distribution in collisions at The maximum is reached at .
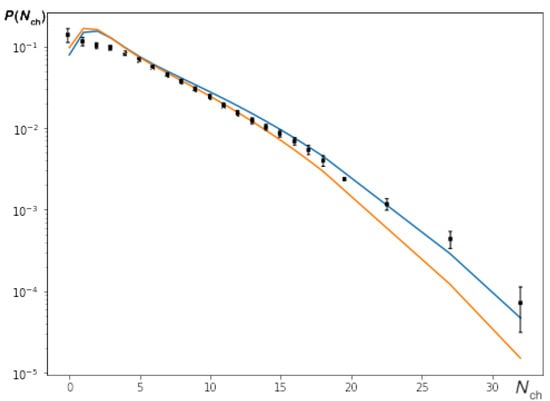
Figure 14.
Multiplicity distribution in collisions at 2.36 Dots—experimental data [101], orange line—model predictions at , blue line—at .
5. Description of Different Particle Yields
According to the modified Schwinger mechanism [13,39], in case of an exchange of n pomerons, the probability of the production of a primary hadron of a given type with transverse momentum is proportional to the value
where is the mass of the particle and is the effective string tension. In the case of and p- collisions:
where t is the tension of a single string and is the parameter responsible for the collectivity. Thus, in , it takes into account, in an efficient way, the increase in string tension due to the string fusion mechanism in the case of n interacting pomerons.
The behavior of parameter as a function of the collision energy was defined from the data on - correlations in and collisions. The value of parameter means no collectivity, and no correlation between transverse momentum and multiplicity. At , the positive (negative) - correlation appears.
The final hadron spectrum of string fragmentation is modified due to the cascade decays of resonances. These decays are effectively taken into account by a cascade branching matrix extracted from the particle decayer built into the THERMINATOR 2 Monte Carlo generator [110] For strangeness and multi-strangeness production for each particle, we applied the dedicated matrix, in which, the particle in question does not decay. Finally, the relative yields of particles with the account of decays of hadrons have the form:
where is the spin of a particle of the type and is the effective branching matrix. The yields of particles are normalized, keeping the total multiplicity .
We consider the application of this formalism in Section 7.
6. Extension of the Multipomeron Exchange Model from to - and - Collisions
The present multipomeron exchange model [13,14,15,16,17,18], can be extended further to the case of p-A and to the more complicated one of A-A collisions.
We obtained the probability of the production of n pomerons in the p-A collision as a convolution of the distribution of the number of participating nucleons with the distribution obtained for the interaction (2) and (3) (see details in [18]). However, because of the obvious uncertainties in the case of A-A collisions, the use of Equations (2) and (3) for the probability of n-pomeron exchange is not possible. We will apply a different approach for calculations of the mean number of pomerons by its relevance to the values of .
We obtained the results for different n pomeron contributions at the given multiplicity in collisions (see the example in Figure 7), and we show that we can use the mean values of as a proxy for the mean number n of pomerons.
We also assume that, at some fixed centrality, the mean multiplicity of charged particles is still related to the mean number of pomerons as (1):
where k is the proportionality coefficient that was obtained earlier and is the rapidity windows size.
For the effective string tension, we use (16) in and p-A collisions. Following the string fusion approach [47,48] for the A-A case, we substitute it by:
where is the nucleus overlapping area, which depends on the impact parameter (b). This is because the string density, and not the string number, matters.
Here, is the radius of the nucleus ( = 7.276 fm for Pb nucleus). For , the characteristic overlapping area in collisions, we took the inelastic nucleon–nucleon cross section ().
We show, in Figure 15, our model calculations of the values of on the dependence of multiplicity in - collisions at = 2.76 TeV. It is the increased string tension that provides, due to the Schwinger mechanism, the hadronization of strongly overlapped fused strings.
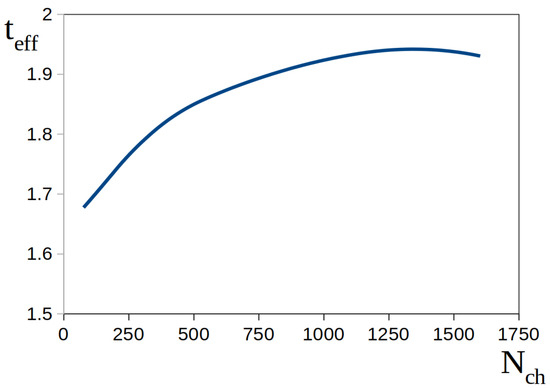
Figure 15.
Dependence of efficient string tension on multiplicity. Our model calculations for - collisions at = 2.76 .
We observe the non-linear growth of with and a tendency for saturation in high-multiplicity events. This behavior is qualitatively similar to the one observed in the - correlation function in collisions.
7. Results and Discussion
7.1. Energy Dependence of the Particle Yields in Collisions
First, the main model parameters obtained by fitting the -multiplicity correlation data at midrapidity were used in the study of the energy dependence of multiplicity density in collisions. We made calculations for yields of charged pions, kaons and protons and compared them to the available experimental data in Figure 16. The model results of Figure 16 demonstrate a satisfactory qualitative agreement with the experiment, which improves with energy growth. We can see some systematic shifts to higher values for kaons. We relate the discrepancies for the yield of protons at a lower energy to the absence of the treatment of a non-zero baryon density in our model.
7.2. Multiplicity Dependence of Strangeness and Multi-Strangeness Production
We calculated, in the framework of the extended multipomeron exchange model, the multiplicity dependences of the strange and multi-strange particle yields (), normalized to charged pion multiplicity. We compare the results in Figure 17 to the experimental data obtained by ALICE at the LHC [11]. Previously, we fixed the parameters of our model calculations: the tension for a single string t is t = , and smooth behavior with energy was used for parameter , approximated by (14). In addition, for the parameter k— the mean multiplicity per rapidity from one string—a smooth logarithmic growth with collision energy was used: (13).
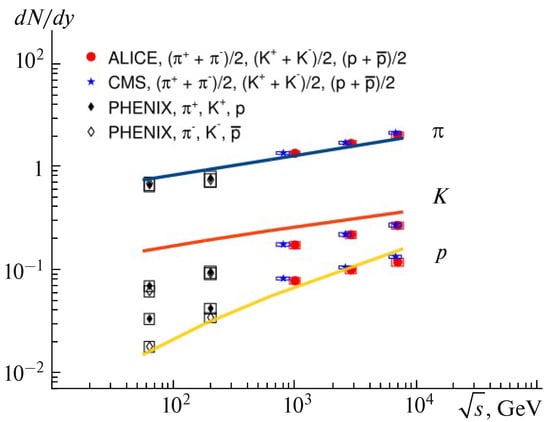
Figure 16.
Energy dependence of the mean multiplicity per rapidity for charged pions, kaons and protons in collisions [17,18]. The lines correspond to model calculations. The points denote experimental data (see references in [111]).
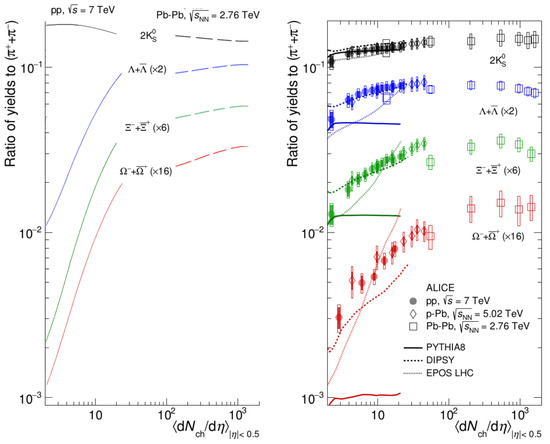
Figure 17.
Multiplicity dependence of the strange and multi-strange particle yields () divided by charged pion multiplicity. Left plot—our model calculation for collisions at 7 (solid lines) and for - collisions (dashed lines) at 2.76 TeV (this work). Right plot [11]—experimental data (dots) and prediction of other models.
The model qualitatively describes the fast increase in the strange and multi-strange yields with charged particle multiplicity in and p-A collisions. The slope of the growth is even higher in the model than in the experimental data. We could relate this to the fact that the parameter effectively considers all mechanisms for the transverse momentum growth observed in the experiment, and not only the modification of the string tension. We observe also, clearly, the trend of the saturation in the yields of strange and multi-strange particles in a smooth transition from the to - collisions, similar to the experimental data.
7.3. Open Charm Relative Yield as the Function of the Multiplicity in , - and - Collisions
The ALICE Collaboration recently found a faster-than-linear growth for the D-meson relative yield with an increasing charged-particle multiplicity in pp collisions [111]. The results of measurements were compared to PYTHIA 8 [76], EPOS 3 [112] and percolation model calculations [113].
In the percolation model, predictions of a faster-than-linear increase of heavy flavor relative production with the relative charged-particle multiplicity were in line with the experiment. All models gave a qualitative description. Detailed discussion of these models’ applications in analysis may be found in [111].
The first analysis based on a string fusion approach to heavy flavor production was performed in the MC event-by-event simulations using a partonic model with color dipoles in [68]. We note that it was suggested in [68] that different mechanisms of charm production in hadronic collisions could be discriminated by the long-range correlation studies.
In this work, we also performed, in the framework of the multipomeron exchange approach, calculations of the relative yields of D mesons in , p- and - collisions as a function of multiplicity. Thus, we are also testing the hypothesis of the multipomeron model soft mechanism of D-meson formation in and - collisions. The results are presented in Figure 18 and compared to the experiment.
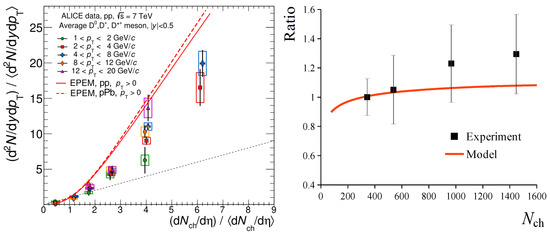
Figure 18.
Left: The relative open charm yield in and p- collisions at = 7 TeV as a function of normalized charged multiplicity, calculated in model [18] and compared with the experimental data [114]. The dotted line shows linear dependence of the yield (proportional to the total charged multiplicity). Right: Multiplicity dependence of D meson production divided by pion multiplicity in - collisions at 2.76 self-normalized in the 30-50% centrality class. The line shows model calculation and the dots show experimental data, which were extracted from the data of papers [114,115].
Therefore, we showed that, in the framework of the multipomeron exchange approach, it is possible to describe both the deviation from linearity in the case of collisions and the slow growth of the D-meson relative yield with multiplicity in - collisions. These results confirm that the production of the open charm behaves very similarly to that of pions, which has been observed in the experimental data (for example, on nucleon modification factors or azimuthal flow).
The benefit of the multipomeron exchange model with the account of collectivity is the low number of parameters, derived through the analysis of the -multiplicity correlation in a broad energy range from ISR to Fermilab and then fixed. We applied the same set of parameters of the multipomeron exchange model in order to catch the gross features of multiparticle production, including strangeness and charm, in soft processes, both in collisions of light and heavy systems.
We note that we use the Schwinger mechanism in our calculations practically in its initial form, without consideration of the effects of the string tension fluctuations. The last ones can account for the “thermal” distribution of a transverse mass of particles created in the decay of a color string [43,44]. We expect that the quantitative agreement of calculations with data could be better with a more careful analysis of the single string tension dependence on the energy of the collision. Further studies in this direction may be discussed and foreseen.
8. Conclusions
We present a new generalization of the multipomeron exchange model for relativistic A-A collisions. The model uses the universal concept of particle production in the hadronization of quark–gluon strings formed at the initial stages of high energy , -A and A-A collisions. It is based on the Regge–Gribov multipomeron approach assuming that, in any nucleon–nucleon interaction, several pomeron exchanges can occur depending on the collision energy. Each pomeron exchange corresponds to a pair of quark–gluon strings in the process of fragmentation, of which, the observed charged particles are produced. The main feature of this approach, in the case of a high density of overlapping strings, is the efficient account of pomeron–pomeron interactions via the quark–gluon string fusion. This fusion provides the formation of new types of particle-emitting sources: strings with a higher tension.
Previously, we defined and fixed the model parameters in the analysis in a wide energy range (from ISR to LHC) of and collision data on the correlations of the mean transverse momentum with the multiplicity of charged particles produced at midrapidity. We do not consider any scenario of string interaction in this work. The effect of string collectivity, associated with a change in string tension due to the fusion process in a certain class of events in , p-A and A-A collisions, is considered by a single parameter .
We also performed a more detailed analysis of the behavior of model parameters and predictions using ML-related methods. We obtained the principal component decompositions for the multiplicity distribution and the -multiplicity (-) correlation function.
We show in the multipomeron exchange model with collectivity that it is the Schwinger mechanism with the efficient tension of fused strings controlled by that handles the growth of multiplicity, the creation of particles with a higher transverse momentum and the increased yield of particles containing strange or charm quarks.
The calculations are performed in the framework of the multipomeron exchange model with the same parameters for , p- and - collisions for the yields, as a function of multiplicity, for the strange and multi-strange particle ().
We found that the results are consistent with the experimental data [11], which show the rather fast rise of the strange particles yield vs. multiplicity for , p-, while the flat dependence is measured for - collisions.
We also calculated in our approach the open charm relative yields in collisions at and of D-mesons in - collisions at . We compared the results to the experiment, thus testing the hypothesis of the soft mechanism of D-meson formation in high-energy , p- and - collisions. The results are also found to be in sufficient agreement with the available experimental data [111,115]. We showed that the generalized multipomeron exchange model can describe the fast deviation from the linearity in the case of collisions and a rather weak behavior of the relative D-meson yield with multiplicity in - collisions.
Author Contributions
Conceptualization, G.F. and V.K.; methodology, G.F. and V.K.; software, V.K.; validation, A.P. and F.V.; formal analysis, V.K., A.P. and F.V.; writing—original draft preparation, G.F. and V.K.; writing—review and editing, G.F., A.P. and V.K.; visualization, V.K.; supervision, G.F.; funding acquisition, G.F. and V.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been conducted with partial financial support from St. Petersburg State University (project No. 93025435). The application of multivariate Bayesian Gaussian process and the principal component decomposition studies was funded by Russian Science Foundation grant No. 17-72-20045.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Authors would like to thank V. Vechernin for fruitful discussions and for permanent interest toward this work.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ISR | Intersecting Storage Rings |
| LHC | Large Hadron Collider |
| RHIC | Relativistic Heavy Ion Collider |
| CGC | Color Glass Condensate |
| SFM | String Fusion Model |
| PSM | Parton String Model |
| QCD | Quantum Chromodynamics |
| QGP | Quark–Gluon Plasma |
| KNO | Koba, Nielsen and Olesen |
| ML | Machine Learning |
| PCA | Principal Component Analysis |
| MC | Monte Carlo |
References
- Niida, T.; Miake, Y. Signatures of QGP at RHIC and the LHC. AAPPS Bull. 2021, 31, 12. [Google Scholar] [CrossRef]
- Gardim, F.G.; Giacalone, G.; Luzum, M.; Ollitrault, J.-Y. Thermodynamics of hot strong-interaction matter from ultrarelativistic nuclear collisions. Nat. Phys. 2020, 16, 615–619. [Google Scholar] [CrossRef]
- Gyulassy, M.; McLerran, L. New forms of QCD matter discovered at RHIC. Nucl. Phys. A 2005, 750, 30–63. [Google Scholar] [CrossRef]
- Tawfik, A.M.; Ganssauge, E. Levy stable law description of the intermittent behavior in Pb + Pb collisions at 158/A-GeV. Acta Phys. Hung. A 2000, 12, 53. [Google Scholar]
- Vechernin, V. Transverse momentum dependence of spectra of cumulative particles produced from droplets of dense nuclear matter. AIP Conf. Proc. 2016, 1701, 060020. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; Frühwirth, R.; et al. Observation of Long-Range Near-Side Angular Correlations in Proton-Proton Collisions at the LHC. JHEP 2010, 9, 91. [Google Scholar] [CrossRef]
- CMS Collaboration. Observation of Long-Range Near-Side Angular Correlations in Proton-Lead Collisions at the LHC. Phys. Lett. B 2013, 718, 795–814. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Observation of Associated Near-Side and Away-Side Long-Range Correlations in sNN=5.02 TeV Proton-Lead Collisions with the ATLAS Detector. Phys. Rev. Lett. 2013, 110, 182302. [Google Scholar] [CrossRef]
- ALICE Collaboration. Long-range angular correlations on the near and away side in p-Pb collisions at sNN=5.02 TeV. Phys. Lett. B 2013, 719, 29–41. [Google Scholar] [CrossRef]
- LHCb Collaboration. Measurements of long-range near-side angular correlations in sNN=5TeV proton-lead collisions in the forward region. Phys. Lett. B 2016, 762, 473–483. [Google Scholar] [CrossRef]
- ALICE Collaboration. Enhanced production of multi-strange hadrons in high-multiplicity proton-proton collisions. Nat. Phys. 2017, 13, 535–539. [Google Scholar] [CrossRef]
- Geiger, K. Space-time description of ultrarelativistic nuclear collisions in the QCD parton picture. Phys. Rept. 1995, 258, 237–376. [Google Scholar] [CrossRef]
- Armesto, N.; Derkach, D.A.; Feofilov, G.A. p(t)-multiplicity correlations in a multi-Pomeron-exchange model with string collective effects. Phys. Atom. Nucl. 2008, 71, 2087–2095. [Google Scholar] [CrossRef]
- Bodnia, E.; Derkach, D.; Feofilov, G.; Kovalenko, V.; Puchkov, A. Multi-pomeron exchange model for pp and collisions at ultra-high energy. PoS QFTHEP2013 2013, 60. [Google Scholar] [CrossRef]
- Bodnya, E.O.; Kovalenko, V.N.; Puchkov, A.M.; Feofilov, G.A. Correlation between mean transverse momentum and multiplicity of charged particles in pp and collisions: From ISR to LHC. AIP Conf. Proc. 2015, 1606, 273–282. [Google Scholar] [CrossRef]
- Kovalenko, V.N.; Puchkov, A.M.; Feofilov, G.A. Production of strange particles in a multi-pomeron exchange model. Bull. Russ. Acad. Sci. Phys. 2016, 80, 966–969. [Google Scholar] [CrossRef]
- Feofilov, G.; Kovalenko, V.; Puchkov, A. Correlation of strange particles production with multiplicity in a multi-pomeron exchange model. arXiv 2017, arXiv:1710.08895. [Google Scholar]
- Feofilov, G.; Kovalenko, V.; Puchkov, A. Correlation between heavy flavour production and multiplicity in pp and p-Pb collisions at high energy in the multi-pomeron exchange model. EPJ Web Conf. 2018, 171, 18003. [Google Scholar] [CrossRef]
- Andronov, E.V.; Kovalenko, V.N. Strongly Intensive Fluctuations Between the Multiplicity and the Total Transverse Momentum in pp Interactions in the Multipomeron Exchange Approach. Theor. Math. Phys. 2019, 200, 1282–1293. [Google Scholar] [CrossRef]
- Dumitru, A.; Gelis, F.; McLerran, L.; Venugopalan, R. Glasma flux tubes and the near side ridge phenomenon at RHIC. Nucl. Phys. A 2008, 810, 91–108. [Google Scholar] [CrossRef]
- Dumitru, A.; Dusling, K.; Gelis, F.; Jalilian-Marian, J.; Lappi, T.; Venugopalan, R. The Ridge in proton-proton collisions at the LHC. Phys. Lett. B 2011, 697, 21–25. [Google Scholar] [CrossRef]
- McLerran, L.; Venugopalan, R. Computing quark and gluon distribution functions for very large nuclei. Phys. Rev. D 1994, 49, 2233–2241. [Google Scholar] [CrossRef] [PubMed]
- McLerran, L.; Venugopalan, R. Gluon distribution functions for very large nuclei at small transverse momentum. Phys. Rev. D 1994, 49, 3352–3355. [Google Scholar] [CrossRef] [PubMed]
- Abramovsky, V.A.; Gedalin, E.V.; Gurvich, E.G.; Kancheli, O.V. Long Range Azimuthal Correlations in Multiple Production Processes at High- energies. JETP Lett. 1988, 47, 337–339. [Google Scholar]
- Braun, M.A.; Pajares, C.; Vechernin, V.V. Ridge from Strings. Eur. Phys. J. A 2015, 51, 44. [Google Scholar] [CrossRef]
- Braun, M.A.; Kolevatov, R.S.; Pajares, C.; Vechernin, V.V. Correlations between multiplicities and average transverse momentum in the percolating color strings approach. Eur. Phys. J. C 2004, 32, 535–546. [Google Scholar] [CrossRef]
- Vechernin, V.V.; Kolevatov, R.S. On multiplicity and transverse-momentum correlations in collisions of ultrarelativistic ions. Phys. Atom. Nucl. 2007, 70, 1797–1808. [Google Scholar] [CrossRef]
- Vechernin, V.V.; Kolevatov, R.S. Long-range correlations between transverse momenta of charged particles produced in relativistic nucleus-nucleus collisions. Phys. Atom. Nucl. 2007, 70, 1809–1818. [Google Scholar] [CrossRef]
- Vechernin, V.V. Correlation between transverse momenta in the string fusion model. Theor. Math. Phys. 2015, 184, 1271–1280. [Google Scholar] [CrossRef]
- Vechernin, V.V. Asymptotic behavior of the correlation coefficients of transverse momenta in the model with string fusion. Theor. Math. Phys. 2017, 190, 251–267. [Google Scholar] [CrossRef]
- Belokurova, S.; Vechernin, V. Long-Range Correlations between Observables in a Model with Translational Invariance in Rapidity. Symmetry 2020, 12, 1107. [Google Scholar] [CrossRef]
- Gribov, V.N.; Pomeranchuk, I.Y.; Ter-Martorosyan, K.A. Moving Branch Points in j Plane and Regge-Pole Unitarity Conditions. Phys. Rev. 1965, 139, B184–B202. [Google Scholar] [CrossRef]
- Abramovsky, V.A.; Gribov, V.N.; Kancheli, O.V. Character of Inclusive Spectra and Fluctuations Produced in Inelastic Processes by Multi - Pomeron Exchange. Sov. J. Nucl. Phys. 1974, 18, 308–317. [Google Scholar]
- Capella, A.; Sukhatme, U.; Tan, C.-I.; Van, J.T.T. Jets in Small p(T) Hadronic Collisions, Universality of Quark Fragmentation, and Rising Rapidity Plateaus. Phys. Lett. B 1979, 81, 68–74. [Google Scholar] [CrossRef]
- Capella, A.; Sukhatme, U.; Tan, C.-I.; Van, J.T.T. Dual parton model. Phys. Rept. 1994, 236, 225–329. [Google Scholar] [CrossRef]
- Kaidalov, A.B. The Quark-Gluon Structure of the Pomeron and the Rise of Inclusive Spectra at High-Energies. Phys. Lett. B 1982, 116, 459–463. [Google Scholar] [CrossRef]
- Kaidalov, A.B.; Ter-Martirosian, K.A. Pomeron as Quark-Gluon Strings and Multiple Hadron Production at SPS Collider Energies. Phys. Lett. B 1982, 117, 247–251. [Google Scholar] [CrossRef]
- Armesto, N.; Pajares, C. Central rapidity densities of charged particles at RHIC and LHC. Int. J. Mod. Phys. A 2000, 15, 2019–2052. [Google Scholar] [CrossRef]
- Schwinger, J.S. On gauge invariance and vacuum polarization. Phys. Rev. 1951, 82, 664–679. [Google Scholar] [CrossRef]
- Wong, C.-Y. Signature of the Fragmentation of a Color Flux Tube. Phys. Rev. D 2015, 92, 074007. [Google Scholar] [CrossRef]
- Wong, C.-Y. Event-by-Event Study of Space-Time Dynamics in Flux-Tube Fragmentation. J. Phys. G 2017, 44, 075102. [Google Scholar] [CrossRef]
- Wong, C.-Y.; Jiang, H.; Yao, N.; Wen, L.; Wang, G.; Huang, H.Z. Clustering properties of produced particles in high-energy pp collisions. Phys. Rev. D 2020, 102, 054007. [Google Scholar] [CrossRef]
- Bialas, A. Fluctuations of the string tension and transverse mass distribution. Phys. Lett. B 1999, 466, 301–304. [Google Scholar] [CrossRef]
- Florkowski, W. Schwinger tunneling and thermal character of hadron spectra. Acta Phys. Polon. B 2004, 35, 799–808. [Google Scholar]
- Braun, M.A.; Pajares, C.; Vechernin, V.V. On the forward—Backward correlations in a two stage scenario. Phys. Lett. B 2000, 493, 54–64. [Google Scholar] [CrossRef]
- Vechernin, V.V. Forward–backward correlations between multiplicities in windows separated in azimuth and rapidity. Nucl. Phys. A 2015, 939, 21–45. [Google Scholar] [CrossRef]
- Armesto, N.; Braun, M.A.; Ferreiro, E.G.; Pajares, C. Percolation approach to quark—Gluon plasma and J/psi suppression. Phys. Rev. Lett. 1996, 77, 3736–3738. [Google Scholar] [CrossRef]
- Braun, M.A.; Pajares, C.; Ranft, J. Fusion of strings versus percolation and the transition to the quark gluon plasma. Int. J. Mod. Phys. A 1999, 14, 2689–2704. [Google Scholar] [CrossRef]
- Nardi, M.; Satz, H. String clustering and J / psi suppression in nuclear collisions. Phys. Lett. B 1998, 442, 14–19. [Google Scholar] [CrossRef]
- Satz, H. The Onset of deconfinement in nuclear collisions. Nucl. Phys. A 1999, 661, 104–118. [Google Scholar] [CrossRef]
- Braun, M.A.; Pajares, C. Implications of percolation of color strings on multiplicities, correlations and the transverse momentum. Eur. Phys. J. C 2000, 16, 349–359. [Google Scholar] [CrossRef]
- Andronov, E.; Vechernin, V. Strongly intensive observable between multiplicities in two acceptance windows in a string model. Eur. Phys. J. A 2019, 55, 14. [Google Scholar] [CrossRef]
- Andronov, E.; Vechernin, V. Multiplicity Correlations with Strongly Intensive Quantities. Phys. Part. Nucl. 2020, 51, 337–339. [Google Scholar] [CrossRef]
- Kochebina, O.; Feofilov, G. Onset of ’ridge phenomenon’ in AA and pp collisions and percolation string model. In Proceedings of the 20th International Baldin Seminar on High Energy Physics Problems: Relativistic Nuclear Physics and Quantum Chromodynamics, Dubna, Russia, 4–9 October 2010. [Google Scholar]
- STAR Collaboration. Anomalous centrality variation of minijet angular correlations in Au-Au collisions at 62-GeV and 200-GeV from STAR. J. Phys. G 2008, 35, 104090. [Google Scholar] [CrossRef]
- Braun, M.; Pajares, C. A Probabilistic model of interacting strings. Nucl. Phys. B 1993, 390, 542–558. [Google Scholar] [CrossRef]
- Koch, P.; Muller, B.; Rafelski, J. Strangeness in Relativistic Heavy Ion Collisions. Phys. Rept. 1986, 142, 167–262. [Google Scholar] [CrossRef]
- Braun, M.; Pajares, C. Probabilistic string interactions in h A and A B collisions. Nucl. Phys. B 1993, 390, 559–586. [Google Scholar] [CrossRef]
- Amelin, N.S.; Braun, M.A.; Pajares, C. Multiple production in the Monte Carlo string fusion model. Phys. Lett. B 1993, 306, 312–318. [Google Scholar] [CrossRef]
- Amelin, N.S.; Braun, M.A.; Pajares, C. String fusion and particle production at high-energies: Monte Carlo string fusion model. Z. Phys. C 1994, 63, 507–516. [Google Scholar] [CrossRef]
- Braun, M.; de Deus, J.D.; Hirsch, A.; Pajares, C.; Scharenberg, R.; Srivastava, B. De-confinement and clustering of color sources in nuclear collisions. Phys. Rep. 2015, 599, 1–50. [Google Scholar] [CrossRef]
- Scharenberg, R.P.; Srivastava, B.K.; Hirsch, A.S.; Pajares, C. Hot Dense Matter: Deconfinement and Clustering of Color Sources in Nuclear Collisions. Universe 2018, 4, 96. [Google Scholar] [CrossRef]
- Bautista, I.; Pajares, C.; Ramírez, J.E. String percolation in AA and p+p collisions. Rev. Mex. Fis. 2019, 65, 197–223. [Google Scholar] [CrossRef]
- Arakelyan, G.H.; Merino, C.; Shabelski, Y.M. Selection Trigger for Rare Quark-Gluon Plasma Formation Events. arXiv 2014, arXiv:1402.6505. [Google Scholar]
- Belokurova, S.N.; Vechernin, V.V. Strongly Intensive Variables and Long-Range Correlations in the Model with a Lattice in the Transverse Plane. Theor. Math. Phys. 2019, 200, 1094–1109. [Google Scholar] [CrossRef]
- Vechernin, V.V.; Belokurova, S.N. The strongly intensive observable in pp collisions at LHC energies in the string fusion model. J. Phys. Conf. Ser. 2020, 1690, 012088. [Google Scholar] [CrossRef]
- Kovalenko, V.; Vechernin, V. Strangeness production and long-range correlations in pp collisions in string fusion approach. J. Phys. Conf. Ser. 2016, 668, 012065. [Google Scholar] [CrossRef]
- Kovalenko, V.; Vechernin, V. Correlation between heavy flavour production and multiplicity in string fusion approach. EPJ Web Conf. 2017, 164, 08002. [Google Scholar] [CrossRef]
- Gorenstein, M.I.; Gazdzicki, M. Strongly Intensive Quantities. Phys. Rev. C 2011, 84, 014904. [Google Scholar] [CrossRef]
- Kovalenko, V. Strongly intensive fluctuations and correlations in ultrarelativistic nuclear collisions in the model with string fusion. EPJ Web Conf. 2019, 204, 03006. [Google Scholar] [CrossRef]
- Vechernin, V. On the interpretation of the balance function. Symmetry 2022, 14, 21. [Google Scholar] [CrossRef]
- Vechernin, V. Short- and long-range rapidity correlations in the model with a lattice in transverse plane. EPJ Web Conf. 2018, 191, 04011. [Google Scholar] [CrossRef]
- Vechernin, V.; Andronov, E. Strongly Intensive Observables in the Model with String Fusion. Universe 2019, 5, 15. [Google Scholar] [CrossRef]
- Biro, T.S.; Nielsen, H.B.; Knoll, J. Color Rope Model for Extreme Relativistic Heavy Ion Collisions. Nucl. Phys. B 1984, 245, 449–468. [Google Scholar] [CrossRef]
- Amelin, N.; Armesto, N.; Pajares, C.; Sousa, D. Monte Carlo model for nuclear collisions from SPS to LHC energies. Eur. Phys. J. C 2001, 22, 149–163. [Google Scholar] [CrossRef]
- Sjostrand, T.; Mrenna, S.; Skands, P.Z. A Brief Introduction to PYTHIA 8.1. Comput. Phys. Commun. 2008, 178, 852–867. [Google Scholar] [CrossRef]
- Flensburg, C.; Gustafson, G.; Lönnblad, L. Inclusive and exclusive observables from dipoles in high energy collisions. J. High Energy Phys. 2011, 2011, 1–45. [Google Scholar] [CrossRef]
- Kalaydzhyan, T.; Shuryak, E. Collective interaction of QCD strings and early stages of high multiplicity pA collisions. Phys. Rev. C 2014, 90, 014901. [Google Scholar] [CrossRef]
- ALICE Collaboration. Higher harmonic anisotropic flow measurements of charged particles in Pb-Pb collisions at sNN = 2.76 TeV. Phys. Rev. Lett. 2011, 107, 032301. [Google Scholar] [CrossRef]
- Feofilov, G.A.; Altsybeev, I.; Kochebina, O. Constraints on string percolation model from anomalous centrality evolution data in Au-Au collisions at sNN = 62 and 200 GeV. In Proceedings of the XXII International Baldin Seminar on High Energy Physics Problems—PoS(Baldin ISHEPP XXII), Dubna, Russia, 14–20 September 2014; Sissa Medialab: Trieste, Italy, 2015. [Google Scholar] [CrossRef]
- Altsybeev, I.; Feofilov, G.; Kochebina, O. Constraints on the percolation model from anomalous centrality evolution of two-particle correlations in Au-Au collisions at sNN = 62 and 200 GeV. AIP Conf. Proc. 2016, 1701, 060011. [Google Scholar] [CrossRef]
- Altsybeev, I. Mean transverse momenta correlations in hadron-hadron collisions in MC toy model with repulsing strings. AIP Conf. Proc. 2016, 1701, 100002. [Google Scholar] [CrossRef]
- ALICE Collaboration. Elliptic flow of identified hadrons in Pb-Pb collisions at sNN = 2.76 TeV. JHEP 2015, 6, 190. [Google Scholar] [CrossRef]
- Bierlich, C.; Gustafson, G.; Lönnblad, L. A shoving model for collectivity in hadronic collisions. arXiv 2016, arXiv:1612.05132. [Google Scholar]
- Ramírez, J.E.; Díaz, B.; Pajares, C. Interacting color strings as the origin of the liquid behavior of the quark-gluon plasma. Phys. Rev. D 2021, 103, 094029. [Google Scholar] [CrossRef]
- Arakelian, G.H.; Capella, A.; Kaidalov, A.B.; Shabelski, Y.M. Baryon number transfer in hadronic interactions. Eur. Phys. J. C 2002, 26, 81–90. [Google Scholar] [CrossRef][Green Version]
- Vechernin, V.; Lakomov, I. The dependence of the number of pomerons on the impact parameter and the long-range rapidity correlations in pp collisions. arXiv 2012, arXiv:1212.2667. [Google Scholar]
- ALICE Collaboration. Pseudorapidity Density of Charged Particles in p+Pb Collisions at sNN = 5.02 TeV. Phys. Rev. Lett. 2013, 110, 032301. [Google Scholar] [CrossRef]
- Capella, A.; Ferreiro, E.G. Charged multiplicities in pp and AA collisions at LHC. Eur. Phys. J. C 2012, 72, 1936. [Google Scholar] [CrossRef]
- Capella, A.; Ferreiro, E.G. Proton-proton multiplicity distributions at LHC and the Pomeron intercept. arXiv 2013, arXiv:1301.3339. [Google Scholar]
- Kovalenko, V.N.; Puchkov, A.M.; Vechernin, V.V.; Diatchenko, D.V. Restrictions on pp scattering amplitude imposed by first diffraction minimum data obtained by TOTEM at LHC. In Proceedings of the 2015 Days on Diffraction (DD), St. Petersburg, Russia, 25–29 May 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Belokurova, S. Study of strongly intense quantities and robust variances in multi-particle production at LHC energies. In Proceedings of the 70th International conference on Nuclear physics and elementary particle physics: Nuclear physics technologies, St. Petersburg, Russia, 12–17 October 2020. [Google Scholar]
- NA49 Collaboration. Transverse momentum fluctuations in nuclear collisions at 158-A-GeV. Phys. Rev. C 2004, 70, 034902. [Google Scholar] [CrossRef]
- Marzo, C.D.; Palma, M.D.; Distante, A.; Favuzzi, C.; Lavopa, P.; Maggi, G.; Posa, F.; Ranieri, A.; Selvaggi, G.; Spinelli, P.; et al. Measurement of the average transverse momentum and of the pion emission volume in proton nucleus and anti-proton nucleus reactions at 200-gev. Phys. Rev. D 1984, 29, 363–367. [Google Scholar] [CrossRef]
- EHS/NA22 Collaboration; Aivazyan, V.V.; Ajinenko, I.V.; Belokopytov, Y.A.; Białkowska, H.; Böttcher, H.; Botterweck, F.; Chliapnikov, P.V.; Crijns, F.; De Roeck, A.; et al. Multiplicity Dependence of the Average Transverse Momentum in π+p, K+p and pp Collisions at 250-GeV/c. Phys. Lett. B 1988, 209, 103–106. [Google Scholar] [CrossRef][Green Version]
- Ames-Bologna-CERN-Dortmund-Heidelberg-Warsaw Collaboration; Breakstone, A.; Campanini, R.; Crawley, H.B.; Dallavalle, G.M.; Deninno, M.M.; Doroba, K.; Drijard, D.; Fabbri, F.; Firestone, A.; et al. Multiplicity Dependence of Transverse Momentum Spectra at ISR Energies. Phys. Lett. B 1983, 132, 463–466. [Google Scholar] [CrossRef]
- UA1 Collaboration; Albajar, C.; Albrow, M.G.; Allkofer, O.C.; Ankoviak, B.A.; Apsimon, R.; Astbury, A.; Aubert, B.; Bacci, C.; Bacon, T.; et al. A Study of the General Characteristics of Collisions at s = 0.2-TeV to 0.9-TeV. Nucl. Phys. B 1990, 335, 261–287. [Google Scholar] [CrossRef]
- Arnison, G.; Astbury, A.; Aubert, B.; Bacci, C.; Bernabei, R.; Bezaguet, A.; Böck, R.; Bowcock, T.J.V.; Calvetti, M.; Carroll, T.; et al. Transverse Momentum Spectra for Charged Particles at the CERN Proton anti-Proton Collider. Phys. Lett. B 1982, 118, 167–172. [Google Scholar] [CrossRef]
- Abe, F.; Amidei, D.; Apollinari, G.; Ascoli, G.; Atac, M.; Auchincloss, P.; Baden, A.R.; Barbaro-Galtieri, A.; Barnes, V.E.; Bedeschi, F.; et al. Transverse Momentum Distributions of Charged Particles Produced in Interactions at s = 630 GeV and 1800 GeV. Phys. Rev. Lett. 1988, 61, 1819. [Google Scholar] [CrossRef] [PubMed]
- Alexopoulos, T.; Allen, C.; Anderson, E.W.; Balamurali, V.; Banerjee, S.; Beery, P.D.; Bhat, P.; Biswas, N.N.; Bujak, A.; Carmony, D.D.; et al. Multiplicity dependence of transverse momentum spectra of centrally produced hadrons in anti-p p collisions at 0.3-TeV, 0.54-TeV, 0.9-TeV, and 1.8-TeV center-of-mass energy. Phys. Lett. B 1994, 336, 599–604. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; Frühwirth, R.; et al. Charged Particle Multiplicities in pp Interactions at s = 0.9, 2.36, and 7 TeV. JHEP 2011, 1, 79. [Google Scholar] [CrossRef]
- Aaboud, M.; Aad, G.; Abbott, B.; Abdallah, J.; Abeloos, B.; Aben, R.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; Abreu, H.; et al. Charged-particle distributions at low transverse momentum in s = 13 TeV pp interactions measured with the ATLAS detector at the LHC. Eur. Phys. J. C 2016, 76, 502. [Google Scholar] [CrossRef]
- Bernhard, J.E.; Moreland, J.S.; Bass, S.A.; Liu, J.; Heinz, U. Applying Bayesian parameter estimation to relativistic heavy-ion collisions: Simultaneous characterization of the initial state and quark-gluon plasma medium. Phys. Rev. C 2016, 94, 024907. [Google Scholar] [CrossRef]
- Kovalenko, V. Determination of the quark-gluon string parameters from the data on pp, pA and AA collisions at wide energy range using Bayesian Gaussian Process Optimization. arXiv 2019, arXiv:1902.11082. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Scikit-Learn Gaussian Process Regressor (python 2.7.12, Sklearn 0.18.1). Available online: http://scikit-learn.org/stable/modules/generated/sklearn.gaussian_process.GaussianProcessRegressor.html (accessed on 6 February 2022).
- Bylinkin, A.A.; Ryskin, M.G. Secondary hadron distributions in two component model. Phys. Rev. D 2014, 90, 017501. [Google Scholar] [CrossRef]
- Benedikt, M.; Mertens, V.; Cerutti, F.; Riegler, W.; Otto, T.; Tommasini, D.; Tavian, L.J.; Gutleber, J.; Zimmermann, F.; Mangano, M.; et al. FCC-hh: The Hadron Collider: Future Circular Collider Conceptual Design Report Volume 3. Eur. Phys. J. ST 2019, 228, 755–1107. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Han, T.; Mangano, M.; Wang, L.-T. Physics opportunities of a 100 TeV proton–proton collider. Phys. Rept. 2016, 652, 1–49. [Google Scholar] [CrossRef]
- Chojnacki, M.; Kisiel, A.; Florkowski, W.; Broniowski, W. THERMINATOR 2: THERMal heavy IoN generATOR 2. Comput. Phys. Commun. 2012, 183, 746–773. [Google Scholar] [CrossRef]
- Adam, J.; Adamová, D.; Aggarwal, M.M.; Aglieri Rinella, G.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmed, I.; Ahn, S.U.; Aimo, I.; et al. Measurement of charm and beauty production at central rapidity versus charged-particle multiplicity in proton-proton collisions at s = 7 TeV. JHEP 2015, 9, 148. [Google Scholar] [CrossRef]
- Drescher, H.J.; Hladik, M.; Ostapchenko, S.; Pierog, T.; Werner, K. Parton based Gribov-Regge theory. Phys. Rept. 2001, 350, 93–289. [Google Scholar] [CrossRef]
- Ferreiro, E.G.; Pajares, C. Open charm production in high multiplicity proton-proton events at the LHC. arXiv 2015, arXiv:1501.03381. [Google Scholar]
- ALICE Collaboration. Centrality dependence of high-pT D meson suppression in Pb-Pb collisions at sNN = 2.76 TeV. JHEP 2015, 11, 205, Addendum: JHEP 2017, 6, 32. [Google Scholar] [CrossRef]
- Abelev, B.; Adam, J.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Aglieri Rinella, G.; Agocs, A.G.; Agostinelli, A.; Aguilar Salazar, S.; Ahammed, Z.; et al. Suppression of high transverse momentum D mesons in central Pb-Pb collisions at sNN = 2.76 TeV. JHEP 2012, 9, 112. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).