Abstract
Recent multi-channel astrophysics observations and the soon-to-be published new measured electromagnetic and gravitation data provide information on the inner structure of the compact stars. These macroscopic observations can significantly increase our knowledge on the neutron star enteriors, providing constraints on the microscopic physical properties. On the other hand, due to the masquarade problem, there are still uncertainties on the various nuclear-matter models and their parameters as well. Calculating the properties of the dense nuclear matter, effective field theories are the most widely-used tools. However, the values of the microscopical parameters need to be set consistently to the nuclear and astrophysical measurements. In this work, we investigate how uncertainties are induced by the variation of the microscopical parameters. We use a symmetric nuclear matter in an extended - model to see the influence of the nuclear matter parameters. We calculate the dense matter equation of state and give the mass-radius diagram for a simplistic neutron star model. We present that the Landau mass and compressibility modulus of the nuclear matter have definite linear relation to the maximum mass of a Schwarzschild neutron star.
1. Introduction
The investigation of the structure of compact astrophysical objects like neutron stars, magnetars, quark- or hybrid stars, etc. is an active novel research area as a child of astrophysics, gravitational theory and experiment and nuclear physics. Thus far, the extreme dense state of the matter can not be produced in today’s Earth-based particle accelerators, thus only celestial objects can be used for tests. Electromagnetic measurements, such as X-ray- and gamma satellites, aim to measure properties of these objects more and more accurately [1,2,3,4]. In parallel, radio array data [5] and the newly discovered gravity waves provide a new way to probe their inner structure [6,7,8]. These observations are particularly important inputs for the theoretical studies of dense nuclear matter [9,10].
From the theoretical point of view, first principle calculations based on lattice field theory are still challenging at high chemical potentials present in compact stars [11,12,13]. Thus, effective theories play an important role in studying the properties of cold dense nuclear matter [14,15]. Recent studies show the importance of the correct handling of the bosonic sector in effective theories of nuclear matter [16,17]; moreover, applying the functional renormalization group (FRG) method on the simplest non-trivial nuclear matter, the effect of the microscopical parameters on neutron star observables were shown in Refs. [18,19].
We note that we use the simplest nuclear matter for neutron stars without crust. Leptonic fields were not included in the model; therefore, no -equlibrium was taken into account. During the calculations of the nuclear equation of state, the condition of charge neutrality was not imposed. We note, however, that this does not lead to the violation of the charge neutrality of the neutron star itself, as there are no energy terms related to the electrical charges of the nucleons, and all the hadronic fields considered are identical. The model effectively describes nuclear matter that consists of interacting neutrons and neutral mesons that are parametrized to describe the saturation properties of symmetric nuclear matter as in the case of the original Walecka-model [20]. These assumptions are restricting but led us to investigate the consequences of varying the nuclear matter parameters in a more clear nuclear environment like e.g., in Ref. [21]. We note that an ongoing extended theoretical work is in progress for a more realistic case to compare astrophysical experimental data to our model.
In this paper, we study the connection between the parametrizations of effective nuclear models and measurable properties of compact stars in three differently extended versions of the - model. All of these include symmetric nuclear matter with various interaction terms in the bosonic sector. After calculating the equation of state (EoS) corresponding to different parametrizations of these models, the mass-radius (M-R) diagrams are calculated by solving the Tollmann–Oppenheimer–Volkoff (TOV) equations. We show how sensitive the mass-radius relation is to differences in the bosonic sector. The dependence of particular properties of compact stars (maximum mass and radius) is presented, influenced by different saturation parameters of the symmetric nuclear matter.
2. The Extended - in the Mean Field Approximation
Here, we apply the most common mean field model of the dense nuclear matter, formulating the extended - model [22,23] with the Lagrange-function taken from Refs. [20,24],
where is the fermionic nucleon field, is the number of nucleons, and , , and are the nucleon, sigma, and omega masses, respectively, for the usual scalar and vector fields. We introduced the and the Yukawa coupling corresponding to the –nucleon and –nucleon interactions is given by and . We denote the general bosonic interaction terms with , which can have thee different forms as the considered modified model cases for certain i,
In the mean field (MF) approximation, the kinetic terms are zero for the mesons and only the fermionic path integral has to be calculated at finite chemical potential and temperature. We consider here the symmetric nuclear matter to be in equilibrium, which includes the baryon number conservation. Taking this into account, the standard procedure was applied minimizing the free energy of the infinite symmetric nuclear matter at the zero temperature limit, where, for the proton () and neutron (), the number of densities are equal, such as the proper chemical potentials, and , respectively:
3. Parameter Fitting in the Extended - Model
As the general procedure, all the models’ considered cases in Equation (2) need to fit to the nucleon saturation data found in e.g., Refs. [20,25]. In parallel to the effective mass, we introduced the definition of the Landau mass
where the Fermi-surface and is the dispersion relation of the nucleons. The Landau mass () and the effective mass () are not independent in relativistic mean field theories,
This is the reason why the Landau mass and the effective mass of the nucleons can not be fitted simultaneously in the models we consider [25]. In this paper, we deal with this problem in the following way. We fit all of the models two times: using the effective mass value from Table 1 and one calculated from Equation (5) to reproduce the Landau mass value from Table 1.

Table 1.
Nuclear saturation parameter data, from Refs. [20,25].
If the models with and type interaction terms are used, then there are not enough free parameters to fit the data in Table 1. In these cases, the nucleon effective mass, saturation density, and binding energy are fitted and the compression modulus is a prediction, given by
which has a simple connection to the thermodynamical compressibility at the saturation density .
In the case of , all four parameters can be fitted simultaneously, and there is another way to incorporate data regarding both Landau and effective mass. For this model, we consider a third fit, where the value of the effective mass is chosen in a way that minimizes the error coming from not fitting the two types of masses correctly. Technically, this value of the effective mass minimized the of the fit, with value
Since the incompressibility is different for the model cases with different interaction terms, we compared them in Table 2. For model cases with and there are two fits, for Landau and effective mass that produce different incompressibility values because they do not have enough free parameters to fit the correct value. However, for there are enough parameters to fit the incompressibility, so it has the same value for all three fits: for the Landau mass, for the effective mass and for the optimal mass. As Table 2 presents incompressibility values for with Landau fit, it is quite close and the results provide the best fit with the saturation nuclear matter parameters in Table 1. These models differ in their predictions for higher densities of nuclear matter, which complicates the description of the compact star interior.

Table 2.
The obtained incompressibility values in different model cases and fits.
4. Properties of Nuclear Matter in the Extended - Model
The nuclear properties of the different model cases were compared with all the possible parameter fits at the equation of state (EOS) level. We used all three types of interaction terms: , , and , and each was considered with two parametrizations corresponding to Landau and effective mass fits. All results were cross-checked with the original - model parameters. In case of the model characterized by interactions, we used a fit which reproduces Eequation (7).
The energy density, pressure and density were calculated in all of these models. The equation of states corresponding to these model and fit cases are shown in Figure 1. The results from the modified - model are compared to other equation of state parametrizations from Refs. [26,27,28] (solid lines). An important feature of Figure 1 is that different model based EoS parametrizations are separated based on whether they are parametrized by the Landau (full symbols) or the effective mass (open symbols). The models which are fitted to reproduce the correct effective mass of nucleons have smaller energy density at a given pressure. This phenomena becomes more prominent as pressure increases. It is also important to note that, in a given band, the incompressibility corresponding to certain equation of states can be very different. For example, in the group that was fitted for the effective mass in the type model, (open rectangles) has the incompressibility 247 MeV, but the type (open circles) has almost double the value, 482 MeV.
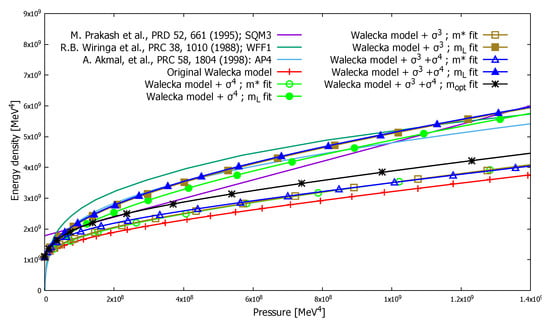
Figure 1.
Equation of state in different models in comparison to Refs. [26,27,28].
Similar grouping can be seen in Figure 2 presenting the binding energy B as the function of the nuclear density n. However, near the minimal B, the value of incompressibility governs the curves because it determines the curvature of the curves around minimum. Effective mass that fits with open symbols has a steeper rise with the increasing density, n, while Landau-mass fit curves with full symbols are wider. We note that, below the saturation density, curves are getting more independent from the model choice and parameter fits.
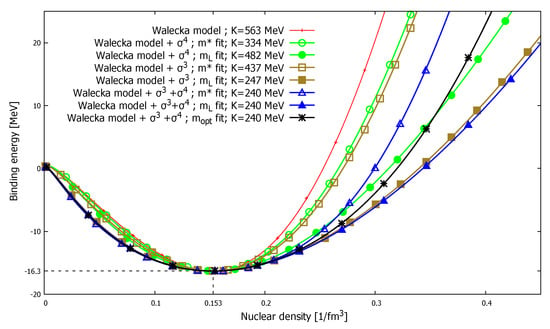
Figure 2.
The density dependence of binding energy with the different models and parametrizations.
5. Compact Star Observables from the Effective Models
The Tolman–Oppenheimer–Volkoff equations provide the general relativistic description of the compact stars assuming spherically symmetric and time independent space-time structure [20],
Here, and are the pressure and energy density as functions of the radius of the star, G is the gravitational constant while is the mass of star that is included in a shell with radius r. To integrate the equations, one needs a connection between and at given r which is provided by the nuclear matter equation of state in the form of the relation . To start the integration, one has to choose a central energy density value for the star as an initial condition.
After solving the Equation (8) using the EoS from the model cases with various fits, the mass (M) and radius (R) of a compact star with a given energy density can be determined. Results corresponding to different energy densities in a given model are summarized on a mass-radius M - R diagram on Figure 3.
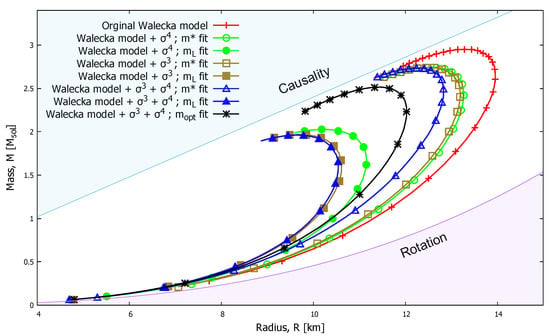
Figure 3.
Mass–radius diagram corresponding to the different parametrizations of the modified - model. The line corresponding to the original - model is also drawn for comparison with a red color.
The model variants inherited the behaviour as in Figure 1 and Figure 2: the curves are grouped based on whether or not they parametrized to reproduce the effective mass or Landau mass. Models with smaller effective mass (open symbols) systematically produce higher maximum mass stars compared to their parametrization with larger effective mass (Landau mass, with full symbols). Moreover, all models fitted for the effective mass value in Table 1 produce higher maximum star mass than the ones fitted for the Landau mass. Since the Landau mass and effective mass are not independent as in Equation (4), the above statement is equivalent to saying that higher effective mass produces smaller maximum star mass. This picture is supported by the curve corresponding to the model case parametrized by the optimal mass in Equation (7), which is the best fit of the model. The maximum star mass in this case is between the values produced by parametrizations described by smaller and larger effective nucleon mass. It is interesting to note that parametrizations corresponding to the effective mass and to the optimal mass value may be ruled out by observations, as they produce much larger maximum star mass and radius than the most recent measurements and theoretical predictions suggest [29].
The value of incompressibility in these models seems to influence very little the maximum star mass; however, at the same time, it has an effect on the compactness by influencing the radius of the star. Thus, it can be seen in Figure 3 by looking at the curves belonging to the fits with the same effective mass (Landau mass). In these model cases, all of the parameters are the same as listed in Table 1 apart from the incompressibility.
6. Connection between Maximum Star Mass and Nuclear Parameters
Our results present a strong connection between the nuclear effective mass, and maximum star mass, . To further study this phenomena, the model variant with interaction term is used and presented below. The couplings in the model are calculated to reproduce all values listed in Table 1 except for the nuclear effective mass and Landau mass that are kept as external parameters. To study the maximum star mass dependence on the effective nucleon mass, many different fits of this model are considered all with different values of effective nucleon mass. The M–R diagrams corresponding to these parametrizations are calculated, and the maximum star mass is determined in each case. This procedure makes it possible to determine the dependence of maximum star mass on nucleon effective mass in this model, if everything else is kept constant. The results are summarized in Figure 4. The connection between maximum star mass and nucleon effective mass is well described by a linear connection, which gives the best fit of the numerical data,
where is given in units of and is given in MeV.
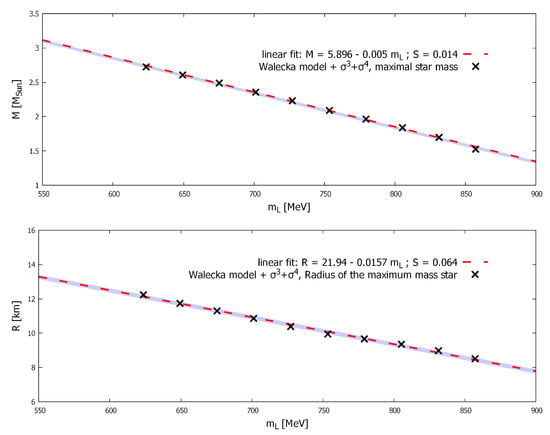
Figure 4.
Maximum star mass, (upper panel) and maximum star size, (lower panel) as a function of the Landau nucleon mass, .
Although the above equation is derived considering only the model with interaction term and taking into account parametrizations that differ only in the value of nucleon effective mass, it generalizes well and it approximates the maximum star mass corresponding to the other model variants we consider with very high accuracy. This seems to indicate that the linear connection is a good approximation regardless of the bosonic interaction term used, and this holds across different model variants.
These observations are further supported by the connection between the radius of the maximum mass star () and nuclear Landau mass. This connection also presents strong linear dependence and holds across all model variants we considered in this paper. The results are shown in Figure 4, where the plotted linear relation is described by
Applying R is given in km units and is given in MeV.
Since besides the nucleon Landau (effective) mass the only parameter that is different in our model variants is the incompressibility, it is worth studying the relation between incompressibility and maximum star mass while keeping every other parameter constant. For this end, in the model with interaction terms, the Landau mass fixed for the value that is listed in Table 1 and the model is solved to reproduce different values of incompressibility. All these different parametrizations give a different dense matter equation of states that predict different M–R diagrams and different maximum mass star parameters, . These results are summarized in the panels of Figure 5.
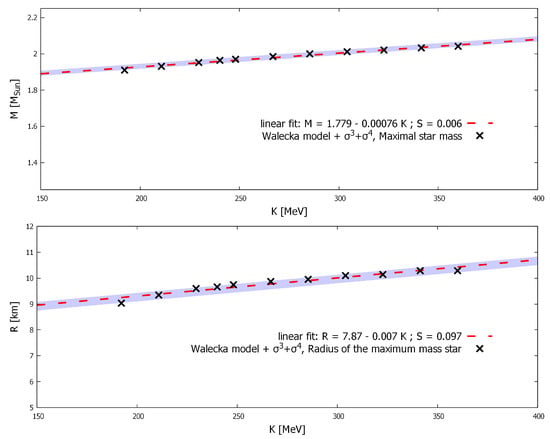
Figure 5.
The maximum mass star mass, (upper panel) and radius, (lower panel) as a function of the compression modulus, K. The dashed line is the best linear fit, which is plotted as guidance.
It can be seen in these plots that the the mass and radius of the maximum mass star are insensitive to the value of the incompressibility. The equations of the best (constant) linear fits are
where is measured in units of , K in MeV units, and is in km.
The slope of both linear functions is tiny and even double the K produces only a few percent of variation in the maximum mass star mass and radius. These results provide a heuristic understanding of the previous results on the dense matter properties: the maximum mass star radius and mass depend strongly on nucleon Landau mass, since its dependence on incompressibility is negligible compared to how strongly it depends on the value of effective mass and all other parameters are kept constant.
7. Conclusions
We investigate the macroscopical observables of neutron stars with a symmetric dense nuclear and matter in the interior. We compared three cases with different general bosonic interactions, and we used variations of the nuclear parameter fit method. We investigated how these bosonic interactions matter in the nuclear equation of state, and especially how the effective mass and Landau mass parameters play role in the nuclear potentials. The applied model is neglecting leptonic fields, and, therefore, there is -equilibrium. Although we had this simplified theoretical case, such a clean nuclear environment led us to explore the effects of its parameters on macroscopical observables of a theoretical compact object.
With variation of these microscopical parameters, we explored the mass-radius groups in the case of a Schwarzschild neutron star model. We presented that the Landau mass of the nuclear matter has a definite linear relation to the maximum mass and maximum radius of the neutron star, considered within the best model case. We also obtained that the effect of the incompressibility is negligible on these macroscopical parameters, with and within the regime 200–400, meaning variation for both cases.
These results support the idea that the evolution equation of the strongly interacting matter saves the magnitude of the uncertainty that originated from the microscopical physical parameters, which appears as deterministic variation of the macroscopical observables as suggested in Refs. [18,19].
Finally, we note that an investigation of the asymmetric nuclear matter version of this study is ongoing, like in Ref. [30,31]. Our preliminary results suggest that taking into account -equilibrium in the asymmetric case does not change much the observed effects, supporting the phenomena summarized in this paper.
Author Contributions
Authors contributed to the paper equally.
Funding
This work is supported by the Hungarian Research Fund (OTKA) under contracts No. K120660, K123815, NKM-81/2016 MTA-UA bilateral mobility program, and PHAROS (CA16214), and THOR (CA15213) COST actions.
Acknowledgments
The authors also acknowledge the computational resources for the Wigner GPU Laboratory.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- NASA. Nicer. Available online: https://www.nasa.gov/nicer (accessed on 1 May 2019).
- Merloni, A.; Predehl, P.; Becker, W.; Böhringer, H.; Boller, T.; Brunner, H.; Brusa, M.; Dennerl, K.; Freyberg, M.; Friedrich, P.; et al. eROSITA Science Book: Mapping the Structure of the Energetic Universe 2012. Available online: http://xxx.lanl.gov/abs/1209.3114 (accessed on 1 May 2019).
- Athena. The Athena X-ray Observatory. Available online: https://www.the-athena-x-ray-observatory.eu/ (accessed on 1 May 2019).
- Ozel, F.; Psaltis, D.; Arzoumanian, Z.; Morsink, S.; Baubock, M. Measuring Neutron Star Radii via Pulse Profile Modeling with NICER. Astrophys. J. 2016, 832, 92. [Google Scholar] [CrossRef]
- Watts, A.L. Constraining the neutron star equation of state using Pulse Profile Modeling. In Proceedings of the Xiamen-CUSTIPEN Workshop on the EOS of Dense Neutron-Rich Matter in the Era of Gravitational Wave Astronomy, Xiamen, China, 3–7 January 2019. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. [The LIGO Scientific Collaboration and the Virgo Collaboration] GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Rezzolla, L.; Takami, K. Gravitational-wave signal from binary neutron stars: A systematic analysis of the spectral properties. Phys. Rev. 2016, D93, 124051. [Google Scholar] [CrossRef]
- Ozel, F.; Psaltis, D.; Guver, T.; Baym, G.; Heinke, C.; Guillot, S. The Dense Matter Equation of State from Neutron Star Radius and Mass Measurements. Astrophys. J. 2016, 820, 28. [Google Scholar] [CrossRef]
- Raithel, C.A.; Özel, F.; Psaltis, D. From Neutron Star Observables to the Equation of State. II. Bayesian Inference of Equation of State Pressures. Astrophys. J. 2017, 844, 156. [Google Scholar] [CrossRef]
- Guenther, J.; Bellwied, R.; Borsányi, S.; Fodor, Z.; Katz, S.; Pásztor, A.; Ratti, C.; Szabó, K. The QCD equation of state at finite density from analytical continuation. Nuclear Phys. A 2017, 967, 720–723. [Google Scholar] [CrossRef]
- Günther, J.; Bellwied, R.; Borsanyi, S.; Fodor, Z.; Katz, S.D.; Pasztor, A.; Ratti, C. The QCD equation of state at finite density from analytical continuation. EPJ Web Conf. 2017, 137, 07008. [Google Scholar] [CrossRef]
- Endrődi, G.; Fodor, Z.; Katz, S.D.; Sexty, D.; Szabó, K.K.; Török, C. Applying constrained simulations for low temperature lattice QCD at finite baryon chemical potential. Phys. Rev. D 2018, 98, 074508. [Google Scholar] [CrossRef]
- Holt, J.W.; Rho, M.; Weise, W. Chiral symmetry and effective field theories for hadronic, nuclear and stellar matter. Phys. Rept. 2016, 621, 2–75. [Google Scholar] [CrossRef]
- Kojo, T. QCD in stars. In Proceedings of the 10th International Workshop on Critical Point and Onset of Deconfinement (CPOD 2016), Wrocław, Poland, 30 May–4 June 2016. [Google Scholar]
- Barnafoldi, G.G.; Jakovac, A.; Posfay, P. Harmonic expansion of the effective potential in a functional renormalization group at finite chemical potential. Phys. Rev. 2017, D95, 025004. [Google Scholar] [CrossRef]
- Kovács, P.; Szép, Z. Critical surface of the SU(3)L×SU(3)R chiral quark model at nonzero baryon density. Phys. Rev. D 2007, 75, 025015. [Google Scholar] [CrossRef]
- Pósfay, P.; Barnaföldi, G.G.; Jakovác, A. The effect of quantum fluctuations in compact star observables. Publ. Astron. Soc. Austral. 2018, 35, 19. [Google Scholar] [CrossRef]
- Pósfay, P.; Barnaföldi, G.G.; Jakovác, A. Effect of quantum fluctuations in the high-energy cold nuclear equation of state and in compact star observables. Phys. Rev. 2018, C97, 025803. [Google Scholar] [CrossRef]
- Glendenning, N.K. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity; Astronomy and Astrophysics Library; Springer: Berlin, Germany, 1997. [Google Scholar]
- Hajizadeh, O.; Maas, A. Constructing a neutron star from the lattice in G2-QCD. Eur. Phys. J. 2017, A53, 207. [Google Scholar] [CrossRef]
- Walecka, J. A theory of highly condensed matter. Ann. Phys. 1974, 83, 491–529. [Google Scholar] [CrossRef]
- Johnson, M.H.; Teller, E. Classical Field Theory of Nuclear Forces. Phys. Rev. 1955, 98, 783–787. [Google Scholar] [CrossRef]
- Schmitt, A. Dense matter in compact stars: A pedagogical introduction. Lect. Notes Phys. 2010, 811, 1–111. [Google Scholar] [CrossRef]
- Meng, J. Relativistic Density Functional for Nuclear Structure; International Review of Nuclear Physics; World Scientific Publishing Company: Singapore, 2016. [Google Scholar]
- Prakash, M.; Cooke, J.R.; Lattimer, J.M. Quark-hadron phase transition in protoneutron stars. Phys. Rev. D 1995, 52, 661–665. [Google Scholar] [CrossRef]
- Wiringa, R.B.; Fiks, V.; Fabrocini, A. Equation of state for dense nucleon matter. Phys. Rev. C 1988, 38, 1010–1037. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef]
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Ann. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y.; Fantina, A.F.; Ducoin, C.; Dutta, A.K.; Goriely, S. Unified equations of state for cold non-accreting neutron stars with Brussels-Montreal functionals—I. Role of symmetry energy. Mon. Not. R. Astron. Soc. 2018, 481, 2994–3026. [Google Scholar] [CrossRef]
- Weissenborn, S.; Chatterjee, D.; Schaffner-Bielich, J. Hyperons and massive neutron stars: The role of hyperon potentials. Nucl. Phys. 2012, A881, 62–77. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).