PHENIX Results of Three-Particle Bose-Einstein Correlations in \({\sqrt{s_{NN}}}\) = 200 GeV Au+Au Collisions

Abstract

Bose-Einstein correlations (BECs) of identical hadrons reveal information about hadron creation from the strongly interacting matter formed in ultrarelativistic heavy-ion collisions. The measurement of three-particle correlations may in particular shed light on hadron creation mechanisms beyond thermal/chaotic emission. In this paper, we show the status of PHENIX measurements of three-pion correlations as a function of momentum differences within the triplets. We analyze the shape of the correlation functions through the assumption of Lévy sources and a proper treatment of the Coulomb interaction within the triplets. We measure the three-particle correlation strength (${\lambda }_3$), which, together with the two-particle correlation strength ${\lambda }_2$, encodes information about hadron creation mechanisms. From a consistent analysis of two- and three-particle correlation strengths, we establish a new experimental measure of thermalization and coherence in the source.

1. Introduction

In particle and nuclear physics, intensity interferometry provides a direct experimental method for the determination of sizes, shapes and lifetimes of particle-emitting sources (for reviews, see [1,2,3,4,5]). In particular, boson interferometry provides a powerful tool for the investigation of the spacetime structure of particle production processes, as Bose-Einstein correlations (BECs) of two or three identical bosons reflect both geometrical and dynamical properties of the particle-radiating source.

The size (radius) of the source in heavy-ion collisions has been found to decrease with increasing transverse momentum, $p_t$, or transverse mass, $m_t=\sqrt{m^2+p_t^2}$, of the bosons. This effect can also be explained by hydrodynamical models [6,7]. The main purpose of the present paper is to determine the three-particle correlation strength (${\lambda }_3$) as a function of transverse momentum. Recently [8], the two-particle correlation strength (${\lambda }_2$) was determined. These measurements of ${\lambda }_2$, when combined with this analysis, may test the limits of the core-halo model [9,10,11] with a thermalized core. For this purpose, we introduce a new parameter, ${\kappa }_3$, which is a function of ${\lambda }_3$ and ${\lambda }_2$. This new parameter is not equal to 1 when there are extra effects in the core, for example, a core not fully thermalized, or when there is partial coherence in the core. The main purpose of the present work is to investigate whether ${\kappa }_3$ indicates extra effects or not.

We start with the definition of the three-particle correlation function:

$$C_3({\mathit{k}}_{\mathbf{1}},{\mathit{k}}_{\mathbf{2}},{\mathit{k}}_{\mathbf{3}})=\frac{N_3({\mathit{k}}_{\mathbf{1}},{\mathit{k}}_{\mathbf{2}},{\mathit{k}}_{\mathbf{3}})}{N_1\left({\mathit{k}}_{\mathbf{1}}\right)N_1\left({\mathit{k}}_{\mathbf{2}}\right)N_1\left({\mathit{k}}_{\mathbf{3}}\right)}$$

(1)

where $N_3$ is the three-particle invariant momentum distribution, defined by

$$N_3({\mathit{k}}_{\mathbf{1}},{\mathit{k}}_{\mathbf{2}},{\mathit{k}}_{\mathbf{3}})=\int \mathcal{S}({\mathit{r}}_{\mathbf{1}},{\mathit{k}}_{\mathbf{1}})\mathcal{S}({\mathit{r}}_{\mathbf{2}},{\mathit{k}}_{\mathbf{2}})\mathcal{S}({\mathit{r}}_{\mathbf{3}},{\mathit{k}}_{\mathbf{3}}){\left|{\mathsf{\Psi }}_{{\mathit{k}}_{\mathbf{1}},{\mathit{k}}_{\mathbf{2}},{\mathit{k}}_{\mathbf{3}}}({\mathit{r}}_{\mathbf{1}},{\mathit{r}}_{\mathbf{2}},{\mathit{r}}_{\mathbf{3}})\right|}^2{\mathsf{\Pi }}_{i=0}^3{d}^4{\mathit{r}}_{\mathit{i}}$$

(2)

and $N_1$ is the single-particle invariant momentum distribution, defined as

$$N_1\left(\mathit{k}\right)=\int \mathcal{S}({\mathit{r}}_1,{\mathit{k}}_1){\left|{\mathsf{\Psi }}_{\mathit{k}}\left({\mathit{r}}_1\right)\right|}^2{d}^4\mathit{r}$$

(3)

In the above equations, ${\mathsf{\Psi }}_{{\mathit{k}}_1,{\mathit{k}}_2,{\mathit{k}}_3}$ is the three-particle wave function, and ${\mathsf{\Psi }}_{\mathit{k}}$ is the single-particle wave function. Furthermore, $S(\mathit{r},\mathit{k})$ is the source distribution, which describes the probability density of particle creation at the spacetime point $\mathit{r}$ with momentum $\mathit{k}$.

Our assumption for the source function is the symmetric Lévy distribution [12,13,14,15,16], which is defined by

$$\begin{array}{c}\hfill L(\alpha ,R,\mathit{r})=\frac{1}{{\left(2\pi \right)}^3}\int {\mathrm{d}}^3\mathit{q}{e}^{i\mathit{q}\mathit{r}}{e}^{-\frac{1}{2}{\left|\mathit{q}R\right|}^{\alpha }}\end{array}$$

(4)

where $\alpha$ is the Lévy index, and R is the Lévy scale. Then $\alpha =2$ gives back the Gaussian case, and $\alpha =1$ yields a Cauchy distribution. For the Lévy stable source distribution, 0 < $\alpha \le 2$ in general.

Assuming properly symmetrized plane-waves for the wave functions and the Lévy distribution as the source function, the three-particle correlation function is given as

$$\begin{array}{c}\hfill C_3^{\left(0\right)}(k_{12},k_{13},k_{23})=1+{\ell }_3{e}^{-0.5\left(\right|2k_{12}R{|}^{\alpha }+|2k_{13}R{|}^{\alpha }+|2k_{23}R{|}^{\alpha })}+{\ell }_2\left(e^{|2k_{12}{R|}^{\alpha }}+e^{|2k_{13}{R|}^{\alpha }}+e^{|2k_{23}{R|}^{\alpha }}\right)\end{array}$$

(5)

where $k_{ij}=|{\mathit{k}}_i-{\mathit{k}}_j|/2$, that is, the half-momentum difference of the ith and jth particles. Furthermore, the ${\ell }_2$ parameter is the two-particle correlation strength parameter in the three-particle correlation function, and ${\ell }_3$ is the three-particle strength parameter.

To be able to fit the model to the data, the correlation function has to be completed with a background that parameterizes possible long-range correlations. In this analysis, we use a simple linear background in every direction, with the same slope. Thus the correlation function is the following:

$$C_{3,\mathrm{fit}}^{\left(0\right)}(k_{12},k_{13},k_{23})=N(1+ϵk_{12})(1+ϵk_{13})(1+ϵk_{23})C_3^{\left(0\right)}(k_{12},k_{13},k_{23})$$

(6)

We also have to take into account the Coulomb interaction, as this decreases the number of particle pairs at low-momentum differences. To add Coulomb correction to the model, we define a Coulomb correction factor:

$$K_3({\mathit{k}}_{\mathbf{12}},{\mathit{k}}_{\mathbf{23}},{\mathit{k}}_{\mathbf{31}})=\frac{\int d^3{\mathit{r}}_{\mathbf{1}}{d}^3{\mathit{r}}_{\mathbf{2}}{d}^3{\mathit{r}}_{\mathbf{3}}\mathcal{S}\left({\mathit{r}}_{\mathbf{1}}\right)\mathcal{S}\left({\mathit{r}}_{\mathbf{2}}\right)\mathcal{S}\left({\mathit{r}}_{\mathbf{3}}\right){\left|{\mathsf{\Psi }}_{{\mathit{k}}_{\mathbf{12}},{\mathit{k}}_{\mathbf{23}},{\mathit{k}}_{\mathbf{31}}}^0({\mathit{r}}_{\mathbf{1}},{\mathit{r}}_{\mathbf{2}},{\mathit{r}}_{\mathbf{3}})\right|}^2}{\int d^3{\mathit{r}}_{\mathbf{1}}{d}^3{\mathit{r}}_{\mathbf{2}}{d}^3{\mathit{r}}_{\mathbf{3}}\mathcal{S}\left({\mathit{r}}_{\mathbf{1}}\right)\mathcal{S}\left({\mathit{r}}_{\mathbf{2}}\right)\mathcal{S}\left({\mathit{r}}_{\mathbf{3}}\right){\left|{\mathsf{\Psi }}_{{\mathit{k}}_{\mathbf{12}},{\mathit{k}}_{\mathbf{23}},{\mathit{k}}_{\mathbf{31}}}^C({\mathit{r}}_{\mathbf{1}},{\mathit{r}}_{\mathbf{2}},{\mathit{r}}_{\mathbf{3}})\right|}^2}$$

(7)

where ${\mathsf{\Psi }}^0$ is the free-particle wave function (symmetrized plane wave), and ${\mathsf{\Psi }}^C$ is the (symmetrized) solution of the full three-particle Coulomb problem. Instead of solving the three-particle Coulomb problem, we use a general approach to handle the three-particle Coulomb interaction, which is called the “Generalized Riverside” method [17]:

$$K_3(k_{12},k_{13},k_{23})\approx K_2\left(k_{12}\right)K_2\left(k_{13}\right)K_2\left(k_{23}\right),\mathrm{with}{K}_2\left(k_{ij}\right)=\frac{\int d^3{\mathit{r}}_{\mathbf{1}}{d}^3{\mathit{r}}_{\mathbf{2}}\mathcal{S}\left({\mathit{r}}_{\mathbf{1}}\right)\mathcal{S}\left({\mathit{r}}_{\mathbf{2}}\right){\left|{\mathsf{\Psi }}_{{\mathit{k}}_{\mathbf{12}}}^0({\mathit{r}}_{\mathbf{1}},{\mathit{r}}_{\mathbf{2}})\right|}^2}{\int d^3{\mathit{r}}_{\mathbf{1}}{d}^3{\mathit{r}}_{\mathbf{2}}\mathcal{S}\left({\mathit{r}}_{\mathbf{1}}\right)\mathcal{S}\left({\mathit{r}}_{\mathbf{2}}\right){\left|{\mathsf{\Psi }}_{{\mathit{k}}_{\mathbf{12}}}^C({\mathit{r}}_{\mathbf{1}},{\mathit{r}}_{\mathbf{2}})\right|}^2}$$

(8)

This approximates the three-particle Coulomb correction well if certain conditions [17] are satisfied, and it does not depend on the directions of the momentum differences, only their magnitude. With this Coulomb correction factor, the full BEC function is

$$C_3(k_{12},k_{13},k_{23})=C_{3,\mathrm{fit}}^{\left(0\right)}(k_{12},k_{13},k_{23})K_{Coulomb}(k_{12},k_{13},k_{23})$$

(9)

By using this approximation, we are able to reuse the Coulomb correction calculation method developed in [18]. After some consistency checks, we conclude that using this approximation can be considered, as the relative systematic error due to this approximation is less than 2%.

The two- and three-particle correlation strengths are defined as the extrapolated intercept of the given correlation function:

$$\begin{array}{cc}\hfill {\lambda }_2& \equiv C_2(k_{12}\to 0)-1\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\lambda }_3& \equiv C_3(k_{12}=k_{13}=k_{23}\to 0)-1\hfill \end{array}$$

(11)

With respect to these, it is important to note that not all pions are created directly from the strongly interacting matter. A significant fraction of pions are secondary, coming from decays. Hence the source will have two components: a core of primordial pions, and a halo consisting of the decay products of long-lived resonances (such as $\eta$, ${\eta }^{\prime }$, $K_s^0$, and $\omega$):

$$S=S_{core}+S_{halo}$$

(12)

In the core-halo model, the fraction of the core is defined by

$$f_c=\frac{N_{\mathrm{core}}}{N_{\mathrm{core}}+N_{\mathrm{halo}}}$$

(13)

where $N_{\mathrm{core}}$ is the number of pions in the core, and $N_{\mathrm{halo}}$ is the number of pions in the halo. If there is partial coherence in the core, a coherence parameter can be introduced [19,20], examining the fraction of coherently produced pions in the core:

$$p_c=\frac{N_{\mathrm{coherent}}}{N_{\mathrm{coherent}}+N_{\mathrm{incoherent}}}$$

(14)

where $N_{\mathrm{coherent}}+N_{\mathrm{incoherent}}=N_{\mathrm{core}}$. With these, ${\lambda }_2$ and ${\lambda }_3$ can be expressed as functions of $f_c$ and $p_c$:

$$\begin{array}{cc}\hfill {\lambda }_2=& f_C^2\left[{(1-p_c)}^2+2p_c(1-p_c)\right]\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\lambda }_3=& 2f_C^3\left[{(1-p_c)}^3+3p_c{(1-p_c)}^2\right]+3f_C^2\left[{(1-p_c)}^2+2p_c(1-p_c)\right]\hfill \end{array}$$

(16)

To be able to investigate the partial coherence within the limits of this model, we have to take Equations (15)–(16) and use the measured ${\lambda }_2$ and ${\lambda }_3$ parameters as input in these equations; we also have to look for $f_c$ and $p_c$ values that solve both equations. To determine whether a solution exists, we can plot $f_c$ as a function of $p_c$ with given ${\lambda }_2$ and ${\lambda }_3$. In this way, we obtain two curves (one from the equation with ${\lambda }_2$, and the other from the equation with ${\lambda }_3$), and if these curves overlap, then the second- and third-order BEC functions are consistent with each other, and the degree of partial coherence can be determined from the region of the overlap.

2. Results

The data used in the analyses were collected by the PHENIX detector in 2010; 7.3 billion minimum bias Au+Au collisions at $\sqrt{s_{NN}}=200$ GeV were recorded. We measured three-particle correlation functions of ${\pi }^{-}{\pi }^{-}{\pi }^{-}$ and ${\pi }^{+}{\pi }^{+}{\pi }^{+}$ triplets in 31 $m_T$ bins ranging from 228 to 871 MeV, with event selection, single track cuts and pair cuts identical to the analysis of [8]. The visualization of three-dimensional fits is difficult; thus instead of showing two-dimensional projections of these three-dimensional fits, we have decided to show, as an illustration, various one-plus-one dimensional slices of them. These slices were obtained by requiring that the two-particle relative momenta $k_{i,j}$ between the pairs $(i,j)=(1,2)$, $(2,3)$ and $(3,1)$ were equal. The ${\chi }^2/NDF$ values and the confidence levels were statistically acceptable. Figure 1 indicates the PHENIX preliminary three-particle correlation data and the fitted curve as a univariate slice of a multi-variate function. We note that no significant long-range correlation was observed: $ϵ$ was close to zero. In these fits, the values of the Lévy scale R and the Lévy index of stability $\alpha$ were taken from PHENIX preliminary two-particle correlation data in the same transverse-momentum bins and in the same selection of minimum-bias $\sqrt{s_{NN}}=200$ GeV Au+Au collisions. (See these preliminary R and $\alpha$ data in [21].) Within one standard deviation, the same parameter values were obtained if we released the values of R and $\alpha$ in these fits, indicating an internal consistency between the two- and three-particle correlation measurements. Given this internal consistency and our focus on the comparison of the strength or intercept parameters ${\lambda }_2$ and ${\lambda }_3$ of the two- and three-particle BEC functions, here we report these values using the R and $\alpha$ values as determined from the two-particle BEC function measurements in minimum-bias $\sqrt{s_{NN}}=200$ GeV Au+Au collisions [21].

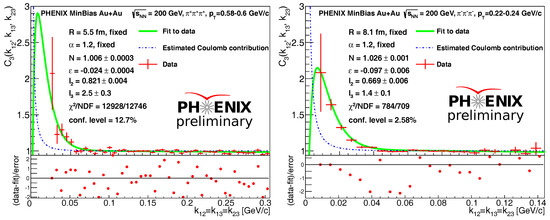
Figure 1. Diagonal visualization of the three-particle Bose-Einstein correlation functions $C_3$ with the results of fits.

2.1. Three-Particle Correlation Strength

The three-particle correlation strength, derived from ${\ell }_2$ and ${\ell }_3$ fit parameters as ${\lambda }_3={\ell }_2+{\ell }_3$, can be seen in Figure 2. According to the core-halo model, ${\lambda }_3$ had to be in the range $[0,5]$, as indicated by a green box in Figure 2. One can see that within errors, this parameter fell in the allowed range. The detailed description of the systematic uncertainty sources is given in [8].

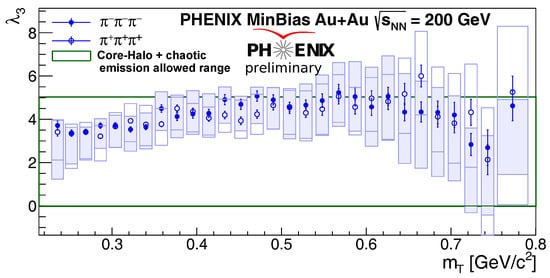
Figure 2. The three-particle correlation strength, ${\lambda }_3$, as a function of $m_T$. Statistical and systematic uncertainties are shown as bars and boxes, respectively.

2.2. core-halo Independent Parameter

In this subsection, the possibility of partial coherence is investigated. We introduce a new parameter, a combination of ${\lambda }_3$ and ${\lambda }_2$, as follows:

$${\kappa }_3=\frac{{\lambda }_3-3{\lambda }_2}{2\sqrt{{\lambda }_2^3}}$$

(17)

This parameter does not depend on the value $f_c$, and its value is unity independently of the transverse mass, if the particle emission has no coherent component or if $p_c=0$ in the core-halo picture of n-particle BECs.

The measured ${\kappa }_3$ parameter is shown in Figure 3 and was calculated by using ${\lambda }_3$ from the fits described in this paper, and ${\lambda }_2$ from [21]. Our errors were still preliminary, and a full systematic analysis is in progress. Figure 3 shows the ${\kappa }_3$ parameter for the average $m_T$ of the triplets.

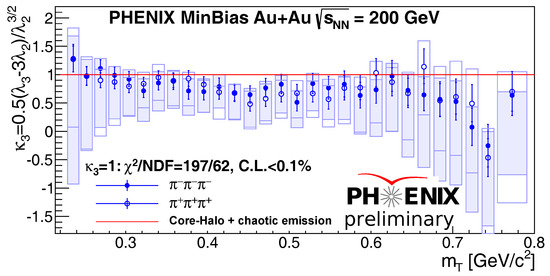
Figure 3. Core-halo independent parameter as a function of $m_T$. Statistical and preliminary systematic uncertainties are shown as bars and boxes, respectively.

We observe that ${\kappa }_3$ was different from unity at $m_T\approx 450$ MeV. The deviation of ${\kappa }_3$ from 1 may indicate some kind of partial coherence; however, the preliminary status of these data points and their error bars prevent us from a more definitive conclusion. Further investigations are ongoing and will be reported elsewhere. Figure 4 shows $f_c$ as a function of $p_c$ for different $m_T$ regions. Here we took Equations (15) and (16) and the measured ${\lambda }_2$ and ${\lambda }_3$ parameters and determined the allowed $(f_c,p_c)$ region, as shown in Figure 4.

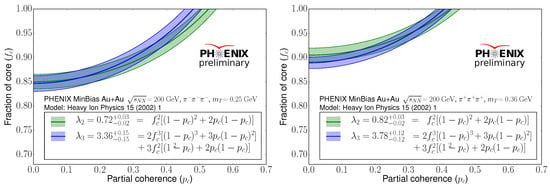
Figure 4. The fraction of the core $f_c$ parameter as a function of coherence parameter $p_c$ for two different $m_T$ values.

3. Conclusions

In this paper, we simultaneously investigated two- and three-particle femtoscopic correlation functions in PHENIX Au+Au collisions at 200 GeV/nucleon collision energy. Lévy distributions yielded correlation functions that provide a statistically acceptable description of the measurements. In this paper, we used the source parameters R and $\alpha$ from two-particle fits and obtained the three-particle correlation strength from the analysis of three-particle correlations. We have investigated the results in view of the core-halo model and derived a core-halo independent parameter ${\kappa }_3$. These preliminary results have been compared to predictions based on chaotic emission, and very small deviations were observed. This, however, needs a detailed final analysis, which we plan to carry out in the near future.