Scaling Properties of Spectra in New Exact Solutions of Rotating, Multi-Component Fireball Hydrodynamics

Abstract

We describe fireballs that rehadronize from a perfect fluid of quark matter, characterized by the lattice QCD equation of state, to a chemically frozen, multi-component mixture, that contains various kinds of observable hadrons. For simplicity and clarity, we apply a non-relativistic approximation to describe the kinematics of this expansion. Unexpectedly, we identify a secondary explosion that may characterize fireball hydrodynamics at the QCD critical point. After rehadronization, the multi-component mixture of hadrons keeps on rotating and expanding together, similarly to a single component fluid. After kinetic freeze-out, the effective temperature $T_i$ of the single-particle spectra of hadron type $h_i$ is found to be a sum of the kinetic freeze-out temperature $T_f$ (that is independent of the hadron type $h_i$) and a term proportional to the mass $m_i$ of hadron type $h_i$. The coefficient of proportionality to $m_i$ is found to be independent of the hadron type $h_i$ but to be dependent on the radial flow and vorticity of collective dynamics.

1. Introduction

In this paper, the main theme of the analysis is the mass systematics of the single particle spectra as measured in relativistic heavy ion collisions, based on exact solutions of fireball hydrodynamics. Interestingly, the NA44 Collaboration observed signals of collective expansion in symmetric heavy-ion collisions in 200 AGeV S+S and 158 AGeV Pb+Pb reactions at CERN SPS: the transverse mass spectra of pions, kaons and protons was found to be nearly exponential in these reactions, with a slope parameter that increased nearly linearly with the mass of the observed hadrons [1]. This linear mass dependence of the slope parameters was interpreted as an evidence of collective transverse flow in these heavy ion induced central collisions.

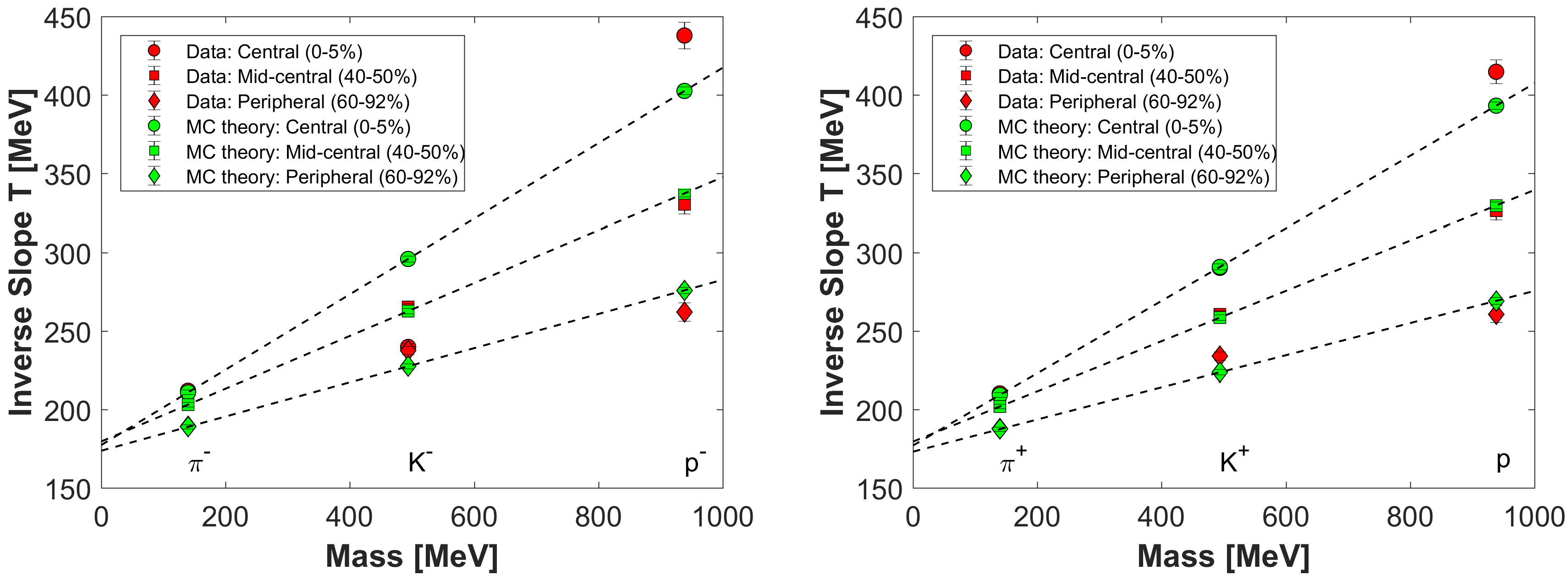
The inverse slope parameters for positively and negatively charged pions and kaons, as well as for protons and anti-protons has subsequently also been measured in various heavy ion collisions, for example in $\sqrt{s_{NN}}=200$ GeV Au+Au collisions by the PHENIX Collaboration in three centrality bins, as is shown very clearly in Figure 10 and in Table IV of [2], reproduced and detailed on Figure 1. These inverse slope parameters were also found to increase with increasing particle mass, in all centrality bins. This increase for central collisions was found to be more rapid for heavier particles, taken as another indication of collective expansion dynamics not only in central but also in peripheral heavy ion reactions at RHIC. Such a behavior was predicted—under certain conditions corresponding to a non-relativistic radial expansion dynamics—in References [3,4,5,6], for central collisions. A similar behaviour was derived for non-central heavy ion collisions as well, in References [7,8].

The early derivations were based on the blast-wave [3], or on the Buda-Lund model [4,5] that focused on a parameterization of the particle emission in phase-space around the time of kinetic freeze-out. It is remarkable that the transverse, radial flows in both the blast-wave and the Buda-Lund parameterization go back to precisely the same exact solution of non-relativistic fireball hydrodynamics, namely the Zimányi-Garpman-Bondorf solution of [9]. A few years after the successfull hydrodynamical parameterizations of the freeze-out phase-space distribution were obtained, the time evolution was also accessed with the help of the first exact solution within the Buda-Lund family of exact solutions of fireball hydrodynamics. The first of such Buda-Lund hydro solutions was found for a spherically symmetric, radially expanding fireball with spatially homogeneous temperature profile and a Gaussian density profile in [6], where the inverse slope parameter of the single particle spectra, $T_{\mathit{eff}}$ has also been shown to scale as an affine-linear function of the particle mass m:

$$T_{\mathit{eff}}(m)=T_f+m{\langle u_T\rangle }^2,$$

(1)

where m is the mass of a single kind of elementary particle with three kinetic degrees of freedom, that consists the expanding medium. The average transverse flow is denoted by $\langle u_T\rangle$ and the kinetic freeze-out temperature is denoted by $T_f$. Although the above relation is typically quoted as a justification for the linear mass dependence of the effective temperature in a hot and dense, hadronic matter, actually the derivations had a much more limited scope, evaluating the mass dependence for one kind of hadrons only, while in the experiment, a mixture of various hadronic components is observed.

Such an experimental result is beautifully illustrated on Figure 10 of [2] and reproduced also on our Figure 1, that compares measured slope parameters in relativistic heavy ion collisions at mid-rapidity with Equation (1), derived in a non-relativistic context. The success of this comparision suggests that the key scaling properties of the transverse mass spectra at mid-rapidity may perhaps be understood in the framework of non-relativistic kinematics. Inspired by this insight, we try to handle the equations of relativistic and non-relativistic hydrodynamics in a similar way in Section 2. For the sake of clarity and brevity, we present new, rotating ellipsoidal exact solutions of fireball hydrodynamics only in the non-relativistic limit, as detailed in Section 3.

Note, however, that all the earlier derivations dealt with a hydrodynamically expanding medium that had only a single component, i.e., only one kind of hadrons, with a given mass m. The linear rise in the data was compared with the results of the calculations by extrapolating the theoretical results as a continuous function of the mass m, that was considered as a smoothly varying parameter of the solution and the resulting effective temperature or slope parameter. However, the experimentally observed mass spectrum of the hadrons is essentially discrete, and not a smoothly varying function. In the data analysis, for example, the slope parameters were measured at the mass of pions, kaons and (anti)protons, as indicated on Figure 1. One of the challenges considered in this work is to generalize the derivation from a single-component hadron gas to a multi-component hadron gas, that is a mixture of hadrons with different discrete values of their masses. Such a derivation seemed to be an almost hopeless theoretical challenge; as far as we know it was not even attempted before. This challenge however is positively solved in this manuscript. We derive a new class of solution for the equations of fireball hydrodynamics for a collectively expanding and rotating, strongly interacting perfect fluid that contains a multi-component hadronic matter. We also obtain the slope parameters for various kinds of hadrons that emerge from the collective expansion after kinetic freeze-out.

For the sake of clarity, we introduce the i index to distinguish the different type of hadrons and thus the contribution of each kind of particle to the inverse slope can be separated. Note that in this way one can find what is really eye-catching in Figure 1: the inverse slope $T_i$ as well as the single particle spectra depends on the particle type only through the mass of the hadrons: the freeze-out temperature $T_f$ and the slope parameter $\langle u_T\rangle$ is independent of the type i of the observed hadrons, furthermore the freeze-out temperature is a static characteristic of the medium, apparently independent of the centrality, while the coefficient of linearity is increasing with increasing centralities. The result is summarized as

$$T_i=T_f+m_i{\langle u_T\rangle }^2.$$

(2)

In this Equation (2), the mass $m_i$ is not a smoothly varying parameter, in contrast to Equation (1), but takes on the discrete values, corresponding to the observable, PDG listed masses of those hadron species $h_i$ that constitute the mixture in the expanding, multi-component hadron gas.

As an extra difficulty, we also consider and are interested in describing the time evolution of fireball hydrodynamics using a realistic, lattice QCD based equation of state of [10]. This exercise is a kind of academic part of our study, motivated by the fact that in lattice QCD simulations, the speed of sound and the ratio of pressure to energy density at vanishing baryochemical potential are known to depend significantly on the temperature [10]. We consider such an equation of state in this work, indicated also in Figure 2, although in a future, even more realistic scenario relativistic kinematics will have to be considered as well. In this sense, our present study is also preparatory, yet a difficult step, aiming at future studies using lattice QCD equation of state in the dynamics, together with relativistic kinematics and a multi-component hadronic matter in the final state.

By this token, the main research topic of this manuscript is given: can the lattice QCD Equation of State and the scaling behaviour, the mass systematics of the slope parameter of the single particle spectra be understood in a self-consistent, hydrodynamical picture?

2. Equations of Relativistic as Well as Non-Relativistic Hydrodynamics

The basic equations of relativistic, perfect fluid hydrodynamics consists of a set of partial differential equations, that express the local consvervation of entropy, momentum and energy:

$${\partial }_{\mu }\left(\sigma u^{\mu }\right)=0,$$

(3)

$${\partial }_{\nu }{T}^{\mu \nu }=0,$$

(4)

where $\sigma$ stands for the entropy density, $T^{\mu \nu }$ is the energy-momentum tensor of a perfect fluid in the co-moving frame:

$$T^{\mu \nu }=\left(\epsilon +p\right)u^{\mu }{u}^{\nu }-p{g}^{\mu \nu }.$$

(5)

Here the metric tensor is denoted by $g^{\mu \nu }=\mathrm{diag}(1,-1,-1,-1)$, and $u^{\mu }=\gamma (1,\mathbf{v})$ is the four-velocity field, normalized as $u^{\mu }{u}_{\mu }=1$. The coordinates are denoted as $x^{\mu }=\left(t,\mathbf{r}\right)=\left(t,r_x,r_y,r_z\right)$ and the four-momentum is defined as $p^{\mu }=\left(E,\mathbf{p}\right)=\left(E,p_x,p_y,p_z\right)$ where the four-momentum is on-shell, $E=\sqrt{m^2+{\mathbf{p}}^2}$.

Equation (3) expresses local entropy conservation, while Equation (4) expresses local conservation of energy and momentum. This equation can be projected to a component parallel to $u^{\mu }$ that yields the energy equation:

$${\partial }_{\mu }\left(\epsilon u^{\mu }\right)+p{\partial }_{\mu }{u}^{\mu }=0,$$

(6)

while the component pseudo-orthogonal to the four-velocity field yields the relativistic Euler equation:

$$\left(\epsilon +p\right)u^{\nu }{\partial }_{\nu }{u}^{\mu }=\left(g^{\mu \nu }-u^{\mu }{u}^{\nu }\right){\partial }_{\nu }p.$$

(7)

Local conservation laws of densities cannot be used generally, because in the initial, hot temperature stage, at vanishing baryochemical potential, the only conserved charge is the net baryon number—which is zero in the considered case. As the medium cools down, quark and gluon degrees of freedom get confined to hadrons. After hadro-chemical freeze-out, this system of equations is supplemented with the continuity equation of particle densities. One new conservation law is obtained for each of the hadrochemically frozen particle types:

$${\partial }_{\mu }\left(n_i{u}^{\mu }\right)=0,\mathrm{for}T\le T_{chem},i=1,2,\dots ,j$$

(8)

where $n_i$ is the particle density of the $i^{th}$ hadron, and j counts that how many kind of hadrons are frozen out hadrochemically.

In the high temperature phase, $T>T_{chem}$, we have five equations, Equations (3), (6) and (7), for six independent variables, the three independent spatial components of the four-velocity field $\mathbf{v}$ and the energy, the pressure and the entropy density, resulting in five equations for six independent quantities. This set of equations becomes closed with the fundamental equation of thermodynamics, that introduces a new variable, the temperature T, and the assumption that the enthalpy is dominated by entropy density times the temperature at such high temperatures, summarized in the left column of

Table 1. We assume, that at high temperature, the enthalpy density is dominated by the entropy term while below the chemical freeze-out temperature of hadrons, their rest mass dominates the same term. In these equations, j counts how many kinds of different hadrons are hadrochemically frozen-out.

QM $\left(T_0\ge T>T_{chem}\right)$	HM $\left(T_{chem}\ge T\ge T_f\right)$
$\epsilon +p=T\sigma +{\sum }_{i=1}^j{\mu }_i{n}_i\approx T\sigma$	$\epsilon +p=T\sigma +{\sum }_{i=1}^j{\mu }_i{n}_i\approx {\sum }_{i=1}^j{m}_i{n}_i$
$p=T\sigma /\left(1+\kappa \right)$	$p={\sum }_{i=1}^j{p}_i=\left({\sum }_{i=1}^j{n}_i\right)T$

. The energy equation can be transformed to a temperature equation, given in

Table 2. The closed system of partial differential equations, corresponding to relativistic hydrodynamics, as specified for quark matter (QM) and for a chemically frozen, multi-component hadronic matter (HM). Utilizing the equations of state from Table 1, we obtain five equations for five unknowns in the high temperature, QM phase, while we obtain $j+4$ equations for $j+4$ unknowns in the chemically frozen, multi-component HM phase, where j counts the number of type of chemically frozen hadrons.

QM $\left(T_0\ge T>T_{chem}\right)$	HM $\left(T_{chem}\ge T\ge T_f\right)$
${\partial }_{\mu }\left(\sigma u^{\mu }\right)=0$	${\partial }_{\mu }\left(n_i{u}^{\mu }\right)=0,i=1,\dots ,j$
$\left[\frac{1+\kappa }{T}\frac{d}{dT}\left(\frac{T\kappa }{1+\kappa }\right)\right]u_{\mu }{\partial }^{\mu }T+{\partial }_{\mu }{u}^{\mu }=0$	$\left[\frac{1}{T}\frac{d}{dT}\left(\kappa T\right)\right]u_{\mu }{\partial }^{\mu }T+{\partial }_{\mu }{u}^{\mu }=0$
$\left[\sigma T\right]u^{\nu }{\partial }_{\nu }{u}^{\mu }=\left(g^{\mu \nu }-u^{\mu }{u}^{\nu }\right){\partial }_{\nu }\left[\frac{\sigma T}{1+\kappa }\right]$	$\left[{\sum }_{i=1}^j{m}_i{n}_i\right]u^{\nu }{\partial }_{\nu }{u}^{\mu }=\left[g^{\mu \nu }-u^{\mu }{u}^{\nu }\right]{\partial }_{\nu }\left[{\sum }_{i=1}^j{n}_{i}T\right]$

, utilizing also the $\epsilon =\kappa (T)p$ equation of state, but replacing the unknown energy density with the unknown temperature field and a known $\kappa (T)$ function.

Let us clarify that the relation $\epsilon =\kappa (T)p$ is only one part of the equation of state, because the new variable T appears as the argument of $\kappa$. So one also has to specify the dependence of the pressure p on the temperature T. In the case of a single component hadronic matter this is usually $p=nT$, as was discussed in earlier publications, see for example [8], where it was demonstrated, that this EoS is a thermodynamically consistent form for any (positive) function of $\kappa (T)$. In the case of a quark matter at zero baryochemical potential, $p=\sigma T/\left(1+\kappa \right)$ where $\sigma$ stands for the entropy density. As far as we know, this kind of EoS was introduced earlier and discussed in detail in Reference [11]. The similarity between the two approaches in the hadron gas and in a baryon-free plasma was discussed in [12]. Let us also clarify that in the plasma phase, at zero baryochemical potential, the speed of sound is simply $c_s^2=1/\kappa (T)$.

The state before the hadronization corresponds to the quark matter (QM) and after the transition the hadronic matter (HM) is formed. Different thermodynamical approaches may be used to describe the different phases. The general form of the fundamental equation of thermodynamics is:

$$\epsilon +p=T\sigma +\sum _i{\mu }_i{n}_i.$$

(9)

In heavy ion collisions at RHIC and LHC energies, the bariochemical potential ($\mu$) of the strongly coupled quark-gluon plasma is close to zero. Consequently in this case we can use the following approximation:

$$\epsilon +p\approx T\sigma .$$

(10)

As the medium cools down and a chemically frozen hadron gas is formed, the hadrochemical potential approaches the particle mass $m_i$ for hadron type i and the $T\sigma$ term becomes negligible compared to the energy of the rest-mass. In this way, in the chemically frozen hadronic matter, one may approximate the enthalpy density as

$$\epsilon +p\approx \sum _i{m}_i{n}_i.$$

(11)

At lower temperatures, $T\le T_{chem}$, we have additional relations, namely the continuity equations for each of the chemically frozen hadronic species. Suppose that there are j such chemically frozen hadrons ($i=1,\dots ,j$), then we have $j-1$ independent new equations, in addition to the entropy conservation. This way we have $j+4$ equations for $j+5$ unknowns, that we take as the j different densities, the temperature, the pressure, and the three independent spatial components of the four-velocity field. Similarly to the high temperature case, the energy equation can be transformed again to a temperature equation, given in the right column of Table 2. Indeed, this transformation utilizes also the $\epsilon =\kappa (T)p$ equation of state, similarly to the high temperature case, and results again in $j+4$ equations for $j+5$ unknowns. The $\kappa (T)$ function is assumed to be known from lattice QCD. This set of equations is closed, similarly to the high temperature phase, with the fundamental equation of thermodynamics, and the assumption that the chemical potentials are given approximately by the masses of hadrons and that the sum over chemical potentials times the corresponding densities is the dominant term in this low temperature phase, as summarized in the right column of Table 1. Actually, such an approximation is justified in the non-relativistic kinematic region, as it leads naturally to the usual form of the non-relativistic Euler equation.

The medium behaves differently before and after the hadronization which is manifested in the different system of equations in the corresponding hydrodynamical description. The relativistic system of equations of the two phases are summarized in Table 2.

From the energy equation, we obtain a differential equation for the temperature (T) by utilizing the equation of state and the expressions for the pressure. Note that this procedure can be followed not only in the case of relativistic kinematics, as summarized in Table 2, but also exactly the same method can be used to obtain the temperature equation in the case of non-relativistic kinematics, and this way one obtains a striking similarity between the system of partial differential equations of fireball hydrodynamics both in the relativistic, and in the non-relativistic kinematic domains. Consequently, in the ${\left|\mathbf{v}\right|}^2\ll 1$ approximation, the system of partial differential equations of relativistic hydrodynamics of Table 2 directly correspond to the system of partial differential equations of non-relativistic hydrodynamics, as summarized in

Table 3. The system of partial differential equations that describes non-relativistic fireball hydrodynamics of quark matter (QM) at high, $T>T_{chem}$ temperatures and a hadrochemically frozen, multi-component hadronic matter (HM) at lower, $T\le T_{chem}$ temperatures. Similarly to the relativistic case, we have obtained five equations for five unknowns in the high temperature, QM phase, while we have $j+4$ equations for $j+4$ unknowns in the chemically frozen, multi-component HM phase.

QM $\left(T_0\ge T>T_{chem}\right)$	HM $\left(T_{chem}\ge T\ge T_f\right)$
${\partial }_t\sigma +\nabla \left(\sigma \mathbf{v}\right)=0$	${\partial }_t{n}_i+\nabla \left(n_i\mathbf{v}\right)=0,i=1,\dots ,j$
$\left[\frac{1+\kappa }{T}\frac{d}{dT}\left(\frac{T\kappa }{1+\kappa }\right)\right]\left({\partial }_t+\mathbf{v}\nabla \right)T+\nabla \mathbf{v}=0$	$\left[\frac{1}{T}\frac{d}{dT}\left(\kappa T\right)\right]\left({\partial }_t+\mathbf{v}\nabla \right)T+\nabla \mathbf{v}=0$
$\left[\sigma T\right]\left({\partial }_t+\mathbf{v}\nabla \right)\mathbf{v}=-\nabla \left[\frac{\sigma T}{1+\kappa }\right]$	$\left[{\sum }_{i=1}^j{m}_i{n}_i\right]\left({\partial }_t+\mathbf{v}\nabla \right)\mathbf{v}=-\nabla \left[{\displaystyle \sum _{i=1}^j}{n}_{i}T\right]$

.

3. Exact and Analytic Solutions of Fireball Hydrodynamics

In this section, we focus on the non-relativistic approximation, for the sake of clarity and simplicity, leaving the discussion of the relativistic kinematics to a follow-up publication. Although such a non-relativistic approximation limits the direct applicability of our results to a detailed comparison with particle production to low transverse momentum and to mid-rapidity, similar simple and exact non-relativistic fireball solutions provided already important insights to the mass systematics of the single-particle spectra at low $p_T$ and at mid-rapidity.

Linear mass dependencies of the slope parameters of the single particle spectra were obtained before in exact solutions of non-relativistic fireball hydrodynamics, where a spatially homogeneous temperature profile was matched with a Gaussian density profile, both for spherically [6] and for ellipsoidally symmetrically expanding fireballs [7,8], corresponding to central and non-central heavy ion collisions, respectively. However, these Gaussian solutions are readily generalized to an arbitrary but still spherically [13] or ellipsoidally symmetric temperature profiles [14], where maxima of the temperature profile function correspond to local minima in the matching density profile functions. Similarly, axially or ellipsoidally symmetric expanding fireballs are described by certain recently found exact solutions of perfect fluid hydrodynamics in the relativistic kinematic domain as well, that are characterized by a scaling variable and an arbitrary positive definite scaling function for the initial temperature profile, that is matched with a corresponding density profile [15,16].

We have summarized in Table 1, Table 2 and Table 3 the systems of partial differential equations of a fireball that is created in (non-)relativistic heavy-ion collisions. It is important to note that in the temperature equation the coefficient of the co-moving derivative of the temperature is the same in both Table 2 and Table 3, and this similarity between the relativistic and non-relativistic kinematics may play a role in subsequent, future studies.

Given such a background, let us present in this section two new, rotating exact solutions of non-relativistic fireball hydrodynamics. Their validity can be straigthforwardly tested with the help of Table 3, so we do not detail their derivation here. These solutions listed in the following subsections are given in the laboratory frame K, assuming a collider type of experiment so that the center of the fireball is at rest in the laboratory frame K.

The exact and analytic solutions that are already known can be grouped in a new manner as well, into three different kind of solutions, noted first in [12].

• The first kind of scaling solutions of fireball hydrodynamics are characterized by spatially homogeneous temperature profiles and corresponding Gaussian (entropy) density profiles. These solutions may also feature a realistic, temperature dependent energy density/pressure ratio, or a corresponding temperature dependent speed of sound, see for example References [6,7,8,12,17,18].
• The second kind of scaling solutions of fireball hydrodynamics are characterized by arbitrary, spatially inhomogeneous temperature profiles and corresponding, matching density profiles. The price for having the freedom of a realistic, arbitrary initial temperature profile is the need to have a temperature independent speed of sound, see References [11,12,13,14,15,16,19].
• The existence of a third kind of scaling solution of fireball hydrodynamics was noted first in [12], but elaborated only in [20]. This third kind of solution may gain further importance in the future, as it allows for the use of a lattice QCD equation of state in a realistic, spatially inhomogeneous, scaling solution of fireball hydrodynamics.

3.1. New Solutions of the First Kind: Exact, Parametric Solutions of Rotating and Expanding Fireballs with Gaussian Density Profiles

The first kind of scaling solution of fireball hydrodynamics corresponds to homogeneous temperature profiles, with a corresponding Gaussian (entropy)density profile, and a temperature dependent $\kappa =\kappa (T)=\epsilon /p$ function.

The equation of state independent part of our new, exact, rotating solutions of fireball hydrodynamics, are given in

Table 4. Equation of state independent part of new, exact, rotating solutions of fireball hydrodynamics, as given in the laboratory frame K, where a rotating ellipsoid with time dependent principal axis X, Y and Z is not only expanding but also spinning around the $r_y$ direction. The time dependent parameter $\vartheta$ stands for the angle between the principal axis X and the impact parameter direction, $r_x$ in the intertia frame K. The first of this kind of solutions was given in [18], which we generalize in this work to quark matter and multi-component hadronic matter scenarios.

Relations Valid Both in Quark Matter (QM) and in Hadronic Matter (HM):
$V={(2\pi )}^{3/2}XYZ$,
$X\left(\ddot{X}-{\omega }^{2}R\right)=Y\ddot{Y}=Z\left(\ddot{Z}-{\omega }^{2}R\right)=D$,
$\dot{\vartheta }\equiv \frac{{\displaystyle \phantom{(}\omega }}{{\displaystyle \phantom{(}2}}$,	$\omega ={\omega }_0\frac{{\displaystyle \phantom{(}{R}_0^2}}{{\displaystyle \phantom{(}{R}^2}}$,	$R=\frac{{\displaystyle \phantom{(}X+Z}}{{\displaystyle \phantom{(}2}}$,
$H_x=\frac{{\displaystyle \phantom{(}\dot{X}}}{{\displaystyle \phantom{(}X}}$,	$H_y=\frac{{\displaystyle \phantom{(}\dot{Y}}}{{\displaystyle \phantom{(}Y}}$,	$H_z=\frac{{\displaystyle \phantom{(}\dot{Z}}}{{\displaystyle \phantom{(}Z}}$,
$s=\frac{{\displaystyle \phantom{(}{r}_x^2}}{{\displaystyle \phantom{(}{X}^2}}+\frac{{\displaystyle \phantom{(}{r}_y^2}}{{\displaystyle \phantom{(}{Y}^2}}+\frac{{\displaystyle \phantom{(}{r}_z^2}}{{\displaystyle \phantom{(}{Z}^2}}+\left(\frac{{\displaystyle 1}}{{\displaystyle \phantom{(}{Z}^2}}-\frac{{\displaystyle 1}}{{\displaystyle \phantom{(}{X}^2}}\right)\left[(r_x^2-r_z^2){sin}^2\vartheta +r_x{r}_{z}sin(2\vartheta )\right]$,
$\mathbf{v}\left(\mathbf{r},t\right)={\mathbf{v}}_H\left(\mathbf{r},t\right)+{\mathbf{v}}_R\left(\mathbf{r},t\right)$,
${\mathbf{v}}_H\left(\mathbf{r},t\right)=\left(\begin{array}{c}(H_x{\cos }^2\vartheta +H_z{\sin }^2\vartheta )r_x\\ H_y{r}_y\\ (H_x{\sin }^2\vartheta +H_z{\cos }^2\vartheta )r_z\end{array}\right)+(H_z-H_x)\frac{{\displaystyle \phantom{(}sin(2\vartheta )}}{{\displaystyle \phantom{(}2}}\left(\begin{array}{c}{r}_z\\ 0\\ r_x\end{array}\right)$ ,
${\mathbf{v}}_R\left(\mathbf{r},t\right)=\dot{\vartheta }\left(\begin{array}{c}{r}_z\\ 0\\ -r_x\end{array}\right)+\dot{\vartheta }\left(\begin{array}{c}\left(\frac{{\displaystyle \phantom{(}X}}{{\displaystyle \phantom{(}Z}}{\cos }^2\vartheta +\frac{{\displaystyle \phantom{(}Z}}{{\displaystyle \phantom{(}X}}{\sin }^2\vartheta \right)r_z\\ 0\\ -\left(\frac{{\displaystyle \phantom{(}X}}{{\displaystyle \phantom{(}Z}}{\sin }^2\vartheta +\frac{{\displaystyle \phantom{(}Z}}{{\displaystyle \phantom{(}X}}{\cos }^2\vartheta \right)r_x\end{array}\right)+\dot{\vartheta }\left(\frac{{\displaystyle \phantom{(}X}}{{\displaystyle \phantom{(}Z}}-\frac{{\displaystyle \phantom{(}Z}}{{\displaystyle \phantom{(}X}}\right)\frac{{\displaystyle \phantom{(}sin(2\vartheta )}}{{\displaystyle \phantom{(}2}}\left(\begin{array}{c}{r}_x\\ 0\\ -r_z\end{array}\right)$,

.

In this subsection we generalize the results of [18], to a quark matter rehadronizing to a multi-component hadron gas. Following [18], we have written up the velocity field as a sum of two terms: a “Hubble-term” ${\mathbf{v}}_H$, and a “rotational term” ${\mathbf{v}}_R$. This form of the velocity field $\mathbf{v}$ and the scaling variable s satisfies the scale equation:

$$\begin{array}{ccc}\hfill \left({\partial }_t+\mathbf{v}\nabla \right)s& =& 0,\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill \mathbf{v}& =& {\mathbf{v}}_H+{\mathbf{v}}_R.\hfill \end{array}$$

(13)

The Hubble term has zero curl (and thus does not contribute to the vorticity of the flow), while the rotational term has zero divergence, hence it does not contribute to the overall expansion of the fluid:

$$\begin{array}{ccc}\hfill \nabla \mathbf{v}& =& \nabla {\mathbf{v}}_H=\frac{\dot{V}}{V},\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill \nabla {\mathbf{v}}_R& =& 0.\hfill \end{array}$$

(15)

The terms in $\mathbf{v}$ that are proportional to the angular velocity $\dot{\vartheta }$ contribute to the rotational flow velocity ${\mathbf{v}}_R$, which determines the vorticity of the solution as

$$\begin{array}{ccc}\hfill \mathbf{\omega }\left(\mathbf{r},t\right)& =& \nabla \times \mathbf{v}=\nabla \times {\mathbf{v}}_R,\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill \nabla \times {\mathbf{v}}_H& =& 0.\hfill \end{array}$$

(17)

The vorticity vector is parallel with the axis of rotation, and the value of its only non-vanishing component in the laboratory frame, $\mathbf{\omega }=({\omega }_x,{\omega }_y,{\omega }_z)$, where the non-vanishing component is given as

$$\begin{array}{cc}\hfill {\omega }_y\left(\mathbf{r},t\right)& =\omega +\frac{\omega }{2}\left(\frac{X}{Z}+\frac{Z}{X}\right).\hfill \end{array}$$

(18)

The equation of state specific parts of the solution are summarized in

Table 5. Equation of state dependent part of new, exact, rotating solutions of fireball hydrodynamics, that completes Table 4. In this table, those parts are shown that are specific to the time evolution of quark matter or hadronic matter.

QM $\left(T_0\ge T>T_{chem}\right)$ Valid in QM Only:	HM $\left(T_{chem}\ge T\ge T_f\right)$ Valid in HM Only:
$T\equiv T(t)$,	$T\equiv T(t)$,
$D=\frac{{\displaystyle \phantom{(}1}}{{\displaystyle \phantom{(}1+\kappa (T)}},$	$D=\frac{{\displaystyle \phantom{(}T}}{{\displaystyle \phantom{(}\langle m\rangle }}$,
$\sigma ={\sigma }_0\frac{{\displaystyle \phantom{(}{V}_0}}{{\displaystyle \phantom{(}V}}exp\left(-s/2\right)$,	$n_i=n_{i,0}\frac{{\displaystyle \phantom{(}{V}_0}}{{\displaystyle \phantom{(}V}}exp\left(-s/2\right)$ $i=1,\dots ,j$,
$\frac{{\displaystyle \phantom{(}\dot{T}}}{{\displaystyle \phantom{(}T}}\left[1+\kappa \right]\frac{{\displaystyle \phantom{(}\mathrm{d}}}{{\displaystyle \phantom{(}\mathrm{d}T}}\left[\frac{{\displaystyle \phantom{(}T\kappa }}{{\displaystyle \phantom{(}1+\kappa }}\right]+\frac{{\displaystyle \phantom{(}\dot{V}}}{{\displaystyle \phantom{(}V}}=0$,	$\frac{{\displaystyle \phantom{(}\dot{T}}}{{\displaystyle \phantom{(}T}}\frac{{\displaystyle \phantom{(}\mathrm{d}}}{{\displaystyle \phantom{(}\mathrm{d}T}}\left[T\kappa \right]+\frac{{\displaystyle \phantom{(}\dot{V}}}{{\displaystyle \phantom{(}V}}=0$.

.

In the same table, based on the results of Reference [21] the acceleration parameter D is related to $\langle m\rangle$, the average mass of the particles in the multi-component hadronic matter:

$$\langle m\rangle =\frac{{\displaystyle \sum _i}{m}_i{n}_i}{{\displaystyle \sum _i}{n}_i}.$$

(19)

In such a multi-component hadronic matter, the average mass is assumed to be time independent, $\langle m\rangle =({\sum }_{i=1}^j{n}_{i,0}{m}_i)/({\sum }_{i=1}^j{n}_{i,0})$.

In this way we reduced the complicated set of partial differential equations to a set of ordinary differential equations. This result generalizes the triaxial, rotating and expanding fireball solution of [18] from a single component hadron gas, characterized by mass m, to a perfect fluid of quark matter that hadronizes to a mixture of hadrons with average mass $\langle m\rangle$. Table 5 indicates that this mixture expands and rotates together, because the scale parameters X, Y and Z as well as the parameters of the rotation $\omega$ are independent of the index i of hadron types $h_i$. These solutions are all (rotating) Gaussian solutions, due to the $exp(-s/2)$ type of terms in the entropy and chemically frozen density profiles given in Table 5, that correspond to a position independent, but time dependent temperature profiles.

3.2. Fireball Explosion at the QCD Critical Point

The last line of Table 5 indicates a beautiful, exact and analytic result: Although the lattice QCD EoS suggests that the function $\kappa (T)$ is a smoothly varying function of the temperature as indicated on Figure 2, the coefficient of $\dot{T}/T$ in the last line of Table 5 actually changes. The difference of these coefficients is

$$\left[1+\kappa \right]\frac{{\displaystyle \phantom{(}\mathrm{d}}}{{\displaystyle \phantom{(}\mathrm{d}T}}\left[\frac{{\displaystyle \phantom{(}T\kappa }}{{\displaystyle \phantom{(}1+\kappa }}\right]-\frac{{\displaystyle \phantom{(}\mathrm{d}}}{{\displaystyle \phantom{(}\mathrm{d}T}}\left[T\kappa \right]=-\frac{{\displaystyle \phantom{(}T\kappa }}{{\displaystyle \phantom{(}1+\kappa }}\frac{{\displaystyle \phantom{(}\mathrm{d}\kappa }}{{\displaystyle \phantom{(}\mathrm{d}T}},$$

(20)

which vanishes at the temperature of $T_{max}\approx 158$ MeV, where the $\kappa (T)$ function has a maximum and changes sign at this point:

• If $T_{chem}>T_{max}$, then the coefficient of $\dot{T}/T$ increases, and the rate of change of the temperature decreases at the same logarithmic derivative of the volume $\dot{V}/V$, characterizing the volume expansion at hadrochemical freeze-out.
• If $T_{chem}=T_{max}$, the time evolution of the temperature changes smoothly at the hadrochemical freeze-out.
• If $T_{chem}<T_{max}$, the coefficient of $\dot{T}/T$ decreases, and the rate of change of the temperature increases at the same logarithmic derivative of the volume $\dot{V}/V$.

As we shall see below, not only the rate of change of the temperature with the increase of the volume is sensitive to quark confinement and subsequent hadrochemical freeze-out, but also the dimensionless measure of the rate of acceleration of the expansion changes at the chemical freeze-out, due to the changes in the expansion dynamics.

We assume that the hadronization and the hadrochemical freeze-out happens nearly simultaneously, as a consequence $T_{chem}\approx T_c$ in this case. Let us clarify that our equation of state at $T_{chem}$ corresponds to a QCD critical point in the sense that $\kappa (T)$ changes continuously, but its derivative jumps. This would correspond to a third order phase transition according to the Ehrenfest classification, however, according to the modern classification of phase transitions this corresponds to a second order phase transition.

For a spatially homogeneous temperature profile, and a simultaneous quark confinement and hadrochemical freeze-out, the boundary conditions are:

$$\begin{array}{cc}\hfill T_Q(t_{chem})& =T_H(t_{chem})=T_{chem},\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\mathbf{v}}_Q(\mathbf{r},t_{chem})& ={\mathbf{v}}_H(\mathbf{r},t_{chem}),\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\kappa }_Q(T_{chem})& ={\kappa }_H(T_{chem}).\hfill \end{array}$$

(23)

Due to these special boundary conditions one can obtain an important relation for D that is a dimensionless measure of the rate of expansions of the scales in the equations of motion:

$$D_Q(T_{chem})=\frac{1}{1+{\kappa }_{chem}}\approx 0.13<D_H(T_{chem})=\frac{T_{chem}}{\langle m\rangle }\approx 0.59.$$

(24)

The expression of the left side in Equation (24) characterizes the dimensionless acceleration parameter $D_Q$ in the quark phase, and the right side of the same relation relates $D_H$ to the acceleration of the hadronic matter. Given that $D_H>D_Q$, the acceleration of the scales jumps at $t_{chem}$ in every direction, so the directional Hubble constants $\dot{X}/X$, $\dot{Y}/Y$ and $\dot{Z}/Z$ have a break at these temperatures, and each of the scales X, Y and Z starts to expand faster as the temperature cools below the hadrochemical freeze-out temperature $T_{chem}$. We propose to call this phenomenon as a second explosion in the Little Bangs or heavy ion collisions. The first explosion is the violent expansion that starts just after the collision, due to large initial energy densities, temperatures and pressure gradients, while this second explosion starts just after the conversion to the hadronic phase and appears due to the role of hadrochemical freeze-out. Thus, this secondary explosion is due to the change of the thermodynamical properties of the hot and strongly interacting matter, namely to the hadrochemical freeze-out: it happens at the hadrochemical freeze-out temperature which in principle may be lower than the hadronization temperature. However, in this manuscript we assume that these are nearly the same temperatures. The effect of the second explosion becomes smoothened, if the average mass in the fireball is increased at $T\approx T_{chem}$. We expect, but cannot detail in this paper that a smooth cross-over may further slow down the expansion dynamics, but the detailed discussion of such a phenomena goes beyond the scope of this manuscript.

Our calculations seem to be laying the ground for similar calculations in the relativistic kinematic domain. Before looking for such new solutions of relativistic hydrodynamics, let us perform a consistency check and see if the single particle spectra from such solutions looks to be realistic or not.

4. Evaluation of the Single-Particle Spectra

The single particle spectra has already been calculated from single-component (SC) hydrodynamical solutions [18,22]. In this section we follow the notations and conventions of these earlier works, without giving the full details, referring also to the introduction for a motivation, and highlighting only the main, characteristic features of our results.

The slope parameters of the single particle spectra are apparently simple also in our multi-component (MC) generalization of rotating and expanding fireballs, when given in the $K^{\prime }$ frame that co-rotates with the fireball:

$$N_{1,i}(p_i^{\prime })\propto exp\{-\frac{1}{2m}\sum _{k,l=1}^3{p}_{k,i}^{\prime }{\left({\mathbf{T}}^{\prime }\right)}_{kl,i}^{-1}{p}_{l,i}^{\prime }\},$$

(25)

where $k,l=\{1,2,3\}=\{x,y,z\}$ and ${\left({\mathbf{T}}^{\prime }\right)}_{kl,i}^{-1}$ is the inverse of the effective temperature matrix or in other words the inverse slope matrix.

Similarly to the hydrodynamical solutions of a single-component hadron gas [18,22], this single particle spectra can be transferred to the laboratory frame and we obtain:

$$N_{1,i}(p_i)\propto exp\{-\frac{1}{2m}\sum _{k,l=1}^3{p}_{k,i}{\left(\mathbf{T}\right)}_{kl,i}^{-1}{p}_{l,i}\}.$$

(26)

We have collected the matrix elements for multi-component (MC) and single component (SC) hadronic matter (HM) in

Table 6. The comparison of the inverse slope parameters after kinetic freeze-out at temperature $T_f$, for a Single Component (SC) and for a Multi-Component (MC) Hadronic Matter (HM) from exact and analytic solutions of fireball hydrodynamics, in the case of rotating and nonrotating ellipsoid as well. In the case of non-rotating fireballs, the temperature matrix is diagonal in the center of mass frame K, $T_{kl}=\mathrm{diag}(T_x,T_y,T_z)$. For rotating fireballs, the temperature matrix is diagonal only in the co-rotating frame $K^{{}^{\prime }}$, where $T_{kl}^{{}^{\prime }}=\mathrm{diag}(T_{xx}^{{}^{\prime }},T_{yy}^{{}^{\prime }},T_{zz}^{{}^{\prime }})$.

	SC HM [8,18,22]	MC HM [21]
	$T_x=T_f+m{\dot{X_f}}^2$	$T_{x,i}=T_f+m_i{\dot{X_f}}^2$
${\omega }_0=0$	$T_y=T_f+m{\dot{Y_f}}^2$	$T_{y,i}=T_f+m_i{\dot{Y_f}}^2$
	$T_z=T_f+m{\dot{Z_f}}^2$	$T_{z,i}=T_f+m_i{\dot{Z_f}}^2$
	$T_{xx}^{\prime }=T_f+m\left({\dot{X_f}}^2+{\omega }_f^2{R}_f^2\right)$	$T_{xx,i}^{\prime }=T_f+m_i\left({\dot{X_f}}^2+{\omega }_f^2{R}_f^2\right)$
${\omega }_0\ne 0$	$T_{yy}^{\prime }=T_f+m{\dot{Y_f}}^2$	$T_{yy,i}^{\prime }=T_f+m_i{\dot{Y_f}}^2$
($K^{\prime }$ frame)	$T_{zz}^{\prime }=T_f+m\left({\dot{Z_f}}^2+{\omega }_f^2{R}_f^2\right)$	$T_{zz,i}^{\prime }=T_f+m_i\left({\dot{Z_f}}^2+{\omega }_f^2{R}_f^2\right)$

, where we denote these final state hadronic observables with the subscript f that denotes kinetic freeze-out. Note that for the non-rotating fireballs, the inverse temperature matrix is diagonal in the center of mass frame K, while for rotating fireballs, the inverse temperature matrix is diagonal only in the co-rotating frame $K^{\prime }$, so an additional transformation to K has to be made, similarly to how it was performed in [22].

We thus find that starting from a high temperature quark matter phase, followed by a nearly simultaneous quark confinement and hadrochemical freeze-out, we obtain apparently thermal single-particle spectra, where the inverse slope parameters have linear mass for each of the hadronic components $h_i$ and they depend on the particle types only through their masses $m_i$, similarly to the experimental data summarized in the introduction. After kinetic freeze-out, the effective temperature $T_i$ of the single-particle spectra of hadron type $h_i$ is found to be a sum of the kinetic freeze-out temperature $T_f$ (that is independent of the hadron type $h_i$) and a term proportional to the mass $m_i$ of hadron type $h_i$. The coefficient of proportionality to $m_i$ is also found to be independent of the hadron type $h_i$ but be dependent on the radial flow (and vorticity) of collective dynamics.

As a conclusion, the presented new class of multi-component, exact solution of fireball hydrodynamics provides a clear-cut, but not-yet-relativistic explanation for the mass-scaling behaviour of the single particle spectra in heavy ion collisions. Scaling violations, corresponding to deviations from the linear mass scaling, may be expected due to relativistic kinematics and temperature gradients, as discussed in [5], or, due to possible non-equilibrium kinetic freeze-out effects [23].

5. Summary

We have presented new, exact, parametric solutions of fireball hydrodynamics for a quark matter hadronizing to a chemically frozen, multi-component hadronic matter. These solutions have spatially homogeneous initial temperature profiles and corresponding Gaussian (entropy) density profiles. Note that these solutions are non-relativistic, so perhaps they can be connected later to scaling solutions discussed in the context of hydrodynamical behaviour of ultra-cold atoms at the Feshbach-resonance [24]. We have identified a change in the time evolution of the temperature that is due to the quark confinement to hadrons and to the simultaneous hadrochemical freeze-out. In addition, we have found a new phenomenon at the hadrochemical freeze-out, that relates to the dynamics of the hadronizing fireball: a second explosion, that seems to be, rather counter-intuitively, the strongest if the energy density to pressure ratio is the largest (frequently referred to as the softest point of QCD). This second explosion is caused by the increase of the acceleration after hadrochemical freeze-out. This effect seems to appear due to the change of the thermodynamics from a quark matter where no conserved charges exist to a chemically frozen hadronic matter, where each of the chemically frozen hadronic types obeys a local continuity equation. We conjecture that this second explosion is washed out if the transition from quark matter to hadronic matter corresponds to a continuous crossover, however, we could not detail this conjecture and elaborate the description of such a cross-over transition in this manuscript.

We have successfully generalized earlier exact and analytic hydrodynamical solutions from a single-component to a multi-component hadronic matter and we have shown that after the hadrochemical freeze-out of the multi-component hadronic matter, the slope parameters of the single particle spectra for various hadrons follow the experimentally observed affine-linear mass-scaling behaviour. Scaling violations, or deviations from such an affine-linear mass-scaling of the slope parameters may also be expected, due to relativistic kinematics and/or temperature gradients [5], or, additional possible non-equilibrium effects [23].