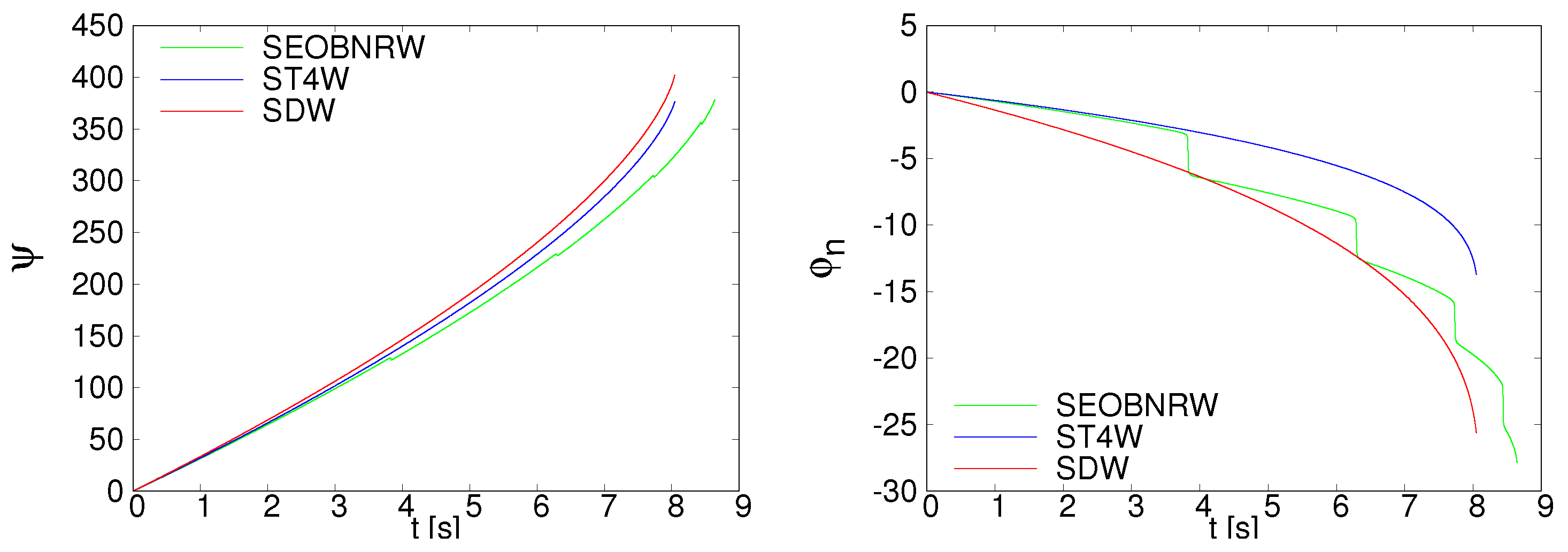Abstract
The sixfold direct detection of gravitational waves opened the era of gravitational wave astronomy. All of these gravitational waves were emitted by black hole or neutron star binaries. The determination of the parameters characterizing compact binaries requires the accurate knowledge of waveforms. Three different waveforms (Spin Dominated, SpinTaylorT4 and Spinning Effective One Body fitted to Numerical Relativity, SEOBNR) are considered in the spin-aligned and precessing cases, in the parameter ranges where the larger spin dominates over the orbital angular momentum. The degeneracy in the parameter space of each waveform is analyzed, then the matches among the waveforms are investigated. Our results show that in the spin-aligned case only the inspiral Spin-dominated and SpinTaylorT4 waveforms agree well with each other. The highest matches of these with SEOBNR are at different parameters as compared to where SEOBNR shows the best match with itself, reflecting SEOBNR being full inspiral-merger-ringdown waveform, with coefficients fitted to numerical relativity, rather than arising from post-Newtonian (PN) calculations. In the precessing case, the matches between the pairs of all waveforms are significantly lower. We identify possible causes of this in (1) the implementation of the angular dynamics carried out at different levels of accuracy for different waveforms; (2) differences in the inclusiveness of the merger process and in the PN coefficients of the inspiral waveforms (Spin-Dominated, SpinTaylorT4) and the full SEOBNR waveform.
1. Introduction
It was forecasted soon after the establishment of general relativity that gravitational waves can emerge from systems undergoing quadrupole deformations [1]. Recently, the LIGO Scientific Collaboration and Virgo Collaboration, based on data acquired by the Advanced LIGO [2] and Advanced Virgo [3] detectors, have announced detections of gravitational waves from coalescing stellar mass black hole binaries [4,5,6,7,8,9] and a neutron star binary [10]. This opened up the era of gravitational wave astronomy.
The motion of compact binaries, i.e black holes and/or neutron stars, under each other’s gravitational fields is divided into three phases: (i) the inspiral; (ii) the merger; (iii) the ringdown, when the newly created compact object evolves to a stable configuration. In this paper we investigate the inspiral phase, characterized by a small post-Newtonian (PN) parameter [11,12]. The order of the PN parameter is given by , where G is the gravitational constant, m is the total mass, r and v are the relative distance and velocity of the compact objects, respectively, and c is the speed of light. Their motion is restricted to a plane when the orbital angular momentum () and the spins () are aligned, or anti-aligned. However if the spins are not parallel with the orbital angular momentum, all vectors , undergo a complicated precession-like motion [12]. As the plane of the motion changes, the gravitational waveforms arising from these systems contain modulations, and they are called precessing waveforms. The purpose of this paper is to compare waveforms (Spin-Dominated, (approximant name: SpinDominatedWf) [13], SpinTaylorT4 [14] (approximant name: SpinTaylorT4), Spinning Effective One Body fitted to Numerical Relativity (approximant name: SEOBNRv3) [15,16]) derived in different approaches for circular orbits, with or without precession. In addition, we analyze the internal parameter degeneracies of the waveforms. These investigations emphasize the dependency of the parameter estimation on the chosen waveform in gravitational wave astronomy.
Previous studies compared several PN approximants and effective-one-body (EOB) models. In [17] the effectualness of PN Taylor approximants (TaylorT1, TaylorT2, TaylorT3, TaylorT4, TaylorEt, TaylorF2) and the EOB model were compared. Each approximant was compared to the others at 2PN, 3PN and 3.5PN orders. It was found that below total mass the PN approximants are consistent with each other at 3PN and 3.5PN orders. For higher masses the late stages of the inspiral (only contained in the EOB model) enter the detector sensitivity band, hence the effectualness of the Taylor approximants drops as compared to EOB. In [18] frequency domain PN (TaylorF2) and phenomenological non-spinning (PhenV1) waveforms were tested for effectualness and accuracy against EOB model. The two closed-form frequency domain models show ≤97% effectualness for advanced LIGO. Analytical waveforms were also compared to numerical relativity (NR) waveforms in [19,20,21,22,23], showing that higher order corrections to the phase evolution follow the phase evolution of NR waveforms more closely. In [23] it is found that both SEOBNR and PN models are effectual for detecting neutron star-black hole systems, the PN models give high bias in parameter recovery. In order to avoid creating excessively long, computer time consuming NR waveforms methods were developed to create hybrid waveforms, built of analytical inspiral and NR waveforms for the late inspiral and merger-ringdown phases. Methods were advanced to determine the required number of cycles of NR waveforms for fitting them accurately to analytical waveforms in [24,25,26,27].
In the inspiral-merger-ringdown consistency test [7], the results of parameter estimation using only the inspiral, and only the ringdown waveforms were compared, finding consistency with general relativity results in both phases. Hence the reliability of inspiral only waveforms is also important. In this paper we carry out a comparative analysis of the inspiral only SpinDominatedWf and SpinTaylorT4 waveforms also with the inspiral-merger-ringdown SEOBNRv3 waveform.
2. Comparison of Gravitational Waveforms
2.1. Method and Waveforms
For comparison of the waveforms the matched filtering algorithm will be used. For this purpose we use the inner product of and which is defined by
where the tilde denotes the Fourier-transforms of time domain functions and is the power-spectral density which is taken as the design sensitivity of the Advanced LIGO detectors [2]. The integration is taken between to , determined by the frequency sensitivity of the detector. The match is an inner product of two normalised waveforms and :
A value of the match (2) close to 1 means that the waveforms agree well. The + polarizations of each waveforms are used in calculating the match.
During the inspiral the order of the ratio of the spin with respect to the orbital angular momentum is
where with component masses and of the binary and . For small mass ratio , the spin dominates over the orbital angular momentum at the end of the inspiral. SpinDominatedWf [13] describes the radiation originating from such binaries. In this case the second spin becomes negligible, the angles between and , also between and the total angular momentum are quasi-constants on conservative timescale (where the effect of radiation backreaction is negligible), resulting in the dynamics being described in terms of two angle variables. These are the longitude of the ascending node (where is a constant axis perpendicular to and ), and the orbital phase [28]. In addition to these variables, the following set of time-independent parameters occur in the parametrization of waveforms: m, , the dimensionless spin parameter
where the hat denotes unit vectors.
When generating gravitational waves, besides the SpinDominatedWf [13], the dynamics of the angular variables should be taken into account. All waveforms used in this paper were generated by the PyCBC software [29,30,31], which implements LALSUITE [32] containing the coded waveforms. As a first approximation, time-dependent SpinDominatedWf was implemented in LALSUITE with the above described approximation for and , but with radiation reaction included in the evolution of the parameters , and the orbital angular frequency . The approximation is supported by the corresponding evolutions of SpinTaylorT4. The waveforms also depend on the direction of the propagation, hence on the parameter which is the angle between and the line of sight. The length of a detectable gravitational waveform depends on the total mass, mass ratio and the frequency band of the detector. The lower frequency for the waveforms was chosen as , the total mass and mass ratio were varied in the ranges respectively. The length of these waveforms is less than 15 s. On this timescale the radiation backreaction only affects significantly the angles , and .
SpinTaylorT4 [14] also applies PN approximation and it is valid for any mass ratio. The evolution of this waveform is characterized by nine variables: the components of orbital angular momentum vector , those of spin unit vectors and of a unit vector determined by and at the start of the evolution as , the orbital angular frequency and the orbital phase . In addition, the time independent quantities m, , and also occur in the parametrization of waveforms. The gravitational radiation backreaction is taken into account by the decrease in the separation of the binary due to energy loss. This separation appears in the equations governing the nine variables. It is to be expected that an additional expansion in a small parameter related to the mass ratio would generate similar results to SpinDominatedWf, although the expansion is subtle [13].
Another popular approach is the spinning effective one body formalism [15,16], also valid for any mass ratio. This description relies on a Hamiltonian formalism, in which the variables are the separation vector between the binary components , its canonically conjugated momentum and the two spin vectors , with two time-independent parameters m, . The time derivatives of , and are related to the derivatives of the Hamiltonian with respect to , and , respectively. In this approach the conservative dynamics is mapped onto an effective one body problem, where the body with reduced mass moves on an effective background. This map results in an effective Hamiltonian in which additional parameters occur. The effects of gravitational radiation backreaction of this system are included by the decrease in the separation of binary due to energy loss. The set of parameters are calibrated such that the resulting SEOBNRv3 matches well with NR waveforms. The calibration procedure has been applied at mass ratios close to one and at the extreme mass-ratio limit, while the waveforms considered in this paper were generated in the mass ratio parameter range . The SEOBNRv3, just like the other waveforms, contains the parameter .
In the comparisons we take two waveforms and calculate the match, which is the overlap maximized over time and phase. The PN waveforms (SpinDominatedWf and SpinTaylorT4) have the same length. However since the SEOBNRv3 waveform is longer than the PN waveforms, the latter are extended by zeros to get the same length in the comparison [33].
2.2. Spin Aligned Case
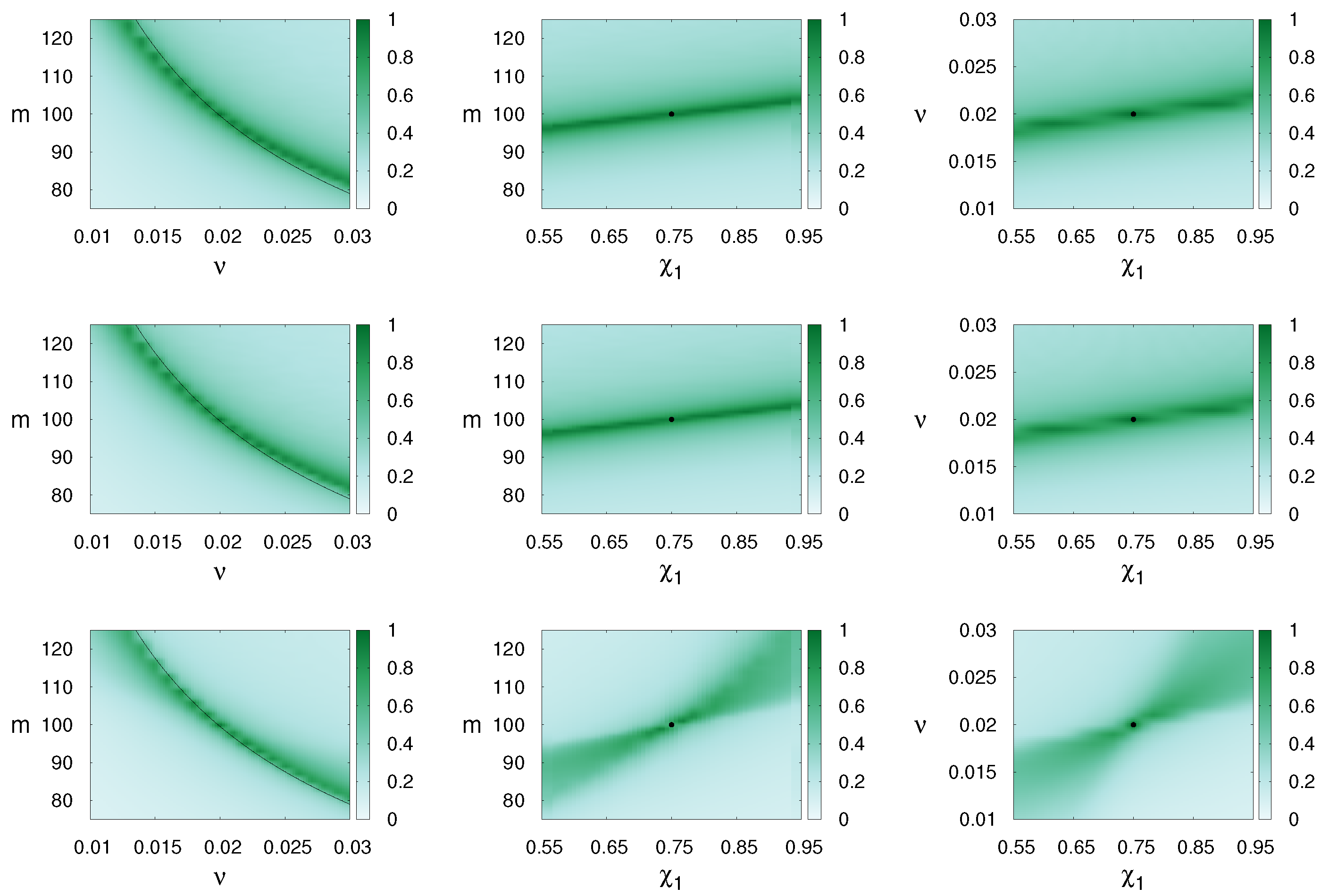
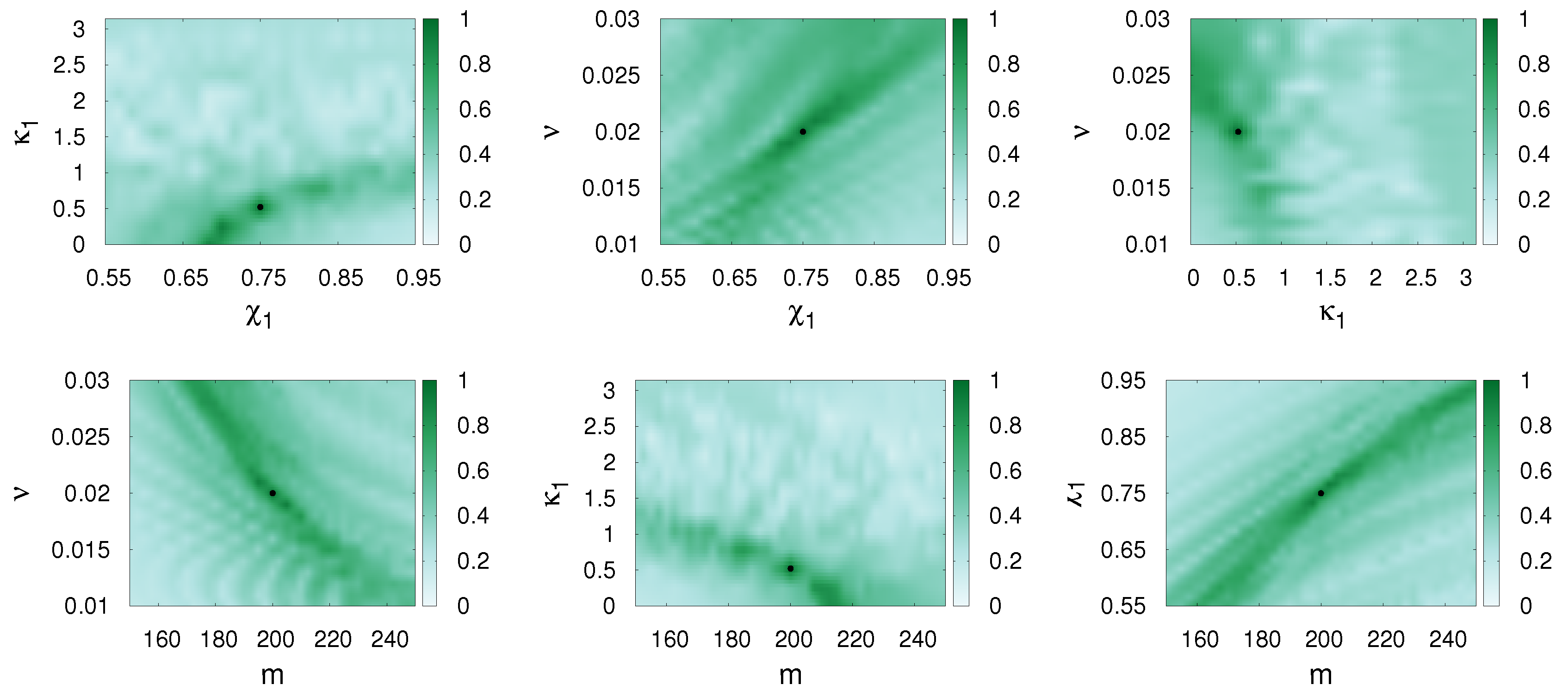
In this case the orbital motion of the binary is constrained to a plane to which the spins are perpendicular. The waveforms are compared within the common region of validity, i.e., for small mass ratios and in the spin-dominated regime. Then the sub-dominant spin is set to zero, hence the waveforms are characterized by m, and . For the exploration of the internal parameter degeneracies we match each waveform with itself such that one of the pair has fixed parameters , and while the other is varied. The matches are plotted on Figure 1 in the parameter spaces (m, ), (m, ) and (, ). The first, the second and the third row contain the comparison of SpinDominatedWf-SpinDominatedWf, SpinTaylorT4-SpinTaylorT4 and SEOBNRv3-SEOBNRv3, respectively. The fixed waveform is indicated by a central dot on all figures. We mention that the global maximum () of the matches coincides with the dots. Nevertheless there are several local maxima of most noticeably appearing in the case of SpinDominatedWf-SpinDominatedWf, but also occurring for SpinTaylorT4-SpinTaylorT4 and SEOBNRv3-SEOBNRv3. The steps on all comparison figures are in total mass, in and in . On each figure, the parameters not represented on the axes have the same values as the signal. The local maxima show up irrespective of the resolution of the sampling and these are always lower than the global maximum.
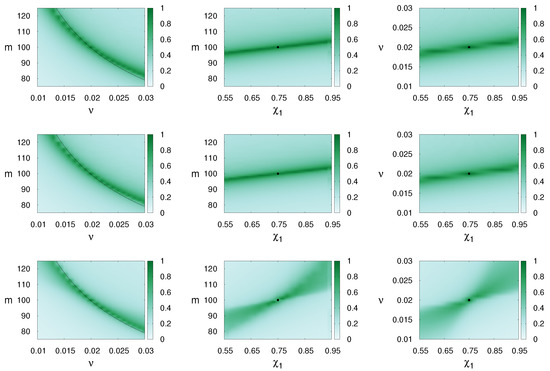
Figure 1.
Match values for two waveforms in the restricted parameter spaces , and from left to right (the three rows representing SpinDominatedWf-SpinDominatedWf, SpinTaylorT4-SpinTaylorT4, SEOBNRv3-SEOBNRv3 matches). The parameters of the first waveform (the template) are varied, while those of the second waveform (the signal, represented by a dot) are fixed as , and . The other parameters were chosen as Hz, The spins are aligned. The black lines on the plots in the first column represent the chirp mass of the signal waveform.
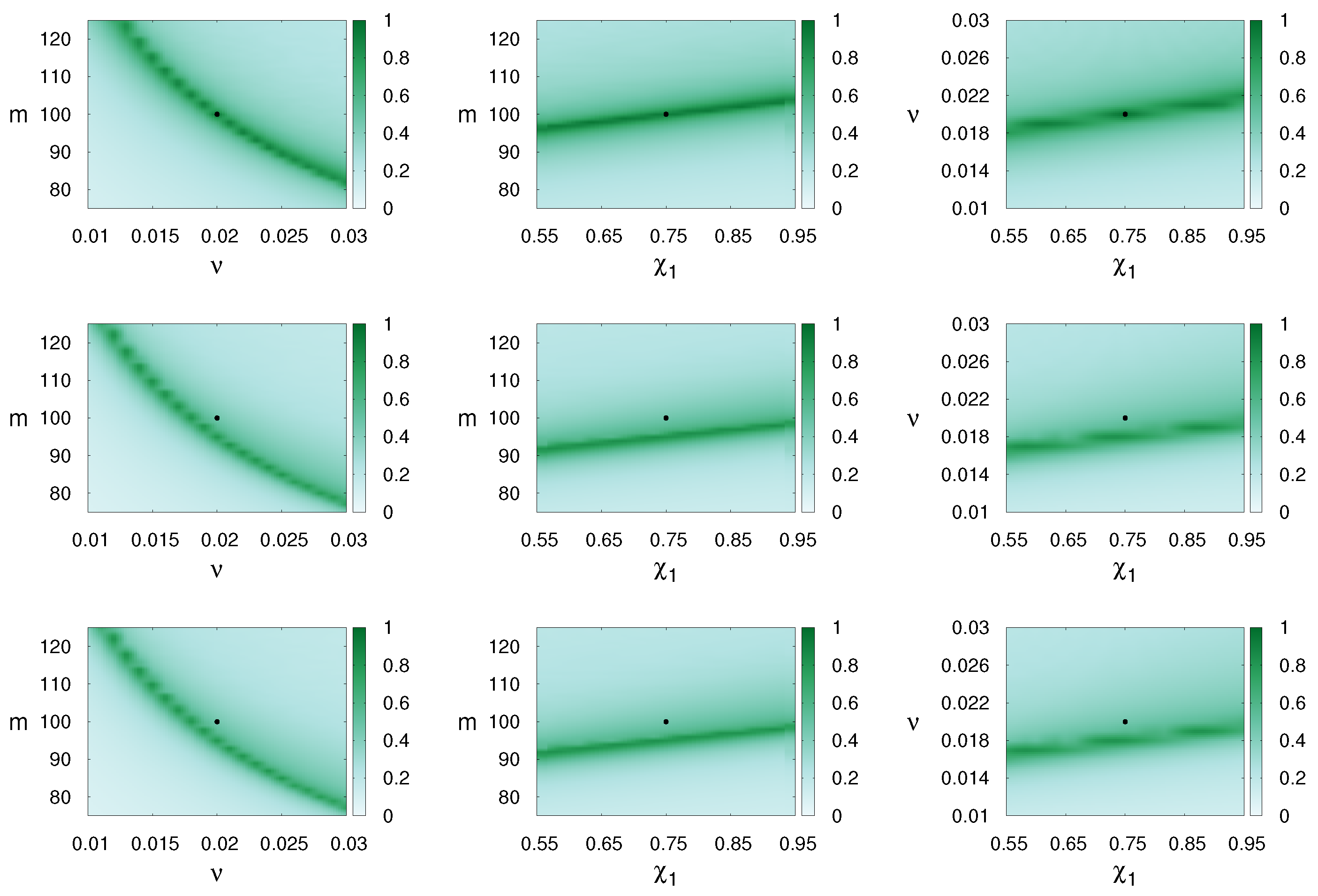
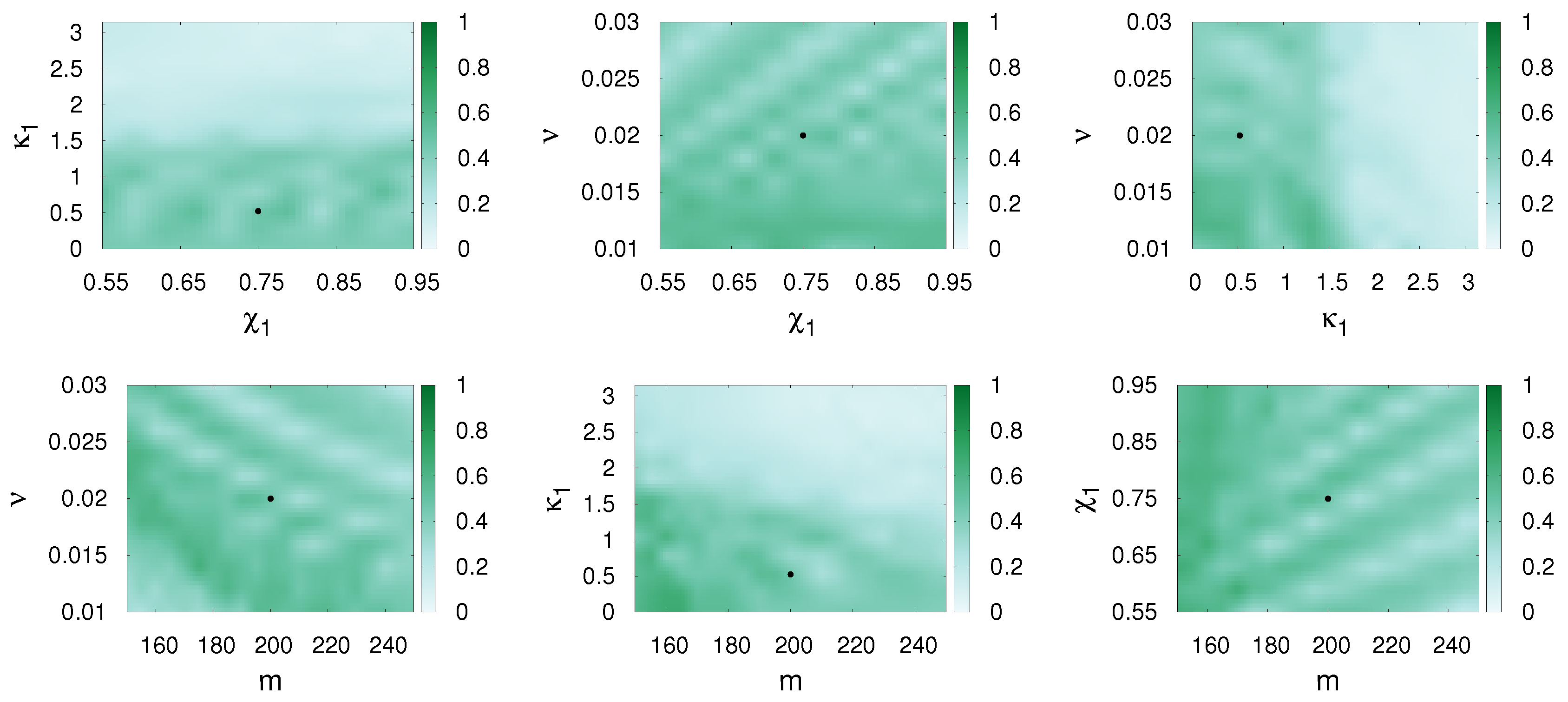
The degeneracies among different waveforms are represented in Figure 2. The matches are calculated with one of the compared waveforms having the fixed parameters , and . The result are shown in the parameter planes (m, ), (m, ) and (, ) for the pairs SpinTaylorT4-SpinDominatedWf, SpinDominatedWf-SEOBNRv3, SpinTaylorT4-SEOBNRv3. In all cases the second waveform has the fixed parameters denoted by a dot on the pictures. The matches between the waveforms SpinDominatedWf-SpinTaylorT4 having the same parameters are very good while those between SpinDominatedWf-SEOBNRv3 and SpinTaylorT4-SEOBNRv3 are unsatisfactory, however this is not entirely surprising as SEOBNRv3 is a full inspiral-merger-ringdown waveform containing coefficients fitted to NR [15], rather than derived analytically. In the case of SpinDominatedWf-SpinTaylorT4, the global maximum occurs at the fixed waveform parameters (indicated by a dot). The matches in the last two rows are best at different parameters as compared to where SEOBNRv3 matched well with itself and the global maxima are below 0.8.
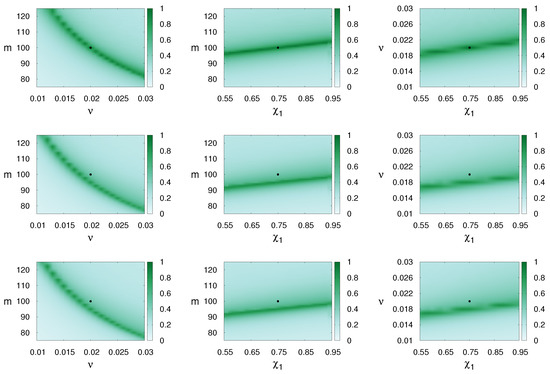
Figure 2.
Match values for two waveforms in the restricted parameter spaces , and from left to right (the three rows representing SpinTaylorT4-SpinDominatedWf, SpinDominatedWf-SEOBNRv3, SpinTaylorT4-SEOBNRv3 matches). The parameters of the first waveform (the template) are varied, while those of the second waveform (the signal, represented by a dot) are fixed as , and . The other parameters were chosen as Hz, The spins are aligned.
2.3. Precessing Spins and Orbital Angular Momentum
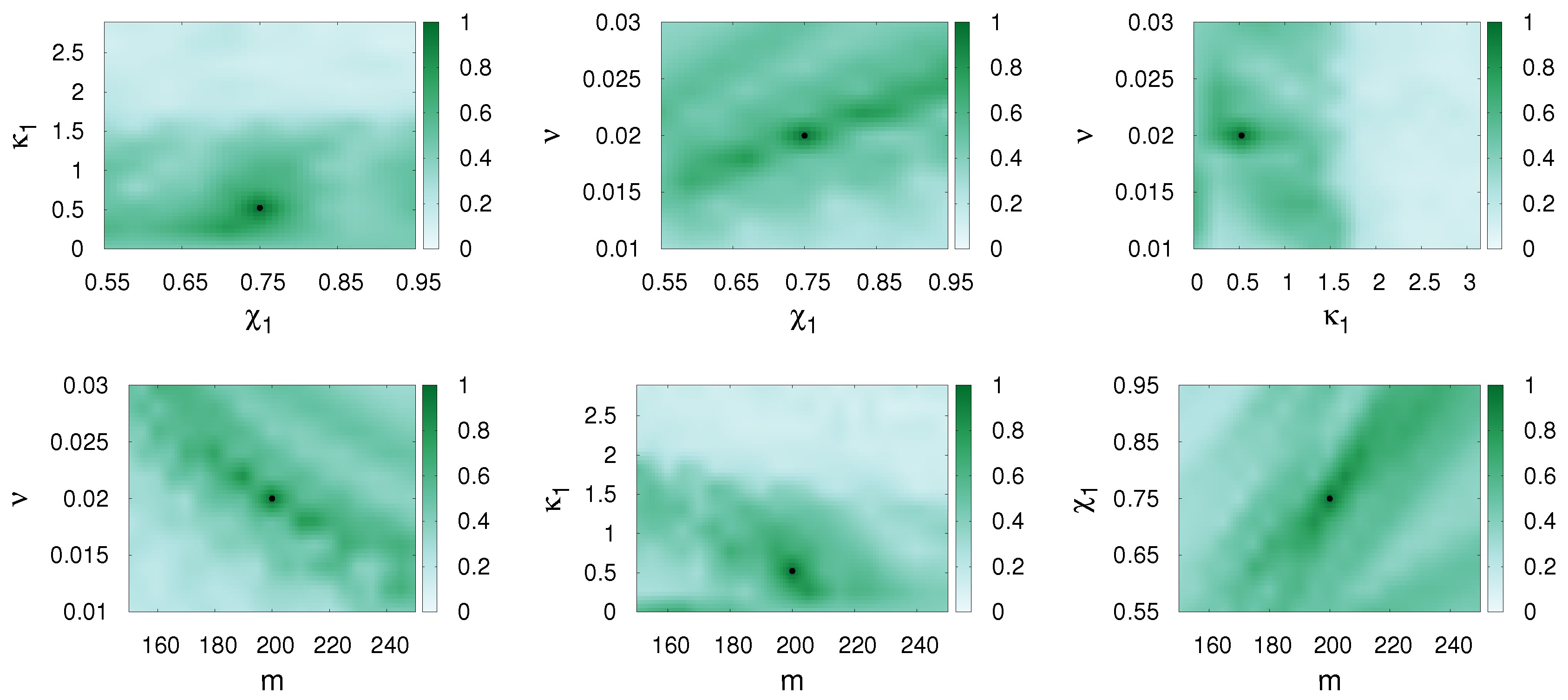
The waveforms arising from precessing binaries are much more complicated. Figure 3, Figure 4 and Figure 5 show the internal degeneracies in the parameter planes (, ), (, ), (, ), (, m), (, m) and (, m).
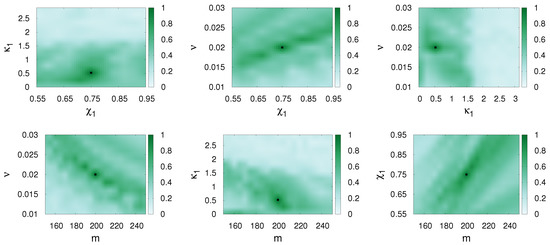
Figure 3.
SpinDominatedWf is matched with itself and match values are presented in different parameter planes (, ), (, ), (, ), (, m), (, m) and (, m). The parameters of the first waveform (the template) are varied, while those of the second waveform (the signal, represented by a dot) are fixed as , , and . The other parameters were chosen as Hz, . Spins are precessing in this case.
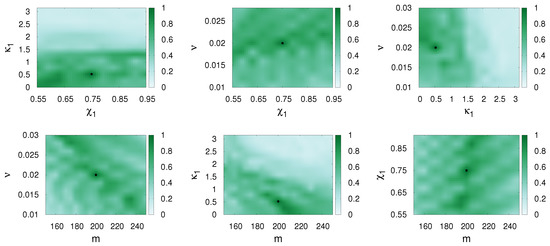
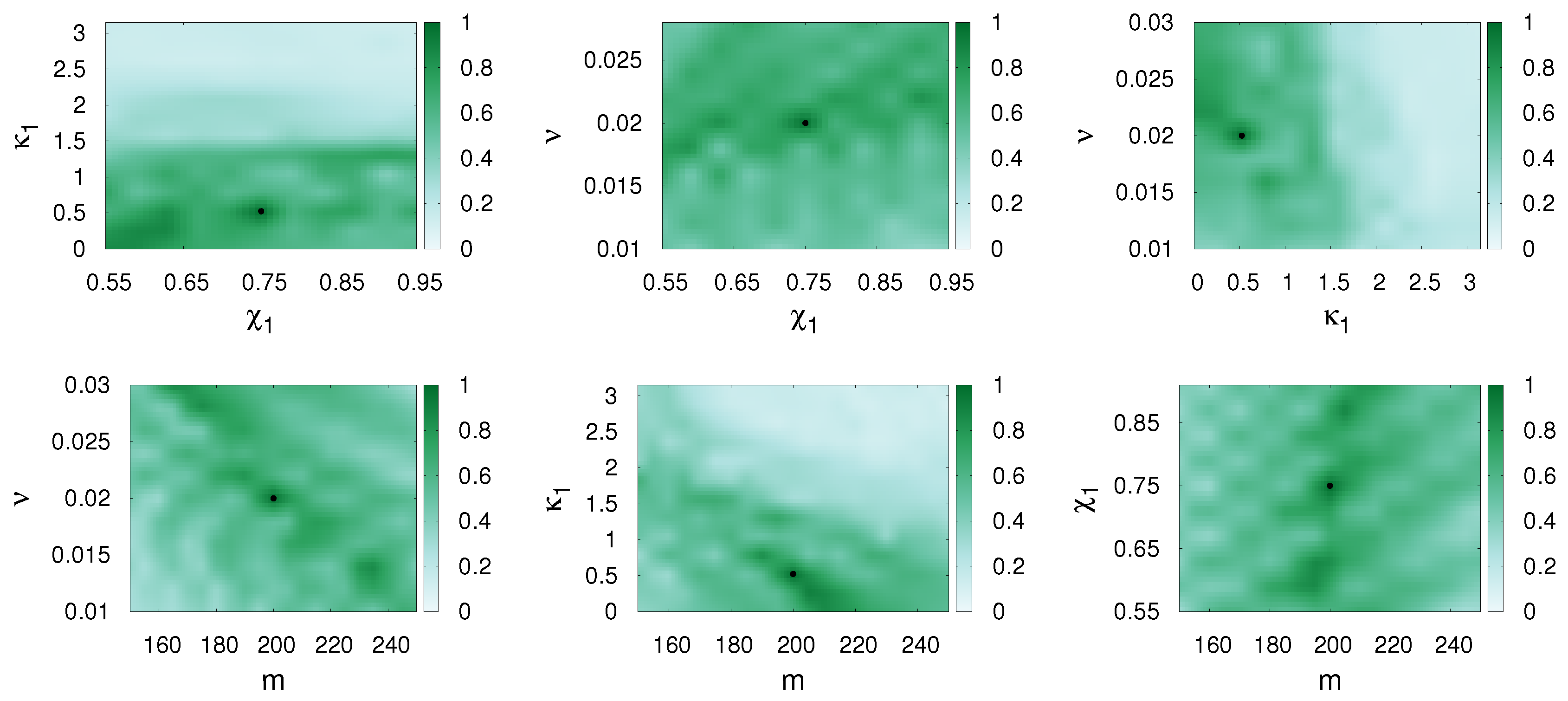
Figure 4.
SpinTaylorT4 is matched with itself and and match values are presented in different parameter planes (, ), (, ), (, ), (, m), (, m) and (, m). The parameters of the first waveform (the template) are varied, while those of the second waveform (the signal, represented by a dot) are fixed as , , and . The other parameters were chosen as Hz, . Spins are precessing in this case.
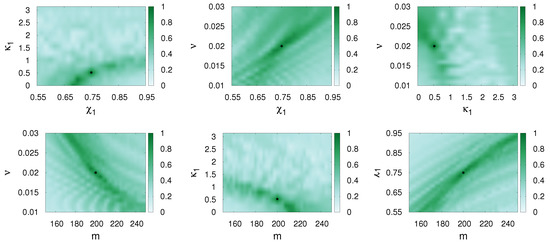
Figure 5.
SEOBNRv3 is matched with itself and and match values are presented in different parameter planes (, ), (, ), (, ), (, m), (, m) and (, m). The parameters of the first waveform (the template) are varied, while those of the second waveform (the signal, represented by a dot) are fixed as , , and . The other parameters were chosen as Hz, . Spins are precessing in this case.
While the match of each waveform with itself is good, showing differences with respect to the aligned case only in the degeneracy patterns, the match between pairs of different waveforms deteriorated severely. The best of them was for SpinTaylorT4 and SpinDominatedWf, represented in Figure 6 with the parameters of the SpinDominatedWf fixed. Compared to the aligned case, the local maxima are spread over a larger region and the global maximum is far from the fixed parameters.
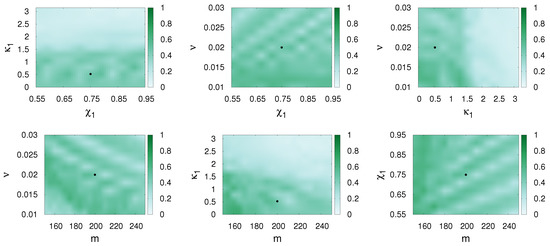
Figure 6.
The match values between SpinTaylorT4 and SpinDominatedWf are presented in the parameter planes (, ), (, ), (, ), (, m), (, m) and (, m). The parameters of the first waveform (the template, SpinTaylorT4) are varied, while those of the second waveform (the signal, SpinDominatedWf, represented by a dot) are fixed as. , , and . The other parameters were chosen as Hz, . Spins are precessing in this case.
3. Conclusions
The match among three waveforms derived in different approximations were investigated in the spin-dominated regime. We calculated the match of the waveforms compared to themselves, with one of the waveforms having fixed parameters, both in the aligned and the precessing cases. For all three waveforms degeneracies appear: several local maxima of also emerge. We also compared the evolutions of the angles , , and implemented in LALSUITE for all three waveform families. For SpinTaylorT4 and SEOBNRv3 we calculated these angles from the available variables.
In the aligned case we calculated the match between each waveform pair. SpinDominatedWf and SpinTaylorT4 match quite well, with values of for the global maximum arising at the fixed parameter values.
However, when either of these two is compared to SEOBNRv3, the global maximum of is shifted noticeably as compared to the parameters of the fixed waveform and its value is reduced to 0.86 and 0.85 for SpinDominatedWf and SpinTaylorT4, respectively. This is expected since the SEOBNRv3 model is fitted to NR waveforms [15], hence the inspiral part will be different from purely analytical waveforms and it also contains the merger and ringdown contributions.
Investigations of the match between waveforms compared to themselves in the precessing case have shown that the local maxima of are closer to the global maximum and they extend over a larger parameter space than in the aligned case, indicating the appearance of additional degeneracies due to the increased parameter space.
Further, the precession heavily deteriorates the matches between any pairs of waveform families. The best of them was between SpinDominatedWf and SpinTaylorT4, with at the global maximum, which occurs at different parameters as compared to where they match best with themselves.
This poor match of the three different waveforms calls for further investigation. We suspect that it can be traced back to (1) different coefficients identified in either being matched to NR results, or identified from PN analytics; (2) differences in the incorporated dynamics, specifically in the level of PN accuracy of their implementation; and (3) differences in the validity of the waveforms, i.e., SpinDominatedWf and SpinTaylorT4 with implemented stopping conditions (having ending frequency of 24 Hz for systems) and until the time of coalescence for SEOBNRv3.
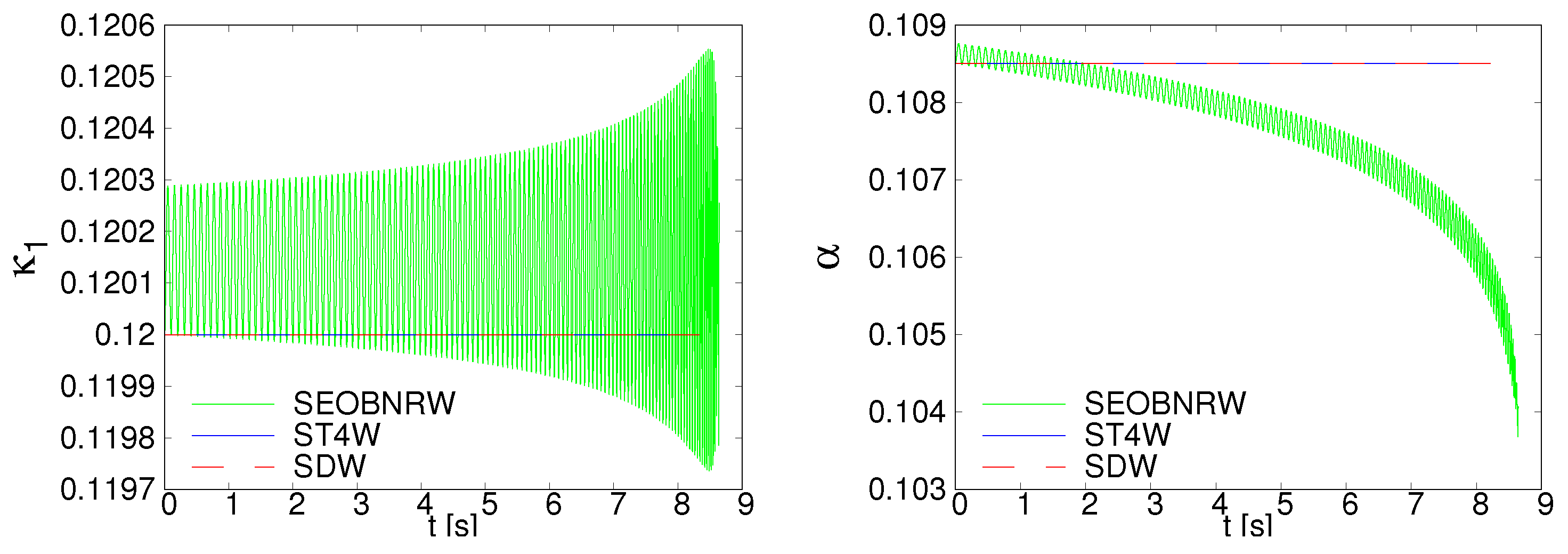
As a first difference we remark that in contrast to SEOBNRv3, the SpinDominatedWf and SpinTaylorT4 explore dynamics averaged over one radial period describing secular effects. This can be seen in Figure 7 presenting the evolutions of the angles and for SEOBNRv3 as compared to their identical constant value in the case of SpinDominatedWf and SpinTaylorT4. The parameters of the system for this figure are as follows: , , , Hz, and . The ending frequency is at 24 Hz for SpinDominatedWf and SpinTaylorT4, while SEOBNRv3 extends until coalescence. The relative changes in and governed by SEOBNRv3 dynamics are of order of 1% and 5%, respectively.
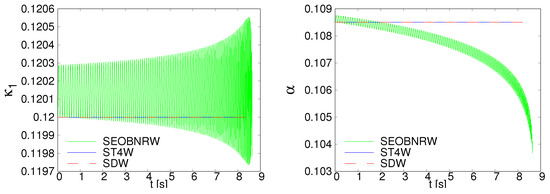
Figure 7.
The evolutions of the angles and for SEOBNRv3 (green), SpinTaylorT4 (blue) and SpinDominatedWf (red).
The evolutions of the orbital phase and the longitude of the ascending node are depicted on Figure 8. A difference of about is accumulated between SpinDominatedWf and SEOBNRv3 at the end of the evolution in the angle , while the respective SpinTaylorT4 evolution runs in between. Similarly, a difference of about appears between the angles of SpinDominatedWf and SpinTaylorT4, with the SEOBNRv3 evolution in between. We traced back the jumps in both angles for SEOBNRv3 to a simultaneous vanishing of the x- and y-components of the orbital angular momentum, leading to a singularity in , indicating a possible coordinate singularity. The evolution equation of the phase (see Equation (3.11) of [34] and Equation (15) of [35]) contains the derivative of the angle . This means that when the precession differs among the waveform families, the phase evolution will be different as well, lowering match values.
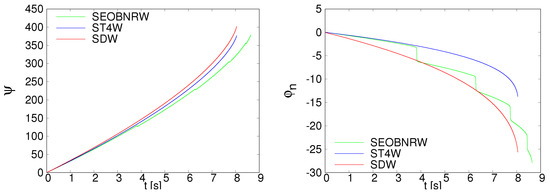
Figure 8.
The evolutions of and are plotted for SEOBNRv3 (green), SpinTaylorT4 (blue) and SpinDominatedWf (red).
The identified differences in the angular dynamics of the three waveform families, including the implementation of radiation reaction to different accuracies are the subject of further investigations meant to improve these waveform families and their match.
Acknowledgments
This work was supported by the Hungarian National Research Development and Innovation Office (NKFI) in the form of the grant 123996. The work of MT was supported by the NTP-NFTÖ-17 National Excellence Program of the Ministry of Human Capacities. The work of ZK was supported by the UNKP-17-4 New National Excellence Program of the Ministry of Human Capacities. MT and ZK were further supported by the European Union, co-financed by the European Social Fund EFOP-3.6.2-16-2017-00005.
Author Contributions
All authors contributed equally to this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Einstein, A. Approximative Integration of the Field Equations of Gravitation. Sitzungsber. K. Preuss. Akad. Wiss. 1916, 1, 688–696. [Google Scholar]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. (The LIGO Scientific Collaboration) Advanced LIGO. Class. Quantum Grav. 2015, 32, 074001. [Google Scholar]
- Acernese, F.; Agathos, M.; Agatsuma, K.; Aisa, D.; Allemandou, N.; Allocca, A.; Amarni, J.; Astone, P.; Balestri, G.; Ballardin, G.; et al. (Virgo Collaboration), Advanced Virgo: A second-generation interferometric gravitational wave detector. Class. Quantum Grav. 2015, 32, 024001. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. (The LIGO Scientific Collaboration, Virgo Collaboration), Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. (The LIGO Scientific Collaboration, Virgo Collaboration), GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. (The LIGO Scientific Collaboration, Virgo Collaboration), Binary Black Hole Mergers in the First Advanced LIGO Observing Run. Phys. Rev. X 2016, 6, 041015. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. (The LIGO Scientific Collaboration, Virgo Collaboration), GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef] [PubMed]
- Abott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. (The LIGO Scientific Collaboration, Virgo Collaboration), GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef] [PubMed]
- Abott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. (The LIGO Scientific Collaboration, Virgo Collaboration), GW170608: Observation of a 19-solar-mass Binary Black Hole Coalescence. arXiv, 2017; arXiv:1711.05578. [Google Scholar]
- Abott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. (The LIGO Scientific Collaboration, Virgo Collaboration), GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Thorne, K.S. Multipole expansions of gravitational radiation. Rev. Mod. Phys. 1980, 52, 299–339. [Google Scholar] [CrossRef]
- Kidder, L.E. Coalescing binary systems of compact objects to (post)5/2-Newtonian order. V. Spin effects. Phys. Rev. D 1995, 52, 821–847. [Google Scholar] [CrossRef]
- Tápai, M.; Keresztes, Z.; Gergely, L.Á. Spin-dominated waveforms for unequal mass compact binaries. Phys. Rev. D 2012, 86, 104045. [Google Scholar] [CrossRef]
- Bounanno, A.; Chen, Y.; Vallisneri, M. Detection template families for gravitational waves from the final stages of binary–black-hole inspirals: Nonspinning case. Phys. Rev. D 2003, 67, 024016. [Google Scholar] [CrossRef]
- Pan, Y.; Buonanno, A.; Taracchini, A.; Kidder, L.E.; Mroué, A.H.; Pfeiffer, H.P.; Scheel, M.A.; Szilágyi, B. Inspiral-merger-ringdown waveforms of spinning, precessing black-hole binaries in the effective-one-body formalism. Phys. Rev. D 2014, 89, 084006. [Google Scholar] [CrossRef]
- Taracchini, A.; Buonanno, A.; Pan, Y.; Hinderer, T.; Boyle, M.; Hemberger, D.A.; Kidder, L.E.; Lovelace, G.; Mroue, A.H.; Pfeiffer, H.P.; et al. Effective-one-body model for black-hole binaries with generic mass ratios and spins. Phys. Rev. D 2014, 89, 061502. [Google Scholar] [CrossRef]
- Buonanno, A.; Iyer, B.R.; Ochsner, E.; Pan, Y.; Sathyaprakash, B.S. Comparison of post-Newtonian templates for compact binary inspiral signals in gravitational-wave detectors. Phys. Rev. D 2009, 80, 084043. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A.; Trias, M. Accuracy and effectualness of closed-form, frequency-domain waveforms for nonspinning black hole binaries. Phys. Rev. D 2011, 83, 024006. [Google Scholar] [CrossRef]
- Campanelli, M.; Lousto, C.O.; Nakano, H.; Zlochower, Y. Comparison of numerical and post-Newtonian waveforms for generic precessing black-hole binaries. Phys. Rev. D 2009, 79, 084010. [Google Scholar] [CrossRef]
- Boyle, M.; Brown, D.A.; Pekowsky, L. Comparison of high-accuracy numerical simulations of black-hole binaries with stationary-phase post-Newtonian template waveforms for initial and advanced LIGO. Class. Quant. Grav. 2009, 26, 114006. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Thierfelder, M.; Brügmann, B. Accuracy of numerical relativity waveforms from binary neutron star mergers and their comparison with post-Newtonian waveforms. Phys. Rev. D 2012, 85, 104030. [Google Scholar] [CrossRef]
- Hinder, I.; Buonanno, A.; Boyle, M.; Etienne, Z.B.; Healy, J.; Johnson-McDaniel, N.K.; Nagar, A.; Nakano, H.; Pan, Y.; Pfeiffer, H.P.; et al. Error-analysis and comparison to analytical models of numerical waveforms produced by the NRAR Collaboration. Class. Quantum Grav. 2014, 31, 025012. [Google Scholar] [CrossRef]
- Kumar, P.; Barkett, K.; Bhagwat, S.; Afshari, N.; Brown, D.A.; Lovelace, G.; Scheel, M.A.; Szilágyi, B. Accuracy and precision of gravitational-wave models of inspiraling neutron star-black hole binaries with spin: Comparison with matter-free numerical relativity in the low-frequency regime. Phys. Rev. D 2015, 92, 102001. [Google Scholar] [CrossRef]
- Ohme, F.; Hannam, M.; Husa, S. Reliability of complete gravitational waveform models for compact binary coalescences. Phys. Rev. D 2011, 84, 064029. [Google Scholar] [CrossRef]
- MacDonald, I.; Nissanke, S.; Pfeiffer, H.P. Suitability of post-Newtonian/numerical-relativity hybrid waveforms for gravitational wave detectors. Class. Quant. Grav. 2011, 28, 134002. [Google Scholar] [CrossRef]
- Boyle, M. Uncertainty in hybrid gravitational waveforms: Optimizing initial orbital frequencies for binary black-hole simulations. Phys. Rev. D 2011, 84, 064013. [Google Scholar] [CrossRef]
- MacDonald, I.; Mroué, A.H.; Pfeiffer, H.P.; Boyle, M.; Kidder, L.E.; Scheel, M.A.; Szilágyi, B.; Taylor, N.W. Suitability of hybrid gravitational waveforms for unequal-mass binaries. Phys. Rev. D 2013, 87, 024009. [Google Scholar] [CrossRef]
- Mikóczi, B.; Vasúth, M.; Gergely, L.Á. Self-interaction spin effects in inspiralling compact binaries. Phys. Rev. D 2005, 71, 124043. [Google Scholar]
- Dal Canton, T.; Nitz, A.H.; Lundgren, A.P.; Nielsen, A.B.; Brown, D.A.; Dent, T.; Harry, I.W.; Krishnan, B.; Miller, A.J.; Wette, K.; et al. Implementing a search for aligned-spin neutron star-black hole systems with advanced ground based gravitational wave detectors. Phys. Rev. D 2014, 90, 082004. [Google Scholar] [CrossRef]
- Usman, S.A.; Nitz, A.H.; Harry, I.W.; Biwer, C.M.; Brown, D.A.; Cabero, M.; Capano, C.D.; Canton, T.D.; Dent, T.; Fairhurst, S.; et al. The PyCBC search for gravitational waves from compact binary coalescence. Class. Quant. Grav. 2016, 33, 215004. [Google Scholar] [CrossRef]
- Nitz, A.; Harry, I.; Brown, D.; Biwer, C.M.; Willis, J.; Canton, T.D.; Pekowsky, L.; Dent, T.; Williamson, A.R.; Capano, C.; et al. ligo-cbc/pycbc: Post-02 Release 3. Available online: https://zenodo.org/record/1058970#.Wp5sUlI4e6c (accessed on 6 March 2018).
- [Virgo Collaboration]. LALSuite. Available online: https://wiki.ligo.org/DASWG/LALSuite (accessed on 15 February 2018).
- [LIGO Collaboration]. Waveforms. Available online: http://pycbc.org/pycbc/latest/html/waveform.html#calculating-the-match-between-waveforms (accessed on 15 February 2018).
- Arun, K.G.; Buonanno, A.; Faye, G.; Ochsner, E. Higher-order spin effects in the amplitude and phase of gravitational waveforms emitted by inspiraling compact binaries: Ready-to-use gravitational waveforms. Phys. Rev. D 2009, 79, 104023. [Google Scholar] [CrossRef]
- Gergely, L.Á. Spinning compact binary inspiral: Independent variables and dynamically preserved spin configurations. Phys. Rev. D 2010, 81, 084025. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).