Study on the Gamma-Ray Radiation Properties of High-Redshift Blazars at z > 2.5

Abstract

The high-redshift blazars are important cosmological probes for exploring the early universe and unraveling the fundamental emission processes and the structure of the active galactic nuclei. The high-energy GeV gamma-ray emissions of 38 high-redshift blazars (z > 2.5) observed by Fermi-LAT were analyzed. Along with the Archive multiwavelength data, we employ one-zone leptonic external Compton (EC) models to reproduce the spectral energy distributions (SEDs) of 38 sources. Both the external photons from the molecular torus (MT) and the broad-line region (BLR) are considered. We obtained the best-fitting parameters for describing the characteristics of the jets and accretion disks. The results indicate that high-redshift blazars exhibit higher $\gamma$-ray luminosities, energy densities, jet powers, kinetic powers, accretion disk luminosities, black hole (BH) masses, radiation efficiencies, and mass accretion rates compared to low-redshift blazars. For high-redshift blazars, the influence of the accretion rate on jet power appears to weaken, and in most cases, the jet power exceeds the total accretion power. We speculate that for high-redshift blazars, rapid accretion may lead to magnetic field saturation, thereby reducing the effectiveness of the Blandford–Payne (BP) process. Consequently, the Blandford–Znajek (BZ) process is likely to play a more dominant role in powering jets in high-redshift blazars compared to low-redshift blazars. Naturally, we acknowledge that selection effects cannot be fully eliminated.

1. Introduction

Blazars are a subclass of active galactic nuclei (AGNs). They have a relativistic jet oriented at a small angle with respect to the line of sight [1]. Relativistic jets are typically powered by either the Blandford–Payne (BP) or Blandford–Znajek (BZ) mechanism [2,3], both of which rely on magnetic fields sustained by the accretion flow, making them ideal laboratories to study the accretion/ejection phenomena. Based on the absence or presence of broad emission lines, blazars are divided into two subclasses: BL Lacertae objects and flat-spectrum radio quasars (FSRQs) [4]. BL Lacertae objects exhibit weak or undetected emission lines, while FSRQs display prominent emission lines.

Blazar spectral energy distributions (SEDs) span from radio to $\gamma$-ray bands, exhibiting a double-peaked structure: a low-energy (LE) peak between infrared (IR) and X-rays, and a high-energy (HE) peak at MeV–TeV $\gamma$-rays. The LE component is generally attributed to synchrotron radiation from highly relativistic electrons in the jet [5,6], while the HE component is thought to result from inverse Compton (IC) scattering, either via synchrotron self-Compton (SSC) (e.g., [7,8]) or external Compton (EC) processes. In BL Lacertae objects, SSC dominates the $\gamma$-ray emission, whereas EC is more important in FSRQs. The source of external photons is debated, with likely candidates being IR emission from the molecular torus (MT) (e.g., [9]) or optical emission from the broad-line region (BLR) (e.g., [10,11,12]).

Increasing amounts of phenomenological evidence suggest that blazars at different redshifts exhibit significantly distinct radiative properties [13,14]. The high-redshift blazars typically show flat or increasing X-ray spectra, especially in the hard X-ray band, have soft $\gamma$-ray spectral indices, and possess $\gamma$-ray luminosities ∼${10}^{48}\mathrm{ergs}{\mathrm{s}}^{-1}$ [15], and Sahakyan et al. [16] even reported jet powers as high as ${10}^{50}\mathrm{ergs}{\mathrm{s}}^{-1}$. The BH masses and accretion disk luminosities of high-redshift blazars can reach maximum values of ∼${10}^9{M}_{\odot }$ and ∼${10}^{46}\mathrm{ergs}{\mathrm{s}}^{-1}$, respectively (e.g., [15,17,18,19,20,21]). In hadronic processes, involving protons may also contribute [22,23,24]. But hadronic cascades tend to overproduce hard X-rays/MeV emission [25], while the observed GeV emission is well reproduced by IC scattering with reasonable parameters. We therefore adopt a leptonic framework in this work.

High-redshift AGN BHs are believed to possess abundant accretable gas, making them more luminous than low-redshift blazars [26] and able to produce powerful jets [27]. Their prominent emission lines may originate from various sources, including the jet, hot accretion flows, disk structures, or cold clumps within the hot flow [28,29,30,31,32,33]. These distant and powerful objects help us understand the physics of relativistic jets and the accretion disk–jet connection in the high-redshift AGNs [34,35].

This connection may differ from that seen in low-redshift blazars. Observational studies have revealed a variety of correlations between jet properties and accretion across different AGN subclasses [36,37,38,39,40]. However, these correlations are generally considered to be redshift-independent, and it remains uncertain whether they evolve with redshift. Therefore, a more focused analysis of accretion and jet connection in high-redshift samples is necessary.

Our primary motivation is to investigate the HE radiation properties of high-redshift blazars through multi-frequency data analysis and theoretical SED modeling, with a particular emphasis on the disk–jet connection. Due to their large distances, high-redshift blazars often have poor observational quality, which causes substantial uncertainties in individual SED fits. To address this, we use average SEDs constructed from 38 blazars, and avoid the limitations of a single blazar.

The rest of the paper is organized as follows. In Section 2, we present the data reduction of the $\gamma$-ray observations and describe the SEDs’ observational characteristics. In Section 3, we provide our theoretical modeling of the broadband SEDs and their results. In Section 4, we conduct an in-depth analysis of the possible physical processes that may be responsible for their high-energy emissions. Throughout this paper, we adopt a flat cosmological model with ${\mathrm{H}}_0=70.5\mathrm{km}{\mathrm{s}}^{-1}{\mathrm{Mpc}}^{-1}$, ${\Omega }_{\mathrm{m}}=0.27$, and ${\Omega }_{\Lambda }=0.73$.

2. High-Energy Emission of High-Redshift Blazars

2.1. Sample and Data Reduction

The HE observations are based on the Fourth Catalog of AGNs Detected by the Fermi-LAT (4LAC-DR3), which reports 117 blazars with redshifts $z>2$ and only 38 with redshifts $z>2.5$ [41].

These 38 high-redshift blazars were selected as our sample. The BH masses are observationally inferred from optical/UV spectroscopy, primarily based on reverberation-mapping calibrations using broad emission lines such as C IV and Mg II. Although host–galaxy scaling relations are also reported, they generally yield only upper limits and are not reliable for individual sources. Therefore, we adopt the BH masses derived from reverberation-mapping throughout this work. Among them, seven blazars lack reliable measurements of BH mass, synchrotron and inverse Compton peak frequency or flux, and accretion disk luminosity. For these objects, the missing values were replaced with the average of the corresponding quantities from the rest of the sample. These average values were used solely for estimating environmental parameters and the Eddington luminosity, and do not affect any subsequent analyses. Detailed information is listed in Table 1.

Table 1. Observations and Environmental Parameters of 38 High-redshift Blazars.

Fermi Name	Source Name	R.A.	Dec.	$log{\mathit{\nu }}_{\mathit{syn}}$	$log\mathit{\nu }{\mathit{F}}_{\mathit{syn}}$	$log{\mathit{\nu }}_{\mathit{IC}}$	$log\mathit{\nu }{\mathit{F}}_{\mathit{IC}}$	$log{\mathit{M}}_{\mathit{BH}}$	$log{\mathit{L}}_{\mathit{disk}}$	${\mathit{R}}_{\mathbf{BLR}}$	${\mathit{R}}_{\mathbf{MT}}$	${\mathit{L}}_{\mathit{Edd}}$	z
				Hz	$\mathrm{erg}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}$	Hz	$\mathrm{erg}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}$	${\mathrm{M}}_{\odot }$	$\mathrm{erg}{\mathrm{s}}^{-1}$	$\times {\mathbf{10}}^{\mathbf{17}}$ (cm)	$\times {\mathbf{10}}^{\mathbf{19}}$ (cm)	$\times {\mathbf{10}}^{\mathbf{47}}$ (erg s−1)
J1510.1+5702	GB 1508+5714	227.54	57.04	12.07	−12.21	20.65	−11.72	8.56	46.80	7.94	1.99	0.46	4.314
J1354.3-0206	PKS 1351-018	208.60	−2.11	11.99	−12.37	20.84	−11.28	9.06	46.50	5.62	1.41	1.45	3.716
J1635.6-3628	MG3 J163554+3629	248.92	36.48	13.22	−12.88	21.60	−11.82	9.08	46.25	4.22	1.05	1.51	3.648
J1219.0+3653	NVSS J121915+365718	184.77	36.89	$12.49$ *	−$12.34$ *	$21.20$ *	−$11.41$ *	$9.13$ *	$46.43$ *	$5.19$ *	$1.30$ *	$1.70$ *	3.528
J0833.4-0458	PMN J0833-0454	128.37	−4.97	12.80	−12.62	21.12	−11.82	9.77	47.17	12.20	3.04	7.42	3.450
J0337.8-1157	PKS 0335-122	54.47	−11.96	12.37	−12.53	21.64	−12.14	8.99	46.21	4.03	1.01	1.23	3.442
J2320.8-0823	PKS 2318-087	350.22	−8.39	12.76	−12.99	20.65	−11.69	9.47	46.48	5.50	1.37	3.72	3.164
J0539.9-2839	PKS 0537-286	84.99	−28.66	11.99	−11.99	20.76	−10.64	10.12	47.04	10.50	2.62	16.61	3.104
J0805.4+6147	TXS 0800+618	121.36	61.79	12.20	−12.24	20.84	−10.80	9.47	46.69	7.00	1.75	3.72	3.033
J1428.9+5406	S4 1427+543	217.23	54.11	12.38	−12.64	21.00	−11.87	9.33	46.19	3.94	0.98	2.69	3.013
J0733.8+0455	GB6 J0733+0456	113.47	4.93	$12.49$ *	−$12.34$ *	$21.20$ *	−$11.41$ *	$9.13$ *	$46.43$ *	$5.19$ *	$1.30$ *	$1.70$ *	3.010
J0746.4+2546	B2 0743+25	116.60	25.77	12.26	−12.31	20.45	−10.60	9.37	46.61	6.38	1.60	2.95	2.987
J0349.8-2103	PKS 0347-211	57.47	−21.06	$12.49$ *	−$12.34$ *	$21.20$ *	−$11.41$ *	$9.13$ *	$46.43$ *	$5.19$ *	$1.30$ *	$1.70$ *	2.944
J1127.4+5648	S4 1124+57	171.86	56.80	12.17	−12.64	20.95	−11.67	8.72	46.80	7.94	1.99	0.66	2.893
J2313.9-4501	PKS 2311-452	348.49	−45.02	12.08	−12.50	20.48	−11.82	8.76	46.25	4.22	1.05	0.73	2.884
J0440.3-4332	PKS 0438-43	70.09	−43.55	11.66	−12.11	20.50	−11.70	9.41	46.59	6.24	1.56	3.24	2.863
J2015.4+6556	S4 2015+65	303.86	65.95	12.59	−12.23	20.75	−11.75	8.82	46.47	5.43	1.36	0.83	2.845
J2145.5+1006	87GB 214302.1+095227	326.38	10.12	$12.49$ *	$-12.34$ *	$21.20$ *	$-11.41$ *	$9.13$ *	$46.43$ *	$5.19$ *	$1.30$ *	$1.70$ *	2.826
J1748.0+3403	MG2 J174803+3403	267.01	34.06	$12.49$ *	−$12.34$ *	$21.20$ *	−$11.41$ *	$9.13$ *	$46.43$ *	$5.19$ *	$1.30$ *	$1.70$ *	2.763
J0836.5-2026	PKS 0834-20	129.13	−20.45	11.90	−11.90	20.85	−10.89	9.48	46.53	5.82	1.46	3.81	2.752
J0224.9+1843	TXS 0222+185	36.23	18.72	12.56	−12.15	20.08	−10.78	9.66	46.73	7.33	1.83	5.76	2.690
J0539.6+1432	TXS 0536+145	84.91	14.54	12.44	−11.94	21.63	−11.33	10.01	46.14	3.72	0.93	12.89	2.690
J0242.3+1102	OD 166	40.6	11.05	12.45	−11.89	21.18	−11.44	8.81	46.77	7.67	1.92	0.81	2.680
J2339.6+0242	CRATES J233930+024420	354.90	2.71	13.09	−12.53	21.38	−11.12	9.05	46.19	3.94	0.98	1.41	2.666
J0910.6+2247	TXS 0907+230	137.67	22.80	12.62	−12.24	21.64	−11.34	8.30	45.93	2.92	0.73	0.25	2.661
J1441.6-1522	PMN J1441-1523	220.41	−15.38	13.00	−12.43	22.28	−11.46	8.39	46.38	4.90	1.22	0.31	2.638
J1054.2+3926	CRATES J105433+392803	163.56	39.43	12.60	−12.98	22.52	−12.38	8.59	45.78	2.45	0.61	0.49	2.634
J1549.6+1710	MG1 J154930+1708	237.41	17.18	$12.49$ *	−$12.34$ *	$21.20$ *	−$11.41$ *	$9.13$ *	$46.43$ *	$5.19$ *	$1.30$ *	$1.70$ *	2.625
J1450.4+0910	TXS 1448+093	222.62	9.18	12.97	−12.13	21.60	−11.83	9.15	46.33	4.62	1.16	1.78	2.611
J0226.5+0938	NVSS J022634+093843	36.63	9.64	13.05	−12.10	22.06	−11.57	10.09	46.61	6.38	1.60	15.50	2.605
J1628.8-6149	LQAC 247-061	247.22	−61.83	11.96	−12.12	21.21	−10.80	9.23	46.04	3.31	0.83	2.14	2.578
J0453.1-2806	PKS 0451-28	73.29	−28.11	12.50	−11.44	20.95	−10.53	9.21	46.88	8.71	2.18	2.04	2.564
J0912.2+4127	B3 0908+416B	138.06	41.46	12.77	−12.23	21.69	−11.58	9.42	45.85	2.66	0.67	3.31	2.563
J1618.0+5139	TXS 1616+517	244.52	51.67	13.60	−12.84	21.27	−11.45	8.78	46.21	4.03	1.01	0.76	2.556
J1625.7+4134	4C+41.32	246.45	41.57	12.03	−12.36	21.21	−11.48	7.85	45.94	2.95	0.74	0.09	2.550
J1345.5+4453	B3 1343+451	206.39	44.88	12.73	−12.59	22.24	−10.84	9.06	46.06	3.39	0.85	1.45	2.534
J1833.6-2103	PKS 1830-211	278.41	−21.06	$12.49$ *	−$12.34$ *	$21.20$ *	−$11.41$ *	$9.13$ *	$46.43$ *	$5.19$ *	$1.30$ *	$1.70$ *	2.507
J2110.2-1021	PKS 2107-105	317.56	−10.36	12.35	−12.27	21.10	−11.54	9.04	46.99	9.89	2.47	1.38	2.500

The observations and environmental parameters are presented in columns 5–14, which include the peak frequency and peak flux of synchrotron radiation and IC scattering, BH mass, accretion disk luminosity, radius of the BLR, inner radius of the MT, Eddington luminosity, and redshift, respectively [42,43]. The BLR and MT are located at distances of $R_{\mathrm{BLR}}\simeq {10}^{17}\sqrt{L_{\mathrm{disk}}/{10}^{45}\mathrm{erg}{\mathrm{s}}^{-1}}$ cm and $R_{\mathrm{MT}}\simeq 2.5\times {10}^{18}\sqrt{L_{\mathrm{disk}}/{10}^{45}\mathrm{erg}{\mathrm{s}}^{-1}}$ cm, respectively [44]. $L_{\mathrm{Edd}}={\displaystyle \frac{4\pi GM{m}_{p}c}{{\sigma }_T}}\approx 1.26\times {10}^{38}\left({\displaystyle \frac{M}{M_{\odot }}}\right)\mathrm{erg}{\mathrm{s}}^{-1}$. Due to missing data, we filled in the gaps using the sample average and marked these values with an asterisk (*).

The sample data, which span from 2008 August 4 to 2025 March 1 (MJD 54,686–60,739), were analyzed using Fermi ScienceTools version 2.0.8 and the P8R3_SOURCE_V3 instrument response function. Data were focused on a 15° radius region of interest (ROI) centered on each sample’s $\gamma$-ray position, within the 100 MeV–500 GeV energy range. High-probability photon events (evclass = 128 and evtype = 3) were selected with the gtselect tool.

A 90° zenith angle cut was applied to minimize contamination from the Earth’s limb. Data were further filtered to include only intervals with good satellite operation and quality, using the gtmktime filter expression (DATA_QUAL>0) && (LAT_CONFIG==1).

The binned data were prepared using the gtbin tool, which allowed for binning the data in the spatial, spectral, and temporal dimensions. A live time cube, which is required for accurate exposure calculations, was created with the gtltcube tool, accounting for variations in the effective area over the entire sky. A likelihood analysis was then performed with the gtlike tool to determine the best-fit spectral parameters of each source.

A model file containing spectral parameters was created using the make4FGLxml.py script based on the 4FGL catalog, covering the user-defined ROI plus an additional 10 degrees. In the likelihood fit, parameters for sources outside the ROI were fixed, while those within the ROI were allowed to vary. Galactic and extragalactic diffuse $\gamma$-ray emissions were modeled using gll_iem_v07.fits and iso_P8R3_SOURCE_V3_v1.txt, respectively. Note that the data used were not corrected for extragalactic background light (EBL) absorption.

2.2. High-Energy Spectra

Two spectral models were applied to analyze the $\gamma$-ray spectral shapes. The first is a simple power law (PL):

$$dN/dE=N_0{\left({\displaystyle \frac{E}{E_0}}\right)}^{-\alpha },$$

(1)

where $N_0$ is the photon number density, $E_0$ is the scale energy and $\alpha$ is the PL index.

The second form is a log-parabola (LP):

$$dN/dE=N_0{\left({\displaystyle \frac{E}{E_0}}\right)}^{-\alpha -\beta log(E/E_0)},$$

(2)

where $\beta$ is the curvature index that describes the curvature around the peak. In our global analysis, the value of $E_0$ is set to a fixed value given by FermiTools.

The last comprehensive multiwavelength study of high-redshift blazars dates back to 2018 [15]. Given that many of these sources may have undergone new flares in the past seven years, an updated analysis is both timely and necessary. We recalculated spectral parameters and fluxes based on the best-fitting spectral models provided in the 4LAC-DR3 catalog [41]. Table 2 presents the best-fit results for the 38 high-redshift blazars. The photon indices are generally soft ($>2$), with the hardest and softest values being $1.65\pm 0.13$ and $3.29\pm 0.35$, respectively. The integrated $\gamma$-ray fluxes (above 0.1 GeV) range from 0.40 to 713.33 $\times \hspace{0.17em}{10}^{-9}\mathrm{ph}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}$. The highest integrated flux is observed for PKS 1830-211, primarily due to a major outburst in 2019 [45,46], but it is strongly affected by gravitational lensing and has therefore been excluded from our final sample. A few blazars exhibit fluxes exceeding those reported by Sahakyan et al. [15], Ajello et al. [41], which is consistent with their high variability1.

Table 2. Best-fitting results of 38 high-redshift blazars.

Fermi Name	${\mathbf{F}}_{0.1–500\mathbf{GeV}}$	${\mathit{\alpha }}_{\mathbf{PL}}$	${\mathit{\alpha }}_{\mathbf{LP}}$	$\mathit{\beta }$	${\mathbf{E}}_{\mathbf{c}}$	$\mathbf{TS}$	Class
	${10}^{-9}\mathrm{ph}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}$				MeV
J1510.1+5702	$13.91\pm 1.49$	−	$2.97\pm 0.07$	$-\mathbf{0.08}\pm \mathbf{0.53}$	524	391	FSRQ
J1354.3-0206	$5.51\pm 1.96$	−	$2.63\pm 0.19$	$3.13\pm 2.48$	577	75	FSRQ
J1635.6-3628	$11.88\pm 2.04$	$2.91\pm 0.12$	−	−	938	156	FSRQ
J1219.0+3653	$0.40\pm 0.20$	−	$2.07\pm 0.27$	$4.77\pm 2.33$	1950	50	BLL
J0833.4-0458	$0.69\pm 0.22$	−	$1.81\pm 0.24$	$6.28\pm 1.95$	1605	130	FSRQ
J0337.8-1157	$5.68\pm 1.77$	$2.70\pm 0.17$	−	−	978	51	FSRQ
J2320.8-0823	$3.17\pm 1.43$	−	$2.62\pm 0.24$	$2.06\pm 1.46$	786	36	FSRQ
J0539.9-2839	$57.18\pm 1.58$	−	$2.71\pm 0.02$	$0.89\pm 0.17$	426	5246	FSRQ
J0805.4+6147	$15.04\pm 1.43$	−	$2.91\pm 0.07$	$\mathbf{0.58}\pm \mathbf{0.59}$	523	366	FSRQ
J1428.9+5406	$3.40\pm 1.00$	$2.45\pm 0.13$	−	−	1078	75	FSRQ
J0733.8+0455	$5.64\pm 1.52$	−	$2.33\pm 0.12$	$0.97\pm 0.71$	787	133	FSRQ
J0746.4+2546	$22.98\pm 1.84$	−	$3.02\pm 0.07$	$1.35\pm 0.72$	437	480	FSRQ
J0349.8-2103	$25.02\pm 1.51$	−	$2.47\pm 0.04$	$1.10\pm 0.28$	504	1704	FSRQ
J1127.4+5648	$9.31\pm 1.24$	−	$2.56\pm 0.08$	$0.74\pm 0.52$	567	418	FSRQ
J2313.9-4501	$2.68\pm 1.10$	−	$3.29\pm 0.35$	$10.46\pm 4.53$	814	97	BCU
J0440.3-4332	$76.97\pm 2.49$	−	$2.64\pm 0.02$	$1.22\pm 0.15$	601	10,430	FSRQ
J2015.4+6556	$4.41\pm 2.42$	$2.62\pm 0.26$	−	−	1249	28	FSRQ
J2145.5+1006	$0.53\pm 0.23$	$1.65\pm 0.13$	−	−	7893	76	BLL
J1748.0+3403	$2.20\pm 0.71$	−	$1.90\pm 0.14$	$2.01\pm 0.77$	1160	258	FSRQ
J0836.5-2026	$15.49\pm 1.88$	−	$3.09\pm 0.12$	$\mathbf{0.22}\pm \mathbf{0.93}$	326	168	FSRQ
J0224.9+1843	$11.51\pm 1.77$	$3.01\pm 0.13$	−	−	293	77	FSRQ
J0539.6+1432	$20.40\pm 2.98$	−	$2.53\pm 0.07$	$0.91\pm 0.47$	722	323	FSRQ
J0242.3+1102	$21.26\pm 2.21$	−	$2.52\pm 0.06$	$1.83\pm 0.49$	560	702	FSRQ
J2339.6+0242	$2.88\pm 1.34$	−	$2.49\pm 0.16$	$3.93\pm 1.82$	1333	133	BCU
J0910.6+2247	$13.99\pm 1.27$	$2.55\pm 0.05$	−	−	963	398	FSRQ
J1441.6-1522	$3.38\pm 1.92$	−	$2.37\pm 0.16$	$1.58\pm 1.00$	2192	91	FSRQ
J1054.2+3926	$3.28\pm 1.17$	$2.52\pm 0.16$	−	−	1011	44	BCU
J1549.6+1710	$1.07\pm 0.63$	$2.01\pm 0.18$	−	−	3904	40	BLL
J1450.4+0910	$6.99\pm 1.40$	−	$2.27\pm 0.08$	$1.97\pm 0.64$	1074	480	FSRQ
J0226.5+0938	$3.45\pm 0.96$	$2.22\pm 0.11$	−	−	1992	78	FSRQ
J1628.8-6149	$26.54\pm 0.44$	−	$2.82\pm 0.01$	$1.92\pm 0.03$	1050	630	FSRQ
J0453.1-2806	$52.01\pm 1.64$	−	$2.57\pm 0.03$	$0.97\pm 0.19$	341	5157	FSRQ
J0912.2+4127	$15.46\pm 1.35$	$2.54\pm 0.05$	−	−	884	703	FSRQ
J1618.0+5139	$8.36\pm 1.28$	$3.14\pm 0.18$	−	−	598	110	FSRQ
J1625.7+4134	$5.94\pm 1.04$	−	$2.27\pm 0.10$	$2.52\pm 0.73$	637	408	FSRQ
J1345.5+4453	$115.54\pm 1.34$	−	$2.24\pm 0.01$	$0.57\pm 0.05$	535	45,448	FSRQ
J1833.6-2103	$713.33\pm 1.52$	−	$2.48\pm 0.001$	$0.96\pm 0.007$	698	124,150	FSRQ
J2110.2-1021	$11.14\pm 1.61$	$2.82\pm 0.11$	−	−	780	99	FSRQ

Column 2 is the global $\gamma$-ray flux. Columns 3–6 are the fitting parameters for each of the two models. Column 7 is the statistical test value. Column 8 provides the subclass of blazars, BLL denotes BL Lacertae objects, and BCU denotes blazar candidates of unknown types. Unavailable parameters are denoted by “-”. When the error of the fitted value is greater than the magnitude of the original data, it is considered an inaccurate parameter and is marked in bold. The source J1833.6–2103 is strongly affected by gravitational lensing, which introduces large uncertainties in its intrinsic luminosity; it has therefore been excluded from the final sample.

We find that the constraints on spectral curvature are generally weak, likely due to the absence of state separation between quiescent and flaring states2. This mixing can cause deviations from standard spectral distribution models, resulting in anomalous parameter values, which we have been explicitly flagged as potentially unreliable.

For each SED data point, the spectral curvature can be neglected due to the narrow width of the corresponding energy bin, and the flux is thus estimated using a simple power-law model. We set $E_0=1$ GeV and $\alpha =2$ in each energy bin, and calculate the flux at each point based on the $N_0$ obtained from the data. Finally, we compile the $\gamma$-ray SEDs for all 38 sources, which serve as the basis for the subsequent evaluation.

3. Broadband Spectral Energy Distribution Modeling

3.1. Modeling the Broadband Emission

To construct broadband SEDs covering the infrared to $\gamma$-ray bands, we collected multiwavelength data using the Space Science Data Center (SSDC) Sky Explorer3. Because the X-ray band can be contaminated by the corona, we do not use it to constrain jet power; where X-ray data are unavailable or unreliable, this choice avoids introducing additional bias. Jet power is instead derived primarily from the $\gamma$-ray SED [47]. In contrast, the $\gamma$-ray band provides a cleaner probe of the jet emission and is thus primarily used to constrain the model. We adopted a standard one-zone leptonic model for the SED modeling. Hereafter, physical quantities with a prime (′) are measured in the comoving frame of the jet, while unprimed quantities refer to the stationary frame of the AGN.

We assume that within the jet, there is a plasma blob with radius $R^{\prime }$ moving along the jet axis with a bulk Lorentz factor $\Gamma$, taken to be approximately equal to the Doppler factor ${\delta }_{\mathrm{D}}$. Inside the blob, there is an isotropic magnetic field of strength $B^{\prime }$. Relativistic electrons are described by a steady-state electron energy distribution (EED), $N_{\mathrm{e}}^{\prime }\left({\gamma }^{\prime }\right)$. Due to the clear deviation of the $\gamma$-ray spectra from a simple PL model, it is likely that the EED has some curvature, which can be modelled with an LP:

$$N_{\mathrm{e}}^{\prime }\left({\gamma }^{\prime }\right)=N_{\mathrm{pk}}^{\prime }{\left({\displaystyle \frac{{\gamma }^{\prime }}{{\gamma }_{\mathrm{pk}}^{\prime }}}\right)}^{-s-rlog({\gamma }^{\prime }/{\gamma }_{\mathrm{pk}}^{\prime })},$$

(3)

where $N_{\mathrm{pk}}^{\prime }$ is the normalization constant at the peak Lorentz factor ${\gamma }_{\mathrm{pk}}^{\prime }$, and s and r are the spectral index and curvature parameter, respectively, which could be indicative of stochastic acceleration of electrons in the jet (e.g., [48,49]). To maintain charge neutrality, we assume the presence of protons that are nearly stationary in the comoving frame. These “cold protons” contribute to the kinetic energy of the jet but do not contribute to its nonthermal radiation. We assume a pure $e^{-}-p$ plasma (zero pair content), and the number density of cold protons is assumed to be 1 times that of the electrons.

We assume an accretion efficiency of $\eta =0.1$, which represents a commonly adopted average value [50,51,52], and the accretion disk is modeled as a geometrically thin, optically thick Shakura–Sunyaev disk [53,54]. It extends from the inner radius $R_{\mathrm{in},\mathrm{d}}=3R_{\mathrm{s}}$ to the outer radius $R_{\mathrm{out},\mathrm{d}}={10}^3{R}_{\mathrm{s}}$, where $R_{\mathrm{s}}\equiv 2G{M}_{\mathrm{BH}}/c^2$ is the Schwarzschild radius and G is the gravitational constant. For additional observational and environmental parameters, see Table 1.

The spectra of the BLR and MT are approximated as isotropic blackbodies peaking at energies corresponding to ∼$10.2$ eV and $3.93k_{\mathrm{B}}{T}_{\mathrm{MT}}$, respectively, where $k_{\mathrm{B}}$ is the Boltzmann constant and $T_{\mathrm{MT}}$ is the characteristic temperature of the MT. The BLR photon energy is based on the strong Ly$\alpha$ line commonly observed in blazars. We assume $T_{\mathrm{MT}}={10}^3$ K for the MT radiation. The fractions of accretion disk luminosity reprocessed by the BLR and MT are adopted as ${\tau }_{\mathrm{BLR}}=0.1$ and ${\tau }_{\mathrm{MT}}=0.2$, respectively.

To determine the appropriate location of the radiation region, we consider potential external photon sources. We assume the dissipation region, $R_{\mathrm{diss}}$, is located near either the BLR or the MT, and we model the emission using the standard one-zone leptonic scenario proposed by Tramacere et al. [49], Jones [55], Dermer and Schlickeiser [56]. For high-redshift blazars, the interaction between HE photons and the EBL can be significant. We account for this by converting the intrinsic $\gamma$-ray flux to observed flux using the EBL model from Finke et al. [57].

As our SEDs are constructed from archival data spanning over a decade, they inevitably blend quiescent and flaring states. Therefore, the fitted SEDs represent time-averaged spectra, the main physical trends remain consistent. Motivated by two considerations, we preprocessed the archival data by adding a 20% fractional systematic uncertainty4: (1) the measurements are not strictly simultaneous; and (2) IR–UV data often have very small or unreported errors relative to the high-energy bands, which could bias the minimizer toward the low-frequency branch.

The LE peak is assumed to be dominated by synchrotron radiation, while the HE peak is primarily due to IC scattering. The seed photons for IC scattering originate from three sources: (1) reprocessed emission from the BLR in the optical–UV range, (2) reprocessed IR emission from the MT, and (3) synchrotron photons produced within the jet [58]. The radio band, which is thought to originate from a larger region outside the jet, is excluded from the fit [59]. Finally, we fit the SEDs from IR to $\gamma$-rays (${10}^{12}$–${10}^{25}$ Hz).

The dissipation region, $R_{\mathrm{diss}}$, is constrained to be near either $R_{\mathrm{BLR}}$ or $R_{\mathrm{MT}}$. In the pre-fit stage, we input ${\nu }_{\mathrm{syn}/\mathrm{IC}}$ and $\nu F_{\mathrm{syn}/\mathrm{IC}}$ values as initial guesses to generate reasonable starting parameters. These inputs are not fixed in the formal MCMC stage. Thus, they do not influence the formal posterior distributions or derived physical quantities. Seven free parameters are included in the formal fit: $N_{\mathrm{pk}}^{\prime }$, s, r, ${\delta }_{\mathrm{D}}$, ${\gamma }_{\mathrm{pk}}^{\prime }$, $B^{\prime }$, and $R^{\prime }$. The SEDs are derived from theoretical modeling, calculated using the publicly available JetSet package [48,49,60], and the parameters are optimized using the emcee sampler [61].

3.2. Spectral Energy Distribution Modeling Results

We collect the peak frequency and peak flux of the synchrotron and IC bumps from Chen et al. [42], Abdollahi et al. [62], while the BH masses and disk luminosities are taken from Xiao et al. [63]. We fix all parameters adopted from Table 1 and leave seven parameters free ($N_{\mathrm{pk}}^{\prime }$, s, r, ${\delta }_{\mathrm{D}}$, ${\gamma }_{\mathrm{pk}}^{\prime }$, $B^{\prime }$, and $R^{\prime }$). We then use the emcee sampler to estimate their posterior uncertainties within physically plausible bounds. The best-fit values and their $1\sigma$ errors are summarized in Table 3 and Table 4.

Table 3. Parameters Obtained from the Modeling by MT.

Fermi Name	$log{\mathbf{N}}_{\mathbf{pk}}^{\prime }$	s	r	${\mathit{\delta }}_{\mathbf{D}}$	$log{\mathit{\gamma }}_{\mathbf{pk}}^{\prime }$	${\mathit{B}}^{\prime }$	$log{\mathbf{R}}^{\prime }$	$log{\mathbf{P}}_{\mathbf{e}}$	$log{\mathbf{P}}_{\mathbf{B}}$	$log{\mathbf{P}}_{\mathbf{p}}$	$log{\mathbf{P}}_{\mathbf{r}}$	$log{\mathbf{P}}_{\mathbf{jet}}$	$log\mathbf{CD}$	${\mathit{\chi }}^2$
	(1/cm3)					(G)	(cm)	(erg s−1)	(erg s−1)	(erg s−1)	(erg s−1)	(erg s−1)
J1510.1+5702	${1.73}_{-0.09}^{+0.08}$	${1.50}_{-0.13}^{+0.12}$	${0.44}_{-0.04}^{+0.04}$	${40.40}_{-3.22}^{+3.21}$	${0.54}_{-0.09}^{+0.08}$	${0.20}_{-0.02}^{+0.02}$	${17.56}_{-0.06}^{+0.05}$	$45.78\pm 1.03$	$46.49\pm 3.55$	$48.21\pm 1.03$	$44.79\pm 1.01$	$48.22\pm 3.55$	$-0.71$	$7.28$
J1354.3-0206	${2.62}_{-0.05}^{+0.05}$	${6.55}_{-0.15}^{+0.15}$	${0.28}_{-0.01}^{+0.01}$	${63.90}_{-3.22}^{+2.91}$	${8.34}_{-0.05}^{+0.05}$	${0.43}_{-0.03}^{+0.03}$	${16.99}_{-0.03}^{+0.03}$	$45.62\pm 0.98$	$46.43\pm 3.20$	$48.35\pm 0.98$	$44.12\pm 0.97$	$48.36\pm 3.20$	$-0.81$	$1.14$
J1635.6-3628	${2.57}_{-0.08}^{+0.08}$	${1.36}_{-0.14}^{+0.11}$	${0.47}_{-0.03}^{+0.04}$	${36.30}_{-3.06}^{+2.70}$	${0.69}_{-0.08}^{+0.07}$	${0.22}_{-0.02}^{+0.02}$	${17.10}_{-0.05}^{+0.05}$	$45.77\pm 0.94$	$45.57\pm 3.52$	$48.03\pm 0.94$	$44.45\pm 0.92$	$48.04\pm 3.52$	$0.19$	$5.31$
J1219.0+3653	${1.45}_{-0.08}^{+0.06}$	${8.36}_{-0.46}^{+0.65}$	${2.45}_{-0.20}^{+0.25}$	${74.70}_{-5.79}^{+3.74}$	${3.69}_{-0.06}^{+0.07}$	${0.81}_{-0.07}^{+0.08}$	${16.05}_{-0.05}^{+0.05}$	$44.45\pm 1.37$	$45.22\pm 2.63$	$45.43\pm 1.37$	$43.41\pm 1.36$	$45.67\pm 2.63$	$-0.77$	$7.05$
J0833.4-0458	${4.48}_{-0.17}^{+0.13}$	${6.42}_{-0.75}^{+0.98}$	${0.45}_{-0.07}^{+0.09}$	${12.30}_{-3.12}^{+3.24}$	${7.66}_{-0.20}^{+0.15}$	${0.02}_{-0.01}^{+0.01}$	${16.43}_{-0.13}^{+0.11}$	$46.57\pm 1.08$	$41.22\pm 4.13$	$47.67\pm 1.08$	$45.32\pm 1.00$	$47.70\pm 4.13$	$5.35$	$7.91$
J0337.8-1157	${2.60}_{-0.08}^{+0.08}$	${2.36}_{-0.10}^{+0.12}$	${0.58}_{-0.05}^{+0.07}$	${14.70}_{-1.20}^{+1.50}$	${3.59}_{-0.08}^{+0.07}$	${0.86}_{-0.10}^{+0.13}$	${15.83}_{-0.05}^{+0.05}$	$44.33\pm 0.32$	$43.45\pm 1.90$	$44.75\pm 0.32$	$44.59\pm 0.26$	$45.08\pm 1.90$	$0.89$	$4.66$
J2320.8-0823	${2.68}_{-0.37}^{+0.24}$	${2.48}_{-1.15}^{+2.32}$	${3.00}_{-1.51}^{+2.75}$	${9.79}_{-3.19}^{+5.73}$	${3.96}_{-0.32}^{+0.24}$	${0.03}_{-0.02}^{+0.03}$	${16.08}_{-0.27}^{+0.21}$	$45.49\pm 1.51$	$40.69\pm 3.49$	$44.97\pm 1.51$	$44.99\pm 1.30$	$45.70\pm 3.49$	$4.81$	$2.81$
J0539.9-2839	${3.08}_{-0.05}^{+0.04}$	${1.10}_{-0.09}^{+0.10}$	${0.77}_{-0.02}^{+0.02}$	${41.00}_{-1.62}^{+1.62}$	${0.91}_{-0.06}^{+0.06}$	${0.11}_{-0.01}^{+0.01}$	${17.19}_{-0.03}^{+0.03}$	$46.77\pm 0.43$	$45.28\pm 4.02$	$48.85\pm 0.43$	$45.54\pm 0.42$	$48.85\pm 4.02$	$1.49$	$7.43$
J0805.4+6147	${1.01}_{-0.08}^{+0.07}$	${1.34}_{-0.12}^{+0.11}$	${0.77}_{-0.03}^{+0.03}$	${67.50}_{-4.40}^{+4.43}$	${0.66}_{-0.07}^{+0.06}$	${0.47}_{-0.03}^{+0.04}$	${17.55}_{-0.04}^{+0.04}$	$45.50\pm 1.30$	$47.66\pm 3.19$	$47.92\pm 1.30$	$44.69\pm 1.29$	$48.11\pm 3.19$	$-2.16$	$6.35$
J1428.9+5406	${3.17}_{-0.07}^{+0.06}$	${2.74}_{-0.04}^{+0.04}$	${0.14}_{-0.01}^{+0.01}$	${73.80}_{-3.93}^{+3.74}$	${1.42}_{-0.08}^{+0.07}$	${0.56}_{-0.04}^{+0.05}$	${16.51}_{-0.04}^{+0.04}$	$45.24\pm 1.18$	$45.84\pm 2.94$	$48.09\pm 1.18$	$43.36\pm 1.17$	$48.09\pm 2.94$	$-0.59$	$0.28$
J0733.8+0455	${2.99}_{-0.08}^{+0.07}$	${2.85}_{-0.08}^{+0.07}$	${0.29}_{-0.03}^{+0.03}$	${22.10}_{-1.76}^{+1.79}$	${2.98}_{-0.07}^{+0.06}$	${0.16}_{-0.01}^{+0.02}$	${17.15}_{-0.06}^{+0.05}$	$45.87\pm 0.53$	$44.96\pm 3.68$	$48.12\pm 0.53$	$44.64\pm 0.50$	$48.12\pm 3.68$	$0.91$	$1.23$
J0746.4+2546	${0.04}_{-0.06}^{+0.05}$	${1.29}_{-0.10}^{+0.09}$	${0.90}_{-0.02}^{+0.02}$	${70.60}_{-2.77}^{+2.62}$	${0.79}_{-0.06}^{+0.05}$	${0.39}_{-0.02}^{+0.02}$	${17.88}_{-0.03}^{+0.03}$	$45.33\pm 0.87$	$48.20\pm 3.51$	$47.65\pm 0.87$	$44.93\pm 0.86$	$48.31\pm 3.51$	$-2.87$	$2.80$
J0349.8-2103	${1.01}_{-0.05}^{+0.05}$	${5.13}_{-0.20}^{+0.21}$	${1.43}_{-0.09}^{+0.09}$	${14.30}_{-0.76}^{+0.81}$	${4.22}_{-0.05}^{+0.05}$	${0.06}_{-0.01}^{+0.01}$	${17.33}_{-0.04}^{+0.03}$	$45.82\pm 0.24$	$44.12\pm 4.01$	$46.14\pm 0.24$	$45.33\pm 0.21$	$46.35\pm 4.01$	$1.69$	$1.66$
J1127.4+5648	${7.02}_{-0.10}^{+0.09}$	${4.36}_{-0.89}^{+0.81}$	${0.49}_{-0.18}^{+0.16}$	${88.30}_{-17.90}^{+13.60}$	${3.50}_{-0.10}^{+0.10}$	${0.34}_{-0.07}^{+0.07}$	${15.00}_{-0.06}^{+0.07}$	$46.61\pm 2.41$	$42.52\pm 3.33$	$49.05\pm 2.41$	$43.64\pm 2.39$	$49.05\pm 3.34$	$4.08$	$1.48$
J2313.9-4501	${7.10}_{-0.07}^{+0.06}$	${7.76}_{-0.66}^{+0.91}$	${0.37}_{-0.04}^{+0.06}$	${34.80}_{-2.98}^{+3.84}$	${8.49}_{-0.07}^{+0.07}$	${0.12}_{-0.01}^{+0.01}$	${15.87}_{-0.05}^{+0.05}$	$47.46\pm 1.08$	$42.54\pm 4.14$	$50.08\pm 1.08$	$44.47\pm 1.07$	$50.08\pm 4.14$	$4.92$	$5.06$
J0440.3-4332	${2.21}_{-0.04}^{+0.04}$	${4.26}_{-0.12}^{+0.13}$	${1.00}_{-0.05}^{+0.05}$	${4.22}_{-0.21}^{+0.26}$	${4.52}_{-0.04}^{+0.04}$	${0.19}_{-0.01}^{+0.02}$	${17.14}_{-0.03}^{+0.03}$	$45.74\pm 1.26$	$43.65\pm 3.86$	$45.87\pm 1.26$	$47.13\pm 1.26$	$47.17\pm 3.86$	$2.09$	$2.85$
J2015.4+6556	${2.73}_{-0.06}^{+0.06}$	${1.53}_{-0.09}^{+0.09}$	${0.48}_{-0.02}^{+0.02}$	${50.00}_{-3.05}^{+2.62}$	${0.51}_{-0.05}^{+0.05}$	${0.50}_{-0.04}^{+0.04}$	${17.00}_{-0.03}^{+0.03}$	$45.77\pm 0.91$	$46.37\pm 2.94$	$48.28\pm 0.91$	$44.32\pm 0.91$	$48.28\pm 2.94$	$-0.59$	$0.22$
J2145.5+1006	${2.06}_{-0.05}^{+0.06}$	${2.39}_{-0.34}^{+0.39}$	${5.26}_{-0.15}^{+0.53}$	${21.50}_{-1.48}^{+1.43}$	${3.50}_{-0.04}^{+0.04}$	${0.37}_{-0.03}^{+0.04}$	${15.96}_{-0.03}^{+0.03}$	$44.94\pm 0.35$	$43.29\pm 2.93$	$44.79\pm 0.35$	$44.55\pm 0.33$	$45.27\pm 2.93$	$1.64$	$\mathbf{14.78}$
J1748.0+3403	${2.32}_{-0.06}^{+0.05}$	${2.95}_{-0.29}^{+0.29}$	${3.86}_{-0.13}^{+0.17}$	${28.00}_{-1.31}^{+1.34}$	${3.19}_{-0.03}^{+0.03}$	${0.55}_{-0.03}^{+0.03}$	${16.09}_{-0.03}^{+0.03}$	$45.28\pm 0.27$	$44.13\pm 3.06$	$45.55\pm 0.27$	$44.72\pm 0.24$	$45.79\pm 3.06$	$1.15$	$\mathbf{20.25}$
J0836.5-2026	${2.87}_{-0.07}^{+0.07}$	${2.75}_{-0.05}^{+0.05}$	${0.20}_{-0.02}^{+0.02}$	${91.10}_{-4.52}^{+3.41}$	${1.11}_{-0.08}^{+0.07}$	${0.83}_{-0.06}^{+0.08}$	${16.64}_{-0.03}^{+0.04}$	$45.36\pm 1.21$	$46.60\pm 2.60$	$48.22\pm 1.21$	$43.59\pm 1.20$	$48.23\pm 2.60$	$-1.24$	$3.95$
J0224.9+1843	${3.82}_{-0.05}^{+0.06}$	${1.69}_{-0.09}^{+0.09}$	${0.54}_{-0.03}^{+0.03}$	${59.60}_{-4.06}^{+3.24}$	${0.30}_{-0.01}^{+0.01}$	${0.48}_{-0.04}^{+0.04}$	${16.91}_{-0.04}^{+0.04}$	$46.63\pm 1.13$	$46.29\pm 3.01$	$49.33\pm 1.13$	$44.77\pm 1.12$	$49.34\pm 3.01$	$0.34$	$0.34$
J0539.6+1432	${3.15}_{-0.06}^{+0.05}$	${3.27}_{-0.17}^{+0.16}$	${0.68}_{-0.04}^{+0.04}$	${22.40}_{-1.38}^{+1.52}$	${2.76}_{-0.06}^{+0.06}$	${0.14}_{-0.01}^{+0.01}$	${17.22}_{-0.05}^{+0.05}$	$46.65\pm 0.36$	$45.04\pm 4.01$	$48.44\pm 0.36$	$45.36\pm 0.32$	$48.45\pm 4.01$	$1.61$	$7.65$
J0242.3+1102	${4.25}_{-0.10}^{+0.08}$	${5.63}_{-0.60}^{+0.91}$	${3.54}_{-0.45}^{+0.61}$	${126.00}_{-6.40}^{+7.82}$	${2.72}_{-0.07}^{+0.09}$	${0.89}_{-0.05}^{+0.07}$	${14.95}_{-0.07}^{+0.07}$	$45.35\pm 1.72$	$43.57\pm 2.98$	$46.49\pm 1.72$	$43.35\pm 1.70$	$46.52\pm 2.98$	$1.79$	$\mathbf{32.50}$
J2339.6+0242	${1.95}_{-0.12}^{+0.12}$	${2.04}_{-0.52}^{+0.71}$	${2.45}_{-0.70}^{+1.13}$	${6.82}_{-0.87}^{+0.99}$	${4.05}_{-0.12}^{+0.12}$	${0.69}_{-0.14}^{+0.16}$	${15.76}_{-0.09}^{+0.08}$	$43.94\pm 0.30$	$42.43\pm 1.66$	$43.27\pm 0.30$	$45.04\pm 0.06$	$45.08\pm 1.66$	$1.52$	$1.17$
J0910.6+2247	${2.94}_{-0.06}^{+0.05}$	${2.59}_{-0.27}^{+0.25}$	${2.96}_{-0.07}^{+0.21}$	${17.00}_{-0.99}^{+0.99}$	${3.54}_{-0.04}^{+0.04}$	${0.11}_{-0.01}^{+0.01}$	${16.08}_{-0.04}^{+0.03}$	$45.80\pm 0.13$	$42.24\pm 4.00$	$45.71\pm 0.13$	$45.34\pm 0.01$	$46.14\pm 4.00$	$3.56$	$6.80$
J1441.6-1522	${2.54}_{-0.09}^{+0.08}$	${2.42}_{-0.41}^{+0.46}$	${4.83}_{-0.54}^{+0.76}$	${16.90}_{-1.33}^{+1.40}$	${3.46}_{-0.06}^{+0.06}$	${0.15}_{-0.01}^{+0.01}$	${16.18}_{-0.05}^{+0.05}$	$45.61\pm 0.33$	$42.73\pm 4.01$	$45.52\pm 0.33$	$45.18\pm 0.27$	$45.95\pm 4.01$	$2.88$	$\mathbf{12.37}$
J1054.2+3926	${2.73}_{-0.06}^{+0.06}$	${2.98}_{-0.15}^{+0.15}$	${1.02}_{-0.06}^{+0.07}$	${20.10}_{-1.59}^{+1.59}$	${3.20}_{-0.05}^{+0.05}$	${0.15}_{-0.01}^{+0.01}$	${16.44}_{-0.05}^{+0.05}$	$45.57\pm 0.43$	$43.41\pm 4.02$	$46.37\pm 0.43$	$44.34\pm 0.40$	$46.43\pm 4.02$	$2.16$	$1.48$
J1549.6+1710	${2.31}_{-0.09}^{+0.09}$	${1.85}_{-0.58}^{+0.61}$	${12.10}_{-2.02}^{+2.04}$	${9.50}_{-0.84}^{+0.82}$	${3.76}_{-0.05}^{+0.04}$	${0.15}_{-0.01}^{+0.02}$	${16.33}_{-0.05}^{+0.05}$	$45.55\pm 0.26$	$42.54\pm 3.65$	$45.08\pm 0.26$	$46.15\pm 0.16$	$46.27\pm 3.65$	$3.02$	$0.68$
J1450.4+0910	${2.52}_{-0.05}^{+0.05}$	${2.96}_{-0.24}^{+0.22}$	${2.32}_{-0.05}^{+0.24}$	${26.00}_{-1.52}^{+1.81}$	${3.13}_{-0.04}^{+0.04}$	${0.19}_{-0.01}^{+0.01}$	${16.37}_{-0.03}^{+0.03}$	$45.79\pm 0.46$	$43.69\pm 4.02$	$46.24\pm 0.46$	$44.80\pm 0.44$	$46.38\pm 4.02$	$2.10$	$\mathbf{11.30}$
J0226.5+0938	${-0.26}_{-0.09}^{+0.08}$	${0.87}_{-0.20}^{+0.18}$	${1.09}_{-0.05}^{+0.06}$	${72.30}_{-5.43}^{+4.40}$	${0.95}_{-0.06}^{+0.06}$	${0.69}_{-0.05}^{+0.07}$	${17.51}_{-0.06}^{+0.06}$	$44.61\pm 1.40$	$47.99\pm 2.81$	$46.63\pm 1.40$	$44.18\pm 1.38$	$48.01\pm 2.81$	$-3.38$	$\mathbf{14.61}$
J1628.8-6149	${1.09}_{-0.08}^{+0.06}$	${3.38}_{-0.82}^{+0.89}$	${14.60}_{-1.04}^{+0.34}$	${45.00}_{-4.15}^{+3.72}$	${3.59}_{-0.04}^{+0.04}$	${4.10}_{-0.56}^{+0.76}$	${15.57}_{-0.05}^{+0.05}$	$43.93\pm 1.20$	$45.24\pm 1.25$	$43.69\pm 1.20$	$44.59\pm 1.19$	$45.36\pm 1.51$	$-1.31$	$1.96$
J0453.1-2806	${6.14}_{-0.04}^{+0.04}$	${1.87}_{-0.07}^{+0.06}$	${0.39}_{-0.03}^{+0.03}$	${68.30}_{-2.48}^{+2.10}$	${0.62}_{-0.06}^{+0.05}$	${0.56}_{-0.02}^{+0.02}$	${15.79}_{-0.03}^{+0.03}$	$46.94\pm 0.73$	$44.30\pm 3.47$	$49.53\pm 0.73$	$44.49\pm 0.72$	$49.54\pm 3.47$	$2.64$	$7.73$
J0912.2+4127	${3.83}_{-0.07}^{+0.06}$	${1.38}_{-0.10}^{+0.10}$	${0.41}_{-0.02}^{+0.02}$	${36.30}_{-1.81}^{+2.02}$	${0.68}_{-0.06}^{+0.05}$	${0.20}_{-0.01}^{+0.01}$	${16.60}_{-0.04}^{+0.04}$	$46.06\pm 0.58$	$44.50\pm 4.04$	$48.30\pm 0.58$	$44.37\pm 0.56$	$48.30\pm 4.04$	$1.55$	$2.78$
J1618.0+5139	${2.26}_{-0.08}^{+0.06}$	${3.25}_{-0.06}^{+0.06}$	${0.27}_{-0.02}^{+0.02}$	${22.70}_{-1.75}^{+1.79}$	${2.92}_{-0.06}^{+0.06}$	${0.16}_{-0.01}^{+0.01}$	${17.69}_{-0.05}^{+0.04}$	$45.86\pm 0.52$	$46.09\pm 4.03$	$48.50\pm 0.52$	$44.46\pm 0.50$	$48.50\pm 4.03$	$-0.23$	$0.86$
J1625.7+4134	${0.32}_{-0.07}^{+0.06}$	${3.61}_{-0.07}^{+0.08}$	${0.48}_{-0.02}^{+0.02}$	${22.80}_{-1.08}^{+1.04}$	${3.16}_{-0.07}^{+0.07}$	${0.09}_{-0.01}^{+0.01}$	${18.20}_{-0.01}^{+0.01}$	$45.41\pm 0.14$	$46.63\pm 4.00$	$47.58\pm 0.14$	$44.87\pm 0.05$	$47.63\pm 4.00$	$-1.22$	$0.77$
J1345.5+4453	${0.97}_{-0.06}^{+0.05}$	${1.22}_{-0.06}^{+0.05}$	${0.44}_{-0.01}^{+0.01}$	${48.40}_{-2.49}^{+2.44}$	${0.81}_{-0.05}^{+0.05}$	${0.08}_{-0.01}^{+0.01}$	${17.48}_{-0.03}^{+0.03}$	$45.40\pm 0.79$	$45.69\pm 4.08$	$47.45\pm 0.79$	$44.96\pm 0.78$	$47.46\pm 4.08$	$-0.28$	$3.42$
J1833.6-2103	${2.50}_{-0.03}^{+0.03}$	${2.43}_{-0.41}^{+0.42}$	${12.70}_{-0.27}^{+0.84}$	${34.50}_{-0.88}^{+0.88}$	${3.20}_{-0.02}^{+0.02}$	${0.13}_{-0.01}^{+0.01}$	${16.39}_{-0.02}^{+0.02}$	$46.38\pm 0.13$	$43.67\pm 4.00$	$46.50\pm 0.13$	$45.77\pm 0.11$	$46.79\pm 4.00$	$2.72$	$\mathbf{63.30}$
J2110.2-1021	${7.24}_{-0.09}^{+0.09}$	${5.54}_{-0.47}^{+0.55}$	${0.51}_{-0.07}^{+0.08}$	${95.20}_{-10.50}^{+8.00}$	${3.58}_{-0.08}^{+0.08}$	${0.53}_{-0.06}^{+0.07}$	${15.57}_{-0.07}^{+0.07}$	$47.62\pm 1.95$	$44.10\pm 3.06$	$50.48\pm 1.95$	$44.49\pm 1.93$	$50.48\pm 3.07$	$3.52$	$2.31$
geometric mean (log)	2.91	3.19	1.66	41.42	2.92	0.44	16.67	45.77	44.69	47.40	44.73	47.69	1.08
geometric mean	8.07 × 102	3.19 × 100	1.66 × 100	4.14 × 101	8.32 × 102	4.40× 10−1	4.72 × 1016	5.88 × 1045	4.87 × 1044	2.51 × 1046	5.33 × 1044	4.90 × 1047	1.21 × 101

Column 2 denotes the electron number density. Columns 3–4 denote the spectral index and curvature of the EED, respectively. Column 5 denotes the Doppler factor. Column 6 denotes the peak Lorentz factor. Column 7 denotes the magnetic field strength. Column 8 denotes the radius of the emitting region. Columns 9–12 are, respectively, the power of the jet in the form of relativistic electrons ($P_{\mathrm{e}}$), the magnetic field ($P_{\mathrm{B}}$), and cold protons ($P_{\mathrm{P}}$) with $n_{\mathrm{e}}/n_{\mathrm{p}}=1$ and the radiation field ($P_{\mathrm{r}}$), where $P_{\mathrm{r}}$ is the sum of all radiative components. Column 13 is the total power ($P_{\mathrm{jet}}=P_{\mathrm{e}}+P_{\mathrm{B}}+P_{\mathrm{r}}+P_{\mathrm{p}}$). Column 14 is the ratio of energy density, i.e., Compton dominant $U_e/U_B$. Column 15 lists the total chi-square for the $\gamma$-ray band, ${\chi }^2={\sum }_j{\left({\displaystyle \frac{{\mathrm{flux}}_j-{\mathrm{flux}}_j^{\prime }}{{\sigma }_{\mathrm{eff},j}}}\right)}^2$, ${\sigma }_{\mathrm{eff},j}=\sqrt{{\mathrm{flux}}_{\mathrm{bar},j}^2+{\left(0.20{\mathrm{flux}}_j\right)}^2}$. For each point, ${\mathrm{flux}}_j^{\prime }$ is the model flux evaluated at the same frequency as each $\gamma$-ray data point (via the interpolation of the fitted curve), ${\mathrm{flux}}_j$ is the observed flux, and ${\mathrm{flux}}_{\mathrm{bar},j}$ is the reported statistical uncertainty; $0.20{\mathrm{flux}}_j$ accounts for a 20% fractional systematic. We bold the fits with chi-square values greater than 10, which are considered unreliable due to poor data quality. The average presented here is calculated after excluding parameter values with ${\chi }^2>10$. The “geometric mean” corresponds to the mean of the logarithmic quantities, which is often more appropriate as it reduces the influence of extreme values.

Table 4. Parameters Obtained from the Modeling by BLR.

Fermi Name	$log{\mathbf{N}}_{\mathbf{pk}}^{\prime }$	s	r	${\mathit{\delta }}_{\mathbf{D}}$	$log{\mathit{\gamma }}_{\mathbf{pk}}^{\prime }$	${\mathit{B}}^{\prime }$	$log{\mathbf{R}}^{\prime }$	$log{\mathbf{P}}_{\mathbf{e}}$	$log{\mathbf{P}}_{\mathbf{B}}$	$log{\mathbf{P}}_{\mathbf{p}}$	$log{\mathbf{P}}_{\mathbf{r}}$	$log{\mathbf{P}}_{\mathbf{jet}}$	$log\mathbf{CD}$	${\mathit{\chi }}^2$
	(1/cm3)					(G)	(cm)	(erg s−1)	(erg s−1)	(erg s−1)	(erg s−1)	(erg s−1)
J1510.1+5702	${3.97}_{-0.06}^{+0.06}$	${7.98}_{-0.63}^{+0.68}$	${2.06}_{-0.18}^{+0.22}$	${16.20}_{-0.77}^{+0.82}$	${3.98}_{-0.07}^{+0.07}$	${2.04}_{-0.16}^{+0.18}$	${15.63}_{-0.04}^{+0.04}$	$44.94\pm 0.25$	$43.87\pm 1.55$	$45.80\pm 0.25$	$45.18\pm 0.20$	$45.94\pm 1.56$	$1.07$	$4.21$
J1354.3-0206	${4.93}_{-0.07}^{+0.06}$	${5.85}_{-0.67}^{+0.70}$	${5.32}_{-1.08}^{+0.88}$	${4.16}_{-0.34}^{+0.31}$	${3.73}_{-0.04}^{+0.05}$	${4.80}_{-0.43}^{+0.55}$	${15.23}_{-0.03}^{+0.04}$	$44.81\pm 0.99$	$42.61\pm 1.16$	$44.76\pm 0.99$	$47.65\pm 0.98$	$47.65\pm 1.34$	$2.20$	$\mathbf{36.21}$
J1635.6-3628	${3.12}_{-0.07}^{+0.06}$	${2.64}_{-0.13}^{+0.11}$	${0.68}_{-0.04}^{+0.04}$	${9.12}_{-0.56}^{+0.55}$	${2.24}_{-0.07}^{+0.06}$	${1.70}_{-0.15}^{+0.15}$	${16.88}_{-0.05}^{+0.05}$	$45.10\pm 0.54$	$45.71\pm 1.73$	$46.95\pm 0.54$	$45.93\pm 0.51$	$47.02\pm 1.73$	$-0.61$	$\mathbf{17.43}$
J1219.0+3653	${2.76}_{-0.14}^{+0.10}$	${5.43}_{-0.79}^{+1.18}$	${5.29}_{-0.79}^{+0.94}$	${26.10}_{-2.51}^{+3.12}$	${2.71}_{-0.07}^{+0.07}$	${10.10}_{-1.14}^{+1.35}$	${15.40}_{-0.08}^{+0.06}$	$43.62\pm 0.94$	$45.22\pm 0.93$	$44.55\pm 0.94$	$44.14\pm 0.90$	$45.34\pm 1.23$	$-1.60$	$\mathbf{13.76}$
J0833.4-0458	${1.73}_{-0.14}^{+0.13}$	${6.05}_{-1.51}^{+2.13}$	${3.30}_{-0.72}^{+0.93}$	${11.50}_{-2.33}^{+2.72}$	${4.43}_{-0.14}^{+0.12}$	${13.00}_{-3.04}^{+3.54}$	${15.30}_{-0.10}^{+0.09}$	$43.07\pm 0.87$	$44.51\pm 1.32$	$42.59\pm 0.87$	$45.00\pm 0.80$	$45.13\pm 1.39$	$-1.45$	$0.53$
J0337.8-1157	${3.70}_{-0.08}^{+0.07}$	${2.32}_{-0.10}^{+0.10}$	${0.61}_{-0.06}^{+0.06}$	${9.98}_{-0.92}^{+0.99}$	${3.26}_{-0.07}^{+0.07}$	${4.96}_{-0.56}^{+0.71}$	${15.36}_{-0.04}^{+0.05}$	$43.89\pm 0.18$	$43.69\pm 0.41$	$44.57\pm 0.18$	$44.99\pm 0.04$	$45.17\pm 0.54$	$0.20$	$2.59$
J2320.8-0823	${2.07}_{-0.21}^{+0.17}$	${4.08}_{-0.39}^{+0.59}$	${0.31}_{-0.10}^{+0.12}$	${4.65}_{-0.95}^{+1.07}$	${3.89}_{-0.22}^{+0.17}$	${0.37}_{-0.09}^{+0.11}$	${18.34}_{-0.09}^{+0.08}$	$45.58\pm 0.42$	$46.72\pm 2.01$	$48.23\pm 0.42$	$46.75\pm 0.01$	$48.26\pm 2.01$	$-1.14$	$3.97$
J0539.9-2839	${4.30}_{-0.05}^{+0.04}$	${8.89}_{-0.44}^{+0.42}$	${2.06}_{-0.11}^{+0.11}$	${4.81}_{-0.20}^{+0.22}$	${5.02}_{-0.06}^{+0.05}$	${0.43}_{-0.02}^{+0.03}$	${15.96}_{-0.03}^{+0.03}$	$45.68\pm 1.36$	$42.12\pm 3.48$	$45.73\pm 1.36$	$47.31\pm 1.36$	$47.33\pm 3.48$	$3.56$	$8.14$
J0805.4+6147	${4.26}_{-0.06}^{+0.06}$	${7.86}_{-1.01}^{+1.09}$	${7.63}_{-0.72}^{+0.73}$	${8.86}_{-0.38}^{+0.44}$	${3.31}_{-0.06}^{+0.06}$	${1.93}_{-0.12}^{+0.13}$	${15.58}_{-0.04}^{+0.04}$	$45.07\pm 0.79$	$43.19\pm 1.97$	$45.45\pm 0.79$	$45.91\pm 0.77$	$46.08\pm 1.97$	$1.88$	$\mathbf{14.71}$
J1428.9+5406	${4.86}_{-0.05}^{+0.05}$	${0.95}_{-0.13}^{+0.13}$	${1.04}_{-0.06}^{+0.07}$	${10.40}_{-0.60}^{+0.66}$	${2.29}_{-0.06}^{+0.06}$	${3.64}_{-0.27}^{+0.30}$	${15.11}_{-0.04}^{+0.04}$	$44.55\pm 0.42$	$42.95\pm 1.16$	$45.26\pm 0.42$	$45.37\pm 0.40$	$45.66\pm 1.18$	$1.60$	$5.57$
J0733.8+0455	${2.46}_{-0.08}^{+0.07}$	${2.26}_{-0.23}^{+0.22}$	${1.37}_{-0.11}^{+0.13}$	${5.80}_{-0.37}^{+0.50}$	${3.65}_{-0.08}^{+0.08}$	${15.00}_{-1.73}^{+2.24}$	${15.48}_{-0.04}^{+0.04}$	$43.20\pm 0.74$	$44.40\pm 0.94$	$43.09\pm 0.74$	$45.56\pm 0.72$	$45.59\pm 1.11$	$-1.21$	$1.59$
J0746.4+2546	${3.31}_{-0.07}^{+0.05}$	${6.60}_{-0.19}^{+0.22}$	${0.78}_{-0.03}^{+0.04}$	${32.80}_{-0.63}^{+1.18}$	${3.63}_{-0.06}^{+0.06}$	${6.95}_{-0.46}^{+0.59}$	${16.55}_{-0.02}^{+0.02}$	$44.93\pm 0.15$	$47.39\pm 0.57$	$47.60\pm 0.15$	$45.57\pm 0.09$	$47.81\pm 0.64$	$-2.46$	$\mathbf{17.85}$
J0349.8-2103	${3.88}_{-0.05}^{+0.05}$	${2.24}_{-0.22}^{+0.19}$	${1.73}_{-0.11}^{+0.11}$	${25.70}_{-1.23}^{+1.30}$	${2.33}_{-0.05}^{+0.05}$	${3.76}_{-0.25}^{+0.26}$	${15.38}_{-0.04}^{+0.04}$	$44.47\pm 0.24$	$44.31\pm 1.21$	$45.62\pm 0.24$	$44.77\pm 0.20$	$45.72\pm 1.21$	$0.16$	$\mathbf{24.12}$
J1127.4+5648	${5.27}_{-0.06}^{+0.06}$	${3.61}_{-0.09}^{+0.09}$	${0.28}_{-0.02}^{+0.02}$	${5.39}_{-0.38}^{+0.41}$	${5.02}_{-0.07}^{+0.06}$	${1.74}_{-0.20}^{+0.23}$	${15.95}_{-0.05}^{+0.05}$	$44.92\pm 0.82$	$43.40\pm 1.56$	$46.77\pm 0.82$	$45.83\pm 0.81$	$46.82\pm 1.58$	$1.52$	$6.40$
J2313.9-4501	${3.93}_{-0.08}^{+0.07}$	${4.77}_{-0.28}^{+0.30}$	${0.81}_{-0.08}^{+0.10}$	${9.05}_{-0.73}^{+0.80}$	${4.67}_{-0.07}^{+0.07}$	${11.40}_{-1.31}^{+1.31}$	${15.13}_{-0.04}^{+0.04}$	$43.63\pm 0.29$	$43.85\pm 0.34$	$44.24\pm 0.29$	$45.05\pm 0.23$	$45.15\pm 0.59$	$-0.22$	$4.03$
J0440.3-4332	${3.28}_{-0.05}^{+0.05}$	${2.56}_{-0.03}^{+0.03}$	${0.27}_{-0.02}^{+0.02}$	${22.70}_{-1.10}^{+1.53}$	${1.65}_{-0.05}^{+0.05}$	${2.52}_{-0.14}^{+0.16}$	${16.65}_{-0.03}^{+0.03}$	$44.81\pm 0.26$	$46.39\pm 1.67$	$47.44\pm 0.26$	$45.61\pm 0.24$	$47.49\pm 1.67$	$-1.58$	$1.37$
J2015.4+6556	${2.93}_{-0.05}^{+0.04}$	${3.18}_{-0.09}^{+0.10}$	${0.77}_{-0.03}^{+0.03}$	${7.89}_{-0.41}^{+0.43}$	${2.60}_{-0.05}^{+0.05}$	${2.01}_{-0.12}^{+0.15}$	${17.05}_{-0.04}^{+0.04}$	$45.23\pm 0.76$	$46.08\pm 1.90$	$46.98\pm 0.76$	$46.14\pm 0.75$	$47.09\pm 1.90$	$-0.84$	$3.50$
J2145.5+1006	${1.68}_{-0.05}^{+0.04}$	${2.75}_{-0.34}^{+0.37}$	${5.28}_{-0.13}^{+0.56}$	${20.80}_{-1.33}^{+1.30}$	${2.93}_{-0.03}^{+0.04}$	${6.16}_{-0.44}^{+0.60}$	${15.69}_{-0.03}^{+0.03}$	$43.39\pm 0.26$	$45.17\pm 0.62$	$43.85\pm 0.26$	$44.25\pm 0.24$	$45.24\pm 0.72$	$-1.78$	$\mathbf{15.15}$
J1748.0+3403	${3.98}_{-0.06}^{+0.05}$	${4.53}_{-0.08}^{+0.09}$	${0.71}_{-0.03}^{+0.03}$	${21.40}_{-1.10}^{+1.21}$	${3.03}_{-0.05}^{+0.04}$	${13.90}_{-0.84}^{+0.84}$	${16.11}_{-0.04}^{+0.04}$	$44.70\pm 0.18$	$46.74\pm 0.21$	$47.01\pm 0.18$	$45.15\pm 0.13$	$47.20\pm 0.48$	$-2.04$	$\mathbf{27.88}$
J0836.5-2026	${4.09}_{-0.07}^{+0.07}$	${4.46}_{-0.33}^{+0.34}$	${0.19}_{-0.05}^{+0.05}$	${47.60}_{-1.36}^{+1.79}$	${4.81}_{-0.16}^{+0.07}$	${16.20}_{-1.48}^{+1.97}$	${15.95}_{-0.03}^{+0.03}$	$44.71\pm 0.42$	$43.46\pm 0.62$	$45.14\pm 0.42$	$46.54\pm 0.39$	$46.56\pm 0.79$	$1.25$	$0.62$
J0224.9+1843	${3.43}_{-0.08}^{+0.07}$	${4.38}_{-0.15}^{+0.15}$	${0.23}_{-0.03}^{+0.03}$	${22.40}_{-0.77}^{+0.71}$	${3.95}_{-0.10}^{+0.09}$	${6.34}_{-0.62}^{+0.78}$	${16.89}_{-0.03}^{+0.03}$	$45.11\pm 0.31$	$47.66\pm 0.41$	$48.06\pm 0.31$	$45.48\pm 0.26$	$48.20\pm 0.63$	$-2.55$	$1.12$
J0539.6+1432	${4.40}_{-0.06}^{+0.06}$	${2.32}_{-0.13}^{+0.13}$	${0.75}_{-0.07}^{+0.07}$	${10.40}_{-0.62}^{+0.58}$	${1.77}_{-0.07}^{+0.07}$	${2.62}_{-0.23}^{+0.25}$	${16.55}_{-0.04}^{+0.04}$	$45.65\pm 0.47$	$45.54\pm 1.32$	$47.68\pm 0.47$	$46.16\pm 0.44$	$47.70\pm 1.33$	$0.11$	$\mathbf{32.94}$
J0242.3+1102	${3.42}_{-0.06}^{+0.06}$	${4.47}_{-0.60}^{+0.90}$	${7.25}_{-1.14}^{+1.49}$	${22.00}_{-1.42}^{+1.52}$	${2.59}_{-0.05}^{+0.06}$	${6.21}_{-0.54}^{+0.71}$	${15.45}_{-0.07}^{+0.06}$	$44.27\pm 0.38$	$44.74\pm 0.54$	$45.15\pm 0.38$	$44.58\pm 0.33$	$45.41\pm 0.73$	$-0.48$	$\mathbf{36.12}$
J2339.6+0242	${0.50}_{-0.16}^{+0.13}$	${7.25}_{-2.27}^{+1.78}$	${0.92}_{-0.34}^{+0.25}$	${45.80}_{-4.94}^{+5.17}$	${5.60}_{-0.16}^{+0.12}$	${3.13}_{-0.65}^{+0.65}$	${15.57}_{-0.10}^{+0.09}$	$42.34\pm 1.45$	$45.03\pm 1.47$	$43.12\pm 1.45$	$43.32\pm 1.41$	$45.05\pm 1.75$	$-2.69$	$1.71$
J0910.6+2247	${3.11}_{-0.05}^{+0.05}$	${2.31}_{-0.24}^{+0.22}$	${2.30}_{-0.03}^{+0.05}$	${13.30}_{-0.59}^{+0.61}$	${2.76}_{-0.05}^{+0.04}$	${2.31}_{-0.13}^{+0.14}$	${15.80}_{-0.04}^{+0.03}$	$44.43\pm 0.46$	$44.16\pm 1.80$	$45.12\pm 0.46$	$44.85\pm 0.44$	$45.39\pm 1.80$	$0.27$	$\mathbf{19.32}$
J1441.6-1522	${2.56}_{-0.09}^{+0.07}$	${2.85}_{-0.55}^{+0.61}$	${4.89}_{-0.54}^{+0.71}$	${8.22}_{-0.70}^{+0.76}$	${3.08}_{-0.06}^{+0.07}$	${2.13}_{-0.21}^{+0.26}$	${16.10}_{-0.05}^{+0.05}$	$44.42\pm 0.33$	$44.26\pm 1.29$	$44.75\pm 0.33$	$45.19\pm 0.27$	$45.41\pm 1.30$	$0.16$	$\mathbf{17.11}$
J1054.2+3926	${2.19}_{-0.06}^{+0.07}$	${3.42}_{-0.12}^{+0.11}$	${0.64}_{-0.04}^{+0.04}$	${11.70}_{-0.96}^{+1.01}$	${2.72}_{-0.06}^{+0.05}$	${2.35}_{-0.20}^{+0.25}$	${16.96}_{-0.05}^{+0.05}$	$44.38\pm 0.16$	$46.37\pm 1.30$	$46.39\pm 0.16$	$45.32\pm 0.01$	$46.70\pm 1.30$	$-1.99$	$4.47$
J1549.6+1710	${2.67}_{-0.07}^{+0.06}$	${8.37}_{-0.88}^{+1.03}$	${6.27}_{-0.55}^{+0.64}$	${25.80}_{-1.88}^{+1.92}$	${3.04}_{-0.05}^{+0.05}$	${10.00}_{-0.99}^{+1.20}$	${15.26}_{-0.04}^{+0.04}$	$43.37\pm 0.58$	$44.91\pm 0.57$	$44.15\pm 0.58$	$43.83\pm 0.56$	$45.02\pm 0.87$	$-1.54$	$1.84$
J1450.4+0910	${2.45}_{-0.06}^{+0.05}$	${2.97}_{-0.18}^{+0.18}$	${1.98}_{-0.03}^{+0.04}$	${18.70}_{-1.03}^{+1.04}$	${2.58}_{-0.04}^{+0.04}$	${4.20}_{-0.25}^{+0.28}$	${16.08}_{-0.03}^{+0.03}$	$44.24\pm 0.13$	$45.52\pm 1.16$	$45.30\pm 0.13$	$45.11\pm 0.03$	$45.83\pm 1.16$	$-1.28$	$\mathbf{20.75}$
J0226.5+0938	${0.58}_{-0.08}^{+0.06}$	${7.30}_{-0.44}^{+0.67}$	${2.83}_{-0.22}^{+0.34}$	${5.62}_{-0.53}^{+0.58}$	${3.65}_{-0.06}^{+0.06}$	${2.00}_{-0.20}^{+0.25}$	${17.33}_{-0.06}^{+0.06}$	$44.23\pm 0.54$	$46.32\pm 1.40$	$44.87\pm 0.54$	$45.90\pm 0.51$	$46.47\pm 1.41$	$-2.10$	$\mathbf{20.51}$
J1628.8-6149	${0.65}_{-0.09}^{+0.07}$	${3.03}_{-0.93}^{+0.81}$	${14.50}_{-1.01}^{+0.43}$	${11.60}_{-0.92}^{+1.02}$	${3.52}_{-0.04}^{+0.03}$	${27.00}_{-3.31}^{+4.74}$	${16.04}_{-0.05}^{+0.05}$	$43.19\pm 0.19$	$46.64\pm 1.21$	$43.00\pm 0.19$	$45.87\pm 0.03$	$46.71\pm 1.22$	$-3.45$	$5.04$
J0453.1-2806	${4.05}_{-0.03}^{+0.04}$	${5.81}_{-0.19}^{+0.18}$	${0.85}_{-0.04}^{+0.04}$	${11.60}_{-0.47}^{+0.43}$	${4.77}_{-0.05}^{+0.04}$	${2.91}_{-0.09}^{+0.10}$	${15.90}_{-0.03}^{+0.03}$	$45.08\pm 0.70$	$44.42\pm 2.16$	$46.12\pm 0.70$	$45.89\pm 0.69$	$46.35\pm 2.16$	$0.65$	$2.57$
J0912.2+4127	${3.47}_{-0.06}^{+0.05}$	${4.89}_{-0.12}^{+0.12}$	${0.41}_{-0.02}^{+0.02}$	${20.20}_{-1.11}^{+1.17}$	${4.58}_{-0.06}^{+0.05}$	${4.03}_{-0.25}^{+0.27}$	${16.35}_{-0.03}^{+0.03}$	$44.46\pm 0.17$	$46.09\pm 1.18$	$46.93\pm 0.17$	$45.02\pm 0.11$	$46.99\pm 1.18$	$-1.63$	$\mathbf{15.73}$
J1618.0+5139	${2.69}_{-0.06}^{+0.06}$	${3.42}_{-0.06}^{+0.06}$	${0.30}_{-0.03}^{+0.02}$	${6.71}_{-0.53}^{+0.55}$	${3.05}_{-0.06}^{+0.06}$	${1.67}_{-0.14}^{+0.16}$	${17.54}_{-0.05}^{+0.05}$	$44.95\pm 0.56$	$46.75\pm 1.74$	$47.57\pm 0.56$	$45.68\pm 0.54$	$47.64\pm 1.74$	$-1.79$	$4.22$
J1625.7+4134	${-0.84}_{-0.05}^{+0.06}$	${2.93}_{-0.08}^{+0.07}$	${0.49}_{-0.02}^{+0.03}$	${9.16}_{-0.35}^{+0.19}$	${2.10}_{-0.07}^{+0.07}$	${1.16}_{-0.05}^{+0.06}$	${18.57}_{-0.01}^{+0.01}$	$43.97\pm 1.14$	$48.77\pm 2.76$	$46.38\pm 1.14$	$45.95\pm 1.14$	$48.77\pm 2.76$	$-4.80$	$\mathbf{21.46}$
J1345.5+4453	${3.51}_{-0.05}^{+0.05}$	${2.72}_{-0.17}^{+0.16}$	${1.51}_{-0.08}^{+0.08}$	${14.40}_{-0.55}^{+0.54}$	${3.24}_{-0.05}^{+0.05}$	${0.59}_{-0.03}^{+0.03}$	${15.75}_{-0.03}^{+0.03}$	$45.05\pm 0.54$	$42.94\pm 3.09$	$45.48\pm 0.54$	$45.71\pm 0.53$	$45.97\pm 3.09$	$2.12$	$\mathbf{33.96}$
J1833.6-2103	${3.28}_{-0.03}^{+0.02}$	${2.45}_{-0.02}^{+0.02}$	${14.10}_{-0.58}^{+0.58}$	${38.20}_{-0.90}^{+0.90}$	${2.41}_{-0.01}^{+0.01}$	${5.48}_{-0.21}^{+0.28}$	${16.61}_{-0.01}^{+0.01}$	$45.02\pm 0.11$	$47.43\pm 1.23$	$47.82\pm 0.11$	$45.98\pm 0.09$	$47.97\pm 1.23$	$-2.41$	$\mathbf{81.40}$
J2110.2-1021	${3.05}_{-0.11}^{+0.10}$	${3.70}_{-0.28}^{+0.29}$	${0.09}_{-0.04}^{+0.04}$	${18.10}_{-2.12}^{+2.12}$	${6.08}_{-0.20}^{+0.16}$	${4.40}_{-0.61}^{+0.66}$	${16.92}_{-0.07}^{+0.06}$	$44.64\pm 0.70$	$47.21\pm 0.77$	$47.55\pm 0.70$	$45.04\pm 0.65$	$47.72\pm 1.01$	$-2.57$	$1.84$
geometric mean (log)	3.09	4.52	1.84	15.48	3.90	6.56	16.15	44.36	45.02	45.59	45.49	46.48	$-0.66$
geometric mean	1.23 × 103	4.52 × 100	1.84 × 100	1.55 × 101	7.95 × 103	6.56 × 100	1.41 × 1016	2.31 × 1044	1.05 × 1045	3.89 × 1045	3.08 × 1045	3.01 × 1046	2.19 × 10−1

Each column represents the same physical quantity as in Table 3.

The goodness of the fit should depend on the gamma-ray band, because most archival data are not simultaneous and many points lack error bars. This can pull the fit toward those bands.

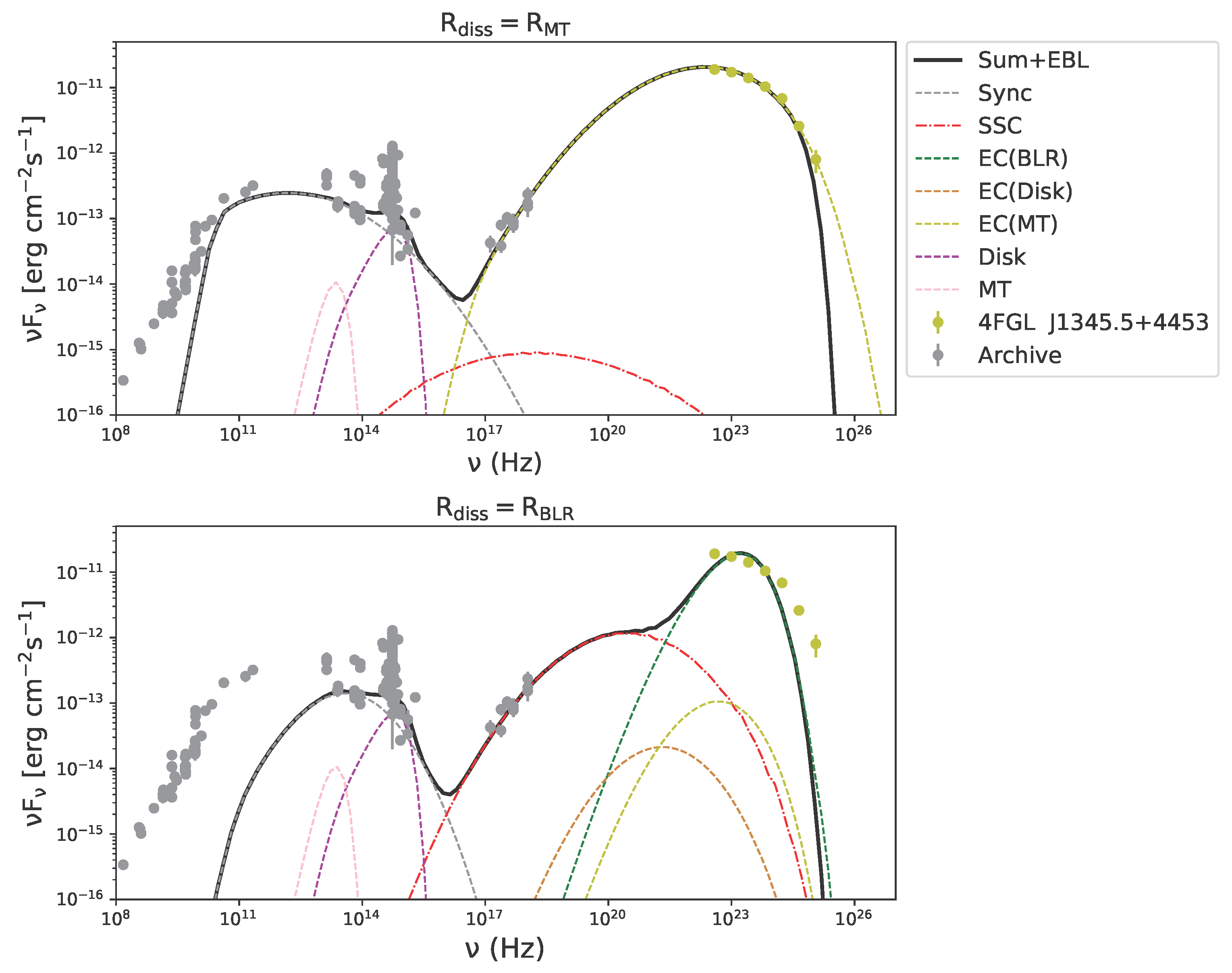
A representative SED fitting result is shown in Figure 1. In the BLR case, the X-ray band is typically dominated by SSC, with gamma rays produced via BLR photons, except for a few sources such as B20743+25, TXS0222+185, and B3 0908+416B. In the MT case, MT photons dominate the high-energy hump and often contribute substantially—sometimes dominantly—to the X-ray band, depending on the source state and parameters. Additionally, we observe a decline in flux around 10²⁵ Hz, which can be attributed to EBL absorption. However, since most of our sources lack data points in this energy range, the impact of the EBL on our results is negligible.

Figure 1. The top and bottom panels represent the best fits with $R_{\mathrm{diss}}=R_{\mathrm{MT}}$ and $R_{\mathrm{diss}}=R_{\mathrm{BLR}}$, respectively. The grey points from the radio to X-ray bands represent the historical data obtained from the SSDC Sky Explorer. Separate synchrotron, MT, accretion disk, SSC, EC-disk, EC-BLR, and EC-MT components are shown. The black solid line in all plots represents the sum of all components, which have been corrected for EBL absorption considering the model of Finke et al. [57].

Following Celotti and Ghisellini [64], we compute, from the seven best fitted parameters, the jet powers carried by the magnetic field ($P_{\mathrm{B}}$), emitting electrons/positrons ($P_{\mathrm{e}}$), radiation ($P_{\mathrm{r}}$), and cold protons ($P_{\mathrm{p}}$) in the jet.

The Compton dominance (CD) is used to characterize the proportion of IC scattering relative to synchrotron radiation. As shown in Table 3 and Table 4, we find that for high-redshift blazars, it is challenging to distinguish between particle-dominated or Poynting-dominated jets directly solely through parameter fitting, consistent with the conclusions of Fan et al. [65]. While equipartition might exist between the magnetic field and nonthermal electron energy density, this balance is disrupted when considering the protons in the jet, whose content/proportion remains uncertain [66].

Table 3 and Table 4 also report the chi-square values for the $\gamma$-ray band fits. Although many MT cases yield relatively low chi-square values, this alone is not sufficient to confirm that the emission region is located near the MT. In the absence of definitive constraints from either theoretical parameter analysis or fit statistics, we follow the common assumption adopted in previous studies of high-redshift blazars—that the emission region lies near the MT—and proceed with the subsequent discussion under this framework [13,15,67].

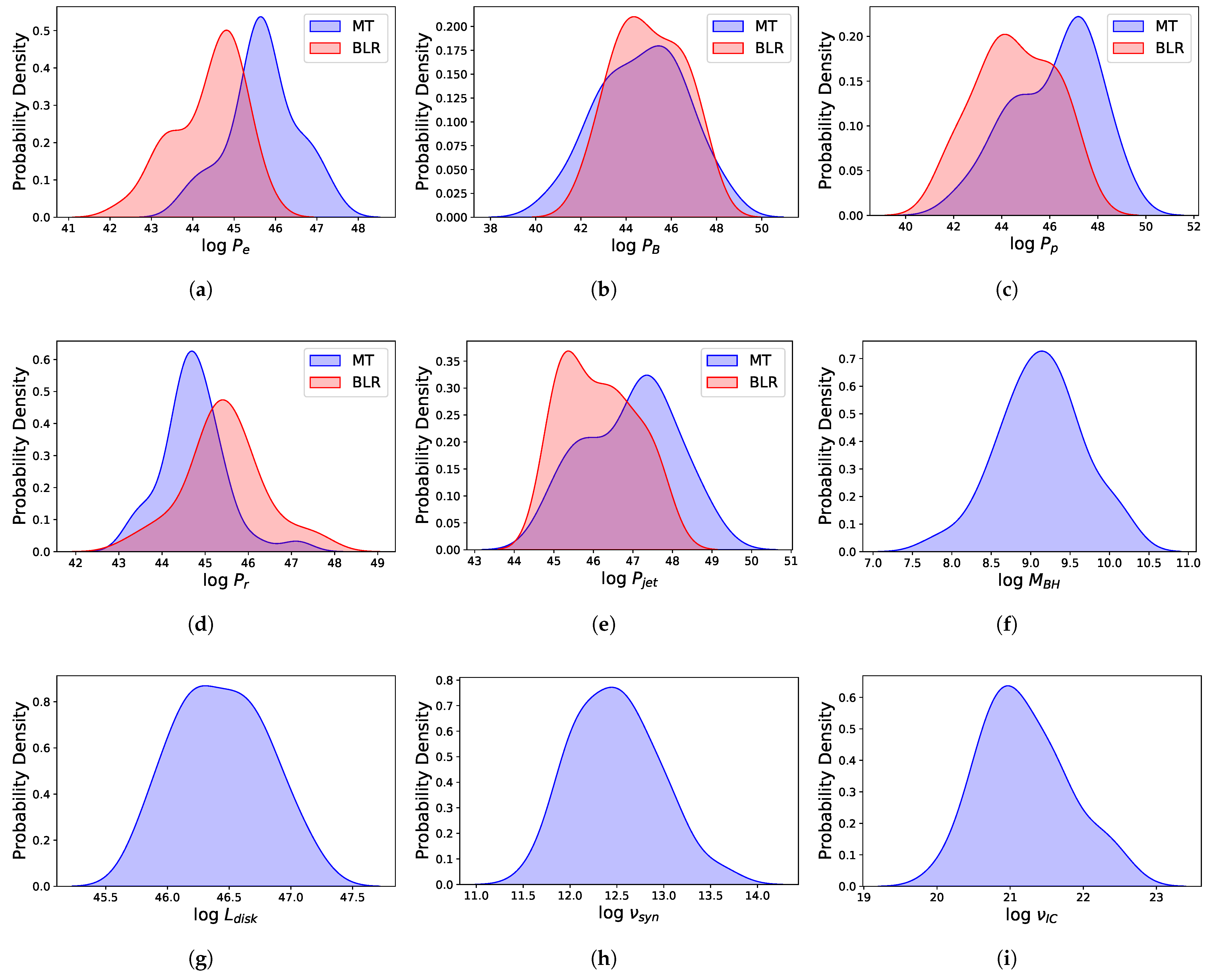
In the MT case, we used kernel density estimation to determine the probability density function of each parameter, as shown in Figure 2. The figure demonstrates that the parameters span similar ranges across the sample, thus allowing us to use the average values for further discussion.

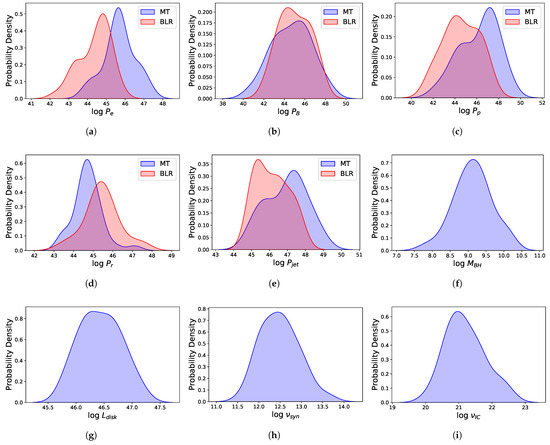
Figure 2. (a–i) The distributions of the physical parameters. The red line is $R_{\mathrm{diss}}=R_{\mathrm{BLR}}$ and the blue line is $R_{\mathrm{diss}}=R_{\mathrm{MT}}$. The last four parameters are identical in both the BLR and MT cases.

4. Discussion and Conclusions

4.1. High-Energy Radiation Properties

The integrated $\gamma$-ray fluxes (above 0.1 GeV) range from $\left(0.40\mathrm{to}713.33\right)\times {10}^{-9}\mathrm{ph}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}$, which is comparable to that of low-redshift blazars [68]. It is possible that the brighter emission observed in these high-redshift blazars is due to denser external photon fields in high-redshift AGNs, which enhance IC emission. Additionally, selection effects can also provide an explanation, as high-redshift blazars must be powerful enough to be detected. Among them, the object with the highest flux is PKS 1830-211, and the lowest is NVSS J121915+365718.

The synchrotron peak frequencies are in the range of $\left(0.46–39.81\right)\times {10}^{12}\mathrm{Hz}$, which is typical for low-synchrotron-peaked blazars. The accretion disk luminosities are between $\left(0.60–14.79\right)\times {10}^{46}\mathrm{erg}{\mathrm{s}}^{-1}$, with an average value of $3.29\times {10}^{46}\mathrm{erg}{\mathrm{s}}^{-1}$; these values are characteristic of powerful blazars.

The BH masses in our sample are generally >${10}^{8.5}{M}_{\odot }$, because blazars with larger disk luminosities have larger BH masses [59,69]. The disk luminosities of these sources do not exceed their Eddington luminosities, however, where the ratio $L_{\mathrm{disk}}/L_{\mathrm{Edd}}\sim 0.001–0.137$. This suggests that high-redshift blazars are likely in a sub-Eddington accretion state, where the typical standard thin disk, i.e., the Shakura–Sunyaev disk, can sufficiently explain their accretion structure [53,54,70].

When the radiation region is near the MT, the average EED spectral index is ∼$3.19$, which deviates from the canonical prediction of shock acceleration theories. Possible explanations include the presence of fast radiative cooling [71], the strong sensitivity of the spectrum to the form of the particle diffusion function along the shock front [72], or the contribution of shock drift acceleration [73]. Therefore, our results remain consistent with the broader expectations of standard particle acceleration scenarios [74,75,76].

Some of the Doppler factors obtained from our SED fits are rather large (>50). We have compared our results with the latest Doppler factor sample derived from broad emission lines in the work of Chen et al. [77], and we find that their values are indeed smaller than those obtained from our modeling. This discrepancy may arise from our simplified assumption that the bulk Lorentz factor equals the Doppler factor, or from differences in the locations of the emission regions probed at different wavelengths (we assume that the emission region is near the MT, where they may not be the same).

For high-redshift blazars, we find that the magnetic energy density of external photons from the MT—mainly IR photons from the MT—is approximately $\left({10}^{-4}–{10}^{-3}\right)\mathrm{erg}{\mathrm{cm}}^{-3}$, while the magnetic energy density of the external photon field near the BLR—mainly UV photons from the BLR—is $\left({10}^{-1}–{10}^0\right)\mathrm{erg}{\mathrm{cm}}^{-3}$.

The total jet power in our sample ranges within $(1.21\times {10}^{45}–3.05\times {10}^{50})\mathrm{erg}{\mathrm{s}}^{-1}$, with an average of $4.90\times {10}^{47}\mathrm{erg}{\mathrm{s}}^{-1}$, significantly exceeding that of low-redshift AGNs [42]. Whether this is driven by selection effects or intrinsic differences, the high-redshift blazars studied here exhibit greater kinetic and jet powers than low-redshift blazars. Some studies suggest that the jet composition may not correspond to exactly zero pair content. However, even when adopting a ratio of $n_{\mathrm{e}}/n_{\mathrm{p}}=0.1$, the average jet power changes only slightly (from $4.90\times {10}^{47}\mathrm{erg}{\mathrm{s}}^{-1}$ to from $1.10\times {10}^{47}\mathrm{erg}{\mathrm{s}}^{-1}$), remaining within the same order of magnitude. We find that $P_{\mathrm{e}}>P_{\mathrm{r}}$, consistent with Tan et al. [78], suggesting that the most energy of the relativistic electrons is dissipated by EC radiation.

In addition, the disk luminosities and jet powers in our sample are generally of the same order of magnitude, consistent with several previous studies [59,79,80,81,82]. This contrasts with the results of Sahakyan et al. [15], Xiong and Zhang [81], because their estimates did not account for the presence of protons in the jet, leading to an underestimation of the true jet power. Given the essential role of protons in counteracting deceleration caused by the Compton rocket effect [17,83], this further supports the reliability of our results.

4.2. Disk–Jet Connection

To examine whether the relationship between the accretion and jet evolves with redshift, we performed a Pearson correlation analysis for high-redshift blazars using their accretion and jet powers, and compared the results with those of Ghisellini et al. [37]. Their sample consists predominantly of 207 low-redshift blazars ($z<2.5$; 181 FSRQs and 26 BL Lacs), and 10 high-redshift sources. To minimize biases arising from intrinsic differences between blazar subclasses, we restricted the comparison to low-redshift FSRQs ($z<2.5$) from their dataset.

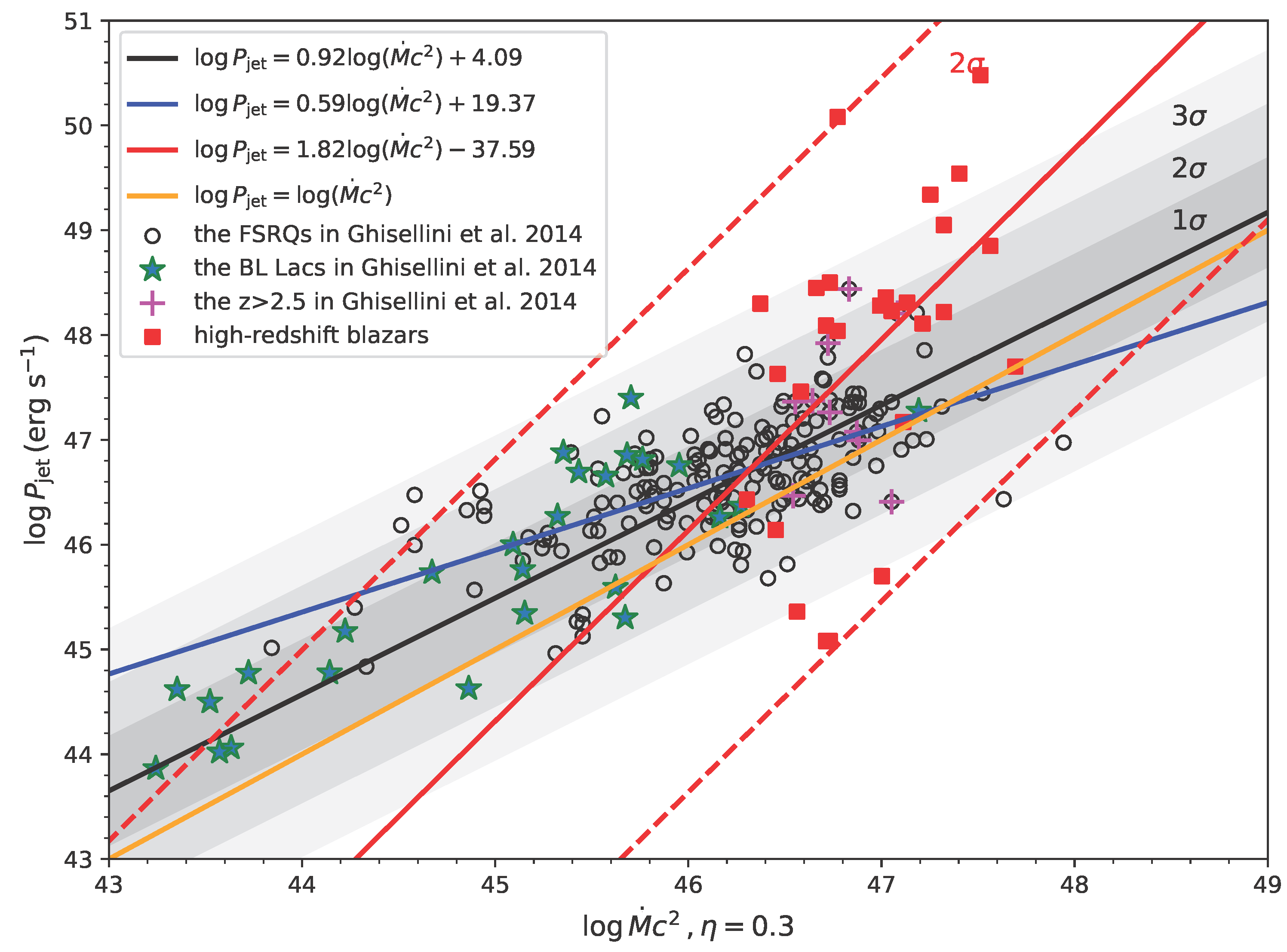
In our sample, the accretion power was derived from the disk luminosity inferred through broad emission lines, adopting the relation $\dot{M}{c}^2=L_{\mathrm{disk}}/\eta$. To ensure reliability, we excluded objects lacking robust accretion–disk luminosity estimates, as well as sources with poor $\gamma$-ray spectral fits (i.e., excessively large ${\chi }^2$ values). The final working sample consists of 27 objects with reliable estimates of both $\dot{M}{c}^2$ and $P_{\mathrm{jet}}$, which were subsequently used in the correlation and least-squares regression analysis. The results are presented in Figure 3.

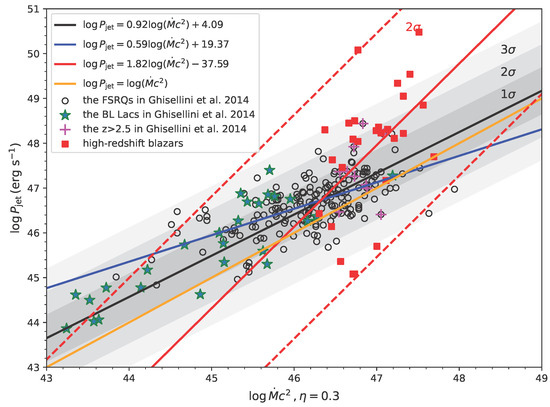
Figure 3. A linear relationship between $log{P}_{\mathrm{jet}}$ and $log\dot{M}{c}^2$ is shown. The black solid line and its shaded uncertainty band correspond to the best-fit relation for the full sample from Ghisellini et al. [37]. The blue line represents the fit obtained by retaining only the low-redshift FSRQs ($z<2.5$) in Ghisellini et al. [37]. “+” symbols mark the $z>2.5$ sources from Ghisellini et al. [37], while pentagrams denote BL Lacs. Red squares indicate our high-redshift blazar sample. The red solid line shows the best-fit relation derived for our sample using the least-squares method, with dashed lines representing the $2\sigma$ confidence interval. The orange solid line denotes the line of equality. The Pearson correlation coefficients for the three relations are 0.76, 0.64, and 0.49, respectively, all with p-values < 0.01.

Figure 3 shows the correlation between jet power and the mass accretion rate, and we find that the high-redshift sample has a higher $\dot{M}$, yet exhibits a weaker Pearson correlation coefficient r. This suggests that at a very high $\dot{M}$, the influence of accretion on jet power becomes weaker. In such cases, the magnetic field may become saturated or enter a magnetically arrested disk (MAD) state [84,85], where the field strength, its configuration, and BH spin likely play a more dominant role than $\dot{M}$. We therefore suggest that at high accretion rates, the BP mechanism becomes less effective, leading to a weaker disk–jet connection in the high-redshift BHs.

Moreover, in our high-redshift sample, assuming a maximal radiative efficiency ($\eta$∼0.3, to be consistent with the parameter values commonly assumed in Ghisellini et al. [37]), we find that jet power increases more steeply with accretion power compared to the low-redshift sample (i.e., a larger slope in the $P_{\mathrm{jet}}$-$\dot{M}{c}^2$ relation). Two possible factors may contribute to this difference in slope. First, BHs with higher spin tend to have higher radiative efficiencies, since $\eta$ is determined by the gravitational energy released at the innermost stable circular orbit (ISCO). A higher spin implies a smaller ISCO radius, allowing more gravitational energy to be converted into radiation. Second, it is widely believed that high accretion rates—particularly in the form of coherent or continuous accretion—tend to spin up BHs over time. This process simultaneously increases the BH’s angular momentum. In contrast, BHs with low accretion rates may experience stochastic, small-scale accretion events with random angular momentum directions, making it difficult to increase spin.

Taken together, these considerations suggest that high-redshift BHs, which generally have a high $\dot{M}$, are likely to possess a consistently high spin and thus a high $\eta$, consistent with Gardner and Done [86]. Adopting a constant $\eta$ may underestimate $\dot{M}$ for some lower-luminosity sources, thereby slightly flattening the observed slope.

Additionally, we find that in many cases, the jet power exceeds the total accretion power, implying a growing and non-negligible contribution from the BZ mechanism as the magnetic field accumulates. The fact that the process of forming and launching relativistic jets is more powerful only in jetactive states does not affect the conclusion that the BZ process becomes more powerful, even if it does not always works at its maximum pace. Our finding is consistent with the conclusions of Ghisellini et al. [37]. Even considering that lower $n_e/n_p$ ratios could reduce the estimated jet power [87], the BZ mechanism still plays a major role.

Our analysis of high-redshift blazars provides valuable insights into the radiation properties of their jets, with most sources showing significant curvature and softer spectral indices. By constructing and analyzing the average SEDs of a sample of high-redshift blazars ($z>2.5$), we reduced the uncertainties caused by lower-quality data typical of individual high-redshift blazars. Compared to low-redshift blazars, high-redshift blazars exhibit higher $\gamma$-ray luminosities, jet power, kinetic power, energy densities, BH mass, accretion disk luminosities, and mass accretion rate. Naturally, we acknowledge that selection effects cannot be fully eliminated. Our purpose is solely to report our fit results and suggest a possible physical mechanism.

All samples have an accretion disk luminosity that is lower than their Eddington luminosity, indicating sub-Eddington accretion. The accretion structure can be explained by the Shakura–Sunyaev disk model. The EED spectral index is ∼$3.19$, and our results remain consistent with the broader expectations of standard particle acceleration scenarios. For high-redshift BHs or those with high accretion rates, jet power may no longer be primarily governed by $\dot{M}$, but rather by magnetic fields and BH spin, or other physical factors, with the BZ process playing a more significant role than in low-$\dot{M}$ systems. We further speculate that high-redshift BHs tend to have higher spins and radiative efficiencies. As redshift decreases, only under conditions of high accretion rates and coherent (i.e., aligned) inflow can a BH maintain a high spin state. Consequently, our results consistently indicate a more crucial role for the BZ process in high-redshift blazars than in low-redshift blazars.