Gravitational Wave Detection with Angular Deviation of Electromagnetic Waves
Abstract
1. Introduction
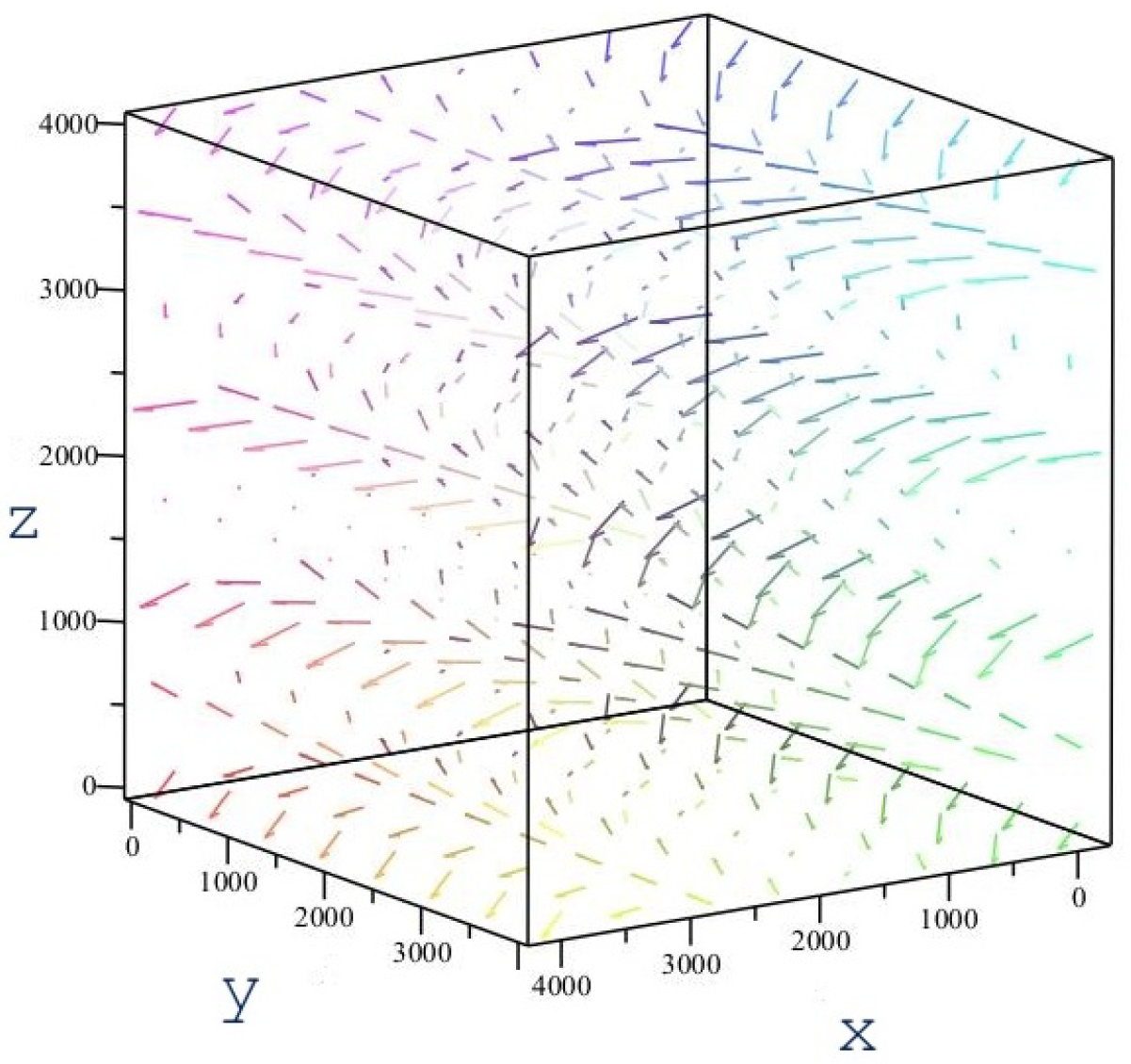
2. Interaction of Gravitational Waves with Electromagnetic Waves
3. Angle Perturbations
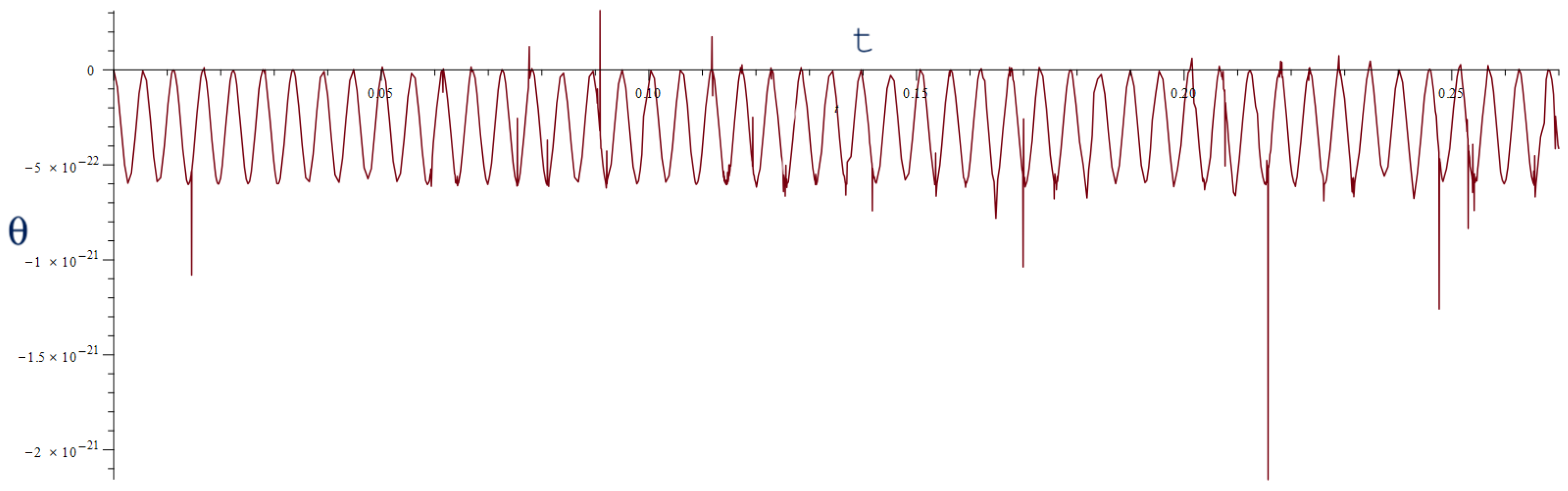
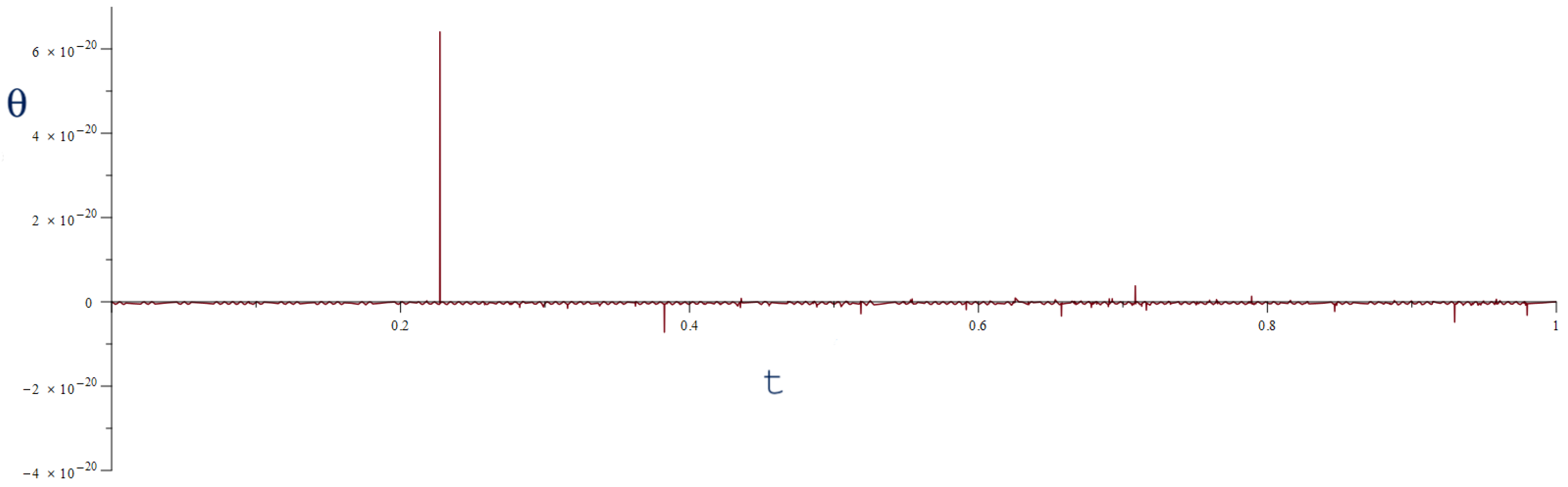
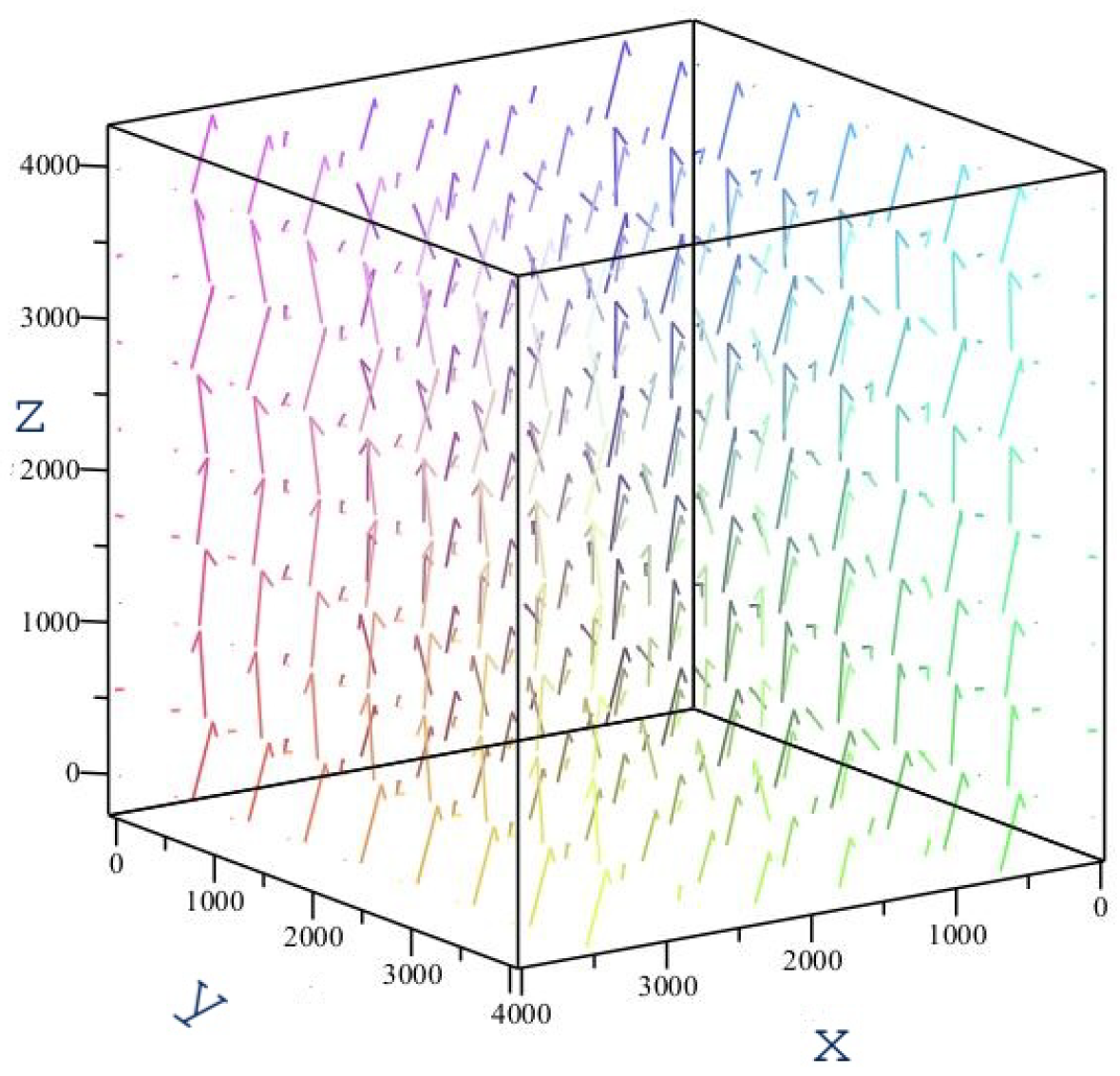
4. Geodynamic Effects on Angle Measurement
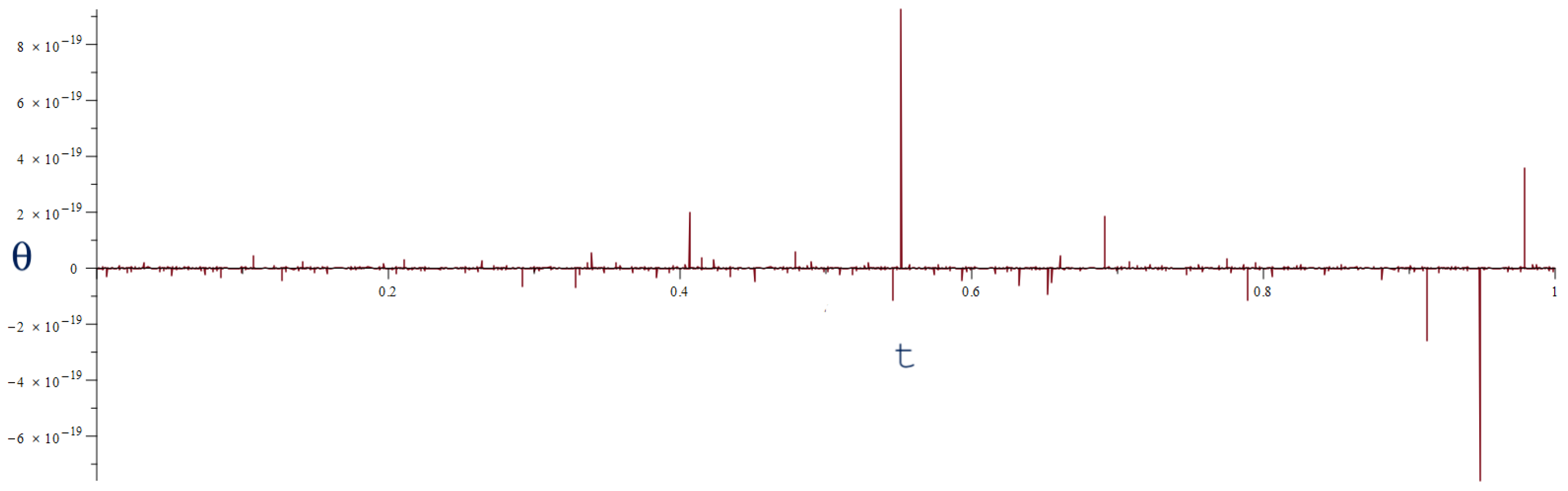
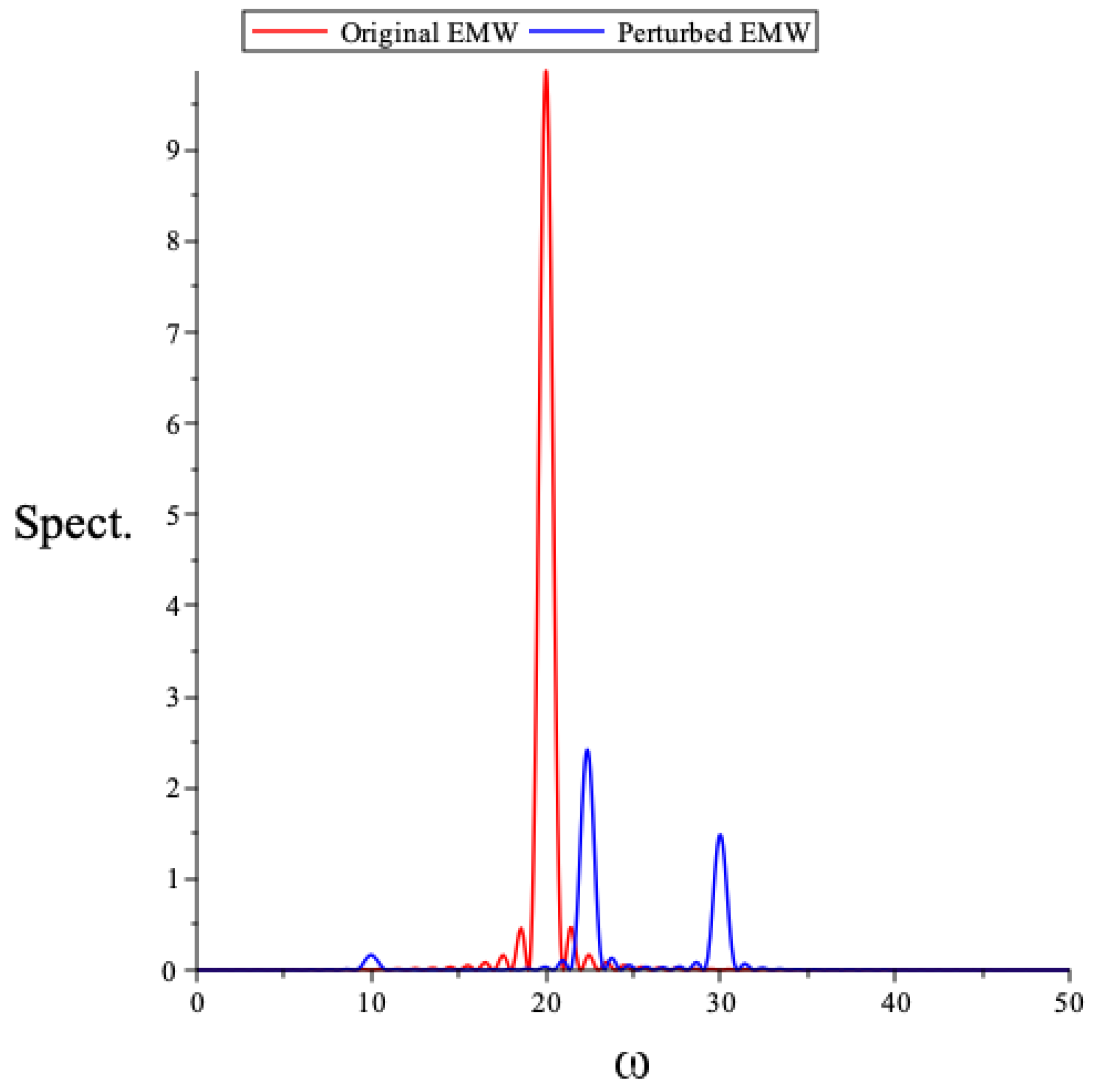
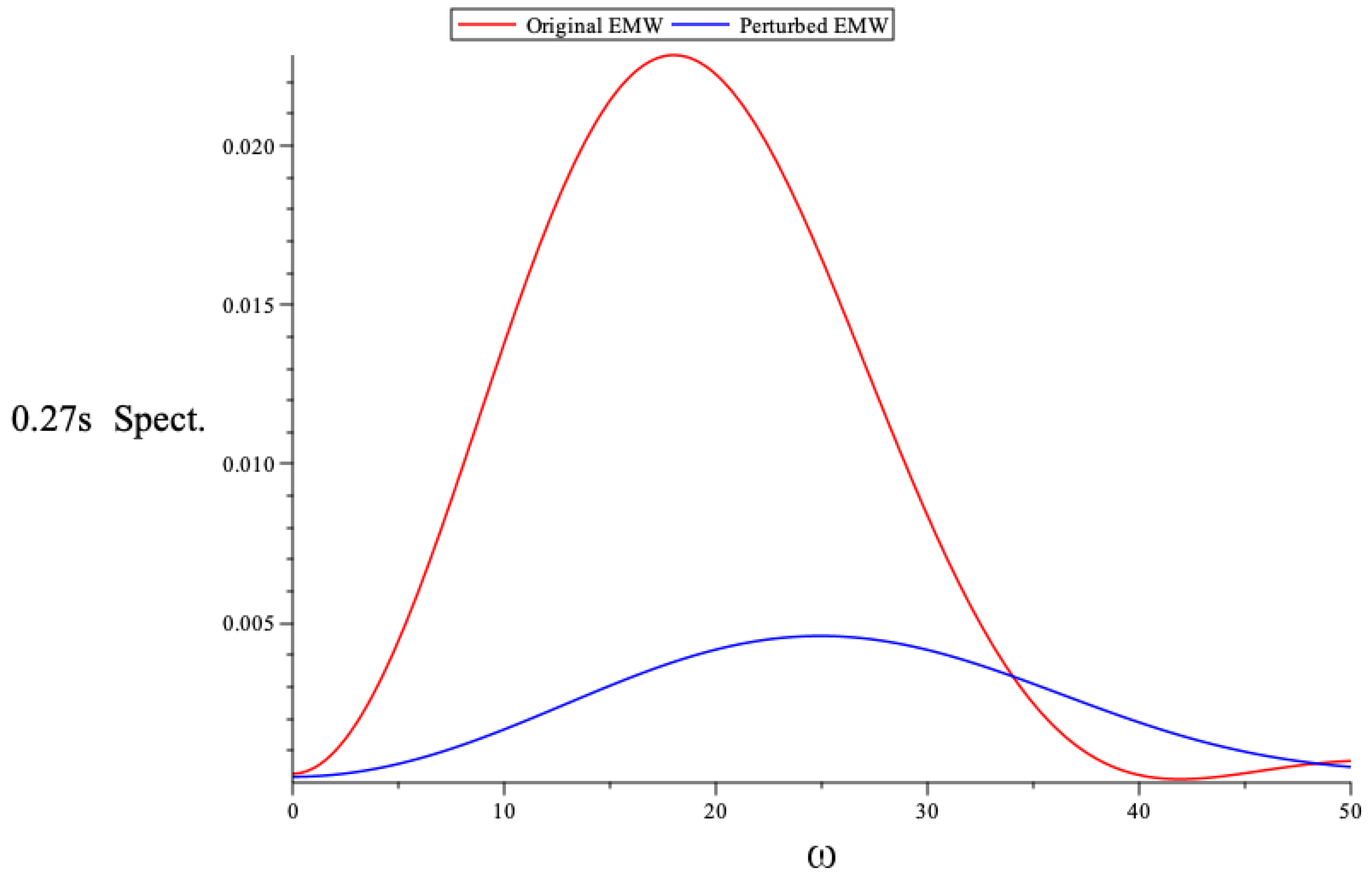
5. Spectral Analysis of the Scattered Beam
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GW | Gravitational Wave |
| EMW | Electromagnetic Waves |
References
- The LIGO Scientific Collaboration Publications. Available online: https://pnp.ligo.org/ppcomm/Papers.html (accessed on 25 May 2025).
- The LISA Interferometer. Available online: https://lisa.nasa.gov/ (accessed on 25 May 2025).
- Abac, A.; Abramo, R.; Albanesi, S.; Albertini, A.; Agapito, A.; Agathos, M.; Albertus, C.; Andersson, N.; Andrade, T.; Andreoni, I.; et al. The Science of the Einstein Telescope. arXiv 2025, arXiv:2503.12263. [Google Scholar]
- Ricciardone, A. Primordial Gravitational Waves with LISA. J. Phys. Conf. Ser. 2017, 840, 012030. [Google Scholar] [CrossRef]
- Aggarwal, N.; Aguiar, O.D.; Bauswein, A.; Cella, G.; Clesse, S.; Cruise, A.M.; Domcke, V.; Figueroa, D.G.; Geraci, A.; Goryachev, M.; et al. Challenges and opportunities of gravitational-wave searches at MHz to GHz frequencies. Living Rev. Relativ. 2021, 24, 4. Available online: https://link.springer.com/article/10.1007/s41114-021-00032-5 (accessed on 25 May 2025). [CrossRef]
- Aggarwal, N.; Aguiar, O.D.; Blas, D.; Bauswein, A.; Cella, G.; Clesse, S.; Cruise, A.M.; Domcke, V.; Ellis, S.; Figueroa, D.G.; et al. Challenges and Opportunities of Gravitational Wave Searches above 10 kHz. arXiv 2025, arXiv:2501.11723. Available online: https://arxiv.org/pdf/2501.11723 (accessed on 30 June 2025).
- Tong, M.; Zhang, Y.; Li, F. Using polarized maser to detect high-frequency relic gravitational waves. Phys. Rev. 2008, D78, 024041. [Google Scholar] [CrossRef]
- Patel, A.; Dasgupta, A. Interaction of Electromagnetic field with a Gravitational wave in Minkowski and de-Sitter space-time. arXiv 2021, arXiv:2108.01788. [Google Scholar]
- Morales, S.; Dasgupta, A. Scalar and Fermion field interactions with a gravitational wave. Class. Quant. Grav. 2020, 37, 105001. [Google Scholar] [CrossRef]
- Gosala, N.R.; Dasgupta, A. Interaction of gravitational waves with Yang–Mills fields. Gen. Rel. Grav. 2024, 56, 36. [Google Scholar] [CrossRef]
- Gosala, N.R.; Dasgupta, A. Effect of gravitational waves on Yang-Mills condensates. Class. Quant. Grav. 2025, 42, 065012. [Google Scholar] [CrossRef]
- Odutola, O.; Dasgupta, A. Gauss’s Law and a Gravitational Wave. Universe 2024, 10, 65. [Google Scholar] [CrossRef]
- Gulian, A.; Foreman, J.; Nikoghosyan, V.; Sica, L.; Abramian-Barco, P.; Tollaksen, J.; Melkonyan, G.; Mowgood, I.; Burdette, C.; Dulal, R.; et al. Gravitational wave sensors based on superconducting transducers. Phys. Rev. Res. 2021, 3, 043098. [Google Scholar] [CrossRef]
- Nicholl, M.; Andreoini, I. Electromagnetic follow-up of gravitational waves: Review and lessons learned. Phil. Trans. R. Soc. A 2025, 383, 20240126. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Adhikari, R.; Ajith, P.; Allen, B.; Allen, G.; Amin, R.S.; Anderson, S.B.; Anderson, W.G.; Arain, M.A.; et al. LIGO: The Laser Interferometer Gravitational-Wave Observatory. Rep. Prog. Phys. 2009, 72, 076901. [Google Scholar] [CrossRef]
- Gertsenshtein, M.E. Wave Resonance of Light and Gravitational Waves. JETP 1962, 14, 84. [Google Scholar]
- Li, J.-K.; Hong, W.; Zhang, T.-J. Polarization Properties of the Electromagnetic Response to High-frequency Gravitational Wave. Astrophys. J. 2025, 985, 137. [Google Scholar] [CrossRef]
- Romano, A.E.; Vallejo-Pena, S.A. Gravitoelectromagnetic quadrirefringence. Phys. Dark. Univ. 2024, 44, 101492. [Google Scholar] [CrossRef]
- Breeze, J.; Salvadori, E.; Sathian, J.; Alford, N.M.; Kay, C.W.N. Continuous-wave room-temperature diamond maser. Nature 2018, 555, 493–496. [Google Scholar] [CrossRef]
- Pravdivtsev, A.N.; Sannichsen, F.D.; Havener, J.B. Continuous Radio Amplification by Stimulated Emission of Radiation using Parahydrogen Induced Polarization (PHIP-RASER) at 14 Tesla. Chemphyschem 2020, 21, 667–670. [Google Scholar] [CrossRef]
- Bishop, N.T.; Rezzolla, L. Extraction of gravitational waves in numerical relativity. Living. Rev. Relativ. 2016, 19, 2. [Google Scholar] [CrossRef]
- Gravitational Waves II: Interferometer Detection (General Relativity). Available online: https://www.youtube.com/watch?v=eUPqA0s5vMU (accessed on 25 May 2025).
- GW170814 Factsheet (2017). Available online: https://www.ligo.caltech.edu/image/ligo20170927f (accessed on 20 July 2025).
- Vacatello, M.; Ardito, S.; Baratti, M.; Bartoli, G.; Bellizzi, L.; Demasi, G.; De Santi, F.; Fidecaro, F.; Fiori, A.; Muccillo, L.; et al. New strategies for seismic attenuation at low frequency for third generation gravitational waves detectors. Nuovo C. 2025, 48, 106. [Google Scholar] [CrossRef]
- Yang, L.; Ding, X.; Biesaida, M.; Liao, K.; Zhu, Z.-H. How Does the Earth’s Rotation Affect Predictions of Gravitational Wave Strong Lensing Rates? Astrophys. J. 2019, 874, 139. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maher, J.; Dasgupta, A. Gravitational Wave Detection with Angular Deviation of Electromagnetic Waves. Universe 2025, 11, 244. https://doi.org/10.3390/universe11080244
Maher J, Dasgupta A. Gravitational Wave Detection with Angular Deviation of Electromagnetic Waves. Universe. 2025; 11(8):244. https://doi.org/10.3390/universe11080244
Chicago/Turabian StyleMaher, John, and Arundhati Dasgupta. 2025. "Gravitational Wave Detection with Angular Deviation of Electromagnetic Waves" Universe 11, no. 8: 244. https://doi.org/10.3390/universe11080244
APA StyleMaher, J., & Dasgupta, A. (2025). Gravitational Wave Detection with Angular Deviation of Electromagnetic Waves. Universe, 11(8), 244. https://doi.org/10.3390/universe11080244






