Abstract
By “nethotron”, from the ancient Greek verb for “to spin”, it is meant here a natural or artificial rotating object, like a pulsar or an artificial satellite, whose rotational axis is cumulatively displaced by the post-Newtonian static (gravitoelectric) and stationary (gravitomagnetic) components of the gravitational field of some massive body around which it freely moves. Until now, both relativistic effects have been measured only by the dedicated space-based mission Gravity Probe B in the terrestrial environment. It detected the gravitoelectric de Sitter and gravitomagnetic Pugh–Schiff spin precessions of four superconducting gyroscopes accumulated within a year after about 50 years from conception to completion of data analysis at a cost of 750 million US dollars to and 19 percent accuracy, respectively. The perspectives to measure them with Earth’s long-lived laser-ranged geodetic satellites, like those of the LAGEOS family or possibly one or more of them to be built specifically from scratch, and pulsars orbiting the supermassive black hole in the Galactic Centre, yet to be discovered, are preliminarily investigated. The double pulsar PSR J0737-3039A/B is examined as well.
1. Introduction
One of the most intriguing, and, to a certain extent, least tested predictions of the General Theory of Relativity (GTR) is the temporal evolution of the spin axis of a gyroscope freely moving in the external gravitational field of a massive, also rotating body of mass M, equatorial radius R, quadrupole mass moment , and angular momentum . Indeed, Newtonian mechanics implies that the spin of the orbiting object experiences a steady, cumulative gravitational precession with respect to distant observers, induced solely by M, only if it is itself nonspherical being endowed with, e.g., an own oblateness [,]. A further Newtonian contribution of gravitational origin to the overall gyroscope’s spin precession may arise if a distant third body is present as well []. Instead, according to GTR, changes cumulatively its orientation with respect to remote stars even if the particle carrying it is spherically symmetric and if there are no other bodies to pull it other than its primary. Furthermore, both M and contribute to the total gyroscope’s spin rate through the static and stationary post-Newtonian (pN) components of the exterior gravitational field of the central source of which they are the mass and angular momentum, respectively. To the first post-Newtonian (1 pN) level, the gravitoelectric and gravitomagnetic precessions of the spin of a pointlike gyroscope of negligible mass due to M and were calculated by de Sitter [] and Fokker [], and Pugh and Schiff [,], respectively. They can be found written in compact, vectorial form, e.g., in1 [,].
At present, the only direct test of both the aforementioned pN gravitoelectromagnetic effects in a dedicated, controlled experiment was conducted in the Earth’s surroundings by the Gravity Probe B (GP-B) space-based mission []. The de Sitter (dS) and Pugh–Schiff (PS) precessions of four superconducting spinning spheres carried onboard a drag-free spacecraft orbiting our planet in a low-altitude, polar orbit were successfully measured to a and 19 percent accuracy [], respectively, compared to an initially estimated much better one [,]. The entire mission, whose duration since the initial conception to completion of data analysis can be estimated to have been around 50 years, cost about 750 million US dollars; the data collection phase lasted a year []. At present, the GP-B remains the only test of the PS spin precession and the only undisputed test ever of a gravitomagnetic effect. As far as the dS precession is concerned, it was measured also with the Lunar Laser Ranging (LLR) technique [] by considering the whole orbit of the Earth-Moon system as a giant gyroscope whose orientation with respect to distant stars is cumulatively displaced during its freely falling in the deformed spacetime of the Sun; the latest tests are accurate to [] and percent []. The generalization of the dS spin precession to a two-body system of comparable masses was measured to a ≃ 13–6 percent accuracy [,] with the double pulsar PSR J0737–3039A/B [,] whose members can be viewed, among other things, as strongly self-gravitating gyroscopes, contrary to the man-made light spheres of GP-B [].
The scope of this paper is to explore the possibility of performing further tests of the 1 pN spin precessions with either artificial or natural pointlike gyroscopes by exploiting existing objects, possibly still to be discovered, or by specifically building new ones that are not excessively expensive. It should be recalled that, in view of its complexity and cost, GP-B is most likely never to be repeated. The role of the negligible mass gyroscope orbiting a massive, rotating primary will be played by both Earth’s artificial satellites and pulsars orbiting a supermassive black hole (SMBH), collectively denoted as “nethotrons”, from the ancient Greek verb (nth), meaning “to spin”, and the suffix-o (-tron) used to make instrument nouns.
As for artificial nethotrons, the first thought immediately goes to geodetic satellites of the LAGEOS type [] tracked with the Satellite Laser Ranging (SLR) technique [], the evolution of whose spin axes has actually been measured for a long time [,,,,,,,,,,,,,,]. Given the relatively modest accuracy of the test of the gravitomagnetic spin precession performed with the very sophisticated and expensive GP-B, built expressly for that purpose, even just the idea of using the simple passive geodetic satellites might seem decidedly bizarre, if not absurd. Nevertheless, it is anyway explored here for the following reasons. (a) There are so many SLR satellites currently in orbit. (b) They are expected to remain there for a virtually indefinite period of time. (c) They are tracked on a nearly continuous basis. (d) Measuring their spin motion is currently one of the main goals of satellite geodesy. (e) The temporal signatures of the pN effects of interest, being generally different from linear trends in view of the non-dedicated satellites’ orbital and spin configurations, may make their detection easier, allowing also for an effective disentangling from the competing signals of classical origin. (f) As if that were not enough, building and launching one or more new LAGEOS-type satellites is feasible at a relatively low cost. The latter would certainly not increase much even if particular care were taken in the manufacturing of such objects. (g) Finally, it is of interest to understand quantitatively where we stand evaluating how much the measurement techniques of the SLR satellites’ spin motion would have to become more precise to allow the measurement of the relativistic signals of interest in possibly implementing one or more low-cost versions of GP-B.
Instead, the best candidate for a natural nethotron would be a pulsar orbiting the SMBH in Sgr A* at the Galactic Centre (GC) in, say, a yr or a 2–5 yr orbit, yet to be discovered; efforts towards this goal have been underway for a long time [,,,]. This eventuality has been long-awaited since it would allow probing the spacetime2 around the hole, with particular attention to its angular momentum [,,,,,]. To this aim, efforts have been focused so far on the secular orbital precessions of the pulsar. Measuring also the 1 pN pulsar’s spin precession(s) would provide, in principle, a further tool to effectively constrain the key parameters of the SMBH’s spacetime which, in the case of a rotating hole [], is believed to be described by the Kerr metric [,]. In principle, the internal structure of a neutron star couples with the external deformed spacetime impacting on both its orbital and rotational dynamics [,,]. Nonetheless, in the present case, the nethotron approximation is also valid for it since it will be shown that the multipolar structure of the pulsar’s self-gravity is negligible for its spin precession already at the Newtonian level.
The paper is organized as follows. The analytical expressions of the 1 pN dS and PS spin precessions along with those of the Newtonian one due to the nethotron’s own oblateness are provided in Section 2. The pN spin axis shifts of the existing SLR satellites LAGEOS, LAGEOS 2 and LARES are numerically produced and displayed in Section 3. In it, also the impact of the satellite’s own oblateness on the evolution of its spin is treated. Moreover, the pN precessions of a hypothetical new satellite, dubbed NethoSAT (NS), are obtained as well. Section 4 deals with the case of a pulsar orbiting the SMBH in Sgr A*. The case of the double pulsar is treated in Section 5. Section 6 summarizes the findings and offers conclusions.
2. Analytical Expressions of the Newtonian and Post-Newtonian Spin Precessions
In the following, G is the Newtonian constant of universal gravitation, c is the speed of light in vacuum, is the standard gravitational parameter of the primary whose mass is M, a is the semimajor axis, is the Keplerian mean motion, e is the eccentricity, is the semilatus rectum, I is the inclination of the orbital plane to the reference plane, and is the longitude of the ascending node. Furthermore, the orbital unit vectors
are defined in such a way that . While is aligned with the orbital angular momentum, and lie within the orbital plane, being directed along the line3 of nodes toward the ascending node.
By parameterizing the nethotron’s spin axis in terms of its right ascension (RA) and declination (decl.) , it can be written as
Thus, the rates of change of and can be expressed as
In view of the following developments, it is useful to introduce the angle
which is the longitude of the ascending node reckoned from the projection of the spin axis onto the reference plane.
It should be stressed that, in any realistic scenario, the orientation of the nethotron’s orbital plane, characterized by I and , does generally change after every orbit because of a variety of physical effects, of gravitational and non-gravitational origin, the most important of which is the quadrupole mass moment of the primary. Next, one finds the gravitomagnetic field itself and possibly the pull of a distant third body. The first two perturbations give rise to []
where
Equations (10) and (11) hold for any orbital configuration and for a generic orientation of the primary’s spin axis in space. Since I and explicitly enter Equations (7) and (8), which are mutually coupled, one containing the variable of the other, the signatures of and are generally not secular trends, being instead long-term harmonic time series modulated by the characteristic time scales of the averaged variations of the orbital plane.
2.1. The Gravitoelectric de Sitter Spin Precession
The averaged gravitoelectric dS spin rate is [,]
In it, the precession velocity vector is given by
where
The resulting spin’s RA and decl. averaged precessions per orbit are
The dS spin precession depends only on the nethotron’s own spin-orbit coupling; it is zero when the orbital and spin angular momenta of the satellite are parallel, being, instead, maximum when they are mutually perpendicular.
2.2. The Gravitomagnetic Pugh–Schiff Spin Precession
The gravitomagnetic PS spin precession is [,]
In it, the precession velocity vector is given by
where is the primary’s spin axis, parameterized in terms of its RA and decl. as
and
The resulting spin’s RA and decl. averaged precessions per orbit are
where
analogously to Equation (9). If, as in the case of the Earth, , Equations (26) and (27) reduce to
2.3. The Newtonian Spin Precession Due to the Gyroscope’s Own Oblateness
The Newtonian gravitational spin precession induced by the coupling of primary’s mass M with the satellite’s quadrupole mass moment is [,]
In it, the precession velocity vector is given by
where
In Equation (33), the expression valid for a homogenous sphere was assumed for the nethotron’s moment of inertia, and
where is its spin period, assumed constant over an orbital revolution. From Equations (31) and (32) it turns out that the classical spin rate due to the nethotron’s own oblateness vanishes if its spin axis is either parallel or perpendicular to its orbital angular momentum.
The resulting spin’s RA and decl. averaged precessions per orbit are
3. The Case of the SLR Satellites
From Equations (15) and (16), Equations (20) and (21), and Equations (31) and (32), it turns out that if the three angular momenta are mutually aligned, as for a nethotron moving along an equatorial orbit with its spin axis parallel to the Earth’s axis, all the precessions of Section 2 vanish. If, instead, lies somewhere in the orbital plane parallel to the Earth’s equatorial one, its RA experiences a combined pN secular shift dominated by the larger dS one, which is prograde, with respect to the smaller retrograde PS one. Both the pN rates depend only on the inclination of the orbital plane. Note that, in this case, the orbital plane would stay parallel to the Earth’s equator since no gravitational torques displace it, as shown by by Equations (10)–(14). Furthermore, the nethotron’s spin would remain perpendicular to the orbital angular momentum since it would move within the orbital plane, only its RA being affected by the overall pN effect. Thus, the Newtonian precession due to would stay equal to zero. This fact would occur even if the pN effects did not exist at all. Indeed, is not classically shifted at all since, for , the right-hand-side of Equation (37) is identically zero over all the time. Thus, if the decl. of the nethotron’s spin axis starts from , it will remain zero forever. This implies that also the right-hand-side of Equation (36) will always be zero by keeping equal to its initial value , whatever it is.
Another orbital configuration that would ideally assure a constant orbital plane would be the polar one, i.e., when the Earth’s spin axis lies within the orbital plane, as it can straightforwardly be inferred by Equations (10)–(14). In this case, and are mutually perpendicular, and the largely dominant Newtonian precessions due to the primary’s oblateness vanish. If starts aligned with , which occurs for , it is slowly displaced parallel to the equatorial plane by the PS effect, changing only its RA in the prograde sense. If, instead, starts within the equatorial plane, perpendicular to both and , i.e., for , its RA undergoes the PS shift, while its decl. experiences the dS variation, as in the GP-B experiment. However, in the case of a polar orbit, the Newtonian precession due to the nethotron’s own oblateness would generally not vanish even if the pN effects were absent. Indeed, contrary to the equatorial case, the right-hand-sides of Equations (36) and (37) are not identically zero.
The spin and orbital configurations of the existing SLR satellites of the LAGEOS-type, listed in Table 1, do not fall in any of the previous cases.

Table 1.
In the first three rows, the relevant spin and orbital parameters of LAGEOS, LAGEOS 2 and LARES are shown as per Tables IV and V of []. The values of the spin’s periods , RA , and decl. refer to 15 May 1976 for LAGEOS, 23 October 1992 for LAGEOS 2 and 13 February 2012 for LARES. The figures for the rates of change of the satellites’ spin periods are inferred from Figures 1, 3 and 5 of []. The dimensionless quadrupole mass moments for each satellite were obtained from the values for their masses , radii , and principal moments of inertia , reported in Table I of [] and in the body of that article, as []. The last row displays the orbital and spin parameters of GP-B retrieved from [].
Figure 1, Figure 2 and Figure 3 show the numerically integrated time series of the dS, PS, and Newtonian shifts of the RA and decl. of the rotational axes of LAGEOS, LAGEOS 2 and LARES.
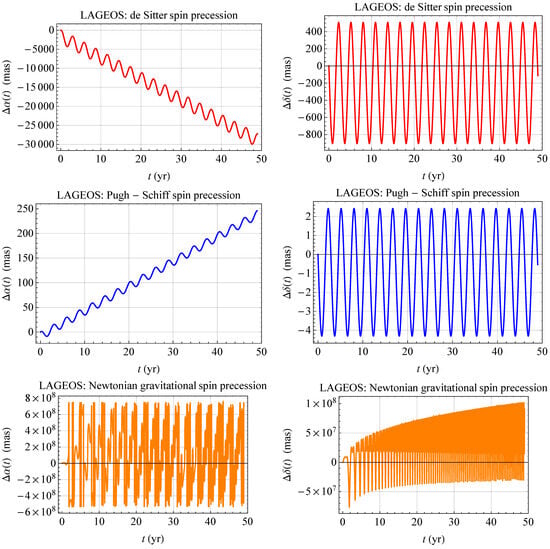
Figure 1.
Numerically integrated time series, in mas, of the dS (upper row), PS (middle row), and Newtonian (lower row) RA and decl. shifts and of the spin axis of LAGEOS over 49 yr. The initial values of the spin and orbital parameters were retrieved from Table 1. For the satellite’s spin period , entering the Newtonian shifts, a linearly varying model [] according to the values of Table 1 for was adopted.
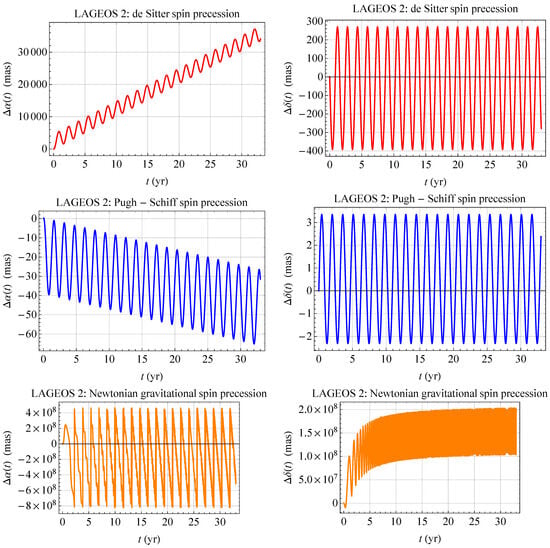
Figure 2.
Numerically integrated time series, in mas, of the dS (upper row), PS (middle row), and Newtonian (lower row) RA and decl. shifts and of the spin axis of LAGEOS 2 over 33 yr. The initial values of the spin and orbital parameters were retrieved from Table 1. For the satellite’s spin period , entering the Newtonian shifts, a linearly varying model [] according to the values of Table 1 for was adopted.
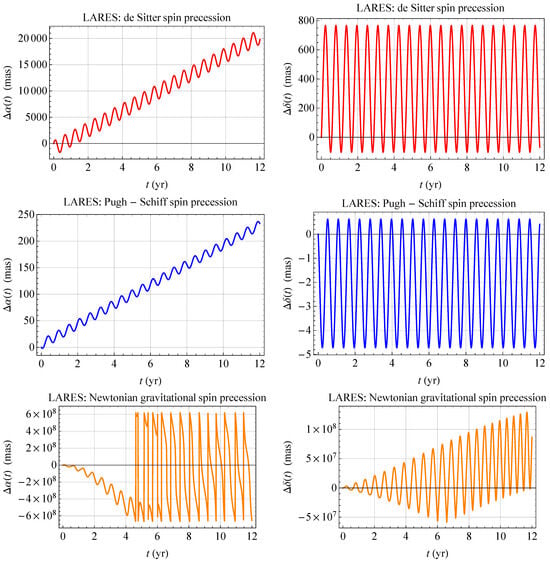
Figure 3.
Numerically integrated time series, in mas, of the dS (upper row), PS (middle row), and Newtonian (lower row) RA and decl. shifts and of the spin axis of LARES over 12 yr. The initial values of the spin and orbital parameters were retrieved from Table 1. For the satellite’s spin period , entering the Newtonian shifts, a linearly varying model [] according to the values of Table 1 for was adopted.
For each satellite, they were obtained by numerically integrating any of the spin rate equations out of Equations (15), (20), and (31) simultaneously with Equations (10) and (11). The time span of the integrations are 49 yr for LAGEOS, 33 yr for LAGEOS 2, and 12 yr for LARES, respectively.
As far as the pN effects are concerned, it turns out that the RA grows steadily with oscillations superimposed on the main trends, while the decl. exhibits oscillatory patterns. The peak-to-peak amplitudes of the decl. signals amount to about a thousand (dS) and five (PS) milliarcseconds (mas), respectively. Instead, the growing RA signatures amount to a few tens of thousands (dS) and a few hundreds (PS) of mas, respectively, over the time spans of the integrations. Instead, the Newtonian shifts, obtained by including the slowdown of the satellites’ spinning periods as per [], are clearly oscillatory, especially the RA signals, with peak-to-peak nominal amplitudes as large as hundreds of millions of mas. Such a peculiar feature turns out to be caused just by the lengthening of , modeled as an increasing linear trend according to Table 1 and []. Should it be neglected by keeping the rotational periods fixed, cleaner and regular trends would be obtained. It has been decided not to show them since they would be unrealistic, at least in the case of LAGEOS, LAGEOS 2, and LARES.
Actually, the spin axis of a LAGEOS-type satellite is displaced also by a number of further torques of non-gravitational origin [,,,,]. One of them is due to the interaction of the Earth’s magnetic field with the magnetic dipole moment acquired by the satellite during its diurnal rotation and orbital revolution through itself. Indeed, being a metallic object, the spacecraft is a conductor; thus, its motions in the external magnetic field of our planet induce parasitic eddy electrical currents within its body, which are just the source of . The possible non coincidence between the satellite’s centre of mass (CoM) and its geometrical center causes a further torque. Finally, another torque arises from the difference in the reflectivity of the two satellite’s hemispheres. A detailed analysis of their impact on the proposed measurement of the pN effects is outside the scope of the present paper.
At present, the spin axis orientation and/or rate of LAGEOS and its cousins are measured by exploiting the fact that either solar or laser radiation hitting the satellite is bounced back by its Corner Cube Retroreflectors (CCRs), which are oriented in rows. The number of spikes can be assessed by performing a frequency analysis so that the spin rate is estimated. The orientation of the satellite’s rotation axis can be inferred by combining the returns of the impinging electromagnetic waves with the geometry of the CCRs and that of the light source, satellite and observatory [,,]. Modern SLR systems characterized by high-repetition rate typically greater than 1 kHz and short pulse duration of the order of 10 ps reach a sub-degree accuracy level of about . It may be difficult to improve this limit since the optical “range” does not translate well to the orientation. Instead, collecting several solar glints during a single pass can lead to a very accurate determination of the satellite’s spin axis orientation, likely one or two orders of magnitude better than SLR. Such an approach is successfully exploited with the fast spinning Ajisai satellite []; in the case of the LAGEOS family, one may use ground-based photon counters to try to detect solar reflections off the satellite’s structure. In the future, continuous wave lasers and interference phenomena may allow for improvements in the accuracy of the laser-based spin determination of slowly rotating SLR satellites. In general, the faster the satellite rotates, the more stable its spin and the more accurately its orientation can be measured. Furthermore, a rapid rotation rate also allows the reduction of the impact of the Newtonian gravitational torque, as per Equation (33).
Figure 4 displays the numerically integrated pN shifts of the spin axis of a hypothetical new satellite, dubbed NethoSAT (NS), with the same spin and orbital configurations of GP-B.
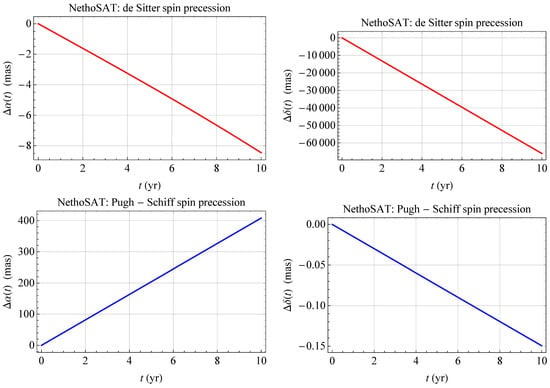
Figure 4.
Numerically integrated time series, in mas, of the dS (upper row) and PS (lower row) RA and decl. shifts and of the spin axis of a hypothetical NethoSAT over 10 yr. The initial values of the spin and orbital parameters of GP-B, retrieved from Table 1, were adopted.
It can be noted that while the largest pN signature affecting the RA is a gravitomagnetic PS linear trend with a slope of 40 mas/yr, the decl. exhibits a huge graviteoectric dS precession of mas/yr. Should NS be a passive geodetic SLR satellite, a careful manufacturing and ground testing of it may, in principle, reduce the competing classical effects to an acceptable level.
4. The Pulsar–Supermassive Black Hole Scenario
Here, the primary will be an extremely massive rotating black hole, and the role of nethotron will be played by a pulsar orbiting it. As far as the effect of the environment (radiation, dust, or even dark energy) in the timing of a pulsar orbiting Sgr A*, see, e.g., []. Some relevant physical properties of black holes and neutron stars are reviewed below.
According to the no-hair theorems [,,], the mass and the spin moments and of degree ℓ [,] of a spinning black hole [], whose external spacetime is described by the Kerr metric [,], are connected by the relation
where is the imaginary unit. From Equation (38), it turns out that the odd mass moments and even spin moments are identically zero. In particular, the mass moment of degree is the hole’s mass , while its spin dipole moment of degree is proportional to its spin angular momentum . For a Kerr BH, it is []
where is the mass moment of degree . If , a naked singularity [,] without a horizon would form, so that causality violations because of closed timelike curves may occur. The cosmic censorship conjecture [,] has not yet been proven; nonetheless, it states that naked singularities may not be formed via the gravitational collapse of a material body. In the following, the SMBH at the GC with [] will be considered as primary. However, it should be noted that a large uncertainty still plagues the value of for Sgr A* which may be as large as according to some recent results [,,].
The dimensionless quadrupole mass moment of a rotating neutron star can be expressed in terms of its dimensional counterpart , having dimensions of a mass times a length squared as
where []
The size of the parameter ranges within
for a variety of equations of state (EOS) and []. In the following, a millisecond pulsar with will be considered as a nethotron orbiting the SMBH in Sgr A*.
In such a scenario, yet to be discovered, predicting the pN spin variations is challenging because all the parameters characterizing the spin and orbital configurations of such a system are virtually unconstrained. It may be useful to recall them: they are the two polar angles of the SMBH’s spin axis, the RA and DEC of the pulsar’ spin axis, and the inclination I and the longitude of the ascending node characterizing the pulsar’s orbital plane.
As far as the holes’s spin axis is concerned, in the following, it will be parameterized as
where is the tilt of with respect to the line of sight, usually assumed as reference z axis. It turns out that are still basically unconstrained. Performed attempts to somehow constrain of Sgr A*Sgr A* with different nondynamical approaches can be found in [,,,,,,], and references therein. On the one hand, it appears that would not be aligned with the line of sight. Indeed, according to, e.g., [], who used polarimetric observations of the near–infrared emission of Sgr A*, it is . [] obtained on the basis of their fit of a simulated Rossby wave–induced spiral pattern in the hole’s accretion disk to the X–ray lightcurve detected with the mission X-ray Multi-Mirror-Newton (XMM–Newton). The authors of [] provided the range by comparing polarized submillimetre infrared observations with spectra computed using three-dimensional general relativistic magnetohydrodynamical simulations. Methods based on gravitational lensing for determining independently of orbital dynamics were outlined, e.g., in []. The authors of [] investigated the possibility of measuring, among other things, from the shape and position of the hole’s shadow under certain assumptions. On the other hand, the first observations by the Event Horizon Telescope (EHT) [] disfavor, among other things, scenarios where the BH is viewed at high inclination .
It turns out that both the dS and the PS spin rates can vanish for certain values of the parameter space: they are
The maximum values for the pN spin rates are obtained for
Figure 5 displays the numerically integrated pN signatures over 10 yr of the RA and decl. of the spin of a hypothetical millisecond pulsar orbiting the SMBH in Sgr A* along a highly eccentric orbit completed in yr, which brings the neutron star as close as Schwarzschild radii4 to the hole. Given that the system’s parameter space is unconstrained, the values of, say, Equation (50) were adopted for the spin and orbital configurations. As far as the pulsar’s quadrupole mass moment is concerned, whose signature is depicted in Figure 5 as well, it was calculated according to Equation (42) with . The size of the pN signatures is remarkable, amounting to tens or hundreds of degrees. Remarkably, the effect of the gravitational torque due to the pulsar’s own oblateness turns out to be completely negligible already at the Newtonian order5. This confirms that the nethotron approximation is also valid for such a compact object in a strong external gravitational field.
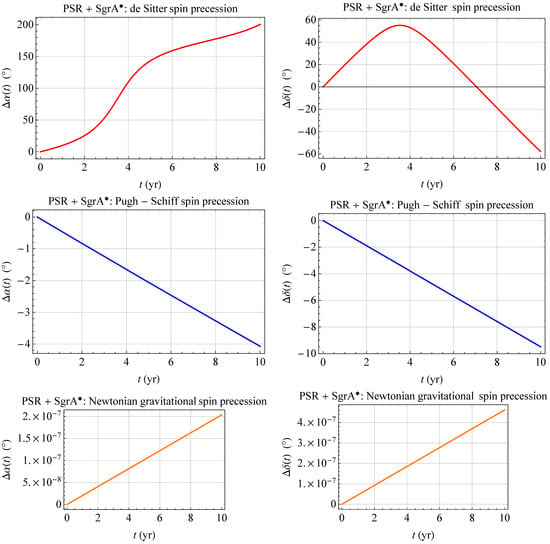
Figure 5.
Numerically integrated time series, in °, of the dS (upper row), PS (middle row), and Newtonian (lower row) RA and decl. shifts and of the spin axis of a millisecond pulsar in a yr orbit around the SMBH in Sgr A* over 10 yr. While the eccentricity was chosen in order to have , the other relevant spin and orbital parameters were retrieved from Equation (50). For the pulsar’s quadrupole parameter, the value was adopted in Equation (42).
If, on the one hand, the non-gravitational torques induced by the possible CoM offset and the asymmetric reflectivity affecting the LAGEOS satellites are absent here, on the other hand, the magnetic torque should be a major competing effect also in this scenario. Indeed, it is well known that pulsars possess extremely huge magnetic moments giving rise to strengths of the magnetic field at their surfaces as large as G []. Furthermore, around the SMBH at the GC, there is a strong magnetic field [,]. In fact, even if the external magnetic field were absent, other electromagnetic torques would affect the pulsar’s spin axis as well because of the misalignment between the latter and the magnetic dipole moment . Indeed, a spherical body endowed with a magnetic dipole field rotating in vacuum experiences two torques acting on it []. The first one arises from the fact that a misaligned spinning magnetic dipole moment emits electromagnetic waves which carry away angular momentum []. The other one is due to the inertia of []. Both are proportional to []. An evaluation of such potentially relevant competing effects is outside the scopes of the present work.
5. The Double Pulsar
Soon after its discovery in 2003 [,], the double pulsar PSR J0737-3039A/B [] became a celestial laboratory of primary importance to test gravitational physics in the strong field regime, primarily through its orbital dynamics and the effects on traveling electromagnetic waves [,]. As far as the spin effects are concerned, on the one hand, it allowed the measurement of the generalization of the gravitoelectric dS-or spin-orbit (SO) in pulsar’s literature-precession to ≃13 percent [] and ≃6 percent accuracy []. On the other hand, there are no reports of attempts made or proposed to measure the gravitomagnetic-or spin-spin (SS) in the pulsar’s literature-shift.
The authors of [,] determined the magnitude of the angular velocity of the spin precession of the B component of the double pulsar to an accuracy of
Here, the predicted magnitude of the angular velocity of the gravitomagnetic SS precession of B’s spin will be calculated and compared with Equation (51).
In the case of a binary system composed of two bodies with comparable masses and angular momenta, the gravitomagnetic precession of the spin of one of them induced by the spin of the other one can be expressed by Equations (20) and (21), provided that the orbital parameters and vectors are referred to the binary’s relative motion []. In the particular case of the double pulsar, entering Equation (20) represents the precessing angular momentum of B, while entering Equation (21) is meant as the angular momentum of A. It is so because , so that the gravitomagnetic precession of the spin of A due to the spin of B is negligible. Indeed, while the spin period of A is ms, the one of B amounts to s []. The moments of inertia of both neutron star were assumed equal to (see [], and references therein). By parameterizing A’s spin axis in terms of its colatitude and azimuth angle in the plane of the sky with respect to the reference x direction in it, from Equation (21) it turns out
which is about 4 orders of magnitude smaller than Equation (51). In order to calculate Equation (52), the range of values obtained in [] for A’s spin direction was adopted.
6. Summary and Conclusions
Measuring the temporal evolution of the orientation of the spin axes of natural and/or artificial nethotrons like pulsars orbiting the supermassive black hole in the Galactic Centre and Earth’s laser-ranged satellites may represent, in principle, a relatively low-cost approach to strengthen the empirical basis supporting the post-Newtonian contributions to such kind of phenomena. Indeed, the sole experiment that has measured the gravitomagnetic Pugh–Schiff spin precession is GP-B, which will likely never be repeated due to its cost and complexity.
Thus, it seems worth investigating the possibilities offered by the existing passive geodetic satellites of the LAGEOS type, whose spin axis orientation has been the subject of long and intense observation campaigns performed with different techniques for many years. Measuring their de Sitter and Pugh–Schiff spin shifts seems, at present, a daunting task. Indeed, the current accuracy in measuring the evolution of the orientation of their rotational axes over the years, being at the level in best cases, is low with respect to the expected sizes of the post-Newtonian signals, of the order of a few tens of thousands or hundreds of milliarcseconds. Furthermore, the Newtonian gravitational torque due to the satellites’ own oblateness is a major source of systematic bias since its nominal effects are several orders of magnitude larger than the relativistic ones. Last but not least, non-gravitational torques like, e.g., that arising from the interaction of the Earth’s magnetic field with the acquired magnetic dipole moments of the satellites, enter the error budget. The situation may become more favorable in the future should one or more carefully manufactured satellites, provisionally dubbed NethoSAT(s), be launched and new observational techniques will be devised.
The size of the relativistic spin precessions of natural nethotrons like pulsars orbiting the supermassive black hole in Sgr A* at the Galactic Centre, long sought because of their high potential as effective probes of the hole’s spacetime, may be as large as some tens or hundreds of degrees for orbital periods as short as yr. In this scenario, major competing effects would be those driven by various electromagnetic torques. Instead, the Newtonian gravitational spin shift attributable to the pulsar’s own quadrupole mass moment would not be of concern. It should be recalled that only the orbital precessions of such hypothesized pulsars have been considered so far as a means to probe the spacetime features of Sgr A*. Measuring also their spin precessions would be an additional resource to aim at such a goal.
As far as the double pulsar is concerned, the gravitomagnetic precession of the spin of its B component due to A’s angular momentum is expected to be about 4 orders of magnitude smaller than the current level of accuracy in measuring it.
Funding
This research received no external funding.
Data Availability Statement
No new data were generated or analysed in support of this research.
Acknowledgments
I am grateful to D. Kucharski for having provided me with important information on the measurement techniques of the spin axes of SLR satellites.
Conflicts of Interest
The author declares no conflicts of interest.
Notes
| 1 | Such papers contain expressions which are also valid in the case of a two-body system whose members both have comparable masses, angular momenta, and quadrupole moments; see also []. |
| 2 | In addition to GTR features, pulsars around Sgr A* may be used to test also modified models of gravity [,] and dark matter distribution in the GC []. |
| 3 | It is the intersection of the orbital plane with the fundamental one. |
| 4 | The Schwarzschild radius is defined as . |
| 5 | In fact, it is of the order of , as per Equation (42). |
References
- Barker, B.M.; O’Connell, R.F. Gravitational two–body problem with arbitrary masses, spins, and quadrupole moments. Phys. Rev. D 1975, 12, 329–335. [Google Scholar] [CrossRef]
- Correia, A.C.M.; Laskar, J.; Farago, F.; Boué, G. Tidal evolution of hierarchical and inclined systems. Celest. Mech. Dyn. Astr. 2011, 111, 105–130. [Google Scholar] [CrossRef]
- de Sitter, W. On Einstein’s theory of gravitation and its astronomical consequences. Second paper. Mon. Not. R. Astron. Soc. 1916, 77, 155–184. [Google Scholar] [CrossRef]
- Fokker, A.D. The geodesic precession: A consequence of Einsteins’s theory of graviation. Proc. K. Ned. Akad. Wet. 1921, 23, 729–738. [Google Scholar]
- Pugh, G.E. Proposal for a Satellite Test of the Coriolis Prediction of General Relativity; Research memorandum; Weapons Systems Evaluation Group, The Pentagon: Washington, DC, USA, 1959. [Google Scholar]
- Schiff, L. Possible new experimental test of general relativity theory. Phys. Rev. Lett. 1960, 4, 215–217. [Google Scholar] [CrossRef]
- Damour, T.; Ruffini, R. Sur certaines vérifications nouvelles de la Relativité générale rendues possibles par la découverte d’un pulsar membre d’un système binaire. C. R. Acad. Sc. Paris Sér. 1974, 279, 971–973. [Google Scholar]
- Barker, B.M.; O’Connell, R.F. The gravitational interaction: Spin, rotation, and quantum effects–a review. Gen. Relativ. Gravit. 1979, 11, 149–175. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; Muhlfelder, B.; Debra, D.B.; Parkinson, B.W.; Turneaure, J.P.; Silbergleit, A.S.; Acworth, E.B.; Adams, M.; Adler, R.; Bencze, W.J.; et al. The Gravity Probe B test of general relativity. Class. Quantum Gravit. 2015, 32, 224001. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; Debra, D.B.; Parkinson, B.W.; Turneaure, J.P.; Conklin, J.W.; Heifetz, M.I.; Keiser, G.M.; Silbergleit, A.S.; Holmes, T.; Kolodziejczak, J.; et al. Gravity Probe B: Final Results of a Space Experiment to Test General Relativity. Phys. Rev. Lett. 2011, 106, 221101. [Google Scholar] [CrossRef]
- Everitt, C.W.F. The Gyroscope experiment-I: General description and analysis of gyroscope performance. In Proceedings of the International School of Physics “Enrico Fermi”. Course LVI. Experimental Gravitation; Bertotti, B., Ed.; Academic Press: Cambridge, MA, USA, 1974; pp. 331–360. [Google Scholar]
- Everitt, C.W.F.; Buchman, S.; Debra, D.B.; Keiser, G.M.; Lockhart, J.M.; Muhlfelder, B.; Parkinson, B.W.; Turneaure, J.P.; Gravity Probe B Team. Gravity Probe B: Countdown to Launch. In Gyros, Clocks, Interferometers …: Testing Relativistic Gravity in Space; Lämmerzahl, C., Everitt, C.W.F., Hehl, F.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 52–82, Volume 562 of Lecture Notes in Physics. [Google Scholar] [CrossRef]
- Will, C.M. Finally, results from Gravity Probe B. Phys. Mag. 2011, 4, 43. [Google Scholar] [CrossRef]
- Biskupek, L.; Müller, J.; Torre, J.-M. Benefit of New High-Precision LLR Data for the Determination of Relativistic Parameters. Universe 2021, 7, 34. [Google Scholar] [CrossRef]
- Williams, J.G.; Folkner, W.M. Lunar Laser Ranging: Relativistic Model and Tests of Gravitational Physics. Bullettin Am. Astron. Soc. 2009, 41, 882. [Google Scholar]
- Hofmann, F.; Müller, J. Relativistic tests with lunar laser ranging. Class. Quantum Gravit. 2018, 35, 035015. [Google Scholar] [CrossRef]
- Breton, R.P.; Kaspi, V.M.; Kramer, M.; McLaughlin, M.A.; Lyutikov, M.; Ransom, S.M.; Stairs, I.H.; Ferdman, R.D.; Camilo, F.; Possenti, A. Relativistic Spin Precession in the Double Pulsar. Science 2008, 321, 104. [Google Scholar] [CrossRef]
- Lower, M.E.; Kramer, M.; Shannon, R.M.; Breton, R.P.; Wex, N.; Johnston, S.; Bailes, M.; Buchner, S.; Hu, H.; Venkatraman Krishnan, V.; et al. A MeerKAT view of the double pulsar eclipses. Geodetic precession of pulsar B and system geometry. Astron. Astrophys. 2024, 682, A26. [Google Scholar] [CrossRef]
- Burgay, M.; D’Amico, N.; Possenti, A.; Manchester, R.N.; Lyne, A.G.; Joshi, B.C.; McLaughlin, M.A.; Kramer, M.; Sarkissian, J.M.; Camilo, F.; et al. An increased estimate of the merger rate of double neutron stars from observations of a highly relativistic system. Nature 2003, 426, 531–533. [Google Scholar] [CrossRef] [PubMed]
- Lyne, A.G.; Burgay, M.; Kramer, M.; Possenti, A.; Manchester, R.N.; Camilo, F.; McLaughlin, M.A.; Lorimer, D.R.; D’Amico, N.; Joshi, B.C.; et al. A Double–Pulsar System: A Rare Laboratory for Relativistic Gravity and Plasma Physics. Science 2004, 303, 1153–1157. [Google Scholar] [CrossRef]
- Freire, P.C.C.; Wex, N. Gravity experiments with radio pulsars. Living Rev. Relativ. 2024, 27, 5. [Google Scholar] [CrossRef]
- Pearlman, M.; Arnold, D.; Davis, M.; Barlier, F.; Biancale, R.; Vasiliev, V.; Ciufolini, I.; Paolozzi, A.; Pavlis, E.C.; Sośnica, K.; et al. Laser geodetic satellites: A high-accuracy scientific tool. J. Geod. 2019, 93, 2181–2194. [Google Scholar] [CrossRef]
- Coulot, D.; Deleflie, F.; Bonnefond, P.; Exertier, P.; Laurain, O.; de Saint-Jean, B. Satellite laser ranging. In Encyclopedia of Solid Earth Geophysics; Gupta, H.K., Ed.; Encyclopedia of Earth Sciences Series; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1049–1055. [Google Scholar] [CrossRef]
- Otsubo, T.; Amagai, J.; Kunimori, H.; Elphick, M. Spin motion of the AJISAI satellite derived from spectral analysis of laser ranging data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1417–1424. [Google Scholar] [CrossRef]
- Vovchyk, Y.; Blahodyr, Y.; Lohvynenko, O.; Bilinskyy, A.; Virun, N.; Klym, B.; Pochapskyy, Y. Electrophotometric observations of artificial objects. Adv. Space Res. 2001, 28, 1309–1313. [Google Scholar] [CrossRef]
- Andrés, J.I.; Noomen, R.; Bianco, G.; Currie, D.G.; Otsubo, T. Spin axis behavior of the LAGEOS satellites. J. Geophys. Res. 2004, 109, B06403. [Google Scholar] [CrossRef]
- Otsubo, T.; Sherwood, R.A.; Gibbs, P.; Wood, R. Spin Motion and Orientation of LAGEOS-2 From Photometric Observation. IEEE Trans. Geosci. Remote Sens. 2004, 42, 202–208. [Google Scholar] [CrossRef]
- Kirchner, G.; Hausleitner, W.; Cristea, E. Ajisai Spin Parameter Determination Using Graz Kilohertz Satellite Laser Ranging Data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 201–205. [Google Scholar] [CrossRef]
- Kucharski, D.; Kirchner, G.; Otsubo, T.; Koidl, F. 22 Years of AJISAI spin period determination from standard SLR and kHz SLR data. Adv. Space Res. 2009, 44, 621–626. [Google Scholar] [CrossRef]
- Kucharski, D.; Otsubo, T.; Kirchner, G.; Koidl, F. Spin axis orientation of Ajisai determined from Graz 2 kHz SLR data. Adv. Space Res. 2010, 46, 251–256. [Google Scholar] [CrossRef]
- Kucharski, D.; Kirchner, G.; Koidl, F. Spin parameters of nanosatellite BLITS determined from Graz 2 kHz SLR data. Adv. Space Res. 2011, 48, 343–348. [Google Scholar] [CrossRef]
- Kucharski, D.; Otsubo, T.; Kirchner, G.; Bianco, G. Spin rate and spin axis orientation of LARES spectrally determined from Satellite Laser Ranging data. Adv. Space Res. 2012, 50, 1473–1477. [Google Scholar] [CrossRef]
- Kucharski, D.; Lim, H.-C.; Kirchner, G.; Hwang, J.Y. Spin parameters of LAGEOS-1 and LAGEOS-2 spectrally determined from Satellite Laser Ranging data. Adv. Space Res. 2013, 52, 1332–1338. [Google Scholar] [CrossRef]
- Kucharski, D.; Otsubo, T.; Kirchner, G.; Lim, H.-C. Spectral response of Experimental Geodetic Satellite determined from high repetition rate SLR data. Adv. Space Res. 2013, 51, 162–167. [Google Scholar] [CrossRef]
- Kucharski, D.; Kirchner, G.; Lim, H.-C.; Koidl, F. Spin parameters of High Earth Orbiting satellites Etalon-1 and Etalon-2 determined from kHz Satellite Laser Ranging data. Adv. Space Res. 2014, 54, 2309–2317. [Google Scholar] [CrossRef]
- Kucharski, D.; Kirchner, G.; Otsubo, T.; Lim, H.-C.; Bennett, J.; Koidl, F.; Kim, Y.-R.; Hwang, J.-Y. Confirmation of gravitationally induced attitude drift of spinning satellite Ajisai with Graz high repetition rate SLR data. Adv. Space Res. 2016, 57, 983–990. [Google Scholar] [CrossRef]
- Koshkin, N.; Shakun, L.; Burlak, N.; Korobeynikova, E.; Strakhova, S.; Melikyants, S.; Terpan, S.; Ryabov, A. Ajisai spin-axis precession and rotation-period variations from photometric observations. Adv. Space Res. 2017, 60, 1389–1399. [Google Scholar] [CrossRef]
- Koshkin, N.; Shakun, L.; Korobeynikova, E.; Melikyants, S.; Strakhova, S.; Dragomiretsky, V.; Ryabov, A.; Terpan, S.; Golubovskaya, T. Determination of the spacecraft’s spin axis orientation. Photometric patterns method. Adv. Space Res. 2024, 74, 5725–5744. [Google Scholar] [CrossRef]
- Zhang, F.; Lu, Y.; Yu, Q. On the Existence of Pulsars in the Vicinity of the Massive Black Hole in the Galactic Center. Astrophys. J. 2014, 784, 106. [Google Scholar] [CrossRef]
- Liu, K.; Desvignes, G.; Eatough, R.P.; Karuppusamy, R.; Kramer, M.; Torne, P.; Wharton, R.; Chatterjee, S.; Cordes, J.M.; Crew, G.B.; et al. An 86 GHz Search for Pulsars in the Galactic Center with the Atacama Large Millimeter/submillimeter Array. Astrophys. J. 2021, 914, 30. [Google Scholar] [CrossRef]
- Carleo, A.; Ben-Salem, B. Effect of environment in the timing of a pulsar orbiting SgrA*. Phys. Rev. D 2023, 108, 124027. [Google Scholar] [CrossRef]
- Torne, P.; Liu, K.; Eatough, R.P.; Wongphechauxsorn, J.; Cordes, J.M.; Desvignes, G.; De Laurentis, M.; Kramer, M.; Ransom, S.M.; Chatterjee, S.; et al. A Search for Pulsars around Sgr A* in the First Event Horizon Telescope Data Set. Astrophys. J. 2023, 959, 14. [Google Scholar] [CrossRef]
- Dong, Y.; Shao, L.; Hu, Z.; Miao, X.; Wang, Z. Prospects for constraining the Yukawa gravity with pulsars around Sagittarius A*. J. Cosmol. Astropart. Phys. 2022, 2022, 51. [Google Scholar] [CrossRef]
- Hu, Z.; Shao, L.; Xu, R.; Liang, D.; Mai, Z.-F. Probing the vector charge of Sagittarius A* with pulsar timing. J. Cosmol. Astropart. Phys. 2024, 2024, 87. [Google Scholar] [CrossRef]
- Hu, Z.; Shao, L.; Zhang, F. Prospects for probing small-scale dark matter models with pulsars around Sagittarius A*. Phys. Rev. D 2023, 108, 123034. [Google Scholar] [CrossRef]
- Wex, N.; Kopeikin, S.M. Frame Dragging and Other Precessional Effects in Black Hole Pulsar Binaries. Astrophys. J. 1999, 514, 388–401. [Google Scholar] [CrossRef]
- Pfahl, E.; Loeb, A. Probing the Spacetime around Sagittarius A* with Radio Pulsars. Astrophys. J. 2004, 615, 253–258. [Google Scholar] [CrossRef]
- Liu, K.; Wex, N.; Kramer, M.; Cordes, J.M.; Lazio, T.J.W. Prospects for Probing the Spacetime of Sgr A* with Pulsars. Astrophys. J. 2012, 747, 1. [Google Scholar] [CrossRef]
- Psaltis, D.; Wex, N.; Kramer, M. A Quantitative Test of the No-hair Theorem with Sgr A* Using Stars, Pulsars, and the Event Horizon Telescope. Astrophys. J. 2016, 818, 121. [Google Scholar] [CrossRef]
- Zhang, F.; Saha, P. Probing the Spinning of the Massive Black Hole in the Galactic Center via Pulsar Timing: A Full Relativistic Treatment. Astrophys. J. 2017, 849, 33. [Google Scholar] [CrossRef]
- Hu, Z.; Shao, L. Measuring the Spin of the Galactic Center Supermassive Black Hole with Two Pulsars. Phys. Rev. Lett. 2024, 133, 231402. [Google Scholar] [CrossRef]
- Bardeen, J.M. Kerr Metric Black Holes. Nature 1970, 226, 64–65. [Google Scholar] [CrossRef]
- Kerr, R.P. Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics. Phys. Rev. Lett. 1963, 11, 237–238. [Google Scholar] [CrossRef]
- Teukolsky, S.A. The Kerr metric. Class. Quantum Gravit. 2015, 32, 124006. [Google Scholar] [CrossRef]
- Mashhoon, B.; Singh, D. Dynamics of extended spinning masses in a gravitational field. Phys. Rev. D 2006, 74, 124006. [Google Scholar] [CrossRef]
- Hackmann, E.; Lämmerzahl, C.; Obukhov, Y.N.; Puetzfeld, D.; Schaffer, I. Motion of spinning test bodies in Kerr spacetime. Phys. Rev. D 2014, 90, 064035. [Google Scholar] [CrossRef]
- Ruangsri, U.; Vigeland, S.J.; Hughes, S.A. Gyroscopes orbiting black holes: A frequency-domain approach to precession and spin-curvature coupling for spinning bodies on generic Kerr orbits. Phys. Rev. D 2016, 94, 044008. [Google Scholar] [CrossRef]
- Iorio, L. General Post-Newtonian Orbital Effects from Earth’s Satellites to the Galactic Center; Cambridge University Press: Cambridge, UK, 2024. [Google Scholar] [CrossRef]
- Visco, M.; Lucchesi, D.M. Comprehensive model for the spin evolution of the LAGEOS and LARES satellites. Phys. Rev. D 2018, 98, 044034. [Google Scholar] [CrossRef]
- Capderou, M. Satellites: Orbits and Missions; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Kahn, R. Gravity Probe B-Post Flight Analysis·Final Report; Technical Report; Stanford University: Stanford, CA, USA, 2007. [Google Scholar]
- Bertotti, B.; Iess, L. The rotation of LAGEOS. J. Geophys. Res. 1991, 96, 2431–2440. [Google Scholar] [CrossRef]
- Farinella, P.; Vokrouhlicky, D.; Barlier, F. The rotation of LAGEOS and its long-term semimajor axis decay: A self-consistent solution. J. Geophys. Res. 1996, 101, 17861–17872. [Google Scholar] [CrossRef]
- Vokrouhlický, D. Non-gravitational effects and LAGEOS’ rotation. Geophys. Res. Lett. 1996, 23, 3079–3082. [Google Scholar] [CrossRef]
- Currie, D.; Kissell, K.; Avizonis, P.; Wellnitz, D. On the Dynamics of the LAGEOS Spin Vector High-Precision and Comparisons to Theoretical Modeling. In IAU Colloq. 165: Dynamics and Astrometry of Natural and Artificial Celestial Bodies; Wytrzyszczak, I.M., Lieske, J.H., Feldman, R.A., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 341–346. [Google Scholar]
- Bianco, G.; Chersich, M.; Devoti, R.; Luceri, V.; Selden, M. Measurement of LAGEOS-2 rotation by satellite laser ranging observations. Geophys. Res. Lett. 2001, 28, 2113–2116. [Google Scholar] [CrossRef]
- Sasaki, M.; Hashimoto, H. Launch and Observation Program of the Experimental Geodetic Satellite of Japan. IEEE Trans. Geosci. Remote Sens. 1987, 25, 526–533. [Google Scholar] [CrossRef]
- Israel, W. Event Horizons in Static Vacuum Space–Times. Phys. Rev. 1967, 164, 1776–1779. [Google Scholar] [CrossRef]
- Carter, B. Axisymmetric Black Hole Has Only Two Degrees of Freedom. Phys. Rev. Lett. 1971, 26, 331–333. [Google Scholar] [CrossRef]
- Robinson, D.C. Uniqueness of the Kerr Black Hole. Phys. Rev. Lett. 1975, 34, 905–906. [Google Scholar] [CrossRef]
- Geroch, R. Multipole Moments. II. Curved Space. J. Math. Phys. 1970, 11, 2580–2588. [Google Scholar] [CrossRef]
- Hansen, R.O. Multipole moments of stationary space–times. J. Math. Phys. 1974, 15, 46–52. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs and Neutron Stars: The Physics of Compact Objects; Wiley: Weinheim, Germany, 1986. [Google Scholar]
- Yodzis, P.; Seifert, H.-J.; Müller Zum Hagen, H. On the occurrence of naked singularities in general relativity. Commun. Math. Phys. 1973, 34, 135–148. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Formation of naked singularities: The violation of cosmic censorship. Phys. Rev. Lett. 1991, 66, 994–997. [Google Scholar] [CrossRef]
- Penrose, R. The Question of Cosmic Censorship. J. Astrophys. Astron. 1999, 20, 233–248. [Google Scholar] [CrossRef]
- Penrose, R. “Golden Oldie”: Gravitational Collapse: The Role of General Relativity. Gen. Relativ. Gravit. 2002, 7, 1141–1165. [Google Scholar] [CrossRef]
- Peißker, F.; Eckart, A.; Zajaček, M.; Britzen, S. Observation of S4716-a Star with a 4 yr Orbit around Sgr A*. Astrophys. J. 2022, 933, 49. [Google Scholar] [CrossRef]
- Dokuchaev, V.I. Spins of Supermassive Black Holes M87* and SgrA* Revealed from the Size of Dark Spots in Event Horizon Telescope Images. Astronomy 2023, 2, 141–152. [Google Scholar] [CrossRef]
- Andrianov, A.S.; Chernov, S.V. Estimation of the Spin of a Supermassive Black Hole in Sagittarius A*. Astron. Rep. 2024, 68, 233–237. [Google Scholar] [CrossRef]
- Daly, R.A.; Donahue, M.; O’Dea, C.P.; Sebastian, B.; Haggard, D.; Lu, A. New black hole spin values for Sagittarius A* obtained with the outflow method. Mon. Not. R. Astron. Soc. 2024, 527, 428–436. [Google Scholar] [CrossRef]
- Laarakkers, W.G.; Poisson, E. Quadrupole Moments of Rotating Neutron Stars. Astrophys. J. 1999, 512, 282–287. [Google Scholar] [CrossRef]
- Falanga, M.; Melia, F.; Tagger, M.; Goldwurm, A.; Bélanger, G. General Relativistic Flux Modulations from Disk Instabilities in Sagittarius A*. Astrophys. J. Lett. 2007, 662, L15–L18. [Google Scholar] [CrossRef][Green Version]
- Meyer, L.; Schödel, R.; Eckart, A.; Duschl, W.J.; Karas, V.; Dovčiak, M. On the orientation of the Sagittarius A* system. Astron. Astrophys. 2007, 473, 707–710. [Google Scholar] [CrossRef][Green Version]
- Broderick, A.E.; Fish, V.L.; Doeleman, S.S.; Loeb, A. Estimating the Parameters of Sagittarius A*’s Accretion Flow Via Millimeter VLBI. Astrophys. J. 2009, 697, 45–54. [Google Scholar] [CrossRef]
- Broderick, A.E.; Fish, V.L.; Doeleman, S.S.; Loeb, A. Evidence for Low Black Hole Spin and Physically Motivated Accretion Models from Millimeter-VLBI Observations of Sagittarius A*. Astrophys. J. 2011, 735, 110. [Google Scholar] [CrossRef]
- Shcherbakov, R.V.; Penna, R.F.; McKinney, J.C. Sagittarius A* Accretion Flow and Black Hole Parameters from General Relativistic Dynamical and Polarized Radiative Modeling. Astrophys. J. 2012, 755, 133. [Google Scholar] [CrossRef]
- Jørgensen, J.H.; Bjælde, O.E.; Hannestad, S. Probing the spin of the central black hole in the Galactic Centre with secondary images. Mon. Not. R. Astron. Soc. 2016, 458, 3614–3618. [Google Scholar] [CrossRef][Green Version]
- Yu, Q.; Zhang, F.; Lu, Y. Prospects for Constraining the Spin of the Massive Black Hole at the Galactic Center via the Relativistic Motion of a Surrounding Star. Astrophys. J. 2016, 827, 114. [Google Scholar] [CrossRef]
- Saida, H. How to measure a black hole’s mass, spin, and direction of spin axis in the Kerr lens effect 1: Test case with simple source emission near a black hole. Prog. Theor. Exp. Phys. 2017, 2017, 053E02. [Google Scholar] [CrossRef]
- Takahashi, R. Shapes and Positions of Black Hole Shadows in Accretion Disks and Spin Parameters of Black Holes. Astrophys. J. 2004, 611, 996–1004. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration. First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophys. J. Lett. 2022, 930, L12. [Google Scholar] [CrossRef]
- Kim, V.; Umirbayeva, A.; Aimuratov, Y. Estimates of the Surface Magnetic Field Strength of Radio Pulsars. Universe 2023, 9, 334. [Google Scholar] [CrossRef]
- Eatough, R.P.; Falcke, H.; Karuppusamy, R.; Lee, K.J.; Champion, D.J.; Keane, E.F.; Desvignes, G.; Schnitzeler, D.H.F.M.; Spitler, L.G.; Kramer, M.; et al. A strong magnetic field around the supermassive black hole at the centre of the Galaxy. Nature 2013, 501, 391–394. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope Collaboration] First Sagittarius A* Event Horizon Telescope Results. VII. Polarization of the Ring. Astrophys. J. Lett. 2024, 964, L25. [Google Scholar] [CrossRef]
- Zanazzi, J.J.; Lai, D. Electromagnetic torques, precession and evolution of magnetic inclination of pulsars. Mon. Not. R. Astron. Soc. 2015, 451, 695–704. [Google Scholar] [CrossRef][Green Version]
- Davis, L.; Goldstein, M. Magnetic-Dipole Alignment in Pulsars. Astrophys. J. Lett. 1970, 159, L81–L86. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H. The double pulsar. Annu. Rev. Astron. Astr. 2008, 46, 541–572. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; McLaughlin, M.A.; Lyne, A.G.; Ferdman, R.D.; Burgay, M.; Lorimer, D.R.; Possenti, A.; D’Amico, N.; et al. Tests of General Relativity from Timing the Double Pulsar. Science 2006, 314, 97–102. [Google Scholar] [CrossRef]
- Kramer, M.; Wex, N. TOPICAL REVIEW: The double pulsar system: A unique laboratory for gravity. Class. Quantum Gravit. 2009, 26, 073001. [Google Scholar] [CrossRef]
- Silva, H.O.; Holgado, A.M.; Cárdenas-Avendaño, A.; Yunes, N. Astrophysical and Theoretical Physics Implications from Multimessenger Neutron Star Observations. Phys. Rev. Lett. 2021, 126, 181101. [Google Scholar] [CrossRef] [PubMed]
- Iorio, L. The impact of the spin–orbit misalignment and of the spin of B on the Lense–Thirring orbital precessions of the double pulsar PSR J0737-3039A/B. Mon. Not. R. Astron. Soc. 2021, 507, 421–430. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).