Abstract
The PPET [mu()on Probe with J-PET] project aims to investigate the “Muon Puzzle” seen in cosmic ray air showers. This puzzle arises from the observation of a significantly larger number of muons on Earth’s surface than that predicted by the current theoretical models. The investigated hypothesis is based on recently observed asymmetries in the parameters for the strong interaction cross-section and trajectory of an outgoing particle due to projectile–target polarization. The measurements require detailed information about muons at the ground level, including their track and charge distributions. To achieve this, the two PET scanners developed at the Jagiellonian University in Krakow (Poland), the J-PET detectors, will be employed, taking advantage of their well-known resolution and convenient location for detecting muons that reach long depths in the atmosphere. One station will be used as a muon tracker, while the second will reconstruct the core of the air shower. In parallel, the existing hadronic interaction models will be modified and fine-tuned based on the experimental results. In this work, we present the conceptualization and preliminary designs of PPET.
1. Introduction: The Muon Puzzle
Cosmic rays (CRs) are a fundamental pillar in our understanding of the physics in the universe, from the life cycle of astrophysical objects to particle acceleration mechanisms. Two key observables are essential for studying CRs: their abundance (expressed as the differential flux as a function of the energy) and their mass composition (the distribution of atomic masses). Cosmic rays at ultra-high energy (UHECRs, GeV) have a low flux, and therefore, their mass cannot be measured directly via, for example, satellites, as that of high-energy ones (HECRs, ) can. Therefore, we rely on indirect ground-based measurements, detecting the secondary particles produced in the extensive air showers (EASs) initiated when primary cosmic rays interact with the Earth’s atmosphere. In this context, the atmosphere acts as a natural calorimeter.
Heitler-Matthews [1] offers a simplified framework for understanding the development of EASs. It approximates hadronic interactions as the pion production occurring at each interaction length 1 with the multiplicity (i.e., the number of pions produced in an interaction): 1/3 as , and 2/3 as . Neutral pions eventually decay electromagnetically, creating a dominant electromagnetic shower. The amount of this component collected at the ground level is related to the energy of the primary particle.
Charged pions either undergo further hadronic interactions (producing additional pions with the same multiplicity) or decay into muons. This cascade continues until the pion’s energy drops below a critical threshold (≈20 GeV in the atmosphere), at which point decay into muons becomes more likely than continued interactions. From this model, the number of muons observed at the ground for a cosmic ray with the initial energy is given by
where is the number of charged particles reaching the ground. The evolution of secondary particle production as a function of atmospheric depth is known as the longitudinal profile of the shower.
The multiplicity and number of charged particles produced in an air shower are closely related to the atomic composition of the primary nucleus and the nucleon–air interaction characteristics. As a result, the mass of the primary cosmic ray can be inferred by analyzing the muons that reach the ground. However, due to the complexity and inherently statistical nature of the parameter , individual mass determinations are not feasible. Instead, the measurement is interpreted in terms of the mass composition, a statistical distribution of the atomic masses across the observed flux.
1.1. The Muon Puzzle
A realistic EAS is more complicated than the simplified model; in addition, relating to Z and A is non-trivial. Therefore, we rely on simulations (CORSIKA [2]) and High-Energy Hadronic Interaction models (HEHIs) to properly simulate complex hadron–air interactions. The most widely used HEHIs are QGSJet-II.04, Sibyll, and EPOS-LHC, along with their respective versions [3,4,5].
A complementary way to extract the primary mass composition is by measuring the slant depth (g ) along the longitudinal development of the shower where the number of secondary particles reaches its maximum: [6]. However, a discrepancy arises between these two methods (counting the particle on the grounds and measuring ), as shown in Figure 1 as an example [7]. The markers show the interpretation of the data in terms of the mass composition from various experiments using different hadronic interaction models. The y-axis is the relative difference in the muon density at the ground (, measured) from the expected density of a pure proton’s composition in a flux (, provided by the simulated model), normalized to the relative difference for the case of a pure iron composition (, also provided by the simulated model): ; therefore, is a flux made of only protons and a flux made only of iron nuclei. The densities are proportional to in Equation (1). The fit of the measured and its uncertainty band are shown by the gray band: it is within the proton–iron limit region (); i.e., the abundance is consistent with what is expected from astrophysical sources. However, as the energy increases, the discrepancy between the methods becomes more pronounced; moreover, the measured muon density at the ground appears to be heavier than that of iron () at the highest energies. This points to a systematic muon deficit in the current simulations.
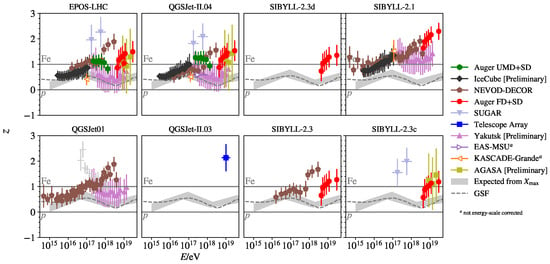
Figure 1.
The mass composition from several experiments (markers) using lateral distributions interpreted using different hadronic interaction models, both newer (EPOS-LHC, QGSJet-II.04, and Sibyll-2.3/d/c) and older [7]. The composition is expressed as ( from the data and and from simulations; see the text): 0 represents pure proton and 1 pure iron fluxes. The fitted measurements with a confidence band are shown as a gray band. The dashed lines are the global spline fits.
The cause of this discrepancy remains unknown and is commonly referred to as the “Muon Puzzle”.
Numerous efforts have been made, and are ongoing, to address it by adjusting the simulations, tuning the hadronic interaction models with accelerator data better, and introducing more sophisticated interaction models [4,5,7,8,9,10]. However, a solution to this puzzle that does not compromise other well-established observables, for example, , has not yet been found. Based on the current understanding, the following can be stated:
- 1.
- The measured values appear consistent with the model predictions [7], suggesting that the unknown phenomenon responsible for the muon excess likely does not occur during the early stages of shower development (i.e., it does not involve high-energy muons, GeV), or its effect at these stages is negligible.
- 2.
- The impact of the unknown mechanism becomes evident at the ground level, implying that it may occur during the later stages of shower development (it involves lower-energy muons, GeV), or it could be a small effect per interaction that accumulates over multiple interactions, ultimately becoming significant by the time the particles reach the ground.
- 3.
- For primary energies below 100 PeV, the observed muon counts and the values show reasonable agreement. This could indicate that the unknown effect either does not accumulate sufficiently at these energies, is partially compensated for by other mechanisms, or does not occur at all.
1.2. PPET and the Tested Hypothesis for Solving the Muon Puzzle
Hadronic interaction models rely on a parton description to simplify the complexity of Quantum Chromo-Dynamics (QCD) calculations in strong interactions. It is well known in the literature that spin polarization of a projectile, a target, or both can alter the cross-section of the interaction and introduce an extra transverse momentum into outgoing particles [11,12,13]. This phenomenon is likely to occur during a particle shower’s development due to the presence of the geomagnetic field. Moreover, recent measurements from HERMES and COMPASS (for example, [14,15]) have found asymmetries in this transverse momentum, the reason for which is still under investigation.
Although modifications to the hadronic interaction cross-section may influence shower development, they are insufficient to resolve the Muon Puzzle without conflicting with other well-established observables, as summarized in [7]. However, an additional transverse momentum imparted to charged particles (from polarization effects) could introduce slight deflections in their trajectories. This would effectively increase the number of radiation lengths that they traversed and shift the atmospheric depth at which their muonic byproducts were produced. In other words, this mechanism could alter the longitudinal development of the muonic component of the shower, potentially leading to the misestimation of the muon content at the ground level.
- In deeper showers (i.e., those initiated by high-energy primaries), the shower maximum occurs closer to the ground. If the muon production is shifted to higher altitudes, due to the pions decaying further from the ground, the predicted muon content at the ground could change, without affecting , dominated by the electromagnetic component. This might justify points 1 and 2 in Section 1.1.
- In shallow showers (i.e., those initiated by low-energy primaries), the shower maximum occurs higher in the atmosphere. In this case, even if polarized pions decay into muons further from the ground, all relevant processes are largely completed by the time the muons reach the surface, rendering the effect negligible. This may account for point 3 in Section 1.1.
In all scenarios, this hypothesis would produce a shift in the expected distribution of the muon trajectory, which would need to be properly propagated through simulations. Other hypotheses are currently under investigation [9,10]. While those efforts focus on improved the modeling of muon multiplicity and processes such as exchange, the hypothesis discussed here proposes a geometric correction to the muon trajectories, offering a distinct and complementary approach to resolving the Muon Puzzle.
PPET (mu()on Probe with J-PET) is a project designed to test this hypothesis by measuring the angular distribution of muon trajectories and comparing it to predictions, with and without the inclusion of polarization-induced effects. The primary observable is therefore the angular distribution of the muons, which is measured using a dedicated muon tracker (Section 2.1). To accurately reconstruct the expected muon trajectories, an array of scintillators is employed (see Section 2.2) to determine the direction of the primary cosmic rays and to detect any charge-dependent asymmetry arising from polarization. To reduce the degrees of freedom, this project focuses on a region of high-energy cosmic rays (HECRs, ), for which the energy spectrum and mass composition are regular and well known.
2. J-PET Detectors
The detectors mentioned in Section 1.2 are two different models of J-PET detectors: Jagiellonian Positron Emission Tomography detectors. A J-PET detector is the first PET scanner developed using plastic scintillator strips [16,17], which makes it cost-effective [18] for scientific research [19,20,21] and medical applications [22,23,24]. One, the muon tracker, is the first full-scale prototype and is referred to as “Big Barrel” (Section 2.1) [25], and the one used as a scintillator array for shower reconstruction is “Modular” (Section 2.2) [26,27]. The DAQ system in both J-PETs uses Field-Programmable Gate Array (FPGA) electronics for efficient real-time processing of multiple data streams through pipelined operations [28].
2.1. The “Big Barrel” J-PET Detector
In Figure 2, the J-PET detector is depicted: an axially symmetric barrel made of three layers of plastic scintillator strips [19,25].

Figure 2.
The Big Barrel J-PET detector.
The two inner layers consist of 48 strips each, placed at 425 mm and 467.5 mm radii, respectively, with the second layer rotated by with respect to the first. The outer layer is composed of 96 EJ-230 scintillator strips at a radius of 575 mm [17,19,25]. Each scintillator strip is mm3, and it is composed of a fast-timing plastic scintillator that is wrapped in two types of foils: an inside foil to reflect the scintillator light and an external foil for optical isolation [17,19,25]. The two extreme ends of the strip (the mm2 surfaces) are coupled with two R9800 Hamamatsu photomultipliers (PMTs) to collect the light signals. Each PMT is equipped with four selectable thresholds: 30, 80, 190, and 300 mV. The time difference in the signals from the two PMTs attached to a particular strip is used to determine the position of the photon interaction along the scintillator strip; the time of the interaction is half the sum of the times of these signals.
2.2. The “Modular” J-PET Detector
The modular J-PET detector (Figure 3) is a newly developed, flexible, and portable variant of the J-PET detector [17,27]. The Modular J-PET detector consists of 24 detection modules that circumscribe a cylinder with a diameter of 73.9 cm, and each module comprises 13 strips of BC404 plastic scintillators with dimensions of mm3 and positioned parallel to the axial axis of the scanner. To improve the light propagation and prevent leakage, the plastic scintillator strips are wrapped in Vikuiti Enhanced Specular Reflector (ESR) foil and DuPont Kapton 100B film. Each scintillator strip is read out at both ends by arrays of matrix Hamamatsu silicon photomultipliers (SiPMs). Each SiPM is equipped with two threshold settings: 30 mV and 70 mV. Upon the interaction of gamma quanta with a scintillator strip, four timestamps are generated across the eight SiPMs. These timestamps are continuously collected by the Data Acquisition System (DAQ) via the front-end electronics.

Figure 3.
The Modular J-PET detector.
3. Expected Trajectory Resolution
As a first approach, we evaluated the Big Barrel’s resolution on the trajectory angle without any dedicated analysis or calibration correction. We simulated 30,000 muons with an energy of 4 GeV using a Monte Carlo (MC) approach to estimating this raw resolution. The simulation was based on the official J-PET-Geant4 framework [29]. In each event, a starting point was randomly generated within the cylindrical volume of the detector, and a random angular direction was assigned such that the trajectory passed through the volume from outside, mimicking a down-going particle. The choice of 4 GeV corresponds to the average energy of muons at sea level [30].
The collected MC simulated data were analyzed using a dedicated analysis framework created in C++ [29]. With the J-PET algorithm, the spatial position of a particle can be reconstructed using the time difference in the signals from the two PMTs (see Section 2) and recorded as the position information for the hit of the particle in the scintillator. To resolve a muon’s direction, we consider the first and last scintillators’ hit information along the down-going particle’s trajectory to resolve its direction. Events that did not register at least two hits were excluded. Defining and as the polar (inclination) and azimuthal angles, respectively, we compared the reconstructed (, ) with the generated (, ) to obtain the raw difference, as shown in Figure 4. As this geometrical problem followed a Cauchy-like distribution, the residuals were fitted using a Breit–Wigner distribution. In both angular components, the fits yielded values within 2 standard deviations from the expected mean for the distribution (, ). The extracted Full Width at Half Maximum (FWHM) values were approximately for and for (reported as “gamma” in the statistic box in the figures), both with a relative uncertainty of about . These values correspond to an effective angular resolution (i.e., the Gaussian-equivalent standard deviation) of .
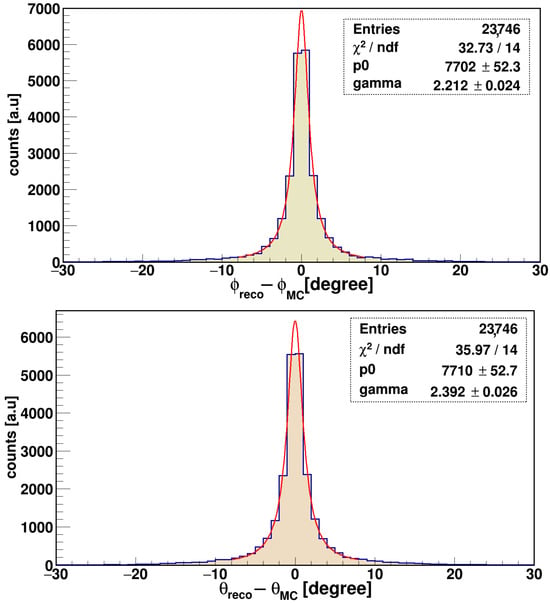
Figure 4.
Resolution of the polar () and azimuthal () angles for a muon crossing the Big Barrel, obtained using the J-PET simulation (histogram). The fit function is a Breit–Wigner distribution (red curve), and its FWHM is reported as “gamma” in the statistic box (p0 is the amplitude of the fit). Uncertainties in the parameters, , and entries are also reported.
4. The Array Design for Shower Reconstruction
As mentioned in Section 1.2, to correctly identify the trajectory of a muon’s track with respect to a shower, reconstruction of its direction and core position is necessary. Using the Modular J-PET scintillators, it is possible to create an array of scintillators, a well-known technique for identifying and reconstructing an EAS [31,32].
4.1. Array Configuration
The array will be placed across the roofs of the campus around the Faculty of Physics, Astronomy, and Applied Computer Science (FAIS) at Jagiellonian University, Krakow, Poland (latitude: N; longitude: E). On the roofs, “Cages” will house the scintillator modules. Each Cage will host a pair of modules next to each other to cover a detection surface of mm2. Given the modules’ mobility, we are also considering testing single or quadruple modules per Cage. Therefore, a total of 24 Cages will be installed, between 40 and 150 m apart from each other, to explore the planned energy region of the primary cosmic ray (). Moreover, we are planning different campaigns of 1–2 months of data collection for different configurations of module groupings per Cage and different sub-arrays of 12 or 6 Cages (still respecting the distance of 40–150 m limits between them).
A first preliminary array configuration is depicted in Figure 5, where the green numbers are the Cage labels (from 1 to 24), the red lines are references for the labels of the relative distances, and the blue pin with a white star shows the Big Barrel’s location. The detector positions were determined using geospatial coordinates and visualized using the Folium library in Python, mapping 24 locations within a ∼500 m radius of the FAIS’s coordinates.
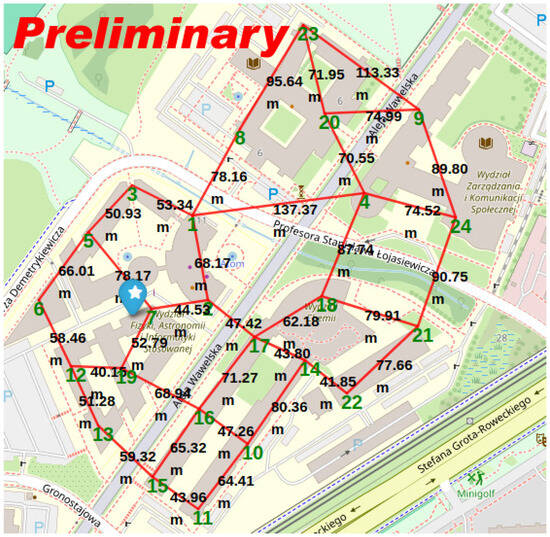
Figure 5.
A preliminary map of the scintillator array on the campus around the Faculty of Physics, Astronomy, and Applied Computer Science (FAIS) at Jagiellonian University. Reported are the positions of the 24 Cages (green numbers) and that of the Big Barrel (blue pin with a star) and the distance labels (black numbers; red lines as references).
Detailed simulations are ongoing to refine the Cages’ positions and the campaign planning; future publications will illustrate our results in detail. The first installation on the FAIS’s roof is expected by June 2026.
4.2. Cages
Housing of the scintillators is necessary to protect them from environmental conditions, animals, sun, etc. We are designing them for permanent installation on the roofs but so that they can still be opened to place and remove the modules easily.
A Cage consists of two elements. The lower part is a steel mounting plate equipped with feet isolating it from the ground, a hermetic power supply, a container for additional electronic systems, and two mounted Peltier modules with radiators for cooling. The upper part is a removable casing: the modules will be placed on the steel plate, covered with the casing, and locked. The upper part’s material is under testing. We are simulating different materials and thicknesses using Geant4 [29] to balance the cost and resistance of the Cage while considering the minimum loss of electrons passing through the casing. Candidates under consideration are Styrofoam, Plexiglass, and PEEK plastic.
In Figure 6, the sketch of a preliminary idea is illustrated: the sizes are still under optimization via simulations. During the spring of 2025, we will test different options and their thermal insulation in the laboratory. By June 2025, a testing campaign of a few Cage candidates on the roof will start to test their resistance. By the end of the summer, one single module will be allocated per Cage candidate, and connections between locations via optical fibers will be tested. The final configuration will be illustrated in future works.
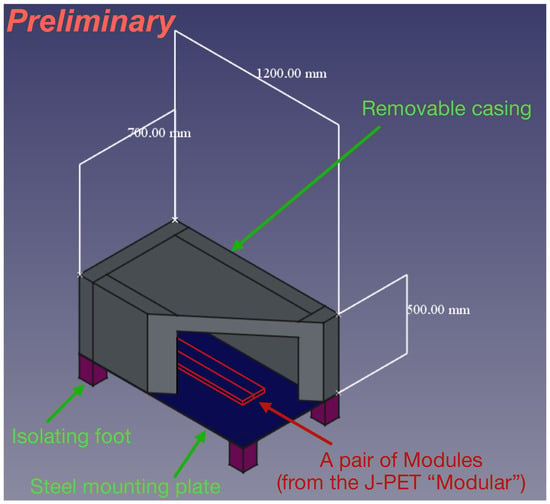
Figure 6.
A sketch of a Cage’s geometry. The sizes are still in the optimization phase.
5. Conclusions
We have presented the PPET project in its initial phase, from the hypothesis to the first preliminary designs. The project exploits the existing J-PET models, the Big Barrel and the Modular, to create a hybrid detector between a classical scintillator array for shower direction and muon tracking.
The Big Barrel demonstrates an angular resolution of approximately 1° for muon trajectory reconstruction, using only the hit geometry and the standard J-PET position reconstruction algorithm—without any refined analysis or calibration. However, the required resolution to detect discrepancies in the muon trajectories between models with and without the proposed hypothesis (outlined in Section 1.2) is still unknown, due to the hypothesis being entirely novel. Any estimate of the expected deviation would require a full EAS simulation, which is not feasible until the hypothesis is implemented in interaction models. To improve the angular resolution, we are planning a dedicated analysis and calibration campaign using state-of-the-art machine learning techniques. Specifically, Convolutional Neural Networks (CNNs) will be employed for calibration, while Physics-Informed Neural Networks (PINNs) will be used for precise localization of the particle interactions within the scintillator. Additionally, Bayesian Neural Networks will be utilized to quantify the uncertainties in the trajectory reconstruction. Our target is to achieve a resolution in the order of fractions of an arcminute. The development and performance of these advanced methods will be presented in future publications.
The Modular detector, instead, is planned to be used as a mobile and reshapable array placed on the roofs of the campus around the FAIS at Jagiellonian University. An advantage of this will be the freedom to test constrained ranges of distances between the shower core and the Big Barrel detector, which remains in a fixed location. Here, too, machine learning techniques, such as a Graph Neural Network (GNN), will be applied to improve the direction reconstruction and reduce event rejection rates.
Future publications will detail the different parts of this project’s design, while the data collection is planned to start in June 2026.
Author Contributions
Conceptualization: A.P.; Methodology: A.P. and G.M.; Software and formal analysis: K.V.E., N.N.P. and D.L.S.; Visualization: A.P., K.V.E., G.M., N.N.P. and D.L.S.; Data curation: K.V.E. and N.N.P.; Investigation and validation: All authors. Writing—original draft preparation: A.P., G.M., K.V.E., N.N.P. and D.L.S.; Writing—review and editing: All authors. Project administration and funding acquisition: A.P.; Supervision: P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by National Science Centre (NCN) grant number 2023/50/E/ST9/ 00576 (A.P.).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We thank the Dean of the Faculty of Physics, Astronomy, and Computer Science, Zbigniew Postawa, and the Vice-Dean for Research and Development, Leszek Motyka, for supporting the J-PET experiment and the PPET project. We thank the supporto of the Ministry of Education and Science and the SciMat and qLife Priority Research Area budgets under the programme Excellence Initiative–Research University at the Jagiellonian University. We acknowledge the technical and administrative support of A. Heczko, M. Kajetanowicz, W. Migdał, and A. Wach.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of this study; in the collection, analyses, or interpretation of the data; in the writing of the manuscript; or in the decision to publish the results.
Note
| 1 | An interaction length is the average distance a particle travels in a medium before undergoing a strong interaction. Similarly to the radiation length, it is expressed as a slant depth X [g ], and it is a characteristic of a material. |
References
- Matthews, J. A Heitler model of extensive air showers. Astropart. Phys. 2005, 22, 387–397. [Google Scholar] [CrossRef]
- Heck, D.; Knapp, J.; Capdevielle, J.N.; Schatz, G.; Thouw, T. CORSIKA: A Monte Carlo code to simulate extensive air showers. Rep. Fzka 1998, 6019, 11. Available online: https://www.iap.kit.edu/corsika/70.php (accessed on 23 May 2025).
- Dedenko, L.G.; Lukyashin, A.V.; Roganova, T.M.; Fedorova, G.F. Testing of the EPOS LHC, QGSJET01, QGSJETII-03 and QGSJETII-04 hadronic interaction models via help of the atmospheric vertical muon spectra. J. Phys. Conf. Ser. 2017, 934, 012017. [Google Scholar] [CrossRef]
- Pierog, T. Air Shower Simulation with a New Generation of post-LHC Hadronic Interaction Models in CORSIKA. PoS 2018, ICRC2017, 1100. [Google Scholar] [CrossRef]
- Riehn, F.; Engel, R.; Fedynitch, A.; Gaisser, T.K.; Stanev, T. Hadronic interaction model Sibyll 2.3d and extensive air showers. Phys. Rev. D 2020, 102, 063002. [Google Scholar] [CrossRef]
- Abdul Halim, A.; Abreu, P.; Aglietta, M.; Allekotte, I.; Almeida Cheminant, K.; Almela, A.; Aloisio, R.; Alvarez-Muñiz, J.; Ammerman Yebra, J.; Anastasi, G.A.; et al. Measurement of the depth of maximum of air-shower profiles with energies between 1018.5 and 1020 eV using the surface detector of the Pierre Auger Observatory and deep learning. Phys. Rev. D 2025, 111, 022003. [Google Scholar] [CrossRef]
- Albrecht, J.; Cazon, L.; Dembinski, H.; Fedynitch, A.; Kampert, K.; Pierog, T.; Rhode, W.; Soldin, D.; Spaan, B.; Ulrich, R.; et al. The Muon Puzzle in cosmic-ray induced air showers and its connection to the Large Hadron Collider. Astrophys. Space Sci. 2022, 367, 27. [Google Scholar] [CrossRef]
- Baur, S.; Dembinski, H.; Perlin, M.; Pierog, T.; Ulrich, R.; Werner, K. Core-corona effect in hadron collisions and muon production in air showers. Phys. Rev. D 2023, 107, 094031. [Google Scholar] [CrossRef]
- Acharya, S.; Agarwal, A.; Rinella, G.A.; Aglietta, L.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmad, S.; Ahn, S.U.; Ahuja, I.; et al. Multimuons in cosmic-ray events as seen in ALICE at the LHC. JCAP 2025, 04, 009. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Canal, C.G.; Kling, F.; Sciutto, S.J.; Soriano, J.F. An explanation of the muon puzzle of ultrahigh-energy cosmic rays and the role of the Forward Physics Facility for model improvement. JHEAp 2022, 34, 19–32. [Google Scholar] [CrossRef]
- Sivers, D.W. Single Spin Production Asymmetries from the Hard Scattering of Point-Like Constituents. Phys. Rev. D 1990, 41, 83. [Google Scholar] [CrossRef]
- Collins, J.C. Fragmentation of transversely polarized quarks probed in transverse momentum distributions. Nucl. Phys. B 1993, 396, 161–182. [Google Scholar] [CrossRef]
- Musch, B.U.; Hagler, P.; Engelhardt, M.; Negele, J.W.; Schafer, A. Sivers and Boer-Mulders observables from lattice QCD. Phys. Rev. D 2012, 85, 094510. [Google Scholar] [CrossRef]
- Airapetian, A.; Akopov, N.; Akopov, Z.; Aschenauer, E.C.; Augustyniak, W.; Avetissian, E.; Avetisyan, A.; Bacchetta, A.; Ball, B.; Bianchi, N.; et al. Observation of the Naive-T-odd Sivers Effect in Deep-Inelastic Scattering. Phys. Rev. Lett. 2009, 103, 152002. [Google Scholar] [CrossRef] [PubMed]
- Parsamyan, B. SIDIS transverse spin azimuthal asymmetries at COMPASS: Multidimensional analysis. PoS 2015, QCDEV2015, 007. [Google Scholar] [CrossRef]
- Moskal, P.; Kowalski, P.; Shopa, R.Y.; Raczyński, L.; Baran, J.; Chug, N.; Curceanu, C.; Czerwiński, E.; Dadgar, M.; Dulski, K.; et al. Test of a single module of the J-PET scanner based on plastic scintillators. Nucl. Instrum. Meth. A 2014, 764, 317–321. [Google Scholar] [CrossRef]
- Moskal, P.; Kowalski, P.; Shopa, R.Y.; Raczyński, L.; Baran, J.; Chug, N.; Curceanu, C.; Czerwiński, E.; Dadgar, M.; Dulski, K.; et al. Simulating NEMA characteristics of the modular total-body J-PET scanner—An economic total-body PET from plastic scintillators. Phys. Med. Biol. 2021, 66, 175015. [Google Scholar] [CrossRef]
- Moskal, P.; Stepien, E.; Khreptak, A. A vision to increase the availability of PET diagnostics in low- and medium-income countries by combining a low-cost modular J-PET tomograph with the 44Ti/44Sc generator. Bio-Algorithms Med-Syst. 2024, 20, 55–62. [Google Scholar] [CrossRef]
- Moskal, P.; Czerwiński, E.; Raj, J.; Bass, S.D.; Beyene, E.Y.; Chug, N.; Coussat, A.; Curceanu, C.; Dadgar, M.; Das, M.; et al. Discrete symmetries tested at 10-4 precision using linear polarization of photons from positronium annihilations. Nat. Commun. 2024, 15, 78. [Google Scholar] [CrossRef]
- Moskal, P.; Gajos, A.; Mohammed, M.; Chhokar, J.; Chug, N.; Curceanu, C.; Czerwiński, E.; Dadgar, M.; Dulski, K.; Gorgol, M.; et al. Testing CPT symmetry in ortho-positronium decays with positronium annihilation tomography. Nat. Commun. 2021, 12, 5658. [Google Scholar] [CrossRef]
- Moskal, P.; Kumar, D.; Sharma, S.; Beyene, E.Y.; Chug, N.; Coussat, A.; Curceanu, C.; Czerwiński, E.; Das, M.; Dulski, K.; et al. Non-maximal entanglement of photons from positron-electron annihilation demonstrated using a novel plastic PET scanner. Sci. Adv. 2025, 11, eads3046. [Google Scholar] [CrossRef] [PubMed]
- Moskal, P.; Dulski, K.; Chug, N.; Curceanu, C.; Czerwiński, E.; Dadgar, M.; Gajewski, J.; Gajos, A.; Grudzień, G.; Hiesmayr, B.C.; et al. Positronium imaging with the novel multiphoton PET scanner. Sci. Adv. 2021, 7, eabh4394. [Google Scholar] [CrossRef]
- Moskal, P.; Baran, J.; Bass, S.; Choiński, J.; Chug, N.; Curceanu, C.; Czerwiński, E.; Dadgar, M.; Das, M.; Dulski, K.; et al. Positronium image of the human brain in vivo. Sci. Adv. 2024, 10, eadp2840. [Google Scholar] [CrossRef] [PubMed]
- Das, M.; Bayerlein, R.; Sharma, S.; Parzych, S.; Niedzwiecki, S.; Badawi, R.D.; Beyene, E.Y.; Chug, N.; Curceanu, C.; Czerwiński, E.; et al. Development of correction techniques for the J-PET scanner. Bio-Algorithms Med-Syst. 2024, 20, 101–110. [Google Scholar] [CrossRef]
- Niedźwiecki, S.; Białas, P.; Curceanu, C.; Czerwinski, E.; Dulski, K.; Gajos, A.; Głowacz, B.; Gorgol, M.; Hiesmayr, B.C.; Jasinsk, B.; et al. J-PET: A new technology for the whole-body PET imaging. Acta Phys. Polon. B 2017, 48, 1567–1577. [Google Scholar] [CrossRef]
- Tayefi Ardebili, F.; Niedźwiecki, S.; Moskal, P. Evaluation of Modular J-PET sensitivity. Bio-Algorithms Med-Syst. 2023, 19, 132–138. [Google Scholar] [CrossRef]
- Tayefi Ardebili, F.; Moskal, P. Assessing the Spatial Resolution of the Modular J-PET Scanner using the Maximum-Likelihood Expectation-Maximization (MLEM) algorithm. Bio-Algorithms Med-Syst. 2024, 20, 1–9. [Google Scholar] [CrossRef]
- Korcyl, G.; Białas, P.; Curceanu, C.; Czerwiński, E.; Dulski, K.; Flak, B. Evaluation of Single-Chip, Real-Time Tomographic Data Processing on FPGA-SoC Devices. IEEE Trans. Med. Imaging 2018, 37, 2526–2535. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in Geant4. Nucl. Instrum. Meth. A 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; Frühwirth, R.; et al. Measurement of the Charge Ratio of Atmospheric Muons with the CMS Detector. Phys. Lett. B 2010, 692, 83–104. [Google Scholar] [CrossRef]
- Anastasi, G.A. AugerPrime: The Pierre Auger Observatory upgrade. Nucl. Instrum. Meth. A 2022, 1044, 167497. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abbasi, R.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Alispach, C.; Allison, P.; Amin, N.M.; et al. IceCube-Gen2: The window to the extreme Universe. J. Phys. G 2021, 48, 060501. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).