Abstract
We present a study of relic gravitational waves based on a foliated gauge field theory defined over a spacetime endowed with a noncommutative algebraic–geometric structure. As an ontological extension of general relativity—concerning manifolds, metrics, and fiber bundles—the conventional space and time coordinates, typically treated as classical numbers, are replaced by complementary quantum dual fields. Within this framework, consistent with the Bekenstein criterion and the Hawking–Hertog multiverse conception, singularities merge into a helix-like cosmic scale factor that encodes the topological transition between the contraction and expansion phases of the universe analytically continued into the complex plane. This scale factor captures the essence of an intricate topological quantum-leap transition between two phases of the branching universe: a contraction phase preceding the now-surpassed conventional concept of a primordial singularity and a subsequent expansion phase, whose transition region is characterized by a Riemannian topological foliated structure. The present linearized formulation, based on a slight gravitational field perturbation, also reveals a high sensitivity of relic gravitational wave amplitudes to the primordial matter and energy content during the universe’s phase transition. It further predicts stochastic homogeneous distributions of gravitational wave intensities arising from the interplay of short- and long-spacetime effects within the non-commutative algebraic framework. These results align with the anticipated future observations of relic gravitational waves, expected to pervade the universe as a stochastic, homogeneous background.
1. Introduction
Different evolution epochs compose the multifaceted mosaic of the chronology of our universe since the primordial times, starting with an era dominated by inflation, followed by dominant phases of radiation, matter, and, currently, according to the prevailing conceptions, the dark energy era, which is supposed to cause the accelerated expansion of the universe.
On a time scale, or conversely, on an inverse temperature scale, the first observed photons (known as the first light) carry remnants of the cosmic microwave background (CMB) radiation, which is assumed as the residual light from the Big Bang. These photons originated during the recombination phase, a crucial epoch marked by the decoupling of matter and radiation. This phase occurred approximately 380 million years after cosmic inflation when the universe had reached a temperature of approximately T ∼ 0.26 eV. During this period, free electrons began to combine with protons to form hydrogen atoms. Prior to the recombination era, the photons present in the universe underwent processes of continuous dispersion by the electric charges that composed the hot, dense primordial plasma. Due to Thomson scattering by free electric charges, these continuous dispersion processes are supposed to render the medium opaque to the propagation of electromagnetic radiation, drastically reducing the mean free path traveled by each photon.
Gravitational waves, ripples in spacetime caused by extreme energetic processes as predicted by Albert Einstein [1,2] and observed for the first time by the LIGO–Virgo collaboration [3], emerge as the most prominent mechanism for accessing information from the evolutionary universe before the recombination era. In this context, speculations point to the possible existence of a stochastic gravitational waves background (SGWB) [3,4,5]. This background signal distribution is expected to be similar to that of CMB radiation and originates from the superposition of countless incoherent sources spread out in all directions. It carries signatures of physical processes in the early universe, such as quantum fluctuations during the inflation era [6,7]. Other mechanisms for generating relic gravitational waves can be mentioned, in particular during the electroweak (EW) phase transition of the primordial universe, such as, for example, colliding bubbles during their expanding phase, the decay of magnetohydrodynamic turbulence produced by bulk motions of the bubbles, and from the propagation of damped sound waves [5]. We will return to these topics later.
In this contribution, using a recently developed branch-cut quantum gravity formulation (BCQG) [8,9] as a starting point, based on Wheeler DeWitt [10] and the Hořava–Lifshitz [11] approaches, we investigate the effects of a mini-superspace of a triad of dual and complementary quantum fields that obey Poisson’s algebra in a noncommutative spacetime environment on relic gravitational wave signals. The present extension allows us to go further into the standard formulations and explore in the future the possibility of introducing complex and pseudo-complex fields with the most distinct Lorentzian natures, involving not only scalar fields but also pseudo-scalar, vector, pseudo-vector, and tensor fields, thus opening up a wide range of descriptive possibilities.
The main reason and motivation for starting this extension with a field inspired by the inflaton [6], although of a distinct (complex) nature, is based on the complementary descriptive proposals for primordial inflation: while the inflation of BCQG is driven by topological structural aspects that acquire a dynamical behavior due to the reconfiguration of matter and energy immersed in spacetime based on an algebraic noncommutative formulation, which generates the capture of the short-range, ultraviolet (UV), and long-distance infrared (IR) scales, Guth’s inflation [6] has another origin, despite complementary to BCQG. More precisely, Guth’s inflation is driven by an “external mechanism" to the structure of spacetime, originated by the presence of matter and energy in the universe that reconfigures in turn spacetime in the presence of a potential that modulates chaotic and non-chaotic inflation. It turns out that both mechanisms touch and complement each other, and moreover, Guth’s model can discriminate chaotic from nonchaotic inflation, while BCQG cannot, leading to the conclusion that the inflation produced by BCQG is nondiscriminatory. Incorporating an inflaton-inspired complex field enables compatibility with known inflationary dynamics while extending the BCQG framework to encode phase transition effects in a more meaningful way. The complex nature of the present inflaton field, unlike the original field, allows its influence to be included in the phase transition region of the BCQG universe, thus going beyond the original formulation. Finally, the inclusion of the inflaton field serves as a theoretical reference for future modeling of BCQG, without such an insertion being strictly necessary.
Finally, it is important to emphasize an important descriptive aspect of both formulations. The standard inflation proposal is based on classical field theory, whereas the present formulation is based on quantum gravity, which implies a series of conceptual elements that bring to light important structural aspects. In particular, in the original formalism, the inflaton as an ‘external’ field does not behave as a fundamental ingredient in either the Friedmann equations or the wave function of the universe. In the present formulation, the non-commutative algebraic structure makes the scale factor , and the quantized fields, and , acquire a quantum entanglement duality, carrying relevant information about the dynamical structure of the universe and becoming fundamental ingredients of the wave function of the universe.
The structure of the paper is as follows. In Section 2, we outline the main features of the BCQG framework, emphasizing the role of the noncommutative algebraic structure and the triad of quantum fields. In Section 3, we present the formulation of relic gravitational waves within the linearized BCQG approach, including the derivation of the corresponding wave equations. Section 4 is devoted to the generation mechanisms of the stochastic gravitational wave background (SGWB), including contributions from early universe phase transitions such as electroweak bubble collisions. We derive the analytical form of the SGWB spectrum and evaluate its observability in future detectors. Section 5 explores additional speculative mechanisms for GW production within BCQG, such as foliation rupture and branch-cut dynamics. In Section 6, we summarize our results and discuss observational implications, particularly in the context of LISA. The appendices provide numerical estimates for the model parameters relevant to the amplitude and spectral shape of the predicted SGWB signal.
2. Branch-Cut Quantum Gravity
Infinities, singularities, and collapse of quantum states associated with observation and/or interactions represent challenging features of a quantum field theory which intensify when dealing with quantum gravity since the entanglement between observer and measuring instruments cannot be eliminated in the presence of gravity. In this realm, the adequacy of Hugh Everett’s [12] proposal for an interpretation of quantum theory applied to systems that include observers and measuring instruments and many-worlds conception as well as its strong connection with the Hawking–Hertog multiverse conception [13], despite being controversial to this day, represents in our view a relevant source of theoretical perspectives. Furthermore, the difficulties associated with describing the observation of quantum gravitational phenomena at the Planck scale occur in an arena where two very successful, apparently irreconcilable, conceptions of space and time confront each other: general relativity and quantum mechanics. In this domain, theories of quantum gravity based on the holographic principle predict the existence of quantum fluctuations of distance measurements that accumulate and exhibit correlations over macroscopic distances, opening a gateway to future observations of quantum gravity phenomena, sensitive to MHz gravitational waves, and dark matter candidates [14].
BCQG is a gauge field theory defined over a spacetime with a noncommutative algebraic–geometric structure, thus representing a consistent theoretical extension of the standard structure of local quantum field theory, introducing crucial elements of nonlocality, such as minimal scale. A non-commutative geometry represents, in turn, an extension of the conceptions that underlie standard geometry with respect to manifolds, metrics, and fiber bundles, insofar as the space and time coordinates, which conventionally correspond to classical numbers, are replaced in the BCQG formulation by a triad of dual and complementary quantum fields.
On the basis of an extended Faddeev–Jackiw deformation of the conventional Poisson algebra, BCQG comprises an extension of Riemannian foliated branch-cut quantum gravity in a non-commutative symplectic spacetime domain (BCQG) [8,9], providing an isomorphic scenario composed of the following triad of canonically conjugate scalar complex quantum fields , , and comprising complementary quantum dualities, resulting in the following super-Hamiltonian (for the details, see [8,9]):
In this scenario, the canonical BCQG cosmic scale factor, , and its complementary quantum counterparts, outlined in the perfect Hermann Weyl fluid domain, , and in addition an inflaton-inspired complex scalar field, shapes an underlying non-commutative spacetime structure. Canonical quantization procedures applied to the Hamiltonian (1), allow the variables , , and along with their corresponding conjugate momenta , , and to be treated as dynamical operators:
In the above equations, the coefficients , , , , and represent effective coupling constants associated with matter, spatial curvature, cubic and quartic self-interactions of the scale factor, and short-range quantum corrections, respectively. The quantity represents a constant reference energy term in the super-Hamiltonian, which may be absorbed into the overall normalization of the wave function or interpreted as a vacuum offset. The parameters , , , , and encode the influence of the noncommutative deformation and characterize the strength of algebraic and topological modifications to the standard Poisson structure. The triad of fields , , and defines the generalized dynamical field variables of the minisuperspace.
Combining Equations (1) and (2), the following expression for the super-Hamiltonian may be obtained:
In this formulation, chaotic inflation is modeled by the potential [6]
while for non-chaotic inflation, by the Fubini potential [15]
According to [16], chaotic inflation corresponds to a scenario of the very early stages of the evolution of the universe where inflation is a natural (and may even be inevitable) consequence of chaotic initial conditions in the early universe. Non-chaotic inflation, also known as non-metric chaotic inflation, is assumed within the context of what is arguably the simplest non-metric extension of Einstein gravity [17].
As previously pointed out [8,9], despite the adoption of an unconventional reverse mapping path for the Faddeev–Jackiw symplectic deformation of the conventional Poisson algebra—which generates a triad of commutative variables from their non-commutative counterparts—the above Equation (1) incorporates the effects of the reconfiguration of the originally commutative super-Hamiltonian by the imposition of a non-commutative symplectic algebra.
The resulting equation, although dependent on commutative variables, represented by , and , accentuates this reconfiguration by imposing a formal structural composition that inserts new dynamic components into the original formalism, modulated by non-commutative algebraic parameters of Poisson type, represented by the symbols , , , . This procedure, unlike a conventional Faddeev–Jackiw transformation, allows us to identify, in a comprehensible and manifest way, the impact of the noncommutative structure compared to the standard formulation, providing a kind of formal logical guide in order to deepen our understanding of the effects inherent to such a transformation on the cosmic acceleration of the universe.
Applying Hamilton equations to the super Hamiltonian (3) we obtain the following dynamical equation for :
In the case of chaotic inflation modeled by expression (4) for , the potential in (6) may be cast as follows (for the details, see [8,9]):
Following a similar procedure, in case of non-chaotic inflation modeled by expression (5) for , we obtain for the potential
By means of an implicit time integration of Equation (6), the following first-order implicit time dynamical equation for the BCQG scale factor may be obtained (for the details see [8,9]):
where the potential is defined as
Equation (9) allows us to formulate a BCQG source for generating relic sub-horizon gravitational waves. The component of the potential (10), , results in the following expression in case of chaotic inflation:
The component of the potential (10), , results in the following expression in case of non-chaotic inflation, assuming the condition :
3. Relic Gravitational Waves
Similarly to the CMB, the gravitational wave background is expected to propagate as a homogeneous noise, although it is supposedly too weak to be measured by current detection systems.
When investigating relic gravitational waves and their production in the first evolutionary stages of the branch-cut universe, we adopt a proposition that follows the conceptual approach of general relativity, the application of perturbation theory to the metric tensor that describes the geometry of spacetime in the weak field domain, assuming a linearized BCQG approach.
Quantum mechanics (QM) and pseudocomplex general relativity (pc-GR), by incorporating theoretical notions of existential closure as well as model completeness and domain extension [18], have expanded their descriptive scope realization to unique theoretical standards. (Augmented) quantum mechanics, by expanding its scope of realization from real variables to the domain of complex variables, and (augmented general relativity) pc-GR by covering the real and pseudo-complex domains have expanded our perception from infinitesimally small to immeasurably large scales.
The incorporation of such notions of descriptive domain extension materialized into physical observable manifestations in quantum mechanics [19,20] while pc-GR, comprising an environment composed of pseudo-complex variables, generated a mechanism for suppressing the primordial gravitational singularity and led to a unique prediction as the accumulation of dark energy around a mass and a generalized Mach principle. For a review on pcGR, see [21,22].
Accordingly, the development of the classical branch-cut gravity formulation was motivated by augmented quantum mechanics and pc-GR, more precisely, by theoretical notions of existential closure, as well as the completeness of the model and domain extension [8,9].
In this respect, the concept of domain extension proved to be fundamental to the theoretical and experimental realization of a quantum version of branched and foliated Riemannian quantum gravity (see the inspiring paper by Paul Adrien Maurice Dirac [23]). Constructed as an image of general relativity, yet analytically continued to the complex plane, BCQG describes a hypothetical set of multiple linearly independent universes, existing in parallel, each emerging from its own singularity.
The imposition is that all multiverses compose a single universe, in the limit of the infinitesimal separation tending to zero, of the originally isolated multiple singularities. When merging, these singularities generate a branch-cut complex continuous structure around a branch point, whose solutions are Riemann-type equations that are analytically continued to the complex plane. It is important to emphasize at this point that BCQG expands the domain of realization of the governing principles of general relativity, as well as its metaphysical commitments, its established relations and the operations that form the basis of its theoretical framework, in addition to evidently establishing a distinct representation of dynamical spacetime.
In this sense, BCQG, more than representing an augmented general relativity, does not suffer from the lack of formal consistency in its propositions, making it possible to overcome, with this expansion of domains, fundamental problems of standard cosmology. At a more elaborate epistemological level, BCQG shares the same methods of logical construction and inferences with general relativity based on systematic logical analysis founded on first principles, to the detriment of ad hoc insertions, axioms, or postulates [24].
In what follows, we develop a linearized formulation of branching gravity following logical steps and stages similar to general relativity. We then introduce a Minkowski-type metric, a field formulation that presents structural similarities to Einstein’s equations of general relativity, Christoffel-type symbols, as well as Riemann-type and Ricci-type tensors, analytically continued to the complex plane and underlying the spacetime of the BCQG universe.
Linearized Equations
Linearized branching cosmology is developed by assuming a metric tensor, analytically continued to the complex plane, decomposed into a Minkowski-type metric, and a small perturbation, in the form
In the BCQG framework, the metric is defined over a complexified spacetime manifold, where both the coordinates and the metric tensor components are analytically continued to the complex plane. Specifically, the Minkowski-type background metric retains its flat-space form but is now embedded in a complex domain, while the perturbation may carry complex components that encode quantum topological fluctuations. This continuation reflects the underlying branch-cut structure of spacetime and allows for multivalued solutions around branch points. The condition in Equation (13) implies that higher orders of are omitted. We thus refer to the linearized BCQG formulation, which corresponds, similarly to general relativity, to a linearized quantum gravity formulation of a rank-2 symmetric tensor field on a flat Minkowskian background with signature . Diffeomorphism invariance, similar to general relativity, due to the ontological character of BCQG, is maintained so that at the linearized level, it takes the form of gauge invariance.
The symmetric tensor comprises, in principle, ten degrees of freedom that are reduced, due to gauge invariance, to the two polarization orientations of gravitational waves and are most apparent in what is called the transverse traceless gauge (TT gauge), which is only valid in vacuum. We do not delve into detail regarding these aspects relating to the polarization of gravitational waves, a topic to be promoted in future studies more centered on future observation of signals from primordial gravitational waves. We will then attempt to construct an Einstein-type BCQG tensor in linear order on and then use it to construct the corresponding linearized equation relating metric perturbations to a form equivalent in BCQG to the stress–energy tensor of general relativity.
In branch-cut quantum gravity (BCQG), the equations that describe the branching universe may be cast in a form similar to Einstein’s equations (see, for instance, [25])
Similarly to general relativity, the branch-cut gravity equations relate the spacetime geometry, encoded in the metric , to matter described by the energy-momentum tensor analytically continued to the complex plane. The corresponding Ricci-type tensor and Ricci-type scalar for the linearized theory are computed following the usual scheme, starting from the analytically continued Christoffel symbol which will lead to an analytically continued Riemann curvature tensor.
From Equation (13), following similar mathematical procedures of the standard theory, we obtain the following for the analytically continued linearized Christoffel-type symbol:
This expression allows us to define the analytically continued Riemann-type curvature tensor in the form
It is crucial to note that in the upper expression, the second-order terms involving do not contribute to the first-order branch-cut equations.
Based on these expressions, the Ricci-type BCQG curvature tensor, analytically continued to the complex plane, may be cast as:
Similarly, the Ricci-type BCQG curvature scalar is
In this expression, is the trace of the metric perturbation, and .
From these expressions, we can construct an Einstein-type BCQG tensor, again to first order in the metric perturbation, as
As usually adopted in standard cosmology, the above equation may be simplified by inserting a trace reversed quantity which, in the present formulation, corresponds to
which results in
4. Stochastic Gravitational Wave Background
Speculations concerning stochastic gravitational wave backgrounds (SGWBs) involve their definition as the superposition of relic gravitational waves with different wave numbers k, encompassing variations in both magnitude and direction. These SGWBs are expected to exhibit characteristics such as isotropy, lack of polarization, and Gaussian distribution. They could originate from diverse sources, encompassing astrophysical and cosmic phenomena such as inflation, the presence of primordial black holes, various primordial cosmic seeds, cosmic strings, and phase transitions. These speculations draw parallels between SGWBs and cosmic microwave background (CMB) radiation originating from the primordial electromagnetic spectrum. The key distinction between these two types of primordial emissions lies in the fact that SGWBs have the potential to provide insight into earlier evolutionary stages of the universe that predate the recombination phase characterized by the decoupling of matter and radiation. This is because gravitational waves can travel freely through a primitive hot plasma, which is not transparent to photons. These considerations are particularly important for BCQG, as one of its scenarios involves a violent transition between two phases of the universe: a contracting phase preceding the conventional concept of a primordial singularity, and a subsequent expanding phase. The region of transition is mediated by a Riemannian foliation structure.
We define the noncommutative gravitation branch-cut metric in the form
where defines the conformal time. Expanding this metric around a flat homogeneous cosmological background , from the previous equations, the linearized field equations for the implicit dependence of the scale factor on the conformal may be expressed as
Following standard procedures, we introduce a Fourier transformation of this expression and we define , so the field Equation (23) may be recast in the form
where k represents the co-moving wave number, denotes the two polarization modes of gravitational waves, and we have set to simplify the notation.
This equation can be simplified by considering two main cases: (1) the sub-horizon case, characterized by the condition , and (2) the super-horizon case, defined by the condition , where . In the following, we briefly discuss the implications of these approximations to establish a connection with the standard formulation.
With respect to the term , we adopt the following representation in tune with the conventional standard Einstein equations:
4.1. First-Order Electroweak (EW) Phase Transition
The EW phase transition marked the separation of the electromagnetic and weak nuclear forces, which were previously unified as a single electroweak force under the Standard Model. Before the transition, the universe was in a symmetric phase where the electroweak symmetry was unbroken. As the universe cooled, the Higgs field underwent spontaneous symmetry breaking, acquiring a nonzero vacuum expectation value, that is, GeV. This broken symmetry gives masses to the W and Z bosons via the Higgs mechanism, while leaving the photon massless.
The character of the EW phase transition depends on the Higgs boson mass and interactions. (a) First-order phase transition: If the transition occurs via bubble nucleation (metastable phases), it produces gravitational waves and possibly enables electroweak baryogenesis that may explain matter-antimatter asymmetry. (b) Crossover transition: In the Standard Model (with a Higgs mass of about 125 GeV), the transition could likely be a smooth crossover, meaning that no violent dynamics occur. However, extensions of the Standard Model (e.g., with additional scalars or higher-temperature effects) could still allow for a first-order transition. Without such a modification, even if the transition is of first order, the amplitude of the generated gravitational waves will be extremely small. It should be emphasized that before the transition, particles like quarks, leptons, and weak gauge bosons were massless (or nearly massless). After the symmetry broke, the fermions acquired mass via Yukawa couplings to the Higgs field, while the W± and Z bosons became massive due to their interaction with the Higgs condensate.
In the context of general relativity and modified versions of this theory, the nature of the electroweak phase transition (case of a first-order transition) and the resulting gravitational wave spectrum can be significantly influenced by theories beyond the Standard Model. These theories may modify the dynamics of the Higgs field, the expansion history of the universe, or the properties of the early plasma, leading to distinct GW signatures.
In the case of a first-order transition, gravitational waves can be generated by the following mechanisms: (a) bubble nucleation of the broken-symmetry phase and (b) shock waves and turbulence in the primordial plasma. The bubble collisions are dominant at high frequencies, while sound waves in the cosmic plasma represent the most energetic contribution. Moreover, there is a broad-band component produced by magnetohydrodynamic (MHD) turbulence. However, there are other possibilities such as the following: (1) Extended Higgs Sectors (e.g., Two-Higgs-Doublet Models, Singlet Extensions)—as a consequence, additional scalar fields modify the Higgs potential, creating a stronger barrier between phases, and enabling a strong first-order transition. This also affects the spectral shape of the GWs, producing a shift of the peak frequency that also depends on the bubble nucleation rate. An enhancement of the wave amplitude will occur because the vacuum energy is larger. (2) Interactions with the dark sector (see, for instance, [26])—in fact, if dark matter couples to the Higgs field, it changes the thermal history, possibly making the transition more abrupt. Moreover, low-frequency bumps will appear in the GW spectrum, since dark matter interactions may suppress turbulence. (3) Non-standard cosmic dynamics—for instance, if the expansion of the universe is dominated by a fast-expanding component (e.g., quintessence or kination), the EWPT may occur earlier or later than the epoch predicted within the Standard Model. In this case, the GW spectrum will be red-shifted if the transition happens earlier or blue-shifted in the opposite case.
Recent reports from the NANOGrav collaboration indicate the detection of a stochastic gravitational wave background at a frequency of approximately Hz and an amplitude of . These values lie well outside the frequency range and amplitude scale expected for gravitational waves generated by cosmological phase transitions at the electroweak scale. The observed signal is therefore more plausibly attributed to an astrophysical background, such as the cumulative emission from a population of inspiraling supermassive black hole binaries [27,28]. The present work, which focuses on higher-frequency relic gravitational waves within a noncommutative quantum gravity framework, does not attempt to account for such low-frequency astrophysical phenomena.
4.2. Power Spectrum and Density Parameter
The energy density of gravitational waves can be written as
On the other hand, we can express the energy density of gravitational waves as
where the time average and the sum is performed over the polarization modes + and ×.
We can now define the dimensionless amplitude of the wave as
Derivation of the equation above and squaring gives
Taking the time average from the previous equation
The integrand can be identified with the power spectral density of the gravitational wave energy, allowing us to express the energy density per unit frequency interval in terms of the Fourier amplitude of the metric perturbations. Replacing (31) in (28) and comparing with (27), we obtain
Defining the density parameter for gravitational waves
with defining the closure density of the universe
with = 67.74 km/s/Mpc.
Introducing the spectral density by the relation
and taking the “averaging” time T as the period of the wave results that . In these conditions
To express the gravitational wave energy density in terms of co-moving spatial scales, we now switch from frequency f to wave number k, using the standard relation in natural units (). This is particularly convenient when connecting to cosmological perturbation theory and the analysis of modes crossing the Hubble horizon. For a statistic, homogeneous, isotropic, unpolarized, and Gaussian GW background, the expression of the energy density of gravitational waves can be written (in a simplified notation), in terms of the wave number k, as
4.3. Time-Evolution of the Metric Perturbation: BCQG Matter–Energy Source
In what follows, we consider solutions of the field equations that describe the time evolution of the perturbation of the metric , within the scope of branch-cut gravity in the sub-horizon mode with a matter–energy source. As the spatio-temporal scales grow beyond the horizon, the amplitude of relic gravitational waves freezes and after the end of inflation, these scales reenter the horizon during radiation and matter-dominated era and would lay imprints on the CMB surface. As pointed out recently by [29], sub-horizon and super-horizon modes will be probed distinctly by the future gravitational wave experiments and the current and future CMB-based experiments, and both modes are relevant for the identification of relic gravitational waves. However, according to [30], the most relevant effect of the sub-horizon mode is a change in the PBH mass function and redshift formation, which may affect, in turn, observables of relic gravitational waves. The authors found, in particular, that sub-horizon PBH formation enhances the isotropic SGWB energy density and the absolute angular power spectrum.
Combining Equations (26) and (10) and the sub-horizon condition, we obtain the following time evolution differential equation for the metric perturbation
with defined in expression (11) for chaotic inflation and in (13) for non-chaotic inflation.
It is worth noting that the dominant contributions to the source term on the right-hand side of Equations (46) and (47) depend sensitively on the behavior of and . For instance, in the limit , the inverse powers , , and can become large, signaling enhanced relic gravitational wave production during early phase transitions. Conversely, for large , quartic and cubic terms (e.g., , ) dominate, corresponding to late-time suppression or damping effects. These asymptotic behaviors emphasize the scale dependence of gravitational wave amplitudes in the BCQG framework.
Figure 1 shows the plot of the sample solution family sampling individual solutions of Equations (46) and (47) for a large range of values assuming a combination of parameters obeying the naturalness condition for long-range and fine-tuning for short-range values of , with , , and the power law , with . The plot in the right image of Figure 1, as expected, shows the gravitational wave background propagating as a homogeneous noise.
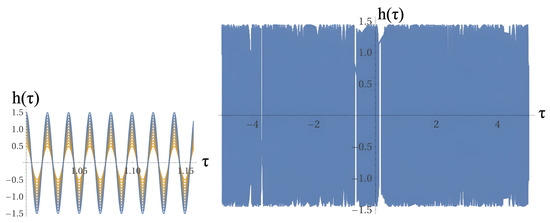
Figure 1.
On the left of the figure is the plot of the sample solution family of Equations (46) and (47) for a large range of values assuming a combination of parameters obeying the naturalness condition for long-range and fine-tuning for short-range values of , with , , , and the power law , with . The colours of the sample solution family correspond to the initial conditions of the individual sample solutions (red corresponding to initial conditions with negative amplitudes and blue the opposite). On the right of the figure is the corresponding plot of the sampling individual solutions.
4.4. Generation of Gravitational Waves: Bubble Collisions
As an application example of our approach, in what follows, we determine the spectral shape of relic gravitational waves produced by bubble collisions [31]:
In the strong regime, and represent the critical value of [5,31]. The parameter represents the characteristic frequency, which is contingent on the duration of the transition, denoted as . Corrected for the redshift effect, and for the case of a strong first-order electroweak phase transition, is given by [5]
which, for a nucleation temperature , , and , yields , placing the predicted peak squarely within the optimal sensitivity range of the LISA detector.
A key quantitative result of this work is a prediction of the shape and amplitude of the SGWB spectrum generated during early universe phase transitions in the BCQG framework.
In the following, due to the formal complexity of the solutions of Equations (46) and (47), and guided by their dominant behavior in the asymptotic domains and , we propose an analytical formulation–given in Equation (A9)—that preserve both the essence of the branch-cut quantum gravity proposal and the main requirements for the spectral shape of the signal.
Building upon the formal developments of Section 4.2, the analytically regularized spectral shape function derived in Equation (A9) captures the main features of the relic gravitational wave signal generated by bubble collisions and topological phase transitions (assuming the convergence condition ; see also Appendix B):
where a and b are positive constants with .
The corresponding energy density per logarithmic frequency interval is estimated from Equation (50) as
where is the amplitude pre-factor obtained from model parameters, given by
Using the parameter estimates discussed in Appendix A, the predicted SGWB spectrum from BCQG peaks near 1 mHz, with a maximum amplitude (see Figure 2)
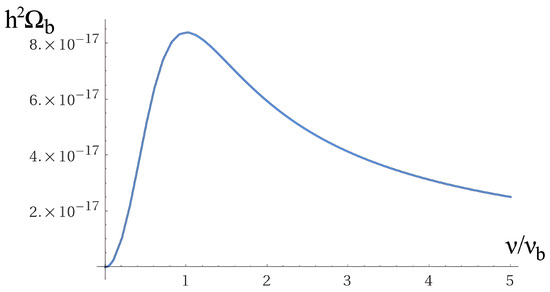
Figure 2.
Typical regularized gravitational wave spectra generated during a strong EW phase transition due to bubble collisions.
By introducing into the formalism a potential that describes the content of the relic universe in terms of mass and energy contributions, in the context of a non-commutative algebraic structure, we arrive at the spectral form of the signal expressed in terms of a convergent and regular series dependent on . The proposal defined in Equation (A9) in turn contemplates the condition that the maximum of the spectral function corresponds to the value of the characteristic frequency , and additionally allows the fitting of the simulated data with the simple choice of the only formulation parameter, a (see, for a more profound discussion of these topics [5]). In the present case, the choice of a corresponds to to fit the simulated data obtained by [32]).
5. Mechanisms for Generation of Gravitational Waves in BCQG
In the following, we speculate about mechanisms for the generation of gravitational waves in BCQG.
5.1. Foliation Rupture Events
Riemannian foliation in BCQG corresponds to a spacetime decomposition into leaves: smooth submanifolds foliated by a transverse structure, similar to layers in a higher-dimensional geometry. In quantum gravity, these leaves may represent discrete Planck-scale geometries, e.g., spin networks in loop quantum gravity (LQG) or n-dimensional anti-de Sitter space (AdSn) layers in holography. In this context, gravitational waves may arise when foliation layers deform or undergo rupture, analogously to seismic waves propagating between tectonic plates. When stress–energy fluctuations exceed a quantum threshold, foliation layers may tear or reconfigure, releasing gravitational wave bursts with high-frequency components originating from Planck-scale dynamics and exhibiting nonpolarization modes due to anisotropic foliation structures.
5.2. Branch-Cut Dynamics
Branch cuts correspond to non-local discontinuities in the metric, like cuts in a complex plane, where spacetime ‘jumps’ between foliation layers. These discontinuities can form in quantum foam regions, where stochastic cuts occur on the Planck scale, where branch cuts behave like topological defects. However, BCQG is expected to incorporate non-perturbative quantum corrections to holonomy through parallel transport around the branch cuts. In addition, one-dimensional branch cuts would behave, if eventually present, as cosmic string snaps (line-like branch cuts as in the multiverse conformation), and its rupture could generate gravitational waves with memory effects, as, for instance, a permanent spacetime strain. Moreover, the merger singularity of highly massive seeds, as relic black hole mergers, may be replaced by a branch-point singularity, emitting gravitational waves with modified quasi-normal modes.
5.3. Stochastic Background from Quantum Foam
Planck-scale branch cuts may fluctuate probabilistically and create a gravitational wave background with burst-like outliers from macroscopic cut mergers.
5.4. BCQG Transition to Complexified Manifolds and Metrics
In BCQG, spacetime is treated as a complex manifold where the metric and curvature can assume complex values. This is motivated by the imposition of analytic continuation from a Lorentzian metric to complex domains, with no-boundary condition, in line with Hartle and Hawking’s proposition [33]. The presence of branch cuts resulting from a scale factor of the universe described by a multivalued helical function, therefore, reconfigures the standard metric and curvature. Underlying this, such a reconfiguration is found in quantum gravity conceptual elements that imply non-smooth geometries and non-trivial metric topologies, where complex phases play a relevant role in suppressing pathological configurations. The transition to complex metrics, as proposed by BCQG, allows, in turn, the resolution of primordial singularities, since the smoothing or overcoming of spacetime divergences finds formal support in complex analysis, a scenario for the genuine implementation of Wick rotations, boundary deformations in gravitational path contours, and introduction of minimal length scales as a result of complex regularization, among others.
Stability problems in quantum gravity approaches are often generated by the presence of ghosts, states with negative norms, due to renormalizability impositions. BCQG, by generating complex metrics, simultaneously generates complex poles and, when summed out over multiple branches, could regulate instabilities, similarly to the alternative structure in particle physics proposed by Lee and Wick in the late 1960s [34].
Classical energy conditions in quantum gravity, on the other hand, are often violated due to quantum fluctuations of dynamic degrees of freedom, gauge fluctuations that carry quantum deformations, and the presence of exotic matter, among others. In BCQG, classical energy conditions acquire new perspectives, focusing on quantum energy constraints, that can be satisfied through branch-cut regularization procedures (see, for instance, [35]).
Branch cuts acting as dynamical regulators ensure stability and enforce energy conditions by constraining the analytic structure of the gravitational and matter field equations. For instance, violations of the energy conditions could be restricted to unphysical layers of the complex manifold leaving the remaining layers as required complying with physical stability and energy conditions. In order to include branch-cut regulators, the gravitational action [8] must be modified in the form
where represents the spacetime manifold, denotes the branch-cut locus in complexified spacetime, and is the BCQG regulator function that depends on the branch-cut variable z and encodes elements of the branch-cut structure.
In the context of quantum field theory, the main obstacle against perturbative renormalizability is that the gravitational coupling constant is dimensionful, with a negative dimension in mass units. The Feynman rules in turn involve the graviton propagator, which scales with the four-momentum , as , with . As an alternative, by considering a linearized branching cosmology and assuming a metric tensor, analytically continued to the complex plane, decomposed into a propagating polarizations of the Minkowski-type metric and a small perturbation (see Equation (13)), the corresponding propagator due to a branch cut is modified as (see [11])
which allows stability via analytic continuation constraints. In this expression, the branch cut along regulates IR/UV divergences and is the BCQG quantum renormalization scale ensuring stability by suppressing unphysical poles and preventing the propagator from diverging in unphysical regions.
5.5. Noncommutative Space Time and the Dark Sector
We outline some implications of non-commutative quantum gravity on the dark matter sector, although at a speculative level, based on non-commutative geometry, quantum gravity, and modified gravity theories.
We begin with the basic aspects of non-commutative geometry that suggest that spacetime coordinates do not commute at small scales, e.g., near the Planck scale:
where is an antisymmetric deformation tensor encoding the non-commutativity and possibly energy dependent. The immediate consequence of such a conception is that the structure of spacetime loses smoothness and may acquire a fractal or simply non-smooth structure, leading to modified dispersion relations and gravitational interactions. Furthermore, such an assumption generates spacetime uncertainty at small scales and modified gravitational dynamics in galactic and cosmological regimes.
In BCQG, in turn, spacetime may have a non-analytic multi-leaves structure, leading to modified propagators and Green’s functions as from instance, from Equation (55)
where is a quantum gravity scale, and encodes the branch-cut structure. The encoding of propagators becomes highly nontrivial due to the non-standard topology and analyticity properties of the spacetime, involving, for instance, quantum gravitational fluctuations as a result of summing over topologic contributions; propagators may be settled on different sheets just connected via monodromy transformations (topological fibers transformation) and may even pick up phase factors or discontinuities and may have different forms in different sheets.
Dark matter (DM) is currently inferred from gravitational effects, e.g., galaxy rotation curves, gravitational lensing, and CMB, among others. By altering the fundamental scales of spacetime, the non-commutative structure affects the gravitational field, matter fields, and new stable quantum states could emerge, expanding the spectrum of new dark matter candidates, an arena where nonlocal interactions could generate dark matter condensates, or even reduce or eliminate the requirements for dark matter. In terms of its effects on current models in the literature, its implications would be palpable in models based on modified Newtonian dynamics, running gravitational constants, or effective dark matter profiles, whose resulting effects could originate from noncommutative corrections to gravity. Furthermore, the implications of the non-commutative structure of spacetime in affecting the dynamics of galaxies would have implications for important structural elements such as dark matter halo structures and lensing anomalies in the CBM power spectra due to quantum gravity corrections, among others. However, more concrete predictions require a fully developed theory that might provide future insight.
When taking into account the presence of effective dark matter/energy terms in BCQG in a non-commutative spacetime, the non-commutative curvature is modified, implying in the modification of the field equations and deformation of the action, which may be encoded as an example, in the replacement (see, for instance, [36])
The symbol ‘★’ represents the Moyal–Weyl product, which provides a comprehensive phase space representation of the underlying dynamics.
A stochastic gravitational wave background, originating from early universe processes such as inflation, cosmic strings, or phase transitions, could carry signatures of quantum gravity, requiring BCQG to modify its spectral shape or correlation functions. To achieve this, BCQG must contemplate a non-smooth spacetime, introducing for example fractal or non-differentiable features on Planck scales. In this context, SBGWs could exhibit anomalous dispersion, decoherence, or non-Gaussian statistics, detectable by future observatories (e.g., in LISA, pulsar timing arrays). One approach that contemplates SBGW signatures is the presence of discrete or logarithmic singularities in gravitational wave propagators, causing certain frequencies in the SBGW spectrum to be enhanced or suppressed, generating resonances with branch cuts. In BCQG, dark matter might emerge from non-local or topological degrees of freedom associated with branch cuts, e.g., gravitational defects in spacetime. Appropriate modifications of the BCQG effective stress–energy tensor at galactic scales could mimic cold dark matter (CDM) without requiring new particles. Nonlocal terms in the quantum-corrected Einstein-type BCQG equations might reproduce, for instance, MOND-like results. Moreover, the coupling of DM to the branch-cut structure, by adopting a non-metric connection, could generate clustering-type properties, different from CDM predictions, and could affect structure formation. The dark energy, in turn, which originated from BCQG renormalization effects, might induce a cosmological constant or dynamical dark energy near branch points. This aspect could be identified as vacuum energy contributions from non-perturbative spacetime fluctuations. Using non-local operators involving integrals over spacetime history, dark energy could arise from ‘memory’ effects of past quantum gravity states, leading to a time-varying gravity constant or phantom energy. There is also another aspect to be mentioned: ‘late-time branch cuts’. When evolving with cosmic time, they might drive late-time acceleration, offering an alternative to quintessence.
5.6. Modified Dispersion and Quantum Foam
In the context of noncommutative quantum gravity frameworks such as BCQG, modified dispersion relations are a natural consequence of the underlying quantum structure of spacetime. These modifications can be attributed to the presence of a non-smooth vacuum, often interpreted as quantum foam, and are expected to induce energy-dependent corrections to the propagation of massless particles. A generic modified dispersion relation can be expressed as
where denotes the quantum gravity scale, is model-dependent and n defines the leading-order correction. These expressions are consistent with previously established quantum-spacetime phenomenology [37,38]. While not central to the present work, such dispersion effects are compatible with the nonlocal structures inherent to BCQG and may serve as a basis for future constraint studies.
6. Summary and Conclusions
In this work, we developed a formulation for relic gravitational waves based on the framework of branch-cut quantum gravity (BCQG), defined over a non-commutative foliated Riemannian spacetime. Starting from a foliated mini-superspace with a triad of canonically conjugate quantum fields, we derived the structure of the super-Hamiltonian governing the cosmic scale factor , the Weyl-type fluid component , and a complex inflaton-inspired scalar field .
The linearized field equations for gravitational perturbations were constructed by analytically continuing the Einstein field equations to the complex plane, revealing a modified wave equation sensitive to both the non-commutative structure and the underlying foliated geometry. The resulting equations predict relic gravitational wave amplitudes that are strongly dependent on the phase transition dynamics and the scale dependence of the BCQG scale factor. Both chaotic and non-chaotic inflationary scenarios were incorporated, and their influence on the relic gravitational wave potential and spectrum was explicitly computed.
We derived the corresponding expressions for the stochastic gravitational wave background (SGWB), including the power spectrum, density parameter, and spectral shape of the signal, with specific attention to contributions from early universe phase transitions such as bubble collisions during the electroweak epoch. Analytical expressions for the time evolution of the metric perturbations under both inflationary regimes were provided, and dominant terms for sub- and superhorizon modes were identified.
The spectrum as shown in Figure 2 is smooth and tunable, with distinct power-law behavior at both low- and high-frequency, and may serve as a signature of non-commutative and topological effects in the early universe. The value SGWBspectrum is below the expected sensitivity threshold of upcoming observatories such as LISA. This aligns with theoretical expectations across both standard and modestly extended electroweak phase transition scenarios, where the resulting gravitational wave signals are generally predicted to be too weak for detection (for a more profound discussion, see [5]). Nonetheless, the spectral shape derived here provides a valuable benchmark for characterizing stochastic gravitational wave backgrounds that could arise in non-standard or strongly BSM-enhanced early universe dynamics. Without such enhancements, the electroweak phase transition is unlikely to produce an observable gravitational wave imprint.
In terms of further predictions, gravitational wave anomalies associated with foliation dynamics may modify the stochastic background in the low-frequency band accessible to LISA, while branch-cut reflections from the merger of compact seed objects could generate high-frequency echoes. Anisotropy associated with foliated layers may also induce non-standard polarization signatures.
Although these predictions are speculative, they provide concrete avenues for testing the signatures of BCQG in future gravitational wave observations. The primary challenge remains the limited sensitivity of current detectors to Planck-scale effects, but the model offers a testable framework that connects non-commutative geometry, topological structure, and early universal gravitational wave physics. Further connections with loop quantum gravity, brane models, and string-theoretic approaches should be explored to deepen and extend this framework.
Author Contributions
Conceptualization, C.A.Z.V.; methodology, C.A.Z.V., J.A.d.F.P., P.O.H., F.W., R.R., B.A.L.B., R.R., D.H. and M.N.-M.; software, C.A.Z.V., B.A.L.B., M.R., M.N.-M., G.N., R.F.d.S. and J.G.G.G.; validation, C.A.Z.V., J.A.d.F.P., P.O.H., F.W., R.R., B.A.L.B. and D.H.; formal analysis, C.A.Z.V., J.A.d.F.P., P.O.H., F.W., D.H. and B.A.L.B.; investigation, C.A.Z.V., J.A.d.F.P., F.W., B.A.L.B., P.O.H., M.R. and M.N.-M.; resources, C.A.Z.V., B.A.L.B., G.N., R.F.d.S. and J.G.G.G.; data curation, C.A.Z.V., B.A.L.B., G.N., R.F.d.S. and J.G.G.G.; writing—original draft preparation, C.A.Z.V.; writing—review and editing, C.A.Z.V., F.W., P.O.H., J.A.d.F.P., R.R., B.A.L.B., D.H., M.R. and M.N.-M.; visualization, C.A.Z.V. and B.A.L.B.; supervision, C.A.Z.V.; project administration, C.A.Z.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the U.S. National Science Foundation under Grant No. PHY-2012152 awarded to F.W. P.O.H. acknowledges financial support from PAPIIT-DGAPA (IN116824).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
In our calculations for the generation of gravitational waves as a result of bubble collisions, we use , and assume (runaway regime) [5]. The parameter plays a crucial role in our analysis, as it quantifies the efficiency of converting latent heat into bulk motion, a pivotal factor in defining the amplitude of GW signals. In reference to [39], is approximately given as . When considering the parameter , from [5] we use Using the above values for and , we obtain
with is given as [40]
Assuming the runaway regime (), we obtain
and
In a first-order phase transition, the bubble nucleation process is fixed by the tunneling probability between the two vacua states of the effective potential (for details, see [5])
The usual standard-model potential does not generate a strong transition required to produce a significant background. In general, the potential must be modified and a minimum change implies additional gauge bosons (at least two new ones), which in practice means modifying the term. The solution for the vacuum states allows for the evaluation of the nucleation temperature, which is on the order of GeV [5]. During the EW phase transition, a fraction of the latent heat is used to excite sound waves, turbulence, and the bulk motion of bubbles, which are able to generate gravitational waves. Thus, the physical conditions of the transition must be used for all mechanisms that are not independent. Once the nucleation temperature is computed (or fixed), the duration of the transition can be estimated from [5]
However, fixing the nucleation temperature to be = 166 GeV, the relation above implies
Appendix B
Combining Equations (44), (46) and (47), due to the complexity of the resulting expression, we have analyzed the behavior of sequences of partial sums to identify a pattern. We arrive at the following partial representation of the spectral shape of the signal:
The series converges for:
Under these conditions, the series converges to the following expression:
References
- Einstein, A. Die Grundlage der allgemeinen Relativitätstheorie. Ann. Phys. 1916, 49, 769. [Google Scholar] [CrossRef]
- Einstein, A. Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie. König.-Preuss. Akad. Wiss. 1917, 142–152. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Binary Black Hole Mergers in the First Advanced LIGO Observing Run. Phys. Rev. X 2016, 6, 041015. [Google Scholar]
- de Freitas Pacheco, J. Cosmological Stochastic Gravitational Waves Background. In New Phenomena and New States of Matter in the Universe: From Quarks to Cosmos; Zen Vasconcellos, C.A., Hess, P.O., Boller, T., Eds.; World Scientific Pub. Co.: Singapore, 2023. [Google Scholar]
- Guth, A. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Guth, A. Carnegie Observatories Astrophysics Series, Vol. 2: Measuring and Modeling the Universe; Freedman, W.L., Ed.; Cambridge University Press: London, UK, 2004. [Google Scholar]
- Zen Vasconcellos, C.A.; Hess, P.O.; de Freitas Pacheco, J.; Weber, F.; Bodmann, B.; Hadjimichef, D.; Naysinger, G.; Netz-Marzola, M.; Razeira, M. The Accelerating Universe in a Noncommutative Analytically Continued Foliated Quantum Gravity. Class. Quantum Gravity 2024, 41, 245004. [Google Scholar] [CrossRef]
- Hess, P.O.; Zen Vasconcellos, C.A.; de Freitas Pacheco, J.; Weber, F.; Ruffini, R.; Hadjimichef, D.; Razeira, M.; Bodmann, B.; Netz-Marzola, M.; Naysinger, G.; et al. Cosmic inflation in an extended non-commutative foliated quantum gravity: The wave function of the universe. Astron. Nachr. 2025, in press. arXiv:2411.09756. [Google Scholar]
- Witt, B.D. Quantum Theory of Gravity. I. The Canonical Theory. Phys. Rev. 1967, 160, 1113. [Google Scholar]
- Hořava, P. Quantum Gravity at a Lifshitz Point. Phys. Rev. D 2009, 79, 084008. [Google Scholar] [CrossRef]
- Hugh Everett, I. The Many-Worlds Interpretation of Quantum Mechanics, The Theory of the Universal Wave Function. Ph.D Thesis, Princeton University, Princeton, NJ, USA, 1957. Available online: https://www.pbs.org/wgbh/nova/manyworlds/pdf/dissertation.pdf (accessed on 6 April 2025).
- Hawking, S.; Hertog, T. A smooth exit from eternal inflation? High Energy Phys. 2018, 4, 147. [Google Scholar] [CrossRef]
- Vermeulen, S.M.; Aiello, L.; Ejlli, A.; Griffiths, W.L.; James, A.L.; Dooley, K.L.; Grote, H. An experiment for observing quantum gravity phenomena using twin table-top 3D interferometers. Class. Quantum Gravity 2021, 38, 085008. [Google Scholar] [CrossRef]
- de Alfaro, V.; Fubini, S.; Furlan, G. Conformal invariance in quantum mechanics. Nuovo Cim. A 1976, 34, 569. [Google Scholar] [CrossRef]
- Linde, A. Chaotic inflation. Phys. Lett. B 1983, 129, 177. [Google Scholar] [CrossRef]
- Enqvist, K.; Koivisto, T.; Rigopoulos, G. Non-metric chaotic inflation. J. Cosmol. Astropart. Phys. 2021, 5, 023. [Google Scholar] [CrossRef][Green Version]
- Manders, K. Domain Extension and the Philosophy of Mathematics. J. Philos. 1989, 86, 553–562. [Google Scholar] [CrossRef]
- Aharonov, Y.; Bohm, D. Significance of electromagnetic potentials in the quantum theory. Phys. Rev. 1959, 115, 485–491. [Google Scholar] [CrossRef]
- Wu, K.D.; Kondra, T.; Rana, S.; Scandolo, C.; Xi-ang, G.Y.; Li, C.F.; Guo, G.C.; Streltsov, A. Operational resource theory of imaginarity. Phys. Rev. Lett. 2021, 126, 090401. [Google Scholar] [CrossRef]
- Hess, P.O.; Schäfer, M.; Greiner, W. Pseudo-Complex General Relativity; Springer: Berlin, Germany, 2015. [Google Scholar]
- Hess, P. Review on the Pseudo-complex General Relativity and Dark Energy. In New Phenomena and New States of Matter in the Universe: From Quarks to Cosmos; Zen Vasconcellos, C.A., Hess, P.O., Boller, T., Eds.; World Scientific Pub. Co.: Singapore, 2023. [Google Scholar]
- Dirac, P. Complex variables in quantum mechanics. Proc. R. Soc. A 1937, 160, 48. [Google Scholar]
- Russell, B. Logical Atomism; Oxford University Press: New York, NY, USA, 2012. [Google Scholar]
- Bodmann, B.; Zen Vasconcellos, C.; Hess, P.; de Freitas Pacheco, J.; Hadjimichef, D.; Razeira, M.; Degrazia, G. A Wheeler–DeWitt Quantum Approach to the Branch-Cut Gravitation with Ordering Parameters. Universe 2023, 9, 278. [Google Scholar] [CrossRef]
- Ghosh, T.; Guo, H.K.; Han, T.; Liu, H. Electroweak phase transition with an SU(2) dark sector. J. High Energy Phys. 2021, 2021, 45. [Google Scholar] [CrossRef]
- Afzal, A.; Agazie, G.; Anumarlapudi, A.; Archibald, A.M.; Arzoumanian, Z.; Baker, P.T.; Bécsy, B.; Blanco-Pillado, J.J.; Blecha, L.; Boddy, K.K.; et al. The NANOGrav 15 yr Data Set: Search for Signals from New Physics. Astrophys. J. Lett. 2023, 951, L11. [Google Scholar] [CrossRef]
- Agazie, G.; Anumarlapudi, A.; Archibald, A.M.; Baker, P.T.; Bécsy, B.; Blecha, L.; Bonilla, A.; Brazier, A.; Brook, P.R.; Burke-Spolaor, S.; et al. The NANOGrav 15 yr Data Set: Constraints on Supermassive Black Hole Binaries from the Gravitational-wave Background. Astrophys. J. Lett. 2023, 952, L37. [Google Scholar] [CrossRef]
- Odintsov, S.; Oikonomou, V. Chirality of gravitational waves in Chern-Simons f(R) gravity cosmology. Phys. Rev. D 2022, 105, 104054. [Google Scholar] [CrossRef]
- Profumo, S.; Yang, F. On the Anisotropy of the Stochastic Gravitational Wave Background from Sub-Horizon-Collapsed Primordial Black Hole Mergers. arXiv 2023, arXiv:2306.07454. [Google Scholar] [CrossRef]
- Caprini, C.; Hindmarsh, M.; Huber, S.; Konstandin, T.; Kozaczuk, J.; Nardini, G.; No, J.M.; Petiteau, A.; Schwaller, P.; Servant, G. Science with the space-based interferometer eLISA. II: Gravitational waves from cosmological phase transitions. J. Cosmol. Astropart. Phys. 2016, 2016, 001. [Google Scholar] [CrossRef]
- Huber, S.; Konstandin, T. Gravitational Wave Production by Collisions: More bubbles. J. Cosmol. Astropart. Phys. 2008, 0809, 22. [Google Scholar] [CrossRef]
- Hartle, J.; Hawking, S. Wave function of the Universe. Phys. Rev. D 1983, 28, 2960. [Google Scholar] [CrossRef]
- Lee, T.; Wick, G. Negative metric and the unitarity of the S-matrix. Nucl. Phys. B 1969, 9, 209–243. [Google Scholar] [CrossRef]
- Motygin, O.V. On regularization of the Heun functions. arXiv 2020, arXiv:2010.09053. [Google Scholar]
- Kontsevich, M.; Segal, G. Wick Rotation and the Positivity of Energy in Quantum Field Theory. Q. J. Math. Adv. 2021, 72, 673–699. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Quantum-spacetime phenomenology. Living Rev. Relativ. 2013, 16, 5. [Google Scholar] [CrossRef] [PubMed]
- Mattingly, D. Modern tests of Lorentz invariance. Living Rev. Relativ. 2005, 8, 5. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, J.; Konstandin, T.; No, J.; Servant, G. Energy Budget of Cosmological First-Order Phase Transitions. J. Cosmol. Astropart. Phys. 2010, 1006, 028. [Google Scholar] [CrossRef]
- Addazi, A.; Marcianò, A.; Pasechnik, R. Probing Trans-Electroweak First Order Phase Transitions from Gravitational Waves. Physics 2019, 1, 92–102. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).