Abstract
As a consequence of the spacetime structure, defined by the tetrad field instead of the metric tensor alone, gravity seems to harbor its own chronology protection agency. When Gott’s pair of moving cosmic strings is considered, it is shown that the requirement of having a global parallelization—i.e., a global smooth field of tetrads– drastically restricts the form of the tetrads on the junction surface between the two strings. The junction conditions on the tetrad field are satisfied only if the corresponding boosts needed to put the strings in motion are null on the matching surface. This seems to throw overboard Gott’s construction from the outset without the need for analyzing the divergence of the expectation value of the energy–momentum tensor on the Cauchy horizon, evading in this way bothersome quarrels concerning the choice of vacuum.
1. Introduction
It is well known that General Relativity (GR) allows the possibility of time travel. Among the various solutions presenting causal anomalies of one sort or another, Gott’s spacetime is perhaps the most peculiar [1]. Being a vacuum solution of Einstein’s equations, the closed timelike curves (CTCs) arising in Gott’s solution are not powered by any form of matter–energy. Furthermore, the two-moving strings spacetime is constructed by pasting two copies of the conical geometry characterizing the exterior metric of an infinitely long cosmic string, so it differs from Minkowski space only in its global properties. Additionally, the spacetime so obtained is geodesically complete, which is the reason why the non-compact region containing causal violations is not affected by fresh information coming from curvature singularities. Finally, the Cauchy horizon in Gott’s solution is not compactly generated, which makes Hawking’s chronology protection conjecture inapplicable [2]. For a detailed, technical description of time travel in GR, we can refer the reader to [3,4].
On physical grounds, Gott’s construction suffers from two drawbacks: first, cosmic strings were not yet detected, a fact that should not worry us too much, especially if we think of the immeasurable advancements achieved in regard to the detection of objects as elusive as black holes and gravitational waves. It is by no means an exaggeration to conceive the possibility of discovering not far ahead in the future topological defects on large scales, such as cosmic strings [5]. Second, if any, cosmic strings are quite likely finite in length, or come in loops, in which case Hawking’s chronology protection conjecture would enter into the scene. However, the expectation value of the stress–energy tensor on the Cauchy horizon is strongly dependent on the choice of vacuum, as was explicitly shown in [6,7] for Misner space. This result is very important because Gott’s two-strings space can be thought as a generalization of Misner space [8]. Hence, it seems unclever to judge by means of this argument whether or not CTCs can survive the perturbations that quantum fields would produce on the metric. Additional physical arguments against the production of CTCs by cosmic strings were considered, for instance, in refs. [9,10,11].
It is our intention here to discuss Gott’s construction in the context of gravity. In order to present a relatively self-contained exposition, we revisit in Section 2 the solutions describing both the interior and exterior structures associated with infinitely long cosmic strings in GR, followed by a concise review of Gott’s two-moving strings space. Section 3.1 deals with the interior and exterior tetrads describing the corresponding cosmic string solutions according to gravity, as well as the junction conditions involved in their matching. Section 3.2 is entirely devoted to the treatment of the two-moving strings space, and to show that no traveler is able to circumnavigate both strings with the aim of visiting his/her own past.
2. Infinitely Long Cosmic Strings in GR and Gott’s Construction
When dealing with just one string, it is convenient to write down the metric in cylindrical coordinates. The interior metric is (we follow [12] in the first part of this section)
which is a solution of Einstein’s field equations , for an energy–momentum tensor , with and . The coordinates in (1) range according to , and . A change of coordinates to gives us
which will be useful in brief. The exterior, vacuum metric, in turn, reads
where is the mass per unit z-length of the string, namely,
where we have used that . It is clear that (3) can be cast in the form
provided ; then, and . So, this is just Minkowski spacetime with an angle deficit .
Due to the fact that the junction surface between the two metrics contains no shells or layers of matter, Israel conditions alluding to the continuity of the extrinsic curvature across the boundary surface reduce to the continuity of the metric and its normal derivatives on it. In the cylindrical coordinates adopted in (2) and (3), this condition simply translates into
From the interior point of view, the boundary surface is defined by . The continuity of the metric on then requires , as viewed from the exterior. Concerning the derivatives, we see that the only non-trivial ones are
So, the value of as well as agree on both sides of the boundary, and the junction conditions are automatically satisfied.
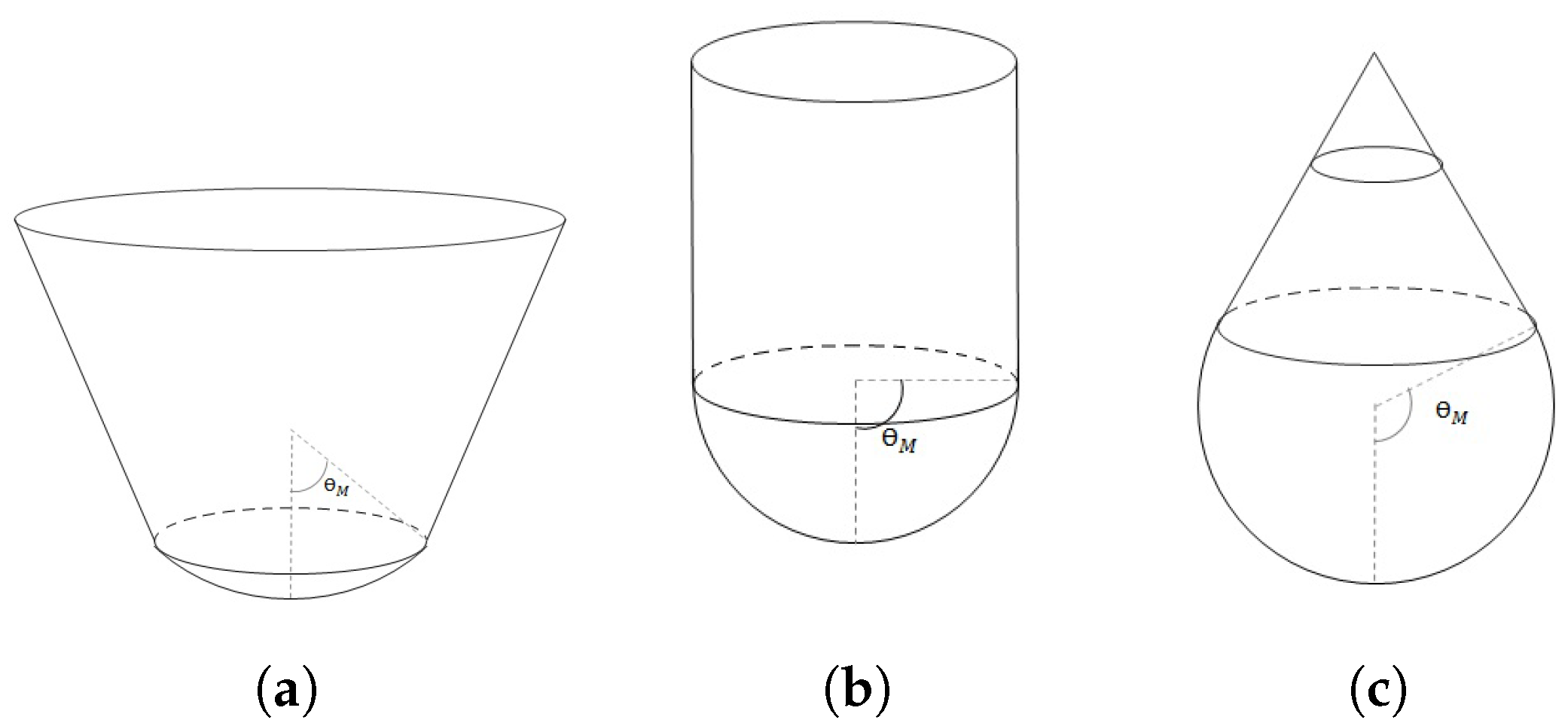
The structure of the strings can be viewed in the embedding diagrams of Figure 1, where the cross sectional geometry , is displayed. When (this is ), we have a spherical cap covering less than a hemisphere for the interior metric, and a cone opening out and extending to infinite for the exterior metric. In turn, when (), the geometry corresponds exactly to a hemisphere for the interior and a cylinder of radius for the exterior. Finally, if (thus, ), the interior is more than a hemisphere and the exterior solution is like a dunce cap sitting on top of the sphere.
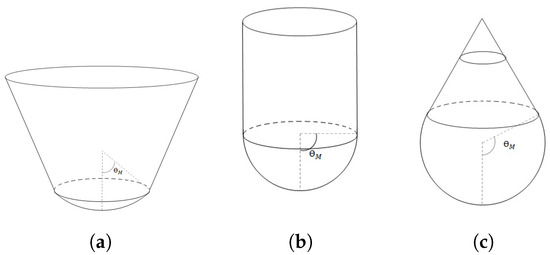
Figure 1.
Embedding diagrams for the cross sectional geometry corresponding to the interior and exterior solutions. (a) , . (b) , . (c) , .
Gott’s construction makes use of the fact that the solution corresponding to two static parallel cosmic strings separated by a distance is easily obtained from the one just discussed. We summarized here the findings made in [1], primarily with the aim of setting the notation. If we adopt Cartesian coordinates
the exterior metric (5) is just , valid in the region , and , as in Figure 1a. Furthermore, we have to identify opposite points on the wedge; hence, and are really the same points. This corresponds to the string whose center is located at a distance d measured along the y-axis. In the same way, we can consider a mirror-image second copy located at ; the two copies obey the matching conditions along the three-surface defined by , which has metric and thus zero intrinsic and extrinsic curvature.
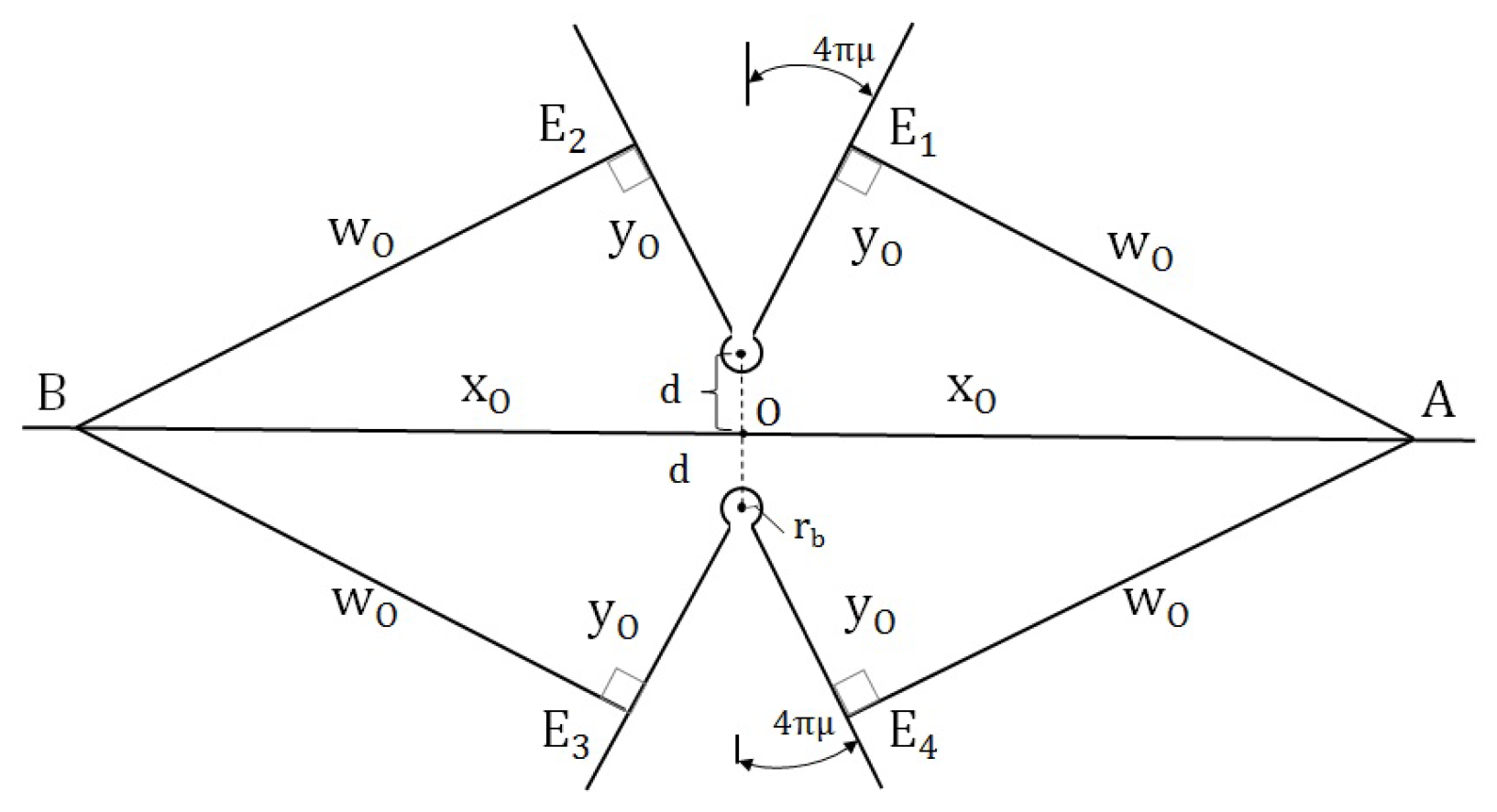
The two-string static solution just constructed has unnerving global properties. Referring to Figure 2, we see that observer B perceives three images of observer A (they are both at rest with respect to the strings). In particular, if a light beam is emitted at A, it can travel directly to B by following the null geodesic passing through the origin O, or by null geodesics passing through the events and , both pairs being respectively identified. According to Figure 2, we have
and the value of is chosen as to minimize , i.e., . Replacing this value into (9), we obtain the simple expression
However, the light beams going around the strings can beat the light beam passing through O only if , which is achieved provided ; the same is true for a rocket travelling at a high enough speed relative to the strings at rest. Concretely, let the rocket start its journey at A (event ) and finish it at B (event ) following the path through , where
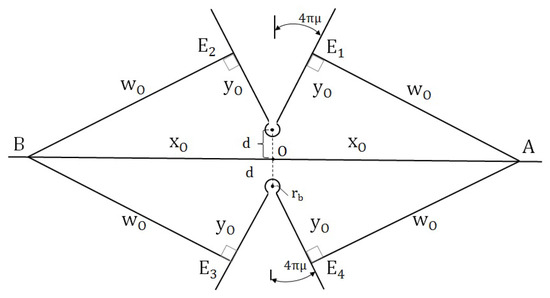
Figure 2.
Static, exterior two-string geometry for constant z.
Notice that the events and are spacelike separated only if . Now, after performing a -boost with velocity in the region, the events and can be made simultaneous if . The same can be done in the region by means of a -boost with the same speed . In this way, the rocket is able to complete a CTC as viewed from the laboratory frame (this is the frame with respect to which the strings have equal but opposite momenta). This CTC is described by the timelike geodesic segments arising as a consequence of the travel from to through , and back from to through .
In ref. [1], it was shown that the closed path just described is actually a CTC only if . In view of Equation (10), we have thus that a necessary and sufficient condition for the existence of such CTC is
Similar conclusions can be obtained by considering a different closed trajectory for the rocket, such as the one described by the segments . In this case, the rocket would undergo acceleration only at the identified events and (as opposed to the situation previously described, where the rocket undergoes acceleration only at and ). Worthy of mention is the fact that, for a given , all the pairs associated with sufficiently large values of are connected by a certain CTC. In other words, CTCs are not limited to exist in a compact region. Details on the global structure of Gott’s spacetime can be found in refs. [8,13,14].
3. Gott’s Construction According to f(T) Gravity
3.1. Infinitely Long Cosmic Strings and the Tetrad Field
In the context of the extended theories of gravity relying on absolute parallelism, the dynamical field is the tetrad , and often it becomes confusing to think of the metric field g as the carrier of the gravitational degrees of freedom, even though the tetrad is required to be orthonormal in the (pseudo) Riemannian sense . In the case of gravity [15,16], the equations of motion governing the full orientation of the tetrad are
where an arbitrary (at least twice differentiable) function f of the Weitzenböck pseudo-invariant appears 1, and primes denote differentiation with respect to T. Here, , are the components of the torsion coming from the Weitzenböck connection, and the components of the superpotential read
where . Let us notice that the tetrad components carry Lorentz-type indexes a as well as spacetime ones . The Equation (12) is derived from the action
which reduces to GR (in its teleparallel equivalent form), when . The energy–momentum tensor appearing in the RHS of the equations is derived from in the usual way. For a bibliographical compendium on gravity, the reader is invited to consult [19].
We proceed now to discuss both string (interior and exterior) solutions within this context. The interior tetrad is just
which corresponds to the form (2) of the interior line element. Due to the simplicity of the tetrad field, just a few components of the torsion and contortion tensor are non-trivial. In spacetime, totally covariant form, they are
It is straightforward to check from these that . This leaves us with only two non-trivial motion equations, namely,
then we obviously have , which implies , as we mentioned before. Due to the null character of T, we see that and for any smooth function f connected to the identity, i.e., . In this way, the equations reduce to the condition . This proves that the tetrad (14) is a solution of the field equations for an energy–momentum tensor verifying , for any smooth deformation of GR.
For the exterior tetrad, we consider again the “square root” of (3); then, we have
which leads us to
This tetrad also conduces to and then it automatically solves the vacuum field equations. The fact that (14) and (16), being GR’s solutions, remain as solutions of the equations, is ultimately a consequence of both having ; this means that (12) reduces to
provided ; these are none other than the TEGR equations with ( vanishes). Therefore, any solution of GR having tetrads leading to remains as a solution of gravity. Diagonal, proper tetrads such as (14) and (16) are rare among solutions of gravity. They only work in very simple and symmetric situations, such as the one corresponding to the constant curvature spaces here considered. The selection of preferred frames is a distinct feature of gravity in its pure-tetrad formulation, opposed (only in nature), to the covariant approach developed in [20]; see the appeasing discussion of ref. [21] in regard to the two approaches.
The tetrads (14) and (16) -match on . As a matter of fact, the continuity of the tetrad and its first derivative on the matching surface follow at once from
being the remaining components trivially matched. This fact ensures that the exterior and interior tetrads together constitute a well-defined global parallelization; see refs. [22,23,24] for further discussions on this subject.
3.2. Gott’s Construction and Remnant Symmetries
Once the general structure of the string is presented, we focus on the exterior, vacuum tetrad (we drop the subscripts + and − from now on). Because we are planning to boost the strings in the x-direction (with opposite speeds), it is convenient to write the tetrad in Cartesian coordinates, defined by (8). The tetrad (16) in these coordinates looks like
which is valid in the region corresponding to the string whose center is at , and we wrote . A similar coordinate change is used to obtain the second copy valid in (this implies to change y by in (18)), which reads
where now . Let us remark that both tetrads are continuous and differentiable on .
In order to put the strings in motion, we now apply coordinate-dependent boosts in . For the moment, we are not forced to consider the same (opposite) speeds for both strings, so we will have after the boosts
for and regions, respectively. In both boosted tetrads, we have (see ref. [25] for a full analysis concerning the role of the booston in 2D toy models). Notice that (20) and (21) have opposite rapidities , so they are boosts in x with opposite speeds. Gott’s construction discussed in Section 2 requires .
Due to the fact that we locally boosted solutions of a theory which is not local Lorentz invariant in general, two questions naturally arise:
(b) Once we established that and are solutions, is that true for ? If that were to be true, it would entail the fulfillment of the junction conditions on .
The answer to the first question resides in the functional form of the Weitzenböck pseudo-invariant T, which clearly is not invariant under local Lorentz transformations in the tangent space. After some work, it can be obtained that
where, from now on, upper signs corresponds to ↑, and lower ones to ↓. This means that the remnant group of transformations associated with the original tetrads (18) and (19), i.e., the local Lorentz transformations leaving invariant the null value of T [17], includes—among many others—position-dependent boosts in the plane. In other words, (20) and (21) are solutions of the vacuum field equations only if alone.
Once we establish that , we proceed to answer question (b) raised above. It is quite evident that on the junction surface (), the tetrad is not ; actually, it is not even continuous due to the jump in the sign. This is so provided that . There is also a discontinuity of the derivatives of on , as witnessed by the presence of several non-null components of the torsion, e.g,
where . Other components of the torsion that do not involve exist as well, for instance,
but they are automatically continuous on , because there. Hence, in order to have a well-defined global parallelization, we need to demand and the continuity of the derivatives across . This simple conclusion puts several constraints on the functional form of near ; in particular, it rules out the case lying behind Gott’s construction.
A crucial aspect in Gott’s construction is the fact that the events and , both belonging to the matching surface defined by , become simultaneous in the laboratory frame after the action of the boosts in both directions of the x-axis; this simply requires , which implies . In contrast, motion equations demand () along the matching surface, thus selecting frames (tetrads) which necessarily undergo accelerated motion, at least within a strip , for non-null, small and .
In effect, in the original static solution for , let us consider the events and described by
where now (see Equation (10)), and is the constant speed of the rocket in . Again, the separation of and is spacelike provided that , and they become simultaneous in the laboratory frame after the action of a -boost with speed . As , we have then , or
However, relation (25) is not consistent with the fact that must go to 0 as ; this simply means that and cannot be simultaneous as . This same conclusion applies to the corresponding events in , which in the static picture have coordinates
where now is the constant speed of the rocket in (perhaps different from ), and . These events can be made simultaneous if a boost in the -direction with speed is performed, but only if is not too small.
In this way, one can conceive a rocket traveling at a high enough speed along a (spatially) closed curve defined by the timelike geodesic segments (through ) and (through ), plus two non-geodesic timelike segments and . Once the two strings are in motion with speeds and in opposite directions, the rocket departs from the position corresponding to and arrives simultaneously to the one of in the laboratory frame. Then, it takes the rocket a time , as measured in the laboratory frame, to cover the non-geodesic segment from to ; during this stage, the rocket experiences a strong accelerated motion due to the fact that it must dramatically change its speed because the boosts go to zero as . Immediately after that, the rocket is able to travel again instantaneously between the positions corresponding to and by using the string moving along in . Finally, it will take another time to go from to its original starting position. The rocket will thus complete a closed spatial circuit in a time according to the laboratory frame. This circuit does not constitute a closed timelike curve. Even though could be very small—this depends on the (unspecified) state of motion along the accelerated stages—the rocket cannot travel back in time to its own past, although it might almost do it.
Things are not much better for the rocket following the closed path , where again, and are identified. After the Lorentz transforms have been made in the region (we are considering now ), the events and are simultaneous in the laboratory frame, just as before. However, the rocket cannot travel from to and from to without crossing the region , where must change its value in order to comply with the matching conditions. More precisely, let us consider the following events in the static frame
These events are none other than the projection of onto the boundary of the accelerated strip. After the corresponding boosts with (constant) opposite speeds are applied in the and regions, these events have coordinates in the laboratory frame
Even though and as well as and are simultaneous in the laboratory frame, a rocket at speed in the same frame will cover the two segments and only if
Again, we can always choose in such a way that , and since , we end up with as before. But we know for certain that goes to zero as , so the last inequality cannot be true in that limit. This simply shows that it is not possible to travel by rocket at speed in the laboratory frame with the aim of joining the simultaneous events and ; in other words, it will take a time (let us say, again) to cover the segment and from the point of view of an observer in the laboratory frame. Obviously, the same conclusion applies to the way back from to . The rocket will spend another time to cover that trip and then a time to circle the two strings.
4. Final Comments
We have seen that the space traveler—having the intention to become a time traveler as well—will spend, roughly, a time to circumnavigate the strings in rapid opposite motion, according to an observer located at the laboratory frame. At the moment the value of is uncertain because it depends on the kinematics unfolding within the accelerated strip, but we do know that . Causal pathologies might then be on the verge of occurring due to the fact that the traveler could still be in the position to influence his/her own past because could be very small. It would be interesting, then, to estimate by analyzing different motions obeying the constraint on , and to inquire whether the results here obtained are present as well in other theories of gravity relying on absolute parallelism such as, for instance, in Born–Infeld gravity [26].
In the original construction of ref. [1], it was mentioned that the strings need not be parallel. In the present context, it would be relevant to figure out what kind of rotations mapping the three-surface into itself also belong to the remnant group associated to the tetrads (18) and (19), with the aim to thus collect further arguments against the formation of CTCs in Gott’s space.
Funding
This research was funded by CONICET and Instituto Balseiro.
Data Availability Statement
No new data were created or anlyzed in this study. Date sharing is not applicable to this article.
Acknowledgments
I would like to express my gratitude to Diego Mazzitelli for reading the manuscript and making valuable comments. The author is a member of Carrera del Investigador Científico (CONICET), and his work is supported by CONICET and Instituto Balseiro (UNCUYO).
Conflicts of Interest
The authors declare no conflicts of interest.
Note
| 1 | Pseudo-invariant means that T is invariant only under general coordinate changes and global Lorentz transformations on the tangent space. It changes by a total derivative when local Lorentz transformations are considered. See refs. [17,18]. |
References
- Richard Gott, J., III. Closed timelike curves produced by pairs of moving cosmic strings: Exact solutions. Phys. Rev. Lett. 1991, 66, 1126. [Google Scholar] [CrossRef] [PubMed]
- Hawking, S.W. Chronology protection conjecture. Phys. Rev. D 1992, 46, 603. [Google Scholar] [CrossRef] [PubMed]
- Earman, J.; Smeenk, C.; Wüthrich, C. Do the laws of physics forbid the operation of time machines? Synthese 2009, 169, 91. [Google Scholar] [CrossRef]
- Krasnikov, S. Back-in-Time and Faster-than-Light Travel in General Relativity; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Xiao, H.; Dai, L.; McQuinn, M. Detecting cosmic strings with lensed fast radio bursts. Phys. Rev. D 2022, 106, 103033. [Google Scholar] [CrossRef]
- Li, L.-X. Must time machine be unstable against vacuum fluctuations? Class. Quantum Grav. 1996, 13, 2563. [Google Scholar] [CrossRef]
- Li, L.-X.; Richard Gott, J., III. A self-consistent vacuum for Misner space and the chronology protection conjecture. Phys. Rev. Lett. 1998, 80, 2980. [Google Scholar] [CrossRef]
- Grant, J.D.E. Cosmic strings and chronology protection. Phys. Rev. D 1993, 47, 2338. [Google Scholar] [CrossRef]
- Deser, S.; Jackiw, R.; ’t Hooft, G. Physical cosmic strings do not generate closed timelike curves. Phys. Rev. Lett. 1992, 68, 267. [Google Scholar] [CrossRef]
- Carroll, S.M.; Farhi, E.; Guth, A.H.; Olum, K.D. Energy-momentum restrictions on the creation of Gott time machines. Phys. Rev. D 1994, 50, 6190. [Google Scholar] [CrossRef]
- Krasnikov, S. A causality preserving evolution of a pair of strings. Universe 2022, 8, 640. [Google Scholar] [CrossRef]
- Richard Gott, J., III. Gravitational lensing effects of vaccum strings: Exact solutions. Astrophys. J. 1985, 288, 422. [Google Scholar] [CrossRef]
- Ori, A. Rapidly moving cosmic strings and chronology protection. Phys. Rev. D 1991, 44, R2214. [Google Scholar] [CrossRef] [PubMed]
- Cutler, C. Global structure of Gott’s two-string spacetime. Phys. Rev. D 1992, 45, 487. [Google Scholar] [CrossRef] [PubMed]
- Ferraro, R.; Fiorini, F. Modified teleparallel gravity: Inflation without inflaton. Phys. Rev. D 2007, 75, 084031. [Google Scholar] [CrossRef]
- Bengochea, G.R.; Ferraro, R. Dark torsion as the cosmic speed up. Phys. Rev. D 2009, 79, 124019. [Google Scholar] [CrossRef]
- Ferraro, R.; Fiorini, F. Remnant group of local Lorentz transformations in f(T) theories. Phys. Rev. D 2015, 91, 064019. [Google Scholar] [CrossRef]
- Bejarano, C.; Ferraro, R.; Fiorini, F.; Guzmán, M.J. Reflections on the covariance of modified teleparallel theories of gravity. Universe 2019, 5, 158. [Google Scholar] [CrossRef]
- Bahamonde, S.; Dialektopoulos, K.F.; Escamilla-Rivera, C.; Farrugia, G.; Gakis, V.; Hendry, M.; Hohmann, M.; Said, J.L.; Mifsud, J.; Valentino, E.D. Teleparallel gravity: From theory to cosmology. Rep. Prog. Phys. 2023, 86, 026901. [Google Scholar] [CrossRef]
- Krššák, M.; Saridakis, E.N. The covariant formulation of f(T) gravity. Class. Quantum Grav. 2016, 33, 115009. [Google Scholar] [CrossRef]
- Blixt, D.; Ferraro, R.; Golovnev, A.; Guzmán, M.J. Lorentz gauge-invariant variables in torsion-based theories of gravity. Phys. Rev. D 2022, 105, 084029. [Google Scholar] [CrossRef]
- Fiorini, F.; Onetto, M. Matching tetrads in f(T) gravity. Phys. Rev. D 2021, 103, 084051. [Google Scholar] [CrossRef]
- de la Cruz-Dombriz, A.; Dunsby, P.K.S.; Saez-Gomez, D. Junction conditions in extended Teleparallel gravities. J. Cosmol. Astropart. Phys. 2014, 1412, 048. [Google Scholar] [CrossRef]
- Velay-Vitow, J.; DeBenedictis, A. Junction conditions for F(T) gravity from a variational principle. Phys. Rev. D 2017, 96, 024055. [Google Scholar] [CrossRef]
- Fiorini, F.; Paliathanasis, A. Role of the remnant symmetries in gravitational theories based on absolute parallelism: A 2D standpoint. Class. Quantum Grav. 2022, 39, 095003. [Google Scholar] [CrossRef]
- Fiorini, F.; Vattuone, N. An analysis of Born-Infeld determinantal gravity in Weitzenböck spacetime. Phys. Lett. B 2016, 763, 45. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).