A Study of Alpha-Particle Scattering on 10B Nuclei at an Energy of 29 MeV
Abstract
1. Introduction
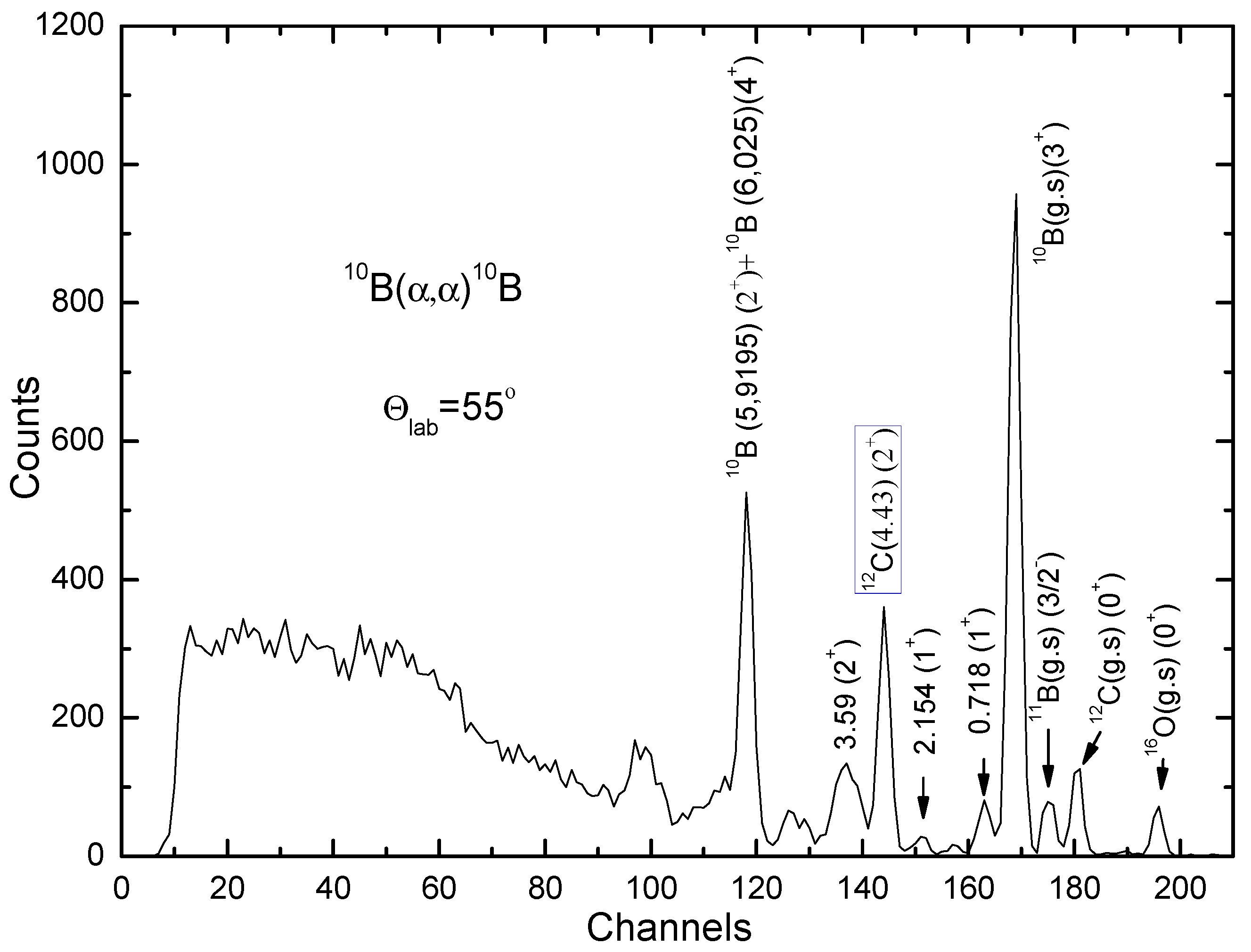
2. Experimental Setup
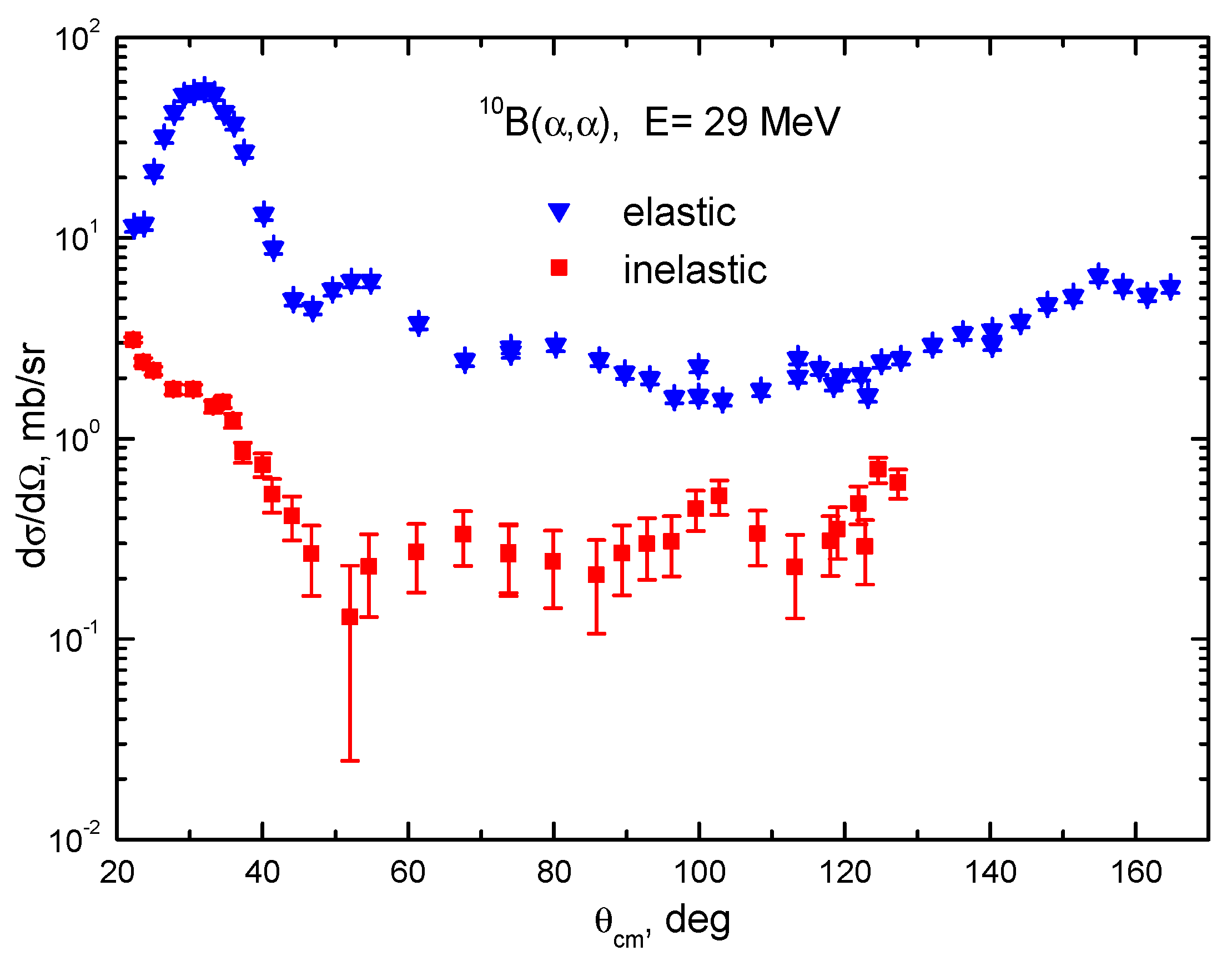
3. Analysis and Discussion of the Results
3.1. Elastic Scattering and Optical Potentials
3.2. Parameterized Phase Analysis of Elastic Scattering
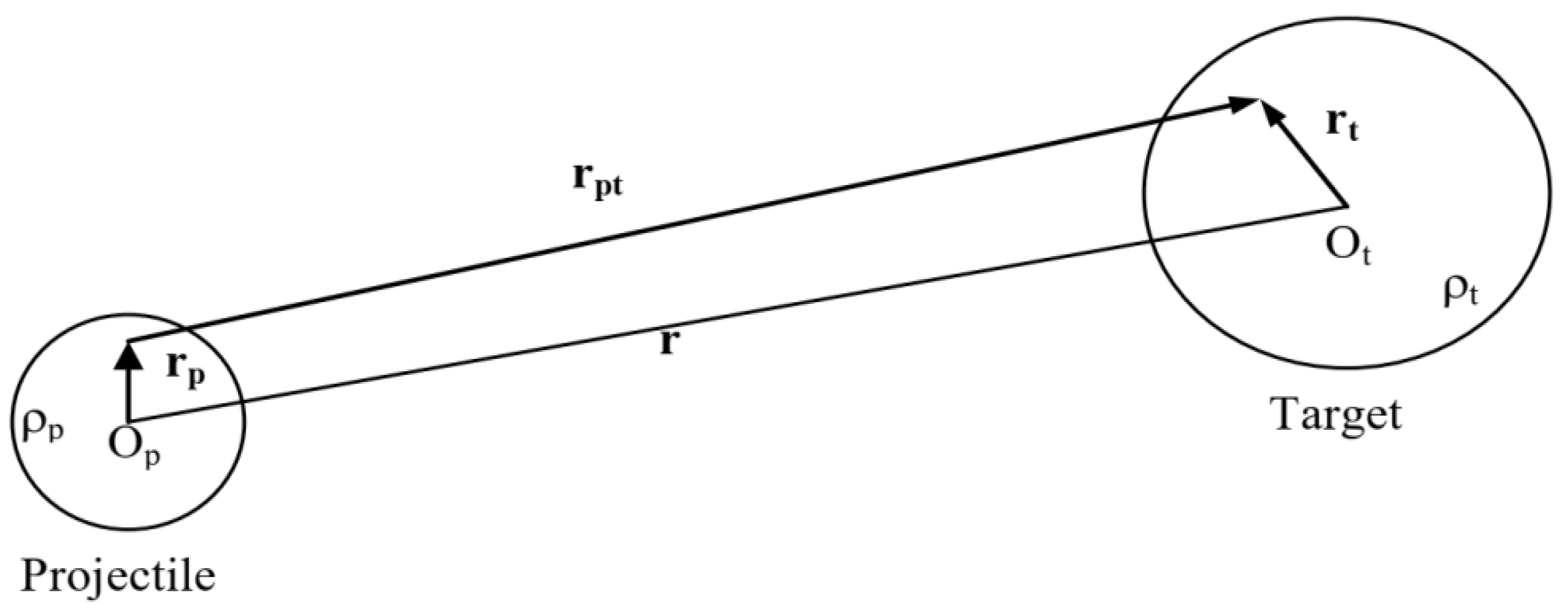
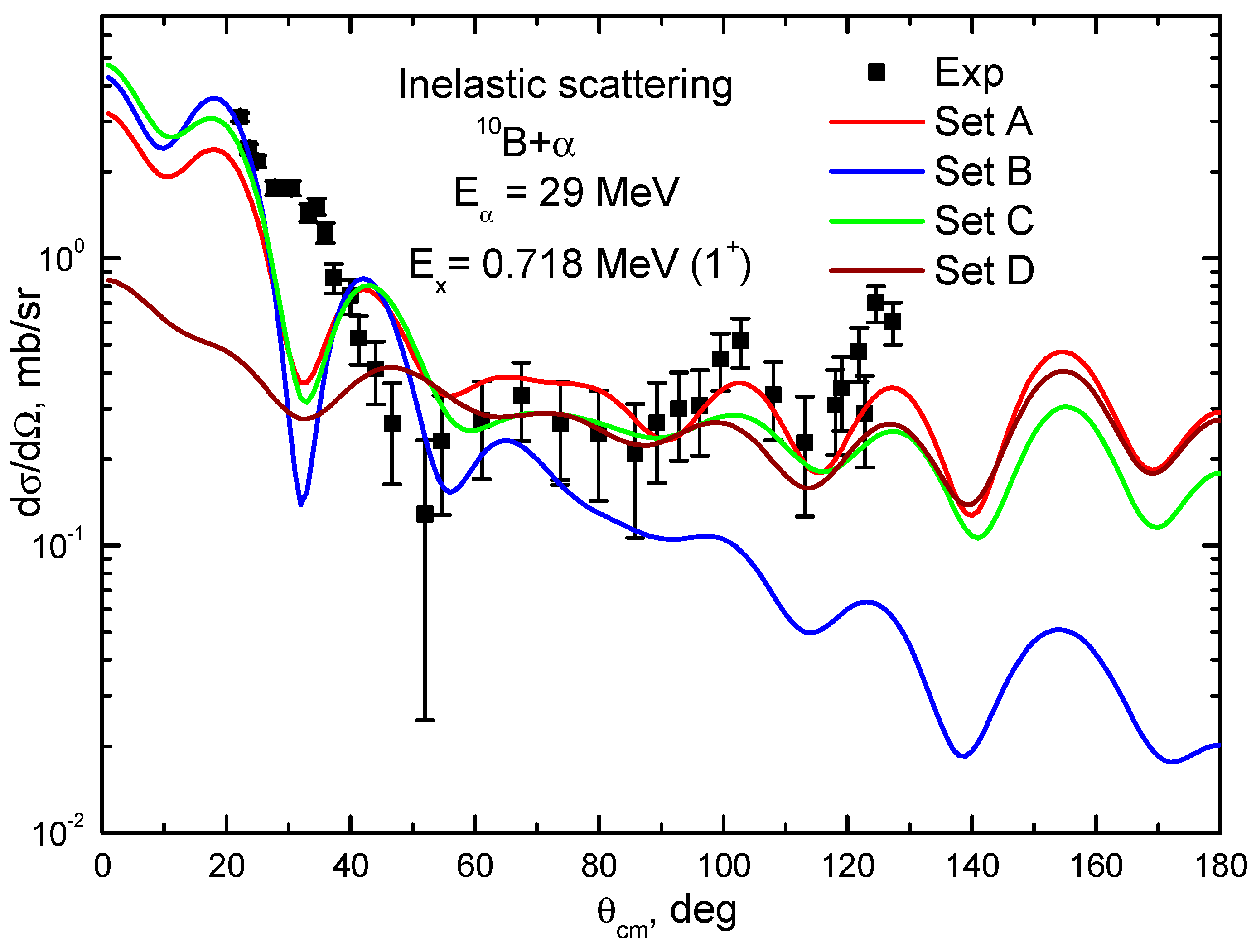
3.3. Coupled-Channel Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| OP | Optical potential |
| OM | Optical model |
| PPA | Parameterized phase analysis |
| AD | Angular distribution |
| CSs | Cross sections |
References
- McFadden, L.; Satchler, J.R. Optical model analysis of the scattering of 24.7 MeV alpha particles. Nucl. Phys. A 1966, 84, 177. [Google Scholar] [CrossRef]
- Igo, G.; Thaler, R.M. Optical model analysis of the elastic scattering of alpha particles. Phys. Rev. C 1957, 106, 126. [Google Scholar] [CrossRef]
- Hodgson, P.E. The nuclear optical model. Rep. Prog. Phys. 1971, 34, 765. [Google Scholar] [CrossRef]
- Goldberg, D.A.; Smith, S.M.; Burdzik, G.F. Refractive behavior in intermediate-energy alpha scattering. Phys. Rev. C 1974, 10, 1362. [Google Scholar] [CrossRef]
- Khoa, D.T. α-nucleus optical potential in the double-folding model. Phys. Rev. C 2001, 63, 034007. [Google Scholar] [CrossRef]
- Satchler, G.R.; Love, W.G. Folding model potentials from realistic interactions for heavy-ion scattering. Phys. Rep. 1979, 55, 183. [Google Scholar] [CrossRef]
- Avrigeanu, M.; Avrigeanu, V. α-particle nuclear surface absorption below the Coulomb barrier in heavy nuclei. Phys. Rev. C 2010, 82, 014606. [Google Scholar] [CrossRef]
- Bryant, H.C.; Jarmie, N. Nuclear glory scattering. Ann. Phys. 1968, 47, 127. [Google Scholar] [CrossRef]
- Budzanowski, A.; Dudek, A.; Dymarz, R.; Grotowski, K.; Jarczyk, L.; Niewodniczański, H.; Strza⌈Kowski, A. Glory effect in the optical-model analysis. In Proceedings of the International Conference on Nuclear Physics, Gatlinburg, Tennessee, 12–17 September 1966; Academic Press: New York, NY, USA, 1967. [Google Scholar]
- Budzanowski, A.; Grotowski, K.; Strzalkowski, A. Back Scattering of Alpha Particles. Acta Phys. Polon. A 1970, 38, 631. [Google Scholar]
- Bertero, B.; Carrassi, M.; Passatore, G.; Viano, G.A. Further Analysis of α-C12 Scattering Process by Regge Representation. Nuovo Cim. 1965, 36, 954. [Google Scholar] [CrossRef]
- Gruhn, C.R.; Wall, N.S. Large-Angle Elastic Scattering of Alpha Particles by 39K, 40Ca, 42Ca, 44Ca and 50Ti. Nucl. Phys. 1966, 81, 161. [Google Scholar] [CrossRef]
- Ceuleneer, R.; Michel, F. Regge Poles and Backward Elastic α-Particle Scattering from 16O. Phys. Lett. B 1973, 43, 365–367. [Google Scholar] [CrossRef]
- Budzanowski, A.; Jarczyk, L.; Kamys, B.; Kapuscik, A. Mechanism of α-Particle Scattering from 28Si Nuclei. Nucl. Phys. A 1976, 265, 461. [Google Scholar] [CrossRef]
- Cowley, A.A.; Heymann, G. Regge Pole Analysis of the Elastic Scattering of α-Particles from 16O. Nucl. Phys. A 1970, 146, 465. [Google Scholar] [CrossRef]
- McVoy, K.W. Regge Poles and Strong Absorption in Heavy-Ion and α-Nucleus Scattering. Phys. Rev. C 1971, 3, 110. [Google Scholar] [CrossRef]
- Frahn, W.E. Angular-momentum matching in the strong-absorption model. Lett. Nuovo Cim. 1971, 1, 561–564. [Google Scholar] [CrossRef]
- von Oertzen, W. On the interaction induced by the exchange of nucleons between two identical nuclear cores. Nucl. Phys. A 1970, 148, 529. [Google Scholar] [CrossRef]
- Gridnev, K.A.; Ogloblin, A.A. Anomalous Backward Scattering and Quasi-molecular Structure of Nuclei. Fiz. Elem. Chastits At. Yadra. 1975, 6, 393, Sov. J. Particles Nucl.1976, 6, 158. [Google Scholar]
- Freer, M. The clustered nucleus–cluster structure in stable and unstable nuclei. Rep. Prog. Phys. 2007, 70, 2149. [Google Scholar] [CrossRef]
- Beck, C. (Ed.) Clusters in Nuclei; Lecture Notes in Physics; Springer Science & Business Media: New York, NY, USA, 2010; Volume 1, p. 818. [Google Scholar]
- Pakou, A.; Sqouros, O.; Soukeros, V.; Cappuzzello, F. Global description and decay rates for continuum excitation of weakly bound nuclei. Eur. Phys. J. A 2021, 57, 25. [Google Scholar] [CrossRef]
- Shapiro, I.S. Dispersion theory of direct nuclear reactions. In Selected Topics in Nuclear Theory; Lectures Given at IAEA, Vienna; International Atomic Energy Agency (IAEA): Vienna, Austria, 1963. [Google Scholar]
- Noble, J.V.; Coelho, H.T. Cluster-Model Vertex Functions for 16O: Backward α-Particle Scattering. Phys. Rev. C 1970, 1, 385. [Google Scholar] [CrossRef]
- Tilley, D.R.; Kelley, J.H.; Godwin, J.L.; Millener, D.J.; Purcell, J.; Sheu, C.G.; Weller, H.R. Energy Levels of Light Nuclei A = 10. Nucl. Phys. A 2004, 745, 155. [Google Scholar] [CrossRef]
- Bohr, A.; Mottelson, B.R. Nuclear Structure. Volume II Nuclear Deformations; World Scientific Publishing Co. Pte. Ltd.: New York, NY, USA; Amsterdam, The Netherlands, 1998. [Google Scholar]
- Burtebayev, N.; Sakuta, S.B.; Nassurla, M.; Saduev, N.; Nassurlla, M.; Sadykov, T.K.; Trzcińska, A.; Wolińska-Cichocka, M.; Khojayev, R. Mechanism of the 11B(α, t)12C reaction at an energy of 40 MeV, role of exchange processes and collective Excitations. Eur. Phys. J. A 2019, 55, 38. [Google Scholar] [CrossRef]
- Nassurlla, M.; Burtebayev, N.; Sakuta, S.B.; Karakozov, B.K.; Nassurlla, M.; Burtebayeva, J.; Khojayev, R.; Sabidolda, A.; Yergaliuly, G. Deuteron scattering and (d, t) reaction on 11B at an energy of 14.5 MeV. Nucl. Phys. A 2022, 1023, 122448. [Google Scholar] [CrossRef]
- David, P.; Debrus, J.; Mommsen, H.; Riccato, A. Elastic scattering of α-particles on 10B for Eα = 5-30 MeV. Nucl. Phys. A 1972, 182, 234. [Google Scholar] [CrossRef]
- Bentheim, F.; David, P.; Debrus, J.; Hinterberger, F.; Jahn, R.; Lubke, F.; Mommsen, H.; Schoenmachers, R.; Schuller, B. Elastic scattering of α-particles on 10B for Eα = 5−50 MeV. Z. Phys. A 1976, 279, 163. [Google Scholar] [CrossRef]
- Jarczyk, L.; Kamys, B.; Rudy, Z.; Strzalkowski, A.; Styczen, B.; Berg, G.P.A.; Magiera, A.; Meissburger, J.; Oelert, W.; Rossen, P.; et al. Triton and helion transfer in the 10B(α,7Li)7Be reaction at Elab= 91.8 MeV. Z. Physic A At. Nucl. 1985, 322, 221. [Google Scholar] [CrossRef]
- Hagino, K.; Ogata, K.; Moro, A.M. Coupled-channels calculations for nuclear reactions: From exotic nuclei to superheavy elements. Prog. Part. Nucl. Phys. 2022, 125, 103951. [Google Scholar] [CrossRef]
- Perey, F. (The Niels Bohr Institute, Copenhagen, Denmark) SPI-GENOA an optical model search code. 1976; (Unpublished work). [Google Scholar]
- Nilsson, B.S. SPI-GENOA an optical model search code. In Niels Bohr Institute Computer Program Library; Niels Bohr Institute: Copenhagen, Denmark, 1975. [Google Scholar]
- Cheston, W.B.; Glassgold, A.E. Elastic scattering of alpha particles with optical model. Phys. Rev. C 1957, 106, 1215. [Google Scholar] [CrossRef]
- Kucuk, Y.; Guimaraes, V.; Carlson, B.V. Towards a systematic optical model potential for A=8 projectiles. Eur. Phys. J. A 2021, 57, 87. [Google Scholar] [CrossRef]
- Baktybaev, M.K.; Basybekov, K.B.; Burtebaev, N.; Artemov, S.V.; Blechman, A.M.; Dyusebaev, B.A.; Duysebaev, A.; Gulamov, I.R.; Ismailov, K.M.; Zhurynbaeva, G.S.; et al. The (a,t) and (a,3He) cross section data at the energies 40.0 and 50.5 MeV. I. In Proceedings of the Eurasia Conference on Nuclear Science and Its Application, Izmir, Turkey, 23–27 October 2000; pp. 534–535. [Google Scholar]
- Thompson, I.J. Coupled reaction channels calculations in nuclear physics. Comput. Phys. Rep. 1988, 7, 167. [Google Scholar] [CrossRef]
- Nolte, M.; Machner, H.; Bojowald, J. Global optical potential for α particles with energies above 80 MeV. Phys. Rev. C 1987, 36, 1312. [Google Scholar] [CrossRef] [PubMed]
- Farid, M.E.A.; Mahmoud, Z.M.M.; Hassan, G.S. Analysis of heavy ions elastic scattering using the double folding cluster model. Nucl. Phys. A 2001, 691, 671. [Google Scholar] [CrossRef]
- Khoa, D.T.; Von Oertzen, W.; Bohlen, H.G. Double-folding model for heavy-ion optical potential: Revised and applied to study C12 and O16 elastic scattering. Phys. Rev. C 1994, 49, 1652. [Google Scholar] [CrossRef] [PubMed]
- Cook, J. DFPOT-A program for the calculation of double folded potentials. Comput. Phys. Commun. 1982, 25, 125. [Google Scholar] [CrossRef]
- Aygun, M.A. Comprehensive analysis of elastic scattering of 14N projectile on 7Li, 9Be, 11B, 12C, 16O, 26Mg, 28Si, 40Ca, 56Fe, 59Co, 60,62Ni, 70,74Ge, 90Zr, 112Cd, 118Sn, 159Tb and 197Au at various incident energies. Chin. J. Phys. 2017, 55, 2559. [Google Scholar] [CrossRef]
- De Vries, H.; De Jager, C.W.; De Vries, C. Nuclear charge-density-distribution parameters from elastic electron scattering. At. Data Nucl. Data Tables 1987, 36, 495. [Google Scholar] [CrossRef]
- Akhiezer, A.I.; Pomeranchuk, I.A. Diffraction Phenomena in Collisions of Fast Particles with Nuclei. UFN 1958, 65, 593. [Google Scholar] [CrossRef]
- Akhiezer, A.I.; Berezhnoy, Y.A.; Pilipenko, V.V. Quantum Interferention and Nuclear Optics. Phys. El. Part. At. Nucl. 2000, 31, 457. [Google Scholar]
- Berezhnoy, Y.A.; Molev, A.S. Interference between diffractive, refractive and Coulomb effects in the cross section for the elastic scattering of light nuclei by nuclei at intermediate energies. Phys. At. Nucl. 2004, 67, 1454. [Google Scholar] [CrossRef]
- Gonchar, V.Y. Investigation of uniqueness of parameters in the method of phase shifts. Phys. At. Nucl. 1969, 9, 987. [Google Scholar]
- Yushkov, A.V. Surface of b(Z, N) Deformation for Nuclei with Z from 2 to 102. Phys. El. Part. At. Nucl. 1993, 24, 348. [Google Scholar]
- Burtebayev, N.; Baktybayev, M.K.; Duisebayev, B.A.; Sakuta, S.B.; Peterson, R.D. Scattering of 40- and 50- MeV α particles from 11B nuclei. Phys. At. Nucl. 2005, 68, 1356–1367. [Google Scholar]
- Spatafora, A.; Cappuzzello, F.; Carbone, D.; Cavallaro, M.; Lay, J.A.; Acosta, L.; Numen Collaboration. 20Ne + 76Ge elastic and inelastic scattering at 306 MeV. Phys. Rev. C 2019, 100, 034620. [Google Scholar] [CrossRef]
- Carbone, D.; Linares, R.; Amador-Valenzuela, P.; Calabrese, S.; Cappuzzello, F.; Cavallaro, M.; Firat, S.; Fisichella, M.; Spatafora, A.; Acosta, L.; et al. Initial State Interaction for the 20Ne + 130Te and 18O + 116Sn Systems at 15.3 AMeV from Elastic and Inelastic Scattering Measurements. Universe 2021, 7, 58. [Google Scholar] [CrossRef]
- Ajenberg-Selove, F. Energy levels of light nuclei A = 5–10. Nucl. Phys. A 1988, 490, 1–225. [Google Scholar] [CrossRef]
- Swiniarski, R.; Resmini, F.G.; Glashausser, C.; Bacher, A.D. Study of 10B by inelastic Scattering of 30.3 MeV protons. Helv. Phys. Acta 1976, 49, 227. [Google Scholar]
- Squier, G.T.A.; McClatchie, E.A.; Johnston, A.R.; Batten, R.J.; England JB, A.; Kingston, F.G. Elastic and Inelastic Scattering of 3He Particles from 10B at 32 MeV. Nucl. Phys. A 1968, 119, 369. [Google Scholar] [CrossRef]

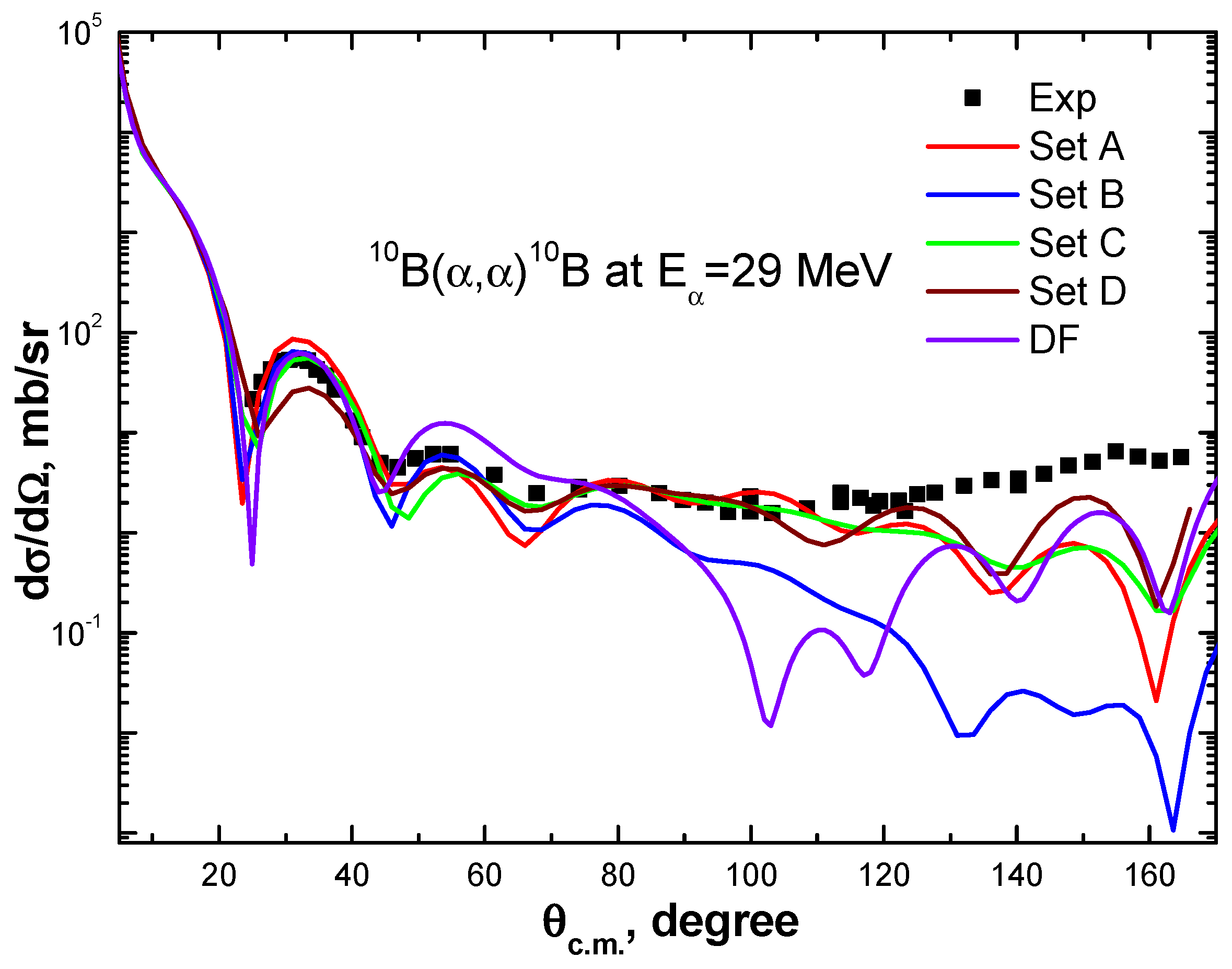
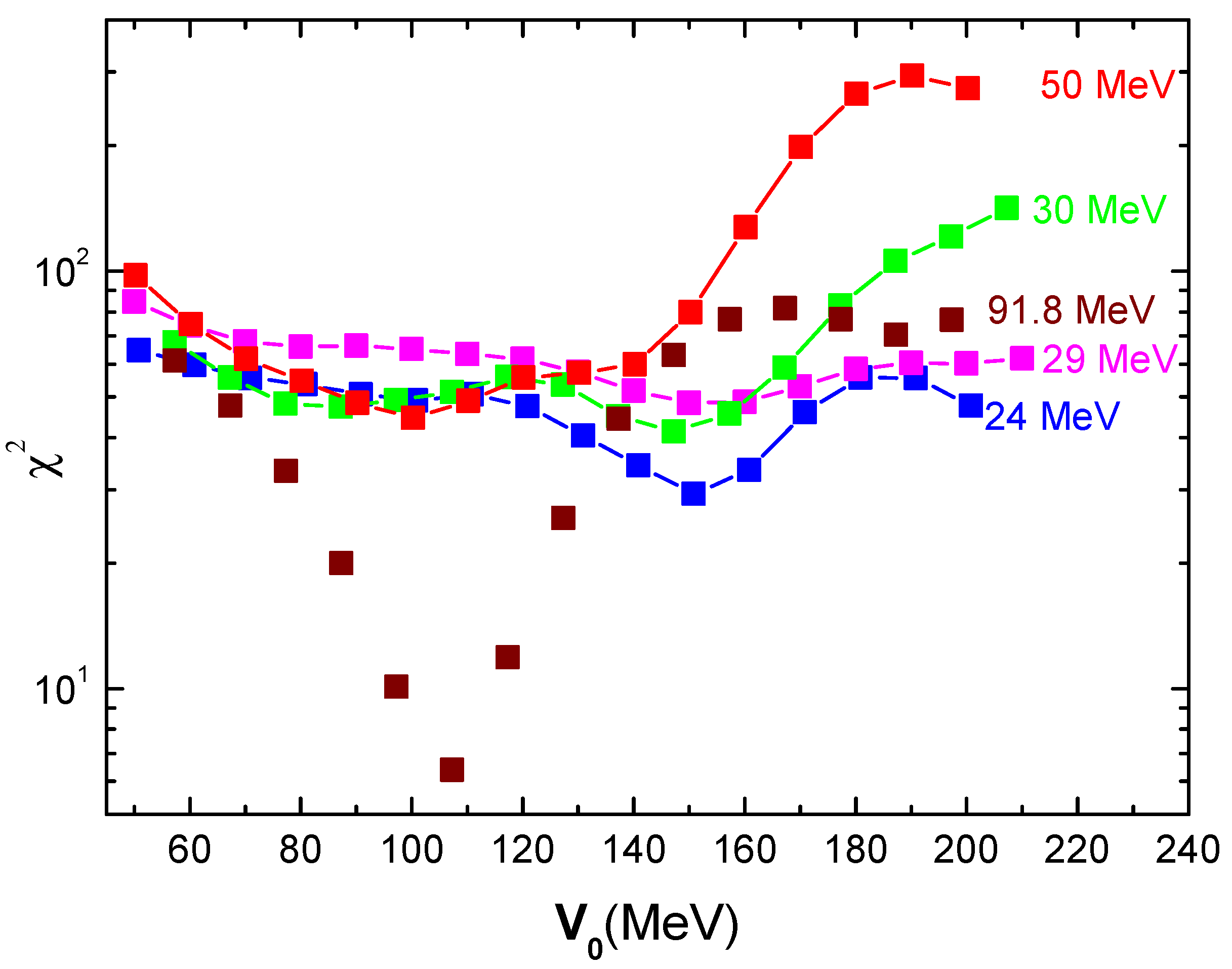
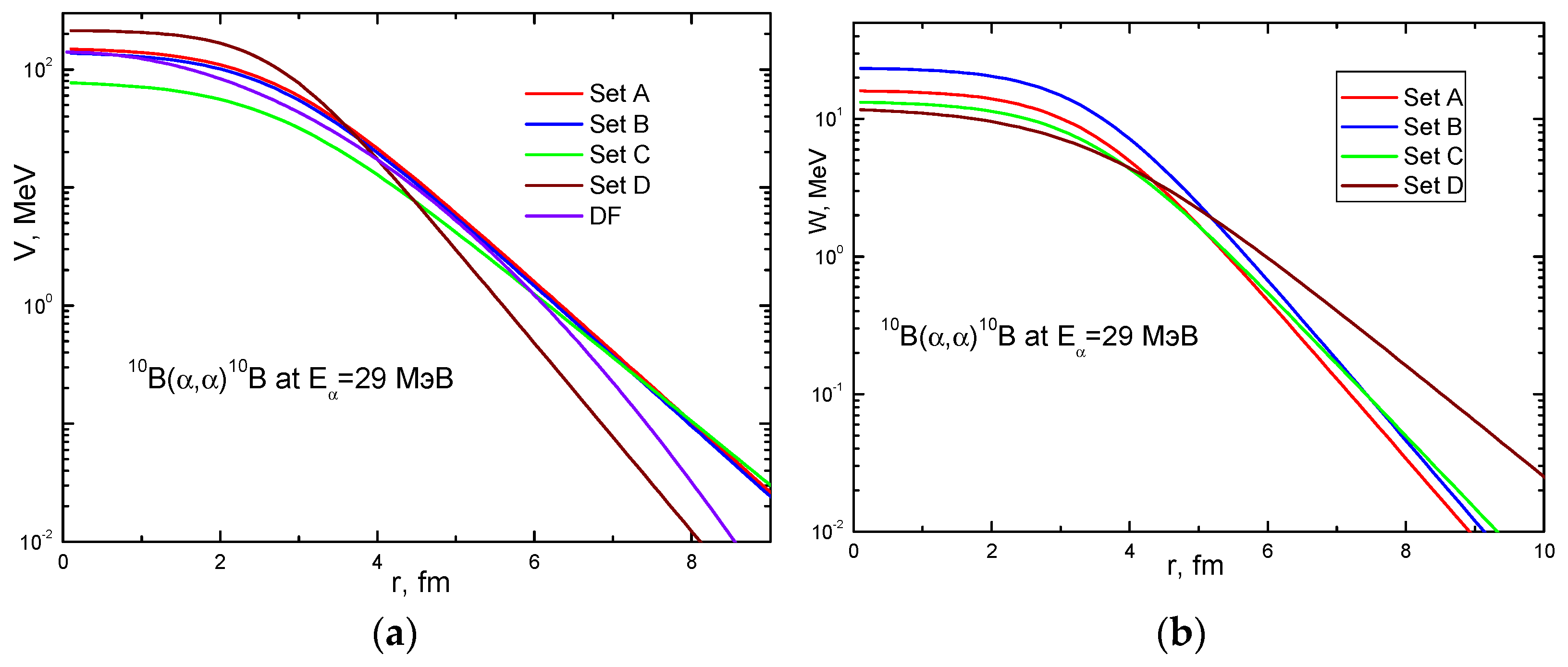
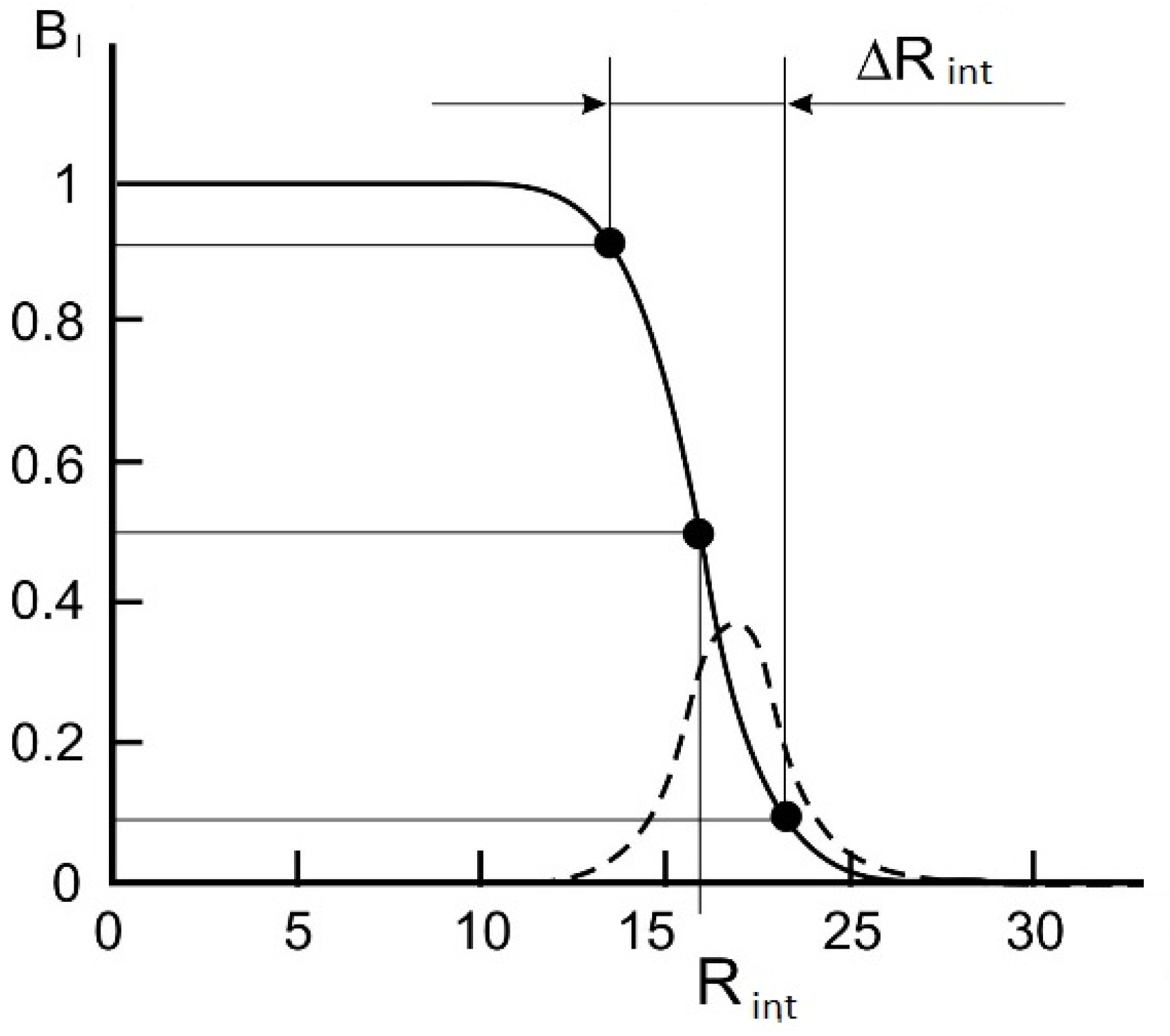
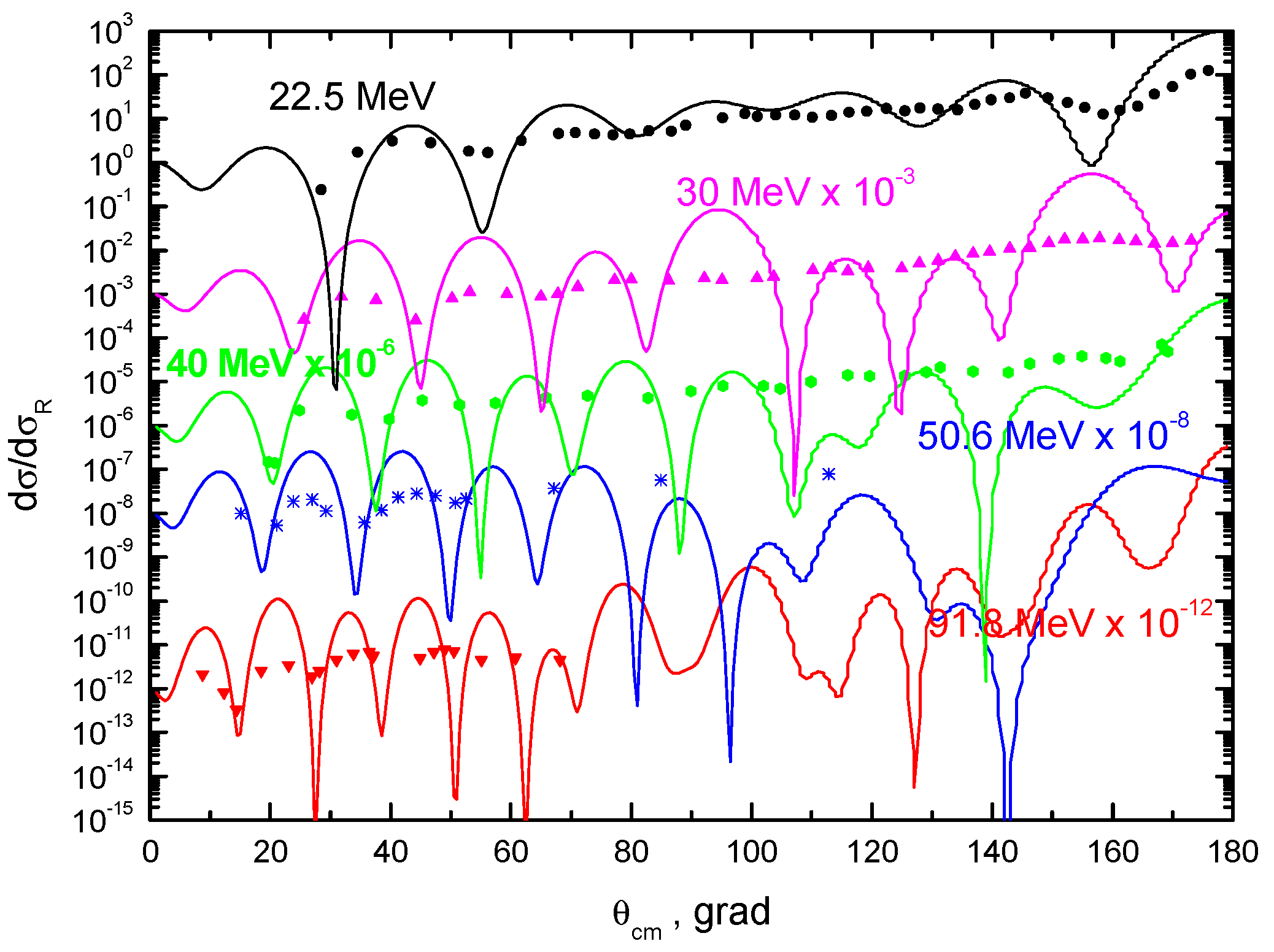
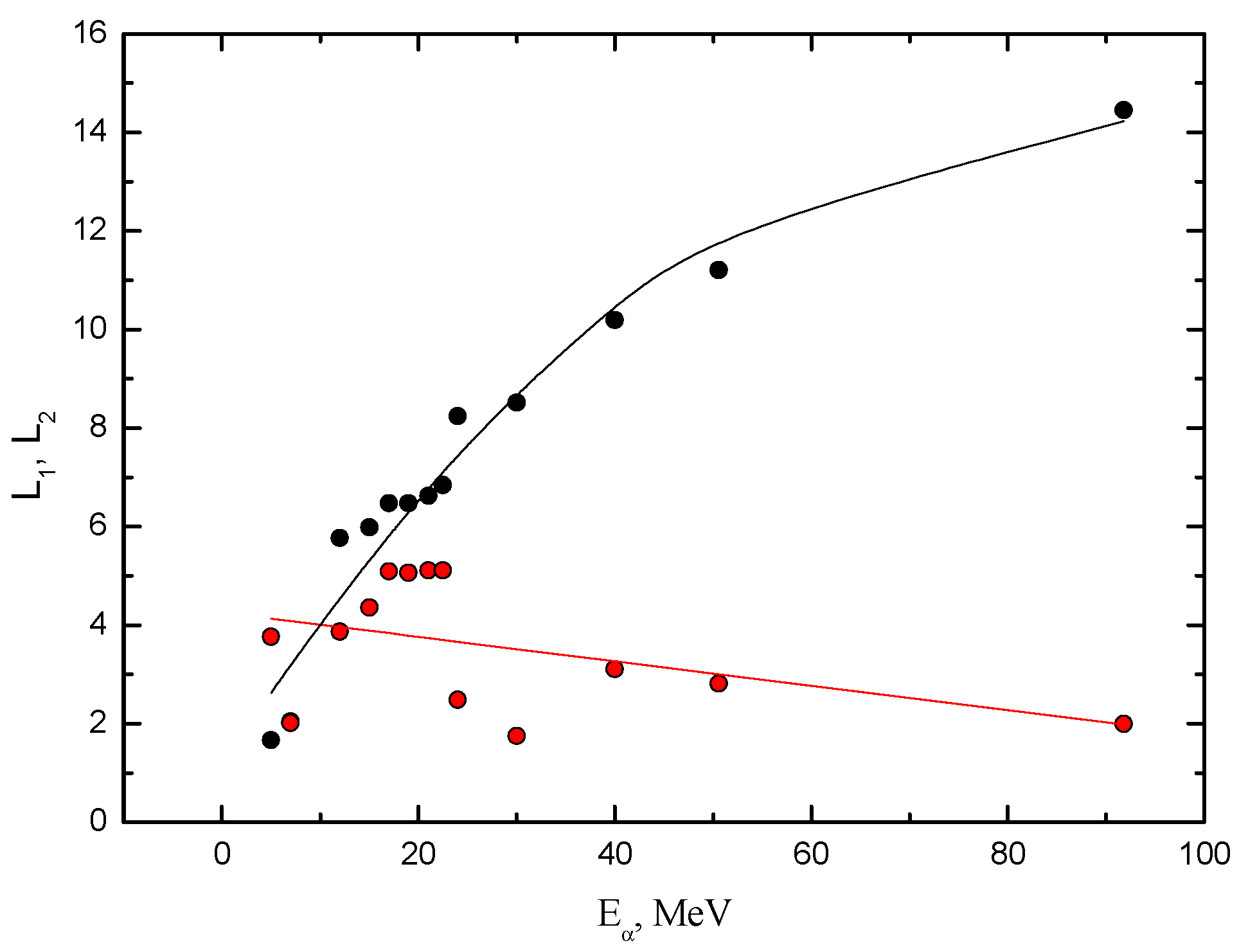
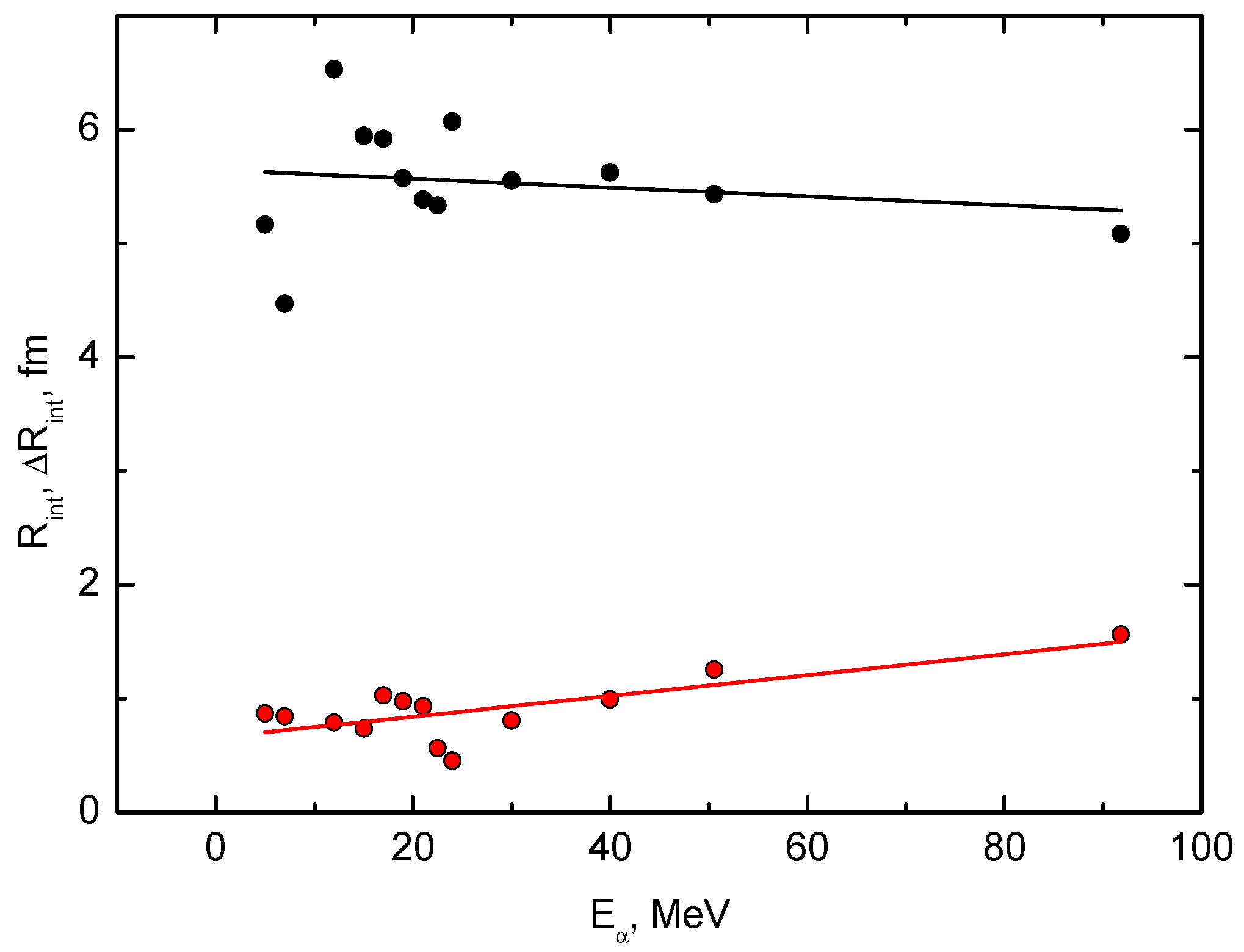
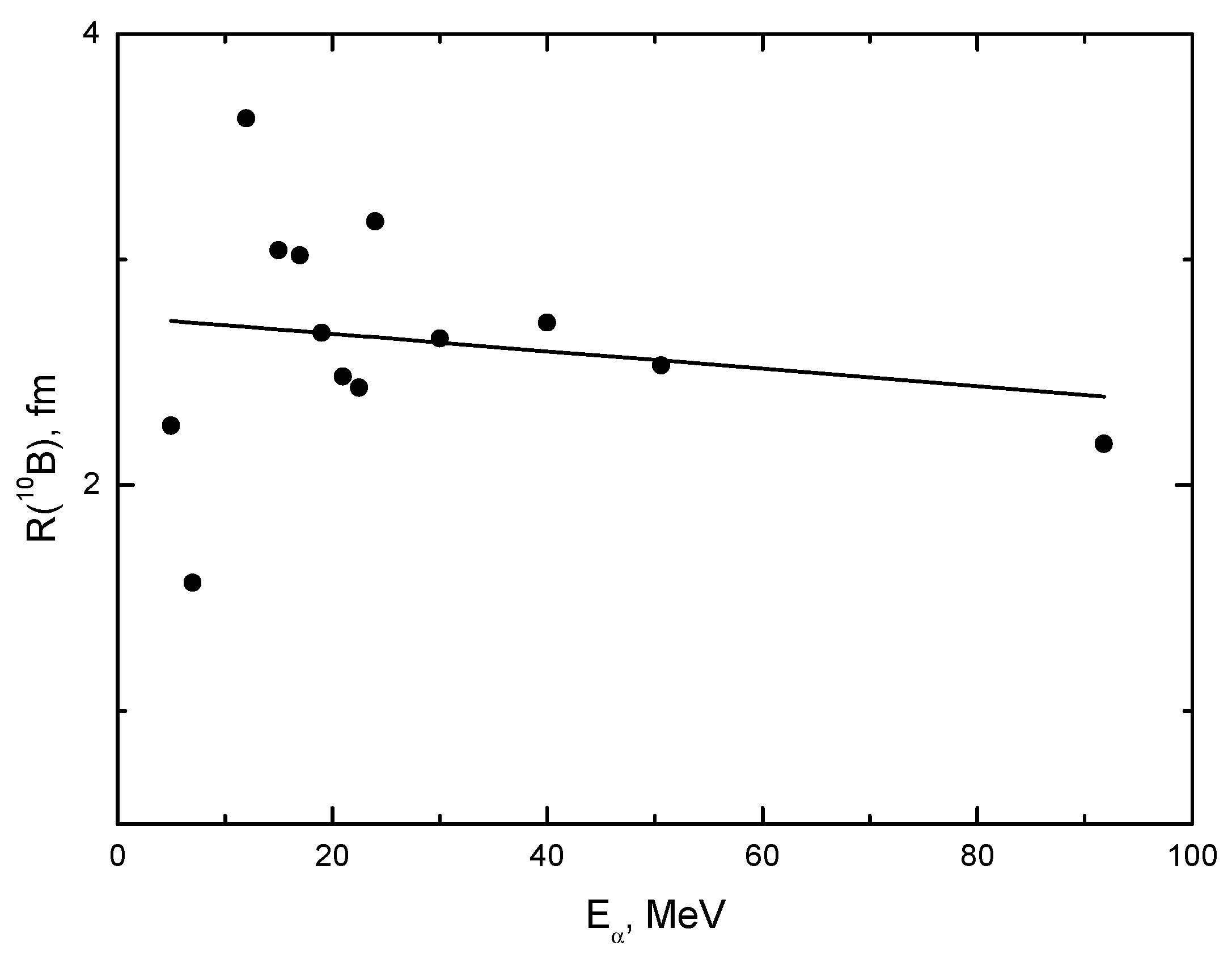
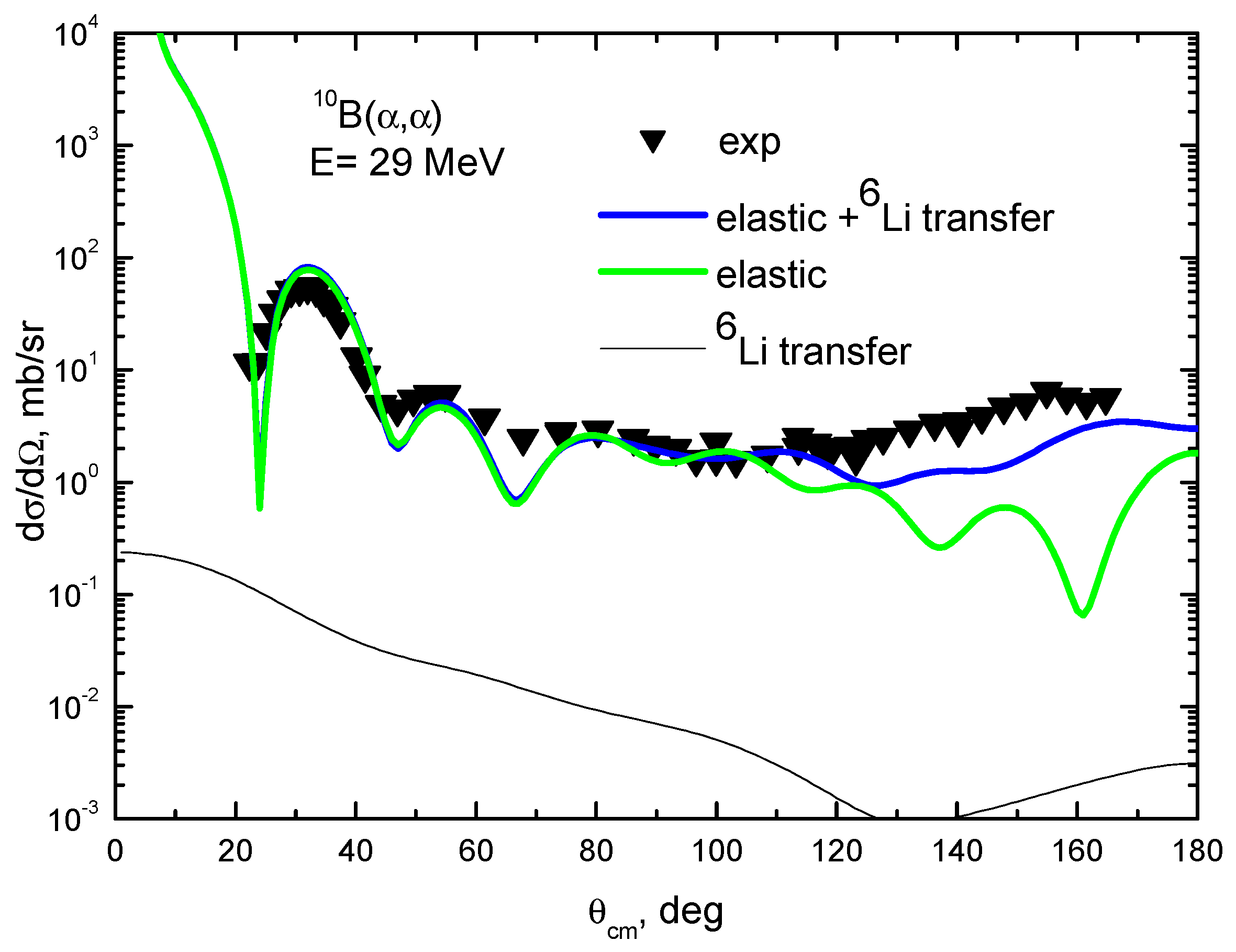
| E, MeV | Set | Vo, MeV | aV, fm | Wo, MeV | aw, fm | JV | JW | χ2/N |
|---|---|---|---|---|---|---|---|---|
| 24 | A | 155.04 | 0.742 | 18.29 | 0.666 | 545.05 | 102.46 | 97.82 |
| B | 152.86 | 0.835 | 11.7 | 0.588 | 599.24 | 58.23 | 65.55 | |
| 29 | A | 152.9 | 0.730 | 16.2 | 0.749 | 530.07 | 97.39 | 45.73 |
| B | 140.9 | 0.730 | 23.63 | 0.740 | 488.25 | 140.96 | 68.46 | |
| C | 79.84 | 0.803 | 13.49 | 0.824 | 301.44 | 86.66 | 39.04 | |
| D | 215.4 | 0.545 | 12.20 | 1.07 | 606.58 | 98.23 | 28.87 | |
| 30 | A | 147.23 | 0.756 | 13.41 | 0.869 | 531.67 | 109.2 | 48.96 |
| B | 143.2 | 0.756 | 13.62 | 0.840 | 512.27 | 88.79 | 42.84 | |
| 50.6 | A | 111.2 | 0.810 | 17.57 | 0.820 | 423.3 | 112.47 | 49.67 |
| B | 119.77 | 0.726 | 15.47 | 0.93 | 413.29 | 109.43 | 31.17 | |
| 91.8 | A | 105.56 | 0.831 | 20.24 | 1.01 | 412.04 | 154.29 | 6.392 |
| B | 104.89 | 0.8 | 15.0 | 0.9 | 394.62 | 147.59 | 11.1 |
| Eα, MeV | l1 | l2 | λ1 | λ2 | B | Rint, fm | ΔRint, fm |
|---|---|---|---|---|---|---|---|
| 5 | 1.662 | 3.762 | 0.23 | 0.146 | 0.476 | 5.164 | 0.868 |
| 7 | 2.041 | 2.014 | 0.23 | 0.146 | 0.476 | 4.468 | 0.842 |
| 12 | 5.768 | 3.87 | 0.219 | 0.866 | 0.941 | 6.526 | 0.79 |
| 15 | 5.986 | 4.357 | 0.224 | 0.909 | 0.722 | 5.941 | 0.735 |
| 17 | 6.468 | 5.086 | 0.329 | 0.661 | 0.45 | 5.919 | 1.027 |
| 19 | 6.473 | 5.062 | 0.329 | 0.948 | 0.722 | 5.574 | 0.976 |
| 21 | 6.619 | 5.111 | 0.329 | 0.956 | 0.702 | 5.381 | 0.934 |
| 22.5 | 6.838 | 5.11 | 0.204 | 0.964 | 0.592 | 5.332 | 0.562 |
| 24 | 8.243 | 2.487 | 0.167 | 1.409 | 1.966 | 6.068 | 0.452 |
| 30 | 8.514 | 1.754 | 0.331 | 0.249 | 0.775 | 5.55 | 0.807 |
| 40 | 10.189 | 3.105 | 0.463 | 0.241 | 0.24 | 5.62 | 0.992 |
| 50.6 | 11.203 | 2.817 | 0.655 | 0.17 | 0.286 | 5.431 | 1.257 |
| 91.8 | 14.446 | 1.991 | 1.083 | 0.39 | 0.581 | 5.083 | 1.563 |
| Eα, MeV | 5 | 7 | 12 | 15 | 17 | 22.5 | 24 | 30 | 40 | 50.6 | 91.8 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| R10B, fm | 2.264 | 1.568 | 3.626 | 3.041 | 3.019 | 2.432 | 3.168 | 2.65 | 2.72 | 2.531 | 2.183 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nassurlla, M.; Burtebayev, N.; Sakuta, S.; Nassurlla, M.; Khojayev, R.; Alimov, D.; Baimbetova, G.; Dyachkov, V.; Zazulin, D.; Sabidolda, A.; et al. A Study of Alpha-Particle Scattering on 10B Nuclei at an Energy of 29 MeV. Universe 2024, 10, 51. https://doi.org/10.3390/universe10010051
Nassurlla M, Burtebayev N, Sakuta S, Nassurlla M, Khojayev R, Alimov D, Baimbetova G, Dyachkov V, Zazulin D, Sabidolda A, et al. A Study of Alpha-Particle Scattering on 10B Nuclei at an Energy of 29 MeV. Universe. 2024; 10(1):51. https://doi.org/10.3390/universe10010051
Chicago/Turabian StyleNassurlla, Maulen, Nassurlla Burtebayev, Stanislav Sakuta, Marzhan Nassurlla, Romazan Khojayev, Dilshod Alimov, Gulzada Baimbetova, Vyacheslav Dyachkov, Denis Zazulin, Avganbek Sabidolda, and et al. 2024. "A Study of Alpha-Particle Scattering on 10B Nuclei at an Energy of 29 MeV" Universe 10, no. 1: 51. https://doi.org/10.3390/universe10010051
APA StyleNassurlla, M., Burtebayev, N., Sakuta, S., Nassurlla, M., Khojayev, R., Alimov, D., Baimbetova, G., Dyachkov, V., Zazulin, D., Sabidolda, A., Mukanov, Y., Issayev, D., & Makhmut, A. (2024). A Study of Alpha-Particle Scattering on 10B Nuclei at an Energy of 29 MeV. Universe, 10(1), 51. https://doi.org/10.3390/universe10010051






