Downlink Training Design for FDD Massive MIMO Systems in the Presence of Colored Noise

Abstract

Massive multiple-input multiple-output (MaMi) systems have attracted much research attention during the last few years. This is because MaMi systems are able to achieve a remarkable improvement in data rate and thus meet the immensely ongoing traffic demands required by the future wireless networks. To date, the downlink training sequence (DTS) for the frequency division duplex (FDD) MaMi communications systems have been designed based on the idealistic assumption of white noise environments. However, it is essential and more practical to consider the colored noise environments when designing an efficient DTS for channel estimation. To this end, this paper proposes a new DTS design by exploring the joint use of spatial channel and noise covariance matrices, when the channel is not reciprocal but the coherence block length remains limited. We derive an analytical solution for the mean square error (MSE) based on the proposed training design with colored noise. In addition, this paper exploits the method of random matrix theory to provide an analytical solution for the downlink (DL) achievable sum rate of the regularized zero forcing beamforming (RZFBF) precoder. Numerical results demonstrate that using the proposed DTS design, the MSE of the channel estimate is significantly reduced compared with the conventional training designs with white noise. Furthermore, the results show that the proposed pilot design markedly improves the DL achievable SR over the conventional training designs, especially at relatively low signal-to-noise-ratio (SNR) levels. This enables FDD MaMi systems to operate under more practical scenarios of colored noise and limited coherence time environments.

1. Introduction

The last decade has witnessed a rapidly increasing growth in the number of wireless devices, which introduces huge demands for data services such as multimedia applications and video streaming [1]. As such, the currently deployed mobile networks are unlikely to support the explosion of the data traffic [2], and thus, new technologies become crucial. The massive multiple-input multiple-output (MaMi) system, which uses a large number of antenna arrays at the base station (BS), is presented as a key technique for the fifth-generation (5G) networks and beyond. A MaMi system is essentially needed to overcome the increasing demands of data traffic [3,4]. Specifically, the massive use of antenna arrays at BS increases the degrees of freedom in the propagation channel, which improves the data rate and link reliability [5]. MaMi systems offer many advantages, such as: (a) ability of providing a uniform quality of service; (b) ability of improving the energy efficiency; (c) capability of mitigating the impact of fast fading and interference; (d) capability of delivering high data rate; and (e) ability of using low complexity linear precoding schemes [6,7]. These key features introduce MaMi transmission as the core technique for the future wireless communications [8]. The performance of MaMi transmission depends entirely on the estimation of channel state information (CSI). In particular, the availability of CSI knowledge depends on the duplexing operation scheme given by the spectrum allocation, i.e., either time division duplex (TDD) or frequency division duplex (FDD) operation mode. The MaMi system is typically assumed to operate in TDD mode, where the required CSI is obtained in the uplink (UL) by transmitting the orthogonal training sequence of length equal to the number of users K [3,4,6,9,10,11,12,13,14]. Although, TDD operation mode has attractive results with MaMi systems, most of the current wireless communications networks operate in FDD mode. In addition, the new 5G radio access technology is expected to support both FDD and TDD duplex operations [8]. However, downlink (DL) training sequence (DTS) and CSI estimation in FDD MaMi systems is a challenging issue with limited coherence time. This is because the number of DTS needs to be linearly scaled with the number of transmit antenna elements N ($N\gg K$) to design the precoder [15,16,17]. As such, the coherence time that is available would be fully consumed by DL channel training, leaving no time for sending useful information to the users.

1.1. Related Works

To overcome the challenge of FDD operation mode in MaMi systems, several research works have investigated the DTS design by exploiting various channel models and design criteria. For example, approaches utilizing compressed sensing (CS) techniques have been proposed in [18,19,20]. In these research works, the channel estimation in the FDD MaMi systems has been reformulated as a CS problem to reduce the DTS overhead for channel estimation. Research investigations, which exploit time and spatial correlations with Kalman-filter (KF) are considered in [21,22,23]. In these works, both the spatial and temporal channel correlations are explored, to reduce the training overhead. In addition, the KF is utilized to track the variation in the DL channel and to improve the mean square error (MSE) performance. Besides the research directions that exploit the spatial and temporal correlations with KF and CS techniques, another line of research studies considers a two-stage precoding approach, termed as joint spatial division and multiplexing (JSDM) [24,25]. The role of JSDM is to partition the users into different groups and to utilize a two-stage precoding process to reduce the DTS length for DL CSI estimation. To come up with the challenge of DL CSI estimation in the desired single-stage precoding process, different studies have considered the design of DTS by exploiting the low-rank structure of the channel covariance matrices [26,27,28,29,30]. In these works, sophisticated iterative algorithms were proposed to optimize the DTS for CSI estimation. However, the aforementioned research works on DTS design and CSI estimation rely on the assumption of weight noise, which limits their applications in more realistic environments. In particular, in practice, the wireless communication systems could exhibit colored noise; therefore, the framework analysis of the DTS developed in [18,19,20,21,22,23,24,25,26,27,28,29,30,31] does not hold for the general scenario of the correlated noise environments. To the best of our knowledge, finding a feasible DTS design for CSI estimation to enable FDD operation with MaMi systems in the presence of colored noise has not been addressed in the literature. Therefore, this paper is the first research that proposes a novel DTS design for DL CSI estimation in the FDD MaMi systems in the presence of spatially correlated colored noise and with limited coherence time.

1.2. Paper Contributions and Findings

In this paper, we address the challenge of DTS design and CSI estimation in the FDD operation in MaMi systems with single-stage precoding and in the presence of spatially colored noise and with limited coherence time. A computational feasible solution for the DTS design and CSI estimation with colored noise environments is proposed by exploring the statistical information denoted by the channel and noise covariance matrices. We analyse the DL CSI estimation with minimum-mean square-error (MMSE) filter and derive a new analytical solution for the MSE, which incorporates a practical impairment of colored noise. Additionally, an asymptotic closed form analytical solution for the achievable sum rate of the regularized zero forcing beamforming (RZFBF) precoder is developed by exploiting a random matrix theory method. This explicit analytical solution allows the achievable sum rate performance of an FDD operation in MaMi system to be straightforwardly obtained without resorting to a computationally demanding exhaustive search. Comparisons between the MSE and sum rate performances of the proposed DTS design and the state-of-the-art DTS designs based on the white noise environments are carried out by considering the one ring (OR) [24,32,33] and Laplacian [26,34] channel models with uniform linear array (ULA) and uniform planar array (UPA) configurations. The results show that the proposed DTS design improves the MSE performance significantly compared with the conventional training designs based on white noise. This improvement results in maximizing the DL achievable sum rate of the FDD MaMi systems considerably, without increasing in the system overhead and design complexity. In particular, this paper shows that a feasible DTS design with minimal overheads can be achieved by jointly considering the eigen-decompositions of the channel and noise covariance matrices. Although the results in this paper are presented for practical antennas sizes, i.e., $N=128$, we believe that the same trends can also be observed for the other antenna arrays sizes. Finally, the results show that the analyses of the MSE and achievable sum are developed in this paper, and greatly agree with the simulations, which underpin the contributions of this work.

Paper organization: In Section 2, we describe the system model and introduce the achievable sum rate of the RZFBF precoding. Section 3 explains the DL channel estimation process based on the DTS design and formalized the optimization problem of the FDD operation in MaMi systems in the presence of colored noise. In Section 4, the proposed DTS design for CSI estimation in the presence of colored noise is developed and the analysis of the MSE is derived. In Section 5, we adopt a random matrix theory to provide an asymptotic analysis for the signal-to-interference-plus-noise ratio (SINR) and the achievable sum rate of the RZFBF precoding. In Section 6, the system geometries of the channel covariance matrices in the ULA and UPA are presented. In Section 7, we characterize the system performance using the proposed training framework by providing some simulation results. Finally, we conclude the paper in Section 8.

Notation: We use an upper boldface symbol for a matrix and lower boldface symbol for a vector. We use the term $\mathbb{E}[·]$ for the expectation operator. The following mathematical operations, trace, transpose, Hermitian transpose, inverse and absolute, are denoted by $\mathrm{tr}(·)$, ${(·)}^{\mathrm{T}}$, ${(·)}^{\mathrm{H}}$, ${(·)}^{-1}$, and $|·|$, respectively.

2. System Model

In this paper, a non-reciprocal DL FDD MaMi communication system with single-cell scenario is considered, where the transmit BS employs antenna array of size N using either ULA or UPA. The BS serves K non-cooperative single antenna users with $N\gg K$. The spatial correlation between the antenna elements would be increased in MAMi systems and each user could have distinct spatial channel characteristics. This paper considers a static block fading transmissions model (i.e., flat-fading wireless channels) based on Rayleigh-correlated fading model and colored noise environments. The overall coherence length for each transmission block in symbols is given by ${\tau }_{}\in {\mathbb{Z}}^{+}$. Figure 1 shows the BS with MaMi system and demonstrates the DL and UL transmissions within each coherence block length. In particular, the available coherence block length consists of resource transmission in time $T_{\mathrm{c}}$ and frequency $B_{\mathrm{c}}$ plane, which represents the time and the frequency intervals over which the channel responses are approximately constant, as considered in the current long term evolution (LTE) wireless networks [35,36]. According to the Nyquist–Shannon sampling theorem, the coherence block length is given as ${\tau }_{}=T_{\mathrm{c}}\times B_{\mathrm{c}}$. The available coherence length $\tau$ for transmission in the UL and DL is freely divided between the training phase $T_{\mathrm{s}}$ and the data transmission phase ${\tau }_{\mathrm{d}}$, both enumerated in symbols. The available energy is divided between the DTS transmission and the useful data transmission.

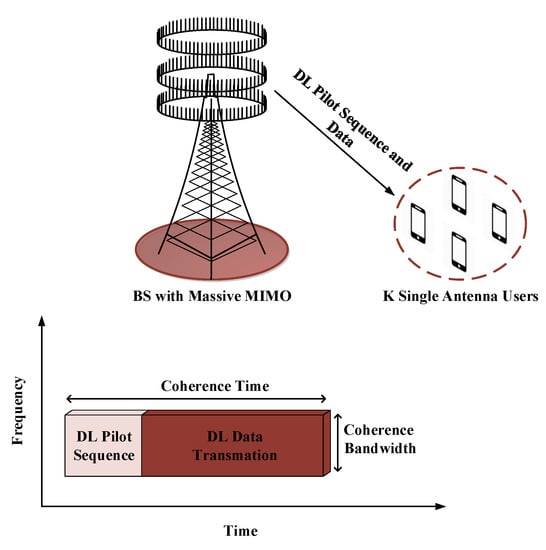
Figure 1. Illustration of a base station (BS) with massive number of antenna elements that serves K users. It also shows the downlink (DL)/uplink (UL) pilot sequence and data transmissions in frequency division duplex (FDD) operation mode.

The received data transmission signal at the k-th user $y_k\in {\mathbb{C}}^K$ can be expressed as [9,10]

$$\begin{array}{c}\hfill y_k^{}=\sqrt{{\rho }_{\mathrm{d}}^{}\xi }{\mathbf{h}}_k^{\mathrm{H}}\mathbf{W}\mathbf{s}+n_k^{},\end{array}$$

(1)

where $\mathbf{s}={[s_1,\dots ,s_K]}^{\mathrm{T}}\in {\mathbb{C}}^K$ is the per-user data symbol, which is modeled as a zero mean circularly symmetric complex Gaussian (CSCG) and satisfied $\mathbb{E}\left[\mathbf{s}{\mathbf{s}}^{\mathrm{H}}\right]={\mathbf{I}}_K$. The parameter $n_k$ is the receiver colored noise, which satisfies ${\mathbf{n}}_k={[n_1,\dots ,n_K]}^{\mathrm{T}}\in {\mathbb{C}}^K\sim \mathcal{CN}(\mathbf{0},{\mathbf{R}}_{\mathrm{n}})$, where ${\mathbf{R}}_{\mathrm{n}}$ denotes the correlated colored noise covariance matrix. The complex precoder matrix at the BS is denoted by $\mathbf{W}=[{\mathbf{w}}_1,\dots ,{\mathbf{w}}_K]\in {\mathbb{C}}^{N\times K}$, which is provided later in (7). The complex channels ${\mathbf{h}}_k$, $k=1,\dots ,K$ are modeled as

$${\mathbf{h}}_k^{}={\mathbf{R}}_{\mathrm{h}}^{1/2}{\mathbf{v}}_k^{},$$

(2)

where ${\mathbf{R}}_{\mathrm{h}}⪰{\mathbf{0}}_N$ denotes a deterministic Hermitian-symmetric positive definite correlation matrix at the BS-side and ${\mathbf{v}}_k$, $k=1,\dots ,K$ depict the fast-fading instantaneous DL channels, which are modeled as uncorrelated wide-sense stationary independent and identically distributed CSCG random vectors with $\sim \mathcal{CN}(\mathbf{0},{\mathbf{I}}_{\mathrm{N}})$. As such, the DL channel ${\mathbf{h}}_k\in {\mathbb{C}}^N$ satisfies ${\mathbf{R}}_{\mathrm{h}}=\mathbb{E}\left[{\mathbf{h}}_k^{}{\mathbf{h}}_k^{\mathrm{H}}\right]\in {\mathbb{C}}^{N\times N}$. The channel covariance matrix is denoted by the spatial correlation effects and the antenna array patterns. Further details about the channel covariance matrix designs can be found in Section 6.

Parameter $\xi =K/\mathbb{E}\left[\mathrm{tr}\left({\mathbf{WW}}^{\mathrm{H}}\right)\right]$ in (1) is the precoding normalization factor, which is considered to ensure that $\mathbb{E}\left[\parallel \sqrt{\xi }\mathbf{W}\mathbf{s}{\parallel }^2\right]=K$, as defined in [10]. Parameter ${\rho }_{\mathrm{d}}$ in (1) denotes the transmit DL signal-to-noise-ratio (SNR).

2.1. Downlink Achievable Sum Rate

In general, the user does not know the exact channel vector and precoding matrix, but instead estimates their average effect through $\sqrt{\xi }\mathbb{E}\left[{\mathbf{h}}_k^{\mathrm{H}}{\mathbf{w}}_k^{}\right]$, as considered in [9]. As such, the DL received signal at the k-th user can be expressed as

$$\begin{array}{c}\hfill y_k^{}=\sqrt{{\rho }_{\mathrm{d}}^{}\xi }\mathbb{E}\left[{\mathbf{h}}_k^{\mathrm{H}}{\mathbf{w}}_k^{}\right]x_k^{}+\sqrt{{\rho }_{\mathrm{d}}^{}\xi }\left({\mathbf{h}}_k^{\mathrm{H}}{\mathbf{w}}_k^{}-\mathbb{E}\left[{\mathbf{h}}_k^{\mathrm{H}}{\mathbf{w}}_k^{}\right]\right)x_k^{}\\ \hfill +\sqrt{{\rho }_{\mathrm{d}}^{}\xi }{\mathbf{h}}_k^{\mathrm{H}}\sum _{i\ne k}^K{\mathbf{w}}_i^{}{x}_i^{}+n_k^{}.\end{array}$$

(3)

The first term in the DL received signal in (3) represents the desired signal at the k-th user. The second term in (3) is the error caused by the imperfect channel knowledge at the user. The third term in (3) represents the residual multiuser interference after precoding. In general, the interference and error introduced by channel estimation terms are neither Gaussian nor independent of the desired information signal. Thus, an ergodic sum rate lower bound is determined by considering that both terms are independent of the desired signal, i.e., a worst-case scenario [9,16]. To this end, the achievable sum rate in the DL of the FDD MaMi systems is given as

$$\mathrm{Rate}=\left(1-\frac{T_{\mathrm{s}}}{{\tau }_{}}\right)·K·{\log }_2^{}\left(1+{\gamma }_{\mathrm{h}}\right)[\mathrm{bit}/\mathrm{s}/\mathrm{Hz}],$$

(4)

where $T_{\mathrm{s}}$ denotes the DTS length in symbol, $\tau$ represents the coherence block length in symbol and ${\gamma }_{\mathrm{h}}$ is the k-th user $\left(\mathrm{SINR}\right)$, which is provided by [9,10]

$${\gamma }_{\mathrm{h}}^{}=\frac{\xi |\mathbb{E}\left[{\mathbf{h}}_k^{\mathrm{H}}{\mathbf{w}}_k^{}\right]{|}^2}{{\sigma }_{\mathrm{d}}+\xi \mathbb{E}\left[|{\mathbf{h}}_k^{\mathrm{H}}{\mathbf{w}}_k^{}-\mathbb{E}\left[{\mathbf{h}}_k^{\mathrm{H}}{\mathbf{w}}_k^{}\right]{|}^2\right]+\xi {\sum }_{i\ne k}^K\mathbb{E}\left[|{\mathbf{h}}_k^{\mathrm{H}}{\mathbf{w}}_i^{}{|}^2\right]}.$$

(5)

The SINR expression in (5) can be re-written as

$${\gamma }_{\mathrm{h}}=\frac{\xi |\mathbb{E}\left[{\mathbf{h}}_k^{\mathrm{H}}{\mathbf{w}}_k^{}\right]{|}^2}{{\sigma }_{\mathrm{d}}+\xi {\sum }_{l=1}^K\mathbb{E}\left[|{\mathbf{h}}_k^{\mathrm{H}}{\mathbf{w}}_l^{}{|}^2\right]-|\mathbb{E}\left[{\mathbf{h}}_k^{\mathrm{H}}{\mathbf{w}}_k^{}\right]{|}^2},$$

(6)

where the term ${\sigma }_{\mathrm{d}}$ is the noise variance. The expectations in (6) are calculated based on different channel variations. These different channel realizations which are determined using extensive Monte Carlo simulations. However, this averaging process is very computationally demanding, because the different expectations in (6) are determined for different choices of ${\sigma }_{\mathrm{d}}$, ${\sigma }_{\mathrm{p}}$, $T_{\mathrm{s}}$, $\tau$ and N values using extensive Monte Carlo simulations. In this paper, a feasible and computationally effective solution for the SINR and the achievable sum rate of the RZFBF precoder in an FDD MaMi system is obtained in Section 5 by exploiting the asymptotic random matrix theory method.

2.2. Linear Precoding Design

The received SINR term in (6) relies on different statistics and the type of precoding scheme used by the BS, which is designed based on the DL channel estimation. In particular, from an information theoretic point of view, the optimum precoding design for multiuser MIMO systems can be obtained using a non-linear precoding, which is known as a dirty-paper coding (DPC) [37,38]. However, due to its design complexity, DPC precoding is to date practically unfeasible [39]. Alternatively, linear precoding can be used to provide a sub-optimum performance with a reduced design complexity [40,41]. Previous research in TDD MaMi systems has shown that the RZFBF precoder achieves a significant improvement in the sum rate performance over the beamforming (BF) precoder [10]. Therefore, this paper considers the RZFBF precoder. To this end, RZFBF precoding is given as

$$\mathbf{W}={\widehat{\mathbf{H}}}^{\mathrm{H}}{\left(\widehat{\mathbf{H}}{\widehat{\mathbf{H}}}^{\mathrm{H}}+N\zeta {\mathbf{I}}_K\right)}^{-1},$$

(7)

where $\zeta$ is a regularization coefficient of RZFBF precoding. In this paper, we follow [10] and consider $\zeta$ as an inverse of the SNR. The term $\widehat{\mathbf{H}}$ is the estimate of the DL channel $\mathbf{H}={[{\mathbf{h}}_1,{\mathbf{h}}_2,\dots ,{\mathbf{h}}_K]}_{}^{\mathrm{H}}\in {\mathbb{C}}^{K\times N}$. Further details about channel estimation based on the DTS are discussed in next section. It should be pointed out that the total average channel power is normalized as $\mathbb{E}\left[\mathrm{tr}\left({\mathbf{H}}^{\mathrm{H}}\mathbf{H}\right)\right]={\sum }_{k=1}^K\mathrm{tr}\left(\mathbb{E}\left[{\mathbf{h}}_k^{}{\mathbf{h}}_k^{\mathrm{H}}\right]\right)=NK$. The following section discusses the DL channel estimation process in an FDD MaMi system in the presence of colored noise.

3. Problem Formulation of Channel Estimation with Colored Noise

Since the performance of precoding scheme in the DL transmission depends on the accuracy of the CSI estimation, designing a feasible DTS for the channel estimation problem is crucial. This section presents the DL channel estimation process using DTS in an FDD MaMi system with a colored noise environment. In particular, the CSI estimation process is conditioned on the received training signal from a known DTS, which can be potentially designed based on the long-term statistical information, i.e., the channel and noise statistics. To obtain the CSI knowledge, the BS first sends a known DTS of length $T_{\mathrm{s}}$ in symbol in a coherent process to all users across the cell during the training transmission. As such, the k-th user received training signal, ${\mathbf{y}}_k\in {\mathbb{C}}^{T_{\mathrm{s}}}$ is expressed as

$${\mathbf{y}}_k^{}={\mathbf{S}}_{}^{\mathrm{H}}{\mathbf{h}}_k^{}+{\mathbf{n}}_k^{},$$

(8)

where ${\mathbf{n}}_k$ denotes the receiver colored noise, which exhibits a CSCG distribution with zero mean and covariance ${\mathbf{R}}_{\mathrm{n}}$. The noise statistic is considered to be stationary i.e., varying slowly over time. The term ${\mathbf{S}}_{}\in {\mathbb{C}}^{N\times T_{\mathrm{s}}}$ is the common training matrix, which satisfies the energy constraint i.e., $\mathrm{tr}\left({\mathbf{S}}_{}^{\mathrm{H}}{\mathbf{S}}_{}^{}\right)={\rho }_{\mathrm{s}}{T}_{\mathrm{s}}$, where ${\rho }_{\mathrm{s}}$ is the average transmitted power during the training-phase. This paper considers ${\rho }_{\mathrm{s}}={\rho }_{\mathrm{d}}$. However, non-uniform power allocations across the users and optimization with respect to different choices of ${\rho }_{\mathrm{s}}$ and ${\rho }_{\mathrm{d}}$ could be considered in future work. Furthermore, CSI feedback compression schemes [42,43,44,45] or using signal compressing methods [46,47] can also be considered in future work. To optimize the DL channel estimation performance, a Bayesian linear estimation based on MMSE filter is used [43,48]. Since the DL channel ${\mathbf{h}}_k$ exhibits a CSCG distribution and the statistics ${\mathbf{R}}_{\mathrm{h}}$ are known, the probability density function (PDF) is given as

$$\begin{array}{c}\hfill f_{{\mathrm{h}}_k}\left({\mathbf{h}}_k\right)=\frac{\exp \left\{-{\mathbf{h}}_{\mathrm{k}}^{\mathrm{H}}{\mathbf{R}}_{\mathrm{h}}^{-1}{\mathbf{h}}_{\mathrm{k}}^{}\right\}}{\det \left(\pi {\mathbf{R}}_{\mathrm{h}}\right)}.\end{array}$$

(9)

Similarly, the PDF of the noise vector with noise temporal correlation matrix is given as

$$\begin{array}{c}\hfill f_{{\mathrm{n}}_k}\left({\mathbf{n}}_k\right)=\frac{\exp \left\{-{\mathbf{n}}_{\mathrm{k}}^{\mathrm{H}}{\mathbf{R}}_{\mathrm{h}}^{-1}{\mathbf{n}}_{\mathrm{k}}^{}\right\}}{\det \left(\pi {\mathbf{R}}_{\mathrm{n}}\right)}.\end{array}$$

(10)

To this end, the PDF of the received signal during training-phase and the conditional PDF of ${\mathbf{y}}_k$ given ${\mathbf{h}}_k$ is provided in (11) and (12), respectively.

$$\begin{array}{c}\hfill f_{{\mathrm{y}}_k}\left({\mathbf{y}}_k\right)=\frac{\exp \left\{-{\mathbf{y}}_k^{\mathrm{H}}{\left({\mathbf{S}}^{\mathrm{H}}{\mathbf{R}}_{\mathrm{h}}\mathbf{S}+{\mathbf{R}}_{\mathrm{n}}\right)}^{-1}{\mathbf{y}}_k\right\}}{\det \left(\pi \left({\mathbf{S}}^{\mathrm{H}}{\mathbf{R}}_{\mathrm{h}}\mathbf{S}+{\mathbf{R}}_{\mathrm{n}}\right)\right)}\end{array}$$

(11)

$$\begin{array}{c}\hfill f_{{\mathbf{y}}_k|{\mathbf{h}}_k}\left({\mathbf{y}}_k\right|{\mathbf{h}}_k)=\frac{\exp \left\{-{\left({\mathbf{y}}_k-{\mathbf{S}}^{\mathrm{H}}{\mathbf{h}}_k\right)}^{\mathrm{H}}{\mathbf{R}}_n^{-1}({\mathbf{y}}_k-{\mathbf{S}}^{\mathrm{H}}{\mathbf{h}}_k)\right\}}{\det \left(\pi {\mathbf{R}}_n\right)}\end{array}$$

(12)

Since the channel ${\mathbf{h}}_k$ and noise ${\mathbf{n}}_k$ vectors are independent Gaussian distributions, by the definition of the posterior probability density function, we have

$$\begin{array}{cc}\hfill f_{{\mathbf{h}}_k|{\mathbf{y}}_k}\left({\mathbf{h}}_k|{\mathbf{y}}_k\right)& =\frac{f_{{\mathbf{h}}_k,{\mathbf{y}}_k}\left({\mathbf{h}}_k,{\mathbf{y}}_k\right)}{f_{{\mathbf{y}}_k}\left({\mathbf{y}}_k\right)}\hfill \\ \hfill & =\frac{f_{{\mathbf{h}}_k}\left({\mathbf{h}}_k\right)f_{{\mathbf{h}}_k|{\mathbf{y}}_k}\left({\mathbf{y}}_k|{\mathbf{h}}_k\right)}{f_{{\mathbf{y}}_k}\left({\mathbf{y}}_k\right)},\hfill \end{array}$$

(13)

substituting (9)–(12) into (13), yields

$$\begin{array}{c}\hfill f_{{\mathbf{h}}_k|{\mathbf{y}}_k}\left({\mathbf{h}}_k|{\mathbf{y}}_k\right)=\frac{\frac{\exp \left\{-{\mathbf{h}}_k^{\mathrm{H}}{\mathbf{R}}_{\mathbf{h}}^{-1}{\mathbf{h}}_k\right\}}{\det \left(\pi {\mathbf{R}}_{\mathbf{h}}\right)}\frac{\exp \left\{-{\left({\mathbf{y}}_k-{\mathbf{S}}^{\mathrm{H}}{\mathbf{h}}_k\right)}^{\mathrm{H}}{\mathbf{R}}_n^{-1}({\mathbf{y}}_k-{\mathbf{S}}^{\mathrm{H}}{\mathbf{h}}_k)\right\}}{\det \left(\pi {\mathbf{R}}_n\right)}}{\frac{\exp \left\{-{\mathbf{y}}_k^{\mathrm{H}}{\left({\mathbf{S}}^{\mathrm{H}}{\mathbf{R}}_{\mathrm{h}}\mathbf{S}+{\mathbf{R}}_{\mathrm{n}}\right)}^{-1}{\mathbf{y}}_k\right\}}{\det \left(\pi \left({\mathbf{S}}^{\mathrm{H}}{\mathbf{R}}_{\mathrm{h}}\mathbf{S}+{\mathbf{R}}_{\mathrm{n}}\right)\right)}}.\end{array}$$

(14)

The expression of the PDF in (14) can be expressed in a canonical Hermitian with Gaussian distribution [48], and thus, the conditional channel covariance matrix of ${\mathbf{h}}_k$ given ${\mathbf{y}}_k$ can be written as

$$\begin{array}{c}\hfill {\mathbf{R}}_{{\mathbf{h}}_k|{\mathbf{y}}_k}=\left({\mathbf{R}}_{\mathrm{h}}^{}-{\mathsf{\Phi }}_{\widehat{\mathrm{h}}}\right),\end{array}$$

(15)

where ${\mathsf{\Phi }}_{\widehat{\mathrm{h}}}$ is the covariance of the MMSE channel estimation that is given by

$${\mathsf{\Phi }}_{\widehat{\mathrm{h}}}={\mathbf{R}}_{\mathrm{h}}^{}{\mathbf{S}}_{}^{}{\left({\mathbf{S}}_{}^{\mathrm{H}}{\mathbf{R}}_{\mathrm{h}}^{}{\mathbf{S}}_{}^{}+{\mathbf{R}}_{\mathrm{n}}^{}\right)}^{-1}{\mathbf{S}}_{}^{\mathrm{H}}{\mathbf{R}}_{\mathrm{h}}^{},$$

(16)

where the expression in (15) is minimised by maximising the expression in (16), which represents the covariance matrix with MMSE channel estimate that is required to be as similar to ${\mathbf{R}}_{\mathrm{h}}$ as possible.

Lemma 1.

For a positive definite matrices $\mathbf{A}$, $\mathbf{U}$, $\mathbf{C}$,$\mathbf{V}$, using the Woodbury matrix identity, the following holds:

$${(\mathbf{A}+\mathbf{U}\mathbf{C}\mathbf{V})}^{-1}={\mathbf{A}}^{-1}-{\mathbf{A}}^{-1}{\mathbf{U}}^{}{({\mathbf{C}}^{-1}+\mathbf{V}{\mathbf{A}}^{-1}\mathbf{U})}^{-1}\mathbf{V}{\mathbf{A}}^{-1}.$$

(17)

Using Lemma 1, the conditional covariance matrix of ${\mathbf{h}}_k$ given ${\mathbf{y}}_k$ can be expressed as

$${\mathbf{R}}_{{\mathbf{h}}_k|{\mathbf{y}}_k}={\left({\mathbf{R}}_{\mathrm{h}}^{-1}+{\mathbf{S}}_{}{\mathbf{R}}_{\mathrm{n}}^{-1}{\mathbf{S}}_{}^{\mathrm{H}}\right)}^{-1}.$$

(18)

Accordingly, the MSE cost function $C_e\in \mathbb{R}$ with MMSE channel estimates can be written as

$$C_e=\mathrm{tr}\left({\mathbf{R}}_{{\mathbf{h}}_k|{\mathbf{y}}_k}\right).$$

(19)

Clearly, the MSE performance depends on the structure of the training matrix $\mathbf{S}$, which explicitly depends on the pilot energy allocated during the training phase, i.e., (${\rho }_{\mathrm{s}}{T}_{\mathrm{s}}$), and on the structure of the channel and noise statistics. Specifically, the MSE performance depends on the eigenstructure of the term ${\left({\mathbf{R}}_{\mathrm{h}}^{-1}+{\mathbf{S}}_{}{\mathbf{R}}_{\mathrm{n}}^{-1}{\mathbf{S}}_{}^{\mathrm{H}}\right)}^{-1}$, i.e., the energy that corresponds to the eigenvalues distribution over the diagonal of this term. This observation motivates the use of the structures of the channel covariance matrix ${\mathbf{R}}_{\mathrm{h}}$ and noise covariance matrix ${\mathbf{R}}_{\mathrm{n}}$ in optimizing the DTS, and thus performance, of the FDD MaMi systems. More details about the structure of the DL training matrix $\mathbf{S}$ are provided in the next section. To this end, minimizing the MSE cost function in the presence of colored noise over the DTS ${\mathbf{S}}_{}^{}$ for a given training phase duration $T_{\mathrm{s}}$ and training power ${\rho }_{\mathrm{s}}$ in the DL MaMi systems equates to the optimization problem defined in (20)

$$\begin{array}{cc}\hfill & \underset{{\mathbf{S}}_{}}{\mathrm{minimise}}\mathrm{tr}\left({\left({\mathbf{R}}_{\mathrm{h}}^{-1}+{\mathbf{S}}_{}{\mathbf{R}}_{\mathrm{n}}^{-1}{\mathbf{S}}_{}^{\mathrm{H}}\right)}^{-1}\right)\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\mathrm{tr}({\mathbf{S}}_{}^{\mathrm{H}}{\mathbf{S}}_{}^{})\le E_{\mathrm{s}},\hfill \end{array}$$

(20)

where $E_{\mathrm{s}}$ is the total energy constraint during the training transition phase, which is given as $E_{\mathrm{s}}={\rho }_{\mathrm{s}}{T}_{\mathrm{s}}$. The following section investigates the optimum DTS design in the presence of colored noise.

4. The Proposed DTS Design and Mean Square Error Analysis in the Presence of Colored Noise

The DL sum rate of RZFBF precoding in an FDD MaMi relies on the channel statistic and noise statistic and the DL channel estimation. In non-reciprocal channels, such as FDD based systems, the BS would need to transmit DL training sequence to the users, and each user will then quantize the received signal and transmit it back to the BS to estimate the DL channels and complete the precoder design. However, in some cases, each user could estimate its own DL channel and send the quantized channel estimates back to the BS. Both approaches are suitable with the poposed design in the paper. This section derives the optimum training sequence that needs to be used to design the precoding at the BS in order to achieve a maximum achievable sum rate in an FDD MaMi system.

In what follows, we provide the proposed DTS framework for an FDD MaMi system in the presence of colored noise. The proposed training design aims to improve the quality of the channel estimation, and thus, achieves a robust sum rate performance with a reduced training overhead. Due to the use of hundreds of antennas at the BS, which are grouped together and packed into a limited physical area, the MaMi channels may be highly correlated. To this end, the channel covariance matrix would exhibit a large eigenvalue spread so that it can be partitioned into a small dimensions, which is effectively less than N. Moreover, a large portion of the energy in the channel can be focused into a few directions (eigenmodes). In what follows, the basic concept of majorization theory is introduced in order to understand the fundamental impact of spatial correlation on the MSE of channel estimate.

Definition 1.

Majorization [49]: Let $\mathbf{x}={[{\mathbf{x}}_1,\dots ,{\mathbf{x}}_N]}^{\mathrm{T}}$ and $\mathbf{z}={[{\mathbf{z}}_1,\dots ,{\mathbf{z}}_N]}^{\mathrm{T}}$ be as two positive real-valued vectors, containing the elements of $\mathbf{x}$ and $\mathbf{z}$, respectively, which are arranged in descending order. Vector $\mathbf{x}$ majorizes $\mathbf{z}$$(\mathbf{x}⪰\mathbf{z})$ if

$$\sum _{i=1}^n\mathbf{x}\ge \sum _{i=1}^n\mathbf{z},$$

(21)

for all$1\le n<N$. If vectors$\mathbf{x}$and$\mathbf{z}$contain eigenvalues of the channel covariance matrices, then by the majorization property, $\mathbf{z}$is less spread out than$\mathbf{x}$and vector$\mathbf{x}$is more spatially correlated than vector$\mathbf{z}$. Similarly, for the MSE cost function under consideration, $C_e\left(\mathbf{x}\right)\le C_e\left(\mathbf{z}\right)$, which implies that the MSE of the stronger eigenvalues are less than the MSE of the weakest eigenvalues. As such, high spatial correlation reduces the estimation error and the eigendirections of${\mathbf{R}}_{\mathrm{h}}$, with large eigenvalues have a smaller estimation error variance than the eigendirections with smaller eigenvalues. Specifically, based on the majorization theory, the MSE performance decreases with increasing spatial channel correlations. As such, the minimum number of DTS length can be chosen to be significantly less thanNin correlated channel scenarios. This is particularly important for the FDD MaMi systems where the MSE needs to be minimised and the sum rate requires being maximized using as little DTS length as possible.

We design the structure of the DTS matrix ${\mathbf{S}}_{}$ with the single stage precoding, based on the second order channel and noise statistics, which are denoted by the covariance matrix and the noise covariance matrix. In particular, the effective eigenvectors denoted by the largest eigenvalues of the channel covariance matrix and noise covariance matrix can be exploited in the pilot design, in order to minimize the MSE while reducing the DTS overhead. This would allow the DL achievable sum rate of the FDD MaMi communications systems to be maximized. Typically, the channel covariance matrix ${\mathbf{R}}_{\mathrm{h}}$ can be decomposed using the eigenvalue decomposition (EVD) as

$${\mathbf{R}}_{\mathrm{h}}^{}={\mathbf{U}}_{\mathrm{h}}^{}{\mathsf{\Lambda }}_{\mathrm{h}}^{}{\mathbf{U}}_{\mathrm{h}}^{\mathrm{H}},$$

(22)

where matrix ${\mathbf{U}}_{\mathrm{h}}=[{\mathbf{u}}_{\mathrm{h},1},\dots ,{\mathbf{u}}_{\mathrm{h},N}]\in {\mathbb{C}}^{N\times N}$ is the eigenvectors and matrix ${\mathsf{\Lambda }}_{\mathrm{h}}\in {\mathbb{R}}^{N\times N}$ corresponds to the eigenvalues of ${\mathbf{R}}_{\mathrm{h}}$, which are ordered as ${\lambda }_{\mathrm{h},1}\ge {\lambda }_{\mathrm{h},2}\ge \cdots \ge {\lambda }_{\mathrm{h},N}$ (Matlab function (svd) provides the unitary matrix arranged in descending order). Using the EVD in (22), the MSE error cost function can be rewritten as

$$C_e=\mathrm{tr}\left({\left({\left({\mathbf{U}}_{\mathrm{h}}^{}{\mathsf{\Lambda }}_{\mathrm{h}}^{}{\mathbf{U}}_{\mathrm{h}}^{\mathrm{H}}\right)}^{-1}+{\mathbf{S}}_{}{\mathbf{R}}_{\mathrm{n}}^{-1}{\mathbf{S}}_{}^{\mathrm{H}}\right)}^{-1}\right).$$

(23)

It is straightforward to re-write (23) as

$$C_e=\mathrm{tr}\left({\left({\mathsf{\Lambda }}_{\mathrm{h}}^{-1}+{\mathbf{U}}_{\mathrm{h}}^{\mathrm{H}}{\mathbf{S}}_{}{\mathbf{R}}_{\mathrm{n}}^{-1}{\mathbf{S}}_{}^{\mathrm{H}}{\mathbf{U}}_{\mathrm{h}}\right)}^{-1}\right).$$

(24)

Similar to channel covariance mtraix, the noise covariance matrix can be decomposed as

$${\mathbf{R}}_{\mathrm{n}}^{}={\mathbf{U}}_{\mathrm{n}}^{}{\mathsf{\Lambda }}_{\mathrm{n}}^{}{\mathbf{U}}_{\mathrm{n}}^{\mathrm{H}},$$

(25)

where ${\mathbf{U}}_{\mathrm{n}}=[{\mathbf{u}}_{\mathrm{h},1},\dots ,{\mathbf{u}}_{\mathrm{n},T_{\mathrm{s}}}]\in {\mathbb{C}}^{T_{\mathrm{s}}\times T_{\mathrm{s}}}$ are the matrix eigenvectors and matrix ${\mathsf{\Lambda }}_{\mathrm{n}}\in {\mathbb{R}}^{T_{\mathrm{s}}\times T_{\mathrm{s}}}$ are the eigenvalues of ${\mathbf{R}}_{\mathrm{n}}$ ordered as ${\lambda }_{\mathrm{h},1}\ge {\lambda }_{\mathrm{h},2}\ge \cdots \ge {\lambda }_{\mathrm{h},T_{\mathrm{s}}}$. To this end, the DTS framework in the presence of colored noise for an FDD MaMi system under consideration is provided in the following proposition.

Proposition 1.

A unique DTS matrix ${\mathbf{S}}_{}\in {\mathbb{C}}^{N\times T_{\mathrm{s}}}$ for the training transmission phase in the FDD MaMi systems with colored noise is constructed from first $T_{\mathrm{s}}$ columns space eigenvectors of the transmit covariance matrix ${\mathbf{R}}_{\mathrm{h}}$, which correspond to $T_{\mathrm{s}}$ largest eigenvalues of ${\mathbf{R}}_{\mathrm{h}}$, multiplied by the columns space eigenvectors of the noise covariance matrix ${\mathbf{R}}_{\mathrm{n}}$ and scaled by the square root of the training power during the training phase, as expressed in (26)

$${\mathbf{S}}_{}^{}=\sqrt{{\rho }_{\mathrm{s}}}{\left[{\mathbf{U}}_{\mathrm{h},T_{\mathrm{s}}}\right]}_{1:T_{\mathrm{s}}}\left[{\mathbf{U}}_{\mathrm{n}}\right],$$

(26)

where ${\mathbf{U}}_{\mathrm{h},T_{\mathrm{s}}}\in {\mathbb{C}}^{N\times T_{\mathrm{s}}}$ is a rectangular matrix consisting of $T_{\mathrm{s}}$ eigenvectors of ${\mathbf{R}}_{\mathrm{h}}$ that correspond to the largest $T_{\mathrm{s}}$ eigenvalues of ${\mathbf{R}}_{\mathrm{h}}$, i.e, ${\mathsf{\Lambda }}_{\mathrm{h},T_{\mathrm{s}}}\in {\mathbb{R}}^{T_{\mathrm{s}}\times T_{\mathrm{s}}}$, and ${\mathbf{U}}_{\mathrm{n}}\in {\mathbb{C}}^{T_{\mathrm{s}}\times T_{\mathrm{s}}}$ is the eigenvectors of the noise covariance matrix ${\mathbf{R}}_{\mathrm{n}}$. This implies that the channel energy, which corresponds to the eigenvectors $[{\mathbf{u}}_{T_{\mathrm{s}}+1},\dots ,{\mathbf{u}}_N]$, is not used in channel estimation process, which reduces the training overhead significantly. The obtained pilot design should satisfy the energy constraint $E_{\mathrm{s}}$ in the training-phase so that $\mathrm{tr}\left({\mathbf{S}}_{}^{\mathrm{H}}{\mathbf{S}}_{}^{}\right)={\rho }_{\mathrm{s}}{T}_{\mathrm{s}}$. Substituting the DTS design in (26) into (24) with some straightforward algebra yields, a novel analytical form for the MSE of the MMSE channel estimate with colored noise as

$$C_e=\mathrm{tr}\left({\left({\mathsf{\Lambda }}_{\mathrm{h},T_{\mathrm{s}}}^{-1}+{\rho }_{\mathrm{s}}{\left({\mathbf{U}}_{\mathrm{n}}^{}\right)}^2{\mathsf{\Lambda }}_{\mathrm{n}}^{-1}{\left({\mathbf{U}}_{\mathrm{n}}^{\mathrm{H}}\right)}^2\right)}^{-1}\right).$$

(27)

For a spacial case of white noise, so that ${\mathbf{R}}_{\mathrm{n}}={\mathbf{I}}_{T_{\mathrm{s}}}$, the MSE expression in (27) can be simplified to

$$C_e=\mathrm{tr}\left({\left({\mathsf{\Lambda }}_{\mathrm{h},T_{\mathrm{s}}}^{-1}+{\rho }_{\mathrm{s}}{\mathbf{I}}_{T_{\mathrm{s}}}\right)}^{-1}\right).$$

(28)

Using the trace property, expression in (28) can be written as

$$C_e=\sum _{t=1}^{T_{\mathrm{s}}^{}}{\left(\frac{1}{{\mathbf{\lambda }}_{\mathrm{h},t}}+{\rho }_{\mathrm{s}}\right)}^{-1}.$$

(29)

Straightforward algebra simplifies (29) to

$$C_e=\sum _{t=1}^{T_{\mathrm{s}}^{}}\frac{{\lambda }_{\mathrm{h},t}}{{\rho }_{\mathrm{s}}{\lambda }_{\mathrm{h},t}+1}.$$

(30)

Substituting the DTS design in (26) into (16) simplifies the trace of the MMSE estimation covariance matrix to

$$\mathrm{tr}\left({\mathsf{\Phi }}_{\widehat{\mathrm{h}}}\right)={\mathsf{\Lambda }}_{\mathrm{h},T_{\mathrm{s}}}^2{\mathbf{U}}_{\mathrm{n}}^{}{\left({\mathbf{U}}_{\mathrm{n}}^{\mathrm{H}}{\mathsf{\Lambda }}_{\mathrm{h},T_{\mathrm{s}}}^{}{\mathbf{U}}_{\mathrm{n}}^{}+\frac{1}{{\rho }_{\mathrm{s}}}{\mathbf{U}}_{\mathrm{n}}^{}{\mathsf{\Lambda }}_{\mathrm{n}}^{}{\mathbf{U}}_{\mathrm{n}}^{\mathrm{H}}\right)}^{-1}{\mathbf{U}}_{\mathrm{n}}^{\mathrm{H}},$$

(31)

and for the spacial scenario of weight noise to

$$\mathrm{tr}\left({\mathsf{\Phi }}_{\widehat{\mathrm{h}}}\right)={\mathsf{\Lambda }}_{\mathrm{h},T_{\mathrm{s}}}^2{\left({\mathsf{\Lambda }}_{\mathrm{h},T_{\mathrm{s}}}^{}+\frac{1}{{\rho }_{\mathrm{s}}}{\mathbf{I}}_{T_{\mathrm{s}}}\right)}^{-1},$$

(32)

which can be further simplified to

$$\mathrm{tr}\left({\mathsf{\Phi }}_{\widehat{\mathrm{h}}}\right)=\sum _{t=1}^{T_{\mathrm{s}}}\frac{{\rho }_{\mathrm{s}}{\lambda }_{\mathrm{h},n}^2}{{\rho }_{\mathrm{s}}{\lambda }_{\mathrm{h},n}+1}.$$

(33)

Clearly, increasing the transmit power during the training phase, i.e., ${\rho }_{\mathrm{s}}$ reduces the MSE.

Remark 1.

Typically, increasing $T_{\mathrm{s}}$ allows for more DTS energy to be collected, which results in reducing the MSE, but it will reduce the achievable sum rate due to a shorter useful information transmission. Hence, it is essential to conduct a suitable system analysis in order to determine a feasible DTS length based on general statistics. This is because the loss in the MSE with shorter pilot length might be minor compared with the gain obtained by carrying out more data transmission. The proposed approach suggests that for a given training power, only the eigennvectors that correspond to the effective eigenvalues of ${\mathbf{R}}_{\mathrm{h}}$, which are deemed as essential, should be exploited in the pilot design. The intuition behind this pilot framework is to take advantage of the strong subspaces (eigendirections) of ${\mathbf{R}}_{\mathrm{h}}$ to send the common pilot signal to the users. The minimum number of DTS symbols is determined by the number of dominant eigenvalues of the spatial correlation matrix. The pilot selection criteria based on the effective eigendirection will be discussed later in Section 7.

Remark 2.

As discussed earlier, the vast majority of the previous studies on the DTS design and CSI estimation in the FDD MaMi systems have assumed an ideal scenario of wight noise environment. Specifically, the impact of colored noise with imperfect CSI estimation on the FDD MaMi systems has not yet been characterized in prior works. In summary, unlike the state-of-the-art research in the FDD MaMi systems where the DL channel estimation is considered by assuming an uncorrelated white noise environment, we focus on DTS design in the colored environments. To the best of our knowledge, this research study is the first work that takes into consideration the noise covariance in pilot design of the FDD MaMi systems. This paper also focuses on investigating the achievable DL sum rate of the proposed DTS design in the limited coherence time. Our approach benefits from the statistical information of the channel covariance matrix and the noise covariance matrix, resulting in a feasible DTS solution during the DL channel estimation, even when the channel coherence time is short.

5. Asymptotic Analysis of the SINR with RZFBF Precoding

This section provides an asymptotic analysis expression that tightly approximates the SINR, and hence DL achievable sum rate, of RZFBF precoding for an FDD MaMi system based on the random matrix theory method [10,39,50]. To this end, an asymptotically approximation of the ${\mathrm{SINR}}_{}$, denoted by ${\overline{\gamma }}_{\mathrm{h}}$, can be obtained as given in (34) when the number of BS antennas N and the number of users K grow asymptotically as

$${\gamma }_{\mathrm{h}}-{\overline{\gamma }}_{\mathrm{h}}\underset{N\to \infty }{\to }0.$$

(34)

Although the asymptotic analysis in this paper is derived under an assumption that $N\to \infty$, consistent with conventional research simulations of asymptotic system analysis [10,39,51,52,53], numerical results show that this asymptotic analysis provides an accurate approximation for the true SINR and the achievable sum rate, of the RZFBF precoder, even with the finite parameter of N. This would allow the SINR ${\gamma }_{\mathrm{h}}$ term in (6) with extensive Monte Carlo simulations to be replaced with the asymptotic approximation given in this section, and thus, straightforward system design evaluation can be achieved. Furthermore, the asymptotic approximation of the SINR of the RZFBF precoder, and hence the sum rate, allows the numerical results to be readily reproducible. The following proposition elaborates the analytical result of the RZFBF precoder using a random matrix theory.

Proposition 2.

Let ${\gamma }^{\mathrm{RZFBF}}$ denote the ${\mathrm{SINR}}_{\mathrm{h}}$ of RZFBF precoding, as defined in (6). An asymptotic SINR approximation with RZFBF precoding of an FDD MaMi system under consideration is provided as

$${\overline{\gamma }}_{\mathrm{h}}^{\mathrm{RZFBF}}=\frac{KN\overline{\xi }{\delta }_{\mathrm{h}}^2}{{\sigma }_{\mathrm{d}}{\left(1+{\delta }_{\mathrm{h}}\right)}^2+\overline{\xi }{K}^2{\overline{\mu }}_{\mathrm{h}}},$$

(35)

where the parameter $\overline{\xi }\in \mathbb{R}$ is the deterministic equivalent of the RZFBF precoding and ${\delta }_{\mathrm{h}}\in \mathbb{R}$ are parameters that arise from the random matrix theory. These parameters can be obtained through the use of an iterative fixed-point algorithm. As such, let a recursion on integer t be $t=1,2,\dots ,$

$${\delta }_{\mathrm{h}}^{\left(t\right)}=\mathrm{tr}\left({\mathsf{\Phi }}_{\widehat{\mathrm{h}}}{\left(\frac{K{\mathsf{\Phi }}_{\widehat{\mathrm{h}}}}{\left(1+{\delta }_{\mathrm{h}}^{(t-1)}\right)}+N\zeta {\mathbf{I}}_N\right)}^{-1}\right),$$

(36)

with an initial value ${\delta }_{\mathrm{h}}^{\left(0\right)}=1/\zeta$ and the parameter ${\delta }_{\mathrm{h}}\in \mathbb{R}$ is determined as

$${\delta }_{\mathrm{h}}^{}=\underset{t\to \infty }{lim}{\delta }_{\mathrm{h}}^{\left(t\right)}.$$

(37)

Solving the fixed-point equations in (36) and (37) leads to obtain

$$\mathbf{T}={\left(\zeta {\mathbf{I}}_N^{}+\frac{K{\mathsf{\Phi }}_{\widehat{\mathrm{h}}}}{N(1+{\delta }_{\mathrm{h}})}\right)}^{-1},$$

(38)

and to determine $\mathbf{T}\in {\mathbb{C}}^{N\times N}$. Matrix $\overline{\mathbf{T}}\in {\mathbb{C}}^{N\times N}$ is given by

$$\overline{\mathbf{T}}=\mathbf{T}\left({\mathbf{I}}_N+\frac{K\overline{{\delta }_{\mathrm{h}}}{\mathsf{\Phi }}_{\widehat{\mathrm{h}}}}{N{(1+{\delta }_{\mathrm{h}})}_{}^2}\right)\mathbf{T},$$

(39)

where $\overline{{\delta }_{\mathrm{h}}}\in \mathbb{R}$ is an auxiliary variable and is given by

$$\overline{{\delta }_{\mathrm{h}}}={\left(1-\frac{\mathrm{tr}\left({\mathsf{\Phi }}_{\widehat{\mathrm{h}}}\mathbf{T}{\mathsf{\Phi }}_{\widehat{\mathrm{h}}}\mathbf{T}\right)}{{\left(N(1+{\delta }_{\mathrm{h}})\right)}^2}\right)}^{-1}\frac{1}{N}\mathrm{tr}\left(\mathbf{T}{\mathsf{\Phi }}_{\widehat{\mathrm{h}}}\mathbf{T}\right).$$

(40)

Parameter $\overline{\xi }\in \mathbb{R}$ denotes the deterministic equivalent of RZFBF precoding normalization, which is provided by substituting matrix $\mathbf{T}$ in (38) and matrix $\overline{\mathbf{T}}$ in (39) into

$$\overline{\xi }={\left(\mathrm{tr}\left(\mathbf{T}\right)-\zeta \mathrm{tr}\left({\overline{\mathbf{T}}}^{}\right)\right)}^{-1}.$$

(41)

The parameter ${\overline{\mu }}_{}\in \mathbb{R}$ is determined by utilizing the dominated convergence theorem and the theorem of the continuous mapping, as provided in [10], and hence, it is obtained in (42)–(44).

$${\overline{\mu }}_{\mathrm{h}}=\frac{1}{N}\mathrm{tr}\left({\mathbf{R}}_{\mathrm{h}}{\mathbf{T}}_{}^{\prime }\right)-\frac{2\mathrm{Re}\left(\mathrm{tr}\left({\mathsf{\Phi }}_{\widehat{\mathrm{h}}}\mathbf{T}\right)\mathrm{tr}\left({\mathsf{\Phi }}_{\widehat{\mathrm{h}}}{\mathbf{T}}_{}^{\prime }\right)\right)\left(1+{\delta }_{\mathrm{h}}\right)-\mathrm{tr}{\left({\mathsf{\Phi }}_{\widehat{\mathrm{h}}}\mathbf{T}\right)}^2{\delta }_{\mathrm{h}}^{\prime }}{{\left(N(1+{\delta }_{\mathrm{h}})\right)}^2}$$

(42)

$${\mathbf{T}}_{}^{\prime }=\mathbf{T}\left({\mathsf{\Phi }}_{\widehat{\mathrm{h}}}+\frac{K{\mathsf{\Phi }}_{\widehat{\mathrm{h}}}{\delta }_{\mathrm{h}}^{\prime }}{N{(1+{\delta }_{\mathrm{h}})}_{}^2}\right)\mathbf{T}$$

(43)

$${\delta }_{\mathrm{h}}^{\prime }={\left(1-\frac{\mathrm{tr}\left({\mathsf{\Phi }}_{\widehat{\mathrm{h}}}\mathbf{T}{\mathsf{\Phi }}_{\widehat{\mathrm{h}}}\mathbf{T}\right)}{{\left(N(1+{\delta }_{\mathrm{h}})\right)}^2}\right)}^{-1}\frac{1}{N}\mathrm{tr}\left(\mathbf{T}{\mathsf{\Phi }}_{\widehat{\mathrm{h}}}\mathbf{T}{\mathsf{\Phi }}_{\widehat{\mathrm{h}}}\right)$$

(44)

The SINR expression given in (35) is a deterministic approximation of the true SINR in (6) that gives a lower bound in (4). The SINR analysis of RZFBF precoding provided in (35) is valid for any spatial correlation model and DTS type. Accordingly, the achievable sum rate expression based on the random matrix theory method can be written as

$$\overline{\mathrm{Rate}}=\left(1-\frac{T_{\mathrm{s}}}{{\tau }_{}}\right)·K·{\log }_2^{}\left(1+{\overline{\gamma }}_{\mathrm{h}}\right)[\mathrm{bit}/\mathrm{s}/\mathrm{Hz}].$$

(45)

The following section discusses the physical channel correlation models based on the ULA and UPA array configurations.

6. Physical Channel Models

Most of the research works on MIMO systems have considered the uncorrelated Rayleigh fading when modeling the channel covariance matrix. In this case, the elements of the covariance matrix are independent and uniformly distributed i.e., ${\mathbf{R}}_{\mathrm{h}}={\mathbf{I}}_N$ for all users. Therefore, in the uncorrelated Rayleigh fading model, all directions become equally important, since the energy is distributed in all directions [54]. However, the condition for the channel coefficients to be spatially uncorrelated is very strict. As mentioned earlier in Section 4, with a large number of BS antennas in MaMi systems, the channel coefficients may be highly correlated due to the spatially dependent of the antennas radiation patterns and near-field scattering environment. Furthermore, practical measurements have shown that MIMO channels are correlated [55,56,57]. Hence, spatial correlation models with different BS design typologies should be considered, in order to characterise a realistic performance assessment of the FDD MaMi systems. In the correlated Rayleigh fading, only few effective paths exist in the angular directions, while the rest of the directions could be ignored so as not to be used in the precoding.

Exploiting the covariance correlation in the channel estimation is crucial for providing a feasible DTS design for the FDD MaMi systems. This is due to the fact that spatial correlation allows a rank deficient covariance matrices. As such, the rank of the channel covariance matrix can be increased sublinearly with N, resulting in affordable DTS overhead for FDD operation mode with MaMi systems. In particular, spatial correlation allows channel training with a minimum duration, which is upper bounded by the rank of the correlation matrix, thus reducing the DTS overhead of MaMi systems.

The degrees of spatial correlation in the channel covariance matrix depends on the statistical information and the array configurations. This paper considers both the ULA and UPA configurations, where the latter is modeled as a three-dimensional (3D) geometrical channel model. In what follows, we present the system geometries of the channel covariance matrix ${\mathbf{R}}_{\mathrm{h}}$ in the one ring and Laplacian scattering channel models with UPA and ULA, respectively. For the UPA, the BS antennas consist of $N=N_{\mathrm{A}}\times N_{\mathrm{E}}$ where each row has an $N_{\mathrm{A}}$ and each column has $N_{\mathrm{E}}$ antennas, where the subscript (A) denotes the azimuth direction and (E) stands for the elevation direction. Figure 2 shows a UPA based on the azimuth (horizontal) and elevation (vertical) directions. We consider a uniform distances between the neighboring antennas of the BS array, i.e., d is considered for both azimuth and elevation directions, i.e., $d_{\mathrm{A}},d_{\mathrm{E}}$, respectively. This implies that $d_{\mathrm{A}}=d_{\mathrm{E}}=d$. Parameters $\theta$ and $\varphi$ represent the azimuth and elevation angles, respectively, where $\theta$ and $\varphi$ $\in [0,\pi ]$. The angular spread in the azimuth and elevation directions are given by ${\alpha }_{\mathrm{A}}$ and ${\alpha }_{\mathrm{E}}$, respectively. The spatial covariance matrix in the UPA, denoted by ${\mathbf{R}}_{\mathrm{h}}$, can be well approximated using the Kronecker model as [22,58]

$${\mathbf{R}}_{\mathrm{h}}^{}={\mathbf{R}}_{\mathrm{h},\mathrm{A}}\otimes {\mathbf{R}}_{\mathrm{h},\mathrm{E}},$$

(46)

where ⊗ is the Kronecker operator and ${\mathbf{R}}_{\mathrm{h},\mathrm{A}}\in {\mathcal{C}}^{N_{\mathrm{A}}\times N_{\mathrm{A}}}$ and ${\mathbf{R}}_{\mathrm{h},\mathrm{E}}\in {\mathcal{C}}^{N_{\mathrm{E}}\times N_{\mathrm{E}}}$ are the covariance matrices in the azimuth and elevation directions, respectively. The channel covariance matrices in the azimuth and elevation directions are given in (47) and (48), respectively,

$${\left[{\mathbf{R}}_{\mathrm{h},\mathrm{A}}\right]}_{i,j}=\frac{1}{\sqrt{2}{\alpha }_{\mathrm{A}}}{\int }_{{\theta }_{}-\pi }^{{\theta }_{}+\pi }{e}^{-\frac{\sqrt{2}}{{\alpha }_{\mathrm{A}}}(x-{\theta }_{})}{e}^{\frac{-j2\pi d}{\lambda }(i-j)\sin \left(x\right)}\mathrm{d}x,$$

(47)

$${\left[{\mathbf{R}}_{\mathrm{h},\mathrm{E}}\right]}_{i,j}=\frac{1}{\sqrt{2}{\alpha }_{\mathrm{E}}}{\int }_{\varphi -\pi }^{\varphi +\pi }{e}^{-\frac{\sqrt{2}}{{\alpha }_{\mathrm{E}}}(x-\varphi )}{e}^{\frac{-j2\pi d}{\lambda }(i-j)\sin \left(x\right)}\mathrm{d}x,$$

(48)

where ${\theta }_{}$ is the angle of arrival of k-th user in the azimuth direction and ${\alpha }_{\mathrm{A}}$ denotes the angular spread in the azimuth direction. The angular spread in elevation direction, denoted by ${\alpha }_{\mathrm{E}}$, and the angle of arrival in elevation direction, denoted by $\varphi$, are given by (49) and (50), respectively [22]

$${\alpha }_{\mathrm{E}}=\frac{1}{2}\left(\arctan \left(\frac{D+s}{h}\right)-\arctan \left(\frac{D-s}{h}\right)\right),$$

(49)

$$\varphi =\frac{1}{2}\left(\arctan \left(\frac{D+s}{h}\right)+\arctan \left(\frac{D-s}{h}\right)\right),$$

(50)

where s denotes the radius of the scattering ring in meter and parameter D denotes the users distance from the BS and h represents the BS height. Note that the narrow angular spread in the azimuth direction provides a low-rank structure for the channel covariance matrix, which implies a strong spatial correlation.

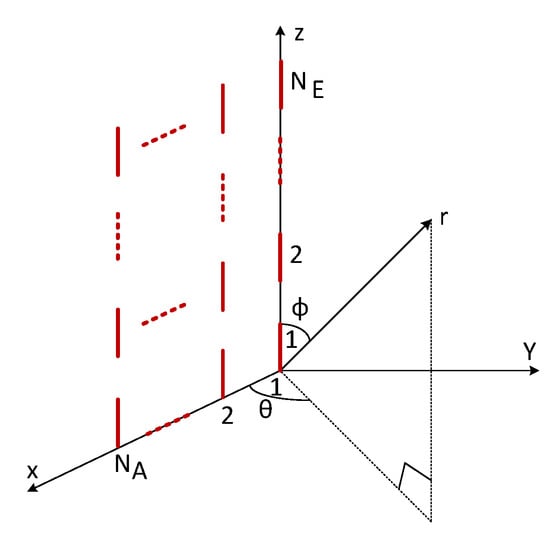
Figure 2. Illustration of a UPA with azimuth and elevation directions based on $x,y,z$ coordinates.

For the ULA, the spatial channel correlation ${\mathbf{R}}_{\mathrm{h}}$ can be modelled as [33]

$${\left[{\mathbf{R}}_{\mathrm{h}}\right]}_{i,j}=\frac{1}{2{\alpha }_A}{\int }_{{\theta }_{}-{\alpha }_A}^{{\theta }_{}+{\alpha }_A}{e}^{\frac{-j2\pi d}{\lambda }(i-j)\sin \left(x\right)}dx,$$

(51)

where ${\alpha }_{\mathrm{A}}$ denotes the angular spread in the azimuth direction. The following section presents several results that characterize the FDD performance in MaMi systems with RZFBF precoding in the ULA and UPA configurations.

7. Results and Findings

This section provides several simulation and theoretical results, which characterize the FDD performance in MaMi, based on the normalized MSE and the achievable sum rate of RZFBF precoding in the FDD MaMi systems. To this end, the performance of the proposed DTS and CSI estimation of FDD operation mode in MaMi systems with colored noise and limited coherence time is evaluated. The simulation parameters that are used in the FDD MaMi evaluation are provided in Table 1. We consider a dense urban scenario where the uses are located within the range of 200 m from the BS. The coherence block length is given as $\tau =100$ symbols and $K=8$ users. The one ring and Laplacian channel models parameters are selected with angular spread ${\alpha }_{\mathrm{A}}=\{5^{\circ },{15}^{\circ }\}$, which imply relatively high spatial channel correlation and weak spatial channel correlation, respectively. Parameter ${\sigma }_{\mathrm{d}}$ is given by ${\sigma }_{\mathrm{d}}=1/\mathrm{tr}\left({\mathbf{R}}_{\mathrm{n}}\right){\rho }_{\mathrm{d}}$, where ${\mathbf{R}}_{\mathrm{n}}$ denotes the colored noise covariance matrix, which is given in [59] as ${\left[{\mathbf{R}}_{\mathrm{n}}\right]}_{i,j}=p^{|j-i|}$ with $0\le p<1$. For relatively high correlated colored noise, we consider $p>0.9$. Each simulated point in our figures is obtained by averaging over ${10}^5$ independent simulation runs.

Table 1. Simulation parameters.

Parameters	Symbol	Value
Number of BS antennas	N	128
Number of users	K	8
Azimuth angular spread	${\alpha }_{\mathrm{A}}$	$\{5^{\circ },{15}^{\circ }\}$
Antenna element separation	$d_{\mathrm{A}}=d_{\mathrm{E}}=d$	$\lambda /2$
Coherence time	$T_{\mathrm{c}}$	1 ms
Coherence frequency	$B_{\mathrm{c}}$	100 kHz
Coherence block length	$\tau$	100 symbols
Training power	${\rho }_{\mathrm{s}}$	−20 dB–10 dB
BS height	h	30 m
Ring radius	s	30 m
Users distance	D	200 m
Azimuth angle	$\theta$	$\pi /6$
BS configurations	BS	{ULA, UPA}

In practice, the channel covariance matrix based on the one ring and Laplacian channel models will not have singular values that are exactly equal zero. As such, programs such as MATLAB might over estimate the effective rank of channel covariance matrix. To overcome this issue, this paper uses a threshold-based pilot selection criteria to provide a feasible DTS length with a reduced overhead for the FDD MaMi systems. In particular, only the effective eigenvalues of the transmit covariance matrix are selected, in order to reduce the overhead of the FDD MaMi systems. To this end, the effective eigenvalues of the transmit covariance matrix that are above a threshold of 0.001, which can be considered as approximately equal zero, are selected for the training transmission phase, while the rest of the eigenvalues are ignored and not used in the training transmission phase, and thus, not used in precoding design and data transmission phase. It is also worth noting that, orthogonal DTS and/or random DTS are ineffective with the FDD MaMi systems, because such sequences would span all the dimensional space. Specifically, the aforementioned sequences do not capture the dominant effective channel dimensions where the energy is concentrated, and thus wasting the resources in the training-phase, which will not be used for broadcasting useful information to the users.

Performance Evaluation of the Proposed DTS Design and CSI Estimation in the Presence of Colored Noise

In what follows, the performance of the proposed DTS design for the FDD MaMi systems is evaluated and compared with the conventional DTS designs, which are proposed based on idealistic assumption of white noise. The performance evaluation is carried out based on the normalized MSE and the achievable sum rate maximization.

The results in Figure 3 and Figure 4 show respectively plots of the normalized MSE and the achievable sum rate versus SNR using the one ring channel model, based on ULA BS with different levels of correlations, i.e., with an azimuth angular spread of ${\alpha }_{\mathrm{A}}=\{5^{\circ },{15}^{\circ }\}$. In particular, the results in Figure 3 and Figure 4 were obtained with $d=1/2$, ${\tau }_{}=100$ symbols, $N=128$ and $K=8$ users. The curves for the normalized MSE are plotted based on Equations (27) and (30), while the curves for the achievable sum rate are plotted based on Equations (4) and (45). The number of pilot sequence lengths are selected based on the threshold-based selection criteria, which is given as $T_{\mathrm{s}}=14$ and $T_{\mathrm{s}}=34$ for the one ring channel model with ${\alpha }_{\mathrm{A}}=5^{\circ }$ and ${\alpha }_{\mathrm{A}}={15}^{\circ }$, respectively.

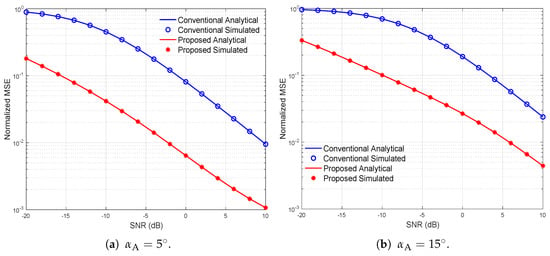
Figure 3. Normalized mean square error (MSE) versus signal-to-noise-ratio (SNR) using the one ring channel model based on uniform linear array (ULA) BS with different levels of correlations, i.e., with an azimuth angular spread of ${\alpha }_{\mathrm{A}}=\{5^{\circ },{15}^{\circ }\}$.

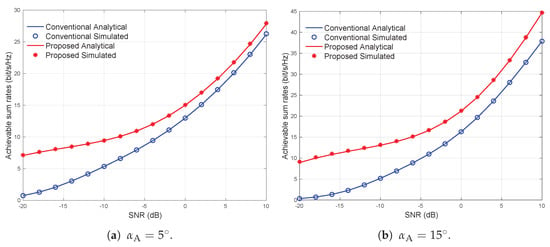
Figure 4. Achievable sum rate versus SNR using the one ring channel model based on ULA BS with different levels of correlations, i.e., with an azimuth angular spread of ${\alpha }_{\mathrm{A}}=\{5^{\circ },{15}^{\circ }\}$.

The results in Figure 3 show that the normalized MSE with proposed DTS design is decreased significantly with increasing the spatial correlation. i.e., with ${\alpha }_{\mathrm{A}}=5^{\circ }$. This indicates that increasing the spatial correlation would reduce the power requirement to achieve the same MSE. In particular, increasing the spatial correlation would allow the power to be focused into the most relevant eigendirections, and thus, these eigendirections become easy to be estimated. In addition, the results demonstrate that the proposed DTS design with colored noise achieves a significant improvement in the MSE performance in comparison to the conventional design with white noise.

Figure 4 demonstrates that remarkable improvement in the achievable sum rate performances are achieved for different level of correlations. Specifically, the results show that in order to obtain a rate of 10 bits/s/Hz with relatively high spatial correction, the proposed DTS design achieves a 5 dB gain compared with the conventional designs with white noise. In addition, the results demonstrate that this gain is increased to almost 10 dB in with relatively low spatial correction in comparison to the conventional designs.

The results show that the gab between the proposed DTS design and the conventional designs is reduced. This can be justified due to the fact that as the SNR increases, the mutual interference is increased, and thus, the ability of RZFBF precoding to mitigate the users interference is reduced. Nonetheless, the proposed DTS design achieves a noticeable gain of approximately 2 dB in comparison to the conventional designs.

Figure 5 and Figure 6 examine respectively the normalized MSE and the achievable sum rate versus SNR using the Laplacian channel model based on UPA BS with different levels of correlations, i.e., with an azimuth angular spread of ${\alpha }_{\mathrm{A}}=\{5^{\circ },{15}^{\circ }\}$. The number of pilot sequence lengths are selected based on the threshold-based selection criteria, which is given as $T_{\mathrm{s}}=15$ and $T_{\mathrm{s}}=24$ for the Laplacian channel model with ${\alpha }_{\mathrm{A}}=5^{\circ }$ and ${\alpha }_{\mathrm{A}}={15}^{\circ }$, respectively. The other salient system parameters remain unchanged.

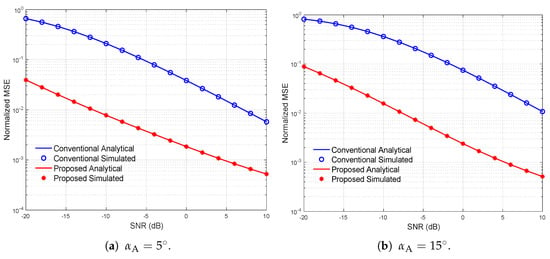
Figure 5. Normalized MSE versus SNR using the Laplacian channel model based on uniform planar array (UPA) BS with different levels of correlations, i.e., with an azimuth angular spread of ${\alpha }_{\mathrm{A}}=\{5^{\circ },{15}^{\circ }\}$.

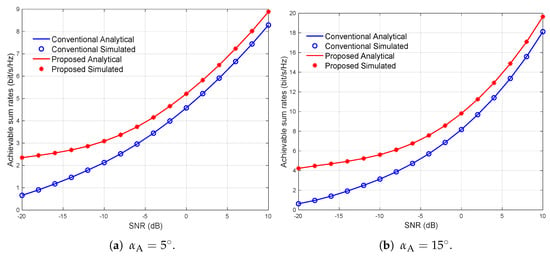
Figure 6. Achievable sum rate versus SNR using the Laplacian channel model based on UPA BS with different levels of correlations, i.e., with an azimuth angular spread of ${\alpha }_{\mathrm{A}}=\{5^{\circ },{15}^{\circ }\}$.

The results show that using the Laplacian channel model with a UPA, the MSE of the proposed DTS design with colored noise is significantly reduced compared with the conventional training designs with white noise. Further, the results demonstrate that using the proposed training design, a noticeable improvement in the DL achievable sum rate is achieved in comparison to the conventional training designs. In particular, the results indicate that in order to obtain a rate of 4 bits/s/Hz, the proposed design achieves a again of 3 dB and 12 dB over the conventional designs with ${\alpha }_{\mathrm{A}}=5^{\circ }$ and ${\alpha }_{\mathrm{A}}={15}^{\circ }$, respectively.

Overall, the results presented in this paper indicate that a feasible DTS for the FDD MaMi systems with colored noise and limited coherence time can be achieved without increasing in the system overhead and design complexity. The findings of this paper are underpinned by accurate analyses, which tightly agree with the simulated results. These analyses support the contributions of this work.

8. Conclusions

This paper has addressed the problem of DTS design and CSI estimation of the FDD MaMi systems in the presence of colored noise environments. To this end, a feasible DTS has been proposed, which is constructed from the effective unitary eigenvectors of channel covariance and noise covariance matrices. In addition, an analytical solution for the MSE based on the MMSE channel estimation was provided. Furthermore, a random matrix theory method was used to obtain an explicit analytical solution for the achievable sum rate of the RZFBF precoder with low-complexity. The MSE and the sum rate performances of the proposed DTS design were compared with the conventional DTS designs based on white noise. The results showed that the porpoised DTS design provides a significant gain in the CSI estimation performance, and thus, the sum rate of FDD operation in MaMi systems is considerably improved in comparison to the conventional designs. The results also demonstrated accurate matching between the theoretical and simulated results, which underpin the main contributions of this paper. The proposed DTS design would allow the FDD to operate with MaMi systems in more realistic scenarios, particularly with limited coherence time and colored noise environments.