Improving the Characteristics of Multi-Level LUT-Based Mealy FSMs

Abstract

Contemporary digital systems include many varying sequential blocks. In the article, we discuss a case when Mealy finite state machines (FSMs) describe the behavior of sequential blocks. In many cases, the performance is the most important characteristic of an FSM circuit. In the article, we propose a method which allows increasing the operating frequency of multi-level look-up table (LUT)-based Mealy FSMs. The main idea of the proposed approach is to use together two methods of structural decomposition. They are: (1) the known method of transformation of codes of collections of outputs into FSM state codes and (2) a new method of extension of state codes. The proposed approach allows producing FPGA-based FSMs having three levels of logic combined through the system of regular interconnections. Each function for every level of logic was implemented using a single LUT. An example of the synthesis of Mealy FSM with the proposed architecture is shown. The effectiveness of the proposed method was confirmed by the results of experimental studies based on standard benchmark FSMs. The research results show that FSM circuits based on the proposed approach have a higher operating frequency than can be obtained using other investigated methods. The maximum operating frequency is improved by an average of 3.18 to 12.57 percent. These improvements are accompanied by a small growth of LUT count.

1. Introduction

Digital systems are widely used in our daily life [1]. They can be viewed as combinations of various sequential and combinational blocks [2,3]. To implement the circuit of a sequential block, it is necessary to formally describe its behavior. Very often, models of finite state machines (FSMs) [4,5] are used for this purpose. The quality of an FSM circuit is determined by a combination of such characteristics as: a chip area occupied by the circuit, maximum operating frequency and consumption of power. As follows from [6], there is a direct relationship between these circuit characteristics. To reduce the occupied chip area, various methods of structural decomposition can be applied [7]. These methods produce circuits with multiple levels of logic, which are significantly slower than their single-level counterparts.

However, very often the performance is a critical factor for a digital system. For example, it is true for real-time embedded systems [8,9]. If a multi-level circuit does not provide the required performance, then the number of levels should be decreased. This conversion must be performed in a way that increases the amount of resources used as little as possible. In this paper, we propose a method for the solution of this problem in the case in which circuits of Mealy FSMs are implemented using field programmable gate arrays (FPGAs).

There are two models of FSMs, namely, Mealy and Moore FSMs [4,5]. Problems related to the synthesis of FSM circuits are discussed in a huge number of scientific articles and books. These works are mainly devoted to the synthesis and design of Mealy automata. This determined our choice of Mealy FSMs in the current research.

To optimize the characteristics of FSM circuits, a designer should use the main features of context in which these circuits are implemented [2,10]. In this article we consider methods of implementing FSM circuits in the context of field programmable gate arrays [11,12,13]. These chips are very popular devices used for implementations of digital systems [2,14,15,16,17,18]. This fact explains our choice of FPGA-based Mealy FSMs as a research object. The current article deals with FSM circuits, which are implemented using look-up table (LUT) elements, flip-flops and programmable interconnections of FPGAs. Since the Xilinx is the largest manufacturer of FPGA chips [13], we focus our research on its solutions.

A LUT is a single-output block having $S_L$ inputs [19,20]. If a Boolean function depends on up to $S_L$ Boolean variables, then its logic circuit includes only one LUT. However, a LUT has a very small number of inputs [11,13]. At the same time, FSMs can be represented by very complex systems of Boolean functions (SBFs) having dozens of arguments [4]. For LUT-based FSMs, this contradiction leads to the necessity of functional decomposition of initial SBFs [21]. In turn, the functional decomposition gives rise to FSM circuits having many logic levels and very complex interconnections [22,23].

To implement a LUT-based FSM circuit, it is necessary to execute the step of technology mapping [24,25,26,27]. The technology mapping is a very important stage of the FPGA-based design process [28]. Its outcome significantly determines the characteristics of a resulting FSM circuit.

As a rule, LUT-based circuits of sequential blocks use five components of FPGA fabric. These components include LUTs, synced memory elements (flip-flops), programmable interconnections, synchronization circuits and blocks of input–output. Our current article is devoted to synthesis of multi-level LUT-based circuits of Mealy FSMs obtained using the methods of structural decomposition. As follows from [24,29], it is very important to optimize the system of interconnections between different elements of a circuit. The article [24] notes that time delays of the interconnection system are starting to play a major role in comparison with logic delays. Additionally, more than 70% of the power dissipation is due to the interconnections [29]. Thus, the optimization of interconnections leads to improving main characteristics of LUT-based FSM circuits. This can be done, for example, using an encoding of collections of outputs.

The main goal of our article is to increase the operating frequency of LUT-based Mealy FSM circuits. To achieve this goal, we try to reduce the number of levels of LUTs between the FSM inputs and FSM outputs. We determine the number of levels of LUTs as the number of LUT elements connected in series in the longest path connecting FSM inputs with FSM outputs. Reducing the number of levels reduces the number of interconnections in the FSM circuit [24]. Since interconnections significantly affect performance [29], a simultaneous decrease in the number of levels of LUTs and the number of interconnections leads to a significant increase in frequency.

Research [19,20] has shown that there is no point in increasing the number of LUT inputs. If the number of inputs exceeds six, it violates the balance between the main characteristics of a LUT circuit. However, the increasing complexity of modern digital systems is accompanied by an increase in the number of arguments in representing FSM functions. Therefore, there is a need for new methods and improvements to existing methods of LUT-based FSM design.

The methods of structural decomposition [7] are designed to reduce the numbers of LUTs in FSM circuits. As a rule, FSM circuits with three levels of logic blocks require the smallest numbers of LUTs. However, three-level FSMs have a much lower operating frequency compared to their single-level counterparts. FSM circuits with two levels of logic blocks represent a compromise on the number of LUTs and operating frequency. The main contribution of this paper is a novel design method aimed at increasing the operating frequency of two-level LUT-based Mealy FSMs. The main idea of the proposed approach is to use together two methods of structural decomposition. They are: (1) the known method of transformation of codes of collections of outputs into FSM state codes and (2) a new method of extension of state codes. Due to it, there are exactly three levels of LUTs in the part of FSM circuit implementing the system of outputs. Additionally, it produces FSM circuits having regular system of interconnections, where each level of logic has its unique systems of inputs and outputs. The proposed method allows obtaining FSM circuits that have slightly more LUTs and a higher operating frequency than their three-level counterparts [30]. The experimental results presented in the article show that the advantage of the proposed approach increases as the number of FSM inputs increases.

The further text of the article includes five sections. Section 2 presents the background of single-level LUT-based Mealy FSMs. Section 3 discusses the methods currently used in design of FPGA-based FSMs. The main idea of our method is considered in Section 4. In Section 5, we discuss an example synthesis, and the main ways for improving the characteristics of the resulting FSM circuit. In Section 6, we present the results of research on the effectiveness of the proposed method for benchmarks FSMs from [31]. The article ends with a brief summary.

2. Single-Level LUT-Based Mealy FSMs

As follows from [13], FPGAs manufactured by Xilinx are based on “island-style” architecture [19,20]. The configurable logic blocks (CLBs) are “islands” surrounded by a “sea” of programmable interconnections that form a general routing matrix [13]. In this paper, we discuss a case of CLBs including LUTs and programmable flip-flops. The flip-flops are used to organize hidden distributed registers keeping FSM state codes [2]. A LUT-based CLB includes a LUT, a flip-flop and a multiplexer (Figure 1).

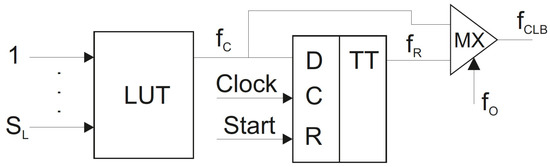
Figure 1. Architecture of a look-up table (LUT)-based configurable logic block (CLB).

A LUT can implement a function $f_c$ dependent on up to $S_L$ arguments. A LUT is a combinational block. Thus, the value of $f_c$ could be changed by changing the values of arguments. Using the pulse of synchronization clock, the current value of $f_c$ is written into the D flip-flop. The output of flip-flop represents a registered function $f_R$. The multiplexer $MX$ selects an appropriate form of CLB’s output. The output $f_{CLB}$ is either combinational ($f_0=0$) or registered ($f_0=1$).

An FSM circuit is represented by some SBF. For practical digital systems, an SBF can include around 50–70 literals [3,4]. However, a LUT has not more than six inputs. This limitation makes it necessary to transform SBFs representing FSM circuits. The transformation is executed using different methods of functional decomposition (FD) [32]. The FD-based transformation leads to FSM circuits with many levels of LUT-based CLBs and systems of unordered (irregular) interconnections. The functional decomposition leads to CLB-based circuits having “spaghetti-type” interconnections [33].

A Mealy FSM is represented as a six-component vector $S=<X,Y,A,\delta ,\lambda ,a_1>$ [34]. The vector S includes a set of inputs $X=\{x_1,\dots ,x_L\}$, a set of outputs $Y=\{y_1,\dots ,y_N\}$, a set of internal states $A=\{a_1,\dots ,a_M\}$, a function of transitions $\delta$, a function of output $\lambda$ and an initial state $a_1\in A$. Various tools can be applied to represent the vector S. The most commonly used tools are: graph-schemes of algorithms [3,34], binary decision diagrams [35,36], state transition graphs [4] and inverter graphs [37]. In this article, we use state transition tables (STTs) to represent Mealy FSMs.

An STT includes the following columns [4]: a current state $a_m$; a state of transition (a next state) $a_s$; an input signal $X_h$ (it determines a transition from $a_m$ to $a_s$); a collection of outputs $Y_h$ (it is generated during the transition from the current state into the next state). The column h includes the numbers of transitions ($h\in \{1,\dots ,H\}$). For example, a Mealy FSM $S_0$ is represented by the STT (Table 1).

Table 1. The state transition table (STT) of Mealy FSM $S_0$.

${\mathit{a}}_{\mathit{m}}$	${\mathit{a}}_{\mathit{s}}$	${\mathit{X}}_{\mathit{h}}$	${\mathit{Y}}_{\mathit{h}}$	h
$a_1$	$a_2$	$x_1$	$y_1$	1
	$a_3$	$\overline{x_1}$	$y_2{y}_3$	2
$a_2$	$a_3$	$x_2$	$y_4$	3
	$a_1$	$\overline{x_2}$	$y_2$	4
$a_3$	$a_1$	1	–	5

As follows from Table 1, the FSM $S_0$ has two inputs, four outputs, three states and five transitions. From Table 1 we can find, for example, that $\delta (a_1,x_1)=a_2$ and $\lambda (a_1,x_1)=y_1$ (these formulae follow from the first row of Table 1). The following steps should be executed to construct SBFs describing logic circuits of FSMs [3,34]: (1) the encoding of FSM states $a_m\in A$ by binary codes $K\left(a_m\right)$; (2) the constructing sets of state variables $T=\{T_1,\dots ,T_R\}$ and input memory functions (IMFs) $\mathsf{\Phi }=\{D_1,\dots ,D_R\}$; and (3) constructing a direct structure table (DST). To encode the states $a_m\in A$, the step of state assignment should be executed [2].

In this paper, we use the style of binary state assignment where the number state variables (R) is determined as

$$R=\lceil lo{g}_{2}M\rceil .$$

(1)

The binary state assignment is used, for example, in the system SIS [38]. The number of bits of the state code can vary from the minimum value determined by (1) to the number of states, M. If $R=M$, then the corresponding state codes are one-hot codes. This style is used, for example, by the academic system ABC [37] of Berkeley.

A special state register ($RG$) keeps FSM state codes. It is controlled by two internal pulses. The pulse start causes the loading of the initial state code into the $RG$. The pulse clock sets the time when the $RG$ can be changed. For CLB-based FSMs, state registers are constructed on the basis of D flip-flops [2]. In this article, we also use state registers based on D flip-flops. The pulse clock allows the functions $D_r\in \mathsf{\Phi }$ to change the $RG$ content.

After the state assignment, each state $a_m\in A$ is represented by its code $K\left(a_m\right)$. The Boolean systems representing an FSM circuit can be derived from a DST. Compared to the initial STT, a DST includes three additional columns: $K\left(a_m\right)$, $K\left(a_s\right)$ and ${\mathsf{\Phi }}_h$. The column ${\mathsf{\Phi }}_h$ includes the symbols $D_r\in \mathsf{\Phi }$ corresponding to 1s in the code of the state $a_s$ from the row h of a DST. A DST is a base for finding the following SBFs:

$$\mathsf{\Phi }=\mathsf{\Phi }(T,X);$$

(2)

$$Y=Y(T,X).$$

(3)

The architecture of a Mealy FSM $U_1$ is defined by these systems of Boolean functions (SBFs). It is shown in Figure 2.

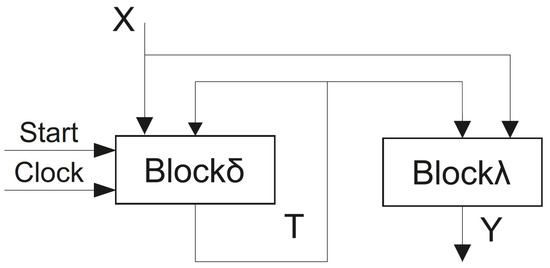
Figure 2. Architecture of LUT-based Mealy FSM $U_1$.

Let us analyze this architecture. The SBF (2) is implemented by $Block\delta$. This block includes the distributed register. The $RG$ is controlled by IMFs (2) and mutual pulses of synchronization and reset. The SBF (3) is implemented using $Block\lambda$. Both blocks are implemented with CLBs (Figure 1).

Analysis of systems $\mathsf{\Phi }$ and Y shows that they depend on the same variables. It is the main peculiarity of Mealy FSMs. Many design methods [7,39] use this specific to reduce the numbers of LUTs in circuits represented by SBFs (2) and (3).

3. State-Of-The-Art

As a rule, the process of designing digital systems involves solving some optimization problems [2,4]. In the case of FPGA-based sequential blocks, these problems are the following [2,24]: (1) the reduction of chip resources required to implement a LUT-based circuit; (2) the decreasing the propagation time (the increasing the maximum operating frequency); and (3) the reducing power consumption. Our current article is devoted to improving the maximum operating frequency of LUT-based Mealy FSMs.

The characteristics of FPGA-based FSM circuits can be improved due to optimal state assignment [2,8,37,38,39,40,41,42]. Additionally, this can be done using embedded memory blocks (EMBs) instead of LUT-based CLBs [43,44,45,46,47,48,49,50]. Let us analyze these approaches.

We call optimal state codes such codes that allow reducing the numbers of arguments in SBFs (2) and (3). For example, the numbers of arguments is significantly reduced by the algorithm JEDI [38]. It is one of the best state assignments algorithms [2]. Due to it, we chose JEDI-based FSMs to compare with FSMs based on our proposed approach.

Modern industrial CAD tools include various state assignment strategies. For example, the following state assignment methods are used in the Xilinx design tool Vivado [40]: automatic state assignment (auto); sequential encoding; the one-hot; Gray encoding and Johnson codes. The same methods can be found in the package XST by Xilinx [51].

The one-hot state assignment is very popular in LUT-based design [41], because FPGAs include many programmable flip-flops. The one-hot state assignment leads to increasing the number of input memory functions compared with (1). However, these IMFs are much simpler than in the case of binary state assignment [2]. As follows from [41], it is better to use the one-hot codes if an FSM has more than 16 states. However, the characteristics of LUT-based FSM circuits significantly depend on the number of inputs [2]. As follows from [42], the binary state encoding allows producing better FSM circuits if $L\ge 10$. Since each approach is good under certain conditions, we compare both of these encoding styles with our proposed method. The method of binary state assignment auto of Vivado is used as a baseline for comparison with the proposed method.

To reduce the power consumption, it is very important to diminish the number of interconnections inside an FSM circuit. Therefore, to diminish the number of interconnections, it is necessary to minimize the numbers of arguments in SBFs (2) and (3) [2]. Thus, it is always useful to apply the optimal state assignment to improve the characteristics of FSM circuits.

The second approach to optimizing CLB-based FSMs is related to using EMBs instead of LUTs [47]. There are many design methods targeting EMB-based FSMs [47,48,49,52,53,54,55,56,57].The survey of different methods of EMB-based design can be found in [47]. In the best case, only a single EMB is necessary to implement an FSM circuit [49]. However, if the number of arguments in systems (2) and (3) exceeds the maximum possible number of EMB address inputs, then an FSM is represented by a network of EMBs. To diminish the number of EMBs in such a network, it is necessary to implement some functions using LUTs [2,49].

Thus, an FSM circuit can be implemented as either a network of EMBs, or a network of LUTs, or a joint network of LUTs and EMBs. In this article, we discuss the second case, when FSM circuits are implemented using LUT-based CLBs. This approach makes sense if: (1) all EMBs are used to implement other parts of a digital system or (2) the number of arguments in SBFs (2) and (3) exceeds 15 (this is a maximum possible number of modern EMBs [11,12,13]).

Denote as $NL\left(f_i\right)$ the number of literals [4] in sum-of-products (SOPs) of functions (2) and (3). If the condition

$$NL\left(f_i\right)\le S_L(i\in \{1,\dots ,N+R\})$$

(4)

takes place, then a logic circuit for any function $f_i\in \mathsf{\Phi }\cup Y$ is represented by exactly one LUT. If $NL\left(f_i\right)>S_L$, then the corresponding logic circuit can be obtained using various methods of FD [21,23,27,35,36,48,58,59]. The FD can be viewed as a process during which decomposed functions are broken down into smaller and smaller components. If any component depends on no more than $S_L$ arguments, the process of FD for a given function is completed. Of course, this results in multi-level LUT-based circuits. For these circuits, it is typical that the same inputs $x_l\in X$ or state variables appear on several logic levels. It significantly complicates the system of interconnection between LUTs of FD-based FSM circuits (with all the ensuing consequences).

In the best case, the LUT count of an FSM circuit is equal to the total number of inputs and state variables. However, if the condition (4) is violated, the LUT count increases by the value of $\left|\mathsf{\Psi }\right|$, where $\mathsf{\Psi }$ is a set of additional functions different from (2) and (3). These additional functions are components of functions (2) and (3) produced during the process of FD. We do not discuss these methods in our article.

The reducing LUT counts in circuits of Mealy FSMs can be achieved using the various methods of structural decomposition [7,39]. These methods eliminate a direct dependence of functions $y_n\in Y$ and $D_r\in \mathsf{\Phi }$ on inputs $x_l\in X$. The methods of structural decomposition are also connected with introducing new functions $f_i\in \mathsf{\Psi }$. Functions $f_i\in \mathsf{\Psi }$ depend on variables $x_l\in X$ and $T_r\in T$. The structural decomposition allows reducing LUT counts if there is

$$\left|\mathsf{\Psi }\right|\ll N+R.$$

(5)

These new functions are divided into subsystems having unique input and output variables. Each subsystem determines a separate LUT-based block of logic. When the condition (5) takes place, the total LUT count for a decomposed FSM is significantly less than it is for equivalent FSM $U_1$. The new functions are arguments of functions (2) and (3). If the condition

$$\left|\mathsf{\Psi }\right|\ll L+R$$

(6)

takes place, then the total LUT count of a decomposed FSM circuit is significantly less than it is for an equivalent multi-level circuit . A survey of different methods of structural decomposition is represented in [7].

In this article, we discuss three known methods of structural decomposition [7,34]: replacement of inputs, encoding of outputs and transformation of codes of collections of outputs into state codes. Consider these approaches.

To reduce the LUT count, the inputs $x_l\in X$ could be replaced by additional variables $p_g\in P=\{p_1,\dots ,p_G\}$, where $G\ll L$ [34]. As a rule, the value of G is determined as [34]:

$$G=max\left(\right|X\left(a_1\right)|,\dots ,|X\left(a_M\right)\left|\right).$$

(7)

The system of additional variables $p_g\in P$ is represented by the SBF

$$P=P(T,X).$$

(8)

The functions $f_i\in \mathsf{\Phi }\cup Y$ are represented by the following SBFs:

$$\mathsf{\Phi }=\mathsf{\Phi }(T,P);$$

(9)

$$Y=Y(T,P).$$

(10)

Collections of outputs (COs) $Y_q\subseteq Y(q\in \{1,\dots ,Q\})$ include functions $y_n\in Y$ generated simultaneously. To synthesize an FSM circuit, it is necessary to represent each CO $Y_q\subseteq Y$ by a binary code $K\left(Y_q\right)$. As a rule, the number of bits in these codes is determined as

$$R_Q=\lceil lo{g}_{2}Q\rceil .$$

(11)

To create codes $K\left(Y_q\right)$, it is necessary to use additional variables $z_r\in Z=\{z_1,\dots ,z_{R_Q}\}$. This allows representing outputs of FSM as the following:

$$Y=Y\left(Z\right).$$

(12)

The additional variables $z_r\in Z$ are represented by the following system:

$$Z=Z(T,X).$$

(13)

To generate functions (13), an additional block of logic should be used.

In the work [30], two known methods of structural decomposition are used for reducing LUT count for FPGA-based Mealy FSMs. It results in Mealy FSM $U_2$ shown in Figure 3.

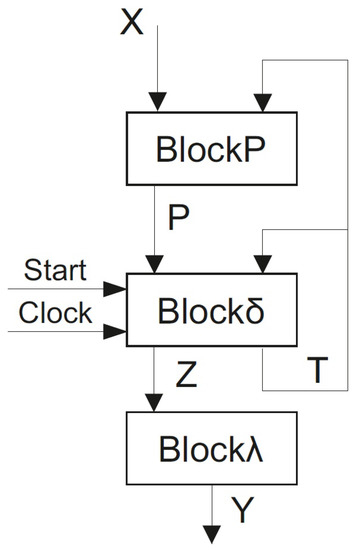
Figure 3. Architecture of Mealy FSM $U_2$.

The logic circuit of Mealy FSM $U_2$ has three logic levels. The $BlockP$ executes the replacement of inputs $x_l\in X$ by additional variables $p_g\in P=\{p_1,\dots ,p_G\}$ and implements the SBF (8). The $Block\delta$ generates input memory functions (9) and additional variables $z_r\in Z$ used for encoding of collections of outputs $Y_q\subseteq Y(q\in \{1,\dots ,Q\})$. This block includes a distributed register keeping state codes. To generate variables $z_r\in Z$, it is necessary to implement the system

$$Z=Z(T,P).$$

(14)

$Block\lambda$ implements the system (12) dependent on additional variables $z_r\in Z$.

As our investigations [30] show, this approach allows significantly reducing the LUT count as compared to equivalent FSM $U_1$. However, this solution has a serious drawback: the performance of FSM $U_2$ is always less than it is for an equivalent Mealy FSM $U_1$.

In [36], different models of Mealy FSMs based on transformation of object codes are discussed. One of the typical methods from this group is a transformation of codes $K\left(Y_q\right)$ into state codes $K\left(a_m\right)$.

The main idea of this approach is the following. For example, some CO $Y_3$ is generated during transitions into states $a_4$ and $a_6$. Using CO $Y_3$, it is possible to determine these states. To do it, it is necessary to use identifiers $I_1$ and $I_2$. Using two pairs $<collectionofoutputs,identifier>$ allows the following representation of these states of transition: $a_4\to <Y_3,I_1>$ and $a_6\to <Y_3,I_2>$. Thus, each state $a_m\in A$ can be represented by one or more pairs $<Y_q,I_{np}>$. To create the set of identifiers $SI=\{I_1,\dots ,I_{NP}\}$, it is necessary to find the maximum amount of pairs ($NP$) including the same CO $Y_q\subseteq Y$.

Each identifier $I_{np}\in I$ is represented by a binary code $K\left(I_{np}\right)$ having $R_I$ bits, where

$$R_I=\lceil lo{g}_{2}NP\rceil .$$

(15)

To encode identifiers, the elements of the set $V=\{v_1,\dots ,v_{RI}\}$ are used.

It allows representing the IMFs by the following system:

$$\mathsf{\Phi }=\mathsf{\Phi }(Z,V).$$

(16)

The variables $v_r\in V$ are represented by the following system:

$$V=V(T,X).$$

(17)

Thus, an FSM based on this principle implements systems (12), (13), (16) and (17). It is an FSM $U_3$ shown in Figure 4.

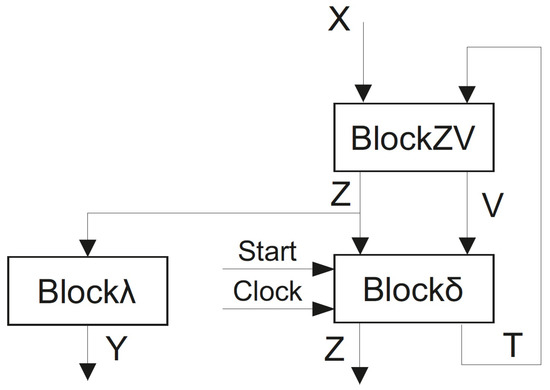
Figure 4. Architecture of Mealy FSM $U_3$.

In FSM $U_3$, the $BlockZV$ implements systems (13) and (17); the $Block\delta$ implements input memory functions represented as (16); the $Block\lambda$ implements the system (12). Thus, there are only two levels of logic between inputs and outputs in the case of FSM $U_3$. As follows from Figure 3, there are three levels of logic between inputs and outputs in the case of FSM $U_2$.

This property of FSM $U_3$ can be used for acceleration of a digital system. As is known [2], outputs (3) of Mealy FSM are not stable. If inputs are changing during a clock cycle, the outputs (3) may also change. This may cause the digital system as a whole to crash. To prevent failures, it is necessary to prohibit the access of incorrect outputs (3) to a digital system. To do it, a special register $SRG$ is introduced (Figure 5).

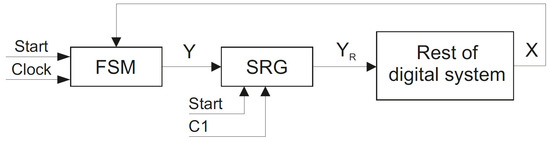
Figure 5. Interaction of FSM with the rest of a digital system.

If all transients in the FSM circuit are completed and the values of outputs are stable, then a pulse of synchronization $C1$ is generated. It allows loading outputs $y_n\in Y$ into $SRG$. Next, the registered outputs $y_n\in Y_R$ enter the digital system. The system executes the corresponding operations and generates the values of inputs $x_l\in X$. Such an interaction should be organized for any model of Mealy FSM.

Thus, in the case of FSM $U_3$, the pulse $C1$ may be generated when the correct values are set for the outputs of two blocks ($BlockZV$ and $Block\lambda$). In the case of FSM $U_2$, the correct outputs are set after all three blocks are triggered sequentially. Thus, the model $U_3$ can provide better performance than the model $U_2$.

There is one very serious disadvantage of FSM $U_3$ compared to equivalent FSM $U_2$. If the relation

$$G<R_I+R_Q$$

(18)

is true, then the number of LUTs (and maybe their levels) in $BlockZV$ is significantly more than in $BlockP$ of equivalent FSM $U_2$. In this article, we propose a method which allows reducing the number of LUTs in FSM $U_3$.

4. Main Idea of the Proposed Method

In this article, we discuss a case when the condition (4) is violated for some functions $f_i\in Z\cup V$. It leads to a multi-level circuit of $BlockZV$ with an irregular system of interconnections. Obviously, it degenerates the performance of FSM $U_3$. To diminish the number of levels of LUTs in the circuit of $BlockZV$, we propose the following approach.

As it is in the case of two-fold state assignment [7,60], we propose to construct a partition $\mathsf{\Pi }=\{A^1,\dots ,A^J\}$ of the set A such that the following condition takes place:

$$R_j+L_j\le S_L(j\in \{1,\dots ,J\}).$$

(19)

Using methods [7,60] allows creating the required partition ${\mathsf{\Pi }}_A$ having the minimum possible number of classes, J.

If a class $A^j\in {\mathsf{\Pi }}_A$ includes $M_j$ states $a_m\in A$,

$$R_j=\lceil lo{g}_2(M_j+1)\rceil$$

(20)

then there are enough state variables to encode the states $a_m\in A^j$. To do it, the state variables $T_r\in T^j\subseteq T$ are used. There are $R_o$ elements in the sets T and $\mathsf{\Phi }$:

$$R_o=\sum _{j=1}^J{R}_j.$$

(21)

If $a_m\notin A^j$, then $T_r=0$ for $T_r\in T^j$. It explains the presence of 1 in (20).

Now, we can encode each state $a_m\in A^j$ by a code $C\left(a_m\right)$ having $R_o$ bits. In this code, $R_o-R_j$ variables are equal to zero. Only variables $T_r\in T^j$ identify a state $a_m\in A$ as an element of $A^j\in {\mathsf{\Pi }}_A$.

As $R_o>R$, the codes $C\left(a_m\right)$ are extended state codes [7]. However, only $R_j<R$ state variables are used to represent functions dependent on states $a_m\in A^j$.

To find SBFs (13) and (17), it is necessary to construct a table of $BlockZV$ ($TZV$). It includes the columns $a_m$, $C\left(a_m\right)$, $a_s$, $Y_q$, $I_{np}$, $X_h$, $K\left(Y_q\right)$, $K\left(I_{np}\right)$, $Z_h$, $V_h$ and h.

A class $A_j\in {\mathsf{\Pi }}_A$ determines a table $TZ{V}_j$ which is a subtable of $TZV$. A table $TZ{V}_j$ determines sets $X^j\subseteq X$, $Z^j\subseteq Z$ and $V^j\subseteq V$. These variables are written in the columns $X_h$, $Z_h$ and $V_h$ of $TZ{V}_j$, respectively. Additionally, a table $TZ{V}_j$ determines SBFs

$$Z^j=Z^j(T^j,X^j);$$

(22)

$$V^j=V^j(T^j,X^j).$$

(23)

Using this preliminary information, we propose an architecture of Mealy FSM $U_4$ (Figure 6).

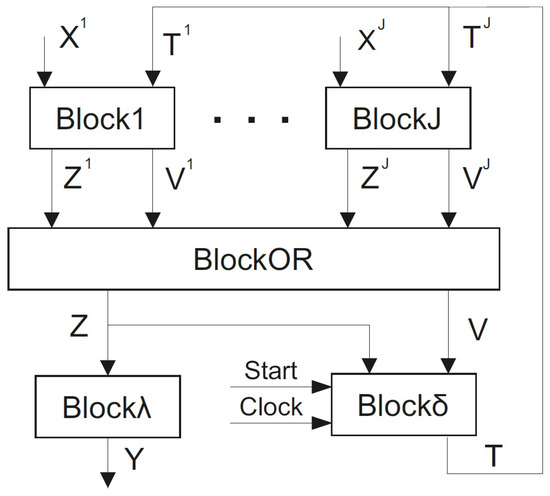
Figure 6. Architecture of Mealy FSM $U_4$.

In FSM $U_4$, the $Blockj$ implements functions (22) and (23). Due to (19), each $Blockj$ has only a single level of LUTs.

$BlockOR$ implements functions $z_r\in Z$ and $v_r\in V$ as disjunctions:

$$z_r=z_r^1\vee z_r^2\vee \dots \vee z_r^j;$$

(24)

$$v_r=v_r^1\vee v_r^2\vee \dots \vee v_r^j.$$

(25)

In (24) and (25), the superscript j means that the corresponding function is generated by the $Blockj$.

If $J\le S_L$, then there is only a single level of LUTs in the circuit of $BlockOR$. Otherwise, it is a multi-level block.

$Block\lambda$ and $Block\delta$ execute the same functions as these blocks in FSM $U_3$. The $Block\lambda$ generates functions (12), the $Block\delta$ the functions (16). If $R_Q\le S_L$, then $Block\lambda$ includes only a single level of LUTs.

Thus, in the best case, there are three levels of LUTs between inputs $x_l\in X$ and outputs $y_n\in Y$. If the condition (4) is violated for equivalent FSM $U_3$, then the FSM $U_4$ provides higher operating frequency.

Comparison of Figure 4 and Figure 6 shows that: (1) $BlockZV$ of $U_3$ is replaced by Block1, …, $BlockJ$, $BlockOR$ and (2) $Block\delta$ of $U_4$ has $R_o>R$ outputs. These two issues are the main specifics of FSM $U_4$.

In this paper, we propose a method of synthesis of finite state machine $U_4$. If an FSM is represented by an STT, then the method includes the following steps:

• Representing states $a_m\in A$ by pairs $P(m,q)$.
• Encoding of collections of outputs and identifiers. Constructing SBF (12) representing $Block\lambda$.
• Constructing the partition ${\mathsf{\Pi }}_A$ of the set A.
• Creating tables $TZ{V}_j$ determining Block1–$BlockJ$.
• Constructing SBFs representing $Block1$–$BlockJ$.
• Constructing SBFs (24) and (25) representing $BlockOR$.
• Constructing SBF (16) representing $Block\delta$.
• Implementing the logic circuit of FSM $U_4$.

The first step is executed using an initial STT. If CO $Y_q\subseteq Y$ is generated during transitions into $m_q$ different states $a_s\in A$, then there are $m_q$ identifiers. Each identifier determines an unique state represented by $Y_q\subseteq Y$. The cardinality of the set $SI$ is determined as

$$NP=max(m_1,\dots ,m_Q).$$

(26)

Step 2 is executed on the basis of STT. The COs should be encoded in a way optimizing the number of literals in SBF (12). Identifiers can be encoded in the trivial way.

The partition ${\mathsf{\Pi }}_A$ is constructed using methods from [7,43]. After finding classes $A^j\in {\mathsf{\Pi }}_A$, we can encode the states $a_m\in A^j$. It gives sets $T^j\subseteq T=\{T_1,\dots ,T_{R_0}\}$ and $\mathsf{\Phi }=\{D_1,\dots ,D_{R_0}\}$.

A table of $Blockj$ has the following columns: $a_m$, $C\left(a_m\right)$, $X_h^j$, $Z_h^j$, $V_h^j$, h. The states $a_m\in A^j$ are written in the column $a_m$. As $T_r=0$ if $T_r\in T^j$, we can write only parts of $C\left(a_m\right)$ created from state variables $T_r\in T^j$. A column $Z_h^j$ includes variables $z_h^j\in Z^j$, a column $V_h^j$ variables $v_h^j\in V^j$. The outcome of step 4 is tables of Block1–BlockJ.

A table $TZ{V}_j$ is a base to derive the SBFs (24) and (25). The terms of corresponding SOPs are conjunctions $A_m·X_h$, where $A_m$ is a conjunction of variables $T_r\in T^j$. All other state variables are treated as insignificant. The SBF (24) and (25) are used to implement circuits of Block1–BlockJ.

The step 6 is executed in the trivial way. If $J\le S_L$, then there is a single level of LUTs in BlockOR. In this case, its circuit includes exactly $R_Q+R_I$ LUTs.

To find the SBF (16), it is necessary to construct a table of $Block\delta$. This table includes the following columns: $Y_q$, $K\left(Y_q\right)$, $I_{n}p$, $K\left(I_{np}\right)$, $a_s$, $C\left(a_s\right)$, ${\mathsf{\Phi }}_h$, h. Each row of this table corresponds to a pair $<Y_q,I_{np}>$ determining the state $a_s\in A$. The terms of SOPs (16) are conjunctions of variables $z_r\in Z$ and $v_r\in V$. The corresponding literals are determined by codes $K\left(Y_q\right)$ and $K\left(I_{np}\right)$.

The last step is executed using standard CAD tools. It is based on program tools translating initial STT into required SBFs. These SBFs are used into VHDL models of FSMs.

Now, we would like to show the difference between the two-fold state assignment [60] and the proposed method. In the first case, there are two sets of state variables. The set $T=\{T_1,\dots T_R\}$ is used to encode states $a_m\in A$ as elements of set A. The set $\tau =\{{\tau }_1,\dots ,{\tau }_{R_0}\}$ is used to encode states $a_m\in A^j$ as elements of sets $A^j(j=\overline{1,J})$. Due to it, there are two levels of logic creating inputs of the Block1–BlockJ. In the proposed approach, the inputs of these block are generated by $Block\delta$. Thus, the proposed approach leads to faster FSMs than for the two-fold state assignment.

5. Example of Synthesis

In this article, we use a symbol $U_i\left(S_j\right)$ to show that an FSM model $U_i$ is used to synthesize an FSM $S_j$. An example of synthesis of Mealy FSM $U_4\left(S_1\right)$ is shown in this section. A Mealy FSM $S_1$ is represented by Table 2.

Table 2. STT of Mealy FSM $S_1$.

${\mathit{a}}_{\mathit{m}}$	${\mathit{a}}_{\mathit{s}}$	${\mathit{X}}_{\mathit{h}}$	${\mathit{Y}}_{\mathit{h}}$	h
$a_1$	$a_2$	$x_1$	$y_1{y}_2$	1
	$a_3$	$\overline{x_1}{x}_2$	$y_3$	2
	$a_4$	$\overline{x_1}\overline{x_2}$	$y_2{y}_4$	3
$a_2$	$a_2$	$x_3{x}_4$	$y_3$	4
	$a_3$	$x_3\overline{x_4}$	$y_5{y}_6$	5
	$a_5$	$\overline{x_3}$	$y_5{y}_7$	6
$a_3$	$a_4$	$x_5$	$y_5{y}_6$	7
	$a_5$	$\overline{x_5}{x}_1$	$y_3{y}_8$	8
	$a_6$	$\overline{x_5}\overline{x_1}$	$y_1{y}_2$	9
$a_4$	$a_3$	$x_6{x}_3$	$y_3$	10
	$a_5$	$x_6\overline{x_3}$	$y_2{y}_4$	11
	$a_2$	$\overline{x_6}$	$y_1{y}_2$	12
$a_5$	$a_6$	1	$y_1{y}_2$	13
$a_6$	$a_1$	$x_5$	–	14
	$a_3$	$\overline{x_5}$	$y_3{y}_8$	15

The following characteristics of $S_1$ follow from Table 2: the number of states $M=6$, the number of transitions $H=15$, the number of inputs $L=6$ and the number of outputs $N=8$. Additionally, the following collections of outputs can be found from Table 2: $Y_1=\varnothing$, $Y_2=\{y_1,y_2\}$, $Y_3=\left\{y_3\right\}$, $Y_4=\{y_2,y_4\}$, $Y_5=\{y_5,y_6\}$, $Y_6=\{y_5,y_7\}$, $Y_7=\{y_3,y_8\}$. Thus, there is $Q=7$.

1. Representing states by pairs $P(m,q)$.

Using STT (Table 2), it is possible to find pairs $<Y_q,I_{np}>$ representing the states $a_m\in A$. For example, the CO $Y_2$ is written in the rows 1, 9, 12 and 13. Additionally, these rows include the states of transitions $a_2$ (rows 1 and 12) and $a_6$ (rows 9 and 13). Thus, it is necessary two identifiers ($I_1$, $I_2$) to distinguish these states: $a_2\to <Y_2,I_1>$, $a_6\to <Y_2,I_2>$.

Using the same approach, we can find all pairs $<Y_q,I_{np}>$ for the given example. The process is shown in Figure 7. Using (26) gives $NP=2$ and $I=\{I_1,I_2\}$.

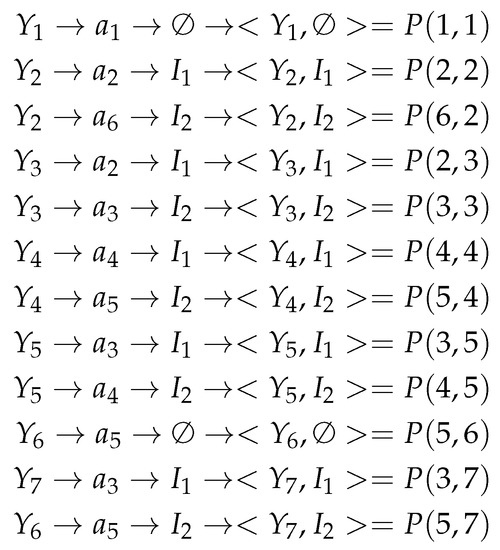
Figure 7. Representation of states by pairs $P(m,q)$.

In the discussed case, there is $H_P=12$, where $H_P$ is a number of pairs $P(m,q)$. Thus, the $Block\delta$ will be represented by the table having 12 rows.

2. Encoding of COs $Y_q\subseteq Y$ and identifiers $I_{np}\in SI$. There is $Q=7$, $NP=2$. Using (11) gives $R_Q=3$ and the set $Z=\{z_1,z_2,z_3\}$. Using (15) gives $R_I=1$ and the set $V=\left\{v_1\right\}$.

There is $R_Q+R_I=4<S_L$. Therefore, each equation from SBF (16) is implemented using only a single look-up table. Thus, there is no need in encoding of COs in a way optimizing (16). Let us encode COs $Y_q\subseteq Y$ in a way optimizing the SBF (12).

Using contents of COs, the following SBF can be obtained:

$$\begin{array}{cc}& y_1=Y_2;y_2=Y_2\vee Y_4;y_3=Y_3\vee Y_7;\\ & y_4=Y_4;y_5=Y_5\vee Y_6;y_6=Y_5;y_7=Y_6;y_8=Y_7.\end{array}$$

(27)

To diminish the number of interconnections between $BlockOR$ and $Block\delta$, it is necessary to reduce the number of literals in functions (12). It can be done using approach [61]. One of the possible solutions is shown in Figure 8.

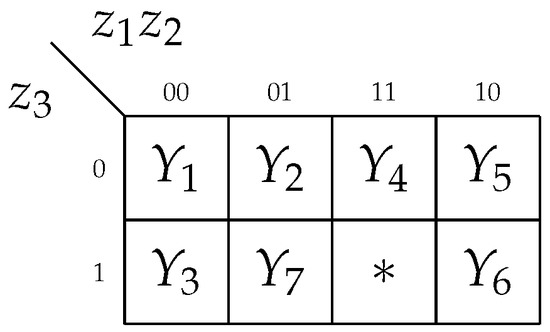
Figure 8. Outcome of encoding of collections of outputs (COs).

Using codes from Figure 8 and rules of minimization [4], we can transform the SBF (27) into the following system:

$$\begin{array}{cc}& y_1=\overline{z_1}{z}_2\overline{z_3};y_2=z_2{z}_3;y_3=\overline{z_1}{z}_3;\\ & y_4=z_1{z}_2;y_5=z_1\overline{z_2};y_6=z_1\overline{z_2}\overline{z_3};\\ & y_7=z_1{z}_3;y_8=z_2{z}_3.\end{array}$$

(28)

The system (28) represents $Block\lambda$ of $U_4\left(S_1\right)$. This block has 18 interconnections with $BlockOR$. In the common case, there are $N·R_Q=8\times 3=24$ literals (and 24 interconnections). Thus, the number of interconnections is reduced by 1.33 times thanks to encoding of COs shown in Figure 8.

The identifiers can be encoded in a trivial way: $K\left(I_1\right)=0$ and $K\left(I_2\right)=1$. Now, the identifier $I_1$ is determined by $\overline{v_1}$, and $I_2$ by $v_1$.

3. Constructing the partition of the set A. There is $S_L=5$ in the discussed example. It means that each block $A^j\in {\mathsf{\Pi }}_A$ should satisfy the condition $L_j+R_j\le 5$.

This step is very important because it determines significantly the characteristics of FSM $U_4$ [60]. We do not discuss this step in detail. Instead, we use the approach [60] to create the partition ${\mathsf{\Pi }}_A=\{A^1,A^2\}$ with classes $A^1=\{a_1,a_3,a_6\}$ and $A^2=\{a_2,a_4,a_5\}$. Using Table 2 gives the sets $X^1=\{x_1,x_2,x_5\}$ and $X^2=\{x_3,x_4,x_6\}$.

Using (20) gives $R_1=R_2=2$, $R_o=4$, $T=\{T_1,\dots ,T_4\}$, $T^1=\{T_1,T_2\}$ and $T^2=\{T_3,T_4\}$. There is $L_1=L_2=3$. It means that $L_1+R_1=L_2+R_2=5=S_L$. Thus, the found partition satisfies the condition (19).

Due to it, state codes $C\left(a_m\right)$ do not affect the number of look-up tables in circuits of Block1 and Block2. We can encode them in the following way: $C\left(a_1\right)=0100$, $C\left(a_2\right)=0001$, $C\left(a_3\right)=1000$, $C\left(a_4\right)=0010$, $C\left(a_5\right)=0011$ and $C\left(a_6\right)=1100$.

4. Creating tables of Block1 and Block2. To do it, we should construct a table of $BlockZV$ of equivalent FSM $U_3\left(S_1\right)$. Next, this table is divided by two tables using classes $A^j\in {\mathsf{\Pi }}_A$ and codes $C\left(a_m\right)$.

Table of $BlockZV$ is constructed using an initial STT. To do it, the states of transitions are replaced by corresponding pairs $P(m,q)$. Additionally, the codes $K\left(Y_q\right)$, $K\left(I_p\right)$ and columns $Z_h$, $V_h$ are introduced instead of the column $Y_h$ of STT. In the discussed example, the $BlockZV$ is represented by Table 3.

Table 3. Table of $BlockZV$ of Mealy FSM $U_3\left(S_1\right)$.

${\mathit{a}}_{\mathit{m}}$	$\mathit{C}\left({\mathit{a}}_{\mathit{m}}\right)$	${\mathit{a}}_{\mathit{s}}$	${\mathit{Y}}_{\mathit{q}}$	${\mathit{I}}_{\mathit{np}}$	${\mathit{X}}_{\mathit{h}}$	$\mathit{K}\left({\mathit{Y}}_{\mathit{q}}\right)$	$\mathit{K}\left({\mathit{I}}_{\mathit{np}}\right)$	${\mathit{Z}}_{\mathit{h}}$	${\mathit{V}}_{\mathit{h}}$	h
$a_1$	0100	$a_2$	$Y_2$	$I_1$	$x_1$	010	0	$z_2$	–	1
		$a_3$	$Y_3$	$I_2$	$\overline{x_1}{x}_2$	001	1	$z_3$	$v_1$	2
		$a_4$	$Y_4$	$I_1$	$\overline{x_1}\overline{x_2}$	110	0	$z_1{z}_2$	–	3
$a_2$	0001	$a_2$	$Y_3$	$I_1$	$x_3{x}_4$	001	0	$z_3$	–	4
		$a_3$	$Y_5$	$I_1$	$x_3\overline{x_4}$	100	0	$z_1$	–	5
		$a_5$	$Y_6$	–	$\overline{x_3}$	101	–	$z_1{z}_3$	–	6
$a_3$	1000	$a_4$	$Y_5$	$I_2$	$x_5$	100	1	$z_1$	$v_1$	7
		$a_5$	$Y_7$	$I_2$	$\overline{x_5}{x}_1$	011	1	$z_2{z}_3$	$v_1$	8
		$a_6$	$Y_2$	$I_2$	$\overline{x_5}\overline{x_1}$	010	1	$z_2$	$v_1$	9
$a_4$	0010	$a_3$	$Y_3$	$I_2$	$x_6{x}_3$	001	1	$z_3$	$v_1$	10
		$a_5$	$Y_4$	$I_2$	$x_6\overline{x_3}$	110	1	$z_1{z}_2$	$v_1$	11
		$a_2$	$Y_2$	$I_1$	$\overline{x_6}$	010	0	$z_2$	–	12
$a_5$	0011	$a_6$	$Y_2$	$I_2$	1	010	1	$z_2$	$v_1$	13
$a_6$	1100	$a_1$	$Y_1$	–	$x_5$	000	–	–	–	14
		$a_3$	$Y_7$	$I_1$	$\overline{x_5}$	011	0	$z_2{z}_3$	–	15

In Table 3, we used codes $K\left(Y_q\right)$ from Figure 8. The pairs <$Y_q,I_{np}$> were taken from Figure 7. To design circuits of Block1–BlockJ, Table 3 should be transformed into a set of tables representing blocks of the first level of logic.

Consider the row $h=1$ of Table 3. It corresponds the pair $P(2,2)$. Thus, the column $Y_q$ includes $Y_2$ and the column $I_{np}$ includes $I_1$. The column $K\left(Y_q\right)$ includes $K\left(Y_2\right)=010$, the column $K\left(I_{np}\right)$ the code $K\left(I_1\right)=0$. It explains the contents of columns $Z_h$ and $V_h$ of the row 1. The column $X_h$ is the same as for initial STT (Table 2). All other rows are filled in the same way.

To create tables of a Blockj, we should: (1) choose state $a_m\in A^j$ and (2) take rows of table of BlockZV for these states. In this case, the Block1 is represented by Table 4 and the Block2 by Table 5. In Table 4 and Table 5 the superscripts 1 and 2 mean that corresponding functions are implemented by Block1 or Block2, respectively.

Table 4. Table of Block1 of Mealy FSM $U_4\left(S_1\right)$.

${\mathit{a}}_{\mathit{m}}$	$\mathit{C}\left({\mathit{a}}_{\mathit{m}}\right)$	${\mathit{X}}_{\mathit{h}}^{\mathbf{1}}$	${\mathit{Z}}_{\mathit{h}}^{\mathbf{1}}$	${\mathit{V}}_{\mathit{h}}^{\mathbf{1}}$	h
$a_1$	01	$x_1$	$z_2^1$	–	1
		$\overline{x_1}{x}_2$	$z_3^1$	$v_1^1$	2
		$\overline{x_1}\overline{x_2}$	$z_1^1$$z_2^1$	–	3
$a_3$	10	$x_5$	$z_1^1$	$v_1^1$	4
		$\overline{x_5}{x}_1$	$z_2^1$$z_3^1$	$v_1^1$	5
		$\overline{x_5}\overline{x_1}$	$z_2^1$	$v_1^1$	6
$a_6$	11	$x_5$	–	–	7
		$\overline{x_5}$	$z_2^1$$z_3^1$	–	8

Table 5. Table of Block2 of Mealy FSM $U_4\left(S_1\right)$.

${\mathit{a}}_{\mathit{m}}$	$\mathit{C}\left({\mathit{a}}_{\mathit{m}}\right)$	${\mathit{X}}_{\mathit{h}}^{\mathbf{1}}$	${\mathit{Z}}_{\mathit{h}}^{\mathbf{1}}$	${\mathit{V}}_{\mathit{h}}^{\mathbf{1}}$	h
$a_2$	01	$x_3{x}_4$	$z_1^2$	–	1
		$x_3\overline{x_4}$	$z_3^2$	–	2
		$\overline{x_3}$	$z_1^2$$z_3^2$	–	3
$a_4$	10	$x_6{x}_3$	$z_3^2$	$v_1^2$	4
		$x_6\overline{x_3}$	$z_1^2$$z_2^2$	$v_1^2$	5
		$\overline{x_6}$	$z_2^2$	–	6
$a_5$	11	1	$z_2^2$	$v_1^2$	7

5. Constructing systems representing blocks of the first level. These systems are constructed using Table 4 and Table 5. Each system includes $R_Q+R_I=4$ equations.

The Block1 is represented by the following SBF:

$$\begin{array}{cc}& z_1^1=T_1\overline{T_2}{x}_5;\\ & z_2^1=\overline{T_1}{T}_2{x}_1\vee \overline{T_1}{T}_2\overline{x_2}\vee T_1\overline{x_5};\\ & z_3^1=\overline{T_1}{T}_2\overline{x_1}{x}_2\vee T_1\overline{T_2}\overline{x_5}{x}_1\vee T_1{T}_2\overline{x_5};\\ & v_1^1=\overline{T_1}{T}_2\overline{x_1}{x}_2\vee T_1\overline{T_2}.\end{array}$$

(29)

The Block2 is represented by the following SBF:

$$\begin{array}{cc}& z_1^2=\overline{T_3}{T}_4{x}_4\vee \overline{T_3}{T}_4\overline{x_3}\vee T_3\overline{T_4}{x}_6\overline{x_3};\\ & z_2^2=T_3\overline{T_4}\overline{x_3}\vee T_3\overline{T_4}\overline{x_6}\vee T_3{T}_4;\\ & z_3^2=\overline{T_3}{T}_4\overline{x_4}\vee \overline{T_3}{T}_4\overline{x_3}\vee T_3\overline{T_4}{x}_6{x}_3;\\ & v_1^2=T_3\overline{T_4}{x}_6\vee T_3{T}_4.\end{array}$$

(30)

6. Constructing the system for BlockOR. This system is constructed in a trivial way. Each function $f_i\in Z\cup V$ is represented by a disjunction of functions of the same name with different upper indexes. It is the following SBF in the discussed case:

$$\begin{array}{cc}& z_1=z_1^1\vee z_1^2;z_2=z_2^1\vee z_2^2;\\ & z_3=z_3^1\vee z_3^2;v_1=v_1^1\vee v_1^2.\end{array}$$

(31)

7. Constructing the system for $Block\delta$. To find the system (16), it is necessary to create a table of $Block\delta$. It is constructed using pairs $P(m,q)$ and codes $K\left(Y_q\right)$, $K\left(I_{np}\right)$ and $C\left(a_s\right)$. In the discussed case, this is Table 6. The table uses data from Figure 7 and Figure 8. The following SBF is derived from Table 6:

$$\begin{array}{cc}& D_1=\overline{z_1}{z}_2\overline{z_3}{v}_1\vee \overline{z_1}\overline{z_2}{z}_3{v}_1\vee z_1\overline{z_2}\overline{z_3}\overline{v_1}\vee \overline{z_1}{z}_2{z}_3\overline{v_1};\\ & D_2=\overline{z_1}\overline{z_2}\overline{z_3}\vee \overline{z_1}{z}_2\overline{z_3}{v}_1;\\ & D_3=z_1{z}_2\overline{z_3}\vee z_1\overline{z_2}\overline{z_3}{v}_1\vee z_1\overline{z_2}{z}_3\vee \overline{z_1}{z}_2{z}_3{v}_1;\\ & D_4=\overline{z_1}{z}_2\overline{z_3}\overline{v_1}\vee \overline{z_1}\overline{z_2}{z}_3\overline{v_1}\vee z_1{z}_2\overline{z_3}{v}_1\vee z_1\overline{z_2}{z}_3\vee \overline{z_1}{z}_2{z}_3{v}_1.\end{array}$$

(32)

Table 6. Table of $Block\delta$ of Mealy FSM $U_4\left(S_1\right)$.

${\mathit{Y}}_{\mathit{q}}$	$\mathit{K}\left({\mathit{Y}}_{\mathit{q}}\right)$	${\mathit{I}}_{\mathit{np}}$	$\mathit{K}\left({\mathit{I}}_{\mathit{np}}\right)$	${\mathit{a}}_{\mathit{s}}$	$\mathit{C}\left({\mathit{a}}_{\mathit{s}}\right)$	${\mathsf{\Phi }}_{\mathit{h}}$	h
$Y_1$	000	–	–	$a_1$	0100	$D_2$	1
$Y_2$	010	$I_1$	0	$a_2$	0001	$D_4$	2
		$I_2$	1	$a_6$	1100	$D_1{D}_2$	3
$Y_3$	001	$I_1$	0	$a_2$	0001	$D_4$	4
		$I_2$	1	$a_3$	1000	$D_1$	5
$Y_4$	110	$I_1$	0	$a_4$	0010	$D_3$	6
		$I_2$	1	$a_5$	0011	$D_3{D}_4$	7
$Y_5$	100	$I_1$	0	$a_3$	1000	$D_1$	8
		$I_2$	1	$a_4$	0010	$D_3$	9
$Y_6$	101	–	–	$a_5$	0011	$D_3{D}_4$	10
$Y_7$	011	$I_1$	0	$a_3$	1000	$D_1$	11
		$I_2$	1	$a_5$	0011	$D_3{D}_4$	12

Now, we have systems for each block of FSM $U_4\left(S_1\right)$. Next step is the implementation of the logic circuit.

8. Implementing the logic circuit of FSM $U_4\left(S_1\right)$. This step is executed using special synthesis tools, e.g., Quartus Prime [50] or Vivado by Xilinx [40]. During this step, each LUT is represented by its truth table. Such complicated tasks are executed as mapping, placement and routing [6]. We just focus on finding the number of LUTs in the circuit and do not discuss this step for our example.

The Block1 is represented by the SBF (29). The corresponding circuit includes four LUTs. The Block2 is represented by the SBF (30). Its circuit also includes four LUTs. Thus, the first level of logic includes eight LUTs having $S_L=5$.

The BlockOR is represented by the SBF (31). To implement its circuit, it is enough to have four LUTs. $Block\lambda$ is represented by the SBF (28). Its circuit consist of 8 LUTs. At last, the system (32) represents $Block\delta$. Its circuit has four LUTs.

Thus, the circuit of FSM $U_4\left(S_1\right)$ includes 24 LUTs. There are three levels of LUTs between inputs $x_l\in X$ and outputs $y_n\in Y$. The same is true for inputs and input memory functions $D_r\in \mathsf{\Phi }$.

This example is very simple. We show it to explain all steps of the proposed method. The next Section shows results of experiments with more complex FSMs.

6. Experimental Results

In this section we show the results of experiments based on benchmark FSMs from the library [31]. There are 48 benchmarks in the library. They are very often used to compare outcomes of different design methods. The benchmark Mealy FSMs are represented in the format KISS2. We do not show the characteristics of these benchmarks in this article. They can be found, for example, in [30].

To implement FPGA-based FSM, we used VHDL-based FSM models. Our CAD tool K2F [2] translated the benchmarks into VHDL-based FSM models. The synthesis and simulation of FSMs were executed by the Active-HDL environment. As a target platform, we used Xilinx VC709 Evaluation Board (Virtex 7, XC7VX690T-2FFG1761C) [62]. This chip includes LUTs having $S_L=6$. To execute the technology mapping and produce reports with characteristics of resulting FSM circuits, we used Xilinx CAD tool Vivado—version 2019.1 [40].

When we investigated FSM $U_2$ [30], we found that this model allows producing circuits with less area and power consumption if $R+L>S_L$. In [30], we divided the benchmarks into five groups using the values of $L+R$ and $S_L$. If $L+R\le 6$, then benchmarks belong to group 0 (trivial FSMs); if $L+R\le 12$, then to group 1 (simple FSMs); if $L+R\le 18$, then to group 2 (average FSMs); if $L+R\le 24$, then to group 3 (big FSMs); otherwise, they belong to group 4 (very big FSMs). As our research [30] shows, the larger the group number, the bigger the gain from using our method. We use the same division of benchmarks in this article too.

Group 0 includes the following benchmarks: bbtas, dk17, dk27, dk512, ex3, ex5, lion, lion9, mc, modulo12 and shiftreg. Group 1 contains the most benchmarks. They are the following: bbara, bbsse, beecount, cse, dk14, dk15, dk16, donfile, ex2, ex4, ex6, ex7, keyb, mark1, opus, s27, s386, s840 and sse. Group 2 consists of the following 12 benchmarks: ex1, kirkman, planet, planet1, pma, s1, s1488, s1494, s1a, s208, styr and tma. There is only a single benchmark: sand in Group 3. Group 4 includes the following benchmarks: s420, s510, s820 and s832.

In the section State-of-the-art, we have justified the choice of three methods for comparison with our approach. We chose the method auto of Vivado as a method based on binary state codes. Additionally, we used the method one-hot of Vivado. Due to its high reputation, we chose JEDI-based FSMs as a basis for comparison too. Our approach is a competitor to the method from work [30]. Thus, we chose $U_2$-based FSMs with three levels of logic blocks as the fourth method used in experiments. The results of experiments are shown in Table 7 (the number of LUTs) and Table 8 (the maximum operating frequency). These results were taken from reports generated by Vivado.

Table 7. Results of experiments (LUT count).

Benchmark	Auto	One-Hot	JEDI	${\mathit{U}}_{\mathbf{2}}$	Our Approach	Group
bbara	17	17	10	10	14	1
bbsse	33	37	24	26	29	1
bbtas	5	5	5	8	9	0
beecount	19	19	14	14	16	1
cse	40	66	36	33	35	1
dk14	16	27	10	12	14	1
dk15	15	16	12	8	11	1
dk16	15	34	12	11	13	1
dk17	5	12	5	8	10	0
dk27	3	5	4	7	9	0
dk512	10	10	9	12	14	0
donfile	31	31	24	21	24	1
ex1	70	74	53	40	44	2
ex2	9	9	8	8	10	1
ex3	9	9	9	11	14	0
ex4	15	13	12	11	13	1
ex5	9	9	9	10	12	0
ex6	24	36	22	21	23	1
ex7	4	5	4	6	8	1
keyb	43	61	40	37	40	1
kirkman	42	58	39	33	35	2
lion	2	5	2	6	8	0
lion9	6	11	5	8	10	0
mark1	23	23	20	19	21	1
mc	4	7	4	6	8	0
modulo12	7	7	7	9	11	0
opus	28	28	22	21	23	1
planet	131	131	88	78	82	2
planet1	131	131	88	78	82	2
pma	94	94	86	72	76	2
s1	65	99	61	54	58	2
s1488	124	131	108	89	93	2
s1494	126	132	110	90	94	2
s1a	49	81	43	38	42	2
s208	12	31	10	9	11	2
s27	6	18	6	6	8	1
s386	26	39	22	20	22	1
s420	10	31	9	8	10	4
s510	48	48	32	22	23	4
s8	9	9	9	9	11	1
s820	88	82	68	52	56	4
s832	80	79	62	50	52	4
sand	132	132	114	99	103	3
shiftreg	2	6	2	4	6	0
sse	33	37	30	26	29	1
styr	93	120	81	70	78	2
tma	45	39	39	30	34	2
Total	1808	2104	1489	1320	1448
Percentage,%	124.86	145.30	102.83	91.16	100

Table 8. Results of experiments (the operating frequency, MHz).

Benchmark	Auto	One-Hot	JEDI	${\mathit{U}}_{\mathbf{2}}$	Our Approach	Group
bbara	193.39	193.39	212.21	183.32	210.21	1
bbsse	157.06	169.12	182.34	159.24	193.43	1
bbtas	204.16	204.16	206.12	194.43	201.47	0
beecount	166.61	166.61	187.32	156.72	194.47	1
cse	146.43	163.64	178.12	153.24	182.62	1
dk14	191.64	172.65	193.85	162.78	201.39	1
dk15	192.53	185.36	194.87	175.42	206.74	1
dk16	169.72	174.79	197.13	164.16	199.14	1
dk17	199.28	167.00	199.39	147.22	172.99	0
dk27	206.02	201.9	204.18	181.73	190.32	0
dk512	196.27	196.27	199.75	175.63	187.45	0
donfile	184.03	184	203.65	174.28	206.83	1
ex1	150.94	139.76	176.87	164.32	180.72	2
ex2	198.57	198.57	200.14	188.95	196.58	1
ex3	194.86	194.86	195.76	174.44	187.26	0
ex4	180.96	177.71	192.83	168.39	196.18	1
ex5	180.25	180.25	181.16	162.56	162.56	0
ex6	169.57	163.8	176.59	156.42	187.53	1
ex7	200.04	200.84	200.6	191.43	204.16	1
keyb	156.45	143.47	168.43	136.49	178.59	1
kirkman	141.38	154.00	156.68	155.36	184.62	2
lion	202.43	204.00	202.35	185.74	195.73	0
lion9	205.3	185.22	206.38	167.28	183.45	0
mark1	162.39	162.39	176.18	153.48	182.37	1
mc	196.66	195.47	196.87	178.02	182.95	0
modulo12	207.00	207.00	207.13	189.7	201.74	0
opus	166.2	166.2	178.32	157.42	186.34	1
planet	132.71	132.71	187.14	174.68	212.45	2
planet1	132.71	132.71	187.14	173.29	212.45	2
pma	146.18	146.18	169.83	156.12	192.43	2
s1	146.41	135.85	157.16	145.32	145.32	2
s1488	138.5	131.94	157.18	141.27	182.14	2
s1494	149.39	145.75	164.34	155.63	186.49	2
s1a	153.37	176.4	169.17	166.36	188.92	2
s208	174.34	176.46	178.76	166.42	192.15	2
s27	198.73	191.5	199.13	185.15	201.26	1
s386	168.15	173.46	179.15	164.65	192.34	1
s420	173.88	176.46	177.25	186.35	218.62	4
s510	177.65	177.65	198.32	199.05	221.19	4
s8	180.02	178.95	181.23	168.32	191.32	1
s820	152.00	153.16	176.58	175.69	195.73	4
s832	145.71	153.23	173.78	174.39	199.18	4
sand	115.97	115.97	126.82	120.07	143.14	3
shiftreg	262.67	263.57	276.26	248.79	253.72	0
sse	157.06	169.12	174.63	158.14	171.18	1
styr	137.61	129.92	145.64	118.02	164.52	2
tma	163.88	147.8	164.14	137.48	182.72	2
Total	8127.08	8061.22	8718.87	7873.36	9005.11
Percentage,%	90.25	89.52	96.82	87.43	100

We use the same organization of Table 7 and Table 8. Their rows are marked by the names of benchmarks, the columns by investigated design methods. The row “Total” includes results of summation for corresponding values. The summarized characteristics of our approach ($U_4$-based FSMs) were taken as 100%. The row “Percentage” shows the percentages of summarized characteristics of FSM circuits implemented by other methods, respectively, compared to benchmarks based on our approach. Let us point out that the model $U_1$ was used for designs with auto, one-hot, and JEDI.

As follows from Table 7, the $U_2$-based FSMs require fewer LUTs than other investigated methods. Our approach produces circuits having 8.84% more LUTs than equivalent $U_2$-based FSMs. However, our approach requires fewer LUTs than auto (24.86% of gain), one-hot (45.3% of gain) and JEDI-based FSMs (2.83% of gain). The higher is the group, the greater is the gain in LUTs respectively auto, one-hot and JEDI-based FSMs. We show these results in Figure 9.

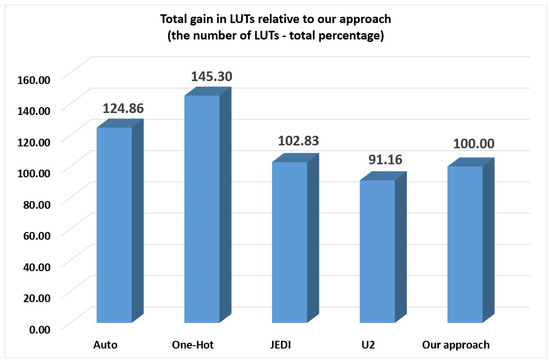
Figure 9. Total gain in LUTs relative to our approach (LUT count—total percentage).

Analysis of Table 8 shows that the $U_4$-based FSMs have the highest operating frequency of the investigated methods. Our method gives us a 9.85% advantage over the auto. The one-hot of Vivado loses 10.48% to our approach. The $U_4$-based FSMs provide a 3.18% gain compared to JEDI-based FSMs. At last, the $U_2$-based FSMs have an average frequency of 12.57% less than it is for FSM based on our approach. These results are shown in Figure 10.

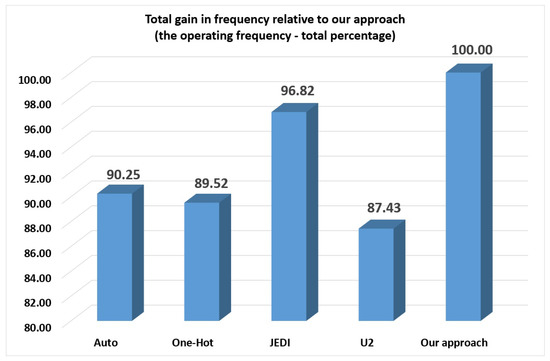
Figure 10. Total gain in frequency relative to our approach (the operating frequency—total percentage).

To clarify how the gain in LUTs depends on the FSM group, we have created Table 9 (gain in LUTs for group 0), Table 10 (gain in LUTs for group 1) and Table 11 (gain in LUTs for groups 2–4). Additionally, we present these results by graphs on Figure 11, Figure 12 and Figure 13, respectively. To clarify how the gain in frequency depends on the FSM group, we have created Table 12 (gain in frequency for group 0), Table 13 (gain in frequency for group 1) and Table 14 (gain in frequency for groups 2–4). Additionally, we present these results by graphs on Figure 14, Figure 15 and Figure 16, respectively.

Table 9. Gain in LUTs for group 0 (LUT count).

Benchmark	Auto	One-Hot	JEDI	${\mathit{U}}_{\mathbf{2}}$	Our Approach	Group
bbtas	5	5	5	8	9	0
dk17	5	12	5	8	10	0
dk27	3	5	4	7	9	0
dk512	10	10	9	12	14	0
ex3	9	9	9	11	14	0
ex5	9	9	9	10	12	0
lion	2	5	2	6	8	0
lion9	6	11	5	8	10	0
mc	4	7	4	6	8	0
modulo12	7	7	7	9	11	0
shiftreg	2	6	2	4	6	0
Total	62	86	61	89	111
Percentage,%	55.86	77.48	54.59	80.18	100

Table 10. Gain in LUTs for group 1 (LUT count).

Benchmark	Auto	One-Hot	JEDI	${\mathit{U}}_{\mathbf{2}}$	Our Approach	Group
bbara	17	17	10	10	14	1
bbsse	33	37	24	26	29	1
beecount	19	19	14	14	16	1
cse	40	66	36	33	35	1
dk14	16	27	10	12	14	1
dk15	15	16	12	8	11	1
dk16	15	34	12	11	13	1
donfile	31	31	24	21	24	1
ex2	9	9	8	8	10	1
ex4	15	13	12	11	13	1
ex6	24	36	22	21	23	1
ex7	4	5	4	6	8	1
keyb	43	61	40	37	40	1
mark1	23	23	20	19	21	1
opus	28	28	22	21	23	1
s27	6	18	6	6	8	1
s386	26	39	22	20	22	1
s8 40	9	9	9	9	11	1
sse	33	37	30	26	29	1
Total	406	525	337	319	364
Percentage,%	111.54	144.23	92.58	87.64	100

Table 11. Gain in LUTs for groups 2–4 (LUT count).

Benchmark	Auto	One-Hot	JEDI	${\mathit{U}}_{\mathbf{2}}$	Our Approach	Group
ex1	70	74	53	40	44	2
kirkman	42	58	39	33	35	2
planet	131	131	88	78	82	2
planet1	131	131	88	78	82	2
pma	94	94	86	72	76	2
s1	65	99	61	54	58	2
s1488	124	131	108	89	93	2
s1494	126	132	110	90	94	2
s1a	49	81	43	38	42	2
s208	12	31	10	9	11	2
styr	93	120	81	70	78	2
tma	45	39	39	30	34	2
sand	132	132	114	99	103	3
s420	10	31	9	8	10	4
s510	48	48	32	22	23	4
s820	88	82	68	52	56	4
s832	80	79	62	50	52	4
Total	1340	1493	1091	912	973
Percentage,%	137.72	153.44	112.13	93.73	100.00

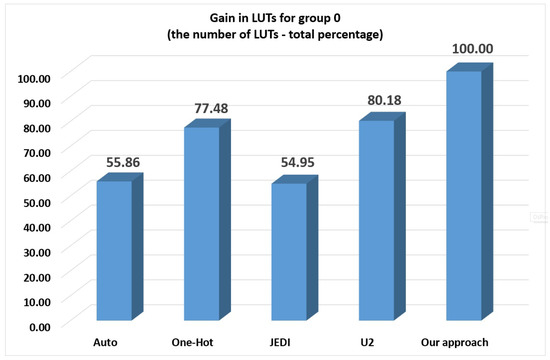
Figure 11. Gain in LUTs for group 0 (LUT count—total percentage).

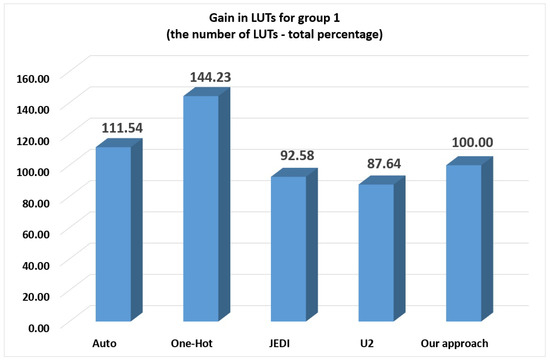
Figure 12. Gain in LUTs for group 1 (LUT count—total percentage).

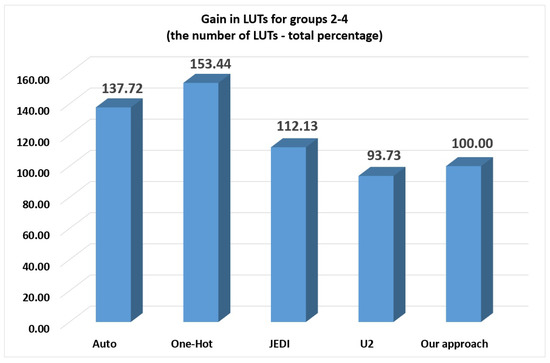
Figure 13. Gain in LUTs for groups 2–4 (LUT count—total percentage).

Table 12. Gain in frequency for group 0 (the operating frequency).

Benchmark	Auto	One-Hot	JEDI	${\mathit{U}}_{\mathbf{2}}$	Our Approach	Group
bbtas	204.16	204.16	206.12	194.43	201.47	0
dk17	199.28	167	199.39	147.22	172.99	0
dk27	206.02	201.9	204.18	181.73	190.32	0
dk512	196.27	196.27	199.75	175.63	187.45	0
ex3	194.86	194.86	195.76	174.44	187.26	0
ex5	180.25	180.25	181.16	162.56	162.56	0
lion	202.43	204	202.35	185.74	195.73	0
lion9	205.3	185.22	206.38	167.28	183.45	0
mc	196.66	195.47	196.87	178.02	182.95	0
modulo12	207	207	207.13	189.7	201.74	0
shiftreg	262.67	263.57	276.26	248.79	253.72	0
Total	2254.90	2199.70	2275.35	2005.54	2119.64
Percentage, %	106.38	103.78	107.35	94.62	100.00

Table 13. Gain in frequency for group 1 (the operating frequency).

Benchmark	Auto	One-Hot	JEDI	${\mathit{U}}_{\mathbf{2}}$	Our Approach	Group
bbara	193.39	193.39	212.21	183.32	210.21	1
bbsse	157.06	169.12	182.34	159.24	193.43	1
beecount	166.61	166.61	187.32	156.72	194.47	1
cse	146.43	163.64	178.12	153.24	182.62	1
dk14	191.64	172.65	193.85	162.78	201.39	1
dk15	192.53	185.36	194.87	175.42	206.74	1
dk16	169.72	174.79	197.13	164.16	199.14	1
donfile	184.03	184	203.65	174.28	206.83	1
ex2	198.57	198.57	200.14	188.95	196.58	1
ex4	180.96	177.71	192.83	168.39	196.18	1
ex6	169.57	163.8	176.59	156.42	187.53	1
ex7	200.04	200.84	200.6	191.43	204.16	1
keyb	156.45	143.47	168.43	136.49	178.59	1
mark1	162.39	162.39	176.18	153.48	182.37	1
opus	166.2	166.2	178.32	157.42	186.34	1
s27	198.73	191.5	199.13	185.15	201.26	1
s386	168.15	173.46	179.15	164.65	192.34	1
s8	180.02	178.95	181.23	168.32	191.32	1
sse	157.06	169.12	174.63	158.14	171.18	1
Total	3339.55	3335.57	3576.72	3158.00	3682.68
Percentage, %	90.68	90.57	97.12	85.75	100.00

Table 14. Gain in frequency for groups 2–4 (the operating frequency).

Benchmark	Auto	One-Hot	JEDI	${\mathit{U}}_{\mathbf{2}}$	Our Approach	Group
ex1	150.94	139.76	176.87	164.32	180.72	2
kirkman	141.38	154	156.68	155.36	184.62	2
planet	132.71	132.71	187.14	174.68	212.45	2
planet1	132.71	132.71	187.14	173.29	212.45	2
pma	146.18	146.18	169.83	156.12	192.43	2
s1	146.41	135.85	157.16	145.32	145.32	2
s1488	138.5	131.94	157.18	141.27	182.14	2
s1494	149.39	145.75	164.34	155.63	186.49	2
s1a	153.37	176.4	169.17	166.36	188.92	2
s208	174.34	176.46	178.76	166.42	192.15	2
styr	137.61	129.92	145.64	118.02	164.52	2
tma	163.88	147.8	164.14	137.48	182.72	2
sand	115.97	115.97	126.82	120.07	143.14	3
s420	173.88	176.46	177.25	186.35	218.62	4
s510	177.65	177.65	198.32	199.05	221.19	4
s820	152	153.16	176.58	175.69	195.73	4
s832	145.71	153.23	173.78	174.39	199.18	4
Total	2532.63	2525.95	2866.80	2709.82	3202.79
Percentage, %	79.08	78.87	89.51	84.61	100.00

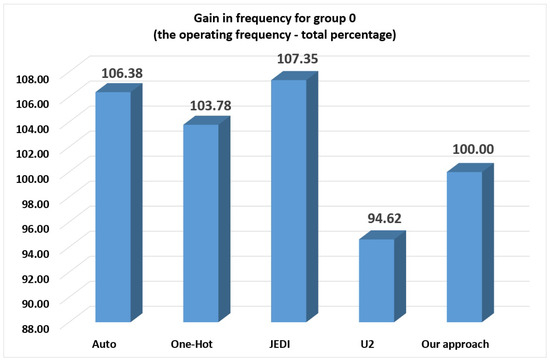
Figure 14. Gain in frequency for group 0 (the operating frequency—total percentage).

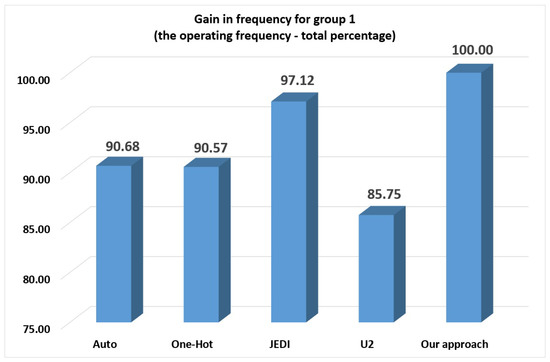
Figure 15. Gain in frequency for group 1 (the operating frequency—total percentage).

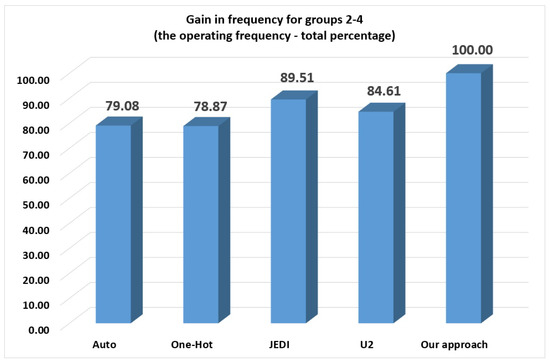
Figure 16. Gain in frequency for groups 2–4 (the operating frequency—total percentage).

Analysis of Table 9 and Figure 10 shows that the $U_4$-based FSMs have more used LUTs than other investigated methods. Our method has the following loss: 44.14% compared to auto, 22.52% compared to one-hot, 45.05% compared to JEDI-based FSMs and 19.82% compared to $U_2$-based FSMs. Thus, this method is not suitable for small FSMs.

As follows from Table 10 and Figure 12, the $U_4$-based FSMs of group 1 required fewer LUTs than FSMs based on auto (11.54% of gain) and one-hot (44.23% of gain). However, we still lose to the JEDI-based FSMs (7.42% of loss) and $U_2$-based FSMs (12.36% of loss). Note that the loss decreased in comparison with the group 0.

As follows from Table 11 and Figure 10, the $U_4$-based FSMs of groups 2–4 required fewer LUTs than FSMs based on auto (37.72% of gain), one-hot (53.44% of gain) and JEDI-based FSMs (12.13% of gain). Only $U_2$-based FSMs have better results and our approach has 6.27% of loss. Note that the loss decreased in comparison with the group 1. Thus, starting from average FSMs, our approach loses only to the $U_2$-based FSMs.

As follows from Table 12 and Figure 14, the $U_4$-based FSMs of group 0 are faster than $U_2$-based FSMs (5.38% of gain). In this group, the best results belong to JEDI-based FSMs. They have the following gains: (1) 0.9% regarding auto; (2) 3.57% regarding one-hot; (3) 12.73% regarding $U_2$-based FSMs; (4) 7.35% regarding our approach. Thus, for the group 0, there is no sense in applying our approach. However, starting from the group 1, our method allows producing faster circuits than the other investigated methods.

The proposed approach produces the best results for FSMs from group 1 (Table 13 and Figure 15). There are the following gains: (1) 9.32% regarding auto; (2) 9.43% regarding one-hot; (3) 2.88% regarding JEDI-based FSMs; and (4) 14.25% regarding $U_2$-based FSMs. Our approach provides even better results (Table 14 and Figure 16) for FSMs from groups 2–4. The gain increases and amounts to: (1) 20.92% regarding auto; (2) 21.13% regarding one-hot; (3) 10.49% regarding JEDI-based FSMs; and (4) 15.39% regarding $U_2$ -based FSMs.

As can be seen from Table 8, the $U_2$-based FSMs require fewer LUTs compared to other methods. Analysis of Table 9 shows that $U_4$-based FSMs are the ones with the highest maximum operating frequency compared to other methods. The overall design quality can be estimated by the product of used resources [63] (for example, chip area occupied by a circuit) and the latency time. As it is in [63], we use the number of LUTs to compare areas required for FSM circuits based on different models (auto, one-hot, JEDI, $U_2$ and $U_4$). As a rule, an FSM is only a part of a digital system. We do not know how many cycles a system needs to perform a required task. Thus, we cannot find absolute values of latency times. However, for a relative evaluation of different models, it is sufficient to know only the time of cycle.

In this article, we have performed a generalized comparison of the models used in experiments. As a generalized assessment, we used the result of multiplying the number of LUTs in an FSM circuit by the cycle time. The numbers of LUTs are taken from Table 7. To calculate the cycle times in nanoseconds, we used the operating frequencies from Table 8. The area-time products measured in $LUTs$ × $ns$ are shown in Table 16.

To better evaluate the chip resources used by FSM circuits, we have created Table 15. It contains the numbers of flip-flops required for implementing the state registers. As follows from Table 15, there are the same number of flip-flops in registers of FSMs obtained using methods auto, JEDI and $U_2$-based FSMs. For these FSMs the number of memory elements is the same. They use the least number of flip-flops determined as $R=\lceil lo{g}_{2}M\rceil$. The largest number of flip-flops is consumed by FSMs based on the one-hot state assignment (eight times more than, for example, $U_2$-based FSMs and 4.97 times more than $U_4$-based FSMs). Our approach gives a gain of 397% compared to one-hot-based FSMs, but loses 37% to other investigated methods. If we find the difference between, for example, the number of flip-flops in registers of $U_2$- and $U_4$-based FSMs, we can see that the difference decreases as the group number decreases.

Table 15. Results of experiments (FFs count).

Benchmark	Auto	One-Hot	JEDI	${\mathit{U}}_{\mathbf{2}}$	Our Approach	Group
bbara	4	12	4	4	6	1
bbsse	5	26	5	5	6	1
bbtas	4	9	4	4	4	0
beecount	4	10	4	4	6	1
cse	5	32	5	5	7	1
dk14	5	26	5	5	8	1
dk15	5	17	5	5	7	1
dk16	7	75	7	7	10	1
dk17	4	16	4	4	4	0
dk27	4	10	4	4	4	0
dk512	5	24	5	5	4	0
donfile	5	24	5	5	6	1
ex1	7	80	7	7	11	2
ex2	5	25	5	5	7	1
ex3	4	14	4	4	4	0
ex4	5	18	5	5	7	1
ex5	4	16	4	4	4	0
ex6	4	14	4	4	6	1
ex7	5	17	5	5	7	1
keyb	5	22	5	5	6	1
kirkman	6	48	6	6	10	2
lion	3	5	3	3	3	0
lion9	4	11	4	4	4	0
mark1	5	22	5	5	7	1
mc	3	8	3	3	3	0
modulo12	4	12	4	4	4	0
opus	5	18	5	5	7	1
planet	7	86	7	7	12	2
planet1	7	86	7	7	12	2
pma	6	49	6	6	11	2
s1	6	54	6	6	10	2
s1488	7	112	7	7	16	2
s1494	7	118	7	7	16	2
s1a	7	86	7	7	14	2
s208	6	37	6	6	11	2
s27	4	11	4	4	5	1
s386	5	23	5	5	7	1
s420	8	137	8	8	18	4
s510	8	172	8	8	21	4
s8	4	15	4	4	5	1
s820	7	78	7	7	16	4
s832	7	76	7	7	17	4
sand	7	88	7	7	14	3
shiftreg	4	16	4	4	4	0
sse	5	26	5	5	8	1
styr	7	67	7	7	13	2
tma	6	63	6	6	12	2
Total	251	2011	251	251	404
Percentage,%	62.13	497.77	62.13	62.13	100

As follows from Table 16, our approach produces FSM circuits with better area-time products than those of other investigated methods. Our approach gives the following gains: (1) 55.24% regarding auto; (2) 79.87% regarding one-hot; (3) 12.28% regarding JEDI-based FSMs; and (4) 8.6% regarding $U_2$-based FSMs. If we compare results for different groups, we can draw the following conclusions. Our approach loses out to all other models for group 0. For group 1, $U_4$-based FSMs lose out only to JEDI-based FSMs (4.46% of loss). However, our approach provides significantly better area-time products for FSMs from groups 2–4. In this case, our approach gives the following gains: (1) 76.79% regarding auto; (2) 97.55% regarding one-hot; (3) 24.71% regarding JEDI-based FSMs; and (4) 12.63% regarding $U_2$-based FSMs.

Table 16. Results of experiments (the generalized assessments, $LUTs\times ns$).

Benchmark	Auto	One-Hot	JEDI	${\mathit{U}}_{\mathbf{2}}$	Our Approach	Group
bbara	87.91	87.91	47.12	54.55	66.60	1
bbsse	210.11	218.78	131.62	163.28	149.93	1
bbtas	24.49	24.49	24.26	41.15	44.67	0
beecount	114.04	114.04	74.74	89.33	82.27	1
cse	273.17	403.32	202.11	215.35	191.65	1
dk14	83.49	156.39	51.59	73.72	69.52	1
dk15	77.91	86.32	61.58	45.60	53.21	1
dk16	88.38	194.52	60.87	67.01	65.28	1
dk17	25.09	71.86	25.08	54.34	57.81	0
dk27	14.56	24.76	19.59	38.52	47.29	0
dk512	50.95	50.95	45.06	68.33	74.69	0
donfile	168.45	168.48	117.85	120.50	116.04	1
ex1	463.76	529.48	299.66	243.43	243.47	2
ex2	45.32	45.32	39.97	42.34	50.87	1
ex3	46.19	46.19	45.97	63.06	74.76	0
ex4	82.89	73.15	62.23	65.32	66.27	1
ex5	49.93	49.93	49.68	61.52	73.82	0
ex6	141.53	219.78	124.58	134.25	122.65	1
ex7	20.00	24.90	19.94	31.34	39.18	1
keyb	274.85	425.18	237.49	271.08	223.98	1
kirkman	297.07	376.62	248.91	212.41	189.58	2
lion	9.88	24.51	9.88	32.30	40.87	0
lion9	29.23	59.39	24.23	47.82	54.51	0
mark1	141.63	141.63	113.52	123.79	115.15	1
mc	20.34	35.81	20.32	33.70	43.73	0
modulo12	33.82	33.82	33.80	47.44	54.53	0
opus	168.47	168.47	123.37	133.40	123.43	1
planet	987.11	987.11	470.24	446.53	385.97	2
planet1	987.11	987.11	470.24	450.11	385.97	2
pma	643.04	643.04	506.39	461.18	394.95	2
s1	443.96	728.74	388.14	371.59	399.12	2
s1488	895.31	992.88	687.11	630.00	510.60	2
s1494	843.43	905.66	669.34	578.29	504.05	2
s1a	319.49	459.18	254.18	228.42	222.32	2
s208	68.83	175.68	55.94	54.08	57.25	2
s27	30.19	93.99	30.13	32.41	39.75	1
s386	154.62	224.84	122.80	121.47	114.38	1
s420	57.51	175.68	50.78	42.93	45.74	4
s510	270.19	270.19	161.36	110.52	103.98	4
s8 40	49.99	50.29	49.66	53.47	57.50	1
s820	578.95	535.39	385.09	295.98	286.11	4
s832	549.04	515.56	356.77	286.71	261.07	4
sand	1138.23	1138.23	898.91	824.52	719.58	3
shiftreg	7.61	22.76	7.24	16.08	23.65	0
sse	210.11	218.78	171.79	164.41	169.41	1
styr	675.82	923.65	556.17	593.12	474.11	2
tma	274.59	263.87	237.60	218.21	186.08	2
Total	12,228.61	14,168.64	8844.90	8554.93	7877.31
Percentage,%	155.24	179.87	112.28	108.60	100

The results of our experiments show that the proposed approach can be used instead of other models starting from simple FSMs. The $U_2$-based FSMs have fewer LUTs than other models. However, starting from average FSMs, our approach allows producing circuits having slightly larger numbers of LUTs with significantly higher maximum operating frequencies. Additionally, our approach provides better area-time products starting from average FSMs. It has rather good potential and can be used in targeting FPGA-based Mealy FSMs.

7. Conclusions

Modern FPGA chips have reached such a level that quite complex systems can be implemented using only a single chip. At the same time, significant parts of the digital systems are implemented using LUTs having rather small numbers of inputs. The value $S_L=6$ is considered as optimal [19,20], but it is too small compared to the number of inputs and outputs of FSMs from modern digital systems. To design these complex FSMs with the use of such simple elements, it is necessary to apply the methods of functional decomposition. As a rule, the functional decomposition results in LUT-based FSM circuits having many logic levels and very complicated systems of interconnections.

Different methods of structural decomposition can be used to optimize the characteristics of FPGA-based FSM circuits. Our research [30,60] shows that the FSM circuits based on structural decomposition possess significantly better characteristics (fewer LUTs, higher maximum operating frequency, lower power consumption) than their counterparts based on functional decomposition. It is very important that the FSM circuits based on structural decomposition have regular systems of interconnections and predicted numbers of levels of logic. In the best case, each logic block of an FSM circuit has only a single level of LUTs.

In this paper, we propose a novel approach aimed at optimization of LUT-based Mealy FSMs. The proposed method leads to Mealy FSM $U_4$. Two methods of structural decomposition are the cornerstones of our approach. They are: (1) the transformation of codes of collections of outputs into state codes and (2) the extension of state codes. The second method is a new one and it is proposed in this paper. To increase the maximum operating frequency, we encode the FSM states using more than the minimum number of state variables determined by (1). Our approach leads to Mealy FSM circuits with three levels of LUTs and regular systems of interconnections. As it is in a single-level FSMs $U_1$, FSM outputs are generated simultaneously with input memory functions. As a result, our approach provides an increase in maximum operating frequency, accompanied by a small increase in the number of LUTs compared to equivalent three-level FSMs.

The results of our experiments clearly show that the proposed approach can be used instead of other models starting from simple FSMs. The $U_2$-based FSMs have fewer LUTs than other models. However, starting from average FSMs, our approach allows producing circuits having slightly larger numbers of LUTs with significantly higher maximum operating frequency. Additionally, our approach provides better area-time products starting from average FSMs. Thus, our approach can be used if either the performance or the area-time product is the dominant characteristic of a digital system.

We are currently considering several areas of research. We intend to explore the possibility of applying the proposed approach to FPGA chips of Intel (Altera). We will also try to adapt this approach for optimizing characteristics of Moore finite state machines.